Electronic and energy descriptors for SACs as tri-functional catalysts towards urea formation and unveiling the C–N coupling mechanism

Abstract

Single atom catalysts (SACs) have rapidly emerged as a cutting-edge trend in electro-catalysis for synthesizing nitrogen-based products such as ammonia, nitric acid and urea. In the present study, we considered NO₂⁻ as a specific N-based molecule, which participated in the simultaneous reduction with CO₂ towards urea formation for 77 SACs. Our investigation demonstrates that among possible nitrogen-containing intermediates generated during the simultaneous electrochemical reduction of CO₂ and NO₂⁻, only the NH₂ intermediate effectively couples with CO to form urea. In the case of simultaneous reduction towards urea formation, the NH₂ free energy serves as an effective energy descriptor for identifying suitable catalysts, exhibiting a strong linear correlation with the limiting potential (R² = 0.93). Additionally, we observed a strong Brønsted–Evans–Polanyi (BEP) relationship (R² = 0.99) between the NH₂ adsorption energy and the activation energy of the coupling intermediate (CONH₂). Furthermore, the out of plane d-sub orbitals (d_xz, d_yz and d_z²) of the transition metal (TM) were analysed to uncover the electronic origins of urea reactivity. Owing to the strong interaction between the d-sub orbitals of the TM and the sp³ hybrid orbitals of NH₂, occupancy of the d_yz orbitals plays a significant role in determining catalytic activity. This is evidenced by a linear correlation (R² = 0.73) between orbital occupancy of d_yz and NH₂ adsorption energy for all systems, identifying it as the electronic origin of urea reactivity. Our interpretation regarding the descriptor is that NH₂ sp³ (HOMO) donates a σ-electron to the TM d-orbital (LUMO), while the TM d-orbital (HOMO) donates a π*-electron back to NH₂ sp³ (LUMO).

---

Introduction

In the agricultural sector, urea serves as a nitrogen-rich (46%) fertilizer, enabling food production that sustains nearly 27% of the world's population.¹ Not only as an agricultural fertilizer, its chemical uses in numerous chemical products as feedstock make it invaluable.^1,2 At present, the energy-intensive Bosch–Meiser process is followed for the industrial production of urea (NH₃ + CO₂ → NH₂CONH₂ + H₂O), (temperature >180 °C and pressure ≡ 150 bar) emitting large amounts of CO₂.^3,4 In stark contrast, synthesis of urea from CO₂ and other alternative N-sources such as N₂, NO₃⁻, NO₂⁻ etc. using an electrochemical cell under ambient conditions complies with sustainability goals.⁵ But, the occurance of many side reactions such as the hydrogen evolution reaction (HER), CO₂ reduction reaction (CO₂RR) and NO₃⁻ reduction reaction (NO₃⁻RR) poses a significant challenge in the electrochemical synthesis of urea.^6–9 Thus, developing catalysts capable of reducing CO₂ and nitrogen-containing species while inhibiting the HER is of critical importance.

To overcome this problem, transition metal-based single-atom catalysts (TM-SACs) have shown significant potential, as they possess superior activities for the electrocatalytic CO₂RR, NRR, NO₂RR, and NO₃RR, while their activity towards the HER remains relatively low. Since 2011, first reported by Zhang et al.,¹⁰ single atom catalysts (SACs) have become a hot topic for various electrocatalytic reactions such as the HER,^11,12 OER,^13–15 NRR^16–18 and CO₂RR,^19–22 due to their unique metallic design and superior catalytic performance.^10,23 Both theoretical and experimental studies point out that the transition metal (TM) centre in TM–N–C SACs is the possible active site for the CO₂RR and NO₂RR. Some studies suggest that single atom catalysts not only can reduce one molecule, but also reduce simultaneously CO₂ and N-based molecules (N₂, NO₂⁻, and NO₃⁻). For example, (i) Shibata et al. reported that TM–Pc SACs could simultaneously reduce CO₂ and nitrite ions towards formation of urea,²⁴ (ii) Ghorai et al. showed recently that Co–Pc supported on MoS₂ could co-reduce N₂ and CO₂ to form urea,⁹ and (iii) recently Cheng et al. explored whether metal-N₄-functionalized graphene can co-reduce NO₃⁻ and CO₂ towards urea formation etc.²⁵

Now, as the intrinsic activity of TM–N–C single-atom catalysts (SACs) for various reduction reactions, including the CO₂RR, N₂RR, NO₃RR, NO₂RR, and ORR, is associated with the electronic structure of both the TM centre and the N-doped carbon support, fundamental understanding of complex electronic behaviour is required in designing superior and cost-effective catalysts. But, screening a large group of catalysts for the multi-step electrocatalytic CO₂RR and NO₂RR fundamentally is quite a challenging task. The same thing applies for urea formation in the simultaneous reduction of CO₂ and NO₂⁻ using SACs, because SACs with strong activity individually for both CO₂ → CO and NO₂⁻ → NH₃ reductions demonstrate higher reactivity for urea formation from the co-reduction of CO₂ and NO₂⁻.²⁶ In this case, single atom catalysts operate as tandem catalysts which can reduce simultaneously CO₂ and N-based molecules (N₂, NO₂⁻ and NO₃⁻) to urea via the Eley–Rideal mechanism even if it has a single transition metal as the active site.^8,27 For that, simple electronic descriptors such as the d-band centre,^28–30 d-band frontier,³¹ width corrected d-band centre³² etc., can provide insight into the origin and help to identify the promising CO₂RR, NO₂RR and their simultaneous reduction (urea formation) catalysts. But, in the case of TM–N–C SACs, the TM d-orbital splits into sub-d orbitals, thus it is better to focus on each sub-d orbital's contribution towards reactivity to find the electronic descriptor which can predict the catalytic activity.^33,34 In addition to this, the mechanism of C–N coupling which is an inevitable process for the formation of urea in the simultaneous reduction of CO₂ and nitrate or nitrite ions, is unclear. Some studies claim that, the co-existence of activated CO-like precursors and ammonia like precursors (NH₂) at the catalyst's surface, formed by simultaneous reduction of CO₂ and NO₂⁻, is the obligatory condition for C–N coupling.^8,24,27,35 But, there is no theoretical proof which can support this point. Several studies with various metal catalysts have been reported, where the urea was synthesized by simultaneous reduction of CO₂ and NO₂⁻ at gas-diffusion electrodes under mild conditions.^24,36,37 Thus, identifying a suitable descriptor that captures the complex electronic behaviour of the catalysts and elucidating the C–N coupling mechanism is crucial for further enhancing the performance of TM–N–C SACs in urea production via the simultaneous reduction of CO₂ and NO₂.

In this DFT study, the hybridization of the d_xz, d_yz, and d_z² orbitals of 3d and 4d transition metals (TMs) with orbitals of the adsorbate during three different reduction reactions, CO₂RR, NO₂RR and their simultaneous reduction on TM–N–C single-atom catalysts (SACs), was found to play a key role in determining catalytic reactivity. The manuscript will discuss that, among these d-orbitals, the d_yz orbital plays the most significant role in predicting catalytic activity, showing strong linear correlations for the CO₂RR, NO₂RR and their simultaneous reduction across all 77 SACs. In the case of simultaneous reduction to produce urea on TM–N–C SACs, taking C–N coupling as an unavoidable phenomenon towards urea formation, we have come up with two mechanisms. Furthermore, the Gibbs free energy of adsorbed NH₂ was identified as an effective energy descriptor for accurately predicting urea formation activity via the two proposed mechanisms in the simultaneous reduction process. Finally using molecular orbital theory, we interpreted why d_yz occupancy is the descriptor to identify catalysts for urea production.

Results and discussion

Structural details and stability

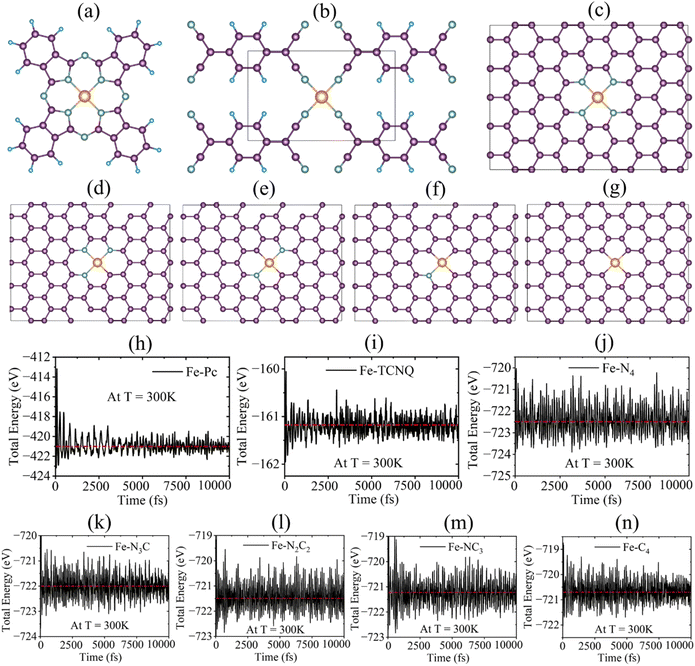
Many studies have explored that single-atomic-layer nitrogen-doped carbon has enough potential for TMs to be anchored, which leads to the formation of single atom catalysts (SACs).^38–41 Hence, in this work, to investigate the effects of N-doped different carbon supports along with TMs on the urea activity of TM–N–C SACs, we have selected seven types of single atom catalysts: TM–Pc, TM–N₄, TM–N₃C, TM–N₂C₂, TM–NC₃, TM–C₄ and TCNQ.⁴² For each and every type of SAC, 11 transition metals, abundant in the earth, Cr, Co, Cu, Fe, Mn, Ni, Ru, Sc, V, Zn and Pd, are taken into account (see SI Fig. 1–3).⁴³ To check the thermodynamic stability for each catalyst we have obtained formation energy calculations (formula details given in the SI). In SI Table 1, we could observe that the most of the catalysts exhibit negative formation energies (specifically TMs coordinated with four N-atoms) which points out that the systems, considered in this work, are all thermodynamically stable. In addition, we have performed AIMD simulations for all types of systems: TM–N₄, TM–N₃C, TM–N₂C₂, TM–NC₃, TM–C₄, TM–Pc and TCNQ with Fe as the TM to cover all SACs for their thermodynamic stability at 300 K with 10 000 fs, each time step has time of 2 fs.⁴⁴ In the case of AIMD simulations, all seven SACs, having Fe as the transition metal, display good stability in terms of total electronic energy (see the Fig. 1h–j). And for the investigations of electrochemical stability, we have performed dissolution potential calculations for all the SACs. The details of the formula and the analysis of electronic stability at different applied potentials are provided in SI Table 6. The positive values of dissolution potentials for the SACs (specifically TMs coordinated with four N-atoms) convey that most of the systems are electrochemically stable (see SI Table 1).

Fig. 1 (a)–(g) The optimized structures of Fe–Pc, Fe–TCNQ, Fe–N₄, Fe–N₃C, Fe–N₂C₂, Fe–NC₃ and Fe–C₄ respectively, and (h)–(n) the plots of total energy vs. time using ab initio molecular dynamics simulation for Fe–Pc, Fe–TCNQ, Fe–N₄, Fe–N₃C, Fe–N₂C₂, Fe–NC₃ and Fe–C₄ at T = 300 K.

Selection of CO catalysts in CO₂ reduction

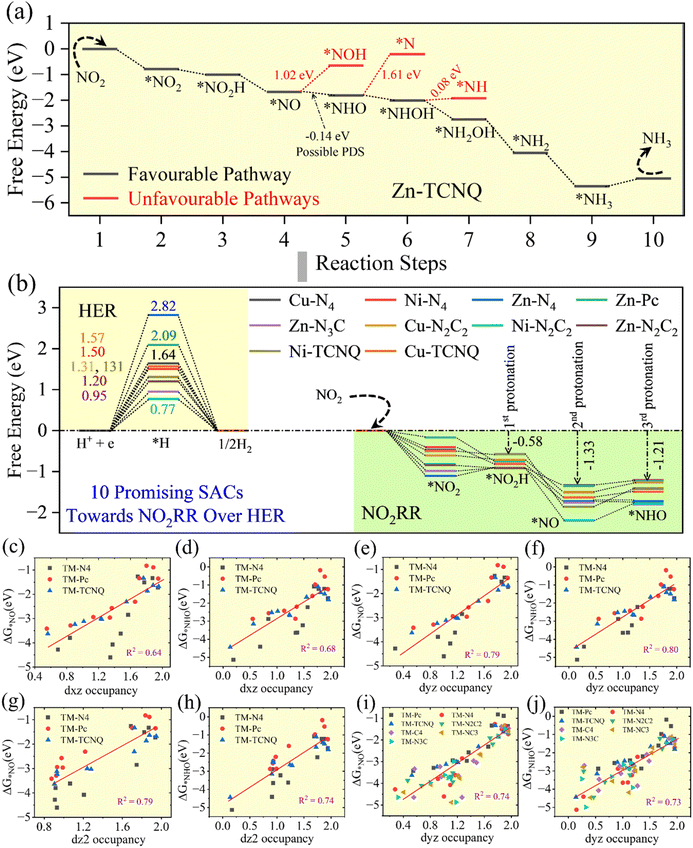
In the simultaneous reduction of CO₂ and nitrogen-based molecules (such as N₂, NO₂⁻, or NO₃⁻) for urea synthesis, CO formed from CO₂ serves as a key intermediate that couples with nitrogen-derived species, unlike other CO₂ reduction products such as HCOOH, CH₄, or C₂H₄, which do not take part in this coupling reaction. Before discussing CO₂ reduction and the potential for CO formation across all 77 SACs, we examined the effects of side reactions (HER) that can hinder the main reaction. Therefore, suppression of the HER is crucial to obtain the CO (g) product over H₂ (g). As the formation of CO₂H or the desorption of CO (g) from the catalyst surface is the potential-determining step in CO₂ reduction, these two intermediates can be used to evaluate the selectivity of the CO₂RR over the HER.²³ For the selectivity analysis, the nine best catalysts out of all 77 SACs, which are capable of suppressing the HER while forming CO (g), are highlighted in Fig. 2a and b. These include Ni–Pc, Zn–Pc, Ni–TCNQ, Pd–TCNQ, Cu–N₄, Ni–N₄, Zn–N₄, Ni–N₂C₂ and Zn–N₂C₂. The results for the remaining catalysts are provided in the SI. Fig. 2a shows that, relative to the reference level of 0.0 eV, all nine catalysts have higher hydrogen adsorption energy barriers than the highest thermodynamic barrier in the CO₂ → CO (g) pathway, which occurs at the first protonation step (* + CO₂ + H⁺ + e⁻ → *CO₂H). For instance, Ni–N₂C₂ exhibits a hydrogen adsorption barrier of 0.77 eV, while the first protonation step in the CO₂ → CO (g) pathway has a barrier of 0.71 eV, which is 0.06 eV lower than the hydrogen adsorption barrier. For Pd–TCNQ, Ni–TCNQ, Zn–N₄, Zn–N₂C₂, Ni–N₄, Cu–N₄, Ni–Pc and Zn–Pc, the values of the first protonation barrier, in the CO₂ → CO (g) pathway are 0.17, 0.07, 2.03, 0.02, 0.05, 0.18, 0.04 and 0.21 eV less than their corresponding hydrogen adsorption barriers, respectively. As shown in Fig. 2b, these nine catalysts favour the formation of CO (g) over CHO formation, which has a higher endothermic barrier. This preference is due to the lower energy required for CO desorption compared to CHO formation, with CHO formation barriers of 0.60, 0.80, 1.12, 1.17, 1.26, 1.38, 1.58, 1.71, and 1.99 eV for Ni–N₂C₂, Pd–TCNQ, Ni–TCNQ, Zn–N₄, Zn–N₂C₂, Ni–N₄, Cu–N₄, Ni–Pc, and Zn–Pc, respectively. The details of the CO₂RR mechanism, full free energy profile and comparison between the CO₂RR and HER for all other SACs are provided in SI Fig. 4–8 and Table 2.

Fig. 2 (a) and (b) the comparison of CO₂RR and HER selectivity and CO (g) formation over CHO with the nine best SACs; (c)–(e) the correlation of occupancies of d_xz, d_yz and d_z² orbitals with the free energy of the first protonation step in the CO₂ → CO (g) pathway for SACs with TMs coordinated with four N-atoms and (f) correlation of the occupancy of d_yz with the free energy of the first protonation step in the CO₂ → CO (g) pathway with all 77 SACs.

In order to identify an electronic descriptor capable of predicting the free energy of the first protonation step (ΔG_*CO2H), which is the highest barrier in the CO₂ → CO (g) pathway and thus determines the activity, we conducted electronic structure analysis. Since CO₂ adsorbs in a horizontal configuration on the surface of single-atom catalysts, its molecular orbitals interact with the out of plane d-orbitals of the transition metal centre in the SAC. Therefore, the characteristics of these d-orbitals can be used to describe CO₂RR activity. Various combinations of these d-orbital contributions were tested to find correlations with the free energy of the first protonation step (ΔG_*CO2H) in the CO₂ → CO (g) pathway. Among all possible orbital combinations, occupancies of d_xz, d_z² and d_yz exhibit a good linear correlation with ΔG_*CO2H, with R² values of 0.68, 0.73 and 0.73, respectively, for SACs where the transition metal is coordinated by four nitrogen atoms (the most stable configurations), as shown in Fig. 2c–e.³⁴ When considering all 77 SACs, the d_yz occupancy remains the most influential descriptor of reactivity, exhibiting an R² value of 0.67 (see Fig. 2f). For a particular sub d-orbital of TMs in SACs, the occupancy is calculated through integrating DOS up to the Fermi level (−∞ to 0), the area under the curve as shown in SI Fig. S36.

Selection of the NH₃ catalyst in reduction of NO₂ ions

Since nitrite ions exhibits a higher capability than nitrate ions for urea production during the simultaneous reduction of CO₂ and nitrogen-based molecules (such as N₂, NO₂⁻, and NO₃⁻), in this study, we focused on the nitrite reduction reaction mechanism for ammonia formation.^35–37 Similar to CO (g) formation during CO₂ reduction, the formation of NH₃ in nitrite reduction is also a necessary prerequisite for C–N coupling in the simultaneous reduction of CO₂ and nitrite ions to produce urea. As the HER is a common side reaction in aqueous medium for any reduction reaction (e.g. CO₂RR, NRR, ORR, NO₃RR, NO₂RR, etc.), examining the NO₂RR selectivity against the HER is inevitable.^{17,23,38,40,45,46} All 77 SACs exhibit higher NO₂⁻ adsorption energies compared to hydrogen adsorption energies, as presented in SI Fig. 5 and Table 3. Consequently, the reaction selectivity shifts towards the nitrite reduction reaction for ammonia production rather than hydrogen evolution.

For the selectivity assessment, the 11 most promising catalysts among the 77 SACs, which effectively suppress the HER while facilitating NH₃ formation, are presented in Fig. 3a and b. Among these 11 promising SACs, Zn–TCNQ emerged as the most reactive catalyst, exhibiting a completely downhill free energy profile up to the *NH₃ intermediate, and having an HER barrier of 0.96 eV, as shown in Fig. 3a. Within this downhill profile, the *NO → *NHO step, which is slightly exothermic with a free energy change of −0.14 eV, can be considered the potential-determining step (PDS). Another 10 promising SACs have been showcased in Fig. 3b, having an endothermic reaction (NO₂RR) barrier (PDS), unlike Zn–TCNQ. For example, Ni–N₂C₂ shows HER limiting potential to be 0.77 eV, whereas in the NO₂RR it is 0.41 eV, noticed at step *NO → *NHO. For Zn–N₃C, Zn–N₂C₂, Ni–TCNQ, Cu–N₂C₂, Ni–N₄, Cu–TCNQ, Cu–N₄, Zn–Pc and Zn–N₄ the values of HER limiting potential are 0.95, 1.20, 1.31, 1.31, 1.50, 1.57, 1.64, 2.09 and 2.82 eV, and that of the NO₂RR are 0.18 (at *NO₂ → *NO₂H), 0.22 (at *NO → *NHO), 0.45 (at *NO → *NHO), 0.23 (at *NO → *NHO), 0.29 (at *NO → *NHO), 0.14 (at *NO → *NHO), 0.12 (at *NO → *NHO), 0.12 (at *NO → *NHO) and 0.30 eV (at *NO₂ → *NO₂H), respectively. The detailed NO₂RR mechanism, full free energy profile and comparison with HER activity and PDS values of other SACs are provided explicitly in SI Fig. 5, 9–11 and SI Table 3.

Fig. 3 (a) Full free energy profile of the NO₂RR on Zn-TCNQ, (b) the mechanisms of the HER vs. NO₂RR with the 10 best SACs, (c)–(h) the linear correlation of the adsorption free energy of NHO and NO with d_xz, d_yz and d_z² occupancies for SACs with TMs coordinated with four N-atoms, and (i) and (j) correlation between occupancy of d_yz and free energy of adsorbed NO and NHO for all 77 SACs.

In the case of NO₂⁻ reduction, configuration of adsorbed nitrite molecules follows an end-on fashion, where N of NO₂ exists on top of the TM of the SAC, as shown in SI Fig. 5. And the activation of the NO₂ molecule can be considered as follows: the hybridized sp² orbital of N@NO₂ couples with the out of plane d-orbitals (d_xz, d_yz and d_z²) of the TM atom. Hence, these d-orbitals might be helpful in demonstrating the NO₂RR activity. Several combinations of these d-orbitals were examined to have a linear correlation with the limiting potential of the catalysts, but nothing worked out. Instead, we have obtained a good linear correlation between the free energy of the two intermediates (*NO and *NHO) and occupancies of d_xz, d_yz and d_z² orbitals of TMs, shown in Fig. 3c–h (considering SACs with TMs coordinated with four nitrogen atoms, showing higher structural stability). Out of these sub-d orbitals, occupancy of d_yz played a significant role in predicting reactivity of the catalysts, having R² values of 0.79 and 0.80 for *NO and *NHO, respectively.³⁴ Furthermore, we tested occupancy of d_yz for all 77 SACs and found R² to be 0.74 and 0.73, which is a good correlation for predicting reactivity (see Fig. 3i and j). Once these two free energies are predicted, we can predict the catalytic activity of a random SAC catalyst, as most of the SACs displayed step *NO → *NHO as the PDS.

We also examined the linear correlation between the d_yz occupancy and ΔG_*CO2H,, ΔG_*NO and ΔG_*NHO after including the Ti–Pc SAC, considering Ti as the transition metal (from the 3d block), and observed no significant change in the R² values (see SI Fig. 35). Therefore, it can be inferred that the R² value would remain nearly unchanged upon including Ti as the transition metal for the other six types of differently coordinated TM–N–C SACs.

Simultaneous reduction of CO₂ and nitrite ions (NO₂⁻)

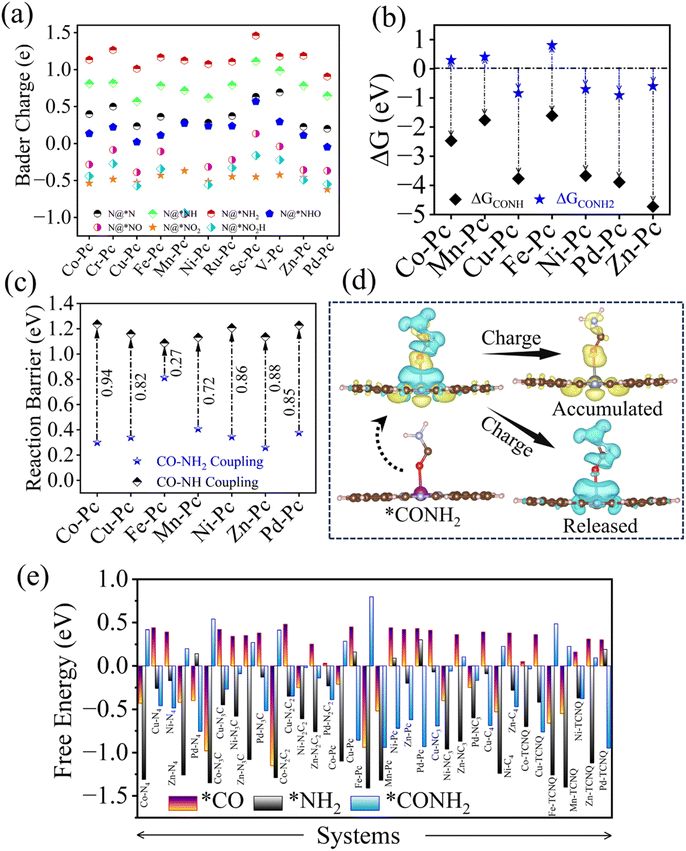
In the above sections, we have elucidated the individual performance of the 77 SACs in cases of CO₂ and nitrite ions reduction reactions. We observed that a greater number of SACs prefer CO (g) as well as NH₃ formation during CO₂ and NO₂⁻ reduction, respectively. For simultaneous reduction of CO₂ and nitrite ions towards urea formation, C–N coupling is a crucial step. Thus, in the simultaneous reduction reaction, which can form CO (g) and NH₃ as well, the generated CO (g) molecule can either couple with N-based intermediates (NO₂, NO₂H, N, and NH, NH₂) or with the NH₂⁻ (amino) radical, leading to the formation of the C–N bond. The N-based intermediates are generated via NO₂⁻ → NH₃ (nitrite ions to ammonia), whereas NH₂⁻ (amino) radicals are generated through interaction of the OH⁻ radical with ammonia (NH₃ + OH⁻ → NH₂⁻). But, single atom catalysts, having the metal centre as the only active site, behave as a tandem catalyst towards C–N bond formation i.e., they follow the Eley–Rideal mechanism for the formation of the C–N bond. Now, because of so many N-based intermediates formed during nitrite ion reduction, finding a suitable N-based intermediate as a precursor for C–N bond formation is an important task. In the case of intermediates *NO₂, *NO₂H and *N, the nitrogen (N)-atom has less charge, because highly electronegative oxygen atoms are connected to nitrogen (N) (for *NO₂ and *NO₂H), and the TM is connected to N (for *N). Thus, C–N coupling through CO and these intermediates cannot be taken into account. On the other hand, the N-atom in NH and NH₂, activated on the catalyst surface, has enough charge, accepted from the bonded hydrogen atom, to couple with CO, forming the C–N bond. But, C–N coupling through CO and NH molecules is very strong, in terms of free energy, which leads to a higher thermodynamic barrier towards urea formation compared to the case of CO and NH₂ coupling (moderate in terms of free energy), as depicted in Fig. 4b and c. Quantitatively, we also confirmed with Bader charge analysis, where we have seen that the charge on N in *NH₂ is comparatively greater than the any other N-based intermediate including *NH, *NO₂, *NO₂H, and *N, as provided in the Fig. 4a. The C–N coupling through CO (pre) and NH₂ (pre) is also agreed by Shibata et al. reported in 2003.²⁴ In their study, TM–Pc SACs: Co–Pc, Cu–Pc, Ni–Pc, Fe–Pc, Mn–Pc, Pd–Pc and Zn–Pc displayed promising catalytic activity in the simultaneous reduction of CO₂ and NO₂⁻ towards urea formation. On the contrary, Cr–Pc, Mo–Pc, Ru–Pc, Sc–Pc and V–Pc were found to be poor catalysts towards urea formation. If C–N coupling occurs through CO and NH, the poor catalysts for urea formation show, in our DFT simulations, moderate C–N coupling in terms of free energy, whereas for promising catalysts opposite phenomena can be observed, i.e.,, strong C–N coupling, leading to a greater reaction barrier. This observation is contradictory to the experimental work for urea formation in the simultaneous reduction of CO₂ and NO₂⁻.²⁴ Therefore, as a nitrogen-based molecule either the amino radical (NH₂⁻) or activated NH₂ intermediate functions as a precursor for C–N coupling in the direction of urea formation.

Fig. 4 (a) The Bader charge of the N-atom in the intermediates *N, *NH, *NH₂, *NO, *NHO, *NO₂ and *NO₂H of all TM–Pc SACs, (b) comparison of Gibbs free energy during CO–NH and CO–NH₂ coupling, (c) the reaction barrier during urea formation for two possible coupling CO–NH and CO–NH₂ pathways and (d) the charge density difference during CO–NH₂ coupling for TM–Pc SACs. (e) Comparison of adsorption energy of *CO, *NH₂ and *CONH₂.

Activation of CO and NH₂ for C–N coupling

Activation of the two precursors CO (pre) and NH₂ (pre), generated through simultaneous reduction of CO₂ and nitrite ions, can be demonstrated by adsorption or binding energy. The value of binding energy for NH₂ (pre) is greater than that of CO (pre) for all 77 SACs, which means that NH₂ (pre) will occupy the metal centre over CO (pre). This can be concluded from the PDOS plots of adsorbed CO and NH₂, where the density of states for NH₂ (pre) observed to be spread over the energy range compared to the case of CO (pre) (see SI Fig. 15–19). In addition, Bader charge analysis of adsorbed NH₂ (pre) and CO (pre) reveals that the NH₂ adsorption, having a greater charge on it, is favoured over CO on the metal site (see SI Table 5). Since SACs have a single metal centre as their active site for any reaction to happen, co-existence of CO (pre) and NH₂ (pre) can be expected for the C–N coupling via the Eley–Rideal mechanism. And the co-existence of precursors can only be possible if the adsorption or desorption free energy for both the precursors is moderate, not more negative than −1.5 eV.

Based on the values of the adsorption energy or desorption barrier of NH₂ (g) and CO (g) in the range of −1.5 to 1.5 eV, we have selected 36 SACs among the 77 SACs, see Fig. 4e. Two mechanisms of urea formation are proposed in the simultaneous reduction of CO₂ and nitrite ions which can be described as follows:

Mechanism-01:

CO + NH₂ + * → CO + *NH₂ (1)

CO + *NH₂ → *CONH₂ (2)

*CONH₂ + NH₂ → *CO(NH₂)₂ (3)

Mechanism-02:

CO + NH₂ + * → CO + *NH₂ (4)

CO + *NH₂ → *CONH₂ (5)

*CONH₂ + NO₂ → *NO₂CONH₂ (6)

*NO₂CONH₂ + H⁺ + e → *NO₂HCONH₂ (7)

*NO₂HCONH₂ + H⁺ + e → *NOCONH₂ + H₂O (8)

*NOCONH₂ + H⁺ + e → *NOHCONH₂ + H₂O (9)

*NOHCONH₂ + H⁺ + e → *NCONH₂ + 2H₂O (10)

*NCONH₂ + H⁺ + e → *NHCONH₂ +2H₂O (11)

*NHCONH₂ + H⁺ + e → *CO(NH₂)₂ + 2H₂O (12)

In the 1st mechanism, first, NH₂ approaches the active site of a given catalyst and gets adsorbed on it. Next, it couples with CO in the 2nd step to form the C–N bond which transforms into CONH₂. Lastly, another NH₂ (pre) approaches towards adsorbed CONH₂ and interacts with it, resulting in the formation of urea (CO(NH₂)₂). Whereas in the 2nd mechanism, upon activation of CONH₂, formed through coupling of CO and NH₂, one nitrite ion (NO₂⁻) approaches the C of adsorbed intermediate *CONH₂, forming *NO₂CONH₂. Next, hydrogenation takes place one by one until CO(NH₂)₂ is formed and finally desorbs from the catalyst.

The reaction steps 1 and 2 of the 1st mechanism resemble the steps 1 and 2 of the 2nd mechanism, and the last step of each mechanism yields urea (CO(NH₂)₂) as the final product. Hence, taking the 2nd mechanism into account, in making the free energy profile towards urea formation, is enough to examine each and every intermediate state whether it is endothermic or exothermic. In the case of TM–Pc SACs, we observed that TMs such as Co, Cu, Ni, Fe, Mn, Zn, and Pd have the ability of producing urea with limiting potential values of 0.28, 0.34, 0.34, 0.8, 0.41, 0.26 and 0.38 V, respectively. On the other hand, other four (Cr–Pc, Ru–Pc, Sc–Pc and V–Pc) are neglected due to the higher binding of NH₂ (<−1.5 eV) to the TM centre, poisoning the catalyst. The PDS values of the reaction mechanism for all these seven catalysts are observed to be either at *NH₂ + CO → *CONH₂ or *CONH₂NO₂ → *CONH₂NO₂H. For Co–Pc, Fe–Pc and Mn–Pc it is at *NH₂ + CO → *CONH₂ and others follow the 2nd one. This agrees with the results reported by Shibata et al. where they demonstrated that the TM–Pc SACs with TMs such as Cr, Mo, Ru, Sc and V were unable to form urea, whereas TM–Pc SACs with Co, Ni, Cu, Fe, Zn, Pd and Cd displayed a better picture in the direction of urea formation.

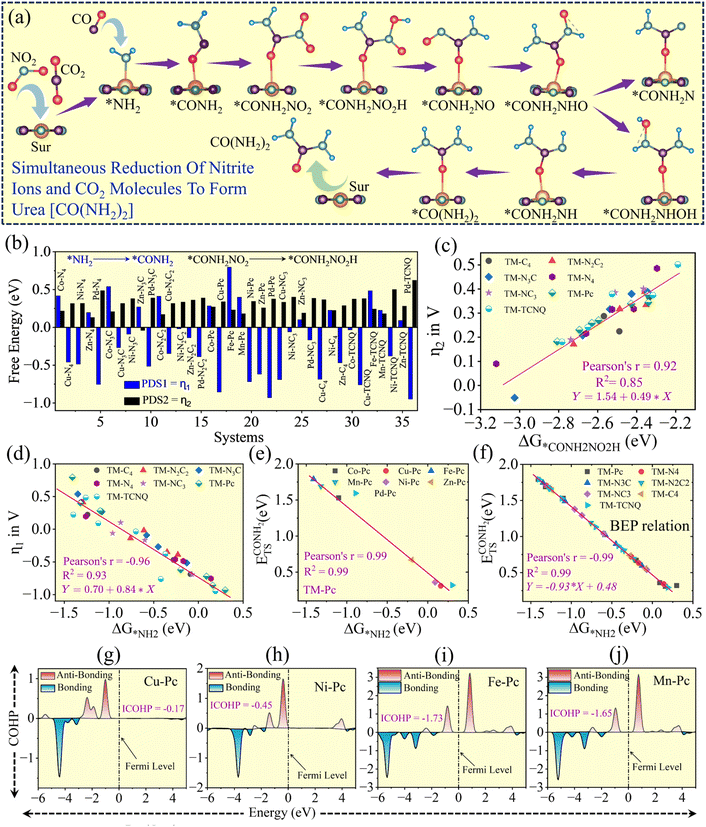
The same concept was applied for the other SACs (TM–N₄, TM–N₃C. TM–N₂C₂, TM–NC₃, TM–C₄ and TCNQ), in the simultaneous reduction of CO₂ and nitrite ions towards urea formation. Most of the catalysts in these other types of SACs, which are able to form urea like TM–Pc SACs, display PDS at *CONH₂NO₂ → *CONH₂NO₂H and some at step *NH₂ + CO → *CONH₂. The detailed explanation of each and every type of SACs, with the full free energy profile, is provided in SI Fig. 12–14. All the PDS values either at *NH₂ + CO → *CONH₂ or *CONH₂NO₂ → *CONH₂NO₂H are presented in Fig. 5b, denoted as PDS1 (η₁) and PDS2 (η₂), respectively.

Fig. 5 (a) The schematic of the full free energy of urea formation, (b) PDS1 and PDS2 of all SACs able to form urea, (c) correlation of PDS2 with the adsorption free energy of CONH₂NO₂H, (d) the correlation of PDS1 with the adsorption free energy of NH₂, (e) the correlation of the transition state energy of *CONH₂ with the adsorption free energy of NH₂, (f) the BEP relation of transition state energy of *CONH₂ with adsorption free energy of NH₂, and (g) to (j) COHP of Cu–Pc, Ni–Pc, Fe–Pc and Mn–Pc.

Among the 36 SACs, which are able to form urea, 13 SACs show an endothermic barrier at *NH₂ + CO → *CONH₂ i.e., during C–N coupling. The remaining 23 SACs display a spontaneous process of C–N bond formation. In addition, we have performed climbed nudged elastic band (NEB) calculations to investigate the kinetic barrier of C–N coupling between NH₂ (pre) and CO (pre), where, NH₂ is considered to be adsorbed on the metal centre and that of CO is on the C-atom near to the metal centre. Catalysts, having an endothermic barrier in the formation of the C–N bond, exhibit a greater kinetic barrier compared to the case of exothermic formation of the C–N bond as shown in SI Fig. 33. Therefore, catalysts displaying spontaneous formation of the C–N bond are considered to be promising catalysts for urea formation in the simultaneous reduction of CO₂ and NO₂⁻. Among 23 SACs, ten are found to be the best catalysts for the reaction: Cu–Pc, Ni–Pc, Zn–Pc, Pd–Pc, Cu–TCNQ, Ni–TCNQ, Pd–TCNQ, Cu–N₄, Ni–N₄ and Pd–N₄.

Correlation of the energy descriptor with limiting potential

In the case of mechanism-01, the coupling intermediate (step 2 *NH₂ + CO → *CONH₂) is the main potential determining step to decide how much external energy needs to be supplied to the system for the reaction to occur. Thus, a linear type of correlation with this coupling free energy, PDS1 (η₁), with an electronic or any intermediate energy parameter can be a great finding. Here, we have tried with CO and NH₂ binding energy to get a linear correlation with this coupling free energy. The adsorption free energy of NH₂, ΔG_*NH2, shows a good linear correlation with this coupling free energy, PDS1 (η₁), with R² = 0.93 as depicted in Fig. 5d. In addition, we also tried, considering TM–Pc SACs, to correlate the transition state barrier with ΔG_*NH2. And we observed a very good correlation between them, having R² = 0.99. Then, considering plots of Fig. 5d and e, we explored all SACs, which are able to form urea, through a BEP relation with R² = 0.99 (see Fig. 5f). Thus, the NH₂ adsorption binding energy functions as an energy descriptor to find the catalytic activity towards urea formation in the simultaneous reduction of CO₂ and NO₂⁻.

In the case of mechanism-02, the potential determining step can be observed either at *NH₂ + CO → *CONH₂ or *CONH₂NO₂ → *CONH₂NO₂H. Thus, either PDS1 (η₁) or PDS2 (η₂) would be the PDS for the mechanism-02. If PDS1 (η₁) > PDS2 (η₂), adsorption energy of NH₂ can be used as an energy descriptor for finding catalytic activity, otherwise we need a new energy parameter for the same. We investigated correlations of the adsorption free energy ΔG_*CONH2NO2 and ΔG_*CONH2NO2H with the limiting potential (η₂). The linear correlation between ΔG_*CONH2NO2 and the limiting potential (η₂) is not up to the mark, whereas in between ΔG_*CONH2NO2H and the limiting potential (η₂) it unveils an interesting result. The linear correlation of ΔG_*CONH2NO2H with η₂ is R² = 0.86 (neglecting 4 SACs, three from 3d block: Zn–N₄, Zn–N₂C₂, Zn–TCNQ and one from 4d block: Pd–TCNQ) (see Fig. 5c). So, ΔG_*CONH2NO2 acts as an energy descriptor to predict catalytic activity in terms of limiting potential in the 2nd mechanism of urea formation from simultaneous reduction of CO₂ and NO₂⁻ (if PDS1 (η₁) < PDS2 (η₂)).

To see the effects of the electric field and water solvent on the adsorption energies of the reaction intermediates and reaction barriers, we performed two types of DFT calculations: one including an external electric field and the other incorporating the effect of a water solvent. For the electric field calculations, a strong field of −0.52 × 10¹⁰ V m⁻¹ was applied, and the adsorption energies were computed for all three types of reactions considered in this work on TM–Pc SACs containing nine transition metals (TM = Co, Cr, Cu, Fe, Mn, Ni, Ru, Sc, and V). Similarly, implicit DFT solvent calculations were performed on the same systems. In both the cases, a constant shift of adsorption energies can be observed (see SI Fig. 37 and 38), which signifies that the overall trend of the reactivity across all the systems remains constant. The explicit values of adsorption energies, required to find reactivity of a catalyst, and the reaction barrier of the nine TM–Pc SACs for the three different reactions have been provided in SI Table 7–12. So, our work performed with DFT using the CHE model remains reliable.

To validate the DFT calculations using the GGA PBE functional, we have used another functional which is the revised GGA PBE. The obtained values of free energies of all possible intermediates required for finding the PDS in the case of all TM–Pc SACs, done with the RPBE functional, are provided in SI Table 4. We observed that the difference of limiting potential for a particular TM–Pc SAC with two different functionals GGA PBE and GGA RPBE is very small. So, our simulated values are validated.

Origin of catalytic activity towards urea formation

To explore the activation of NH₂ (axial ligand) on the TM in SACs, we presented a molecular orbital diagram in Fig. 6a. Here, we have shown that the sp³ hybrid orbital of NH₂ (HOMO) is donating an electron (σ-donation) to the unoccupied d-orbital of the TM (LUMO), while the occupied d-orbital of the TM (HOMO) is donating an electron (π*-donation) back to the unoccupied antibonding orbital of sp³ of NH₂. The pronounced σ donation and π* back-donation during NH₂ adsorption at the TM sites are responsible for its enhanced activation as first reported by the Blyholder model for CO activation.⁴⁷ Furthermore, we evaluated the NH₂ binding strength through three different analyses. Firstly, we investigated the position of the frontier orbitals (FOs) of the transition metal (TM) centres in the single-atom catalysts (SACs). These FOs, electronic states located near to the Fermi level, play a crucial role in governing the interaction between the TM site and the adsorbate. When the energy gap between the TM's FOs and the HOMO or LUMO of the NH₂ molecule is small, a reasonable orbital overlap and charge transfer occur, leading to stronger binding. Conversely, when the FOs of the TM are located farther from the Fermi level, the orbital interaction with NH₂ becomes less efficient, resulting in weaker adsorption strength (see the SI Fig. 21, 23 and 25).⁴⁸ Secondly, we examined the contribution of individual d-sub orbitals to the coupling: in the case of coupling between TM–N–C SACs and NH₂, the out of plane orbitals (d_xz, d_yz, and d_z²) are responsible for TM–NH₂ bond formation (see Fig. 6b–g from the orbital and partial density of states point of view). The more the orbitals are coupled, the stronger the bond becomes. Thirdly, we performed crystal orbital Hamiltonian population (COHP) analysis: in order to identify the bonding and antibonding states below the Fermi level, COHP of the NH₂ bond with TM–N–C SACs is performed.^49–51 If the occupied bonding states are greater than the occupied anti-bonding states, the bond is considered to be enough strong to bind NH₂ or vice versa (see Fig. 5g–j and SI Fig. 27). By taking these three electronic points into account, we have examined thirty possible electronic features to correlate with the free energy of adsorbed NH₂, ΔG_*NH2 (see SI Fig. 28–32), thus determining the urea activity. Among the 30 performed possible electronic features (namely d-band centre, d-band occupancy, d_xz, d_yz and d_z² centres and occupancy-based features with spin up and spin down components), occupancies of d_xz, d_yz and d_z² orbitals exhibit a very good linear correlation with ΔG_*NH2, as presented in Fig. 6h–j having an R² value of 0.75, 0.83 and 0.76, respectively (presented for SACs with TMs coordinated with four nitrogen atoms).³⁴ As occupancy of d_yz plays an important role in predicting urea reactivity of catalysts, we tested on all 77 SACs and found R² to be 0.73 (see Fig. 6k). Therefore, occupancy of d_yz behaves as an electronic descriptor to accurately predict the urea activity on TM–N–C SACs. Overall, we can infer that the catalysts, having moderate orbital coupling and greater occupied anti-bonding states which lead to the moderate binding of NH₂ with TMs, will show superior activity in the simultaneous reduction of CO₂ and NO₂⁻ towards urea formation such as Cu-Pc, Cu–N₄, Cu–TCNQ, Ni–Pc, Ni–N₄, Ni–TCNQ, Zn–N₄, Zn–Pc, Zn–TCNQ, Pd–Pc, Pd–N₄ and Pd–TCNQ. For further validation, linear regression with cross-validation was carried out, and the corresponding MAE (Mean Absolute Error) and RMSE (Root Mean Squared Error) values along with the 95% confidence band are presented in SI Fig. 39.

Fig. 6 (a) The orbital interaction between adsorbed NH₂ with the TM of the SAC, (b) schematic of hybridization of the free NH₂ molecule, (c) and (d) schematic of coupling of the sp³ hybridized orbitals of NH₂ with d_xz, d_yz and d_z² orbitals of the TM of the SAC, (e)–(g) the PDS of adsorbed NH₂ and the sub-d orbital of the TM of the SAC showing coupling between total DOS of adsorbed NH₂ with d_xz, d_yz and d_z² orbitals of the TM, (h)–(j) correlation of occupancies of d_xz, d_yz and d_z² with free energy of adsorbed NH₂ for SACs with TMs coordinated with four N-atoms and (k) correlation between occupancy of d_yz and free energy of adsorbed NH₂ for all SACs.

Conclusion

In summary, we have successfully performed DFT simulations for the screening of (i) CO catalysts during CO₂ reduction, (ii) ammonia catalysts from nitrite ions reduction and (iii) urea catalysts in the simultaneous reduction of CO₂ and nitrite ions, respectively. In the case of CO₂ reduction, the number of CO (g) promising catalysts is found to be nine from all types of SACs which can suppress the HER and CHO formation as well. For the NO₂RR, the number of best ammonia catalysts is eleven which can suppress the HER among all types of SACs (total 77). In the case of urea formation in the simultaneous reduction, we proposed two mechanisms and illustrated the C–N coupling mechanism comparing the reaction energy barrier and using Bader charge analysis. And we found out that only the intermediate NH₂ can couple with CO for the given reaction. In further studies, we obtained NH₂ adsorption free energy as the energy descriptor to accurately find the catalytic activity towards urea formation which has a good linear correlation with limiting potential (R² = 0.93) and transition state energy of intermediate CONH₂ (R² = 0.99). Another energy descriptor ΔG_*CONH2NO2H was identified for the simultaneous reduction of CO₂ and nitrite ions which also has a good correlation with the catalytic activity in terms of limiting potential (R² = 0.86). From the electronic point of view, d-sub orbitals especially out of plane orbitals are observed to be the origin of urea activity. The occupancy of d_yz shows a very good linear correlation with the adsorption free energy of NH_2, with an R² value of 0.83 for SACs where the transition metal is coordinated by four nitrogen atoms, and 0.73 when considering all 77 SACs. Overall, this descriptor-based theoretical study encourages, in the field of materials science, designing efficient SACs for urea formation in the simultaneous reduction of CO₂ and nitrite ions, and further motivates exploration of different groups of catalysts (metal, metal-based alloy, metal oxide etc.) for urea formation by the simultaneous reduction of CO₂ and N-based molecules (N₂, NO₂⁻ and NO₃⁻).

Author contributions

Narad Barman: contributed to conceptualization, data curation, investigation, methodology (done all the calculations), formal analysis, data visualization, writing original draft, and manuscript review and editing. Chiranjib Majumder: formal analysis, validation, and review and editing of the manuscript. Ranjit Thapa: conceptualized and designed the project, supervised the project, data curation, validation, writing the original draft, manuscript review and editing, and funding acquisition.

Conflicts of interest

The authors declare no conflict of interest.

Data availability

The data supporting this article have been included as part of the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5sc06657c.

Acknowledgements

NB thanks the University Grants Commission (UGC) for supporting the Fellowship under NFSC (No. F. 82-44/2020 (SA-III)). RT thanks the Board of Research in Nuclear Sciences (BRNS), India, for the financial support (Grant No. 58/14/13/2023-BRNS) and the Anusandhan National Research Foundation (ANRF), India (Grant No. CRG/2021/000620). The authors thank the SRM University-AP, Andhra Pradesh, for providing the central computational facility and National Supercomputing Mission (NSM) for providing access to PARAM Rudra for conducting DFT based computation. Thanks to Mr Sourav Ghosh for helping in estimation of MAE/RMSE.

References

1. J. Liu, S. C. Smith, Y. Gu and L. Kou, C–N Coupling Enabled by N–N Bond Breaking for Electrochemical Urea Production, Adv. Funct. Mater., 2023, 33(47), 2305894,  DOI:10.1002/adfm.202305894.
2. X. Zhang, E. A. Davidson, D. L. Mauzerall, T. D. Searchinger, P. Dumas and Y. Shen, Managing Nitrogen for Sustainable Development, Nature, 2015, 51–59,  DOI:10.1038/nature15743.
3. C. Smith, A. K. Hill and L. Torrente-Murciano, Current and Future Role of Haber-Bosch Ammonia in a Carbon-Free Energy Landscape, Energy Environ. Sci., 2020, 13(2), 331–344,  10.1039/c9ee02873k.
4. X. Wei, Y. Liu, X. Zhu, S. Bo, L. Xiao, C. Chen, T. T. T. Nga, Y. He, M. Qiu, C. Xie, D. Wang, Q. Liu, F. Dong, C. L. Dong, X. Z. Fu and S. Wang, Dynamic Reconstitution Between Copper Single Atoms and Clusters for Electrocatalytic Urea Synthesis, Adv. Mater., 2023, 35(18), 2300020,  DOI:10.1002/adma.202300020.
5. M. Sun, G. Wu, J. Jiang, Y. Yang, A. Du, L. Dai, X. Mao and Q. Qin, Carbon-Anchored Molybdenum Oxide Nanoclusters as Efficient Catalysts for the Electrosynthesis of Ammonia and Urea, Angew. Chem., Int. Ed., 2023, 62(19), e202301957,  DOI:10.1002/anie.202301957.
6. J. Shao, N. Meng, Y. Wang, B. Zhang, K. Yang, C. Liu, Y. Yu and B. Zhang, Scalable Electrosynthesis of Formamide through C–N Coupling at the Industrially Relevant Current Density of 120 MA Cm⁻², Angew. Chem., Int. Ed., 2022, 61(44), e202213009,  DOI:10.1002/anie.202213009.
7. X. Zhu, X. Yuan, Y. Wang, M. Ge and Y. Tang, Advancing Electrocatalytic Urea Synthesis: Insights from 2D Benzenehexathiolate Coordination Nanosheets, J. Catal., 2024, 429, 115218,  DOI:10.1016/j.jcat.2023.115218.
8. Y. Gao, J. Wang, M. Sun, Y. Jing, L. Chen, Z. Liang, Y. Yang, C. Zhang, J. Yao and X. Wang, Tandem Catalysts Enabling Efficient C–N Coupling toward the Electrosynthesis of Urea, Angew. Chem., Int. Ed., 2024, 63(23), e202402215,  DOI:10.1002/anie.202402215.
9. J. Mukherjee, S. Paul, A. Adalder, S. Kapse, R. Thapa, S. Mandal, B. Ghorai, S. Sarkar and U. K. Ghorai, Understanding the Site-Selective Electrocatalytic Co-Reduction Mechanism for Green Urea Synthesis Using Copper Phthalocyanine Nanotubes, Adv. Funct. Mater., 2022, 32(31), 2200882,  DOI:10.1002/adfm.202200882.
10. B. Qiao, A. Wang, X. Yang, L. F. Allard, Z. Jiang, Y. Cui, J. Liu, J. Li and T. Zhang, Single-Atom Catalysis of CO Oxidation Using Pt1/FeOx, Nat. Chem., 2011, 3(8), 634–641,  DOI:10.1038/nchem.1095.
11. F. Ullah, K. Ayub and T. Mahmood, High Performance SACs for HER Process Using Late First-Row Transition Metals Anchored on Graphyne Support: A DFT Insight, Int. J. Hydrogen Energy, 2021, 46(76), 37814–37823,  DOI:10.1016/j.ijhydene.2021.09.063.
12. T. He, C. Zhang and A. Du, Single-Atom Supported on Graphene Grain Boundary as an Efficient Electrocatalyst for Hydrogen Evolution Reaction, Chem. Eng. Sci., 2019, 58–63,  DOI:10.1016/j.ces.2018.03.028.
13. L. Zong, K. Fan, W. Wu, L. Cui, L. Zhang, B. Johannessen, D. Qi, H. Yin, Y. Wang, P. Liu, L. Wang and H. Zhao, Anchoring Single Copper Atoms to Microporous Carbon Spheres as High-Performance Electrocatalyst for Oxygen Reduction Reaction, Adv. Funct. Mater., 2021, 31(41), 2104864,  DOI:10.1002/adfm.202104864.
14. L. Yang, D. Cheng, H. Xu, X. Zeng, X. Wan, J. Shui, Z. Xiang and D. Cao, Unveiling the High-Activity Origin of Single-Atom Iron Catalysts for Oxygen Reduction Reaction, Proc. Natl. Acad. Sci. U. S. A., 2018, 115(26), 6626–6631,  DOI:10.1073/pnas.1800771115.
15. H. Niu, X. Wang, C. Shao, Y. Liu, Z. Zhang and Y. Guo, Revealing the Oxygen Reduction Reaction Activity Origin of Single Atoms Supported on G-C3N4 Monolayers: A First-Principles Study, J. Mater. Chem. A, 2020, 8(14), 6555–6563,  10.1039/d0ta00794c.
16. S. Kapse, S. Narasimhan and R. Thapa, Descriptors and Graphical Construction for in Silico Design of Efficient and Selective Single Atom Catalysts for the ENRR, Chem. Sci., 2022, 13(34), 10003–10010,  10.1039/d2sc02625b.
17. R. Thapa, N. Barman and S. Kapse, Electronic Descriptor to Identify the Activity of SACs for E-NRR and Effect of BF3 as Electrolyte Ion, ChemSusChem, 2024, 18(2), e202400902,  DOI:10.1002/cssc.202400902.
18. K. Liu, J. Fu, L. Zhu, X. Zhang, H. Li, H. Liu, J. Hu and M. Liu, Single-Atom Transition Metals Supported on Black Phosphorene for Electrochemical Nitrogen Reduction, Nanoscale, 2020, 12(8), 4903–4908,  10.1039/c9nr09117c.
19. Z. Liu, A. Ma, Z. Wang, Z. Ding, Y. S. Pang, G. Fan and H. Xu, Single-Atom Anchored on Curved Boron Nitride Fullerene Surface as Efficient Electrocatalyst for Carbon Dioxide Reduction, Mol. Catal., 2024, 559, 114040,  DOI:10.1016/j.mcat.2024.114040.
20. F. Xu, X. Wang, X. Liu, C. Li, G. Fan and H. Xu, Computational Screening of TMN4 Based Graphene-like BC6N for CO2 Electroreduction to C1 Hydrocarbon Products, Mol. Catal., 2022, 530, 112571,  DOI:10.1016/j.mcat.2022.112571.
21. Q. Chang, Y. Liu, J. H. Lee, D. Ologunagba, S. Hwang, Z. Xie, S. Kattel, J. H. Lee and J. G. Chen, Metal-Coordinated Phthalocyanines as Platform Molecules for Understanding Isolated Metal Sites in the Electrochemical Reduction of CO2, J. Am. Chem. Soc., 2022, 144(35), 16131–16138,  DOI:10.1021/jacs.2c06953.
22. T. Liu, G. Wang and X. Bao, Electrochemical CO2Reduction Reaction on 3d Transition Metal Single-Atom Catalysts Supported on Graphdiyne: A DFT Study, J. Phys. Chem. C, 2021, 125(47), 26013–26020,  DOI:10.1021/acs.jpcc.1c07681.
23. Z. Wang, A. Ma, Z. Liu, Z. Ding, Y. Pang, G. Fan and H. Xu, Density Functional Theory Study of Transition Metal Dual-Atom Anchored Phthalocyanine as High-Performance Electrocatalysts for Carbon Dioxide Reduction Reaction, Appl. Surf. Sci., 2024, 669, 160532,  DOI:10.1016/j.apsusc.2024.160532.
24. M. Shibata and N. Furuya, Electrochemical Synthesis of Urea at Gas-Diffusion Electrodes Part VI. Simultaneous Reduction of Carbon Dioxide and Nitrite Ions with Various Metallophthalocyanine Catalysts, J. Electroanal. Chem., 2001, 507(1–2), 177–184,  DOI:10.1016/S0022-0728(01)00363-1 , https://www.elsevier.com/locate/jelechem.
25. T. J. Lin, W. S. Chen, H. C. Li, C. Y. Chen, H. Choi, Y. Kwon and M. J. Cheng, Metal-N4-Functionalized Graphene as Highly Active Catalysts for C-N Bond Formation in Electrochemical Urea Synthesis, J. Phys. Chem. C, 2025, 129(7), 3424–3436,  DOI:10.1021/acs.jpcc.4c07971.
26. M. Shibata and N. Furuya, Electrochemical Synthesis of Urea at Gas-Diffusion Electrodes Part VI. Simultaneous Reduction of Carbon Dioxide and Nitrite Ions with Various Metallophthalocyanine Catalysts, J. Electroanal. Chem., 2001, 507, 177–184,  DOI:10.1016/S0022-0728(01)00363-1 , https://www.elsevier.com/locate/jelechem.
27. Y. Huang, T. Fan and Y. Ji, Are Transition Metal Phthalocyanines Active for Urea Synthesis via Electrocatalytic Coupling of CO2 and N2?, Phys. Chem. Chem. Phys., 2025, 27, 531–538,  10.1039/d4cp04047c.
28. F. H. B. Lima, J. Zhang, M. H. Shao, K. Sasaki, M. B. Vukmirovic, E. A. Ticianelli and R. R. Adzic, Catalytic Activity - d-Band Center Correlation for the O2 Reduction Reaction on Platinum in Alkaline Solutions, J. Phys. Chem. C, 2007, 111(1), 404–410,  DOI:10.1021/jp065181r.
29. D-Band_position.
30. J. Zhang, H. Jin, M. B. Sullivan, F. C. H. Lim and P. Wu, Study of Pd-Au Bimetallic Catalysts for CO Oxidation Reaction by DFT Calculations, Phys. Chem. Chem. Phys., 2009, 11(9), 1441–1446,  10.1039/b814647k.
31. G. Zhan, Y. Yao, F. Quan, H. Gu, X. Liu and L. Zhang, D-Band Frontier: A New Hydrogen Evolution Reaction Activity Descriptor of Pt Single-Atom Catalysts, J. Energy Chem., 2022, 72, 203–209,  DOI:10.1016/j.jechem.2022.05.012.
32. E. E. Siddharthan, S. Ghosh and R. Thapa, Site Specific Descriptors for Oxygen Evolution Reaction Activity on Single Atom Catalysts Using QMML, J. Mater. Chem. A, 2024, 12(30), 19176–19186,  10.1039/d4ta02610a.
33. K. Liu, J. Fu, Y. Lin, T. Luo, G. Ni, H. Li, Z. Lin and M. Liu, Insights into the Activity of Single-Atom Fe-N-C Catalysts for Oxygen Reduction Reaction, Nat. Commun., 2022, 13(1), 2075,  DOI:10.1038/s41467-022-29797-1.
34. Y. Wang, Y. Liang, T. Bo, S. Meng and M. Liu, Orbital Dependence in Single-Atom Electrocatalytic Reactions, J. Phys. Chem. Lett., 2022, 13(25), 5969–5976,  DOI:10.1021/acs.jpclett.2c01381.
35. M. Shibata, K. Yoshida and N. Furuya, Electrochemical synthesis of urea on reduction of carbon dioxide with nitrate and nitrite ions using Cu-loaded gas-diffusion electrode, J. Electroanal. Chem., 1995, 387(1–2), 143–145,  DOI:10.1016/0022-0728(95)03992-P.
36. M. Shibata, K. Yoshida and N. Furuya, Electrochemical Synthesis of Urea at Gas-Diffusion Electrodes: IV. Simultaneous Reduction of Carbon Dioxide and Nitrate Ions with Various Metal Catalysts, J. Electrochem. Soc., 1998, 145, 2348,  DOI:10.1149/1.1838641.
37. M. Shibata, K. Yoshida and N. Furuya, Eleetrochemical Synthesis of Urea at Gas-diffusion Eleetrodes V. Simultaneous Reduction of Carbon Dioxide and Nitrite Ions with Various Boride Catalysts, Denki Kagaku, 1998, 66(6), 584–589.
38. A. Biswas, S. Kapse, B. Ghosh, R. Thapa, R. Sundar Dey and Lewis, Acid-Dominated Aqueous Electrolyte Acting as Co-Catalyst and Overcoming N₂ Activation Issues on Catalyst Surface, Proc. Natl. Acad. Sci. U. S. A., 2022, 119(33), e2204638119,  DOI:10.1073/pnas.2204638119.
39. S. Paul, S. Sarkar, A. Adalder, S. Kapse, R. Thapa and U. K. Ghorai, Strengthening the Metal Center of Co-N4 Active Sites in a 1D-2D Heterostructure for Nitrate and Nitrogen Reduction Reaction to Ammonia, ACS Sustain. Chem. Eng., 2023, 11(16), 6191–6200,  DOI:10.1021/acssuschemeng.2c07114.
40. A. Adalder, S. Paul, N. Barman, A. Bera, S. Sarkar, N. Mukherjee, R. Thapa and U. K. Ghorai, Controlling the Metal-Ligand Coordination Environment of Manganese Phthalocyanine in 1D-2D Heterostructure for Enhancing Nitrate Reduction to Ammonia, ACS Catal., 2023, 13(20), 13516–13527,  DOI:10.1021/acscatal.3c02747.
41. B. B. Sarma, F. Maurer, D. E. Doronkin and J. D. Grunwaldt, Design of Single-Atom Catalysts and Tracking Their Fate Using Operando and Advanced X-Ray Spectroscopic Tools, J. Am. Chem. Soc., 2023, 11, 379–444,  DOI:10.1021/acs.chemrev.2c00495.
42. C. Ling, Y. Ouyang, Q. Li, X. Bai, X. Mao, A. Du and J. Wang, A General Two-Step Strategy–Based High-Throughput Screening of Single Atom Catalysts for Nitrogen Fixation, Small Methods, 2019, 3(9), 1800376,  DOI:10.1002/smtd.201800376.
43. S. Bhattacharjee, U. V. Waghmare and S. C. Lee, An Improved D-Band Model of the Catalytic Activity of Magnetic Transition Metal Surfaces, Sci. Rep., 2016, 6, 35916,  DOI:10.1038/srep35916.
44. E. Paquet and H. L. Viktor, Computational Methods for Ab Initio Molecular Dynamics, Adv. Chem., 2018, 2018, 1–14,  DOI:10.1155/2018/9839641.
45. A. Adalder, K. Mitra, N. Barman, R. Thapa, S. Bhowmick and U. K. Ghorai, Magneto-Electrochemical Ammonia Synthesis: Boosting Nitrite Reduction Activity by the Optimized Magnetic Field Induced Spin Polarized System, Adv. Energy Mater., 2024, 14(42), 2403295,  DOI:10.1002/aenm.202403295.
46. S. Kapse, N. Barman and R. Thapa, Identification of ORR Activity of Random Graphene-Based Systems Using the General Descriptor and Predictive Model Equation, Carbon, 2023, 201, 703–711,  DOI:10.1016/j.carbon.2022.09.059.
47. C. Yates and D. J. Rlyholder, I'iiper 1-38, I'roceedirlgs of the Third International Congress on Catalysis, McQraw-Hill Rook Co., Inc, 1961, vol. 65.
48. Z. Fu, B. Yang and R. Wu, Understanding the Activity of Single-Atom Catalysis from Frontier Orbitals, Phys. Rev. Lett., 2020, 125(15), 156001,  DOI:10.1103/PhysRevLett.125.156001.
49. S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, LOBSTER: A Tool to Extract Chemical Bonding from Plane-Wave Based DFT, J. Comput. Chem., 2016, 37(11), 1030–1035,  DOI:10.1002/jcc.24300.
50. S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, Analytic Projection from Plane-Wave and PAW Wavefunctions and Application to Chemical-Bonding Analysis in Solids, J. Comput. Chem., 2013, 34(29), 2557–2567,  DOI:10.1002/jcc.23424.
51. V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, Crystal Orbital Hamilton Population (COHP) Analysis as Projected from Plane-Wave Basis Sets, J. Phys. Chem. A, 2011, 115(21), 5461–5466,  DOI:10.1021/jp202489s.

---