Open Access Article
Open Access ArticleSolvation strategies for free-energy calculations in a halogen-bonded complex: implicit, explicit, and machine learning approaches
Jaroslav
Vacek
 abc,
Dávid
Vrška
abc,
Dávid
Vrška
 ad,
Debashree
Manna
ad,
Debashree
Manna
 *a,
Rabindranath
Lo
*a,
Rabindranath
Lo
 *a and
Pavel
Hobza
*a and
Pavel
Hobza
 *ab
*ab
aInstitute of Organic Chemistry and Biochemistry, Czech Academy of Sciences, Flemingovo náměstí 542/2, 160 00 Prague, Czech Republic. E-mail: debashree.manna@uochb.cas.cz; rabindranath.lo@uochb.cas.cz; pavel.hobza@uochb.cas.cz
bIT4Innovations, VŠB-Technical University of Ostrava, 17. Listopadu 2172/15, 708 00 Ostrava-Poruba, Czech Republic
cFaculty of Science, Palacký University Olomouc, 17. Listopadu 1192/12, 779 00 Olomouc, Czech Republic
dDepartment of Physical and Theoretical Chemistry, Faculty of Natural Sciences, Comenius University in Bratislava, Mlynská dolina, Ilkovičova 6, 842 15 Bratislava, Slovakia
First published on 27th October 2025
Abstract
In pursuit of an efficient solvation approach for the halogen bonded complex between molecular iodine and tetramethylthiourea that reliably reproduces experimental trends, we investigated a range of solvent models, from implicit representations to periodic metadynamics simulations alongside micro-solvation and ONIOM-based methods as robust alternatives. Implicit solvent models fail to describe halogen-bonded complexes in high-polar solvents but provide surprisingly accurate estimates of binding free energies in all low to moderately polar solvents. For accurate and reliable modeling, especially in polar media, explicit solvent representations are essential. Periodic metadynamics simulations typically provide enhanced accuracy in calculating free energy differences, particularly for systems with complex solvation behavior. However, they are computationally demanding and restricted to generalized gradient approximation functionals (GGA). To overcome this limitation and improve accuracy, we employed the machine learning perturbation theory technique, enabling the estimation of free energies at levels of theory beyond the GGA.
Introduction
The solvent environment plays a critical role in modulating halogen bonding (X-bonding), significantly affecting both the strength and geometry of these noncovalent interactions. Understanding and modelling these solvent effects is crucial, as they impact a wide range of applications,1–3 including drug design,4–6 supramolecular self-assembly,7 protein engineering, catalysis, molecular recognition, and chemical sensing.8,9In aqueous or other polar environments, noncovalent interactions are often attenuated due to competitive solvation by the surrounding solvent molecules. However, it is evident that the effect of the solvent largely depends on the nature of the interactions between the subsystems. When electrostatic interactions are predominant, the dielectric constant of the medium plays a crucial role, as polar solvents tend to screen these interactions, thereby weakening them. Systems dominated by polarization are moderately affected by the solvent, and the solvent effect varies proportionally with the extent of polarization. Charge transfer interactions can be stabilized or destabilized depending on how well the solvent stabilizes the charge-separated resonance forms. Recently, we have shown that the stability of neutral hydrogen-bonded (H-bonded) complexes increases in a more polar solvent, provided there is substantial charge transfer between the subsystems.10,11 This is against the conventional belief that the stability of H-bonded complexes decreases in a more polar solvent.12–19 In the case of halogen bonds (XBs), solvent effects do not follow a simple or universal trend. Research on neutral halogen bonded (X-bonded) systems in solution is still limited and often contradictory.20–26 For example, Carlsson et al. suggested that neutral XBs are slightly stabilized with an increase in solvent polarity.27 Hunter et al. reported that the X-bonded complex between molecular iodine (I2) and tetramethylthiourea (TMTU) is rather insensitive to solvent polarity.25 Conversely, Fan-Hagenstein et al. found that the formation of X-bonded complexes between pyridine and perfluoroalkyl iodides is significantly influenced by the solvent, with polar solvents enhancing the stability of these complexes.23 Theoretical investigations into neutral XBs in solution also remain relatively sparse.28–32 For the complexes formed by a series of aromatic XB acceptors and donors, Frontera et al. found that the interaction energies are less favourable in solution compared to those in the gas phase.32 However, several studies by Cabot et al. on perfluorohexyl iodide, and by Li et al. on BrCl⋯H2CS and HOX⋯H2CS (where X = F, Cl, and Br), indicate that solvent effects can stabilize XBs.17,33,34 Both Carlsson et al. and Taylor et al. argued that a purely electrostatic model fails to adequately describe X-bonding behaviour in solution.22,27
Given these diverse findings, identifying an appropriate and efficient computational solvent model for X-bonded systems is both timely and necessary. To evaluate computational solvent models, we utilize the extensive experimental data available for the TMTU⋯I2 system investigated by Hunter and co-workers.25 The paper presents data on two H-bonded and two X-bonded complexes in nine low to moderately polar and six highly polar solvents. The results are, at first glance, surprising since binding free energies of X-bonded complexes measured in various solvents differ by less than 2 kcal mol−1 and, furthermore, they are systematically larger in low to moderately polar solvents. This paper serves as a unique source of high-quality binding free energy data for X-bonded complexes across different solvents. The complexity of solvent interactions, particularly in biological contexts, makes the accurate modelling of XB behaviour in solution challenging and underscores the need for quantum mechanical (QM) methods. Implicit solvent models are widely employed across various fields of chemistry and biochemistry due to their computational efficiency and cost-effectiveness. While implicit solvent models35–37 capture general solvent trends, they oversimplify solute–solvent interactions by treating the solvent as a uniform dielectric continuum.38 This prevents accurate modelling of competitive binding scenarios, in which solvent molecules interact directly with donor or acceptor sites. As a result, explicit solvation models are often required to account for specific, localized solute–solvent interactions that can alter both the binding strength and geometry.
A rigorous computational modelling is crucial for designing and optimizing molecules that rely on noncovalent interactions in solutions, particularly when applied in medicinal chemistry, enzyme design, or material synthesis.
Computational details
Implicit solvent models
All geometries were initially optimized at the DFT-D39 level using the PBE0-D3 functional40–42 with zero damping and the def2-TZVPP basis set.43,44 These calculations were performed with the Gaussian 16 program package.45 To account for solvent effects, we employed the COSMO, SMD, and C-PCM continuum solvation models,35–37 as well as periodic explicit solvent models and a combined explicit–implicit micro-solvation approach. The geometries were further refined using the range-separated hybrid meta-GGA functional ωB97M-V, which includes VV10 nonlocal correlation46 and is known to deliver reliable results for non-covalent systems. These calculations were carried out with ORCA 6.0.47,48 The ΔG values were computed using the rigid rotor–harmonic oscillator–ideal gas approximation at the PBE0 level, while thermodynamic corrections at the ωB97M-V level were derived using the Quasi-RRHO approach.49To evaluate the total interaction energies ΔE (eqn (1)), we calculated the energy difference between the bound state (complex) and the separated state (monomers). This corresponds to the binding process TMTU + I2 → TMTU⋯I2.
| ΔE = Ecomplex − Emonomer 1 − Emonomer 2 | (1) |
Analogously, the binding free energy differences ΔG were obtained according to eqn (2a):
| ΔG = Gcomplex − Gmonomer 1 − Gmonomer 2 | (2a) |
The following formula was used for Helmholtz free energy (ΔA):
| ΔA = Acomplex − Amonomer 1 − Amonomer 2 | (2b) |
Two different charge models are used to estimate the charge transfer: CT1, calculated using Hirshfeld charges,50 and CT2, calculated using Löwdin charges.51,52
Explicit–implicit solvent models
The binding free energy was computed as the energy difference,
| GONIOM/MSbinding = GONIOM/MSclose − GONIOM/MSfar. |
Periodic models
The TMTU⋯I2 complex was simulated with more sophisticated periodic descriptions of solvents. Due to the high computational cost of this approach, the number of solvent molecules was limited to 24 per system for carbon tetrachloride and dichloromethane solvents. For methanol, 28 explicit solvent molecules were used. Including more solvent molecules would have exceeded our available computational resources.At the beginning, the TMTU⋯I2 complex solvated with 24 molecules of the solvents, which were placed in a large unit cell (50 Å × 50 Å × 50 Å). Initial geometry optimizations were performed using classical force fields via the QuantumATK package.59,60 Subsequently, the system was pre-equilibrated using force-field molecular dynamics (MD) in the NpT ensemble, employing the Martyna–Tobias–Klein (MTK) algorithm61 keeping the pressure p and the temperature T constant. The number of particles N is constant by design.
The resulting pre-equilibrated structures were further optimized using the Vienna Ab initio Simulation Package (VASP),62–64 followed by ab initio MD in the NpT ensemble. For this purpose, the Parrinello–Rahman algorithm65,66 was used. After NpT equilibration, a final ab initio MD simulation was performed in the NVT ensemble – number of particles, volume, and temperature (the Nosé–Hoover thermostat67–70 was employed) were constant, using the average unit cell volume obtained from the previous NpT run. Final cell volumes for each investigated system are summarized in Table S1 in the SI.
All ab initio MD and metadynamics simulations were carried out using the VASP at the PBE-D3 level of theory, with the Becke–Johnson damping function.39,71,72 A plane-wave basis set was employed to describe the valence electron region, while the projector-augmented wave (PAW) method73,74 was used to treat the core electrons. The ALGO = Fast was employed and the energy cutoff and precision mode parameters were set as follows: ENCUT = 400 eV and PREC = NORMAL. To determine the equilibration period of the MD trajectories (see Table S2 in the SI), we employed the Mann–Kendall tests.75
Once equilibrium was reached, the resulting structure was used as the starting point for ab initio metadynamics.76,77 The S–I distance was chosen as the collective variable (CV) for the TMTU⋯I2 system. A very fine bias potential was applied to ensure high precision in the metadynamics simulations: the height of the Gaussian hill was set to 0.0005 eV and the width of the Gaussian hill was 0.005 Å, added after every two steps in a metadynamics run.
Since the canonical (NVT) ensemble is used, we work with Helmholtz free energy A instead of Gibbs free energy G. We report the free energy of reaction ΔA(R→P) (in our case, the binding process of TMTU with the iodine dimer from separated TMTU + I2 (R) to bound TMTU⋯I2 (P) in different solvents) defined in eqn (3):
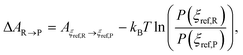 | (3) |
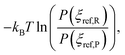 represents a correction that accounts for the normalized probabilities of observing the specific reactant P(ξref,R) and product P(ξref,P) configuration. These probabilities are obtained from molecular dynamics trajectories, for instance using histogram methods. Although the specific values ξref,R and ξref,P can be chosen arbitrarily, in practice we select the maximum value of the corresponding normalized histograms. Here, kB denotes the Boltzmann constant and T is the thermodynamic temperature of simulation (340 K in our case). The statistical errors were determined using the block averaging method78 with a 95% confidence interval. The overall sum of errors was calculated as follows:
represents a correction that accounts for the normalized probabilities of observing the specific reactant P(ξref,R) and product P(ξref,P) configuration. These probabilities are obtained from molecular dynamics trajectories, for instance using histogram methods. Although the specific values ξref,R and ξref,P can be chosen arbitrarily, in practice we select the maximum value of the corresponding normalized histograms. Here, kB denotes the Boltzmann constant and T is the thermodynamic temperature of simulation (340 K in our case). The statistical errors were determined using the block averaging method78 with a 95% confidence interval. The overall sum of errors was calculated as follows: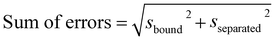 | (4) |
Machine learning perturbation theory
For free energy calculations in an improved level of theory, the Machine Learning Perturbation Theory (MLPT)79–81 technique was employed. This approach connects Δ-ML82 where a model is trained to predict energy differences of the target level (i.e. more accurate and computationally more demanding method), relative to a reference method (i.e. computationally low-cost, production method), with thermodynamic perturbation theory (PT).83In our case, the production method is the GGA-type PBE functional supplemented by the Grimme dispersion correction and the Becke–Johnson damping function D3(BJ). As target methods, we selected two DFT functionals from the hybrid rung of Jacob's ladder,84 both enhanced with D3(BJ) corrections: range-separated HSE06 (ref. 85) and unscreened PBE0.40–42 For these target functionals in all solvents, we chose a time step value of TIME = 0.7 within the Damped algorithm, and we set the energy cutoff (ENCUT) of 520 eV and “Accurate” precision.
Thus, MD data were generated using the PBE-D3(BJ) functional (for more details, see Section “Periodic models”) with a Hamiltonian H(p,x). Using MLPT, simulation at the target levels described by the Hamiltonian ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) (p,x) requires only a few dozen single-point calculations (we selected every (Ndata/100)-th configuration, where Ndata is the total number of configurations obtained from the production MD run) for training the ML model. The rest of the simulation is predicted based on this training. In this way, MLPT enables simulations that are several orders of magnitude faster without sacrificing accuracy.
(p,x) requires only a few dozen single-point calculations (we selected every (Ndata/100)-th configuration, where Ndata is the total number of configurations obtained from the production MD run) for training the ML model. The rest of the simulation is predicted based on this training. In this way, MLPT enables simulations that are several orders of magnitude faster without sacrificing accuracy.
Several applications of the MLPT technique in the efficient determination of various properties, such as adsorption enthalpies,79,81,86 free activation energies80,87 or fully anharmonic dimerization thermodynamics at challenging target levels, including CCSD(T)88 have been found.
The formula for the target free energy difference between two stable states ΔÃR→P is known (see, for instance, ref. 80 and 89):
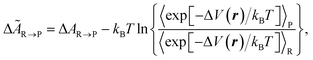 | (5) |
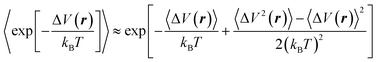 | (6) |
Note that the term ΔV(r) in eqn (5) and (6) denotes the difference in potential energy between the target and the production Hamiltonians. More generally, ΔH(r,p) represents the Hamiltonian difference, but if the two Hamiltonians differ only in their potential energy contributions, the free energy expression can be written equivalently using ΔV(r) instead of ΔH(r,p): ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) (r,p) − H(r,p) = Ṽ(r) − V(r) = ΔV(r).
(r,p) − H(r,p) = Ṽ(r) − V(r) = ΔV(r).
The statistical errors were determined using the block averaging method78 in the same way as in the case of the production method (see eqn (4)).
A kernel ridge regression91 model trained on a small set of target-level calculations is used to predict energy differences ΔV(r) for the full ensemble, employing the REMatch kernel92 with SOAP descriptors93 as implemented in the DScribe94 and scikit-learn94,95 libraries, respectively.
Details about minimizing errors in ML predictions are presented in Tables S3 and S4 in the SI.
Results and discussion
Implicit models
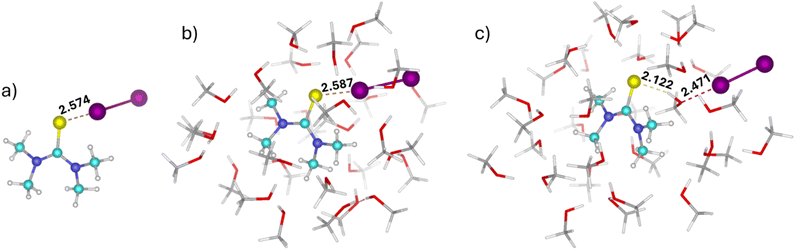
Although implicit solvent models do not capture specific solvent–solute interactions as accurately as explicit models, they provide a very reasonable approximation for bulk solvation effects, like electrostatic stabilization, solvation free energy, and dielectric screening. Therefore, we begin by evaluating the performance of the implicit COSMO35 solvation models against the experimentally observed trends in binding free energies ΔG. These experimental ΔG values are derived from association constants reported by Hunter and co-workers.25Table 1 presents the interaction energies (ΔE), Gibbs free energies (ΔG) and Helmholtz free energies (ΔA) at temperature T = 298 K, of the X-bonded TMTU⋯I2 complex in different solvents at the PBE0-D3/def2-TZVPP level of theory. The results indicate that the stability of the TMTU⋯I2 complex increases steadily with increasing solvent polarity. However, this trend is supported by experimental data only for low to moderately polar solvents (Table 1 and Fig. 1a). When a highly polar solvent is used, the correlation between polarity and stability of the complex is lost. Thus, an implicit solvent model can only be used for low to moderately polar solvents, where its performance is incredible. The correlation between calculated and experimental ΔG for six non-polar/low-polar solvents with ε between 1.9 and 8.9 is as high as 0.960 (Table 1 and Fig. 1b). A strong correlation was also observed between the experimental and calculated ΔG values and the solvent dielectric constant (Fig. 1b). Nevertheless, this relationship deteriorates markedly in the case of highly polar solvents. To elucidate the underlying reasons for this deviation, a more detailed investigation was undertaken using three representative solvents, each chosen to reflect a distinct range of dielectric properties. Carbon tetrachloride (CCl4) was selected as a low-polar solvent (ε = 2.23), dichloromethane (CH2Cl2) as a moderately polar solvent (ε = 8.93), and methanol (CH3OH) as a high-polar solvent (ε = 32.61). We started with evaluating the performance of three widely used implicit solvation models (COSMO, SMD, and CPCM) against the experimental ΔG trends, as summarized in Table 2. All implicit solvent models examined yielded consistent results, predicting a steady increase in complex stability with increasing solvent polarity; none captured the trend observed for more polar solvents. Tables 2 and S5 in the SI also list the S⋯I bond lengths (r) and charge transfer (CT) values. To assess the functional dependency, values are also reported with the ωB97M-V functional with the COSMO solvation model in Table S6 in the SI. Tables 2 and S5 in the SI further show a significant charge transfer from I2 to TMTU upon complex formation. Additionally, the S⋯I bond length decreases systematically with increasing solvent polarity, while the corresponding charge transfer (CT) values increase substantially. All the charge models (Hirshfeld, Löwdin, NBO and CM5) consistently indicate that the CT values for this complex are indeed significant. The strong charge-transfer nature of the interaction is further supported by the UV/Vis spectrum of the TMTU⋯I2 complex, which displays a distinct charge-transfer band in the 330–340 nm range.25 Previously, we have shown that when the charge transfer (CT) between the subsystems is significant, it leads to stabilization of the X-bonded complex with increasing solvent polarity.96 However, when the CT is low, the opposite trend may be observed. Since the CT is significant for the TMTU⋯I2 complex, its stabilization with increasing solvent polarity is consistent with our expectations, provided there are no substantial specific solvent–solute interactions.| Solvent | Dielectric constant (ε) | ΔE | ΔGcalc./ΔAcalc. | ΔGexp. | K a |
|---|---|---|---|---|---|
| a From ref. 25, measured by UV/vis. b From ref. 25, measured by 1H NMR titration. c From ref. 25, the errors were determined as 2× the standard deviation from multiple titration repeats. | |||||
| n-Octane | 1.94 | −16.94 | −6.52/−7.83 | −5.38 | 8800 ± 900a |
| Carbon tetrachloride | 2.23 | −17.19 | −6.74/−8.07 | −5.27 | 7300 ± 600a |
| Toluene | 2.38 | −17.31 | −6.84/−8.17 | −5.51 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 1600a 000 ± 1600a |
| Chloroform | 4.81 | −18.50 | −7.88/−9.25 | −5.86 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 1000a 000 ± 1000a |
| 1,1,2,2-Tetrachloroethane | 8.4 | −19.27 | −8.62/−10.00 | −6.46 | 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 15 000 ± 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000a 000a |
| Dichloromethane | 8.93 | −19.34 | −8.68/−10.07 | −6.50 | 58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 10 000 ± 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000b 000b |
| Acetone | 20.7 | −20.02 | −9.35/−10.74 | −4.47 | 1900 ± 300b |
| Methanol | 32.61 | −20.24 | −9.58/−10.97 | −4.68 | 2700 ± 200b |
| Acetonitrile | 37.5 | −20.27 | −9.61/−11.00 | −4.70 | 2800 ± 70b |
| Water | 78.4 | −20.47 | −9.81/−11.21 | — | — |
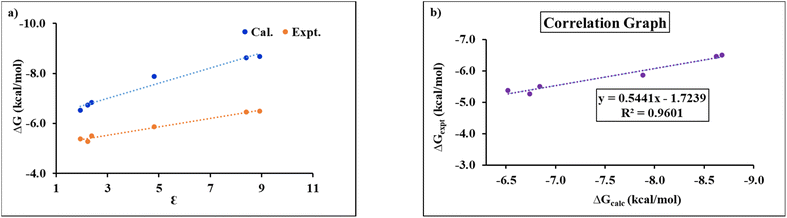 | ||
| Fig. 1 Plots of (a) ΔG (kcal mol−1) vs. ε from experimental and calculated free energy values and (b) ΔGexp. (kcal mol−1) vs. ΔGcalc. (kcal mol−1). | ||
| Solvent | COSMO | SMD | CPCM | Exp. | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ΔE | ΔG/ΔA | r | CT1/CT2 | ΔE | ΔG/ΔA | r | CT1/CT2 | ΔE | ΔG/ΔA | r | CT1/CT2 | ΔGexp.a | |
| a From ref. 25. | |||||||||||||
| Carbon tetrachloride | −17.19 | −6.74/−8.07 | 2.724 | −0.408/−0.376 | −17.86 | −7.55/−8.81 | 2.731 | −0.416/−0.383 | −17.08 | −6.79/−8.08 | 2.735 | −0.413/−0.381 | −5.27 |
| Dichloromethane | −19.34 | −8.68/−10.07 | 2.610 | −0.549/−0.510 | −20.84 | −11.05/−12.28 | 2.631 | −0.545/−0.507 | −18.84 | −8.43/−9.76 | 2.637 | −0.536/−0.499 | −6.50 |
| Methanol | −20.24 | −9.58/−10.97 | 2.574 | −0.607/−0.564 | −21.98 | −13.02/−14.26 | 2.599 | −0.593/−0.552 | −19.52 | −9.18/−10.52 | 2.606 | −0.580/−0.540 | −4.68 |
In contrast, for the tetramethylurea⋯I2 complex, another system studied by Hunter and co-workers,25 both experimental and computational results show destabilization with increasing solvent polarity. We have demonstrated that the CT values for this complex are significantly lower, which in turn leads to this opposite trend (Table S7, SI).
Explicit–implicit solvent models
Thus, calculations were carried out using 30 explicit solvent molecules, each embedded in a continuous solvent environment described by the COSMO implicit solvent model. The incorporation of explicit solvent molecules significantly destabilizes the TMTU⋯I2 complex in CH3OH, aligning well with experimental observations (Table 3). In contrast, a slight stabilization is observed when moving from CCl4 to CH2Cl2. This is again in line with the experimental trend. The differences in the S⋯I bond length, with or without explicit solvation, are negligible (Table 3). We extended the study by using four more low-energy conformers from MD simulation trajectories. We used these as starting points to construct complexes with 30 solvent molecules of CCl4, CH2Cl2, and CH3OH. Table S8 in the SI shows the free energy order for all the conformers, and Table 3 lists the ΔG values for the most stable conformer with 30 solvent molecules. Destabilization occurs for the TMTU⋯I2 complex in CH3OH, as the separated systems are stabilized by both conventional hydrogen bonding and bridging hydrogen bonding with CH3OH (Fig. 2c). In particular, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S⋯H and O⋯I–I types of hydrogen and halogen bonds formed through the bridging CH3OH molecule contribute to the stabilization of the separated systems. Please note that these calculations are highly computationally demanding; thus, the number of solvent molecules included in the micro-solvation model is restricted by computational cost. Additionally, the ONIOM approach was employed to evaluate the strength of the X-bonded complex in the presence of 50 explicit solvent molecules, treating the complex as the high layer (PBE0-D3/def2-TZVPP) and the solvent molecules as the low layer (PM7). For each solvent, five different conformers are considered in the ONIOM calculations (Table S9, SI), and the Gibbs free energy (ΔG) is reported for the most stable conformation (Table 3). ONIOM calculations also reproduce the experimental trends (Table 3). However, both micro-solvation and ONIOM significantly overestimate the experimental ΔG values.
S⋯H and O⋯I–I types of hydrogen and halogen bonds formed through the bridging CH3OH molecule contribute to the stabilization of the separated systems. Please note that these calculations are highly computationally demanding; thus, the number of solvent molecules included in the micro-solvation model is restricted by computational cost. Additionally, the ONIOM approach was employed to evaluate the strength of the X-bonded complex in the presence of 50 explicit solvent molecules, treating the complex as the high layer (PBE0-D3/def2-TZVPP) and the solvent molecules as the low layer (PM7). For each solvent, five different conformers are considered in the ONIOM calculations (Table S9, SI), and the Gibbs free energy (ΔG) is reported for the most stable conformation (Table 3). ONIOM calculations also reproduce the experimental trends (Table 3). However, both micro-solvation and ONIOM significantly overestimate the experimental ΔG values.
Calculations of free energies of dimerization of TMTU + I2 in explicitly defined solvents for temperature T = 340 K in periodic models
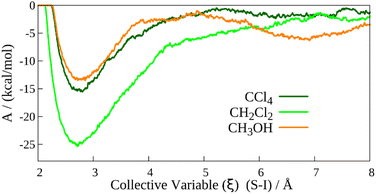
To increase computational accuracy, we investigated the interactions between TMTU and the iodine molecule in a periodic model. Periodic simulations are generally expected to provide improved accuracy compared to droplet models, particularly for systems exhibiting complex solvation behaviour. The periodic boundary model offers several advantages over the droplet model approach. For example, it eliminates the risk of molecules “boiling off” during a MD run. Moreover, unlike the droplet model, the periodic approach has no surface, thereby avoiding artificial interactions between the system and vacuum that could distort the results. In summary, the periodic approach enables long MD simulations while preserving stability and ensuring reliable results.Metadynamics simulations of the TMTU⋯I2 molecule (Fig. 3) were performed in three different solvents: 24 explicitly defined molecules for two low to moderately polar solvents (CCl4 and CH2Cl2) and 28 explicit solvent molecules for one high-polar solvent (CH3OH), under periodic boundary conditions. We initiated the simulations from the more stable (bound) states and introduced a bias potential constructed in the space of the CV (ξ) chosen as the distance between the sulphur and iodine atoms (Fig. 3). This allowed us to reach a second stable state corresponding to the separated states. It should be noted that although we considered a binding reaction (i.e. from the separated state to a bound state), the direction of the CV change is irrelevant in metadynamics.
After taking into account the probabilities of the occurrence of the concrete ξ values obtained from MD trajectories of both states, we were able to determine the free energy differences as functions of CV, ΔA(ξ), according to eqn (3). This methodology successfully reproduces the experimentally observed stability trends, with the corresponding values summarized in Table 4.
While the approach captures the correct qualitative trend, it tends to significantly overestimate both absolute (ΔA) and relative (ΔΔA) free energy differences compared with the experimental reference, similar to micro-solvation and ONIOM-based methods. Moreover, the periodic metadynamics method is computationally more expensive than micro-solvation or ONIOM approaches and can accommodate comparatively fewer solvent molecules. Due to computational cost, we restricted this approach to the PBE-D3(BJ) level of theory.
Free energy finite-T calculations beyond GGA functionals
The MLPT-corrected free energy differences, ΔÃHSE06-D3(BJ), yield values closer to the experimental references compared to the ΔAPBE-D3(BJ) baseline (see Table 4) across all three solvents. By contrast, the ML-correction with the PBE0-D3(BJ) functional, ΔÃPBE0-D3(BJ), exhibits a larger deviation from the experimental reference in CCl4 than the corresponding baseline value.
This inverse trend arises because the difference between the target and production methods, calculated via the cumulant expansion (CE), is evaluated separately for the reactant (separated state) and the product (bound state). When the CE value (i.e., the energy difference between target and production methods) is more negative for the reactant than for the product, the resulting correction – defined as the difference between these two CE values (see the second term of eqn (5)) – is positive. Adding this positive correction to the (already negative) ΔAPBE-D3(BJ) reduces the absolute value of the free energy. This scenario applies to CH3OH and CH2Cl2 for both the functionals, as well as to CCl4 with HSE06-D3(BJ). Conversely, when the CE value is lower for the product, as observed with PBE0-D3(BJ) in CCl4, the correction is negative, making the overall free energy even more negative. We attribute this to an artifact arising from the combination of the unscreened functionals and the solvent, possibly due to a preference of a (significantly) different density, i.e., a different unit cell volume for the reactant and/or product.
Apart from this outlier, all other ML-corrected values are closer to the experimental reference than the PBE-D3(BJ) baseline. The closest agreements are observed as follows: in CCl4 with HSE06-D3(BJ), the error is 5.07 ± 1.35 kcal mol−1; in CH2Cl2 with PBE0-D3(BJ), 12.16 ± 1.37 kcal mol−1; and in CH3OH with PBE0-D3(BJ), 2.46 ± 1.09 kcal mol−1. These values are highlighted in bold in Table 5.
Relative free energy differences between different solvents (ΔΔA) are overestimated compared with experimental data, similar to production PBE-D3(BJ) level results. Among the functionals, the ΔΔA differences between the two low to moderately polar solvents are as follows: ΔΔAPBE0-D3(BJ) = 4.68 kcal mol−1 and ΔΔAHSE06-D3(BJ) = 9.04 kcal mol−1. The differences between the high-polar CH3OH and moderately polar CH2Cl2 remain nearly constant, 11.52 kcal mol−1 for PBE0-D3(BJ) and 11.85 kcal mol−1 for HSE06-D3(BJ). For CH3OH and the low-polarity solvent, CCl4, the spread is slightly wider: 2.81 kcal mol−1 with HSE06-D3(BJ) and 6.84 kcal mol−1 with PBE0-D3(BJ).
Critical evaluation of different techniques for estimation of binding free energies of X-bonded complexes in a solvent provides the following take:
(i) Continuous solvent cannot be used for both apolar and polar solvents. The model, however, provides very good estimates of ΔG for low to moderately polar solvents. COSMO and CPCM provide not only qualitative but even quantitative estimates of ΔG.
(ii) The micro-solvation and ONIOM models, contrary to the continuous models, provide reasonable qualitative agreement of ΔG for all three solvents considered, though their absolute values are strongly overestimated.
(iii) Theoretically justified periodic calculations performed at the PBE level also provide qualitative estimates of ΔG for all solvents considered, but their quantitative values are overestimated even more than in the previous case.
(iv) Upon considering the ML-corrected values, the situation is changed only slightly. HSE06 and PBE0 methods qualitatively agree with experimental values, though, again, the respective absolute values are strongly overestimated.
Conclusions
Solvent effects play a critical role in modulating the XB between molecular iodine and tetramethylthiourea in solution and their theoretical estimates are tedious and represent a challenge to current computational chemistry. The complex exhibits significant charge-transfer character and are notably stabilized in low-polarity environments (dielectric constant ε ≤ 10) with moderate increases in solvent polarity. However, in highly polar solvents, the XB weakens due to the stabilization of charge-separated species via competitive solvation of the individual components. While implicit solvent models are valuable for identifying general trends and for initial screening of molecular systems, they inherently oversimplify solute–solvent interactions by neglecting specific, directional, and dynamic solvent effects. The method cannot be used for high-polar solvents, but for low to moderately polar solvents, it provides good estimates of binding free energies. To address these shortcomings, explicit solvent models are essential. By providing a detailed, dynamic representation of solvation, explicit models enable more reliable predictions of free energy trends in solution.By systematically comparing implicit and explicit solvent models, incorporating periodic boundary conditions to better capture realistic solvation environments, and applying machine learning perturbation theory to balance computational cost and accuracy, we provide a robust framework for evaluating solvent effects. Although the current error margins (2.5–12 kcal mol−1) are too large for reliable predictive applications in catalysis, materials design, or molecular recognition, the approach effectively captures the trends observed in experimental association constants across multiple solvents. More broadly, this study contributes to the development of general strategies for modeling noncovalent interactions in complex solvent environments, which is essential for advancing both fundamental chemistry and practical applications. We also acknowledge that achieving more quantitative agreement is necessary for the direct predictive use of the free energy data.
Author contributions
D. M. and R. L. evaluated the implicit solvent models and performed micro-solvation and ONIOM calculations. J. V. performed the metadynamics simulations. D. V. calculated the free energies using machine learning perturbation theory. D. M., D. V., R. L., J. V. and P. H. prepared the manuscript. P. H. coordinated the study.Conflicts of interest
There are no conflicts to declare.Data availability
Additional data are available at ZENODO (https://doi.org/10.5281/zenodo.17452749).Tables S1–S9, figure, and supplementary data associated with this article are provided in the supplementary information (SI). See DOI: https://doi.org/10.1039/d5sc06336a.
Acknowledgements
The authors would like to thank Associate Professor Tomáš Bučko for fruitful discussions in the field of free energy calculations, which greatly helped them. This work was carried out with the financial support of the European Union under the REFRESH – Research Excellence for Region Sustainability and High-tech Industries project number CZ.10.03.01/00/22_003/0000048 via the Operational Programme Just Transition (P. H.). J. V. acknowledges the financial support of Palacký University through the Internal Grant Association, project IGA_PrF_2025_003.Notes and references
- Halogen bonding I: Impact on materials chemistry and life sciences, ed. P. Metrangolo and G. Resnati, Springer, Switzerland, 2015 Search PubMed.
- Halogen Bonding, Fundamentals and Applications, ed. P. Metrangolo and G. Resnati, Springer-Verlag, Berlin, Heidelberg, 2008, https://link.springer.com/book/10.1007/978-3-540-74330-9 Search PubMed.
- P. Politzer, P. Lane, M. C. Concha, Y. Ma and J. S. Murray, J. Mol. Model., 2007, 13, 305–311 CrossRef CAS PubMed.
- C. Bissantz, B. Kuhn and M. Stahl, J. Med. Chem., 2010, 53, 5061–5084 CrossRef CAS PubMed.
- Y. Lu, Y. Liu, Z. Xu, H. Li, H. Liu and W. Zhu, Expert Opin. Drug Discovery, 2012, 7, 375–383 CrossRef CAS PubMed.
- M. R. Scholfield, C. M. V. Zanden, M. Carter and P. S. Ho, Protein Sci., 2013, 22(2), 139–152 CrossRef CAS PubMed.
- L. C. Gilday, S. W. Robinson, T. A. Barendt, M. J. Langton, B. R. Mullaney and P. D. Beer, Chem. Rev., 2015, 115, 7118–7195 CrossRef CAS PubMed.
- G. Cavallo, P. Metrangolo, R. Milani, T. Pilati, A. Priimagi, G. Resnati and G. Terraneo, Chem. Rev., 2016, 116, 2478–2601 CrossRef CAS PubMed.
- B. Li, S.-Q. Zang, L.-Y. Wang and T. C. W. Mak, Coord. Chem. Rev., 2016, 308, 1–21 CrossRef CAS.
- D. Manna, R. Lo, J. Vacek, V. M. Miriyala, P. Bouř, T. Wu, Z. Osifová, D. Nachtigallová, M. Dračínský and P. Hobza, Angew. Chem., Int. Ed., 2024, 63, e202403218 CrossRef CAS PubMed.
- R. Lo, D. Manna, J. Vacek, P. Bouř, T. Wu, Z. Osifová, O. Socha, M. Dračínský and P. Hobza, Angew. Chem., Int. Ed., 2025, 64, e202422594 CrossRef CAS PubMed.
- M. D. Driver, M. J. Williamson, J. L. Cook and C. A. Hunter, Chem. Sci., 2020, 11, 4456–4466 RSC.
- J. L. Cook, C. A. Hunter, C. M. R. Low, A. Perez-Velasco and J. G. Vinter, Angew. Chem., Int. Ed., 2007, 46, 3706–3709 CrossRef CAS PubMed.
- A. J. A. Aquino, D. Tunega, G. Haberhauer, M. H. Gerzabek and H. Lischka, J. Phys. Chem. A, 2002, 106, 1862–1871 CrossRef CAS.
- C. C. Robertson, J. S. Wright, E. J. Carrington, R. N. Perutz, C. A. Hunter and L. Brammer, Chem. Sci., 2017, 8, 5392–5398 RSC.
- C. A. Hunter, Angew. Chem., Int. Ed., 2004, 43, 5310–5324 CrossRef CAS PubMed.
- R. Cabot and C. A. Hunter, Chem. Commun., 2009, 2005–2007 RSC.
- N. Y. Meredith, S. Borsley, I. V. Smolyar, G. S. Nichol, C. M. Baker, K. B. Ling and S. L. Cockroft, Angew. Chem., Int. Ed., 2022, 61, e202206604 CrossRef CAS PubMed.
- R. J. Burns, I. K. Mati, K. B. Muchowska, C. Adam and S. L. Cockroft, Angew. Chem., Int. Ed., 2020, 59, 16717–16724 CrossRef CAS PubMed.
- M. Erdélyi, Chem. Soc. Rev., 2012, 41, 3547 RSC.
- P. Klaeboe, J. Am. Chem. Soc., 1967, 89, 3667–3676 CrossRef CAS.
- M. G. Sarwar, B. Dragisic, L. J. Salsberg, C. Gouliaras and M. S. Taylor, J. Am. Chem. Soc., 2010, 132, 1646–1653 CrossRef CAS PubMed.
- B. Hawthorne, H. Fan-Hagenstein, E. Wood, J. Smith and T. Hanks, Int. J. Spectrosc., 2013, 2013, 1–10 CrossRef.
- O. Dumele, D. Wu, N. Trapp, N. Goroff and F. Diederich, Org. Lett., 2014, 16, 4722–4725 CrossRef CAS PubMed.
- C. C. Robertson, R. N. Perutz, L. Brammer and C. A. Hunter, Chem. Sci., 2014, 5, 4179–4183 RSC.
- J. Cao, X. Yan, W. He, X. Li, Z. Li, Y. Mo, M. Liu and Y.-B. Jiang, J. Am. Chem. Soc., 2017, 139, 6605–6610 CrossRef CAS PubMed.
- A.-C. C. Carlsson, A. X. Veiga and M. Erdélyi, Halogen Bonding in Solution, in Halogen Bonding II, ed. P. Metrangolo and G. Resnati, Topics in Current Chemistry, Springer, Cham, 2014, vol. 359, pp. 49–76 Search PubMed.
- Y. Lu, H. Li, X. Zhu, W. Zhu and H. Liu, J. Phys. Chem. A, 2011, 115, 4467–4475 CrossRef CAS PubMed.
- Y. Lu, H. Li, X. Zhu, H. Liu and W. Zhu, Int. J. Quantum Chem., 2012, 112, 1421–1430 CrossRef CAS.
- A. Forni, S. Rendine, S. Pieraccini and M. Sironi, J. Mol. Graphics Modell., 2012, 38, 31–39 CrossRef CAS PubMed.
- K. E. Riley and K. M. Merz, J. Phys. Chem. A, 2007, 111, 1688–1694 CrossRef CAS PubMed.
- A. Bauzá, D. Quiñonero, A. Frontera and P. M. Deyà, Phys. Chem. Chem. Phys., 2011, 13, 20371 RSC.
- Q. Li, R. Li, Z. Zhou, W. Li and J. Cheng, J. Chem. Phys., 2012, 136, 014302 CrossRef PubMed.
- Q.-Z. Li, B. Jing, R. Li, Z.-B. Liu, W.-Z. Li, F. Luan, J.-B. Cheng, B.-A. Gong and J.-Z. Sun, Phys. Chem. Chem. Phys., 2011, 13, 2266 RSC.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 5, 799–805 RSC.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS PubMed.
- J. Zhang, H. Zhang, T. Wu and Q. Wang, J. Chem. Theory Comput., 2017, 13, 1034–1043 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982–9985 CrossRef CAS.
- M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036 CrossRef CAS.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- N. Mardirossian and M. Head-Gordon, J. Chem. Phys., 2016, 144, 214110 CrossRef PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2025, 15, e70019 Search PubMed.
- S. Grimme, Chem.–Eur. J., 2012, 18, 9955–9964 CrossRef CAS PubMed.
- F. L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129–138 CrossRef CAS.
- P.-O. Löwdin, J. Chem. Phys., 1950, 18, 365–375 CrossRef.
- P.-O. Löwdin, On the Nonorthogonality Problem, in Advances in Quantum Chemistry, Elsevier, 1970, vol. 5, pp. 185–199 Search PubMed.
- R. B. Sunoj and M. Anand, Phys. Chem. Chem. Phys., 2012, 14, 12715–12736 RSC.
- C. Hadad, E. Florez, N. Acelas, G. Merino and A. Restreppo, Int. J. Quantum Chem., 2019, 119, e25766 CrossRef.
- G. N. Simm, P. L. Türtscher and M. Reiher, J. Comput. Chem., 2020, 41, 1144–1145 CrossRef CAS PubMed.
- Y. Basdogan, M. C. Groenenboom, E. Henderson, S. De, S. B. Rempe and J. A. Keith, J. Chem. Theory Comput., 2020, 16, 633–642 CrossRef PubMed.
- M. Svensson, S. Humbel, R. D. J. Froese, T. Matsubara, S. Sieber and K. Morokuma, J. Phys. Chem., 1996, 100, 19357–19363 CrossRef CAS.
- J. J. P. Stewart, J. Mol. Model., 2013, 19, 1–32 CrossRef CAS PubMed.
- J. Schneider, J. Hamaekers, S. T. Chill, S. Smidstrup, J. Bulin, R. Thesen, A. Blom and K. Stokbro, Model. Simul. Mater. Sci. Eng., 2017, 25, 085007 CrossRef.
- S. Smidstrup, T. Markussen, P. Vancraeyveld, J. Wellendorff, J. Schneider, T. Gunst, B. Verstichel, D. Stradi, P. A. Khomyakov, U. G. Vej-Hansen, M.-E. Lee, S. T. Chill, F. Rasmussen, G. Penazzi, F. Corsetti, A. Ojanperä, K. Jensen, M. L. N. Palsgaard, U. Martinez, A. Blom, M. Brandbyge and K. Stokbro, J. Phys.: Condens. Matter, 2020, 32, 015901 CrossRef CAS PubMed.
- G. J. Martyna, D. J. Tobias and M. L. Klein, J. Chem. Phys., 1994, 101, 4177–4189 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- M. Parrinello and A. Rahman, Phys. Rev. Lett., 1980, 45, 1196–1199 CrossRef CAS.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- S. Nosé, Prog. Theor. Phys. Suppl., 1991, 103, 1–46 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef PubMed.
- D. Frenkel and B. Smit, Understanding Molecular Simulation: From Algorithms to Applications, Computational science series, Academic Press, San Diego, 2nd edn, 2002 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- S. K. Schiferl and D. C. Wallace, J. Chem. Phys., 1985, 83, 5203–5209 CrossRef CAS.
- A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12566 CrossRef CAS PubMed.
- M. Iannuzzi, A. Laio and M. Parrinello, Phys. Rev. Lett., 2003, 90, 238302 CrossRef PubMed.
- H. Flyvbjerg and H. Petersen, J. Chem. Phys., 1989, 91, 461–466 CrossRef CAS.
- B. Chehaibou, M. Badawi, T. Bučko, T. Bazhirov and D. Rocca, J. Chem. Theory Comput., 2019, 15, 6333–6342 CrossRef CAS PubMed.
- T. Bučko, M. Gešvandtnerová and D. Rocca, J. Chem. Theory Comput., 2020, 16, 6049–6060 CrossRef PubMed.
- B. Herzog, M. Chagas da Silva, B. Casier, M. Badawi, F. Pascale, T. Bučko, S. Lebègue and D. Rocca, J. Chem. Theory Comput., 2022, 18, 1382 CrossRef CAS PubMed.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. von Lilienfeld, J. Chem. Theory Comput., 2015, 11, 2087–2096 CrossRef CAS PubMed.
- A. Pohorille, C. Jarzynski and C. Chipot, J. Phys. Chem. B, 2010, 114, 10235–10253 CrossRef CAS PubMed.
- J. P. Perdew and K. Schmidt, AIP Conf. Proc., 2001, 577, 1 CrossRef CAS.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106–224111 CrossRef PubMed.
- B. Herzog, A. Gallo, F. Hummel, M. Badawi, T. Bučko, S. Lebègue, A. Grüneis and D. Rocca, npj Comput. Mater., 2024, 10, 68 CrossRef.
- J. Rey, A. Gomez, P. Raybaud, C. Chizallet and T. Bučko, J. Catal., 2019, 373, 361–373 CrossRef CAS.
- D. Vrška, M. Pitoňák and T. Bučko, J. Chem. Phys., 2024, 160, 174106 CrossRef PubMed.
- M. Gešvandtnerová, D. Rocca and T. Bučko, J. Catal., 2021, 396, 166 CrossRef.
- C. Chipot and A. Pohorille, Calculating free energy differences using perturbation theory, in Free Energy Calculations Theory and Applications in Chemistry and Biology, Springer, Berlin, Heidelberg, 2007 Search PubMed.
- M. Rupp, Int. J. Quantum Chem., 2015, 115, 1058–1073 CrossRef CAS.
- S. De, A. P. Bartók, G. Csányi and M. Ceriotti, Phys. Chem. Chem. Phys., 2016, 18, 13754 RSC.
- A. P. Bartók, R. Kondor and G. Csányi, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 184115 CrossRef.
- L. Himanen, M. O. Jäger, E. V. Morooka, F. Federici Canova, Y. S. Ranawat, D. Z. Gao, P. Rinke and A. S. Foster, Comput. Phys. Commun., 2020, 247, 106949 CrossRef CAS.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- R. Lo, A. Mašínová, M. Lamanec, D. Nachtigallová and P. Hobza, J. Comput. Chem., 2023, 44, 329 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2025 |