Open Access Article
Open Access ArticleSimulation of ultrafast transient absorption spectra of a perylene-based light harvesting antenna†
Royle
Perez-Castillo
 a,
Victor M.
Freixas
a,
Victor M.
Freixas
 b,
Aliezer
Martinez-Mesa
c,
Llinersy
Uranga-Piña
cf,
Maxim F.
Gelin
d,
Sergei
Tretiak
b,
Aliezer
Martinez-Mesa
c,
Llinersy
Uranga-Piña
cf,
Maxim F.
Gelin
d,
Sergei
Tretiak
 e and
Sebastian
Fernandez-Alberti
e and
Sebastian
Fernandez-Alberti
 *a
*a
aDepartamento de Ciencia y Tecnologia, Universidad Nacional de Quilmes/CONICET, B1876BXD Bernal, Argentina. E-mail: sfalberti@gmail.com
bDepartment of Chemistry and Physics and Astronomy, University of California, Irvine, California 92697-2025, USA
cDynAMoS (Dynamical Processes in Atomic and Molecular Systems), Facultad de Física, Universidad de La Habana, San Lázaro y L, La Habana 10400, Cuba
dSchool of Sciences, Hangzhou Dianzi University, Hangzhou 310018, China
eTheoretical Division, Center for Nonlinear Studies (CNLS), Center for Integrated Nanotechnologies (CINT), Los Alamos National Laboratory, Los Alamos, NM 87545, USA
fLaboratoire Collisions Agrégats Réactivité (FeRMI), UMR 5589, Université de Toulouse, F-31062 Toulouse Cedex 09, France
First published on 23rd June 2025
Abstract
Atomistic simulations of photo-induced responses in artificial light-harvesting molecular systems help to reveal the mechanisms of ultrafast intramolecular energy transfer between individual chromophores. These light-induced processes mimic the primary events occurring in natural photosynthesis. Modeling studies contribute to the design of more efficient molecular architectures enabling performance optimization for applications in light harvesting, energy conversion, and optoelectronics. Within this context, the direct comparison between simulated and experimental transient absorption pump–probe (TA-PP) spectra are especially valuable for validating theoretical approaches and deepening mechanistic understanding. Herein, we investigate the photoinduced dynamics of an antenna system composed of two naphthalene monoimides donor units covalently linked to a perylene derived acceptor. Following photoexcitation, the exciton rapidly self-traps on one of the donor units. Thereafter, efficient ultrafast energy transfer to the acceptor unit takes place via two possible pathways: either through transient exciton localization on the second donor unit or by direct transfer to the acceptor. The simulated TA-PP spectra clearly capture these distinct energy transfer pathways and enable a detailed comparison of their relative efficiencies. This highlights the system's potential for tunable exciton dynamics towards advancing light-harvesting and optoelectronic molecular materials.
1 Introduction
Efficient artificial light-harvesting antenna systems are essential for solar energy conversion by enabling the capture of a significant portion of incident light.1,2 Their design is often inspired by natural photosynthesis, where energy is absorbed, transferred to the reaction center, and used for charge separation in a highly efficient sequence.3–6 These artificial systems are typically composed of carefully arranged chromophores with distinct chemical structures and complementary optical absorption profiles, allowing for optimal utilization of solar light spectrum.7,8For robust performance, a light-harvesting antenna must not only efficiently capture energy, but also ensure smooth energy transfer among its chromophores, directing it toward the reactive site for downstream processes.9,10 To achieve this, the electronic properties of the chromophores must be precisely matched, minimizing competing photoinduced processes that could reduce efficiency. By emulating nature's strategies, researchers aim to enhance energy collection and conversion for advanced solar-powered applications.11
The synthetic realization of new artificial multi-chromophoric antenna enables detailed investigations into the efficiency of processes affecting light-harvesting performance.12–16 The rates of these excitation energy transfer processes can vary widely, spanning a range from several nanoseconds to tens of femtoseconds. The presence of multiple energy transfer pathways with varying efficiencies, along with competing energy dissipation mechanisms, such as solvent relaxation, determines the overall performance of artificial light harvesters as potential components for solar cells.6
Over the past decade, atomistic on-the-fly non-adiabatic excited-state molecular dynamics has emerged as a robust method for exploring the photophysics of realistic molecular and material systems.17–31 Photoinduced dynamics in multichromophore systems involve the interplay of multiple coupled excited states, undergoing nonadiabatic transitions and vibrational relaxation. These processes unfold through distinct energy transfer pathways with varying degrees of efficiency, leading to transient exciton re-localization among different chromophores as the system evolves through its excited-state landscape. Whitin this context, the NEXMD software package31 has been developed for simulating large conjugated molecules featuring multiple coupled electronic excited states. This code has been previously employed to explore the relative efficiencies of energy transfer pathways in various light harvesting antenna systems.32–37
Transient-absorption pump–probe (TA-PP) spectroscopy allows for precise monitoring of ultrafast photoinduced non-adiabatic dynamics in complex molecular systems.38–43 These experimental advancements can be effectively complemented by emerging modeling approaches that employ direct nonadiabatic molecular dynamics simulations.44,45 One practical approach combines the classical approximation to the doorway-window (DW) representation introduced by Mukamel and coworkers,46–48 with the on-the-fly trajectory-based simulations. This methodology has been successfully applied to the simulations of TA-PP signals of pyrazine,44 phenylene ethynylene dendrimers building blocks,49 azomethane,50 a tetra-branched perylene-core dendrimer,51 and extended to the simulation of electronic two dimensional spectroscopic signals.52,53 The TA-PP signal is computed as the product of the doorway operator (evaluated at the initial time, t = 0) and the window operator (defined at the time delay t between the pump and probe pulses), averaged over an ensemble of quantum-classical nonadiabatic trajectories. These simulations are commonly performed using trajectory surface hopping (TSH) algorithms.54,55
In the present work, the photoinduced dynamics of a prototypical antenna system, composed of two naphthalene monoimides donors linked to a perylene derived acceptor (D2A2), see Fig. 1(a) is explored using nonadiabatic molecular dynamics simulations.31 Both dynamical observables and TA-PP signals are evaluated. D2A2 belongs to the family of perylene-3,4,9,10-tetracarboxylic acid (PTCA) derivatives, that have been utilized for the construction of artificial light-harvesting antennas owing their exceptional photo(chemical) stability, strong UV-Vis absorption, high electron affinities, and structural versatility that allows for precise molecular tuning.5,16,56 Previous reports have shown that PTCA and naphthalene monoimide (NMI) derivatives act as an ideal chromophore pair owing to their complementary electronic properties and a combined spectral coverage up to 600 nm.13,14,57 Light-harvesting antenna molecules consisting of NMI moieties attached to the 1- and 7-bay positions of PTCA derivatives exhibit a quantitative and ultrafast (∼1 ps) electronic energy transfer.13 The energy donors have been linked at the 1,7-bay-positions of the perylene derivatives, thus leaving the peri positions free for further functionalization and device construction. A highly stable and rigid structure, with no electronic communication between the donor and acceptor components, has been realized via an all-aromatic non-conjugated phenoxy spacer between the constituent chromophores. According to femtosecond TA-PP experiments performed by W. F. Jager and coworkers,13 an ultrafast intramolecular energy transfer from donor naphthalene chromophores to the acceptor perylene is observed, without evidences of electron transfer. These observations of fast and efficient energy transfer alongside with broad visible-light absorption, made these antenna systems promising candidates for solar-to-electric and solar-to-fuel conversion technologies, where effective light harvesting and rapid exciton dynamics are critical for performance.
2 Results and discussion
The photoinduced dynamics of the D2A2 antenna has been studied at the atomistic level using nonadiabatic excited-state molecular dynamics simulations. D2A2 is a relatively floppy molecular system exhibiting free rotations at room temperature around the dihedral angles that connect its constituent chromophores. This conformational flexibility is evident from the superposition of D2A2 structures sampled during ground state molecular dynamics simulations under ambient conditions, shown in Fig. 1(b) (see section Methods for details). The average values of dihedral angles connecting each donor and acceptor units are 55 ± 21° and 78 ± 42° for dihedral angles connecting the donor(blue) and donor (orange) with the acceptor (see Fig. 1(a)), revealing differences in the flexibility of both connections that were also observed during excited state simulations. We expect that the exciton localization and delocalization patterns during excited-state dynamics would be likely influenced by this conformational diversity. Fig. 1(c) shows the simulated absorption spectra based on the conformers in Fig. 1(b), with delineated contributions from various excited states. A good agreement with the experimental absorption spectra has been achieved,13 showing a low energy band at approximately 2.4 eV (∼520 nm) corresponding to the S1 state, along with a more intense larger peak centered around 2.9 eV (∼420 nm). The vertical excitation energies of the five lowest electronic states obtained at the ground state optimal geometry, are listed in Table 1, together with their respective transition dipole moments μx,y,z,tot. These dipole components are defined with respect to a body-fixed reference frame, where the x and y axes lie in the plane of the pyrene moiety, as illustrated in ESI Fig. S1.†| VEE (eV) | μ (a.u.) | |||||
|---|---|---|---|---|---|---|
| x | y | z | tot | X | ||
| S1 | 2.41 | 1.42 | 3.45 | −0.23 | 3.74 | A |
| S2 | 2.93 | 3.02 | 1.26 | −1.47 | 3.59 | Da |
| S3 | 2.94 | −0.33 | −0.08 | 0.20 | 0.49 | Db |
| S4 | 3.06 | 0.03 | 0.00 | 0.07 | 0.08 | |
| S5 | 3.09 | −0.46 | 0.18 | −0.04 | 0.50 | |
The insets in Fig. 1(c) display the spatial distributions of electronic transition densities for the S2 and S1 states, computed in the ground-state optimal geometry. The corresponding orbital plots for the S3–5 states are provided in ESI Fig. S1.† S1 is contained to the perylene acceptor. In contrast, while S2 and S3 states are localized in the naphthalene monoimide donors, S4 and S5 states are localized in the perylene-derived acceptor. In fact, the S2 and S3 states are nearly degenerate at the ground state optimal geometry, with their small energy splitting reflecting weak electronic coupling between the terminal naphthalene monoimides. However, this degeneracy is lifted by thermal fluctuations under ambient conditions (see Fig. 1(c)), leading to localization of the S2 and S3 wavefunctions on individual units. Not surprisingly, the D2A2 absorption spectra closely resemble the sum of the spectra of its constituent chromophores.13 The high structural flexibility triggered by thermal fluctuations (Fig. 1(b)), combined with weak electronic coupling between the chromophores, substantiates exciton localization on individual units. ESI Fig. S2† summarizes the fraction of transition density across the donor and acceptor units for the S1–5 electronic states, based on molecular geometries shown in Fig. 1(b). All excited states are localized on individual chromophore units. While S1 is primarily localized on the acceptor, S2 and S3 are localized on a single donor unit. However, S4 and S5 exhibit fluctuating localization between the donor and acceptor, driven by thermal fluctuations that can alter their energy ordering. Photoexcitation to different excited states leads to exciton localization on one of the chromophore units. Since the initial experimental pump pulse mainly populates the S2 and S3 states, the primary pathway for exciton redistribution during internal conversion involves energy transfer from donor to acceptor units. Moreover, our analysis of the natural transition orbitals for various excited states, as shown in ESI Fig. S3,† confirms that all excited states of interest exhibit Frenkel-exciton character, with no indication of charge transfer processes. This observation is consistent with previous experimental results indicating that ultrafast energy transfer occurs from the donor excited state to the acceptor, while charge transfer processes remain minimal, even over longer time scales.13,14
Fig. 2 presents a concise overview of the photoexcited state population dynamics in D2A2, providing a mechanistic view on energy migration between different excited states. Panel (a) depicts the evolution of electronic state populations for low-lying excited S1–S5 states. We assume that the pump pulse, centered at Epu = 2.90 eV, primarily excites the S2 and S3 states. As shown in Fig. 2(a), an ultrafast S3 → S2 energy transfer takes place within the first ∼100 fs, followed by a slower S2 → S1 relaxation process. The population of S1 state experiences an ultrafast rise that follows a single exponential rise profile 1 − exp(t/τ), with a time constant τ = 0.5 ps. This is somewhat faster than the experimentally reported value of 1.16 ps.13 A deeper insight into the internal conversion process can be obtained by monitoring changes in the spatial localization of the transition density across the different chromophore units. This is illustrated in Fig. 2(b), which depicts the time evolution of the average fraction of the transition density, δαX(t), across different chromophores. To perform this analysis, donor units were identified based on their initial excitation levels following photoexcitation. Specifically, the monomer exhibiting the higher transition density was labeled as Da, while the one with the lower transition density was designated as Db. This distinction reflects the fact that, at the moment of excitation, Da absorbs a larger fraction of the excitation energy and is thus more strongly photoexcited than Db. An ultrafast exchange between donors leads to a subsequent donor-to-acceptor, (Da/b) → (A), population transfer. Importantly, Fig. 2(b) reveals the existence of two distinct energy transfer pathways: a direct pathway from Da → A, and an indirect pathway involving Da → Db → A steps. These alternative energy migration routes between chromophore units can be further characterized and distinguished using the transition density flux analysis58,59 (see ESI† Transition density flux analysis section). This method directly tracks the distinct pathways of energy redistribution among chromophore units following initial photoexcitation. During nonadiabatic simulations, the effective change in transition density, δαX(t) (see eqn (1)), is monitored by the flow matrix f(t). This matrix has zero-valued diagonal elements, while the off-diagonal elements, fXY(t), represent the amount of δαX(t) transferred between units X and Y.59Fig. 3 shows the time evolution of the transition density accumulated fluxes fXY(t). We observe that the direct Da → A pathway, described by fDaA(t), accounts for approximately 60% of the intramolecular energy transfer, while the indirect Da → Db → A pathway, described by the combined fluxes fDaDb(t) and fDbA(t), contributes to the remaining ∼40%. This quantitative breakdown reflects the presence of competing energy transfer routes and the relative importance of sequential exciton migration in the overall photoinduced dynamics. The exciton exchange between donors (i.e. fDaDb(t)) takes place at the early times after photoexcitation, i.e., within the first ∼100 fs, that corresponds to the ultrafast S3 → S2 energy transfer. Furthermore, nonadiabatic excited-state trajectories can be classified based on the specific energy transfer pathways they follow during our simulations. To accomplish this, trajectories in which the exciton becomes transiently localized on the Db unit at any point during the excited-state dynamics—specifically, those where δαDb(t) > 0.5 at any moment—are associated with the indirect Da → Db → A pathway. In contrast, trajectories where δαDb(t) remains below 0.5 throughout the entire simulation time, indicating that only one donor (Da) participates in the transfer process, are associated with the direct Da → A pathway. The corresponding evolution of the average populations of electronic states and fraction of the transition density δαX(t) are displayed in ESI Fig. S4 and S5.† The two pathways exhibit two different time scales of donor → acceptor energy migration. The direct Da → A energy transfer pathway leads to an ultrafast population of the S1 state, characterized by a rapid rise following the function A − B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(t/τ) with a time-constant τ = 0.2 ps. In contrast, the indirect Da → Db → A pathway involves a slower step-wise transfer with a characteristic rise time of approximately τ = 0.8 ps, reflecting the additional intermediate exciton relocalization step prior to reaching the acceptor.
exp(t/τ) with a time-constant τ = 0.2 ps. In contrast, the indirect Da → Db → A pathway involves a slower step-wise transfer with a characteristic rise time of approximately τ = 0.8 ps, reflecting the additional intermediate exciton relocalization step prior to reaching the acceptor.
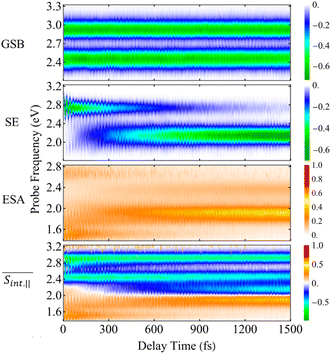
Further analyses of the ultrafast photoinduced non-adiabatic dynamics after photoexcitation of the D2A2 antenna are directly related to time-resolved spectroscopic measurements. Fig. 4 and 5 showcase the net TA-PP signals simulated using the on-the-fly DW approach (see Methods). The results are shown for both parallel (spu = spr) and perpendicular (spu⊥spr) linear polarizations of the pump and probe pulses, respectively.
 | ||
Fig. 5 Same as Fig. 4 but for the  TA-PP signal obtained for the pump and probe pulses with orthogonal polarizations, spu⊥spr. TA-PP signal obtained for the pump and probe pulses with orthogonal polarizations, spu⊥spr. | ||
Fig. 4 and 5 summarize the individual contributions of the ground-state bleaching (GSB), stimulated emission (SE), excited-state absorption (ESA), as well as the total TA-PP signal. To analyze these spectra, we delineate relevant electronic states into 3 distinct manifolds: manifold {0} includes ground state only (S0), manifold {I} comprises low-lying S1–S5 excited states interrogated by the optical pump, and finally manifold {II} encompasses higher-lying S6–S200 excited states, which are involved in the optical probe excitations. In the frequency domain, the signals extend across a broad energy range, reflecting multiple electronic transitions. These include transitions between the ground state and the low-lying excited state of manifold {I}, as well as transition between the states within manifold {I} and higher-lying excited states of manifold {II}. In the time domain, GSB exhibits underdamped oscillations, while SE and ESA signals display slightly damped oscillations, reflecting the wavepacket motion within manifolds {0} and {I}, respectively. Due to the large number of nuclear degrees of freedom involved—most of which are anharmonic—the oscillations observed in the signal lack a clearly defined period. Nevertheless, the separation between the first two SE maxima is around 20 fs. These oscillations are most likely associated with double bond stretching vibrations. According to the distribution of the average fraction of the transition density matrix (δαX(t)) displayed in Fig. 2, excited states S2 and S3 are mainly localized in the naphthalene monoimides donor units. Therefore, oscillations initially present in the SE and ESA signals can be associated with the double CC bonds in the naphthalene monoimides donor units. ESI Fig. S7(a)† shows the nonadiabatic coupling vector (NACR32) associated to S3 → S2 energy transfer. NACR32 represents the direction of the force acting on the nuclei during the S3 → S2 transition. We can observe its delocalization between both naphthalene monoimides donor units. The projection of NACR32 on the D2A2 normal modes (ESI Fig. S7(b)†) reveals main overlaps with normal modes with periods around 20 fs, in agreement with oscillations initially observed in the SE and ESA signals. Normal modes with the highest overlap are also shown. The analysis of the nonadiabatic coupling vector (NACR21) associated to S2 → S1 energy transfer is shown in ESI Fig. S8(a).† NACR21 is delocalized between one of the naphthalene monoimides donor units and the acceptor, as it is expected by the distribution of the average fraction of the transition density matrix (δαX(t)) displayed in Fig. 2, where S2 is mainly localized in one of the naphthalene monoimides donor unit while S1 is localized in the acceptor. As in the case of NACR32, the projection of NACR21 on the D2A2 normal modes (ESI Fig. S8(b)†) reveals main overlaps with normal modes with periods around 20 fs. Nevertheless, the main normal modes involved in these transitions present different spatial localization, being mostly localized in the acceptor. Similar spectral features have been previously reported in a light harvesting dendrimer analyzed using broadband, high-resolution TA-PP spectroscopy.49,51,60
The GSB signal describes the motion of the “hole” punched by the pump pulse in the electronic ground state. This hole in the nuclear phase space is described by the doorway function D_in of eqn (2). It creates non-stationary nuclear distribution in the electronic ground state. This nonstationary distribution, in turn, produces moving vibrational wavepackets in the electronic ground state which are monitored by the GSB signal. The GSB signal probes transitions from manifold {0} (S0) to manifold {I} states. In the case of the averaged parallel polarization signal,  (Fig. 4), the spectrum exhibits two contributions of comparable intensity centered around Epr ≈ 2.9 eV, and ≈2.4 eV. These features correspond to electronic transitions from S0 to S1 and S2/3, respectively. In contrast, for the averaged parallel polarization signal,
(Fig. 4), the spectrum exhibits two contributions of comparable intensity centered around Epr ≈ 2.9 eV, and ≈2.4 eV. These features correspond to electronic transitions from S0 to S1 and S2/3, respectively. In contrast, for the averaged parallel polarization signal,  , the GSB signal at ≈2.4 eV is stronger than the one at ≈2.9 eV (Fig. 5). This difference arises from the distinct orientations of the transition dipole moments, μ01vs. μ02/3 (see Table 1 and ESI Fig. S1†), demonstrating that polarization schemes in the detection of TA-PP spectra of dendrimers can be tuned to be sensitive to specific transitions. On the other hand, the underdamped oscillations observed the GSB signals expose the wavepacket motion within the electronic ground state. As noted in previous studies,49,51 these oscillations are a hallmark of significant non-Condon effects, which result from the strong dependence of transition dipole moments between manifolds {0} and {I} on the nuclear configurations.
, the GSB signal at ≈2.4 eV is stronger than the one at ≈2.9 eV (Fig. 5). This difference arises from the distinct orientations of the transition dipole moments, μ01vs. μ02/3 (see Table 1 and ESI Fig. S1†), demonstrating that polarization schemes in the detection of TA-PP spectra of dendrimers can be tuned to be sensitive to specific transitions. On the other hand, the underdamped oscillations observed the GSB signals expose the wavepacket motion within the electronic ground state. As noted in previous studies,49,51 these oscillations are a hallmark of significant non-Condon effects, which result from the strong dependence of transition dipole moments between manifolds {0} and {I} on the nuclear configurations.
The SE signal captures the projection of the nuclear wavepacket motion in manifold {I} onto the ground state, offering deeper insight into nonadiabatic transitions beyond the population dynamics depicted in Fig. 2(a). The ultrafast S3 → S2 internal conversion is evident as a redshift in the SE signal in the frequency domain. Initially centered around Epr ≈ 2.9 eV, the SE spectrum shifts toward lower energies within 50 fs of photoexcitation. Subsequently, the S2 → S1 transition depletes the population of the S2 state, which is centered at Epr ≈ 2.8 eV, further shifting the signal to Epr ≈ 2.2 eV, thereby revealing the emergence of the S1 state. After approximately 400 fs, half of the excited state population has transferred to the S1 state, as indicated by the crossing of the intensities of the SE signal for Epr ≈ 2.8 eV and 2.2 eV.
As previously noted, intramolecular donors-to-acceptor energy transfer occurs during the photoinduced dynamics within manifold {I} (see Fig. 3). This process is also reflected in the SE signal, which clearly captures the inter-state population-transfer timescales. Interestingly, the initial SE intensity at Epr ≈ 2.8 eV of the  signal (Fig. 4) is higher than that of the
signal (Fig. 4) is higher than that of the  signal (Fig. 5). However, this trend reverses for Epr ≈ 2.2 eV at longer times. Despite this, the SE contribution at Epr ≈ 2.8 eV persists somewhat longer in the
signal (Fig. 5). However, this trend reverses for Epr ≈ 2.2 eV at longer times. Despite this, the SE contribution at Epr ≈ 2.8 eV persists somewhat longer in the  signal compared to the
signal compared to the 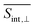 signal. This behavior arises from the orthogonal orientations of μ02 and μ03 relative to μ01, and can be used for enhancing or suppressing specific contributions to the TA-PP signal.
signal. This behavior arises from the orthogonal orientations of μ02 and μ03 relative to μ01, and can be used for enhancing or suppressing specific contributions to the TA-PP signal.
The manifold {II} comprises 195 high-lying excited states that frequently intersect during dynamical simulations, making it challenging to track specific dominant states. However, we can estimate and analyze key transition energies, as the ESA maxima in the energy domain correspond to the energy gaps between states in manifolds {II} and {I}. For instance, the ESA contribution at Epr ≈ 1.8 eV primarily originates from the S1 state, and its intensity increases as the S1 population grows. As expected, this effect is more pronounced in 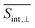 than in
than in  . Importantly, the simulated signals align well with the experimentally observed broad ESA band spanning 620–900 nm,13 further reinforcing the accuracy of our theoretical predictions. In principle, both the SE and ESA signals contain information about the photoinduced nuclear wavepacket dynamics in manifold {I}, but they do so through different “spectacle” states onto which this wavepacket motion is promoted: SE projects the wavepacket motion onto the electronic ground state, whereas ESA projects it onto the high-lying states of manifold {II}. Hence, the ESA signal at Epr ≈ 2.4 eV and the SE signal at Epr ≈ 2.2 eV appear qualitatively similar, as both are shaped by the same wavepacket dynamics. On the other hand, the ESA signal at Epr ≈ 1.8 eV and the SE signal at Epr ≈ 2.8 eV show qualitatively different behavior, due to the fact that manifold {II} contains many states which are optically allowed from manifold {I}. Fortunately, the rise of intensity of the Epr ≈ 1.8 eV ESA signal and the loss of intensity of the Epr ≈ 2.8 eV SE signal, are both driven by the same underlying process: the internal conversion from S2 to S1. These observations illustrate how different spectroscopic features can be interconnected and used to infer the same underlying excited-state dynamics through complementary perspectives.
. Importantly, the simulated signals align well with the experimentally observed broad ESA band spanning 620–900 nm,13 further reinforcing the accuracy of our theoretical predictions. In principle, both the SE and ESA signals contain information about the photoinduced nuclear wavepacket dynamics in manifold {I}, but they do so through different “spectacle” states onto which this wavepacket motion is promoted: SE projects the wavepacket motion onto the electronic ground state, whereas ESA projects it onto the high-lying states of manifold {II}. Hence, the ESA signal at Epr ≈ 2.4 eV and the SE signal at Epr ≈ 2.2 eV appear qualitatively similar, as both are shaped by the same wavepacket dynamics. On the other hand, the ESA signal at Epr ≈ 1.8 eV and the SE signal at Epr ≈ 2.8 eV show qualitatively different behavior, due to the fact that manifold {II} contains many states which are optically allowed from manifold {I}. Fortunately, the rise of intensity of the Epr ≈ 1.8 eV ESA signal and the loss of intensity of the Epr ≈ 2.8 eV SE signal, are both driven by the same underlying process: the internal conversion from S2 to S1. These observations illustrate how different spectroscopic features can be interconnected and used to infer the same underlying excited-state dynamics through complementary perspectives.
In the frequency domain, the total signals are dominated by ESA at lower Epr and by the GSB + SE at higher Epr. At short times (<300 fs), the S2 contribution is more intense in 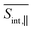 (Fig. 4) compared to that in
(Fig. 4) compared to that in  (Fig. 5). At longer times, the S1 state signatures become more pronounced in
(Fig. 5). At longer times, the S1 state signatures become more pronounced in  . As explained above, this effect is attributed to the transition dipole moment reorientations in the S1 state. Importantly, while the S3 → S2 and S2 → S1 transitions are clearly visible in the SE signal, they become obscured in the total TA-PP signal due to the dominant GSB contribution masking the weaker SE features. However, as discussed above, information about the S2 → S1 internal conversion can be readily extracted from the ESA signal centered around Epr ≈ 1.8 eV, which is well separated spectrally in the total TA-PP spectrum. This spectral separation allows for selective monitoring of excited-state population dynamics, indicating the value of ESA as a sensitive probe of nonadiabatic transitions when GSB and SE signals overlap spectrally.
. As explained above, this effect is attributed to the transition dipole moment reorientations in the S1 state. Importantly, while the S3 → S2 and S2 → S1 transitions are clearly visible in the SE signal, they become obscured in the total TA-PP signal due to the dominant GSB contribution masking the weaker SE features. However, as discussed above, information about the S2 → S1 internal conversion can be readily extracted from the ESA signal centered around Epr ≈ 1.8 eV, which is well separated spectrally in the total TA-PP spectrum. This spectral separation allows for selective monitoring of excited-state population dynamics, indicating the value of ESA as a sensitive probe of nonadiabatic transitions when GSB and SE signals overlap spectrally.
To compare our simulations with the experimental TA-PP spectra reported in ref. 13 and Fig. 6(a) shows the total TA-PP spectrum,  , evaluated at the magic angle between pump- and probe-pulse polarizations. This orientation averages out anisotropic contributions and provides a spectrum that is qualitatively similar to both
, evaluated at the magic angle between pump- and probe-pulse polarizations. This orientation averages out anisotropic contributions and provides a spectrum that is qualitatively similar to both  and
and  . For deeper analysis, we focus on spectral cuts presented in Fig. 6(b). The experimental TA-PP spectra from ref. 13 exhibit negative bands in the range of approximately 460–620 nm (∼2.0–2.7 eV). ESI Fig. S5† displays individual contributions from GSB, SE, and ESA. The band around 510 nm is attributed to GSB, while the one around 580 nm corresponds to SE. Wavelengths longer than 620 nm are predominantly assigned to ESA signals. Our simulations (Fig. 6(b)) successfully reproduce the overall shape and key features of the experimental spectra (Fig. 6(c)). However, some differences are apparent, with the most significant discrepancy being the signal intensity at wavelengths longer than 700 nm, where the simulated ESA signal deviates more substantially from the experiment. This indicates that while the simulated GSB and SE components show strong agreement with experiment, the ESA signals show stronger deviations being more sensitive to the lower accuracy of calculated higher-lying excited states, besides the missing of double excitations in the current method. This direct comparison with experiments, shown in Fig. 6(b and c), evidence the faster relaxation observed in our simulations (∼0.5 ps) with respect to experiments (1.16 ps), previously discussed in the fitting of the population rise of S1 state to a single exponential shown in Fig. 2. This indicates that while the simulated GSB and SE components show strong agreement with experiment, the ESA signals show stronger deviations being more sensitive to the lower accuracy of calculated higher-lying excited states. Additionally, the present methodology does not address electronic excitations that have correlated nature such as double excitations. This direct comparison with experiments, shown in Fig. 6(b and c), evidence the faster relaxation observed in our simulations (∼0.5 ps) with respect to experiments (1.16 ps), previously discussed in the fitting of the population rise of S1 state to a single exponential shown in Fig. 2. We note that calculated non-radiative decay rate is extremely sensitive to the values of gaps between states61 so that this disagreement is expected.
. For deeper analysis, we focus on spectral cuts presented in Fig. 6(b). The experimental TA-PP spectra from ref. 13 exhibit negative bands in the range of approximately 460–620 nm (∼2.0–2.7 eV). ESI Fig. S5† displays individual contributions from GSB, SE, and ESA. The band around 510 nm is attributed to GSB, while the one around 580 nm corresponds to SE. Wavelengths longer than 620 nm are predominantly assigned to ESA signals. Our simulations (Fig. 6(b)) successfully reproduce the overall shape and key features of the experimental spectra (Fig. 6(c)). However, some differences are apparent, with the most significant discrepancy being the signal intensity at wavelengths longer than 700 nm, where the simulated ESA signal deviates more substantially from the experiment. This indicates that while the simulated GSB and SE components show strong agreement with experiment, the ESA signals show stronger deviations being more sensitive to the lower accuracy of calculated higher-lying excited states, besides the missing of double excitations in the current method. This direct comparison with experiments, shown in Fig. 6(b and c), evidence the faster relaxation observed in our simulations (∼0.5 ps) with respect to experiments (1.16 ps), previously discussed in the fitting of the population rise of S1 state to a single exponential shown in Fig. 2. This indicates that while the simulated GSB and SE components show strong agreement with experiment, the ESA signals show stronger deviations being more sensitive to the lower accuracy of calculated higher-lying excited states. Additionally, the present methodology does not address electronic excitations that have correlated nature such as double excitations. This direct comparison with experiments, shown in Fig. 6(b and c), evidence the faster relaxation observed in our simulations (∼0.5 ps) with respect to experiments (1.16 ps), previously discussed in the fitting of the population rise of S1 state to a single exponential shown in Fig. 2. We note that calculated non-radiative decay rate is extremely sensitive to the values of gaps between states61 so that this disagreement is expected.
 | ||
Fig. 6 (a) The total TA-PP spectrum  evaluated at the magic angle (54.7°) between polarizations of the pump and probe pulses evaluated at the magic angle (54.7°) between polarizations of the pump and probe pulses  , (b) simulated and (c) experimental13 spectral cuts at selected delay times t indicated in panel (b). , (b) simulated and (c) experimental13 spectral cuts at selected delay times t indicated in panel (b). | ||
At this point it is interesting to mention that our non-adiabatic molecular dynamics simulations address non-radiative decay between S3/S2 and S1 excited states. These states are separated by about 0.5 eV gap in the ground state conformations (see absorption spectrum in Fig. 1(c)). As a result, we do not see frequent direct crossing between PES between these states. Subsequently, the calculated no-radiative decay rate is still ultrafast, about 0.5 ps (Fig. 2), as reflected in TA-PP spectra (Fig. 4 and 5) in agreement with experiment (Fig. 6(c)) and in line with typical internal conversion rates in molecules.
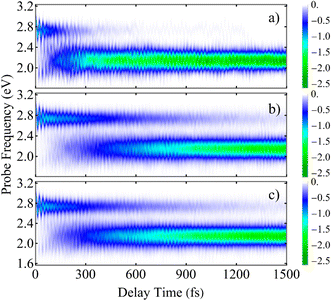
A deeper understanding of the microscopic origin of the TA-PP signal can be gained by analyzing the individual contributions from the direct Da → A and indirect Da → Db → A energy transfer pathways. Fig. 7 and ESI S6† show the SE spectra evaluated using trajectories corresponding to each of these distinct pathways. The direct Da → A pathway leads to a considerably faster decrease of the SE signal at Epr ≈ 2.8 eV during the first ∼100 fs, followed by an increase of the signal at Epr ≈ 2.2 eV (Fig. 6(a)). In contrast, the SE signal produced by the trajectories following the indirect Da → Db → A pathway experience this spectral shift at longer times, beyond 300 fs (Fig. 6(b)). This delay manifests the additional step of exciton relocalization on the second donor unit before reaching the acceptor. The total SE signal (Fig. 6(c)) is a superposition of these two distinct relaxation mechanisms. Furthermore, ESI Fig. S6† shows that the SE signals produced by the two pathways have markedly different spectral shapes at various delay times. These differences reflect the moving nonadiabatic nuclear wavepacket within manifold {I} across different potential energy surfaces associated with excited states. This analysis illustrates the pathway-dependent nature of the excited-state dynamics and emphasizes the importance of nonadiabatic nuclear wavepacket motion in shaping the time-resolved spectroscopic response.
3 Conclusions
This study presents a computational investigation of photoinduced donor-to-acceptor energy transfer in the D2A2 antenna system, which is composed of two naphthalene monoimide donors linked to a perylene-derived acceptor, using atomistic nonadiabatic excited-state molecular dynamics simulations. The system's high structural flexibility, driven by thermal fluctuations, combined with the weak electronic coupling between chromophores, results in transient exciton localization on individual chromophore units. Consequently, photoexcitation to different excited states leads to exciton confinement on a specific chromophore, establishing localized initial conditions for subsequent energy transfer dynamics.Our analysis identifies two distinct energy transfer pathways that define internal conversion in the D2A2 system. The first is a faster and more efficient direct Da → A pathway, where the exciton initially localizes on donor Da and subsequently transfers directly to the acceptor. The second is a slower indirect Da → Db → A pathway, which involves transient exciton localization on the secondary donor unit Db before ultimately reaching the acceptor. These pathways operate at different relaxation rates, and their relative contributions significantly affect the shape and evolution of the simulated TA-PP spectra. Information about the dynamics and efficiencies of each pathway can be extracted from the spectral features, offering powerful means to decode exciton migration mechanisms from time-resolved spectroscopic measurements.
Overall, our simulations demonstrate a fast and efficient donor-to-acceptor energy transfer in the D2A2 antenna, underscoring its potential for emerging solar energy conversion technologies. The ability of these systems to rapidly and effectively funnel excitation energy toward the acceptor site minimizes energy losses and maximizes light-harvesting efficiency, showing promises for solar-to-electric and solar-to-fuel applications. The presence of well-defined energy transfer pathways and ultrafast internal conversion dynamics suggests that such architectures could be integrated into artificial photosynthetic systems or photovoltaic devices, enhancing light absorption, charge separation, and energy conversion. Furthermore, the tunability of their structural and electronic properties opens avenues for optimizing their performance under different environmental conditions.
We would like to conclude with a remark on the accuracy and reliability of the on-the-fly simulation methodologies. Nowadays, there is a surging interest in benchmarking trajectory-based nonadiabatic molecular dynamics simulation protocols against their fully quantum-mechanical analogs using carefully selected model systems.62 In this broader context, the comparison between experimental and simulated spectroscopic signals offers an additional, highly valuable opportunity for validation of theoretical approaches. In the present work, our simulation methodology has shown good agreement with experimental observations, particularly in reproducing key features of the TA-PP spectra. This outcome suggests the robustness and predictive power of our NEXMD techniques and supports the application of this code to realistic, complex photoactive systems. We show that atomistic on-the-fly non-adiabatic excited-state molecular dynamics provides a powerful and complementary to experiment approach for investigating multichromophoric and even supramolecular conjugated systems and polymers of relatively large size. This method enables a deeper understanding of excited-state behavior and can effectively disentangle distinct energy transfer pathways, such as long-range versus short-range transfer, thus providing valuable insights into the fundamental mechanisms governing these complex systems.
4 Methods
The photoinduced excited-state molecular dynamics in the D2A2 antenna system, depicted in Fig. 1(a), has been simulated using Non-adiabatic EXcited state Molecular Dynamics (NEXMD) software.29,31 This code is designed for on-the-fly simulations of non-adiabatic photoexcited dynamics in multichromophoric molecular systems, enabling the treatment of multiple coupled electronic states via a range of hybrid quantum-classical approaches. In this study, we employ Tully's Fewest Switches Surface Hopping (FSSH) algorithm.63 As implemented in NEXMD, the excited-state energies, energy gradients and non-adiabatic coupling terms are computed using configuration interaction singles (CIS) approach and the semiempirical Austin Model 1 (AM1) Hamiltonian model.64 NEXMD has been successfully applied in previous studies to simulate light-induced dynamics in various light-harvesting antenna systems, proving its utility in modeling photoexcited energy relaxation, exciton dynamics, and energy transfer mechanisms in complex molecules.34,36,51,65–68Within the NEXMD framework, spatial exciton localization is evaluated using the fraction of the transition density ρ0α, which represents the contribution of the ground-to-excited state α transition density that is localized on each chromophore. It is formally expressed as:
 | (1) |
Our excited-state simulations are performed using initial conditions sampled from a 1 ns equilibrated ground-state molecular dynamics simulation of the dendrimer at room temperature (T = 300 K), using a Langevin thermostat with a friction coefficient of γ = 20.0 ps−1. The subsequent nonadiabatic excited-state dynamical simulations are carried out under constant energy (microcanonical) conditions, during which 500 individual excited-state trajectories are propagated. For each trajectory, the initially (subscript “in”) populated excited state α is selected based on a positively defined doorway function,45
 | (2) |
 | (3) |
 and Epu represent the spectral profile and the carrier frequency of the pump pulse, respectively, and E0α is the energy of the αth state with respect to the ground state. A total of 200 excited states are included to simulate TA-PP signals, capturing a broad range of electronic transitions. The pump pulse is centered at the absorption spectrum maximum, Epu = 427 nm (2.9 eV), see Fig. 1(c). In the time domain, its time profile follows a Gaussian envelope,
and Epu represent the spectral profile and the carrier frequency of the pump pulse, respectively, and E0α is the energy of the αth state with respect to the ground state. A total of 200 excited states are included to simulate TA-PP signals, capturing a broad range of electronic transitions. The pump pulse is centered at the absorption spectrum maximum, Epu = 427 nm (2.9 eV), see Fig. 1(c). In the time domain, its time profile follows a Gaussian envelope, 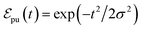 , where σ = 42.5 fs corresponds to a Full Width at Half Maximum (FWHM) of 100 fs. For classical nuclear trajectory propagation, time steps of 0.5 and 0.1 fs are used in the ground state and excited state simulations, respectively. A quantum time step of 0.025 fs is selected to propagate the electronic coefficients in the time-dependent Schrodinger equation. Further technical details on the treatments of decoherence and handling trivial unavoided crossings, as well as the overall theoretical framework, implementation, and testing parameters of the NEXMD package can be found elsewhere.29,31
, where σ = 42.5 fs corresponds to a Full Width at Half Maximum (FWHM) of 100 fs. For classical nuclear trajectory propagation, time steps of 0.5 and 0.1 fs are used in the ground state and excited state simulations, respectively. A quantum time step of 0.025 fs is selected to propagate the electronic coefficients in the time-dependent Schrodinger equation. Further technical details on the treatments of decoherence and handling trivial unavoided crossings, as well as the overall theoretical framework, implementation, and testing parameters of the NEXMD package can be found elsewhere.29,31
The details of the TA-PP simulation have been previously described in ref. 51. Here, we provide a brief summary of this approach. Our simulations follow the DW simulation protocol,44,45 which assumes that the integral TA-PP can be evaluated using (semi)classical trajectories. This methodology also incorporates orientational averaging and polarization-sensitive detection of TA-PP signals.49,51 Thus, we evaluate the partial TA-PP signals S(abcd)int(t,Epr), where a, b, c, d = x, y, z specify the corresponding components of the transition dipole moments interacting with the pump (a, b) and probe (c, d) pulses in an arbitrary reference frame. Epr denotes the probe pulse carrier frequency.
According to the DW simulation protocol, the partial TA-PP signals are computed as
 | (4) |
 | (5) |
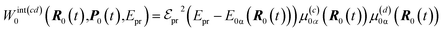 | (6) |
 | (7) |
 | (8) |
 is the spectrum of the probe pulse.
is the spectrum of the probe pulse.
To maintain consistency with the initial 0 → α excitations (eqn (2)), α → β excitations for the ESA contribution are selected similarly. At each time step, a β state is chosen with a weight proportional to  .
.
After computing the partial S(abcd)int(t,Epr) components, the orientationally-averaged TA-PP signal can be evaluated as
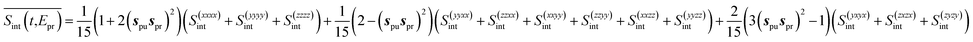 | (9) |
 . The corresponding signals are denoted as
. The corresponding signals are denoted as  ,
,  , and
, and  where the subscript M represent the magic angle. These signals satisfy the relation
where the subscript M represent the magic angle. These signals satisfy the relation  .
.
Data availability
All study data are included in the article and/or ESI.†Author contributions
R. P.-C. performed the non-adiabatic simulations and calculated and analyzed the TA-PP signals. V. M. F. helped in derived, computing and analyzing the TA-PP signals and supervised the project. A. M.-M., and L. U.-P. contributed to write the manuscript. S. T. contributed wrote the manuscript and supervised the project. M. F. G. derived, supervised the calculation and analysis of the TA-PP signals and contributed to write the manuscript. S. F.-A. designed and supervised the project and wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. T. acknowledges support from the U.S. DOE, Office of Science, Office of Basic Energy Sciences under Triad National Security, LLC (“Triad”) contract grant #89233218CNA000001 (FWP: LANLE3T1). This work was performed in part at the Center for Integrated Nanotechnology (CINT) at Los Alamos National Laboratory (LANL), a U.S. DOE and Office of Basic Energy Sciences user facility. This research used resources provided by the LANL Institutional Computing Program. S. F.-A., and R. P.-C. acknowledge the support of CONICET. We would like to thank Prof. Wolter F. Jager for his predisposition to share experimental results. M. F. G. acknowledges support from the National Natural Science Foundation of China (No. 22373028). L. U.-P. acknowledges the support of the Horizon Europe research and innovation programme, under the Marie Skłodowska-Curie grant agreement no. 101155733.Notes and references
- A. Harriman, Artificial Light-harvesting Arrays for Solar Energy Conversion, Chem. Commun., 2015, 51, 11745–11756 RSC.
- P. Frischmann, K. Mahata and F. Wurthner, Powering the future of molecular artificial photosynthesis with light-harvesting metallosupramolecular dye assemblies, Chem. Soc. Rev., 2013, 42, 1847–1870 RSC.
- S. Pramanik and S. Mukherjee, Bio-templated energy transfer system for constructing artificial light-harvesting antennae, white light generation, and photonic nanowires, Chem. Phys. Rev., 2023, 4, 031306 CrossRef CAS.
- Y. Kim, J. H. Lee, H. Ha, S. W. Im and K. T. Nam, Material science lesson from the biological photosystem, Nano Convergence, 2016, 3(1), 19 CrossRef PubMed.
- A. M. Philip, C. C. Hsu, Z. Wei, M. B. Fridriksson, F. C. Grozema and W. F. Jager, Directing charge transfer in perylene based light-harvesting antenna molecules, J. Chem. Phys., 2020, 153, 144302 CrossRef CAS PubMed.
- C. S. Ponseca, P. Chábera, J. Uhlig, P. Persson and V. Sundström, Ultrafast Electron Dynamics in Solar Energy Conversion, Chem. Rev., 2017, 117, 10940–11024 CrossRef CAS PubMed.
- H. Imahori, Giant multiporphyrin arrays as artificial light-harvesting antennas, J. Phys. Chem. B, 2004, 108, 6130–6143 CrossRef CAS PubMed.
- P. Porcu, M. Vonlanthen, A. Ruiu, I. González-Méndez and E. Rivera, Energy transfer in dendritic systems having pyrene peripheral groups as donors and different acceptor groups, Polymers, 2018, 10(10), 1062 CrossRef PubMed.
- T. Mirkovic, E. E. Ostroumov, J. M. Anna, R. Van Grondelle, Govindjee and G. D. Scholes, Light absorption and energy transfer in the antenna complexes of photosynthetic organisms, Chem. Rev., 2017, 117, 249–293 CrossRef CAS PubMed.
- R. Ziessel and A. Harriman, Artificial light-harvesting antennae: Electronic energy transfer by way of molecular funnels, Chem. Commun., 2011, 47, 611–631 RSC.
- T. S. Balaban, Tailoring porphyrins and chlorins for self-assembly in biomimetic artificial antenna systems, Acc. Chem. Res., 2005, 38, 612–623 CrossRef CAS PubMed.
- N. Auerhammer, A. Schulz, A. Schmiedel, M. Holzapfel, J. Hoche, M. I. S. Röhr, R. Mitric and C. Lambert, Dynamic exciton localisation in a pyrene-BODIPY-pyrene dye conjugate, Phys. Chem. Chem. Phys., 2019, 21, 9013–9025 RSC.
- R. K. Dubey, D. Inan, S. Sengupta, E. J. R. Sudhölter, F. C. Grozema and W. F. Jager, Tunable and highly efficient light-harvesting antenna systems based on 1,7-perylene-3,4,9,10-tetracarboxylic acid derivatives, Chem. Sci., 2016, 7, 3517 RSC.
- R. K. Dubey, D. Inan, A. M. Philip, F. C. Grozema and W. F. Jager, Efficacious elimination of intramolecular charge transfer in perylene imide based light-harvesting antenna molecules, Chem. Commun., 2020, 56, 5560–5563 RSC.
- S. M. Waly, J. K. G. Karlsson, P. G. Waddell, A. C. Benniston and A. Harriman, Light-Harvesting Crystals Formed from BODIPY-Proline Biohybrid Conjugates: Antenna Effects and Excitonic Coupling, J. Phys. Chem. A, 2022, 126, 1530–1541 CrossRef CAS PubMed.
- R. K. Dubey, N. Westerveld, S. J. Eustace, E. J. R. Sudhölter, F. C. Grozema and W. F. Jager, Synthesis of Perylene-3,4,9,10-tetracarboxylic Acid Derivatives Bearing Four Different Substituents at the Perylene Core, Org. Lett., 2016, 18, 5648–5651 CrossRef CAS PubMed.
- R. Crespo-Otero and M. Barbatti, Recent Advances and Perspectives on Nonadiabatic Mixed Quantum-Classical Dynamics, Chem. Rev., 2018, 118, 7026–7068 CrossRef CAS PubMed.
- B. F. E. Curchod and T. J. Martínez, Ab Initio Nonadiabatic Quantum Molecular Dynamics, Chem. Rev., 2018, 118, 3305–3336 CrossRef CAS.
- M. Barbatti, M. Ruckenbauer, F. Plasser, J. Pittner, G. Granucci, M. Persico and H. Lischka, Newton-X: A surface-hopping program for nonadiabatic molecular dynamics, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 26–33 CAS.
- S. Mai, P. Marquetand and L. González, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1370 Search PubMed.
- M. Barbatti, G. Granucci, M. Persico, M. Ruckenbauer, M. Vazdar, M. Eckert-Maksić and H. Lischka, The on-the-fly surface-hopping program system Newton-X: Application to ab initio simulation of the nonadiabatic photodynamics of benchmark systems, J. Photochem. Photobiol., A, 2007, 190, 228–240 CrossRef CAS.
- M. Richter, P. Marquetand, J. González-Vázquez, I. Sola and L. González, SHARC: Ab initio molecular dynamics with surface hopping in the adiabatic representation including arbitrary couplings, J. Chem. Theory Comput., 2011, 7, 1253–1258 CrossRef CAS PubMed.
- S. Mai, P. Marquetand and L. González, Nonadiabatic Dynamics: The SHARC Approach, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1370 Search PubMed.
- F. Plasser, S. Gómez, M. Menger, S. Mai and L. González, Highly efficient surface hopping dynamics using a linear vibronic coupling model, Phys. Chem. Chem. Phys., 2019, 21, 57–69 RSC.
- A. V. Akimov and O. V. Prezhdo, The PYXAID program for non-adiabatic molecular dynamics in condensed matter systemsmics in condensed matter systems, J. Chem. Theory Comput., 2013, 9, 4959–4972 CrossRef CAS.
- A. V. Akimov and O. V. Prezhdo, Advanced capabilities of the PYXAID program: Integration schemes, decoherence effects, multiexcitonic states, and field-matter interaction, J. Chem. Theory Comput., 2014, 10, 789–804 CrossRef CAS.
- H. Song, S. A. Fischer, Y. Zhang, C. J. Cramer, S. Mukamel, N. Govind and S. Tretiak, First Principles Nonadiabatic Excited-State Molecular Dynamics in NWChem, J. Chem. Theory Comput., 2020, 16, 6418–6427 CrossRef CAS PubMed.
- H. Song, V. M. Freixas, S. Fernandez-Alberti, A. J. White, Y. Zhang, S. Mukamel, N. Govind and S. Tretiak, An Ab Initio Multiple Cloning Method for Non-Adiabatic Excited-State Molecular Dynamics in NWChem, J. Chem. Theory Comput., 2021, 17, 3629–3643 CrossRef CAS PubMed.
- T. R. Nelson, A. J. White, J. A. Bjorgaard, A. E. Sifain, Y. Zhang, B. Nebgen, S. Fernandez-alberti, D. Mozyrsky, A. E. Roitberg and S. Tretiak, Non-adiabatic Excited-State Molecular Dynamics : Theory and Applications for Modeling Photophysics in Extended Molecular Materials, Chem. Rev., 2020, 120, 2215–2287 CrossRef CAS PubMed.
- W. Malone, B. Nebgen, A. White, Y. Zhang, H. Song, J. A. Bjorgaard, A. E. Sifain, B. Rodriguez-Hernandez, V. M. Freixas, S. Fernandez-Alberti, A. E. Roitberg, T. R. Nelson and S. Tretiak, NEXMD Software Package for Nonadiabatic Excited State Molecular Dynamics Simulations, J. Chem. Theory Comput., 2020, 16, 5771–5783 CrossRef CAS PubMed.
- V. M. Freixas, W. Malone, X. Li, H. Song, H. Negrin-Yuvero, R. Pérez-Castillo, A. White, T. R. Gibson, D. V. Makhov, D. V. Shalashilin, Y. Zhang, N. Fedik, M. Kulichenko, R. Messerly, L. Mohanam, S. Sharifzadeh, A. Bastida, S. Mukamel, S. Fernandez-Alberti and S. Tretiak, NEXMD v2.0 Software Package for Nonadiabatic Excited State Molecular Dynamics Simulations, J. Chem. Theory Comput., 2023, 19, 5356–5368 CrossRef CAS PubMed.
- H. Negrin-Yuvero, V. M. Freixas, D. Ondarse-Alvarez, L. Alfonso-Hernandez, G. Rojas-Lorenzo, A. Bastida, S. Tretiak and S. Fernandez-Alberti, Vibrational Funnels for Energy Transfer in Organic Chromophores, J. Phys. Chem. Lett., 2023, 14, 4673–4681 CrossRef CAS PubMed.
- L. Alfonso-Hernandez, N. Oldani, S. Athanasopoulos, J. M. Lupton, S. Tretiak and S. Fernandez-Alberti, Photoinduced Energy Transfer in Linear Guest-Host Chromophores: A Computational Study, J. Phys. Chem. A, 2021, 125, 5303–5313 CrossRef CAS.
- M. C. Aguilera, A. E. Roitberg, V. D. Kleiman, S. Fernandez-Alberti and J. F. Galindo, Unraveling Direct and Indirect Energy Transfer Pathways in a Light-Harvesting Dendrimer, J. Phys. Chem. C, 2020, 124, 22383–22391 CrossRef CAS.
- V. M. Freixas, D. Ondarse-Alvarez, S. Tretiak, D. V. Makhov, D. V. Shalashilin and S. Fernandez-Alberti, Photoinduced non-adiabatic energy transfer pathways in dendrimer building blocks, J. Chem. Phys., 2019, 150, 124301 CrossRef CAS PubMed.
- D. Ondarse-Alvarez, N. Oldani, A. E. Roitberg, V. Kleiman, S. Tretiak and S. Fernandez-Alberti, Energy transfer and spatial scrambling of an exciton in a conjugated dendrimer, Phys. Chem. Chem. Phys., 2018, 20, 29648–29660 RSC.
- S. Fernandez-Alberti, A. E. Roitberg, V. D. Kleiman, T. Nelson and S. Tretiak, Shishiodoshi unidirectional energy transfer mechanism in phenylene ethynylene dendrimers, J. Chem. Phys., 2012, 137, 22A526 CrossRef CAS.
- A. H. Khundkar and L. R. Zewail, Ultrafast Molecular Reaction Dynamics in Real-Time: Progress Over a Decade, Annu. Rev. Phys. Chem., 1990, 41, 15–60 CrossRef.
- M. H. Martin and J. L. Vos, Femtosecond Biology, Annu. Rev. Biophys. Biomol. Struct., 1992, 21, 199–222 CrossRef PubMed.
- G. Beddard, Molecular Photophysics, Rep. Prog. Phys., 1993, 56, 63–171 CrossRef CAS.
- M. Fushitani, Applications of Pump-Probe Spectroscopy, Annu. Rep. Prog. Chem., Sect. C: Phys. Chem., 2008, 104, 272–297 RSC.
- T. Elsaesser, Introduction: Ultrafast Processes in Chemistry, Chem. Rev., 2017, 117, 10621–10622 CrossRef CAS PubMed.
- M. Maiuri, M. Garavelli and G. Cerullo, Ultrafast Spectroscopy: State of the Art and Open Challenges, J. Am. Chem. Soc., 2020, 142, 3–15 CrossRef CAS PubMed.
- M. F. Gelin, X. Huang, W. Xie, L. Chen, N. Došlić and W. Domcke, Ab Initio Surface-Hopping Simulation of Femtosecond Transient-Absorption Pump-Probe Signals of Nonadiabatic Excited-State Dynamics Using the Doorway-Window Representation, J. Chem. Theory Comput., 2021, 17, 2394–2408 CrossRef CAS PubMed.
- W. Gelin, M. F. Chen and L. Domcke, Equation-of-motion methods for the calculation of femtosecond time-resolved 4-wave-mixing and n-wave-mixing signals, Chem. Rev., 2022, 122, 17339–17396 CrossRef.
- S. Yan, Y. J. Fried and L. E. Mukamel, Ultrafast pump-probe spectroscopy: femtosecond dynamics in Liouville space, J. Phys. Chem., 1989, 93, 8149–8162 CrossRef.
- S. Yan and Y. J. Mukamel, Femtosecond pump-probe spectroscopy of polyatomic molecules in condensed phases, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 41, 6485–6504 CrossRef PubMed.
- S. Fried and L. E. Mukamel, A classical theory of pump−probe photodissociation for arbitrary pulse durations, J. Chem. Phys., 1990, 93, 3063–3071 CrossRef.
- D. Hu, J. Peng, L. Chen, M. F. Gelin and Z. Lan, Spectral Fingerprint of Excited-State Energy Transfer in Dendrimers through Polarization-Sensitive Transient-Absorption Pump-Probe Signals: On-the-Fly Nonadiabatic Dynamics Simulations, J. Phys. Chem. Lett., 2021, 12, 9710–9719 CrossRef CAS.
- C. Xu, K. Lin, D. Hu, F. L. Gu, M. F. Gelin and Z. Lan, Ultrafast internal conversion dynamics through the on-the-Fly simulation of transient absorption pump–probe spectra with different electronic structure methods, J. Phys. Chem. Lett., 2022, 13, 661–668 CrossRef CAS.
- R. Perez-Castillo, V. M. Freixas, S. Mukamel, A. Martinez-Mesa, L. Uranga-Piña, S. Tretiak, M. F. Gelin and S. Fernandez-Alberti, Transient-absorption spectroscopy of dendrimers via nonadiabatic excited-state dynamics simulations, Chem. Sci., 2024, 15, 13250–13261 RSC.
- X. Huang, W. Xie, N. Došlić, M. F. Gelin and W. Domcke, Ab initio quasiclassical simulation of femtosecond time-resolved two-dimensional electronic spectra of pyrazine, J. Phys. Chem. Lett., 2021, 12, 11736–11744 CrossRef CAS.
- J. Zhang, J. Peng, D. Hu, M. F. Gelin and Z. Lan, What Two-Dimensional Electronic Spectroscopy Can Tell Us about Energy Transfer in Dendrimers: Ab Initio Simulations, J. Phys. Chem. Lett., 2025, 1007–1015 Search PubMed.
- J. C. Tully, Molecular dynamics with electronic transitions, J. Chem. Phys., 1990, 93, 1061–1071 CrossRef CAS.
- O. V. Wang, L. J. Akimov and A. Prezhdo, Recent progress in surface hopping: 2011−2015, J. Phys. Chem. Lett., 2016, 7, 2100–2112 CrossRef PubMed.
- F. Würthner, C. R. Saha-Möller, B. Fimmel, S. Ogi, P. Leowanawat and D. Schmidt, Perylene Bisimide Dye Assemblies as Archetype Functional Supramolecular Materials, Chem. Rev., 2016, 116, 962–1052 CrossRef.
- D. Inan, R. K. Dubey, W. F. Jager and F. C. Grozema, Tailoring Photophysical Processes of Perylene-Based Light Harvesting Antenna Systems with Molecular Structure and Solvent Polarity, J. Phys. Chem. C, 2019, 123, 36–47 CrossRef CAS.
- M. A. Soler, A. Bastida, M. H. Farag, J. Zúñiga and A. Requena, A method for analyzing the vibrational energy flow in biomolecules in solution, J. Chem. Phys., 2011, 135, 204106 CrossRef PubMed.
- L. Alfonso Hernandez, T. Nelson, M. F. Gelin, J. M. Lupton, S. Tretiak and S. Fernandez-Alberti, Interference of Interchromophoric Energy-Transfer Pathways in π-Conjugated Macrocycles, J. Phys. Chem. Lett., 2016, 7, 4936–4944 CrossRef CAS PubMed.
- D. Huo, M. Li, Z. Zhao, X. Wang, A. Xia, P. Lu and Y. Wan, Delocalized Excitation or Intramolecular Energy Transfer in Pyrene Core Dendrimers, J. Phys. Chem. Lett., 2021, 12, 7717–7725 CrossRef CAS PubMed.
- V. M. Freixas, T. Nelson, D. Ondarse-Alvarez, P. Nijjar, A. Mikhailovsky, C. Zhou, S. Fernandez-Alberti, G. C. Bazan and S. Tretiak, Experimental and theoretical study of energy transfer in a chromophore triad: What makes modeling dynamics successful?, J. Chem. Phys., 2020, 153, 244114 CrossRef CAS PubMed.
- R. A. Ingle, L. E. Cigrang and B. F. E. Curchod, et al., Roadmap for Molecular Benchmarks in Nonadiabatic Dynamics, J. Phys. Chem., 2025 Search PubMed , in press.
- J. C. Tully, Molecular dynamics with electronic transitions, J. Chem. Phys., 1990, 93, 1061–1071 CrossRef CAS.
- M. J. S. Dewar, E. G. Zoebisch, E. F. Healy and J. J. P. Stewart, The development and use of quantum-mechanical molecular-models.76.AM1 - A new general purpose quantum-mechanical molecular-model, J. Am. Chem. Soc., 1985, 107, 3902–3909 CrossRef CAS.
- V. Bonilla, V. M. Freixas, S. Fernandez-Alberti and J. F. Galindo, Impact of the core on the inter-branch exciton exchange in dendrimers, Phys. Chem. Chem. Phys., 2023, 25, 12097–12106 RSC.
- V. M. Freixas, D. Keefer, S. Tretiak, S. Fernandez-Alberti and S. Mukamel, Ultrafast coherent photoexcited dynamics in a trimeric dendrimer probed by X-ray stimulated-Raman signals, Chem. Sci., 2022, 13, 6373–6384 RSC.
- J. F. Galindo, E. Atas, A. Altan, D. G. Kuroda, S. Fernandez-Alberti, S. Tretiak, A. E. Roitberg and V. D. Kleiman, Dynamics of Energy Transfer in a Conjugated Dendrimer Driven by Ultrafast Localization of Excitations, J. Am. Chem. Soc., 2015, 137, 11637–11644 CrossRef CAS PubMed.
- D. Ondarse-Alvarez, S. Kömürlü, A. Roitberg, G. Pierdominici-Sottile, S. Tretiak, S. Fernandez-Alberti and V. Kleiman, Ultrafast electronic energy relaxation in a conjugated dendrimer leading to inter-branch energy redistribution, Phys. Chem. Chem. Phys., 2016, 18, 25080–25089 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Fig. S1 shows chemical structure of the dendrimer T1 indicating the x, y, and z directions of the body-fixed reference frame, spatial distributions of electronic transition densities and transition dipole moments (μ) for the five lowest energy electronic states; Fig. S2 presents distribution of the average fraction of the transition density matrix localized on the different chromophores; populations of electronic states at short times; Fig. S3 displays excited state natural orbitals; and Fig. S4 and S5 show the analysis of trajectories following the different energy transfer pathways; Fig. S6 displays SE contribution to the TA-PP signal at different times for the different energy relaxation pathways. Fig. S7 and S8 shows nonadiabatic coupling vectors associated to the different energy transfer between states, their projection onto D2A2 normal mode and normal modes with the highest contributions. See DOI: https://doi.org/10.1039/d5sc03157e |
| This journal is © The Royal Society of Chemistry 2025 |