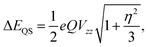Deciphering potential-driven dynamics in Fe–N–C catalysts: ab initio insights into Fe–N switching and spin-state transition

Abstract

Pyrolyzed Fe–N–C materials are cost-effective alternatives to Pt for the acidic oxygen reduction reaction (ORR), yet the atomic and electronic structures of their active centers remain poorly understood. Operando spectroscopic studies have identified potential-induced reversible Fe–N switching in the FeN_x active centers of D1 type, which provides a unique opportunity to decode their atomic structures, but the mechanism driving this behavior has been elusive. Herein, using constant-potential ab initio molecular dynamics (CP-AIMD), we reveal that pyridinic FeN₄ sites transit reversibly between planar OH*–Fe³⁺N₄ and out-of-plane H₂O*–Fe²⁺N₄ configurations at 0.8 V, mirroring the experimental Fe–N switching phenomenon. This shift arises from a spin-state transition: intermediate-spin Fe³⁺ (S = 3/2) converts to high-spin Fe²⁺ (S = 2) as potential decreases, driven by the pseudo Jahn–Teller effect and strong H₂O binding on the high-spin Fe²⁺ center. Additionally, a metastable 2H₂O*–Fe^2.5+N₄ configuration exists, acting as a transitional state during the reversible switching process. Calculated X-ray absorption and Mössbauer spectra based on CP-AIMD align closely with experimental data, bridging the theoretical predictions and experimental observations. Crucially, this dynamic Fe–N switching is unique to pyridinic FeN₄ sites, challenging the long-held assumption that D1 sites are pyrrolic FeN₄. This study clarifies the potential-driven dynamics and active center structures in Fe–N–C catalysts and will help to precisely design Fe-based ORR catalysts.

---

1 Introduction

Iron and nitrogen co-doped carbon (Fe–N–C) catalysts have emerged as promising platinum-free electrocatalysts for the oxygen reduction reaction (ORR) in proton exchange membrane fuel cells, primarily due to their atomically dispersed FeN_x active sites.^1–5 Despite their notable ORR activity, the practical application of these catalysts is hindered by insufficient activity and durability under operational conditions.⁶ To address these limitations, a precise understanding of the active site structure is essential, yet it remains elusive. Experimental efforts have focused on employing operando characterization techniques, such as X-ray absorption spectroscopy (XAS) and Mössbauer spectroscopy (MS), to investigate the atomic and electronic structures of these active sites. Under operando conditions, FeN_x centers often exhibit potential-dependent structural and electronic evolution, offering insights into their dynamic behavior. Nevertheless, deciphering the complex interplay between applied potential, structural dynamics, and spin-state transitions—and correlating these behaviors with specific FeN_x structures—remains a significant challenge due to inherent complexities and the lack of a robust theoretical framework.^7–9

Spectroscopic investigations have started to shed light on these complexities. In situ X-ray absorption spectroscopy (XAS) studies demonstrated reversible structural switching between out-of-plane Fe²⁺N₄ and planar O_x–Fe³⁺N₄ configurations,^9–11 which correspond to the D1 state observed in Mössbauer spectra. Specifically, the out-of-plane displacement of Fe in the D1 sites occurs during the decrease in potential when Fe³⁺ is reduced to Fe²⁺. The behavior contrasts with the typical out-of-plane displacement expected in OH*–Fe³⁺N₄, where OH* adsorption induces a pulling effect on the Fe center. Distinctly, the coexisting D2 state exhibited no potential-dependent structural changes. Notably, the dynamic switching behavior of D1 sites is proposed to be a key factor underlying their intrinsically high ORR activity compared to the static D2 sites.^9,11 This is attributed to the in-plane movement of the D1 site upon its oxidation to Fe³⁺, which significantly mitigates the overly strong Fe–O binding energy that is otherwise detrimental to ORR activity.

A recent operando Mössbauer spectroscopic study by Li et al. revealed that the D1 sites can reversibly transit between a low-potential (D1L) and a high-potential (D1H) state, while further confirming the static nature of the D2 sites.⁸ By combining experimental observations with theoretical calculations of Mössbauer parameters, the D1 site was assigned to FeN₄ centers with pyrrolic nitrogen coordination. The reversible potential-dependent transition between D1L and D1H was attributed to a redox-driven process involving high-spin Fe²⁺N₄ (S = 2) and high-spin OH*–Fe³⁺N₄ (S = 5/2) states. Importantly, the study highlighted that the dynamic D1 site, despite exhibiting high ORR activity, is significantly less stable under ORR operational conditions compared to the static D2 site.

There is a growing consensus that the D1 site undergoes potential-driven structural and spin-state transitions, while the D2 site remains relatively static under operando conditions. However, the precise structural assignments of the D1 and D2 active sites remain a subject of debate. Herranz's time-resolved XAS study suggested that porphyrin-derived Fe–N–C catalysts undergo planarization upon potential reduction, whereas MOF-derived catalysts exhibit ligand loss and symmetry breaking below 0.5 V, likely due to out-of-plane displacement of the Fe center.¹² A plausible hypothesis for the active site structure in porphyrin-derived Fe–N–C catalysts is the pyrrolic FeN₄ configuration, given the inherent atomic structure of the porphyrin molecule. However, the relatively static behavior of porphyrin-derived Fe–N–C catalysts contrasts with the dynamic characteristics of D1 sites, which align more closely with the behavior observed in MOF-derived catalysts. Furthermore, a recent study utilizing molecular model catalysts with well-defined structures demonstrated that a pyridinic FeN₄ macrocycle molecule ((phen₂N₂)Fe) more accurately mimics the active sites of pyrolyzed Fe–N–C catalysts compared to pyrrolic iron phthalocyanine (FePc) or iron octaethylporphyrin (FeOEP) molecules.¹³

The key to unambiguously assigning the active site structures of Fe–N–C catalysts lies in deciphering the potential-induced dynamic behavior of FeN_x centers at an atomic level. Density functional theory (DFT) has provided initial insights into the potential-driven structural and spin transitions of pyridinic FeN₄ sites.^14–17 Our previous constant-potential DFT study revealed a potential-dependent spin crossover (intermediate-spin Fe²⁺ ↔ high-spin Fe²⁺) near 0.5 V, accompanied by an out-of-plane displacement of the Fe atom.¹⁴ Additionally, our calculations demonstrated that high-spin pyridinic FeN₄ sites bind oxygenated species more strongly than their intermediate- or low-spin counterparts, aligning with experimental observations.^14,18 These findings underscore the significant role of spin effects in determining the oxygen reduction reaction (ORR) activity of Fe–N–C catalysts. However, these static calculations, which rely on implicit solvent models, fall short in adequately capturing solvent effects and the dynamic behavior at electrified electrode/electrolyte interfaces—a critical limitation highlighted by recent ab initio molecular dynamics (AIMD) studies of such interfaces.^19–25

The intriguing and distinctive potential-induced dynamic behavior of FeN_x active centers has motivated us to employ constant-potential ab initio molecular dynamics (CP-AIMD) simulations to model the Fe–N–C/electrolyte interface with explicit solvent. This approach aims to elucidate the experimentally observed potential-driven structural and spin transitions in Fe–N–C catalysts, which could significantly advance the identification of active site structures. In this study, by simulating the pyridinic FeN₄/water interface across a potential range of 0–1.0 V, we identify two distinct regimes: (1) below 0.8 V, water adsorption stabilizes non-planar high-spin (HS) H₂O*–Fe²⁺N₄ complexes (S = 2); (2) above 0.8 V, oxidation leads to planar intermediate-spin (IS) OH*–Fe³⁺N₄ configurations (S = 3/2). These opposite Fe–N switching behaviors (termed “opposite” because the out-of-plane FeN₄ configuration is typically expected for OH*–Fe³⁺N₄ due to OH* adsorption-induced pulling) align well with experimental observations.⁹ Furthermore, we validate our theoretical findings by simulating potential-dependent XAS and MS quadrupole splitting energies based on CP-AIMD trajectories, quantitatively reproducing experimental spectral features in operando conditions. Since the dynamic behavior is distinctly exhibited in the pyridinic FeN₄ site rather than in the pyrrolic FeN₄ site, we tentatively assign the D1 site, with its potential-induced spin crossover and structural dynamics, to the pyridinic FeN₄ structure. Our findings provide new insights into the long-standing debates surrounding the dynamics of the D1 site and its structural assignment, establishing a robust mechanistic foundation for the active site engineering of Fe–N–C catalysts.

2 Computational methods

Spin-polarized DFT calculations were conducted using the Vienna Ab Initio Simulation Package (VASP).²⁶ The electron–ion interactions were modeled with projector augmented-wave (PAW) potentials, and the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional was utilized. A plane-wave basis set with a cutoff energy of 400 eV was adopted. Brillouin zone sampling was performed on a 3 × 3 × 1 Γ-centered k-point mesh. For Fe's 3d orbitals, to mitigate self-interaction errors, we applied the DFT + U method,²⁷ assigning an effective Hubbard U parameter (U_eff) of 3.29 eV. This value accurately reflected the relative stability of various spin states in Fe²⁺N₄ and OH*–Fe³⁺N₄ complexes as determined by hybrid functionals like PBE0 and HSE06.¹⁴ Structural optimizations required atomic forces to converge below 0.05 eV Å⁻¹. We achieved different spin configurations of Fe ions within Fe–N–C catalysts by customizing the occupation matrix of the 3d orbitals using the occupation matrix control plugin.²⁸ Following initial structural relaxation under these constraints, further optimization proceeded without them to achieve full optimization at the desired spin state. Electron population analysis around Fe ions used Bader charge decomposition.^29–31

For simulating electrode/electrolyte interfaces at constant potential, our computational framework for electronically grand-canonical ensemble automatically adjusted the number of electrons in the system to match the target electrode potential, thereby maintaining the electronic chemical potential (μ_e). The electric potential (U) relative to the standard hydrogen electrode (SHE) was calculated from U = −4.6 V − Φ_q/e, where −4.6 V is the SHE potential and −Φ_q represents the work function for the system doped with charge q.

Structural dynamics simulations at constant potential employed CP-AIMD methods under μ_eNVT conditions, similar to the approach developed by Liu et al.^19,22 Temperature control was achieved through a Nóse–Hoover thermostat set at 298 K. Time integration was carried out with a time-step of 1 fs for a total of at least 15 ps to ensure equilibrium. Adjustments to the number of electrons occurred every five steps to maintain the target potential. To reduce computational load, a single Γ-point was utilized for the Brillouin zone sampling during AIMD simulations. The interfacial environment of the pyridinic FeN₄ system was simulated at a series of potentials: 0, 0.2, 0.4, 0.6, 0.8, and 1.0 V. For comparison, CP-AIMD simulations of the pyrrolic FeN₄ system were conducted at two representative potentials: low (0.2 V) and high (1.0 V).

The Fe–N–C electrode was represented by a p(5 × 3) rectangular graphene sheet with six carbon atoms substituted by an FeN₄ moiety. An explicit solvent layer of 72 water molecules at a density of 1 g cm⁻³ was positioned above the electrode, topped by an implicit solvent region modeled using the linear polarizable continuum approach in VASPsol^32,33 for bulk water. To systematically assess the limited influence of Fe site density on potential-dependent observables, we constructed additional models with higher and lower Fe densities relative to the original p(5 × 3) model. A detailed analysis is provided in ESI Fig. S1.†

Simulated Fe K-edge XAS spectra were derived from CP-AIMD trajectories at various potentials. After equilibration for 10 ps, at least 500 independent snapshots were averaged for XAS calculations. X-ray absorption near-edge structure (XANES) of Fe K-edge was simulated using the FDMNES software.³⁴ Extended X-ray absorption fine structure (EXAFS) simulations of Fe K-edge included multiple scattering paths within a 4.0 Å radius around the photo-absorbing Fe atom were considered and their phase shifts, amplitudes, and mean-free paths were calculated with FEFF6-lite.³⁵ Amplitude reduction factor S₀² and energy origin correction ΔE₀ were set to 0.88 and 2.90 eV, respectively. Fourier transformation of the k²-weighted EXAFS data produced R-space spectra over the k-range of 2.0–8.0 Å⁻¹. The method has been successfully employed to simulate EXAFS of nanoparticles and single-atom catalyst.^36–39

The quadruple splitting energy (ΔE_QS) was computed by considering the coupling between the nuclear quadrupole moment (Q) of the ⁵⁷Fe nucleus and the principal components V_ii (i = x, y, z) of the electric field gradient (EFG) tensor using the equation⁴⁰

where e is the electron charge, and η is the asymmetry parameter, which is calculated as η = (V_xx − V_yy)/V_zz, where |V_zz| ≥ |V_yy| ≥ V_xx. The nuclear quadrupole moment, Q, for the J = 3/2 state is set to 0.1 barn.

3 Results and discussion

3.1 Convergence of CP-AIMD simulations

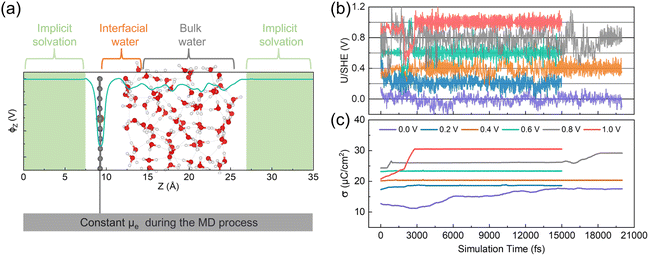
We performed CP-AIMD simulations on the electrochemical Fe–N–C/H₂O interface with a pyridinic FeN₄ site at various applied potentials: 0.0, 0.2, 0.4, 0.6, 0.8, and 1.0 V vs. SHE. An illustrative atomic configuration from these simulations is presented in Fig. 1a. Superimposed on the atomic model in Fig. 1a is the plane-averaged local electrostatic potential profile along the z-axis (ϕ_z). The ϕ_z stabilizes in the implicit solvation region, allowing us to use it as an energy reference for the calculation of the work function, −Φ_q, which is used to determine the system's potential level relative to the SHE. As demonstrated in Fig. 1b, our CP-AIMD simulations achieved proper convergence to the intended applied potentials. The simulated potentials fluctuate within approximately ±0.1 V of the target values, primarily due to the orientational dynamics of polar water molecules. On a macroscopic scale, however, the time-averaged potential remains stable over the entire simulation. Moreover, the surface charge density (σ), calculated as the total surface charge divided by the surface area, also reached a stable state at each simulated potential (see Fig. 1c). The electronically grand canonical free energy of the system also showed similar convergence (see ESI Fig. S2†). Due to the weak intermolecular interactions of H₂O and the complex electrode/electrolyte interface, extended simulation times are typically required to achieve full convergence in Fe–N–C/H₂O systems.^41,42 However, given the significant computational cost of CP-AIMD simulations, we employ relatively shorter trajectories (15 to 20 ps) while validating our findings through static calculations and comparison with experimental spectroscopic data.

Fig. 1 (a) Side view of the electrochemical Fe–N–C/H₂O interface used in the CP-AIMD simulations. The superimposed green curve represents the profile of the xy-plane averaged electrostatic potential. (b) Evolution of the simulated electrode potential vs. SHE. (c) Evolution of surface charge density of the electrode.

3.2 Potential-induced interfacial solvent reorientation

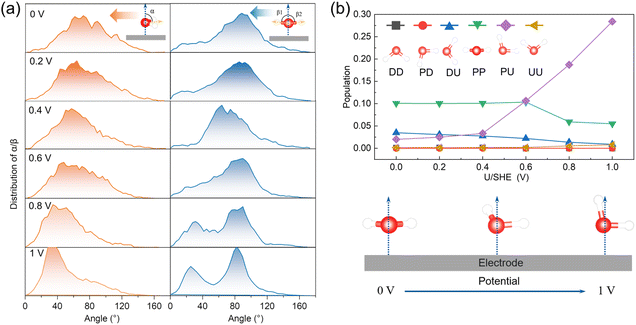
The interfacial water molecules adjust their orientations in response to changes in the surface charge density at varying applied potentials. To explore how the orientation of these water molecules evolves, we analyzed the distributions of two angles—α and β—for describing the orientation of water molecules. Their definitions are visually illustrated in Fig. 2a and detailed in the corresponding caption. Specifically, we evaluated α and β for interfacial water molecules located within 3.8 Å from the graphene plane, as depicted in Fig. 2a.

Fig. 2 (a) Distribution of α and β angles of the interfacial water molecules as a function of applied potential. α angle: this is defined as the angle between the bisector of the water molecule's O–H bonds and the surface normal. A smaller α angle signifies an H-up configuration, while a larger α suggests an H-down configuration. β angle: this measures the alignment of the O–H bond with respect to the surface normal vector. Each water molecule has two β angles corresponding to its two O–H bonds, denoted as β₁ and β₂. (b) The potential-dependent population of six orientation categories of the interfacial water molecules. A schematic plot is shown in the bottom panel for the potential-dependent change in the orientation of interfacial water molecules (bottom panel). DD (down–down): 170° < α < 180° and 117° < β < 137°. PD (parallel–down): 113° < α < 153°, 37° < β < 57° DU (down–up): 80° < α < 100° and 37° < β < 57°. PP (parallel–parallel): 80° < α < 100° and 80° < β < 100°. PU (parallel–up): 27° < α < 47° and 80° < β < 100°. UU (up–up): α < 10° and 43° < β < 63°.

Our findings indicate that as the applied potential increases, the average α angle decreases, suggesting that H-up water molecules become more prevalent at higher voltages. This shift occurs because of the attractive electrostatic interactions between the increasingly positively charged surface and the negatively charged oxygen atoms of the water molecules. Additionally, the β angles tend to split into two prominent peaks around 25° and 85° with increasing potential, indicating that one O–H bond aligns closely with the surface normal direction while the other tilts away.

To further analyze the orientation of interfacial water molecules, we categorized them into six groups based on combinations of α and β values. Their definitions are visually illustrated in Fig. 2b and detailed in the corresponding caption. The population distribution among these six orientation groups shifts with the applied potential, as shown in Fig. 2b. At lower potentials, the PP orientation—where both O–H bonds lie parallel to the surface—is predominant. However, at higher potentials (>0.4 V), the PU orientation becomes more common, with one O–H bond aligns with the surface normal and the other tilts away. The schematic illustration in the bottom panel of Fig. 2b visually represents this solvent reorientation driven by potential changes.

3.3 Potential-driven transitions of pyridinic FeN₄

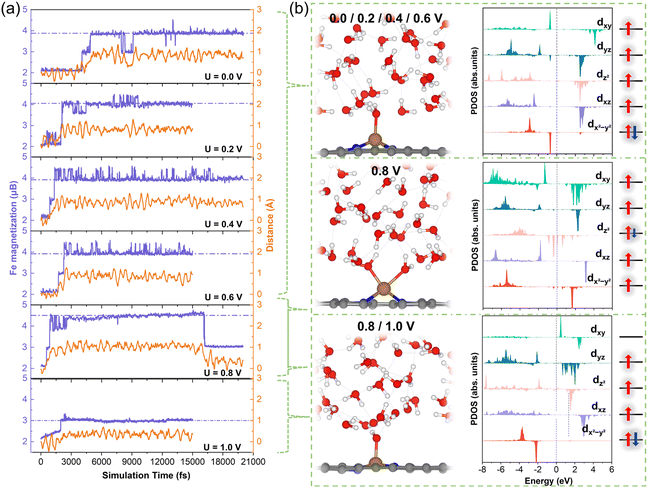
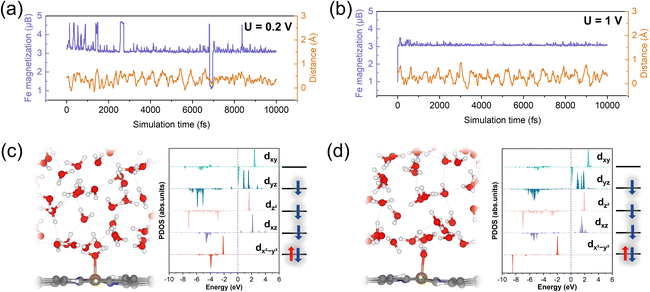
We further investigated the structural and spin-state transformations of pyridinic FeN₄ active sites under varying potentials. In CP-AIMD simulations, initially the Fe²⁺N₄ sites were set to an IS state, characterized by a d-orbital occupation of (d_xy)⁰(d_xz)¹(d_z²)¹(d_yz)²(d_x²−y²)². Our previous research has established this IS state as the ground state under potential of zero charge (PZC) conditions.¹⁴ Under constant-potential conditions with implicit solvation, however, a HS state—with a d-orbital occupation of (d_xy)¹(d_xz)¹(d_z²)²(d_yz)¹(d_x²−y²)¹—exhibits comparable stability, particularly at higher potentials. Nonetheless, the IS state remains more stable. ESI Fig. S3† offers additional details into the IS state and the relative stability of the IS and HS states.

During CP-AIMD simulations with explicit water solvent, the IS state of the Fe²⁺N₄ center is observed to be transient. Specifically, at applied potentials ranging from 0 to 0.6 V, a water molecule from the solvent approaches and adsorbs onto the iron site, leading to the formation of a penta-coordinated H₂O*–FeN₄ structure. The adsorption process can be tracked by monitoring the reduction in the Fe–O bond length over time, as shown in ESI Fig. S4.† Representative snapshots of the atomic configuration at the FeN₄/H₂O interface under potentials between 0 and 0.6 V are provided in Fig. 3b.

Fig. 3 CP-AIMD simulations of pyridinic FeN₄/H₂O interface. (a) Evolution of Fe magnetization (purple curve) and height of the Fe atom above the graphene plane (orange curve). (b) Representative structures of the Fe–N–C/H₂O interface and the PDOS of the corresponding Fe atom and the orbital occupancy from the CP-AIMD simulations at potentials.

The spin transition of the Fe center consistently coincides with the adsorption of water molecules. As illustrated in Fig. 3a, the magnetization of the ferrous Fe²⁺ (represented by the purple curves), which reflects the difference between majority and minority spins, evolves from the IS state (magnetization, m = 2μ_B) to a HS state (m = 4μ_B). This HS state is characterized by a d-orbital occupation of (d_xy)¹(d_xz)¹(d_z²)¹(d_yz)¹(d_x²−y²)². The detailed Fe 3d orbital occupations at various potentials are presented in ESI Table S1.† The projected density of states (PDOS) for the 3d orbitals of the Fe active center are depicted in Fig. 3b. Upon transitioning to the HS state, the Fe atom experiences an out-of-plane displacement, as evidenced by the significant increase in its z-coordinate, shown by the orange curves in Fig. 3a. This out-of-plane displacement is a hallmark of the HS of the pyridinic FeN₄ center, as previously demonstrated in our research.¹⁴

The out-of-plane HS state of the ferrous Fe²⁺ center, observed in CP-AIMD simulations within the potential range of 0.0–0.6 V, is stabilized against the in-plane IS state through water adsorption on the Fe site. To investigate this stabilization effect, we decomposed the water-adsorption-induced IS-to-HS transition into two subprocesses: the IS-to-HS transition under implicit solvation conditions and the subsequent water adsorption on the HS Fe center. The energies associated with these subprocesses are denoted as ΔE₁ and ΔE₂, respectively, with their sum (ΔE₁ + ΔE₂) representing the overall driving force for the water-adsorption-induced IS-to-HS transition.

As shown in Fig. 4b, ΔE₁ is positive at approximately 0.15 eV, reflecting the unfavorable nature of the IS-to-HS transition in the absence of water adsorption under implicit solvation. Although ΔE₁ is positive, the out-of-plane displacement of the Fe center is electronically facilitated by the pseudo Jahn–Teller effect, which gains addition Fe–N covalency by breaking the square-planar symmetry of the FeN₄ center. Specifically, in the in-plane FeN₄ configuration, there is zero interaction between Fe-d_z² and N-p_z because of orbital orthogonality as evidenced by the projected and integrated Crystal Orbital Hamilton Populations (pCOHP and ICOHP) shown in Fig. 4a. In the out-of-plane configuration, nonzero overlap between Fe-d_z² and N-p_z is evident (−ICOHP = 0.30 eV) as shown in Fig. 4a. However, this energy barrier of IS-to-HS transition (ΔE₁) is significantly offset by the strong binding of water to the HS Fe center, as indicated by the negative ΔE₂ value of about −0.6 eV. Consequently, the total energy change (ΔE₁ + ΔE₂) is negative, indicating that the transition from a bare IS state to a water-adsorbed HS Fe²⁺N₄ structure is energetically favorable. Furthermore, the adsorption energy of water on the IS Fe center (ΔE₃), also depicted in Fig. 4b, is positive, which suggests that water adsorption does not stabilize the IS state, thus excluding the possibility of a water stabilized IS configuration. The strong water adsorption on the HS Fe center could be attributed to the out-of-plane configuration, which promotes the hybridization between Fe 3d_z² and O 2p_z orbitals.

Fig. 4 (a) Crystal orbital Hamilton population (COHP) and integrated COHP (ICOHP) between Fe-d_z² and N-p_z orbitals of in-plane and out-of-plane FeN₄ configurations. Insets show the corresponding orbital overlaps. (b) Energies related to the water-adsorption induced spin transitions as a function of applied potential. (c) Energy difference between IS and HS OH*–FeN₄ as a function of H–O distance. (d) Magnetization and net electron of the O atom in OH* as a function of H–O distance.

To ensure the reliability of the observed potential-induced spin and structural transitions and to prevent CP-AIMD simulations from being trapped in local minima, we conducted additional CP-AIMD simulations that last for 15 ps at potentials of 0 and 0.4 V, starting from the HS state. These extended simulations confirm that the HS H₂O*–FeN₄ structure is the equilibrium state at these potentials. Further details are provided in ESI Fig. S5.†

At 0.8 V, the Fe atom sequentially binds with two water molecules during the simulation: the first binding occurs at approximately 0.5 ps, followed by a second binding around 2.6 ps, leading to the formation of a hexa-coordinated 2H₂O*–FeN₄ structure, as illustrated in Fig. 3b. The out-of-plane displacement of the Fe atom is pronounced and exceeds that observed for the HS state at lower potentials.

Based on the PDOS of the Fe 3d orbitals shown in Fig. 3b and the Fe magnetization of 4.5μ_B depicted in Fig. 3a, the occupancy of the Fe 3d orbitals can be approximated as (d_xy)¹(d_xz)¹(d_z²)^1.5(d_yz)¹(d_x²−y²)¹. This orbital configuration indicates a HS state with fewer than six electrons in the Fe 3d orbitals, suggesting an oxidation state intermediate between Fe²⁺ and Fe³⁺, indicative of the beginning of Fe^2+/3+ redox.

At approximately 16 ps, desorption of a water molecule from the Fe site triggers a transition from the 2H₂O*–Fe^2.5+N₄ configuration to an H₂O*–Fe³⁺N₄ structure. The PDOS for the Fe 3d orbitals (Fig. 3b) reveals a five-electron configuration of (d_xy)⁰(d_xz)¹(d_z²)¹(d_yz)¹(d_x²−y²)², corresponding to an IS state of Fe³⁺. This transition induces the in-plane movement of the Fe atom (Fig. 3a).

To rationalize these observations, we conducted static calculations (ESI Fig. S6†) to assess the thermodynamics of water adsorption/desorption at the Fe center. Our results reveal that the first H₂O molecule binds strongly to the Fe site with a binding energy of about −1.0 eV, while the second binds more weakly (∼−0.5 eV in binding energy). When accounting for the entropy of a free water molecule (∼0.67 eV at 300 K), the second H₂O adsorption becomes metastable, which is consistent with the occasional appearance of a magnetic configuration with an Fe magnetization of 4.5μ_B observed at 0 to 0.6 V in Fig. 3a. This indicates that the 2H₂O*–Fe^2.5+N₄ configuration is unlikely to remain stable over extended periods, whereas the H₂O*–Fe²⁺N₄ structure remains the most stable and dominant configuration at low potentials. These results indicate that the Fe²⁺/Fe³⁺ redox transition occurs around ∼0.8 V, with the HS 2H₂O*–Fe^2.5+N₄ configuration representing a transient state.

At 1 V, the Fe center retains the IS (S = 3/2) spin state and in-plane geometry observed at 0.8 V (Fig. 3a). Notably, the adsorbed H₂O* is deprotonated to form an OH* group bound to the FeN₄ center (Fig. 3b), further supporting the conclusion that the Fe²⁺/Fe³⁺ redox transition occurs near 0.8 V.

To verify the transitions in both spin and oxidation states, additional CP-AIMD simulations were conducted starting from the HS state of OH*–Fe³⁺N₄. These simulations confirm that the HS Fe³⁺ state is not stable at 1 V. Instead, it spontaneously transitions to the IS state shortly after the simulation begins, as detailed in ESI Fig. S7.† This finding underscores the stability of the IS state of Fe³⁺ under electrochemical conditions at 1 V.

However, previous work employing static implicit solvent models predict the HS state of OH*–Fe³⁺N₄ is more favorable than the IS state (see ESI Fig. S8†).¹⁴ The CP-AIMD simulation with only implicit solvation also confirms the initial IS state transits to the HS state shortly after the beginning of the simulation (see ESI Fig. S9†). The discrepancy between implicit and explicit solvation models suggest that implicit solvent models may inadequately capture solvation effects on the active center, leading to erroneous prediction of the stable spin state under electrochemical environment.

To investigate the origin of this discrepancy, we employed a model system consisting of OH*–FeN₄, one H₂O molecule, and a Zundel H₅O₂⁺ proton. In this model, we gradually reduced the distance between the H₅O₂⁺ ion and the OH* group. As shown in Fig. 4c, the energy difference between the IS and HS states (ΔE^IS–HS) of OH*–FeN₄ decreases as the H–O distance (between the H atom in H₅O₂⁺ and the O atom in *OH) shortens. At a distance of 1.2 Å, the IS state becomes energetically favorable, whereas beyond this distance, the HS state is more stable.

As the H–O distance decreases, the magnetization of the O atom in OH* decreases from 0.21 to 0.13μ_B, indicating a transition from an OH˙ radical-like species to a close-to-OH⁻ species (see Fig. 4d). Correspondingly, a greater negative charge accumulates on the OH* group (see Fig. 4d). These results suggest that in the fully solvated interface of the CP-AIMD simulations, OH* is more likely to exist as an OH⁻ species, thereby stabilizing the IS state of Fe³⁺. The observed trend can be explained by the difference in ligand field strength between OH⁻ and OH˙. OH⁻, as a negatively charged ligand, is significantly stronger than the charge-neutral OH˙ radical. This stronger ligand field induces a larger splitting of the Fe 3d orbitals, thereby stabilizing the IS state as compared to the HS.

To further validate this theory, we calculated the energy difference between the IS and HS states (ΔE^IS–HS) for Fe³⁺ using H₂O and F⁻ as axial ligands on FeN₄. Since H₂O has a ligand field strength comparable to OH⁻, while F⁻ is weaker,⁴³ the results show that H₂O*–Fe³⁺N₄ stabilizes in the IS state, whereas F⁻-Fe³⁺N₄ prefers the HS state (see ESI Fig. S10†). These findings are consistent with our interpretation for the different preferred spin states in OH*–FeN₄ with different solvation models. Moreover, we observed that at 1.0 V, the axial ligand of FeN₄ alternates between OH* and H₂O (see ESI Fig. S11†), while Fe remains in the 3+ oxidation state. This dynamic ligand exchange further rationalizes the stability of the IS state of Fe³⁺.

3.4 Simulation of potential-dependent XAS

The CP-AIMD results discussed above demonstrate significant potential-induced structural, oxidation state, and spin transitions in the pyridinic FeN₄ center. To relate our computational insights with experimental findings, we simulated potential-dependent Fe K-edge XANES spectra using atomic configurations from potential-dependent CP-AIMD trajectories. The method is validated by the simulation of XANES of iron phthalocyanine (FePc) as shown in ESI Fig. S12.† The obtained XANES spectra (Fig. 5a) reveal a shift in the absorption edge to lower energies as the potential decreases, indicative of a reduction in the average Fe oxidation state. This is consistent with the decreased average Bader charge of Fe ion as the electrode potential reduces (see Fig. 5b). The continuous reduction of the Fe center at potentials lower than the Fe^2+/3+ redox potential of 0.8 V results from the gradual disappearance of the HS Fe^2.5+ state with decreasing potential, as demonstrated in ESI Fig. S13.† The white line intensity—a spectral feature corresponding to 1s → 4p electronic transitions—increases at 1.0 V, reflecting ligand environment changes associated with OH*–Fe³⁺N₄ formation. These simulated spectral features align closely with published experimental data (Fig. 5c).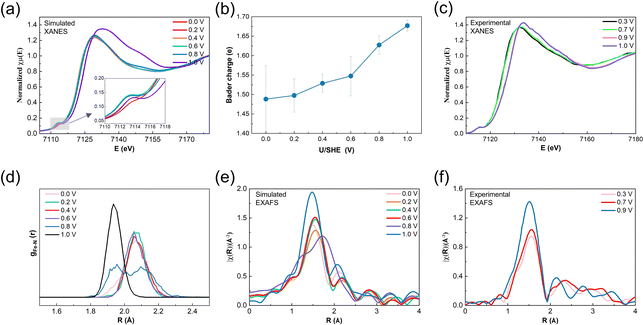

Fig. 5 (a) Modeled potential-dependent XANES of the Fe K-edge. (b) Average Bader charge of the Fe ion as a function of applied potential. (c) Experimental potential-dependent XANES of the Fe K-edge of the poly(N-vinylamine guanidine) (PVAG)–Fe catalyst collected in oxygen-free 0.1 M HClO₄ electrolyte under in situ conditions. (d) Potential-dependent pair distribution function (PDF) of the Fe–N bonds. (e) Modeled potential-dependent k²-weighted Fourier transformed EXAFS of the Fe K-edge. (f) Experimental potential-dependent EXAFS of the Fe K-edge of the PVAG–Fe catalyst collected in oxygen-free 0.1 M HClO₄ electrolyte under in situ conditions. Experimental data in (e) and (f) are reproduced from ref. 10.

Potential-induced structural changes in the FeN₄ center are further quantified through Fe–N bond pair distribution function (PDF) analysis (Fig. 5d). At 0–0.6 V, the average Fe–N bond length remains stable at ∼2.07 Å. However, at 0.8 V, bond elongation to ∼2.1 Å occurs due to enhanced out-of-plane Fe displacement following a second water adsorption. Additionally, a second peak emerges in the PDF at ∼1.95 Å, attributed to the reduced out-of-plane displacement during the transition from HS Fe²⁺ to IS Fe³⁺ at the later stage of the CP-AIMD trajectory. By 1.0 V, the Fe–N bond remains at ∼1.95 Å. Notably, the narrowing Fe–N bond distribution at this potential reflects reduced thermal vibrational amplitudes, indicating stronger Fe–N bonding due to the planar structure.

EXAFS simulations of the Fe K-edge (Fig. 5e) reflects these structural trends. The k²-weighted Fourier-transformed EXAFS spectra show Fe–N peak shifts that mirror the PDF observations. At 0.8 V, the coexistence of the out-of-plane 2H₂O*–Fe^2.5+N₄ configuration and the in-plane H₂O*–Fe³⁺N₄ configuration leads to a shift of the main Fe–N peak toward higher R values, accompanied by the emergence of an additional peak at lower R values. At 1.0 V, the peak shifts back to lower R values as out-of-plane displacement decreases. The increased peak intensity arises not from coordination changes but from a reduced Debye–Waller factor of Fe–N bonds, signifying shorter, stronger Fe–N bonds due to the reduced degree of out-of-plane displacement. These simulated spectral features align closely with published experimental data (Fig. 5f).

ESI Fig. S14† summarizes our current understanding of how the geometric and electronic properties of pyridinic FeN₄ active sites evolve with applied electrode potential, based on insights from CP-AIMD and XAS simulations. In the figure, we systematically compare experimental interpretations of these potential-induced changes, including oxidation state redox, spin-state transitions, and structural rearrangements against our simulation results. The quantitative agreement reveals that the potential-dependent XAS signatures could be attributed to the IS OH*–Fe³⁺N₄ to HS H₂O*–Fe²⁺N₄ transition as the potential decreases. This insight aligns with experimental discussions previously reported by Jia and Mukerjee, and more recently by Herranz et al.^9,11,12

3.5 Potential-induced shifts in ΔE_QS values

The quadruple splitting energy (ΔE_QS) derived from ⁵⁷Fe Mössbauer spectroscopy serves as a prominent parameter for determining oxidation and spin states of iron sites in experiment. In this study, potential-dependent ΔE_QS values were computed through DFT calculations using CP-AIMD trajectories, enabling direct correlation with spectroscopic doublet signals for precise Fe site assignment.

Fig. 6a displays the potential-dependent ΔE_QS with error bars calculated from 12 randomly chosen CP-AIMD snapshots after equilibrium at each applied potential. The ΔE_QS shifts from 1.30–1.39 mm s⁻¹ to 2.23–2.40 mm s⁻¹ upon reducing the potential from 0.8–1.0 V to 0.0–0.6 V. This transition corresponds to the in-plane IS Fe³⁺ to out-of-plane HS Fe²⁺ conversion in the above discussion. Experimentally, analogous potential-dependent ΔE_QS behavior has been observed in D1 states. Notably, Li et al. recently reported ΔE_QS values of ∼2.0 mm s⁻¹ at 0.2 V and ∼1.1 mm s⁻¹ at 0.8 V for D1 states,⁸ which is quantitatively consistent with our theoretical prediction.

Fig. 6 (a) Potential-dependent ΔE_QS calculated from CP-AIMD trajectory. The insets show the structures characteristics and dominant spin state of Fe center at 0.0–0.6, 0.8 and 1.0 V. (b) Calculated ΔE_QS values two inter-convertible states at low potentials. The error bars represent the standard deviation derived from 12 independent calculations at 0.4 V. The insets show the corresponding d-orbital occupancies and structures of the two states.

Our CP-AIMD simulations reveal dynamic spin-state interconversion at lower potentials (Fig. 3a). Two predominant configurations emerge: (d_xy)¹(d_xz)¹(d_z²)¹(d_yz)¹(d_x²−y²)² (m = 4μ_B) and (d_xy)¹(d_xz)¹(d_z²)^1.5(d_yz)¹(d_x²−y²)¹ (m = 4.5μ_B), with the former exhibiting higher prevalence at 0–0.6 V (ESI Fig. S13†). These distinct spin states demonstrate significantly different ΔE_QS values (Fig. 6b), i.e. 2.43 mm s⁻¹ for the 4μ_B state versus 1.39 mm s⁻¹ for the 4.5μ_B configuration.

3.6 Assignment of the D1 site

While previous experimental studies have ascribed the potential-dependent in-plane/out-of-plane structural transitions (D1 signature) to FeN₄ centers with pyrrolic nitrogen coordination,^8,44,45 our CP-AIMD simulations establish a distinct picture. The structural switching phenomenon is uniquely associated with pyridinic FeN₄ moieties, as demonstrated by quantitative agreement with experimental XAS data and potential-dependent ΔE_QS.

To further validate our findings, we conducted CP-AIMD simulations of pyrrolic-N-coordinated FeN₄ centers at both low (0.2 V) and high (1 V) potentials (Fig. 7). Similar to pyridinic-N FeN₄, these pyrrolic FeN₄ centers spontaneously adsorb water molecules from the electrolyte. However, unlike their pyridinic counterparts, the Fe sites maintain a near-in-plane configuration after H₂O adsorption. Representative interfacial configurations at both potentials are shown in Fig. 7c and d.

Fig. 7 CP-AIMD simulations of pyrrolic FeN₄/H₂O interface. (a and b) Evolution of Fe magnetization (purple curve) and height of the Fe atom above the graphene plane (orange curve). Representative structures of the Fe–N–C/H₂O interface and the PDOS of the corresponding Fe atom and the orbital occupancy from the CP-AIMD simulations at 0.2 (c) and 1 V (d).

Notably, the Fe sites preserve this in-plane geometry across both potential regimes, as demonstrated by consistently low z-coordinates relative to the graphene plane (orange curves in Fig. 7a and b). Complementary static DFT calculations under implicit solvation of various spin states of pyrrolic H₂O*–FeN₄ revealed no distortions in z direction (ESI Fig. S15†), corroborating our CP-AIMD observations. This structural rigidity of pyrrolic FeN₄ stands in stark contrast to the significant structural rearrangements characteristic of experimental D1 sites, highlighting fundamental differences in their behavior.

These collective results demonstrate that the potential-dependent structural and spin-state transitions observed experimentally in D1 sites specifically correspond to pyridinic FeN₄ configurations, not pyrrolic N coordination. Our theoretical evidence compellingly challenges current experimental assignments of D1 sites to pyrrolic FeN₄ centers, suggesting these identifications may require reconsideration.

4 Conclusion

In summary, we investigate potential-dependent structural and spin-state transitions in pyridinic FeN₄ active sites of Fe–N–C catalysts using CP-AIMD simulations with explicit solvent modeling. Our simulations reveal the potential-driven structural and electronic evolution of pyridinic FeN₄ active sites: (i) above 0.8 V, FeN₄ sites adopt a near-planar OH*-coordinated Fe³⁺N₄ configuration with an intermediate spin state (S = 3/2). (ii) Below 0.8 V, strong water adsorption induces structural distortion, leading to non-planar H₂O*-stabilized Fe²⁺N₄ complexes with a high-spin configuration (S = 2). Moreover, as a key potential for the Fe²⁺/Fe³⁺ redox transition, 0.8 V also features a metastable, partially oxidized 2H₂O*–Fe^2.5+N₄ configuration that serves as an intermediate state during the conversion. The potential-dependent XAS and ΔE_QS simulated from these configurations show quantitative agreement with experimental measurements, validating the potential-induced changes in coordination environment and spin state. Our findings explicitly attribute the potential-driven structural and spin-state switching behavior—a signature of D1 sites—to pyridinic FeN₄ moieties, challenging conventional assignments to pyrrolic FeN₄ configurations. By elucidating how applied potential modulates the atomic-level structure, redox properties, and spin states, this work provides fundamental insights for the rational design and optimization of Fe–N–C catalysts. It is worth noting that certain limitations remain in this study. For instance, the limited simulation timescale may preclude the observation of some potential metastable states or magnetic configurations.

Data availability

The data that support the findings of this study are available from the corresponding author, Z. D., upon reasonable request.

Author contributions

H. L., Z. D., and F. T. contributed to the design of the research. H. L. performed DFT calculations. H. L. and Z. D. contributed to the analysis of the results. H. L., Z. D. and F. T. contributed to the writing of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The work is supported by the National Natural Science Foundation of China (52272238) and the Key Research and Development Plan of Tibet Autonomous Region (XZ202401ZY0043).

References

1. F. Jaouen, E. Proietti, M. Lefèvre, R. Chenitz, J.-P. Dodelet, G. Wu, H. T. Chung, C. M. Johnston and P. Zelenay, Recent Advances in Non-Precious Metal Catalysis for Oxygen-Reduction Reaction in Polymer Electrolyte Fuel Cells, Energy Environ. Sci., 2011, 4(1), 114–130.
2. A. Zitolo, V. Goellner, V. Armel, M.-T. Sougrati, T. Mineva, L. Stievano, E. Fonda and F. Jaouen, Identification of Catalytic Sites for Oxygen Reduction in Iron- and Nitrogen-Doped Graphene Materials, Nat. Mater., 2015, 14(9), 937–942.
3. K. Strickland, E. Miner, Q. Jia, U. Tylus, N. Ramaswamy, W. Liang, M.-T. Sougrati, F. Jaouen and S. Mukerjee, Highly Active Oxygen Reduction Non-Platinum Group Metal Electrocatalyst without Direct Metal–Nitrogen Coordination, Nat. Commun., 2015, 6, 7343–7351.
4. G. Wu, K. L. More, C. M. Johnston and P. Zelenay, High-Performance Electrocatalysts for Oxygen Reduction Derived from Polyaniline, Iron, and Cobalt, Science, 2011, 332(6028), 443–447.
5. Y.-C. Wang, W. Huang, L.-Y. Wan, J. Yang, R.-J. Xie, Y.-P. Zheng, Y.-Z. Tan, Y.-S. Wang, K. Zaghib, L.-R. Zheng, S.-H. Sun, Z.-Y. Zhou and S.-G. Sun, Identification of the Active Triple-Phase Boundary of a Non-Pt Catalyst Layer in Fuel Cells, Sci. Adv., 2022, 8(44), eadd8873.
6. X. b. Gao, Y. Wang, W. Xu, H. Huang, K. Zhao, H. Ye, Z.-Y. Zhou, N. Zheng and S.-G. Sun, Mechanism of Particle-Mediated Inhibition of Demetalation for Single-Atom Catalytic Sites in Acidic Electrochemical Environments, J. Am. Chem. Soc., 2023, 145(28), 15528–15537.
7. V. A. Saveleva, K. Ebner, L. Ni, G. Smolentsev, D. Klose, A. Zitolo, E. Marelli, J. Li, M. Medarde, O. V. Safonova, M. Nachtegaal, F. Jaouen, U. I. Kramm, T. J. Schmidt and J. Herranz, Potential-Induced Spin Changes in Fe/N/C Electrocatalysts Assessed by In Situ X-ray Emission Spectroscopy, Angew. Chem., Int. Ed., 2021, 60(21), 11707–11712.
8. J. Li, M. T. Sougrati, A. Zitolo, J. M. Ablett, I. C. Oğuz, T. Mineva, I. Matanovic, P. Atanassov, Y. Huang, I. Zenyuk, A. Di Cicco, K. Kumar, L. Dubau, F. Maillard, G. Dražić and F. Jaouen, Identification of Durable and Non-Durable FeN_x Sites in Fe–N–C Materials for Proton Exchange Membrane Fuel Cells, Nat. Catal., 2020, 4(1), 10–19.
9. J. Li, S. Ghoshal, W. Liang, M.-T. Sougrati, F. Jaouen, B. Halevi, S. McKinney, G. McCool, C. Ma, X. Yuan, Z.-F. Ma, S. Mukerjee and Q. Jia, Structural and Mechanistic Basis for the High Activity of Fe–N–C Catalysts toward Oxygen Reduction, Energy Environ. Sci., 2016, 9(7), 2418–2432.
10. U. Tylus, Q. Jia, K. Strickland, N. Ramaswamy, A. Serov, P. Atanassov and S. Mukerjee, Elucidating Oxygen Reduction Active Sites in Pyrolyzed Metal–Nitrogen Coordinated Non-Precious-Metal Electrocatalyst Systems, J. Phys. Chem. C, 2014, 118(17), 8999–9008.
11. Q. Jia, N. Ramaswamy, H. Hafiz, U. Tylus, K. Strickland, G. Wu, B. Barbiellini, A. Bansil, E. F. Holby, P. Zelenay and S. Mukerjee, Experimental Observation of Redox-Induced Fe N Switching Behavior as a Determinant Role for Oxygen Reduction Activity, ACS Nano, 2015, 9(12), 12496–12505.
12. K. Ebner, A. H. Clark, V. A. Saveleva, G. Smolentsev, J. Chen, L. Ni, J. Li, A. Zitolo, F. Jaouen, U. I. Kramm, T. J. Schmidt and J. Herranz, Time-Resolved Potential-Induced Changes in Fe/N/C-Catalysts Studied by In Situ Modulation Excitation X-Ray Absorption Spectroscopy, Adv. Energy Mater., 2022, 12(14), 2103699.
13. T. Marshall-Roth, N. J. Libretto, A. T. Wrobel, K. J. Anderton, M. L. Pegis, N. D. Ricke, T. V. Voorhis, J. T. Miller and Y. Surendranath, A Pyridinic Fe-N₄ Macrocycle Models the Active Sites in Fe/N-Doped Carbon Electrocatalysts, Nat. Commun., 2020, 11(1), 5283.
14. T. Zheng, J. Wang, Z. Xia, G. Wang and Z. Duan, Spin-Dependent Active Centers in Fe–N–C Oxygen Reduction Catalysts Revealed by Constant-Potential Density Functional Theory, J. Mater. Chem. A, 2023, 11(36), 19360–19373.
15. P. Hutchison, P. S. Rice, R. E. Warburton, S. Raugei and S. Hammes-Schiffer, Multilevel Computational Studies Reveal the Importance of Axial Ligand for Oxygen Reduction Reaction on Fe–N–C Materials, J. Am. Chem. Soc., 2022, 144(36), 16524–16534.
16. M. Yu, A. Li, E. Kan and C. Zhan, Substantial Impact of Spin State Evolution in OER/ORR Catalyzed by Fe–N–C, ACS Catal., 2024, 14(9), 6816–6826.
17. Z. Duan and G. Henkelman, Surface Charge and Electrostatic Spin Crossover Effects in CoN₄ Electrocatalysts, ACS Catal., 2020, 10(20), 12148–12155.
18. J. Xie and Z. Duan, Spin-Orientation-Dependent O₂ Adsorption Mechanism in Fe Single-Atom Catalysts, J. Phys. Chem. C, 2024, 128(49), 20819–20826.
19. S. Yu, Z. Levell, Z. Jiang, X. Zhao and Y. Liu, What Is the Rate-Limiting Step of Oxygen Reduction Reaction on Fe–N–C Catalysts?, J. Am. Chem. Soc., 2023, 145(46), 25352–25356.
20. Y. Wang, B. Li, B. Xue, N. Libretto, Z. Xie, H. Shen, C. Wang, D. Raciti, N. Marinkovic, H. Zong, W. Xie, Z. Li, G. Zhou, J. Vitek, J. G. Chen, J. Miller, G. Wang and C. Wang, CO Electroreduction on Single-Atom Copper, Sci. Adv., 2023, 9(30), eade3557.
21. X. Bai, X. Zhao, Y. Zhang, C. Ling, Y. Zhou, J. Wang and Y. Liu, Dynamic Stability of Copper Single-Atom Catalysts under Working Conditions, J. Am. Chem. Soc., 2022, 144(37), 17140–17148.
22. X. Zhao and Y. Liu, Origin of Selective Production of Hydrogen Peroxide by Electrochemical Oxygen Reduction, J. Am. Chem. Soc., 2021, 143(25), 9423–9428.
23. X. Zhao and Y. Liu, Unveiling the Active Structure of Single Nickel Atom Catalysis: Critical Roles of Charge Capacity and Hydrogen Bonding, J. Am. Chem. Soc., 2020, 142(12), 5773–5777.
24. J.-W. Chen, Z. Zhang, H.-M. Yan, G.-J. Xia, H. Cao and Y.-G. Wang, Pseudo-Adsorption and Long-Range Redox Coupling during Oxygen Reduction Reaction on Single Atom Electrocatalyst, Nat. Commun., 2022, 13(1), 1734.
25. N. Yang, Theoretically Probing the Possible Degradation Mechanisms of an FeNC Catalyst during the Oxygen Reduction Reaction, Chem. Sci., 2021, 12(37), 12476–12484.
26. G. Kresse and J. Furthmüller, Efficiency of Ab Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set, Comput. Mater. Sci., 1996, 6(1), 15–50.
27. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Electron-Energy-Loss Spectra and the Structural Stability of Nickel Oxide: An LSDA+U Study, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57(3), 1505–1509.
28. J. P. Allen and G. W. Watson, Occupation Matrix Control of D- and f-Electron Localisations Using DFT + U, Phys. Chem. Chem. Phys., 2014, 16(39), 21016–21031.
29. G. Henkelman, A. Arnaldsson and H. Jónsson, A Fast and Robust Algorithm for Bader Decomposition of Charge Density, Comput. Mater. Sci., 2006, 36(3), 354–360.
30. E. Sanville, S. D. Kenny, R. Smith and G. Henkelman, Improved grid-based algorithm for Bader charge allocation, J. Comput. Chem., 2007, 28(5), 899–908.
31. W. Tang, E. Sanville and G. Henkelman, A Grid-Based Bader Analysis Algorithm without Lattice Bias, J. Phys.: Condens. Matter, 2009, 21(8), 084204.
32. K. Mathew, R. Sundararaman, K. Letchworth-Weaver, T. A. Arias and R. G. Hennig, Implicit Solvation Model for Density-Functional Study of Nanocrystal Surfaces and Reaction Pathways, J. Chem. Phys., 2024, 140(8), 084106–084114.
33. K. Mathew, V. S. C. Kolluru, S. Mula, S. N. Steinmann and R. G. Hennig, Implicit Self-Consistent Electrolyte Model in Plane-Wave Density-Functional Theory, J. Chem. Phys., 2019, 151(23), 234101.
34. O. Bunău and Y. Joly, Self-Consistent Aspects of X-Ray Absorption Calculations, J. Phys.: Condens. Matter, 2009, 21(34), 345501.
35. S. I. Zabinsky, J. J. Rehr, A. Ankudinov, R. C. Albers and M. J. Eller, Multiple-Scattering Calculations of X-Ray-Absorption Spectra, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52(4), 2995–3009.
36. J. Guan, Z. Duan, F. Zhang, S. D. Kelly, R. Si, M. Dupuis, Q. Huang, J. Q. Chen, C. Tang and C. Li, Water Oxidation on a Mononuclear Manganese Heterogeneous Catalyst, Nat. Catal., 2018, 1(11), 870–877.
37. Z. Duan, J. Timoshenko, P. Kunal, S. D. House, H. Wan, K. Jarvis, C. Bonifacio, J. C. Yang, R. M. Crooks, A. I. Frenkel, S. M. Humphrey and G. Henkelman, Structural Characterization of Heterogeneous RhAu Nanoparticles from a Microwave-Assisted Synthesis, Nanoscale, 2018, 10(47), 22520–22532.
38. Z. Duan, Y. Li, J. Timoshenko, S. T. Chill, R. M. Anderson, D. F. Yancey, A. I. Frenkel, R. M. Crooks and G. Henkelman, A Combined Theoretical and Experimental EXAFS Study of the Structure and Dynamics of Au147 Nanoparticles, Catal. Sci. Technol., 2016, 6(18), 6879–6885.
39. P.-Y. Zhang, X. Xu, W.-S. Yu, Z.-Y. Duan, H. Huang, T. Wang, G. Fu, Z.-Y. Zhou, Y.-C. Wang and S.-G. Sun, Enzyme-Inspired Single Selenium Site for Selective Oxygen Reduction, Angew. Chem., Int. Ed., 2025, 64(8), e202418897.
40. T. Mineva, I. Matanovic, P. Atanassov, M.-T. Sougrati, L. Stievano, M. Clémancey, A. Kochem, J.-M. Latour and F. Jaouen, Understanding Active Sites in Pyrolyzed Fe–N–C Catalysts for Fuel Cell Cathodes by Bridging Density Functional Theory Calculations and ⁵⁷Fe Mössbauer Spectroscopy, ACS Catal., 2019, 9(10), 9359–9371.
41. P. S. Rice, Z.-P. Liu and P. Hu, Hydrogen Coupling on Platinum Using Artificial Neural Network Potentials and DFT, J. Phys. Chem. Lett., 2021, 12(43), 10637–10645.
42. M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford University Press, 2nd edn, 2017.
43. D. R. Evans and C. A. Reed, Reversal of H2O and OH- Ligand Field Strength on the Magnetochemical Series Relative to the Spectrochemical Series. Novel 1-Equiv Water Chemistry of Iron(III) Tetraphenylporphyrin Complexes, J. Am. Chem. Soc., 2000, 122(19), 4660–4667.
44. U. I. Kramm, J. Herranz, N. Larouche, T. M. Arruda, M. Lefèvre, F. Jaouen, P. Bogdanoff, S. Fiechter, I. Abs-Wurmbach, S. Mukerjee and J.-P. Dodelet, Structure of the Catalytic Sites in Fe/N/C-Catalysts for O₂-Reduction in PEM Fuel Cells, Phys. Chem. Chem. Phys., 2012, 14(33), 11673.
45. L. Ni, C. Gallenkamp, S. Wagner, E. Bill, V. Krewald and U. I. Kramm, Identification of the Catalytically Dominant Iron Environment in Iron- and Nitrogen-Doped Carbon Catalysts for the Oxygen Reduction Reaction, J. Am. Chem. Soc., 2022, 144(37), 16827–16840.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sc03057a

---