Unusual polar ordering and room-temperature blue phase stabilization in tetrafluorinated bent-shaped mesogens

Abstract

The growing demand for advanced photonic and electro-optical devices necessitates the rational design of novel functional materials. Liquid crystals (LCs) are particularly promising due to their highly tunable electro-optical properties. Building on this potential, we synthesized a series of polar bent-core LCs, F4-na (dipole moment ∼9.4 D), featuring a tetrafluorinated terminal motif and varying terminal chains. Distinct structure–property relationships are observed in this series of compounds, with the shorter chain homologues forming polar cybotactic clusters (N_cyb phase) alongside nematic and tilted smectic phases. Dielectric spectroscopy reveals non-trivial dipolar ordering, attributed to short-range polar order within cybotactic clusters, notably present without net macroscopic polarization. Under an AC field, the materials form electroconvection patterns, suggesting potential for optical modulation devices. Furthermore, the F4-na materials, particularly the lower homologues showing cybotactic clusters, stabilize the otherwise unstable blue phase (BP) at room temperature when doped with a chiral additive, achieving a maximum BP range of 22.9 °C. This overcomes the challenges in achieving room-temperature BP with our easily synthesizable materials, holding strong potential for 3D photonic applications. Overall, our findings offer promising opportunities for advancing room-temperature photonic and electro-optical devices while enhancing the understanding of self-assembly in soft functional materials.

---

Introduction

The advancement of electro-optical and photonic devices hinges on the judicious design of novel functional materials that are responsive to electric fields. Liquid crystals (LCs), owing to their easily tunable electro-optical properties and high responsiveness to external stimuli, are promising candidates for advanced applications. In liquid crystalline systems, the molecular shape, structure, and composition play a pivotal role in defining their properties. Bent-shaped LCs, owing to their distinct geometry, introduce chirality and polarity into the supramolecular assembly. These features can result in the formation of polar-responsive assemblies or clusters, giving rise to phenomena such as electroconvection, ferroelectricity, and flexoelectricity.¹ Thus the presence of these polar clusters directly influences the electro-optical and dielectric characteristics of the material. Bent-core molecules are designed to induce polar ordering by varying the terminal substituents and incorporating polar functional groups. Considerable effort has been devoted to understand the fundamental molecular interactions that influence the phase structures and physical properties of various bent-core systems.

To date, numerous symmetrical and asymmetrical bent-core molecules have been reported to exhibit polar nematic (N), smectic (Sm), and cybotactic nematic (N_cyb) phases. These phases are predominantly observed in molecules featuring polar substituents such as cyano, nitro, and azo groups, as well as in hydrogen-bonded systems, oxadiazole cores, terminal polycatenars,² and halogenated structures, all of which display distinct polar switching behavior.^1,3,4 Among these, fluorinated systems stand out due to their enhanced ability to induce such properties in bent-core LCs.^5–8 The electronegativity and small steric effects of fluorine contribute to the induction of polar behavior, with the number and positioning of fluorine atoms significantly influencing these properties.^9–12 In the pursuit of developing novel polar bent-core LCs with improved electro-optical properties, we designed and synthesized a series of achiral polar bent-core LCs (Fig. 1), incorporating a tetrafluorinated aromatic ring as the terminal motif on the short arm. This highly fluorinated system is connected to a methylated core, featuring ester and salicylaldimine linkages, resulting in a polar bent-shaped molecule designated as F4-na (with F4 indicating tetrafluorination and ‘na’ denoting varying terminal chain lengths of the molecule's longer arm). Here, ‘n’ represents the terminal chain lengths (8, 12, 14, 16, 18), as illustrated in Fig. 1.

Fig. 1 (a) Molecular structure of the F4-na series of compounds (with n representing various homologues) (b) a plausible model illustrating the formation of cybotactic clusters in these compounds (n̂ at the bottom indicating the average director direction).³

Preliminary investigations of pristine bent-core compounds F4-na by polarized optical microscopy (POM) and differential scanning calorimetry (DSC) revealed monotropic LC behavior, (with higher homologues n = 16 and 18 also showing short temperature-range LC phase in heating cycle). Temperature-dependent X-ray scattering measurements confirmed the presence of the intervening N_cyb phase (smectic clusters in the nematic phase), in addition to the nematic (N) and tilted smectic (SmC) phases. Dielectric spectroscopy measurements indicated the presence of polar cybotactic clusters in certain homologues (with varying n), exhibiting short-range polar ordering despite the absence of macroscopic polarization in any of the mesophases, which is an unusual observation. Interestingly, the F4-na compounds exhibited electroconvection patterns upon the application of an AC field, reinforcing the dielectric findings on the presence of short-range polar clusters. The electroconvection phenomena observed under an AC field showed distinct patterns across homologues, emphasizing the significant role of terminal alkoxy chain length on the nature and evolution of these non-equilibrium states. Electroconvection in LCs provides exciting opportunities for applications involving optical modulation and dynamic material systems under non-equilibrium conditions.

Building on our exploration of polar behavior in fluorinated achiral bent-core LCs F4-na, we extend our investigation to the role of tetrafluorination in stabilizing LC phases, with a focus on chiral composites based on these materials. Fluorinated molecules exhibit a unique potential to expand the temperature range of otherwise unstable mesophases, while also inducing polar behavior and improving electro-optical properties.^13–15 Complementing these properties, the bent molecular shape plays a crucial role in stabilizing disclination lines within self-assembled supramolecular lattices, particularly in frustrated chiral LC phases such as blue phases (BPs).¹⁶ These unique phases show great potential for use in 3D photonic devices owing to their periodic lattice structure and low-voltage tunability of optical properties. However, BP-based devices have not yet been much developed due to stability issues at room temperature. To address this, we utilized the synergistic effects of tetrafluorination and bent molecular architecture in our molecular system by combining these materials with a chiral dopant to form a stable BP composite at room temperature.

BPs have been observed in single-molecule systems, composite materials,¹⁷ and polymeric formulations, including both rod-shaped and bent-core fluorinated LCs.^18,19 Despite these advances, there remains substantial potential for developing easily synthesizable materials that can exhibit room-temperature BPs. In our study, we successfully utilized F4-na materials in combination with the chiral dopant S811 and room-temperature LC 5CB to induce and stabilize BPs at ambient temperature. By incorporating S811 into F4-8a, we achieved a maximum BP range of ∼22.9 °C near room temperature, which was further stabilized down to room temperature for ∼8.9 °C range by using 5CB as an additional dopant. This study revealed a systematic dependence of the relative concentrations of the host achiral fluorinated bent-core materials F4-na with the dopants 5CB and S811, providing unique insights into the self-assembly behavior involved in the formation of BP lattices. Additionally, some previous reports^20–22 indicate that cybotactic clusters (N_cyb) may play a significant role in stabilizing BPs. However, the relationship between cybotactic clusters and chirality amplification within these phases remains largely unexplored. A deeper understanding of structural factors influencing cybotactic cluster formation and BP behavior is essential for developing advanced lasers, photonic devices, and display technologies. Our detailed investigation enriches this understanding by exploring the structural interplay between macroscopic polarization, cybotactic clusters, and BP stabilization under ambient conditions.

Results and discussion

Synthesis and characterization

The synthesis of the F4-na (n: 8, 12, 14, 16, 18) series of compounds involves incorporating a highly fluorinated aromatic ring through an ester linkage as the short terminal arm of a bent-shaped molecule. This molecule features a central methylated core and an extended ring system with flexible terminal chains of varying lengths, forming the long arm, as shown in Fig. 1a. The detailed synthetic scheme and procedures are provided in ESI (Scheme S1†). The ester linkage is crucial for optimizing flexibility within the molecular structure, thereby facilitating LC behavior. The fluorinated short arm is attached to a methyl-substituted core, with the methyl group positioned at the transverse site, a key factor in promoting mesomorphism in bent-shaped LCs. Subsequently, this core connects through hydrogen bonding-stabilized Schiff base linkages with an extended ring system bearing terminal chains of varying lengths. The Schiff base linkage plays a pivotal role in molecular design, contributing significantly to the stability of LC behavior. The synthesized intermediate and final compounds have been characterized using ¹H NMR, ¹³C NMR, ¹⁹F NMR, IR and UV-vis spectroscopy (details provided in ESI, Fig. S1–S7†).

The F4-na series of compounds (with n = 8, 12, 14) exhibits monotropic LC behavior. Specifically, the emergence of the nematic phase featuring cybotactic clusters (N_cyb, Fig. 1b)³ along with the conventional nematic (N) and smectic C (SmC) phases is observed. Analysis of the structure–property relationship across different homologues reveals distinct patterns: lower homologues of the series with n = 8, 12, and 14 demonstrate a sequence of N, N_cyb, and SmC phases, whereas n = 16 shows the absence of the N_cyb phase, primarily exhibiting short-range N and predominant SmC phases. Conversely, n = 18 exclusively displays the SmC phase. The LC phase is also observed in the heating cycle for n = 16 and 18 for short-temperature range. The investigation of mesomorphic behavior and structure–property relationships has been conducted employing POM, DSC, and temperature-dependent small-angle and wide-angle X-ray scattering (SAXS/WAXS) techniques.

POM studies on F4-na materials were conducted at varying temperatures (at cooling rates of 5 °C min⁻¹ and 10 °C min⁻¹) by placing the sample on a glass slide with a coverslip. The sample F4-8a, upon cooling from the isotropic phase, at 108 °C exhibited a transition to the N phase, as evidenced by the emergence of birefringence under crossed polarizers conditions (Fig. 2a). Subsequently, as the temperature further decreased, the birefringence vanished, transitioning to a dark texture with intermittent bright spots (Fig. 2b). This observation underscores the pronounced tendency of the molecules to spontaneously align homeotropically within the N phase. Such inherent tendency of molecules to align homeotropically is advantageous, resulting in lower threshold voltages for electric-field-driven switchability and faster response times, thereby improving energy efficiency and device performance. Upon further cooling, another transition to the SmC phase occurs at 80.9 °C, as evidenced by distinct textures (Fig. 2c). The tilted orientation of the SmC phase was confirmed under homeotropic anchoring conditions, where the textures show distinctive features instead of a dark appearance, indicating molecular tilt. Additional features are elaborated in the birefringence studies. These findings are further supported by SAXS/WAXS measurements (detailed in the next section). In a homeotropic cell with a thickness of 18.3 μm, the observed behavior is similar to that on a standard glass slide, with the appearance of birefringence upon transition to the N phase (at 101.5 °C), followed by a dark texture with some birefringent spots. Upon further cooling, birefringence texture emerges on transition to a tilted smectic phase, followed by crystallization of the sample (Fig. S8, ESI†).

Fig. 2 POM textures observed for F4-8a on a glass slide, illustrating (a) the appearance of birefringence in the N phase, (b) birefringent spots within homeotropic-like dark textures in the N phase, and (c) textures observed in the SmC phase (cooling rate 5 °C min⁻¹).

The F4-na samples with n = 12, 14, and 16 exhibit similar behavior upon cooling from the isotropic phase on a glass slide, transitioning to a birefringent texture which subsequently changes into a homeotropic alignment until converts to the Smectic phase. These samples display variations in their textures, presenting unique patterns when observed in both planar and homeotropic cells. The detailed phase sequences and textures for these samples are provided in the ESI (Fig. S9–S11, S18 and S19†). In contrast, the sample with n = 18, which exclusively displays the SmC texture, exhibits distinct Schlieren textures with focal conic textures overlaying on a glass slide, while showing characteristic focal conic textures of the smectic phase when observed in a planar cell (detailed in the ESI, Fig. S12†). The phase transition temperatures and their corresponding enthalpy changes as determined through DSC, are provided in Table 1 and Fig. S13 (ESI†). These findings are further corroborated by SAXS/WAXS measurements, as elaborated in the next section.

Table 1 Phase transition temperatures for F4-na series of compounds (Iso: isotropic, N: nematic, N_cyb: nematic with cybotactic clusters, SmC: smectic C; Cr: crystal)

Compound	Transition temperatures (°C) and enthalpy change (kJ mol^−1) [in Brackets]; *transitions confirmed by POM studies; ^#designated by SAXS/WAXS studies
F4-8a	Heating: Cr1 45.4 [−10.6] Cr2 109.3* [14.7] Iso
	Cooling: Iso 108.0* N 91.0^# Ncyb 80.9 [−0.3] SmC 69.2* Cr
F4-12a	Heating: Cr 103.7 [6.5] Iso
	Cooling: Iso 103.4 [−0.9] N 99.0^# Ncyb 94.2 [−0.8] SmC 59.4 [−4.6] Cr
F4-14a	Heating: Cr 104.1 [27.1] Iso
	Cooling: Iso 102.3 N 98.3 Ncyb 92.0^# SmC 62.0 [−40.7] Cr
F4-16a	Heating: Cr1 77.5 [−5.7] Cr2 94.9 [24.0] SmC 98.7* N 104.0* Iso
	Cooling: Iso 103.7* N 98.8 [−2.5] SmC 67.7 [−38.8] Cr
F4-18a	Heating: Cr1 83.6 [−3.1] Cr2 98.3 [39.4] SmC 103.3 [3.0] Iso
	Cooling: Iso 102.1 [−3.4] SmC 74.0 [−44.0] Cr

---

SAXS/WAXS measurements

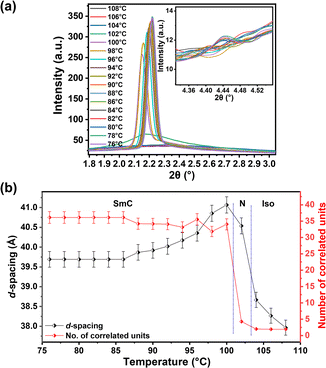
The detailed mesomorphic analysis of F4-na compounds was conducted through temperature-dependent SAXS/WAXS measurements, employing small temperature intervals of 2 °C and a cooling rate of 5 °C min⁻¹ from the isotropic to crystal phase. This investigation unveiled the presence of cybotactic clusters in the nematic phase of samples with n = 8, 12, and 14, as evidenced by variations in correlation length derived from the SAXS data (detailed in ESI†). Throughout the LC range, a distinct small-angle peak and a wide-angle peak are consistently observed. Conversely, compounds with n = 16 and 18 exhibit an additional small-angle peak, indicating the layered structure.

The occurrence of the N_cyb phase in compound F4-14a has been discussed in detail (Fig. 3). The d-spacing obtained from the diffused wide-angle peak is ∼4.5 Å, attributed to fluid alkyl chain–chain correlations. The small-angle peak is broad at higher temperatures, becoming sharp and intense as the temperature decreases. To understand the mesomorphism exhibited by these compounds, the variation of the correlation length, expressed in terms of the number of correlated units, has been calculated (details in ESI†). In the isotropic phase (at 110 °C), the sample shows diffused peaks in both the small and wide-angle regions. As the temperature decreases and the sample transitions to the N phase (at 100 °C), the intensity of the small-angle peak increases. Further transition to the SmC phase at lower temperatures is intervened by the N_cyb phase, characterized by the observation of smectic clusters in the nematic phase. This is evident in Fig. 3c and d (at 95 °C), showing a relatively sharp peak, further validated by the calculation of variations in correlation length (Fig. 4b and Table S3†). The d-spacing variation ranges from 36 Å to 38.5 Å, and the number of correlated units ranges from 2 to 31. In the isotropic and N phases, the number of correlated units is about 2, increasing to 3–15 in the N_cyb phase and more than 20 in the SmC phase. The d-spacing in the SmC phase is less than the molecular length L (obtained from DFT optimized structure, Table S8 and Fig. S26–S28, detailed in ESI†), confirming a tilted phase.²³ The behavior of F4-12a is similar, as shown in Fig. 4a and Table S2.† The presence of the N_cyb phase is also observed in F4-8a for a temperature range of ∼10 °C. However, F4-8a exhibits N phase for a wider temperature range compared to other homologues (structure–property relation presented in Fig. S17†). In contrast, the higher homologues F4-16a and F4-18a, do not exhibit the N_cyb phase. Instead, a layered periodic structure is inferred in the SmC phase, indicated by the presence of two small-angle peaks with a d-spacing ratio of 1 : 1/2. Notably, the N phase is completely absent in the F4-18a. Detailed SAXS data and the corresponding d-spacing calculations for these homologues are provided in the Fig. 5, S14–S16, and Tables S1–S5 (ESI†).

Fig. 3 (a) Temperature-dependent WAXS data for the F4-14a sample, showing a small-angle peak and a diffuse wide-angle peak (b) SAXS data for F4-14a, displaying the variation in intensity as a function of 2θ (scattering angle), showing the temperature-dependent behavior of the small-angle peak (c) SAXS peaks expressed in q-space (q = 4π × sinθ/λ is the scattering wave vector) at different phases: Iso (110 °C), N (100 °C), N_cyb (95 °C), and SmC (72 °C) and (d) the corresponding 2D pattern of the SAXS peak in different phases.

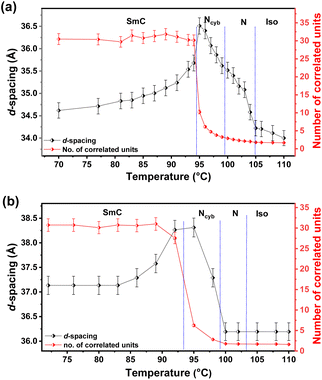Fig. 4 Temperature-dependent variation of d-spacing and the number of correlated units in different phases observed for (a) F4-12a and (b) F4-14a.

Fig. 5 (a) Temperature-dependent SAXS data for F4-16a. The inset shows an additional small-angle peak confirming the periodic layered structure of the SmC phase. (b) Variation of d-spacing and the number of correlated units with respect to temperature for F4-16a.

Analysis of birefringence properties

To investigate the optical properties of the materials with varying temperatures, birefringence studies were conducted. The birefringence (Δn) measurements were made using an optical spectral technique²⁴ for which a planar aligned cell (cell thickness d = 9 μm, antiparallel buffing) filled with the sample (F4-8a, F4-12a, F4-14a) was kept under a microscope with crossed polarizers, and the angle (ψ) between the rubbing (R) direction and the polarizer (P)/analyzer (A) was fixed at 45°. The samples exhibited homogeneously ordered textures in the N and N_cyb phases, with broken fan textures observed in the SmC phase within planar cells. In homeotropic cells, small defects emerged in the N_cyb phase, increasing in size as the temperature decreased, eventually forming the Schlieren texture characteristic of the SmC phase. These defects are associated with cybotactic clusters, which are more difficult to orient homeotropically and expand as the sample cools (Fig. S18 and S19, ESI†). The transmittance (T) spectra of the LC sample as a function of wavelength were recorded at different temperatures using a spectrometer. The transmitted light passed through an LC cell can then be expressed as²⁵here, I₀ is the intensity of the plane polarized light that falls on the cell, α is the angle between the LC director and the polarizer (kept at 45° in the current measurements), Δn is the birefringence of the sample, d is the thickness of the cell, λ is the wavelength of light, and D is an offset signal which accounts for leakage of light through the cell. Now, Δn also depends on the wavelength of incident light (λ) due to dispersion, which is governed by an extended Cauchy equation given by^26,27where k is a temperature-dependent scaling factor proportional to the order parameter (S). In contrast, λ* is a temperature-independent dispersion parameter. The recorded transmittance data is fitted to eqn (1) by considering Δn as a function of wavelength given by eqn (2). The dispersion parameter λ* was found to be 214 nm for the studied compounds, from fitting the highest temperature spectrum, which is just below the Iso–N transition temperature. As mentioned above, the value of λ* is temperature independent (i.e., dispersion remains the same under temperature variation) when the measurements are being performed in the absence of electric field. Fig. 6a and b display the variation of Δn as a function of temperature for F4-12a and F4-14a at a wavelength of 550 nm, respectively. The insets in Fig. 6 illustrate the temperature dependence of the scaling factor, k, for (a) F4-12a and (b) F4-14a.

Fig. 6 Temperature-dependent variation of birefringence (Δn) for (a) F4-12a and (b) F4-14a at a wavelength of 550 nm, measured in a planar-aligned cell with a thickness of 9 μm. The insets display the temperature dependence of the scaling factor, k, for the respective compounds.

The plot shows a sharp increase in Δn near the Iso–N transition temperature, followed by a more gradual rise in Δn as the temperature continues to decrease. The gradual increase in Δn with decreasing temperature can be attributed to enhanced molecular ordering as the sample cools further. Notably, a distinct jump in Δn is observed at the N/N_Cyb-SmC transition, reflecting the phase change. The abrupt increase in Δn near the SmC phase is primarily due to the introduction of translational ordering in the LC matrix upon entering the smectic phase (increased ordering), compared to the purely orientational ordering present in the N phase.^28,29 Additionally, the N to N_cyb transition is observed as a slight change in the slope of the Δn vs. T curve, indicating increased molecular ordering due to the formation of larger cybotactic clusters in the N_cyb phase.

Dielectric properties

In order to understand the polar behavior of the observed clusters and the dielectric characteristics of various homologues in the F4-na series, we employed the dielectric relaxation spectroscopy technique. The F4-na series of compounds have a net dipole moment of ∼9.4 D (from DFT calculations, Table S8 and Fig. S26–S28, ESI†). The LC samples (F4-8a, F4-12a, F4-14a showing N_cyb) were first heated above their isotropic transition temperature, and dielectric measurements were then performed during slow cooling with a temperature step of 0.5 °C. A small voltage of 0.1 V was applied across the samples, with measurements taken over a frequency range of 1 Hz to 10 MHz. The temperature of the samples was stabilized to within ±0.02 °C. Fig. 7a and d present the dielectric loss spectra of F4-12a as a function of temperature and frequency in homeotropic and planar cells, respectively. Three relaxation processes H1, H2, and P1 of varying magnitude can be observed in homeotropic and planar cells, respectively. In both alignments, high-frequency processes H_ITO and P_ITO, were detected beyond the presented data (∼15 MHz) which can be assigned to the finite resistance (∼10 Ω □⁻¹) of the ITO-coated electrodes in series with the cell capacitance. The H1, H2, and P1 peaks are temperature-dependent and hence can be related to the relaxation process of the LC sample. The observed dielectric spectra were analyzed by fitting the experimentally recorded complex permittivity (ε*) to the Havriliak–Negami (HN) equation to calculate the dielectric relaxation frequencies (f_r) and corresponding strengths (δε) of the relaxation modes.

Fig. 7 (a) and (d) Dielectric loss spectra (ε′′) of F4-12a as a function of temperature and frequency in homeotropic and planar cells, respectively. (b) and (e) Dielectric loss spectra fitted with the HN equation for homeotropic and planar cells at T = 100 °C, highlighting the presence of three relaxation modes in each case (c) and (f) Temperature dependence of relaxation frequencies (f_r) and corresponding dielectric strengths (δε) for F4-12a, showing the relaxation modes observed in homeotropic and planar cells.

WINFIT software of Novocontrol GmbH was used to fit the dielectric spectra data. The HN equation is given as^30,31

where ε′ is the dielectric permittivity, ε′′ is the dielectric loss, ε_∞ is the limiting value of dielectric permittivity at a high frequency that depends on the electronic and atomic polarizabilities of the material, ω = 2πf is the angular frequency of the probe field, ε₀ is the permittivity of free space, σ_DC is DC conductivity, τ_k is the relaxation time and δε_k is the dielectric strength of the k_th process, α_k and β_k are the symmetric and asymmetric broadening parameters which determine the distribution of the relaxation times of the k_th process. Fitting the dielectric spectra reveals that both the low- and high-frequency processes in homeotropic and planar cells are of the Cole–Cole type (β = 1).

Fig. 7b and e show the fitted dielectric loss spectra to eqn (3) for F4-12a in homeotropic and planar cells at T = 100 °C, respectively. The HN fitting aids in understanding the origin and evolution of the three prominent peaks observed for F4-12a (Fig. 7a and d). The high-frequency peaks (H2), with low dielectric strengths (δε < 2), are attributed to individual molecular rotations around the short axis. In contrast, the lower frequency processes (H1, P1), with large dielectric strengths (δε > 70), correspond to the collective fluctuations of cybotactic clusters formed by bent-core molecules across all mesophases, including the isotropic phase.^32–35 The fitted spectra also reveal an additional relaxation peak (P2) in the planar cell, characterized by a small dielectric strength δε ≈ 0.1 and a relaxation frequency (f_r) of 2.55 × 10⁵ Hz in planar cell. The P2 process is similar to H2 but exhibits ∼10 times weaker dielectric strength, suggesting it is also associated with the molecular rotation of F4-12a molecules around their short axis. This difference in dielectric strength between the P2 and H2 processes was previously noted by Shanker et al.,³² and was attributed to a significant pretilt of the director relative to the substrate and the low smectic orientational order parameter (S) of the molecular system.

The variation of relaxation frequencies and corresponding dielectric strengths of the H1 and P1 modes with temperature is illustrated in Fig. 7c and f. The P2 process exhibits very low dielectric strength across the entire temperature range. The strength of the H2 process, as shown in Fig. 7c, is also small (δε ≈ 0.4) in the isotropic phase, but it begins to increase near the isotropic-to-N transition, stabilizing at about δε ≈ 1 below this transition. Similar behavior for relaxation modes associated with molecular rotation around the short axis has been observed in bent-core molecules.^32,36 The low-frequency H1 and P1 processes are attributed to the collective motion of cybotactic clusters, which begin to form deep within the isotropic phase due to dipolar interactions among bent-core molecules.^37–39 This relaxation mode persists even in the isotropic phase, with its strength remaining relatively constant as the temperature decreases below the Iso–N transition. While similar behavior has been observed in polar bent-core molecules, where the dielectric strength of collective motion increases below this transition due to macroscopic polarization leading to larger cluster sizes and enhanced dielectric strength with decreasing temperature,^30,40 no such macroscopic polarization was observed in the F4-na compounds. Consequently, there is no related enhancement in the dielectric strength of the H1 and P1 processes. However, the relaxation frequency of this collective motion decreases with decreasing temperature, which can be explained by the increasing viscosity of the LC material that restricts the motion of molecular clusters.

Similar results were observed for F4-14a and F4-8a, as shown in Fig. 8 and S20,† respectively. The planar cell filled with F4-14a exhibited two LC-based processes with origins and characteristics similar to those observed in F4-12a. In the homeotropic cell filled with F4-14a, results akin to those for F4-12a were also noted, although the collective cluster relaxation process shifted to an even lower frequency (∼5 Hz), merging with the parasitic ionic relaxation caused by the separation and accumulation of ions on the polymeric alignment layers. Consequently, an increased dielectric strength of the collective relaxation process was observed in homeotropic cells filled with F4-14a. However, in F4-na series of compounds, despite the existence of clusters, there is no ferroelectric-like response in any of the LC phases of the studied homologues (detailed in spontaneous polarization studies, Fig. S22 and S23, ESI†). Further, a similar trend was also noticed through the dielectric permittivity ε′ for all three compounds (Fig. S21†). The ε′ measurements didn't show any mesoscopic enhancement of the permittivity values which is a characteristic feature of macroscopic polar ordering in bent-core LCs.

Fig. 8 (a) and (b) Dielectric loss spectra (ε′′) of F4-14a as a function of temperature and frequency in homeotropic and planar cells, respectively. (c) Temperature variation of relaxation frequencies and corresponding dielectric strength for F4-14a in planar cell.

Response of cybotactic clusters under DC electric field

To further investigate the behavior of the collective relaxation mode (P1) of cybotactic clusters, we examined the dielectric spectra under DC bias voltage. The dielectric loss spectra were recorded for F4-na compounds exhibiting N phases (n = 8, 12, 14, 16). For clarity, we subtracted the parasitic effects of ITO and the DC conductivity factor. Fig. 9 illustrates the variation in dielectric loss spectra (ε′′) for the low-frequency collective relaxation mode (P1) as a function of frequency for different bias voltages. Interestingly, while the P1 mode is present in all the homologues, it showed contrasting results under DC voltage among the shorter terminal chain compounds (F4-8a and F4-12a) and those with longer chains (F4-14a and F4-16a). In the longer-chain molecules, the P1 process initially shifts to a lower frequency with a small DC voltage (∼5 V), but as the DC bias increases, the collective relaxation process becomes completely suppressed (Fig. 9b). This suppression of the low-frequency collective relaxation under DC bias in bent-core compounds with cybotactic clustering has previously been noted only in ferroelectric bent-core molecules.^33,41,42 This variation in the P1 response further supports the conclusion that the low-frequency process is related to cybotactic clusters rather than ionic effects.

Fig. 9 Effect of DC bias voltage on the P1 relaxation mode at T = 100 °C (N phase) in (a) F4-12a and (b) F4-14a compounds, filled in planar cell of thickness 9 μm.

In homologues with shorter terminal chains, the application of DC bias results in a shift of the P1 relaxation frequency to lower values, while the dielectric strength remains largely unchanged, indicating no effective suppression even at higher DC bias (Fig. 9a). This kind of variation in the relaxation frequency and dielectric strength of the low frequency collective relaxation process have not been observed previously and can be attributed to the characteristics of non-polar cybotactic clusters. The suppression of the P1 relaxation in long chain molecules suggests the presence of small-scale polar ordering within the clusters. Although this ordering does not yield macroscopic polarization, it facilitates the reorientation of the clusters in response to the applied DC field. In contrast, the short-chain molecules exhibited no suppression under DC bias for the low-frequency process, indicating that the small polar clusters are strong enough to withhold the DC bias. Thus, as the chain length increases, the strength of dipole–dipole interactions inside the polar clusters decrease and hence we observe the two contrary behaviors of the low-frequency relaxation process under the application of DC bias. These findings underscore the critical influence of terminal chain length on the properties and behavior of cybotactic clusters in bent-core LCs.

Electroconvection (EC) patterns under AC voltage

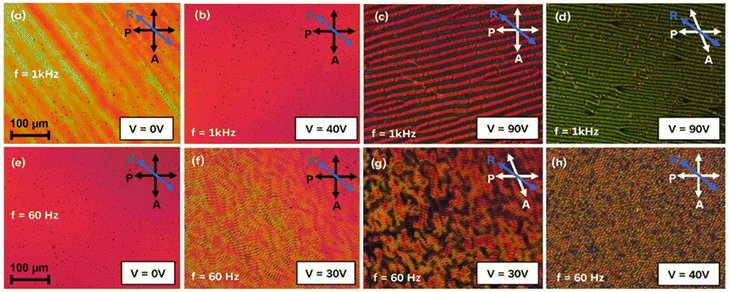
To understand and control their dynamic electro-optical behaviors, LC samples have been studied under an AC field. Particularly, the investigation of field-induced structured patterned states in N LCs represents a significant avenue in the study of nonequilibrium systems.^43,44 Understanding and predicting the effects of external electric fields in nonlinear systems like LCs, which are sensitive to pattern-forming instabilities, is crucial for both research and technological applications such as beam steering and optical switches.^45,46 When an external electric field is applied to a LC, it typically induces a collective molecular reorientation known as the Freedericksz transition (FT), which is foundational for modern LC-based displays and sensors.^47,48 However, the electric field often fails to produce uniform reorientation (uniform FT), instead leading to spatially periodic and localized distortions that form 3D patterns. These patterns result from several factors, with electroconvection (EC) theory providing a comprehensive framework for understanding the periodic modulation of the director in LC pattern formation. In EC pattern formation, director modulation because of macroscopic polarization, material flow, and space charge ordering significantly contributes towards the origin and evolution of these patterns. The formation of EC patterns is influenced by factors such as the geometry of the cell (planar or homeotropic) and the anisotropies within the LC system. The Carr-Helfrich model, often referred to as the standard model of EC patterns (s-EC), was one of the first to describe these phenomena. However, patterns that cannot be explained by this model are termed non-standard EC patterns (ns-EC). In our study of the EC patterns in F4-na molecules, we observed several intriguing ns-EC patterns, a few of which are presented here (Fig. 10 and S24†).

Fig. 10 Optical micrographs depicting the EC patterns in the N phase (T = 93 °C) of the F4-8a molecule under crossed polarizers, with the rubbing direction (R) oriented at 45° to both the polarizer and analyzer. When the frequency of the applied sine wave AC voltage (V_pp) is set to 1 kHz (a)–(d), the resulting transverse wavy stripes are distinctly visible and appear thicker (c). In contrast, lowering the frequency to 60 Hz (e)–(h) produces smaller and less stable transverse stripes (f). Notably, changing the analyzer angle does not result in a color interchange at either frequency (d) and (g).

The development of EC patterns in the N phase of F4-8a and F4-12a under different AC voltages (V) and frequencies (1 kHz and 60 Hz) is illustrated in Fig. 10 and S24.† In F4-8a, a clear formation of transverse wavy stripes appears perpendicular to the rubbing direction (R) when a 1 kHz AC voltage is applied (Fig. 10c). At 60 Hz, the stripes become thinner and more unstable (Fig. 10f). These results are similar to the prewavy pattern reported⁴⁹ by Tanaka et al. However, no color interchange was observed when the analyzer was rotated (Fig. 10d and g). Additionally, at 60 Hz, the stripes become dynamic, with thin transverse stripes overlapping thicker longitudinal ones (refer ESI Video†), forming a mesh-like pattern as the voltage increases (Fig. 10h). This dynamic behavior is not typically associated with prewavy patterns but is more characteristic of other forms of non-standard EC (ns-EC) patterns.⁴³ Further analysis is required to better understand the origin and dynamics of these EC patterns. Similar measurements were conducted on the N phase of F4-12a (details in ESI, Fig. S24†) and other homologues. These studies revealed intriguing behaviors that require further investigation. A more in-depth exploration of these findings is currently underway and will be the subject of a separate manuscript.

Blue phase induction at room temperature

Building on our investigation of polar behavior in fluorinated achiral bent-core LCs F4-na, we now explore how tetrafluorination aids in stabilizing LC phases. Fluorinated systems have shown notable success in stabilizing BPs across broad temperature ranges, as mentioned earlier. Furthermore, these systems enhance the electro-optical properties of BPs, including the Kerr constant.⁵⁰ In our study, F4-na fluorinated bent-core compounds were explored for their potential to induce and stabilize BP through doping with the room-temperature LC 5CB and a chiral dopant S811 (refer to ESI† for structures and detailed methods, Fig. S25†). As discussed earlier, we have explored these materials in inducing the BP owing to the synergistic effects of tetrafluorination and the bent shape of the molecules. Various homologues of F4-na (n = 8, 12, 14, 16, 18) were doped with an optimized concentration of 5CB and S811 following iterative trials. Interestingly, while the higher homologues, F4-16a and F4-18a, failed to induce the BP, those with n = 8, 12, and 14 were successful. Among these, the samples with n = 8 and 12 (lower terminal chain lengths) exhibited a greater tendency to induce the BP, likely related to the stability of the N phase observed in the 8 and 12 homologues.

A graphical representation of the temperature ranges observed for the BP across various mixtures containing different homologues of bent-core compounds is provided in Fig. 11. As previously discussed, homologues with n = 8 and 12 show higher efficacy in inducing BP. The presence of N_cyb phase in these compounds appears to play a key role in contributing to this property of induction and stabilization of BP. In the mixtures depicted in Fig. 11, with varying homologues and concentrations, BP ranges of ∼8 °C were observed, albeit above room temperature. Detailed information regarding the temperature ranges is provided in Table S6 (ESI†). Corresponding POM textures illustrating platelet formations for some of the mixtures are displayed in Fig. 12.

Fig. 11 Graphical representation illustrating the temperature range of BP formation as a function of varying homologues of F4-na series (a)–(c) correspond to compositions of 35 : 45 : 20, 25 : 45 : 30, and 45 : 25 : 30 weight percent of F4-na:5CB:S811, respectively.

Fig. 12 POM textures illustrating BP formation (platelet textures) in (a) doped mixture F4-8a:5CB:S811, (b) doped mixture F4-12a:5CB:S811, and (c) doped mixture F4-8a:5CB:S811, weight percent ratios are indicated in the respective images.

Subsequent optimization of relative concentrations focused on the F4-8a homologue, with varying concentrations of 5CB and S811. Initial attempts at direct doping with S811 at different concentrations revealed phase separation beyond a 50 : 50 weight percent ratio. The optimal stabilization of the BP was achieved at a concentration of 20–30 wt% of the chiral dopant S811. The results, including a maximum BP temperature range of approximately 22.9 °C (for 80 : 20 mixture) are summarized in Fig. 13a and Table S7 (ESI†). These observations offer two key insights into BP formation in bent-core molecules. First, the successful induction of BP in non-ferroelectric F4-na compounds indicates that formation is dependent on cybotactic cluster tendencies rather than macroscopic polar ordering. Second, BP efficacy is influenced by terminal chain length, favoring shorter chains (F4-8a and F4-12a) over longer ones (F4-14a). Further, as discussed previously, the cybotactic clusters of shorter-chain molecules exhibited different behavior compared to those of longer-chain molecules, demonstrating non-polar characteristics even at the microscopic level. This suggests that their enhanced BP formation may be linked to this non-polar nature, which requires further exploration to better understand the underlying physical mechanisms.

Fig. 13 Graphical representation illustrating the temperature range of BP formation as a function of varying weight percent concentrations of different components: (a) with F4-8a and S811 without 5CB; (b) with fixed concentration of S811 and varying weight percent of F4-8a and 5CB; and (c) with fixed concentration of 5CB and varying weight percent of F4-8a and S811. Each bar represents the boundaries within which BP is stable, providing insights into the phase behavior of the system.

Further efforts aimed to achieve BP at room temperature involved the addition of 5CB. Concentration optimization was conducted through multiple iterations where at room temperature, a maximum temperature range of ∼8.9 °C was achieved for ∼30 wt% concentration of F4-8a and S811 each. The POM textures obtained for the BP in various mixtures are presented in Fig. 14. The formation of BP is influenced by both the cooling rate and the type of substrate employed. Nevertheless, the general trend observed with changes in relative concentrations remain consistent, as depicted in Fig. 13. The temperature range details are provided in Table S7 (ESI†). The classification of the blue phase (BP I, II, III) utilizing detailed analyses such as Kossel diagrams and selective reflection studies is deferred to future research, which will be communicated in the extension of this work. Extended investigations are currently underway to elucidate these aspects comprehensively. Furthermore, these materials can be integrated as gels or free-standing films for functioning at room temperature for various sensing and photonic device applications such as three-dimensional BP lasers and diffraction gratings.^51,52

Fig. 14 Various mixtures exhibiting BP (a) Glass slide (against a black background) displaying the blue color reflected under ambient light at room temperature (∼28 °C) for three different mixtures. (b)–(d) POM textures showing BP in various mixtures. Composition ratios are mentioned in the images as weight percent of F4-8a:5CB:S811.

Conclusions

We have successfully synthesized and investigated a series of polar unsymmetrical bent-core LCs, F4-na, featuring tetrafluorinated terminal motif and varying alkoxy chain lengths (n = 8, 12, 14, 16, 18). The compounds exhibited monotropic LC behavior, with lower homologues (n = 8, 12, 14) displaying the N_cyb phase, while higher homologues (n = 16, 18) predominantly exhibited SmC phases (alongwith short-range LC behaviour in heating cycle). Detailed characterization through POM, DSC, and temperature-dependent SAXS/WAXS measurements confirmed the phase transitions. Furthermore, DS studies revealed the presence of cybotactic clusters not only in the liquid crystalline phases but also in the isotropic phase, underscoring the complex behavior of these materials. Interestingly, despite large cybotactic clustering and large molecular dipole moments (∼9.34 D), no macroscopic polar ordering was observed in any LC phase (P_s = 0). The behavior of cybotactic clusters varied with the length of the alkoxy chain, as demonstrated by DS measurements under DC bias, where lower homologues exhibited a shift in the relaxation frequency, and higher homologues showed suppression of relaxation processes. These variations were further reflected in the different electroconvection patterns observed across the homologues, revealing the role of terminal alkoxy chain length in defining macroscopic LC properties. These materials hold potential for applications in light-scattering technologies and non-equilibrium-based materials, given the diversity of their electro-optical behaviors.

Furthermore, we have successfully induced room-temperature BP in these bent-core compounds over a temperature range of ∼22.9 °C using S811 as a chiral additive. We further stabilized the BP down to room temperature for a range of ∼8.9 °C by incorporating 5CB as an additional dopant. BP induction was most proficient in the lower homologues, particularly those exhibiting the N_cyb phase, with F4-8a and F4-12a demonstrating the easiest stabilization, followed by F4-14a. This trend underscores the critical role of terminal alkoxy chain length in both stabilizing the BP and influencing the LC properties. While the role of cybotactic clusters in stabilizing BPs has been noted in only a few reports, our work extends this model through systematic concentration optimization, elucidating their dual function as both host systems and dopants. The ability of cybotactic clusters to stabilize BPs, especially in non-ferroelectric systems, underscores the broader applicability of these materials in advanced photonic devices. Our findings in this work suggest that these materials can offer significant potential for advancing room-temperature photonic and electro-optical devices.

Data availability

The data supporting this article have been included as part of the ESI.†

Author contributions

AB, VP and SKP conceptualized the project. AB, MS and NY performed the experiments. SPG, JKV and VM assisted in data analysis. SKP did the overall project administration, reviewed, edited, and finalized the manuscript. All authors have approved the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Santanu Kumar Pal and Santosh Prasad Gupta acknowledge SERB-TARE (TAR/2021/000146) for their generous financial support. The work in Dublin was funded by the Research Ireland, under the US-Ireland program, project number SFI 21/US/3788. Anshika Baghla thanks Ministry of Education (MoE), Govt. of India for Prime Minister's Research Fellowship (PMRF). We are also thankful to IISER Mohali for their financial support, as well as their departmental and central research facilities, including NMR. We also acknowledge the National Institute of Pharmaceutical Education and Research (NIPER), Mohali, for their central facility for DSC measurements. Some images in the DFT studies are processed using Chemcraft software. Fig. 1b and some elements in graphical abstract are drawn using Microsoft PowerPoint and Chemcraft.

Notes and references

1. S. Kaur, V. Punjani, N. Yadav, A. Barthakur, A. Baghla, S. Dhara and S. K. Pal, Liq. Cryst., 2022, 49, 1078–1146.
2. M. Alaasar, J. C. Schmidt, X. Cai, F. Liu and C. Tschierske, J. Mol. Liq., 2021, 332, 115870.
3. A. K. Nasir and M. Rahman, Liq. Cryst., 2024, 51, 503–535.
4. F. Vita, I. Placentino, E. Samulski and O. Francescangeli, Mol. Cryst. Liq. Cryst., 2013, 573, 46–53.
5. M. Derbali, A. Guesmi, N. B. Hamadi and T. Soltani, J. Mol. Liq., 2020, 319, 113768.
6. Y. Uchida, T. Akita, K. Hanada, D. Kiyohara and N. Nishiyama, J. Mater. Chem. C, 2022, 10, 6621–6627.
7. C. Yang, F. Ye, X. Huang, J. Li, X. Zhang, Y. Song, S. Aya and M. Huang, Liq. Cryst., 2024, 51, 558–568.
8. M. Alaasar, M. Prehm and C. Tschierske, RSC Adv., 2016, 6, 82890–82899.
9. P. Kirsch and M. Bremer, ChemPhysChem, 2010, 11, 357–360.
10. T. Abhilash, H. Varghese, M. Czerwiński, K. Czupryński and A. Chandran, J. Mol. Liq., 2021, 341, 117392.
11. W. Zhang, Z. Peng, Q. Pan, S. Liu and J. Zhao, ACS Appl. Polym. Mater., 2022, 5, 141–151.
12. M. Hird, Chem. Soc. Rev., 2007, 36, 2070–2095.
13. W. He, G. Pan, Z. Yang, D. Zhao, G. Niu, W. Huang, X. Yuan, J. Guo, H. Cao and H. Yang, Adv. Mater., 2009, 21, 2050–2053.
14. W. Hu, L. Wang, M. Wang, T. Zhong, Q. Wang, L. Zhang, F. Chen, K. Li, Z. Miao and D. Yang, Nat. Commun., 2021, 12, 1440.
15. K. Orzechowski, M. Tupikowska, O. Strzeżysz, T.-M. Feng, W.-Y. Chen, L.-Y. Wu, C.-T. Wang, E. Otón, M. M. Wójcik and M. Bagiński, ACS Nano, 2022, 16, 20577–20588.
16. K. Bagchi, T. Emeršič, J. A. Martínez-González, J. J. de Pablo and P. F. Nealey, Sci. Adv., 2023, 9, eadh9393.
17. T. Pawale, S. Cheng, N. Hnatchuk and X. Li, J. Mater. Chem. C, 2022, 10, 13778–13788.
18. O. Chojnowska, R. Dąbrowski, J. Yan, Y. Chen and S. Wu, J. Appl. Phys., 2014, 116, 213505.
19. A. Yoshizawa, RSC Adv., 2013, 3, 25475–25497.
20. W. Nishiya, Y. Takanishi, J. Yamamoto and A. Yoshizawa, J. Mater. Chem. C, 2014, 2, 3677–3685.
21. H.-C. Jeong, S. Aya, S. Kang, F. Araoka, K. Ishikawa and H. Takezoe, Liq. Cryst., 2013, 40, 951–958.
22. S. Taushanoff, K. Van Le, J. Williams, R. J. Twieg, B. Sadashiva, H. Takezoe and A. Jákli, J. Mater. Chem., 2010, 20, 5893–5898.
23. Y. Arakawa, Y. Ishida, Y. Sasaki, S. Sasaki, M. Tokita and H. Tsuji, Mater. Adv., 2022, 3, 3218–3228.
24. O. Panarina, Y. P. Panarin, F. Antonelli, J. K. Vij, M. Reihmann and G. Galli, J. Mater. Chem. C, 2006, 16, 842–849.
25. R. Qiu, J. T. Ho and S. Hark, Phys. Rev. A, 1988, 38, 1653.
26. J. Li and S. T. Wu, J. Appl. Phys., 2004, 95, 896–901.
27. A. Chakraborty, M. K. Das, B. Das, U. Baumeister and W. Weissflog, J. Mater. Chem. C, 2013, 1, 7418–7429.
28. A. Chakraborty, M. K. Das, B. Das, A. Lehmann and C. Tschierske, Soft Matter, 2013, 9, 4273–4283.
29. P. Sathyanarayana, S. Radhika, B. Sadashiva and S. Dhara, Soft Matter, 2012, 8, 2322–2327.
30. S. Kaur, G. Mohiuddin, N. Yadav and S. Kumar Pal, ChemPhysChem, 2023, 24, e202300133.
31. Y. P. Panarin, S. P. Sreenilayam, J. K. Vij, A. Lehmann and C. Tschierske, Beilstein J. Nanotechnol., 2018, 9, 1288–1296.
32. G. Shanker, M. Prehm, M. Nagaraj, J. K. Vij, M. Weyland, A. Eremin and C. Tschierske, ChemPhysChem, 2014, 15, 1323–1335.
33. S. Patranabish, G. Mohiuddin, N. Begum, A. R. Laskar, S. K. Pal, N. V. Rao and A. Sinha, J. Mol. Liq., 2018, 257, 144–154.
34. L. Marino, A. T. Ionescu, S. Marino and N. Scaramuzza, J. Appl. Phys., 2012, 112, 114113.
35. S. Ghosh, N. Begum, S. Turlapati, S. K. Roy, A. K. Das and N. V. Rao, J. Mater. Chem. C, 2014, 2, 425–431.
36. G. Shanker, M. Nagaraj, A. Kocot, J. K. Vij, M. Prehm and C. Tschierske, Adv. Funct. Mater., 2012, 22, 1671–1683.
37. V. Domenici, M. Geppi, C. A. Veracini, R. Blinc, A. Lebar and B. Zalar, J. Phys. Chem. B, 2005, 109, 769–774.
38. D. Wiant, S. Stojadinovic, K. Neupane, S. Sharma, K. Fodor-Csorba, A. Jakli, J. T. Gleeson and S. Sprunt, Phys. Rev. E, 2006, 73, 030703.
39. V. Domenici, Soft Matter, 2011, 7, 1589–1598.
40. N. Sebastián, S. Belau, A. Eremin, M. Alaasar, M. Prehm and C. Tschierske, Phys. Chem. Chem. Phys., 2017, 19, 5895–5905.
41. S. Kaur, G. Mohiuddin, V. Punjani, R. K. Khan, S. Ghosh and S. K. Pal, J. Mol. Liq., 2019, 295, 111687.
42. J. Kumar and V. Prasad, J. Phys. Chem. B, 2018, 122, 2998–3007.
43. S. Kaur, A. Belaissaoui, J. W. Goodby, V. Görtz and H. F. Gleeson, Phys. Rev. E, 2011, 83, 041704.
44. P. Tadapatri, U. S. Hiremath, C. Yelamaggad and K. Krishnamurthy, J. Phys. Chem. B, 2010, 114, 10–21.
45. N. Éber, P. Salamon and Á. Buka, Liq. Cryst. Rev., 2016, 4, 101–134.
46. A. Buka and N. Éber, Flexoelectricity in Liquid Crystals: Theory, Experiments and Applications, World Scientific, 2012.
47. L. M. Blinov and V. G. Chigrinov, Electrooptic Effects in Liquid Crystal Materials, Springer Sci. Bus. Media., 2012.
48. P. G. De Gennes and J. Prost, The Physics of Liquid Crystals, Oxford Univ. Press., 1993.
49. S. Tanaka, S. Dhara, B. Sadashiva, Y. Shimbo, Y. Takanishi, F. Araoka, K. Ishikawa and H. Takezoe, Phys. Rev. E, 2008, 77, 041708.
50. R. K. Khan, G. Mohiuddin, N. Begum, S. Turlapati, R. V. Nandiraju, B. K. Debbarma and S. Ghosh, ACS Appl. Mater. Interfaces, 2022, 14, 42628–42634.
51. S. S. Gandhi and L. C. Chien, Adv. Mater., 2017, 29, 1704296.
52. F. Castles, F. Day, S. Morris, D. Ko, D. Gardiner, M. Qasim, S. Nosheen, P. Hands, S. Choi and R. Friend, Nat. Mater., 2012, 11, 599–603.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sc01530h

‡ Joint first authors.

---