P≡B and As≡B triple bonds in the linear PB₂O⁻ and AsB₂O⁻ species

Abstract

Due to its electron deficiency, boron triple bonds are relatively scarce. We use high-resolution photoelectron imaging to investigate the structures and bonding of the EB₂O⁻ (E = P, As) type of clusters, which are found to have [E≡B–B≡O]⁻ closed-shell linear structures with E≡B triple bonds. The B atoms in the linear EB₂O⁻ species undergo sp hybridization, while the E atoms also undergo sp hybridization to form a σ bond with the sp orbital of B along with two π bonds formed by the p_x and p_y orbitals. The high-resolution photoelectron imaging data reveal detachment transitions from the EB₂O⁻ (¹Σ⁺) anions to the EB₂O (²Π) neutrals. The electron affinities of PB₂O and AsB₂O are measured to be 3.592(1) eV and 3.432(1) eV, respectively; the vibrational frequencies for the E–B, B–B, and B–O stretching modes are measured for both species. The spin–orbit splitting of the ²Π state to ²Π_3/2 and ²Π_1/2 is measured to be 153 cm⁻¹ and 758 cm⁻¹ for PB₂O and AsB₂O, respectively.

---

1. Introduction

Borylene (:BR) is the boron analogue of carbene (:CR₂).¹ The HOMO of borylene is an sp hybridized σ-type orbital, while the LUMO and LUMO+1 are the two empty p (p_x and p_y) orbitals. Compared with carbenes, borylenes are more reactive due to their two vacant p orbitals. This also makes borylenes better π-acceptors and they can be stabilized by favourable back-donation of d electrons from transition metals. The first borylene complex was synthesized within the ligand sphere of a stable transition metal complex in 1998 with the form of L_nMBR.² Since then, many borylene complexes have been synthesized.³ Owing to their ability to form π bonds by the two vacant p orbitals, borylenes have the potential to form triple bonds with transition metals. Transition metal–boron triple-bond characters were first hinted in the [(OC)₅Cr=BSi(SiMe₃)₃] complex,^3f in which the Cr–B bond length is slightly shorter than a Cr=B double bond. The shortest transition metal–boron bond length was reported in an L_nFeBF compound⁴ with an Fe–B bond length comparable to the Fe≡B triple-bond. Transition metal–boron triple bonds have been observed in the linear ReB₂O⁻ and IrB₂O⁻ gaseous anions.⁵ Interestingly, RhB₂O⁻ was found to have a bent structure with a short Rh–B bond, leading to the discovery of the first Rh[quadruple bond, length as m-dash]B quadruple bond.⁶ These gaseous anions were produced by laser vaporization, in which the stable BO boronyl unit was readily formed due to trace amounts of oxygen contaminants, serving as a convenient monovalent substituent in the simple borylene model of :B–BO.

In contrast to transition metal–boron complexes, main group elements are more challenging to form triple bonds with boron due to the absence of d electrons. However, the B≡B triple bond can be formed using donor ligands, such as in [OC → B≡B ← CO] or the first isolated B≡B stabilized by two bulky carbenes.⁷ If B acquires an electron, B⁻ is isoelectronic to C and can form B≡B triple bonds, such as in the dianion [OB–B≡B–BO]²⁻ and [Bi≡B–BO]^– or the recent Bi≡BH⁻ species.^8–10 Triple bonds between group 15 elements with boron are particularly interesting because they are analogous to C≡C triple bonds. Numerous iminoborane R–N≡B–R′ moieties featuring a N≡B triple bond have been synthesized, as evidenced by their linear structures and short N–B bond lengths.¹¹ However, as one moves down the periodic table, R–E≡B–R′ type compounds start to exhibit bent structures, especially on the R–E side.¹² For example, the simplest HPBH molecule, which is isoelectronic with alkynes, is predicted to be bent,¹³ indicating a P–B bond order lower than three. The bending is a result of less s-orbital overlap as one descends the periodic table.^12,14 The reduced s orbital contribution by the E atom in the RE side leads to a shift from sp to sp² hybridization, transforming the geometry from linear to bent. In sp² hybridization, only one p orbital remains available to form a π bond. Equivalently, in the MO picture under the bent geometry, the in-plane π bonding orbital has the same symmetry as the antibonding σ orbital. This leads to significant mixing between the two orbitals, weakening the in-plane π bond and making it more like a lone pair, consistent with the valence bond perspective. Thus, the bent geometry inherently reduces the bond order below three. The few synthesized phosphaborene (R–P=B–R′) and arsaborene (R–As=B–R′) molecules are found to exhibit bent geometries with P=B and As=B double bonds.¹⁵

Thus, it is challenging to synthesize molecules with P≡B or As≡B triple bonds. No compounds with such triple bonds have been isolated in the bulk except a theoretical suggestion of a P≡B triple bond protected by bulky groups.¹⁶ Alternatively, molecules containing P≡B or As≡B triple bonds can be prepared in the gas phase or low temperature matrices, where it is possible to form linear molecules with bare P or As atoms unprotected by ligands. The PBH radical was observed in a low temperature matrix, an open-shell species with three π electrons and a P–B bond order of 2.5.¹⁷ In this article, we use high-resolution photoelectron imaging (PEI) to study EB₂O⁻ (E = P, As) clusters produced by a laser vaporization source. High-resolution photoelectron spectra from photoelectron imaging (PEI) of cryogenically cooled anions and theoretical calculations confirm that the EB₂O⁻ species are electron-precise linear molecules, [E≡B–B≡O]^–, containing a terminal E≡B triple bond (E = P, As). The electron affinities (EAs), vibrational frequencies, and spin–orbit (SO) splitting of the neutral EB₂O radicals are obtained for the first time.

2. Experimental and theoretical methods

2.1. Experimental methods

The experiment was carried out on a high-resolution PEI apparatus newly equipped with a cryogenically cooled 3D Paul trap. The PEI apparatus has been described in detail previously,¹⁸ and has been proven to be effective to cool anionic clusters generated from a laser vaporization source.¹⁹ In the current work, the PB₂O⁻ and AsB₂O⁻ clusters were produced by laser vaporization of cold-pressed P/¹⁰B and As/¹⁰B targets, respectively. The boronyl species were generated due to trace amounts of oxide impurity on the target surface. In fact, the PB₂O⁻ and AsB₂O⁻ clusters were particularly prominent in the mass spectra, indicating that they are highly stable thermodynamically. A helium carrier gas was used to quench the laser-induced plasma. Clusters formed inside the nozzle were entrained by the helium carrier gas and underwent a supersonic expansion. After passing through a skimmer, the collimated cluster beam travelled directly into the 3D Paul trap cooled down to 4.2 K by a two-stage closed-cycle helium refrigerator. Clusters of interest were selected and intercepted by a detachment laser in the interaction zone of a velocity map imaging (VMI) system. Photodetachment was performed using the frequency-doubled output of a dye laser, as well as the third harmonic output from an Nd:YAG laser. Photoelectrons were projected onto a set of microchannel plates coupled with a phosphor screen and a charge-coupled-device camera. The VMI lens was calibrated using PEI of Bi⁻ at various photon energies. The photoelectron images were analysed by the maximum entropy method (MEVELER).²⁰ The resolution of the VMI system was ∼0.6% for electrons with high kinetic energies and as low as 1.2 cm⁻¹ for very slow photoelectrons.¹⁸

Photoelectron angular distributions (PADs) can be obtained from photoelectron images, characterized by an anisotropy parameter (β). Under the electric dipole approximation, when an electron with angular momentum l is detached from an atom, the outgoing photoelectron carries an angular momentum of l ± 1. If an electron is detached from an s atomic orbital (l = 0), the outgoing photoelectron will have l = 1 (pure p-wave) with β = 2. If an electron is detached from an atomic p orbital, the outgoing electron will carry s + d partial waves with β = −1.²¹ While the β value is non-trivial to interpret for electron detachment from molecular orbitals (MOs),²² it provides qualitative information about the symmetries of the MOs.

2.2. Theoretical methods

We employed the ABCluster software to perform the global minimum search.²³ Several initial structures were optimized using density functional theory (DFT) at the B3LYP/6-311+G* (ref. 24) level with the Gaussian 09 package.²⁵ Additional calculations were also done at the TPSSh/aug-cc-pVTZ level of theory.²⁶ Frequency calculations were carried out to compare with the experimental data and to ensure that the optimized structures were true minima. To account for SO interactions, we first utilized the state-averaged (SA)-complete active space self-consistent field (CASSCF) method²⁷ followed by multi-reference configuration interaction (MRCI) calculations²⁸ to get the low-lying electronic states. An active space consisting of 17 electrons and 9 orbitals was chosen for both PB₂O and AsB₂O. Then we carried out SO coupling calculations using the Breit-Pauli Hamiltonian in Molpro.^29,30 The aug-cc-pVTZ basis set was applied for the SO coupling calculations. Franck–Condon (FC) factors were computed using the ezFCF program.³¹ Chemical bonding analyses were done using adaptive natural density partitioning (AdNDP).³²

3. Experimental and theoretical results

3.1. Experimental results

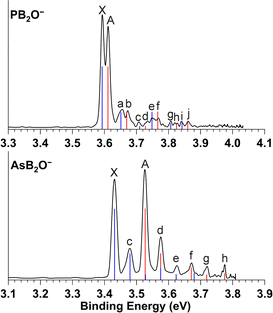
High-resolution PEI data of cryogenically cooled PB₂O⁻ at 3.809 eV and 4.023 eV are shown in Fig. 1. The 4.023 eV spectrum (Fig. 1b) reveals two prominent peaks, X and A, which have similar intensities and are followed by numerous weak vibrational features labelled as peaks a–j. In the 3.809 eV spectrum (Fig. 1a), peaks a–f are better resolved, revealing that peaks X and A, as well as the pairs of a and b, c and d, and e and f, all have similar spacings and intensity patterns. It turns out that peaks g and h, and peaks i and j in the 4.023 eV spectrum, are similar pairs. These observations suggest that the pairs of peaks originate from two electronic states with parallel potential energy surfaces, likely corresponding to two SO-split states. Peaks X and A should be the 0–0 transitions to the two SO states of the neutral PB₂O molecule. Peak X defines an accurate electron affinity (EA) of 3.592 eV for PB₂O, while the spacing between X and A yields a SO splitting energy of 153 cm⁻¹. The presence of SO splitting suggests that PB₂O⁻ and PB₂O should have linear structures and the HOMO of PB₂O⁻ must be a π orbital.

Fig. 1 Photoelectron images and spectra of cryogenically cooled PB₂O⁻ at (a) 3.809 eV and (b) 4.032 eV. The double arrow below the image indicates the laser polarization.

The photoelectron angular distributions provide further insights into the nature of the HOMO, from which an electron is detached. In the 4.023 eV spectrum, all peaks exhibit s + d-type angular distributions, indicating that they are due to electron detachment from a π-type MO. At the lower photon energy of 3.809 eV, peaks that are closer to the detachment threshold, such as e and f, exhibit more isotropic angular distributions, due to the significant suppression of higher-order partial waves near the detachment threshold. The binding energies of all the observed peaks, their shifts relative to peaks X and A, and the assignments are given in Table 1.

Table 1 The measured binding energies (BE), assignments, and shifts relative to peaks X and A for the fine features observed in the spectra of PB₂O⁻

	BE (eV)^a	Assignment	Shift (cm^−1)
a The numbers in the parentheses represent the uncertainty in the last digit.
X	3.592(1)	^2Π3/2 (00^0)	0
A	3.611(1)	^2Π1/2 (00^0)	153	0
a	3.651(1)	^2Π3/2 (30^1)	476
b	3.668(1)	^2Π1/2 (30^1)		460
c	3.714(1)	^2Π3/2 (30^2)	984
d	3.729(1)	^2Π1/2 (30^2)		952
e	3.749(1)	^2Π3/2 (20^1)	1266
f	3.765(1)	^2Π1/2 (20^1)		1245
g	3.807(1)	^2Π3/2 (30^120^1)	1734
h	3.825(3)	^2Π1/2 (30^120^1)		1726
i	3.840(1)	^2Π3/2 (10^1)	2000
j	3.862(1)	^2Π1/2 (10^1)		2024

---

High-resolution PEI data of cryogenically cooled AsB₂O⁻ at 3.496 eV and 3.809 eV are shown in Fig. 2. The 3.809 eV spectrum (Fig. 2b) reveals two strong peaks X and A, similar to those observed in PB₂O⁻. Peaks c, e and f, and peaks d, g and h form two sets of similar vibrational progressions following peaks X and A. In addition to the better resolved peaks X and c, the 3.496 eV spectrum (Fig. 2a) also reveals two very weak peaks, a and b. The overall similarity between the spectra of AsB₂O⁻ and PB₂O⁻ suggests that AsB₂O⁻ also adopts a linear structure, with peaks X and A being the 0–0 transitions to two SO states. Peak X defines an accurate EA of 3.432 eV for AsB₂O, and the spacing between peaks X and A gives a SO splitting of 758 cm⁻¹. As expected from the periodic trend from P to As, the EA of AsB₂O decreases and the SO effect increases. All the resolved peaks for AsB₂O in the 3.809 eV spectrum display s + d-type angular distributions and become more isotropic in the near-threshold spectrum at 3.496 eV, similar to the observation in the spectra of PB₂O. The binding energies of all the observed peaks, their shifts relative to peaks X and A, and the assignments are given in Table 2.

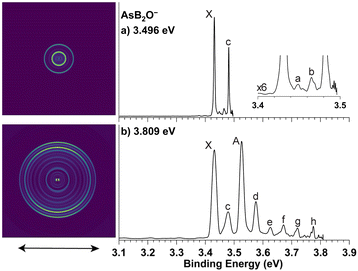Fig. 2 Photoelectron images and spectra of cryogenically cooled AsB₂O⁻ at (a) 3.496 eV and (b) 3.809 eV. The double arrow below the image indicates the laser polarization.

Table 2 The measured binding energies (BE), assignments, and shifts relative to peaks X and A for the fine features observed in the spectra of AsB₂O⁻

	BE (eV)^a	Assignment	Shift (cm^−1)
a The numbers in the parentheses represent the uncertainty in the last digit.
X	3.432(1)	^2Π3/2 (00^0)	0
a	3.449(1)	^2Π3/2 (40^1)	137
b	3.465(1)	^2Π3/2 (40^2)	266
c	3.482(1)	^2Π3/2 (30^1)	403
A	3.526(1)	^2Π1/2 (00^0)	758	0
		^2Π3/2 (30^2)	758
d	3.576(1)	^2Π1/2 (30^1)		403
		^2Π3/2 (20^1)	11615
e	3.626(1)	^2Π1/2 (30^2)		807
		^2Π3/2 (30^120^1)	1565
f	3.672(1)	^2Π1/2 (20^1)		1178
		^2Π3/2 (10^1)	1936
g	3.719(1)	^2Π1/2 (30^120^1)		1557
h	3.775(1)	^2Π1/2 (10^1)		2008

---

3.2. Theoretical results

The global minimum (GM) structures and low-lying isomers of PB₂O⁻ and AsB₂O⁻ are presented in Fig. S1.† The GM structures of EB₂O⁻ (E = P, As) are found to have closed-shell linear structures with C_∞v symmetry and a 1σ²2σ²3σ²4σ²1π⁴5σ²2π⁴ (¹Σ⁺) electronic configuration. All other isomers are much higher in energy. The optimized geometries at the B3LYP level for EB₂O⁻ and neutral EB₂O are shown in Fig. 3. The calculated vibrational frequencies of the neutral radicals are compared with the experimental values in Table 3. The results calculated at the TPSSh level agree well with those at the B3LYP level, as compared in Fig. S1 and S2 and Table S1.† The MOs for EB₂O⁻ are given in Fig. S3.† The HOMOs of EB₂O⁻ are π bonding orbitals essentially localized on the E–B bond. Detachment of an electron from the HOMO yields a ²Π state for the neutral molecule with an electron configuration of …1π⁴5σ²2π³. The ²Π state splits into ²Π_3/2 and ²Π_1/2 due to SO coupling, with the ²Π_3/2 SO state being lower in energy. The calculated EAs to the ²Π neutral ground state for both molecules at the B3LYP/6-311+G* level, in which SO coupling is not considered explicitly, are compared with the experimental values in Table 3. We computed the ²Π state and an additional low-lying ²Σ⁺ state using the SA3-CASSCF(17,9) and MRCI methods, and these states were included in the calculations of SO splitting between ²Π_1/2 and ²Π_3/2. The resulting SO splitting is computed to be 145 and 740 cm⁻¹ for PB₂O and AsB₂O, respectively, as summarized in Table 3.

Fig. 3 The optimized structures of PB₂O⁻ and AsB₂O⁻ and the corresponding neutrals at the B3LYP/6-311+G* level. The point group symmetries and electronic states are also given. The bond lengths are given in Å.

Table 3 The experimental EAs, spin–orbit (SO) splitting, and vibrational frequencies for EB₂O, compared with the calculated values

	EA (eV)^a		SO splitting (cm^−1)		Frequency (cm^−1)^b
	Exp.	Cal.	Exp.	Cal.	Exp.^c	Cal.
a Spin–orbital coupling is not considered in the computed EAs. b Calculated frequencies are scaled by a factor of 0.97. ν1 = B–O stretching, ν2 = B–B stretching, ν3 = E–B stretching, ν4 = cis-bending. The scaling factor is based on the NIST computational chemistry comparison and benchmark database (https://cccbdb.nist.gov/vibscalejustx.asp). c The experimental uncertainty is estimated to be ±10 cm^−1.
PB2O	3.592	3.52	153	145	2010 (ν1)	2010
					1260 (ν2)	1254
					470 (ν3)	472
AsB2O	3.432	3.39	758	740	2000 (ν1)	2003
					1165 (ν2)	1161
					400 (ν3)	389
					135 (ν4)	143

---

4. Discussion

4.1. Comparison between experiment and theory

The calculated EAs for the linear structures, 3.52 eV for PB₂O and 3.39 eV for AsB₂O at the B3LYP level, are in good agreement with the experimental data of 3.592 eV and 3.432 eV, respectively. The computed SO splitting for the ²Π state, 145 cm⁻¹ for PB₂O and 740 cm⁻¹ for AsB₂O, also agrees well with the spacing between peaks X and A: 153 cm⁻¹ for PB₂O and 758 cm⁻¹ for AsB₂O. The excellent agreement between theory and experiment confirms that peaks X and A indeed correspond to the two SO states and validates the linear structures of EB₂O⁻ (E = P, As).

To understand the observed vibrational structures, we computed the FC factors using the optimized geometries and vibrational frequencies at the B3LYP/6-311+G* level, as shown in Fig. 4, where the blue and red bars represent FC factors for transitions to the ²Π_3/2 and ²Π_1/2 states, respectively. The overall FC profiles agree well with the experimental spectra, further validating the linear structures. For detachment transitions from the linear anions to linear neutrals, FC-active modes can only involve stretching vibrations. In the case of PB₂O, we observed all three stretching modes, which are essentially the P–B, B–B, and B–O vibrations, designated as modes ν₃, ν_2, and ν₁ (Fig. S4†). Using the FC simulations, we can readily assign the observed vibrational peaks for PB₂O (Table 1). Peaks a and b correspond to ν₃ of the two SO states, while peaks c and d correspond to the overtone of ν₃ of the two SO states. Peaks e and f are from ν₂ of the two SO states. Peaks g and h represent the combination modes of ν₃ and ν₂ for the two SO states. Peaks i and j correspond to ν₁ of the two SO states.

Fig. 4 Comparison of the calculated Franck–Condon factors (vertical lines) with the PE spectra of PB₂O⁻ at 4.032 eV and AsB₂O⁻ at 3.809 eV. The blue and red colours represent the Franck–Condon factors of the ²Π_3/2 and ²Π_1/2 states, respectively.

In the spectra of AsB₂O⁻ (Table 2), peak c corresponds to excitation to the ν₃ mode of the ²Π_3/2 state, while its overtone overlaps with the 0–0 transition of the ²Π_1/2 state, resulting in peak A appearing slightly more intense than peak X. The ν₂ excitation of the ²Π_3/2 state also overlaps with the excitation of the ν₃ mode of the ²Π_1/2 state, causing peak d to appear slightly more intense than peak c. Peak e is the overlap of the overtone of ν₁ of the ²Π_1/2 state and the combination of ν₃ and ν₂ of the ²Π_3/2 state. Peak f is dominated by excitation to ν₂ of the ²Π_1/2 state with minor contribution from ν₁ of the ²Π_3/2 state. Peaks g and h are from the combination of ν₁ and ν₂ of the ²Π_1/2 state and ν₁ of the ²Π_1/2 state, respectively.

In the 3.496 eV spectrum of AsB₂O⁻ (Fig. 2a), two very weak peaks a and b are observed. These peaks do not correspond to any FC-active modes. Instead, their frequencies agree with the calculated fundamental and overtone of the cis-bending mode ν₄ (Fig. S4†). For linear molecules, overtones of bending modes are symmetry-allowed, while the fundamental of the bending mode is forbidden. In a previous PES study on BiBH⁻,¹⁰ which has a similar linear structure, we also found a weak bending vibrational feature attributed to vibronic coupling between the ²Π state and a higher-lying ¹Σ⁺ excited state. The observation of the weak 4₀¹ bending feature in the spectrum of AsB₂O⁻ could also come from vibronic coupling.

4.2. Chemical bonding in PB₂O⁻ and AsB₂O⁻

We analysed the chemical bonding in EB₂O⁻ using the AdNDP method (Fig. 5) and the MOs (Fig. S3†). The AdNDP results for EB₂O⁻ (E = P, As) are nearly identical. We can identify two lone pairs on E and O, a triple bond between E and B, a B–B single bond and another triple bond between B and O. Thus, the two EB₂O⁻ species are electron-precise molecules [E≡B–B≡O]^–. The triple bonds can also be readily seen from the HOMO and HOMO-1 (Fig. S3†), representing the E–B π and σ bonds, respectively. We calculated the Wiberg bond index matrix on the natural atomic orbital (NAO) basis. The Wiberg bond orders for the P≡B and As≡B bonds in PB₂O⁻ and AsB₂O⁻ are 2.84 and 2.83, respectively, consistent with the AdNDP and MO analyses. PB₂O⁻ and AsB₂O⁻ are the first molecules observed to contain P≡B and As≡B triple bonds. In the valence bond model, the B atom undergoes sp hybridization, where one of the sp hybridized orbitals forms a σ bond with BO and the other sp orbital forms another σ bond with P or As. The P and As atoms also undergo sp hybridization, so that the s orbital from P or As makes considerable contribution to the σ bond. One of the sp orbitals forms a σ bond with the B atom, and the other sp orbital gives rise to the lone pair on P/As. The calculated atomic orbital composition shows that the s orbital contributes 34% to the P sp hybridized orbitals, while it contributes 31% to the As sp hybridized orbitals. The 2p_x and 2p_y orbitals of B form two π bonds with the corresponding p orbitals of P or As, giving rise to the P≡B and As≡B triple bond. The contribution of the valence s orbital to the σ bond in P≡B and As≡B is quite different from the weak triple bond in Bi≡B, where the 6s orbital is basically a lone pair.^9,10 The strong relativistic effects significantly stabilize the 6s orbital relative to the 6p orbitals, making it unfavourable for sp hybridization.

Fig. 5 AdNDP chemical bonding analyses for (a) PB₂O⁻ and (b) AsB₂O⁻.

The P–B and As–B bond lengths in PB₂O⁻ and AsB₂O⁻ are also consistent with their triple bond nature. According to Pyykko's additive covalent radii,³³ the P≡B and As≡B triple bond lengths are 1.67 Å and 1.79 Å, respectively, in excellent agreement with the calculated P–B and As–B bond lengths of 1.68 Å and 1.78 Å in PB₂O⁻ and AsB₂O⁻ (Fig. 3). In the PB₂O and AsB₂O neutrals, removal of an electron from the π bonding orbital (HOMO in Fig. S3†) weakens the P–B and As–B bonds, resulting in a bond order of 2.5. Consequently, the P–B and As–B bond lengths in the neutral species increase to 1.72 Å and 1.83 Å, respectively, indicating the significant strength of the π bond in PB₂O⁻ and AsB₂O⁻. It should be noted that the P–B bond length in PB₂O is consistent with that in the linear PBH (1.72 Å) species observed in a low temperature matrix, where the P–B bond order is also 2.5.¹⁷ It is interesting to point out that the sp lone pair on the terminal P or As atoms in PB₂O⁻ and AsB₂O⁻ may be able to coordinate to a bulky Lewis acid to allow the isolation of the first P≡B and As≡B triple bonds.

5. Conclusion

In conclusion, we report a high-resolution photoelectron imaging investigation of PB₂O⁻ and AsB₂O⁻. The electron affinities of neutral PB₂O and AsB₂O are measured to be 3.592 eV and 3.432 eV, respectively. Vibrationally resolved photoelectron imaging, combined with computational chemistry, confirms that PB₂O⁻ and AsB₂O⁻ have linear structures, [P≡B–B≡O] ^– and [As≡B–B≡O]^–, with P≡B and As≡B triple bonds. Both PB₂O⁻ and AsB₂O⁻ are closed-shell with a ¹Σ⁺ electronic state, whereas their neutrals are open shell with a ²Π_3/2 ground state. The spin–orbit split ²Π_1/2 excited state is determined to be 153 cm⁻¹ and 758 cm⁻¹ higher in energy for PB₂O and AsB₂O, respectively. The PB₂O⁻ and AsB₂O⁻ species represent the first molecules containing P≡B and As≡B triple bonds, which can serve as benchmarks for studying P–B and As–B multiple bonds and may be viable for bulk syntheses.

Data availability

The data that supports the findings of this study is available from the corresponding author upon request.

Author contributions

H. W. G. and J. H. did the experiment. H. W. G. analysed the data and wrote the first draft of the manuscript. J. H. did the calculations. L. S. W. guided and advised the project, and revised and finalized the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the U.S. National Science Foundation (Grant No. CHE-2403841). The calculations were performed using resources at the Centre for Computation and Visualization (CCV) of Brown University.

References

1. (a) A. W. Ehlers, E. V. Barends, F. M. Bickelhaupt and U. Radius, Chem.–Eur. J., 1998, 4, 210; (b) D. Vidovic, G. A. Pierce and S. Aldridge, Chem. Commun., 2009, 1157; (c) H. Braunschweig, R. D. Dewhurst and V. H. Gessner, Chem. Soc. Rev., 2013, 42, 3197; (d) M. Soleilhavoup and G. Bertrand, Angew. Chem., Int. Ed., 2017, 56, 10282.
2. (a) H. Braunschweig, C. Kollann and U. Englert, Angew. Chem., Int. Ed., 1998, 37, 3179; (b) A. H. Cowley, V. Lomelf and A. Voigt, J. Am. Chem. Soc., 1998, 120, 6401.
3. (a) H. Braunschweig, M. Colling, C. Kollann, H. G. Stammler and B. Neumann, Angew. Chem., Int. Ed., 2001, 40, 2298; (b) D. L. Coombs, S. Aldridge, C. Jones and D. J. Willock, J. Am. Chem. Soc., 2003, 125, 6356; (c) D. L. Coombs, S. Aldridge, A. Rossin, C. Jones and D. J. Willock, Organometallics, 2004, 23, 2911; (d) H. Braunschweig, M. Burzler, T. Kupfer, K. Radacki and F. Seeler, Angew. Chem., Int. Ed., 2007, 46, 7785; (e) H. Braunschweig, K. Radacki and K. Uttinger, Angew. Chem., Int. Ed., 2007, 46, 3979; (f) B. Blank, M. Colling-Hendelkens, C. Kollann, K. Radacki, D. Rais, K. Uttinger, G. R. Whittell and H. Braunschweig, Chem.–Eur. J., 2007, 13, 4770; (g) H. Braunschweig, M. Forster, T. Kupfer and F. Seeler, Angew. Chem., Int. Ed., 2008, 47, 5981; (h) G. Alcaraz, U. Helmstedt, E. Clot, L. Vendier and S. Sabo-Etienne, J. Am. Chem. Soc., 2008, 130, 12878; (i) S. Bertsch, H. Braunschweig, B. Christ, M. Forster, K. Schwab and K. Radacki, Angew. Chem., Int. Ed., 2010, 49, 9517.
4. M. J. Drance, J. D. Sears, A. M. Mrse, C. E. Moore, A. L. Rheingold, M. L. Neidig and J. S. Figueroa, Science, 2019, 363, 1203.
5. T. Chen, L. F. Cheung, W. J. Chen, J. Cavanagh and L. S. Wang, Angew. Chem., Int. Ed., 2020, 59, 15260.
6. L. F. Cheung, T. T. Chen, G. S. Kocheril, W. J. Chen, J. Czekner and L. S. Wang, J. Phys. Chem. Lett., 2020, 11, 659.
7. (a) M. Zhou, N. Tsumori, Z. Li, K. Fan, L. Andrews and Q. Xu, J. Am. Chem. Soc., 2002, 124, 12936; (b) H. Brauschweig, R. D. Dewhurst, K. Hammond, J. Mies, K. Radacki and A. Vargas, Science, 2012, 336, 1420.
8. S. D. Li, H. J. Zhai and L. S. Wang, J. Am. Chem. Soc., 2008, 130, 2573.
9. T. Jian, L. F. Cheung, T. T. Chen and L. S. Wang, Angew. Chem., Int. Ed., 2017, 56, 9551.
10. H. W. Gao, J. Hui and L. S. Wang, Chem. Commun., 2023, 59, 12431.
11. (a) P. Paetzold, A. Richter, T. Thijssen and S. Würtenberg, Chem. Ber., 1979, 112, 3811; (b) J. Wang, P. Jia, W. Sun, Y. Wei, Z. Lin and Q. Ye, Inorg. Chem., 2022, 61, 8879.
12. R. C. Fischer and P. P. Power, Chem. Rev., 2010, 110, 3877.
13. J. D. Watts and L. C. V. Zant, Chem. Phys. Lett., 1996, 251, 119.
14. P. P. Power, Nature, 2010, 463, 171–177.
15. (a) E. Rivard, W. A. Merrill, J. C. Fettinger, R. Wolf, G. H. Spikes and P. P. Power, Inorg. Chem., 2007, 46, 2971; (b) J. Li, Z. Lu and L. L. Liu, J. Am. Chem. Soc., 2022, 144, 23691; (c) A. Koner, B. Morgenstern and D. M. Andrada, Angew. Chem., Int. Ed., 2022, 61, e202203345; (d) E. Rivard, W. A. Merrill, J. C. Fettinger and P. P. Power, Chem. Commun., 2006, 36, 3800; (e) M. Wen, R. Medel, P. V. Zasimov, C. Müller and S. Riedel, Chem. Sci., 2024, 15, 8045; (f) E. A. LaPierre, B. O. Patrick and I. Manners, J. Am. Chem. Soc., 2023, 145, 7107.
16. J. S. Lu, M. C. Yang and M. D. Su, ACS Omega, 2018, 3, 76.
17. L. Wang, X. Jiang, G. Wang, X. Zeng and M. Zhou, Chem.–Eur. J., 2023, 29, e202203704.
18. I. León, Z. Yang, H. T. Liu and L. S. Wang, Rev. Sci. Instrum., 2014, 85, 083106.
19. (a) G. S. Kocheril, H. W. Gao, D. F. Yuan and L. S. Wang, J. Chem. Phys., 2022, 157, 171101; (b) G. S. Kocheril, H. W. Gao and L. S. Wang, Mol. Phys., 2024, 122, e2182610; (c) G. S. Kocheril, H. W. Gao and L. S. Wang, J. Chem. Phys., 2023, 158, 236101; (d) H. W. Gao, H. W. Choi, J. Hui, W. J. Chen, G. S. Kocheril and L. S. Wang, J. Chem. Phys., 2023, 159, 114301; (e) H. W. Gao, H. W. Choi, J. Hui and L. S. Wang, J. Phys. Chem. A, 2024, 128, 3579.
20. B. Dick, Phys. Chem. Chem. Phys., 2019, 21, 19499.
21. J. Cooper and R. N. Zare, J. Chem. Phys., 1968, 48, 942.
22. A. Sanov and R. Mabbs, Int. Rev. Phys. Chem., 2008, 27, 53.
23. J. Zhang and M. Dolg, Phys. Chem. Chem. Phys., 2015, 17, 24173.
24. C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B:Condens. Matter Mater. Phys., 1988, 37, 785.
25. M. J. Frisch et al. , Gaussian 09, Revision A.1, Gaussian, Inc., Wallingford, CT, 2009.
26. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
27. H. J. Werner and P. J. Knowles, J. Chem. Phys., 1985, 82, 5053.
28. H. J. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803.
29. A. Berning, M. Schweizer, H. J. Werner, P. J. Knowles and P. Palmieri, Mol. Phys., 2000, 98, 1823.
30. H. J. Werner et al., MOLPRO, a package of ab initio programs, see http://www.molpro.net.
31. S. Gozem and A. I. Krylov, WIREs Comp. Mol. Sci., 2021, 12, e1546.
32. D. Y. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207.
33. P. Pyykko, J. Phys. Chem. A, 2015, 119, 2326.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sc00812c

---