Open Access Article
Open Access ArticleTuning the modal coupling in three-dimensional Au@Cu2O@Au core–shell–satellite nanostructures for enhanced plasmonic photocatalysis†
Yahui
Yang
a,
Binbin
Zhang
a,
Xuehao
Sun
a,
Yunlong
Tao
a,
Guizeng
Yang
a,
Chuang
Liu
a,
Zixu
Wang
a,
Lichao
Sun
*ab and
Qingfeng
Zhang
 *a
*a
aCollege of Chemistry and Molecular Sciences, Hubei Key Laboratory of Electrochemical Power Sources, Wuhan University, Wuhan 430072, China. E-mail: lichaosun@whu.edu.cn; zhangqf@whu.edu.cn
bSuzhou Institute of Wuhan University, Suzhou 215123, China. E-mail: lichaosun@whu.edu.cn
First published on 31st March 2025
Abstract
The fascinating optical properties of coupled plasmonic nanostructures have attracted great attention and emerged as a promising platform for applications in catalysis, sensing, and photonics. When two resonant modes interact strongly, the coupled modes are formed with mixed properties inherited from the basic modes. However, limitations still exist in the understanding of the coupling between optical modes in individual structures. In addition, how the coupling in hybrid plasmonic structures correlated with their efficiencies in promoting photocatalysis remains an important and challenging question. Here we demonstrate that coupling in individual Au@Cu2O@Au core–shell–satellite hybrid structures can be tuned through rationally designing the structural features for enhancing plasmonic photocatalysis. To further comprehend the optical phenomena of different coupled nanostructures, a model was developed based on the Mie theory, which provided a different perspective to analyze coupling qualitatively in individual nanoparticles. The insights gained from this work not only shed light on the underlying mechanisms of modal coupling in individual structures but also provide an important knowledge framework that guides the rational design of coupled plasmonic nanostructures for plasmonic photochemistry and photocatalysis.
Introduction
Noble metal nanoparticles (NPs) are well known for their capacity to enhance the interactions between light and matter, exhibiting fascinating colors.1 For an individual particle, the collective oscillation of its free electrons results in a localized surface plasmon resonance (LSPR) at a certain frequency determined by the size/shape of the NP and its dielectric environment. When two or more NPs are close enough to each other, the LSPR of the individual NPs interacts through their optical near fields, forming coupled oscillation modes and generating a significant change in the optical response.2,3 Furthermore, coupling systems with more complex structures exhibit some strikingly different optical properties, such as plasmon hybridization,4 Fano resonance,5–7 electromagnetically induced transparency (EIT),8 and plasmonic waveguiding,9 which are widely applied from sensing10 to energy harvesting,11,12 and subwavelength optical imaging.13 Thus, plasmon coupling is the fundamental principle by which the optical resonances in NP assemblies are tuned. Moreover, plasmon coupling of the hybrid nanostructure can induce significant electromagnetic field enhancement, which is beneficial for plasmon-enhanced spectroscopy,14,15 artificial photosynthesis,16 and plasmon-enhanced catalysis.17–19In the face of the increasingly serious energy crisis, one expects to maximize the conversion of solar energy into usable chemical energy through plasmon-enhanced photocatalysis.20 Noble metal NPs combined with semiconductors were developed to form heterostructures where plasmonic metal acts as antennae, enhancing the light absorption and photogenerated carrier lifetime in semiconductors greatly.21–24 Recent advances in tuning the surface/interfacial structures of the hybrid plasmonic nanocatalysts have shown great promise for their application in photocatalysis.25–29 Notably, strong coupling can enhance the interaction between light and matter, which has been employed to modulate the catalytic activities and selectivity. For instance, the coupling between the LSPR and optical modes such as whispery gallery modes,30 waveguide modes,9,31 and Bloch waves32 has been demonstrated for broadband optical responses. In particular, Misawa and coworkers demonstrated that coupling between the LSPR mode and Fabry–Pérot (F–P) nanocavity mode has been shown to achieve optical responses over a broad range of wavelengths, which can promote water splitting.33 In addition, the coupling strength can be tuned by varying the dielectric constant and the embedding depth of NPs.34,35 However, limitations still exist in the understanding of the coupling between optical modes in individual 3D structures. The core–shell–satellite structures have been constructed in some previous studies for plasmon-enhanced nanocatalysis;36,37 however, the quantitative correlations between structural features and modal coupling in hybrid structures remain a challenge yet to be addressed. Moreover, how the modal coupling in hybrid structures correlated with their activities in enhancing plasmonic photocatalysis remains unclear. Therefore, tuning the modal coupling in 3D hybrid plasmonic structures through precise control over geometric features and quantitative optical characterization studies is urgent for developing highly efficient plasmonic photocatalysts.
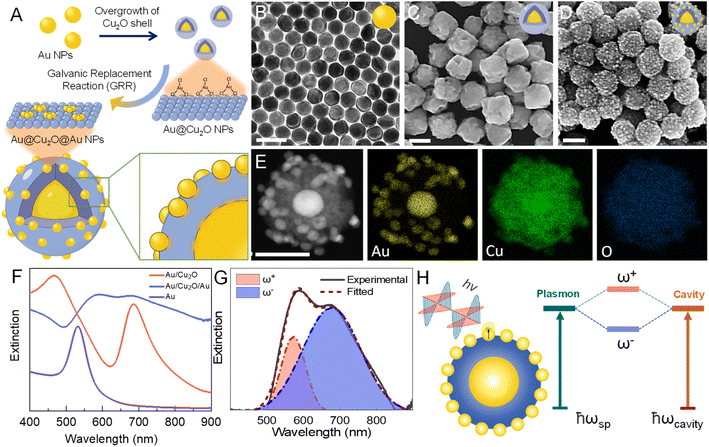
Herein, we present an Au@Cu2O@Au (ACA) core–shell–satellite hybrid structure with tunable plasmon coupling for enhanced plasmon photocatalysis. In this structure, Au@Cu2O NPs support a nanocavity mode in the visible spectral region. Furthermore, the growth of Au NPs as satellites with tailored sizes induces a modal splitting in the extinction spectra, suggesting the formation of a modal coupling. By deliberately controlling the thickness of the Cu2O shell and the size of Au satellites, the coupling can be tuned and understood using a two-harmonic resonator model. The modal splitting in scattering spectra was also revealed through single-particle dark-field scattering (DFS) measurements. More importantly, the ACA NPs show much better catalytic activities than Cu2O@Au NPs toward plasmon-driven chemical reactions revealed by in situ surface-enhanced Raman scattering (SERS) measurements. Ultrafast transient absorption (TA) spectroscopy and photoelectrochemical (PEC) measurements further show the superior performance of the ACA hybrid structure toward plasmonic photocatalysis.
Results and discussion
As schematically illustrated in Fig. 1A, we developed a two-step method for the construction of the ACA core–shell–satellite nanostructure (see experimental details in the ESI†). Au rhombicuboctahedral (RCO) NPs, which are single-crystalline in nature and ∼55 nm in size, were employed as the plasmonic core (Fig. 1B and S1†). Firstly, the Cu2O shell was grown on the surfaces of the Au NPs to form the Au@Cu2O structure with tunable shell thickness (Fig. 1C and S1, S2†). The range of Cu2O shell thickness in Au@Cu2O NPs can be tuned from ∼27 nm to ∼65 nm by simply changing the amount of Cu2+ precursors (Fig. S2†). Secondly, ACA NPs can be obtained by reacting the Cu2O shell with HAuCl4 through a galvanic replacement reaction (GRR) process (Fig. 1D and S3†). The core–shell–satellite structure can be then clearly visualized by HAADF-STEM imaging and corresponding EDS mapping of an individual ACA particle (Fig. 1E). X-ray diffraction (XRD) patterns further verify the composition of Au and Cu2O in the ACA NPs and none of the Cu0 elements or CuAu alloy phase can be found (Fig. S4†). By deliberately controlling the amount of HAuCl4, the size and density of the Au satellite in ACA NPs can be finely modulated, resulting in a different modal coupling mode that will be discussed later (Fig. S5†). The as-prepared ACA NPs exhibit excellent uniformity in both the overall size of ACA NPs and the density of the Au satellites, which will benefit the investigations of plasmon coupling in the ensemble extinction spectra (Fig. S6†). In the ACA structure, Cu2O not only acts as a medium allowing light to spread but also as a spacer to control the distance between the cavity and Au satellites, which is similar to the spacer of NPs on thin film systems.33 Moreover, the in situ GRR process could create close contacts between Au satellites and the Cu2O shell (Fig. S5†), which could potentially enhance the plasmon coupling in contrast to the method that used long alkyl chain ligands as the linker to assemble the Au satellites.38 Notably, the Au core could serve as an Au mirror in the ACA structure, which could improve the optical distance effectively when light undergoes repeated mirror reflection in the nanostructure. Therefore, it is envisioned that the ACA hybrid structure provides the superb capability to confine the electromagnetic field of light into a dielectric layer and enhance the coupling between light and matter vastly.The formation of a core–shell–satellite coupled structure introduced intriguing modifications to the optical properties. Fig. 1F shows the extinction spectra of Au, Au@Cu2O, and ACA NPs in aqueous solution. Au NPs exhibit a dipole resonance peak localized at ∼530 nm, whereas Au@Cu2O NPs show a dipole resonance peak located at ∼685 nm. Interestingly, the original dipole resonance peak of Au@Cu2O splits into two peaks after the formation of Au satellites on the surface of Au@Cu2O NPs. The Gaussian or Lorentzian fittings of the dual extinction bands of ACA NPs further show the peak splitting in the extinction spectrum of ACA NPs (Fig. 1G and S7†). The newly fitted peaks are labeled as ω+ and ω−, which are localized at ∼590 nm and ∼690 nm, respectively. Inspired by the modal strong coupling system developed by Misawa and coworkers,33 we proposed that the observed peak splitting in our case is akin to the energy-level splitting into upper and lower modes generated by the modal coupling (Fig. 1H). Note that Fig. 1H shows the enhanced light reflection and absorption in the ACA structure but not a whispering gallery mode (WGM). Energy-level diagram of the coupling between the nanocavity mode in the Cu2O layer and the LSPR mode of the Au satellite NPs was showed in the right panel of Fig. 1H. The ωsp and ωcavity are the resonant frequencies of plasmon and nanocavity modes. The LSPR mode of Au satellites is thought to be coupled with the nanocavity mode of the Au@Cu2O layer in the ACA structure upon light excitation, leading to the peak splitting in the ensemble extinction spectrum. Although the nanocavity mode here is not a traditional F–P cavity mode as Misawa and coworkers demonstrated in their cases,33,34 the inner Au@Cu2O core in the ACA structure could be considered as a nanocavity mode when interacting with light and the Au satellites for enhanced light absorption. To satisfy the strong coupling regime between two oscillators, the frequency of the coupled system should be higher than the dephasing time of both oscillators.39,40 However, it's very difficult for us to estimate the splitting energy on account of the thickness change of Cu2O and the variation in Au satellite size during the process of loading Au satellites, so we couldn't obtain meaningful results such as the inverse cross curve of strong coupling.33 Therefore, we use a modal coupling mechanism to account for the optical properties that we observed on the ACA structure and further propose another system for understanding the plasmon coupling in the three-dimensional ACA hybrid structures.
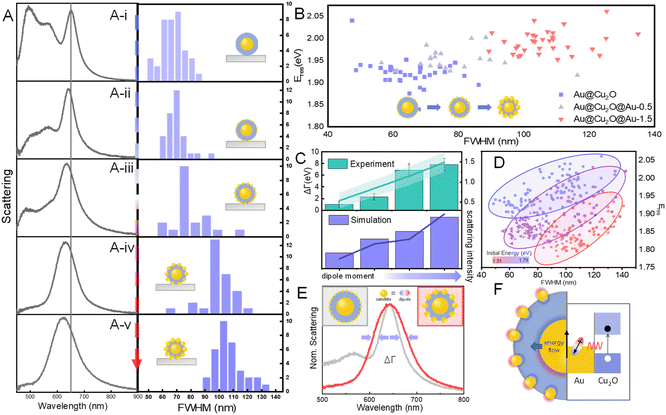
For the plasmonic NPs with a coupling system, it is well known that the size, permittivity, shape, and distance between NPs determine the optical properties of the coupled system.41–45 Thus, we further tuned the structural features and plasmon coupling of ACA NPs by controlling the size and density of Au satellites (Fig. 2). By simply changing the amount of Au precursors involved in the GRR with the Cu2O shell, ACA NPs with tunable size and density of Au satellites can be obtained (Fig. 2C–H and S8†). The thickness of the Cu2O shell in ACA NPs is found to gradually decrease as the amount of HAuCl4 increases (Fig. S8†). As shown in Fig. 2A, a gradual broadening of the dipole resonance peak of ACA NPs can be observed as the size and density of Au satellites first increase. A further increase in the size of Au satellites generates a shoulder peak (∼600 nm), which may indicate the formation of dual-extinction bands due to the peak splitting induced by modal coupling (Fig. S9†). The shoulder peak becomes stronger, so eventually, a broad extinction band was observed (Fig. 2A: F curve), suggesting the superposition of two peaks. As we proposed in Fig. 1H, these two peaks are classified as ω+ and ω−, indicating modal coupling between the nanocavity mode and LSPR mode of Au satellites. As the amount of HAuCl4 further increases, the ω+ mode blueshifts and the ω− mode redshifts, ultimately exhibiting two obvious individual peaks (Fig. 2A: G curve). Also, the extinction band of Cu2O located at ∼470 nm decreases gradually during the GRR between the Cu2O shell and HAuCl4, suggesting the changes in the thickness of the Cu2O shell in ACA NPs.
To gain more quantitative insights into the optical properties of coupled structures, we calculated the extinction spectra of ACA NPs with different densities and sizes of Au satellites using the finite-difference-time-domain (FDTD) method (Fig. 2B). The simulation models were constructed according to the TEM images of a single particle (Fig. 2C–H). The simulated results are in excellent agreement with our experimental observations, indicating that the coupling between the LSPR of Au satellites and the nanocavity mode of the Au@Cu2O layer strongly affects their optical properties through peak splitting. Notably, the aggregated larger satellites could potentially affect the optical properties of ACA NPs. The plasmon–plasmon coupling between Au satellites cannot be completely excluded for sure. Our simulation models, as shown in Fig. 2, have already accounted for the aggregated states for larger Au satellites. However, it is very difficult to experimentally control the density of aggregated Au satellites for a quantitative comparison. Thus, to quantitatively show the impact of plasmon–plasmon coupling between Au satellites on the optical properties of ACA NPs, we have further carried out the FDTD simulations on ACA NPs with discrete and aggregated Au satellites, respectively. As shown in Fig. S10,† the aggregated Au satellites with a size of 8 nm have a negligible impact on the overall optical properties of ACA NPs. In contrast, for Au satellites with a size of 15 nm, broadening of the plasmon peaks of ACA NPs can be observed as the number of aggregated Au satellites increases. The dependence of optical properties on the coupling between Au satellites and the Au@Cu2O layer can also be observed and tuned in ACA NPs using anisotropic Au NPs as initial seeds instead of spherical Au NPs (Fig. S11†).
We further investigated the impact of the Cu2O shell on the modal splitting in the extinction spectra of ACA NPs by varying the thickness of the Cu2O layer (Fig. 3). We constructed ACA NPs with 5 different Cu2O thicknesses (the dipole resonance peak located at 630, 650, 667, 685, and 695 nm, respectively). As shown in Fig. 2A and S12,† distinct spectral evolution of extinction bands of ACA NPs with different Cu2O thicknesses can be observed as a function of the amount of Au precursor. To further qualitatively investigate the spectral differences in different shell thicknesses, two Au@Cu2O NPs with their dipole resonance peaks located at 630 nm and 667 nm were chosen for a detailed analysis of modal splitting (Fig. 3A and B). The red and blue curves indicate the Gaussian fitting of the dual extinction bands (ω− and ω+), which clarifies the transient state from overlapping to the separation of dual-extinction bands. For the peak locations, ω+ blue shifts to a shorter wavelength while ω− red shifts to a longer wavelength as the amount of Au precursor increases. As the amount of Au precursor increases, the dipole moment (proportional to the radius of the Au particle) of Au satellites becomes larger, which significantly enhances the modal coupling between the cavity mode and the LSPR mode. Thus, the enhanced modal coupling leads to the blueshift of ω+ and the redshift of ω− with a larger modal splitting in extinction spectra. The amount of HAuCl4 is found to play a crucial role in tuning the modal coupling in the ACA structure because it affects not only the dipole of the Au satellites but also the thickness of the Cu2O shell in between. Therefore, an increase in the peak intensities of ω+ and ω− modes was observed due to the enhanced modal coupling as the amount of HAuCl4 increased at first with well-defined cavity mode coupling with the dipole modes of Au satellites. However, the peak intensity started to decrease when the amount of HAuCl4 was in excess, leading to the overgrowth of Au satellites and the ill-defined Cu2O shell, i.e., the less-defined nanocavity mode with weaker modal coupling (Fig. 3A and B). Therefore, the dual-extinction bands can be observed in Fig. 3B while not obvious in Fig. 3A because of the different degrees of separation between the two modes. However, the dual-extinction bands can't be observed in the case where the Cu2O shell is very thick (Fig. S12D†). We further compared the full width at half maximum (FWHM) and the peak area changes in both cases (Fig. 3C). Both FWHM and peak area follow the trend of first increasing and then decreasing (Fig. 3C). To further understand the results of FWHM and peak area with the satellite variation, we compared the changes in FWHM and peak area for ACA NPs with 5 different Cu2O thicknesses (Fig. S13†). All the samples showed a consistent variation trend with an increase first and a decrease later as the amount of HAuCl4 increased. In particular, sample S13D with proper Cu2O shell thickness represents the optimum condition for the modal coupling, which was preserved even with a higher amount of HAuCl4. Therefore, our experimental observations suggested that the shell thickness of the Cu2O layer plays a crucial role in modulating the modal splitting of optical extinction spectra.
To better understand the effect of Au satellites and Cu2O shells on the optical properties of ACA NPs, the Mie theory was employed for a deeper analysis. We consider Au@Cu2O NPs as the LSPR core coated with a dielectric shell, which is also in line with previous studies.26,29,46,47 For the Au@Cu2O NPs, an individual dipole resonance peak in the ensemble extinction spectra (Fig. 1F) was observed instead of a complicated multipolar optical mode,48,49 which is also in excellent agreement with our simulation results (Fig. 2B). Also, it is difficult to simply consider it as a Mie resonator due to the presence of the Au core in Au@Cu2O NPs which significantly changes its optical response.50 For NPs much smaller than the wavelength of the absorbing light, only the dipole term is assumed to contribute to the absorption, while quadrupole resonances and other high-order modes are neglected.51 Thus, as depicted by Christian, both the cavity and the orbit of satellites independently form purely dipolar polarization states.52 It has been reported that a strong red shift and spectral peak broadening occur when the Au spherical monomer forms the dimer. Therefore, the spectral line shapes of extinction spectra reflect the interaction between two plasmonic metal NPs to a certain extent. The simplest description of this interaction, the coupling of two nearby oscillators, is in the coupling of two nearby dipoles. The interaction energy is given by53
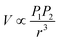 | (1) |
 | (2) |
To simplify the ACA system, we make the following transformations analogous to self-consistent field theory in solving multi-electron atomic wave functions. If we separately consider the individual components in the coupled nanostructures, the EM field distribution and optical performance of one component will be influenced by the induced interaction of dipolar resonances with other nearby components. Under the incident light, the dipole moment of a metal NP is proportional to the size of the particle, while the vector sum of dipole moments of the cavity and other satellites can be described as follows:
 | (3) |
To further quantify the spectral change before and after loading Au satellites on ACA NPs, we defined an equation described by the ratio of the skewness (Δλ, Fig. S14†) of the peak to the full peak width as follows:
 | (4) |
We compared the Gfactor of ACA NPs with different Cu2O shell thicknesses as a function of the amount of Au precursor. The Gfactor was color-coded with different shades and shown with corresponding values. As shown in Fig. 3D, the value of the Gfactor follows a volcano curve as the amount of HAuCl4 increases for ACA NPs with thinner Cu2O shells. In contrast, the Gfactor value of ACA NPs with thicker Cu2O shells gradually increases as the amount of Au precursors increases, which could be attributed to the dominance of the ω− mode. Note that there are no specific physical meanings of the G value as we designed, so we are not able to claim whether the system satisfies the strong coupling regime or not based on the G values.
To more quantitatively understand the impact of plasmon coupling on the optical properties of the ACA hybrid structure, we further carried out the single-particle DFS measurements on the ACA NPs (Fig. 4). The scattering spectra of ∼30 randomly selected particles for each sample were measured using a hyperspectral detection system (Fig. S15,† see experimental details in the ESI†).56 We used the Au@Cu2O NPs whose scattering peak is located at 650 nm as a model system to investigate the spectral evolution of scattering spectra before and after forming Au satellites with different sizes and densities (Fig. 4A). The dipole scattering peak at ∼650 nm of Au@Cu2O NPs shows a slight blueshift as the amount of Au precursors increases. More importantly, the scattering peak becomes significantly broadening along with increases in FWHM, as revealed by the statistical histogram of each dataset. As shown in Fig. 4B, we further correlated the resonance energy (Eres) of the scattering peak with the FWHM (Γ). Again, it is found that the Eres increases along with the increases in FWHM as the size of Au satellites increases, which is also in excellent agreement with the simulated results (Fig. 4C). Note that the thickness of the Cu2O shell decreases as more Au precursors react with the shell through the GRR, which in turn increases the coupling strength that leads to the increase in FWHM. We also designed and fabricated Au@Cu2O NPs with two different shell thicknesses to tune the plasmon coupling when forming ACA NPs with different thicknesses of Cu2O cavities (Fig. S16 and S17†). We then classified them into coupled structures with different initial energies of 1.91 eV (blue), 1.85 eV (purple), and 1.79 eV (red), as shown in Fig. 4D. It is worth noting that as we added HAuCl4 to the system, it is difficult to ensure that each particle undergoes the same changes. However, single-particle spectroscopy has an advantage over ensemble extinction spectroscopy, which allows one to count the changes in each particle. Thus, we counted all the samples with different HAuCl4 added at the same initial Cu2O thickness, and the trend of FWHM and peak position at that thickness can be obtained from the scatter plot (Fig. 4D). By comparing the scatter plots of Au@Cu2O NPs with three different initial energies, we found that the resonance energy of Au@Cu2O with higher initial energy varies faster with the FWHM. While the modal peak splitting cannot be observed in the single-particle scattering spectra, the dramatic broadening of scattering plasmonic modes also indicates the enhanced coupling between the plasmon mode of the Au satellite and the nanocavity mode of the inner Au@Cu2O layer.
We further compared the FWHM of scattering spectra of ACA NPs with significantly different sizes of Au satellites (Fig. 4E). It is observed that the larger Au satellite induces significantly more plasmon damping, resulting in the broadening of the scattering peak and an increase in FWHM. The changes in FWHM could be attributed to the enhanced electron–phonon relaxation when surface adsorbates induce an electric dipole at the particle surfaces,57 which has also been previously demonstrated using single-particle spectroscopy.58 Recent studies have further demonstrated that energy transfer can cause a decrease in the electron temperature, which in turn decreases the electron–phonon relaxation time.59 In the model of the ACA system, Au satellites serving as dipoles can accelerate the electron–phonon relaxation of the Au core, which accelerates the energy transfer process. The electron–phonon coupling time (τe–ph) is determined by the electronic temperature. The dependence of τe–ph can be described using the following equation,60 according to the well-established two-temperature model for describing the electron dynamics of metal NPs.
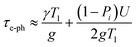 | (5) |
To further explore the significance of the Au core on the enhanced coupled plasmonic properties of ACA NPs, we carried out the plasmon-driven dimerization of 4-nitrothiophenol (4-NTP) to 4,4′-dimercaptoazobenzene (DMAB) on ACA NPs; in this case, the Au satellites serve as the catalytically active sites (Fig. 5). Time-resolved SERS was used as a spectroscopic tool to monitor the molecular transformation from 4-NTP to DMAB upon laser excitation, in which the characteristic SERS peaks of 4-NTP and DMAB have been carefully demonstrated by previous studies (Fig. S18†).61,62 Similar to plasmonic NPs on mirror systems, the Au core is expected to serve as a plasmonic mirror to confine the electromagnetic field of light into a dielectric layer and significantly enhance the plasmonic near-fields.63–67 As illustrated in Fig. 5A, a CW excitation laser was focused on a 2 μm diameter focal spot by using a confocal Raman microscope. ACA NPs and Cu2O@Au NPs with roughly similar sizes and densities of Au satellites were employed as the single-particle bifunctional substrates (Fig. S19†). Fig. 5B and C show the temporal evolution of SERS spectral features under isolated air at an excitation wavelength (λex) of 785 nm on ACA NPs and Cu2O NPs, respectively. Since the tests were performed in the presence of water, we excluded photothermal effects on the reaction and only considered carrier effects. At the initial stage, three SERS peaks located at 1078, 1338, and 1572 cm−1 are observed in the Raman spectrum, corresponding to the characteristic C–S bond stretching (νC–S), symmetric nitro stretching (νNO2) and aromatic ring stretching (νring) modes of 4-NTP.68–70 After the laser excitation, four new SERS bands signifying the formation of DMAB emerged at 1143, 1181, 1444, and 1472 cm−1, all of which became progressively more intense as the dimerization reaction proceeded.70–72 The overall trend of 4-NTP on Cu2O@Au follows the same law, despite some details different from ACA NPs, which is attributed to the different coupling rates (Fig. S19 and S20†). We further calculated the apparent fractions of DMAB and 4-NTP, denoted as θDMAB and θNTP, respectively, based on the relative intensities of the SERS peaks at 1438 cm−1 (νN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N of DMAB) and 1338 cm−1 (νNO2 of 4-NTP) with respect to the νring mode at 1572 cm−1 (see details in the ESI†). As shown in Fig. 5D and E, the temporal evolutions of θDMAB and θNTP both obey an apparent first-order rate law, which can be described using the following rate equations:
N of DMAB) and 1338 cm−1 (νNO2 of 4-NTP) with respect to the νring mode at 1572 cm−1 (see details in the ESI†). As shown in Fig. 5D and E, the temporal evolutions of θDMAB and θNTP both obey an apparent first-order rate law, which can be described using the following rate equations:
| θDMAB(t) = θt=∞(t) × (1 − e−kt) | (6) |
| θNTP(t) = 1 − θt=∞ + θt=∞ × e−kt | (7) |
Strong electromagnetic field enhancement can promote hot carrier separation more efficiently in metal-semiconductor nanostructures for photocatalysis, which has been widely studied.73–75 We propose that the different reaction behaviors between ACA NPs and Cu2O@Au NPs in plasmon-driven dimerization of 4-NTP could be attributed to the different excitation strengths of plasmonic near-fields. To gain deep insights into the plasmonic near-field properties of different structures, we have further used FDTD to calculate the near-field enhancement of ACA, Cu2O@Au, and Au@Cu2O NPs (Fig. 5F). Fig. 5F shows the cross-sectional views of calculated near-field enhancements of ACA, Cu2O@Au, and Au@Cu2O NPs (|E/E0|2 plotted on a logarithmic scale) under 638 nm and 785 nm laser excitation, respectively. Near-field enhancement of Au@Cu2O NPs is mainly concentrated at the interface between the core and shell layer while weak on the outer surface of NPs. For Cu2O@Au NPs, the external electric field of NPs is excited, while the internal near-field enhancement is weak. The enhanced electric field in Fig. 5F (center: Cu2O@Au NPs) is due to the presence of Au satellites that create inter-particle hotspots on the surface of Cu2O NPs. In contrast, ACA NPs exhibit an enormous enhancement of both external and internal near-fields, and this synergistic effect greatly enhances the overall electromagnetic field for plasmonic photochemistry.
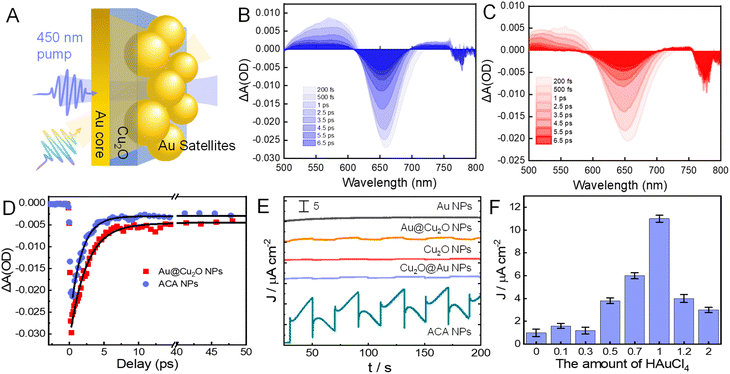
We further employed ultrafast TA spectroscopy to investigate the dynamics of plasmon decay of ACA hybrid structures in comparison to the corresponding Au@Cu2O NPs (Fig. 6A). Both TA spectra of ACA and Au@Cu2O NPs exhibit a bleaching signal at the plasmon resonance accompanied by two positive wings on both sides due to induced absorption (Fig. 6B and C). The electron–electron scattering occurred during the initial fast rise due to the high electron density of metals (Fig. 6D). In addition, a longer absorption rise can be observed for ACA NPs compared with Au and Au@Cu2O NPs (Fig. S22–S24†), which is consistent with previous observations under coupling conditions.66 The ultrafast decay arises from electron–phonon scattering on the order of a few picoseconds followed by the lattice cooling at a longer time scale. The fitted data revealed electron–phonon relaxation times (τe–ph) of 2.45 and 1.65 ps for Au@Cu2O and ACA NPs (Table S1†), which is consistent with our inference that the Au satellites on the surface of the ACA NPs act as dipoles, accelerating the electron–phonon relaxation process of the Au core. In contrast, the Au NPs exhibited a long τe–ph (4.89 ps), which is in line with previous studies.
To investigate the photocatalytic activities of the as-constructed ACA hybrid structures, we measured the photocurrents of ACA NPs in a three-electrode system using a Xe lamp as the light source (see details in the ESI†). Notably, charge recombination is significantly suppressed in PEC measurement with an applied bias voltage, allowing us to focus on how plasmonic charge density affects photocatalytic reactions. Fig. 6E shows the comparison of the photocurrent response among the Au, Au@Cu2O, Cu2O, Cu2O@Au, and ACA NPs. No significant photocurrent response is observed in the Au NP, whereas a stronger photocurrent response occurs in Au@Cu2O NPs. Remarkably, at an applied potential of −0.3 V, the photocurrent density of ACA NPs is 5-fold with respect to that of Au@Cu2O NPs. Additionally, Cu2O and Cu2O@Au NPs show similar photocurrents to the Au@Cu2O NPs, suggesting that the formation of ACA NPs plays a crucial role in the enhanced photocurrents. As shown in Fig. 6F, we further compared the photocurrent response of ACA NPs with different densities and sizes of Au satellites (samples as shown in Fig. 2A). First, all the ACA NPs exhibit significantly higher photocurrent responses compared to the Au@Cu2O NPs. Moreover, the photocurrent responses of ACA follow the same trend of increasing and then decreasing (Fig. 2F and S25†), consistent with our analysis of changes in the line width and peak area (Fig. 3C) as well as previous work on photocatalytic hydrogenation.37 While the correlation is very intriguing, the underlying mechanism could be much more complicated than we expected and require further scrutiny. Overall, our experimental observations strongly demonstrate the superior performance of the ACA hybrid structure toward plasmonic photocatalysis.
Finally, the method for constructing the core–shell–satellite structure that we developed here also shows versatility for creating unconventional hybrid plasmon structures for various optical applications (Fig. S26 and S27†). For instance, by using a chiral Au rhombic dodecahedron (RD) as the initial core,76 we were able to demonstrate the plasmon coupling between the Au satellite and chiral nanocavity through the construction of chiral Au RD@Cu2O@Au hybrid structures (Fig. S26†).77 By simply controlling the amount of Au precursors that react with the Cu2O shell through the GRR, the chiral ACA NPs with tunable chiral couplings and chiroptical activities can be obtained (Fig. S26 and S27†). Moreover, significantly enhanced electromagnetic fields were observed for chiral ACA structures because of the intense chiral plasmon coupling in the core–shell–satellite structure (Fig. S27†), and this phenomenon has also been observed in the mentioned achiral ACA NPs (Fig. 5F). FDTD simulations further revealed the chiral near-field distributions when excited using 824 nm left/right-handed circularly polarized (LCP/RCP) light (Fig. S27†). It is envisioned that the chiral ACA structure with significantly enhanced plasmon coupling and chiral near-fields could provide a promising platform for chirality-dependent plasmonic photocatalysis.78–82
Conclusions
In summary, we have demonstrated a general approach for constructing core–shell–satellite coupled nanostructures with tunable optical properties for enhanced plasmon photocatalysis. By deliberately changing the size of Au satellites and the shell thickness of Cu2O, we experimentally and theoretically demonstrated the modal splitting in the extinction spectra of the hybrid structures. We further employed single-particle scattering to show the spectral changes of plasmon bands on each particle. Moreover, the coupled nanostructures with tunable plasmon coupling exhibit excellent photocatalytic activities toward plasmon-driven chemical reactions, as revealed by in situ SERS measurements. TA spectroscopy and PEC measurements also show the superior performance of the hybrid structure toward plasmonic photocatalysis. Finally, this strategy can also be employed to construct chiral coupled nanostructures for applications in chirality-dependent plasmonic photocatalysis. It is envisioned that integrating plasmon coupling and excellent catalytic activity within the 3D coupled nanostructure represents a promising approach for applications in photonics and plasmonic photocatalysis.Data availability
A data availability statement (DAS) is required to be submitted alongside all articles. Please read our full guidance on data availability statements for more details and examples of suitable statements you can use.Author contributions
The manuscript was written through the contributions of all authors. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 22174104, 22472119, and 22405195). This work was also funded by the Basic Research Program of Jiangsu (Grant No. BK20240448 to L. S.). The authors also acknowledge the support of the Large-scale Instrument and Equipment Sharing Foundation of Wuhan University and the Core Facility of Wuhan University. We also thank the Core Research Facility of the College of Chemistry and Molecular Sciences at Wuhan University for SEM and TEM characterization studies.Notes and references
- W. L. Barnes, A. Dereux and T. W. Ebbesen, Surface plasmon subwavelength optics, Nature, 2003, 424, 824–830 CrossRef CAS PubMed.
- F. J. García de Abajo, Nonlocal Effects in the Plasmons of Strongly Interacting Nanoparticles, Dimers, and Waveguides, J. Phys. Chem. C, 2008, 112, 17983–17987 CrossRef.
- P. K. Jain, S. Eustis and M. A. El-Sayed, Plasmon Coupling in Nanorod Assemblies: Optical Absorption, Discrete Dipole Approximation Simulation, and Exciton-Coupling Model, J. Phys. Chem. B, 2006, 110, 18243–18253 CrossRef CAS PubMed.
- E. Prodan, C. Radloff, N. J. Halas and P. Nordlander, A Hybridization Model for the Plasmon Response of Complex Nanostructures, Science, 2003, 302, 419–422 CrossRef CAS PubMed.
- Y. Bao, Z. Hu, Z. Li, X. Zhu and Z. Fang, Magnetic Plasmonic Fano Resonance at Optical Frequency, Small, 2015, 11, 2177–2181 CAS.
- N. Verellen, Y. Sonnefraud, H. Sobhani, F. Hao, V. V. Moshchalkov, P. V. Dorpe, P. Nordlander and S. A. Maier, Fano Resonances in Individual Coherent Plasmonic Nanocavities, Nano Lett., 2009, 9, 1663–1667 CAS.
- S. Zhang, K. Bao, N. J. Halas, H. Xu and P. Nordlander, Substrate-Induced Fano Resonances of a Plasmonic Nanocube: A Route to Increased-Sensitivity Localized Surface Plasmon Resonance Sensors Revealed, Nano Lett., 2011, 11, 1657–1663 CrossRef CAS PubMed.
- N. Liu, L. Langguth, T. Weiss, J. Kästel, M. Fleischhauer, T. Pfau and H. Giessen, Plasmonic analogue of electromagnetically induced transparency at the Drude damping limit, Nat. Mater., 2009, 8, 758–762 CrossRef CAS PubMed.
- P. Zeng, J. Cadusch, D. Chakraborty, T. A. Smith, A. Roberts, J. E. Sader, T. J. Davis and D. E. Gómez, Photoinduced Electron Transfer in the Strong Coupling Regime: Waveguide–Plasmon Polaritons, Nano Lett., 2016, 16, 2651–2656 CrossRef CAS PubMed.
- N. S. King, L. Liu, X. Yang, B. Cerjan, H. O. Everitt, P. Nordlander and N. J. Halas, Fano Resonant Aluminum Nanoclusters for Plasmonic Colorimetric Sensing, ACS Nano, 2015, 9, 10628–10636 CAS.
- A. Aubry, D. Y. Lei, A. I. Fernández-Domínguez, Y. Sonnefraud, S. A. Maier and J. B. Pendry, Plasmonic Light-Harvesting Devices over the Whole Visible Spectrum, Nano Lett., 2010, 10, 2574–2579 CrossRef CAS PubMed.
- D. Liu and C. Xue, Plasmonic Coupling Architectures for Enhanced Photocatalysis, Adv. Mater., 2021, 33, 2005738 CAS.
- S. Kawata, Y. Inouye and P. Verma, Plasmonics for near-field nano-imaging and superlensing, Nat. Photonics, 2009, 3, 388–394 CrossRef CAS.
- H. Baida, D. Mongin, D. Christofilos, G. Bachelier, A. Crut, P. Maioli, N. Del Fatti and F. Vallée, Ultrafast Nonlinear Optical Response of a Single Gold Nanorod near Its Surface Plasmon Resonance, Phys. Rev. Lett., 2011, 107, 057402 CrossRef CAS.
- X. Hu, Y. Zhang, Y. Fu, H. Yang and Q. Gong, Low-Power and Ultrafast All-Optical Tunable Nanometer-Scale Photonic Metamaterials, Adv. Mater., 2011, 23, 4295–4300 CrossRef CAS PubMed.
- T. Oshikiri, K. Ueno and H. Misawa, Plasmon-Induced Ammonia Synthesis through Nitrogen Photofixation with Visible Light Irradiation, Angew. Chem., Int. Ed., 2014, 53, 9802–9805 CrossRef CAS PubMed.
- S. Li, P. Miao, Y. Zhang, J. Wu, B. Zhang, Y. Du, X. Han, J. Sun and P. Xu, Recent Advances in Plasmonic Nanostructures for Enhanced Photocatalysis and Electrocatalysis, Adv. Mater., 2021, 33, 2000086 CrossRef CAS PubMed.
- L. A. Zhou, J. M. P. Martirez, J. Finzel, C. Zhang, D. F. Swearer, S. Tian, H. Robatjazi, M. H. Lou, L. L. Dong, L. Henderson, P. Christopher, E. A. Carter, P. Nordlander and N. J. Halas, Light-driven methane dry reforming with single atomic site antenna-reactor plasmonic photocatalysts, Nat. Energy, 2020, 5, 61–70 CrossRef CAS.
- T. Kawawaki, T. Nakagawa, M. Sakamoto and T. Teranishi, Carrier-Selective Blocking Layer Synergistically Improves the Plasmonic Enhancement Effect, J. Am. Chem. Soc., 2019, 141, 8402–8406 CrossRef CAS PubMed.
- M. Cai, Z. Wu, Z. Li, L. Wang, W. Sun, A. A. Tountas, C. Li, S. Wang, K. Feng, A.-B. Xu, S. Tang, A. Tavasoli, M. Peng, W. Liu, A. S. Helmy, L. He, G. A. Ozin and X. Zhang, Greenhouse-inspired supra-photothermal CO2 catalysis, Nat. Energy, 2021, 6, 807–814 CrossRef CAS.
- C. Clavero, Plasmon-induced hot-electron generation at nanoparticle/metal-oxide interfaces for photovoltaic and photocatalytic devices, Nat. Photonics, 2014, 8, 95–103 CAS.
- S. K. Cushing, J. Li, F. Meng, T. R. Senty, S. Suri, M. Zhi, M. Li, A. D. Bristow and N. Wu, Photocatalytic Activity Enhanced by Plasmonic Resonant Energy Transfer from Metal to Semiconductor, J. Am. Chem. Soc., 2012, 134, 15033–15041 CAS.
- R. Long, K. Mao, M. Gong, S. Zhou, J. Hu, M. Zhi, Y. You, S. Bai, J. Jiang, Q. Zhang, X. Wu and Y. Xiong, Tunable Oxygen Activation for Catalytic Organic Oxidation: Schottky Junction versus Plasmonic Effects, Angew. Chem., Int. Ed., 2014, 53, 3205–3209 CAS.
- K. Song, H. Lee, M. Lee and J. Y. Park, Plasmonic Hot Hole-Driven Water Splitting on Au Nanoprisms/P-Type GaN, ACS Energy Lett., 2021, 6, 1333–1339 CAS.
- J. W. Hong, D. H. Wi, S.-U. Lee and S. W. Han, Metal–Semiconductor Heteronanocrystals with Desired Configurations for Plasmonic Photocatalysis, J. Am. Chem. Soc., 2016, 138, 15766–15773 CAS.
- H. Jia, F. Li, T. H. Chow, X. Liu, H. Zhang, Y. Lu, J. Wang and C.-y. Zhang, Construction of Spatially Separated Gold Nanocrystal/Cuprous Oxide Architecture for Plasmon-Driven CO2 Reduction, Nano Lett., 2022, 22, 7268–7274 CAS.
- S. Linic, S. Chavez and R. Elias, Flow and extraction of energy and charge carriers in hybrid plasmonic nanostructures, Nat. Mater., 2021, 20, 916–924 CAS.
- R. Long, Z. Rao, K. Mao, Y. Li, C. Zhang, Q. Liu, C. Wang, Z.-Y. Li, X. Wu and Y. Xiong, Efficient Coupling of Solar Energy to Catalytic Hydrogenation by Using Well-Designed Palladium Nanostructures, Angew. Chem., Int. Ed., 2015, 54, 2425–2430 CAS.
- W. Xu, J. Jia, T. Wang, C. Li, B. He, J. Zong, Y. Wang, H. J. Fan, H. Xu, Y. Feng and H. Chen, Continuous Tuning of Au–Cu2O Janus Nanostructures for Efficient Charge Separation, Angew. Chem., Int. Ed., 2020, 59, 22246–22251 CAS.
- J. Zhang, X. Jin, P. I. Morales-Guzman, X. Yu, H. Liu, H. Zhang, L. Razzari and J. P. Claverie, Engineering the Absorption and Field Enhancement Properties of Au–TiO2 Nanohybrids via Whispering Gallery Mode Resonances for Photocatalytic Water Splitting, ACS Nano, 2016, 10, 4496–4503 CAS.
- P. Ding, E. Liang, G. Cai, W. Hu, C. Fan and Q. Xue, Dual-band perfect absorption and field enhancement by interaction between localized and propagating surface plasmons in optical metamaterials, J. Opt., 2011, 13, 075005 Search PubMed.
- J. Yang, Q. Sun, K. Ueno, X. Shi, T. Oshikiri, H. Misawa and Q. Gong, Manipulation of the dephasing time by strong coupling between localized and propagating surface plasmon modes, Nat. Commun., 2018, 9, 4858 Search PubMed.
- X. Shi, K. Ueno, T. Oshikiri, Q. Sun, K. Sasaki and H. Misawa, Enhanced water splitting under modal strong coupling conditions, Nat. Nanotechnol., 2018, 13, 953–958 CAS.
- Y. Suganami, T. Oshikiri, X. Shi and H. Misawa, Water Oxidation under Modal Ultrastrong Coupling Conditions Using Gold/Silver Alloy Nanoparticles and Fabry–Pérot Nanocavities, Angew. Chem., Int. Ed., 2021, 60, 18438–18442 CrossRef CAS.
- Y. Cao, X. Shi, T. Oshikiri, S. Zu, Y. Sunaba, K. Sasaki and H. Misawa, Near-field engineering for boosting the photoelectrochemical activity to a modal strong coupling structure, Chem. Commun., 2021, 57, 524–527 RSC.
- X. Yu, X. Liu, B. Wang, Q. Meng, S. Sun, Y. Tang and K. Zhao, An LSPR-based “push–pull” synergetic effect for the enhanced photocatalytic performance of a gold nanorod@cuprous oxide-gold nanoparticle ternary composite, Nanoscale, 2020, 12, 1912–1920 RSC.
- H. Ren, J.-L. Yang, W.-M. Yang, H.-L. Zhong, J.-S. Lin, P. M. Radjenovic, L. Sun, H. Zhang, J. Xu, Z.-Q. Tian and J.-F. Li, Core–Shell–Satellite Plasmonic Photocatalyst for Broad-Spectrum Photocatalytic Water Splitting, ACS Mater. Lett., 2021, 3, 69–76 CrossRef CAS.
- Y. Kim, D. H. Wi, J. W. Hong and S. W. Han, Plasmonic Nanocrystal Assembly–Semiconductor Hybrids for Boosting Visible to Near-Infrared Photocatalysis, ACS Nano, 2023, 17, 18641–18651 CAS.
- A. F. Kockum, A. Miranowicz, S. De Liberato, S. Savasta and F. Nori, Ultrastrong coupling between light and matter, Nat. Rev. Phys., 2019, 1, 19–40 Search PubMed.
- R. Houdre, J. L. Gibernon, P. Pellandini, R. P. Stanley, U. Oesterle, C. Weisbuch, J. Ogorman, B. Roycroft and M. Ilegems, Saturation of the Strong-Coupling Regime in a Semiconductor Microcavity - Free-Carrier Bleaching of Cavity Polaritons, Phys. Rev. B, 1995, 52, 7810–7813 CAS.
- T. H. Chow, Y. Lai, X. Cui, W. Lu, X. Zhuo and J. Wang, Colloidal Gold Nanorings and Their Plasmon Coupling with Gold Nanospheres, Small, 2019, 15, 1902608 CrossRef PubMed.
- W. Chen, S. Zhang, Q. Deng and H. Xu, Probing of sub-picometer vertical differential resolutions using cavity plasmons, Nat. Commun., 2018, 9, 801 CrossRef PubMed.
- G.-C. Li, Y.-L. Zhang, J. Jiang, Y. Luo and D. Y. Lei, Metal-Substrate-Mediated Plasmon Hybridization in a Nanoparticle Dimer for Photoluminescence Line-Width Shrinking and Intensity Enhancement, ACS Nano, 2017, 11, 3067–3080 CrossRef CAS PubMed.
- W. Q. Li, G. Wang, X. N. Zhang, H. P. Geng, J. L. Shen, L. S. Wang, J. Zhao, L. F. Xu, L. J. Zhang, Y. Q. Wu, R. Z. Tai and G. Chen, Geometrical and morphological optimizations of plasmonic nanoarrays for high-performance SERS detection, Nanoscale, 2015, 7, 15487–15494 RSC.
- H. J. Kim, S. H. Lee, A. A. Upadhye, I. Ro, M. I. Tejedor-Tejedor, M. A. Anderson, W. B. Kim and G. W. Huber, Plasmon-Enhanced Photoelectrochemical Water Splitting with Size-Controllable Gold Nanodot Arrays, ACS Nano, 2014, 8, 10756–10765 CrossRef CAS PubMed.
- L. Zhang, D. A. Blom and H. Wang, Au-Cu2O Core-Shell Nanoparticles: A Hybrid Metal-Semiconductor Heteronanostructure with Geometrically Tunable Optical Properties, Chem. Mater., 2011, 23, 4587–4598 CAS.
- H. Jing, N. Large, Q. F. Zhang and H. Wang, Epitaxial Growth of Cu2O on Ag Allows for Fine Control Over Particle Geometries and Optical Properties of Ag-Cu2O Core-Shell Nanoparticles, J. Phys. Chem. C, 2014, 118, 19948–19963 CrossRef CAS.
- T. Oshikiri, T. Hayakawa, H. Niinomi and M. Nakagawa, Strong Light Confinement by a Plasmon-Coupled Parabolic Nanoresonator Array, J. Phys. Chem. C, 2024, 128, 5271–5279 CrossRef CAS.
- P. Gu, M. J. Wan, W. Y. Wu, Z. Chen and Z. L. Wang, Excitation and tuning of Fano-like cavity plasmon resonances in dielectric-metal core-shell resonators, Nanoscale, 2016, 8, 10358–10363 RSC.
- H. Sugimoto, T. Okazaki and M. Fujii, Mie Resonator Color Inks of Monodispersed and Perfectly Spherical Crystalline Silicon Nanoparticles, Adv. Opt. Mater., 2020, 8, 2000033 CrossRef CAS.
- S. Link and M. A. El-Sayed, Spectral Properties and Relaxation Dynamics of Surface Plasmon Electronic Oscillations in Gold and Silver Nanodots and Nanorods, J. Phys. Chem. B, 1999, 103, 8410–8426 CrossRef CAS.
- R. P. M. Höller, M. Dulle, S. Thomä, M. Mayer, A. M. Steiner, S. Förster, A. Fery, C. Kuttner and M. Chanana, Protein-Assisted Assembly of Modular 3D Plasmonic Raspberry-like Core/Satellite Nanoclusters: Correlation of Structure and Optical Properties, ACS Nano, 2016, 10, 5740–5750 CrossRef PubMed.
- N. J. Halas, S. Lal, W.-S. Chang, S. Link and P. Nordlander, Plasmons in Strongly Coupled Metallic Nanostructures, Chem. Rev., 2011, 111, 3913–3961 CrossRef CAS PubMed.
- K. M. Kosuda, J. M. Bingham, K. L. Wustholz and R. P. Van Duyne, in Comprehensive Nanoscience and Technology, ed. D. L. Andrews, G. D. Scholes and G. P. Wiederrecht, Academic Press, Amsterdam, 2011, pp. 263–301 Search PubMed.
- S. Sheikholeslami, Y.-w. Jun, P. K. Jain and A. P. Alivisatos, Coupling of Optical Resonances in a Compositionally Asymmetric Plasmonic Nanoparticle Dimer, Nano Lett., 2010, 10, 2655–2660 CAS.
- Q. F. Zhang, T. Hernandez, K. W. Smith, S. A. H. Jebeli, A. X. Dai, L. Warning, R. Baiyasi, L. A. McCarthy, H. Guo, D. H. Chen, J. A. Dionne, C. F. Landes and S. Link, Unraveling the origin of chirality from plasmonic nanoparticle-protein complexes, Science, 2019, 365, 1475–1478 CAS.
- S. L. Westcott, R. D. Averitt, J. A. Wolfgang, P. Nordlander and N. J. Halas, Adsorbate-Induced Quenching of Hot Electrons in Gold Core−Shell Nanoparticles, J. Phys. Chem. B, 2001, 105, 9913–9917 CrossRef CAS.
- B. Foerster, V. A. Spata, E. A. Carter, C. Sönnichsen and S. Link, Plasmon damping depends on the chemical nature of the nanoparticle interface, Sci. Adv., 2019, 5, eaav0704 Search PubMed.
- G. Tagliabue, J. S. DuChene, M. Abdellah, A. Habib, D. J. Gosztola, Y. Hattori, W.-H. Cheng, K. Zheng, S. E. Canton, R. Sundararaman, J. Sá and H. A. Atwater, Ultrafast hot-hole injection modifies hot-electron dynamics in Au/p-GaN heterostructures, Nat. Mater., 2020, 19, 1312–1318 CAS.
- D. C. Ratchford, A. D. Dunkelberger, I. Vurgaftman, J. C. Owrutsky and P. E. Pehrsson, Quantification of Efficient Plasmonic Hot-Electron Injection in Gold Nanoparticle–TiO2 Films, Nano Lett., 2017, 17, 6047–6055 Search PubMed.
- Q. Zhang, Y. Zhou, X. Fu, E. Villarreal, L. Sun, S. Zou and H. Wang, Photothermal Effect, Local Field Dependence, and Charge Carrier Relaying Species in Plasmon-Driven Photocatalysis: A Case Study of Aerobic Nitrothiophenol Coupling Reaction, J. Phys. Chem. C, 2019, 123, 26695–26704 CAS.
- Y. Li, Z. Zhang, A. Du, X. Du, A. Zhu, C. Zhang, Y. Gao, Y. Hu, Y. Wang, X. Yang, L. Yang and W. Xie, Hot-Electron-Driven Interfacial Chemistry Using Non-Noble Plasmonic Cu under Visible-Light Irradiation, ACS Photonics, 2023, 10, 3181–3187 CAS.
- R. Chikkaraddy, V. A. Turek, N. Kongsuwan, F. Benz, C. Carnegie, T. van de Goor, B. de Nijs, A. Demetriadou, O. Hess, U. F. Keyser and J. J. Baumberg, Mapping Nanoscale Hotspots with Single-Molecule Emitters Assembled into Plasmonic Nanocavities Using DNA Origami, Nano Lett., 2018, 18, 405–411 Search PubMed.
- J.-H. Huh, J. Lee and S. Lee, Comparative Study of Plasmonic Resonances between the Roundest and Randomly Faceted Au Nanoparticles-on-Mirror Cavities, ACS Photonics, 2018, 5, 413–421 Search PubMed.
- J. J. Baumberg, J. Aizpurua, M. H. Mikkelsen and D. R. Smith, Extreme nanophotonics from ultrathin metallic gaps, Nat. Mater., 2019, 18, 668–678 CAS.
- Y. Gao, Q. Zhu, S. He, S. Wang, W. Nie, K. Wu, F. Fan and C. Li, Observation of Charge Separation Enhancement in Plasmonic Photocatalysts under Coupling Conditions, Nano Lett., 2023, 23, 3540–3548 CAS.
- S. Hu, E. Elliott, A. Sánchez-Iglesias, J. Huang, C. Guo, Y. Hou, M. Kamp, E. S. A. Goerlitzer, K. Bedingfield, B. de Nijs, J. Peng, A. Demetriadou, L. M. Liz-Marzán and J. J. Baumberg, Full Control of Plasmonic Nanocavities Using Gold Decahedra-on-Mirror Constructs with Monodisperse Facets, Adv. Sci., 2023, 10, 2207178 CAS.
- M. Sun and H. Xu, A Novel Application of Plasmonics: Plasmon-Driven Surface-Catalyzed Reactions, Small, 2012, 8, 2777–2786 CrossRef CAS.
- Q. Zhang, Y. Zhou, E. Villarreal, Y. Lin, S. Zou and H. Wang, Faceted Gold Nanorods: Nanocuboids, Convex Nanocuboids, and Concave Nanocuboids, Nano Lett., 2015, 15, 4161–4169 CrossRef CAS.
- H.-K. Choi, K. S. Lee, H.-H. Shin and Z. H. Kim, Identification of the First Elementary Step in the Photocatalytic Reduction of Nitrobenzenethiols on a Metallic Surface, J. Phys. Chem. Lett., 2016, 7, 4099–4104 CrossRef CAS PubMed.
- Y.-F. Huang, H.-P. Zhu, G.-K. Liu, D.-Y. Wu, B. Ren and Z.-Q. Tian, When the Signal Is Not from the Original Molecule To Be Detected: Chemical Transformation of para-Aminothiophenol on Ag during the SERS Measurement, J. Am. Chem. Soc., 2010, 132, 9244–9246 CrossRef CAS PubMed.
- Q. Zhang and H. Wang, Mechanistic Insights on Plasmon-Driven Photocatalytic Oxidative Coupling of Thiophenol Derivatives: Evidence for Steady-State Photoactivated Oxygen, J. Phys. Chem. C, 2018, 122, 5686–5697 CrossRef CAS.
- D. B. Ingram and S. Linic, Water Splitting on Composite Plasmonic-Metal/Semiconductor Photoelectrodes: Evidence for Selective Plasmon-Induced Formation of Charge Carriers near the Semiconductor Surface, J. Am. Chem. Soc., 2011, 133, 5202–5205 CrossRef CAS PubMed.
- Z. Liu, W. Hou, P. Pavaskar, M. Aykol and S. B. Cronin, Plasmon Resonant Enhancement of Photocatalytic Water Splitting Under Visible Illumination, Nano Lett., 2011, 11, 1111–1116 CrossRef CAS PubMed.
- H. Jin, M. Herran, E. Cortés and J. Lischner, Theory of Hot-Carrier Generation in Bimetallic Plasmonic Catalysts, ACS Photonics, 2023, 10, 3629–3636 CrossRef CAS PubMed.
- X. Sun, J. Yang, L. Sun, G. Yang, C. Liu, Y. Tao, Q. Cheng, C. Wang, H. Xu and Q. Zhang, Tunable Reversal of Circular Dichroism in the Seed-Mediated Growth of Bichiral Plasmonic Nanoparticles, ACS Nano, 2022, 16, 19174–19186 CrossRef CAS PubMed.
- G. Yang, Y. Tao, Q. Cheng, C. Liu, B. Zhang, X. Sun, Y. Yang, D. Lu, J. Yang, L.-L. Deng, L. Sun, H. Xu, S.-Y. Xie and Q. Zhang, Shell Dependence of Highly Tunable Circular Dichroism in Chiral Hybrid Plasmonic Nanomaterials for Chiroptical Applications, ACS Nano, 2025, 19, 2961–2074 CrossRef CAS PubMed.
- F. Wang, W. Yang, Q. Ding, X. Xing, l. xu, H. Lin, C. Xu and S. Li, Chiral Au@CeO2 Helical Nanorods with Spatially Separated Structures for Polarization-dependent N2 Photofixation, Angew. Chem., Int. Ed., 2024, e202415031 Search PubMed.
- C. L. Hao, L. G. Xu, W. Ma, X. L. Wu, L. B. Wang, H. Kuang and C. L. Xu, Unusual Circularly Polarized Photocatalytic Activity in Nanogapped Gold-Silver Chiroplasmonic Nanostructures, Adv. Funct. Mater., 2015, 25, 5816–5822 CAS.
- Y. Negrin-Montecelo, A. Movsesyan, J. Gao, S. Burger, Z. M. M. Wang, S. Nlate, E. Pouget, R. Oda, M. Comesana-Hermo, A. O. Govorov and M. A. Correa-Duarte, Chiral Generation of Hot Carriers for Polarization-Sensitive Plasmonic Photocatalysis, J. Am. Chem. Soc., 2022, 144, 1663–1671 CAS.
- W. Fu, Q. Gao, C. Zhang, L. Tan, B. Jiang, C. Xiao, M. Liu and P.-p. Wang, Exploring Geometric Chirality in Nanocrystals for Boosting Solar-to-Hydrogen Conversion, Angew. Chem., Int. Ed., 2024, 63, e202411871 CrossRef CAS PubMed.
- G. Yang, L. Sun, Y. Tao, Q. Cheng, X. Sun, C. Liu and Q. Zhang, Chiral AuCu heterostructures with site-specific geometric control and tailored plasmonic chirality, Sci. China Chem., 2023, 66, 3280–3289 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sc00610d |
| This journal is © The Royal Society of Chemistry 2025 |