Open Access Article
Open Access ArticleStructure–property relationships for the force-triggered disrotatory ring-opening of cyclobutene†
Brandon H.
Bowser
a,
Cameron L.
Brown
a,
Jan
Meisner‡
 b,
Tatiana B.
Kouznetsova
a,
Todd J.
Martinez
*b and
Stephen L.
Craig
b,
Tatiana B.
Kouznetsova
a,
Todd J.
Martinez
*b and
Stephen L.
Craig
 *a
*a
aDepartment of Chemistry, Duke University, Durham, NC, USA. E-mail: stephen.craig@duke.edu
bDepartment of Chemistry, Stanford University, Stanford, CA, USA. E-mail: todd.martinez@stanford.edu
First published on 11th February 2025
Abstract
Symmetry forbidden reactions are notoriously difficult to study experimentally, for the simple reason that their competing symmetry allowed pathways typically dominate. Covalent polymer mechanochemistry offers an opportunity to broaden access to symmetry forbidden reactions, through the judicious placement of polymer handles on mechanophore reactants. Here, single molecule force spectroscopy and computation are used to evaluate substituent effects on the disrotatory ring opening reaction of cyclobutene to butadiene. Theory and experiment reveal that the formally forbidden reaction is more sensitive to substituents on the scissile carbon–carbon bond than on the alkene, with each of two Me substituents providing approximately 1.5–2 kcal mol−1 of stabilization and a trimethylsilyl alkyne substituent approximately 4.5–6.5 kcal mol−1.
Introduction
Electrocyclizations serve as an important class of reactions for both understanding fundamental aspects of chemical reactivity1,2 and for stereospecific synthesis.3 The typically high stereospecificity of electrocyclic reactions has inspired theoretical treatments of reactivity.4 In the specific case of the paradigmatic thermal ring-opening reaction of cyclobutene (CBE), theoretical models account for the experimental observation that ring-opening occurs via a preferential conrotatory motion at the atoms in the 3 and 4 positions (Fig. 1). In fact, the conrotatory mechanism is so favourable that it is typically designated to be “allowed,” in contrast to its “forbidden” disrotatory analogue. As a natural result, experimental studies that probe substituent effects on the conrotatory reaction abound,5–7 whereas those that explore the disrotatory reaction are exceptionally rare.8–10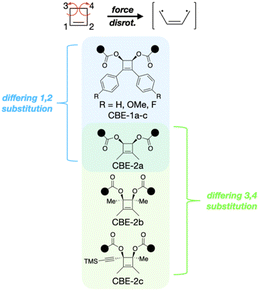 | ||
| Fig. 1 Force applied through ester substituents is used to drive the disrotatory ring opening of a range of cyclobutene mechanophores with different substituents. | ||
The emergence of covalent polymer mechanochemistry, however, has motivated a greater attention to the historically under-studied class of disrotatory cyclobutene reactions. Mechanochemistry has increasingly been used to drive various molecules,11 including CBE,12–14 down electrocyclic paths that are otherwise thermally forbidden, making these reactions more accessible and practically relevant for applications that include stress-strengthening materials.15 Seminal work by Hickenboth et al. demonstrated that pulling on benzocyclobutene (BCB) mechanically via cis-substituted polymer handles leads to a disrotatory process, whereas trans attachments facilitated the conrotatory mechanism.16 Wang et al. later used single-molecule force spectroscopy (SMFS) as a method to probe and quantify differences in the force-coupled reactivities of these allowed and forbidden processes of BCB.17 Understanding the factors that influence disrotatory reactivity in the parent CBE ring-opening reaction is of particular interest, and we recently used SMFS to probe differences in the energetics of the mechanically-induced conrotatory and disrotatory ring-opening of CBE and BCB.13 The SMFS methodology experimentally validated the differences in “forbidden-ness” between the two systems, first calculated by Sakai.18,19
Herein we extend the combination of SMFS and computation as a tool for probing symmetry forbidden reactivity, focusing on substituent effects in the disrotatory reaction of the parent CBE system. We synthesized and characterized a range of CBEs with differing 1,2-(CBE-1a–c and CBE-2a) and 3,4-substitutions (CBE-2a–c, Fig. 1). In parallel, the experimental systems are examined computationally, enabling this range of substituent effects on symmetry-forbidden CBE ring opening reactions to be elucidated for the first time. Prior computational reports13,20,21 suggest that the nature of the transition state for the mechanically-induced disrotatory reaction consists of substantial diradical character, and we further explore this conceptual framework as a guide for molecular design principles that govern the energetics of the disrotatory mechanism. Finally, we consider how substituent effects can be leveraged for stress-reporting optical signals, by using the latent conjugation that is unveiled by mechanical ring-opening to create detectable spectroscopic signatures, as seen in other stress-reporting mechanophores.22
Experimental
Synthesis of monomers and copolymers
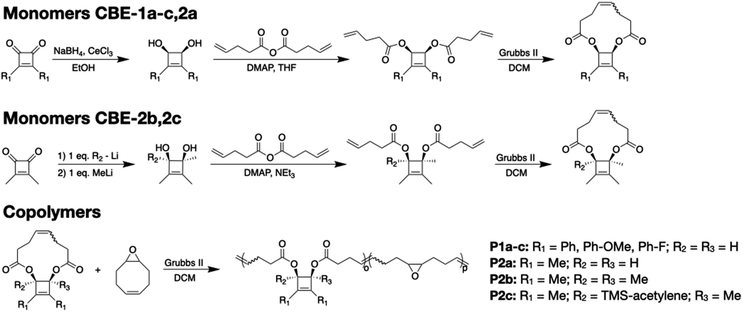
Synthesis of monomers CBE-1b–c and CBE-2a followed that previously reported for CBE-1a,13 starting from the respective diketones (Scheme 1, top). The initial Luche reduction23–25 conditions generated cis-diols exclusively, which ultimately led to cis-substituted polymer “handles” that, when pulled, couple to the desired disrotatory ring-opening reaction.13,17 A slightly modified approach was adopted for the synthesis of more highly substituted CBE-2b–c (Scheme 1, middle). Instead of sodium borohydride as the reducing agent, the appropriate organolithium reagents were added sequentially to the diketone, resulting again in cis-diols. The tertiary diols could not be esterified using the same conditions employed in the synthesis of CBE-1-a–c and CBE-2a, and so a slightly modified procedure was adopted wherein the reaction is conducted in NEt3 rather than tetrahydrofuran (THF).26 The resulting diene undergoes facile ring-closing metathesis similar to the other derivatives, yielding the appropriate monomers.Copolymers containing CBE mechanophores were synthesized using methods based on entropy-driven ring-opening metathesis polymerization27,28 (ED-ROMP; Scheme 1, bottom), which has proven to be a robust approach for these types of CBE monomers.13 CBE monomers were copolymerized with epoxycyclooctene to both generate polymers of sufficiently high molecular weight for SMFS and sonication (Mn > 30 kDa) and to install mechanically inert epoxides onto the backbone as a source of adhesion to the tip of the atomic force microscope.29
The mechanophore content of the copolymers was determined by 1H NMR, and the molecular weights were characterized using gel permeation chromatography equipped with a multi-angle light scattering detector (GPC-MALS). Polymers were diluted in THF to ∼1 mg mL−1 and the resulting solution was used for both SMFS and sonication experiments.
Single-molecule force spectroscopy
The procedure used to characterize the polymers via SMFS has been reported previously,13 and further details are provided in the ESI.† Briefly, pulling experiments were conducted in toluene under ambient conditions using a homemade AFM. Force curves were collected in dSPACE (dSPACE Inc., Wixom, MI) and analysed using Matlab (The MathWorks, Inc., Natick, MA). The data were subsequently calibrated and plotted using homemade software written in Matlab language.All pulls that reached forces up to 2 nN exhibited a characteristic plateau region in the force curve, wherein the polymer lengthens as a result of the irreversible ring-opening of cyclobutene mechanophores. The polymer contour length before (L1) and after (L2) this plateau was determined by fitting the pre- and post-plateau regions of the curve with an extended freely jointed chain model (e-FJC) according to literature precedent.29–31 The experimentally observed polymer extension (L2/L1) is compared to the extension that is predicted based on computational modelling of the individual monomer contour lengths in order to corroborate that the plateau region corresponds to the expected disrotatory reaction.
The individual monomer contour lengths were calculated using our previously reported approach based on the CoGEF computational methodology,32 which employs a relaxed potential energy scan across a range of fixed end-to-end distances to calculate monomer contour lengths as a function of an applied force. The contour lengths found at forces relevant to the SMFS experiment are used to extrapolate a force-free contour length, which is the computational equivalent of the extrapolation that is performed on the experimental curves, described above. See Fig. S1–S19, Tables S2–S6, and associated descriptions in the ESI.†
Sonication
Polymers were subjected to the high elongational forces produced by sonication using well-established procedures described previously.33–35 The dilute polymer solutions were first sparged with N2(g) for 30 min to remove oxygen, then sonicated in alternating sequence of one second on, one second off at a power of 8.7 W cm−2. Changes in polymer molecular weight and UV-absorbance were monitored by GPC, and changes in chemical structure of the polymer were monitored by 1H NMR.Calculations
We used broken-symmetry density functional theory (B3LYP/6-31G* (ref. 36–40)) in combination with the approach of a force-modified potential energy surface (FMPES)21 to compute free energy reaction barriers for the conrotatory and the disrotatory ring-opening mechanisms.A constant, adaptive force was applied to push the outermost atoms of the model away from each other. Reactant and transition structures are optimized on the force-modified potential energy surfaces in 0.5 nN steps and at the experimentally determined plateau forces (f*). For cis-substituted CBEs, conrotatory and disrotatory ring-opening mechanisms were investigated. For trans-substituted CBEs, only the conrotatory ring-opening mechanism was calculated. Increasing the force reduces the free energy barrier height for both conrotatory and disrotatory mechanisms. At forces above a system-dependent critical value (see Tables S6 and S7 in the ESI†) the respective FMPES does not exhibit a stable reactant structure and the potential turns into a slide.
Below a system-dependent threshold force (see Tables S6 and S7 in the ESI†), transition state optimizations for the disrotatory ring-opening of cis-substituted CBEs converged to the conrotatory transition structures. For all cis-CBEs, a conrotatory reaction mechanism could be found in the low-force regime. At higher forces, however, the conrotatory reaction channel disappears and only the reaction path of the disrotatory ring-opening can be optimized. This is a strong indication for two transition states coalescing (a so-called catastrophe41,42 that provide an interesting topic for future in-depth studies.
Results and discussion
The ED-ROMP methodology successfully produced high molecular weight (Mn > 30 kDa) copolymers that contained multiple CBE repeats (10–40% mechanophore content). Copolymer composition and molecular weights are summarized in Table S1.† We first discuss SMFS and sonication results for CBE mechanophores in which the 1,2-substituents (those on the unsaturated carbons of the CBE alkene) are varied while the 3,4-substituents are held constant (i.e., CBE-1a–c and CBE-2a). We then consider the influence of 3,4-substitution (those on the saturated carbons of the scissile bond) within a CBE scaffold in which the 1,2-substituents are held constant (i.e., CBE-2a–c).Effect of 1,2-substituents on reactivity
To compare the force-coupled reactivity of CBEs with different 1,2-substitution, we analyse the force curves for polymers containing diphenyl (P1a), diphenyl-p-OMe (P1b), diphenyl-p-F (P1c), and dimethyl (P2a) substituted CBEs, all with cis-O-ester handles for pulling at the 3 and 4 positions. Representative force curves for P1a–c and P2a are shown in Fig. 2. We note that the curve for P1a has been reported previously and is included here for ease of comparison.13All polymers exhibit a characteristic plateau region in the force range of 1400–1600 pN, wherein there is a minimal change in the applied force (∼100 pN) but an appreciable increase in polymer contour length. As is the case for other multi-mechanophore systems, we attribute this plateau region to the ring-opening reaction of all mechanophore units. The plateau for each curve can be characterized by a single force, termed the “plateau force”, determined by taking the second derivative of the force-separation curve and finding the inflection point (Fig. S20–S22†), which provides a benchmark value for the ring-opening force within a particular polymer.13,43 We take the average and standard deviation of the plateau force across several pulls to obtain an average plateau force (f*) for each mechanophore, which are reported in Fig. 2 and are representative of force-coupled reactivities (lower force = more reactive).
When comparing the reactivities for these derivatives with different 1,2-substitution patterns, we find that the f* values all fall within a force range of ∼160 pN (Fig. 2). While noticeable, differences in f* of less than 200 pN are relatively small, especially when compared to the ∼500 pN difference that was observed in our prior study of CBE-1a and its mechanically more reactive cis-BCB analogue. The larger difference between CBE and BCB has been attributed in significant part to the substantial ring strain in BCB speeding up its force-coupled reaction relative to CBE,13 whereas the ring strains in CBE1-a–c and CBE-2a are likely similar and do not lead to large differences in force-coupled reactivities.
The force-coupled reactions that occur at f* can theoretically correspond to either the thermally allowed conrotatory pathway, providing the E,Z butadiene product, or the thermally forbidden disrotatory pathway, providing the E,E product. Prior work has shown that for cyclobutene derivatives, when the force is applied through cis-substituted polymer “handles,” as is the case here, the disrotatory reaction is favoured and the E,E product is obtained.13,16,17 Recently, however, Tian et al. have reported a cyclobutene derivative where there exists a competition between disrotatory and conrotatory ring-opening at low forces, and thus both E,E and E,Z products were observed.12 Similar behavior was reported in our previous study of cyclobutenes,13 and unintuitive reaction motions opposite to the nominal direction of pulling have been observed even at very high forces in cyclopropane derivatives.44 Because a direct characterization of ring-opened products is not possible in our SMFS experiments, we instead employed two approaches for determining which mechanism is at play at the observed f*s: (1) computing and comparing energy barriers for both conrotatory and disrotatory ring-opening at f*, and (2) comparing the experimentally observed changes in polymer contour length with those expected from CoGEF for both processes.
We first addressed the question of reaction outcome computationally. In doing so, it is important be mindful that the barrier does not vanish completely at the experimental f* values.45 Rather, the application of the external force reduces the free activation energy to such an extent that the thermal fluctuations are sufficient to overcome this barrier, so that the lifetime of the mechanophore is of the order of the experiment. In order to elucidate the ring-opening, both conrotatory and disrotatory mechanisms were computationally investigated at the experimental f* for each mechanophore using the FMPES approach described in the Experimental section. We find that the calculated free-energy barriers at the respective experimental plateau forces all fall within a range of 14–19 kcal mol−1 (Table 1), which correspond to rate constants of ∼0.1–1000 s−1 at 298 K and are similar to the actual rate constants inferred from the SMFS experiments (1–55 s−1).46 For the phenyl-substituted CBEs 1a–c, the computed free energy barrier for the thermally allowed conrotatory process is similar to the thermally forbidden disrotatory process at f* (differences less than 0.5 kcal mol−1, see Fig. 2 and Table S7 in the ESI†). These findings are in agreement with our prior SMFS and computational work on CBE and support that the disrotatory reaction is being induced in the force regimes examined herein, even though it is likely that there is some contribution of competitive conrotatory processes.13 We conclude that, under the SMFS conditions employed, both conrotatory and disrotatory processes contribute. We are aware of no reason why this should be a general property of electrocyclic mechanochemical reactions, but in this particular case the observed kinetics reflects both the disrotatory and conrotatory reactions. The activation energy associated with either is probably <1 kcal mol−1 above the activation energy inferred from the combined reactivity. Moreover, the trends in the force-coupled competition between disrotatory and conrotatory processes are similar across the CBE derivatives. Taken together, these results support the use of the SMFS experiments to infer trends in the disrotatory reactions.
| Reactant | f*(exp), nN | ΔG‡dis(f*), kcal mol−1 | dΔG‡dis/df, kcal mol−1 nN | dΔG‡con/df, kcal mol−1 nN |
|---|---|---|---|---|
| 1a | 1.52 | 17.3 | −15.3 | −11.7 |
| 1b | 1.58 | 16.3 | −15.3 | −12.6 |
| 1c | 1.44 | 19.1 | −16.1 | −11.4 |
| 2a | 1.42 | 17.4 | −16.1 | −13.1 |
| 2b | 1.24 | 16.2 | −21.6 | −19.8 |
| 2c | 1.08 | 14.3 | −19.4 | −14.6 |
Further support for the predominance of the disrotatory pathway is provided by the structural transition in the SMFS experiments. We compared the experimentally obtained change in polymer contour length pre- and post-plateau (L2/L1) to the expected change in length if all CBE's ring-open in either a disrotatory (E,E-product) or conrotatory (E,Z-product) fashion, as predicted by the CoGEF-based modelling of contour length. The experimental and computational results are presented in Tables S1–S5† and are more supportive of the expected disrotatory ring-opening process; however, we note that the calculated difference in L2/L1 between E,E and E,Z products is small (differing by less than 2% of the initial contour length in some instances), meaning contributions from conrotatory ring-opening cannot be definitively ruled out by this analysis alone.
The experimental and theoretical studies support several insights into the forbidden, disrotatory reaction. First, when attempting to derive structure–property relationships for the disrotatory reaction, one cannot simply rely on trends observed in their conrotatory analogues. For example, the force-free conrotatory ring-opening is faster for CBE-2a than CBE-1a,47,48 but the force-coupled disrotatory ring-opening is slower. This reversal of the relative reactivity could be due to a confluence of electronic and mechanical coupling effects, which we did not seek to disentangle here. The change in mechanism from synchronous (conrotatory) to asynchronous (disrotatory) bond breaking/forming requires a change in how we think about substituent effects on the ring-opening process, especially in the context of mechanically driven reactions. A similar “flipping” of relative reactivity through substituent effects was reported previously in a comparison of CBE-1a to BCB.13
Lastly, both the relatively close f* values for CBE-1a–c and CBE-2a observed experimentally and the associated calculations suggest that changing the 1,2-substituents of CBE does not significantly alter the force-coupled reactivity for disrotatory ring-opening. This also largely holds true for the thermal conrotatory ring-opening of CBE, which has been extensively studied,49 but this is the first known report of such an analysis on the disrotatory process. It is likely that these substituents on the 1 and 2 positions do not greatly influence reactivity because they are largely decoupled from the primary reactive site of the disrotatory ring-opening process – namely the breaking σ-bond that develops substantial diradical character in the transition state. This provides motivation for exploring the effects of different 3,4-substituents, which are connected to this breaking σ-bond and are better suited to either stabilize or destabilize the diradical transition state, which we achieve by examining the reactivities of CBE-2a–c.
Effect of 3,4-substituents on reactivity
Using the same organolithium approach shown in the middle of Scheme 1, we first attempted to synthesize various CBEs with aryl groups attached at both the 3 and 4 positions, which are known to greatly decrease the activation barrier for conrotatory ring-opening.48 However, these CBEs are too reactive and ring-opened faster than we could isolate them (data not shown). We were therefore motivated to explore alkyl substituents on the 3 and 4 positions, and we identified the tetramethyl CBE core synthesized previously by Banert et al. as an opportunity to compare methyl (P2b) versus hydrogen (P2a) substituents at the 3 and 4 positions.50Further, we successfully synthesized polymer P2c, in which one of the methyl (Me) groups on the 3,4-position is replaced with trimethylsilylacetylene (TMSA). The use of P2c offers an opportunity for further exploring the effect of π-substituents at the α carbon of the scissile bond.
Representative force curves for P2b and P2c are shown in Fig. 3 (with P2a shown again to facilitate comparison). Similarly to P1a–c and P2a, both polymers exhibit a characteristic plateau region, indicative of cyclobutene ring-opening. Also similar to P1a–c and P2a, the fits to experimentally observed extensions in polymer contour length pre- and post-plateau (L2/L1 = 1.08) agree well with computational models (L2/L1 = 1.06 and 1.08 for P2b and P2c, respectively) if all CBEs are assumed to open to the E,E-butadiene product (and thus ring-open in a disrotatory fashion).
Using the same method described above, we obtain average plateau forces (f*) over a variety of pulls for P2b and P2c, reported in Fig. 3. FMPES calculations of the conrotatory and disrotatory processes at these respective f* values reveal that the barrier for disrotatory ring-opening is ∼3 kcal mol−1 lower than that of the corresponding conrotatory process for CBE-2a and CBE-2b, and we conclude that the disrotatory ring opening is the dominant mechanism being probed at these forces. The disrotatory barriers for CBE-2a (18.0 kcal mol−1) and CBE-2b (16.6 kcal mol−1) fall within the expected range of 16–18 kcal mol−1 calculated for the previous derivatives. The calculated disrotatory and conrotatory barriers at f* for the opening of CBE-2c (14.3 and 14.7 kcal mol−1) are slightly lower than expected. In this case, again, both mechanisms are almost equally important.
Across these three derivatives that are identical in their 1,2-substitution (Me) but differ in their 3,4-substitution (H,H; Me,Me; and TMSA,Me), we find that  . To explain this trend in reactivity, we examine potential differences in the two primary factors that govern mechanochemical reactivity: (1) mechanochemical coupling (i.e., how efficiently the force is coupled to the reaction path) and (2) the intrinsic reactivity of the mechanophore (i.e. the force-free activation energy for ring-opening).
. To explain this trend in reactivity, we examine potential differences in the two primary factors that govern mechanochemical reactivity: (1) mechanochemical coupling (i.e., how efficiently the force is coupled to the reaction path) and (2) the intrinsic reactivity of the mechanophore (i.e. the force-free activation energy for ring-opening).
Minor perturbations in mechanophore structure can often lead to marked differences in how efficiently an applied force is coupled to a mechanochemical transformation. For example, ferrocenophane mechanophores are much more mechanically labile than their ferrocene analogues due to enhanced mechanical coupling that arises from the distal conformational “locks” imposed by the alkyl bridge between cyclopentadiene ligands.43 We were therefore curious if changing the substituents connected to CBE has an effect on mechanical coupling. One method for determining the efficiency with which mechanical force is coupled to a given reaction is to computationally model how the activation barrier changes as a function of force near the forces relevant for ring-opening. We recently employed this approach to compare the mechanical coupling between cis-CBE/BCB to trans-CBE/BCB and verified that there was greater coupling to the cis-substituted mechanophores. In the energy-barrier-versus-force plots, the slopes of the cis-substituted mechanophores were larger than the trans analogues, indicative of greater mechanical coupling.
Plots of activation barrier versus force for the six CBEs are shown in Fig. 2 and 3. In all cases, the force dependence is close to linear across the force regime relevant to the SMFS experiments (1–2 nN), and the slopes of those fits are provided in Table 1. The plateau forces for the mechanophores under investigation range over more than 400 pN, but the barrier vs. force slopes reveal similarities in mechanical coupling. We therefore conclude that the stereochemistry of the pulling attachments (cis), rather than the other substituents, is therefore likely to be the dominant factor that governs the mechanical coupling for CBE mechanophores.
The differences in force-coupled reactivity are therefore best explained by the differences in the intrinsic (force-free) activation energies between the mechanophores, which are influenced by both steric and electronic effects of the disrotatory process (Fig. 4).
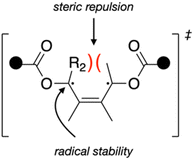 | ||
| Fig. 4 Schematic showing how substituents that are anti to the pulling attachments and on the scissile bond generate increased steric repulsion in a disrotatory process. | ||
By combining the computationally derived mechanical coupling parameter for these CBE mechanophores (ΔG‡/df, average of the slopes taken from a range of forces ±400 pN from the observed f* of the two CBE derivatives under consideration) along with the experimentally observed plateau forces, we can extrapolate an approximate difference in the apparent barriers for the force-free disrotatory processes of various CBE derivatives:
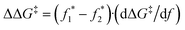 | (1) |
 and
and  correspond to the plateau forces for two different CBE derivatives and dΔG‡/df corresponds to the average in the slopes (−18.8 kcal mol−1 nN−1 for CBE-2avs.CBE-2b, and −17.7 kcal mol−1 nN−1 for CBE-2avs.CBE-2c). Essentially, the SMFS data provide a force necessary to achieve a similar activation energy for different reactions. The coupling parameter dΔG‡/df converts that force difference to an energy difference in the mechanochemical processes at a common force. The similarity in calculated dΔG‡/df of the different derivatives is consistent with the preserved core structure across the series, and so this approach provides a reasonable basis for experimentally assessing the energetic impact of the various substituents on the disrotatory process.
correspond to the plateau forces for two different CBE derivatives and dΔG‡/df corresponds to the average in the slopes (−18.8 kcal mol−1 nN−1 for CBE-2avs.CBE-2b, and −17.7 kcal mol−1 nN−1 for CBE-2avs.CBE-2c). Essentially, the SMFS data provide a force necessary to achieve a similar activation energy for different reactions. The coupling parameter dΔG‡/df converts that force difference to an energy difference in the mechanochemical processes at a common force. The similarity in calculated dΔG‡/df of the different derivatives is consistent with the preserved core structure across the series, and so this approach provides a reasonable basis for experimentally assessing the energetic impact of the various substituents on the disrotatory process.
When comparing CBE-2b to CBE-2a and CBE-2c to CBE-2a using the above equation, we obtain experimentally derived values of ΔΔG‡ = −3 kcal mol−1 and −6 kcal mol−1, respectively. By comparison, the purely computational differences in activation energies at 1200 pN are −3.8 kcal mol−1 and -8.8 kcal mol−1, respectively. Taken together, this means that in the force-triggered disrotatory reaction, each Me substituent is providing ∼1.5–2 kcal mol−1 of stabilization and the TMSA substituent is providing ∼4.5–6.5 kcal mol−1 of stabilization. It has been well established computationally,9,18,20 including most recently for CBE-1a,13 that both in the presence and absence of force, the transition state of the disrotatory ring-opening has considerable diradical character. Thus, a major influence on the lability of the breaking σ-bond for disrotatory ring-opening is the stability of the developing diradical. Previous reports suggest that a Me substituent should provide an additional 2–3 kcal mol−1 of electronic stabilization to a secondary radical,51 while an alkynyl substituent should provide an additional 8–11 kcal mol−1 of stabilization to a primary radical52 (although the latter value is presumably slightly less for an initially more stable secondary radical). The general trend in radical stabilization derived from these BDEs matches what we observe in the SMFS experiments: substituents that better stabilize the developing radical(s) also lower the force required for ring-opening. Quantitatively, however, the theoretical differences in intrinsic activation energy due to diradical stabilization (e.g., ∼10 kcal mol−1 for CBE-2c compared to CBE-2c at the same pulling forces, see Table S8 in the ESI†) are slightly larger than differences obtained using eqn (1) for the CBE mechanophores (which leads to ∼6 kcal mol−1 for CBE-2c compared to CBE-2a).
There are other aspects of the CBE structure, apart from the H/Me/TMSA substituents being probed, that likely account for some of this discrepancy between the simple stabilization model based on BDEs and those observed experimentally for CBE. In contrast to the model system, homolytic scission in CBE is accelerated by ring-strain, and leads to the formation of radicals that are stabilized by allylic character and lone pair donation from the acetoxy substituent.53 The additional stabilization that comes from replacing an H atom with a Me or TMSA substituent is likely “blunted” by these other factors that are also present in CBE. In addition to this potential “saturation” effect, the stabilization brought by replacing the H atom can be offset by a concurrent “weakening” of other stabilizing effects. For example, the acetoxy substituent provides less stabilization as the ordinality of the carbon-centered radical increases.53 Replacement of H with Me or TMSA leads to competing stabilizing/destabilizing effects that mitigate the resulting stability. Lastly, it is possible that at the TS of CBE ring-opening, the radicals are not yet fully developed, so the comparison to fully developed radicals in model compounds breaks down.
In addition to the interplay of electronic factors that blunt the effective stabilization of a Me or TMSA substituent, it is also very likely that the radical-stabilizing interactions are counterbalanced by a destabilizing geometric factor, namely steric congestion as the ring-opening reaction progresses (Fig. 4). The vector of applied force causes the acetoxy polymer “handles” to rotate outwards, and therefore the H/Me/TMSA substituents rotate inwards from their initial cis orientation. Lee et al. found that for a CBE derivative where the 3 and 4 positions each had an H and Me substituent, disrotatory ring-opening is faster when the H atoms are cis and rotate inwards compared to when the H and Me groups are cis and clash upon inward rotation, invoking steric interactions as the primary cause for the difference.9
Spectroscopy of ring-opened products
Looking beyond substituent effects on mechanochemical reactivity, we were also curious how the choice of substituents impacts the changes in the photophysical properties of the polymer that are observed upon mechanical activation. Depending on the nature of the substitution pattern, the extent of conjugation and therefore electronic communication between substituents can either be created or destroyed upon ring-opening. This control over the conjugation pathway translates to CBE's potential utility as a stress-reporting mechanophore. We therefore sonicated P1a, P2a, and P2c in order to characterize changes in the absorbance/emission properties of the mechanophores upon activation.Sonication of P1a and P2a for 1 h leads to a decrease in polymer molecular weight (Fig. S23–S27†), meaning that forces large enough for backbone bond scission are experienced. These large forces are also enough to achieve mechanophore activation, as evidenced by changes in the 1H NMR spectra. From the spectra, we calculate that 63% of CBE-1a and 65% CBE-2a mechanophores were activated (Fig. S25 and S27†). This level of activation allows changes in UV-absorbance to be characterized using an in-line UV-vis detector coupled to the GPC. UV-absorption profiles for pre-sonicated and post-sonicated samples of P2a are shown in Fig. S26.†
The activation of P1a disrupts conjugation between the nascent 1,2-diaryl substituents, transforming a stilbene-like π-system to a pair of isolated styrene-type π-systems. As a result, λmax blue shifts from roughly 300 nm to 260 nm. In contrast, P2a exhibits an appreciable increase in total UV absorbance above 250 nm, due to the transformation of a 2π electron ethylene-like π-system to the 4π electron π-system of the butadiene product.
The most dramatic changes, however, occur upon sonication of P2c, which generates a conjugated π system that incorporates the alkyne. Sonication of P2c (Fig. 5a) for 1 h leads to a decrease in polymer molecular weight (56 kDa to 28 kDa) and 53% mechanophore activation (Fig. S29†). When the pre-sonicated and post-sonicated solutions (1 mg mL−1 in THF) are placed under a handheld UV lamp at 365 nm, a clear difference in fluorescence intensity can be seen by the unaided eye (Fig. 5b) and verified by pre- and post-sonication emission spectra (Fig. 5d). This change in spectral properties along with the irreversible nature of the ring-opening reaction means that CBEs can be added to the growing list of “turn-on” mechano-chromophores and mechano-fluorophores, which include, e.g., ferrocene- and anthracene-based mechanophores.43,54 Similar to prior work on anthracene-based stress-reporters, additional extension of CBE's pi-system through the alkyne substituent of CBE-2c may be an attractive route for further exploring and enhancing its fluorescence properties.55
Conclusions
For CBE-type mechanophores we now have the beginnings of a molecular toolkit for both tuning and quantifying changes in reactivity and photophysical properties, allowing us to begin tailoring the system to specific applications. Beyond what is shown here for disrotatory CBE ring-opening, pulling from trans-ester substituents or using the related BCB framework offers even more opportunities for altering these properties. Future work is merited to explore the potential utility of these types of CBE mechanophores as stress-reporters within bulk polymer materials. We believe the TMSA substituted CBE could serve as a powerful platform for further exploration of the structure–property space of CBEs in general, as the TMS group can readily be removed under basic conditions and replaced with a variety of aryl groups in a late-stage modular fashion via Sonogashira coupling.SMFS coupled with computation serves as a powerful combination strategy for experimentally exploring the rich structure–property space of the disrotatory CBE ring-opening reaction. We believe these findings will help with the future molecular-level design of mechanically responsive CBEs, allowing us to better understand how to both control and exploit CBE reactivity based on the substituents with which we decorate it.
Data availability
Details of experimental procedures, characterization data, materials employed, and additional data reference in the main text are available in the ESI.† Input and output files for all computations are available via public repository at https://zenodo.org/records/14838019.56Author contributions
B. Bowser: conceptualization, methodology, investigation, writing; C. Brown: conceptualization, methodology, investigation, writing; J. Meisner: conceptualization, methodology, investigation, writing; T. Kouznetsova: methodology, investigation; T. Martínez: funding acquisition, supervision, writing; S. Craig: conceptualization, funding acquisition, supervision, writing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Science Foundation through grants CHE-2304884 (S. L. C.) and CHE-2350170 (T. J. M.) and Duke University.Notes and references
- R. Hoffmann and R. B. Woodward, Acc. Chem. Res., 1968, 1, 17–22 CrossRef CAS.
- J. A. Berson, Acc. Chem. Res., 1972, 5, 406–414 CrossRef CAS.
- M. Bian, L. Li and H. Ding, Synthesis, 2017, 49, 4383–4413 CrossRef CAS.
- M. J. S. Dewar, Tetrahedron, 1966, 22, 75–92 CrossRef.
- K. Rudolf, D. C. Spellmeyer and K. N. Houk, J. Org. Chem., 1987, 52, 3708–3710 CrossRef CAS.
- W. R. Dolbier, H. Koroniak, K. N. Houk and C. Sheu, Acc. Chem. Res., 1996, 29, 471–477 CrossRef CAS.
- M. Hasegawa, I. Usui, S. Konno and M. Murakami, Org. Biomol. Chem., 2010, 8, 4169–4175 RSC.
- J. E. Baldwin, A. H. Andrist and R. K. Pinschmidt, Acc. Chem. Res., 1972, 5, 402–406 CrossRef CAS.
- P. S. Lee, S. Sakai, P. Hörstermann, W. R. Roth, E. A. Kallel and K. N. Houk, J. Am. Chem. Soc., 2003, 125, 5839–5848 CrossRef CAS PubMed.
- G. A. Doorakian and H. H. Freedman, J. Am. Chem. Soc., 1968, 90, 5310–5311 CrossRef CAS.
- E. Izak-Nau, D. Campagna, C. Baumann and R. Gostl, Polym. Chem., 2020, 11, 2274–2299 RSC.
- Y. Tian, X. Cao, X. Li, H. Zhang, C.-L. Sun, Y. Xu, W. Weng, W. Zhang and R. Boulatov, J. Am. Chem. Soc., 2020, 142, 18687–18697 CrossRef CAS PubMed.
- C. L. Brown, B. H. Bowser, J. Meisner, T. B. Kouznetsova, S. Seritan, T. J. Martinez and S. L. Craig, J. Am. Chem. Soc., 2021, 143, 3846–3855 CrossRef CAS PubMed.
- Q.-Z. Yang, Z. Huang, T. J. Kucharski, D. Khvostichenko, C. Joseph and B. Roman, Nat. Nano, 2009, 4, 302–306 CrossRef CAS PubMed.
- J. Wang, I. Piskun and S. L. Craig, ACS Macro Lett., 2015, 4, 834–837 CrossRef CAS PubMed.
- C. R. Hickenboth, J. S. Moore, S. R. White, N. R. Sottos, J. Baudry and S. R. Wilson, Nature, 2007, 446, 423–427 CrossRef CAS PubMed.
- J. Wang, T. B. Kouznetsova, Z. Niu, M. T. Ong, H. M. Klukovich, A. L. Rheingold, T. J. Martinez and S. L. Craig, Nat. Chem., 2015, 7, 323–327 CrossRef CAS PubMed.
- S. Sakai, J. Mol. Struct.:THEOCHEM, 1999, 461, 283–295 CrossRef.
- S. Sakai, J. Phys. Chem. A, 2000, 104, 11615–11621 CrossRef CAS.
- G. S. Kochhar, A. Bailey and N. J. Mosey, Angew. Chem., Int. Ed., 2010, 49, 7452–7455 CrossRef CAS PubMed.
- M. T. Ong, J. Leiding, H. Tao, A. M. Virshup and T. J. Martínez, J. Am. Chem. Soc., 2009, 131, 6377–6379 CrossRef CAS PubMed.
- M. Stratigaki and R. Gostl, ChemPlusChem, 2020, 85, 1095–1103 CrossRef CAS PubMed.
- J. L. Luche, J. Am. Chem. Soc., 1978, 100, 2226–2227 CrossRef CAS.
- J.-L. Luche, L. Rodriguez-Hahn and P. Crabbé, J. Chem. Soc., Chem. Commun., 1978, 601–602 RSC.
- A. L. Gemal and J. L. Luche, J. Am. Chem. Soc., 1981, 103, 5454–5459 CrossRef CAS.
- G. Höfle, W. Steglich and H. Vorbrüggen, Angew. Chem., Int. Ed. Engl., 1978, 17, 569–583 CrossRef.
- A. J. Hall and P. Hodge, React. Funct. Polym., 1999, 41, 133–139 CrossRef CAS.
- S. Strandman, J. E. Gautrot and X. X. Zhu, Polym. Chem., 2011, 2, 791–799 RSC.
- H. M. Klukovich, T. B. Kouznetsova, Z. S. Kean, J. M. Lenhardt and S. L. Craig, Nat. Chem., 2013, 5, 110–114 CrossRef CAS PubMed.
- D. Wu, J. M. Lenhardt, A. L. Black, B. B. Akhremitchev and S. L. Craig, J. Am. Chem. Soc., 2010, 132, 15936–15938 CrossRef CAS PubMed.
- G. R. Gossweiler, T. B. Kouznetsova and S. L. Craig, J. Am. Chem. Soc., 2015, 137, 6148–6151 CrossRef CAS PubMed.
- B. H. Bowser, S. Wang, T. B. Kouznetsova, H. K. Beech, B. D. Olsen, M. Rubinstein and S. L. Craig, J. Am. Chem. Soc., 2021, 143, 5269–5276 CrossRef CAS PubMed.
- Y. Lin, T. B. Kouznetsova and S. L. Craig, J. Am. Chem. Soc., 2020, 142, 99–103 CrossRef CAS PubMed.
- Y. Lin, T. B. Kouznetsova and S. L. Craig, J. Am. Chem. Soc., 2020, 142, 2105–2109 CrossRef CAS PubMed.
- Z. Wang and S. L. Craig, Chem. Commun., 2019, 55, 12263–12266 RSC.
- P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B:Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- M. Wollenhaupt, C. Schran, M. Krupička and D. Marx, ChemPhysChem, 2018, 19, 837–847 CrossRef CAS PubMed.
- Z. Chen, X. Zhu, J. Yang, J. A. Mercer, N. Z. Burns, T. J. Martinez and Y. Xia, Nat. Chem., 2020, 12, 302–309 CrossRef CAS PubMed.
- Y. Zhang, Z. Wang, T. B. Kouznetsova, Y. Sha, E. Xu, L. Shannahan, M. Fermen-Coker, Y. Lin, C. Tang and S. L. Craig, Nat. Chem., 2021, 13, 56–62 CrossRef CAS PubMed.
- Z. Wang, T. B. Kouznetsova and S. L. Craig, Synlett, 2022, 33, 885–889 CrossRef CAS.
- Y. Sun, I. Kevlishvili, T. B. Kouznetsova, Z. P. Burke, S. L. Craig, H. J. Kulik and J. S. Moore, Chem, 2024, 10(10), 3055–3066 CAS.
- T. B. Kouznetsova, J. Wang and S. L. Craig, ChemPhysChem, 2017, 18, 1486–1489 CrossRef CAS PubMed.
- H. M. Frey, B. M. Pope and R. F. Skinner, Trans. Faraday Soc., 1967, 63, 1166–1170 RSC.
- M. Pomerantz and P. H. Hartman, Tetrahedron Lett., 1968, 9, 991–993 CrossRef.
- P. Nava and Y. Carissan, Phys. Chem. Chem. Phys., 2014, 16, 16196–16203 RSC.
- K. Banert, S. Grimme, R. Herges, K. Heß, F. Köhler, C. Mück-Lichtenfeld and E.-U. Würthwein, Chem.–Eur. J., 2006, 12, 7467–7481 CrossRef CAS PubMed.
- S. J. Blanksby and G. B. Ellison, Acc. Chem. Res., 2003, 36, 255–263 CrossRef CAS PubMed.
- C. W. Bauschlicher and S. R. Langhoff, Chem. Phys. Lett., 1992, 193, 380–385 CrossRef CAS.
- M. L. Poutsma, J. Org. Chem., 2011, 76, 270–276 CrossRef CAS PubMed.
- G. R. Gossweiler, G. B. Hewage, G. Soriano, Q. Wang, G. W. Welshofer, X. Zhao and S. L. Craig, ACS Macro Lett., 2014, 3, 216–219 CrossRef CAS PubMed.
- R. Gostl and R. P. Sijbesma, Chem. Sci., 2016, 7, 370–375 RSC.
- J. Meisner, Computational Data to “Structure-property relationships for the force-triggered disrotatory ring-opening of cyclobutene”, Zenodo, 2025, DOI:10.5281/zenodo.14838019.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sc00253b |
| ‡ Present address: Heinrich-Heine University, Düsseldorf, Germany. |
| This journal is © The Royal Society of Chemistry 2025 |