Open Access Article
Open Access ArticleComputational framework for discovery of degradation mechanisms of organic flow battery electrolytes†
Xiaotong
Zhang
and
Piotr
de Silva
 *
*
Department of Energy Conversion and Storage, Technical University of Denmark, Anker Engelunds Vej 301, 2800 Kongens Lyngby, Denmark. E-mail: pdes@dtu.dk
First published on 7th April 2025
Abstract
The stability of organic redox-active molecules is a key challenge for the long-term viability of organic redox flow batteries (ORFBs). Electrolyte degradation leads to capacity fade, reducing the efficiency and lifespan of ORFBs. To systematically investigate degradation mechanisms, we present a computational framework that automates the exploration of degradation pathways. The approach integrates local reactivity descriptors to generate reactive complexes and employs a single-ended process search to discover elementary reaction steps, including transition states and intermediates. The resulting reaction network is iteratively refined with heuristics and human-guided validation. The framework is applied to study the degradation mechanisms of quinone- and quinoxaline-based electrolytes under acidic and basic aqueous conditions. The predicted reaction pathways and degradation products align with experimental observations, highlighting key degradation modes such as Michael addition, disproportionation, dimerization, and electrochemical transformation. The framework provides a valuable tool for in silico screening of stable electrolyte candidates and guiding the molecular design of next-generation ORFBs.
Introduction
Redox flow batteries (RFBs) are a promising technology for large-scale energy storage as they have decoupled energy and power densities.1–3 This decoupling is achieved by storing the electroactive electrolytes in external tanks and pumping them through an electrochemical cell, where reversible redox reactions occur. Such a design allows for flexible scaling of energy capacity and power output independently, making RFBs particularly suitable for applications requiring substantial energy storage and high-power delivery over extended periods. Among various types of RFBs, organic RFBs (ORFBs) have gained significant attention due to their potentially low cost, safety, and environmental sustainability factors. The key to the performance and longevity of ORFBs lies in the stability of the organic redox-active electrolytes and reversibility of their electrochemical reactions.1 However, one of the critical challenges impeding the widespread adoption of ORFBs is the degradation of these organic electrolytes over time, which leads to capacity fade and reduced efficiency.4–8Identifying degradation products and understanding the corresponding reaction mechanisms is critical for overcoming the stability issue, yet it poses significant challenges due to the complexity and diversity of the chemical reactions involved. Organic electroactive molecules can degrade through various pathways, including hydrolysis,9–11 gem-diol formation,12 Michael addition,13–15 nucleophilic substitution,4 disproportionation,16,17 dimerization,18 and tautomerization,19,20 often producing transient intermediates that are difficult to detect. These reactions can be also highly sensitive to operating conditions like temperature and pH, which adds another level of complexity to their analysis. Furthermore, the presence of multiple components in the electrolyte system, including solvents and other additives, can alter the reaction mechanisms. Experimentally, the analysis of degradation products and mechanisms often employs techniques such as mass spectrometry,21,22 cyclic voltammetry,23,24 NMR spectroscopy,25,26 and UV-Vis spectroscopy.27,28 These techniques have been employed to uncover various degradation pathways in ORFB electrolytes and guide molecular engineering of more stable compounds. For example, Pang et al. synthesized amino acid-functionalized phenazines (AFPs) for use as negolytes in AORFBs. The 1,6-substituted AFPs showed superior electrochemical stability and lower capacity fade rates compared to 1,8 and 2,7-substituted AFPs, which suffered from rapid capacity decay due to tautomerization.29 The development of 2,6-dihydroxyanthraquinone (DHAQ) as an negolyte in ORFBs initially demonstrated promise due to its favorable electrochemical properties and solubility.30 However, it was soon identified that DHAQ underwent electrochemical decomposition, as confirmed through NMR.31 To address this, more stable quinone derivatives like 2-2-PEAQ were developed by incorporating functional groups to suppress degradation, resulting in significantly improved stability and extended cycle life.32 These findings highlight how molecular engineering, through functional group modification, can mitigate capacity decay in ORFBs. However, experimental approaches can be constrained by the complexity of side reactions and the challenges in isolating transient intermediates. The identification of unexpected or unknown degradation products further complicates this task, requiring advanced analytical techniques and comprehensive screening.
Considering the limitations of experimental techniques, computational methods offer valuable insights into chemical stability by exploring potential energy surfaces (PES), identifying transition state (TS), and estimating activation energy barriers. The kinetics of degradation reactions can then be assessed using Transition State Theory (TST). To study unknown reaction mechanisms, some approaches, like chemical flooding33 and metadynamics,34–36 rely on predetermined reactive coordinates to guide molecular dynamics simulations along specific paths. Methods based on system properties to approximate reactive coordinates, such as the Nudged Elastic Band (NEB),37–41 eigenvector following,42 dimer method,43 synchronous transit,44 and the string methods,45–47 offer flexibility and detailed insights into the reaction landscape. However, double-ended methods, like NEB require prior knowledge of both reactants and products of elementary reaction steps, which is not suitable for scenario where the products are unknown a priori. On the other hand, the one-ended process search, using minimum-mode following, stands out for its efficacy in scenarios where only the initial structure is provided. This method employs saddle point search techniques, such as the dimer method,43 and the growing string method (GSM),48,49 that directly seek TS without needing predefined reaction coordinates. Additionally, advanced techniques like machine learning are increasingly used to predict reaction mechanisms from large datasets and simulate the temporal evolution of reactions.50,51
While these methods are effective in studying reaction mechanisms, they typically require some hypotheses about the involved reaction intermediates, which subsequently can be validated through transition state searches. Such approach, often based on trial and error, can be tedious, relies heavily on human chemical intuition, and is prone to overlooking various possibilities due to the vast and complex chemical space. Consequently, critical products and reaction pathways on the PES might be missed. Efforts have been made to expedite this process through automated reaction network discovery algorithms.52–64 The first step in such automated approaches usually is to identify the possible reactive sites of the studied system, typically based on some preexisting reaction templates, chemical heuristics or conceptual electronic structure descriptors. One such framework is Conceptual Density Functional Theory (CDFT), which aims at predicting chemical reactivity through quantitative descriptors like electrophilicity and nucleophilicity indices. These reactivity descriptors measure a molecule's tendency to either accept or donate electrons.65–77 The Fukui function maps reactive sites within a molecule, while the dual descriptor refines this prediction by indicating whether a specific region is more susceptible to nucleophilic or electrophilic attacks. Additionally, local electrophilicity and nucleophilicity provide a detailed evaluation of the tendency of specific regions within a molecule to donate or accept electrons during chemical reactions.78
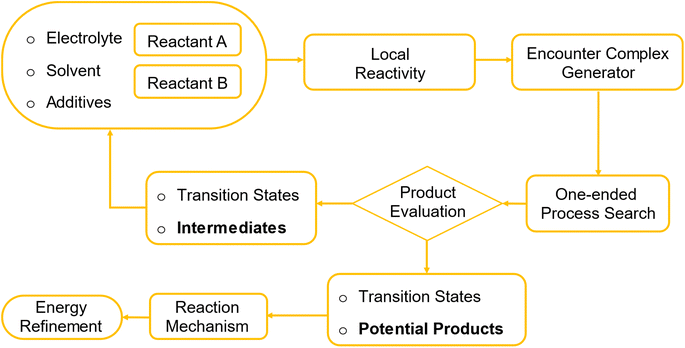
Building on this foundation, we introduce a computational framework that automates some steps in the degradation reaction mechanism discovery process. Such reactions are intrinsically slow; therefore, characterized by high activation barriers of the elementary steps. The procedure starts with creation of encounter complexes using local nucleophilicity and electrophilicity descriptors, systematically integrating chemical intuition into an automated process. It then employs a single-ended process search to explore the PES, successively identifying elementary reaction steps including the corresponding transition states and intermediates. The complexity of the emerging reaction network is managed by heuristic rules and facilitated by human expertise. Since the procedure requires many evaluations of energy and its derivatives, the computational cost is a major consideration. We keep it moderate by relying on semiempirical methods in the exploration phase, but the final energies can be a posteriori refined at a higher level. While the applicability domain can be generalized to any class of molecules, we tailor it to study the degradation reactions of aqueous organic flow battery electrolytes.
To calibrate and validate our framework, we have investigated the degradation pathways of several organic electroactive molecules, including substituted quinones and quinoxaline, which are prevalent in organic redox flow battery (ORFB) electrolytes. The choice is dictated by the knowledge of their primary degradation products and the corresponding mechanisms, while the objective is to reproduce these mechanisms without assuming a priori what they are. To test the robustness of our approach, we considered electrolytes in both acidic and basic aqueous solutions, as well as considered both chemical and electrochemical degradation reactions. To this end we choose four cases of ORFB electrolyte degradation reactions: (a) 1,2-benzoquinone 3,5-disulfonic acid (BQDS), a posolyte materials which was found to suffer significant degradation through Michael addition of water,79–81 in conjunction with 3,6-dihydroxy-2,4-dimethylbenzenesulfonic acid (DHDMBS), which was introduced as a posolyte stable against Michal addition but later reported to undergo desulfonation;6 (b) anthraquinone (AQ) as a model for AQ-based negolytes, which decompose to anthrone at medium to low pH values via a bimolecular reaction involving two AQ intermediates;82 (c) dihydroxyanthraquinone (DHAQ), which undergoes an electrochemical reduction in a basic solution followed by dimerization;83,84 (d) quinoxaline (QXL) which degrades from its electrochemically reduced form to a non-electroactive product under neutral to acidic conditions through a tautomerization reaction.85 These compounds are ideal model systems for our framework to study due to their well-documented degradation mechanisms. This framework not only streamlines the exploration of complex reaction networks but also proves highly effective in elucidating the degradation pathways of these ORFB electrolytes.
Simulation details
The simulation starts with defining the reactant library, which is composed of a subset of chemical species present in the electrolyte in operando. The species included are decided by the user and may comprise posolyte or negolyte molecules in the relevant redox state, solvent, supporting salts, other additives, and potentially their dissociation or tautomerization products (Fig. 1). The library is continuously updated with new intermediates discovered in the search process. All the intermediates and transition states are also stored in a database that is used to generate the final reaction network. Elementary steps of the possible degradation reactions are assumed to occur between two species from the library. For each molecule, the user assigns possible oxidation states based on its chemical structure and known redox behavior. At the initial step, the user selects the two reacting species. After the first iteration, identified intermediates are added to the reactant library. In subsequent iterations, these intermediates can be used as reactants for further simulations, facilitating continuous exploration of new reaction pathways and products.For a selected pair of molecules, the possible reaction sites are determined by local reactivity descriptors, local nucleophilicity and local electrophilicity.78 The algorithm ranks these regions based on their reactivity to generate potential encounter complexes. User can specify the number of reactive sites to include, either by percentage (e.g., top 10%) or by a specific number (e.g., 5 atoms). The algorithm then generates encounter complexes accordingly. For example, if 5 atoms are selected in molecule A and 3 in molecule B, the algorithm will generate 30 possible geometries (5 × 3 × 2). The factor of 2 comes from the fact that either molecule can act as the nucleophile or electrophile in the reaction. An example is illustrated in Fig. 2, where ortho-benzoquinone and water are used as the interacting pair. The algorithm identifies the aromatic carbon of ortho-benzoquinone (highlighted in yellow) as an electrophilic site and the oxygen atom of water (highlighted in green) as a nucleophilic site. The reactive sites are placed in close proximity, separated by a fixed distance (R).
Since the initial orientation of molecules is arbitrary, non-reactive atoms can obstruct the approach between the reactive sites, as shown in the left-side structure in Fig. 2. To address this, the algorithm optimizes the relative orientation of the two molecules through constrained minimization, adjusting their positions to maximize the separation of non-active atoms, ensuring no steric hindrance.
For each active atom pair, the algorithm begins by calculating the distances between all non-active atoms from molecule A and B. The distance between non-active atom i from molecule A (rA,i) and non-active atom j from molecule B (rB,j) is given by the Euclidean distance (dij): (eqn (1)). Here, r refers to the position vector of the i/j-th atom in molecule A/B, respectively.
| dij = |rA,i − rB,j| | (1) |
The algorithm aims to maximize the minimum distance between all pairs of non-active atoms to avoid steric clashes:
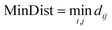 | (2) |
To achieve this, the algorithm performs translations on a sphere and rotations of molecule B relative to molecule A. The reactive site of molecule A (e.g., the electrophilic carbon on ortho-benzoquinone) is fixed at the origin of a spherical polar coordinate system. Molecule B (e.g., water) is then positioned near this reactive site, ensuring that the distance between the two reactive sites (rA,reactive and rB,reactive) is maintained at a fixed value R. For each pair of non-active atoms, i from molecule A and j from molecule B, the angle ωij between the lines connecting these non-active atoms to the reactive sites is computed:
 | (3) |
The algorithm ensures that ωij satisfies the user-defined constraint:
| ωij ≥ ωmin | (4) |
The optimization process aims to maximize the minimum distance between non-active atoms, subject to the constraints on the reactive site distance R and the minimum angle ωmin. The objective function to be maximized is described as:
 | (5) |
The minimization is performed using a genetic algorithm implemented in the Geatpy module,86 which iteratively optimizes the positioning and orientation of the molecules by adjusting the variables α, β, θx, θy, and θz. The genetic algorithm efficiently explores the search space to identify the optimal molecular configuration that satisfies the distance and angular constraints while maximizing the separation between non-active atoms.
After further relaxing the encounter complexes via geometry optimization, we employed a single-ended process search in the Amsterdam Simulation Suite (AMS) to identify TS for elementary reaction steps.43,87–90 This method uses multiple “expeditions” that consists of numbers of “explorers” to navigate the PES departing from an initial structure (encounter complex). To enhance search efficiency, specific atoms can be nudged along a predefined reaction coordinate or the direction of an imaginary frequency. The dimer method,43 along with other minimum mode methods like Lanczos,90 searches for transition states by following the gradient direction to converge to a saddle point. Once identified, the Intrinsic Reaction Coordinate (IRC) method traces the minimum energy path from the transition state to reactants and products, detailing the reaction mechanism. Identified intermediates and products become potential reactants for subsequent steps, successively mapping out reaction pathways.
The results of the process search, i.e. structures and energies of transition states and intermediates are recorded in a database. Potential products are identified based on criteria that ensure chemical plausibility, avoiding unrealistic scenarios such as breaking aromatic rings with exceptionally high transition state energies. Dissociated fragments are identified by detecting atoms or groups of atoms that are more than 2 Å away from their original connecting atom, and these fragments are excluded from the following step in the reactant library to reduce complexity. The complexity of the emerging reaction network is managed by applying energy filters, ensuring that only reactions leading to viable products are recognized, with human guidance confirming the chemical plausibility of the products. For computational efficiency, DFTB-3 (ref. 91) is used for initial exploration, with identified reaction paths further refined using ωB97XD/6-311++G**92 with the implicit solvation model PCM.93–95 Final free energies used in the analysis include zero-point energy (ZPE) and thermal corrections to Gibbs free energy. Transition state theory is employed to estimate kinetic properties, considering the step with the highest activation barrier as the rate-limiting step, with a pre-exponential factor of kbT/h = 6 × 1012 s−1.96
Results and discussion
We applied the framework in four separate case studies of possible degradation reactions: (1) Michael addition reaction and desulfonation of benzoquinone derivatives, (2) disproportionation and anthrone formation of anthraquinone, (3) electrochemical reduction of dihydroxyanthraquinone to anthrone and anthranol followed by an electrochemical dimerization, and (4) electrochemical degradation of quinonaxaline. Since the mechanisms of the main degradation reaction have been proposed in the literature, these simulations serve as proof-of-principle tests to calibrate the protocols and validate our framework for discovering degradation reaction mechanisms.Case study 1
We selected BQDS and DHDMBS as model systems, both initially proposed as promising ORFB electrolytes but later found to degrade in acidic media. BQDS was observed to undergo degradation through MA reaction, with estimated kinetic rate constant of 3.768 × 10−4 s−1 (activation barrier of 0.74 eV).80,81,96,97 Conversely, DHDMBS was engineered to resist MA reactions but has been reported to experience desulfonation, presenting a different stability concern.98 These cases underscore the important role of molecular engineering in shaping degradation pathways in benzoquinone derivatives.The initial reactant libraries for both systems included BQDS or DHDMBS molecules in their oxidized states, H2O molecule as the solvent, and a H3O+ ion to account for the acidic condition. The energy of the hydronium ion was calculated with H3O+ hydrogen-bonded to three H2O molecules, Fig. S1.†97,99 The energies of H2O molecules required to balance the elementary steps were evaluated using tetramers or pentamers in their optimized geometries. The energy of a single H2O molecule was determined from the energy difference between (H2O)5 and (H2O)4 clusters.97 Given the limitations of the DFTB3 method in handling highly charged systems, the sulfonic groups on both BQDS and DHDMBS were protonated despite their negative pKas.100,101
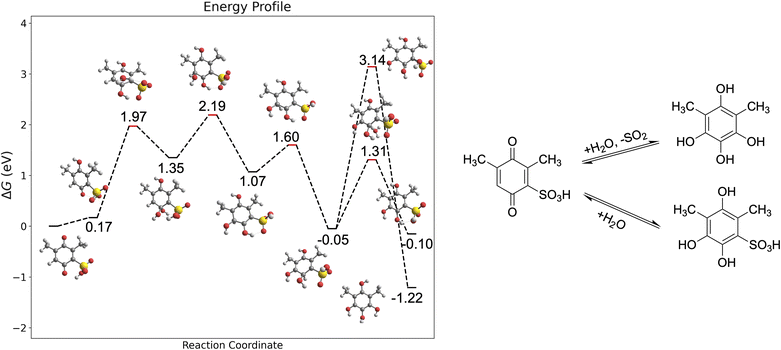
Scheme 1 shows the proposed degradation mechanisms of BQDS (Scheme 1A) and DHDMBS (Scheme 1B) as reported in the literature.6,96,97,102 For BQDS, the primary degradation pathway is MA, where a water molecule attacks the β-carbon of the α,β-unsaturated sulfonyl compound, forming an intermediate adduct. This adduct then undergoes re-aromatization and deprotonation, resulting in the final product. For DHDMBS, the primary mechanism is desulfonation, where the sulfonate group is cleaved under acidic conditions, through protonation. Fig. 3 illustrates the primary degradation mechanisms, MA, of BQDS revealed by our framework, which are in good agreement with the literature. Key points identified through the one-ended process search are shown in Fig. S2.† In addition to the primary degradation products, by using our framework, we also identified potential side product resulting from desulfonation of BQDS. Both MA and desulfonation are thermodynamically favorable, with Gibbs free energy changes (ΔG) of −0.58 eV for desulfonation and −1.06 eV for MA. However, kinetics differs significantly. Our results are qualitatively consistent with previous studies, which reported an MA kinetic rate of 3.768 × 10−4 s−1 and an activation barrier of 0.74 eV using transition state theory with a pre-exponential factor of 6 × 1012 s−1.96 In our simulations, we observed a higher activation barrier of 1.26 eV for the rate-limiting step, which is the protonation of BQDS by hydronium. The discrepancy likely results from the oversimplified explicit model of the solvent, artificial protonation of sulfonic groups, and the limitations of the implicit solvation model in simulating charged systems. The MA mechanism begins with the protonation of one carbonyl group of BQDS. This is followed by the attachment of a water molecule to the carbon between the two sulfonic groups, forming an unstable intermediate. This intermediate rapidly rearranges as the proton from the newly added water is transferred to the adjacent sulfonic group. Subsequent proton transfers occur from the sulfonic group to the unprotonated carbonyl, leading to the deprotonation of the intermediate, returning the proton to the solvent, and forming the final product. The activation barrier for desulfonation (the third TS in Fig. 3), where the second sulfonic group is about to cleave, is notably high at 3.13 eV. This indicates that desulfonation is kinetically unfavorable, explaining its absence in experimental observations. The reaction begins with the cleavage of one sulfonic group, followed by the protonation of a carbonyl group. The rate-limiting step is the subsequent cleavage of the second sulfonic group. This is followed by a proton transfer from a hydroxyl group to the adjacent carbonyl, leading to the formation of the final product.
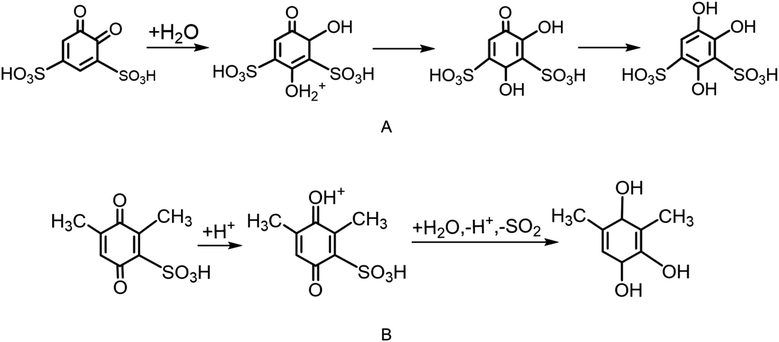 | ||
| Scheme 1 The proposed degradation mechanisms for Michael addition (A) in BQDS and desulfonation (B) in DHDMBS, respectively. | ||
Fig. 4 shows the degradation mechanisms of DHDMBS predicted using our framework. Key points identified through the process search are shown in Fig. S3.† The primary degradation product of desulfonation aligns well with experimental findings. Additionally, our framework predicts the formation of a Michael addition (MA) product as a potential side reaction. Unlike BQDS, where both degradation products are thermodynamically favorable, the MA product of DHDMBS degradation is only slightly more stable than the reactant (ΔG = −0.1 eV), while the desulfonation product is significantly more stable (ΔG = −1.22 eV). For DHDMBS, both reactions begin with protonation, followed by the splitting of a water molecule, where the hydrogen attaches to the sulfonic group and the hydroxyl group attaches to the carbonyl carbon adjacent to the sulfonic group, which is the rate-limiting step for MA. The hydroxyl group is then transferred to a nearby carbon atom, and the proton moves from the hydroxylated carbon to its neighboring carbon, forming the last intermediate (ΔG = −0.05 eV relative to the reactant, Fig. 4). From this intermediate, the reaction can proceed via desulfonation (ΔGTS = 3.09 eV) or deprotonation (ΔGTS = 1.26 eV). Although desulfonation is kinetically less favorable than the MA reaction for DHDMBS, the significant thermodynamic stability of the desulfonation product (ΔG = −1.22 eV) makes it the predominant degradation pathway. The calculated reaction barrier might be also overestimated for the same reasons as in BQDS. The marginal stability of the MA product (ΔG = −0.1 eV) relative to the reactant explains its absence in experiments. In this case, thermodynamic stability is the primary determinant of the degradation pathway, favoring desulfonation over the less stable MA product.
Case study 2
Anthraquinone (AQ) derivatives are an important class of organic negolytes;103 however, they are prone to degradation in both acidic and basic conditions, especially in their reduced state. Anthrahydroquinone (HAQ), the reduced form of AQ, has been reported to undergo a disproportionation reaction in cold concentrated sulfuric acid (Scheme 2).16 While no kinetic data is available for this reaction, it is proposed to begin with the protonation and dehydration of tautomeric oxanthrol.104 This reaction is particularly interesting and challenging for our framework due to its bimolecular nature and the involvement of tautomerization—a process formally involving a proton transfer from one site in the molecule to another, making it difficult to capture with our PES exploration algorithm.To simulate this reaction, we initially included HAQ and hydronium ion in the library. The reaction was expected to proceed through protonation and dehydration of oxanthrol (tautomer form of HAQ), then disproportionation with another HAQ. However, this approach failed to capture the disproportionation reaction, likely due to the difficulty in capturing the tautomerization process on the single-molecule PES. To address this issue, we explicitly included oxanthrol in the initial library as a shortcut to establish the starting structure. By doing so, we successfully predicted the formation of anthrone and AQ as the final products, with a total free energy change of −1.11 eV. All critical points identified during process search are shown in Fig. S4.† Starting with the slightly more stable oxanthrol (ΔG = −0.19 eV relative to HAQ, Fig. 5), protonation by the solvent occurs first, followed by a hydride shift to the solvent, leading to the formation of a charged anthrone intermediate (ΔG = 0.47 eV). This charged anthrone then acts as an electrophile, reacting with another oxanthrol molecule acting as the nucleophile. The disproportionation reaction proceeds through a TS with an energy barrier of 0.33 eV, during which the charged anthrone is reduced and the oxanthrol is oxidized, forming an intermediate species (ΔG = −0.35 eV). This intermediate subsequently undergoes deprotonation of the hydroxyl group, yielding the final products: anthrone and AQ. Our result is strongly supported by experimental data, where anthrone was confirmed using NMR and IR spectroscopy.16 These results highlight the feasibility of our framework to capture bimolecular reactions of electrolytes if the user explicitly allows for such a possibility. Since we found that tautomerization, which is often a crucial step in the degradation mechanism, is difficult to capture by the algorithm, we include tautomers in the library explicitly as part of the framework.
Case study 3
The two cases considered so far are chemical reactions, i.e. leading to the degradation of electrolyte even when the electrical current is not flowing. However, some degradation processes are happening only under electrochemical cycling conditions due to the involvement of oxidized or reduced intermediates. A well-described example is an electrochemical degradation of 2,6-dihydroxy-anthraquinone (DHAQ4−) in basic conditions to 2,6-dihydroxy-anthrone (DHA2−) and the electrochemical dimerization of DHA2− to (DHA)24−.83,84To consider the possibility of an electrochemical reaction, the charge of the species in the reactant library needs to be allowed to vary according to the applied electrode potential. Since the reaction in Scheme 3 happens during charging with a potential hold and two electrons are necessary to convert to the degradation products, we start the algorithm with DHAQ6− as the initial reactant. During the optimization we find that the first reaction follows a mechanism where DHAQ6− undergoes a barrierless stepwise protonation of two carbonyl groups via ionization of water molecules, forming intermediates intermediate 1 and 2 (Fig. 6). For the convenience of visualization, we set the energy of intermediate 2 as zero in Fig. 6. A subsequent proton transfer from a third water molecule facilitates hydroxyl departure through the transition state TS1 (ΔG = 0.62 eV), leading to intermediate 3 (ΔG = −1.72 eV, charge −3). Finally, a fourth water molecule protonates intermediate 3 through TS2 (ΔG = −1.56 eV), yielding DHAL2− (ΔG = −4.18 eV), which can tautomerize into DHA2− (ΔG = −3.7 eV compared to DHAL2−). These results align well with the experimental findings.84 All critical points identified during the process search are shown in Fig. S5.†
 | ||
| Fig. 6 The electrochemical degradation reaction of DHAQ4− under basic conditions discovered using our framework. | ||
The electrochemical dimerization of DHA2− to (DHA)24− (Scheme 4) begins with the oxidation of DHA2−, which then reacts with a hydroxide ion from the environment. This interaction leads to the departure of a water molecule and the formation of a radical intermediate (intermediate, ΔG = −0.57 eV, Fig. 7). Subsequently, two radical intermediates dimerize, forming the final product (ΔG = −1.67 eV) as identified in the experiment. Beyond recovering the known degradation products, the presented framework provided detailed insights into the mechanism, showing that after an initial electrochemical oxidation/reduction the degradation is strongly thermodynamically and kinetically favored. Capturing these two electrochemical reaction steps supports the effectiveness of our framework in uncovering electrochemical degradation pathways of organic redox flow battery electrolytes.
 | ||
| Fig. 7 The electrochemical dimerization pathway of DHA2− under basic conditions discovered using our framework. | ||
Case study 4
To validate the framework beyond quinone electrolytes we considered quinoxaline (QXL), which is as a potential negolyte undergoing a parasitic electrochemical oxidation reaction.85 It is proposed that the reduced form of QXL, in neutral and acidic conditions, can undergo a Michael addition (MA) reaction during the reoxidation, converting it to a hydroxy derivative that isomerizes to a lactam tautomer (Scheme 5).Our initial simulation setup included the reduced form of QXL (1,4-dihydroquinoxaline) and one water molecule in the library. Since the degradation is known to happen during the electrochemical oxidation, we initiate the analysis by removing two electrons from 1,4-dihydroquinoxaline. The reaction was expected to proceed with water addition to the molecule, followed by the sequential loss of two protons to the solvent, leading to tautomerization into the final product (Fig. 8). We found that the degradation of reduced QXL is triggered by the addition of water to the carbon atom adjacent to the nitrogen (in position 2), forming an unstable intermediate (ΔG = 2.40 eV). This intermediate quickly loses a proton to the solvent, resulting in a more stable intermediate with a single positive charge (ΔG = −0.40 eV). However, the search algorithm stalled at this structure, failing to capture the final deprotonation process. We note that this intermediate is a cation with two neighboring carbon atoms that have three and four bonds, respectively, so the usual valency rules are not satisfied. The proper valency can be restored in the neutral final product by removing one of the two possible protons. Realizing that a single explicit water molecule might inadequately represent the solvent environment, and that the counterion (chloride ion in the experimental reference) may influence the process, we revised our model. We included a water cluster with five molecules and a chloride ion solvated by six water molecules as possible reactants in the library (Fig. S6†). Both clusters facilitated the reaction, producing results consistent with experimental findings (see critical points from process search in Fig. S7†). The water cluster yielded a final product with ΔG = −1.27 eV, while the chloride ion cluster led to a tautomer with ΔG = −0.45 eV. This example illustrates that representing the solvent reactant a single water molecule might be insufficient in some cases. Whether the model needs to be extended to include water clusters or counterions should be decided on a case-by-case basis. We anticipate that it might be necessary whenever the algorithm stops at a structure that does not follow the usual valency rules like it is the case in this example.
The introduced computational framework has proven effective in elucidating mechanisms of four different degradation reactions of aqueous organic flow battery electrolytes. We have recovered the experimentally identified degradation products and key intermediates of the proposed mechanisms. The identified reaction mechanisms should be considered as plausible, as there is no guarantee that a more favorable pathway does not exist. The calculated barriers for the rate-limiting steps seem overestimated compared to the experiments, which may result either from the existence of alternative lower-energy intermediates or from the deficiencies of the methods. In particular, we recognize that modeling of charged molecules in non-neutral aqueous environments is particularly difficult mostly due to the limitations of semiempirical electronic structure methods, co-operativity effects in hydrogen-bonded networks, and deficiencies of implicit solvation models. Nevertheless, the framework allows for flexibility in adapting to specific challenges like incorporating a tautomer of anthrahydroquinone or using solvent clusters and counterions in quinoxaline. The analysis of BQDS and DHDMBS degradation mechanisms showed that the preference for a degradation product might be driven by reaction kinetics rather than thermodynamics, rationalizing the different products found experimentally for these electrolytes.
Conclusion
We developed a partially automated framework for identifying degradation mechanisms of organic electroactive molecules used in ORFB electrolytes. The protocol automates the process of keeping track of possible reactants, identifying the reactive sites, generating reactive complexes, and finding the transition state and corresponding product in a single-ended search. The latter implies that the algorithm does not assume the knowledge of the products or intermediates at any stage. However, the complexity of the problem so far prevents the procedure from being free of user interventions. Experimental evidence or chemical intuition may be needed to select the library of possible reactants and often to guide the reaction pathways in the anticipated direction. A ranking based on reactivity descriptors can be used for an exhaustive search through the possible encounter complexes, but we have not attempted such approach due to its poor computational scaling. The proof-of-principle application of the framework was successful, enabling elucidation of several multistep degradation mechanism, where the resulting products and intermediates are fully consistent with the experimental data. It also enabled us to calibrate the methodology for this class of problems, for example by realizing that the explicit consideration of tautomers, counterions or larger water clusters may be necessary. At this point, we present the framework as a useful computational tool for molecular engineering of stable electrolytes. A detailed understanding of the degradation mechanism allows for developing effective mitigation strategies, based either on thermodynamics or kinetics of the elementary steps. The framework can be readily used e.g. to computationally validate a hypothesis that a derivative is more stable than the parent compound or as a part of in silico screening studies where stability is one of the criteria. Such stability analysis could supplement other use cases for molecular modeling in ORFB electrolytes development.105–107 With some user expertise, the method is also useful in the discovery of a priori unknown degradation products of newly developed materials. Future developments will focus on further automatization of the process (e.g. by developing more robust heuristics), improving user interface, automating choices of solvent models, and expanding the framework's applicability to a broader range of materials.Data availability
The data supporting this article have been included as part of the ESI.† The code for the automated generation of reactants can be found at https://doi.org/10.5281/zenodo.15007828.Author contributions
X. Z. developed the software, performed the calculations, and analyzed the results. P. de S. conceptualized and supervised the project. Both authors contributed to writing and revising the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project has received funding from the European Union's Horizon 2020 research and innovation programme under Grant Agreement No. 875489.References
- C. G. Cannon, P. A. A. Klusener, N. P. Brandon and A. R. J. Kucernak, ChemSusChem, 2023, 16, e202300303 CrossRef CAS PubMed.
- A. Z. Weber, M. M. Mench, J. P. Meyers, P. N. Ross, J. T. Gostick and Q. Liu, J. Appl. Electrochem., 2011, 41, 1137 CrossRef CAS.
- W. Wang, Q. Luo, B. Li, X. Wei, L. Li and Z. Yang, Adv. Funct. Mater., 2013, 23, 970 CrossRef CAS.
- D. G. Kwabi, Y. Ji and M. J. Aziz, Chem. Rev., 2020, 120, 6467 CrossRef CAS PubMed.
- K. Wedege, E. Dražević, D. Konya and A. Bentien, Sci. Rep., 2016, 6, 39101 CrossRef CAS PubMed.
- A. Murali, A. Nirmalchandar, S. Krishnamoorthy, L. Hoober-Burkhardt, B. Yang, G. Soloveichik, G. K. S. Prakash and S. R. Narayanan, J. Electrochem. Soc., 2018, 165, A1193 CrossRef CAS.
- S. Khwa Museveni, G. Nakitare Nambafu and N. Kollongei, Mater. Sci. Energy Technol., 2023, 6, 561 CAS.
- V. Singh and H. R. Byon, ACS Appl. Energy Mater., 2024, 7, 7562 CrossRef CAS.
- T. Harayama, Y. Tezuka, T. Taga and F. Yoneda, J. Chem. Soc., Perkin Trans. 1, 1987, 75 RSC.
- K. Lin, R. Gómez-Bombarelli, E. S. Beh, L. Tong, Q. Chen, A. Valle, A. Aspuru-Guzik, M. J. Aziz and R. G. Gordon, Nat. Energy, 2016, 1, 1 Search PubMed.
- A. R. Surrey and F. C. Nachod, J. Am. Chem. Soc., 1951, 73, 2336 CrossRef CAS.
- D. P. Tabor, R. Gómez-Bombarelli, L. Tong, R. G. Gordon, M. J. Aziz and A. Aspuru-Guzik, J. Mater. Chem. A, 2019, 7, 12833 RSC.
- D. G. Kwabi, K. Lin, Y. Ji, E. F. Kerr, M.-A. Goulet, D. De Porcellinis, D. P. Tabor, D. A. Pollack, A. Aspuru-Guzik, R. G. Gordon and M. J. Aziz, Joule, 2018, 2, 1907 CrossRef.
- Y. Ji, M.-A. Goulet, D. A. Pollack, D. G. Kwabi, S. Jin, D. De Porcellinis, E. F. Kerr, R. G. Gordon and M. J. Aziz, Adv. Energy Mater., 2019, 9, 1900039 CrossRef.
- B. Huskinson, M. P. Marshak, C. Suh, S. Er, M. R. Gerhardt, C. J. Galvin, X. Chen, A. Aspuru-Guzik, R. G. Gordon and M. J. Aziz, Nature, 2014, 505, 195 CrossRef CAS PubMed.
- F. Beck and G. Heydecke, Berichte der Bunsengesellschaft für physikalische Chemie, 1987, 91, 37 CrossRef CAS.
- T. J. Carney, S. J. Collins, J. S. Moore and F. R. Brushett, Chem. Mater., 2017, 29, 4801 CrossRef CAS.
- M.-A. Goulet and M. J. Aziz, J. Electrochem. Soc., 2018, 165, A1466 CrossRef CAS.
- C. Wang, Z. Yang, Y. Wang, P. Zhao, W. Yan, G. Zhu, L. Ma, B. Yu, L. Wang, G. Li, J. Liu and Z. Jin, ACS Energy Lett., 2018, 3, 2404 CrossRef CAS.
- L. Tong, M.-A. Goulet, D. P. Tabor, E. F. Kerr, D. De Porcellinis, E. M. Fell, A. Aspuru-Guzik, R. G. Gordon and M. J. Aziz, ACS Energy Lett., 2019, 4, 1880 CrossRef CAS.
- B. Hu, H. Fan, H. Li, M. Ravivarma and J. Song, Adv. Funct. Mater., 2021, 31, 2102734 CrossRef CAS.
- D. Xu, C. Zhang, Y. Zhen and Y. Li, ACS Appl. Mater. Interfaces, 2021, 13, 35579 CrossRef CAS PubMed.
- D. Pinheiro, M. Pineiro and J. S. S. de Melo, Commun. Chem., 2021, 4, 1 CrossRef PubMed.
- I. L. Escalante-García, J. S. Wainright, L. T. Thompson and R. F. Savinell, J. Electrochem. Soc., 2014, 162, A363 CrossRef.
- W. Liu, Z. Zhao, T. Li, S. Li, H. Zhang and X. Li, Sci. Bull., 2021, 66, 457 CrossRef CAS PubMed.
- C. Wang, B. Yu, Y. Liu, H. Wang, Z. Zhang, C. Xie, X. Li, H. Zhang and Z. Jin, Energy Storage Mater., 2021, 36, 417 CrossRef.
- G. Kwon, S. Lee, J. Hwang, H.-S. Shim, B. Lee, M. H. Lee, Y. Ko, S.-K. Jung, K. Ku, J. Hong and K. Kang, Joule, 2018, 2, 1771 CrossRef CAS.
- L. Liu, Y. Yao, Z. Wang and Y.-C. Lu, Nano Energy, 2021, 84, 105897 CrossRef CAS.
- S. Pang, X. Wang, P. Wang and Y. Ji, Angew. Chem., Int. Ed., 2021, 60, 5289 CrossRef CAS PubMed.
- M.-A. Goulet, L. Tong, D. A. Pollack, D. P. Tabor, S. A. Odom, A. Aspuru-Guzik, E. E. Kwan, R. G. Gordon and M. J. Aziz, J. Am. Chem. Soc., 2019, 141, 8014 CrossRef CAS PubMed.
- E. W. Zhao, T. Liu, E. Jónsson, J. Lee, I. Temprano, R. B. Jethwa, A. Wang, H. Smith, J. Carretero-González, Q. Song and C. P. Grey, Nature, 2020, 579, 224 CrossRef CAS PubMed.
- K. Amini, E. F. Kerr, T. Y. George, A. M. Alfaraidi, Y. Jing, T. Tsukamoto, R. G. Gordon and M. J. Aziz, Adv. Funct. Mater., 2023, 33, 2211338 CrossRef CAS.
- E. M. Müller, A. de Meijere and H. Grubmüller, J. Chem. Phys., 2002, 116, 897 CrossRef.
- A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562 CrossRef CAS PubMed.
- B. Ensing, M. De Vivo, Z. Liu, P. Moore and M. L. Klein, Acc. Chem. Res., 2006, 39, 73 CrossRef CAS PubMed.
- M. Iannuzzi, A. Laio and M. Parrinello, Phys. Rev. Lett., 2003, 90, 238302 CrossRef PubMed.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978 CrossRef CAS.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 1999, 111, 7010 CrossRef CAS.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901 CrossRef CAS.
- D. Sheppard, R. Terrell and G. Henkelman, J. Chem. Phys., 2008, 128, 134106 CrossRef PubMed.
- J.-W. Chu, B. L. Trout and B. R. Brooks, J. Chem. Phys., 2003, 119, 12708 CrossRef CAS.
- H. B. Schlegel, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 790 CAS.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 1999, 111, 7010 CrossRef CAS.
- C. Peng, P. Y. Ayala, H. B. Schlegel and M. J. Frisch, J. Comput. Chem., 1996, 17, 49 CrossRef CAS.
- W. E, W. Ren and E. Vanden-Eijnden, J. Chem. Phys., 2007, 126, 164103 CrossRef PubMed.
- W. E, W. Ren and E. Vanden-Eijnden, J. Phys. Chem. B, 2005, 109, 6688 CrossRef CAS PubMed.
- S. K. Burger and W. Yang, J. Chem. Phys., 2007, 127, 164107 CrossRef PubMed.
- P. M. Zimmerman, J. Comput. Chem., 2015, 36, 601 CrossRef CAS PubMed.
- B. Peters, A. Heyden, A. T. Bell and A. Chakraborty, J. Chem. Phys., 2004, 120, 7877 CrossRef CAS PubMed.
- P. Raccuglia, K. C. Elbert, P. D. F. Adler, C. Falk, M. B. Wenny, A. Mollo, M. Zeller, S. A. Friedler, J. Schrier and A. J. Norquist, Nature, 2016, 533, 73 CrossRef CAS PubMed.
- M. A. Kayala, C.-A. Azencott, J. H. Chen and P. Baldi, J. Chem. Inf. Model., 2011, 51, 2209 CrossRef CAS PubMed.
- M. Woulfe and B. M. Savoie, J. Chem. Theory Comput., 2025, 21, 1276 CrossRef CAS PubMed.
- V. Singla, Q. Zhao and B. M. Savoie, Digital Discovery, 2024, 3, 1729 RSC.
- T. Weymuth, J. P. Unsleber, P. L. Türtscher, M. Steiner, J.-G. Sobez, C. H. Müller, M. Mörchen, V. Klasovita, S. A. Grimmel, M. Eckhoff, K.-S. Csizi, F. Bosia, M. Bensberg and M. Reiher, J. Chem. Phys., 2024, 160, 222501 CrossRef CAS PubMed.
- J. P. Unsleber, J. Chem. Inf. Model., 2023, 63, 3392 CrossRef CAS PubMed.
- Q. Zhao and B. M. Savoie, Angew. Chem., Int. Ed., 2022, 61, e202210693 CrossRef CAS PubMed.
- C. Lavigne, G. Gomes, R. Pollice and A. Aspuru-Guzik, Chem. Sci., 2022, 13, 13857 RSC.
- A. Hashemi, S. Bougueroua, M.-P. Gaigeot and E. A. Pidko, J. Chem. Theory Comput., 2022, 18, 7470 CrossRef CAS PubMed.
- M. Steiner and M. Reiher, Top. Catal., 2022, 65, 6 CrossRef CAS PubMed.
- J. P. Unsleber, S. A. Grimmel and M. Reiher, J. Chem. Theory Comput., 2022, 18, 5393 CrossRef CAS PubMed.
- T. A. Young, J. J. Silcock, A. J. Sterling and F. Duarte, Angew. Chem., Int. Ed., 2021, 60, 4266 CrossRef CAS PubMed.
- A. L. Dewyer, A. J. Argüelles and P. M. Zimmerman, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1354 Search PubMed.
- C. W. Gao, J. W. Allen, W. H. Green and R. H. West, Comput. Phys. Commun., 2016, 203, 212 CrossRef CAS.
- P. M. Zimmerman, J. Comput. Chem., 2013, 34, 1385 CrossRef CAS PubMed.
- M. Berkowitz, S. K. Ghosh and R. G. Parr, J. Am. Chem. Soc., 1985, 107, 6811 CrossRef CAS.
- M. Franco-Pérez, C.-A. Polanco-Ramírez, P. W. Ayers, J. L. Gázquez and A. Vela, Phys. Chem. Chem. Phys., 2017, 19, 16095 RSC.
- J. Martínez, Chem. Phys. Lett., 2009, 478, 310 CrossRef.
- W. Yang and R. G. Parr, Proc. Natl. Acad. Sci. U.S.A., 1985, 82, 6723 CrossRef CAS PubMed.
- R. G. Parr, L. v. Szentpály and S. Liu, J. Am. Chem. Soc., 1999, 121, 1922 CrossRef CAS.
- J. Yu, N. Q. Su and W. Yang, JACS Au, 2022, 2, 1383 CrossRef CAS PubMed.
- R. G. Parr and W. Yang, J. Am. Chem. Soc., 1984, 106, 4049 CrossRef CAS.
- D. Hait and M. Head-Gordon, J. Phys. Chem. Lett., 2018, 9, 6280 CrossRef CAS PubMed.
- R. Parthasarathi, J. Padmanabhan, V. Subramanian, B. Maiti and P. K. Chattaraj, J. Phys. Chem. A, 2003, 107, 10346 CrossRef CAS.
- T. Fievez, N. Sablon, F. De Proft, P. W. Ayers and P. Geerlings, J. Chem. Theory Comput., 2008, 4, 1065 CrossRef CAS PubMed.
- I. G. Ryabinkin and V. N. Staroverov, J. Chem. Phys., 2014, 141, 084107 CrossRef PubMed.
- J. I. Martínez-Araya, Front. Chem., 2022, 10, 869110 CrossRef PubMed.
- P. Geerlings and F. D. Proft, Phys. Chem. Chem. Phys., 2008, 10, 3028 RSC.
- C. Morell, J. L. Gázquez, A. Vela, F. Guégan and H. Chermette, Phys. Chem. Chem. Phys., 2014, 16, 26832 RSC.
- B. Yang, L. Hoober-Burkhardt, F. Wang, G. K. Surya Prakash and S. R. Narayanan, J. Electrochem. Soc., 2014, 161, A1371 CrossRef CAS.
- J. Rubio-Garcia, A. Kucernak, A. Parra-Puerto, R. Liu and B. Chakrabarti, J. Mater. Chem. A, 2020, 8, 3933 RSC.
- J. D. Hofmann, S. Schmalisch, S. Schwan, L. Hong, H. A. Wegner, D. Mollenhauer, J. Janek and D. Schröder, Chem. Mater., 2020, 32, 3427 CrossRef CAS.
- F. Beck and G. Heydecke, Berichte der Bunsengesellschaft für physikalische Chemie, 1987, 91, 37 CrossRef CAS.
- E. W. Zhao, E. Jónsson, R. B. Jethwa, D. Hey, D. Lyu, A. Brookfield, P. A. A. Klusener, D. Collison and C. P. Grey, J. Am. Chem. Soc., 2021, 143, 1885 CrossRef CAS PubMed.
- Y. Jing, E. W. Zhao, M.-A. Goulet, M. Bahari, E. M. Fell, S. Jin, A. Davoodi, E. Jónsson, M. Wu, C. P. Grey, R. G. Gordon and M. J. Aziz, Nat. Chem., 2022, 14, 1103 CrossRef CAS PubMed.
- M. Aleksic, J. Pantic and V. Kapetanovic, Facta Univ., Ser.: Phys., Chem. Technol., 2014, 12, 55 CrossRef.
- J. Jazzbin, http://www.geatpy.com/, accessed 2020.
- J. Kästner and P. Sherwood, J. Chem. Phys., 2008, 128, 014106 CrossRef PubMed.
- S. T. Chill, M. Welborn, R. Terrell, L. Zhang, J.-C. Berthet, A. Pedersen, H. Jónsson and G. Henkelman, Modell. Simul. Mater. Sci. Eng., 2014, 22, 055002 CrossRef.
- A. Heyden, A. T. Bell and F. J. Keil, J. Chem. Phys., 2005, 123, 224101 CrossRef PubMed.
- R. Malek and N. Mousseau, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 7723 CrossRef CAS PubMed.
- M. Gaus, Q. Cui and M. Elstner, J. Chem. Theory Comput., 2011, 7, 931 CrossRef CAS PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615 RSC.
- F. Lipparini and B. Mennucci, J. Chem. Phys., 2016, 144, 160901 CrossRef PubMed.
- M. Cossi, G. Scalmani, N. Rega and V. Barone, J. Chem. Phys., 2002, 117, 43 CrossRef CAS.
- J. Andzelm, C. Kölmel and A. Klamt, J. Chem. Phys., 1995, 103, 9312 CrossRef CAS.
- S. V. Modak, W. Shen, S. Singh, D. Herrera, F. Oudeif, B. R. Goldsmith, X. Huan and D. G. Kwabi, Nat. Commun., 2023, 14, 3602 CrossRef CAS PubMed.
- S. Nandi, L. E. de Sousa, T. Vegge and P. de Silva, Batteries Supercaps, 2023, 6, e202200443 CrossRef CAS.
- L. Hoober-Burkhardt, S. Krishnamoorthy, B. Yang, A. Murali, A. Nirmalchandar, G. K. S. Prakash and S. R. Narayanan, J. Electrochem. Soc., 2017, 164, A600 CrossRef CAS.
- Y. Zeng, A. Li and T. Yan, J. Phys. Chem. B, 2020, 124, 1817 CAS.
- M. Kubillus, T. Kubař, M. Gaus, J. Řezáč and M. Elstner, J. Chem. Theory Comput., 2015, 11, 332 CrossRef CAS PubMed.
- S. Stepanovic, R. Lai, M. Elstner, M. Gruden, P. Garcia-Fernandez and Q. Cui, Phys. Chem. Chem. Phys., 2020, 22, 27084 RSC.
- L. Hoober-Burkhardt, S. Krishnamoorthy, B. Yang, A. Murali, A. Nirmalchandar, G. K. S. Prakash and S. R. Narayanan, J. Electrochem. Soc., 2017, 164, A600 CrossRef CAS.
- M. R. Gerhardt, L. Tong, R. Gómez-Bombarelli, Q. Chen, M. P. Marshak, C. J. Galvin, A. Aspuru-Guzik, R. G. Gordon and M. J. Aziz, Adv. Energy Mater., 2017, 7, 1601488 CrossRef.
- M. A. Matthews, J. Chem. Soc., 1926, 129, 236 RSC.
- R. P. Fornari and P. de Silva, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1495 CAS.
- R. P. Fornari, M. Mesta, J. Hjelm, T. Vegge and P. de Silva, ACS Mater. Lett., 2020, 2, 239 CrossRef CAS.
- R. P. Fornari and P. de Silva, Molecules, 2021, 26, 3978 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc07640k |
| This journal is © The Royal Society of Chemistry 2025 |