Charge-transfer mediated J-aggregation in red emitting ultra-small-single-benzenic meta-fluorophore crystals

Abstract

Red emission in crystals has been observed with an ultra-small-single-benzenic meta-fluorophore (MF) with a molecular weight (MW) of only 197 Da, bettering the literature report of fluorophores with the lowest MW = 252 Da. Supramolecular extensive hydrogen-bonding and J-aggregate type centrosymmetric discrete-dimers or a 1D chain of MFs led to red emission (λ^max_em = 610–636 nm) in MF crystals. Unlike in the solution phase showing one absorption band, in thin films and in crystals the transition from the S₀ state to both the S₁⁻ state and S₁⁺ state becomes feasible. The angle between the transition dipole moments has been obtained to be 66.99° and the exciton splitting energy has been obtained to be (−) 55.7 meV. Significant overlap have been observed and the extent of overlaps integrals between the HOMOs and the LUMOs were assessed to be 0.0068 and (−) 0.00024, respectively. Planar molecules are shown to be involved in anti-parallel stacking with a slip-angle of 44.05° and an inter-planar longitudinal distance of 3.40 Å. A large magnitude of ΔE_ES (energy difference between the S₁⁻ state and S₁⁺ state) (0.83 eV) has been obtained. A much higher magnitude of the CT coupling constant (−0.708 for MF2) has been noted in comparison to the coulombic coupling constant (0.016 for MF2). The excited-state-lifetime has been shown to increase from 5.98 ns (in hexane) to 30.90 ns in the crystal. All these extra-ordinary optical properties point to the existence of a charge-transfer mediated J-aggregation phenomenon in these MF crystals. Based on these fascinating observations, highly stable, bright and colour pure white LEDs could be generated.

---

Introduction

Meta-fluorophores (MFs), (in which single charge-transfer-donor (CTD) and single charge-transfer-acceptor (CTA) groups are oriented in the meta direction in a single-benzenic fluorophore) are coming up in a big way, as a potentially much improved optical fluorophores than the corresponding para-fluorophores.¹ Novel designs of MFs for red emission in the solution phase are at a promising stage,^2–8 whereas the designing of MFs, towards obtaining hitherto unknown red emission in the solid state, is non-existent. To achieve red emission in a fluorophore for different applications such as light emitting diodes (LEDs), bioimaging, etc.,^9–16 researchers have adopted different strategies (Chart 1): e.g. (i) introduction of two pairs of ortho-oriented CTD and CTA groups in a single-benzenic structure (Chart 1a, b and Table S1†);^17–24 (ii) fusing several polycyclic aromatic hydrocarbons (Table S2†), and (iii) extending π-conjugation between CTD and CTA groups (Table S2†).⁹ By these strategies, the excited state dipole moment becomes much higher than that of the ground state.⁹ However, due to π–π stacking, dipole–dipole interaction, etc. the photo-luminescence (PL) quantum yield (ϕ) of these large sized fluorophores gets reduced very significantly in the solid state.^9,25–29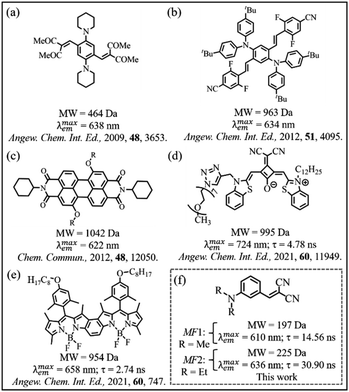

Chart 1 (a–e) Molecular structures of reported red-emitting crystals and (f) red emissive MF crystals explored in this work.

To circumvent such quenching effects, bulky groups were incorporated in the main fluorophore structures (Chart 1d and e).^30–33 However, by such strategies, not only the molecular weight (MW) or size increases, the synthesis and purification of these red-emitting fluorophores become cumbersome^17–24 (Chart 1c–e). Moreover, these fluorophores show poor optical properties, e.g. lesser Stokes shift (Table S2†), lesser solvatochromic shift, etc., thereby jeopardizing PL multiplexing experiments.

Herein, in this article, we introduce a couple of ultra-small (w.r.t. MW)^3,15 red-emitting (with the emission maximum i.e. λ^max_em > 600 nm) MFs (MF1 and MF2, Chart 1f) in the crystal. (i) Synthesis and purification of these ultra-small MFs (MW = 197–225 Da) are much less cumbersome (Scheme S1 and Fig. S1–S4†). Moreover, these two MFs exhibit much improved (Table S3†) optical properties, e.g. (ii) an exorbitantly large Stokes shift (as high as 256 nm), (iii) a large solvatochromic shift of 194 nm, (iv) a high ϕ of ∼0.45, and (v) nearly 20 000 times enhanced excited-state-lifetime (τ) (in comparison to similar para-fluorophores) in the solution phase, for such an ultra-small fluorophore of MW = 197–225 Da. Please note that similar para-fluorophores of MW ∼200 Da, exhibit a Stokes shift of only ∼37–82 nm, solvatochromic shift of only ∼30 nm, ϕ < 0.03, and τ of only ∼1 ps, in the solution phase (Table S4†).³⁴ The reasons behind large solvatochromic shift, high ϕ (∼0.4 in both solution and solid phase) and much longer τ (>25 ns in both solution and solid phase), have been investigated in great detail, and CT-mediated J-aggregation phenomenon has been shown to be responsible for such extraordinary optical behaviour in the solid state. Interestingly, the crystals also show a mechano-fluorochromic hypsochromic shift upon mechanical grinding.

Results and discussion

Photophysical behaviour

Solution phase. Solution phase optical behaviour is summarized in Fig. 1 and Table 1 (and Fig. S5 and S6†).

Fig. 1 (a) UV illuminated solution phase pictures in cuvettes, and (b) emission spectra and (c) PL decay behaviour of MF1 in different solvents. PL decays have been monitored at the respective λ^max_em, λ_ex = 405 nm.

Table 1 Photophysical properties of MF1 and MF2 in different solvents

Solvent	ϕ		τ (ns)
	MF1	MF2	MF1	MF2
Mesitylene	0.35	0.45	23.69	24.36
Toluene	0.45	0.40	22.72	25.29
Benzene	0.34	0.44	21.50	25.40

---

Such ultra-small MFs (with MW ≤ 225 Da) exhibit (i) a large solvatochromic shift of ∼194 nm (green to deep red emission, Fig. 1a, b and Table S3†), (ii) an intense Stokes shift value of 256 nm (Table S3†), (iii) high ϕ of 0.45 (Table 1) and (iv) large τ of 21–25 ns (Table 1). As mentioned earlier, similar small para-fluorophores of MW ∼197–291 Da, exhibit a Stokes shift of only ∼37–82 nm, solvatochromic shift of only 25–33 nm, and ϕ of only 0.01–0.03 (Table S4†).³⁴ Moreover, both MF1 and MF2 exhibit unique single exponential PL decay (Fig. 1c and S6c†) in all solvents studied (Table S3†). Similar ultra-small para-fluorophores (with MW ∼ 197–291 Da) exhibit a τ of only 0.7–1.4 ps in the solution phase (Table S4†),³⁴ whereas, MF1 and MF2 exhibit a comparatively 20 000 times larger τ of ∼21.5–25.4 ns.

Solid state optical behaviour

Although optical properties of MFs have been reported in the solution phase,^1–8 a detailed literature report of steady-state and time-resolved optical properties of red-emitting ultra-small MFs in the crystal state is non-existent. Quite impressively, the crystals of MF2 exhibit bright red emission (Fig. 2a and b) (for MF1, see Fig. S7†). Mechano-fluorochromic solid state optical behaviour of MF2 is depicted in Fig. 2c (for MF1 see Fig. S7†). For MF2, in a pristine crystal, λ^max_em = 636 nm and the emission gets hypsochromically (∼25 nm) shifted to 610 nm upon grinding or heating (Fig. 2c) (for MF1, see Fig. S7†). The extent of blue shift is even more pronounced in polymer films (∼70 nm). In a polymethylmethacrylate (PMMA) film the emission is in orange (λ^max_em = 582 nm) and in polystyrene (PS) film the emission is in yellow (λ^max_em = 568 nm). Thus, with the same MF it is possible to obtain yellow to red colour in the solid state. We have obtained quite a high ϕ of 0.37 in the solid state (for MF1, see Table S5†).

Fig. 2 Crystal images of MF2 (a) under daylight and (b) under UV-illumination. (c) Emission spectra and (d) PL decay behaviour in mechano-fluorochromic solid states of MF2. PL decays are monitored at the respective λ^max_em, λ_ex = 405 nm.

Quite interestingly, both these MFs exhibit single exponential PL decay (Fig. 2d) with a comparatively larger τ of 30 ns or higher (for fluorophores with MW ≤ 225 Da) (Tables 2 and S6†). In comparison, τ values of red-emitting solids of small and large fluorophores are in the range of 6–12 ns (Table S7†). Through the PXRD pattern, IR and differential scanning calorimetry (DSC) analyses, etc., no significant change in the structural crystalline state, or presence of any polymorph of these MFs upon grinding or heating (Fig. S8–S10†) for MF crystals could be observed.

Table 2 Solid state optical properties of MF2

Sample	λ ^maxem (nm)	ϕ	τ (ns)
Crystal	636	0.19	30.90
PMMA film	582	0.31	30.02
PS film	568	0.37	33.09

---

Estimation of mechanical properties by nanoindentation

Mechanical properties are fundamental properties of a material which are quite useful to assess the applicability of a material towards device fabrication. Softer crystalline materials are ideal for flexible and durable optoelectronics. In order to study the interesting mechanical behaviour of the crystals, we quantified the mechanical properties^35–38 of these MF crystals by employing the nano-indentation technique.^39–41

The value of Young's modulus (E) for MF1 (5.50 ± 0.30 GPa) is obtained to be slightly higher than that of MF2 (5.36 ± 0.14 GPa) (Fig. S11a, ESI IIg and Table S8†), signifying that the MF1 crystal is marginally stiffer than MF2. However, the magnitudes of hardness (H) of MF1 (0.24 ± 0.02 GPa) and MF2 (0.24 ± 0.01 GPa) are the same (Fig. S11a and Table S8†). The E and H values as well as the significant residual depths of the indent impressions upon unloading, confirm that both the crystals are soft in nature as compared to most other molecular crystals.⁴⁰ This is understandable as there are no conventional strong hydrogen-bonding interactions in the crystals. The mechanical softness makes these crystals promising candidates for flexible optoelectronics.

Single crystal structural analyses

MF1 and MF2 have the same basic chemical structure (Chart 1f), except the NR₂ group (for MF1, R = Me and for MF2, R = Et). Such a small change should not affect the optical behaviour significantly in the solid state based on the knowledge obtained from the solution phase. However, on going from MF1 to MF2, the λ^max_em changes from 610 nm to 636 nm, ϕ changes from 0.06 to 0.19 (∼3 times) and τ changes from 14.56 ns to 30.90 ns (∼2 times) (Table S9†). In order to investigate the underlying reason(s) it was necessary to know what kinds of interactions are present in these crystals, and how do their nature, extent and energetics change on going from MF1 to MF2.

Although chemical structures are similar, MF1 and MF2 crystallize differently (Table S10†); the former crystallizes in the monoclinic with P2₁/c space group, whereas, the latter crystallizes in triclinic with P1̄ space group. Careful and deeper analysis of the single crystals (Fig. 3a and b) indicate that (i) there is an intermolecular hydrogen-bonding between –CN and H of the N–CH₃ group in MF1 (shown as the white dotted line in Fig. 3a and e), because of which MF1 forms a continuous one-directional (1D) chain (Fig. 3e) and such an interaction is absent in MF2, (ii) there are double intermolecular hydrogen-bonding interactions between –CN and H of C=C in MF2 (shown as the yellow dotted line in Fig. 3b and f), leading to the formation of a J-aggregate⁴² type of supramolecular centrosymmetric “discrete-dimer” structure in MF2 (Fig. 3f), which is absent in MF1.

Fig. 3 Differential single crystal X-ray structure of MFs showing major interactions. Different types of hydrogen-bonding interactions of (a) MF1 and (b) MF2, the π–π stack orientation of (c) MF1 and (d) MF2, and crystal packing of (e) MF1 and (f) MF2.

In depth crystal structural analyses results mentioned above suggest that in MF1 crystal the molecules form 1D chain along b (b axis) direction by weak C–H⋯N (d/Å, θ/°: 2.61 Å and 174.55°) hydrogen-bonding, while in MF2 crystal the molecules form centrosymmetric discrete-dimer and are further packed by π–π (Fig. 3c for MF1 and Fig. 3d for MF2) and van der Waals interactions (d/Å, θ/°: 2.68 Å and 164.64°) (Table S11†). Moreover, supramolecular aggregated structures with a brick-work arrangement of molecular units have been observed for MF2 in the crystal (Fig. 3f). As a next step we have measured the distance between the hydrogen-bond donor and acceptor atoms (d) and hydrogen-bond angle (θ) (Fig. S12†).^43–45 The shorter the value of d and closer the value of θ to 180°, the stronger the hydrogen-bond.⁴³ The presence of double intermolecular hydrogen-bonding leads to centrosymmetric discrete-dimer formation which effectively rigidifies the planar molecular conformation in MF2 (Fig. 3f). There is no significant interaction between/among the discrete-dimers in MF2. Fig. S12† clearly shows that the extent of hydrogen-bonding is much higher in MF2 than in MF1. All these very important points mentioned above categorically explain the observed difference in the optical responses i.e. (a) longer λ^max_em (because of discrete-dimer formation), (b) higher ϕ (because of rigidification), (c) longer τ (reduction of the nonradiative pathway because of rigidification), and (d) narrower PL emission (as there is nearly no interaction in between or among discrete-dimers) in the MF2 crystal in comparison to the MF1 crystal (Table S9†).

As the collective resistance of the 1D hydrogen-bonded chains in MF1 is more effective than discrete-dimers in MF2, the elastic deformation is comparatively less facile against the external stress in MF1 in comparison to MF2. That is why the magnitude of Young's Modulus of MF1 is marginally higher than that of MF2.

The mechano-fluorochromic hypsochromic shift of λ^max_em upon grinding (Fig. 2b) can be understood in terms of mechanical softness of the crystals, facilitating structural change in the deformed microcrystals. Upon applying mechanical stress, breakage of intermolecular interactions leads to formation of defects within the crystals. Thus, the excited state stabilization, observed in the crystal state, gets affected very significantly in the ground or heated samples, leading to the hypsochromic shift of the λ^max_em (Table S6†). These defect-states initiate additional nonradiative process(es), thereby reducing the τ (26 ns, 20 ns, and 19 ns in 10 minute ground, 60 minute ground, and after heating samples of MF2) (for MF1, see Table S6†).

Energy framework calculations

In order to obtain deeper details regarding the optical response, from an energetics point of view, pairwise energy framework calculations⁴⁶ were explored for the (i) entire crystal, as well as (ii) along the intermolecular hydrogen-bond direction for both MF1 (Fig. S13–S17) and MF2 (Fig. S18–S22†).

Pairwise energy calculations in the entire crystal reveal that the magnitudes of dispersion energy, Coulomb energy and total energy are similar in MF1 and in MF2 (Table S12†). However, pairwise energy calculations along the intermolecular hydrogen-bond direction in paired hydrogen-bonded molecular units revealed that the magnitudes of (a) electrostatic Coulomb energy, (b) dispersion energy, and the (c) total energy, for the MF2 crystal, are much higher than those for the MF1 crystal, signifying comparatively stronger hydrogen-bonded dimeric interaction in MF2 than in MF1 (Fig. S12†). To estimate the percentage of different sub-molecular interactions, Hirshfeld surface analyses⁴⁶ (Fig. S23–S26†) were performed, which showed that the percentage of strong interactions like C–H⋯N, C–N⋯H and C–C⋯C are slightly higher in MF1 than MF2 (Fig. S25, S26 and Table S13†) signifying the marginally stiffer nature of the MF1 crystal than the MF2 crystal.

Charge-transfer mediated J-aggregation

In order to obtain the in-depth understanding of the nature of the aggregation of MF1 and MF2 in the crystal, we have investigated crystal structural and optical spectroscopic properties, as well as performed quantum chemical calculations based on these crystals. In isolated molecules having discrete S₀ and S₁ states, only one absorption band is observed. However, in the aggregated state the excited state gets split into two states through Coulombic coupling (Fig. 4a).^47–51 These two energy-states will have energy either lower or higher than the S₁ energy state.^47–51 Out of these two energy states, one energy state will have a null dipole moment which makes the transition incorporating the S₀ energy state and this particular state not feasible.^47–51 As documented in the literature,^47–51 in the classical H-aggregated state the transition between the S₀ state and the lower energy state (S₁⁻ state) is not feasible, but the transition between the S₀ state and the higher energy state (S₁⁺ state) is feasible.^47–51 Conversely, in the classical J-aggregated state, the transition between the S₀ state and the lower energy state (S₁⁻ state) is feasible, but the transition between the S₀ state and the higher energy state (S₁⁺ state) is not feasible (Fig. 4a).^47–51 However, in the newly discovered CT mediated J-aggregation (in thin films and in crystals), in contrast to the long range in contrast to the long range Coulombic (LRC) coupling observed for classical H-type & J-type molecular aggregates, the molecules are quite close (longitudinal distance <4 Å) and there exists a large spatial (structural) overlap (Fig. 4b) and such conditions favour intermolecular wavefunction overlap, leading to short-range intermolecular charge transfer (SRICT) coupling.^52,53

It has been opined that unlike classical H-aggregates and classical J-aggregates, the interplay between LRC and SRICT coupling makes the transition between the S₀ state and both the S₁⁻ state and S₁⁺ state feasible. The energy separation between the S₁⁻ state and S₁⁺ state is denoted as (ΔE_ES) and it has been opined that strong exciton coupling would cause a large magnitude of ΔE_ES. The magnitude of large ΔE_ES increases from the thin film to crystal. To date, there have been only a few reports on very interesting molecular aggregates in which none of these two newly originating energy states (S₁⁻ and S₁⁺ states) have a null dipole moment.^47–51

Interestingly, in the MF2 crystal, the attractive intramolecular hydrogen-bonding interactions between the –CH₂ (of the –NR₂ group) and –CN group and also between phenyl H and the –CN group are evident from the reduced density gradient iso-surface of the monomer and reduced density gradient (RDG) scatter diagram (Fig. S27c and d†). These interactions make the individual molecule planar. Moreover, the bulky –NEt₂ group induces steric repulsion (Fig. S27c and d†). In the RDG iso-surface plot and RDG scatter diagram of the dimer, attractive hydrogen-bonding interactions (both intramolecular and intermolecular) are observed (Fig. 4c and d). Moreover, the intermolecular steric repulsion between the bulky –NEt₂ groups disfavours the side-by-side stacking (necessary for H-aggregate formation), and rather the head-to-tail oriented slip-stacking is favoured (necessary for J-aggregation).^54,55

From the density functional theory (DFT) calculations, it has been observed that the electron cloud in the highest occupied molecular orbital (HOMO) is mostly concentrated on the donor –NEt₂ group and the electron cloud in the lowest unoccupied molecular orbital (LUMO) is mostly concentrated on the acceptor i.e. on the –CN group (Fig. S28a†). The calculated CT amount has been observed to be 0.82 and thus consistent with the electron clouds in the HOMO and LUMO, signifying the existence of strong intramolecular CT. Experimentally it has been observed that the λ^max_em gradually red shifts, and a large solvatochromic shift of 164 nm has been observed upon going from nonpolar hexane to polar acetonitrile (Fig. S6a, b and Table S3†). All these observations clearly verify the existence of strong intramolecular CT in MF2. The orientations of the transition dipole moment (TDM) have been shown as green arrows (Fig. 4e) and the angle between the TDMs has been obtained to be 66.99° (Fig. 4e). From the direction of the TDM and molecular packing structure, the exciton splitting energy has been obtained to be (−) 55.7 meV and can be understood from the Frenkel exciton model (ESI, IIn†).^44,56

Fig. 4 (a) Excited-states of the thin film & crystal and a three-level energy-diagram of charge-transfer (CT)-mediated J-aggregates with excited-state energy separation (ΔE_ES). (b) Different kinds of molecular stacking arrangements showing variation in the extent of overlap in classical J-aggregates (left) and CT-mediated J-aggregates (right). (c) Reduced density gradient iso-surface, (d) plot of the reduced density gradient (RDG) versus sign(λ₂)ρ of the dimer, (e) molecular packing structure obtained from the single-crystal X-ray structure, where the computationally derived π–π stacked slip-angle (α) between the S₀ to S₁ transition dipole moment (TDM) has been shown (TDM directions are shown as a green arrow), (f) estimated HOMO–HOMO overlap & LUMO–LUMO overlap of a characteristic dimer, (g) experimentally derived π–π stacked slip-angle from the crystal packing, and comparison of (h) absorption, (i) excitation and (j) excited-state-lifetime in hexane, the thin film and the crystal, for the MF2 crystal.

Such dimers in the slip-stacked J-aggregates exhibit significant overlap between the HOMOs and the LUMOs (Fig. 4f) and the magnitude of overlap integrals were assessed to be 0.0068 and (−) 0.00024 respectively, indicating the CT nature within the slip-stacked J-aggregates in the crystal structure.

In such stacked molecular aggregates both Coulombic as well as CT coupling would be present.⁴⁸ However, in order to ascertain which coupling is more prevalent than the other in MF1 and MF2, it is necessary to quantify the magnitude of these coupling constants, i.e. the CT coupling constant (J_CT) and Coulombic coupling constant (J_Coulomb). We have performed quantum chemical calculations (ESI, IIn†) to obtain the magnitudes of J_CT and J_Coulomb for both MF1 and MF2 and the values of both coupling constants have been tabulated below (Table 3).

Table 3 Quantum chemical estimation of J_CT and J_Coulomb for MF1 and MF2

MFs	J CT	J Coulomb
MF1	−0.6296	0.0028
MF2	−0.7083	0.0155

---

As can be seen from the above table, the magnitude of J_CT is much higher than J_Coulomb for both MF1 and MF2. In other words the magnitude of J_Coulomb is negligible in comparison to J_CT. A high (and negative) magnitude of J_CT confirms strong CT-mediated J-aggregation, in accordance with the literature report.⁴⁸ Thus, we can conclude that in the molecular aggregates of both MF1 and MF2, CT coupling is near-explicitly present and the extent of Coulombic coupling is negligible.

Experimental crystal structural evidence

From the single crystal structural analyses, in MF2, it is observed that the molecule is planar with anti-parallel stacking of the molecules with a slip-angle of 44.05° (Fig. 4g). In the crystal structure it is observed that the donor –NEt₂ moiety attached to the benzene ring is spatially quite close to the acceptor =C–(CN)₂ and forms a slip-stacked dimer with a vertical inter-planar distance of 3.40 Å (i.e. <4 Å) (Fig. 4g). These experimental crystal structural parameters are consonant with the literature reports of CT-mediated J-aggregation.^{47,49,51,57–59}

Absorption & excitation spectral evidence

In order to understand the nature of the aggregate in the thin film and in the crystal we have recorded the absorption (Fig. 4h) and PL excitation (PLE) spectra (Fig. 4i) of both the thin film and the crystal of MF2 and compared them with those obtained in hexane solvent. In hexane there is only one absorption band with the absorption maximum (λ^max_abs) at 454 nm (Fig. 4h). However, in the thin film, we observed two absorption bands with peaks at 412 nm and 520 nm (Fig. 4h). In the crystal also, we have observed two absorption bands with the peaks at 412 nm and 563 nm (Fig. 4h). The PLE spectrum in hexane has one band with the maximum at 453 nm (Fig. 4i). In the thin film the PLE spectrum has two bands with the peaks at 412 nm and 523 nm (Fig. 4i). The PLE spectrum of the crystal has two bands with the peaks at 412 nm and 570 nm (Fig. 4i). All these experimental observations clearly indicate that the S₁ state (observed in hexane) gets split into S₁⁺ and S₁⁻ states as expected for CT-mediated J-aggregation (Fig. 4a) and the transitions from S₀ state to both S₁⁻ and S₁⁺ states are quite feasible indicating CT-mediated J-aggregation in the thin film and crystal of MF2. The energy difference between these two states (ΔE_ES) has been calculated from both absorption (0.63 eV and 0.81 eV for the thin film and crystal respectively) and PLE (0.64 eV and 0.83 eV for the thin film and crystal respectively). Thus, not only we have observed CT-mediated J-aggregation in MF2, but we also have obtained a very significant magnitude of ΔE_ES and these values are comparable with those in the few literature reports obtained so far (Table S16†).^{47,49,51,57–59} We should note that the magnitude of ΔE_ES is higher in the crystal than in the thin film, as expected, indicating stronger aggregation in the crystal state than in the thin film.

PL decay dynamical evidence

Moreover, we have recorded the PL decay of MF2 in both the thin film and in the crystal and compared the same with that obtained in hexane (Fig. 4j). We would like to report how the CT-mediated J-aggregation affects the PL decay of MF2 strongly both in the thin film and in the crystal state. In comparison to hexane solvent, the PL decay in both the thin film and in the crystal becomes much slower. In the thin film and in the crystal, the τ has been obtained to be 21.39 ns and 30.90 ns, respectively, which is much longer than the τ obtained in hexane (5.98 ns). Thus, because of CT-mediated J-aggregation there is a gigantic enhancement of the τ, which is due to the restricted environment in the thin film and in the crystal (in comparison to the same in hexane), and thus, the extent of non-radiative decay gets reduced very significantly leading to huge enhancement of τ. Enhancement of τ in CT-mediated J-aggregates is in accordance with the other few literature studies reported to date (Table S16†).

Thus, all these quantum chemical, crystal structural as well as steady-state and time resolved optical spectroscopic results clearly indicate that there exists strong CT-mediated J-aggregation in the thin film and crystal of MF2. A comparison table of quantum chemical as well as experimental parameters obtained for the other molecule MF1 (Fig. S30 and Table S17†) and other literature reported molecules exhibiting CT-mediated J-aggregation are depicted in Table S16.†

Yellow and white LED generation

Employing a low-cost microcontroller board (Arduino-Uno) and open source electronic platform, it was possible to generate both yellow and white light LEDs with MF2 (Fig. 5a and b; for MF1 see Fig. S31a and d†).

Fig. 5 Intense (a) yellow and (b) white LEDs generated using MF2.

For MF2, the CIE (“Commission Internationale de l'Éclairage”) coordinates of a colour pure yellow LED were obtained to be (0.47, 0.51) with a correlated colour temperature (CCT) value of 3215 K (Fig. S32b and c†) (for MF1 see Fig. S31b, c and Table S18†). The CIE coordinates of a colour pure white LED using MF2 were obtained to be (0.32, 0.34), with a CCT value of 6073 K (Fig. S32e and f†) (for MF1 see Fig. S31e, f and Table S18†). These LEDs are very stable, and the intensity of yellow LEDs decreases by only ∼20%; whereas, the intensity of white LEDs doesn't show any significant decrease in intensity, even after continuous illumination for 12 hours (Fig. S33c and d; for MF1, see Fig. S33a and b†).

Conclusions

In conclusion, we report red emission in the crystal of an ultra-small MF (MW = only 197 Da) in comparison to the literature report of fluorophores with the lowest MW = 252 Da. Supramolecular extensive hydrogen-bonding and J-aggregate type centrosymmetric discrete-dimers or a 1D chain of MFs yielded red emission (λ^max_em = 610–636 nm) in the soft crystals of tiny MFs of MW = 197–225 Da. These tiny MFs exhibited 20 000 times enhanced τ in comparison to para-fluorophores having a similar MW (∼200 Da). Chemically similar MFs exhibit different crystal-structural properties. The MF1 crystal exhibits a 1D chain, whereas supramolecular extensive hydrogen-bonding and J-aggregate type centrosymmetric discrete-dimer nature is present in the MF2 crystal leading to a more red shifted emission (λ^max_em = 636 nm in MF2 against 610 nm in MF1), much higher ϕ (0.19 in MF2 against 0.06 in MF1), narrower PL emission (FWHM of 76 nm in MF2 against 85 nm in MF1) and much longer τ (30.90 ns in MF2 against 14.56 ns in MF1) for a tiny fluorophore of MW = 225 Da in the crystal. Nano-indentation studies reveal that both the MF crystals are soft in nature. Energy framework calculations distinctly show why these chemically similar MFs exhibit differential optical behaviours. Unlike the single absorption band observed in the solution phase, in both the thin film and crystal, two absorption bands are observed depicting the transitions from the S₀ state to both the S₁⁻ state and S₁⁺ state. Computationally, the angle between the TDMs of the monomers in the π-stacked dimers has been obtained to be 66.99°. The exciton splitting energy has been observed to be (−) 55.7 meV. The magnitudes of the overlap integral between the HOMOs and between the LUMOs were estimated to be 0.0068 and (−) 0.00024, respectively. Planar molecules involved in anti-parallel π-stacking exhibit a slip-angle of 44.05° and an inter-planar longitudinal distance of 3.40 Å. A significantly high magnitude of the energy gap between the S₁⁻ state and S₁⁺ state (ΔE_ES = 0.83 eV) has been obtained. A comparatively much higher magnitude of the CT coupling constant (−0.708 for MF2) in comparison to the Coulombic coupling constant (0.016 for MF2) has been noted. Upon going from the solution state to the crystal state, an about five times enhancement in the τ has been observed (5.98 ns (in hexane) to 30.90 ns (in the crystal)). All these observations clearly exhibit the existence of the CT-mediated J-aggregation phenomenon in the MF crystals, which is responsible for the extra-ordinary optical properties shown by these MF crystals. Based on these very interesting observations, highly stable, bright and colour pure white LEDs could be generated.

Data availability

The data supporting this article have been included as part of the ESI.†

Author contributions

PKM envisaged the project. MM and SM (Sukumar) synthesized and characterized the fluorophores, and performed spectroscopic studies in the solution phase. Solid state spectroscopic studies and LED application studies were performed by MM, SM (Sukumar), SG, SM (Saptarshi) and SM (Soumen). Crystal structural analyses were performed by MM, SM (Sukumar), AS and TC. Computational calculations were performed by MM, SM (Sukumar), MS and RP (under the supervision of MD). Crystal structure based interaction energy, RDG, etc., calculations were performed by SM (Sukumar), AS, MS and RD. Nanoindentation studies were performed in the group of CMR with the help of SB. MM, SM (Sukumar), CMR, MD, and PKM wrote the manuscript. All authors have gone through the manuscript and agreed upon this final version of the manuscript for submission.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

MD and PKM thank IISER Kolkata for financial help and instrumental facilities. Financial support from the SERB-DST India (Projects No. CRG/2019/003605 and CRG/2023/005125) and CSIR-India (Project No. 01/3133/23/EMR-II) is gratefully acknowledged (PKM). MM and TC thank CSIR-India, SM (Sukumar), SG, RP, SB, and SM (Soumen) thank DST-INSPIRE, AS thanks NPDF, MS thanks IISER Kolkata (IPDF), SM (Saptarshi) thanks IISER Kolkata, and RD thanks UGC-India, for their respective fellowships.

References

1. T. Chatterjee, M. Mandal, S. Mardanya, M. Singh, A. Saha, S. Ghosh and P. K. Mandal, Chem. Commun., 2023, 59, 14370–14386.
2. M. Mandal, T. Chatterjee, A. Das, S. Mandal, A. Sen, M. Ta and P. K. Mandal, J. Phys. Chem. C, 2019, 123, 24786–24792.
3. M. Mandal, T. Chatterjee, D. Roy, A. Das, C. K. De, S. Mandal, S. Ghosh, A. Sen, M. Ta and P. K. Mandal, J. Phys. Chem. C, 2020, 124, 27049–27054.
4. T. Chatterjee, D. Roy, A. Das, A. Ghosh, P. P. Bag and P. K. Mandal, RSC Adv., 2013, 3, 24021–24024.
5. T. Chatterjee, M. Mandal, V. Gude, P. P. Bag and P. K. Mandal, Phys. Chem. Chem. Phys., 2015, 17, 20515–20521.
6. T. Chatterjee, M. Mandal and P. K. Mandal, Phys. Chem. Chem. Phys., 2016, 18, 24332–24342.
7. T. Chatterjee, M. Mandal, A. Das, K. Bhattacharyya, A. Datta and P. K. Mandal, J. Phys. Chem. B, 2016, 120, 3503–3510.
8. T. Chatterjee, F. Lacombat, D. Yadav, M. Mandal, P. Plaza, A. Espagne and P. K. Mandal, J. Phys. Chem. B, 2016, 120, 9716–9722.
9. J. R. Lakowicz, Principles of Fluorescence Spectroscopy, Springer, New York, 3rd edn, 2006.
10. Z. R. Grabowski, K. Rotkiewicz and W. Rettig, Chem. Rev., 2003, 103, 3899–4032.
11. J. B. Grimm, B. P. English, J. Chen, J. P. Slaughter, Z. Zhang, A. Revyakin, R. Patel, J. J. Macklin, D. Normanno and R. H. Singer, et al. , Nat. Methods, 2015, 12, 244–250.
12. E. Kim, M. Koh, B. J. Lim and S. B. Park, J. Am. Chem. Soc., 2011, 133, 6642–6649.
13. H. Lu, J. Mack, Y. Yang and Z. Shen, Chem. Soc. Rev., 2014, 43, 4778–4823.
14. L. Yuan, W. Lin, K. Zheng, L. He and W. Huang, Chem. Soc. Rev., 2013, 42, 622–661.
15. H. Kobayashi, M. Ogawa, R. Alford, P. L. Choyke and Y. Urano, Chem. Rev., 2010, 110, 2620–2640.
16. A. S. Klymchenko, Acc. Chem. Res., 2017, 50, 366–375.
17. M. Shimizu, Y. Takeda, M. Higashi and T. Hiyama, Angew. Chem., Int. Ed., 2009, 48, 3653–3656.
18. B. Tang, C. Wang, Y. Wang and H. Zhang, Angew. Chem., Int. Ed., 2017, 56, 12543–12547.
19. B. Liu, Q. Di, W. Liu, C. Wang, Y. Wang and H. Zhang, J. Phys. Chem. Lett., 2019, 10, 1437–1442.
20. H. Liu, S. Yan, R. Huang, Z. Gao, G. Wang, L. Ding and Y. Fang, Eur. J. Chem., 2019, 25, 16732–16739.
21. Z. Xiang, Z. Y. Wang, T. B. Ren, W. Xu, Y. P. Liu, X. X. Zhang, P. Wu, L. Yuan and X. B. Zhang, Chem. Commun., 2019, 55, 11462–11465.
22. J. N. Zhang, H. Kang, N. Li, S. M. Zhou, H. M. Sun, S. W. Yin, N. Zhao and B. Z. Tang, Chem. Sci., 2017, 8, 577–582.
23. R. Huang, B. Liu, C. Wang, Y. Wang and H. Zhang, J. Phys. Chem. C, 2018, 122, 10510–10518.
24. R. Zhou, Y. Cui, J. Dai, C. Wang, X. Liang, X. Yan, F. Liu, X. Liu, P. Sun and H. Zhang, et al. , Adv. Opt. Mater., 2020, 8, 1902123–1902131.
25. Y. Hong, J. W. Y. Lam and B. Z. Tang, Chem. Soc. Rev., 2011, 40, 5361–5388.
26. J. Luo, Z. Xie, J. W. Y. Lam, L. Cheng, H. Chen, C. Qiu, H. S. Kwok, X. Zhan, Y. Liu and D. Zhu, et al. , Chem. Commun., 2001, 18, 1740–1741.
27. B. Liu, H. Liu, H. Zhang, Q. Di and H. Zhang, J. Phys. Chem. Lett., 2020, 11, 9178–9183.
28. A. Matsumoto, T. Tanaka, T. Tsubouchi, K. Tashiro, S. Saragai and S. Nakamoto, J. Am. Chem. Soc., 2002, 124, 8891–8902.
29. H. Liu, Z. Lu, Z. Zhang, Y. Wang and H. Zhang, Angew. Chem., Int. Ed., 2018, 57, 8448–8452.
30. M. J. Lin, Á. J. Jiménez, C. Burschka and F. Würthner, Chem. Commun., 2012, 48, 12050–12052.
31. M. Shimizu, R. Kaki, Y. Takeda, T. Hiyama, N. Nagai, H. Yamagishi and H. Furutani, Angew. Chem., Int. Ed., 2012, 51, 4095–4099.
32. C. A. Shen, D. Bialas, M. Hecht, V. Stepanenko, K. Sugiyasu and F. Würthner, Angew. Chem., Int. Ed., 2021, 60, 11949–11958.
33. A. Patra, L. J. Patalag, P. G. Jones and D. B. Werz, Angew. Chem., Int. Ed., 2021, 60, 747–752.
34. H. Jin, M. Liang, S. Arzhantsev, X. Li and M. Maroncelli, J. Phys. Chem. B, 2010, 114, 7565–7578.
35. S. Varughese, M. S. R. N. Kiran, U. Ramamurty and G. R. Desiraju, Angew. Chem., Int. Ed., 2013, 52, 2701–2712.
36. J. R. Morris, H. Bei, G. M. Pharr and E. P. George, Phys. Rev. Lett., 2011, 106, 165502.
37. U. Ramamurty and J. i. Jang, CrystEngComm, 2014, 16, 12–23.
38. C. Wei, L. Li, Y. Zheng, L. Wang, J. Ma, M. Xu, J. Lin, L. Xie, P. Naumov and X. Ding, et al. , Chem. Soc. Rev., 2024, 53, 3687–3713.
39. B. Bhattacharya, D. Roy, S. Dey, A. Puthuvakkal, S. Bhunia, S. Mondal, R. Chowdhury, M. Bhattacharya, M. Mandal and K. Manoj, et al. , Angew. Chem., Int. Ed., 2020, 59, 19878–19883.
40. G. R. Krishna, M. S. R. N. Kiran, C. L. Fraser, U. Ramamurty and C. M. Reddy, Adv. Funct. Mater., 2013, 23, 1422–1430.
41. W. C. Oliver and G. M. Pharr, J. Mater. Res., 1992, 7, 1564–1583.
42. F. Würthner, T. E. Kaiser and C. R. Saha-Möller, Angew. Chem., Int. Ed., 2011, 50, 3376–3410.
43. T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 48–76.
44. M. Kasha, H. R. Rawls and M. A. El-Bayoumi, Pure Appl. Chem., 1965, 11, 371–392.
45. S. J. Yoon, J. W. Chung, J. Gierschner, K. S. Kim, M. G. Choi, D. Kim and S. Y. Park, J. Am. Chem. Soc., 2010, 132, 13675–13683.
46. M. J. Turner, J. J. McKinnon, S. K. Wolff, D. J. Grimwood, P. R. Spackman, D. Jayatilaka and M. A. Spackman, CrystalExplorer17, University of Western Australia, 2017, http://hirshfeldsurface.net.
47. U. Mayerhöffer, K. Deing, K. Gruß, H. Braunschweig, K. Meerholz and F. Würthner, Angew. Chem., Int. Ed., 2009, 48, 8776–8779.
48. N. J. Hestand and F. C. Spano, J. Chem. Phys., 2015, 143, 244707.
49. J. Fang, P. Li, L. Zhang, X. Li, J. Zhang, C. Qin, T. Debnath, W. Huang and R. Chen, J. Am. Chem. Soc., 2024, 146, 961–969.
50. M. P. Lijina, A. Benny, E. Sebastian and M. Hariharan, Chem. Soc. Rev., 2023, 52, 6664–6679.
51. J. H. Kim, T. Schembri, D. Bialas, M. Stolte and F. Würthner, Adv. Mater., 2022, 34, 2104678.
52. N. J. Hestand and F. C. Spano, Chem. Rev., 2018, 118, 7069–7163.
53. N. J. Hestand and F. C. Spano, Acc. Chem. Res., 2017, 50, 341–350.
54. Z. Yang, Z. Mao, C. Xu, X. Chen, J. Zhao, Z. Yang, Y. Zhang, W. Wu, S. Jiao and Y. Liu, et al. , Chem. Sci., 2019, 10, 8129–8134.
55. Z. Mao, Z. Yang, C. Xu, Z. Xie, L. Jiang, F. L. Gu, J. Zhao, Y. Zhang, M. P. Aldred and Z. Chi, Chem. Sci., 2019, 10, 7352–7357.
56. E. G. McRae and M. Kasha, in The Molecular Exciton Model, Academic Press, New York, USA, 1964.
57. M. Gsänger, E. Kirchner, M. Stolte, C. Burschka, V. Stepanenko, J. Pflaum and F. Würthner, J. Am. Chem. Soc., 2014, 136, 2351–2362.
58. N. J. Hestand, C. Zheng, A. R. Penmetcha, B. Cona, J. A. Cody, F. C. Spano and C. J. Collison, J. Phys. Chem. C, 2015, 119, 18964–18974.
59. S. Wu, W. Zhang, C. Li, Z. Ni, W. Chen, L. Gai, J. Tian, Z. Guo and H. Lu, Chem. Sci., 2024, 15, 5973–5979.

---

Footnotes

† Electronic supplementary information (ESI) available. 2017383 and 2042111. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4sc06851c

‡ These authors contributed equally.

---