Open Access Article
Open Access ArticleGrappa – a machine learned molecular mechanics force field
Leif
Seute
*ab,
Eric
Hartmann
ab,
Jan
Stühmer
ac and
Frauke
Gräter
 *abd
*abd
aHeidelberg Institute for Theoretical Studies, Schloss-Wolfsbrunnenweg 35, 69118 Heidelberg, Germany. E-mail: leif.seute@h-its.org
bInterdisciplinary Center for Scientific Computing, Heidelberg University, INF 205, 69120 Heidelberg, Germany
cInstitute for Anthropomatics and Robotics, Karlsruhe Institute of Technology, Kaiserstr. 12, 76131 Karlsruhe, Germany
dMax Planck Institute for Polymer Research, Ackermannweg 10, 55128 Mainz, Germany. E-mail: graeter@mpip-mainz.mpg.de
First published on 15th January 2025
Abstract
Simulating large molecular systems over long timescales requires force fields that are both accurate and efficient. In recent years, E(3) equivariant neural networks have lifted the tension between computational efficiency and accuracy of force fields, but they are still several orders of magnitude more expensive than established molecular mechanics (MM) force fields. Here, we propose Grappa, a machine learning framework to predict MM parameters from the molecular graph, employing a graph attentional neural network and a transformer with symmetry-preserving positional encoding. The resulting Grappa force field outperforms tabulated and machine-learned MM force fields in terms of accuracy at the same computational efficiency and can be used in existing Molecular Dynamics (MD) engines like GROMACS and OpenMM. It predicts energies and forces of small molecules, peptides, and RNA at state-of-the-art MM accuracy, while also reproducing experimentally measured values for J-couplings. With its simple input features and high data-efficiency, Grappa is well suited for extensions to uncharted regions of chemical space, which we show on the example of peptide radicals. We demonstrate Grappa's transferability to macromolecules in MD simulations from a small fast-folding protein up to a whole virus particle. Our force field sets the stage for biomolecular simulations closer to chemical accuracy, but with the same computational cost as established protein force fields.
1 Introduction
In recent years, advances in geometric deep learning have led to the development of highly accurate machine learned force fields, reshaping the field of computational chemistry and Molecular Dynamics (MD) simulations. E(3) equivariant neural networks1–4 are capable of predicting energies and forces of small molecules to great accuracy with lower computational cost than quantum mechanical (QM) methods. However, these models are several orders of magnitude more expensive than Molecular Mechanics (MM) force fields, which employ a simple physics-inspired functional form to parametrize the potential energy surface of a molecular system, hence trading off accuracy in favor of efficiency. For MD simulations of large systems such as proteins and polynucleotides, MM force fields are well established and widely used. Established MM force fields rely on lookup tables with a finite set of atom types characterized by chemical properties of the atom and its bonded neighbors for parameterization. Recently, Espaloma5 and GB-FFs6 have demonstrated that machine learning can be used to increase the accuracy of MM force fields by learning to assign parameters based on a graph representation of the molecule with chemical properties that rely on expert knowledge, such as orbital hybridization states or formal charge, as input features.In this work, we propose a novel machine learning framework, Grappa (Graph Attentional Protein Parametrization), to learn MM parameters directly from the molecular graph, improving accuracy on a broad range of chemical space and eliminating the need for hand-crafted features. Grappa employs a graph attentional neural network to construct atom embeddings capable of representing chemical environments based on the 2D molecular graph, followed by a transformer7 with symmetry-preserving positional encoding. Since MM parameters only have to be predicted once per molecule, Grappa can be incorporated into highly optimized MM engines such as GROMACS8 and OpenMM.9 This allows energy and force evaluations with the same computational cost as traditional force fields, at state-of-the-art MM accuracy.
We show that Grappa outperforms traditional MM force fields and the machine-learned MM force field Espaloma on the Espaloma dataset,10 which contains over 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules and more than one million conformations, covering small molecules, peptides and RNA. We evaluate the potential energy landscape of dihedral angles of peptides, where we find that Grappa can match the performance of Amber FF19SB without requiring CMAPs and closely reproduces experimentally measured J-couplings. We also show that Grappa improves upon the calculated folding free energy of the small protein chignolin. To the best of our knowledge, Grappa is the first machine learned MM force field that uses no hand-crafted chemical features, allowing facile extension to uncharted regions of chemical space, which we demonstrate on the example of peptide radicals. Grappa is transferable to individual macromolecules and assemblies such as proteins and viruses, which exhibit similar dynamics as established force fields. Starting from an unfolded initial state, MD simulations of small proteins parametrized by Grappa recover experimentally determined folding structures of small proteins, suggesting that Grappa captures the physics underlying protein folding. We demonstrate the efficiency of Grappa, which is inherited from MM, by simulating a system of one million atoms with the proposed force field on a single GPU, with a similar number of timesteps per second as a highly performant E(3) equivariant neural network1 on over 4000 GPUs.
000 molecules and more than one million conformations, covering small molecules, peptides and RNA. We evaluate the potential energy landscape of dihedral angles of peptides, where we find that Grappa can match the performance of Amber FF19SB without requiring CMAPs and closely reproduces experimentally measured J-couplings. We also show that Grappa improves upon the calculated folding free energy of the small protein chignolin. To the best of our knowledge, Grappa is the first machine learned MM force field that uses no hand-crafted chemical features, allowing facile extension to uncharted regions of chemical space, which we demonstrate on the example of peptide radicals. Grappa is transferable to individual macromolecules and assemblies such as proteins and viruses, which exhibit similar dynamics as established force fields. Starting from an unfolded initial state, MD simulations of small proteins parametrized by Grappa recover experimentally determined folding structures of small proteins, suggesting that Grappa captures the physics underlying protein folding. We demonstrate the efficiency of Grappa, which is inherited from MM, by simulating a system of one million atoms with the proposed force field on a single GPU, with a similar number of timesteps per second as a highly performant E(3) equivariant neural network1 on over 4000 GPUs.
1.1 Molecular mechanics
In MM, the potential energy of a system with a given molecular graph is expressed as a sum of contributions from different interactions. Bonded interactions are described by functions of E(3)-invariant internal coordinates such as the lengths rij of bonds between two atoms, angles θijk between three consecutive atoms and dihedrals ϕijkl of two planes spanned by four atoms. For the dihedrals, one considers interactions between four atoms that are either consecutively bonded (torsions) or where three atoms are bonded to a central atom, often referred to as impropers, which are used to maintain planarity of certain chemical groups. One commonly uses harmonic potentials for bond stretching and angle bending and a periodic function for the dihedral potential. The potential energy of all interactions along bonds then is given by | (1) |
| ξ ≡ {ξij…(l)|l ∈ {bonds, angles, torsions, impropers}}. | (2) |
For the periodic dihedral potential, a common choice is a Fourier series with the constraint that the dihedral potential is extremal at and symmetric around zero, which eliminates the need for sine terms. Additionally, atom pairs that are not included in such N-body bonded interaction terms contribute to the potential energy through pairwise nonbonded interaction, typically described by Lennard-Jones and Coulomb potentials.
Traditional MM force fields define a finite set of atom types determined by hand-crafted rules, which are used to assign the free parameters {kij, r(0)ij, …} based on lookup tables for possible combinations of atom types. In Grappa, we replace this scheme by learning the parameters from the molecular graph directly, which allows for a more flexible and transferable description of the potential energy surface.
A fundamental limitation of standard MM is the assumption of a constant molecular graph topology, which is enforced by the use of harmonic bond potentials. While this restricts accuracy and prohibits the description of bond-changing chemical reactions, the physical interpretability of the potential energy function ensures that simulated systems remain stable, even in states that are poorly described by the force field. Grappa builds on this advantage, and also inherits the superb efficiency that MM force fields achieve through this assumption.
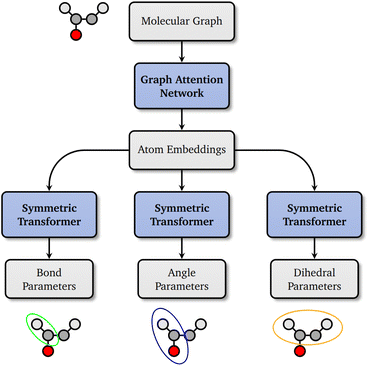
2 Grappa
Inspired by the atom typing with hand-crafted rules in traditional MM force fields and in analogy to Wang et al.,5 Grappa first predicts d-dimensional atom embeddings, | (3) |
 , where the set of nodes
, where the set of nodes  represents the atoms and the set of edges
represents the atoms and the set of edges  represents the bonds. In a second step (Fig. 1), for each interaction type l MM parameters ξ(l) are predicted from the embeddings of the atoms involved in the respective energy contribution,
represents the bonds. In a second step (Fig. 1), for each interaction type l MM parameters ξ(l) are predicted from the embeddings of the atoms involved in the respective energy contribution,| ξij…(l) = ψ(l)(νi, νj, …), | (4) |
| E(x) = EMM(x, ξ). | (5) |
Since the mapping from molecular graph to energy is differentiable with respect to the model parameters and spatial positions, it can be optimized on predicting QM energies and forces end-to-end, as visualized in Fig. 3. Notably, the machine learning model prediction does not depend on the spatial conformation of the molecule, thus it has to be evaluated only once per molecule and the computational cost of each subsequent energy evaluation is given by the MM energy functional.
Grappa currently only predicts bonded MM parameters since we expect that nonbonded interactions are not covered sufficiently by the monomeric datasets used for training, rendering the nonbonded parameters underdetermined. The nonbonded parameters are taken from established MM force fields that can reproduce solute interactions and melting points, which we expect to be strongly dependent on nonbonded interactions.
2.1 Permutation symmetries in MM
For the mapping from atom embeddings ν to MM parameters, we postulate certain permutation symmetries that the model should respect. To derive these symmetries, we consider the energy function of MM as a decomposition into contributions from subgraphs of the featurized molecular graph that correspond to bonds, angles, torsions and improper dihedrals. We demand invariance of the energy contribution under node permutations that induce isomorphisms of the respective subgraph. For bonds, angles and torsions, these permutations leave the respective spatial coordinate invariant, thus we can achieve invariance of the energy contribution by demanding invariance of the MM parameters,| ξ(bond)ij = ξ(bond)ji, | (6) |
| ξ(angle)ijk = ξ(angle)kji, | (7) |
| ξ(torsion)ijkl = ξ(torsion)lkji. | (8) |
For improper dihedrals, however, not all subgraph isomorphisms leave the dihedral angle invariant and demanding parameter invariance under those permutations would lead to an energy contribution that is not invariant. In Grappa, we solve this problem by decomposing the improper torsion contributions into three terms, as described in Section A.4.
2.2 The Grappa architecture
To predict atom embeddings from the molecular graph, Grappa employs a graph attentional neural network inspired by the transformer architecture.7 Multi-head dot-product attention on graph edges11 is followed by feed-forward layers with residual connections12 and layer normalization,13 which has been demonstrated to enhance the expressivity of attention layers.14For the map from these embeddings to MM parameters, it is desirable to use an architecture that respects the permutation symmetries (eqn (6)–(8)) by design, constraining the space of possible models to those that are physically sensible. In the proposed symmetric transformer architecture, we use permutation equivariant layers followed by final symmetric pooling. However, since we do not require invariance under all permutations but only under permutations as defined in eqn (6)–(8), we can increase expressivity by allowing the model to break symmetries that are not required.
Following these considerations, we use multi-head dot-attention layers, which are permutation equivariant by design, and introduce a positional encoding that is invariant under the required permutation symmetries but can break others. For example for angles, this positional encoding is given by
 | (9) |
 ,
, | (10) |
 -invariant output to obtain parameter scores z. We call this combination of permutation invariant positional encoding with permutation equivariant layers and symmetric pooling the symmetric transformer, which is illustrated in Fig. 2. The symmetric transformer can be generalized to permutation symmetries of arbitrary subgraphs by using the eigenvectors of the graph Laplacian15 as positional encoding.
-invariant output to obtain parameter scores z. We call this combination of permutation invariant positional encoding with permutation equivariant layers and symmetric pooling the symmetric transformer, which is illustrated in Fig. 2. The symmetric transformer can be generalized to permutation symmetries of arbitrary subgraphs by using the eigenvectors of the graph Laplacian15 as positional encoding.
 | ||
| Fig. 3 Grappa predicts one set of parameters per molecule. With the MM energy functional (eqn (5)), the parameters can be mapped to energies and forces of given conformations, whose deviation from the ground truth (QM) is minimized during training. Functions are represented in blue, conformation-specific quantities in green and molecule-specific quantities in grey. | ||
Finally, we map the scores z to the range of physically sensible parameters, e.g. (0, ∞) for bond and angle force constants or (0, π) for equilibrium angles θ(0). To this end, we use scaled and shifted versions of ELU and the sigmoid function as described in A.2.3. While one could also use the exponential for mapping to (0, ∞), ELU's linear behaviour towards large inputs is favorable for producing stable gradients during optimization. With the scaling we ensure that a normally distributed output of the neural network is mapped to a distribution with mean and standard deviation that is suitable for the respective MM parameter, which can be seen as a normalization technique.13 For predicting dihedral parameters ξijkl, we use a sigmoid gate, which allows the model to suppress dihedral modes that are not needed.
As input feature, we use one-hot encodings of the atomic number, the number of neighbors of the respective node and membership in loops of length 3 to 8, which can be directly calculated from the molecular graph. The assignment of nonbonded MM parameters is done using a traditional force field of choice. Since the bonded parameters predicted by Grappa may depend on the scheme by which nonbonded parameters are assigned, we pass the partial charge of each atom as input feature to Grappa, which also allows to encode the total charge of a molecule without breaking graph symmetries as one would potentially do by assigning atomwise formal charges instead.
2.3 Training
We train Grappa to minimize the mean squared error (MSE) between QM energies EQM and forces −∇xEQM, whose contribution we weight by the hyperparameter λF, and its prediction, E and ∇xE respectively, which includes the non-learnable nonbonded contribution. At the start of training, we also include the deviation of predicted bond, angle and torsion MM parameters to those of a given traditional force field, weighted by λtrad and, for regularization, the L2 norm of dihedral MM parameters ξ(dih)ijkl, weighted by λdih as in ref. 10. That is, we use the loss function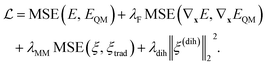 | (11) |
Since MM can only predict energy differences of states, not formation energies, we subtract the mean of target and predicted energies for each molecule. As shown previously for other machine learned force fields,4,16 we find training on forces −∇xE in addition to energies important also in our setting, for two reasons. First, the energy is a global, pooled quantity and thus less expressive than the forces, which are local and by a factor of 3N more numerous. Second, as shown in,17 learning derivatives of the target with respect to the input can lead to improved generalization and data efficiency, effectively smoothing the learned potential energy surface. Details on the training procedure and hyperparameters can be found in A.3.
3 Results and discussion
3.1 Grappa is state-of-the-art
To demonstrate that Grappa is the current state-of-the-art MM force field in terms of accuracy, we train and evaluate a Grappa model on the dataset reported in the follow-up paper10 to Espaloma, which contains 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 427 unique molecules and over one million conformations. Our training and test partition is identical with the one from Espaloma, where the molecules were divided into 80% training, 10% validation and 10% test set, based on isomeric SMILES strings. The dataset covers small molecules, peptides and RNA with states sampled from the Boltzmann distribution at 300 K and 500 K, from optimization trajectories and from torsion scans. The nonbonded contribution is calculated using the OpenFF-2.0.0 force field18 and partial charges from the AM1-BCC method, as in Espaloma. We train the model for 1000 epochs on an A100 GPU, which takes about one day.
427 unique molecules and over one million conformations. Our training and test partition is identical with the one from Espaloma, where the molecules were divided into 80% training, 10% validation and 10% test set, based on isomeric SMILES strings. The dataset covers small molecules, peptides and RNA with states sampled from the Boltzmann distribution at 300 K and 500 K, from optimization trajectories and from torsion scans. The nonbonded contribution is calculated using the OpenFF-2.0.0 force field18 and partial charges from the AM1-BCC method, as in Espaloma. We train the model for 1000 epochs on an A100 GPU, which takes about one day.
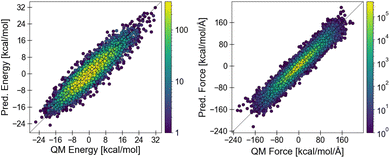
For all types of molecules, Grappa outperforms established MM force fields and Espaloma in terms of energy and force accuracy on Boltzmann-sampled states as shown in Table 1 and Fig. 4a. While the Boltzmann samples are the more relevant benchmarking data for using Grappa in MD simulations, we also evaluate it on torsion scans and optimization trajectories (Table 7). There, we find Grappa and Espaloma to be competitive, while Grappa is more accurate for forces and less accurate for energies. Grappa also outperforms the baselines if only trained on a fraction of Espaloma's training set (Fig. 19), indicating high data efficiency.
| Dataset | Test mols | Confs | RMSE | Grappa | Espaloma | Gaff-2.11 | ff14SB, RNA.OL3 | Mean predictor |
|---|---|---|---|---|---|---|---|---|
| SPICE-PubChem | 1411 | 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 853 853 |
Energy | 2.3 | 2.3 | 4.6 | 18.4 | |
| Force | 6.1 | 6.8 | 14.6 | 23.4 | ||||
| SPICE-DES-Monomers | 39 | 2032 | Energy | 1.3 | 1.4 | 2.5 | 8.2 | |
| Force | 5.2 | 5.9 | 11.1 | 21.3 | ||||
| SPICE-Dipeptide | 67 | 2592 | Energy | 2.3 | 3.1 | 4.5 | 4.6 | 18.7 |
| Force | 5.4 | 7.8 | 12.9 | 12.1 | 21.6 | |||
| RNA-Diverse | 6 | 357 | Energy | 3.3 | 4.2 | 6.5 | 6.0 | 5.4 |
| Force | 3.7 | 4.4 | 16.7 | 19.4 | 17.1 | |||
| RNA-Trinucleotide | 64 | 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 811 811 |
Energy | 3.5 | 3.8 | 5.9 | 6.1 | 5.3 |
| Force | 3.6 | 4.3 | 17.1 | 19.7 | 17.7 |
Chemical properties based on expert knowledge, e.g. hybridization and aromaticity, have long been used to assign MM parameters,18,19 also when those are machine-learned.5,10 With Grappa, we show that accurate MM parameters can be predicted directly from the molecular graph, without relying on hand-crafted chemical input features.
3.2 Grappa is extensible across chemical space
If a certain kind of chemistry is not part of the training set of a machine learned force field, predictions can go awry. While the current datasets already cover a significant part of chemical space, extensions should be straightforward and accessible. To demonstrate Grappa's extensibility to rather uncommon molecules, we train it on peptide radicals, which play a role in enzyme catalysis23 and as mechanoradicals24 and for which we generate a dataset as described in A.5.In Table 2, we report the accuracy of Grappa on a test set of unseen peptide radicals with and without training on other peptide radicals. Grappa can, indeed, learn to predict more accurate parameters for radicals. Additionally, we demonstrate that Grappa can learn the effect of radical atoms on optimized geometries with an example of an alanine radical in Fig. 5. We report no baseline values since, to the best of our knowledge, Grappa is the first MM force field that covers this part of chemical space. On the other datasets from Espaloma, Grappa remains competitive, as can be seen in Table 8.
| RMSE | Grappa-radicals | Grappa | Mean predictor |
|---|---|---|---|
| Energy | 3.1 ± 0.3 | 4.1 ± 0.3 | 7.0 ± 0.5 |
| Force | 8.5 ± 0.2 | 13.6 ± 0.3 | 40.6 ± 1.2 |
The extension to peptide radicals indicates that Grappa can learn new chemistries accurately without negatively affecting the performance on the original datasets. Due to Grappa's limited complexity of input features – only connectivity, atomic numbers and partial charges – the chemical space accessible for parameterization is vast. As long as a molecule has a fixed connectivity and the MM energy functional is a reasonable approximation, Grappa can be trained to predict parameters for it. For extending machine learned force fields to new chemistries, it is usually required to generate additional training data. Grappa's high data efficiency (Fig. 19) suggests that it requires less of such additional training data than other machine learned MM force fields.
3.3 Grappa is compatible with multiple nonbonded parameter schemes
In order to make Grappa compatible with partial charges from the popular ff99SB25 and CHARMM36 (ref. 26) protein force fields, we calculate the nonbonded contributions of these force fields for the SPICE-Dipeptides and Protein-Torsion datasets used only with the contribution from AM1-BCC charges in Espaloma. We train Grappa on the resulting dataset, incentivizing it to predict bonded parameters that can be combined with the respective partial charges, which it receives as input as described in Section 2.2.We conduct an ablation study on the effect of using different nonbonded parameters on the accuracy of Grappa on the SPICE-Dipeptides dataset (Table 3). We find that, in combination with either of the charge models above, Grappa can predict energies and forces of dipeptides to higher accuracy than established force fields (Table 1), even if only trained on AM1-BCC charges. Training Grappa to be compatible with nonbonded contributions from ff99SB and CHARMM36 improves its accuracy to the same level as achieved with AM1-BCC charges. In practice, this means that Grappa can be used in existing workflows where proteins are parametrized with the established protein force fields ff99SB and CHARMM36 by overwriting bonded parameters in the resulting topology.
| Nonbonded parameters | RMSE | Grappa | Grappa-base |
|---|---|---|---|
| AM1BCC | Energy | 2.4 ± 0.1 | 2.4 ± 0.1 |
| Force | 5.5 ± 0.1 | 5.6 ± 0.1 | |
| ff99SB | Energy | 2.3 ± 0.1 | 2.6 ± 0.1 |
| Force | 5.5 ± 0.1 | 6.1 ± 0.1 | |
| CHARMM36 | Energy | 2.5 ± 0.1 | 3.1 ± 0.1 |
| Force | 5.5 ± 0.1 | 6.4 ± 0.1 |
3.4 Grappa reproduces known features of relaxed dihedral scans
Protein dynamics are largely governed by the free energy landscape of the backbone dihedral angles ϕ and ψ. While Grappa achieves a high accuracy with respect to vacuum QM energies on the Protein-Torsion test set (Table 8), we also investigate its free energy landscape by performing relaxed dihedral scans of the Ace–Ala–Nme peptide with implicit solvent and compare with Amber ff14SB and Amber ff19SB (Fig. 6).27In several regions, Grappa's energy profile resembles that of Amber ff19SB, which was found to be in good agreement with the QM profile.27 For example, the diagonal shape and extension of the αr helix basin at (ϕ, ψ) = (−80°, −20°) and the minimum in the α helix – β sheet transition region (−90°, 80°) are captured by Grappa without requiring CMAPs, which were specifically fitted on the respective QM profile in the case of Amber ff19SB. We investigate further how Grappa achieves this behaviour (Fig. 16). Grappa not only tunes the parameters of the dihedrals involved, but also those of neighboring dihedrals and angles, which we find to have a significant contribution to the dihedral free energy landscape. This indicates that learning all parameters at once, as in Grappa and Espaloma, has important advantages over fitting individual parameters separately as commonly done for established force fields.
3.5 All bonded interactions have a large potential for improvement
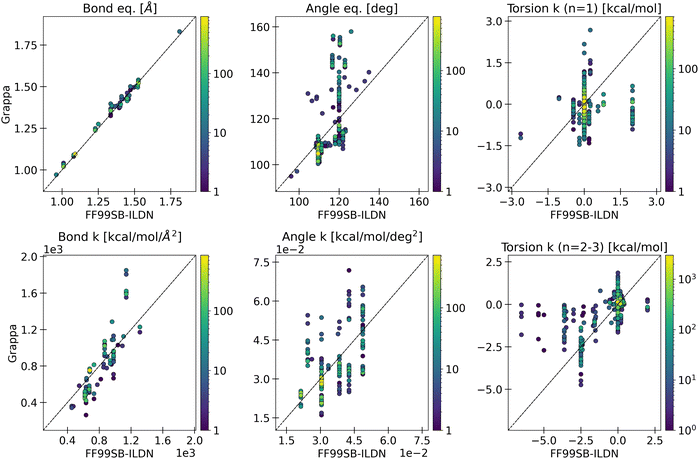
Grappa's modular formulation allows for learning only a certain type of interaction while keeping the others fixed to those of an established force field. To quantify the improvement of Grappa over the widely used protein force field Amber ff99SB-ILDN,25 we train Grappa models that predict only certain types of MM parameters and evaluate their accuracy in Table 4.| Learnable interaction | RMSE | |||
|---|---|---|---|---|
| Bond | Angle | Dihedral | Energy | Force |
| ✓ | ✓ | ✓ | 2.5 | 5.9 |
| ✓ | ✓ | 3.0 | 6.1 | |
| ✓ | 3.9 | 7.4 | ||
| ✓ | 3.8 | 9.2 | ||
| ✓ | 3.5 | 11.0 | ||
| 4.1 | 11.8 | |||
For each interaction, replacing the ff99SB-ILDN parameters with those predicted by Grappa improves the energy RMSE. The extent of this improvement varies to some extent, with dihedral interactions having a low and the bond interaction the highest impact on the force RMSE. Taken together, we show that complementing ff99SB-ILDN with Grappa parameters for either type of bonded interaction improves the accuracy of the resulting force field compared to ff99SB-ILDN.
3.6 Grappa is interpretable
3.7 A tabulated Grappa protein force field
Trust in a particular force field grows over several benchmark and application studies during which the strengths and limitations become clear.28,29 To facilitate the comparison with tabulated force fields, as well as to provide a force field with a low barrier to entry, we construct a reduced tabulated protein force field from Grappa. The resulting force field has unique, independent parameters for every residue and for interresidue bonded interactions. Details on the construction of the tabulated force field can be found in A.7.On a test dataset of dipeptides sampled at 300 K, the tabulated force field has an RMSE of 2.6 kcal mol−1 for the energy and 6.0 kcal mol−1 Å−1 for forces (Fig. 15). In the tabulated case, the parameters depend only on the residues involved in the bonded interaction, whereas in Grappa, the same residue may have different parameters depending on the sequence context. With the current hyperparameters (Table 5), Grappa's field of view on the molecular graph includes all atoms reachable within seven bonds and can thus reach beyond the residues of atoms involved in the bonded interaction. For the investigated dipeptide dataset, this increased field of view only has a marginal effect on energy and force RMSE, corroborating the efficiency of tabulated force fields for regular polymers such as proteins.
With the tabulated Grappa force field, we provide a highly accurate force field with fixed parameters that can be used and analyzed the very same way as traditional force fields.
4 Force field validation
Especially for large biomolecules, force fields are not only required to predict energies and forces as accurately as possible, but their predictions should behave in such a way that certain macroscopic properties such as stability and consistency with experimentally determined folding states are fulfilled in MD simulations. Grappa is well suited to overcome the gap between empirically validated, established protein force fields and machine learned force fields.In this section, we demonstrate that Grappa is on par with established force fields when it comes to MD simulations of proteins over timescales of hundreds of nanoseconds and that it captures the physics that cause stability of protein folds. All simulations mentioned in this section were performed with GROMACS, for which the Grappa package† provides a command line interface, briefly described in A.1. Using this interface (or a similar one for OpenMM), large biomolecular systems with over 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms are parameterized within minutes on a CPU (Fig. 11).
000 atoms are parameterized within minutes on a CPU (Fig. 11).
4.1 Grappa keeps large proteins stable during MD
A basic check for a protein force field is if a native protein structure remains stable over time during an MD simulation. QM methods and E(3) equivariant neural networks suffer from the problem that while their end-to-end predictions are accurate, they might fail in yielding stable simulations because of diverging gradients of the potential energy surface when extrapolating beyond regions covered by the training dataset. Particularly over long timescales, the system might drift out of the range of validity of the model and small errors might accumulate, leading to instabilities of the system and a potential crash of the simulation. MM with its interpretable, physics-inspired energy function, with parameters that are conformation-independent, ensures a higher degree of stability, and we indeed did not observe simulation crashes.However, since it is not ensured a priori that macrostates such as protein folds remain stable during MD, we next assess Grappa's capability of keeping protein folds close to their experimentally determined structure. As example system, we use ubiquitin (PDB ID: 1UBQ), which is a protein with 76 amino acids whose fold contains a beta-sheet and an alpha-helix. We perform a 200 nanoseconds MD simulation of ubiquitin in aqueous solution with Grappa and Amber ff99SB-ILDN,25 for which details are given in A.8.3. We find that the C-alpha RMSD from the initial state is bounded by about 4 Å in 200 ns simulation with both Grappa and Amber ff99SB-ILDN (Fig. 7c), indicating that the folded state of the protein is stable. Structural fluctuations on timescales of up to 2 ns are of similar magnitude (Fig. 7b).
4.2 Grappa reproduces the experimental folding free energy of a small protein
In order to assess Grappa's capability of capturing the physics responsible for protein folding, we simulate a variant of the small protein chignolin (CLN025) at its melting temperature of 340 K, where its folding free energy is expected to be zero, with ff99SB nonbonded parameters and TIP3P water.30 During two simulations of 4 μs length, we observe multiple folding and unfolding events (Fig. 8b) and obtain a calculated folding free energy of −3.0 kT, which is closer to the experimental reference than the value of −4.0 kT reported by Shabane et al.31 for Amber ff99SB with the same water model. The improvement is achieved by tuning only intramolecular bonded parameters, however, the choice of protein nonbonded parameters32,33 has a sizeable impact on MD-derived folding free energies and is a potential source for further improvement.Moreover, clustering structures from the simulations by their Cα distances shows that the central structure of the most populated cluster is in good agreement with the experimentally determined structure34 with a Cα RMSD of 0.77 Å (Fig. 8a, right).
4.3 Grappa reproduces experimental peptide J-couplings
Having observed improved accuracy of Grappa with respect to quantum mechanical energies and forces, the question remains whether this translates to stronger agreement with experimental ensemble properties compared to other MM force fields. J-Couplings, which are measurable with NMR, can serve as such test property as they can also be calculated from the statistics of dihedral angles obtained in MD simulation via the Karplus equation and have been target of extensive force field refinement.20,27,33We validate Grappa on a J-coupling benchmark dataset consisting of 13 small peptides at pH 2 (ref. 35–39) and find that Grappa with nonbonded parameters from ff99SB achieves a slightly lower χ2 and RMSE than Espaloma with AM1-BCC charges and much better performance than the established ff14SB force field (Fig. 9a).
For one of the peptides from the benchmark, Ala–Ala–Ala with protonated C-terminus, we also show the dihedral free energy landscape of the compared force fields, calculated by the statistics of visited states during 1.5 μs of simulation in Fig. 9b. Both Espaloma and Grappa show an increased sampling of transition regions consistent with recent improvements on peptide backbone parameters.27
4.4 Grappa can be finetuned for challenging molecules
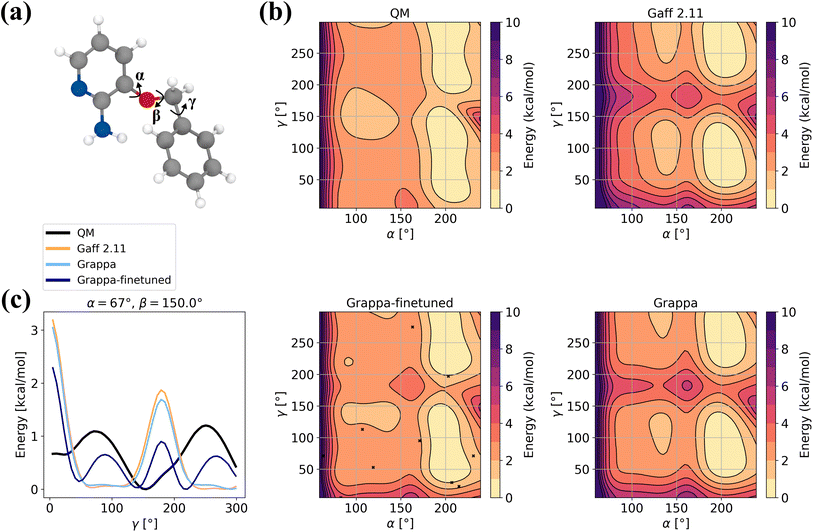
In order to assess Grappa's performance on challenging molecules where applicability of molecular mechanics is limited, we evaluate it on the 3BPA dataset40 of states of the drug-like molecule 3-(benzyloxy)pyridin-2-amine (Fig. 10a), which was used to test the extrapolation capability of the E(3) equivariant model MACE.2 Since the Espaloma dataset used for training Grappa does not contain 3BPA, we also report the values for a Grappa model that was finetuned on states sampled with MD at 300 K, as in ref. 2 and 40. Additionally, we include 10 states from the relaxed β = 150° dihedral slice. | ||
| Fig. 10 Example for finetuning Grappa. (a) The 3BPA molecule with the dihedral angles α, β and γ. (b) Potential energy along the gamma dihedral for fixed α and β and relaxed other degrees of freedom as described in ref. 40. (c) Potential energy on the relaxed β = 180° slice. We subtract the minimal energy on the slice for each force field. | ||
We find that while Grappa achieves similar performance as the established force field Gaff-2.11 without additional training, it can be finetuned to capture more intricate characteristics of the potential energy surface of the β = 180° slice (Fig. 10b and c) that are not represented by Gaff-2.11. We note that in order to perform well not only on Boltzmann-sampled states but also on relaxed dihedral slices, it is necessary to include a few relaxed states from other slices, which we investigate further in Appendix A.9. In Table 6, we also report accuracies for different temperatures and more slices, where we find that Grappa outperforms Gaff-2.11 in terms of energy and force RMSE even without finetuning.
4.5 Grappa is orders of magnitude more resource-efficient than E3 equivariant models
Efficiency of force fields is crucial; otherwise the computational cost for simulating large systems on long timescales can prohibit their application in simulations of many systems of interest. To demonstrate Grappa's efficiency, which it inherits from molecular mechanics, and to also showcase its capability of jointly parametrizing RNA and proteins, we simulate the virus STMV41 in solution – a system with approximately one million atoms, visualized in Fig. 14a. For this system simulated with Grappa, we measure a performance of 101 timesteps per second on a single A100 GPU in GROMACS8 without system-specific optimizations.A recently proposed machine learned force field relying on an E(3) equivariant neural network with state-of-the-art accuracy and efficiency, Allegro,1 has been shown to be capable of performing near-quantum-accuracy simulations of systems of unprecedented size. This is achieved by using a strictly local architecture, which allows parallelization across thousands of GPUs. Since they are not constrained by the energy functional of MM, E(3) equivariant models like Allegro, NequIP42 or MACE2 have greatly improved accuracy but are orders of magnitude more expensive than MM force fields like Grappa. For the system at hand, Allegro reports a performance of 106 timesteps per second on 4000 A100 GPUs.43 Hence, at reduced accuracy and incapable of describing topological changes directly, Grappa has more than three orders of magnitude higher efficiency than Allegro for simulating the example system.
5 Conclusions
With Grappa, we propose a machine learning framework for molecular mechanics force fields with state-of-the-art accuracy that can be used seamlessly in established MD engines. Our validations show that Grappa reproduces experimental results and is transferable to large biomolecules like proteins and viruses, which sets the stage for large scale simulations at improved accuracy, with the same computational efficiency as established MM force fields.Unlike most traditional MM force fields, Grappa is not specialized to a certain chemical species, but offers consistent parameterization of molecules with different chemistries, such as a wide range of small molecules, peptides and nucleotides, with a single model at a higher level of accuracy than previous MM force fields. Grappa not only enhances existing parameter sets, but also reaches previously inaccessible regions of chemical space, such as non proteinogenic amino acids or protein radicals.
Since current state-of-the-art E(3) equivariant neural network potentials like Allegro and MACE are several orders of magnitude more expensive than molecular mechanics and might also be less robust under large perturbations as for example in high temperature simulations, we regard machine learned molecular mechanics approaches like Grappa as suitable method for simulating large systems, especially if computational resources are limited or when it is not necessary to simulate all parts of a system at quantum accuracy.
6 Outlook
While Grappa achieves high computational efficiency through molecular mechanics, it also inherits its fundamental limitations, including restricted accuracy and the inability to directly describe chemical reactions. However, Grappa is well suited for efficient reparametrization of large molecules that undergo local topological changes induced by chemical reactions, e.g. in kinetic Monte Carlo simulations.44 This is due to both, Grappa's finite field-of-view, which ensures locality on the molecular graph, as well as the lack of hand-crafted chemical features, which allows to apply the parametrization to cut-out regions of molecules.Grappa is a general and versatile framework to obtain MM parameters for a broad range of molecules and can be seamlessly extended to new chemistries, lowering the barrier for simulating rarely studied systems that have been neglected due to the absence of established MM parameters. To this end, the Grappa package implements workflows for retraining on the provided and custom new datasets.
While we consider the consistency with established nonbonded parameters an advantage of Grappa, an extension of the framework to nonbonded parameters is a straightforward next step. It would render Grappa fully independent from traditional MM force fields and could potentially improve its accuracy further.
Data availability
Grappa is released as open source software under the GNU General Public License v3.0‡ along with the Grappa dataset and SMILES strings used for the train–val–test partition and configuration files to reproduce Table 1. A repository for creating the radical peptide and dipeptide datasets§ is publicly available. All results reported in the validation section were obtained with Grappa-1.4.0.Author contributions
Leif Seute: methodology, conceptualization, software, writing – original draft, investigation, visualization, data curation. Eric Hartmann: conceptualization, software, verification, visualization, writing – review and editing. Jan Stühmer: formal analysis, writing – review and editing. Frauke Gräter: supervision, conceptualization, writing – review and editing.Conflicts of interest
There are no conflicts to declare.A Appendices
A.1 The Grappa package
Grappa utilizes PyTorch45 and DGL46 in its implementation. The package is released as open source software under the GNU General Public License v3.0 and is available on GitHub¶ and on PyPi:pip install torch -f https://download.pytorch.org/whl/cpu
pip install grappa-ff.
It brings a command line interface to reparametrize a GROMACS topology file obtained from a traditional force field:
grappa_gmx -f topol.top -o new_topol.top.
For OpenMM, we provide a class that can be used to reparametrize a system with Grappa:
Pretrained released models can be accessed by using a tag; the model weights are downloaded automatically from the respective release on GitHub. Released models also contain a dictionary with results on test datasets, a list of identifiers for molecules used for training and validation and a configuration file to reproduce training on the same dataset. Further details on the package can be found on GitHub .
A.2 Model architecture
In this section, we provide a detailed description of the architecture of Grappa, including the graph attentional neural network and the symmetric transformer.After initializing the node features νi as described below, we apply a single nodewise linear layer followed by an exponential linear unit (ELU),47
νi ← ELU(Wνi + b), W ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) d × din, b ∈ d × din, b ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) d, d, | (12) |
Then, we apply LGNN graph attentional layers, each of which is given by
| νi ← LayerNorm(νi), | (13) |
 | (14) |
 | (15) |
 | (16) |
 | (17) |
| νi ← LayerNorm(Vi) + νi, | (18) |
νi ← ELU(W2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ELU(W1νi + b1) + b2) + νi, ELU(W1νi + b1) + b2) + νi, | (19) |
 is the set of neighbors of node i including the node itself, (k) denotes the attention head and where the weights
is the set of neighbors of node i including the node itself, (k) denotes the attention head and where the weightsW(k) ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) d×d/Nheads, d×d/Nheads, | (20) |
WO ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) d×d, d×d, | (21) |
W1 ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 4d×d, 4d×d, | (22) |
W2 ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) d×4d. d×4d. | (23) |
νi ← Wνi, W ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) demb×d. demb×d. | (24) |
As initial node features we choose a one-hot encoding of the atomic number, a one-hot encoding of whether the node is in a loop, a one-hot encoding of the potential loop size and the degree of the node. Since Grappa only predicts bonded parameters, we have to ensure consistency with the nonbonded parameters from the traditional force field, which is why we one-hot encode the traditional force field used for the nonbonded contribution of the respective state if we train on a dataset that contains data from different nonbonded methods. We also include the partial charges (the scalar value concatenated with a 16-dimensional binning between −2e and 2e) as node input features, which allows us to describe differently charged conformations of the same molecule without resorting to global or graph-symmetry breaking features like the formal charge.
As described in Section 2.2, we add a symmetric positional encoding to the node features, as in (9), that is invariant under the desired set of permutations but can break symmetries that are not necessary to make the model more expressive while keeping equivariance under the permutations that we use for invariant pooling (10) later on. From the symmetries eqn (6)–(8), and from the considerations for improper dihedrals in Section A.4, we can derive the following positional encodings
| PEangle = (0, 1, 0), | (25) |
| PEtorsion = (0, 1, 1, 0), | (26) |
| PEimproper = (0, 1, 1, 0). | (27) |
The bond positional encoding is not needed because the permutations of the bond parameters are the full group S2 and there is no symmetry that needs to be broken. For torsions and impropers, the positional encoding does not break all unnecessary symmetries, for example the symmetry ijkl → ljki is still present with positional encoding, and will be broken later.
We then apply a transformer acting one nodes that represent the atoms involved in the interaction, that is, after a projection on features of dimension dT,
νi ← ELU(Wνi + b), W ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) dT×demb, b ∈ dT×demb, b ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) dT, dT, | (28) |
We apply LT transformer layers, each of which is given by scaled dot-product attention with NT-heads heads and a 2-layer MLP with hidden dimension 4dT, skip connections, dropout and layer normalization as in the original transformer architecture.7
We then apply a symmetry pooling operation by passing permuted versions of concatenated node embeddings to a Lpool-layer MLP with hidden dimension dpool and summing over all permutations σ in the respective symmetry group  ,
,
 | (29) |
The two dimensional scores zij for bonds and zijk for angles are finally mapped to the range of the respective set of MM parameters by scaled and shifted versions of ELU and the sigmoid function,
| kij = ToPos(zij,0), | (30) |
| r(0)ij = ToPos(zij,1), | (31) |
| kijk = ToPos(zijk,0), | (32) |
| θ(0)ijk = ToRange(0,π)(zijk,0), | (33) |
| kijkl,m = zijkl,2m+1 × sigmoid(zijkl,2m). | (34) |
For mapping to positive values, we use
 | (35) |
 | (36) |
We can see that the mean and standard deviation of the output are indeed close to the target mean and standard deviation if we consider the asymptotic behavior of the sigmoid function and ELU as their input approaches zero,
 | (37) |
 | (38) |
| 〈ToRange(z)〉 ≈ γ(1/2 + 4σ/γ〈z〉) = γ/2 |
For mapping to positive values, we expand ELU in μ/σ − 1 + z around zero, which is reasonable if μ/σ ≈ 1, and find in analogy that target mean and standard deviation are recovered to first order in μ/σ − 1 + z.
A.3 Hyperparameters and training details
For all models discussed in this work, we use the hyperparameters listed in Table 5 and a dihedral periodicity of nperiodicity = 3. All relative weights between energies, forces and MM parameters rely on units formed by kcal mol−1, Å and radian. We train the models using the Adam49 optimizer with ε = 10−8, β1 = 0.9, β2 = 0.999.| Hyperparameter | Variable | Value |
|---|---|---|
| Graph neural network | ||
| Layers | L GNN | 4 |
| Hidden dimension | d | 512 |
| Attention heads | N heads | 16 |
| Embedding dimension | d emb | 256 |
| Dropout probability | 0.3 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| Symmetric transformer | ||
| Transformer layers | L T | 1 |
| Transformer hidden dim | d T | 512 |
| Attention heads | N T-heads | 8 |
| Pooling layers | L pool | 3 |
| Pooling hidden dim | d pool | 256 |
| Dropout probability | 0.5 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| Training setup | ||
| Learning rate | 10−5 | |
| Molecules per batch | 32 | |
| States per molecule | 32 | |
| Force weight | λ F | 0.8 |
| Dihedral L2 weight | λ dih | 1 |
| Traditional MM weight | λ trad | 0 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| MM | ||
| Torsion periodicities | {1, 2, 3} | |
| Improper periodicities | {2} | |
First, we train for 2 epochs on traditional MM parameters only, which can be interpreted as a form of pretraining that is efficient in bringing the model in a state where the gradients of the QM-part of the loss functions are informative. We start the training on energies and forces with λtrad = 10−3, which we set to zero after 100 epochs, preventing the model from converging towards unphysical local minima of the QM-part of the loss function. When changing weights of terms of the loss function as described above, we re-initialize the optimizer with random moments and apply a warm restart,50 during which we linearly increase the learning rate in 500 training steps to decorrelate the optimizer state from the gradient updates of the previous loss function. Besides pretraining on traditional MM parameters directly, we have found penalizing large torsion and improper force constants ξ(dih) to benefit generalizability across conformational space.
As validation loss, we use a linear combination of the energy and force root mean squared error (RMSE) on the sub-datasets (the rows in Table 1), averaged over all sub-datasets, with a weight of 1 for the energy RMSE and 3 for the force RMSE to prevent overfitting on a molecule type. We use this validation loss for early stopping and for learning rate scheduling. For the model trained on the Espaloma dataset (Table 1), the validation loss did not improve after 1000 epochs, which corresponds to about 25 hours of training on an A100 GPU.
A.4 Improper dihedrals
As discussed in Section 2.2, we postulate that the energy contributions from the different interactions are symmetric under certain permutations of the embeddings and spatial positions of the atoms involved. These permutations are given by the isomorphisms of the respective subgraph that describes the interaction. In the case of angles, bonds and torsions, these symmetries are given by eqn (6)–(8), for improper dihedrals, the symmetries are given by all six permutations that leave the central atom invariant, as can be seen from the structure of the subgraphs in Fig. 13. For bonds, angles and torsions, the interaction coordinates distance, angle and the cosine of the dihedral angle are invariant under the respective permutations, which is why we can construct an invariant energy contribution simply by enforcing invariance of the MM parameters under the respective permutations. | ||
| Fig. 13 The subgraphs of the molecular graph that correspond to bonded MM interactions, namely bonds (a), angles (b), torsions (c) and improper dihedrals (d). | ||
For improper dihedrals, this is not the case, as the dihedral angle is not invariant under all six permutations mentioned above and a model with improper force constants that are invariant under these permutations would not have invariant improper energy contributions. In Grappa, we solve this problem by introducing more terms for improper dihedrals. For example
Eimproper = kijkl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ϕijkl) + kjikl cos(ϕijkl) + kjikl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ϕjikl), cos(ϕjikl), | (39) |
| Cos(ϕijkl) = cos(ϕljki), | (40) |
| k(improper)ijkl = k(improper)ljki. | (41) |
A.5 Datasets
as it is done in Espaloma 0.3.
As in Espaloma, we report the RMSE of centered energies, which means that, for a given molecule and a given force field, we subtract the mean of the predicted energies before comparing them to values predicted by another force field, for which we also center the predicted energies. This is done because molecular mechanics can only predict energy differences between states of a given molecule. Thus constant shifts in energy should have no influence on the quality measure of the prediction, which is ensured by subtracting the mean energy per molecule.
A.6 Contributions to the dihedral potential energy landscape
As described in Section 3.4, we find that Grappa reproduces characteristics of the Amber ff19SB potential energy landscape with implicit solvent in dihedral scans. Grappa does not require CMAPs to achieve this, but uses the same MM energy functional as Amber ff14SB, thus we decided to investigate how different contributions are combined in Grappa to obtain features such as the diagonal shape and extension of the αr helix basin at (ϕ, ψ) = (−80°, −20°).We find that next to the dihedrals involved in the scan, neighboring dihedrals, angles and nonbonded interactions also contribute to the energy landscape 16.
A.7 Tabulated force field construction
With the intent of constructing a tabulated Grappa protein force field, we extract MM parameters for each residue from small peptides that we parametrize with the original Grappa force field. The resulting force field contains parameters for all natural amino acids, including protonation states for Lys, Arg, Asp, Glu, His and Cys and, if possible, terminal variants, the unnatural amino acids hydroxyproline and DOPA and the capping groups Ace and Nme. For parameters of an individual non-terminal amino acid, a BLXLZ sequence is chosen, where B and Z are the capping groups, L is leucine and X is the amino acid of interest. For terminal amino acids, the sequences are BLX and XLZ, respectively. Capping group parameters are obtained from a BLLZ peptide. Inter-residue bonded parameters are obtained from peptides with the sequence BLXYLZ and corresponding sequences for terminal amino acids and capping groups, where Y denotes a second amino acid of interest.The parameters of these peptides are then extracted and arranged in the required force field format for OpenMM or GROMACS. Per amino acid variant (C-terminal, N-terminal, non-terminal, protonation states) a single residue type entry with a unique atom type for every atom is built. Atom types are not shared between residues. Parameters for intra-residue bonded interactions are taken from the respective peptide with a single amino acid of interest. Inter-residue bonded interactions are parametrized from the peptides containing this specific interaction.
A.8 MD simulations
Molecular dynamics simulations are performed with GROMACS version 2023 (ref. 8) using the Amber ff99SB-ILDN force field,25 Grappa with Amber ff99SB-ILDN nonbonded parameters and Espaloma-0.3 (ref. 10) with EspalomaCharge54 partial charges. For all three force fields the TIP3P water model30 and Joung and Cheatham ions,55 2 fs time steps with LINCS constraints56 on H-bonds were employed. Simulations for the J-coupling benchmark were run at 300 K, for the folding simulations, a temperature of 340 K was maintained with v-rescale thermostat57 and Parrinello–Rahman pressure coupling58 was used to maintain a pressure of 1 bar. We apply a Coulomb and Lennard-Jones cutoff of 1.0 nm. After system preparation, energy minimization, NVT and NPT equilibration simulations are conducted. The code for reproducing the simulations is publicly available at https://github.com/LeifSeute/validate-grappa.We follow the ref. 59 by defining three separate states: folded, intermediate and extended. The backbone RMSD compared to the experimental structure was binned in 0.2 Å steps.
Fig. 14b shows the RMSD of protein C-alpha and RNA carbon atoms during 30 ns of MD simulation with Grappa parameters for protein and RNA, which indicates that Grappa keeps the virus stable. For large scale conformational changes or artificial viral capsid disruption, higher RMSD values would be expected .
 | ||
| Fig. 14 (a) The virus STMV, containing proteins (blue) and RNA (red). (b) RMSD of protein C-alpha and RNA carbon atoms of the virus in solution during a 30 ns MD simulation with Grappa. | ||
A.9 Finetuning Grappa on 3BPA
As described in Section 4.4, we observe that, if finetuned on the 300 K training set of the 3BPA dataset40 and 10 states from the β = 150° slice, Grappa can capture features of the dihedral energy landscape on another slice (β = 180°). In Fig. 17, we show the potential energy prediction across another unseen slice, β = 120° and in Fig. 18, we show Grappa's performance on the β = 150° slice it was trained on. We also report accuracies for Grappa, Grappa finetuned, and Grappa finetuned only on the training set of 300 K states in Table 6. From the table we see that by including states from the relaxed β = 150° dihedral slice, Grappa's performance on unseen slices is improved further. We note this necessity of including partially relaxed states for training as limitation of Grappa if compared to more flexible E(3) equivariant models MACE, where this is not necessary, but as advantage over tabulated MM force fields like Gaff-2.11. | ||
| Fig. 17 (a) The 3BPA molecule with the dihedral angles α, β and γ. (b) Potential energy along the gamma dihedral for fixed α and β and relaxed other degrees of freedom as described in ref. 40. (c) Potential energy on the relaxed β = 120° slice. We subtract the minimal energy on the slice for each force field. | ||
 | ||
| Fig. 18 (a) The 3BPA molecule with the dihedral angles α, β and γ. (b) Potential energy along the gamma dihedral for fixed α and β and relaxed other degrees of freedom as described in ref. 40. (c) Potential energy on the relaxed β = 150° slice. We show the states used during the training of Grappa-finetuned as black dots. As before, the minimal energy on the slice for each force field is subtracted. | ||
| Dataset | Confs | RMSE | Gaff-2.11 | Grappa | Grappa-finetuned | Grappa-finetuned-300 K |
|---|---|---|---|---|---|---|
| Slice β = 180° | 2350 | Energy | 3.1 | 2.7 | 2.5 | 2.6 |
| Force | 11.8 | 7.1 | 4.2 | 4.4 | ||
| Slice β = 150° | 2350 | Energy | 1.3 | 1.0 | 0.7 | 0.9 |
| Force | 11.1 | 6.3 | 2.6 | 2.9 | ||
| Slice β = 120° | 2347 | Energy | 1.4 | 1.3 | 1.1 | 1.2 |
| Force | 10.7 | 6.0 | 3.2 | 3.5 | ||
| Test 300 K | 1669 | Energy | 3.1 | 1.7 | 1.2 | 1.2 |
| Force | 12.8 | 8.1 | 5.4 | 5.4 | ||
| Test 600 K | 2138 | Energy | 4.4 | 2.7 | 2.4 | 2.3 |
| Force | 14.2 | 9.9 | 8.1 | 8.1 | ||
| Test 1200 K | 2139 | Energy | 8.5 | 6.7 | 6.5 | 6.4 |
| Force | 19.4 | 16.3 | 14.9 | 14.7 |
A.10 Learning curve
We provide a learning curve for Grappa trained on subsets of the Espaloma dataset in Fig. 19.A.11 Grappa's MM parameters
In Fig. 20, the MM parameters predicted by Grappa and ff99SB-ILDN for the protein ubiquitin are visualized.A.12 Force accuracy
In analogy to Fig. 4, Grappa's accuracy for predicted force components is visualized in Fig. 21.A.13 Extensive tables
We provide tables with errors for the full Espaloma dataset and the Grappa extension with ff99SB and CHARMM36 nonbonded parameters and radical peptides in Tables 7 and 8.| Dataset | Test mols | Confs | Grappa | Espaloma | Gaff-2.11 | ff14SB, RNA.OL3 | Mean predictor | |
|---|---|---|---|---|---|---|---|---|
| Boltzmann sampled | ||||||||
| SPICE-PubChem | 1411 | 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 853 853 |
Energy | 2.3 ± 0.1 | 2.3 ± 0.1 | 4.6 | 18.4 | |
| Force | 6.1 ± 0.3 | 6.8 ± 0.1 | 14.6 | 23.4 | ||||
| SPICE-DES-Monomers | 39 | 2032 | Energy | 1.3 ± 0.1 | 1.4 ± 0.3 | 2.5 | 8.2 | |
| Force | 5.2 ± 0.2 | 5.9 ± 0.5 | 11.1 | 21.3 | ||||
| SPICE-Dipeptide | 67 | 2592 | Energy | 2.3 ± 0.1 | 3.1 ± 0.1 | 4.5 | 4.6 | 18.7 |
| Force | 5.4 ± 0.1 | 7.8 ± 0.2 | 12.9 | 12.1 | 21.6 | |||
| RNA-Diverse | 6 | 357 | Energy | 3.3 ± 0.2 | 4.2 ± 0.3 | 6.5 | 6.0 | 5.4 |
| Force | 3.7 ± 0.1 | 4.4 ± 0.1 | 16.7 | 19.4 | 17.1 | |||
| RNA-Trinucleotide | 64 | 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 811 811 |
Energy | 3.5 ± 0.1 | 3.8 ± 0.2 | 5.9 | 6.1 | 5.3 |
| Force | 3.6 ± 0.1 | 4.3 ± 0.1 | 17.1 | 19.7 | 17.7 | |||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| Torsion scan | ||||||||
| Gen2-Torsion | 131 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 890 890 |
Energy | 1.7 ± 0.2 | 1.6 ± 0.3 | 2.7 | 4.7 | |
| Force | 4.0 ± 0.4 | 4.7 ± 0.6 | 9.4 | 5.5 | ||||
| Protein-Torsion | 9 | 6624 | Energy | 2.2 ± 0.4 | 1.9 ± 0.2 | 3.0 | 3.5 | |
| Force | 3.8 ± 0.5 | 3.5 ± 0.3 | 9.7 | 5.1 | ||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| Optimization | ||||||||
| Gen2-Opt | 154 | 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 055 055 |
Energy | 1.8 ± 0.2 | 1.7 ± 0.5 | 3.0 | 3.9 | |
| Force | 3.8 ± 0.2 | 4.5 ± 0.8 | 9.7 | 5.1 | ||||
| Pepconf-Opt | 55 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 884 884 |
Energy | 3.2 ± 0.3 | 2.8 ± 0.3 | 5.1 | 4.1 | 6.3 |
| Force | 3.6 ± 0.2 | 4.0 ± 0.4 | 10.2 | 10.2 | 5.3 | |||
| Dataset | Test mols | Confs | Grappa | Espaloma | Gaff-2.11 | ff99SB-ILDN | Mean predictor | |
|---|---|---|---|---|---|---|---|---|
| SPICE-PubChem | 1411 | 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 853 853 |
Energy | 2.3 ± 0.1 | 2.3 ± 0.1 | 4.6 ± 0.1 | 18.8 | |
| Force | 6.1 ± 0.3 | 6.8 ± 0.1 | 14.6 ± 0.3 | 41.3 | ||||
| SPICE-DES-Monomers | 39 | 2032 | Energy | 1.3 ± 0.1 | 1.4 ± 0.3 | 2.5 ± 0.2 | 8.6 | |
| Force | 5.3 ± 0.2 | 5.9 ± 0.5 | 11.1 ± 0.6 | 37.4 | ||||
| SPICE-Dipeptide | 67 | 2592 | Energy | 2.4 ± 0.1 | 3.1 ± 0.1 | 4.5 ± 0.1 | 19.1 | |
| Force | 5.6 ± 0.1 | 7.8 ± 0.2 | 12.9 ± 0.3 | 38.4 | ||||
| SPICE-Dipeptide (FF99SB) | 67 | 2592 | Energy | 2.3 ± 0.1 | 4.5 ± 0.1 | 19.1 | ||
| Force | 5.6 ± 0.1 | 12.8 ± 0.3 | 38.4 | |||||
| SPICE-Dipeptide (CHARMM36) | 67 | 2592 | Energy | 2.5 ± 0.1 | 19.1 | |||
| Force | 5.5 ± 0.1 | 38.4 | ||||||
| RNA-Diverse | 6 | 357 | Energy | 3.2 ± 0.2 | 4.2 ± 0.3 | 6.5 ± 0.1 | 6.1 | |
| Force | 3.7 ± 0.0 | 4.4 ± 0.1 | 16.8 ± 0.1 | 30.2 | ||||
| RNA-Trinucleotide | 64 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 811 811 |
Energy | 3.5 ± 0.0 | 3.8 ± 0.2 | 6.0 ± 0.1 | 6.1 | |
| Force | 3.6 ± 0.0 | 4.3 ± 0.1 | 17.0 ± 0.0 | 31.2 | ||||
| Radical-Dipeptides (ff99SB) | 28 | 272 | Energy | 3.3 ± 0.3 | 8.7 | |||
| Force | 6.8 ± 0.2 | 41.3 | ||||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| Optimization | ||||||||
| Gen2-Opt | 154 | 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 055 055 |
Energy | 1.7 ± 0.1 | 1.7 ± 0.5 | 2.8 ± 0.2 | 4.2 | |
| Force | 4.5 ± 0.2 | 4.5 ± 0.8 | 9.8 ± 0.3 | 8.7 | ||||
| Pepconf-Opt | 55 | 9084 | Energy | 2.9 ± 0.2 | 2.8 ± 0.3 | 4.7 ± 0.3 | 6.5 | |
| Force | 3.9 ± 0.2 | 4.0 ± 0.4 | 10.4 ± 0.3 | 9.4 | ||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| Torsion scan | ||||||||
| Gen2-Torsion | 131 | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 290 290 |
Energy | 1.7 ± 0.1 | 1.6 ± 0.3 | 2.6 ± 0.1 | 4.7 | |
| Force | 4.2 ± 0.2 | 4.7 ± 0.6 | 9.5 ± 0.4 | 8.9 | ||||
| Protein-Torsion | 9 | 6024 | Energy | 2.0 ± 0.2 | 1.9 ± 0.2 | 2.9 ± 0.2 | 3.5 | |
| Force | 5.3 ± 0.3 | 3.5 ± 0.3 | 9.8 ± 0.4 | 9.0 | ||||
| Protein-Torsion (FF99SB) | 9 | 6024 | Energy | 2.4 ± 0.2 | 3.5 | |||
| Force | 6.2 ± 0.3 | 9.0 | ||||||
| Protein-Torsion (CHARMM36) | 9 | 6024 | Energy | 2.3 ± 0.2 | 3.5 | |||
| Force | 6.0 ± 0.3 | 9.0 | ||||||
Acknowledgements
This research was supported by the Klaus Tschira Foundation. The project has also received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement no. 101002812) [F. G.]. We thank Kai Riedmiller and Jannik Buhr for application and software related discussions, Fabian Grünewald, Camilo Aponte-Santamaria and Vsevolod Viliuga for discussions on future applications and Daniel Sucerquia for conversations on the role of internal coordinates in MM.References
- A. Musaelian, S. Batzner, A. Johansson, L. Sun, C. J. Owen, M. Kornbluth and B. Kozinsky, Learning local equivariant representations for large-scale atomistic dynamics, Nat. Commun., 2023, 14, 579 CrossRef CAS PubMed.
- I. Batatia, D. P. Kovacs, G. Simm, C. Ortner and G. Csanyi, MACE: Higher Order Equivariant Message Passing Neural Networks for Fast and Accurate Force Fields, Advances in Neural Information Processing Systems, 2022, 11423–11436 Search PubMed.
- O. T. Unke, M. Stöhr, S. Ganscha, T. Unterthiner, H. Maennel, S. Kashubin, D. Ahlin, M. Gastegger, L. M. Sandonas, J. T. Berryman, A. Tkatchenko and K.-R. Müller, Biomolecular dynamics with machine-learned quantum-mechanical force fields trained on diverse chemical fragments, Sci. Adv., 2024, 10, eadn4397 CrossRef CAS PubMed.
- K. Schütt, O. Unke and M. Gastegger, Equivariant message passing for the prediction of tensorial properties and molecular spectra, in Proceedings of the 38th International Conference on Machine Learning, 2021, pp. 9377–9388 Search PubMed.
- Y. Wang, J. Fass, B. Kaminow, J. E. Herr, D. Rufa, I. Zhang, I. Pulido, M. Henry, H. E. B. Macdonald, K. Takaba and J. D. Chodera, End-to-end differentiable construction of molecular mechanics force fields, Chem. Sci., 2022, 13, 12016–12033 RSC.
- G. Chen, T. Jaffrelot Inizan, T. Plé, L. Lagardère, J.-P. Piquemal and Y. Maday, Advancing Force Fields Parameterization: A Directed Graph Attention Networks Approach, J. Chem. Theory Comput., 2024, 20, 5558–5569 CrossRef CAS PubMed.
- A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, L. u. Kaiser and I. Polosukhin, Attention Is All You Need, Advances in Neural Information Processing Systems, 2017, pp. 6000–6010 Search PubMed.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, GROMACS: high performance molecular simulations through multi-level parallelism from laptops to supercomputers, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- P. Eastman, M. S. Friedrichs, J. D. Chodera, R. J. Radmer, C. M. Bruns, J. P. Ku, K. A. Beauchamp, T. J. Lane, L.-P. Wang, D. Shukla, T. Tye, M. Houston, T. Stich, C. Klein, M. R. Shirts and V. S. Pande, OpenMM 4: A Reusable, Extensible, Hardware Independent Library for High Performance Molecular Simulation, J. Chem. Theory Comput., 2013, 9, 461–469 CrossRef CAS PubMed.
- K. Takaba, A. J. Friedman, C. E. Cavender, P. K. Behara, I. Pulido, M. M. Henry, H. MacDermott-Opeskin, C. R. Iacovella, A. M. Nagle, A. M. Payne, M. R. Shirts, D. L. Mobley, J. D. Chodera and Y. Wang, Machine-learned molecular mechanics force fields from large-scale quantum chemical data, Chem. Sci., 2024, 15, 12861–12878 RSC.
- P. Veličković, G. Cucurull, A. Casanova, A. Romero, P. Liò and Y. Bengio, Graph Attention Networks, in International Conference on Learning Representations, 2018 Search PubMed.
- K. He, X. Zhang, S. Ren and J. Sun, Deep Residual Learning for Image Recognition, arXiv, 2015, preprint, arXiv:1512.03385, DOI:10.48550/arXiv.1512.03385.
- J. L. Ba, J. R. Kiros and G. E. Hinton, Layer Normalization, arXiv, 2016, preprint, arXiv:1607.06450, DOI:10.48550/arXiv.1607.06450.
- S. Brody, U. Alon and E. Yahav, On the Expressivity Role of LayerNorm in Transformers' Attention, arXiv, 2023, preprint, arXiv:2305.02582, DOI:10.48550/arXiv.2305.02582.
- S. Yun, M. Jeong, R. Kim, J. Kang and H. J. Kim, Graph Transformer Networks, arXiv, 2020, preprint, arXiv:1911.06455, DOI:10.48550/arXiv.1911.06455.
- K. Schütt, P.-J. Kindermans, H. E. Sauceda Felix, S. Chmiela, A. Tkatchenko and K.-R. Müller, SchNet: a continuous-filter convolutional neural network for modeling quantum interactions, Advances in Neural Information Processing Systems, 2017, pp. 992–1002 Search PubMed.
- W. M. Czarnecki, S. Osindero, M. Jaderberg, G. Świrszcz and R. Pascanu, Sobolev Training for Neural Networks, arXiv, 2017, preprint, arXiv:1706.04859, DOI:10.48550/arXiv.1706.04859.
- S. Boothroyd, P. Behara, O. Madin, D. Hahn, H. Jang, V. Gapsys, J. R. Wagner, J. T. Horton, D. L. Dotson, M. W. Thompson, J. Maat, T. Gokey, L.-P. Wang, D. J. Cole, M. K. Gilson, J. D. Chodera, C. I. Bayly, M. R. Shirts and D. L. Mobley, Development and Benchmarking of Open Force Field 2.0.0 — The Sage Small Molecule Force Field, J. Chem. Theory Comput., 2023, 19(11), 3251–3275 CrossRef CAS PubMed.
- X. He, V. Man, W. Yang, T.-S. Lee and J. Wang, A fast and high-quality charge model for the next generation general AMBER force field, J. Chem. Phys., 2020, 153, 114502 CrossRef CAS PubMed.
- J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser and C. Simmerling, ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters from ff99SB, J. Chem. Theory Comput., 2015, 11, 3696–3713 CrossRef CAS PubMed.
- M. Zgarbová, M. Otyepka, J. Šponer, A. Mládek, P. Banáš, T. E. C. Cheatham III and P. Jurečka, Refinement of the Cornell et al. Nucleic Acids Force Field Based on Reference Quantum Chemical Calculations of Glycosidic Torsion Profiles, J. Chem. Theory Comput., 2011, 7, 2886–2902 CrossRef PubMed.
- P. Eastman, P. K. Behara, D. L. Dotson, R. Galvelis, J. E. Herr, J. T. Horton, Y. Mao, J. D. Chodera, B. P. Pritchard, Y. Wang, G. De Fabritiis and T. E. Markland, SPICE, A Dataset of Drug-like Molecules and Peptides for Training Machine Learning Potentials, Sci. Data, 2023, 10, 11 CrossRef CAS PubMed.
- H. Lebrette, V. Srinivas, J. John, O. Aurelius, R. Kumar, D. Lundin, A. S. Brewster, A. Bhowmick, A. Sirohiwal, I. Kim, S. Gul, C. Pham, K. D. Sutherlin, P. Simon, A. Butryn, P. Aller, A. M. Orville, F. D. Fuller, Alonso, A. Batyuk, N. K. Sauter, V. K. Yachandra, J. Yano, V. R. I. Kaila, B. Sjöberg, J. Kern, K. Roos and M. Högbom, Structure of a ribonucleotide reductase R2 protein radical, Science, 2023, 382, 109–113 CrossRef CAS PubMed.
- C. Zapp, A. Obarska-Kosinska, B. Rennekamp, M. Kurth, D. M. Hudson, D. Mercadante, U. Barayeu, T. P. Dick, V. Denysenkov, T. Prisner, M. Bennati, C. Daday, R. Kappl and F. Gräter, Mechanoradicals in tensed tendon collagen as a source of oxidative stress, Nat. Commun., 2020, 11, 2315 CrossRef CAS PubMed.
- K. Lindorff-Larsen, S. Piana, K. Palmo, P. Maragakis, J. Klepeis, R. Dror and D. Shaw, Improved side-chain torsion potentials for the Amber ff99SB protein force field, Proteins, 2010, 78, 1950–1958 CrossRef CAS PubMed.
- J. Huang and A. D. MacKerell Jr, CHARMM36 all-atom additive protein force field: validation based on comparison to NMR data, J. Comput. Chem., 2013, 34, 2135–2145 CrossRef CAS PubMed.
- C. Tian, K. Kasavajhala, K. A. A. Belfon, L. Raguette, H. Huang, A. N. Migues, J. Bickel, Y. Wang, J. Pincay, Q. Wu and C. Simmerling, ff19SB: Amino-Acid-Specific Protein Backbone Parameters Trained against Quantum Mechanics Energy Surfaces in Solution, J. Chem. Theory Comput., 2020, 16, 528–552 CrossRef PubMed.
- K. Lindorff-Larsen, P. Maragakis, S. Piana, M. P. Eastwood, R. O. Dror and D. E. Shaw, Systematic Validation of Protein Force Fields against Experimental Data, PLoS One, 2012, 7, e32131 CrossRef CAS PubMed.
- S. Rauscher, V. Gapsys, M. J. Gajda, M. Zweckstetter, B. L. de Groot and H. Grubmüller, Structural Ensembles of Intrinsically Disordered Proteins Depend Strongly on Force Field: A Comparison to Experiment, J. Chem. Theory Comput., 2015, 11, 5513–5524 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, Comparison of simple potential functions for simulating liquid water, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- P. S. Shabane, S. Izadi and A. V. Onufriev, General Purpose Water Model Can Improve Atomistic Simulations of Intrinsically Disordered Proteins, J. Chem. Theory Comput., 2019, 15, 2620–2634 CrossRef CAS PubMed.
- K. Lindorff-Larsen, S. Piana, R. O. Dror and D. E. Shaw, How Fast-Folding Proteins Fold, Science, 2011, 334, 517–520 CrossRef CAS PubMed.
- J. Huang, S. Rauscher, G. Nawrocki, T. Ran, M. Feig, B. L. de Groot, H. Grubmüller and A. D. MacKerell, CHARMM36m: an improved force field for folded and intrinsically disordered proteins, Nat. Methods, 2017, 14, 71–73 CrossRef CAS PubMed.
- S. Honda, T. Akiba, Y. S. Kato, Y. Sawada, M. Sekijima, M. Ishimura, A. Ooishi, H. Watanabe, T. Odahara and K. Harata, Crystal Structure of a Ten-Amino Acid Protein, J. Am. Chem. Soc., 2008, 130, 15327–15331 CrossRef CAS PubMed.
- M. Hennig, W. Bermel, H. Schwalbe and C. Griesinger, Determination of ψ Torsion Angle Restraints from 3J(Cα, Cα) and 3J(Cα, HN) Coupling Constants in Proteins, J. Am. Chem. Soc., 2000, 122, 6268–6277 CrossRef CAS.
- J.-S. Hu and A. Bax, Determination of φ and χ1 Angles in Proteins from 13C13C Three-Bond J Couplings Measured by Three-Dimensional Heteronuclear NMR. How Planar Is the Peptide Bond?, J. Am. Chem. Soc., 1997, 119, 6360–6368 CrossRef CAS.
- K. Ding and A. M. Gronenborn, Protein Backbone 1HN13Cα and 15N13Cα Residual Dipolar and J Couplings: New Constraints for NMR Structure Determination, J. Am. Chem. Soc., 2004, 126, 6232–6233 CrossRef CAS PubMed.
- B. Vögeli, J. Ying, A. Grishaev and A. Bax, Limits on Variations in Protein Backbone Dynamics from Precise Measurements of Scalar Couplings, J. Am. Chem. Soc., 2007, 129, 9377–9385 CrossRef PubMed.
- J. Wirmer and H. Schwalbe, Angular dependence of 1J(Ni, Cαi) and 2J(Ni, Cαi−1) coupling constants measured in J-modulated HSQCs, J. Biomol. NMR, 2002, 23, 47–55 CrossRef CAS PubMed.
- D. P. Kovács, C. v. d. Oord, J. Kucera, A. E. A. Allen, D. J. Cole, C. Ortner and G. Csányi, Linear Atomic Cluster Expansion Force Fields for Organic Molecules: Beyond RMSE, J. Chem. Theory Comput., 2021, 17, 7696–7711 CrossRef PubMed.
- The Amber Project, Amber23 Benchmark, 2023 Search PubMed.
- S. Batzner, A. Musaelian, L. Sun, M. Geiger, J. P. Mailoa, M. Kornbluth, N. Molinari, T. E. Smidt and B. Kozinsky, E(3)-equivariant graph neural networks for data-efficient and accurate interatomic potentials, Nat. Commun., 2022, 13, 2453 CrossRef CAS PubMed.
- B. Kozinsky, A. Musaelian, A. Johansson and S. Batzner, Scaling the Leading Accuracy of Deep Equivariant Models to Biomolecular Simulations of Realistic Size, in Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, New York, NY, USA, 2023 Search PubMed.
- B. Rennekamp, F. Kutzki, A. Obarska-Kosinska, C. Zapp and F. Gräter, Hybrid Kinetic Monte Carlo/Molecular Dynamics Simulations of Bond Scissions in Proteins, J. Chem. Theory Comput., 2020, 16, 553–563 CrossRef PubMed.
- A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein, L. Antiga, A. Desmaison, A. Köpf, E. Yang, Z. DeVito, M. Raison, A. Tejani, S. Chilamkurthy, B. Steiner, L. Fang, J. Bai and S. Chintala, PyTorch: An Imperative Style, High-Performance Deep Learning Library, arXiv, 2019, preprint, arXiv:1912.01703, DOI:10.48550/arXiv.1912.01703.
- M. Wang, D. Zheng, Z. Ye, Q. Gan, M. Li, X. Song, J. Zhou, C. Ma, L. Yu, Y. Gai, T. Xiao, T. He, G. Karypis, J. Li and Z. Zhang, Deep Graph Library: A Graph-Centric, Highly-Performant Package for Graph Neural Networks, arXiv, 2020, preprint, arXiv:1909.01315, DOI:10.48550/arXiv.1909.01315.
- D.-A. Clevert, T. Unterthiner and S. Hochreiter, Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs), arXiv, 2016, preprint, arXiv:1511.07289, DOI:10.48550/arXiv.1511.07289.
- N. Srivastava, G. Hinton, A. Krizhevsky, I. Sutskever and R. Salakhutdinov, Dropout: A Simple Way to Prevent Neural Networks from Overfitting, Journal of Machine Learning Research, 2014, 15, 1929–1958 Search PubMed.
- D. P. Kingma and J. Ba, A Method for Stochastic Optimization, arXiv, 2017, preprint, arXiv:1412.6980, DOI:10.48550/arXiv.1412.6980.
- I. Loshchilov and F. Hutter, Stochastic Gradient Descent with Warm Restarts, arXiv, 2017, preprint, arXiv:1608.03983, DOI:10.48550/arXiv.1608.03983.
- A. Blondel and M. Karplus, New formulation for derivatives of torsion angles and improper torsion angles in molecular mechanics: elimination of singularities, J. Comput. Chem., 1996, 17, 1132–1141 CrossRef CAS.
- A. D. Boese and J. M. L. Martin, Development of density functionals for thermochemical kinetics, J. Chem. Phys., 2004, 121, 3405–3416 CrossRef CAS PubMed.
- D. G. A. Smith, L. A. Burns and e. a. Simmonett, Psi4 1.4: Open-Source Software for High-Throughput Quantum Chemistry, J. Chem. Phys., 2020, 184108 CrossRef CAS PubMed.
- Y. Wang, I. Pulido, K. Takaba, B. Kaminow, J. Scheen, L. Wang and J. D. Chodera, EspalomaCharge: Machine Learning-Enabled Ultrafast Partial Charge Assignment, J. Phys. Chem. A, 2024, 128, 4160–4167 CrossRef CAS PubMed.
- I. S. Joung and T. E. I. Cheatham, Determination of Alkali and Halide Monovalent Ion Parameters for Use in Explicitly Solvated Biomolecular Simulations, J. Phys. Chem. B, 2008, 112, 9020–9041 CrossRef CAS PubMed.
- B. Hess, P-LINCS: A Parallel Linear Constraint Solver for Molecular Simulation, J. Chem. Theory Comput., 2007, 4, 116–122 CrossRef PubMed.
- G. Bussi, D. Donadio and M. Parrinello, Canonical sampling through velocity rescaling, J. Chem. Phys., 2008, 126, 014101 CrossRef PubMed.
- M. Parrinello and A. Rahman, Polymorphic transitions in single crystals: a new molecular dynamics method, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- R. Anandakrishnan, A. Drozdetski, R. C. Walker and A. V. Onufriev, Speed of Conformational Change: Comparing Explicit and Implicit Solvent Molecular Dynamics Simulations, Biophys. J., 2015, 108, 1153–1164 CrossRef CAS PubMed.
- L. Wang, P. K. Behara, M. W. Thompson, T. Gokey, Y. Wang, J. R. Wagner, D. J. Cole, M. K. Gilson, M. R. Shirts and D. L. Mobley, The Open Force Field Initiative: Open Software and Open Science for Molecular Modeling, J. Phys. Chem. B, 2024, 128, 7043–7067 CrossRef CAS PubMed.
Footnotes |
| † https://github.com/graeter-group/grappa. |
| ‡ https://github.com/graeter-group/grappa. |
| § https://github.com/LeifSeute/grappa-data-creation. |
| ¶ https://github.com/graeter-group/grappa. |
| || https://github.com/graeter-group/grappa/blob/master/dataset_creation/get_espaloma_split/load_esp_ds.py. |
| ** https://github.com/choderalab/refit-espaloma/blob/main/openff-default/02-train/joint-improper-charge/charge-weight-1.0/train.py, commit 3ccc44d. |
| †† https://github.com/LeifSeute/grappa-data-creation. |
| ‡‡ https://github.com/openforcefield/proteinbenchmark/tree/main/proteinbenchmark. |
| This journal is © The Royal Society of Chemistry 2025 |