Plasmon hybridization model in molecules: molecular jackhammers

Abstract

We recently demonstrated molecular plasmons in cyanine dyes for the conversion of photon energy into mechanical energy through a whole-molecule coherent vibronic-driven-action. Here we present a model, a molecular plasmon analogue of molecular orbital theory and of plasmon hybridization in metal nanostructures. This model describes that molecular plasmons can be obtained from the combination or hybridization of elementary molecular fragments, resulting in molecules with hybridized plasmon resonances in the electromagnetic spectrum. We applied our approach to the hybridization of the benzoindole and heptamethine fragments for understanding of the resonance frequencies in cyanines using UV-vis and Raman spectroscopy. The molecular plasmon resonances in cyanines are tunable by engineering molecular structure modifications and controlling the dielectric constant of the medium in which the cyanines are dissolved. We measured the plasmonicity index, an easy-to-use and powerful tool to predict and quantify if an organic molecule in solution is a molecular plasmon. This is done by analyzing the UV-vis spectrum as a function of the change of the dielectric constant of the solvent. Our model provides a tool for understanding how to manipulate chemical structures and their interaction with light at the molecular scale as plasmon-driven molecular jackhammers for applications at the interface with biological structures.

---

Introduction

A plasmon resonance in nanostructured metals is the collective oscillation of conduction band electrons, which is driven by the electric field of incident light and oscillates at nearly the same frequency as the excitation photons.^1–3 Research on optical plasmons has been conducted almost exclusively in metallic or semimetallic nanomaterials for applications in optoelectronic devices, sensors, cancer theranostics, solar energy harvesting, and photocatalysis.^4–8 Although plasmons in molecules have been theoretically proposed, they have only been investigated experimentally in a few cases.^9–11 We recently showed that cyanine dyes act as plasmon-driven molecular jackhammers (MJH) through vibronic mode activation, a large amplitude vibrational motion coupled to electronic resonance, that causes the molecule to stretch longitudinally and axially through coherent whole-molecule vibration.¹² The actuation of these intrinsic molecular plasmon resonances in cyanines upon near-infrared (NIR) light excitation enables the conversion of photonic energy to mechanical energy.¹² Upon application to lipid bilayers followed by NIR light activation, plasmon-driven MJH mechanically opens cellular membranes, eradicating cancer cells in culture and tumors in mice.¹²

Identifying plasmons in small molecular systems is challenging since only a few electrons are involved.^13–15 Not every organic molecule can sustain molecular plasmon resonances, and a challenge arises from the difficulty in evaluating the theoretical and experimental underpinnings of these plasmon-induced movements in molecules. Our recent theoretical and experimental demonstration, along with additional evidence provided in this study, confirms the existence of molecular plasmons in MJH (an optical excitation of collective electronic and vibrational modes in a cyanine molecule). Our quantum mechanical calculations on molecular plasmons in cyanines and their associated whole-molecule vibrations have resolved the controversy regarding whether a dominant vibration or a collection of single excited vibrations occurs in cyanines.¹² When vibrational and electronic modes are coupled, by absorbance of a suitable energy of light, a molecule's collective electronic excitations hybridize with the molecule's vibrational modes to induce the vibronic mode.^11,16 For clarification, in cyanines, this is a special type of vibronic mode that involves collective electronic excitations, a plasmon, in contrast to the classical concept of a single-electron excited vibronic mode.^11,12 Previously Yang et al. resolved, among others, a vibrational frequency at 1310 cm⁻¹ using wavelength-resolved femtosecond pump-probe spectra of cyanine 1,1′,3,3,3′,3′-hexamethyl-4,4′,5,5′-dibenzo-2,2′-indotricarbocyanine (HDITC) when the molecule was optically excited.¹⁷ However, the identity of this vibration was not explained in that study. Our Time-Dependent Density Functional Theory (TDDFT) analysis strongly supports that this reported vibration band at 1310 cm⁻¹ corresponds to the concerted whole-molecule vibration.¹² In agreement with this, the frequency has been reported to correspond to one unique vibration with a nearly constant value of approximately 1310–1375 cm⁻¹ among different indocyanine structures.¹⁸ The TDDFT calculations and vibrational analyses allowed the generation of a video of the atoms moving synchronously in a continuous loop. First, the molecule stretches lengthwise and contracts axially simultaneously. Then, it contracts lengthwise and stretches axially, giving the impression that the molecule is “breathing”. This is the so-called whole-molecule vibration responsible for the mechanical action exerted by MJH.¹²

The precise control of molecular motion through the actuation of a molecular plasmon could be facilitated by the establishment of general design principles. Here we provide a model that is the combination of plasmons of elementary molecular fragments arising into larger and more complex hybrid molecular plasmons. This model is an analogue of molecular orbital theory^19–21 and of the plasmon hybridization in metal nanostructures.²² In 1928 both Robert Mulliken and Friederich Hund developed a quantum interpretation of the spectra of diatomic molecules, the molecular orbital theory, which describes the behavior of electrons in a molecule in terms of combinations of atomic wavefunctions.^19–21,23 In 2003 Emil Prodan et al. proposed a plasmon hybridization model for plasmonic metal nanostructures, an analogue to the molecular orbital theory.²² We applied an analogue to the hybridization of the benzoindole and heptamethine fragments for understanding of the resonance frequencies in cyanines. We detected and assigned the resonance frequency of the individual fragments and of the entire hybridized molecule. This was possible through analysis of Raman and UV-vis spectra of the molecular fragments and cyanine molecules. Previously, we studied a large library of cyanine-based MJH and established structure-activity relationships using experimental plasmonicity index (EPI) measurements to assess their plasmonic character in mechanical opening cell membranes.²⁴ Here, in contrast, we systematically demonstrate how to differentiate a molecular plasmon within MJH structures and assess the role of the molecular fragments using a plasmon hybridization model.

According to our knowledge, a model for plasmon hybridization in molecules and its implications for whole-molecule vibration has not been proposed before. What makes this model particularly interesting is its ability to explain the emergence of plasmon resonances in the optical spectra of cyanine molecules, as well as the whole-molecule vibrational frequencies in the Raman spectra. Specifically, we demonstrate how this model provides insights for manipulating chemical structures to control the activation and deactivation of whole-molecule vibrational modes in the Raman spectra by selectively adding or removing molecular fragments in the molecule.

Results and discussion

Cyanines are molecular plasmons

Cyanine molecules, or molecular jackhammers (MJH) when excited with light, support plasmon resonances with oscillation frequencies that are dependent on the number atoms that participate in the π-conjugation longitudinally through the heptamethine bridge and axially through the polycyclic aromatic hydrocarbon at the benzoindole as illustrated in Fig. 1.^12,24 When a molecular plasmon resonance is photoactivated, the electronic and vibrational oscillations are coupled in a vibronic mode. It is important to clarify that molecular plasmon resonance occurs when multiple electrons interact with the electromagnetic field of incident light and then oscillate coherently. This collective oscillation, which decays coherently, induces an electron density at the interface, resulting in an induced electric field.^15,25 Therefore, plasmonic excitation continues as damped oscillations decay after the driving incident light is turned off. In contrast, when a single electron excitation occurs in a molecule interacting with light, there is no large induced field beyond the screened internal Coulomb interaction between the hole and the electron. Consequently, the induced electric field is weaker in this case.¹⁵ Rabi oscillations generate a dipolar field while the incident light is present. However, once the light stops, the electron and hole recombine in a monotonic manner. This process does not exhibit collective behavior in the same way as a plasmon. In summary, the collective motion of the electrons in a plasmon mode is mainly influenced by its self-induced surface charges, while the dynamics of a pure electron–hole pair excitation (in the context of a classical vibronic transition) are primarily controlled by the incident light. In this article, when we mention collective electron excitations in a molecular plasmon coupling with the vibrational motions, we are referring to a whole-molecule collective vibronic mode, as multiple electrons are involved in coherent motions. It is important to note that in this study, we are not discussing the classical concept of single-electron vibronic transitions.

Fig. 1 Molecular plasmon model and the calculated induced charged density in the optically excited cyanines (MJH). (a) Absorption experimental spectrum of BL-141-1 (Cy7.5) at 2.7 μM in ethanol and assignment of four major molecular plasmon modes (ω₁−ω₄). The frequencies ω₁−ω₄ correspond to the levels ω₁−ω₄ in (b). The absorption shoulder ω₂ is the major vibronic mode, a concerted whole molecule oscillation of the plasmon longitudinally and transversally. The mode ω₁ is a longitudinal molecular plasmon (LMP). The mode ω₄ is a transversal molecular plasmon (TMP). The mode ω₃ is a minor quadrupolar mode of the electronic oscillation longitudinally and transversally with low absorbance. These assignments are supported by time-dependent DFT (TDDFT) calculations from a former study.¹² (b) The assignment of the four molecular plasmon modes to the corresponding pictorial model of the electron density distribution in the cyanine molecule; also supported by the TDDFT calculations. Adapted with permission from John Wiley & Sons, copyright 2023.²⁴ (c) The calculated electron density distribution in the cyanine molecule from the TDDFT calculations. Adapted with permission from Springer Nature, copyright 2023.¹²

The absorption shoulder ω₂ in Fig. 1a is the major vibronic mode, a concerted whole molecule oscillation of the plasmon longitudinally and transversally. The mode ω₁ is a longitudinal molecular plasmon (LMP). The mode ω₄ is a transversal molecular plasmon (TMP). The assignment of ω₁ (LMP) and ω₄ (TMP) was initially done by analogy with the well-known plasmon modes in gold nanorods, where the high wavelength peak (low energy) is a plasmon that oscillates along the longitudinal axis of the nanoparticle while the low wavelength peak (high energy) is a plasmon that oscillates across the transversal axis.²⁶ These assignments were later confirmed by TDDFT calculations.¹² UV-vis spectral analysis of a comprehensive library of cyanines has shown a sensitive dependence of the plasmon resonance frequency on the molecular structure and the dielectric constant of the solvent.²⁴ Here we summarize a systematic series of cyanine structures that illustrate the strong shift of plasmon resonance frequency and change of absorption intensity that depends on the dielectric constant of the solvent (Fig. 2a, 3 and Table 1). This sensitive optical response with respect to the molecular structure and dielectric constant of the solvent is analogous to the behavior of plasmon resonances in metal nanostructures.^27–29 The design and synthesis of molecules (Fig. 2a) are equivalent to the engineering of the size and shape of metal nanostructures while the plasmon resonance shift (Fig. 3) in molecules is equivalent to the localized surface plasmon resonance (LSPR) shift in the metallic counterparts.^6,10,30,31 Based on the sensitive dependence of the plasmon resonance frequency and the absorption intensity as a function of the polarity of the medium, we developed a method to measure the EPI.²⁴ The plasmonicity index measures the plasmonic character of a molecule or nanomaterial. This is important to predict and quantify if an organic molecule can behave as a molecular plasmon. The plasmonicity index is directly proportional to the number of electrons that can participate in the collective plasmon oscillation. Determining the plasmonicity index in molecules by theoretical quantum mechanical methods is a challenging process.^15,32,33 In contrast, the EPI is an easy-to-use and powerful tool to predict and quantify if an organic molecule in solution is a molecular plasmon. The EPI measures the plasmonic character of each molecule based on its plasmon resonance response with respect to the dielectric constant of the medium in which the molecule is dissolved. Molecular plasmons are associated with electron oscillations that are highly polarizable by the polarity of the solvent. Therefore, changes in the dielectric constant (κ) of the solvent affect the light absorption response of a molecular plasmon. This is accomplished by measuring the UV-vis-NIR spectra in different solvents and quantifying the optical response by analyzing the absorption intensity as a function of the solvent polarity (Fig. 4). The EPI represents the slope of the linear correlation between the absorption intensity and the solvent polarity, multiplied by a factor of −1000 to obtain integer positive values since the slope is negative (Fig. 4). A higher value of EPI means that the molecule has a stronger plasmonic character. It is observed that the EPI predicts consistently higher values for structures with a higher number of atoms involved in the π-conjugation, the presence of a 6-carbon ring, which we hypothesize introduces a more rigid structure for better electronic oscillation along the heptamethine bridge, and the presence of an electron-withdrawing group, N,N-dimethylamine-, that induces a perturbation of the molecular plasmon (Fig. 2a, 4 and Table 1). This perturbation is analogous to the perturbation of a large metallic plasmonic nanostructure by a tiny metallic sphere.³⁴ Interestingly, this is another aspect where plasmons in molecules behave similarly to the plasmons in metallic nanostructures; in both cases, the perturbation of a plasmon by a charge induces the degeneration of the energy levels of the dipole (peak) and quadrupole (shoulder) modes resulting in a combined plasmon mode (Fig. S2 of the ESI,† BL-204 and GL-308-2 spectra in water). It is important to clarify that in the case of metal nanoparticles the charge perturbation arises from the induced transient dipole while in the case of cyanine it arises from a permanent charge at the N,N-dimethylamine group. To verify some organic molecules cannot behave as molecular plasmon, we synthesized a control molecule BL-250, having an aromatic benzene ring connected to the heptamethine bridge with both nitrogen atoms charged, impeding the free oscillation of the molecular plasmon longitudinally as shown in Table 1 and Fig. 2c. Therefore, the control molecule BL-250 lacks plasmonicity. The experimental evidence suggests that this model for understanding of the molecular plasmons in molecules is consistent with the knowledge of plasmons in metallic nanostructures.

Fig. 2 Chemical structures of molecular jackhammers (cyanines). (a) Different cyanine structures and systematic increase of the expected plasmonicity from left to right and top to bottom. BL-250 is a control molecule that lacks plasmonicity. The structure of BL-250 contains two positive charges and a benzene ring in the middle that might impede the longitudinal oscillation of the plasmon resonance. Three elements increase the plasmonicity: (1) the number of atoms involved in the π-conjugation system, (2) the 6C-member ring in the middle increases the rigidity and (3) the dimethyl amine facilitates plasmonicity as an electron withdrawing group. (b) Representation of resonant structures of BL-141-1 showing π-electrons moving along the heptamethine bridge. (c) Representation of resonant structures of BL-250 reveals that moving π-electrons along the heptamethine bridge is not feasible because it would require disrupting the highly stabilizing aromaticity of the benzene ring in the middle.

Fig. 3 Plasmon resonance (λ_max) shift as a function of the dielectric constant. IPA = isopropanol (dielectric constant, κ = 19.43), EtOH = ethanol (κ = 24.35), MeOH = methanol (κ = 32.6), water (κ = 78.3). BL-250 is a control molecule that does not behave as molecular plasmon and therefore lacks the property of plasmon resonance shift (λ_max shift) as a nearly linear function of the dielectric constant. The λ_max of BL-250 does not show a linear correlation with the dielectric constant.

Table 1 Tunability of the molecular plasmon resonance and EPI in molecular jackhammers^a

Entry	IPA		EtOH		MeOH		Water
	λ max/nm	Abs	λ max/nm	Abs	λ max/nm	Abs	λ max/nm	Abs	EPI
a Control molecule BL-250 does not support a whole-molecule vibration and lacks plasmonicity. The molecules were analyzed at 2.7 μM concentration. The wavelengths in nm units are converted to eV units and are presented in Table S1 of ESI.
GL-176	743	0.603	742	0.588	739	0.570	735	0.452	2.6
BL-264	749	0.584	748	0.576	744	0.565	741	0.400	3.2
GL-362-1	782	0.455	780	0.432	777	0.425	773	0.240	3.7
BL-141-1	787	0.409	785	0.398	781	0.386	776	0.179	4.0
BL-308-2	784	0.444	784	0.428	780	0.412	762	0.179	4.6
BL-204	789	0.404	787	0.373	783	0.362	767	0.125	4.7
BL-250	432	0.077	427	0.079	414	0.051	426	0.083	−0.2

---

Fig. 4 Experimental plasmonicity index predicts the expected plasmonic character. The experimental plasmonicity index (EPI) for each molecule. Solvents are IPA = isopropanol (dielectric constant, κ = 19.43), EtOH = ethanol (κ = 24.35), MeOH = methanol (κ = 32.6), water (κ = 78.3). The absence of plasmonicity in BL-250 is reflected by a negative EPI value of −0.2 and a poor linear correlation coefficient (R² = 0.11) between the absorbance and the dielectric constant of the solvent.

The plasmonicity index is different than solvatochromism

It is important to clarify that the optical response of a molecular plasmon resonance as a function of the polarity of the solvent is beyond the classical concept of solvatochromism. Solvatochromism can occur indistinctively in molecules with or without plasmon resonances. However, only molecular plasmons in cyanine molecules exhibit two types of linear correlations in their optical response as the polarity of the solvent increases: (1) a negative shifting of the λ_max (Fig. 3) and (2) a decrease of the absorption intensity (Fig. 4). In contrast, solvatochromism does not necessarily exhibit these linear correlations, and it can result in a positive shift (bathochromic) or a negative shift (hypsochromic) or even a reversed shift (a bathochromic shift followed by a hypsochromic shift or vice versa).^35–37 A clear example is the control molecule BL-250, which shows reversed solvatochromism (a hypsochromic shift followed by a bathochromic shift with increasing solvent polarity) and clearly does not exhibit plasmonicity (Fig. 3 and 4). Also, molecules with higher plasmonicity (BL-204 and GL-308-2) show a nearly perfect linear correlation (R² = 0.99), as illustrated in Fig. 3 and 4. This linearity decreases as the plasmonicity of the molecule decreases, and becomes almost zero (R² = 0.01) for the molecule BL-250, which lacks plasmonicity. Overall, studying such optical responses in the context of molecular plasmons provides insights into understanding the photophysical properties of cyanines.

Molecular plasmon fragment hybridization model

We now describe a way in which the plasmon response of a cyanine can be understood as the combination or hybridization of plasmons supported by the molecular fragments; these are the C7 heptamethine bridge and the benzoindole (Fig. 5). Each fragment can support two main electronic oscillation modes: (1) longitudinal (LMP) and (2) transversal (TMP). In principle, there is a third mode which is perpendicular to the plane of LMP and TMP oscillations. However, the contribution of this mode can be considered negligible relative to the intensity of the LMP and TMP modes, as has been shown before.¹² Each orientation of electronic oscillation (LMP or TMP) in each fragment can combine (hybridize) with the respective electronic oscillation in the fragment pair. For example, the LMP of the C7 heptamethine bridge can couple with the LMP of the benzoindole resulting in the major LMP mode ω₁ in the molecule. Similarly, the LMP of the C7 heptamethine can couple with the TMP of the benzoindole resulting in the mode ω₂, and so forth. In summary, this hybridization results in the shifting and splitting of the resonance frequencies resulting in four distinctive plasmon resonance frequencies: a longitudinal dipolar oscillation ω₁, a quadrupolar oscillation ω₂, a quadrupolar oscillation ω₃, and a transversal dipolar oscillation ω₄, which have been assigned and verified with the help of time-dependent DFT calculations as shown in Fig. 1.¹² The same behavior is observed for the hybridization of indole and C7 heptamethine bridge in BL-264, (Fig. S3†). However, in the case of BL-264, the hybrid structure shows a smaller transversal mode ω₄ in the absorption intensity since the indole only contains one benzenoid ring, which reduces the π-conjugation along the transversal axis. This is also evident in a shift of the resonance frequency (a lower λ_max). Therefore, the shift is mainly determined by the number of electrons in the π-conjugation within the heptamethine bridge and the benzoindole.

Fig. 5 Construction of molecular plasmon hybridization model in BL-141-1 (Cy7.5 cyanine). This model is analogous to a combination of molecular orbital theory and plasmon hybridization theory in metallic nanoparticles. (a) Hybridization of molecular fragments give rise to hybridized molecular plasmon. (b) Spectrum of benzoindole fragment. (c) Spectrum of heptamethine bridge. (d) Spectrum of hybridized molecular plasmon.

Raman spectroscopy supports the molecular plasmon hybridization model

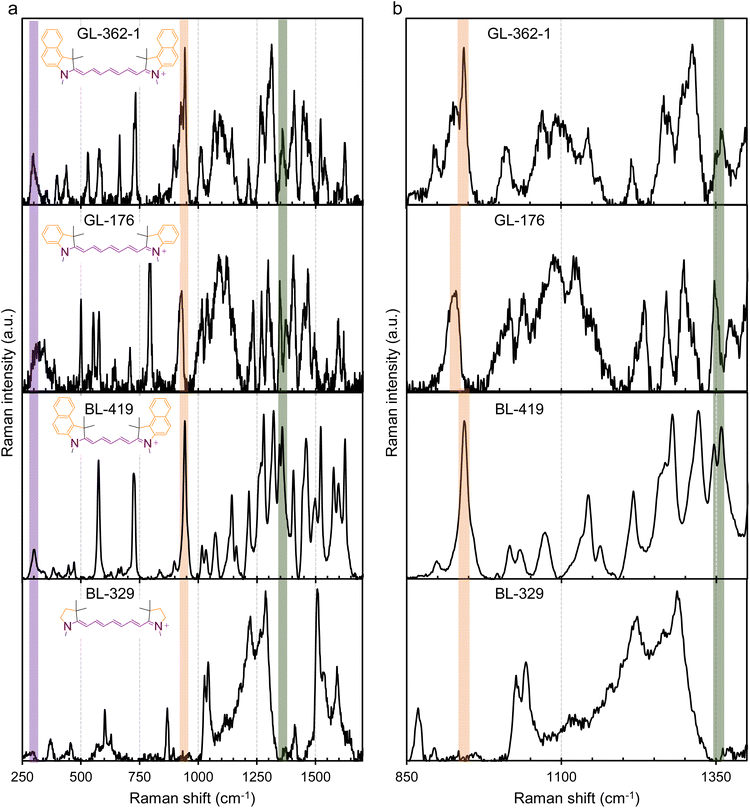
To further validate molecular plasmons in cyanines and the molecular plasmon hybridization model, we conducted Raman spectroscopy studies on the cyanines Cy7.5 (BL-141-1) and Cy7 (BL-264) and their respective molecular fragments. The major vibrational modes associated with the molecular plasmon oscillation in cyanines were resolved by Raman spectroscopy (Fig. 6 and S4 of ESI†). The Raman spectra of the fragments and the non-plasmonic BL-250 control were critical for the assignment. The vibration associated with the LMP resonance is highlighted by the purple band at ∼300 cm⁻¹ for BL-141-1 and BL-264 and at ∼280 cm⁻¹ for BL-328 in Fig. 6 and S4.† The vibration associated with the TMP resonance is highlighted by the orange band at ∼940 cm⁻¹. The concerted whole-molecule vibration associated with the quadrupolar resonance is highlighted by the green band at ∼1345–1355 cm⁻¹ in Fig. 6, S4, and summarized in Table S2 of ESI.† These Raman frequency assignments are supported by the literature.¹⁸ Both molecules, Cy7.5 and Cy7, show LMP and TMP and whole-molecule vibrations. Interestingly, the heptamethine fragment (BL-328) shows the vibrational band associated with the LMP resonance at ∼280 cm⁻¹ but they lack the whole-molecule vibration at ∼1345–1355 cm⁻¹ and the ∼945 cm⁻¹ associated with the TMP resonance, as expected from the plasmon hybridization model in Fig. 5. The control molecule BL-250 (Fig. S2†), which lacks an LMP mode in the UV-vis spectrum, displays a band at ∼945 cm⁻¹ since only the oscillation along the benzoindole is possible, as expected and predicted from the EPI measurements. The spectrum of the benzoindole (fragment BL-68) shows the vibrational band associated with the TMP resonance at ∼940 cm⁻¹ but it lacks LMP-associated vibration and whole-molecule vibration in agreement with the model (Fig. 6). The spectrum of the indole (fragment BL-263) shows the vibrational band associated with the TMP resonance as expected (Fig. S4 of ESI†). However, BL-263 shows a broad and low-intensity peak at ∼1350 cm⁻¹. This peak has different characteristics than the whole molecule-vibration peak which is usually a distinctive narrow and high-intensity peak as is observed in BL-264 in Fig. S4† and BL-141-1 in Fig. 6. Similar analyses of GL-362-1 and GL-176, both without the six-membered carbon ring in the middle, and their respective fragment (BL-329) are shown in Fig. 7. These show that the LMP, TMP, and whole-molecule-associated vibrations can be assigned to their respective longitudinal, axial, and whole-molecule contributions in the cyanine molecules. In the molecular fragment (BL-329), the LMP vibration at ∼295 cm⁻¹ can be assigned to its respective longitudinal contribution. In this case, the LMP vibration of the BL-329 fragment closely matches the LMP vibration of the whole-molecule GL-362-1 at ∼298 cm⁻¹. The results are summarized in Table S2 of ESI.† It is interesting to note that the oscillation frequencies of the whole-molecule concerted vibrations (Raman peak ∼1345–1355 cm⁻¹) are very fast molecular motions at ∼40 × 10¹² s⁻¹ which is equivalent to 25 fs per a single oscillation. Fast whole-molecule concerted vibrations are important in MJH for the mechanical opening of cellular membranes in cancer treatment. The oscillation rates were calculated by converting the Raman vibrational frequencies in cm⁻¹ units to frequencies in hertz (s⁻¹) units. Overall, these observations support that larger and more complex molecular plasmons can be synthesized utilizing a more elementary molecular plasmon as a building block through plasmon hybridizations.

Fig. 6 Major vibrational-plasmon modes in MJH (cyanines) resolved by Raman spectroscopy. The spectrum in column (a) is for the extended Raman shift range (250–1700 cm⁻¹) and the spectrum in (b) is for a narrow Raman shift range (850–1400 cm⁻¹) for better observation of the peaks. The LMP vibration is highlighted by the purple band at ∼298 cm⁻¹ for BL141-1 and at ∼280 cm⁻¹ for BL-328, the TMP vibration is highlighted by the orange band ∼945 cm⁻¹ and the concerted whole-molecule vibration is highlighted by the green band ∼1345–1355 cm⁻¹. The Raman spectrum of BL-141-1 (Cy7.5) shows the LMP and TMP and whole-molecule vibration. The spectrum of control molecule BL-250 lacks the LMP mode and whole-molecule vibration as expected and predicted by the EPI measurement (Fig. 4). The spectrum of the benzoindole (BL-68) shows the TMP but lacks LMP and the whole-molecule vibration. The spectrum of the heptamethine bridge (BL-328) shows the LMP mode and lacks the TMP and the whole-molecule vibration mode as expected.

Fig. 7 Conservation of major vibrational-plasmon modes among different MJH structures (cyanines). The spectrum in column (a) is for the extended Raman shift range (250–1700 cm⁻¹) and the spectrum in (b) is for a narrow Raman shift range (850–1400 cm⁻¹) for better observation of the peaks. The LMP vibration is highlighted by the purple band at ∼300 cm⁻¹, the TMP vibration is highlighted by the orange band ∼945 cm⁻¹ for BL-362-1 and ∼926 cm⁻¹ for BL-176, and the concerted whole-molecule vibration is highlighted by the green band ∼1345–1355 cm⁻¹. The Raman spectra of BL-362-1, BL-176, and BL-419 show the LMP and TMP and whole-molecule vibration. The spectrum of the heptamethine bridge (BL-329) shows the LMP mode and lacks the TMP and the whole-molecule vibration mode as expected.

It was observed that cyanines with a polymethine bridge containing 7 carbons (Cy7.5) have a relatively low-intensity whole-molecule vibration band in the Raman spectrum (∼1350 cm⁻¹) relative to other peaks with high intensity. This observation is also made for the molecules BL-141-1 (Fig. 6) and GL-362-1 (Fig. 7). This weak intensity of the whole-molecule vibration in BL-141-1 and GL-362-1 might be attributed to the observation that the wavelength of the laser (633 nm) for the excitation at the Raman microscope is less capable of exciting whole-molecule vibronic modes in comparison to the Cy7 counterparts BL-264 and GL-176. The Cy7.5 molecules BL-141-1 and GL-362-1 have the whole-molecule vibronic shoulder in solution at ∼720 nm while the Cy7 molecules BL-264 and GL-176 have it at ∼680 nm in solution as shown in the UV-vis spectrum (Fig. S2†). The Raman spectra were acquired from solid powder samples while the UV-vis spectra were acquired in solution. Therefore, the position of the Raman absorption for the whole-molecule vibration in solid form is expected to be different than the UV-vis absorption in solution. However, the relative positions should be conserved. This implies that the more red-shifted absorption spectra of the molecules BL-141-1 and GL-362-1 in the UV-vis spectra in solution should be more red-shifted in the solid samples relative to the Cy7 molecules BL-264 and GL-176. Overall, this explains why the excitation lasers of 532 nm and 633 nm in the Raman microscope are more capable of exciting the whole-molecule vibronic shoulder in Cy7 molecules as shown in Fig. S5 of ESI.† Therefore, a higher intensity whole-molecule vibronic mode is detected in Cy7 molecules than in Cy7.5 molecules. To verify that this observation is correct, we further analyzed a Cy5.5 molecule with 5 carbons in the polymethine bridge as shown in Fig. 7. For Cy5.5 molecules the whole-molecule vibronic shoulder in the UV-vis spectrum is blue-shifted to ∼640 nm.^12,24 Based on this result, the 533 nm laser in the Raman microscope was better for exciting the whole-molecule vibronic shoulder and produced a more intense signal in the Raman spectrum ∼1350 cm⁻¹, relative to the other peaks (Fig. 7). It is important to clarify that a better signal-to-noise ratio was observed when the laser-excited a wavelength that was offset to the left of the position of the vibronic shoulder. When the laser was used to excite a wavelength more towards the peak or shoulder of the absorption spectrum, a strong fluorescence signal was observed. These observations led us to choose the best available laser for the excitation of each molecule as described in materials and methods.

Conclusion

In conclusion, we provide further experimental evidence for the existence of molecular plasmons in cyanines. This molecular plasmon is associated with a concerted whole-molecule vibration that is detected and confirmed by Raman spectroscopy. A control molecule, BL-250, in which the free oscillation of the molecular plasmon was impeded, was synthesized. The control molecule lacks the whole-molecule vibration as indicated in its Raman spectrum, while cyanines consistently show the concerted-whole molecule vibration at ∼1345–1355 cm⁻¹. Likewise, the molecular plasmon in cyanines shows similar physical behaviors to those observed in the plasmonic metallic nanostructure counterparts such as plasmon resonance tunability, obtained by engineering molecular structure modifications and controlling the dielectric constant of the medium in which the cyanines are dissolved. The plasmon hybridization model in molecules can be regarded conceptually as a combination of molecular orbital theory and plasmon hybridization model in metal nanoparticles. Our proposed plasmon hybridization model in cyanine molecules could lead to the understanding and synthesis of larger and more complex molecular plasmons using elementary molecular plasmons as building blocks through plasmon hybridizations.

Materials and methods

Solvents

The following solvents were used to carry out the optical measurements in the molecular plasmons that are sensitive to the purity of the solvent. Methanol, (ACS spectrophotometric grade, >99.9%, Millipore-Sigma, catalog #154903); ethanol (200 proof, anhydrous, Decon Labs, Inc., catalog #2716); isopropanol, (HPLC spectrophotometric grade, Supelco, catalog #PX1834-6); and deionized water that was obtained with a Millipore water purifier system.

Experimental plasmonicity index (EPI)

EPI is a newly determined parameter that we recently developed.²⁴ To calculate the EPI, each molecule was solubilized in various solvents at 2.7 μM and the UV-vis spectra were measured. The solvents were chosen to cover a wide range of dielectric constants at 25 °C: isopropanol (κ = 19.43), ethanol (κ = 24.35), methanol (κ = 32.6), water (κ = 78.3).^38,39 Then the absorbance at the λ_max was plotted as a function of the dielectric constant and the EPI is the slope of the linear correlation function multiplied by a factor of −1000 to obtain integer positive values since the slope is negative EPI = −1000 × slope.

Raman spectroscopy

The Raman spectra were measured in a Renishaw inVia Raman microscope. For option A acquisition settings, an extended acquisition mode, 633 nm laser, 10 s exposure time, 0.5% laser power, 50× objective lens, 15 accumulations per analysis, cosmic ray subtraction, and background subtraction were used. For option B acquisition settings, an extended acquisition mode, 532 nm laser, 10 s exposure time, 0.1% laser power, 50× objective lens, 10 accumulations per analysis, cosmic ray subtraction, and background subtraction were used. The acquisition settings in option A were applied to molecules BL-141-1, BL-264, GL-176, and GL-362-1. The acquisition settings in option B were applied to BL-68, BL-263, BL-250, BL-328, BL-329, GL-176, GL-362-1 and BL-419. Different acquisition parameters (option A or option B) were used to obtain the best signal-to-noise ratio. WiRE 5.6 software was used to process the data collection and analysis. The samples were in powder form. A calibration with a silicon standard (Raman peak centered at 520.5 cm⁻¹) was performed.

Data availability

Additional graphs, charts, NMR spectra and synthesis details are provided in the ESI.† Essential data are provided in the main text and ESI.† Additional data are available from the corresponding author on reasonable request.

Author contributions

C. A.-O. conceptualized the model, the designs of the molecular fragments and elements of the model, and their photophysical characterization and interpretation. B. L. synthesized most of the cyanine molecules and molecular fragments. G. L. synthesized some cyanine molecules. J. M. T. oversaw the research and obtained the financial support. C. A.-O. wrote the initial version of the manuscript. The final version of the article was written through the contributions of all authors.

Conflicts of interest

Rice University owns intellectual property on the use of MJH for permeabilization of cell membranes. The authors declare no other potential conflicts.

Acknowledgements

This research was supported by The Discovery Institute and The Welch Foundation C-2017-20220331. We thank Dr D. K. James for editing and revising the manuscript. We thank Professor Peter Nordlander for the helpful discussions on plasmon physics.

References

1. W. A. Murray and W. L. Barnes, Adv. Mater., 2007, 19, 3771–3782.
2. N. J. Halas, S. Lal, W. S. Chang, S. Link and P. Nordlander, Chem. Rev., 2011, 111, 3913–3961.
3. X. Zhang, J. He, Y. Wang and F. Liu, Sci. Rep., 2016, 6, 1–8.
4. E. Ozbay, Science, 2006, 311, 189–193.
5. H. A. Atwater and A. Polman, Nat. Mater., 2010, 9, 205–213.
6. J. N. Anker, W. P. Hall, O. Lyandres, N. C. Shah, J. Zhao and R. P. Van Duyne, Nat. Mater., 2008, 7, 442–453.
7. R. Bardhan, S. Lal, A. Joshi and N. J. Halas, Acc. Chem. Res., 2011, 44, 936–946.
8. Z. Zheng, W. Xie, B. Huang and Y. Dai, Chem. Eur. J., 2018, 24, 18322–18333.
9. A. Manjavacas, F. Marchesin, S. Thongrattanasiri, P. Koval, P. Nordlander, D. Sánchez-Portal and F. J. García De Abajo, ACS Nano, 2013, 7, 3635–3643.
10. A. Lauchner, A. E. Schlather, A. Manjavacas, Y. Cui, M. J. McClain, G. J. Stec, F. J. García De Abajo, P. Nordlander and N. J. Halas, Nano Lett., 2015, 15, 6208–6214.
11. Y. Cui, A. Lauchner, A. Manjavacas, F. J. García De Abajo, N. J. Halas and P. Nordlander, Nano Lett., 2016, 16, 6390–6395.
12. C. Ayala-Orozco, D. Galvez-Aranda, A. Corona, J. M. Seminario, R. Rangel, J. N. Myers and J. M. Tour, Nat. Chem., 2024, 16, 456–465.
13. C. M. Krauter, S. Bernadotte, C. R. Jacob, M. Pernpointner and A. Dreuw, J. Phys. Chem. C, 2015, 119, 24564–24573.
14. C. M. Krauter, J. Schirmer, C. R. Jacob, M. Pernpointner and A. Dreuw, J. Chem. Phys., 2014, 141, 104101.
15. R. Zhang, L. Bursi, J. D. Cox, Y. Cui, C. M. Krauter, A. Alabastri, A. Manjavacas, A. Calzolari, S. Corni, E. Molinari, E. A. Carter, F. J. García De Abajo, H. Zhang and P. Nordlander, ACS Nano, 2017, 11, 7321–7335.
16. F. F. Kong, X. J. Tian, Y. Zhang, Y. J. Yu, S. H. Jing, Y. Zhang, G. J. Tian, Y. Luo, J. L. Yang, Z. C. Dong and J. G. Hou, Nat. Commun., 2021, 12, 1–8.
17. T.-S. Yang, M.-S. Chang, R. Chang, M. Hayashi, S. H. Lin, P. Vöhringer, W. Dietz and N. F. Scherer, J. Chem. Phys., 1999, 110, 12070.
18. H. Mustroph and A. Towns, ChemPhysChem, 2018, 19, 1016–1023.
19. R. S. Mulliken, Phys. Rev., 1928, 32, 186.
20. J. E. Lennard-Jones, Trans. Faraday Soc., 1929, 25, 668–686.
21. G. G. Hall, Adv. Quant. Chem., 1991, 22, 1–6.
22. E. Prodan, C. Radloff, N. J. Halas and P. Nordlander, Science, 2003, 302, 419–422.
23. F. Hund, J. Phys., 1928, 51, 759–795.
24. C. Ayala-Orozco, G. Li, B. Li, V. Vardanyan, A. B. Kolomeisky and J. M. Tour, Adv. Mater., 2024, 36, 2309910.
25. L. Bursi, A. Calzolari, S. Corni and E. Molinari, ACS Photonics, 2014, 1, 1049–1058.
26. P. K. Jain, S. Eustis and M. A. El-Sayed, J. Phys. Chem. B, 2006, 110, 18243–18253.
27. S. J. Oldenburg, R. D. Averitt, S. L. Westcott and N. J. Halas, Chem. Phys. Lett., 1998, 288, 243–247.
28. E. Prodan, A. Lee and P. Nordlander, Chem. Phys. Lett., 2002, 360, 325–332.
29. M. D. Malinsky, K. L. Kelly, G. C. Schatz and R. P. Van Duyne, J. Am. Chem. Soc., 2001, 123, 1471–1482.
30. K. A. Willets and R. P. Van Duyne, Annu. Rev. Phys. Chem., 2007, 58, 267–297.
31. J. Zhang, G. Kolhatkar and A. Ruediger, J. Mater. Chem. C, 2021, 9, 6960–6969.
32. L. Bursi, A. Calzolari, S. Corni and E. Molinari, ACS Photonics, 2016, 3, 520–525.
33. S. Gil-Guerrero, Á. Peña-Gallego and M. Mandado, J. Phys. Chem. C, 2019, 124, 1585–1593.
34. L. Shao, C. Fang, H. Chen, Y. C. Man, J. Wang and H. Q. Lin, Nano Lett., 2012, 12, 1424–1430.
35. A. Marini, A. Muñoz-Losa, A. Biancardi and B. Mennucci, J. Phys. Chem. B, 2010, 114, 17128–17135.
36. A. S. Klymchenko, Acc. Chem. Res., 2017, 50, 366–375.
37. A. Mishra, R. K. Behera, P. K. Behera, B. K. Mishra and G. B. Behera, Chem. Rev., 2000, 100, 1973–2012.
38. A. Chmielewska, M. Zurada, K. Klimaszewski and A. Bald, J. Chem. Eng. Data, 2009, 54, 801–806.
39. C. G. Malmberg and A. A. Maryott, J. Res. Natl. Bur. Stand., 1956, 56, 2641.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc04846f

‡ These authors contributed equally to this work.

§ Present address: Cy Therapeutics, Missouri City, Texas 77459, United States.

---