Open Access Article
Open Access ArticleDynamic flow experiments for Bayesian optimization of a single process objective†
Federico
Florit
 a,
Kakasaheb Y.
Nandiwale
a,
Kakasaheb Y.
Nandiwale
 b,
Cameron T.
Armstrong
b,
Cameron T.
Armstrong
 b,
Katharina
Grohowalski
b,
Angel R.
Diaz
b,
Jason
Mustakis
b,
Steven M.
Guinness
b and
Klavs F.
Jensen
b,
Katharina
Grohowalski
b,
Angel R.
Diaz
b,
Jason
Mustakis
b,
Steven M.
Guinness
b and
Klavs F.
Jensen
 *a
*a
aMassachusetts Institute of Technology, Department of Chemical Engineering, Cambridge, MA 02139, USA. E-mail: kfjensen@mit.edu
bChemical Research and Development, Pfizer Worldwide Research and Development, Groton, Connecticut 06340, USA
First published on 11th December 2024
Abstract
A new method, named dynamic experiment optimization (DynO), is developed for the current needs of chemical reaction optimization by leveraging for the first time both Bayesian optimization and data-rich dynamic experimentation in flow chemistry. DynO is readily implementable in automated systems and it is augmented with simple stopping criteria to guide non-expert users in fast and reagent-efficient optimization campaigns. The developed algorithms is compared in silico with the algorithm Dragonfly and an optimizer based on random selection, showing remarkable results in Euclidean design spaces superior to Dragonfly. Finally, DynO is validated with an ester hydrolysis reaction on an automated platform showcasing the simplicity of the method.
When novel chemical reactions are discovered or modifications to existing reactions are done, optimization is a required step of the chemistry development procedure, while also being a crucial need in current research development.1 For this task, fast and possibly automated optimization methods of black-box functions are needed,2,3 as a full chemical kinetics characterization may be an excessive endeavor with classical methodologies, especially if the reaction is new, and the mechanism unknown.4,5 Also, when the experiments involve expensive reactants, optimization should proceed with reduced amounts of chemicals and waste.6 Furthermore, it has been shown that such computational methods outperform human intuition and led to faster/cheaper optimization campaigns.7
Bayesian optimization (BO) methods have seen an increasing application in as a solution to obtain data-driven optimization campaigns.2 These methods are very efficient for automatic optimization with very minor human intervention, making their implementation in chemistry discovery appealing. These methods find applications in both batch (discontinuous) and flow (continuous) reactors, showing the flexibility of the approach.
BO methods have seen applications in chemistry in combination with simple response-surface methods.8 Several parameters (which number would be excessive for classical, user-based experimentation and interpretation) have also been considered simultaneously using recently the TSEMO9 and the BOAEI10 algorithms. Also, cost-aware parallelized BO algorithms (CAPBO) have been developed11 to underline that the relevant goal in chemistry optimization is the cost of the experimentation and not the number of experiments performed. Efficient, automated sampling becomes thus critical for optimal conduction of BO campaigns.12 BO has also been applied for fast chemical reactions in combination with mass spectroscopy.13 It is worth noting that, given the complexity of the algorithms, non-expert users should be guided, possibly with simple interfaces and instructions.14
An emerging tool to explore a chemical design space is dynamic experiments (DynE) in flow chemistry, that is, optimization parameters are changed over time in a continuous reactor which is not operated at steady state. These methods can produce rich data sets with advantages over classical, steady experiments, as more data can be collected in shorter times, while saving reagents and time.15 The change of the parameters over time effectively creates trajectories which sample the design space in an ordered fashion. DynE best work in Euclidean, continuous design spaces, typical of chemical reactions where optimization variables are continuous (residence time, inlet composition, temperature, light intensity, wavelength, voltage, …). Such variables usually represent the majority of the optimization parameters, while discrete (categorical) variables (e.g., choice of solvent and catalyst) may be set from previous discovery experiments or can be treated as separate systems. A workaround for discrete variables is to transform them in continuous ones: for example, solvent choice (among two or three candidates) can become a problem of binary/ternary solvent mixture optimization.16
The early works of several groups17–20 have set foundation for newer and sophisticated methods aimed at optimization and chemical kinetics analysis with DynE. Optimization procedures using gradient-based methods were adapted to DynE by alternating circular trajectories (around a central point in the design space) and gradient search with linear trajectories (to move the central point to a better location).6 Kinetic analysis has been performed with DynE changing up to five parameters simultaneously9 and by leveraging a digital twin.21 Kinetic parameters were found even in multi-phase systems (catalytic reactor with gas–liquid stream) ramping reactant flow rates at different (constant) temperatures.5
In this work, we develop for the first time a dynamic experiment optimization method (DynO) in a Bayesian optimization framework to combine the advantages of both function optimization and data-rich experimentation. DynO is compared with the widely used algorithm Dragonfly22 in a parametric analysis using a simulated reaction as a case study with three optimization parameters (residence time, reactant ratio, and temperature) to highlight the advantages of DynO in terms of experimental time and reagent consumption. Finally, DynO is validated experimentally in tubular reactor on a Polar Bear Plus Flow™ reactor (Uniqsis) for an ester hydrolysis reaction. The experiment is run with two parameters (residence time and reactants ratio) to best display the algorithmic steps, which lead to an optimal result in the explored domain with only two experiments, while also collecting an important amount of data which could be used for kinetic studies.
1 Materials and methods
1.1 DynO algorithm development
A brief summary of the use of dynamic flow experiments (DynE) will be presented in section 1.1.1, while some details on BO can be found in section S1 in the ESI.† These tools will be combined in section 1.1.2, where the detailed development of the proposed optimization methodology is presented. In this work, without loss of generality, we focus on the maximization of an objective (minimization can be done with the same algorithms by maximizing the negative objective).The value of the objective Y measured at each time t in a DynE corresponds to the value obtained at steady-state for some particular set of conditions (reconstructed parameters, X). Such variables are not necessarily corresponding to the ones set at time t (instantaneous parameters, XI), as a plug-flow introduces a time delay corresponding to the plug residence time, τ. Therefore, a DynE is a trajectory in the design space provided a proper reconstruction of the conditions that produced a certain value of the objective.
Parameters can be classified as inlet variables (set at the inlet of the reactor, such as the composition) and reactor-wide variables (that affect the entire reactor, such as temperature, voltage, light intensity). The former type is reconstructed by observing the value of the instantaneous parameter back in time by a residence time; the latter variables are reconstructed by taking the integral average of the parameter over a time span equal to the current residence time.23 This means:
 | (1) |
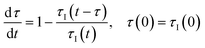 | (2) |
The choice of the shape of XI(t) (and thus also τI(t)) is arbitrary; in this work we use sinusoidal variations of such parameters, extending the definition used in a previous work.23 Sinusoidal variations were chosen for their flexibility in describing trajectories in the design space. In fact, if the wave parameters are chosen properly (following the Lissajous curves constraints), the obtained trajectory in the design space can also describe a polynomial shape, thus making commonly used trajectories (usually linear or circular) a particular case of the used sinusoidal variations. The general equation for the variations reads:
 | (3) |
 | (4) |
The main advantage of DynE is that they are data-rich experiments, providing more information than steady-state experiments with reduced amounts of chemicals employed and over a shorter experimental time. In a DynE, a steady-state is initially established by waiting for a time equal to a selected number of residence times, nτ, after which (at t = 0) the sinusoidal variations of the parameters take effect (usually nτ ≥ 3).
It is possible to evaluate a priori the volume of chemicals required in a DynE, VDynE, in relation to the reactor volume, Vrxt, as:
 | (5) |
 . The user should also provide the sampling time ΔtS. DynO is summarized in Algorithm 1 and described hereafter.
. The user should also provide the sampling time ΔtS. DynO is summarized in Algorithm 1 and described hereafter.
As for every BO algorithm, initialization is required to predict a new trajectory to test experimentally. This can be done by using data both collected using dynamic or steady experiments. For steady data, randomization is usually the best choice. For initialization with dynamic experiments we suggest using Lissajous curves able to explore the whole design space while satisfying the slow-variations criterion (eqn (4)). The trajectory is centered at the center of the design space, thus:
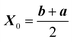 | (6) |
 | (7) |
![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) (corresponding to the largest period considered) and a factor f ∈
(corresponding to the largest period considered) and a factor f ∈ ![[Doublestruck N]](https://www.rsc.org/images/entities/char_e171.gif) (giving the shape of the Lissajous curve) via:
(giving the shape of the Lissajous curve) via: | (8) |
 | (9) |
Once initialization is completed the GP can be trained. The design space is normalized to a unitary hypercube  to simplify calculations, given the boundedness of the domain. In this work an anisotropic 3/2 Matérn kernel is used, but any other functional is allowed. During training of the GP, measurement noise is evaluated as an hyperparameter, which will also account for all non-idealities of the DynO methodology, treating them as independent and identically distributed noise. GP regression is performed with the readily available Python package Scikit-Learn.24
to simplify calculations, given the boundedness of the domain. In this work an anisotropic 3/2 Matérn kernel is used, but any other functional is allowed. During training of the GP, measurement noise is evaluated as an hyperparameter, which will also account for all non-idealities of the DynO methodology, treating them as independent and identically distributed noise. GP regression is performed with the readily available Python package Scikit-Learn.24
It should be noted that other similar kernels, such as the commonly used 5/2 (or larger) Matérn kernels and radial basis functions, may restrict the objective to very smooth shapes, possibly being unable to capture (rare) sharp changes in the objective; the 3/2 kernel is able to predict both sharp and smooth objectives. Other kernels (periodic, dot product) can be used, but have generally few applications for common flow chemistry objectives such as yield, productivity, and environmental indexes.
With a trained GP it is possible to maximize an acquisition function to obtain the new experiment parameters (X0, δ, T, φ, NS). The present acquisition function (based on UCB25) was developed to consider the contribution of each individual point of the trajectory with the addition of a repulsive term to avoid the collapse of the trajectory to a single point. The parameters of the new trajectory are then obtained by iteratively maximizing:
 | (10) |
 | (11) |
The maximization of α is done via a differential evolution algorithm from SciPy in Python. It is worth noting that the solution to this problem is not unique for a trajectory: as a trivial example, the same trajectory in the design space can be traced in two opposite directions, producing similar (if not equal) values of α. Nevertheless, the area in which the trajectory is located will hardly change and only its shape may vary.
A new proposed experiment can then be run and the GP retrained. Now new experimental conditions can be suggested again, and the procedure repeated up to convergence. Convergence can be assessed by observing different measures and we considered:
C.0 similarity between optima found experimentally and estimated from the GP (using a 10% significance Z-test);
C.1 similarity between such optima locations (distance lower than d0);
C.2 low uncertainty of the GP-estimated optimum (standard deviation lower than 5%);
C3 similarity of location distance over iterations (distance with last optimum lower than d0).
A combination of these criteria can also be used, as it will be observed in the parametric analysis in section 2.
1.2 Experimental setup
Dynamic optimization of a case study reaction, ester hydrolysis, was performed in 5 mL plug flow reactors (PFRs) on a Polar Bear Plus Flow™ reactor (Uniqsis) (Fig. S1 and S2†) to validate the proposed model. A schematic of the ester hydrolysis reaction is in shown Fig. S3.†LabVIEW™ (National Instrument, NI ver. 2021.0) and MATLAB® & SIMULINK® (MathWorks, Inc., ver. R2022a) were used to enable automated dynamic experimentation. The LabVIEW virtual instrument (VI) automation user interface was designed and written completely in-house for controlling the Polar Bear Plus Flow reactor (Uniqsis), VICI Milligat six pumps array (Global FIA, VICI M6), flow rate manipulation, temperature control, online ultra high-performance liquid chromatography (UHPLC) sampling, and analysis (Fig. S4 and S5†). We achieved the automated dynamic experimentation by the integration of sinusoidal trajectories (eqn (3)) with the MATLAB-Script node in LabVIEW.
The analysis of product mixture was carried out with Agilent 1260 Infinity II online UHPLC with an IClass QDA mass spectrometer (MS). NI USB 6009 Data Acquisition (DAQ) with digital I/O (DIO) device was used for automated sampling and analysis on UHPLC via enhanced remote interface (ERI) signal. The Agilent 1260 Infinity II online sample manager (G3167AA) set comprised of the Agilent 1260 Infinity II online sample manager (G3167A) and the Agilent 1290 Infinity II valve drive (G1170A) with external sampling valve (Fig. S2†). The external valve drive (G1170A) with a valve head (3-position/6-port FI) served as an external sampling interface, which was synchronized with the inner injection valve of the online sample manager. The online UHPLC provided enhanced injection flexibility of process samples with flexible sampling and injection volumes (0.1 to 100 μL). In addition, it allowed direct injections, automated dilutions (up to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1000), reaction quenching, and sample archiving via online retain-sample functionality.
1000), reaction quenching, and sample archiving via online retain-sample functionality.
2 Parametric analysis and algorithmic comparison
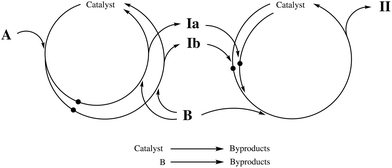
To showcase the capabilities of DynO, a synthetic case study is conducted on a test reaction with selectivity issues in a simulated tubular reactor. A reaction (following the scheme of a Suzuki–Miyaura coupling) is considered between a di-halogenated species A and phenylboronic acid B as from Fig. 1. Also, catalyst deactivation and protodeboronation of B are considered. Ia and Ib are mono-substituted products (in the two possible positions) and II is the di-substituted product. Each reaction follows the Suzuki coupling mechanism where oxidative addition (OA) and transmetallation (TM) are considered, while reductive elimination is assumed to be instantaneous. The following parametric analysis considers the optimization of an objective at different values of the reaction rate constants, in particular at changing value of the ratio between OA and TM rate constants. Further details can be found in section S4 in the ESI.†The objective to be maximized corrects yield of Ia by considering the use of reactants (favoring solutions using smaller amounts of chemicals) and residence time (favoring lower residence times slightly):
 | (12) |
The analysis is run optimizing the reaction with DynO considering different initialization methods (random/steady vs. dynamic), speeds of variation of the parameters (i.e., the values of K), and sampling times (slow vs. fast analysis methods, e.g., HPLC vs. FTIR) for 60 different sets of kinetic constants (see ESI†), according to Table 1. Cases 1–4 were also repeated with the state-of-art algorithm Dragonfly22 and a purely random (steady) optimizer to compare the results, all algorithms being initialized with the same data. Cases 5–7 study the effect of initializing DynO with a DynE (Lissajous trajectory) instead of random points.
The learning curves of the algorithms were observed by reporting relative regret (i.e., the difference between the optimal objective and the objective that is achieved relative to the true optimum value) against number of data points used in the optimization campaign, experimental time (i.e., time required for running the experiments in real life), and volume of reagents needed for the optimization campaign (divided by the reactor volume). It should be stressed that in a real-life scenario experimental time and volume of reagents are the variables of interest for a successful optimization campaign, rather than the number of samples, if the cost of the analysis is negligible compared to equipment up-time and chemicals cost, which is generally the case. Additionally, the possible presence of noise in the objective was analyzed for all considered cases, with the objective being tainted with independent and identically distributed noise equal to 1% of the optimum value. All learning curves are analyzed in terms of geometric average of the regret (average of log-regret) and geometric standard deviation.
DynO is run for a maximum of 10 iterations after initialization, while Dragonfly and the random optimizer are run for a maximum of 65 data points after initialization.
The learning curves for cases 1–4 using the three algorithms are reported in Fig. 2 when no noise in the objective is considered. DynO seems to always be outperformed by Dragonfly and to behave similarly to or worse than random in the classical view of sample complexity. This behavior is expected as DynO is a data-rich method, while Dragonfly and random rely on steady experiments to collect data. On the other hand, in the majority of the cases, DynO learns faster then Dragonfly in terms of both experimental time and volume of reagents, the quantities that are important to practical optimization. The learning curves imply that DynO is able to collect data more efficiently than Dragonfly (and random).
In cases 1 and 2 (low speed of variation, steady state reached in 3 times the residence time), DynO is able to decrease regret in a sub-linear fashion (on the bi-logarithmic plot) since the beginning, while Dragonfly behaves similarly to random at the beginning of the optimization procedure. The comparison of cases 1 and 2 for DynO shows that there is no real advantage in doubling the number of initialization points (from 10 to 20) as similar regrets can be reached with lower time/volume complexity with fewer initialization points.
When cases 3 and 4 are considered (high speed of variation), DynO behaves efficiently with a linear or super-linear trend. Notably for there cases, the time waited to reach steady state is lower (1.5 times the residence time), yet DynO outperforms Dragonfly on the long run, reaching very low values of regret. Comparing cases 3 and 4 for DynO shows that the algorithm is slightly more efficient in regret reduction when a fast sampling method is used, exploiting the data-richness of the underlying DynE.
Overall, this analysis demonstrates that DynO outperforms and, at worst, behaves as Dragonfly. Additionally, on long runs DynO steadily decreases regret, while Dragonfly tends to a plateau, suggesting that DynO behaves as a no-regret optimization method (as it is based on UCB, which is no-regret25).
When a noisy objective is considered, the learning curves change to those reported in Fig. 3 (a dashed line also reports the noise level). All considerations above remain unchanged, with DynO outperforming Dragonfly and quickly reaching a regret lower than the noise level.
Fig. 4 helps comparing the different ways of initialization for DynO, with steady or dynamic experiments in a noise-free setting. A couple of cases are compared: 1 and 5 have slow variations and slow sampling method, 3 and 6 have fast variations and slow sampling, while 4 and 7 have fast variations and fast sampling. In all cases, using a DynE to initialize DynO helps regret reduction in terms of time (i.e., it requires a lower or equal time to reach the same regret). No advantage is observed in terms of volume, which is in any case lower than the one required by Dragonfly as per the discussion above.
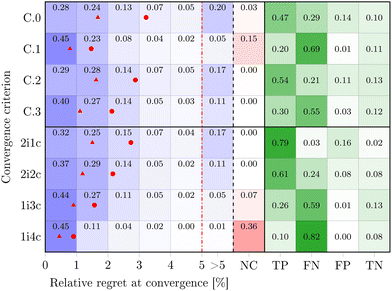
Finally, we analyzed different convergence criteria. The data summarized in Fig. 5 are based on using the average values obtained in all considered cases. The regret at convergence of the analyzed cases is reported for the four basic criteria (C.0–C.3) individually and four new combined criteria. The plot uses a linear scale, as in real-life scenarios errors between 1 and 5% are acceptable and any error analysis below 1% becomes meaningless due to experimental error and noise. The arithmetic and geometric average regret at convergence are reported as a red dot and a red triangle, respectively. Also, the fraction of cases which did not reach convergence (NC) and the confusion matrix are reported. In general, a confusion matrix indicates at a glance the goodness of a classification model (e.g., a convergence criterion) based on four performance indicators: true positive fraction (TP), false negative fraction (FN), false positive fraction (FP), and true negative fraction (TN). For the case of convergence criteria, TP indicates the ability of the criterion to correctly indicate convergence when convergence is effectively achieved (the regret is small), while TN the ability to correctly indicate that no convergence is reached when the regret is large; FN indicates the cases when the criterion deemed not to have reached convergence even if the regret was small (this corresponds to wasting iterations in practice and to the so-called type II error); FP shows the cases when the criterion deemed to have reached convergence even if the regret was large (this corresponds to a premature stop of the algorithm and to the so-called type I error). All the proposed basic criteria for DynO individually are able to indicate convergence, on average, correctly below 5% regret, yet they may also incorrectly report convergence or never converge in some cases. This can be seen in the confusion matrix, where the base criteria display a sum of FN and FP between 30 and 70%.
A combination of the basic criteria (possibly imposing a minimum number of DynO algorithm iterations) was found to be helpful to decrease FP, while decreasing the average regret at convergence. Requiring three or all four base criteria to be met at the same time (1i3c and 1i4c in Fig. 5) leads to low regret, at the cost of an excessive number of wasted iterations (large FN) and at the risk of not reaching convergence within 10 iterations. When instead at least two iterations are required together with one (2i1c) or two (2i2c) criteria, the best balance between true and false outcomes is obtained, with reduced average regret. The proposed criteria and their combinations allow the user to select different levels of risk (to incur in type I or II errors) instead of only relying on the expertise of the user in judging convergence, as usually done in BO. Nevertheless, all combination criteria have a regret distribution that is skewed to the left with a significant fraction of cases (greater than 30%) reaching convergence with less than 1% regret, which is more than acceptable for the majority of the practical scenarios in chemistry optimization.
3 Experimental validation with ester hydrolysis
DynO was tested with an experimental test case, ester hydrolysis in a Polar Bear PFR reactor (Fig. S1–S3†). The objective was to maximize the yield of the hydrolyzed product. The LabVIEW automation user interface enabled automated execution of dynamic experiments for ester hydrolysis (Fig. S4 and S5†). The hydrolysis reaction mixture was divided into two streams: stream 1 consisting of ester starting material in 2-methyltetrahydrofuran (2-MeTHF) and stream 2 consisting of potassium hydroxide (KOH) in methanol.The design space was composed of two variables (D = 2):
1. Residence time: 5 to 30 min;
2. equivalents of KOH w.r.t. ester: 1 to 3.
Sampling was performed approximately every ΔtS = 8 min using the automated online UHPLC (details of the method in the ESI†). The values of K were set to 0.3 for both residence time and KOH equivalents to avoid excessively conservative trajectories in terms of speed.
3.1 Initialization
Prior to starting the hydrolysis experimentation, the Polar Bear temperature was set to 25 °C and both streams, and the reactor were flushed with mixture of 2-MeTHF and methanol under ambient pressure, followed by pressurizing the system to 20 psi with a Zaiput BPR. Pressure relief lines with 250 psi cartridge BPRs (Upchurch, IDEX) were inserted directly after the pump head as a standard flow safety protocol. After the system was flushed and pressurized, a steady state was established in the reactor with residence time of 17.5 min at 2 equiv. of KOH and held for three residence times after equilibration of set temperature. Afterwards the LabVIEW automation software executed the dynamic portion of the experiment setting the flowrates to determine the residence time the ratio of flow rates (stream 1 and 2) to determine the equivalents of reagents with the parameters reported in Table 2 (iteration 0) and graphically reported in Fig. 6a and b over time. Upon completion of the dynamic experiment the system was flushed with mixture of 2-MeTHF and methanol.| Iter. | t exp [min] | Var. | X 0 | δ [−] | T [min] | φ [rad] |
|---|---|---|---|---|---|---|
| 0 | 360 | τ | 17.50 min | 0.7100 | 260.0 | 0 |
| χ | 2.00 | 0.5000 | 183.0 | 0 | ||
| 1 | 96 | τ | 18.51 min | 0.6117 | 258.7 | 0.074 |
| χ | 2.39 | 0.2530 | 187.3 | 1.486 | ||
| 2 | 96 | τ | 20.23 min | 0.4748 | 213.17 | −0.060 |
| χ | 2.26 | 0.2721 | 187.40 | 1.470 |
The data collected in the DynE over time (Fig. 6c) is used to reconstruct the steady-equivalent design space using eqn (1) and to train the GP. Fig. 6d–f are obtained, where contour plots indicate the GP predictions (average, standard deviation, and UCB) in the whole design space based on the experimental data on the reconstructed trajectory. Fig. 6g is a 3D representation of the predicted objective together with experimental data. The response surface obtained is rather smooth, as expected for a chemical reaction of this type and the optimum is visually observed close to a corner of the domain.
The experimental and GP-predicted maxima are reported in Table 3 (iteration 0) where an almost-corner point is indicated. At this moment the combined convergence criteria are not met as no iteration after initialization was performed, thus the optimization needs proceed. The large range of values of the objective and the low GP standard deviation produce an UCB with a similar shape to the average, encouraging exploitation in the following iteration with a minor component of exploration. A DynO trajectory prediction was run to obtain the parameters for the following iteration, reported in Table 2 (iteration 1).
| Iter. | Optimum location | Optimum value | ||||
|---|---|---|---|---|---|---|
| Exp. | GP | Exp. | GP | |||
| τ [min] | χ [−] | τ [min] | χ [−] | [%] | [%] | |
| 0 | 29.60 | 2.96 | 30.00 | 2.77 | 90.97 | 91.20 ± 1.17 |
| 1 | 29.59 | 2.43 | 30.00 | 2.40 | 92.57 | 92.24 ± 1.79 |
3.2 Iteration 1
Similarly to initialization, a steady state was established with residence time of 19.35 min at 2.99 equiv. of KOH (these values differ from X0 because φ is not a multiple of π) after equilibration of set temperature at 25 °C. The LabVIEW automation software subsequently executes the dynamic part of the trajectory automatically.The trajectory over time and the collected data is reported in Fig. 7a–c. The reconstructed trajectory in the design space is used to retrain the GP and Fig. 7d–g are obtained. As expected, DynO computed a trajectory that crosses the region of maximum UCB at the previous iteration, while also going through unexplored parts of the domain (balanced by the UCB in the acquisition function) with minor overlap with the previous trajectory (effect of repulsion in the acquisition function). The obtained results confirm that the shape of the previous iteration and the points where the new trajectory crosses the old one have the same objective value. This is a sanity check of the DynE and a confirmation of the good choice for the values of K: crossing points with same results indicate that the DynE is representative of steady states and the error done by using DynE instead of discrete, steady conditions is negligible.23
The experimental and GP-predicted maxima are reported in Table 3 (iteration 1) and interestingly the maximum has moved to lower KOH equivalents while keeping the maximum residence time. At this iteration the combined criterion 1i3c was satisfied (three of the four base criteria C.0–C.3 met). This should be expected as the domain has low dimensionality and initialization was done with a DynE (in accordance to the parametric analysis, Fig. 4, where very low regret is achieved). Based on 1i3c convergence analysis (Fig. 5), a regret lower than 2% is expected. As convergence is reached with a strong criterion, there is no need to further proceed with optimization. If DynO was asked to calculate a new trajectory, the parameters in Table 2 (iteration 2) would have been obtained.
Conclusions
This work presents for the first time the use of Bayesian optimization in the context of dynamic flow experiments. The DynO algorithm was developed specifically for chemistry and chemical engineering problems, leveraging the fundamental behavior of continuous tubular reactor, exploiting the data richness of dynamic experiments in combination with the flexibility of Gaussian processes in describing response surfaces. The algorithm is able to guide the user from initialization (using steady or dynamic experiments) to the end of the optimization procedure thanks to useful convergence criteria, which were proposed for the first time together with an estimate of the regret reached. Based on a parametric analysis, DynO was compared to Dragonfly optimization algorithm (and a random optimizer), showing remarkable performance in terms of experiment time saving and reagent volume reduction. The procedure was validated with a reaction of ester hydrolysis, showing that DynO can be easily implemented experimentally and allows to evaluate optimal reaction conditions with a limited number of experiments. It should be noted that DynO is designed for Euclidean domains, thus discrete variables cannot yet be included.Data availability
The code for the DynO algorithm can be found in Python on GitHub (https://github.com/fflorit/DynOpt) under a BSD 3-Clause License.Author contributions
FF, JM, KFJ and KYN formulated the project. FF conceptualized, wrote, implemented, tested, and analyzed the dynamic Bayesian optimization algorithm. CA, AD, KG, and KYN designed, built, and ran the experimental system and analyzed the experimental data. SMG, JM, KFJ, and KYN provided feedback and guidance on the algorithm development and experiments. FF wrote the initial manuscript. FF, KFJ, and KYN edited the manuscript, and all authors reviewed the manuscript. JM, KFJ, and KYN supervised the project and secured the funding.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by Pfizer.Notes and references
- P. Bollini, M. Diwan, P. Gautam, R. L. Hartman, D. A. Hickman, M. Johnson, M. Kawase, M. Neurock, G. S. Patience, A. Stottlemyer, D. G. Vlachos and B. Wilhite, ACS Eng. Au, 2023, 3, 364–390 CrossRef CAS.
- A. M. K. Nambiar, C. P. Breen, T. Hart, T. Kulesza, T. F. Jamison and K. F. Jensen, ACS Cent. Sci., 2022, 8, 825–836 CrossRef CAS PubMed.
- D. J. Griffin, C. W. Coley, S. A. Frank, J. M. Hawkins and K. F. Jensen, Org. Process Res. Dev., 2023, 27, 1868–1879 CrossRef CAS.
- C. J. Taylor, J. A. Manson, G. Clemens, B. A. Taylor, T. W. Chamberlain and R. A. Bourne, React. Chem. Eng., 2022, 7, 1037–1046 RSC.
- S. Martinuzzi, M. Tranninger, P. Sagmeister, M. Horn, J. Williams and C. O. Kappe, React. Chem. Eng., 2024, 9, 132–138 RSC.
- J. P. McMullen and B. M. Wyvratt, React. Chem. Eng., 2023, 8, 137–151 RSC.
- C. J. Taylor, A. Pomberger, K. C. Felton, R. Grainger, M. Barecka, T. W. Chamberlain, R. A. Bourne, C. N. Johnson and A. A. Lapkin, Chem. Rev., 2023, 123, 3089–3126 CrossRef CAS PubMed.
- M. I. Jeraal, N. Holmes, G. R. Akien and R. A. Bourne, Tetrahedron, 2018, 74, 3158–3164 CrossRef CAS.
- P. Sagmeister, C. Schiller, P. Weiss, K. Silber, S. Knoll, M. Horn, C. A. Hone, J. D. Williams and C. O. Kappe, React. Chem. Eng., 2023, 8, 2818–2825 RSC.
- A. D. Clayton, E. O. Pyzer-Knapp, M. Purdie, M. F. Jones, A. Barthelme, J. Pavey, N. Kapur, T. W. Chamberlain, A. J. Blacker and R. A. Bourne, Angew. Chem., Int. Ed., 2023, 62, e202214511 CrossRef CAS PubMed.
- R. Liang, H. Hu, Y. Han, B. Chen and Z. Yuan, AIChE J., 2024, 70, e18316 CrossRef CAS.
- T. M. Dixon, J. Williams, M. Besenhard, R. M. Howard, J. MacGregor, P. Peach, A. D. Clayton, N. J. Warren and R. A. Bourne, Digital Discovery, 2024, 3, 1591–1601 RSC.
- C. Lehmann, K. Eckey, M. Viehoff, C. Greve and T. Röder, Org. Process Res. Dev., 2024, 28, 3108–3118 CrossRef CAS.
- J. A. G. Torres, S. H. Lau, P. Anchuri, J. M. Stevens, J. E. Tabora, J. Li, A. Borovika, R. P. Adams and A. G. Doyle, J. Am. Chem. Soc., 2022, 144, 19999–20007 CrossRef CAS PubMed.
- J. D. Williams, P. Sagmeister and C. O. Kappe, Curr. Opin. Green Sustainable Chem., 2024, 47, 100921 CrossRef.
- D. Drelinkiewicz, T. J. A. Corrie and R. J. Whitby, React. Chem. Eng., 2024, 9, 379–387 RSC.
- J. S. Moore and K. F. Jensen, Angew. Chem., Int. Ed., 2014, 53, 470–473 CrossRef CAS PubMed.
- C. A. Hone, N. Holmes, G. R. Akien, R. A. Bourne and F. L. Muller, React. Chem. Eng., 2017, 2, 103–108 RSC.
- K. C. Aroh and K. F. Jensen, React. Chem. Eng., 2018, 3, 94–101 RSC.
- B. M. Wyvratt, J. P. McMullen and S. T. Grosser, React. Chem. Eng., 2019, 4, 1637–1645 RSC.
- K. Silber, P. Sagmeister, C. Schiller, J. D. Williams, C. A. Hone and C. O. Kappe, React. Chem. Eng., 2023, 8, 2849–2855 RSC.
- K. Kandasamy, K. R. Vysyaraju, W. Neiswanger, B. Paria, C. R. Collins, J. Schneider, B. Poczos and E. P. Xing, J. Mach. Learn. Res., 2020, 21, 1–27 Search PubMed.
- F. Florit, A. M. K. Nambiar, C. P. Breen, T. F. Jamison and K. F. Jensen, React. Chem. Eng., 2021, 6, 2306–2314 RSC.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- N. Srinivas, A. Krause, S. M. Kakade and M. W. Seeger, IEEE Trans. Inf. Theory, 2012, 58, 3250–3265 Search PubMed.
- H. Hu, P. Li and J. Z. Huang, 2018 IEEE/ACM International Conference on Computer-Aided Design (ICCAD), 2018, pp. 1–8 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Mathematical and experimental details. See DOI: https://doi.org/10.1039/d4re00543k |
| This journal is © The Royal Society of Chemistry 2025 |