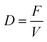DOI:
10.1039/D4RE00280F
(Paper)
React. Chem. Eng., 2025,
10, 2490-2501
Experimental and computational study of a packed-bed bioreactor for the continuous production of succinic acid†
Received
10th June 2024
, Accepted 13th August 2024
First published on 23rd August 2024
Abstract
In this work we present a packed-bed bioreactor system packed, with immobilised cells in sodium alginate beads, for the biological conversion of glycerol to succinic acid. We simulate this continuous bioreactor system by constructing a partial differential equation, multi-phase, convection–diffusion model, which uses the intrinsic kinetics for the fermentation of glycerol with A. succinogenes. The model is validated by conducting a series of fermentation experiments at different operating conditions and is subsequently used to successfully predict the dynamics and the species profiles throughout the length of the bioreactor. The model is then exploited for optimising the continuous bioprocess. The computed optimal conditions are experimentally validated. The succinic acid concentration at the end effluent of the bioreactor reached 51.16 g L−1, with the substrate being fully consumed. The maximum succinic acid productivity was calculated to be 2.15 g L−1 h−1, a value which is the highest recorded for the bioproduction of succinic acid with glycerol.
1 Introduction
Succinic acid is a platform chemical with a wide range of applications in the chemical, pharmaceutical and food industries.1–3 It is a product of the petrochemical industry, as it is mainly produced by the catalytic hydrogenation of maleic acid or maleic anhydrite.4 Nevertheless, it is also a chemical intermediate of the citric acid cycle and an essential part of the cell metabolism.5 Therefore it can also be produced biologically. There are several candidate bacteria that are natural succinic acid over-producers and can be exploited for succinic acid bioproduction.6–9Actinobacillus succinogenes, is an excellent microorganism for bioproducing succinic acid as it can grow on a wide range of substrates, it secretes the procured succinic acid extracellularly, and it is able to produce high yields of succinic acid.10–13 The use of glycerol as a fermentation substrate is of particular interest, as it is the main by-product of the biodiesel industry,14 therefore the biological production of succinic acid from glycerol can be part of a biodiesel biorefinery, aiming to increase its sustainability and profitability.15
Succinic acid is mainly produced using batch bioprocesses, e.g. ref. 12 and 15–17 however, continuous processes have also been developed,18,19 based on continuous stirred-tank bioreactors (CSTBRs), which have superior performance compared to a batch process with the same microorganism and substrate.20 Nevertheless, the use of a CSTBR has its own limitations. More, specifically, the effluent contains both bacterial biomass and unconverted substrate, which have to be separated during downstream processing (DSP), adding extra complexity and cost to the overall process. In addition, both the fermentation products, as well as the substrate can inhibit the growth of the microorganisms, while the operational conditions of the process can lead to the wash-out of the culture. The immobilisation of the cells, has been proposed as a remedy for these challenges and it has been applied with promising results.21,22
A mode of operation that is of particular interest is continuous bioprocesses using immobilized bacterial cultures. Bradfield and Nicol,23 developed a continuous fermentation system, where A. succinogenes can get attached and develop biofilm in a special polypropylene fitting fixed on the fermentor's agitator shaft, and produce succinic acid from xylose-enriched hydrolysate. Succinic acid productivity reached 1.77 g L−1 h−1. A fibre-bed bioreactor was used by Yan et al.,24 where A. succinogenes cells were immobilised on the surface of a cotton fibrous matrix. The reactor was then operated in batch and fed-batch mode using a glucose-based fermentation medium and successfully produced succinic acid with a maximum succinic acid productivity of 3.61 g L−1 h−1. Ferone et al.25 developed a packed bed biofilm bioreactor. The reactor was filled with support which allowed the biofilm to grow on it and succinic acid was produced by fermenting a synthetic glucose–arabinose–xylose carbon source. Succinic acid productivity reached 35 g L−1 h−1. Another method of immobilising bacterial cultures is the adhesion or entrapment of the cells in porous matrices. Corona-González et al.,26 have studied the immobilisation of succinic acid with both adhesion and entrapment methods, using various support matrices such as zeolite and activated carbon for adhesion, and agar, alginate and polyacrylamide hydrogels for the entrapment. After successful immobilisation, batch fermentation experiments were conducted using a glucose-based medium reaching productivity as high as 2.83 g L−1 h−1. Pateraki et al.,13 used alginate and delignified wood sawdust, to immobilise A. succinogenes and performed a series of batch fermentations, using spent sulphite liquor as a substrate. Productivity reached 0.65 g L−1 h−1 and the immobilised cells were used in multiple batches, without their ability to produce succinic acid being significantly reduced. Bumyut et al., were successful in immobilising A. succinogenes, in alginate and producing succinic acid using both pure and crude glycerol with batch fermentations, reaching a concentration of 10.8 g L−1 and yield of 1.25 gSA gGly−1.27 The majority of the literature concerned with the production of succinic acid with entrapped cells revolves around batch and fed-batch fermentation. Recent studies have explored the use of entrapped cells, in a continuous fermentation process. Ercole et al.28 developed a fluidized bed bioreactor, to produce succinic acid via glucose fermentation. The bioreactor was packed with A. succinogenes entrapped into alginate beads and a productivity of 35.6 g L−1 h−1 was reached.
In this work, we have developed a continuous packed-bed bioreactor with immobilised A. succinogenes cells in alginate beads, in conjunction with a computational model of our continuous bioprocess. The construction of a robust process model is essential for bioprocess development as it can reduce the number of time-consuming and expensive experiments and help in the investigation of optimal control strategies for the bioprocess system.29 A model developed with the purpose of performing optimal control of the bioprocess must be able to simulate the dynamic behaviour of the system, in our case the bacterial growth, as well the diffusion of the metabolites and fluid convection inside the bioreactor.
Different types of models have been proposed to simulate continuous or batch bioprocesses with immobilised cells, however most of them tend to use other immobilisation techniques.30–34 For the scope of this work the construction of a new model is better fit for purpose, as it can easier capture the nuances of the fermentation system.
Over the years, a number of different modelling approaches have been proposed for packed-bed bioreactors, resulting in different models that can be categorised based on the number of phases, dimensions, and transport phenomena they take into account. Concerning reactor phases, packed-bed reactor models can be classified into pseudo-homegeneous and heterogeneous models. In the former, the solid-(bio) catalyst and fluid phases can be assumed as a single medium and in the latter, they are treated as two separate phases described through their own sets of equations.35,36 Both of these approaches come with their own limitations, namely a less realistic depiction of the real system in the case of pseudo-homogeneous models and high computational demands in the case of heterogeneous models.36 Therefore, depending on the desired goal of the model implementation (computational speed vs. more realistic modelling) each of these modelling approaches is employed. In this work, the heterogeneous modelling approach is used as the calculations are relatively computationally tractable and we opted for increased modelling insights.
2 Materials and methods
2.1 Cells entrapment in sodium alginate
The microorganism used for the experiments, Actinobacillus succinogenes (DSM No. 22257), was acquired from the Deutsche Sammlung von Mikroororganismen und Zellkulturen (DSMZ) (Braunschweig, DE). The cell culture was initially revived, by batch cultivation for 48 h, using a 30 g L−1 tryptic soy broth (TSB) medium. The activated culture was then stored in cryopreservation vials (−80 °C) containing 30% glycerol. The stock culture was adapted to high glycerol concentrations using the method described by Vlysidis et al.11 For the fermentation, a semi-defined medium11 was used. The medium was sterilised for 15 min at 121 °C. Initially the content of the cryopreservation vial was let to thaw and subsequently it was added in flasks containing a 100 mL medium consisting of 15 g L−1 TSB and 30 g L−1 glycerol. The culture was then placed on a rotary shaker and incubated for 24 h at 37 °C. A 5% w/v sodium alginate, as well as a 20% w/v CaCl2 solution, were prepared and sterilised for 15 min at 121 °C. The sodium alginate solution was then mixed with the cell culture in 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio, reaching a final concentration of 4% w/v sodium alginate. The sodium alginate-cell culture mixture was subsequently added to a burette, placed approximately 15 cm from the surface of a beaker containing the CaCl2 solution, which was stirred gently using a magnetic stirrer. As soon as the droplets touched the liquid the Na+ ions were replaced by the Ca2+ ions forming firm calcium alginate beads.37 The median diameter of the beads was 0.3 cm. The median weight of pure (without entrapped cells) calcium alginate beads was 0.33 g per 10 beads. All reactants were purchased from Sigma-Adlrich UK. After immobilisation, the beads were used in a series of batch fermentations to grow and stabilise their biomass content. A semi-defined medium11 was employed. The glycerol concentration was 30 g L−1. After three subsequent fermentation cycles, the biomass concentration (Cbiomass (gbiomass L−1)) was stabilized at around 2.65 Cbiomass gbeads−1 as can be seen in Fig. 1. Biomass concentration inside the beads was measured by dissolving them in a 0.2 M sodium citrate solution. The successful fermentation runs, were also proof of the successful cell immobilisation.
1 ratio, reaching a final concentration of 4% w/v sodium alginate. The sodium alginate-cell culture mixture was subsequently added to a burette, placed approximately 15 cm from the surface of a beaker containing the CaCl2 solution, which was stirred gently using a magnetic stirrer. As soon as the droplets touched the liquid the Na+ ions were replaced by the Ca2+ ions forming firm calcium alginate beads.37 The median diameter of the beads was 0.3 cm. The median weight of pure (without entrapped cells) calcium alginate beads was 0.33 g per 10 beads. All reactants were purchased from Sigma-Adlrich UK. After immobilisation, the beads were used in a series of batch fermentations to grow and stabilise their biomass content. A semi-defined medium11 was employed. The glycerol concentration was 30 g L−1. After three subsequent fermentation cycles, the biomass concentration (Cbiomass (gbiomass L−1)) was stabilized at around 2.65 Cbiomass gbeads−1 as can be seen in Fig. 1. Biomass concentration inside the beads was measured by dissolving them in a 0.2 M sodium citrate solution. The successful fermentation runs, were also proof of the successful cell immobilisation.
 |
| | Fig. 1 Biomass concentration variation per experimental run. | |
2.2 Fermentation medium
The same semi-defined medium was used for the fermentation in the packed-bed bioreactor. The glycerol concentration changed in order to accommodate the need for different initial experimental conditions. The amount of MgCO3 used in the fermentation medium was 60% greater than the amount used in the batch experiments (16 g L−1). This was done for two reasons: Firstly to saturate the fermentation medium with dissolved CO2 (dCO2), which is important as a second substrate12 and secondly as a mean to control the process pH and stabilise it around the optimal, for A. succinogenes growth, value of 6.4.
The concentration of dCO2 in both the inlet and the effluent of the bioreactor was around 0.3 gdCO2 L−1, meaning that it remained constant throughout the length of the bed.
2.3 Packed-bed bioreactor
After the biomass concentration is stabilised, the bioreactor is packed with the beads containing the immobilised cells. A Liebig condenser was used as the tubular bioreactor. The condenser was chosen for its convenient size as well as for its double wall, which allows for warm water to circulate, maintaining a temperature of 37 °C. Different length bioreactors were utilised. All of them had an average diameter of 0.5 cm and were packed with the number of beads necessary in order to achieve a void fraction of 0.55 cmpacking3 cmreactor−3. The beads were inserted aseptically inside the reactor, packed and then, sterile water was used in order to measure the volume of the empty space inside the tubular reactor. For the reported experiments, two different tube lengths were chosen, 20 and 40 cm, respectively. The packing was held into place through the use of glass beads at the top and the bottom of the working length of the bioreactor. Fresh medium was transferred into the bioreactor with the use of a peristaltic pump (Watson Marlow 505U). For the reactor temperature control, a water bath with an integrated water pump (Haake DC10) was used. Sampling was performed through a sampling port right after the exit point of the reactor. The packed bed bioreactor can be seen in Fig. 2.
 |
| | Fig. 2 The packed bed bioreactor: A photo of the experimental setup, B process flow diagram of the packed bed bioreactor. | |
2.4 Analytical methods
The residual glycerol and the fermentation products were simultaneously measured using High Pressure Liquid Chromatography (HPLC) (ThermoScientific Diomex UltiMate 3000). Glycerol was detected by a Refractive Index detector (ERC RefractoMax 520) and the fermentation products (succinic, acetic and formic acid) by a Diode Array detector (ThermoScientific Diomex UltiMate 3000 DAD). The column used was Aminex HPX-87H 300 mm × 7.8 mm (Bio-Rad, USA). The concentration of the dissolved CO2 at the inlet and effluent of the reactor was measured with a dCO2 electrode (InPro 5000, Mettler Toledo).
3 Bioprocess model
For the bioprocess, a 2-phase heterogeneous model of the packed-bed reactor35 was developed. Two control volumes are used: the largest is the entire volume of the bioreactor and the smallest is the volume of an individual alginate bead. Here, by explicitly considering the reaction taking place inside the alginate beads the mass transfer limitations can be taken into account and a more accurate estimation of the reaction rate can be calculated.
The main assumption in this work is that the immobilised cells follow the intrinsic kinetics of the free cells. The results of batch experiments with immobilised cells also support this. The fermentation broth is considered saturated with carbon dioxide and due to the small length of the reactor, the CO2 concentration remains steady throughout the length of the bioreactor. The concentration of biomass is considered to have reached a steady state, which is proven experimentally since after three consecutive batch runs, biomass concentration is not altered.
The intrinsic kinetics of the continuous bioprocess is described by the following set of differential-algebraic equations (DAEs)20eqn (1)–(4):
| |  | (1) |
| | 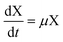 | (2) |
| |  | (3) |
| |  | (4) |
| |  | (5) |
| |  | (6) |
Here, Gly, CO
2, SA, FA, AA, X, are the concentration of glycerol, carbon dioxide, succinic, acetic, and formic acid (g L
−1),
μ and
μmax the specific and the maximum specific growth rate of
A. succinogenes respectively (h
−1), and
KSGly and
KSCO2 the substrate saturation constants for glycerol and CO
2 (g L
−1).
KIGly is the substrate inhibition constant for glycerol (g L
−1), SA* the critical succinic acid concentration for product inhibition (g L
−1),
nSA the product inhibition exponent (−), and
αi (g
i g
biomass−1) and
βi (g
i (g
biomass−1 h
−1)) the growth and non-growth associated production rates for each species i (Gly, SA, FA, AA), correspondingly.
The growth rate of A. succinogenes is calculated by eqn (1). μ is then used in eqn (2) to compute both the production rate and the concentration of the biomass X, which in turn is used in eqn (4) to compute the consumption of glycerol and in eqn (3), (5) and (6), to calculate the production of succinic, acetic, and formic acid.
By combining eqn (2) with eqn (3)–(6), the rates of production for the substrate, the primary product, and the byproducts and the consumption rate of glycerol as a function only of the growth rate μ and the biomass concentration X are given by eqn (7)–(10).
| | | rSA = (αSAμ + βPSA)·Xia | (7) |
| | | rGly = −(αGlyμ + βGly)·Xia | (10) |
X
ia being the biomass concentration inside the alginate beads [g
DCW g
beads−1]. As the culture inside the alginate beads is stabilised, we assume that there is no cell growth. Using
eqn (7) to (10), the consumption rate of glycerol and the production rates of succinic, acetic and formic acid inside the alginate beads can be calculated, taking into account the inhibition effects of the substrate and the product on the production of succinic acid.
The values of the model kinetic parameters are taken directly from our previous work, which developed a continuous stirred-tank bioreactor with cell recycle20 without any refitting or adjustment and are presented in Table 1. It is also worthwhile to note that the identifiability of the model parameters was extensively studied in our recent work.38
Table 1 Kinetic parameters of the intrinsic cell kinetics
|
|
Value |
Units |
|
μ
max
|
0.2568 |
h−1 |
|
K
S
Gly
|
5.4 |
g L−1 |
|
K
I
Gly
|
119.99 |
g L−1 |
|
K
S
CO2
|
0.03 |
g L−1 |
|
n
SA
|
5 |
— |
| SA* |
45.6 |
g L−1 |
|
α
SA
|
4.5 |
gSA gX−1 |
|
β
SA
|
0.21 |
gSA gX−1 h−1 |
|
α
Gly
|
2.39 |
gGly gX−1 |
|
β
Gly
|
0.187 |
gGly gX−1 h−1 |
|
β
AA
|
0.0056 |
gAA gX−1 h−1 |
|
β
FA
|
0.011 |
gFA gX−1 h−1 |
The concentration profiles of glycerol and succinic, formic, and acetic acid in the bulk fluid phase can be calculated by implementing the convection–diffusion equation:
| |  | (11) |
where
Ci and ∇
Ci are the concentration and the concentration gradient of species i (Gly, CO
2, SA, FA, AA), respectively,
Di is the diffusion coefficient of species i,
v is the superficial fluid velocity and
Rtot is the reaction source term. Here we implement a 1-dimensional model, hence we assume that convection occurs only over the bioreactor length (
x-axis) and
eqn (11) takes the following form:
| |  | (12) |
Because of the difference in the time scales between convection and diffusion of the species in the bulk phase and the reactions inside the alginate beads, which are much faster, we consider that a steady-state is reached instantaneously in the beads phase, thus the reaction throughout the radius of the bead is described by a steady state second order partial differential equation. Hence, the concentration profiles of glycerol, succinic, formic, and acetic acid inside an alginate bead can be calculated by implementing the reaction–diffusion equation in spherical coordinates:
| |  | (13) |
where
Ci,in is the concentration of species i (Gly, CO
2, SA, FA, AA),
r is the radial direction of the spherical beads,
Dia is the diffusion coefficient of species i inside the alginate beads and
Ri,a is the reaction rate of each species i inside the beads. The convection term is omitted as the only transport mechanism inside the alginate beads is diffusion.
To determine the effect of convection and diffusion terms on the concentration profiles, the dimensionless Peclet number is calculated by eqn (14):
| |  | (14) |
In the packed bioreactor system the Peclet number in the fluid phase has an order of magnitude in the area of 105, hence, it is safe to assume that transport is convection dominated. The value of the Peclet number in relation to the inlet flow rate for the bioreactor system can be seen in Fig. 3. Therefore, for the shake of simplifying the model, the diffusion term can be omitted from the convection–diffusion equation for the bulk fluid phase (eqn (11)), yielding eqn (15)
| |  | (15) |
The mass conservation equations for the bulk liquid phase become:
| |  | (16) |
| |  | (17) |
| |  | (18) |
| |  | (19) |
With Gly, SA, FA, AA (g L
−1) being the concentration of each species in the bulk liquid and ∈ the void fraction of the packed bed its value being 0.55 m
packing3 m
reactor−3 and
RtotGly,
RtotSA,
RtotAA,
RtotFA the total reaction rate for each species (g L
−1 h
−1).
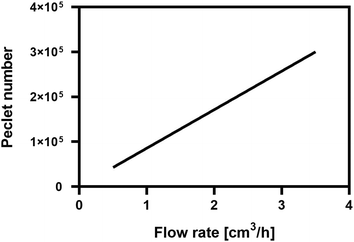 |
| | Fig. 3 Peclet number correlation with inlet flowrate. | |
The component balance equations for the alginate bead phase in spherical coordinates become:
| |  | (20) |
| |  | (21) |
| |  | (22) |
| |  | (23) |
With Gly
a, SA
a, FA
a, AA
a (g L
−1) being the concentration of each species in the alginate beads,
DGly,a,
DSA,a,
DAA,a,
DFA,a the diffusivity of each species inside the beads (cm
2 h
−1) and
RGlya,
RSAa,
RAAa,
RFAa the reaction rate of each species inside the beads (g L
−1 h
−1). Then the total reaction rate for each species i,
Rtot,i can be computed by the definite integral of the species i reaction rate over the bead's radius,
r:
39| |  | (24) |
where
ρa is the density of the alginate bead (1000 g L
−1).
The boundary conditions for the system are presented in eqn (25) to (40).
For the bulk fluid:
| |  | (29) |
| |  | (30) |
| |  | (31) |
| |  | (32) |
In the bulk liquid at the beginning of the bioreactor (
x = 0), the concentration of glycerol is equal to the glycerol concentration of the feed (
eqn (25)), whereas the concentration of succinic, formic and acetic acid is 0 (
eqn (26) to (28)). At the end of the bioreactor (
x =
L), no change in the species concentrations is assumed (
eqn (29) to (32)).
For the alginate bead at position x = xp of the bioreactor:
| |  | (37) |
| |  | (38) |
| |  | (39) |
| |  | (40) |
We assume that on the surface of the bead (
r =
R), the concentration of all glycerol, succinic, acetic and formic acid is equal to the concentration of the bulk liquid surrounding the bead (
eqn (33) to (36)) and symmetry conditions are imposed at the centre of the bead (
r = 0) (
eqn (37) to (40)).
For the calculation of the diffusion coefficients of each of the process species (Gly, SA, FA, AA) the Wilke–Chang correlation (eqn (41))40 was used and the calculated values are given in Table 2.
| | 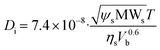 | (41) |
where
ψs is the association parameter (for aqueous solutions
ψs = 2.6), MW
s = 18.01528 g mol
−1 is the molecular weight of the solvent (water),
T = 36 °C is the temperature of the solution,
ηs = 0.7058 cP is the viscosity of the solution (assumed equal to the viscosity of water at 36 °C) and
Vb is the molar volume of the solute (glycerol, succinic, acetic and formic acid) at the normal boiling point.
Vb was calculated for its solute using the Schroeder method (ESI
†).
Table 2 Reaction–diffusion model parameters
|
|
Value |
Units |
|
D
Gly,a
|
0.00989 |
cm2 h−1 |
|
D
SA,a
|
0.00989 |
cm2 h−1 |
|
D
AA,a
|
0.01384 |
cm2 h−1 |
|
D
FA,a
|
0.01835 |
cm2 h−1 |
| ∈ |
0.55 |
mpacking3 mreactor−3 |
The diffusivity of each species inside the alginate beads was assumed to be equal to their corresponding diffusivity in water (as all the species modeled are in ionic form and have low molecular weights (≪20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da)41,42). These diffusivities were calculated using eqn (41) and are shown in Table 2.
000 Da)41,42). These diffusivities were calculated using eqn (41) and are shown in Table 2.
4 Numerical methods
The reactor system is described as a system of partial differential eqn (16) to (23) solved numerically. Both the liquid and the bead phase were discretised in 100 finite differences each using central and backward finite differences and a first-order upwind scheme was used to convert the boundary value problem (eqn (1) to (9) and eqn (16) to (24)) into a system of index 1 differential-algebraic equations (DAEs), which can be easily solved by numerical integration. MATLAB (v. 2018a) was used to solve the resulting system employing an ODE solver (ode113). The two domains were coupled by eqn (24), which calculates the total reaction rate of a species over the radius of an alginate bead using the reaction rates calculated from eqn (20) to (23), which was then used in eqn (16) to (19).
The volume integrals in eqn (24) were calculated using the trapezoidal rule, implemented using the MATLAB routine (trapz). The simulations were performed on a 2020 MacBook Air, with a 1.1 GHz Intel Core i5 processor.
5 Experimental and computational results
5.1 Evaluation of immobilised cells
After the cell immobilisation was carried out, a series of batch fermentations were performed, with the goal of evaluating the effectiveness of the immobilised cell system. Conical flasks were loaded with 100 ml of fermentation medium and 5 g of immobilised cells. In each consecutive fermentation, the loading of the previous flask was used. This was done, in order to evaluate the long-term viability of cell immobilisation. After 3 batches the biomass concentration is stabilised, remaining at 2.65 Cbiomass gbeads−1 for the rest of the experimental runs (Fig. 4).
 |
| | Fig. 4 Immobilised biomass concentration during 5 consecutive fermentation batches. | |
In each fermentation, glycerol was consumed completely and the values of succinic acid productivity and yield were similar to the values obtained with free cell experiments20 (Fig. 5). The cell immobilisation was regarded as successful and the alginate beads were used as packing for the packed-bed bioreactor.
 |
| | Fig. 5 Glycerol and succinic acid concentration during 5 consecutive fermentation batches. | |
5.2 Continuous fermentation results and comparisons with model
Experiments were conducted using different bioreactor lengths and experimental conditions to validate the model. The varied experimental conditions were: the substrate concentration in the bioreactor feed (Gly0), the feed flow rate (ḟ) and the reactor length (L). The system was ran long enough to ensure that it reached steady state. The concentrations of glycerol, succinic, acetic and formic acid, were measured over time and their profiles were plotted against the corresponding simulation results.
As it can be seen in Fig. 6–8, the agreement between experiments and simulations is excellent as both dynamics and steady states can be successfully captured for succinic acid and byproducts production as well as glycerol consumption. The error between the experimental data and the predicted values for the experimental and the model results from Fig. 6–8 was calculated using eqn (42) and it ranges from 2% to 4%.
| |  | (42) |
with
nexp. p, being the number of experimental points,
ti each experimental time point and
yexp,
ycalc the corresponding experimental and model result for this particular time point respectively.
 |
| | Fig. 6 Results for fermentation with initial substrate of 15 g L−1, bioreactor length 40 cm and feed flow rate 0.1 cm3 h−1 (0.003 h−1). (a): Succinic acid and glycerol concentration, (b): acetic and formic acid concentration. | |
 |
| | Fig. 7 Results for fermentation with initial substrate of 15 g L−1, bioreactor length 20 cm and feed flow rate 1.2 cm3 h−1 (0.076 h−1). (a): Succinic acid and glycerol concentration, (b): acetic and formic acid concentration. | |
 |
| | Fig. 8 Results for fermentation with initial substrate of 60 g L−1, bioreactor length 40 cm and feed flow rate 1.2 cm3 h−1 (0.038 h−1). (a): Succinic acid and glycerol concentration, (b): acetic and formic acid concentration. | |
In the fermentation conducted using a bioreactor with a length of 20 cm (Fig. 7), the substrate is not fully consumed due to the smaller residence time. Increasing the reactor length (which leads to an increase of residence time), results in the full conversion of the substrate (Fig. 6). High substrate feed concentration also leads to decreased glycerol conversion (Fig. 8), despite the high residence time. As expected, substrate conversion is a function of residence time and feed substrate concentration. The validated model was subsequently used with confidence to optimise the productivity and substrate conversion of the bioprocess.
5.3 Bioprocess optimisation
As mentioned above, the developed validated model was used in optimisation studies to optimise the overall bioprocess. The optimisation goal was to simultaneously maximise the productivity (p) (eqn (45)) and the yield (y) (eqn (46)) of succinic acid and the conversion (c) (eqn (47)) of glycerol. The process parameters that have the biggest effect on productivity, yield and conversion and at the same time can be easily manipulated are the dilution rate (D) (eqn (44)) – by changing the feed flow rate – and the initial substrate concentration (Glyf). These variables are contained in the vector pp (eqn (43)).| | 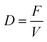 | (44) |
| |  | (46) |
| |  | (47) |
Succss,L and Glyss,L being the steady-state concretion of succinic acid and glycerol at the exit of the bioreactor (g L−1), respectively.
The following optimisation problem is constructed, to determine the optimal values of the process parameters pp:
| |  | (48) |
where lb and ub are the vectors containing the lower and upper bounds of the process parameters.
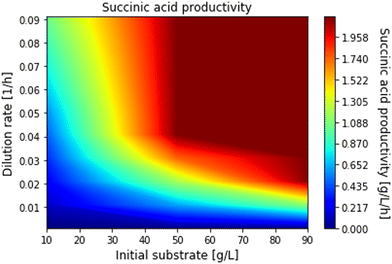
We first scanned the space of process parameters pp to explore the bioreactor performance and in addition to determine realistic optimisation boundaries. This was achieved by solving the packed bioreactor model multiple times using different combinations of dilution rate (from 0.01 to 0.09 h−1, incrementally increased by 0.01 h−1) and initial substrate concentration (from 10 to 90 g L−1, incrementally increased by 10 g L−1) and then calculating the productivity, yield and glycerol conversion for each of the combinations. The computed conversions, productivities and yields as a function of dilution rate and initial substrate are given in Fig. 9–11 respectively, where the operating regions for maximum productivity, yield and conversion can be clearly seen. In addition, the range of upper and lower bounds for dilution rate and initial substrate concentration for the optimisation problem in eqn (48) were determined by identifying the parameter values, on the graphs, where productivity, yield and glycerol conversion are close to their maximum values. The optimisation bounds were hence set between 40 g L−1 and 50 g L−1 for the feed glycerol concentration and 0.04 h−1 to 0.05 h−1 for the dilution rate.
 |
| | Fig. 9 Glycerol conversion for different dilution rates and initial substrate concentrations. | |
 |
| | Fig. 10 Succinic acid productivity for different dilution rates and initial substrate concentrations. | |
 |
| | Fig. 11 Succinic acid yield for different dilution rates and initial substrate concentrations. | |
The maximisation problem was then solved to precisely locate the optimal operating conditions, with the use of the Matlab (version 2018a, Mathworks) optimisation toolbox. A combination of stochastic and deterministic algorithms was used:20 initially, a genetic algorithm with multiple restarts was employed to search and locate a family of solutions close to the optimal area avoiding the possibility of being trapped at a local extremum,43 then the final optimal solutions were pinpointed through the Matlab subroutine fmincon (a successive quadrative programming method).44
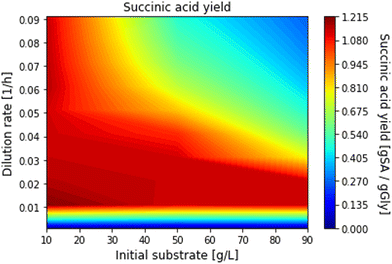
Three Pareto fronts are constructed from the solutions of the multiobjective optimisation problem (eqn (48)), representing the 3 possible optimisation parameter combinations: glycerol conversion (c) – succinic acid yield (y) (Fig. 12A), glycerol conversion (c) – succinic acid productivity (p) (Fig. 12B), succinic acid yield (y) – succinic acid productivity (p) (Fig. 12C). All figures also include the experimental validation points. Moreover, in Fig. 13, a 3D Pareto surface representing the optimal combinations of glycerol conversion (c), succinic acid yield (y) and succinic acid productivity is given.
 |
| | Fig. 12 Pareto fronts for the 3 possible optimisation parameter combinations: A. glycerol conversion (c) – succinic acid yield (y), B. glycerol conversion (c) – succinic acid productivity (p), C. succinic acid yield (y) – succinic acid productivity (p). | |
 |
| | Fig. 13 Pareto surface representing the optimal combinations of glycerol conversion (c), succinic acid yield (y) and succinic acid productivity (p). | |
From Fig. 12 and 13 it is clear that achieving high values for all, glycerol conversion (c), succinic acid yield (y) and succinic acid productivity (p) is feasible. In Fig. 12C, it is observed that there is a small compromise between achieving the highest possible succinic acid yield (1.2 gSA gGly−1) and the maximum possible succinic acid productivity (6% difference). Thus this compromise can be practically considered insignificant. In the upper right corner of Fig. 13, we can see that there is a feasible combination of c, y and p, with total substrate conversion, high yield and productivity higher than the productivity of other batch and continuous process with the same glycerol/A. succinogenes input.20
The optimal productivity, succinic acid yield and substrate conversion combination were then identified for a feed substrate concentration of 45 g L−1 and dilution rate of 0.042 h−1. For these operating conditions, succinic acid productivity was 2.13 g L−1 h−1, succinic acid yield was 1.128 gSA gGly−1 and substrate conversion was complete.
To validate the computed optimisation results, a continuous fermentation experiment was subsequently conducted, using the calculated optimal operating conditions. In Fig. 14 a comparison between the results of the optimal fermentation experiment and the computed optimal performance can be seen.
 |
| | Fig. 14 Results for fermentation with optimal initial conditions: substrate of 45 g L−1, and dilution rate 0.042 h−1. (a): Succinic acid and glycerol concentration, (b): acetic and formic acid concentration. | |
The average succinic acid concentration at the effluent of the bioreactor is measured at 51.16 g L−1 leading to a succinic acid productivity of 2.15 g L−1 h−1 and succinic acid yield of 1.14 gSA gGly−1, which is in excellent agreement with the optimisation calculations. As the process model is able to confidently simulate the bioprocess, it can be used as a very powerful tool for further bioprocess development. In addition, this is the highest ever productivity reported for the bioproduction of succinic acid from glycerol using A. succinogenes. This system is 4.15 times more productive than the continuous system with cell recycling and 4.57 times more productive than the batch system, with the same substrate and using the same microorganism.20 Moreover, the fermentation substrate is fully consumed. This, combined with the absence of biomass in the effluent can lead to less costly downstream processing (DSP), which can amount up to 80% of the total bioprocessing cost.45,46 Hence, this efficient packed-bed bioreactor design can help in increasing the economical feasibility of bio-succinic acid, making it competitive against succinic acid produced from petrochemical derived feedstocks. Nevertheless, a thorough technoeconomic and environmental and social impact analysis is needed to further assess the potential of this process. The succinic acid productivity and final concentration are the highest reported in the literature for a process involving the fermentation of glycerol and other alternative feedstocks to succinic acid using entrapped cells, with a final succinic acid titer 3.8 times higher than the one reported by Bumyut et al. and a productivity 2.3 times higher than the productivity achieved by Pateraki et al. and 0.2 times more than the productivity reported by Bradfield and Nicol for xylose enriched hydrolysate. When a glucose-based substrate is used higher productivities have been reported. However, the succinic acid to substrate yield was either equal or lower than the highest yield achieved in this work.25,26,28
6 Conclusions
In this work we have achieved for the first time design and operation of a continuous fermentation system, based on a packed-bed bioreactor, for the production of succinic acid from glycerol. A. succinogenes can be successfully immobilised with sodium alginate and can be viable for use through multiple fermentation cycles. We have also developed a model that can reliably simulate the continuous fermentation, which is used to optimise the productivity, yield and substrate conversion of this bioprocess. This productivity (2.15 g L−1 h−1) and yield (1.14 gSA gGly−1) are, to the best of our knowledge, the highest ever reported for this particular substrate and microorganism combination. Moreover, the conversion of glycerol is the highest presented for the continuous production of succinic acid with A. succinogenes, reaching 100% substrate consumption at the exit of the bioreactor.
We believe that this study has reliably demonstrated that the use of a packed bed bioreactor with immobilised A. succinogenes has great potential as the best bioprocessing option for the bioconversion of glycerol to succinic acid, overperforming both the batch and the CSTR systems.
Data availability
The data supporting this article have been included as part of the ESI.†
Author contributions
Ioannis Zacharopoulos: conceptualization, investigation, methodology, data curation, writing – original draft, writing – review & editing, visualisation. Min Tao: investigation, methodology, writing – review & editing. Constantinos Theodoropoulos: supervision, methodology, conceptualization, investigation, data curation, writing – original draft, writing – review & editing, visualization.
Conflicts of interest
The authors have no conflict of interest to declare.
Acknowledgements
The University of Manchester Presidential Doctoral Scholarship Award to IZ and the joint University of Manchester-China Scholarship Council scholarship to MT are gratefully acknowledged.
References
- J. G. Zeikus, M. K. Jain and P. Elankovan, Appl. Microbiol. Biotechnol., 1999, 51, 545–552 CrossRef CAS.
-
R. K. Saxena, S. Saran, J. Isar and R. Kaushik, Current Developments in Biotechnology and Bioengineering, Elsevier, 2017, pp. 601–630 Search PubMed.
- M. Sauer, D. Porro, D. Mattanovich and P. Branduardi, Trends Biotechnol., 2008, 26, 100–108 CrossRef CAS PubMed.
-
B. Cornils and P. Lappe, Ullmann's Encyclopedia of Industrial Chemistry, American Cancer Society, 2014, pp. 1–18 Search PubMed.
-
B. Alberts, D. Bray, A. Johnson, J. Lewis, M. Raff, K. Roberts and P. Walter, Essential Cell Biolog, Garland Science, 2013 Search PubMed.
- M. Gallmetzer, J. Meraner and W. Burgstaller, FEMS Microbiol. Lett., 2002, 210, 221–225 CrossRef CAS PubMed.
- D. Cimini, O. Argenzio, S. D'Ambrosio, L. Lama, I. Finore, R. Finamore, O. Pepe, V. Faraco and C. Schiraldi, Bioresour. Technol., 2016, 222, 355–360 CrossRef CAS PubMed.
- P. Lee, S. Lee, S. Hong and H. Chang, Appl. Microbiol. Biotechnol., 2002, 58, 663–668 CrossRef CAS PubMed.
- M. V. Guettler, D. Rumler and M. K. Jain, Int. J. Syst. Evol. Microbiol., 1999, 49, 207–216 CrossRef CAS PubMed.
- M. Binns, A. Vlysidis, C. Webb, C. Theodoropoulos, P. de Atauri and M. Cascante, Comput.-Aided Chem. Eng., 2011, 29, 1421–1425 CAS.
- A. Vlysidis, M. Binns, C. Webb and C. Theodoropoulos, Biochem. Eng. J., 2011, 58–59, 1–11 CrossRef CAS.
- A. Rigaki, C. Webb and C. Theodoropoulos, Biochem. Eng. J., 2019, 107391 Search PubMed.
- C. Pateraki, M. Patsalou, A. Vlysidis, N. Kopsahelis, C. Webb, A. A. Koutinas and M. Koutinas, Biochem. Eng. J., 2016, 112, 285–303 CrossRef CAS.
- M. R. Monteiro, C. L. Kugelmeier, R. S. Pinheiro, M. O. Batalha and A. da Silva César, Renewable Sustainable Energy Rev., 2018, 88, 109–122 CrossRef CAS.
- A. Vlysidis, M. Binns, C. Webb and C. Theodoropoulos, Energy, 2011, 36, 4671–4683 CrossRef CAS.
- I. A. Escanciano, M. Ladero, N. Blanco and V. E. Santos, Biomass Bioenergy, 2024, 181, 107034 CrossRef CAS.
- E. Stylianou, C. Pateraki, D. Ladakis, M. Cruz-Fernández, M. Latorre-Sánchez, C. Coll and A. Koutinas, Biotechnol. Biofuels, 2020, 13, 72 CrossRef CAS PubMed.
- S. Y. Kim, S. O. Park, J. Y. Yeon and G.-T. Chun, Biotechnol. Bioprocess Eng., 2021, 26, 125–136 CrossRef CAS.
- C. D. van Heerden and W. Nicol, Biochem. Eng. J., 2013, 73, 5–11 CrossRef CAS.
- I. Zacharopoulos and C. Theodoropoulos, Bioresour. Technol., 2023, 386, 129518 CrossRef CAS.
- U. Uysal and H. Hamamcı, Bioresour. Technol. Rep., 2021, 16, 100829 CrossRef CAS.
- M. Alexandri, H. Papapostolou, L. Stragier, W. Verstraete, S. Papanikolaou and A. A. Koutinas, Bioresour. Technol., 2017, 238, 214–222 CrossRef CAS PubMed.
- M. F. A. Bradfield and W. Nicol, Biochem. Eng. J., 2014, 85, 1–7 CrossRef CAS.
- Q. Yan, P. Zheng, S.-T. Tao and J.-J. Dong, Biochem. Eng. J., 2014, 91, 92–98 CrossRef CAS.
- M. Ferone, F. Raganati, A. Ercole, G. Olivieri, P. Salatino and A. Marzocchella, Biotechnol. Biofuels, 2018, 11, 138 CrossRef.
- R. I. Corona-González, R. Miramontes-Murillo, E. Arriola-Guevara, G. Guatemala-Morales, G. Toriz and C. Pelayo-Ortiz, Bioresour. Technol., 2014, 164, 113–118 CrossRef PubMed.
- A. Bumyut, V. Champreda, C. Singhakant and S. Kanchanasuta, Biomass Convers. Biorefin., 2022, 12, 643–654 CrossRef CAS.
- A. Ercole, F. Raganati, P. Salatino and A. Marzocchella, Biochem. Eng. J., 2021, 169, 107968 CrossRef CAS.
-
C. Theodoropoulos and C. Sun, Comprehensive Biotechnology, Pergamon, Oxford, 3rd edn, 2019, pp. 663–680 Search PubMed.
- T. Menegatti, I. Plazl and P. Žnidaršič-Plazl, Chem. Eng. J., 2024, 483, 149317 CrossRef CAS.
- E. Yatmaz, M. Germec, S. B. Erkan and I. Turhan, Biomass Convers. Biorefin., 2022, 12, 5241–5255 CrossRef CAS.
- S. B. Erkan, E. Yatmaz, M. Germec and I. Turhan, J. Food Process. Preserv., 2021, 45, e14635 CAS.
- A. Damayanti, Z. A. S. Bahlawan and A. C. Kumoro, Cogent Eng., 2022, 9, 2049438 CrossRef.
- M. Carrié, H. Velly, F. Ben-Chaabane and J.-C. Gabelle, Biochem. Eng. J., 2022, 180, 108355 CrossRef.
-
G. F. Froment and K. B. Bischoff, Chemical Reactor Analysis and Design, Wiley, 1979 Search PubMed.
-
R. Khanna and J. H. Seinfeld, Mathematical modeling of packed bed reactors: numerical solutions and control model development, in Advances in Chemical Engineering, ed. J. Wei, Academic Press, New York, 1987, vol. 13, pp. 113–191 Search PubMed.
- O. Smidsrød and G. Skjak-Brk, Trends Biotechnol., 1990, 8, 71–78 CrossRef.
- M. Binns, A. Usai and C. Theodoropoulos, Comput. Chem. Eng., 2024, 186, 108683 CrossRef CAS.
-
K. J. Beers, Numerical Methods for Chemical Engineering: Applications in MATLAB, Cambridge University Press, Cambridge, 2006 Search PubMed.
- C. R. Wilke and P. Chang, AIChE J., 1955, 1, 264–270 CrossRef CAS.
- J. M. C. Puguan, X. Yu and H. Kim, Colloids Surf., A, 2015, 469, 158–165 CrossRef CAS.
- W. van Beinum, J. C. L. Meeussen, A. C. Edwards and W. H. van Riemsdijk, Water Res., 2000, 34, 2043–2050 CrossRef CAS.
- L. J. Park, C. H. Park, C. Park and T. Lee, Med. Biol. Eng. Comput., 1997, 35, 47–49 CrossRef CAS PubMed.
- P. T. Boggs and J. W. Tolle, Acta Numer., 1995, 4, 1–51 CrossRef.
- R. Kumar, B. Basak and B.-H. Jeon, J. Cleaner Prod., 2020, 277, 123954 CrossRef CAS.
- M. F. A. Bradfield and W. Nicol, Bioprocess Biosyst. Eng., 2016, 39, 233–244 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *
*
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio, reaching a final concentration of 4% w/v sodium alginate. The sodium alginate-cell culture mixture was subsequently added to a burette, placed approximately 15 cm from the surface of a beaker containing the CaCl2 solution, which was stirred gently using a magnetic stirrer. As soon as the droplets touched the liquid the Na+ ions were replaced by the Ca2+ ions forming firm calcium alginate beads.37 The median diameter of the beads was 0.3 cm. The median weight of pure (without entrapped cells) calcium alginate beads was 0.33 g per 10 beads. All reactants were purchased from Sigma-Adlrich UK. After immobilisation, the beads were used in a series of batch fermentations to grow and stabilise their biomass content. A semi-defined medium11 was employed. The glycerol concentration was 30 g L−1. After three subsequent fermentation cycles, the biomass concentration (Cbiomass (gbiomass L−1)) was stabilized at around 2.65 Cbiomass gbeads−1 as can be seen in Fig. 1. Biomass concentration inside the beads was measured by dissolving them in a 0.2 M sodium citrate solution. The successful fermentation runs, were also proof of the successful cell immobilisation.
1 ratio, reaching a final concentration of 4% w/v sodium alginate. The sodium alginate-cell culture mixture was subsequently added to a burette, placed approximately 15 cm from the surface of a beaker containing the CaCl2 solution, which was stirred gently using a magnetic stirrer. As soon as the droplets touched the liquid the Na+ ions were replaced by the Ca2+ ions forming firm calcium alginate beads.37 The median diameter of the beads was 0.3 cm. The median weight of pure (without entrapped cells) calcium alginate beads was 0.33 g per 10 beads. All reactants were purchased from Sigma-Adlrich UK. After immobilisation, the beads were used in a series of batch fermentations to grow and stabilise their biomass content. A semi-defined medium11 was employed. The glycerol concentration was 30 g L−1. After three subsequent fermentation cycles, the biomass concentration (Cbiomass (gbiomass L−1)) was stabilized at around 2.65 Cbiomass gbeads−1 as can be seen in Fig. 1. Biomass concentration inside the beads was measured by dissolving them in a 0.2 M sodium citrate solution. The successful fermentation runs, were also proof of the successful cell immobilisation.


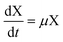


























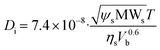
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da)41,42). These diffusivities were calculated using eqn (41) and are shown in Table 2.
000 Da)41,42). These diffusivities were calculated using eqn (41) and are shown in Table 2.