 Open Access Article
Open Access ArticleAn integrated molecular–thermodynamic framework for analyzing nanobubbles in supersaturated liquids
Ali Ghamartalea,
Ehsan Shahini a,
Aditya Jainb,
Rogerio Manica
a,
Aditya Jainb,
Rogerio Manica c,
Peter Bergd and
Tian Tang
c,
Peter Bergd and
Tian Tang *a
*a
aDepartment of Mechanical Engineering, University of Alberta, Edmonton, Alberta T6G 1H9, Canada. E-mail: tian.tang@ualberta.ca
bDepartment of Mechanical Engineering, Delhi Technological University, New Delhi, Delhi 110042, India
cDepartment of Mathematical and Statistical Sciences, University of Alberta, Edmonton, Alberta T6G 2G1, Canada
dDepartment of Physics, Brock University, St. Catharines, Ontario L2S 3A1, Canada
First published on 26th November 2025
Abstract
Nano-sized gas bubbles have attracted significant interest in electro-chemical applications due to their durability and longevity. Accurately predicting nanobubble formation and their size is critical for advancing technologies such as electrolysis and fuel cell systems. This study presents an integrated framework combining molecular dynamics (MD) simulations and thermodynamic modelling to determine nanobubble formation and size in a closed system under isothermal–isobaric condition. Assuming the nanobubble consists of a van der Waals (vdW) gas, the vdW constants are extracted from MD simulations of pure gas systems. A thermodynamic model is then developed for a closed system by combining the vdW equation with the assumption of chemical and mechanical equilibrium, which establishes a predictive relationship between nanobubble size and gas concentration. To validate the framework, MD simulations are performed for hydrogen in water under supersaturation, and the results are compared with thermodynamic model predictions. Comparisons are also made with experimental reports of nanobubbles. Our findings reveal that nanobubbles only form above a critical supersaturation threshold. The framework accurately predicts nanobubble radii in hydrogen–water systems, matching MD results while requiring minimal computational effort. When the pressure inside the nanobubble is approximated from the vdW equation of state, the Young–Laplace equation is shown to be valid even at sub-10 nm scales, with a negligible Tolman length. In contrast, the assumption of an ideal gas in thermodynamic modelling leads to considerable discrepancy with MD simulations. Overall, the proposed approach—bridging MD and thermodynamic modelling—paves the way toward a quantitative understanding of nanobubble formation and size in supersaturated liquids.
1. Introduction
Nanobubble technology has been experiencing a huge growth over the past two decades, emerging as a valuable global market with applications in energy, food, biomedical, and environmental sectors.1 Nanoscopic bubbles are categorized into surface nanobubbles or bulk nanobubbles,2 with bulk nanobubbles showing strong potential to enhance processes in various industries.3 However, despite their positive impact, basic knowledge regarding the formation, stability, size and dynamics of bulk nanobubbles, are still limited, which is the focus of this study.The International Standard ISO-20480-1-2017 defines nanobubbles as bubbles with a diameter of less than 100 nm that remain suspended in liquid and undergo Brownian motion, unlike larger bubbles that rise to the surface and burst.4 The exceptional stability and high surface area-to-volume ratio of nanobubbles result in unique properties, such as enhanced gas solubility, which distinguish them from both dissolved molecules and macroscopic bubbles.1,5,6 Due to their distinctive characteristics, nanobubbles can alter fluid properties resulting in more efficient heat transfer in geothermal systems.7 They can enhance nutrient permeability in skin care product, leading to effective anti-aging treatments.8 Of particular interest are hydrogen nanobubbles, which are becoming important in various industries5 due to their ability to neutralize reactive oxygen species, coupled with high cell penetration and biological compatibility.9 Hydrogen nanobubbles are typically generated via electrochemical methods, such as electrolysis, where hydrogen is produced in hydrogen evolution reactions—found in processes like water splitting—and subsequently forms nanobubbles.1,10 Understanding bubble properties and dynamics in hydrogen-based applications are crucial for optimizing energy use and enhancing process efficiency in such systems.10
Classical theories predict that nanobubbles should either collapse or grow once they reach a critical radius.11 According to the Young–Laplace model, internal pressures in nanobubbles should be exceptionally high (e.g., ∼300 atm for a 5 nm radius bubble), leading to rapid dissolution.1,12 However, experimental observations reveal that nanobubbles can persist for weeks or months under favourable conditions.13,14 Techniques, such as dynamic light scattering,2,15 zeta potential analysis,16 and cryo-electron microscopy,17 have advanced the understanding of nanobubble behaviour, yet the prediction of their properties such as size and shape continue to be elusive and debated topics. For instance, while some studies attribute nanobubble longevity to charged liquid–gas interfaces and concentration gradients,12 others emphasize surface polarization independent of bubble charge.18 Measuring nanobubble size and understanding its dependence on gas supersaturation are unanswered questions in both experimental and computational studies. In addition, bridging molecular view of nanobubbles with their thermodynamic understanding remains a challenge. On this front, some statistical mechanical models have been developed to include molecular interactions into free energy formulations. For example, Yu and Wu19 proposed a density functional approach that combined the modified fundamental measure theory for hard-sphere interaction with Wertheim's first-order thermodynamic perturbation theory (TPT1) for studying inhomogeneous associating fluids. This framework was applied in Zhou et al.20 to predict the interfacial properties and bubble nucleation of air–water mixtures near a hydrophobic wall. Compared with classical theories, such models are more detailed and capable of predicting non-uniform density distributions of gas and liquid in the system, while requiring more computations.
Molecular dynamics (MD) simulation is another tool used in the literature to study the formation and stability of nanobubbles in liquid. Table 1 provides a detailed review of MD simulations that investigated nanobubbles. In these works, the term ‘stable’ describes a nanobubble that remains structurally intact and exhibits no spontaneous dissolution over the duration of the MD simulations (tens of nanoseconds), a convention that will also be used to describe nanobubble state in our MD simulations. While providing valuable insights, such as nanobubble size, at the nanoscale,8 studies listed in Table 1 rarely compared the MD output with thermodynamic modelling to fill the gap of scalability. When a comparison was made in some works, the focus was often on the validity of the Young–Laplace equation, and whether a Tolman correction was needed for the surface tension.2,12 In the closest effort, Weijs et al.21 attempted to develop a connection between MD simulation and thermodynamics modelling. The modelling was significantly simplified by considering a 2D gas cylinder instead of a 3D gas bubble. A key gap exists in establishing a robust, generalized relationship between the gas supersaturation and the resulting nanobubble size, a connection that has so far been accessible only through MD studies on a case-by-case basis.
| Solvent, forcefield | Gas, forcefield | Concen.a (g L−1) | Supersat.b | T (K), P (atm) | Ensemble, MD package | Key findings reported | Ref. |
|---|---|---|---|---|---|---|---|
a Unless otherwise specified, mass concentration of the gas (CgT) is calculated from molecular numbers according to CgT = (NgMg)/(NLML/ρL), where Ng and NL are number of gas and liquid molecules respectively, Mg and ML are molecular weight of gas and liquid respectively, and ρL is liquid density.b Unless otherwise specified, supersaturation = CgT/(saturated concentration) is calculated using column 3 (Concen). Saturated concentration reported by the National Institute of Standards and Technology (NIST)33 for N2, O2, CH4 and He are 0.017, 0.042, 0.022, and 0.00152 g L−1, respectively.c Parameters provided in Table 2.d Atomic type and molecular weight not given,21 Ng = 333−837, NL = 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 236−52 236−52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 489. 489. |
|||||||
| Argonc | Vacuum | N/A | N/A | 99, N/A | NVT, not mentioned | • Stable NBs when the non-dimensional average density is below a critical value of 0.6625 | 24 |
| • Simulation domain size significantly impacts NBs instability. Larger domains allow more stable NBs formation | |||||||
| • Surface tension of NBs is slightly larger (up to 15%) than that of a planar interface and decreases very slightly with increasing NB size | |||||||
| H2O, TIP4P | Vacuum | N/A | N/A | 300, N/A | Not mentioned | • Young–Laplace equation is valid for NBs, with small dependency of surface tension on NB size | 25 |
| • Threshold radius of unstable NBs is 1 nm, below which NBs shrink and vanish | |||||||
| Liquidc | Gasc | N/Ad | N/A | 300, 1 | NPT, not mentioned | • Stable NB when the distance from its periodic image is small (<15 nm) | 21 |
| • Larger distances (>30 nm) lead to NB dissolution, unless sufficient gas is present | |||||||
| • Equilibrium radius of stable NB matches 2D continuum model predictions, but insufficient gas concentration prevents NB nucleation in simulation, even if predicted to be stable theoretically | |||||||
| H2O, SPC/Fw | He, CHARMM | 1.085–16.93 | 713.8–11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 138.1 138.1 |
298.15, N/A | NVT-NVE, NAMD | • Preformed NBs below the critical radius of 1 nm are thermodynamically unstable | 26 |
| • Inner pressure grows with decreasing radius, resulting in NB instability below the critical radii | |||||||
| • Calculated Tolman length is not constant and can be positive or negative depending on the NB size, leading to under- or overestimation of surface tension in some cases | |||||||
| H2O, TIP3P | N2c | 13–26 | 722.2–1444.4 | 300, 1 | NPT, GROMACS | • NBs exhibit a sharp transition from dispersed to assembled states when N2 concentration exceeds a critical threshold corresponding to supersaturation ≈1050 | 27 |
| • Density of N2 inside NB is significantly higher than in the dispersed state and increases as N2 concentration rises beyond the critical threshold | |||||||
| • Formation of NBs occurs within a short time frame (around 20 ns) | |||||||
| H2O, SPC/E | O2c | 0.042–35.7 | 1–850 | 300, 1 | NPT-NVT, LAMMPS | • Stable NBs' radii range from 20 to 400 nm with internal pressure from 120 to 4 atm | 28 |
| • Surface tension of water decreases with increasing supersaturation | |||||||
| • For high supersaturation (>200), surface tension drops significantly | |||||||
| H2O, CHARMM27 | Vacuum | N/A | N/A | 300, N/A | NVT, GROMACS | • Stable NB radius range 1.33 to 3.37 nm depending on system size and initial bubble radius | 29 |
| • Water surface tension remains nearly constant (∼64.18 mN m−1) regardless of the NB radius | |||||||
| • A maximum inter-bubble distance is proposed below which NBs stay stable. The maximum inter-bubble distance ∝ (bubble radius)4/3 | |||||||
| H2O, TIP4P/2005 | O2, N2c | Atomistic: O2: 21.14–29.17 | O2: 503.3–694.5 | 298, 1 | NPT, LAMMPS | • Gas molecules of pre-formed NBs exhibit confined diffusion, with most gas molecules (more than 50%) remaining inside the NB over the simulation period | 30 |
| CG: N2: 19.41–21.11 | N2: 1078.33–1172.78 | • Inner pressures for the NBs are 62.1, 52.3, and 46.9 MPa for bubble radius = 1.88, 2.27, and 2.55 nm, respectively, resulting in ultra-high density inside the NB. | |||||
| • NBs exhibit a double-layer surface charge, with inner layer positively charged and outer layer negatively charged | |||||||
| H2O, TIP4P/ice, CGc | CH4, OPLS-UA, CGc | 47.13 | 2142.27 | 270, 98.7 | NPT, GROMACS/LAMMPS | • Young–Laplace equation is valid for pre-formed NBs with radius larger than 5 nm, while smaller NBs are unstable | 31 |
| • Minimum center-of-mass distance required to prevent coalescence between two NBs is 20–25 nm, varying slightly with NB size and methane concentration | |||||||
| H2O, SPC/E | O2c | 1.042–13.16 | 24.81–313.3 | 293–303 | NVT-NPT, LAMMPS | • High supersaturation (>1454.41) supports NB formation by limiting gas diffusion from NB. | 12 |
| 1 | • Calculated surface tension decreases with supersaturation, averaging 58–68 mN m−1 | ||||||
| • Elevated temperatures increase gas diffusion and instability | |||||||
| H2O, SPC/E | N2c | 21.01–41.67 | 1167.2–2315 | 300, 1 | NPT-NVE, LAMMPS | • Small NB (radius = 14 Å) has a high internal pressure (792 atm) and a thicker gas–liquid interface (6.8 Å) compared to large NB (radius = 22 Å, 518 atm, interface thickness 4.4 Å) | 2 |
| • Small NB has almost double the diffusion rate of large NB, facilitating faster dissolution | |||||||
| • Young–Laplace equation is valid, with surface tension in the range of 55–58 mN m−1, and Henry's law corroborates solubility predictions for different NB sizes | |||||||
| Pb–Li eutecticc | Hec | 1.62–8.41 | N/A | 1000, 773.75 as calculate average | NVT, LAMMPS | • NBs exhibit thermodynamic irreversibility when the ratio of gas molecules in the NB to dissolved gas exceeds 0.5, preventing dissolution even under disturbances | 32 |
| • Diffusive-shielding effect, driven by background supersaturation, enhances NB formation by reducing gas leakage to the surrounding liquid | |||||||
| εij (kcal mol−1) | σij (Å) | Ref. | |
|---|---|---|---|
| Argon | 0.240 | 3.4 | 24 |
| Liquid | 0.717 | 3.4 | 21 |
| Gas | 0.239 | 5 | 21 |
| N of N2 | 0.069 | 3.26 | 27 |
| O of O2 | 0.095 | 3.094 | 12 and 28 |
| O of O2 | 0.086 | 3.159 | 30 |
| N2 | 0.382 | 3.6 | 30 |
| N of N2 | 0.072 | 3.32 | 2 |
| H2O–CH4 | Stillinger–Weber potential | 31 | |
| Helium | Extended Tang–Toennies–Sheng | 32 | |
| Pb–Li | Embedded-atom method | 32 | |
In response to this challenge, we propose a streamlined framework to predict nanobubble size by integrating molecular properties of the gas, macroscopic parameters such as surface tension, and thermodynamic conditions. The focus is on bulk nanobubbles, without the presence of a nearby surface. Surface nanobubble is another intriguing topic, with many ongoing studies. For instance, Zhang & Lohse22 combined MD with a generalized Lohse–Zhang model that considers reaction-driven gas influx and a real-gas (vdW) law, predicting the size evolution and detachment of single electrolytic nanobubbles on nanoelectrodes. Perez Sirkin et al.23 used MD to simulate the nucleation and stationary states of gas bubbles on nanoelectrodes, by mimicking electrochemical production of gas at the electrodes. In contrast to these studies, the present work addresses nanobubble formation and size in a closed, non-reactive system under isothermal–isobaric condition. While involving both MD and thermodynamic modelling, our approach does not invoke strict scale separation; rather, we integrate MD outputs with thermodynamic relations calibrated to those outputs.
The rest of the paper is organized as follows: Section 2 describes the theoretical framework including thermodynamic modelling and MD simulation. Section 3 is dedicated to Results and discussion including validation of the framework with MD simulations and experiments. Finally, the conclusion is provided in Section 4.
2. Theoretical framework
The theoretical framework begins by incorporating the vdW equation of state, tuned for the specific gas using MD simulations, into the thermodynamic model (Section 2.1) for a closed system as illustrated in Fig. 1(a). This real-gas treatment parallels recent surface-nanobubble theory at high Laplace pressures.22 The values of constants in the vdW equation of state are obtained by molecular simulation of pure gas without any liquid (illustrated in Fig. 1(b)), and they reflect the intermolecular interactions that dictate nanobubble behaviour (Section 2.2). Different MD simulations are undertaken to validate the framework, following the methodology described in Section 2.2. A generic picture of the gas-in-liquid simulations is shown in Fig. 1(c) before nanobubble formation and in Fig. 1(d) after nanobubble formation.2.1. Thermodynamic modelling
Consider a closed system with controlled pressure and temperature, i.e., it operates under the isothermal–isobaric (NPT) condition with prescribed pressure in the liquid PL (Fig. 1(a)). Mass conservation of the gas implies| ngT = ngB + ngL, | (1) |
 | (2) |
| ngL = kPgBVL, | (3) |
| VL = (ngLvgL + nLvL)NA, | (4) |
| ngT = ngB + kPgB[(ngT − ngB)vgL + nLvL]NA. | (5) |
Assuming the gas–liquid interface has a uniform curvature, and the system is free from external forces or dynamic effects, then mechanical equilibrium holds and is described by the Young–Laplace equation
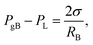 | (6) |
It is common in the literature to model the gas in the system using the ideal gas law, which only accurately predicts gas behaviour at low pressure and high temperature. The nanobubble can hold a very high pressure1,12 at room temperature, and hence an equation of state that captures intermolecular interactions is more appropriate. In this work, the vdW gas law is adopted for the gas in the bubble,
 | (7) |
 | (8) |
Theoretically, eqn (5)–(8) can be used to collectively solve ngB, PgB, RB and VgB, provided that other parameters in these equations are prescribed. However, to reduce the total number of physical quantities and regulate their magnitude in numerical calculations, the equations are non-dimensionalized using the following definitions, with quantities carrying a bar being dimensionless.
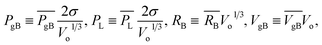 | (9) |
 | (10) |
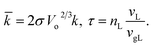 | (11) |
Likewise, eqn (6) and (8) can be recast as
 | (12) |
 | (13) |
 | (14) |
 | (15) |
For the purpose of comparison and emphasizing the importance of a good gas model, the results for ideal gas will be obtained by setting the vdW constants ā = ![[b with combining macron]](https://www.rsc.org/images/entities/i_char_0062_0304.gif) = 0 in eqn (14), leading to
= 0 in eqn (14), leading to
 | (16) |
Fig. 2 shows the flowchart to establish a relationship between the normalized nanobubble radius  and the amount of gas in the system, ngT. Rather than specifying ngT and solving for
and the amount of gas in the system, ngT. Rather than specifying ngT and solving for  , which is numerically more challenging, the strategy here is to specify
, which is numerically more challenging, the strategy here is to specify  and solve the corresponding ngT. With a given
and solve the corresponding ngT. With a given  , the normalized gas pressure
, the normalized gas pressure  and volume
and volume  can be calculated directly using eqn (12) and (13), for a specified liquid pressure
can be calculated directly using eqn (12) and (13), for a specified liquid pressure  . Next, parallel paths are taken to calculate ngB via eqn (14) and (16), respectively for the vdW and ideal gases. The determined ngB value is then fed into eqn (10) to calculate ngT. This process is repeated for a range of
. Next, parallel paths are taken to calculate ngB via eqn (14) and (16), respectively for the vdW and ideal gases. The determined ngB value is then fed into eqn (10) to calculate ngT. This process is repeated for a range of  , establishing its relationship with ngT. Other relationships can be easily determined based on
, establishing its relationship with ngT. Other relationships can be easily determined based on  vs. ngT, e.g., between RB and cgL. In Experimental settings, it is often not possible to separately measure the amount of gas in the bubbles and that in the liquid. Alternatively, the total mass concentration of the gas in the system (in g L−1) can be calculated from the aforementioned quantities by
vs. ngT, e.g., between RB and cgL. In Experimental settings, it is often not possible to separately measure the amount of gas in the bubbles and that in the liquid. Alternatively, the total mass concentration of the gas in the system (in g L−1) can be calculated from the aforementioned quantities by
 | (17) |
 | ||
Fig. 2 Flowchart to determine the relationship between normalized bubble radius  and total moles of gas, ngT, in the system. and total moles of gas, ngT, in the system. | ||
2.2. Molecular dynamics
Molecular dynamics simulations are conducted, following a structured workflow that includes three main steps: selecting forcefields, designing the simulation systems, and defining system settings. These steps are described in detail below, followed by the post-processing calculations applied to analyze the simulation outputs and relate them to thermodynamic modelling.The pure hydrogen system is simulated to extract the vdW gas constants required in the thermodynamic modelling. In these simulations, the number of hydrogen molecules remains constant (500), while pressure and temperature are varied across a specified range: temperature (200, 250, 300, 325, 400 K), pressure (0.1, 5, 7.5, 10, 15, 20, 25, 30, 35 bar). Arbitrary combinations of these temperature and pressure values lead to a total of 45 simulations. Each simulation starts with a cubic box (initial side length of 3 nm), and undergoes three steps: minimization, NVT/NPT equilibration and NPT production run. The simulation begins with energy minimization using the steepest descent algorithm to stabilize the system and reduce the maximum force in the system to below 100 kJ mol−1 nm−1. The second step is equilibration under the NVT ensemble for 1.5 ns to adjust the temperature, followed by equilibration under the NPT ensemble for 10 ns to stabilize the system and reach the target temperature and pressure. Once equilibration is completed, a 10 ns production run under NPT is performed to collect data. Temperature control is achieved using the V-rescale thermostat with coupling time constant of 0.1 ps. Pressure is maintained using the C-rescale barostat with coupling time constant of 2 ps. System compressibility is set to 3 × 10−3 bar−1 following the data from NIST.33 Periodic boundary condition is applied in all three directions to mimic infinite bulk behaviour and eliminate edge effects. The cut-off radius for short-range non-bonded interactions is set to 1.2 nm. Since the hydrogen beads in the Buch forcefield have zero charge, there are no electrostatic interactions. The leap-frog integrator with 1 fs time step is used to solve the equations of motion.
The second set of systems containing both hydrogen and water are designed to study bubble dynamics across a range of hydrogen concentrations. Four distinct system sizes of small (3000 water molecules), medium (6000 water molecules), intermediate (9000 water molecules) and large (12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 water molecules) are considered each with four different hydrogen concentrations (Table 4). The hydrogen molecules are initially randomly dispersed in the water box using the Packmol package,38 which ensures optimal spatial distribution of molecules within the simulation box while avoiding overlaps. Table 4 also shows the initial box dimension for each system. The determination of CgT and supersaturation follows the same method specified in the footnote of Table 1, with the saturation concentration of H2 = 0.00157 g L−1, extracted from NIST data.33 This calculation of CgT is consistent with the definition in eqn (17) for the thermodynamic model, provided that the volume of dissolved gas is much smaller than the volume of the liquid.
000 water molecules) are considered each with four different hydrogen concentrations (Table 4). The hydrogen molecules are initially randomly dispersed in the water box using the Packmol package,38 which ensures optimal spatial distribution of molecules within the simulation box while avoiding overlaps. Table 4 also shows the initial box dimension for each system. The determination of CgT and supersaturation follows the same method specified in the footnote of Table 1, with the saturation concentration of H2 = 0.00157 g L−1, extracted from NIST data.33 This calculation of CgT is consistent with the definition in eqn (17) for the thermodynamic model, provided that the volume of dissolved gas is much smaller than the volume of the liquid.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 water molecules
000 water molecules
| System | #H2O | #H2 | CgT (g L−1) | Supersaturation | Initial box side length (nm) |
|---|---|---|---|---|---|
| S1 | 3000 | 175 | 6.53 | 4157.89 | 5 |
| S2 | 3000 | 200 | 7.46 | 4751.88 | |
| S3 | 3000 | 225 | 8.39 | 5345.86 | |
| S4 | 3000 | 250 | 9.33 | 5939.85 | |
| M1 | 6000 | 300 | 5.60 | 3563.91 | 6 |
| M2 | 6000 | 350 | 6.53 | 4157.89 | |
| M3 | 6000 | 400 | 7.46 | 4751.88 | |
| M4 | 6000 | 450 | 8.39 | 5345.86 | |
| I1 | 9000 | 450 | 5.60 | 3563.91 | 7 |
| I2 | 9000 | 525 | 6.53 | 4157.89 | |
| I3 | 9000 | 600 | 7.46 | 4751.88 | |
| I4 | 9000 | 675 | 8.39 | 5345.86 | |
| L1 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
600 | 5.60 | 3563.91 | 7.5 |
| L2 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
700 | 6.53 | 4157.89 | |
| L3 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
800 | 7.46 | 4751.88 | |
| L4 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
900 | 8.39 | 5345.86 |
Each hydrogen–water system is first subjected to energy minimization using the steepest descent algorithm, to reduce the forces below 100 kJ mol−1 nm−1. Equilibration is then conducted using the NPT ensemble for 20 ns with a Nose–Hoover thermostat and a Parrinello–Rahman barostat, controlling the system's temperature and pressure at 300 K and 1 bar, respectively. The subsequent production phase, 80 ns for data collection under the NPT ensemble, uses the same thermostat and barostat. Bond constraints for water molecules are applied using the LINCS algorithm. Periodic boundary conditions are applied in all three dimensions, and short-range non-bonded interactions are cut off at 1.2 nm. Long-range electrostatic interactions are handled using the Particle Mesh Ewald (PME) method. The leap-frog integrator is used to solve the equations of motion with a 2 fs time step. Trajectories are saved every 100 ps for post-simulation analysis. Equilibrium indicators (e.g., energy and pressure fluctuations), are evaluated using built-in GROMACS tools.
Bubble size in the hydrogen–water systems is determined by first detecting the nanobubbles. A distance-based criterion, derived from the radial distribution function (RDF), is introduced to identify the nanobubbles. Fig. 3 shows the RDF between hydrogen molecules for two systems of M2 and L4, representing the fundamental characteristics of all systems. A prominent peak in the RDF is observed between 0.2 and 0.6 nm, which corresponds to the close packing of hydrogen molecules within a nanobubble. The distance of 0.6 nm is therefore selected within which two hydrogen molecules are considered to be in the same nanobubble. Custom Python scripts,39 built on the MD analysis library,40 complement this analysis by visualizing and validating nanobubble formation. Once the nanobubbles are detected, the radius (RB) of each nanobubble is calculated based on its gyration radius (RG). Specifically, by approximating each nanobubble as a sphere, RB and RG are related by
 | (18) |
The calculated RB is substituted into eqn (8) to calculate the bubble volume, VgB. Attempt is also made to compute VgB by approximating the nanobubble as an ellipsoid, leading to  , where (λ1, λ2, λ3) are the principal moments of the gyration tensor. Comparison between the two approaches shows less than 3% difference, confirming the validity of the spherical nanobubble assumption.
, where (λ1, λ2, λ3) are the principal moments of the gyration tensor. Comparison between the two approaches shows less than 3% difference, confirming the validity of the spherical nanobubble assumption.
3. Results
3.1. Extracting van der Waals constants from MD simulations
The Nelder–Mead algorithm is used to iteratively determine the vdW constants a and b, based on initial guesses adopted from experimental values reported for hydrogen: a = 24 L2 kPa mol−2 and b = 0.01 L mol−1. The optimization renders a = 17.2577 L2 kPa mol−2 and b = 0.0193 L mol−1. Fig. 4 shows the good agreement between the MD-calculated hydrogen density, the fit to the vdW equation of state, and the density reported from NIST database.33 | ||
| Fig. 4 Comparison of the pure hydrogen density from MD simulations (filled shapes), NIST data (hollow shapes), and fitting using the vdW equation of state (dashed lines). | ||
3.2. Existence of minimum supersaturation for bubble formation
Our investigation begins with the S systems presented in Table 4. At low hydrogen concentrations (simulations are also conducted for 50, 75, 125 and 150 hydrogen molecules in addition to those listed in Table 4), the initially dissolved molecules remain dispersed throughout the simulation. However, as the concentration increases, clusters begin to form, eventually resulting in a stable nanobubble when the number of H2 molecules reaches 200. At this critical concentration (CgT = 7.46 g L−1) the bubble persists throughout the simulation timeframe. Simulations with 225 and 250 hydrogen molecules are then performed to provide three data points for this system size. A similar approach is used for system sizes of M, I and L, presented in Table 4, and a concentration of 6.53 g L−1 is identified as the threshold above which stable nanobubbles exist for these systems.3.3. Validity of Young–Laplace equation
In continuum theory, surface tension is considered size-independent. However, at the nanoscale, surface tension may exhibit deviations from its macroscopic counterpart, raising questions about the applicability of the Young–Laplace equation in this regime.41 To investigate this effect, the internal pressure, PgB, of each nanobubble is calculated from its volume using the vdW equation of state (eqn (7)), with a and b values derived from MD simulations (Section 3.1). This should be recognized as an approximation (although more realistic than the ideal gas model used in many studies), since the gas inside a nanobubble is not uniformly distributed, and strictly speaking pressure inside the nanobubble is a position-dependent property. The pressure difference across the hydrogen–water interface, ΔP, is then computed as ΔP = PgB − PL, where PL = 1 bar. ΔP is plotted against 1/RB for all systems in Fig. 5. For each system, all data during the last 25 ns of the simulations are shown by scattered point and represented by a distinct marker type and color. The variability in the data is due to the dynamic nature of the nanobubble where the hydrogen molecules in the bubble can exchange with those in the bulk liquid. The pressure and bubble radius averaged from all the data are obtained for each system and shown with a hollow symbol in Fig. 5. The averaged data reveal a linear trend with little deviation from the black dash line plotted using the Young–Laplace equation (eqn (6)) and σ = 72.0 mN m−1. An attempt is also made to fit the data using the Tolman correction:41
 | (19) |
3.4. Prediction of bubble size
Using the thermodynamic model established in Section 2.1, the nanobubble radius (RB) is calculated as a function of CgT and the analytical predictions are plotted in Fig. 6 for systems with different amount of water using either solid (assuming vdW gas) or dashed (assuming ideal gas) lines. Average RB from the last 25 ns of the MD trajectory is shown in the same figure, along with the corresponding standard deviation. The results reveal a nearly perfect alignment between the simulation data and the theoretical predictions based on the vdW equation of state (solid lines). While the theoretical predictions based on the ideal gas model (dashed lines) deviate significantly from the simulation data. This comparison underscores the robustness of the framework in predicting nanobubble size when intermolecular interactions are taken into account. Notably, solving bubble size using the numerical scheme in Fig. 2 is highly efficient, without the computational expense of simulating each molecular system individually. | ||
| Fig. 6 Nanobubble radius (RB) vs. total mass concentration of gas (CgT), obtained from thermodynamic modelling (curves) and MD simulation (symbols). | ||
An important observation in Fig. 6 is the absence of simulation data on the lower branch of the theoretical curves. For the range of hydrogen concentrations studied in our MD simulations, this branch corresponds to nanobubbles with radii between 2.5 and 3.4 Å. Such radii represent minuscule clusters containing only 2–3 hydrogen molecules, which lack the cohesive interactions required for stability, leading to rapid dissolution into the bulk liquid.
3.5. Comparison with experiments
Before our attempt to make a comparison with existing experiments in the literature, it is acknowledged that while our model predicts the size of a single nanobubble, in an experimental setup there is usually a distribution of nanobubbles which can co-exist with larger bubbles due to the more complex experimental conditions. It is hence extremely difficult to isolate a single bubble in experiments for direct comparison. However, it is possible to consider the model prediction as a representative nanobubble size in the experimental system, mimicking the situation where individual nanobubbles are not strongly interacting with each other.In one set of experiments by Michailidi et al.,13 air and oxygen nanobubbles were generated using a low-energy nanobubble generator based on hydrodynamic cavitation. Their setup operated under an elevated pressure of approximately 3 bar (≈3 atm), and the nanobubble size distribution was determined using dynamic light scattering (DLS) along with stability analyses via ζ-potential and free radical measurements. In a separate study by Wang et al.,42 nanobubbles containing N2, O2, and CO2 were produced by a periodic pressure change device. The device first pre-saturated the solution with gas and then induced pressure fluctuations—where the pressure in the U-tube was observed to increase by roughly 0.8 atm above the ambient (≈1 atm), yielding an effective pressure of about 1.8 atm during the pressurization phase.
The above experimental reports did not specify the gas concentrations in their systems. To enable the comparison of experimental results with our theoretical model, the best we can do based on the provided data is to estimate the molar concentrations of dissolved gas in water (cgL) using Henry's law, eqn (2). Then, the nanobubble radii under the same cgL are predicted from our analytical framework. The Henry's constants are adopted from the literature as follows: O2: 1.3 × 10−5, N2: 6.4 × 10−6, air: 7.8 × 10−6, and CO2: 3.4 × 10−4 mol m−3 Pa−1.33 The volume of the liquid chamber in Michailidi et al.13 was 4 L and that in Wang et al.42 was 3 mL. These numbers are used to obtain nL required by the model. The analytical predictions are compared with experimental measurements in Fig. 7, which shows a systematic discrepancy: the analytical model yields larger bubble radii than those observed experimentally. To quantify this deviation, we introduce a ratio  , where
, where  is the effective gas concentration required in our model to match the experimentally observed nanobubble radius, and cgL,est is the concentration estimated using Henry's law. As shown in Fig. 7, this ratio is greater than one in all cases. For example, in the study by Michailidi et al.,13 the analytical and experimental radii converge when the effective concentration is about 1.6 times cgL,est. This is likely because Henry's law assumes ideal, equilibrium conditions, whereas experimental systems are subject to dynamic mixing and local non-equilibrium effects that may result in higher effective concentrations of dissolved gas.
is the effective gas concentration required in our model to match the experimentally observed nanobubble radius, and cgL,est is the concentration estimated using Henry's law. As shown in Fig. 7, this ratio is greater than one in all cases. For example, in the study by Michailidi et al.,13 the analytical and experimental radii converge when the effective concentration is about 1.6 times cgL,est. This is likely because Henry's law assumes ideal, equilibrium conditions, whereas experimental systems are subject to dynamic mixing and local non-equilibrium effects that may result in higher effective concentrations of dissolved gas.
Another source of discrepancy is the time over which the experimental observations are made. Michailidi et al.13 observed that the nanobubble size increased by approximately 1.5 times after 3 months compared to its initial size after 5 days. This temporal evolution indicates that prolonged equilibration leads to bubble growth, which may result in better agreement with the theoretical model built on strict enforcement of equilibrium. Compared to Michailidi et al.,13 the data from Wang et al.42 differ more from the analytical prediction, likely reflecting the shorter equilibration time reported −48 hours for N2 and O2, and 24 hours for CO2—which prevented the system from reaching full equilibrium. In view of these points, better agreement is expected when parameter values in the model are made more faithful to experimental conditions. For instance, rather than applying the ideal Henry's law to estimate the dissolved gas concentrations, one could use activity/fugacity-based estimates tied to the actual gas partial pressures and the true mixture composition (air as O2/N2/CO2 rather than a single-component proxy). An effective γ may be adopted to reflect interfacial conditions present in the measurements (e.g., ionic strength, surface-active species, and dynamic changes in interfacial tension).
Despite these deviations, the overall agreement between the analytical predictions and experimental data remains within a reasonable range, underscoring the robustness and adaptability of our framework when extrapolated to larger systems.
3.6. Discussion
Fig. 6 not only validates our framework against MD simulations but also reveals interesting behaviour when extended to larger volumes. For each system size—from the smallest 1.25 × 10−19 ml (MD simulation box containing 3000 molecules) to a hypothetical 1 ml volume—the analytical solution yields two mathematical branches. In MD simulation, only the upper branch corresponds to a stable nanobubble. The lower branch, which would imply radii of just a few angstroms, is thermodynamically unfavourable and the nanobubble disappears rapidly through dissolution. As system size grows, both branches move upwards. For the 0.001 and 1 ml systems shown in Fig. 6, the lower branch occupies a region that could, in principle, host equilibrium bubbles on the order of tens to hundreds of nanometres, while the upper branch corresponds to unrealistically large radii on the order of mm to cm. Therefore, for large systems, it is expected that the lower branch would provide predictions that better align with experiments. Another interesting observation from Fig. 6 is that once the lower branch becomes physically accessible, its predicted radii for different system sizes collapse onto a single curve. This is in contrast to the separation of the upper branches which are physically realistic for small systems. Therefore, in large systems, equilibrium bubble size depends solely on the gas concentration and not on the liquid volume, while in small systems, liquid volume impacts bubble size, in agreement with findings previously reported in the literature.21,29The sharp “elbow” in each analytical curve of Fig. 6 marks the minimum gas concentration (CgT) required for a bubble to be in equilibrium. Below this concentration, the thermodynamic model has no real solution for RB, suggesting that gas remains dispersed rather than forming a bubble. As system volume increases, we observe that the minimum CgT steadily decreases which means larger liquid reservoirs require a lower degree of supersaturation to overcome the Laplace pressure barrier. This negative correlation between the critical concentration and system size is confirmed in our MD simulations: the smallest (S) systems exhibit a threshold near 7.5 g L−1, whereas medium, intermediate, and large systems all transition around 6.5 g L−1. Such a trend has also been reported in previous computational studies21,24—for example, Park et al. (2001) observed stable bubbles at lower supersaturations for larger simulation cells.24
Despite the overall agreement in trend, the MD-derived thresholds lie substantially above the analytical predictions—for instance, our large systems (containing 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 water molecules) yield a minimum CgT of ∼6.5 g L−1 in MD versus ∼2.8 g L−1 analytically. Several effects contribute to this gap. First, the thermodynamic model assumes a perfectly smooth, spherical interface with a constant macroscopic surface tension, whereas in molecular simulations the bubble surface has rough edges, and it is not perfectly spherical—both of which can increase the local Laplace pressure and raise the barrier for bubble equilibration. Second, Henry's law is used to relate dissolved gas concentration to bubble pressure which, strictly speaking, only applies to ideal dilute solutions. Therefore, at high supersaturations, the thermodynamic model may underestimate the dissolved (and hence the total) gas concentration when an equilibrium bubble is present. Finally, finite-size and periodic-boundary effects in MD can introduce interactions between periodic images, and hinder nanobubble stabilization.
000 water molecules) yield a minimum CgT of ∼6.5 g L−1 in MD versus ∼2.8 g L−1 analytically. Several effects contribute to this gap. First, the thermodynamic model assumes a perfectly smooth, spherical interface with a constant macroscopic surface tension, whereas in molecular simulations the bubble surface has rough edges, and it is not perfectly spherical—both of which can increase the local Laplace pressure and raise the barrier for bubble equilibration. Second, Henry's law is used to relate dissolved gas concentration to bubble pressure which, strictly speaking, only applies to ideal dilute solutions. Therefore, at high supersaturations, the thermodynamic model may underestimate the dissolved (and hence the total) gas concentration when an equilibrium bubble is present. Finally, finite-size and periodic-boundary effects in MD can introduce interactions between periodic images, and hinder nanobubble stabilization.
While our primary focus is hydrogen-based nanobubbles due to their importance in various applications, the methodology is broadly applicable to nanobubbles formed by other gases. When we substitute nitrogen or oxygen for hydrogen in the large system (12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 water molecules), the same two-branch trend emerge (Fig. 6), but the predicted bubble sizes shrink. At the same CgT, bubble radii for the three gases follow the order of H2 > N2 > O2.
000 water molecules), the same two-branch trend emerge (Fig. 6), but the predicted bubble sizes shrink. At the same CgT, bubble radii for the three gases follow the order of H2 > N2 > O2.
Within the nanobubble literature, the closest research to ours was performed by Weijs et al.,21 but with differences in three fundamental aspects. First, the bubbles were modeled as 2D cylinders in Weijs et al.21 while we consider 3D geometry which is more realistic. Second, while Weijs et al. employed an ideal gas description in their continuum model—focusing on diffusive shielding effects in nanobubble clusters—we explicitly incorporate non-ideal gas behavior using the vdW equation of state. This modification is critical because nanobubbles experience extremely high internal pressures, where the ideal gas law becomes inadequate. Fig. 6 shows the importance of considering the non-ideal gas law when predicting the bubble size. The third improvement is the incorporation of parameters derived at microscopic scale into a macroscopic model. These parameters include molecular volumes for the liquid and dissolved gas, vL and vgL. Under the isothermal–isobaric condition, the pressure in the liquid is prescribed while the system volume is not known a priori. Incorporating vL and vgL in the model removes the need for an empirical equation of state for the liquid that specifies a relationship between pressure and volume. In addition, while the vdW constants a and b can be determined using experimental sources (e.g., NIST database33), they are calibrated in our work using MD simulation data, an approach that can be extended to any gases (in pure or mixed forms) especially when experimental data are unavailable. This integration of molecular-level details into a thermodynamic framework enhances the predictive capability of our model for the nanoscale systems studied.
It is important to recognize the practical constraints of MD simulations in exploring the full range of nanobubble behaviour. While our theoretical curves in the inset of Fig. 6 indicate that ever-larger bubbles should form as CgT increases, intrinsic limitations in box size and computational cost prevent MD from reaching those regimes. For example, at CgT ≈ 13.50 g L−1 the model predicts a bubble radius of 34.8 Å, yet a cubic simulation cell with side length L = 80.4 Å cannot physically accommodate such a bubble without significant interaction between periodic images. In this example, L − 2RB ≈ 10.8 Å, which falls below the 12 Å cut-off distance for nonbonded interactions. Under such conditions, the bubble is artificially distorted into a cylindrical shape, as shown in the inset of Fig. 6. The thermodynamic framework, on the other hand, does not have these limitations or the high computational cost of MD, offering reliable bubble-size predictions across supersaturation levels and volumes far beyond current simulation feasibility.
As acknowledged earlier, the gas density inside a nanobubble is intrinsically non-uniform. A rigorous route for predicting the radial density profile together with the curvature-dependent interfacial tension is provided by classical density functional theory (cDFT). For example, Peng and Yu showed that cDFT can self-consistently capture non-uniform gas densities and interfacial properties at nanometre scales.43 In contrast, the present study adopts a simplified but practical closure: the nanobubble's internal pressure is assumed to be uniform and approximated from a real-gas (vdW) equation of state whose parameters are calibrated to MD. This approach trades some microscopic details for computational efficiency and direct comparability with MD outputs. Extending our framework to a cDFT-based description of the gas phase and interface is a natural direction for future work and may further improve quantitative accuracy when strong inhomogeneities are present.
In addition, it is worth investigating whether the strong applicability of the Young–Laplace equation, discovered here for hydrogen in water, is also valid for other gas/liquid combinations or corrections for nanoscale effects might be required. Moreover, the application of Henry's law warrants careful discussion. Our MD calculations yield dissolved gas concentrations ranging 0.697–1.658 g L−1, which are significantly higher than the saturation concentration (0.00157 g L−1 (ref. 33)), thereby violating the dilute-solution assumption underlying Henry's law. Despite this, the model appears to capture the nanobubble behavior well, both qualitatively and quantitatively. Future improvements could involve adopting a modified solubility law or incorporating non-linear concentration dependencies into the thermodynamic model, thereby providing a more accurate description of the equilibrium states in supersaturated systems.
4. Conclusions
An integrated framework is developed that synergistically combines molecular dynamics (MD) simulations of pure gases with a van der Waals gas-based thermodynamic model to predict the equilibrium size of nanobubbles in supersaturated liquid. Our results indicate that equilibrium bulk nanobubbles emerge only when the gas concentration exceeds a critical threshold, below which bubble formation is thermodynamically unfavored. The Young–Laplace equation, with nanobubble pressure approximated from the van der Waals equation of state, effectively captures the interfacial pressure jump even at radii as small as a few nanometers, without the need for Tolman correction. The van der Waals constants tuned to the MD data enable this framework to reproduce nanobubble radii observed in hydrogen–water simulations with significantly reduced computational overhead. The comparison between theory and simulation highlights the importance of considering intermolecular interactions when the gas is under ultra-high pressure inside a nanobubble. Henry's law, although originally formulated for dilute solutions, can still offer a reasonable baseline for modelling gas solubility in nanoscale contexts. Overall, this work underscores the robustness and flexibility of uniting molecular and continuum descriptions to investigate nanobubbles. Future research could integrate effects such as dynamic gas exchange, external fields, and interfacial charge to address a broader array of conditions with potential applications across energy, biotechnology, and soft matter systems.Author contributions
Ali Ghamartale: conceptualization, data curation, formal analysis, investigation, methodology, software, validation, visualization, writing – original draft. Ehsan Shahini: data curation, formal analysis, investigation, methodology, software, validation, visualization, writing – original draft. Aditya Jain: data curation, investigation, methodology, software. Rogerio Manica: conceptualization, writing – review & editing. Peter Berg: conceptualization, formal analysis, project administration, supervision, writing – review & editing. Tian Tang: conceptualization, formal analysis, funding acquisition, methodology, project administration, resources, supervision, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Data availability
Data for this article will be made available upon request.Supplementary information (SI): forcefield verification using nanobubble density analysis. See DOI: https://doi.org/10.1039/d5ra07908j.
Acknowledgements
Digital Research Alliance of Canada is acknowledged for providing the computing resources and technical support. TT acknowledges financial support from the Natural Sciences and Engineering Research Council of Canada (NSERC; Grant number: NSERC AICO 580362-22) and the Canada Research Chair program (CRC; Grant number: TIER1 2021-00023). PB also acknowledges financial support from the Natural Sciences and Engineering Research Council of Canada (NSERC; Grant number: RGPIN-2018-03809). The authors appreciate helpful discussions with Prof. Michael Eikerling, Prof. Kristina Tschulik and Dr Tobias Binninger.References
- A. W. Foudas, R. I. Kosheleva, E. P. Favvas, M. Kostoglou, A. C. Mitropoulos and G. Z. Kyzas, Chem. Eng. Res. Des., 2023, 189, 64–86 CrossRef CAS.
- J. Lei, D. Huang, W. Zhao, S. Liu and Y. Yue, Int. J. Heat Mass Transfer, 2024, 225, 125407 CrossRef CAS.
- G. S. Manning, Phys. Chem. Chem. Phys., 2020, 22, 17523–17531 RSC.
- E. D. Michailidi, G. Bomis, A. Varoutoglou, E. K. Efthimiadou, A. C. Mitropoulos and E. P. Favvas, in Interface science and technology, Elsevier, 2019, vol. 30, pp. 69–99 Search PubMed.
- H. Bao, Y. Zhang, S. Lv, S. Liu and W. Fan, Environ. Int., 2024, 109126 CrossRef CAS PubMed.
- S. Wang, Y. Liu, T. Lyu, G. Pan and P. Li, ACS ES&T Water, 2020, 1, 376–387 Search PubMed.
- M. Soltani, F. M. Kashkooli, M. A. Fini, D. Gharapetian, J. Nathwani and M. B. Dusseault, Renewable Sustainable Energy Rev., 2022, 167, 112729 CrossRef CAS.
- Y. Tanaka and N. Miwa, Hydrogen, 2022, 3, 161–178 CrossRef CAS.
- I. Ohsawa, M. Ishikawa, K. Takahashi, M. Watanabe, K. Nishimaki, K. Yamagata, K.-i. Katsura, Y. Katayama, S. Asoh and S. Ohta, Nat. Med., 2007, 13, 688–694 CrossRef CAS PubMed.
- A. Angulo, P. van der Linde, H. Gardeniers, M. Modestino and D. F. Rivas, Joule, 2020, 4, 555–579 CrossRef CAS.
- M. Blander and J. L. Katz, AIChE J., 1975, 21, 833–848 CrossRef CAS.
- S. A. Hewage and J. N. Meegoda, Colloids Surf., A, 2022, 650, 129565 CrossRef.
- E. D. Michailidi, G. Bomis, A. Varoutoglou, G. Z. Kyzas, G. Mitrikas, A. C. Mitropoulos, E. K. Efthimiadou and E. P. Favvas, J. Colloid Interface Sci., 2020, 564, 371–380 CrossRef CAS PubMed.
- K. Ohgaki, N. Q. Khanh, Y. Joden, A. Tsuji and T. Nakagawa, Chem. Eng. Sci., 2010, 65, 1296–1300 CrossRef CAS.
- L. Zhou, S. Wang, L. Zhang and J. Hu, Curr. Opin. Colloid Interface Sci., 2021, 53, 101439 CrossRef CAS.
- B. H. Tan, H. An and C.-D. Ohl, Phys. Rev. Lett., 2020, 124, 134503 CrossRef CAS PubMed.
- F. Eklund, M. Alheshibri and J. Swenson, Curr. Opin. Colloid Interface Sci., 2021, 53, 101427 CrossRef CAS.
- M. R. Ghaani, P. G. Kusalik and N. J. English, Sci. Adv., 2020, 6, eaaz0094 CrossRef CAS PubMed.
- Y.-X. Yu and J. Wu, J. Chem. Phys., 2002, 116, 7094–7103 CrossRef CAS.
- D. Zhou, Z. H. Ansari and J. Mi, J. Phys.: Condens. Matter, 2013, 25, 184004 CrossRef PubMed.
- J. H. Weijs, J. R. Seddon and D. Lohse, ChemPhysChem, 2012, 13, 2197–2204 CrossRef CAS PubMed.
- Y. Zhang and D. Lohse, J. Fluid Mech., 2023, 975, R3 CrossRef.
- Y. A. Perez Sirkin, E. D. Gadea, D. A. Scherlis and V. Molinero, J. Am. Chem. Soc., 2019, 141, 10801–10811 CrossRef CAS PubMed.
- S. Park, J. Weng and C. Tien, Int. J. Heat Mass Transfer, 2001, 44, 1849–1856 CrossRef CAS.
- M. Matsumoto, J. Fluid Sci. Technol., 2008, 3, 922–929 CrossRef.
- T. Yamamoto and S. Ohnishi, Phys. Chem. Chem. Phys., 2011, 13, 16142–16145 RSC.
- M. Zhang, Y.-s. Tu and H.-p. Fang, Appl. Math. Mech., 2013, 34, 1433–1438 CrossRef.
- S. Jain and L. Qiao, AIP Adv., 2017, 7, 045001 CrossRef.
- S.-N. Hong, S.-H. Choe, U.-G. Jong, M.-S. Pak and C.-J. Yu, Fluid Phase Equilib., 2019, 487, 45–51 CrossRef CAS.
- Z. Gao, W. Wu, W. Sun and B. Wang, Langmuir, 2021, 37, 11281–11291 CrossRef CAS PubMed.
- Y. Lu, L. Yang, Y. Kuang, Y. Song, J. Zhao and A. K. Sum, Phys. Chem. Chem. Phys., 2021, 23, 27533–27542 RSC.
- A. S. Al-Awad, L. Batet, R. Rives and L. Sedano, J. Chem. Phys., 2024, 161, 024503 CrossRef CAS PubMed.
- R. Sander, NIST Standard Reference Database, 2017 Search PubMed.
- C. Vega and E. de Miguel, J. Chem. Phys., 2007, 126, 154707 CrossRef CAS PubMed.
- I. N. Tsimpanogiannis, S. Maity, A. T. Celebi and O. A. Moultos, J. Chem. Eng. Data, 2021, 66, 3226–3244 CrossRef CAS.
- V. Buch, J. Chem. Phys., 1994, 100, 7610–7629 CrossRef CAS.
- M. Abraham, A. Alekseenko, C. Bergh, C. Blau, E. Briand, M. Doijade, S. Fleischmann, V. Gapsys, G. Garg, S. Gorelov, G. Gouaillardet, A. Gray, M. E. Irrgang, F. Jalalypour, J. Jordan, C. Junghans, P. Kanduri, S. Keller, C. Kutzner, J. A. Lemkul, M. Lundborg, P. Merz, V. Miletić, D. Morozov, S. Páll, R. Schulz, M. Shirts, A. Shvetsov, B. Soproni, D. v. d. Spoel, P. Turner, C. Uphoff, A. Villa, S. Wingbermühle, A. Zhmurov, P. Bauer, B. Hess and E. Lindahl, Zenodo, 2024, DOI:10.5281/zenodo.11104865.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- A. Ghamartale, S. Zendehboudi and N. Rezaei, Energy Fuels, 2020, 34, 13186–13207 CrossRef CAS.
- R. J. Gowers, M. Linke, J. Barnoud, T. J. E. Reddy, M. N. Melo, S. L. Seyler, J. Domanski, D. L. Dotson, S. Buchoux and I. M. Kenney, MDAnalysis: a Python Package for the Rapid Analysis of Molecular Dynamics Simulations, Report 2575-9752, Los Alamos National Laboratory (LANL), Los Alamos, NM (United States), 2019 Search PubMed.
- R. C. Tolman, J. Chem. Phys., 1949, 17, 333–337 CrossRef CAS.
- Q. Wang, H. Zhao, N. Qi, Y. Qin, X. Zhang and Y. Li, Sci. Rep., 2019, 9, 1118 CrossRef PubMed.
- B. Peng and Y.-X. Yu, Langmuir, 2008, 24, 12431–12439 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2025 |


![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif)








