 Open Access Article
Open Access ArticleTribology-driven modulation of piezoelectricity in 2D CdS bilayers: a first-principles investigation
A. S. M. Jannatul Islam a,
Md. Sherajul Islam
a,
Md. Sherajul Islam *a,
Ashraful G. Bhuiyana,
Catherine Stampfl
*a,
Ashraful G. Bhuiyana,
Catherine Stampfl b and
Jeongwon Park
b and
Jeongwon Park c
c
aDepartment of Electrical and Electronic Engineering, Khulna University of Engineering &Technology, Khulna 9203, Bangladesh. E-mail: sheraj_kuet@eee.kuet.ac.bd
bSchool of Physics, The University of Sydney, New South Wales 2006, Australia
cDepartment of Electrical and Biomedical Engineering, University of Nevada, Reno, NV 89557, USA
First published on 11th December 2025
Abstract
The pronounced electronegativity difference and exceptional non-centrosymmetricity of two-dimensional (2D) cadmium sulfide (CdS) offer an exceptional piezoelectric effect, positioning it as a promising material for next-generation energy-harvesting devices. This study examines the piezoelectric properties of 2D CdS bilayers driven by tribological effects and assesses their feasibility for nano energy harvesting applications. Two types of tribological effects, namely in-plane sliding motion and out-of-plane compression, are applied to a CdS bilayer to investigate its piezoelectric properties, including potential energy, polarization deviations, charge density, shear strength, induced voltage, and power density. The results indicate that in-plane sliding, which transitions the bilayer structure from an A–B to an A–A stacking pattern, leads to a significant increase in out-of-plane piezoelectricity. Upon vertical compression, we find that the range of maximal energy corrugation is 724–1365 meV, and the range of shear strength is 49.79–99.20 GPa. Additionally, due to vertical compression, an induced voltage of 0.35 V is found for bilayer 2D CdS. Finally, a compressive-sliding motion-based nanogenerator model is proposed for a 2D CdS bilayer structure that can engender an output power density of up to 51.72 mW cm−2. These outcomes pave the way for new opportunities in nanoenergy extraction from the tribo-piezoelectric effect of CdS structures, advancing the development of wearable electronics, self-powered devices, and wireless technologies.
1 Introduction
The fast development of wearable electronics, self-powered devices, and wireless technologies has raised the necessity for novel energy-harvesting materials that can effectively transform mechanical energy into electrical energy.1–6 Among several energy-harvesting methodologies, piezoelectric and triboelectric energy harvesting have emerged as two of the most promising strategies.7–11 Piezoelectric energy-generating utilizes materials that produce electrical charges when subjected to mechanical stress, rendering it suitable for applications demanding great sensitivity and efficiency.12,13 Conversely, triboelectric energy harvesting employs the contact and separation of materials with distinct triboelectric polarities to generate electrical energy, providing scalability and design adaptability.7,13–15 Both methods leverage mechanical movements, including vibrations, compression, and sliding, to deliver sustainable energy solutions.In this context, several piezoelectric materials have been investigated, each presenting distinct benefits and obstacles. Conventional piezoelectric materials, including lead zirconate titanate (PZT) nanofibers, gallium nitride (GaN), aluminum nitride (AlN), and quartz, have historically prevailed in the domain owing to their robust piezoelectric responses.8,13,16–19 Nonetheless, these materials have intrinsic obstacles. PZT, despite its superior performance, is plagued by environmental issues associated with its lead concentration. GaN and AlN have exceptional thermal stability; yet, their high production costs and stiffness restrict their use in flexible and wearable electronics. Emerging materials such as zinc oxide (ZnO) nanostructures and polyvinylidene fluoride (PVDF) have broadened the potential for energy harvesting. ZnO nanowires, especially in lateral configurations, provide significant piezoelectric sensitivity and scalability; however, need meticulous alignment and structural integrity for best performance. Conversely, PVDF offers flexibility and simplicity of production, but its inferior piezoelectric coefficients relative to inorganic materials limit its use in high-output systems.
Amid this landscape, two-dimensional (2D) materials have of late gained immense interest for advancing nanoscale ambient energy harvesting devices, owing to their exceptional properties such as remarkable quantum Hall effects, ultra-thin structure, mechanical stability, biocompatibility, flexibility, and high carrier mobility.20–27 It has been revealed that due to their characteristics of high piezoelectric constants, and breakdown of inversion symmetry, layered 2D materials—for instance, WSe2,28 MoS2,29 SnS,30 and MXenes31 can reveal strong in-plane piezoelectricity. The out-of-plane response is often limited to odd-numbered layers and gradually declines with increasing thickness. Several 2D systems, such as CuInP2S6, LiNbO3, In2Se3, and NbOI2, have shown significant out-of-plane piezoelectricity.32–37 This is due to twist-angle-dependent symmetry destroying, interface-engineered nanostructures, and ferroelectric composite interactions. However, these techniques frequently rely on extensive surface modification steps and have limited tunability, resulting in significant variation in piezoelectric performance.
Tribological phenomena, including lateral sliding, out-of-plane compression, and interfacial friction-driven variation of polarization, have recently emerged as a possible alternative method for increasing piezoelectricity. Such tribo-piezoelectric phenomena have been observed in nitride bilayers and Janus TMD bilayers;38–42 however, the induced voltage, power density, shear strength, and out-of-plane polarization are all moderate. These limitations highlight the need for new bilayer systems that can generate stronger and more robust tribo-piezoelectric responses. Inspired by this issue, the current investigation explores group-II sulfides, with a specific emphasis on bilayer CdS, to investigate their potential as a next-generation 2D energy-harvesting material. 2D CdS exhibits excellent thermodynamic stability, an impressive electronic bandgap (2.5 eV), a low work function, high mechanical strength, strong excitonic binding energy, and remarkable optical properties.43–46 In addition, CdS belongs to the family of 2D II–VI chalcogenides that can be synthesized through well-established techniques such as chemical vapor deposition and solution-mediated exfoliation, ensuring the practical representativeness of the system.47–50 Applications of 1D and 2D CdS nanostructures have been proven in many different domains, including waveguides, dye-sensitized solar cells, photoconductors, thermo-electronics, field emitters, and logic gates.43–46 Although 2D CdS is considered a promising piezoelectric material owing to the substantial electronegativity difference between Cd (1.69) and S (2.58) atoms, a comprehensive understanding of tribology-induced piezoelectric responses in bilayer 2D CdS is still missing.
This work uses a comprehensive first-principles density functional theory (DFT) analysis to study the tribo-piezoelectricity of 2D CdS bilayers. We show that bilayer CdS might be stimulated to undergo vertical polarization by in-plane sliding along a specific route of two CdS monolayers. The polarization amplification is connected to greater vertical piezoelectricity and interfacial charge transmission once the CdS bilayer overcomes the in-plane sliding obstacle and transforms into the A–A stacking configuration. The potential energy variation, polarization deviation, and shear strength alteration with interlayer gap change reveal tunable piezoelectric properties. Both the vertical charge polarization and the horizontal sliding energy resistance of a CdS bilayer are improved with decreasing interlayer spacing. In-plane sliding and associated opposition are tribological activities. Nevertheless, there is a remarkable strengthening of out-of-plane polarization, and no triboelectric charges are produced during interlayer sliding in the transition from A–B to A–A assembling pattern with a given interlayer spacing. This suggests that stronger vertical polarization has been triggered by tribological energy, resulting in piezoelectricity instead of triboelectricity. It should be noted that, because interlayer sliding does not produce any triboelectric charges, this type of tribo-piezoelectricity differs from traditional piezo-triboelectricity. Since a variation in the interlayer movement can produce vertical piezoelectricity, a compressive slipping nanoenergy harvester with a CdS bilayer arrangement is suggested based on the tribo-piezoelectric influence and can deliver a generated voltage as high as ∼0.35 V and output power density of up to 51.72 mW cm−2.
2 Computational details
Initially, a bilayer of CdS is taken into consideration to examine the in-plane sliding and vertical compression. Bilayer CdS has a rhombus unit cell made up of 2-Cd and 2-S atoms. The top CdS layer incorporates transverse sliding, whereas the bottom CdS monolayer remains fixed following structural relaxation and optimization. The configuration, therefore, translates to various locations in the XY-plane. Every location undergoes atomic geometry relaxation with the S atoms in the upper and bottom layers kept at a fixed interlayer spacing. The potential energy surface (PES) is computed when the top layer is moving in-plane across its x–y axis at an interlayer distance:| EPES(x,y) = E(x,y) − Elowest | (1) |
 | (2) |
| ΔP(x,y) = Pd(x,y) − PFn | (3) |
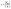 | (4) |
In this study, DFT is used for all computations, and the plane wave self-consistent field (PWscf) suite of Quantum Espresso is utilized.51,52 The exchange-correlation functional is taken to be the PBE functional for the generalized gradient approximation.53 The electron–ion interactions in the PWscf program are described by Kresse–Joubert projector augmented wave (KJPAW) potentials.54 The weak intermolecular van-der Waals (vdW) relations are represented by the optB86b-vdW functional.55,56 The initial PBE vdW-DF is altered by optB86b-vdW relations to guarantee correct replication for the interatomic distances and energies at equilibrium.55–58 A 2D-centered Monkhrost–Pack k-mesh grid with dimensions of 15 × 15 × 1 is used to carry out the Brillouin zone integration. An energy cut-off value of 10−8 a.u. is utilized to ensure correct convergence of the ground state electron density. The charge densities and wave function have kinetic energy cut-offs of 350 Ry and 45 Ry, respectively. Furthermore, for precise stress and force computations, a force convergence cutoff of 10−3 eV nm−1 is employed. To prevent direct contact between the monolayers and bilayers, a 20 Å vacuum space is applied.
3 Results and discussion
The structural optimization of the CdS monolayer is used as the starting point for the investigation. With zero buckling height, the lattice constant determined after relaxation is 4.25 Å. Our findings are in good agreement with other studies.59,60 Our study investigates three stacking configurations, namely A–A, A–B, and A–C stacking patterns. In the A–A stacking arrangement, the Cd (S) atoms of the top layer are vertically aligned with the Cd (S) atoms of the bottom layer. Conversely, the S and Cd atoms in the A–B stacking arrangement are positioned above the Cd atom and the hexagon center in the base layer, while in the A–C packing arrangement, the Cd and S atoms of the upper layer are positioned at the S atom and the hexagon center (as shown in Fig. 1). An interlayer spacing, determined between the upper and bottom S atoms, separates the CdS monolayers. The equilibrium interlayer distances for the A–B and A–C stacking configurations are determined to be 3.14 Å based on binding energy calculations, and this value is consistent with the findings of L. Chhana et al.61 The binding energy of the bilayers is defined as: Eb = Ebilayer − 2Emonolayer. A stable structure is indicated by a negative binding energy, where a larger negative value denotes greater stability than a smaller value.62 Moreover, as the minimum binding energy point represents the local equilibrium geometry, it results in stable electronic properties. Here, the A–B and A–C configurations exhibit binding energies of −2.713 eV and −2.702 eV, respectively, indicating excellent structural stability. On the other hand, the A–A stacking arrangement is notably less favorable as seen from its binding energy (−1.133 eV) curve in Fig. 1. This binding energy calculation for the A–B, A–C, and A–A stacking patterns of bilayer CdS is consistent with previous studies.60,61,63 To evaluate the sensitivity of key results e.g., equilibrium interlayer distance and binding energy to the choice of vdW correction, additional simulations are performed using Grimme D2, DFT-D3, and the optB86b-vdW functional for bilayer CdS. As expected, the D2 scheme exhibits a tendency to overbind, resulting in a slightly reduced interlayer spacing. In contrast, both DFT-D3 and optB86b-vdW produce highly consistent equilibrium interlayer distances and binding energies, in excellent agreement with values typically reported for layered II–VI chalcogenides.64–66 This consistency confirms that optB86b-vdW provides a reliable description of interlayer interactions for the CdS system studied here. A consolidated comparison of these results is provided in Table S1 of the SI. In addition to binding energy, prior first-principles investigations have demonstrated the dynamical, thermal, and mechanical stability of 2D CdS, including bilayer configurations.60,67 Mohanta et al.68 conducted ab initio molecular-dynamics simulations and phonon studies of CdS bilayers and found no soft phonon modes or structural changes under finite-temperature conditions, indicating both dynamic and thermal stability. The same study also reveals that the estimated elastic constants meet the 2D Born stability criterion, indicating mechanical stability. It is noteworthy that the calculated binding energies for the CdS bilayer (A–B and A–C stacking patterns) remain negative within the interlayer distance range of 3.14 to 2.74 Å. This interlayer distance range is then taken into consideration as a parameter for choosing the limit for the steady interlayer spacing to use out-of-plane compressive slipping of the upper CdS layer to attain superior maximum energy corrugation.The two distinct interlayer distances (3.14 Å and 2.84 Å) are used to examine the impact of transverse sliding. Fig. 2 presents the calculated PES and PDS distributions at various sliding positions. As would be expected from the equilibrium geometry of the flat honeycomb constructed CdS, the PES and PDS maps exhibit periodic repetition.59 As seen in Fig. 2, very strong vertical polarization is shown when the original arrangement slides to resemble the A–A stacking arrangement. Moreover, with a smaller interlayer separation, this strong vertical polarization increases as well. However, when the interlayer spacing changes, the A–B stacking arrangement yields comparatively little vertical polarization. In addition, the A–B stacking responds to interlayer spacing far less strongly than the A–C stacking. Consequently, the A–B stacking arrangement is considered the starting state, and the A–A stacking arrangement will achieve the greatest polarization improvement. Nevertheless, the A–A stacking is not energetically favorable in the absence of an outside mechanical input or constraint. Only an in-plane pushing force stronger than the shear strength and interlayer resistive force may cause a switch to the A–A arrangement during the lateral slipping of the A–B configuration.
The resistance that accompanies interlayer sliding is a tribological phenomenon, but vertical polarization is greatly enhanced when A–A stacking is used with equilibrium interlayer spacing. Therefore, transverse interlayer slipping in the CdS bilayer may be considered as the cause of the vertical polarization amplification, which can be explained as a tribo-piezoelectric phenomenon. Through tribological energy transformation, the energy obstruction of sliding resistance is overcome, leading to piezoelectricity. Outside external force and compression are needed to push the CdS bilayer to the A–A state, which is equivalent to transforming tribological energy into electrical power. The triboelectric effect is maintained at a given interlayer spacing through the procedure of overwhelming the energy barrier associated with interlayer shear strength and resistive force. Therefore, the tribo-piezoelectric action will be the cause of the vertical plane slipping that resulted in vertical polarization. In our work, the tribological energy generates piezoelectricity, in contrast to earlier research where the triboelectric effect results in static charges.9,13 Cai et al. have also discovered analogous tribo-piezoelectric behaviors in Janus TMD bilayers.69 Thus, out-of-plane interlayer resistive frictions determine the corrugated energy (ΔE) in the PES of the CdS bilayer; greater interlayer resistance and friction would result in a larger energy corrugation.70
The energy corrugation (ΔE) determines how much tribo-piezoelectricity is generated. The compressive fluctuation of the interlayer separation from 3.14 Å to 2.74 Å is shown in Fig. 3(a), which shows the greatest polarization deviation (ΔPmax) and maximum energy corrugation (ΔEmax). Fig. 3(a) shows that when the maximum energy corrugation increases, the maximum polarization deviation escalates linearly. The stronger the magnitude of vertical polarization, the more energy will be needed to overwhelm the interlayer sliding friction. Relative shear strength can be obtained from eqn (4) by using the greatest static resistance force acting on the sliding progression. The shear strength at an interlayer spacing between 2.74 Å and 3.14 Å is revealed in Fig. 3(b). Throughout the vertical compressive displacement of the CdS layer, the highest energy barrier variation (724–1670 meV) and shear strength (49–125 GPa) are greater than those attained with the Janus TMD bilayers (180–480 meV) and (2.5–7.2 GPa), correspondingly.69 The CdS bilayer may also yield a larger vertical polarization value (1.73–2.44 pC m−1) than the Janus TMD bilayers (0.6–2.3 pC m−1).69 A decrease in the interlayer spacing results in a quadratic rise in the values of maximum corrugated energy and shear strength. To obtain a greater triboelectric to electrical energy conversion, vertical compressive pressure is therefore an effective method. The discrepancies are principally due to CdS's highly ionic Cd–S bonds with strong polarity, which induce significant interlayer electrostatic attraction and charge redistribution during sliding. This results in a conspicuous corrugated potential-energy landscape and high resistance to lateral motion, particularly under compression, where Cd-5s/S-3p orbital overlap improves interlayer coupling. Janus TMDs are characterized by weak vdW interactions and limited interlayer charge transfer that provide low-energy sliding routes. Moreover, because of the impact of in-plane strain brought on by vertical tension, a structural variation has been seen throughout this procedure. The bilayer's atoms' interaction is affected by the change in interlayer distance; this impact is greater when the bilayer is positioned at a smaller interlayer gap than the equilibrium one. At the optimal interlayer spacing of 3.14 Å, the lattice constant was found to be 4.251 Å. However, reducing the interlayer distance lowers the lattice constant. The lattice constant decreases to 4.225 Å and 4.219 Å, respectively, with spacings of 2.84 Å and 2.74 Å. Upon applying vertical tension, the system is relaxed each time, and the computations account for variations in the lattice constant.
The charge density differences (CDD) in the CdS bilayer are studied to illustrate the charge involvement in the observed tribo-piezoelectric characteristic. The CDD at two interlayer distances (3.14 Å and 2.84 Å) between the CdS monolayers is shown in Fig. 4. The CDD may be expressed as follows:
| Δρ = ρtotal − ρtop − ρbottom | (5) |
 | (6) |
 | (7) |
 and
and  with zero average forces. The typical fluctuations in charge density with interlayer distances ranging from 3.14 to 2.74 Å are depicted in Fig. 5(a) and (b). It is observed that an increase in the mean charge density inside the layers is caused by a decrease in the interlayer spacing. In the A–B stacking pattern, a larger charge density is seen at the bottom layer than at the top layer due to vertical compressive movement concerning the layers. In the A–A stacking arrangement, the charge density of the upper layer predominates at the same time. The charge allocation in the CdS upper and lower monolayers is in good accord with the CDD plot (Fig. 4).
with zero average forces. The typical fluctuations in charge density with interlayer distances ranging from 3.14 to 2.74 Å are depicted in Fig. 5(a) and (b). It is observed that an increase in the mean charge density inside the layers is caused by a decrease in the interlayer spacing. In the A–B stacking pattern, a larger charge density is seen at the bottom layer than at the top layer due to vertical compressive movement concerning the layers. In the A–A stacking arrangement, the charge density of the upper layer predominates at the same time. The charge allocation in the CdS upper and lower monolayers is in good accord with the CDD plot (Fig. 4).
Unlike conventional triboelectric nanogenerators—where electrical output relies on interaction between two different materials with dissimilar electron affinities—the bilayer CdS system is composed of two identical CdS sheets. Because the two surfaces possess the same electron affinity, significant interfacial charge transmission through the triboelectric effect is not demanded. As a substitute, the measured output originates solely from piezoelectric polarization, which is generated when lattice asymmetry is introduced during mechanical deformation (sliding or compression). To verify this mechanism, we performed Bader charge analysis39 for various stacking configurations and interlayer distances. The results confirm that the net charge transfer between the two layers is negligible, indicating that triboelectric contributions are minimal. The polarization response is therefore dominated by intralayer electron-density redistribution induced by mechanical perturbation, fully consistent with a piezoelectric rather than triboelectric origin. A summary of the Bader charge values for bilayer CdS under different structural conditions is provided in Table 1.
| Stacking pattern | Interlayer distance (Å) | Net Bader charge transfer (e) |
|---|---|---|
| A–A | 3.14 | −0.046855 |
| A–B | 3.14 | +0.040976 |
| A–A | 2.84 | −0.006575 |
| A–B | 2.84 | +0.071818 |
Compressive-sliding nanogenerators can be developed by taking into consideration the charge reallocation between the atoms and layers. Since most of the charge builds up around the S-atoms, the electron density surrounding the S-surface will be larger than the electron density at the interface between the layers. As depicted in Fig. 5(c), assigning electrodes to the upper and lower surfaces can provide a little voltage. As seen in Fig. 5(d), a greater concentration of inductive charges is observed close to the interface for the A–A stacking pattern. As a result, creating a nanogenerator with the A–A stacking arrangement will enable the extraction of a higher voltage. Moreover, Fig. 5(e) shows the charge gain in the upper and lower layers during the out-of-plane compression procedure. The charge gain is determined by detracting the single layer charges between the unit cells of the A–A and A–B assembling arrangements.
Subsequently, taking the A–A assembling arrangement, the electrostatic potential variations (ΔU) between the S atoms in the upper and lower layers are analyzed to calculate the maximum generated voltage. At the monolayer surfaces, a variation in the electrostatic potential differences with interlayer change can be determined by:
| ΔU = ΔUT − ΔUB | (8) |
 | (9) |
 | (10) |
 and
and  denote the conforming cases at zero average forces. As seen in Fig. 6, a reduction in the interlayer spacing results in a rise in out-of-plane polarization and a rise in the electrostatic potential at both the upper and lower layers. During the procedure, an induced voltage between 0.23 and 0.35 V can be obtained by using the formula,
denote the conforming cases at zero average forces. As seen in Fig. 6, a reduction in the interlayer spacing results in a rise in out-of-plane polarization and a rise in the electrostatic potential at both the upper and lower layers. During the procedure, an induced voltage between 0.23 and 0.35 V can be obtained by using the formula,  , where q denotes the unit charge and φ represents the induced voltage, to account for the electrostatic potential and unit charges.
, where q denotes the unit charge and φ represents the induced voltage, to account for the electrostatic potential and unit charges.
To utilize the suggested bilayer CdS configuration as a nanogenerator, Fig. 7 presents the construction of a compression-sliding motion model. Using the nanoscale probing technique, force or rotation on a single layer or many layers of material at a certain route and trend may be incorporated to experimentally build the suggested nanogenerator.69,71–73 In this instance, a tiny CdS flake moves on a large CdS substrate in response to transverse and vertical motion imparted by means of the probe tip. The bilayer CdS is connected to two electrodes at its edges, with the upper electrode linked to a probe for controlling the mobility of the flake. The probe is set up to perform as a conductor, joining the lower electrode.74 In this concept, Au electrodes that are frequently utilized can be employed. Our further studies show that the adhesion force between the Au electrode and the CdS monolayer surface is greater than the force between two CdS monolayers. Moreover, the Au contact has minimal effect on the tribo-piezoelectric properties of the CdS bilayer, as shown in Fig. 8. The compression-sliding method is durable and strong with the CdS bilayer, as shown by our findings and previous research on the Au/2D materials contact.
 | ||
| Fig. 7 Diagrammatic representation of a prototype CdS bilayer nanogenerator based on compression-sliding motion. The probe is represented in blue, and the electrodes are shown in yellow. | ||
Taking a relaxed Au-supported CdS structure, as seen in Fig. 8(a), the impact of applying a metallic Au electrode on the CdS monolayer is investigated. The computations are performed in the same manner as described in Section 2. To align with the lattice constant of the Au substrate, the CdS's lattice constant was compressed by approximately 1.9%. The details of the lattice mismatch between CdS and Au, as well as the supercell matching strategy, are provided in the SI. Between the Au and CdS layers, an optimal interlayer gap of 2.74 Å is found. The Au–CdS contact will thus exhibit physical adsorption. For the Au/CdS and CdS bilayers, the calculated binding energies are −2.935 eV and −2.713 eV, respectively. The adhesion force between the Au electrode and the CdS monolayer surface is considerably greater than the force generated between two CdS monolayers. An analogous outcome was also discovered at the Au–TMD interface.69 Additionally, we have illustrated the projected density of states of the Cd and S atoms for the CdS monolayer and Au/CdS interface, as seen in Fig. 8(c) and (d). At the Au/CdS interface, the monolayer CdS's Fermi level is pinned close to the conduction band, suggesting that the interface is an n-type contact. Charge carrier transport between the Au and CdS interfaces is therefore restricted as a result of the creation of an interlayer Schottky barrier with a superior contact resistance between the Au/CdS contact. Moreover, we have extended the contact analysis beyond the PDOS by including a band structure diagram (Fig. S1) in the SI, which explicitly shows the relative positions of the Fermi level and the conduction- and valence-band edges at the Au/CdS interface. This diagram clearly confirms the formation of an n-type Schottky barrier, consistent with the high work function of Au and its tendency to pin the Fermi level near the CdS conduction band. Our results are consistent with previous theoretical investigations of the metal–2D material contact.75,76 The tribo-piezoelectricity process demonstrated in Fig. 5 states that inductive charges are generated when the electrode comes into contact with the CdS layer and that no charge is transferred from the CdS to the electrode. The Schottky barrier at the interface will obstruct the charge flow between the CdS layer and the metal electrode. Consequently, the tribo-piezoelectricity of the CdS bilayer is mostly insensitive to the metal contact. Additionally, recent Au/TMD tests have shown similar electrical characteristics, suggesting that the Au electrode has a minimal impact on the TMD layer.77,78
Mechanical energy is transformed into electrical energy by the interlayer resistive and sliding forces. Consequently, the majority of the electrical energy (Eelec) produced during the sliding operation will come from tribological energy (Etribo). The relation can be used to determine the quantity of Eelec generation if a conversion coefficient (δ) is taken,
| Eelec = δEtribo ≈ Pt | (11) |
 | (12) |
 | (13) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 715 µW cm−2 for sliding velocities between 1 and 100 nm s−1, and ΔEmax for the case where the interlayer gap is decreased to 2.84 Å, supposing complete conversion of tribological energy to electrical energy. Experimental findings13 indicate that a tribo-piezoelectric generator has a power density of 7 µW cm−2. According to earlier studies, the power density output of triboelectric nanogenerators82 and piezoelectric nanogenerators ranges79 from 400 to 50
715 µW cm−2 for sliding velocities between 1 and 100 nm s−1, and ΔEmax for the case where the interlayer gap is decreased to 2.84 Å, supposing complete conversion of tribological energy to electrical energy. Experimental findings13 indicate that a tribo-piezoelectric generator has a power density of 7 µW cm−2. According to earlier studies, the power density output of triboelectric nanogenerators82 and piezoelectric nanogenerators ranges79 from 400 to 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 µW cm−2 and 4.41 to 5.92 µW cm−2, respectively. A reasonable supreme power density and a significant induced electrical output voltage are seen by the predicted CdS bilayer nanogenerator. This is comparable to the triboelectric nanogenerators of GaN nanowire,83 Janus TMD bilayers,69 h-BN polypropylene,84 monolayer MoS2 flake,29 PVDF–TrFE, and graphene oxide,79 which are presented in Table 2.
000 µW cm−2 and 4.41 to 5.92 µW cm−2, respectively. A reasonable supreme power density and a significant induced electrical output voltage are seen by the predicted CdS bilayer nanogenerator. This is comparable to the triboelectric nanogenerators of GaN nanowire,83 Janus TMD bilayers,69 h-BN polypropylene,84 monolayer MoS2 flake,29 PVDF–TrFE, and graphene oxide,79 which are presented in Table 2.
| Offered material | Highest power density (mW cm−2) | Highest induced output voltage (V) | ||
|---|---|---|---|---|
| Theoretical | Experimental | Theoretical | Experimental | |
| Planned bilayer 2D CdS | ∼52 | 0.35 | ||
| Double layer of 2D BeO85 | ∼30 | 0.22 | ||
| Double layer of 2D h-BN42 | ∼25 | 0.172 | ||
| Double layer of 2D InN86 | ∼74 | 0.20 | ||
| Nanowire array of GaN83 | — | — | 0.15–0.35 | |
| Janus TMD double layers69 | ∼29.64 | 0.25 | ||
| Monolayer MoS2 flake29 | — | ∼2 × 10−4 | 0.01825 | 0.015 |
| h-BN polypropylene84 | — | ∼29 × 10−4 | 2.3 | |
| Bilayer PVDF–TrFE and graphene oxide79 | 4.41 × 10−3 | 4 | ||
Furthermore, we expanded our investigation by taking into account a 3 × 3 CdS supercell bilayer structure, which yields a power density of around 519.16 to 51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 916 µW cm−2, negligibly higher than the values obtained with the CdS unit cells. The supercell structure has an induced voltage of 0.233 V and a polarization of 1.735 pC m−1, whereas the unit cell structure exhibits values of 0.231 V and 1.73 pC m−1, respectively. Hence, the consistency between the unit cell and supercell results highlights the periodicity effects and affirms the reliability of our DFT first-principles calculations. Regarded as a potential choice for energy harvesting applications, the CdS nanogenerator shows promise, particularly for low-power devices and self-powered sensors.87 Recently, there have been enormous advancements and research efforts to create CdS-based devices, such as water-splitters,43,44,63 photovoltaics,45 nanowires, and thin-film-based piezo-electric transducers,46 photodetectors,88–90 and nano thin-film transistors.91 Additionally, CdS-based nanowires and other structures are constantly improving.12 Therefore, it is anticipated that in the near future, the experimental construction of a 2D CdS-based tribo-piezoelectric nanogenerator will be viable and sustainable.
916 µW cm−2, negligibly higher than the values obtained with the CdS unit cells. The supercell structure has an induced voltage of 0.233 V and a polarization of 1.735 pC m−1, whereas the unit cell structure exhibits values of 0.231 V and 1.73 pC m−1, respectively. Hence, the consistency between the unit cell and supercell results highlights the periodicity effects and affirms the reliability of our DFT first-principles calculations. Regarded as a potential choice for energy harvesting applications, the CdS nanogenerator shows promise, particularly for low-power devices and self-powered sensors.87 Recently, there have been enormous advancements and research efforts to create CdS-based devices, such as water-splitters,43,44,63 photovoltaics,45 nanowires, and thin-film-based piezo-electric transducers,46 photodetectors,88–90 and nano thin-film transistors.91 Additionally, CdS-based nanowires and other structures are constantly improving.12 Therefore, it is anticipated that in the near future, the experimental construction of a 2D CdS-based tribo-piezoelectric nanogenerator will be viable and sustainable.
4 Conclusions
In conclusion, first-principles calculations have been used to discover the tribology-driven tunability of piezoelectric properties in 2D CdS bilayers. For a given interlayer separation, the in-plane sliding movement of the top CdS monolayer induces significant out-of-plane polarization in the vertical direction. Instead of static charges, piezoelectric polarization is produced by tribological energy. Tribo-piezoelectric energy produced by A–A assembling is much superior than that of A–B assembling. The interfacial sliding resistive force and the degree of shear strength define the amount of tribological energy. During lateral sliding, the A–A stacking structure, as opposed to the A–B and A–C stacking structures, exhibits the highest potential energy (1365 meV) for the CdS bilayer. The bilayer systems that mimic the A–A structure also exhibit the highest level of vertical polarization (2.44 pC m−1). A voltage of approximately 0.35 V is produced by the vertical compressive sliding that occurs outside of the plane in the CdS bilayer. The nanogenerator can give a maximum adjustable electrical output of 517.15 to 51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 715 µW cm−2 by modulating the tension on the probe tip. The results of this study indicate that CdS bilayers have the potential to be employed in the development of a highly efficient, innovative, and stable nanogenerator that can translate and harvest energy at the nanoscale.
715 µW cm−2 by modulating the tension on the probe tip. The results of this study indicate that CdS bilayers have the potential to be employed in the development of a highly efficient, innovative, and stable nanogenerator that can translate and harvest energy at the nanoscale.
Author contributions
A. S. M. Jannatul Islam: conceptualization, investigation, methodology, software, writing – original draft preparation. Md. Sherajul Islam: conceptualization, supervision, writing – reviewing and editing. Catherine Stampfl: writing – reviewing and editing. Ashraful G. Bhuiyan: supervision, writing – reviewing and editing. Jeongwon Park: supervision, writing – reviewing and editing.Conflicts of interest
The authors declare no conflicts of interest.Data availability
The structures and data files used and/or analyzed in this study are provided in the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5ra07830j.Acknowledgements
This work was supported by the UGC-funded research project (Grant No. CASR-59/24, 2021–2022) administered by the Centre for Advanced Research in Sciences (CASR) at Khulna University of Engineering & Technology, Bangladesh.References
- P. C. Lee, Y. L. Hsiao, J. Dutta, R. C. Wang, S. W. Tseng and C. P. Liu, Nano Energy, 2021, 82, 105702 CrossRef CAS.
- S. Akram, S. Ou, I. U. Haq, X. Zhu, Z. Fang, M. Tayyab and M. T. Nazir, Surf. Interfaces, 2024, 52, 104835 CrossRef CAS.
- V. Natraj, V. Mohan, P. Pazhamalai, K. Krishnamoorthy and S.-J. Kim, Surf. Interfaces, 2024, 53, 105031 CrossRef CAS.
- Q. Wang, B. Xu, D. Tan, X. Hu, Y. Yang, J. Huang, Y. Gao and X. Liu, Nano Energy, 2024, 121, 109217 CrossRef CAS.
- H. Wu, C. Shan, S. Fu, K. Li, J. Wang, S. Xu, G. Li, Q. Zhao, H. Guo and C. Hu, Nat. Commun., 2024, 15, 6558 CrossRef CAS PubMed.
- Q. Zhu, X. Song, X. Chen, D. Li, X. Tang, J. Chen and Q. Yuan, Nano Energy, 2024, 127, 109741 CrossRef CAS.
- J. He, T. Wen, S. Qian, Z. Zhang, Z. Tian, J. Zhu, J. Mu, X. Hou, W. Geng, J. Cho, J. Han, X. Chou and C. Xue, Nano Energy, 2018, 43, 326–339 CrossRef CAS.
- S. A. Han, J. Lee, J. Lin, S. W. Kim and J. H. Kim, Nano Energy, 2019, 57, 680–691 CrossRef CAS.
- S. Cherumannil Karumuthil, S. P. Rajeev and S. Varghese, Nano Energy, 2017, 40, 487–494 CrossRef CAS.
- Y. Cheng, H. Yuan, X. Li, L. Zhang, Z. Liu, Y. Wang and T. Jiao, Surf. Interfaces, 2025, 56, 105657 CrossRef CAS.
- C. Cheng, U. Jung, W. Heo, W. Park and J. Park, Surf. Interfaces, 2023, 41, 103177 CrossRef CAS.
- W. Zhang, H. Yang, L. Li, S. Lin, P. Ji, C. Hu, D. Zhang and Y. Xi, Nanotechnology, 2020, 31, 385401 CrossRef CAS PubMed.
- X. Yang and W. A. Daoud, Adv. Funct. Mater., 2016, 26, 8194–8201 CrossRef CAS.
- Z. L. Wang, ACS Nano, 2013, 7, 9533–9557 CrossRef CAS PubMed.
- H. Zhang, Y. Yang, Y. Su, J. Chen, C. Hu, Z. Wu, Y. Liu, C. Ping Wong, Y. Bando and Z. L. Wang, Nano Energy, 2013, 2, 693–701 CrossRef CAS.
- G. Zhu, R. Yang, S. Wang and Z. L. Wang, Nano Lett., 2010, 10, 3151–3155 CrossRef CAS PubMed.
- X. Chen, S. Xu, N. Yao and Y. Shi, Nano Lett., 2010, 10, 2133–2137 CrossRef CAS PubMed.
- Z. L. Wang and J. Song, Science, 2006, 312, 242–246 CrossRef CAS PubMed.
- L. Dong, J. Lou and V. B. Shenoy, ACS Nano, 2017, 11, 8242–8248 CrossRef CAS PubMed.
- A. S. M. J. Islam, Md. S. Islam, N. Z. Mim, Md. S. Akbar, Md. S. Hasan, Md. R. Islam, C. Stampfl and J. Park, ACS Omega, 2022, 7, 4525–4537 CrossRef CAS PubMed.
- A. S. M. J. Islam, M. S. Islam, N. Ferdous, J. Park and A. Hashimoto, Phys. Chem. Chem. Phys., 2020, 22, 13592–13602 RSC.
- A. S. M. J. Islam, M. S. Islam, N. Ferdous, J. Park, A. G. Bhuiyan and A. Hashimoto, Nanotechnology, 2019, 30, 445707 CrossRef CAS PubMed.
- Md. R. Islam, A. S. M. J. Islam, K. Liu, Z. Wang, S. Qu and Z. Wang, Chem. Phys., 2021, 551, 111334 CrossRef CAS.
- A. S. M. J. Islam, Md. S. Islam, Md. S. Hasan, Md. S. Akbar and J. Park, ACS Omega, 2022, 7, 14678–14689 CrossRef CAS PubMed.
- M. S. Islam, I. Mia, A. S. M. J. Islam, C. Stampfl and J. Park, Sci. Rep., 2022, 12, 1–15 CrossRef PubMed.
- A. S. M. J. Islam, Md. S. Hasan, Md. S. Islam and J. Park, Comput. Mater. Sci., 2021, 200, 110824 CrossRef CAS.
- A. S. M. J. Islam, M. S. Islam, M. R. Islam, C. Stampfl and J. Park, Nanotechnology, 2021, 32, 435703 CrossRef CAS PubMed.
- K. Datta, Z. Li, Z. Lyu and P. B. Deotare, ACS Nano, 2021, 15, 12334–12341 CrossRef CAS PubMed.
- W. Wu, L. Wang, Y. Li, F. Zhang, L. Lin, S. Niu, D. Chenet, X. Zhang, Y. Hao, T. F. Heinz, J. Hone and Z. L. Wang, Nature, 2014, 514, 470–474 CrossRef CAS PubMed.
- H. Khan, N. Mahmood, A. Zavabeti, A. Elbourne, Md. A. Rahman, B. Y. Zhang, V. Krishnamurthi, P. Atkin, M. B. Ghasemian, J. Yang, G. Zheng, A. R. Ravindran, S. Walia, L. Wang, S. P. Russo, T. Daeneke, Y. Li and K. Kalantar-Zadeh, Nat. Commun., 2020, 11, 3449 CrossRef CAS PubMed.
- D. Tan, C. Jiang, N. Sun, J. Huang, Z. Zhang, Q. Zhang, J. Bu, S. Bi, Q. Guo and J. Song, Nano Energy, 2021, 90, 106528 CrossRef CAS.
- Y. Wu, I. Abdelwahab, K. C. Kwon, I. Verzhbitskiy, L. Wang, W. H. Liew, K. Yao, G. Eda, K. P. Loh, L. Shen and S. Y. Quek, Nat. Commun., 2022, 13, 1884 CrossRef CAS PubMed.
- X. Jiang, X. Zhang, R. Niu, Q. Ren, X. Chen, G. Du, Y. Chen, X. Wang, G. Tang, J. Lu, X. Wang and J. Hong, Adv. Funct. Mater., 2023, 33, 2213561 CrossRef CAS.
- F. Xue, J. Zhang, W. Hu, W.-T. Hsu, A. Han, S.-F. Leung, J.-K. Huang, Y. Wan, S. Liu, J. Zhang, J.-H. He, W.-H. Chang, Z. L. Wang, X. Zhang and L.-J. Li, ACS Nano, 2018, 12, 4976–4983 CrossRef CAS PubMed.
- L. Lapčinskis, K. Mālnieks, A. Linarts, J. Blūms, K. Šmits, M. Järvekülg, M. Knite and A. Šutka, ACS Appl. Energy Mater., 2019, 2, 4027–4032 CrossRef.
- H. Yao, P. Zheng, S. Zhang, C. Hu, X. Fang, L. Zhang, D. Ling, H. Chen and X. Ou, Nat. Commun., 2024, 15, 5002 CrossRef CAS PubMed.
- X. Wang, W. Shi and J. Wan, J. Appl. Phys., 2021, 130, 015113 CrossRef CAS.
- L. Dong, J. Lou and V. B. Shenoy, ACS Nano, 2017, 11, 8242–8248 CrossRef CAS PubMed.
- J. Y. Damte and J. Houska, Sustainable Energy Fuels, 2024, 8, 4213–4220 RSC.
- H. Cai, Y. Guo, H. Gao and W. Guo, Nano Energy, 2019, 56, 33–39 CrossRef CAS.
- S. Yuan, Y. Zhang, M. Dai, Y. Chen, H. Yu, Z. Ma, W. F. Io, X. Luo, P. Hou and J. Hao, Adv. Electron. Mater., 2024, 10, 2300741 CrossRef CAS.
- M. Y. Zamil, M. S. Islam, C. Stampfl and J. Park, ACS Appl. Mater. Interfaces, 2022, 14, 20856–20865 CrossRef CAS PubMed.
- Y. Zhao, Z. B. Fang, W. Feng, K. Wang, X. Huang and P. Liu, ChemCatChem, 2018, 10, 3397–3401 CrossRef CAS.
- Y. Zhao, X. Huang, F. Gao, L. Zhang, Q. Tian, Z. B. Fang and P. Liu, Nanoscale, 2019, 11, 9085–9090 RSC.
- D. Shvydka, J. Drayton, A. D. Compaan and V. G. Karpov, Appl. Phys. Lett., 2005, 87, 1–3 CrossRef.
- B. Yang, H. Chen, X. Guo, L. Wang, T. Xu, J. Bian, Y. Yang, Q. Liu, Y. Du and X. Lou, J. Mater. Chem. C, 2020, 8, 14845–14854 RSC.
- Z. Han, R. Zhang, M. Li, L. Li, D. Geng and W. Hu, J. Mater. Chem. C, 2022, 10, 13324–13350 RSC.
- B. T. Diroll, B. Guzelturk, H. Po, C. Dabard, N. Fu, L. Makke, E. Lhuillier and S. Ithurria, Chem. Rev., 2023, 123, 3543–3624 CrossRef CAS PubMed.
- L. Jie, X. Gao, X. Cao, S. Wu, X. Long, Q. Ma and J. Su, Mater. Sci. Semicond. Process., 2024, 176, 108288 CrossRef CAS.
- T. Taniguchi, L. Nurdiwijayanto, R. Ma and T. Sasaki, Appl. Phys. Rev., 2022, 9, 021313 CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. De Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- P. Giannozzi, O. Baseggio, P. Bonfà, D. Brunato, R. Car, I. Carnimeo, C. Cavazzoni, S. De Gironcoli, P. Delugas, F. Ferrari Ruffino, A. Ferretti, N. Marzari, I. Timrov, A. Urru and S. Baroni, J. Chem. Phys., 2020, 152(154105) CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- J. Klimeš, D. R. Bowler and A. Michaelides, J. Phys.: Condens. Matter, 2009, 22, 022201 CrossRef PubMed.
- J. Klime, D. R. Bowler and A. Michaelides, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195131 CrossRef.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B, 1976, 13, 5188 CrossRef.
- D. Yuan, H. Liao and W. Hu, Phys. Chem. Chem. Phys., 2019, 21, 21049–21056 RSC.
- P. Garg, S. Kumar, I. Choudhuri, A. Mahata and B. Pathak, J. Phys. Chem. C, 2016, 120, 7052–7060 CrossRef CAS.
- W. K. Alaarage, A. H. Abo Nasria, B. Tamadhur, A. Hussein and H. I. Abbood, RSC Adv., 2024, 14, 5994–6005 RSC.
- L. Chhana, B. Lalroliana, R. C. Tiwari, B. Chettri, D. P. Rai, L. Vanchhawng, L. Zuala and R. Madaka, J. Electron. Mater., 2022, 51, 6556–6567 CrossRef CAS.
- M. S. Hassan, M. S. Islam and J. Park, Nanotechnology, 2021, 32, 305707 CrossRef CAS PubMed.
- J. Deb, R. Majidi and U. Sarkar, ACS Appl. Opt. Mater., 2023, 1, 201–208 CrossRef CAS.
- S. A. Tawfik, T. Gould, C. Stampfl and M. J. Ford, Phys. Rev. Mater., 2018, 2, 034005 CrossRef CAS.
- L. Shulenburger, A. D. Baczewski, Z. Zhu, J. Guan and D. Tománek, Nano Lett., 2015, 15, 8170–8175 CrossRef CAS PubMed.
- T. Björkman, J. Chem. Phys., 2014, 141, 074708 CrossRef PubMed.
- G. Perin, D. Kuritza, R. Barbosa, G. Tresco, R. B. Pontes, R. H. Miwa and J. E. Padilha, Phys. Rev. Mater., 2023, 7, 104003 CrossRef CAS.
- M. K. Mohanta and A. De Sarkar, ACS Appl. Mater. Interfaces, 2020, 12, 18123–18137 CrossRef CAS PubMed.
- H. Cai, Y. Guo, H. Gao and W. Guo, Nano Energy, 2019, 56, 33–39 CrossRef CAS.
- Y. Guo, J. Qiu and W. Guo, Nanoscale, 2015, 8, 575–580 RSC.
- S. W. Liu, H. P. Wang, Q. Xu, T. B. Ma, G. Yu, C. Zhang, D. Geng, Z. Yu, S. Zhang, W. Wang, Y. Z. Hu, H. Wang and J. Luo, Nat. Commun., 2017, 8, 1–8 CrossRef PubMed.
- C. C. Vu, S. Zhang, M. Urbakh, Q. Li, Q. C. He and Q. Zheng, Phys. Rev. B, 2016, 94, 081405 CrossRef.
- H. Li, J. Wang, S. Gao, Q. Chen, L. Peng, K. Liu and X. Wei, Adv. Mater., 2017, 29, 1701474 CrossRef PubMed.
- J. Liu, A. Goswami, K. Jiang, F. Khan, S. Kim, R. McGee, Z. Li, Z. Hu, J. Lee and T. Thundat, Nat. Nanotechnol., 2017, 13, 112–116 CrossRef PubMed.
- I. Popov, G. Seifert and D. Tománek, Phys. Rev. Lett., 2012, 108, 156802 CrossRef PubMed.
- D. Çakir, C. Sevik and F. M. Peeters, J. Mater. Chem. C, 2014, 2, 9842–9849 RSC.
- J. H. Lee, J. Y. Park, E. B. Cho, T. Y. Kim, S. A. Han, T. H. Kim, Y. Liu, S. K. Kim, C. J. Roh, H. J. Yoon, H. Ryu, W. Seung, J. S. Lee, J. Lee and S. W. Kim, Adv. Mater., 2017, 29, 1606667 CrossRef PubMed.
- C. J. Brennan, R. Ghosh, K. Koul, S. K. Banerjee, N. Lu and E. T. Yu, Nano Lett., 2017, 17, 5464–5471 CrossRef CAS PubMed.
- V. Bhavanasi, V. Kumar, K. Parida, J. Wang and P. S. Lee, ACS Appl. Mater. Interfaces, 2016, 8, 521–529 CrossRef CAS PubMed.
- Z. L. Wang, Adv. Energy Mater., 2020, 10, 2000137 CrossRef CAS.
- S. Niu and Z. L. Wang, Nano Energy, 2015, 14, 161–192 CrossRef CAS.
- S. Wang, Y. Xie, S. Niu, L. Lin, C. Liu, Y. S. Zhou and Z. L. Wang, Adv. Mater., 2014, 26, 6720–6728 CrossRef CAS PubMed.
- C. T. Huang, J. Song, W. F. Lee, Y. Ding, Z. Gao, Y. Hao, L. J. Chen and Z. L. Wang, J. Am. Chem. Soc., 2010, 132, 4766–4771 CrossRef CAS PubMed.
- Y. Liu, J. Ping and Y. Ying, Adv. Funct. Mater., 2021, 31, 2009994 CrossRef CAS.
- M. S. Islam, M. Y. Zamil, N. Ferdous, C. Stampfl and J. Park, ACS Appl. Electron. Mater., 2023, 5, 7034–7044 CrossRef CAS.
- M. S. Islam, M. Y. Zamil, M. R. H. Mojumder, C. Stampfl and J. Park, Sci. Rep., 2021, 11, 1–12 CrossRef PubMed.
- S. Mishra, S. Potu, R. S. Puppala, R. K. Rajaboina, P. Kodali and H. Divi, Mater. Today Commun., 2022, 31, 103292 CrossRef CAS.
- I. Ibrahim, H. N. Lim, R. Mohd Zawawi, A. Ahmad Tajudin, Y. H. Ng, H. Guo and N. M. Huang, J. Mater. Chem. B, 2018, 6, 4551–4568 RSC.
- B. G. An, H. R. Kim, Y. W. Chang, J. G. Park and J. C. Pyun, J. Korean Ceram. Soc., 2021, 58, 631–644 CrossRef CAS.
- K. Deng and L. Li, Adv. Mater., 2014, 26, 2619–2635 CrossRef CAS PubMed.
- Y. Ye, B. Yu, Z. Gao, H. Meng, H. Zhang, L. Dai and G. Qin, Nanotechnology, 2012, 23, 194004 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2025 |







