 Open Access Article
Open Access ArticleA kinetic interpretation of the effect of extractant and acid on neodymium(III) extraction by a diglycolamide
Wyatt S. Nobley a,
Johnathan J. Klein
a,
Johnathan J. Klein a and
Mark P. Jensen
a and
Mark P. Jensen *ab
*ab
aChemistry Department, Colorado School of Mines, 1500 Illinois Street, Golden, CO 80401, USA. E-mail: mjensen@mines.edu; Tel: +1-303-273-3785
bNuclear Science and Engineering Program, Colorado School of Mines, 1500 Illinois Street, Golden, CO 80401, USA
First published on 18th November 2025
Abstract
With an increasing demand for rare earth elements in modern technologies, it is crucial to develop a full understanding of the purification process for lanthanides. Recent studies have focused heavily on the separation of lanthanides using solvent extraction with diglycolamide extractant ligands. These completely incinerable extractants, especially N,N,N′,N′-tetra(n-octyl)diglycolamide (TODGA), provide best-in-class thermodynamic separation for the early-middle lanthanides. Thermodynamic parameters are well characterized for lanthanide extraction from nitric acid media by TODGA, but there exists a lack of knowledge about the kinetics. We developed a greater understanding of the rates and mechanism of lanthanide extraction by TODGA using operando visible spectroscopy to monitor changes in a coordination-sensitive neodymium(III) absorbance band. Due to the dynamic interplay between equilibrium metal distribution and the rate of mass transfer, determining these parameters across a wide range of component concentrations revealed novel thermodynamic and kinetic findings. An activity-based treatment of the non-linear dependence of metal extraction on acidity allowed us to quantitatively identify the changes in speciation across the acidity range. Plateau and linear regions in the kinetic data are directly related to slopes in the equilibrium data, which, together, provide the reaction orders with respect to each component. Extraction and stripping rate laws follow the interfacial two-step consecutive reactions mechanism, where adsorption and desorption of neodymium(III) complexes at the interface govern the rate limiting steps, while TODGA, nitrate anions, and nitric acid adducts associate and dissociate in fast equilibria.
Introduction
Lanthanide elements are critical to a range of high-performance magnetic and optical materials, but individual lanthanides are difficult to separate from one another due to their chemical similarity.1–3 Most separation chemistry for the purification of lanthanide elements uses organic extractants to form lanthanide complexes that are soluble in organic solvents, and the small differences in the lanthanide ionic radii can then be exploited to separate the lanthanides by liquid–liquid extraction.4 However, the selectivity for specific lanthanide elements is poor, and hundreds of individual extraction stages are often required to achieve high purity for one lanthanide.5 Understanding the physicochemical features underlying lanthanide separation processes and developing more efficient separating ligands are key areas of research for reducing the resources consumed in lanthanide production.The diglycolamide (DGA) ligand N,N,N′,N′-tetra(n-octyl)diglycolamide (TODGA)6 (Fig. 1) and its derivatives7 have emerged as promising extractants for lanthanide(III) cations with intra-lanthanide separation capabilities comparable to the best-in-class organophosphorus extractants. While some questions remain, thermodynamic aspects of the extraction, such as the degree of lanthanide(III) extraction and the equilibrium organic phase complexes formed by TODGA or other common tetraalkyldiglycolamides, have received considerable attention.8–10 Since DGAs are solvating extractants, they tend to form supramolecular complexes that also contain the lanthanide cation, charge-balancing anions, water, and mineral acids from the aqueous phase.11 Consequently, extractions involving tetraalkyl-DGAs have an unusually strong and complex dependence on the concentration of aqueous acid, which has been difficult to reproduce with an equilibrium thermodynamic model.12,13
The kinetic aspects of DGA extraction systems, such as rate laws, rate constants, and mechanisms, have rarely been characterized, likely due to the difficulty in obtaining and interpreting quantitative kinetic data for liquid–liquid extraction systems.14,15 The Lewis cell16 and rotating membrane cell17,18 techniques have been used to probe the TODGA-HNO3 system and found varying results. Using a Lewis cell, the extraction of Am(III) was found to be first order with respect to TODGA, HNO3, and Am(III). A chemically-controlled reaction mechanism was proposed to rationalize the results;16 however, the authors conclude that the extraction is at least partially controlled by the rate of diffusion rather than chemical reactions in their Lewis cell.16 A comprehensive study of Eu(III) and Am(III) extraction by TODGA in 5 vol% 1-octanol/hydrogenated tetrapropylene using a rotating membrane cell indicated decreasing forward and reverse rate constants with increasing TODGA concentration, while increasing the acidity led to faster forward (extraction) rates and slower reverse (stripping) rates.18 In that study, the increasing metal extraction with increasing TODGA concentration was primarily attributable to the decrease in the rate of the stripping reaction.
To develop a better understanding of the reaction orders and mechanism under conditions where the chemical reactions are rate controlling, we used operando UV/visible absorption spectroscopy to study the kinetics of Nd(III) partitioning between solutions of TODGA in n-dodecane and aqueous nitric acid. Our findings with this highly-stirred technique shed new light on the mechanisms of lanthanide phase transfer in diglycolamide-based separations, and they provide insight into the extraction and equilibrium speciation in the bulk organic phase.
Experiment
TODGA (>99%) was synthesized and purified in our lab according to the procedure in the SI. Nitric acid (ACS grade) was purchased from Sigma-Aldrich and n-dodecane (99%) was purchased from ThermoFisher Scientific. DI water (18.2 MΩ) was obtained from a Millipore Direct-Q water purifier. A stock solution containing 0.478 M Nd(NO3)3 was diluted to prepare all the aqueous Nd-containing solutions.Organic solutions were prepared by dissolving the appropriate mass of TODGA in n-dodecane. Aqueous phases were prepared by diluting appropriate masses of concentrated HNO3 and the Nd(NO3)3 stock solution with DI water. For the acid dependency experiments, solutions were prepared over a range of HNO3 concentrations (0.20–3.0 M) while the concentration of TODGA and Nd(III) were held at 0.10 M and 4.87 ± 0.04 mM, respectively. The concentration range for the TODGA dependency was 0.060–0.40 M TODGA, while the HNO3 and Nd(III) concentrations were held at 0.50 M and 4.91 ± 0.04 mM, respectively. For each condition, 15 mL of organic phase was pre-equilibrated with an equal volume of the corresponding metal-free acid solution. Phases were vortexed at 2000 rpm for 10 min using a Benchmark Scientific Benchmixer Vortex Mixer and centrifuged for 5 min. The aqueous phase was removed, and the process repeated. After two pre-equilibrations, the organic phase was separated for continued use. Extraction experiments were performed by contacting equal volumes of pre-equilibrated organic phase and metal-loaded aqueous phase for 5 min and subsequent centrifugation. All extractions were performed in triplicate at 295 ± 1 K. The initial and equilibrium Nd concentrations were determined by Inductively Coupled Plasma – Optical Emission Spectroscopy using a PerkinElmer Avio 220 Max analyzing two emission wavelengths in both radial and axial viewing modes. The distribution ratio (D) at equilibrium was calculated according to eqn (1), where organic phase species are indicated by an overbar, while aqueous species have none, subscript init represents the initial concentration, and subscript eq represents the equilibrium concentration.
 | (1) |
Interfacial tension measurements of TODGA solutions in contact with varying concentrations of nitric acid were collected by the pendant drop method on a Biolin ThetaFlex at 293 ± 1 K. The densities of the organic and aqueous phase were determined using an Anton Parr DMA 1001 with a precision of ±0.1 mg mL−1 to correct the recorded tension values. The pre-equilibrated organic phase (20 µL) was dispensed into fresh aqueous solution by a 14-gauge hooked needle, and 140 frames of images over 10 seconds were analyzed. All solutions were measured in duplicate.
Kinetic experiments were performed under pseudo first order reaction conditions with at least 12-fold excess of nitric acid and TODGA. The chemical form and phase distribution of the Nd(III) species in the mixture were followed as a function of time using the OLIS RSM-1000 spectrophotometer with CLARiTY attachment. This dual-monochromator instrument equipped with 1200 lines/mm gratings can acquire 1–100 scans per second over a wavelength range of approximately 70 nm with high resolution. The CLARiTY attachment uses an 8 mL round-bottom sample cell surrounded by a reflective coating that reflects the light throughout the cell multiple times before being collected and amplified by PMTs, leading to longer effective pathlengths and larger absorbance values for a given sample volume. A custom-made overhead stirrer was used in these experiments, which closed the system from stray light, and provided precise stirring speed control.
All kinetic experiments were performed following this sequence: the aqueous phase (3.95 mL), and then the pre-equilibrated organic phase (3.95 mL) were each carefully added to the cell to avoid pre-emptive mixing of the phases. The overhead stirrer was lowered into the cell, then data collection and stirring were started. The two phases were stirred vigorously at 57 rps in the round bottom cell at 295 ± 0.5 °C. Spectra were collected from 547 – 618 nm at 3.1 scans per second over 50 seconds to monitor the 4I9/2 → 4G5/2, 2G7/2 hypersensitive electronic transitions of Nd(III). Spectra were corrected with an instrumental background and further baseline corrected using the msbackadj function in the MATLAB Bioinformatics Toolbox. The resulting 3-dimensional data (spectral changes over time) were analyzed with the OLIS GlobalWorks software.
The specific interfacial area of the stirred samples was determined from the Sauter mean diameter of the organic droplets in the stirred mixture across the range of TODGA and nitric acid concentrations studied. Images of the stirred phases were acquired at 150 fps using a microscopic camera that was focused on an identical 8 mL round-bottom cell and stirrer without the external reflective coating or housing that replicated the dimensions of the CLARiTY cell. These images were randomly sampled and analyzed in ImageJ for the drop diameter after calibration of the images against those of 95 ± 5 µm polystyrene beads. The mean diameter of the drops ranged from 169 to 199 µm across the solution conditions considered.
All uncertainties are given at the 95% confidence level.
Results and discussion
Equilibrium analysis
Equilibrium analysis of Nd extraction by TODGA is useful for understanding the stoichiometries of the Nd complexes present in the bulk aqueous and organic phases at equilibrium. It is also necessary for analysis of the kinetic experiments. A general form of the extraction equilibrium for the partitioning of Nd between aqueous nitric acid solutions and TODGA/n-dodecane can be written as
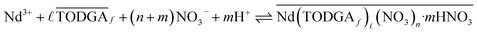 | (2) |
 | (3) |
 represents the free concentration of TODGA in the organic phase that is neither bound to metal nor nitric acid, and the approximation {H+} ≈ {NO3−} is used.
represents the free concentration of TODGA in the organic phase that is neither bound to metal nor nitric acid, and the approximation {H+} ≈ {NO3−} is used.
The effects of varying  at constant acidity and varying the aqueous nitrate activity at constant TODGA concentration are shown in Fig. 2. Linear least squares fitting of eqn (3) to the data in Fig. 2A, yields a value of
at constant acidity and varying the aqueous nitrate activity at constant TODGA concentration are shown in Fig. 2. Linear least squares fitting of eqn (3) to the data in Fig. 2A, yields a value of  for the average equilibrium Nd:TODGA stoichiometry in the organic phase. This indicates that there is a mixture of Nd complexes containing 3 or 4 TODGA molecules in the organic phase under these conditions, which agrees well with the literature, where slopes between 3 and 4 are found for lanthanide(III) extraction by TODGA from nitric acid into aliphatic and aromatic diluents.19–21 Previous EXAFS studies of the extracted Nd-TODGA complexes in the bulk organic phase were consistent with coordination of three tridentate TODGA molecules with the counter anions residing in clefts between the coordinated TODGA molecules.9 With this core Nd(TODGA)3(NO3)3 structure, the fourth TODGA molecule and any coextracted HNO3 would reside in the outer sphere of a lanthanide-centered supramolecular assembly.22
for the average equilibrium Nd:TODGA stoichiometry in the organic phase. This indicates that there is a mixture of Nd complexes containing 3 or 4 TODGA molecules in the organic phase under these conditions, which agrees well with the literature, where slopes between 3 and 4 are found for lanthanide(III) extraction by TODGA from nitric acid into aliphatic and aromatic diluents.19–21 Previous EXAFS studies of the extracted Nd-TODGA complexes in the bulk organic phase were consistent with coordination of three tridentate TODGA molecules with the counter anions residing in clefts between the coordinated TODGA molecules.9 With this core Nd(TODGA)3(NO3)3 structure, the fourth TODGA molecule and any coextracted HNO3 would reside in the outer sphere of a lanthanide-centered supramolecular assembly.22
 | ||
| Fig. 2 Variation in equilibrium Nd distribution ratios between aqueous nitric acid and TODGA/n-dodecane at 295 K. (A) Extraction from 0.50 M HNO3 ({NO3−} = 0.37) by varying concentrations of TODGA with an initial aqueous Nd concentration of 4.91 × 10−3 M. (B) Extraction from varying aqueous concentrations of nitric acid into 0.1 M TODGA/n-dodecane with an initial aqueous Nd concentration of 4.89 × 10−3 M. Lines represent the best fit of eqn (3) (panel A) or SI eqn S9 (panel B). | ||
The equilibrium and extraction rate experiments cover a wide range of aqueous phase nitric acid concentrations (0.20–3.0 M). The activity coefficients of the aqueous species are well-known to vary significantly over this range, therefore the aqueous phase nitrate ion activity was used to model the nitric acid dependence of the extraction.23 However, as expected from previous studies of lanthanide-DGA extraction, the equilibrium nitrate activity dependence of Nd extraction at constant TODGA concentration (Fig. 2B) is non-linear over the range of nitric acid concentrations studied6,19 and cannot be modeled well using eqn (3) with a single set of stoichiometric coefficients and Kex values. At low nitrate activity, the Nd distribution ratios in Fig. 2B show the expected third-power dependence on the nitrate activity, but at higher nitrate activities, the measured distribution ratio exceeds a fourth-power dependence on the aqueous nitrate activity.
The possible reasons for this very steep acid dependence have been discussed elsewhere,12,13,19 but the presence of two distinct nitrate dependence slopes in this data implies that multiple species containing different numbers of nitrate anions (n) and nitric acid molecules (m) are present in the organic phase at equilibrium. Consequently, a more complete model that accounts for the presence of multiple organic phase complexes and also considers changes in the activity coefficients of other aqueous species, for example Nd, was used to model the data as summarized in the SI and Fig. S1–S3. The experimental distribution data is well fit by this equilibrium model with three Nd complexes in the organic phase (Fig. 2B and SI Fig. S2). The first complex,  , predominates at low nitric acid concentrations ([HNO3] ≤ 0.50 M, {NO3−} ≤ 0.37) where the nitrate dependence slope of eqn (3) is (n + 2m) = 3.03 ± 0.08, and from charge balance considerations n = 3 and m = 0. At higher aqueous nitrate activities, a mixture of
, predominates at low nitric acid concentrations ([HNO3] ≤ 0.50 M, {NO3−} ≤ 0.37) where the nitrate dependence slope of eqn (3) is (n + 2m) = 3.03 ± 0.08, and from charge balance considerations n = 3 and m = 0. At higher aqueous nitrate activities, a mixture of 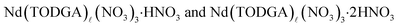 exists in the organic phase, and intermediate slopes are observed. For the highest nitrate activities studied, the nitrate dependence slope of eqn (3) corrected for the activity coefficients of the aqueous species is (n + 2m) = 6.9 ± 0.4. This is consistent with organic phase complexes that contain 3 NO3− and 2.0 ± 0.2 HNO3 molecules at the highest acidities studied. These results agree with previous findings with TODGA19 and a similar branched tetraalkyldiglycolamide,12 where an average of 1–2 HNO3 molecules were determined to associate with organic phase lanthanide complexes when the acidity rises.
exists in the organic phase, and intermediate slopes are observed. For the highest nitrate activities studied, the nitrate dependence slope of eqn (3) corrected for the activity coefficients of the aqueous species is (n + 2m) = 6.9 ± 0.4. This is consistent with organic phase complexes that contain 3 NO3− and 2.0 ± 0.2 HNO3 molecules at the highest acidities studied. These results agree with previous findings with TODGA19 and a similar branched tetraalkyldiglycolamide,12 where an average of 1–2 HNO3 molecules were determined to associate with organic phase lanthanide complexes when the acidity rises.
Therefore, from the perspective of equilibrium thermodynamics, the unusually large dependence of the measured distribution ratio on the aqueous nitrate activity can be understood as the result of the formation of organic phase Nd complexes that contain both the 3 nitrate anions required to form a neutral Nd(III) complex and an additional 1 or 2 nitric acid molecules.12,19
Interfacial tension
The interfacial tensions between solutions of TODGA in n-dodecane and aqueous solutions of nitric acid were measured across a range of compositions (Fig. 3). The constant slope regions of the interfacial tension curves show that the aqueous-organic interface is saturated with TODGA molecules when the TODGA concentration exceeds 1 × 10−5 M for all the aqueous acidities studied, with an interfacial excess corresponding to an average interfacial area of 166 ± 4 Å2/TODGA. Furthermore, the interfacial behavior of TODGA is consistent and predictable to at least 0.1 M TODGA across the range of acidities studied. TODGA solutions in contact with 0.46 M HNO3, which represent the specific solution compositions used in the TODGA kinetic experiments below, also show no sign of reverse micelle formation in the organic phase at high TODGA concentrations.Mass transfer kinetics
Measurements of the Nd reaction kinetics in this system provide a complementary perspective on the extraction process. The spectra for the extraction of Nd from 2.6 M HNO3 into 0.10 M TODGA/n-dodecane are shown in Fig. 4, along with the changes in absorbance observed at three of the most prominent wavelengths. Similar data for Nd extraction from 0.4 M HNO3 also are reported in SI Fig. S4. Increasing the aqueous acidity clearly increases the amount of metal extracted into the organic phase and the rate at which the reaction reaches equilibrium. At 0.40 M HNO3, DNd = 0.53 ± 0.04 and the extraction reached equilibrium in approximately 25 s, leading to kobs = 0.18 ± 0.01 s−1. At 2.6 M HNO3, the equilibrium distribution ratio climbed to DNd = 1106 ± 54 and Nd extraction reached equilibrium within 15 s with kobs = 0.30 ± 0.05 s−1. The spectra for Nd(III) isolated in either the aqueous phase or in the organic phase are provided in Fig. S5 for comparison.The spectral changes over time were first analyzed by singular value decomposition of the data into absorbance and kinetic eigenvectors using the OLIS GlobalWorks software. Under all the conditions studied, this analysis always indicated the presence of two unique light-absorbing Nd species with two significant kinetic eigenvectors. Fitting all of the absorbance data from an experiment using a simple two-species irreversible model yielded an overall pseudo first order rate constant (kobs) for the transfer of Nd between the aqueous and organic phases. This observed mass transfer coefficient was decoupled into a forward (extraction or aqueous → organic) rate constant for mass transfer (kao) and a reverse (stripping or organic → aqueous) rate constant for mass transfer (koa) using the distribution ratio, DNd, and eqn (4) and (5), where A/V is the specific interfacial area24 for our systems.
 | (4) |
 | (5) |
The forward and reverse mass transfer rate constants derived from kobs using eqn (5) were used as initial values for a two-species reversible kinetic fit of all the spectra from an experimental run in GlobalWorks, which fit the data well and yielded the final, refined kao and koa values for the Nd phase transfer reaction.
These interfacial area independent rate constants were used to determine the reaction orders in the rate law for the forward and reverse reactions.14,25,26 Logarithmic plots of the pseudo-first-order rate constants as functions of the concentration of free TODGA (Fig. 5) provide information about the reaction order. From the linear regions of the curves, limiting slopes of 3.0 ± 0.4 in the extraction direction and −3.1 ± 0.2 in the stripping direction are obtained. With respect to  and at constant [HNO3], the rate laws for the forward and reverse reactions take the general functional forms,
and at constant [HNO3], the rate laws for the forward and reverse reactions take the general functional forms,
 | (6) |
 | (7) |
The mathematical forms of the rate laws describing this solvent extraction system eqn (6)–(9) are consistent with the complex curvature and saturation at low and high concentrations observed in the [TODGA] and {NO3−} dependence data presented in Fig. 5 and 6. As will be discussed in more detail, this form of rate law is consistent with the interfacial two step consecutive reactions mechanism, which has been derived for metal solvent extraction systems previously.14,27 If the phase transfer reaction rate is controlled by chemical reactions, the cn coefficients in eqn (6) and (7) will be composed of the appropriate rate constants for the individual elementary steps of the chemical reactions and the interfacial absorption coefficients of TODGA,14 since the interfacial tension data imply that the interface is saturated with TODGA molecules under these experimental conditions. If, on the other hand, the reaction is diffusion controlled, the values of cn will be determined by the appropriate diffusion coefficients. The best fits of the data were obtained when parameters c1–c4 and the TODGA reaction order were varied simultaneously. This decreased χ2 for the fit by a factor of 2.5 and yielded a 3.25 ± 0.11 power dependence on TODGA for both the forward and reverse reaction rates. The data could also be modelled equally well assuming two parallel reaction paths involving 3 or 4 TODGA molecules. However, the presence of additional lower order TODGA-containing terms in the rate equation did not improve the fits.
The pseudo-first order kinetic results for the nitrate anion dependence are shown in Fig. 6A. They demonstrate that the extraction reactions are governed by different factors over different nitrate anion activity regimes. At low activities (i.e. {NO3−} < 0.5 which is [HNO3] < 0.67 M), the stripping rate constant, koa, is independent of nitrate activity, but is the primary contributor to the overall rate constant, kobs, and the reaction rate over most of that range. Consequently, the extraction rate constant, kao, steadily rises over this range of nitrate activities with an effective reaction order that matches the equilibrium nitrate activity dependence, 3.03 ± 0.08. The opposite behavior is observed in the higher nitrate activity region (i.e. 0.5 < {NO3−} ≤ 2.7 or 0.67 M < [HNO3] ≤ 3 M). In this range of nitrate activities kao plateaus but koa decreases steadily (Fig. 6A) with an observed reaction order of −4.73 ± 0.12 with respect to aqueous nitrate activity. The form of the rate laws with respect to the aqueous nitrate activity at constant TODGA concentration have the same general form as the TODGA-based rate expressions,
 | (8) |
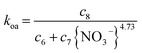 | (9) |
Because kao is much larger than koa at high nitrate activities, and kao is constant, the overall mass transfer rate constant, kobs, also plateaus (SI Fig. S6). Interestingly, although the kinetic constant, kobs, plateaus at high nitrate activity, the thermodynamic quantity describing the overall extraction, DNd, continues to climb rapidly. Fig. 6B compares koa−1 and DNd to highlight the similarity between the rapid decrease in stripping rate and the large increase in DNd in the higher nitrate activity region. All of the increase in DNd with increasing nitrate activity is accounted for by the decrease in koa over the same range. Given the requirement of charge neutrality for the organic phase complexes, and the direct correspondence of the nitrate activity slopes of koa−1 and DNd depicted in Fig. 6B, the observed order of the stripping reaction with respect to nitrate implies the loss of all HNO3 molecules bound to the extracted complex as well as the three NO3− in the overall stripping reaction.
The mathematical forms of our observed rate laws are known to arise in two particular categories of solvent extraction reactions when interfacial processes dominate the rates.24 For solvent extraction systems where the mass transfer kinetics is determined by the rates of chemical reactions at or near the interface, rate laws with the forms of eqn (6)–(9) are expected for systems where the elementary steps for the adsorption and desorption of Nd3+ and a neodymium complex at the aqueous-organic interface are rate controlling.14 In solvent extraction, this type of reaction has been referred to as an interfacial two-step consecutive reaction (ITSCR).27 However, this is not the only reaction mechanism that is consistent with eqn (6)–(9). Rate expressions with identical dependences on reactant concentrations also govern certain systems when the mass transfer rate is controlled by diffusion through the interface.25,27
Solvent extraction reactions controlled by interfacial chemical reactions can be rigorously distinguished from diffusion-controlled reactions in systems where the rate can be studied as a function of the thickness of the diffusion layers, but that is not possible in our highly-stirred cell. Nevertheless, multiple lines of evidence are most consistent with partitioning rates that are controlled by the chemical reactions. First, we observe a plateau in the mass transfer rates at high stirring speeds (SI Fig. S7), which is a necessary, but not sufficient condition for chemical kinetic control of the reaction.30 Second, using a rotating membrane cell with well-defined hydrodynamics, Vu et al., observed that the mass transfer reactions of Am(III) by 0.2 M TODGA in 5% 1-octanol/hydrogenated tetrapropylene were substantially slower than the diffusion limit.18 Third, the average drop sizes, volume fractions, diffusion coefficients, and mass transfer rates, appear inconsistent with diffusive models that do not include slow chemical reactions. Correcting for differences in solvent viscosity, we used previously reported diffusion coefficients for Am18 to estimate the diffusion coefficient of Nd(TODGA)3(NO3)3 in n-dodecane to be 12.3% larger than the reported diffusion coefficient of Am(TODGA)3(NO3)3 in 5% 1-octanol/hydrogenated tetrapropylene, or 1.3 × 10−6 cm2 s−1. The diffusion coefficient of Nd3+ in 0.5 M HNO3 was taken to be 4.94 × 10−6 cm2 s−1.18 With these values for the diffusion coefficients, the apparent thickness of the diffusion layer deduced from two-film theory31 appears too large in the continuous, well-stirred, aqueous phase of our system at 50–70 µm, when the average separation between the dispersed organic droplets is on the order of 150 µm. Moreover, the average surface residence time of the aqueous layer at the surface of the dispersed organic droplets predicted by Danckwertz surface renewal theory,32 8.4 ± 0.7 seconds, appears much too long for our well-stirred reaction cell. Together these facts lead us to prefer the ITSCR model over diffusion-controlled mass transfer to explain the kinetic observations.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 4
1 and 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 TODGA : Nd complexes at an average stoichiometry of 3.25
1 TODGA : Nd complexes at an average stoichiometry of 3.25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. On the aqueous side of the interface, the other slow step would be coordination of Nd(III) to a ligand at the interface and release from the interfacial complex into the aqueous phase. Because lanthanide(III)-nitrate equilibria are very fast,34 it is quite likely that the interfacial ligand that Nd binds to in this rate-limiting step is a TODGA molecule, which saturates the interface for all the solution compositions studied.
1. On the aqueous side of the interface, the other slow step would be coordination of Nd(III) to a ligand at the interface and release from the interfacial complex into the aqueous phase. Because lanthanide(III)-nitrate equilibria are very fast,34 it is quite likely that the interfacial ligand that Nd binds to in this rate-limiting step is a TODGA molecule, which saturates the interface for all the solution compositions studied.The reaction orders with respect to the nitrate present a more complicated picture of the reactions involved in the phase transfer. Three nitrates are required to form the requisite neutral Nd complex, but complexes containing 1 or 2 additional HNO3 molecules also form in the equilibrium organic phase. Because the aqueous activity of H+ varies directly with the activity of NO3−, each molecule of HNO3 extracted should show a second power dependence of the equilibrium on {NO3−} or {H+}. This is clearly observed in the equilibrium DNd values when they are corrected for variations in the activity coefficients of Nd3+, H2O, and the formation of aqueous Nd(NO3)2+ and Nd(NO3)2+, in addition to the changes in {NO3−}. These corrections are not easily applied to the kinetic reaction orders for the mass transfer. At low aqueous concentrations of HNO3 the reaction order in the extraction direction at low concentrations is 3 (eqn (8) and Fig. 6A). Combined with the TODGA dependence data discussed above, this is consistent with  being the complexes that detach from the interface in the extraction direction.
being the complexes that detach from the interface in the extraction direction.
Different behavior is observed for the stripping reaction at higher nitrate activities. Under these conditions kao plateaus, and the stripping rate, koa, decreases with an observed order of 4.7 with respect to {NO3−} without correction for changes in the activity coefficients of other aqueous species (eqn (9)). Because the reaction order for the stripping direction with respect to nitrate is greater than 3, the stripping reaction will involve dissociation of HNO3 from the Nd complex prior to the rate determining steps. But, since the forward rate has plateaued at high nitrate activities (Fig. 6A), according to eqn (4) all the increase in DNd is associated with a strong decrease in koa (Fig. 6B), which makes the effective reaction order for koa match the nitrate dependence slope of DNd after the full activity correction, which is 6.9 at the highest acidities. Therefore, all three nitrates and all the coordinated nitric acid in the complex must be released in the stripping steps by the time the transition state forms in the final complex. This final step would then be release of Nd3+ from the aqueous side of the interface.
Combining these reaction orders, the rate laws imply that within an ITSCR mechanism (1) nitrate ions and TODGA molecules react with Nd adsorbed in the interface region in a series of fast elementary equilibria that occur between the rate-controlling interfacial adsorption and desorption elementary reactions, and (2) the addition of the solvating HNO3 to the  complex takes place as a set of fast equilibria in the organic phase after desorption of the
complex takes place as a set of fast equilibria in the organic phase after desorption of the  complex from the interface. For the complex containing 3 TODGA molecules the reactions would be
complex from the interface. For the complex containing 3 TODGA molecules the reactions would be
| Nd3+ + TODGAi ⇌ Nd(TODGA)i | (10) |
| Nd(TODGA)i + 2TODGAi + 3NO3− ⇌ Nd(TODGA)3(NO3)3,i | (11) |
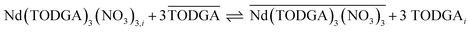 | (12) |
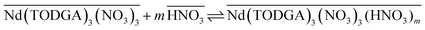 | (13) |
This multi-step mechanism is also consistent with the temperature dependence data for the extraction reactions. The overall extraction equilibrium (eqn (2)) is exothermic with ΔH0 = −57 ± 4 kJ mol−1 for Nd extraction from 0.50 M HNO3 into 0.1 M TDOGA/n-dodecane (SI Fig. S8). However, the temperature dependencies of kao and koa show opposite trends from each other (SI Fig. S9). The forward rate slows down as the temperature increases with an apparent activation energy of −40 ± 2 kJ mol−1, while the reverse rate increases with an apparent activation energy of 16 ± 4 kJ mol−1. The negative apparent activation energy observed for kao is consistent with mechanisms where a fast exothermic equilibrium, such as the one summarized by equilibrium (11), are followed by a slow step where the activation energy, Ea, for the slow step is less than −ΔH0 of the equilibrium.35
Conclusions
The operando UV/visible spectroscopic measurement of solvent extraction kinetics under strong stirring allowed determination of the mass transfer parameters in the Nd(III)/HNO3–TODGA/n-dodecane solvent extraction system for reactions that reached equilibrium in as little as 10 seconds. While these measurements were conducted under conditions resembling practical reaction conditions (i.e. TODGA and HNO3 concentrations were varied over a practical range and efficient phase mixing was implemented), fundamental information about the extraction mechanism could be discerned. As expected for extraction of neutral nitrate salts by water-insoluble neutral ligands, the rate constants for extraction increased with a third order dependence on the concentrations of both TODGA and HNO3, eventually reaching plateaus at high concentrations. This is in contrast to the confounding findings of Vu et al., who report Am(III) and Eu(III) extraction rates weakly decrease with increasing TODGA concentrations in a similar extraction system.18 The stripping rates showed the reverse behavior with plateaus in the TODGA and NO3− dependencies at low concentrations and decreasing rates at higher concentrations. Similar decreasing stripping rates at high TODGA concentrations were also observed by Vu et al.18 Certain key differences exist between the current study and their investigations, such as our focus on neodymium(III), using n-dodecane as the organic diluent, and our employment of a highly-stirred tank technique. This differs from the study by Vu et al. which focused on europium(III) and americium(III), using the highly-branched hydrogenated tetrapropylene with 5 volume percent 1-octanol as the organic diluent, and a rotating membrane cell to study the kinetics. It is likely that the discrepancies between the two studies are due to a combination of these differences.From a mechanistic perspective, the kinetic data can be interpreted according to the interfacial two-step consecutive reactions mechanism, where adsorption to and desorption from the interface of Nd species are rate-controlling. During extraction, 3 nitrate anions and 3 or 4 TODGA molecules bind to Nd at the interface in a series of equilibria before desorption of the neutral 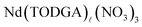 complex from the interface into the organic phase. In the reverse process, strong inverse dependence of koa on the TODGA concentration and aqueous nitrate activity indicate that the
complex from the interface into the organic phase. In the reverse process, strong inverse dependence of koa on the TODGA concentration and aqueous nitrate activity indicate that the  complex fully dissociates, releasing Nd3+ to the aqueous phase in a slow step.
complex fully dissociates, releasing Nd3+ to the aqueous phase in a slow step.
This kinetic picture of lanthanide extraction by TODGA from nitric acid solutions also provides an alternate interpretation of the varied and strong dependence of the equilibrium distribution ratio DNd on the nitric acid concentration. At the lowest nitric acid concentrations and nitrate activities, Nd complexes containing no nitric acid adducts are the most prevalent species in the organic phase (SI Fig. S3), koa is constant and all of the increase in DNd is attributable to the increase in the forward rate. At approximately {NO3−} = 0.6 (or [HNO3] = 0.8 M), the situation reverses. At that point, kao becomes constant, koa begins to decrease precipitously, and nitric acid adducts come to dominate the organic phase speciation. As illustrated in Fig. 6B, under these conditions it is the changes in koa that drive the changes in DNd, and the nitrate dependence of DNd achieves a much higher slope than it has when the forward rate determines the changes in DNd. Thus, from this perspective, the kinetic difficulty in losing all of the nitrate counter ions and nitric acid molecules from the organic phase Nd-TODGA complexes hinders the reverse reaction at high nitric acid concentrations which proportionately increases the equilibrium distribution ratio.
Author contributions
Wyatt S. Nobley – conceptualization, formal analysis, investigation, methodology, visualization, writing – original draft, writing – review and editing. Johnathan J. Klein – investigation, visualization, writing – original draft. Mark P. Jensen – conceptualization, formal analysis, supervision, funding acquisition, visualization, project administration, writing – review and editingConflicts of interest
There are no conflicts to declare.Data availability
Data for this article, including the equilibrium distribution ratios is archived in the Separation Archive for Elements at https://safe.lanl.gov/, while interfacial tension measurements and rate constant data are given in the Supplementary Information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5ra06672g.Acknowledgements
The authors want to thank Ed Dempsey, Instrument Engineer/Designer for the Chemistry Department at the Colorado School of Mines, for the design and implementation of the stirring assembly used in the kinetic experiments conducted in this study. This work was supported by U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under award DE-SC0022217. The views expressed in the article do not necessarily represent the views of the DOE or the U.S. Government. The U.S. Government retains and the publisher, by accepting the article for publication, acknowledges that the U.S. Government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this work, or allow others to do so, for U.S. Government purposes.References
- J. H. L. Voncken, The Rare Earth Elements: an Introduction, Springer International Publishing AG Switzerland, 2016 Search PubMed.
- D. S. Sholl and R. P. Lively, Seven Chemical Separations to Change the World, Nature, 2016, 532, 435–437 CrossRef PubMed.
- K. Binnemans, P. T. Jones, B. Blanpain, T. Van Gerven, Y. Yang, A. Walton and M. Buchert, Recycling of Rare Earths: A Critical Review, J. Cleaner Prod., 2013, 51, 1–22 CrossRef CAS.
- F. Xie, T. A. Zhang, D. Dreisinger and F. Doyle, A Critical Review on Solvent Extraction of Rare Earths from Aqueous Solutions, Miner. Eng., 2014, 56, 10–28 CrossRef CAS.
- T. Cheisson and E. J. Schelter, Rare Earth Elements: Mendeleev's Bane, Modern Marvels, Science, 2019, 363, 489–493 CrossRef CAS.
- Y. Sasaki, Y. Sugo, S. Suzuki and S. Tachimori, The Novel Extractants, Diglycolamides for the Extraction of Lanthanides and Actinides in HNO3-n-Dodecane System, Solvent Extr. Ion Exch., 2001, 19, 91–103 CrossRef CAS.
- D. Stamberga, M. R. Healy, V. S. Bryantsev, C. Albisser, Y. Karslyan, B. Reinhart, A. Paulenova, M. Foster, I. Popovs, K. Lyon, B. A. Moyer and S. Jansone-Popova, Structure Activity Relationship Approach toward the Improved Separation of Rare-Earth Elements Using Diglycolamides, Inorg. Chem., 2020, 59, 17620–17630 CrossRef CAS.
- S. A. Ansari, P. Pathak, P. K. Mohapatra and V. K. Manchanda, Chemistry of Diglycolamides: Promising Extractants for Actinide Partitioning, Chem. Rev., 2012, 112, 1751–1772 CrossRef CAS PubMed.
- D. M. Brigham, A. S. Ivanov, B. A. Moyer, L. H. Delmau, V. S. Bryantsev and R. J. Ellis, Trefoil-Shaped Outer-Sphere Ion Clusters Mediate Lanthanide(III) Ion Transport with Diglycolamide Ligands, J. Am. Chem. Soc., 2017, 139, 17350–17358 CrossRef CAS PubMed.
- A. A. Peroutka, S. S. Galley and J. C. Shafer, Elucidating the Speciation of Extracted Lanthanides by Diglycolamides, Coord. Chem. Rev., 2023, 482, 1–31 CrossRef.
- S. Nave, G. Modolo, C. Madic and F. Testard, Aggregation Properties of N,N,N’,N’-tetraoctyl-3-oxapentanediamide (TODGA) in n-Dodecane, Solvent Extr. Ion Exch., 2004, 22, 527–551 CrossRef CAS.
- E. Campbell, V. E. Holfeltz, G. B. Hall, K. L. Nash, G. J. Lumetta and T. G. Levitskaia, Extraction Behavior of Ln(III) Ions by T2EHDGA/n-Dodecane from Nitric Acid and Sodium Nitrate Solutions, Solvent Extr. Ion Exch., 2018, 36, 331–346 CrossRef CAS.
- T. Yaita, A. W. Herlinger, P. Thiyagarajan and M. P. Jensen, Influence of Extractant Aggregation on the Extraction of Trivalent f-Element Cations by a Tetraalkyldiglycolamide, Solvent Extr. Ion Exch., 2004, 22, 553–571 CrossRef CAS.
- P. R. Danesi, R. Chiarizia and C. F. Coleman, The Kinetics of Metal Solvent Extraction, Crit. Rev. Anal. Chem., 1980, 10, 1–126 CrossRef.
- G. A. Picayo and M. P. Jensen, in Handbook on the Physics and Chemistry of Rare Earths, Elsevier B.V., 2018, vol. 54, pp. 145–225 Search PubMed.
- W.-B. Zhu, G.-A. Ye, F.-F. Li and H.-R. Li, Kinetics and Mechanism of Am(III) Extraction with TODGA, J. Radioanal. Nucl. Chem., 2013, 298, 1749–1755 Search PubMed.
- M. A. Bromley and C. Boxall, A Study of Cerium Extraction Kinetics by TODGA in Acidified and Non-Acidified Organic Solvent Phases in the Context of Fission Product Management, Prog. Nucl. Sci. Technol., 2018, 5, 70–73 CrossRef.
- T. H. Vu, J.-P. Simonin, A. L. Rollet, R. J. M. Egberink, W. Verboom, M. C. Gullo and A. Casnati, Liquid/Liquid Extraction Kinetics of Eu(III) and Am(III) by Extractants Designed for the Industrial Reprocessing of Nuclear Wastes, Ind. Eng. Chem. Res., 2020, 59, 13477–13490 CrossRef.
- Y. Sasaki, P. Rapold, M. Arisaka, M. Hirata, T. Kimura, C. Hill and G. Cote, An Additional Insight into the Correlation between the Distribution Ratios and the Aqueous Acidity of the TODGA System, Solvent Extr. Ion Exch., 2007, 25, 187–204 CrossRef.
- S. A. Ansari, P. N. Pathak, V. K. Manchanda, M. Husain, A. K. Prasad and V. S. Parmar, N,N,N′,N′-tetraoctyl diglycolamide (TODGA): A Promising Extractant for Actinide-Partitioning from High-Level Waste (HLW), Solvent Extr. Ion Exch., 2005, 23, 463–479 CrossRef.
- I. Kajan, M. Florianova, C. Ekberg and A. V. Matyskin, Effect of Diluent on the Extraction of Europium(III) and Americium(III) with: N,N,N′,N′-tetraoctyl diglycolamide (TODGA), RSC Adv., 2021, 11, 36707–36718 RSC.
- R. J. Ellis, D. M. Brigham, L. Delmau, A. S. Ivanov, N. J. Williams, M. N. Vo, B. Reinhart, B. A. Moyer and V. S. Bryantsev, “Straining” to Separate the Rare Earths: How the Lanthanide Contraction Impacts Chelation by Diglycolamide Ligands, Inorg. Chem., 2017, 56, 1152–1160 CrossRef PubMed.
- A. V. Levanov, O. Y. Isaikina and V. V. Lunin, Dissociation Constant of Nitric Acid, Russ. J. Phys. Chem. A, 2017, 91, 1221–1228 CrossRef.
- P. R. Danesi, in Principles and Practices of Solvent Extraction, ed. J. Rydberg, C. Musikas and G. R. Choppin, Marcel Dekker, New York, 1992, pp. 157–207 Search PubMed.
- P. R. Danesi and G. F. Vandegrift, Kinetics and Mechanism of the Interfacial Mass Transfer of Eu3+ and Am3+ in the System Bis(2-ethylhexyl) Phosphate-n-Dodecane-NaCl-HCl-Water, J. Phys. Chem., 1981, 85, 3646–3651 CrossRef.
- H. P. Ting, G. L. Bertrand and D. F. Sears, Diffusion of Salts across a Butanol-Water Interface, Biophys. J., 1966, 6, 813–823 CrossRef PubMed.
- P. R. Danesi, G. F. Vandegrift, E. P. Horwitz and R. Chiarizia, Simulation of Interfacial Two-Step Consecutive Reactions by Diffusion in the Mass-Transfer Kinetics of Liquid-Liquid Extraction of Metal Cations, J. Phys. Chem., 1980, 84, 3582–3587 CrossRef.
- S. Kumar, Studies for Mutual Solubility of TODGA and Water at 298.15 K and 0.1 MPa, J. Radioanal. Nucl. Chem., 2024, 333, 4995–5001 CrossRef.
- X. Liu, X. Huang, Y. Wang, Z. Wang, Q. Yu, H. Zhou, R. Li and S. Ding, Solvent Extraction of TODGA in the Presence of Phase Modifiers of TBP, n-Octanol, and DHOA Dissolved in n-Dodecane: Thermodynamics, Kinetics and Aggregation Studies, Inorg. Chim. Acta., 2025, 583, 122710 CrossRef.
- P. R. Danesi, in Solvent Extraction Principles and Practice, Revised and Expanded, ed. J. Rydberg, M. Cox, C. Musikas and G. R. Choppin, CRC Press, Boca Raton, 2nd edn, 2004 Search PubMed.
- E. L. Cussler, Diffusion: Mass Transfer in Fluid Systems, Cambridge University Press, 3rd edn, 2009 Search PubMed.
- G. Astarita, Mass Transfer with Chemical Reaction, Elsevier, 1967 Search PubMed.
- J. H. Espenson, Chemical Kinetics and Reaction Mechanisms, McGraw-Hill, New York, 1981 Search PubMed.
- H. B. Silber, N. Scheinin, G. Atkinson and J. J. Grecsek, Kinetic Investigation of the Lanthanide(III)-Nitrate Complexation Reaction, J. Chem. Soc., Faraday Trans., 1972, 1(68), 1200–1212 RSC.
- L. E. Revell and B. E. Williamson, Why Are Some Reactions Slower at Higher Temperatures?, J. Chem. Educ., 2013, 90, 1024–1027 CrossRef.
| This journal is © The Royal Society of Chemistry 2025 |





