Open Access Article
Open Access ArticleStark effects of the fluorescence spectra in InP core and InP/ZnSe core/shell quantum dots under an external electric field
Ning Du * and
Hongshan Chen
* and
Hongshan Chen
College of Physics and Electronic Engineering, Northwest Normal University, Lanzhou 730070, China. E-mail: duning@nwnu.edu.cn
First published on 12th November 2025
Abstract
Investigating the optical response of quantum dots subjected to an external electric field offers key insights into their suitability for nanoelectronic device integration. In this study, we employ first-principles calculations to elucidate the Stark effect in both InP core and InP/ZnSe core/shell quantum dots. Our analysis reveals three characteristic Stark shift behaviors, including quadratic, linear, and hybrid quadratic-linear responses, where each is directly linked to the evolution of the excitonic dipole moment, reflecting the intrinsic electron–hole separation (D0i, where i = x, y, z) in the absence of an applied field. Calculated electron densities for excited states demonstrate that spectral energy ΔE increases as |Di| decreases under an external electric field, reaching a maximum when |Di| approaches zero. For all the QDs examined, D0x is approximately zero, so an applied field along the x-direction consistently enlarges |Dx|, resulting in a red shift. In contrast, the spectral response along the y or z axes depends on the alignment of the field orientation relative to D0i: fields aligning with the electron–hole vector enhance separation (red shift), while opposing fields reduce it (blue shift). The magnitude of |D0i| is primarily determined by core/shell electronic structure: small-core (InP)10(ZnSe)67 exhibits quasi-type II behavior with large |D0z|, while larger-core (InP)27(ZnSe)50 and pure (InP)77 show type-I-like localization with small |D0i|. These findings indicate that the Stark shift characteristics of InP/ZnSe QDs can be tailored by adjusting the thickness of the core or shell layer of QDs.
1 Introduction
Quantum dots (QDs) are nanoscale semiconductor crystals characterized by discrete energy levels and size-dependent optical properties. When subjected to an external electric field or photon excitation, QDs emit light at tunable frequencies by varying their sizes, a phenomenon commonly referred to as the quantum confinement effect. Through precise control of both particle size and chemical composition, the emission spectra of QDs can span the entire visible range, enabling dynamic modulation of their optical output. This tunability, alongside features such as broad absorption, narrow and intense emission, high photostability, and superior color purity, has propelled QDs to the forefront of research in optoelectronics, bioimaging, and energy technologies. Among the wide range of available QD materials, cadmium-based systems have reached a high level of technological maturity, and Cd-based quantum dot light-emitting diodes (QLEDs) now fulfill commercial display requirements.1,2 However, concerns over toxicity and environmental impact restrict their widespread deployment. Indium phosphide (InP) QDs, as a cadmium-free alternative, possess a Bohr radius near 10 nm and exhibit emission that can be tuned throughout the visible spectrum by controlling particle size. Substantial advances in the synthesis and surface engineering of InP QDs have led to marked improvements in their performance, rendering them increasingly attractive for applications in displays.3–5 For instance, the external quantum efficiency (EQE) of red and green QLED reached 22.56%,6 and 16.3%,7 respectively.Although blue-emitting InP quantum dots with a photoluminescence quantum yield greater than 80% can usually be obtained by constructing core–shell or alloy-type quantum dots,8,9 the corresponding QLED still exhibits poor EQE (2.8%).10 This indicates the EQE of InP QLED is determined by the combined effect of multiple factors. One of them is that QDs embedded in QLED architectures are susceptible to spectral diffusion under external electric fields, primarily as a consequence of the quantum-confined Stark effect (QCSE). Furthermore, the spectral diffusion may affect the rate of radiation combination as well as EQE.
Experimental studies have documented field-induced emission phenomena in InP QDs. For example, Suh et al.11 observed a significant redshift and broadening in the electroluminescence spectra of blue InP QLEDs compared to photoluminescence spectra, while Yu et al. reported a maximum redshift of 19 nm (from 465 to 484 nm).12 This electric-field-induced spectral modulation, often termed the Stark effect, is attributed to alterations in the band-edge energy landscape and reduction in effective bandgap.13 In contrast, a recent study by Daibagya14 found no observable Stark shift in the photoluminescence spectra of CdTe/SiO2 QDs with a mean radius of 1.74 nm, attributing this to strong spatial confinement that suppresses field-induced dipole formation. Further investigations have revealed material and structure-dependent variations in the QCSE. Usman15 studied GaBixAs1−x/GaAs quantum wells, showing that at a low Bi content (x = 3.125%), the Stark shift is unconventional due to strong localization of hole states caused by the presence of Bi clusters, while at higher Bi concentrations, a conventional quadratic dependence on the electric field emerges, regardless of field direction, similar to traditional III–V materials. Field polarity can also produce asymmetric spectral responses; for example, blue shifts are observed under fields opposing the intrinsic dipole direction.16 Additionally, Heyn et al.17 highlighted that the geometry of QDs, such as cones versus symmetric dots, significantly influences both the magnitude and symmetry of the Stark shift, correlating with the electron–hole spatial separation in the absence of an applied field.
The complex behavior of field-induced spectral shifts in QDs is commonly interpreted through contributions from both permanent dipole moments and linear polarizability. The direction and magnitude of the shift—red or blue—depend on the interplay between these two factors, with permanent dipole moments enabling bidirectional shifts and polarizability causing exclusively red shifts. Such dependencies have been exploited in several studies to extract exciton dipole moments and polarizabilities by fitting the quadratic relation between the Stark energy shift and applied field strength.18–23
Encapsulation of QDs in core–shell architectures has been shown to mitigate surface defect states and enhance fluorescence quantum yield.24 This work systematically explores how external electric fields modulate the fluorescence response, with a focus on the field-induced Stark effect within InP/ZnSe core/shell engineered nanostructures.
2 Calculation methods
In this work, a nearly spherical indium phosphide nanocrystal, denoted as (InP)77 with an approximate diameter of 2.0 nm, was derived by isolating a cluster from the bulk cubic lattice structure.25–27 This undoped nanocluster exhibits C3v point group symmetry. To generate core/shell architectures, the outer indium atoms on the InP cluster were selectively replaced with zinc, while phosphorus atoms were substituted with selenium, yielding two distinct configurations: (InP)10(ZnSe)67, representing a smaller core, and (InP)27(ZnSe)50, representing a large core. To eliminate unsatisfied surface bonds, pseudo-hydrogen atoms with fractional charges were used for surface passivation. These pseudo-atoms were assigned effective nuclear charges tailored to compensate for the valence of the surface atoms, following the electron counting principle, where the fractional charge is given by (8 − Z)/4 and Z represents the valence electron count of the surface species.28 In this work, the passivating pseudo-hydrogen bonded to surface In, Zn, P, and Se were set to assigned nuclear charges of 1.25, 1.50, 0.75, and 0.50, respectively, maintaining the system's overall charge neutrality.All model geometries were fully relaxed in their electronic ground states using density functional theory (DFT) as implemented in the Gaussian 16 software.29 The PBE0 hybrid exchange-correlation functional30 was selected for its demonstrated accuracy in modeling the structural and electronic features of indium phosphide nanomaterials.25,31,32 Atomic orbitals for each element were described using the LanL2DZ effective core potential basis set.33,34 SCF cycles and geometry optimizations were achieved using the default convergence criteria of the Gaussian 16 software:10−8 hartree for the self-consistent field convergence, maximum force of 0.000450 hartree/bohr, RMS force of 0.000300 hartree/bohr, maximum displacement of 0.001800 bohr, and RMS displacement of 0.001200 bohr. Structural analysis revealed that the optimized (InP)77-G and (InP)10(ZnSe)67-G exhibit C3v, whereas (InP)27(ZnSe)50-G adopts Cs symmetry in its relaxed configuration (see Fig. 1).
 | ||
| Fig. 1 Optimized ground-state (-G) and the lowest singlet excited-state (-E) geometries of (InP)77, (InP)10(ZnSe)67, and (InP)27(ZnSe)50. | ||
Following the electron excitation, each nanostructure undergoes rapid geometry relaxation, reaching a new equilibrium on the picosecond timescale. According to Kasha's rule, fast internal conversion between higher excited states and the lowest singlet (S1) state ensures that fluorescence emission is governed by the S1 →  transition.35 This electron transition model is clearly illustrated in Fig. S1 of the SI. Therefore, the influence of the electric field-induced Stark shifts was examined using the S1-relaxed geometries. The energy gap between S1 and
transition.35 This electron transition model is clearly illustrated in Fig. S1 of the SI. Therefore, the influence of the electric field-induced Stark shifts was examined using the S1-relaxed geometries. The energy gap between S1 and 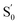 directly yields the emission energy ΔE. The same computational approach, including functionals, pseudopotentials, and basis sets, was employed in the time-dependent DFT (TDDFT) calculations for optimizing S1 geometries. The lowest singlet excited-state structures of (InP)77-E, (InP)10(ZnSe)67-E, and (InP)27(ZnSe)50-E are given in Fig. 1. The corresponding atom coordinates are listed at the end of the SI. Since the cluster models are derived from the bulk cubic lattice structure and have an approximate diameter of 2.0 nm, the structural distortion after being excited was not significant, but only a decrease in symmetry (Cs or C1). We use the root mean square displacement to measure the difference between the ground and excited state geometries.
directly yields the emission energy ΔE. The same computational approach, including functionals, pseudopotentials, and basis sets, was employed in the time-dependent DFT (TDDFT) calculations for optimizing S1 geometries. The lowest singlet excited-state structures of (InP)77-E, (InP)10(ZnSe)67-E, and (InP)27(ZnSe)50-E are given in Fig. 1. The corresponding atom coordinates are listed at the end of the SI. Since the cluster models are derived from the bulk cubic lattice structure and have an approximate diameter of 2.0 nm, the structural distortion after being excited was not significant, but only a decrease in symmetry (Cs or C1). We use the root mean square displacement to measure the difference between the ground and excited state geometries.
 | (1) |
 ,
,  and
and  are the coordinates of i-th atom in the S1 structure. Computed RMSD values are 0.034 Å for (InP)77, 0.090 Å for (InP)10 (ZnSe)67 and 0.042 Å for (InP)27 (ZnSe)50. Therefore, it is difficult to observe clear changes through static graphics.
are the coordinates of i-th atom in the S1 structure. Computed RMSD values are 0.034 Å for (InP)77, 0.090 Å for (InP)10 (ZnSe)67 and 0.042 Å for (InP)27 (ZnSe)50. Therefore, it is difficult to observe clear changes through static graphics.
The influence of external electric fields on these systems was probed by introducing a “field” keyword during calculations. The field's magnitude and direction were controlled by the parameter M ± N, where M indicates multipolarity and N×0.0001 specifies the field strength in atomic units (a.u.). For instance, specifying “Field = z + N” applies a field from the positive z-direction to the negative z-direction, while “Field = z − N” orients it oppositely. In this work, the fields along the x,y, and z-axes were incremented from −0.0010 to +0.0010 a.u. in steps of 0.0002 a.u.(1 a.u. = 5.14 × 1011 V m−1),36 such as ±0.0002, ±0.0004, ±0.0006, ±0.0008 a.u….
The total energy of the system under an applied electric field was expanded as a Taylor series37,38
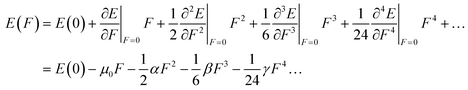 | (2) |
and
 | (3) |
3 Results and discussion
3.1 Energy profiles of ground and excited states in applied electric fields
As outlined in computational methodology, the total energy of each nanostructure subjected to an electric field can be represented as a Taylor expansion. Table 1 summarizes the permanent dipole moments µ0i and static polarizabilities αii calculated by Gaussian 16 for both ground and excited states of (InP)77-E, (InP)10(ZnSe)67-E, and (InP)27(ZnSe)50-E, corresponding to the linear and quadratic terms in the expansion. Substituting these values into the truncated Taylor series (excluding higher-order terms), analytic expressions for the energies in -state and S1-state were derived for fields oriented along the x, y, and z axes. The explicit forms of these equations are provided in SI (eqn S1–S18). Meanwhile, the computed DFT energies of both electronic states and differences are listed in Tables S1–S3 (see SI).
-state and S1-state were derived for fields oriented along the x, y, and z axes. The explicit forms of these equations are provided in SI (eqn S1–S18). Meanwhile, the computed DFT energies of both electronic states and differences are listed in Tables S1–S3 (see SI).
 -state and S1-state, as well as the difference between these two states, and the percentage contribution of orbital transitions HOMO → LUMO to the electron excitation
-state and S1-state, as well as the difference between these two states, and the percentage contribution of orbital transitions HOMO → LUMO to the electron excitation
In Fig. 2, the computed DFT energies (symbols) are compared to the values generated from the analytic equations (curves), showing excellent agreement and a predominantly quadratic relationship between the energy and the magnitude of the applied field. The most special one is the energy of  in (InP)10(ZnSe)67-E when the electronic field is applied in the z-axis. Within the range of the applied electric field, no inflection point of the parabola was observed, presenting a linear-like characteristic. This is because the absolute value of the permanent dipole moment µ0i of
in (InP)10(ZnSe)67-E when the electronic field is applied in the z-axis. Within the range of the applied electric field, no inflection point of the parabola was observed, presenting a linear-like characteristic. This is because the absolute value of the permanent dipole moment µ0i of  -state is up to 3.9311 a.u., resulting in the linear term gaining more dominance.
-state is up to 3.9311 a.u., resulting in the linear term gaining more dominance.
3.2 Stark modulation of fluorescence emission energy
The fluorescence emission energy (ΔE), defined as the energy difference between the S1 and -states, is directly influenced by the presence of an external electric field. ΔE under various field conditions is computed as described by eqn (4)–(6), incorporating the excitation-induced changes in permanent dipole moment and polarizability.21,39–42 Changes in the dipole moment upon excitation Δµ0i result in a linear field dependence of the transition energy, while modifications in polarizability Δαii yield a quadratic response.
-states, is directly influenced by the presence of an external electric field. ΔE under various field conditions is computed as described by eqn (4)–(6), incorporating the excitation-induced changes in permanent dipole moment and polarizability.21,39–42 Changes in the dipole moment upon excitation Δµ0i result in a linear field dependence of the transition energy, while modifications in polarizability Δαii yield a quadratic response.
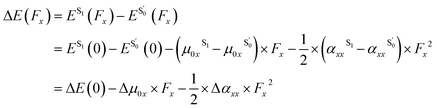 | (4) |
similarly
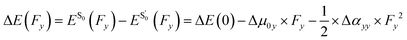 | (5) |
 | (6) |
As depicted in Fig. 3, the emission energy ΔE, as obtained from the analytical approach, agrees well with the numerical DFT results under varying electric field orientations. For (InP)77 quantum dots, the ΔE shows a clear parabolic response to the field applied in the x direction, peaking when the field is absent. This pattern means the spectral peak consistently shifts to lower energies, no matter the direction of the field. Along the y and z axes, however, the response is more complex, combining both linear and nonlinear behaviors. When the field is aligned with the z axis, the energy shift curve becomes asymmetric, and a slight shift to higher energy is observed at stronger positive fields. Along y, larger changes in the dipole (1.3663 a.u.) result in an even more pronounced blue shift, with the parabola's symmetry notably offset. These observations demonstrate that, despite homogeneousness, the field response of InP QDs can be strongly directional, which is consistent with prior reports for other types of nanocrystals, such as CdSe, where field alignment and nanocrystal orientation both significantly influence the Stark effect.43
 | ||
| Fig. 3 Field-dependent emission energy ΔE for (a) (InP)77-E, (b) (InP)10(ZnSe)67-E, and (c) (InP)27(ZnSe)50-E. Calculated data points (black, red, blue) indicate DFT results for electric fields applied along x, y, and z axes, respectively. The corresponding colored curves show theoretical fits based on the analytic eqn (4)–(6). The date above the boundary line indicates a blue shift, while the area below it indicates a red shift. | ||
For (InP)10(ZnSe)67 QDs, core/shell nanocrystals, the field-induced emission energy variation is mainly quadratic in the x direction, but shows a strong linear shift along z, resulting in red or blue shifts depending on the field orientation. With the field along y, both quadratic and linear tendencies appear, leading to an asymmetric curve, though the overall magnitude of shift is less than in the linear-dominated case.
For (InP)27(ZnSe)50 (Fig. 3c), the shift follows a broadly similar pattern to (InP)77 across all three field directions. Overall, these comparisons indicate that the observed field sensitivity of the fluorescence spectrum depends not only on the direction of the applied field, but also on the internal structure and core thickness of the quantum dots. Adjusting the core size or composition can thus serve as a practical way to tune Stark shifts in engineered QD systems.
3.3 Spatial separation of electrons and holes in core/shell quantum dots
The nature of the Stark effect in fluorescence emission is dictated by the behavior of the dipole moment change upon excitation. When this change is close to zero, the Stark shift follows a purely quadratic trend; when it is large, a predominantly linear dependence appears, while most cases exhibit a blend of both characteristics. This dipole change is fundamentally linked to the spatial redistribution of positive and negative charges after exciton formation. Specifically, it reflects the intrinsic dipole moment of the exciton p0i, proportional to the average electron–hole distance at zero field (D0i, where i = x, y, z), as expressed by p0i = qD0i, with q as the elementary charge.19,44,45 The centroid-based electron–hole separation Di, where i = x, y, z, can be defined as the difference between the mean positions of electrons (X/Y/Ze) and holes (X/Y/Zh):| Dx = Xh − Xe = ∫xρh(r)dr − ∫xρe(r)dr | (7-1) |
| Dy = Yh − Ye = ∫yρh(r)dr − ∫yρe(r)dr | (7-2) |
| Dz = Zh − Ze = ∫zρh(r)dr − ∫zρe(r)dr | (7-3) |
 → S1 excitation is dominated by a HOMO → LUMO transition, accounting for around 95% (listed in Table 1) of the transition character. Fig. 4 displays the spatial distribution of electrons and holes, as well as the relevant molecular orbitals at zero field, generated with Multiwfn.47,48 The close similarity between the electron/hole and orbital distributions supports this simplified model, with additional perspectives available in SI (see Fig. S2 and S3).
→ S1 excitation is dominated by a HOMO → LUMO transition, accounting for around 95% (listed in Table 1) of the transition character. Fig. 4 displays the spatial distribution of electrons and holes, as well as the relevant molecular orbitals at zero field, generated with Multiwfn.47,48 The close similarity between the electron/hole and orbital distributions supports this simplified model, with additional perspectives available in SI (see Fig. S2 and S3).
 | ||
| Fig. 4 Electron and hole spatial distributions, HOMO, and LUMO at zero field of (a) (InP)77-E, (b) (InP)10(ZnSe)67-E and (c) (InP)27(ZnSe)50-E. | ||
Using eqn (7), the computed initial electron–hole spatial separations D0i (in Å) at zero field are obtained: 0.000 (x), 2.477 (y), −0.383 (z) for (InP)77; 0.004, 1.179, 4.213 for (InP)10(ZnSe)67; 0.000, −2.700, −0.365 for (InP)27(ZnSe)50. These correspond to the intrinsic exciton dipole moment p0i (in a.u.): 0.000 (x), 4.502 (y), −0.696 (z) for (InP)77; 0.007, 2.190, 7.832 for (InP)10(ZnSe)67; 0.000, −4.972, −0.671 for (InP)27(ZnSe)50. By comparison, changes of dipole moment Δµ0i fitted via Stark shift analysis (see Table 1) are smaller, highlighting the fact that centroid-based separation (carried out by Multiwfn) uses unrelaxed excited-state densities, essentially an instantaneous snapshot after excitation, whereas Stark-fit values reflect post-relaxation densities, thus providing a more accurate physical representation. This distinction explains why direct experimental determination of electron–hole separation is often challenging, and why many studies rely on Stark effect measurements to infer dipole characteristics.
Under applied electric fields, the separation between electrons and holes is dynamically modulated: the field can either stretch or compress this distance, as summarized in Tables S4–S6 (see SI). Fig. 5 presents how the emission energy ΔE (left axis) and electron–hole separation Di (right axis) evolve with field strength. Notably, ΔE changes in a quadratic or linear function with the field, while Di changes linearly. There is a clear anti-correlation: as |Di| decreases, ΔE increases and reaches a maximum near |Di| = 0. This pattern matches findings from studies on geometry-dependent Stark effects in other nanostructures, such as GaAs quantum dots.17 In these, systems with zero initial electron–hole offset exhibit symmetric (parabolic) Stark responses, while those with pre-existing charge separation display asymmetric shifts. To more clearly demonstrate the influence of the electric field on dipole alignment, Fig. 6 presents the distribution of electrons and holes under various electric fields in the x-axis for (InP)77. The results of the other two structures belonging to the x and y directions, respectively, are depicted in Fig. S4 and S5 of the SI. Although the differences are subtle, a careful comparison still reveals that the applied fields do not affect the symmetry of the holes and electrons, but just slightly shift the distribution of the electrons and holes (the holes move along the direction of the electric field, while the electrons move in the opposite direction of the electric field).
 | ||
| Fig. 5 Relationship between emission energy (ΔE, left Y-axis) and electron–hole separation (Di for x, y, z; right axis) in (a) (InP)77-E, (b) (InP)10(ZnSe)67-E and (c) (InP)27(ZnSe)50-E. | ||
 | ||
| Fig. 6 Distribution of holes and electrons under various electronic fields in the x-axis for (InP)77-E. A vivid diagram that presents the interaction between the electric field and the dipole aligns is given in Fig. S6 of the SI. For all studied QDs, the initial x-direction electron–hole separation is negligible, so an electric field in this axis always increases |Dx|, resulting in a consistent red shift. Along y and z, larger separations exist at zero field. If the external field aligns with D0i, the electron and hole are pulled further apart (red shift); if opposed, the two are pushed together, potentially producing a blue shift. This blue shift ceases once the separation reaches zero, after which further field application increases |Di| again, restoring the red shift. Overall, these data clearly demonstrate the inverse relationship between emission energy and spatial charge separation, consistent with earlier experimental observations.49–51 | ||
Fig. 5b shows that for (InP)10(ZnSe)67, ΔE exhibits a linear dependence on the z-oriented electric field. This occurs because |D0z| is already large (4.213 Å) at zero field, so the field range used cannot reduce the electron–hole distance to zero or create a ΔE maximum. This substantial separation stems from the intrinsic electronic arrangement of the core/shell structure. Fig. 7 illustrates the total and core-projected density of states for (InP)77, (InP)10(ZnSe)67, and (InP)27(ZnSe)50 QDs. In the pure (InP)77, two projected density distributions were made, corresponding to the (InP)10 (blue line) and (InP)27 (red line) at the core, respectively. Although the composition of the core atoms was set to be uniform, the InP/ZnSe core/shell structure shows a greater contribution of the core to the HOMO and LUMO levels than pure InP. This is because the pure (InP)77 can be regarded as the type I energy band structure with the shell layer removed.51 The composition of its HOMO and LUMO does not show any significant localization but exhibits something related to the number of atoms.
 | ||
| Fig. 7 Total and core-projected density of states for (a) (InP)77-E, (b) (InP)10(ZnSe)67-E, and (c) (InP)27(ZnSe)50-E. | ||
InP, which forms the core, has a narrower band gap than ZnSe, resulting in higher-lying HOMO and lower-lying LUMO relative to the shell. As a result, InP/ZnSe quantum dots generally display a type-I band alignment, confining both electrons and holes to the core region.52–54 However, in (InP)10(ZnSe)67, the HOMO remains predominantly localized in the core (∼70%), while the LUMO is delocalized between the core and shell (48% core, 52% shell), indicating a hybridized state. This finding is corroborated by orbital distributions in Fig. 4 and aligns with previous observations that energy level proximity between core and shell leads to hybridization.55 The minimal LUMO offset in (InP)10(ZnSe)67 QDs gives rise to characteristics similar to quasi-type-II nanostructures, such as CdSe/CdS with small cores.56 In contrast, both frontier orbitals in (InP)27(ZnSe)50, are strongly core-localized (85% HOMO, 60% LUMO), typical of type-I alignment. Recent works confirm that shrinking InP core size57 or expanding the ZnS shell thickness58 decreases the band offset between core and shell. In larger quantum dots, the energy band distribution of the core and shell material is closer to that of the bulk material, so the energy level distribution may be closer to the assumed situation (as shown in Fig. S7), and thus the localized states will also exist.
In addition, the atomic composition of the density of states is also given in Fig. S8 of the SI. In pure (InP)77, the occupied orbitals (valence band) are mainly contributed by P atoms, while the unoccupied orbitals (conduction band) are more dominated by In. Upon the addition of the ZnSe shell to the InP system (going from (InP)77 to (InP)10(ZnSe)67 and (InP)27(ZnSe)50), the bandgap for the system decreases (by 0.92 eV and 0.26 eV), as anticipated due to the ability for the wavefunction to diffuse into the shell. Examination of the density of states plot for the (InP)10(ZnSe)67 structure shows that the partial density of states of In atoms and P atoms is significantly lower than that of Zn atoms and Se atoms due to the difference in the number of atoms. The occupied orbitals are mainly contributed to by Se atoms, except that the HOMO is derived from P. The unoccupied orbitals are more dominated by Zn. In (InP)27(ZnSe)50, the partial density of states of In atoms and P atoms have risen than those in (InP)10(ZnSe)67. The occupied orbitals are also mainly contributed to by Se atoms and P atoms, except that the HOMO is derived from P. The unoccupied orbitals are more dominated by Zn and In. The above results are essentially consistent with the results of the core/shell project density of states.
The partial band delocalization in (InP)10(ZnSe)67 favors electron–hole separation under an applied field. Depending on the field direction, this can push charge carriers toward or away from the interface, resulting in blue or red shifts in the emission spectrum, respectively. Behavior reminiscent of the quantum-confined Stark effect (QCSE) observed in other colloidal quantum dots and nanorods.51 Typically, type-I structures show a parabolic (quadratic) response to field strength, while type-II systems tend to exhibit a more linear dependence.
According to experimental studies, Mei et al.10 found a redshift of 10 nm in electroluminescence compared to photoluminescence in blue pure InP quantum dots, which belong to the Type I band structure. Suh et al.11 also observed a significant redshift and broadening in the electroluminescence spectra of blue InP/ZnS QLEDs. The core and shell sizes of the samples used in the experiment are 1.80 nm and 4.95 nm. In addition, Yu et al. reported a maximum redshift of 19 nm (from 465 to 484 nm)12 in a blue InP/ZnS QLED. The InP core and ZnS shell sizes of the samples used in the experiment are 2.50 nm and 4.80 nm. Due to the differences in the shell material, we cannot directly determine which type of band distribution the above two InP/ZnS QDs belong to. However, regardless of the type of energy band structure it belongs to, the spectrum generally undergoes a redshift in most cases when an electric field is applied (see Fig. 3), unless the direction and magnitude of the applied electric field are strictly controlled. This is in correspondence with the redshift phenomenon observed in the above three experiments.
4 Conclusions
First-principles calculations were used to evaluate the Stark shifts of fluorescence spectra in InP core and InP/ZnSe core/shell quantum dots subjected to varying field strengths and orientations. Three classes of field-dependent spectral shifts: quadratic, linear, and mixed modes were revealed. Pure quadratic shifts arise when the dipole moment change upon excitation is negligible, while large dipole changes yield predominantly linear behavior. Intermediate cases display both effects.The permanent exciton dipole, which depends on the intrinsic electron–hole separation at zero field, is central to understanding these effects. Analysis of excited-state densities provides quantitative insight: along the x axis, the electron–hole separation is negligible at zero field, so any applied field increases this distance and induces a red shift. Along y and z, initial separations are more substantial. A field aligned from electron to hole simplifies the distance (leading to a redshift), while an opposing field can reduce separation and cause blue shifts. Across all cases, the emission energy increases as the electron–hole separation decreases, with a maximum near zero separation.
The magnitude of intrinsic electron–hole separation is dictated by the quantum dot's electronic structure. In (InP)10(ZnSe)67, the small core and band structure promote quasi-type-II behavior with pronounced electron–hole separation, especially along z. For (InP)27(ZnSe)50, and pure (InP)77, both charge carriers remain largely confined to the core, resembling type-I alignment. The calculations demonstrate that adjusting the thickness of the InP core and the ZnSe shell provides a route for tuning the magnitude and character of Stark shifts in InP/ZnSe quantum dots. In fact, the Stark effect of the fluorescence spectra can also influence the radiative lifetime of quantum dots as well as the efficiency of the device. This is a topic that needs to be explored in the future.
Author contributions
Ning Du: conceptualization; data curation; methodology; funding acquisition; and writing – original draft. Hongshan Chen: resources; supervision; and writing – review & editing.Conflicts of interest
There are no conflicts of interest to declare.Data availability
The data supporting this article are included within the main text or the supplementary information (SI). Supplementary information: explicit energy equations for fields oriented along the x, y, and z axes, schematic diagram of electron transition, electron and hole spatial distributions, electronic energy levels of selected III–V and II–VI semiconductors, total and atomic composition of the density of states, computed DFT energy of -state and S1-state, electron–hole separation lengths, coordinates of all three structures. See DOI: https://doi.org/10.1039/d5ra06323j.
-state and S1-state, electron–hole separation lengths, coordinates of all three structures. See DOI: https://doi.org/10.1039/d5ra06323j.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (NSFC, Grant No. 12404464) and Northwest Normal University of China (NWNU-LKQN2022-06). The authors also appreciate Brandi M. Cossairt for offering the coordinate file of (InP)77 cluster.References
- J. Song, O. Wang, H. Shen, Q. Lin, Z. Li, L. Wang, X. Zhang and L. S. Li, Adv. Funct. Mater., 2019, 29, 1808377 CrossRef.
- Y. Deng, F. Peng, Y. Lu, X. Zhu, W. Jin, J. Qiu, J. Dong, Y. Hao, D. Di, Y. Gao, T. Sun, M. Zhang, F. Liu, L. Wang, L. Ying, F. Huang and Y. Jin, Nat. Photonics, 2022, 16, 505–511 CrossRef CAS.
- G. Almeida, R. F. Ubbink, M. Stam, I. du Fossé and A. J. Houtepen, Nat. Rev. Mater., 2023, 8, 742–758 CrossRef CAS.
- Z. Cui, D. Yang, S. Qin, Z. Wen, H. He, S. Mei, W. Zhang, G. Xing, C. Liang and R. Guo, Adv. Opt. Mater., 2023, 11, 2202036 CrossRef CAS.
- H. Seo, J. H. Park, O. H. Kwon, O. P. Kwon, S. K. Kwak and S.-W. Kim, Nanoscale Adv, 2020, 2, 5615–5622 RSC.
- H. Li, Y. Bian, W. Zhang, Z. Wu, T. K. Ahn, H. Shen and Z. Du, Adv. Funct. Mater., 2022, 32, 2204529 CrossRef CAS.
- W.-C. Chao, T.-H. Chiang, Y.-C. Liu, Z.-X. Huang, C.-C. Liao, C.-H. Chu, C.-H. Wang, H.-W. Tseng, W.-Y. Hung and P.-T. Chou, Comm. Mater., 2021, 2, 96 CrossRef CAS.
- H. Zhang, X. Ma, Q. Lin, Z. Zeng, H. Wang, L. S. Li, H. Shen, Y. Jia and Z. Du, J. Phys. Chem. Lett., 2020, 11, 960–967 CrossRef CAS PubMed.
- K.-H. Kim, J.-H. Jo, D.-Y. Jo, C.-Y. Han, S.-Y. Yoon, Y. Kim, Y.-H. Kim, Y. H. Ko, S. W. Kim, C. Lee and H. Yang, Chem. Mater., 2020, 32, 3537–3544 CrossRef CAS.
- G. Mei, Y. Tan, J. Sun, D. Wu, T. Zhang, H. Liu, P. Liu, X. W. Sun, W. C. H. Choy and K. Wang, Appl. Phys. Lett., 2022, 120, 091101 CrossRef CAS.
- Y. H. Suh, S. Lee, S. M. Jung, S. Y. Bang, J. Yang, X. B. Fan, S. Zhan, C. Samarakoon, J. W. Jo, Y. Kim, H. W. Choi, L. G. Occhipinti, T. H. Lee, D. W. Shin and J. M. Kim, Adv. Opt. Mater., 2022, 10, 2102372 CrossRef CAS.
- P. Yu, Y. Shan, S. Cao, Y. Hu, Q. Li, R. Zeng, B. Zou, Y. Wang and J. Zhao, ACS Energy Lett., 2021, 6, 2697–2703 CrossRef CAS.
- J. P. A. de Jesus, M. Z. Jimenez and F. d. A. La Porta, Comp. Mater. Sci., 2021, 188, 110147 CrossRef CAS.
- D. S. Daibagya, S. A. Ambrozevich, I. A. Zakharchuk, A. V. Osadchenko, M. S. Smirnov, O. V. Ovchinnikov and A. S. Selyukov, Opt. Mater., 2024, 150, 115297 CrossRef CAS.
- M. Usman, J. Phys. Condens. Matter., 2019, 31, 415503 CrossRef CAS PubMed.
- B. Lv, T. Zhu, Y. Tang, Y. Lv, C. Zhang, X. Wang, D. Shu and M. Xiao, Phys. Rev. Lett., 2021, 126, 197403 CrossRef CAS PubMed.
- C. Heyn, L. Ranasinghe, M. Zocher and W. Hansen, J. Phys. Chem. C, 2020, 124, 19809–19816 CrossRef CAS.
- D. Rana and A. Materny, Spectrochim. Acta. A, 2021, 253, 119565 CrossRef CAS PubMed.
- J. D. Mar, J. J. Baumberg, X. L. Xu, A. C. Irvine and D. A. Williams, Phys. Rev. B, 2017, 95, 201304 CrossRef.
- L. Alaerts, Y. Xiong, S. Griffin and G. Hautier, Phys. Rev. Mater., 2024, 8, 106201 CrossRef CAS.
- J. Seufert, M. Obert, M. Scheibner, N. A. Gippius, G. Bacher, A. Forchel, T. Passow, K. Leonardi and D. Hommel, Appl. Phys. Lett., 2001, 79, 1033–1035 CrossRef CAS.
- L. Zhang, B. Lv, H. Yang, R. Xu, X. Wang, M. Xiao, Y. Cui and J. Zhang, Nanoscale, 2019, 11, 12619–12625 RSC.
- H. Huang, D. Csontosová, S. Manna, Y. Huo, R. Trotta, A. Rastelli and P. Klenovský, Phys. Rev. B, 2021, 104, 165401 CrossRef CAS.
- E. Alexander, M. Kick, A. R. McIsaac and T. Van Voorhis, Nano Lett., 2024, 24, 7227–7235 CrossRef CAS PubMed.
- N. Park, F. W. Eagle, A. J. DeLarme, M. Monahan, T. LoCurto, R. Beck, X. Li and B. M. Cossairt, J. Chem. Phys., 2021, 155, 084701 CrossRef CAS PubMed.
- E. Cho, H. Jang, J. Lee and E. Jang, Nanotechnology, 2013, 24, 215201 CrossRef PubMed.
- E. Cho, T. Kim, S.-m. Choi, H. Jang, K. Min and E. Jang, ACS Appl. Nano Mater., 2018, 1, 7106–7114 CrossRef CAS.
- L.-W. Wang and J. Li, Phys. Rev. B, 2004, 69, 153302 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. C.02, Wallingford, CT, 2019 Search PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- P. T. Snee, J. Phys. Chem. C, 2021, 125, 11765–11772 CrossRef CAS.
- A. Hassan, X. Zhang, C. Liu and P. T. Snee, J. Phys. Chem. C, 2018, 122, 11145–11151 CrossRef CAS.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310 CrossRef CAS.
- W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284–298 CrossRef CAS.
- M. E. Bathen, L. Vines and J. Coutinho, J. Phys. Condens. Matter., 2020, 33, 075502 CrossRef PubMed.
- P. K. Bhattacharyya, Comput. Theor. Chem., 2015, 1057, 43–53 CrossRef CAS.
- D. M. Bishop, Rev. Mod. Phys., 1990, 62, 343–374 CrossRef CAS.
- D. Rayane, A. R. Allouche, E. Benichou, R. Antoine, M. Aubert-Frecon, P. Dugourd, M. Broyer, C. Ristori, F. Chandezon, B. A. Huber and C. Guet, Eur. Phys. J. D, 1999, 9, 243–248 CrossRef CAS.
- F. C. Grozema, R. Telesca, H. T. Jonkman, L. D. A. Siebbeles and J. G. Snijders, J. Chem. Phys., 2001, 115, 10014–10021 CrossRef CAS.
- P. Kjellberg, Z. He and T. Pullerits, J. Phys. Chem. B, 2003, 107, 13737–13742 CrossRef CAS.
- I. Zhigulin, J. Horder, V. Ivády, S. J. U. White, A. Gale, C. Li, C. J. Lobo, M. Toth, I. Aharonovich and M. Kianinia, Phys. Rev. Appl., 2023, 19, 044011 CrossRef CAS.
- Y. Xie, Y. Cui, L. Zhang and M. Yang, J. Phys. Chem. C, 2023, 127, 2603–2611 CrossRef CAS.
- S. A. Empedocles and M. G. Bawendi, Science, 1997, 278, 2114–2117 CrossRef CAS PubMed.
- T. Karin, X. Linpeng, M. M. Glazov, M. V. Durnev, E. L. Ivchenko, S. Harvey, A. K. Rai, A. Ludwig, A. D. Wieck and K.-M. C. Fu, Phys. Rev. B, 2016, 94, 041201 CrossRef.
- M. Sugisaki, H.-W. Ren, S. V. Nair, K. Nishi and Y. Masumoto, Phys. Rev. B, 2002, 66, 235309 CrossRef.
- X.-Y. Liu, Z.-W. Li, W.-H. Fang and G. Cui, J. Phys. Chem. A, 2020, 124, 7388–7398 CrossRef CAS PubMed.
- T. Lu and F. Chen, J. Comp. Chem., 2011, 33, 580–592 CrossRef PubMed.
- T. Lu, J. Chem. Phys., 2024, 161, 082503 CrossRef CAS PubMed.
- A. W. Achtstein, A. V. Prudnikau, M. V. Ermolenko, L. I. Gurinovich, S. V. Gaponenko, U. Woggon, A. V. Baranov, M. Y. Leonov, I. D. Rukhlenko, A. V. Fedorov and M. V. Artemyev, ACS Nano, 2014, 8, 7678–7686 CrossRef CAS PubMed.
- J. Muller, J. M. Lupton, P. G. Lagoudakis, F. Schindler, R. Koeppe, A. L. Rogach, J. Feldmann, D. V. Talapin and H. Weller, Nano Lett., 2005, 5, 2044–2049 CrossRef CAS PubMed.
- K. Park, Z. Deutsch, J. J. Li, D. Oron and S. Weiss, ACS Nano, 2012, 6, 10013–10023 CrossRef CAS PubMed.
- Q. Zheng, J. Wang, F. Huang, Z. Huang, S. Tian, Q. Chen, Y. Pei, K. Zheng and J. Tian, ACS Energy Lett., 2024, 9, 2358–2366 CrossRef CAS.
- S. Kim, J. Park, T. Kim, E. Jang, S. Jun, H. Jang, B. Kim and S. W. Kim, Small, 2010, 7, 70–73 CrossRef PubMed.
- P. Cavanaugh, X. Wang, M. J. Bautista, I. Jen-La Plante and D. F. Kelley, J. Chem. Phys., 2023, 159, 134704 CrossRef CAS PubMed.
- K. Jain, S. Kishor, K. S. Singh, M. Odelius and L. M. Ramaniah, J. Phys. Chem. C, 2021, 125, 27046–27057 CrossRef CAS.
- D. Kong, Y. Jia, Y. Ren, Z. Xie, K. Wu and T. Lian, J. Phys. Chem. C, 2018, 122, 14091–14098 CrossRef CAS.
- D. Respekta, P. Schiettecatte, L. Giordano, N. De Vlamynck, P. Geiregat, J. I. Climente and Z. Hens, ACS Nano, 2025, 19, 19831–19840 CrossRef PubMed.
- S. Savchenko, A. Vokhmintsev, M. Karabanalov, Y. Zhang, A. Henaish, A. Neogi and I. Weinstein, Phys. Chem. Chem. Phys., 2024, 26, 18727–18740 RSC.
| This journal is © The Royal Society of Chemistry 2025 |