Electrode selection framework for oxygen evolution reaction catalysts involving density functional theory and finite element method

Abstract

The design of durable and high-performance electrodes for the oxygen evolution reaction (OER) is important for producing green hydrogen via water electrolysis. In this work, we present a multiscale modeling framework that effectively integrates Density Functional Theory (DFT) with Finite Element Modeling (FEM) for the electrodes of polymer electrolyte membrane electrolysers. The framework connects atomic-scale mechanisms of the four electrocatalysts with their half-cell-level redox performance. The redox performance of the catalyst was modelled using the FEM. Cyclic voltammograms (CV) of IrO₂, RuO₂, Co–Pt, and Ni–Fe are obtained and validated with experimental results. The atomic-scale calculations of all electrocatalysts provide agreeable electronic structure, surface energetics, and reaction intermediates of the electrocatalysts without any experimental input. The half-cell system-level behavior and atomistic characteristics are obtained by linking quantum-level reaction pathways with continuum-scale electrochemical performance of electrodes. The combination of DFT and CV framework helps to compare and identify activity-limiting steps of the catalysts. The cell polarization data obtained using the half-cell studies specific to individual electrode performance are validated with results obtained by the proposed framework. A perovskite-based material is used as a baseline to compare the characteristics of the OER. Our predictive design framework shows RuO₂ as a promising OER catalyst due to its low HOMO–LUMO gap, optimal structure (2.686 Å), acceptable exchange current density (3.3 × 10⁻⁸ A cm⁻²) and double layer capacitance (0.36 F m⁻²), charge distribution, and enhanced reaction kinetics. The results are in good agreement with the experimental findings reported in the literature.

---

1. Introduction

The combustion of fossil fuels contributes to over 75% of global greenhouse gas emissions, causing a profound crisis in climate stability and undermining the foundations of long-term energy security.^1,2 The global energy market is heavily reliant on fossil fuels, a trajectory marked by significant environmental and geopolitical concerns. As the worldwide energy demand continues to rise, it is imperative to transition toward green and renewable energy sources. Green hydrogen has recently emerged as a transformative fuel and energy vector in the energy market. It has been widely adopted in the transportation, power generation, and heavy industries. Water electrolysis stands out among the green hydrogen production methods, offering a remarkably clean and viable solution to generate high-purity hydrogen without any CO₂ emissions.^2–4 Both alkaline and acidic electrolysis configurations are suitable for clean hydrogen production. Both electrolyzers have been studied extensively over the past two decades. Alkaline hydrogen electrolyzers offer advantages, such as reduced operational costs, improved safety, and better performance under high current densities. However, they are unsuitable for dynamic applications.^5–7 Proton Exchange Membrane Water Electrolyzers (PEMWEs) facilitate the generation of hydrogen free from pollutants. PEMWE stacks are compact, efficient, possess a modular design, and can be adjusted to dynamic operational conditions. In accordance with ambitious global decarbonization goals, they have been identified as candidates for accelerating the commercial scalability of hydrogen technology. Therefore, the Department of Energy has set a target to reduce the cost of electrolyzers by 30% by 2030.⁸

Hydrogen produced via these two electrochemical pathways has the potential to serve as a clean fuel for fuel cells and combustion engines. The emerging energy transition toward hydrogen depends on identifying suitable electrocatalysts and charting a recipe for sustainable components for the PEMWE catalyst layers. However, remarkable progress has been made in the development of electrocatalysts since the year 2000. This is primarily driven by a deeper understanding of the surface reaction mechanisms at the quantum level. Noble metal oxides, such as IrO₂ and RuO₂ have been identified as baseline standards for the next generation of oxygen evolution reactions (OER) in acidic environments.^9–11 The binding energies of these two catalysts with water molecules and critical reaction intermediates, such as *OH, *O, and *OOH species, exhibit higher water splitting efficiencies. Furthermore, these two electrocatalysts have d-band centers and robust metal–oxygen covalency, which help to improve catalytic turnover rates.^12,13 For example, IrO₂ catalysts deliver exceptional mass activities, which are higher than 1.0 A mg⁻¹ at 1.6 V (vs. RHE) at low overpotentials approximately (315 mV) and current density (10 mA cm⁻²). Cyclic voltammetry (CV) profiles typically reveal broad redox features associated with Ir³⁺/Ir⁴⁺ transitions and shifts in peak current density during cycling highlight critical structural reconstruction, rationale for higher activity, and surface oxidation processes.^14–16 However, long-term durability or performance is often compromised by dissolution and morphological instability, particularly under rigorous potential changes. Therefore, quantum-based models are required to explain the water-splitting mechanism. The rationale for choosing and comparing these different catalyst systems is based on their electrochemical performance, availability, cost, and structural diversity as reported in the literature.¹⁷ A summary of these materials and their properties is presented in Table 1.

Table 1 Selected catalysts and their properties^a,b,c,d,e,f

Catalyst system	Advantages	Issues	OER activity	TOF (s^−1)	Stability (T50% or chrono duration)	Cost ($ per g)	Degradation rate (loss/10 h)	Ref.
a OER activity (η @ 10 mA cm^−2).b η: overpotential required to reach 10 mA cm^−2.c TOF: turnover frequency – reflects intrinsic activity.d T50%: time to 50% activity drop; chronoamperometry/stability test.e Cost: market estimate as of recent literature or suppliers (2022–2024).f Degradation rate: approximated based on chronoamperometry or cycling tests in OER conditions.
IrO2	High intrinsic activity, stable in acid	Expensive, rare	0.28–0.35 V	0.1–0.2	>100 h stable	200–300	∼2–5% in 10 h	5
RuO2	High conductivity, fast kinetics	Poor long-term stability	0.25–0.30 V	0.05–0.1	∼10–20 h	100–150	∼10–20% in 10 h	6
Ni–Fe LDH	Abundant, cost-effective	Lower activity in acid	0.29–0.35 V	0.02–0.05	>200 h (alkaline)	<$1	<1% in 24 h (alkaline)	7
Co–Pt alloy	Good synergy, conductivity	Pt cost, underexplored	0.27–0.32 V	∼0.08	∼50 h	∼$30	∼5–8% in 10 h	58
LaNiO3	Stable perovskite, flexible doping	Synthesis complexity	0.30–0.38 V	∼0.01–0.03	50–100 h (stable in alkaline)	$2–3	∼3–5% in 10 h	59

---

Core–shell structures, such as RuO₂@IrO₂ provide enhanced durability by addressing performance metrics, including the electrochemical catalyst surface area and activity. In such systems, the Ir shell helps protect the Ru core from harsh corrosive electrochemical environments, thereby conserving the catalytic function for longer operation.^18–20 These architectures showed low overpotentials (∼275 mV at 10 mA cm⁻²) and acceptable redox hysteresis in CV scans, even after durability tests, demonstrating enhanced charge transfer and stability.¹⁶ For the hydrogen evolution reaction (HER), Pt is a benchmark catalyst that efficiently enables hydrogen oxidation and reduction. In contrast, PtCo binary alloys improve oxygen evolution reaction (OER) performance in alkaline media by promoting the formation of Co-oxo intermediates. The electronic interactions between the Co 3d and Pt 5d orbitals modulate the density of states, thereby improving the adsorption energies and catalytic activity. CV analyses of Co–Pt systems display symmetric Co²⁺/Co³⁺ redox peaks and quasi-reversible HER behavior on Pt, although the HER onset potential often shifts positively compared to that of pure Pt, highlighting the presence of synergistic effects. However, challenges remain, including dynamic surface segregation and the need for robust quantum-level modeling to fully interpret these behaviors.^21–25

Most experimental studies have reported a loss of catalytic activity due to Pt migration and Co leaching. This reveals an urgent need to expedite a quantum-level understanding of alloy configurations to assess their instability. For alkaline electrolyzers, Ni–Fe (oxy)hydroxides are widely recognized as electrocatalysts for OER. Their activity depended on the ability of Fe to regulate the electronic structure of Ni. A clear DFT calculation is required to enhance Ni–O covalency and destabilization of Ni sites. Several CVs demonstrate sharp reversible redox peaks linked to both Ni²⁺/Ni³⁺ and Ni³⁺/Ni⁴⁺ transitions, which evolve during potential cycling. The experimental results^26–28 reported show the emergence of catalytically active γ-NiOOH. Adding Fe reduces the overpotential at which Ni²⁺/Ni³⁺ and Ni³⁺/Ni⁴⁺ transitions occur and elevates peak current densities. These results are consistent with the accelerated charge transfer kinetics reported elsewhere. Despite the good performance of Ni–Fe, degradation during prolonged CV cycling, as evidenced by redox peak broadening and baseline current drift, highlights structural reorganization or Fe leaching, emphasizing the critical need for operando quantum chemical studies to monitor evolving surface states.

Recently, Perovskite oxides with the formula ABO₃ have gained attention as OER catalysts. ABO₃ is largely altered or influenced by the B-site cations. Likewise, in LaNiO₃ (LNO), the electrocatalytic performance is governed by Ni cations,^5–7 particularly the Ni³⁺ species. This species transition is crucial for the OER. Similar to other electrocatalysts, quantum chemical descriptors, including orbital occupancy, charge transfer energies, and oxygen vacancy formation energies, are directly linked to the catalytic efficiency and require thorough computational analysis and.^29,30 LaNiO₃ demonstrates moderate OER activity compared to high-performing perovskites such as Ba_0.5Sr_0.5Co_0.8Fe_0.2O_3−δ (BSCF). It shows pseudocapacitive behavior in the CV analysis, which highlights the reversible Ni³⁺/Ni⁴⁺ transitions. The observed surface amorphization suggests that LaNiO₃ acts more as a dynamic precursor than as a static phase during cycling. No OER models that can correlate the performance of LNO with alloy catalysts are available in the literature.

Despite extensive experimental investigations of all four electrocatalysts, our understanding of their behavior at the quantum level remains limited.^31–39 This knowledge gap leads to the pressing need for a design framework that interlinks cyclic voltammetry (CV) data with an orbital-resolved understanding of the electronic structures. Density Functional Theory (DFT) calculations are particularly adept at navigating the complexities of electron correlation and solvent polarization, making them invaluable for exploring these phenomena. In parallel, employing finite element methods to model CV allows for precise redox fingerprinting of active sites, providing a quantitative tool to analyze their performance. A direct comparison of the experimental CV results with ab initio simulations can illuminate the evolution of these active sites under operating conditions, enriching our understanding of their dynamic behavior. Furthermore, this integrated approach promises to unravel the intricate interplay between spin states and catalytic activity.^40–46 The variability observed in the experimental results, particularly regarding the polarization behavior during current–voltage sweeps, adds another layer of complexity and highlights the necessity of comprehending how polarization rearrangements transpire during these processes. Therefore, it is imperative to develop robust theoretical workflows to bridge these significant gaps. These workflows should incorporate operando CV measurements and polarization data, informing sophisticated quantum models capable of capturing the nuanced details of the redox processes. This strategy has the potential to substantially advance the rational design of next-generation catalysts, ultimately propelling the field toward breakthroughs in efficiency and effectiveness. To address this research gap, the following objectives are outlined.

• Using DFT to study electronic properties, including the HOMO–LUMO energy levels, charge distributions, and bond lengths.

• Obtaining optimized molecular structure and bond lengths.

• Modeling Cyclic Voltammetry (CV) and polarization curves to compare and contrast the catalytic activity and stability of the electrochemical cell.

CV reveals redox events, active sites, and catalytic performance, whereas DFT provides the electronic structure and reaction pathways. Correlating CV peaks with DFT-predicted energy states links the redox processes to specific catalyst sites, facilitating redox fingerprinting. This integrated approach enhances our understanding of catalytic mechanisms and advances the rational design of more efficient catalysts. Additionally, modeling the polarization curve provides the kinetic losses in the layer, which requires a Butler–Volmer-driven approach. Operando cyclic voltammetry, quantum modeling, and polarization data are essential characterization tools that can accelerate the rational design of modern electrocatalysts.

2. Methods and materials

2.1 Theory

2.1.1 Density functional theory. Although several quantum-based methods have been employed to predict the redox characteristics of electrocatalysts, Ab initio methods based on solving the Schrödinger equation provide clear molecular insights. However, they are computationally expensive and unsuitable for alloy systems. Therefore, the Schrödinger equation and Hamiltonian operator underpin the electronic structure computations, offering accuracy at a high computational cost.^41–51 The DFT computations were based on the Kohn–Sham formulation. This provides an accurate and efficient computation of binary and ternary catalyst alloys. It has been widely adopted to predict the electronic structure and reaction pathways.^44–49 Such models lead to a many-electron system as non-interacting particles under a potential composed of Hartree, external, and exchange–correlation terms (eqn (1)):

v_ks^(r) = v_ext^(r) + v_H^(r) + v_xc^(r) (1)

where v_ext^(r) is the external potential due to the nuclei, v_H^(r) is the classical Hartree (electrostatic) potential representing electron–electron repulsion, v_xc^(r) is the exchange–correlation potential, accounting for quantum mechanical effects such as exchange interaction and electron correlation.

2.1.2 Cyclic voltammetry. Cyclic voltammetry (CV) is a powerful tool for evaluating electrocatalyst performance, particularly for quantifying the electrochemically active surface areas and optimizing catalyst design.^52–55 CV simulations provided the time-dependent electrochemical behavior of a cell comprising working and counter electrodes, where the working electrode was treated as a dynamic boundary subjected to a time-varying applied potential. The resulting current response arises from two contributions: (i) faradaic reactions, which involve charge transfer, and (ii) non-faradaic (capacitive) effects owing to double-layer charging. The Butler–Volmer equation describes the electrochemical kinetics at the electrode surface, whereas the Nernst–Planck equation, which accounts for both diffusion and migration, governs the mass transport of ionic species in the electrolyte. These coupled nonlinear partial differential equations are solved numerically using the finite element method (FEM), offering a high spatial and temporal resolution of species concentrations, electric potential, and current density throughout the cell. Fitting simulated current–voltage responses to experimental CV data enables the extraction of key electrochemical parameters, including diffusion coefficients. Charge transfer rate constants and exchange current densities: the simulation domain consisted of a 1D representation of the electrolyte, with length L corresponding to the effective diffusion layer thickness. To ensure numerical convergence and physical relevance, L is chosen to exceed the maximum diffusion layer thickness during the voltammetry sweep, given by (eqn (2))

L = 6√Dt_max (2)

where D is the diffusion coefficient and t_max is the duration of the cyclic voltammogram. The electroanalysis interface has chemical transport equations for the respective reactant and product species. Fick's second law is used as the domain equation to describe the chemical transport of the electro active species, and the equation (eqn (3)) is given belowwhere D_i is the diffusion coefficient of the species c_i and ∇c_i is the concentration gradient. At the bulk boundary (x = L), a uniform concentration, equal to the bulk concentration of the reactant, was assumed. Therefore, the product has zero concentration at the length, as in the bulk. The Butler–Volmer equation, which accounts for both anodic and cathodic polarizations, is used to model the redox process (eqn (4)):where, k₀ is the heterogeneous rate constant of the reaction, a_c is the cathodic transfer coefficient, η is the overpotential at the working potential of the redox couple.

Faraday's laws of electrolysis were then applied to compute the flux of the reactant and product species, which is proportional to the current density drawn from the cell. The equation below provides the details (eqn (5)).

Furthermore, the 1D approximation is computed because the total current is related to the current density. Thereby, the computed current is multiplied by the electrode area A, as given in the equation below (eqn (6)).

I_el = i_locA (6)

The polarization (iV) curve for the oxygen evolution reaction (OER) is an effective tool for assessing the electrocatalytic performance of the electrode materials proposed in this study. Our model generated a steady-state current density (j) against the applied potential (E) under controlled conditions. A key metric is the overpotential (η) required to reach a specified current density, which was obtained from the relevant literature and logit regression. The following sections detail the governing equations and thermodynamics, including calculations of the overall cell potential and overpotentials adjusted for the iR drop and reference electrode alignment. Overall cell potential was calculated using the method described by Chu and Srinivasan (eqn (7)).⁵⁷

V_cell = E_rev + η_act + η_ohmic + η_mt (7)

where E_rev is the reversible voltage, and MT is the activation, ohmic overpotential and mass transport overpotential. This equation describes the voltage loss, because the electrochemical reaction is not infinitely fast. At low currents, the reaction requires additional energy (voltage) to push electrons through the reaction barrier. By adding the activation, ohmic and mass transfer overpotential as given by,^56,57 eqn (7) can be rewritten as eqn (8)where R is the gas constant, T is the temperature (K), α is the charge transfer coefficient, n is the number of electrons, F is the Faraday constant, i is the current density (A cm⁻²), i₀ is the exchange current density (A cm⁻²), and R_ohmic is the resistance of membrane and the cell. Where, is the limiting current density.

3. Methods and modeling tools

3.1 DFT calculations

The molecular structures of IrO₂, RuO₂, Co–Pt, and Ni–Fe were constructed using Avogadro (v1.2.0) and pre-optimized using molecular mechanics. These initial geometries served as starting points for full quantum mechanical optimization in Gaussian or VASP. DFT calculations for all the four catalysts were performed using the Gaussian 16 software package. Geometry optimizations and electronic structure calculations were performed using the B3LYP hybrid functional, which offers a balance between computational efficiency and accuracy for systems involving transition metals. The calculations performed using Gaussian 16 were verified with ab initio simulations to confirm the reproducibility of the catalyst models. For the cluster catalyst models of IrO₂, RuO₂, Co–Pt, and Ni–Fe, calculations were performed using Gaussian 16 with the B3LYP hybrid functional and LANL2DZ basis sets for heavy atoms. Benchmark calculations were performed using B3LYP/Def2-TZVP on the IrOx molecule models. Key parameters, such as bond lengths and adsorption energies, were evaluated to validate the reliability of our approach. These results are in agreement with those of LANL2DZ. In systems containing 3d transition metals (Co, Ni, Fe), strong electron correlation effects were observed with the DFT + U approach. The Hubbard parameters were applied to the d-orbitals. The chosen initial U_eff values used in the computations were Co 3d: 3.2 eV; Ni 3d: 6.2 eV, and Fe 3d: 4.0 eV. Furthermore, all geometry optimizations and adsorption energy calculations were carried out with and without Hubbard correction to assess its impact. All the structures were verified to be minima via frequency analysis. For periodic slab calculations, the projector augmented wave (PAW) method with the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional was employed.

The DFT + U scheme was applied to 3d transition metals using the rotationally invariant approach for the U_eff parameters, as in Gaussian calculations. The modeled slabs consisted of atomic layers, where the bottom layers were fixed to the bulk positions to simulate the bulk environment, while the top layers and adsorbates were fully relaxed. Vacuum spacing is not included, as the aim is not to assess slab–slab interactions. Dipole corrections were applied along the surface normal to correct asymmetric charge distributions. Geometry optimizations converged until the residual forces were less than 0.02 eV Å⁻¹. The adsorption energies and electronic properties from the VASP calculations were consistent with those from the Gaussian molecular models, validating the chosen methods and parameters. All computational results were benchmarked against the available experimental data and previous theoretical studies for reliability. The LANL2DZ basis set with effective core potentials was used to account for scalar relativistic effects for catalysts, such as iridium oxide (IrOx) and cobalt–platinum alloy (Co–Pt). Lighter atoms were treated with the default 6-31G(d) basis set unless otherwise noted. All self-consistent field (SCF) procedures used tight convergence criteria, and quadratic convergence was enabled to ensure numerical stability.

3.2 Cyclic voltammetry

To assess and compare the OER performance of four electrocatalysts—RuO₂, IrO₂, Ni–Fe, and LaNiO₃ we selected them and followed a structured modeling approach for both cyclic voltammetry (CV) and polarization behavior based on the literature. The simulations were meticulously executed under acidic and alkaline electrolyte conditions (0.5–1 M H₂SO₄ and 2 M KOH, respectively),^55–61 reflecting the operational environment one would expect in a standard electrolyzer half-cell testing setup. The physicochemical properties and constants used in the CV and I–V curve generation are provided in Table 3. A time-based model for CV at a planar anode was developed using COMSOL Multiphysics 6.2. It uses the transport of diluted species across the cell. This simulation was aimed at the diffusion-controlled electrochemical reaction of a lone redox-active species in a 2D setting, ranging from the electrode surface from x = 0 to x = L = 100 μm. The Dirichlet boundary condition was applied to assess the oxidized species concentration at the bulk level. The simulation, too, has a time-dependent solver with a relative tolerance set at 10–4 with a time step of 0.01 s to track the current response during the sweep. A non-uniform triangular mesh approach was adopted as the computational domain was split into 700 elements, with a fine mesh. The element size was approximately 1 × 10–8 m. We diligently reconstructed the experimental CV and polarization (iV) curves and thoroughly validated them against established datasets to ensure the reliability of our findings. Concurrently, the polarization curves were modeled using MATLAB, where solving the Butler–Volmer equation under steady-state conditions, ensuring a solid foundation for our findings, derived the current–voltage relationships. To replicate each experimental curve, we sourced all the necessary parameters directly from the literature whenever possible. In instances where data was not complete, specifically regarding the exchange current densities of the Ni–Fe and LaNiO₃ system, we have applied the Tafel equation to estimate these values. In doing so, we maintained clarity in our approach, and meticulously fitted values with Tafel equations were integrated into our simulation framework, enabling us to effectively reproduce the observed electrochemical responses. The final curves not only closely matched their experimental counterparts but also underscored the robustness of our computational model. This thorough assessment functionally validates our chosen approach and reveals the dynamic performance characteristics of the selected electrocatalysts in the context of OER.

4. Results

An overall comparison of the DFT data reported in different studies is given in Tables 2, 4–7. Details were obtained using different optimization and imaging techniques. Hence, these numbers can be used as rough estimates to probe all four catalysts using the DFT-FEM framework. The selected results from this work were compared with values reported in the literature (Tables 1 and 2) to assess consistency and establish reference benchmarks.

Table 2 DFT parameters and their impact on catalytic activity reported in literature^a,b,c,d,e

Parameter	Co–Pt alloy	Pure Pt (benchmark)	Reference
a Electronic energy: represents the total ground-state energy after geometry optimization. Lower (more negative) values indicate higher thermodynamic stability, though excessively low values may reduce catalytic reactivity.b RMS gradient norm: measures the degree of convergence; values approaching zero confirm that the structure is optimized and lies near a true energy minimum on the potential energy surface.c Dipole moment: indicates molecular charge separation. Higher dipole moments improve electrostatic interaction with OER intermediates and facilitate electron transfer.d Mulliken charge: estimates partial atomic charges. Positive values on metal centers promote OH^− adsorption, while negative charges on oxygen atoms stabilize key reaction intermediates.e Bond length: denotes the distance between bonded atoms, typically metal–oxygen. Optimal bond lengths reflect a balanced structure, supporting both stability and catalytic activity.
Electronic energy	Intermediate; tuned via alloying	Lower stability for OOH/O binding	60
RMS gradient norm	∼0.01–0.02	∼0.01	Typical DFT convergence (VASP/Gaussian user guides; general convergence criterion <0.03)
Dipole moment	∼3 debye	∼2.5–3.0 debye	11
Mulliken charge	Co/Pt: +0.9 to +1.2e; O: −0.6e	Pt: +0.6–0.9e; O: −0.5 to −0.6e
M–O bond length	Co–O: ∼2.05 Å; Pt–O: ∼2.00 Å	Pt–O: ∼1.95–2.00 Å	62 and 63

---

4.1 DFT analysis of four catalysts

To effectively compare and contrast the electronic and structural properties pertinent to OER catalysis, DFT calculations were applied to four promising materials: IrO₂, RuO₂, CoPt, and FeNi and their results are provided in Tables 3–8. The calculations utilized the hybrid B3LYP functional (Becke, 3-parameter, Lee–Yang–Parr) along with the LANL2DZ basis set, chosen for its optimal shows higher computational efficiency and accuracy, particularly suitable for Co–Pt and Ni alloy systems. This approach facilitates the extraction of crucial electronic energy levels and optimized geometries, which are essential for evaluating the catalytic potential of these materials. The ground-state electronic energy was minimized with respect to the electron density, providing valuable insight into the thermodynamic stability and facilitating the comparison of intrinsic reactivity across different catalysts. In addition, the root-mean-square (RMS) gradient was reported during geometry optimization. This measurement reflects the average magnitude of the atomic forces, and achieving convergence near zero is indicative of structural stability, ensuring minimized forces with no imaginary frequencies.

Table 3 Physicochemical parameters used in the CV modeling and half-cell polarization curve

Parameter inputs for cyclic voltammetry for OER
Catalyst	Exchange current density (A cm^−2)	Double layer capacitance (F m^−2)	Bulk concentration (mmol L^−1)	Starting potential (V)	Switching potential (V)	Ref. 41–49
RuO2	3.3 × 10^−8	0.36	0.5	0.05	1.2	65
IrO2	4.68 × 10^−5	0.020	0.5	−0.01	0.5	64
Ni–Fe	3.60 × 10^−7	6.6 × 10^−4	0.5	0	1	14
LaNiO3	0.000112	0.172	1	−0.2	0.7	66

---

Parameter inputs for polarization curve for OER
Catalyst	Area-specific resistance	Exchange current density (A cm^−2)	Reference
RuO2	0.00033	3.3 × 10^−8	65
IrO2	0.001	4.68 × 10^−5	64
Ni–Fe	0.0624	7.70 × 10^−8	14
LaNiO3	2.32 × 10^−5	0.000112	66 and 39

---

Table 4 IrO₂ DFT results

Atom number	Bond length
	Original structure (Å)	Optimized structure (Å)	Literature review (Å) (ref. 41–49)
Ir1–O1	2.02	2.015	2.037
Ir1–O2	2.02	1.982	1.917
Ir1–O4	2.02	1.982	1.917
Ir1–O3	1.98	2.015	2.037
Ir2–O3	1.98	1.982	1.917

---

Details of the optimized structure
Property	Value
Electronic energy	−897.67538271487115 Eh
RMS gradient norm	0.0000259925 hartree per bohr
Dipole moment	3.412693525 debye
Mulliken charges	Atom number	Atom	Mulliken charge (a.u.)
	1	Ir	0.971375
	2	Ir	0.406013
	3	O	−0.304719
	4	O	−0.355709
	5	O	−0.361251
	6	O	−0.355709

---

Table 5 RuO₂ DFT results

Bond length data
Atom number	Original structure (Å)	Optimized structure (Å)	Literature Review^41–49 (Å)
Ru1–Ru2	3.576	2.686	3.535
Ru1–O1	1.964	1.735	1.942
Ru1–O2	1.964	1.735	1.942
Ru1–O3	2.006	1.778	1.984
Ru1–O4	2.006	2.058	1.984
Ru2–O4	1.964	1.784	1.942

---

Details of the optimized structure
Property	Value
Electronic energy	−488.453471324 Eh
RMS gradient norm	0.000059914 hartree per bohr
Dipole moment	7.2519 debye
Mulliken charges	Atom number	Atom	Mulliken charge (a.u.)
	1	Ru	0.915769
	2	Ru	0.561485
	3	O	−0.352542
	4	O	−0.352542
	5	O	−0.360691
	6	O	−0.411480

---

Table 6 Co–Pt DFT data

Bond length data
Atom number	Original structure (Å)	Optimized structure (Å)	Literature review (Å) (ref. 41–49)
Co–Pt	2.667	2.416	2.66

---

Details of the optimized structure
Property	Value
Electronic energy	−264.176573375 Eh
RMS gradient norm	0.000001959 hartree per bohr
Mulliken charges	Atom number	Atom	Mulliken charge (a.u.)
	1	Co	0.402610	2.125301
	2	Pt	−0.402610	−1.125301

---

Table 7 FeNi DFT data

Bond length data
Atom number	Original structure (Å)	Optimized structure (Å)	Literature review (Å) (ref. 41)
Fe–Fe	2.448	2.262	2.15
Fe–Ni1	2.442	2.352	2.34
Fe–Ni2	2.797	2.350	2.34
Ni1–Ni2	2.448	2.262	2.38

---

Details of the optimized structure
Property	Value
Electronic energy	−585.219519944 Eh
RMS gradient norm	0.000408523 hartree per bohr
Dipole moment	0.5523 debye
Mulliken charges	Atom number	Atom	Mulliken charge (a.u.)
	1	Fe	−0.045424
	2	Fe	−0.045424
	3	Ni	0.045424
	4	Ni	0.045424

---

Table 8 HOMO–LUMO, energy gap for 4 catalysts

Molecule	IrO2	RuO2	Co–Pt	Fe–Ni
Structure
Energy gap	0.02806	0.00955	0.00	0.07637
Space group	P/42	P42/mnm	P4/mmm	R3̄m
Unit cell dimensions	a = 4.545 Å	a = 4.543 Å	a = 2.698 Å	a = 4.380 Å
	b = 4.545 Å	b = 4.543 Å	b = 2.698 Å	b = 4.380 Å
	c = 3.190 Å	c = 3.140 Å	c = 3.727 Å	c = 4.380 Å
	α = 90	α = 90	α = 90	α = 33.384
	β = 90	β = 90	β = 90	β = 33.384
	γ = 90	γ = 90	γ = 90	γ = 33.384
Volume	65.884	64.809	27.135	22.648

---

The dipole moments were calculated to ascertain the molecular polarity and charge distribution. It further illustrates intermolecular interactions. Higher dipole moments generally associated with increased catalytic activity owing to enhanced charge separation. To further refine our analysis, partial atomic charges were derived through Mulliken population analysis, offering insights into charge localization and local reactivity, which can reveal potential sites of catalytic activity. Extracting optimized bond lengths between catalytically active centers and surrounding ligands allows us to gauge bond strength and electronic delocalization, both of which are critical for facilitating rapid electron transfer and stable adsorption of reaction intermediates in OER catalysts. To reduce the computational cost, a representative unit cell was extracted from the crystalline structure of each molecule. The reduced model maintained the key symmetry and bonding features necessary for describing local electronic environments. Post-optimization and computation of electronic properties were performed using GaussView 6.0. We confirmed that all the optimized geometries represented minima on the potential energy surface by ensuring the absence of imaginary vibrational frequencies. Further analysis was conducted using GaussView, which allowed us to extract essential electronic properties, including dipole moments, bond lengths, Polarizability, and Mulliken atomic charges. We also obtained the frontier molecular orbitals (HOMO and LUMO) and the corresponding energy gaps to thoroughly evaluate the electronic behavior and stability of the catalytic structures, including the IrO₂ and Co–Pt complexes. All the optimized structures were reconfirmed as true minima on the potential energy surface by vibrational frequency analysis, ensuring that no imaginary frequencies were present.

4.1.1 Estimation of the electronic properties, charge distributions, and bond lengths. DFT calculations were conducted to thoroughly examine the structural and electronic properties of the four leading oxygen evolution reaction (OER) catalysts: IrO₂, RuO₂, CoPt, and NiFe. Each structure was meticulously optimized to its ground-state geometry using the B3LYP functional, and the resulting structural parameters were rigorously validated against existing experimental data to ensure the robustness of our computational approach (Tables 4–8). The optimized bond lengths of all catalysts exhibited impressive agreement with the crystallographic data. For example, the Ir–O bonds in IrO₂ were found to be between 1.982 and 2.015 Å, closely aligned with the reported value of approximately 2.037 Å.²² Similarly, Ru–O bonds in RuO₂ span from 1.735 Å to 2.058 Å, conforming to the literature values of 1.942 Å to 1.984 Å.¹¹ The NiFe and CoPt systems also demonstrated only minor structural discrepancies, confirming that the DFT-optimized structures accurately represented their solid-state counterparts.^11–15

At the quantum level, the total electronic energies of the optimized systems revealed significant insights into the stability of their electron densities. IrO₂ stood out with the most negative total energy (−897.67 Eh), indicating a highly stabilized wavefunction—facilitated by relativistic effects and robust coordination symmetry surrounding the Ir atoms. These low-energy configurations arise from strong metal–oxygen orbital interactions and extensive delocalized bonding networks, particularly in 4d and 5d transition metal oxides, which show remarkable overlap between metal d orbitals and O 2p orbitals. This degree of orbital hybridization not only enhances the density of states near the Fermi level but also fosters efficient electron transfer, which is essential for effective electrocatalytic processes. The dipole moment analysis provided vital insights into the electronic polarity and charge distribution within the catalysts. RuO₂ exhibited the highest dipole moment (7.25 D), followed closely by IrO₂ (3.41 D), indicating significant polarization throughout these molecules. This pronounced dipolar character is attribute to the asymmetric charge localization driven by uneven orbital occupation and pronounced electronegativity differences between the metal and oxygen atoms. From a quantum electrochemical perspective, a higher molecular dipole augments the interaction between the catalyst surface and polar intermediates (e.g., H₂O, OH⁻, OOH), thereby reducing the energy barrier for adsorption and stabilizing transition states at the electrochemical interface.

Mulliken population analysis sheds further light on the charge distribution within the systems. In both IrO₂ and RuO₂, the metal centers carried partial positive charges of +0.97 and +0.91 a.u., respectively, while the surrounding oxygen atoms exhibited negative charges, underscoring the strong metal–oxygen polarization. This polarization significantly facilitates nucleophilic attack during the OER, thereby enabling the activation of water molecules and facilitating the formation of O–O bonds. CoPt showed effective charge separation due to d–d orbital overlap between Co and Pt atoms, while NiFe presented a more neutral charge distribution, suggesting a weaker orbital polarization with a reduced ability to facilitate electron redistribution during catalytic cycles. The small RMS gradient norms for all systems (ranging from 10⁻⁴ to 10⁻⁶ hartree per bohr) affirm that the optimizations successfully reached valid quantum mechanical minima on the potential energy surface. These results verify that the systems comply with the Born–Oppenheimer approximation at equilibrium, bolstering the reliability of the subsequent electronic property calculations, including frontier molecular orbital energies and metrics relevant to electronic reactivity.

4.1.2 HOMO–LUMO energy levels molecular structure. Parameters such as HOMO–LUMO energy levels and gaps, dipole moments, bond lengths, polarizability, and Mulliken atomic charges were used to evaluate electronic stability, charge distribution, and reactivity trends across all systems studied. In-depth analysis of the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) energies yielded further critical insights into the electronic behavior of the catalysts. The HOMO–LUMO gap serves as an essential quantum descriptor of a material's reactivity and electron transport efficiency. RuO₂ exhibited the smallest gap (0.00955 a.u.), suggesting exceptional electronic mobility and robust propensity for electron exchange during redox events. IrO₂ followed closely, with a gap of 0.02806 a.u., indicative of similarly impressive charge-transfer capabilities. CoPt displayed a near-zero gap due to the overlap of spin-resolved α and β orbitals, signifying metallic behavior with highly delocalized electrons, which potentially facilitates efficient current conduction, although the catalytic specificity may remain uncertain. Conversely, NiFe presented the largest HOMO–LUMO gap (0.07637 a.u.), indicating strong electronic stability but a limited charge transfer potential, which is an undesirable trait for rapid catalytic turnover. These electronic characteristics are intrinsically linked to the electrochemical performance.

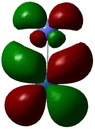
In the OER, the formation of high-energy intermediates such as OOH* or O₂ necessitates flexible electron redistribution and transient oxidation states, which are predominantly favored by the small HOMO–LUMO gaps (Fig. 1) and pronounced orbital delocalization. Furthermore, the dipole moment and charge distribution directly affected the interaction of the catalyst surface with the adsorbed species and the electric field within the double layer. For instance, the high dipole moment combined with a narrow HOMO–LUMO gap creates optimal conditions for both charge transfer and stabilization of transition states, making it particularly suitable for aqueous OER applications. In summary, the DFT findings compellingly identify RuO₂ as the most promising OER catalyst among those evaluated. Its unique combination of quantum delocalization, high dipole polarity, narrow HOMO–LUMO gap, and favorable charge distribution enhances its electronic reactivity and exceptional catalytic potential. IrO₂ shares many of these advantageous characteristics, establishing it as a compelling alternative with comparable stability and reactivity. CoPt, while lacking significant polarity, demonstrates metallic conductivity that could be beneficial in hybrid or composite catalyst systems. In contrast, although structurally sound, the NiFe system displays quantum features, such as a low dipole moment and a wide energy gap, which are less favorable for the OER; however, cooperative electronic interactions between Ni and Fe centers may still confer practical advantages. Based on these quantum-electrochemical descriptors, RuO₂ unequivocally represents the most viable candidate for further advancement in OER catalysis.

Fig. 1 HOMO–LUMO, energy gap for 4 catalysts.

4.2 Modeling cyclic voltammetry (CV)

Voltammetry analysis was meticulously conducted on the oxide catalysts in both acidic and alkaline electrolytes to gain a comprehensive understanding of their electrochemical properties. Cyclic voltammograms (CVs) were captured at three distinct scan rates (50 mV s⁻¹, 100 mV s⁻¹, and 150 mV s⁻¹) for four catalysts—RuO₂, IrO₂, NiFe, and LaNiO₃—allowing for an in-depth exploration of their redox kinetics and capacitive behaviors. As depicted in Fig. 2, the CV of RuO₂ reveals a pronounced cathodic peak between 0.05–0.3 V vs. RHE, which can be attributed to the absorption of hydrogen into the oxide lattice and grain boundaries. This current response is influenced by both faradaic contributions from the formation of surface hydroxides and capacitive charging at the interface between the electrode and the electrolyte. DFT calculations further validated these findings, showing strong hydrogen adsorption energies and stable lattice configurations at low potentials. The analysis of the partial density of states (PDOS) illustrates that the active Ru d-orbitals effectively interact with the O p-states, thereby promoting reversible redox reactions.

Fig. 2 Cyclic voltammogram of RuO₂ at 50 mV s⁻¹, 100 mV s⁻¹, 150 mV s⁻¹.

Fig. 3 highlights the compelling behavior of IrO₂, distinguished by its striking pseudocapacitive characteristics and pronounced scan-rate-dependent redox peaks. The sharper peaks and their asymmetry, when compared to those of RuO₂, suggest that Ir undergoes more dynamic and specialized redox transitions. DFT simulations reinforced these observations, indicating the variable oxidation states of Ir and remarkably low activation energy for electron transfer. The enhanced electronic conductivity, evidenced by the dense density of states near the Fermi level, perfectly aligns with the robust current responses observed in the CV data. In Fig. 4, the voltammogram for the NiFe catalysts is presented, showing a notably low onset potential for the oxygen evolution reaction (OER) along with features indicative of both surface-confined and diffusion-controlled redox processes. DFT analysis revealed that the incorporation of Fe into the Ni matrix introduced localized electronic states near the Fermi level, which not only facilitated oxygen intermediate adsorption, but also significantly enhanced the catalytic efficiency. These theoretical insights elucidate the early onset and broad redox characteristics of CV.

Fig. 3 Cyclic voltammogram of IrO₂ at 50 mV s⁻¹, 100 mV s⁻¹, 150 mV s⁻¹.

Fig. 4 Cyclic voltammogram of Ni–Fe at 50 mV s⁻¹, 100 mV s⁻¹, 150 mV s⁻¹.

Fig. 5 shows the behavior of LaNiO₃, where the increase in the peak current with the scan rate and the symmetry of the peaks suggest quasi-reversible kinetics. The DFT results indicate that La doping dramatically alters the electronic structure of Ni, promoting charge delocalization and improving charge transfer dynamics. The hybridization of the Ni 3d and O 2p states reinforces the stabilization of intermediates, which is consistent with the reversible redox behavior revealed in the CV profiles. The compelling correlation between the CV responses and DFT predictions not only reinforces the fundamental mechanisms at play but also establishes a powerful predictive framework for designing innovative catalyst combinations. The success of the DFT-CV modeling framework demonstrates its effectiveness in accurately capturing the nuances of electrochemical behavior, allowing the identification of materials that exhibit optimal adsorption energies, low overpotentials, and electronic structures that facilitate rapid charge transfer, thereby prioritizing them for synthesis.

Fig. 5 Cyclic voltammogram of LaNiO₃ at 50 mV s⁻¹, 100 mV s⁻¹, 150 mV s⁻¹.

By leveraging computational screening to identify the most promising candidates for experimental validation, researchers can expedite the development process significantly. Moreover, the intricate relationship between redox kinetics (from CV) and atomic-level electronic properties (from DFT) enables precise engineering of hybrid or doped catalysts. Tailored combinations, such as Ni-doped La-based perovskites or Ru–Ir mixed oxides, can be systematically designed to optimize both activity and stability under specific electrochemical conditions. These insights not only pave the way for prototyping advanced electrodes and catalytic interfaces for energy devices, including electrolyzers, metal-air batteries, and supercapacitors, but also effectively link nanoscale properties to macroscopic performance metrics. Thus, the integration of CV analysis and DFT modeling represents a formidable, synergistic approach for the discovery and optimization of high-performance electrochemical materials, driving us closer to the future of energy technologies. The successful application of this DFT-CV modeling framework exemplifies how advanced computational techniques can significantly enhance our understanding and development of the next-generation catalysts.

4.3 Modeling polarization curve

The polarization behavior of the various catalysts was rigorously analyzed using data from the Table 3, with polarization curves (Fig. 6 and 7) assessed at three distinct operating temperatures: 25 °C, 60 °C, and 80 °C. Table 8 presents the details of optimized crystal structure. This multi-temperature evaluation provides a robust framework for comparing the catalytic activity and kinetic performance of benchmark and cost-effective materials. RuO₂ identified as the superior catalyst by exhibiting the lowest overpotential for the onset of the OER and attaining the highest current densities at low overpotential at elevated temperatures. The overpotential is required to drive the OER, and the binding energies of the reaction intermediates, such as (*OH, *O, and *OOH). The catalyst surface is key to achieving high catalyst activity during electrolysis. Thereby, the efficiency of the OER is controlled by the reaction mechanism. The process starts with the electrochemical conversion of hydroxide species (OH⁻) into adsorbed hydroxyl (*OH) by the release of a single electron. This step is followed by the interaction between *OH with another OH⁻ to form adsorbed oxygen (*O). In this process, a water molecule is released while expunging an electron. Next, *O reacts with OH⁻ to form adsorbed peroxospecies (*OOH), and *OOH reacts with OH⁻ to provide oxygen gas (O₂), water, and an electron while regaining the active site. Herein, the rate-limiting step often relies on the catalyst, and the rate of the formation or desorption of *OOH. Our DFT study indicates that the binding energies of the intermediates form a scaling relationship to determine the minimum overpotential to proceed for the reaction.

Fig. 6 Polarization curve for RuO₂, IrO₂, LaNiO₃, Ni–Fe at different temperatures.

Fig. 7 Polarization curve for RuO₂, IrO₂, LaNiO₃, Ni–Fe at 25C.

This process is influenced by many key parameters during the OER. One such parameter is overpotential (η), where our calculation predicts a theoretical minimum of 0.37 V; however, many binary catalysts tested in this study show over 0.4–0.6 V, chiefly due to kinetic losses. The study presents d-band center theory for transition metal-based catalysts, such as cobalt, nickel, and iron. All of them exhibit tuneable electronic structures that describe how intermediates are getting adsorbed and, consequently, improve the overall OER activity. Furthermore, the electronic conductivity and surface area of materials are estimated using the FEM model, which shows how the electrochemical surface areas facilitate the charge transport. OER is an energy-consuming process during water splitting. The total energy required to split water is roughly 1.23 eV per electron under standard conditions; in real-time cells, electrolysis starts at 1.6 due to the influence of overpotential. It is important to note that the energy produced is not derived directly from the OER but instead from the recombination of hydrogen (H₂) and oxygen (O₂) in fuel cells, with potential energy efficiencies reaching up to approximately 60%.

5. Discussion

The integration of insights from density functional theory (DFT), experimental kinetics through cyclic voltammetry (CV), and macro-level behavior observed in polarization curves form a robust framework essential for understanding oxygen evolution reaction (OER) catalyst performance. This comprehensive framework leverages key parameters provided by DFT, such as the adsorption energies of OER intermediates (O*, OH*, OOH*), d-band center (ε_d), Mulliken charges, dipole moments, and metal–oxygen bond lengths. These elements shape the ability of a catalyst to facilitate multi-electron transfer steps and impact reaction energetics. For instance, alloying cobalt with platinum alters the d-band center and weakens the binding energies of oxygen intermediates, aligning the catalyst closer to the optimal adsorption strength required for efficient OER. Cyclic voltammetry validates the theoretical insights within this framework by probing the OER kinetics and mechanistic pathways. The enhanced onset potentials for oxygen evolution observed with Co–Pt-based catalysts, compared to pure cobalt or commercial platinum catalysts, confirmed the activity predicted by DFT calculations. Tafel slopes ranging from 60 to 70 mV per decade indicate favorable reaction kinetics and suggest shifts in the rate-determining step, consistent with electronic structure modifications. Increases in double-layer capacitance and peak current density reflect larger electrochemically active surface areas and heightened charge polarization, which is in line with theoretical predictions regarding dipole moments and charge transfer for alloyed surfaces.

At the device level, the polarization curves highlight the practical impact of these OER catalysts. Co–Pt alloy catalysts in water electrolysis cells exhibit lower activation overpotentials and higher current densities at specific applied voltages compared to pure Pt catalysts. These advancements arise from optimized intermediate adsorption energies that reduce kinetic barriers for the OER, reinforcing theoretical expectations. The strength of this framework lies in its ability to synthesize DFT, CV, and polarization models into a cohesive approach that enhances the rational design of OER catalysts. It establishes clear relationships between the structure, activity, and performance, enabling rapid screening and optimization of alloy compositions prior to experimental synthesis. By merging the DFT-derived adsorption free energy differences (ΔG_OOH − ΔG_O) with Tafel slopes and polarization curves from CV, the framework allows for the precise tuning of the Co : Pt ratios for optimal OER kinetics. Additionally, it facilitates the diagnosis of performance limitations; discrepancies between DFT predictions and CV results may indicate surface passivation or morphological issues, whereas deviations in polarization can reveal mass transport or electrode architecture concerns. Ultimately, this multi-scale framework accelerates the development and deployment of highly efficient and durable OER catalysts, which are crucial without any experiments for advancing sustainable energy technologies, including water electrolysis.

RuO₂ has emerges as the clear leader in catalytic activity, as evidenced by its lowest overpotential for the onset of the oxygen evolution reaction (OER) and its highest current densities at low overpotential, particularly at elevated temperatures. IrO₂ closely follows, demonstrating similarly low onset potentials and impressive activities, reinforcing its position as a premier OER catalyst. In stark contrast, NiFe and LaNiO₃ exhibit significantly higher onset potentials, indicating slower reaction kinetics and inherently lower activity under identical conditions. Nevertheless, these materials offer undeniable advantages in terms of earth abundance and cost, positioning them as highly attractive candidates for non-precious-metal OER catalysts, particularly when integrated into hybrid or doped frameworks. The performance trend is unequivocal: RuO₂ > IrO₂ >> LaNiO₃ ≈ NiFe—consistent across all tested temperatures, confirming the superior electrochemical kinetics of Ru- and Ir-based oxides. These results highlight the critical trade-off between performance and material cost, strongly suggesting that the design of composites or doped structures that retain the high activity of Ru/Ir while leveraging the economic advantages of Ni/Fe-based oxides is a strategic direction for future catalyst development.

6. Conclusion

This study establishes a robust multiscale strategy that effectively integrates Density Functional Theory (DFT) and Finite Element Method (FEM) modeling to expedite the identification and validation of high-performance oxygen evolution reaction (OER) catalysts. At the atomic scale, DFT delivers critical electronic descriptors, including HOMO–LUMO energy gaps, bond lengths, dipole moments, and charge distributions, which are essential for deciphering and predicting catalytic behavior. These insights are rigorously validated through FEM simulations that accurately replicate near-real electrochemical conditions, whereas computational results are reinforced by experimental electrochemical data (CV and Tafel analysis), highlighting the predictive strength of the combined approach. Based on this comprehensive investigation, the following pivotal conclusions can be drawn:

• DFT modeling enables the rational selection of catalysts by elucidating the relationship between structure, charge transfer, and reactivity at the atomic level.

• FEM simulations generate current density and polarization profiles that closely correspond with theoretical predictions, affirming the practical applicability of the models.

• The synergy between theory and experiment enhances the reliability of catalyst screening while substantially reducing experimental costs and time.

• RuO₂ is identified as the most promising OER catalyst due to its low HOMO–LUMO gap, optimal charge distribution, and favorable Ru–O bonding environment—collectively lowering energy barriers and enhancing reaction kinetics.

• In comparison to IrO₂, RuO₂ offers not only comparable activity and stability but also significant advantages concerning cost, abundance, and industrial scalability.

• Future enhancements are achievable through strategies such as surface modification, alloying, and Nano structuring to further elevate catalytic efficiency and durability.

This overarching framework sets a strong precedent for computationally directed catalyst development, with RuO₂ positioned as a leading candidate for scale-up in electrolyzers and broader hydrogen energy systems. In summary, the integrated DFT-FEM-experimental workflow presented in this study serves as a potent toolset for advancing green hydrogen production technologies, facilitating the transition to a carbon-neutral energy future.

Conflicts of interest

All authors have no conflict of interest.

Data availability

Data will be available upon request. Most of the data are disseminated as figures and tables in this manuscript.

References

1. C. W. Forsberg, Int. J. Hydrogen Energy, 2007, 32, 431–439,  DOI:10.1016/j.ijhydene.2006.08.003.
2. S. Ke, C. Rui, G. Chen and X. Ma, Energy Fuels, 2021, 35, 9723–9730,  DOI:10.1021/acs.energyfuels.1c02056.
3. R. A. Marcus, Annu. Rev. Phys. Chem., 1993, 44, 155–179,  DOI:10.1146/annurev.pc.44.100193.001103.
4. T. A. Rees and R. E. Jones, J. Chem. Phys., 1999, 110, 4200–4212,  DOI:10.1063/1.478306.
5. X. Rong, PhD thesis, Massachusetts Institute of Technology, 2018.
6. L. Chen, Structural Characterization, Physical Properties, Electrocatalytic Activity and Energy Storage Behavior of the Hydrothermal Y₂CoMnO₆ Double Perovskite Nanorods, thesis/report, 2024.
7. W. G. Hardin, PhD thesis, University of Austin, 2017.
8. J. Zaveri, S. R. Dhanushkodi, M. W. Fowler, B. A. Peppley, D. Taler, T. Sobota and J. Taler, Energies, 2025, 18, 1022,  DOI:10.3390/en18051022.
9. Y. Jiao, Y. Zheng, M. Jaroniec and S. Z. Qiao, Chem. Soc. Rev., 2015, 44, 2060–2086,  10.1039/c4cs00470a.
10. Y. Liu, D. Wang and S. Zhang, Nat. Mater., 2016, 15, 282–286,  DOI:10.1038/nmat4522.
11. F. Jiao, Y. Zheng and W. Chen, Nat. Mater., 2015, 14, 94–100,  DOI:10.1038/nmat4167.
12. G. A. Mabbott, J. Chem. Educ., 1983, 60, 697,  DOI:10.1021/ed060p697.
13. P. Sabatier, La catalyse en chimie organique, Librairie Polytechnique, ed. C. Béranger, Paris, 1913.
14. J. Greeley, T. F. Jaramillo, J. Bonde, I. Chorkendorff and J. K. Nørskov, J. Phys. Chem. B, 2002, 106, 4665–4673,  DOI:10.1021/jp020161h.
15. K. Zhu, X. Zhu and W. Yang, Angew. Chem., Int. Ed., 2019, 58, 1252–1265,  DOI:10.1002/anie.201802923.
16. T. Audichon, E. Mayousse, T. W. Napporn, C. Morais, C. Comminges and K. B. Kokoh, Electrochim. Acta, 2014, 132, 284–291,  DOI:10.1016/j.electacta.2014.03.141.
17. B. C. Beard and P. N. Ross, J. Electrochem. Soc., 1990, 137, 3368,  DOI:10.1149/1.2086208.
18. D. A. McKeown, P. L. Hagans, L. P. Carette, A. E. Russell, K. E. Swider and D. R. Rolison, J. Phys. Chem. B, 1999, 103, 4825–4832.
19. Q. Feng, Q. Wang, Z. Zhang, Y. Xiong, H. Li, Y. Yao, X. Z. Yuan, M. C. Williams, M. Gu and H. Chen, et al., Appl. Catal., B, 2019, 248, 18–26.
20. M. A. Hubert, A. M. Patel, A. Gallo, Y. Liu, E. Valle and M. Ben Naim, et al., ACS Catal., 2020, 10, 12182–12196,  DOI:10.1021/acscatal.0c03478.
21. D. Roth and M. Sadeghi, J. Chem. Phys., 2020, 153, 104105,  DOI:10.1063/5.0022934.
22. J. A. Pople and M. S. Gordon, in Advances in Chemical Physics, Academic Press, 2001.
23. J. G. Harris and R. O. Jones, Comput. Mater. Sci., 2008, 42, 318–326.
24. H. B. Schlegel, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 790–809.
25. E. Borguet, S. B. E. Osborn, D. J. A. Ramírez and M. J. Toomey, J. Phys. Chem. C, 2017, 121, 9863–9873,  DOI:10.1021/acs.jpcc.7b02534.
26. D. González, M. Sodupe, L. Rodríguez Santiago and X. Solans Monfort, J. Catal., 2022, 412, 78–86,  DOI:10.1016/j.jcat.2022.05.029.
27. H. A. Gasteiger, S. S. Kocha, B. Sompalli and F. T. Wagner, Appl. Catal., B, 2005, 56, 9–35,  DOI:10.1016/j.apcatb.2004.06.021.
28. F. Calle-Vallejo, J. I. Martínez, J. M. García-Lastra, P. Sautet and D. Loffreda, Angew. Chem., Int. Ed., 2014, 53, 8316–8319,  DOI:10.1002/anie.201402927.
29. M. Sakthivel, S. Bhandari and J. F. Drillet, ECS Electrochem. Lett., 2015, 4, A56,  DOI:10.1149/2.0081506eel.
30. A. Grimaud, K. J. May and C. E. Carlton, et al., Nat. Commun., 2013, 4, 2439,  DOI:10.1038/ncomms3439.
31. J. G. Harris and R. O. Jones, Comput. Mater. Sci., 2008, 42, 318–326,  DOI:10.1016/j.commatsci.2007.06.028.
32. J. K. Nørskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Nat. Chem., 2009, 1, 37–46,  DOI:10.1038/nchem.121.
33. D. J. Burkholder, W. R. McCurdy and M. S. Linehan, J. Chem. Theory Comput., 2006, 2, 1342–1350,  DOI:10.1021/ct060089t.
34. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865,  DOI:10.1103/PhysRevLett.77.3865.
35. J. A. Steckel and D. Sholl, Density Functional Theory—A Practical Introduction, Wiley, Hoboken, 2009,  DOI:10.1002/9780470447710.
36. E. Engel, Density Functional Theory, Springer-Verlag, Berlin, 2011,  DOI:10.1007/978-3-642-14090-7.
37. H. Eschrig, The Fundamentals of Density Functional Theory, Teubner, Stuttgart, 1996.
38. K. Burke, J. Chem. Phys., 2012, 136, 150901,  DOI:10.1063/1.4704546.
39. A. Jain, Y. Shin and K. A. Persson, Nat. Rev. Mater., 2016, 1, 16002,  DOI:10.1038/natrevmats.2016.2.
40. W. Yang, J. Yi and W. H. Sun, Macromol. Chem. Phys., 2015, 216, 1125–1133,  DOI:10.1002/macp.201500007.
41. L. Yang and C. Liu, Catal. Sci. Technol., 2020, 10, 6386–6395,  10.1039/D0CY01026J.
42. G. Levi, A. V. Ivanov and H. Jónsson, Faraday Discuss., 2020, 224, 448–466,  10.1039/C9FD00115A.
43. J. C. Zapata and L. K. McKemmish, J. Phys. Chem. A, 2020, 124, 7538–7548,  DOI:10.1021/acs.jpca.0c06736.
44. V. Choudhary, A. Bhatt, D. Dash and N. Sharma, J. Comput. Chem., 2019, 40, 2354–2363,  DOI:10.1002/jcc.26012.
45. T. Cheng, H. Xiao and W. A. Goddard, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 1795–1800,  DOI:10.1073/pnas.1701185114.
46. J. A. Gauthier, C. F. Dickens, H. H. Heenen, S. Vijay, S. Ringe and K. Chan, J. Chem. Theory Comput., 2019, 15, 6895–6906,  DOI:10.1021/acs.jctc.9b00717.
47. B. Schlegel, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 790–809,  DOI:10.1002/wcms.34.
48. J. E. Dennis and R. B. Schnabel, Numerical Methods for Unconstrained Optimization and Nonlinear Equations, SIAM, Philadelphia, 1996,  DOI:10.1137/1.9781611971200.
49. S. Liu, D. Zhao, X. Gao and J. Li, J. Catal., 2019, 377, 335–343,  DOI:10.1016/j.jcat.2019.07.030.
50. A. Badreldin, O. Bouhali and A. Abdel Wahab, Adv. Funct. Mater., 2024, 34, 2312425,  DOI:10.1002/adfm.202312425.
51. X. Liao, R. Lu, L. Xia, Q. Liu, H. Wang, K. Zhao and Y. Zhao, Energy Environ. Mater., 2022, 5, 157–185,  DOI:10.1002/eem2.12204.
52. R. M. Darling and M. L. Perry, J. Electrochem. Soc., 2014, 161, A1381–A1387,  DOI:10.1149/2.0941409jes.
53. A. J. Bard and L. R. Faulkner, Electrochemical Methods: Fundamentals and Applications, Wiley, New York, 2nd edn, 2001,  DOI:10.1002/9780470477021.
54. R. S. Nicholson and I. Shain, Anal. Chem., 1964, 36, 706–723,  DOI:10.1021/ac60210a007.
55. W. Sheng, H. A. Gasteiger and Y. Shao-Horn, J. Electrochem. Soc., 2010, 157, B1529–B1536,  DOI:10.1149/1.3483106.
56. J. He, J. Xie, Y. Zhang, X. Yang, Z. Wei, Q. Liu, T. Yao, X. Yang, L. Zhang and B. Liu, et al., Nat. Commun., 2017, 8, 237,  DOI:10.1038/ncomms14371.
57. K. L. Chu and S. Srinivasan, J. Electrochem. Soc., 1995, 142, L116–L118,  DOI:10.1149/1.2044152.
58. L. Han, S. Dong and E. Wang, Adv. Mater., 2016, 28, 9266–9291,  DOI:10.1002/adma.201602270.
59. X. Zhao and K. Sasaki, Acc. Chem. Res., 2022, 55, 1226–1236,  DOI:10.1021/acs.accounts.2c00057.
60. L. Zhang, G. Wang, W. Wang, Y. Xiong and Y. Wang, J. Phys. Chem. C, 2015, 119, 12027–12035,  DOI:10.1021/acs.jpcc.5b02021.
61. I. Matanovic, S. S. Kocha and K. C. Neyerlin, J. Phys. Chem. C, 2011, 115, 10636–10643,  DOI:10.1021/jp200666c.
62. J. Rossmeisl, Z. W. Qu, H. Zhu, G. J. Kroes and J. K. Nørskov, J. Electroanal. Chem., 2007, 607, 83–89,  DOI:10.1016/j.jelechem.2007.01.008.
63. J. Rossmeisl, Z. W. Qu, H. Zhu, G. J. Kroes and J. K. Nørskov, J. Phys. Chem. B, 2005, 109, 10392–10398,  DOI:10.1021/jp053383q.
64. S. Czioska, K. Ehelebe, J. Geppert, D. Escalera-López, A. Boubnov and E. Saraçi, et al., ChemElectroChem, 2022, 9, e202200514,  DOI:10.1002/celc.202200514.
65. H. Ma, C. Liu, J. Liao, Y. Su, X. Xue and W. Xing, J. Mol. Catal. A: Chem., 2006, 247, 7–13,  DOI:10.1016/j.molcata.2005.11.013.
66. J. F. Drillet, ECS Electrochem. Lett., 2015, 4, A56,  DOI:10.1149/2.0081506eel.

---