Shale-hosted vanadium occupation in typical silicate mineral structures

Abstract

Vanadium is one kind of critical rare metal elements. Recently the domestic demand for vanadium has increased, and its market price has gradually climbed. In-depth study of vanadium extraction technology from shale holds obviously strategic and economic benefits. However, the difficulty of shale-hosted vanadium leaching varies due to the diverse occupancy states and grades in vanadium shale. Additionally, the complex and diverse mineral compositions, severe carbonaceous impregnation and interweaving, and poor lattice integrity complicate the localization of vanadium atoms with current detection technology, making it difficult to elucidate the impact of structural properties on vanadium release. In this paper, we use the first-principles-based density-functional theory (DFT) approach to determine that vanadium is most likely present in the octahedra of silicate mineral minerals, especially Mg–O octahedra, from both energetic and structural perspectives. This study accurately determines the occupancy of vanadium atoms in shale on an atomic scale, clarifies the nature of the ore, identifies targets for disrupting the mineral structure, and serves as a guide for the leaching of vanadium from shale.

---

1. Introduction

The black shale system is a general term for marine fine-grained sedimentary rocks characterized by their richness in organic matter. It is often economically important because it preserves valuable metals,^1–4 such as V, Ni, Mo, U, PGE (platinum-group elements), Se, Au, Ag, Cd, Ti, Y, REE (rare earth elements), Ba, phosphorus, and other precious metals, as well as rare-earth, rare, and dispersed elements and radioactive elements.^5–12 Among the valuable metal-rich mineral species, vanadium shale is a kind of unique black rock sedimentary mineral resource in China, and shale-hosted vanadium accounts for nearly 50% of China's total vanadium reserves. Refined vanadium, as an important strategic rare metal, is critical for production of advanced iron and steel materials, titanium alloys, as well as storage of new energy.^13–17

Vanadium shale consists mainly of carbonaceous matters, carbonate minerals, sulfide and silicate minerals.¹⁸ According to literature studies,^17,19–21 the shale-hosted vanadium mainly exits as the valence of V(III) in silicate minerals, including mica, kaolinite, chlorite, tourmaline, garnet and possibly quartz and feldspar (Table 1). Silicate minerals are categorized into five types of structures according to their crystal structure: layered, cyclic, island, framework and chain. Among the minerals that may host vanadium, mica, kaolinite and chlorite are layered minerals, tourmaline is cyclic, garnet is insular, and quartz and feldspar are framework minerals. The relative mass fraction of Si(IV)²² on the surfaces of framework-structured minerals is the largest, exceeding 20%; the mass fraction of Si⁴⁺ on the surfaces of cyclic-structured minerals is the second largest, 17.37%; the relative mass fraction of Si(IV) on the surfaces of island -structured minerals ranges from 10–13%; and the mass fraction of Si(IV) on the surfaces of layered-structured minerals is around 10%. This reflects the great difference between different types of silicate minerals. In addition, vanadium atoms in the structures of these vanadium-bearing minerals can isomorphism replacement of their central atoms, especially Al, Mg, and Fe,^18,23 which may lead to a complex vanadium occupation in vanadium shale.

Table 1 Vanadium-bearing minerals in shales discovered to date^a

Mineral name	Chemical formula
a R is a metal element such as Mg, Fe, Mn, Ga, etc.
Mica	KAl2(Si3Al)O10(OH)2
Kaolinite	[Al2(OH)4]Si2O5
Chlorite	Mg(Si3Al)O10(OH)8
Tourmaline	Na(R)3Al6(BO3)3(Si6O18)(OH)4
Garnet	(R)3Al2(SiO4)3
Feldspar	KAlSi3O8
Quartz	SiO2

---

Scanning Electron Microscope-Energy Dispersive Spectrometer (SEM-EDS), X-ray diffraction (XRD), Mineral Quantitative Analysis System (MLA) and other detections are commonly used for mineral composition analysis. However, these conventional detections cannot determine the exact location of atoms in a mineral. Unlike conventional analytical techniques, density functional theory (DFT) enables the simulation of atomic occupancy in mineral lattices with high spatial precision. While natural minerals often contain structural defects, impurities, and amorphous components that cannot be fully captured by idealized DFT models, DFT remains one of the most effective tools currently available for probing the site-specific behavior of atoms at the atomic scale. Some scholars²⁴ investigated the effects of different elemental occupancy positions on the stability, photovoltaic, thermoelectric, and elastic properties of halide double perovskite, and obtained the molecular structure with optimal electrical conductivity, in order to serve as a guideline for realizing the application of this material in the field of solar energy. Other scholars²⁵ studied the selective occupation, structure and thermal stability of high-entropy (CoCrFeMnNi)₃O₄ spinel, and obtained the optimal structure of high entropy spinel oxide (HESO) at high temperatures, which provides a theoretical basis for the application of HESO at high temperatures. At present, DFT based on periodic boundary conditions and pseudopotentials has been widely used to study the crystal structure, elasticity, and thermodynamic properties of minerals.

In the field of vanadium research, some researchers²⁶ used DFT to clarify the distribution of vanadium in three minerals, namely mica, feldspar, and quartz, confirming that mica is the main vanadium mineral, a conclusion that was verified by testing. Due to the diversity of vanadium morphology in shales, there are fewer studies of vanadium-bearing minerals in vanadium-bearing shales, which are mainly concentrated in mica, and it is necessary to study the occupancy of a variety of vanadium-bearing silicate minerals. The minerals in the shale are extremely difficult to obtain and the localization of vanadium elements is extremely difficult to do by traditional detection means. Therefore, the use of quantum chemical methods to analyze elements that cannot be localized in complex minerals is a commonly used method. Meanwhile, Crundwell²⁷ discussed the effects of layered, cyclic, island, framework, and chain silicate minerals in acidic and alkaline solutions and proposed a new theory to explain the dissolution kinetics of these minerals. A new dissolution mechanism is proposed that divides the dissolution process of silicate minerals in acids and bases into three stages: (1) the reaction of surface metal atoms with H⁺ or OH⁻, (2) the detachment of silicate tetrahedra (SiO₄)ⁿ⁻ from the solid surface, and (3) the subsequent reaction of these products with substances in solution to form the final dissolution product. The breaking of the metal–O bond is considered to be the decisive step. The combination of quantum chemical methods with Cromwell's theory also gives us access to the solubility of silicate minerals in shale.

In this paper, the occupancy of vanadium atoms in vanadium-bearing minerals is modeled using density-functional theory (DFT). A total of eleven vanadium-bearing minerals of four types, layered, cyclic, island and framework minerals, were considered in the calculations. By comparing the energy changes and degrees of distortion of vanadium within different mineral structures, the most likely vanadium-bearing minerals and the optimal sites for vanadium incorporation were identified. The ease of vanadium release from the eleven minerals was further inferred by combining mineral occupancy and solubility. This study summarizes the substitution pattern of vanadium atoms in vanadium shales and enhances the data on shale process mineralogy.

2. Materials and methods

2.1 Mineral structure model

The initial structures of the eleven minerals were obtained from the Crystallographic Open Database (COD) and their initial parameters are shown in Table 2.^28–36 In layer minerals, all three mica structures are monoclinic, with single cells formed by TOT stacking, where two tetrahedral layers (T) sandwich an octahedral layer (O). The difference between muscovite and phlogopite and biotite is that the octahedral central atom of muscovite is aluminum, and only two of the three octahedral cavities under the six-membered ring holes are filled with Al, classifying it as a dioctahedral structure. In phlogopite and biotite, the octahedral center atoms are Mg and Fe, with all three octahedral cavities filled, classifying them as trioctahedral structures. Kaolinite has a triclinic crystal structure, with single cells consisting of stacked tetrahedral (T) and octahedral (O) layers. The octahedral center atom of kaolinite is aluminum, classifying it as a dioctahedral structure, similar to muscovite. Chlorite has a monoclinic structure, with single cells consisting of stacked TOT-O layers, where two tetrahedral (T) layers sandwich an octahedral (O) layer, with another octahedral (O) layer beneath the TOT layer. The octahedral center atom of chlorite is Mg, with all three octahedral cavities under the six-membered ring pores filled with Mg, making it a trioctahedral structure.

Table 2 Initial structural parameters of nine minerals

Mineral name	Chemical formula	Space group	References	A (Å)	b (Å)	c (Å)	α (°)	β (°)	γ (°)	COD ID
Muscovite	KAl2(Si3Al)O10(OH)2	C2/c	Catti's	5.29	9.12	20.26	90.00	90.00	95.83	9005013
Phlogopite	KMg2(Si3Al)O10(OH)2	C2/m	Aiqing	5.39	9.30	10.21	90.00	90.00	101.91	8104627
Biotite	KFe2(Si3Al)O10(OH)2	C2/m	Brigatti M. F.	5.34	9.26	10.23	90.00	90.00	100.26	1000038
Kaolinite	[Al2 (OH)4]Si2O5	C/i	Gruner W. J'.	5.14	8.89	14.49	91.76	105.31	89.80	1011045
Chlorite	Mg(Si3Al)O10(OH)8	C2/c	McMurchy G. C.	5.34	9.26	14.42	90.25	97.28	89.99	1011015
Dravite	NaMg3Al6(BO3)3(Si6O18)(OH)4	R/3m	Bosi F.	15.97	15.97	7.20	90.00	90.00	120.00	1556971
Schorl	NaMg3Al6(BO3)3(Si6O18)(OH)4	R/3m	Bosi F.	15.97	15.97	7.20	90.00	90.00	120.00	1556971
Pyrope	Mg3Al2(SiO4)3	Ia/3̄d	Lager G. A.	11.85	11.85	11.85	90.00	90.00	90.00	1531652
Grossular	Ca3Al2(SiO4)3	Ia/3̄d	Lager G. A.	11.46	11.46	11.46	90.00	90.00	90.00	1531652
Feldspar	KAlSi3O8	C2/m	Organova N. I.	8.69	13.15	7.27	90.00	90.00	115.75	1521702
Quartz	SiO2	P3221	Wright A. F.	4.98	4.98	5.46	90.00	90.00	120.00	1100019

---

Among the cyclic minerals, tourmaline has a tripartite crystal structure, differing in whether the octahedral center atoms are Fe or Mg. Garnets are island minerals with an equiaxial crystal structure, and the difference between the two types of garnets is whether the atoms coordinated to O are Mg or Ca. Feldspar and quartz are two representative framework minerals; quartz is composed of pure SiO₂, while feldspar also has K, Al assigned to it. To avoid concentration differences caused by varying atomic numbers in the single-cell structure, the number of atoms for each mineral was maintained at approximately 150. The following supercells were used: 2 × 1 × 1, 2 × 1 × 2, 2 × 1 × 2, 2 × 1 × 1, 2 × 1 × 1, 1 × 1 × 2, and 2 × 2 × 2 supercells were used to represent the structures of muscovite, phlogopite, biotite, chlorite, kaolinite, feldspar, and quartz, respectively. This facilitated vanadium substitution for Si, Al, Mg, and Fe atoms. Tourmaline and garnet cells have more atoms and do not require supercells. The substitution and formation energies allow us to determine the likelihood of substitution reactions and the stability of the resulting new structures. The equations for the two energies are as follows:³⁷

The substitution energy (E_s) definition:

E_s = E_all − E₀ + E_α − E_V (1)

The energy of formation (E_f) definition:

E_f = E₁^f − E₀^f (2)

(1) Where E_all is the total structural energy of the substituted α-atoms in the mineral, E₀ is the total structural energy of the unsubstituted mineral, and E_α and E_V are the ground state energies of the substituted atoms α and vanadium-substituted atoms, respectively. The lower the substitution energy value, the easier the substitution occurs and the more stable the structure of the substituted vanadium-bearing mica.

(2) Where E₀^f is the formation energy of the mineral structure without substitution and E₁^f is the formation energy of the mineral structure after substitution. The larger the negative value of the formation energy, the more stable the mineral structure after substitution.

2.2 Structural optimization and data processing methods

DFT calculations were performed using the VASP module within the MedeA software package, employing the generalized gradient approximation (GGA) method³⁸ with the Perdew–Burk–Ernzerhof (PBE)³⁹ generalization for processing exchange-correlation energy, and the projector augmented wave (PAW) method⁴⁰ for electronic interactions. A kinetic truncation energy of 400 eV is employed to ensure high-precision calculations of vanadium occupancy, with convergence criteria set at 1 × 10⁻⁵ eV for energy and 5 × 10⁻² eV Å⁻¹ for force in all calculations. The structural optimizations were performed using the conjugate gradient algorithm for the ionic steps and the normal blocked Davidson method for the electronic steps. A displacement tolerance of 0.015 Å was used to determine the convergence of atomic relaxation, with a normal setting for the overall calculation accuracy. A Methfessel–Paxton smearing method was employed, with a smearing width of 0.2 eV. The projection operators were evaluated in reciprocal space, incorporating non-spherical corrections and auxiliary support grids for the accurate evaluation of augmentation charges. A k-point spacing of 0.3 Å⁻¹ was used for Brillouin zone sampling. No long-range dispersion correction was applied during the structural relaxations. The projector-augmented wave (PAW) potentials used were as follows: H, B, O, Mg, Al, Si, Fe, Na_pv, K_sv, Ga_sv, and V_sv. All calculations employed the potpaw.54 PAW dataset version. To ensure full relaxation, the symmetry of all structures (initially assigned to space group P1) was disregarded during optimization, and all atomic positions were allowed to relax without constraints.

The structural aberration data were analyzed by separately evaluating changes in bond lengths and angles before and after aberrations. The extent of aberrations in different minerals was compared by assessing the variations in bond lengths and angles following facet substitutions, with the results visualized as lengths in the Fig. 6 and 7. The numerical ranges shown in Fig. 6 and 7 represent the magnitude of distortion. Data positioned to the left of zero indicate a reduction in bond lengths and angles post-substitution, whereas data on the right indicate an increase. For the band charge data, the analysis focused on the differential charge transfer observed before and after vanadium entered the structure for bonding. The line graph in Fig. 9 shows the amount of charge transferred after bonding for different minerals, while the bar graph shows the total amount of charge after bonding.

3. Results and discussion

3.1 Assigned positions of vanadium atoms

3.1.1 Occupancy of vanadium atoms in the layered structures.
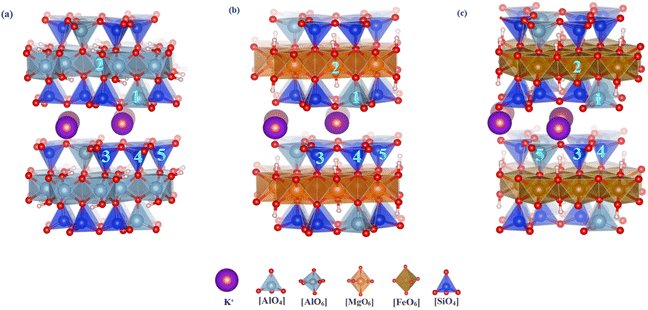
3.1.1.1 Mica-type minerals. In vanadium shale, mica minerals are the primary vanadium-bearing mineral phases. However, the sub-classes of mica are highly diverse. In this study, we selected three representative mica structures: dioctahedral muscovite and trioctahedral phlogopite and biotite. The substitution of vanadium atoms at different positions within these mineral structures leads to varying degrees of structural disruption and the ease with which V–O bonds break to release vanadium. Therefore, the energy differences associated with the substitution of four elements—Al, Mg, Si, and Fe—by vanadium in these three types of mica were investigated, in which two sites for Al (tetrahedral and octahedral), three tetrahedral sites for Si, and one octahedral site for Mg and Fe were considered respectively. The interlayer K⁺ is disregarded because it is free from the interlayer. Fig. 1 shows the substitution positions, while Table 3 lists the changes in lattice parameters and substitution energies of three types of mica before and after substitution. It was found that the c-axis of muscovite and phlogopite expanded by 0.12–0.16 Å and 0.08–0.11 Å, respectively, while the c-axis of biotite contracted by 0.54–0.59 Å. The c-axis changes in all three mica types were larger than those in the a-axis and b-axis, indicating that vanadium substitution causes more deformation along the c-axis. For the three mica types, the substitution energy of Al–O octahedron in muscovite is −1.12 eV, Mg–O octahedron in phlogopite is −4.93 eV, and Fe–O octahedron in biotite is 1.31 eV, all lower than tetrahedral substitution energies by 0.32–3.4 eV. In mica, the octahedral substitution energies are generally lower. The formation energies of new minerals produced by vanadium substitution in the octahedra of muscovite, phlogopite, and biotite are respectively 330.00 eV, −1.80 eV, and 104.00 eV, all much lower than other substitution sites. Given the substitution and formation energies, vanadium is most likely to be present in phlogopite among the three mica types.

Fig. 1 Substitution site of vanadium in mica [(a)-muscovite(1-[Al_IV] 2-[Al_VI] 3-[Si_IV]₁ 4-[Si_IV]₂ 5-[Si_IV]₃); (b)-phlogopite (1-[Al_IV] 2-[Mg_VI] 3-[Si_IV]₁ 4-[Si_IV]₂ 5-[Si_IV]₃); (c)-biotite(1-[Al_IV] 2-[Fe_VI] 3-[Si_IV]₁ 4-[Si_IV]₂ 5-[Si_IV]₃)].

Table 3 Lattice parameters and two energies of 11 minerals sat different substitution sites of vanadium (the following supercells were used: 2 × 1 × 1, 2 × 1 × 2, 2 × 1 × 2, 2 × 1 × 1, 2 × 1 × 1, 1 × 1 × 2, and 2 × 2 × 2 supercells were used to represent the structures of muscovite, phlogopite, biotite, chlorite, kaolinite, feldspar, and quartz, respectively.)

Substitution type	Substitution site	a (Å)	b (Å)	c (Å)	α (°)	β (°)	γ (°)	Es/eV	Ef/eV
Muscovite	M	10.58	9.12	20.26	90.00	90.00	95.83	—
Al–O octahedron	M[AlVI]	10.54	9.12	20.36	90.01	90.00	95.73	−1.12	330.00
Al–O tetrahedron	M[AlIV]	10.55	9.12	20.38	90.01	90.00	95.73	2.28	486.00
Si–O tetrahedron	M[SiIV]1	10.57	9.14	20.42	90.00	90.00	95.74	2.22	580.00
Si–O tetrahedron	M[SiIV]2	10.57	9.15	20.42	90.00	90.01	95.77	2.23	600.00
Si–O tetrahedron	M[SiIV]3	10.57	9.15	20.42	90.00	90.02	95.73	2.21	590.00
Phlogopite		10.74	9.30	20.70	90.01	89.99	101.56	—
Mg–O octahedron	P[MgVI]	10.74	9.30	20.80	90.00	89.99	101.40	−4.93	−1.80
Al–O tetrahedron	P[AlIV]	10.76	9.32	20.78	89.11	89.99	101.50	−3.26	315.41
Si–O tetrahedron	P[SiIV]1	10.77	9.33	20.81	90.00	90.00	101.50	−3.25	155.60
Si–O tetrahedron	P[SiIV]2	10.77	9.33	20.81	90.00	90.00	101.50	−3.12	160.00
Si–O tetrahedron	P[SiIV]3	10.77	9.33	20.81	89.99	89.99	101.47	−3.11	154.50
Biotite		10.69	9.26	20.45	90.00	90.00	100.26	—
Fe–O octahedron	B[FeVI]	10.42	9.06	19.90	90.16	90.19	100.18	1.31	104.00
Al–O tetrahedron	B[AlIV]	10.46	9.08	19.91	89.95	90.03	100.40	1.63	443.70
Si–O tetrahedron	B[SiIV]1	10.43	9.07	19.85	89.91	90.01	100.50	3.17	504.15
Si–O tetrahedron	B[SiIV]2	10.44	9.08	19.88	89.90	90.04	100.35	3.18	550.61
Si–O tetrahedron	B[SiIV]3	10.45	9.08	19.86	89.92	90.03	100.44	3.18	506.15
Kaolinite	K	10.25	8.89	14.49	91.76	105.31	89.80	—
Al–O octahedron	K[AlVI]	10.25	8.89	14.49	91.76	105.31	89.80	−0.47	338.94
Si–O tetrahedron	K[SiIV]	10.25	8.89	14.50	92.12	105.51	89.83	0.26	393.06
Chlorite	C	10.58	9.19	14.26	90.10	97.14	90.06	—
Mg–O octahedron	C[MgVI]1	10.59	9.17	14.21	90.19	97.22	90.02	−10.93	−395.50
Mg–O octahedron	C[MgVI]2	10.58	9.18	14.26	90.10	97.14	90.06	−7.02	−201.43
Al–O tetrahedron	C[AlIV]	10.60	9.20	14.37	90.11	97.13	90.04	−4.79	−90.46
Si–O tetrahedron	C[SiIV]1	10.59	9.20	14.33	90.07	97.10	90.06	−2.79	−39.46
Si–O tetrahedron	C[SiIV]2	10.60	9.19	14.32	90.08	97.14	90.14	−2.43	−35.50
Si–O tetrahedron	C[SiIV]3	10.61	9.18	14.32	90.09	97.12	90.05	−2.66	−34.35
Dravite	D	15.94	15.94	7.087	90.00	90.00	120.00
Mg–O octahedron	D[MgVI]	15.93	15.94	7.079	90.00	90.01	120.02	−10.42	−263.87
Al–O octahedron	D[AlVI]	15.95	15.96	7.069	89.98	90.03	120.05	−4.30	−150.86
Si–O tetrahedron	D[SiIV]	15.97	15.96	7.072	89.94	89.98	120.03	−2.69	1.77
Na–O 9 coordination	D[NaIX]	15.91	15.91	7.064	90.00	90.00	120.00	−7.33	−102.94
Schorl	S	15.84	15.84	7.048	90.00	90.00	120.00	—
Fe–O octahedron	S[FeVI]	15.82	15.85	7.038	90.00	90.08	120.07	−2.72	−209.13
Al–O octahedron	S[AlVI]	15.85	15.84	7.047	89.93	90.05	120.15	−1.12	213.80
Si–O tetrahedron	S[SiIV]	15.85	15.88	7.030	89.99	89.85	120.07	−0.27	230.22
Na–O 9 coordination	S[NaIX]	15.85	15.85	7.020	90.00	90.00	120.00	−1.77	499.50
Pyrope	P	11.43	11.43	11.43	90.00	90.00	90.00	—
Al–O octahedron	P[AlVI]	11.44	11.44	11.44	90.00	90.02	90.02	−0.70	375.19
Mg–O dodecahedron	P[MgVIII]	11.44	11.43	11.43	90.03	90.00	90.00	−2.54	251.94
Si–O tetrahedron	P[SiIV]	11.44	11.46	11.44	90.00	90.00	90.00	−0.24	420.03
Grossular	G	11.84	11.84	11.84	90.00	90.00	90.00	—
Al–O octahedron	G[AlVI]	11.85	11.85	11.85	90.09	90.09	90.09	−1.11	206.90
Ga–O dodecahedron	G[CaVIII]	11.83	11.82	11.83	90.00	89.96	90.00	−0.89	546.87
Si–O tetrahedron	G[SiIV]	11.85	11.86	11.85	90.00	90.00	90.00	−0.44	293.87
Feldspar	F	8.70	13.12	14.62	90.00	115.78	90.00	—
Al–O tetrahedron	F[AlIV]1	8.73	13.15	14.67	90.01	115.78	90.02	−0.54	230.61
Al–O tetrahedron	F[AlIV]2	8.73	13.15	14.67	89.99	115.77	89.99	−0.59	229.32
Si–O tetrahedron	F[SiIV]1	8.74	13.17	14.69	89.98	115.77	90.00	−0.52	396.64
Si–O tetrahedron	F[SiIV]2	8.74	13.17	14.69	90.00	115.76	89.99	−0.54	397.58
Si–O tetrahedron	F[SiIV]3	8.74	13.17	14.69	90.01	115.77	90.00	−0.53	396.21
Quartz	Q	9.95	9.95	10.89	89.99	90.10	120.00	—
Si–O tetrahedron	Q[SiIV]	10.03	10.03	10.99	90.01	89.99	120.01	−0.58	231.39

---

3.1.1.2 Non-mica-type minerals (kaolinite and chlorite). In the non-mica layered silicates, we selected two representative minerals (2 : 1 type chlorite and 1 : 1 type kaolinite). For these two minerals, we investigated the energy differences at seven vanadium substitution sites. In chlorite, three substitution environments were examined: Si–O tetrahedral sites, Al–O tetrahedral sites, and Mg–O octahedral sites. In kaolinite, the occupation of vanadium atoms in Al–O and Si–O tetrahedral sites was investigated. The substitution sites for both minerals are shown in Fig. 2. The lattice parameters and substitution energies for kaolinite and chlorite are listed in Table 3. In both layered minerals, vanadium replacement changes the crystal cell along the c-axis, similar to mica-like minerals. The substitution energy of the Al–O octahedron in kaolinite is −0.47 eV, and the formation energy is 338.94 eV, both lower than those of the Si–O tetrahedron. In chlorite, the difference for the substitution energies range from 2.0 to 2.13 eV for the Al–O tetrahedra and Mg–O octahedra, whereas for Si–O tetrahedra and Mg–O octahedra these differences range from 4.23 to 8.5 eV. Regarding the formation energies, these range from 110.97 to 305.04 eV for Al–O tetrahedra and Mg–O octahedra, and from 118.54 to 355.65 eV for Si–O tetrahedra and Mg–O octahedra. The two energies of Mg–O octahedra are much lower than those of the two tetrahedra. At the same time, the energies of the two different Mg–O octahedral substitution sites are also quite different, due to the fact that chlorite is stacked by tot-o cells, and the first substitution site is a separate octahedral layer, while the second is an octahedral layer sandwiched by two tetrahedral layers. Since the first substitutional site is not encapsulated by tetrahedral layer, vanadium entry is easier and requires less energy than in the second substitutional site. Considering the substitution and formation energies, vanadium is less likely to be present in kaolinite among both layered minerals.

Fig. 2 Substitution site of vanadium in non-mica-type minerals [(a)-kaolinite(1-[Al_VI] 2-[Si_IV]) (b)-chlorite(1-[Al_IV] 2-[Mg_VI]₁ 3-[Mg_VI]₂ 4-[Si_IV]₁ 5-[Si_IV]₂ 6-[Si_IV]₃)].

3.1.2 Occupancy of vanadium atoms in the cyclic structures.
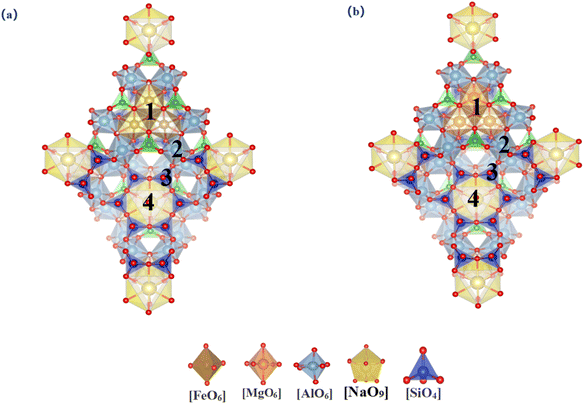
3.1.2.1 Tourmaline (dravite and schorl). Tourmaline is a representative cyclic silicate mineral. Given the nearly identical atomic environments within the unit cell, there is only one substitution site for each element. We examined the differences across eight substitution sites, as illustrated in Fig. 3. Table 3 summarizes the lattice parameters and substitution energies for various sites within two types of tourmalines. It was observed that the lattice parameters of tourmaline primarily undergo deformation along the c-axis following vanadium substitution, which is consistent with the behavior seen in layered structures. In Dravite, the substitution energy of Mg–O octahedral sites is −10.42 eV, and the formation energy of newly formed minerals post-substitution is −263.87 eV. In Schol, the substitution energy of Fe–O octahedral sites is −2.72 eV, and the formation energy of newly formed minerals post-substitution is −209.13 eV. Considering both the substitution and formation energies, vanadium is more likely to be accommodated within the Mg–O octahedral sites in Dravite among the tourmaline minerals.

Fig. 3 Vanadium substitution sites in tourmaline [(a)-dravite(1-[Mg_VI] 2-[Al_VI] 3-[Si_IV] 4-[Na_IX]); (b)-Schorl (1-[Fe_VI] 2-[Al_VI] 3-[Si_IV] 4-[Na_IX])].

3.1.3 Occupancy of vanadium atoms in the island structures.
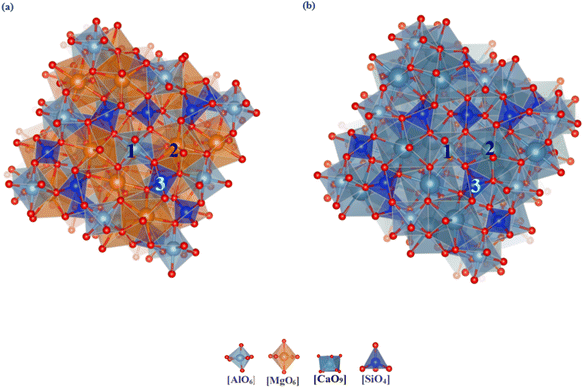
3.1.3.1 Garnet (pyrope and grossular). Garnet is a typical island aluminum silicate mineral. Due to the unique characteristics of this structure, the atomic environments within the unit cell are essentially identical. Six substitution sites were selected for study, as illustrated in Fig. 4. Table 3 provides the lattice parameters and substitution energies for different substitution sites in two types of garnet. The lattice parameters of garnet show almost no change after vanadium substitution at various sites. This stability is mainly because the tetrahedral structure in garnet can alleviate deformation caused by vanadium substitution through multidimensional twisting, resulting in minimal changes in the unit cell parameters. However, this also leads to increased internal stress, making substitution reactions within the garnet unit cell relatively difficult. For the Ga–O dodecahedral substitution site in grossular garnet, the substitution energy is −0.89 eV, and the formation energy of the newly formed mineral post-substitution is 546.87 eV and the substitution energy of Mg–O dodecahedral in pyrope garnet is −2.54 eV, and the formation energy of the newly formed mineral post-substitution is 251.94 eV. Considering both the substitution and formation energies, grossular garnet is less favorable for vanadium incorporation compared to other garnet types. However, the values of both energies are large, so the possibility of vanadium bearing in garnet is low.

Fig. 4 Vanadium substitution sites in garnet [(a)-pyrope(1-[Al_VI] 2-[Mg_VIII] 3-[Si_IV]); (b)-grossular (1-[Al_VI] 2-[Ca_VIII] 3-[Si_IV])].

3.1.4 Occupancy of vanadium atoms in the framework structures.
3.1.4.1 Feldspar and quartz. Feldspar and quartz are two framework silicate minerals. Since quartz is composed of pure SiO₂, there is only one substitution site in the lattice. Feldspar, on the other hand, has a total of five substitution sites for Al and Si with different coordination environments. We investigated the differences between the two minerals with a total of six substitution sites, as shown in Fig. 5. The lattice parameters and substitution energies of feldspar and quartz are listed in Table 3. After the substitution of both minerals, the cell is expanded in the c-axis direction, which is consistent with the changes occurring in the rest of the silicate minerals. In feldspar, the best Al–O tetrahedral site has a substitution energy of −0.59 eV, and the formation energy of the newly formed mineral after substitution is 229.32 eV, suggesting that this is the most stable configuration in feldspar. Vanadium is more likely to be present in feldspars, given the replacement and formation energies of vanadium. It is less likely that vanadium is endowed in both minerals.

Fig. 5 Vanadium substitution sites in two minerals [(a)-feldspar(1-[Al_IV]₁ 2-[Al_IV]₂ 3-[Si_IV]₁ 4-[Si_IV]₂ 5-[Si_IV]₃); (b)-quartz (1-[Si_IV])].

3.2 Structural distortions induced by vanadium substitution

The macroscopic changes in lattice parameters are inherently a result of alterations in atomic interactions. Thus, it is essential to analyze the local structural variations caused by vanadium substitution at different sites within each mineral. The probability of garnet, feldspar, and quartz bearing vanadium is low based on energetic determinations, and only the remaining seven silicate minerals classified as layered and cyclic will be discussed here (Fig. 6 and 7). This analysis aims to further elucidate the trends in internal structural changes induced by vanadium substitution across various minerals and to identify the substitution sites that result in the minimal internal stress.

Fig. 6 Changes of bond length and angle after vanadium substituting in two structures.

Fig. 7 Changes of bond angle after vanadium substituting in two structures.

3.2.1 Mica-type minerals. Based on the changes in bond length and bond angle shown in Fig. 6 and 7, it can be concluded that in mica like layered minerals, bond lengths grow by 0 to 0.20 Å during tetrahedral substitution in muscovite, and the V–O–Si(Al) bond angles change by −5° to 5°. During substitution, the expansion of vanadium-oxygen tetrahedra, confined by surrounding stable tetrahedra, expels bridging oxygen atoms toward the interlayer. This is because the V–O bond is longer than the Si–O bond, leading to a change in the V–O–Si(Al) bond angle. This primarily causes the deformation of the entire unit cell along the c-axis direction. After octahedral substitution of aluminum, bond length increases do not exceed 0.11 Å, and the V–O–Al bond angle changes are less than 3.2°. The surrounding octahedra exhibit good plasticity during octahedral substitution of aluminum, mitigating expansion deformation caused by larger vanadium atoms. In phlogopite, bond length fluctuations after octahedral substitution are less than 0.03 Å, and V–O–Al bond angle variations are less than 0.01°, much lower than the tetrahedral structural aberration. The localized structural features after vanadium substitution in biotite are similar to those in the other two micas. Following the octahedral substitution, the bond lengths changed by 0 to 0.18 Å, and the bond angles varied between −8.5° and 30°. This behavior can be attributed to the relatively large atomic radius of iron. This behavior can be attributed to the relatively large atomic radius of iron. When vanadium replaces iron, the central atom is shifted, leading to fluctuations in bond lengths; however, these changes in bond lengths within the lattice are limited due to the high plasticity of the octahedral unit. As a result, internal distortions lead to significant changes in some bond angles within the substituted octahedral lattice. Of the three mica species, phlogopite shows the least deformation upon substitution.

(The bar lengths in the figure indicate the range of mineral bond length variation, with dark blue, light blue, and purple corresponding to tetrahedral, octahedral, and Na–O dodecahedral variations in the minerals, respectively.)

3.2.1.1 Non-mica-type minerals (kaolinite and chlorite). The changes in bond length and bond angle before and after the substitution of kaolinite and chlorite are shown in Fig. 6 and 7. In kaolinite, tetrahedral substitution increased the bond length by 0 to 0.20 Å and changed the V–O–Si bond angle by −4° to 5°. After octahedral replacement, the bond lengths increased by 0 to 0.16 Å and the V–O–Al bond angles changed by −1 to 3°. In chlorite, tetrahedral substitution increased the bond length by 0 to 0.19 Å and the V–O–Si(Al) bond angle by −4° to 4°. After octahedral replacement, the bond lengths change by 0 to 0.15 Å and the V–O–Mg bond angles increase by 0° to 3.1°. Of the two layered minerals, chlorite shows the least deformation after replacement.

Analyzing from the perspective of octahedral structures, muscovite and kaolinite are classified as dioctahedral minerals, while phlogopite, biotite, and chlorite are classified as trioctahedral minerals. Upon octahedral substitution in dioctahedral minerals, the changes in bond lengths and bond angles range from 0 to 0.16 Å and from −2° to 3°, respectively. For trioctahedral minerals, excluding biotite, where the cell parameters change drastically due to the larger iron atom radius, the changes in bond lengths and bond angles after octahedral substitution range from 0 to 0.14 Å and from 0° to 3.1°, which are smaller than the changes observed in dioctahedral minerals. Considering parameters such as substitution energy, formation energy, and structural distortion, the trioctahedral layered minerals exhibit greater compatibility with vanadium atoms. Consequently, vanadium is more likely to be accommodated in the trioctahedral layered minerals.

3.2.1.2 Tourmaline (dravite and schorl). In the tetrahedral substitution of vanadium in the dravite, the bond length increases by 0.11 Å, and the V–O–Si bond angle enlarges by −3 to 3°. For octahedral substitutions, the increase in bond length is less than 0.05 Å, and the V–O–Al (Mg) bond angle changes by less than 3°. In the structure of schorl, tetrahedral substitution results in bond lengths increasing by 0 to 0.19 Å and bond angles increasing by −7° to 9°. In the case of octahedral substitution, bond lengths increase by 0.17 Å and bond angles by −7° to 30° (Fig. 6 and 7). The local structural features of the vanadium-substituted octahedra are similar to those found in biotite. However, since the shelf-structured tourmaline does not have an octahedral layer like the layered structure, after the central atom of the Fe–O octahedron is substituted, it is not possible to mitigate the deformation caused by the substitution by a stable octahedral layer, so not only the angle within the octahedron changes drastically, but the bond lengths also change drastically due to the lack of a stable constraint from the octahedral layer. The unstable Na–O dodecahedron in tourmaline undergoes a large change in bond lengths and angles when it is replaced by vanadium because it does not have the same stability as the octahedron. Among the tourmalines, dravite exhibits the least structural distortion upon substitution.

(The bar lengths in the figure indicate the range of in mineral bond angle variation, with dark blue, light blue, and purple corresponding to tetrahedral, octahedral, and Na–O dodecahedral variations in the minerals, respectively.)

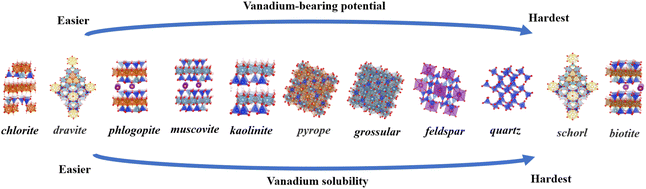
Comparing the two types of minerals, layered and cyclic, we exclude the two types of biotite and schorl, which have drastic structural distortions, and the iron-atom-bearing silicate minerals are unsuitable for vanadium bearing. In the layered structures, following tetrahedral substitution, the bond lengths change by 0 to 0.20 Å, and the bond angles change by −5° to 5°. After octahedral substitution, the bond lengths change by 0 to 0.16 Å, and the bond angles change by −2° to 3.1°. In cyclic structures, tetrahedral substitution leads to changes in bond lengths by 0 to 0.19 Å and bond angles by −3° to 9°. Octahedral substitution results in bond length changes from 0 to 0.09 Å and bond angle changes from −1 to 3°. The structural distortion in cyclic structures is less significant compared to that in layered structures. Vanadium-bearing minerals in four different types of silicate minerals are, from the easiest to the hardest: cyclic, layered, island and framework. Precisely eleven minerals are: chlorite, dravite, phlogopite, muscovite, kaolinite, pyrope, grossular, feldspar, quartz, schorl and biotite. Furthermore, octahedral sites are found to be more compatible with the presence of vanadium atoms Regardless of the silicate mineral structure, octahedral coordination remains the most favorable position for vanadium-bearing.

3.3 Formation of V–O bonds

3.3.1 Electron localization function and electric charge. In the previous section, it was determined that the octahedral structure is more favorable for vanadium in silicate minerals. Among the octahedra, there are three types, Mg–O, Al–O and Fe–O. The best minerals for each octahedron were selected: chlorite, muscovite, and schorl. In the field of quantum chemistry, the ELF (electron localization function) method is not only applicable for characterizing covalent bonds, but can also reveal information about the strength of bonding/binding from them.^41,42 The ELF diagrams of these octahedra are shown in Fig. 8. From the ELF analysis, we observed that upon vanadium substitution at the octahedral central position, the local electron density around the V and O atoms increases significantly. This indicates that the localized electronic character of the six surrounding oxygen atoms in the octahedron becomes more pronounced, confirming the formation of V–O bonds after substitution. During the bonding process, vanadium atoms lose electrons, while oxygen atoms gain electrons. Consequently, the localized electron intensity around the oxygen atoms surpasses that around the central vanadium atom, as depicted in The ELF diagrams. And among them, the electron density of the oxygen in the Mg–O octahedral structure is significantly larger than that of the remaining octahedra, suggesting that a strong electron transfer occurs in it.

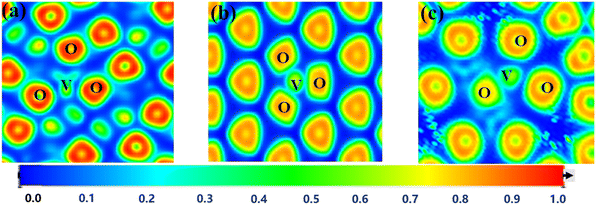Fig. 8 ELF plots of different octahedra in the three best minerals ((a)-chlorite; (b)-muscovite; (c)-schorl; the darker color of the octahedron in the figure indicates more electrons transferred).

During the formation of V–O bonds, the number of bonding electrons in the molecule directly affects the strength of the bonds formed. The charge distribution of the vanadium atoms in the three octahedral structures after substitution is shown in Fig. 9. Vanadium typically has 13 electrons in its outer shell. In the Mg–O octahedron, the amount of electron transfer to vanadium after substitution varies as follows, from highest to lowest: 2.62, 2.05 and 1.75. For the Al–O octahedron, the electron transfer amounts are 1.84–1.85, which is lower than that of the Mg–O octahedron. In the Fe–O octahedron, the electron transfer values are 1.73 and 1.64, the lowest among the three octahedral types. Thus, the strongest change in valence electrons in the Mg–O octahedron occurs when vanadium replaces the central atom of the octahedron.

Fig. 9 Charge of vanadium after formation of V–O bonds in octahedra of different elements.

3.3.2 The stability of the V–O bond. Density of states (DOS) is a widely utilized concept in Density Functional Theory (DFT), and the shift in DOS peaks can indicate the occurrence of a reaction and the stability of bond formation. As V enters the octahedral system displacing the central atom, vanadium provides electrons while the oxygen atom in the octahedral cavity accepts electrons and the V–O bond is formed. Oxygen plays a very crucial role in the formation of V–O bond. By analyzing the difference in DOS before and after oxygen substitution in different octahedra, the stability of the V–O bond can be determined. The DOS graphs of oxygen atoms in the Mg–O octahedra, Al–O octahedra, and Fe–O octahedra before and after substitution are illustrated in Fig. 10.

Fig. 10 DOS plots of different elements before and after octahedral substitution. (Mg–O: (a)-chlorite; (b)-dravite; (c)-phlogopite; Al–O: (d)-muscovite; (e)−kaolinite; Fe–O: (f)-schorl; (g)-biotite)

Our findings indicate that upon vanadium substitution, the DOS plots for oxygen in all three types of octahedra shift to the left, signifying a move towards lower energy states, leading to the formation of V–O bonds. For minerals containing Mg–O octahedra, the displacements values are 5, 4.5, and 4.44 eV for chlorite, dravite, and phlogopite depicted in Fig. 10(a)–(c), respectively, with an average shift of 3.91 eV. Notice that chlorite has the largest offset for the minerals containing Mg–O octahedra in panel (a). Regarding the minerals with Al–O octahedra, the displacement ranges from 3.38 to 3.77 eV, with an average of 3.57 eV, as extracted from Fig. 10 (d) and (e), respectively. Here muscovite shows the largest offset in Fig. 10(d). Lastly, for the Fe-octahedra cases depicted in Fig. 10(f) and (g), the maximum shift only is 0.28 eV for schorl shown in panel (f), which is significantly lower than the shifts observed in Mg-octahedra and Al-octahedra. Incorporating the conclusions drawn from the analysis, the formation of V–O bonds in the Mg–O octahedral structure is the most stable and robust when vanadium replaces the central atom in the system. Therefore, V–O bonds in the Mg–O octahedral structure are more stable than in other octahedral structures.

This comprehensive analysis suggests that minerals with Mg–O octahedra exhibit the largest DOS shifts. This indicates that after substitution, the system moves towards lower energy states, with V–O bonds formed in Mg–O octahedra being stronger and more stable. Therefore, Mg-octahedra are more favorable for vanadium bearing.

3.4 Interaction between vanadium occupation and its solubility

Above all, the ranking of vanadium-bearing potential across nine minerals, from the easiest to the hardest is: chlorite, dravite, phlogopite, muscovite, kaolinite, pyrope, grossular, feldspar, quartz, schorl and biotite (Fig. 11). According to Cromwell's theory, the dissolution process of silicate minerals in acids and bases is divided into three stages, where the cleavage of the Metal–O bond occurs in the first stage, while the breaking of the Si–O bond is considered to be the rate-limiting step in the dissolution process of silicates.⁴³

Fig. 11 Ranking of vanadium-bearing potential and vanadium solubility for eleven minerals.

Based on Sections 3.1 and 3.2, it was concluded that the octahedral central atom in silicate minerals is the most favorable site for vanadium bearing, and the breaking of metal-O bonds in aluminosilicate minerals usually occurs in the first stage. It is hypothesized that the relative difficulty of vanadium solubility from nine minerals can be determined by comparing the energy levels of three octahedral structures. The optimal octahedral substitution energies for 11 minerals are summarized in Table 3 as follows: chlorite (−10.93 eV), dravite (−10.42 eV), phlogopite (−4.93 eV), schorl (−2.72 eV), pyrope (−2.54 eV), muscovite (−1.12 eV), grossular (−1.11 eV), feldspar (−0.59 eV), quartz (−0.58 eV), kaolinite (−0.47 eV), and biotite (1.31 eV). In view of the unsuitability of Fe-bearing silicate minerals, island and framework silicate minerals for vanadium-bearing, these minerals were placed at the bottom of the vanadium solubility ranking (Fig. 11). Sort the eleven minerals by octahedral type: Mg–O octahedra (chlorite, dravite, phlogopite) >Al–O octahedra (muscovite, kaolinite, pyrope, grossular)> Al–O tetrahedron (feldspar) >Si–O tetrahedron (quartz)>Fe–O octahedra (schorl, biotite). Muscovite is the most common and representative vanadium-bearing mineral in vanadium shale. Using muscovite as a yardstick, the three minerals that lie ahead of muscovite in the ranking are easier in terms of vanadium-bearing potential and vanadium solubility and the seven minerals following the muscovite are more difficult in terms of vanadium potential and vanadium solubility. In the extraction of vanadium from shale, the ease of vanadium release can be obtained by comparing the differences in the ordering of the vanadium-bearing minerals with that of muscovite. From there, the amount of acid and leaching time conditions can be adjusted relative to each other to find the optimum leaching conditions for a particular shale more quickly.

4. Conclusion

Vanadium preferentially resides in minerals such as mica, chlorite, and tourmaline, rather than in kaolinite, garnet, feldspar or quartz. Among mica types, phlogopite shows the highest suitability for vanadium retention compared to muscovite and biotite. In tourmaline, vanadium exhibits a stronger affinity for dravite. Based on energetic variations and structural distortions, the ranking of vanadium-bearing potential across eleven minerals, from the easiest to the hardest is: chlorite, dravite, phlogopite, muscovite, kaolinite, pyrope, grossular, feldspar, quartz, schorl and biotite.

When vanadium replaces central atoms in the octahedral lattices of these minerals, the system stabilizes with minimal structural distortion and achieves its lowest energy configuration. In layered minerals, trioctahedral structures are more compatible with vanadium than dioctahedral ones. Additionally, vanadium substitution in Mg–O octahedra leads to the most stable V–O bonds in these silicate minerals. These findings suggest that vanadium leaching is strongly influenced by the mineral's crystal structure, with the destruction of octahedra being key to the release of vanadium from shale.

The vanadium solubility rankings of the eleven minerals were determined from the energy variations, and the vanadium solubility rankings were positively correlated with the rankings of the minerals' vanadium-bearing potentials. In the extraction of vanadium from shale, by clarifying the composition of the mineral and the main vanadium-bearing minerals, and comparing them with the muscovite in the middle of the sequence, the difficulty of vanadium dissolution of the mineral can be derived more quickly to determine the range of the acid, which reduces the cost of the experiments and reduces the time of the experiments. Further exploration of the differences in leaching behavior among various silicate minerals will be presented in future papers.

Data availability

Data for this article, including Crystal CIF files are available at Crystallography Open Database (COD) at [https://www.crystallography.net/cod/result.php]. The Crystal CIF files in the text have all been marked with COD ID. The calculation software is: MedeA version 3.0; MedeA is a registered trademark of Materials Design, Inc., San Diego, USA.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by Hubei Science and Technology Innovation Talents and Services Special Program (2022EJD002), National Natural Science Foundation of China (52174260) and National Natural Science Foundation of China Youth Foundation (52104311).

References

1. H. Falk, U. Lavergren and B. Bergbäck, Metal mobility in alum shale from Öland, Sweden, J. Geochem. Explor., 2006, 90(3), 157–165.
2. C. Scott, J. F. Slack and K. D. Kelley, The hyper-enrichment of V and Zn in black shales of the Late Devonian-Early Mississippian Bakken Formation (USA), Chem. Geol., 2017, 452, 24–33.
3. P. F. Greenwood, J. J. Brocks and K. Grice, et al., Organic geochemistry and mineralogy. I. Characterisation of organic matter associated with metal deposits, Ore Geol. Rev., 2013, 50, 1–27.
4. A. Parviainen and K. Loukola-Ruskeeniemi, Environmental impact of mineralised black shales, Earth-Sci. Rev., 2019, 192, 65–90.
5. C. Zou, R. Zhu and Z. Q. Chen, et al., Organic-matter-rich shales of China, Earth-Sci. Rev., 2019, 189, 51–78.
6. Y. Ju, Y. Sun and J. Tan, et al., The composition, pore structure characterization and deformation mechanism of coal-bearing shales from tectonically altered coalfields in eastern China, Fuel, 2018, 234, 626–642.
7. Z. Abdi, S. M. Rimmer and H. D. Ro we, et al., Trace-metal enrichment mechanisms in Bakken Formation black shales, Williston Basin, North Dakota, USA, Chem. Geol., 2024, 646, 121892.
8. L. Yang, Z. Li and Y. Ouyang, et al., Mannardite as the main vanadium-hosting mineral in black shale-hosted vanadium deposits, South China, Am. Mineral., 2024, 109(2), 359–373.
9. S. Y. Jiang, Y. Q. Chen and H. F. Ling, et al., Trace-and rare-earth element geochemistry and Pb–Pb dating of black shales and intercalated Ni–Mo–PGE–Au sulfide ores in Lower Cambrian strata, Yangtze Platform, South China, Miner. Deposita, 2006, 41, 453–467.
10. Q. S. Cai, M. Y. Hu and B. M. Zhang, et al., Source of silica and its implications for organic matter enrichment in the Upper Ordovician-Lower Silurian black shale in western Hubei Province, China: insights from geochemical and petrological analysis, Pet. Sci., 2022, 19(1), 74–90.
11. J. Mao, B. Lehmann and A. Du, et al., Re-Os dating of polymetallic Ni-Mo-PGE-Au mineralization in Lower Cambrian black shales of South China and its geologic significance, Econ. Geol., 2002, 97(5), 1051–1061.
12. R. B. Perkins and C. E. Mason, The relative mobility of trace elements from short-term weathering of a black shale, Appl. Geochem., 2015, 56, 67–79.
13. K. D. Kelley, C. Scott and D. E. Polyak, et al. Vanadium[R], US Geological Survey, 2017.
14. P. Hu, L. Liang and G. Xie, et al., Effect of slurry conditioning on flocculant-aided filtration of coal tailings studied by low-field nuclear magnetic resonance and X-ray micro-tomography, Int. J. Min. Sci. Technol., 2020, 30(6), 859–864.
15. Y. Dong, L. I. U. Yue and L. Hai, et al., Improving vanadium extraction from stone coal via combination of blank roasting and bioleaching by ARTP-mutated Bacillus mucilaginosus, Trans. Nonferrous Met. Soc. China, 2019, 29(4), 849–858.
16. P. Zuo, Q. Chen and Z. Xiao, et al., Geology and mineral assemblages of the early Cambrian black shales in the South Qinling: implications for vanadium and barium mineralization, Ore Geol. Rev., 2023, 105624.
17. Z. Zhou, J. Jin and Y. Zhu, et al., Effect of roasting temperature on vanadium extraction, kinetics, phase transformation, and microstructure evolution of vanadium-bearing shale during suspension oxidation roasting process, Adv. Powder Technol., 2023, 34(11), 104233.
18. N. Xue, Y. Zhang and J. Huang, et al., Separation of impurities aluminum and iron during pressure acid leaching of vanadium from stone coal, J. Cleaner Prod., 2017, 166, 1265–1273.
19. B. Yan, D. Wang and L. Wu, et al., A novel approach for pre-concentrating vanadium from stone coal ore, Miner. Eng., 2018, 125, 231–238.
20. M. R. Li, D. Y. Liang and X. J. He, Process mineralogical study of a stone-coal type vanadium ore in Hubei, Metal Mining, 2015,(2), 87–91.
21. X. Zeng, F. Wang and H. Zhang, et al., Extraction of vanadium from stone coal by roasting in a fluidized bed reactor, Fuel, 2015, 142, 180–188.
22. W. Z. Yin and C. Y. Sun, X-ray photoelectron spectrometric analysis on surface property of silicate minerals, J. Northeast. Univ., Nat. Sci., 2002, 23, 156–159.
23. Y. M. Zhang, S. X. Bao and T. Liu, et al., The technology of extracting vanadium from stone coal in China: History, current status and future prospects, Hydrometallurgy, 2011, 109(1–2), 116–124.
24. M. Q. Shah, M. Shafiq and A. Naeem, et al., Effect of position occupancy of different elements on the structural stability, optoelectronic, thermoelectric and elastic properties of Cs2CuAsX6 (X: Cl, Br, I) halide double perovskite: DFT analysis, Mater. Sci. Semicond. Process., 2024, 174, 108187.
25. Y. He, L. Zhang and H. Xiong, et al., The selective site occupation, structural and thermal stability of high entropy (CoCrFeMnNi) 3O4 spinel, J. Alloys Compd., 2023, 965, 171428.
26. Q. Zheng, Y. Zhang and N. Xue, et al., Vanadium occupation and its leachability differences in trioctahedral and dioctahedral mica, RSC Adv., 2019, 9(47), 27615–27624.
27. F. K. Crundwell, The mechanism of dissolution of minerals in acidic and alkaline solutions: Part II Application of a new theory to silicates, aluminosilicates and quartz, Hydrometallurgy, 2014, 149, 265–275.
28. M. Catti, G. Ferraris and S. Hull, et al., Powder neutron diffraction study of 2M1 muscovite at room pressure and at 2 GPa, Eur. J. Mineral., 1994, 6(2), 171–178.
29. C. Aiqing and Z. Lixue, Crystal structure of Al-rich fluorophlogopite, K1. 0 (Mg2. 8Al0. 2)(Si2. 8Al1. 2) O10F2, Z. fur Krist. - New Cryst. Struct., 2021, 236(5), 931–933.
30. M. F. Brigatti and P. Davoli, Crystal-structure refinements of 1M plutonic biotites, Am. Mineral., 1990, 75(3–4), 305–313.
31. J. W. Gruner, The crystal structure of kaolinite, Z. fur Krist. - New Cryst. Struct., 1932, 83(1–6), 75–88.
32. R. C. McMurchy, The crystal structure of the chlorite minerals, Z. fur Krist.–New Cryst. Struct., 1934, 88(1–6), 420–432.
33. F. Bosi, L. Z. Reznitskii and E. V. Sklyarov, Oxy-vanadium-dravite, NaV3 (V4Mg2)(Si6O18)(BO3) 3 (OH) 3O: crystal structure and redefinition of the “vanadium-dravite” tourmaline, Am. Mineral., 2013, 98(2–3), 501–505.
34. G. A. Lager, R. T. Downs and M. Origlieri, et al., High-pressure single-crystal X-ray diffraction study of katoite hydrogarnet: evidence for a phase transition from Ia3d → I4̄3 d symmetry at 5 GPa, Am. Mineral., 2002, 87(5–6), 642–647.
35. N. I. Organova, I. M. Marsii and I. V. Rozhdestvenskaya, et al., Structures of the K-and Na-components of two-phase feldspar from primore, Crystallography, 1999, 44(5), 829–834.
36. A. F. Wright and M. S. Lehmann, The structure of quartz at 25 and 590 C determined by neutron diffraction, J. Solid State Chem., 1981, 36(3), 371–380.
37. Q. Zheng, Y. Zhang and T. Liu, et al., Optimal location of vanadium in muscovite and its geometrical and electronic properties by DFT calculation, Minerals, 2017, 7(3), 32.
38. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865.
39. M. Ernzerhof and G. E. Scuseria, Assessment of the Perdew–Burke–Ernzerhof exchange-correlation functional, J. Chem. Phys., 1999, 110(11), 5029–5036.
40. G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(3), 1758.
41. A. Savin, R. Nesper and S. Wengert, et al., ELF: The electron localization function, Angew Chem. Int. Ed. Engl., 1997, 36(17), 1808–1832.
42. K. Koumpouras and J. A. Larsson, Distinguishing between chemical bonding and physical binding using electron localization function (ELF), J. Phys.: Condens. Matter, 2020, 32(31), 315502.
43. E. L. Lippert and M. R. Truter, 968. The stereochemistry of acetylacetone complexes of zinc. Part I. The crystal structure of monoaquobisacetylacetonezinc, J. Chem. Soc., 1960, 4996–5006.

---