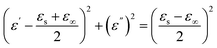DOI:
10.1039/D5RA03621F
(Paper)
RSC Adv., 2025,
15, 24679-24695
Improving the multiferroic properties and ability to absorb electromagnetic microwaves of NFO/BZT-BCT composites
Received
23rd May 2025
, Accepted 27th June 2025
First published on 14th July 2025
Abstract
Multiferroic composites of xNiFe2O4/(1 − x)(0.5BaZr0.2Ti0.8O3-0.5Ba0.7Ca0.3TiO3) (NFO/BZT-BCT with x = 0, 0.2, 0.4, 0.6, 0.8 and 1.0) with an average particle size of 100 nm was prepared by high-energy ball milling combined with the thermal annealing methods. The X-ray diffraction patterns indicate the presence of both NiFe2O4 (NFO) and BaZr0.2Ti0.8O3-Ba0.7Ca0.3TiO3 (BZT-BCT) phases in the multiferroic composites. As the ferromagnetic phase content increases, the ferroelectric and ferromagnetic properties of the material are significantly improved. For an applied electric field below 10 kV cm−1, the values of the residual polarization (Pr) and the coercive field (Ec) are found to be 0.02–0.064 μC cm−2 and 2.06–5.67 kV cm−1, corresponding to x = 0–0.8, respectively. The loss of energy density increases from 0.035 to 0.18 mJ cm−3 and the stored energy density decreases from 82.6 to 17.4%, with NFO content increasing from 0 to 0.8. The material has the ability to strongly absorb electromagnetic waves (EMW) in the frequency range of 2–18 GHz corresponding to thicknesses of 1.5–5 mm. With a thickness of 2.5 mm, the minimum reflection loss (RLmin) value reaches −41.87 dB occurring at 13.06 GHz for the NFO sample; RLmin = −38.51 dB for the BZT-BCT sample at 12.5 GHz and RLmin = −33.91 dB for the NFO/BZT-BCT with x = 0.4 (NBZ4) sample at 9.62 GHz. The research results show the potential for developing electromagnetic wave absorption applications of the material in a wide range of investigated frequencies from 2–18 GHz.
Introduction
Nowadays, multiferroic composites are widely used in many different fields in advanced electronic components such as DRAM, MRAMs, FeRAMs, magnetic transducers, actuators.1–4 Their unique combination of ferroelectric and magnetic properties makes them promising candidates for advanced electronic applications, sensors, and ultra-high-speed telecommunications absorb electromagnetic wave (EMW)5–8 and so on. Multiferroic composites are engineered materials that bring together at least two distinct phases with different physical and chemical properties: a ferroelectric phase and a ferromagnetic or ferrimagnetic phase. These are not single materials with inherent multiferroic properties, but rather a combination of different materials designed to exhibit both ferroelectricity and ferromagnetism. The quest for multiferroic materials that exhibit coupling effects between electric and magnetic properties is a fascinating area in materials engineering.9 The structure of multiferroic composites can vary significantly depending on the fabrication method and desired properties.10–12 They absorb electromagnetic waves through a combination of energy dissipation mechanisms inherent to their ferroelectric and ferromagnetic components, influenced by their structural arrangement and the coupling between the two phases. Their electromagnetic wave absorption properties depend on the properties, structure and ration between phases, and as well as the frequency of the electromagnetic wave.7,10,13 The ferroelectric component contributes to absorption through dielectric polarization and subsequent energy dissipation as heat.14–16 The magnetic component absorbs electromagnetic wave through magnetic losses arises from the interaction of the oscillating magnetic field of the wave with the material's magnetic moments.11,14,17 The ability of multiferroic composites to absorb electromagnetic wave depends on the influence of dielectric constant and permeability in the electromagnetic field. An increase in ferrite content in a composite can affect the dielectric constant and resistivity. With increased ferrite content, resistivity might decrease as the ferrite phase often has lower resistivity than the ferroelectric phase, forming conductive chains. Therefore, the selection of materials that act as ferroelectric and ferromagnetic phases of multiferroic composites is considered important in adjusting the ability to absorb electromagnetic wave.18
For the ferromagnetic phase, spinel ferrites such as MFe2O4, (M is Fe, Ni, Co, Zn, Mn…) are chosen as the typical materials. They have some advanced characters, such as high permeability, high saturation magnetization, and high resistivity. For magnetic materials with spinel structure, and their interaction with the magnetic component of an EMW leads to energy dissipation. Factors like the anisotropy energy and saturation magnetization of the spinel oxide influence the natural resonance frequency.18,19 Spinel oxides absorb electromagnetic waves through a complex interplay of magnetic and dielectric loss mechanisms. The specific contributions of each mechanism depend on the material's intrinsic properties, its microstructure, and the frequency of the incident electromagnetic radiation. Designing spinel oxide-based materials with controlled morphology, composition, and heterostructures is a key strategy for achieving high-performance microwave absorption.19,20 A typical example is NiFe2O4 (NFO). This is a soft ferromagnetic material, characterised by low coercivity and high saturation magnetisation. These magnetic properties contribute to its ability to interact with and absorb electromagnetic waves through magnetic losses.8–10 NiFe2O4 is a potential component in microwave absorbing materials (MAMs) and radar absorbing materials (RAM) that operate in the GHz frequency range like the making it useful in microwave absorption applications, often in composites where its properties can be combined with other materials to enhance performance.17–21 Spinel ferrite nanoparticles, particularly NiFe2O4, show promise in electromagnetic wave absorption technology due to their magnetic and dielectric loss capabilities. However, their application still faces several limitations. Single-phase spinel ferrite nanoparticles often have limited absorption bandwidth, require high material thickness, and possess high density, reducing their practicality as EMI shielding materials.22 Additionally, they frequently encounter poor impedance matching, leading to a significant portion of waves being reflected rather than absorbed.23 Spinel ferrites primarily rely on magnetic loss mechanisms, but achieving optimal performance necessitates a balance with dielectric loss. A lack of or imbalance between these two mechanisms can diminish absorption efficiency.24 Furthermore, the scalability of manufacturing effective millimeter-scale absorbing materials remains limited, especially for Ni-ferrite.25
To overcome these limitations and enhance the permeability of NiFe2O4, the combined method of solid-state reaction (SSR) and high-energy ball milling (HEBM) offers several advantages. The annealing process in SSR helps atoms rearrange into a stable crystalline structure, minimizing lattice defects and improving magnetic properties, including high permeability. Although HEBM can initially introduce defects, its use as a pre-treatment step to homogenize and reduce precursor size facilitates the subsequent calcination process. This “heals” defects and promotes better crystalline structure formation, leading to higher permeability. HEBM also allows for better control over precursor particle size, which in turn optimizes the final NiFe2O4 particle size through adjusted milling and calcination parameters, helping achieve the highest permeability.
For ferroelectric phase, a typical example is BaTiO3. This is a lead-free material with a high dielectric constant, high spontaneous polarization, large piezoelectric coefficient, its chemical versatility for property tuning, and compatibility with ferromagnetic phase.26–29 These factors make it a versatile building block for designing novel multiferroic materials with tailored properties for various applications. Recently, studies on the electromagnetic wave absorption ability of BaTiO3-based materials in the frequency range of 2–18 GHz have attracted much attention. The results indicate that BaTiO3/TiO2@PPy HoMSs exhibit improved microwave absorption compared with BaTiO3/TiO2 HoMSs. In particular, tripled-shelled BaTiO3/TiO2@PPy HoMS has the most excellent absorbing performance. The best reflection loss can reach up to −21.80 dB at 13.34 GHz with a corresponding absorber thickness of only 1.3 mm, and the qualified absorption bandwidth of tripled-shelled BaTiO3/TiO2@PPy HoMS is up to 4.2 GHz.27 In addition, recent results indicate that the electromagnetic wave absorption ability of multiferroic materials combining BaTiO3 substrate with ferromagnetic materials with spinel structure has a peak value of reflection loss shifted to the frequency from 8 to 12 GHz.7,11,14,26 The electrical properties of BaTiO3 can be altered by substituting ions at either the barium (Ba) site or the titanium (Ti) site in its perovskite structure with elements like calcium (Ca) or zirconium (Zr).10,31 For instance, calcium substitution (Ba1−xCaxTiO3: BCT) can lead to a phase transition from rhombohedral to cubic, while zirconium substitution (BaZryTi1−yO3: BZT) can result in a tetragonal to cubic phase transition.28 Doping with elements like strontium (Sr) can also enhance the dielectric constant and piezoelectric properties.11,30 The high piezoelectric coefficient of systems like Ba1−xCaxZryTi1−yO3 (derived from BaTiO3) is attributed to the presence of such a boundary.10,17,31 Among the BaTiO3-based materials, BZT-BCT material is considered as a typical lead-free piezoelectric material. Compositions of BZT-BCT near the morphotropic phase boundary (MPB) have been reported to exhibit significantly higher piezoelectric coefficients (d33 ∼ 620 pC N−1) compared to pure BaTiO3 (d33 ∼ 150–190 pC N−1).31 The existence of an MPB, where multiple phases coexist, is often associated with enhanced piezoelectric properties, which are crucial for strong magnetoelectric coupling in composites relying on strain transfer mechanisms.32 This enhanced piezoelectricity is attributed to the coexistence of different ferroelectric phases, leading to a lower energy barrier for polarization rotation and thus a larger piezoelectric response to applied stress.28 The higher piezoelectric coefficient of BZT-BCT suggests an even greater potential for enhanced (magnetoelectric) ME coupling when combined with a magnetostrictive phase. Studies have indeed shown promising ME coefficients in composites using BZT-BCT derivatives.32 Based on the above characteristics and properties of spinel ferrite NFO and piezoelectric material BZT-BCT, we can see that they can be combined into multiferroic materials with many potential applications, especially electromagnetic wave absorption applications. However, research on multiferroic materials by combining BZT-BCT with NFO oriented for electromagnetic wave absorption represents a new idea that has not been mentioned before. In this study, we investigate the fabrication and properties of xNiFe2O4/(1 − x)(0.5BaZr0.2Ti0.8O3-0.5Ba0.7Ca0.3TiO3) (denoted as NFO/BZT-BCT) composites and examine their ability to absorb electromagnetic waves in the frequency range of 2–18 GHz. This research is a pioneering effort involving the NFO/BZT-BCT material family. The findings in this work will contribute to expanding the potential applications of multiferroic composites in the areas of electromagnetic wave absorption and shielding at high frequencies.
Experiment
Multiferroic composites of NFO/BZT-BCT were synthesized for values of x = 0.0, 0.2, 0.5, 0.8, and 1.0. These samples were prepared using a combination of high-energy mechanical milling and thermal annealing methods. The raw materials included BaCO3, CaCO3, TiO2, ZrO2, NiO, and Fe2O3 powders, all with a purity of 99.9% or higher. The particulate composites containing the BZT-BCT compound and the NFO compound were fabricated separately. The raw chemical powder mixtures of the BZT-BCT and NFO phases were ground and mixed by high-energy ball milling for 30 min. After mixing, the powder mixtures were pressed into pellets under a pressure of 7000 kg cm−2. Each set of pellets were subsequently sintered for 5 h in air at 1300 °C for BZT-BCT sample and at 1000 °C for NFO sample with a heating rate of 5 °C min−1. After that the samples were cooled naturally with the furnace to room temperature. Following sintering, the NFO and BZT-BCT samples were subjected to high-energy ball milling for 2 h in the air, resulting in fine powders as the final products. The NFO and BZT-BCT powders were measured according to the molar ratios of xNFO/(1 − x)BZT-BCT with x = 0, 0.2, 0.4, 0.6, 0.8, 1, labeled as BZT-BCT, NBZ2, NBZ4, NBZ6, and NBZ8, NFO, respectively. Herein, high-energy ball milling processes have used a SPEX SamplePrep 8000D Mixer/Mill machine with a speed of 875 rpm in air at room temperature with a ball/powder weight ratio of 24/5. After weighing the powders, the mixtures were thoroughly combined and pressed into pellets under a pressure of 7000 kg cm−2. These pellets were then heat-treated at 800 °C for 6 h to form solid pellets of uniform size, 12 mm in diameter and 1 mm in thickness. The structure of all samples was analyzed using the X-ray diffraction (XRD) patterns obtained from a Thermo Scientific Equinox 5000 device, utilizing a wavelength of λ = 1.54056 Å from Cu-Kα radiation. Raman spectra of samples have been measured at room temperature using Raman spectroscopy instruments, powered by LabSpec 6 HORIBA (Japan). The morphology and particle size of the samples were determined using the field emission scanning electron microscopy (FE-SEM) with equipment of Hitachi S4800. The chemical elements' composition and the substances' distribution within the samples were analyzed using Aztec energy dispersive spectroscopy (EDS) equipment from Oxford Instruments (UK). The samples' characteristic ferromagnetic and ferroelectric properties were assessed using M(H) and P(E) hysteresis curves. These measurements were conducted at room temperature with a vibrating sample magnetometer VersaLab (Quantum design) and a Precision LC II Model 609 system. Herein, an external voltage of 1 kV was applied, corresponding to an applied electric field of 10 kV cm−1 for P(E) hysteresis measurements. To investigate the microwave absorption properties of the samples, we measured the S-parameters using a vector network analyzer (VNA, PNA-X, Keysight). Where, the final NFO/BZT-BCT powders were mixed with paraffin in a volume ratio of 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60, and then were formed into toroidal devices using a punch, which had inner and outer diameters of 3.04 mm and 7 mm, respectively. After collecting the S-parameter data, we used the Nicolson–Ross–Weir (NRW) method to extract the complex permittivity and complex permeability of the samples. Finally, the microwave absorption performance was calculated using transmission line theory.
60, and then were formed into toroidal devices using a punch, which had inner and outer diameters of 3.04 mm and 7 mm, respectively. After collecting the S-parameter data, we used the Nicolson–Ross–Weir (NRW) method to extract the complex permittivity and complex permeability of the samples. Finally, the microwave absorption performance was calculated using transmission line theory.
Result and discussion
XRD patterns at room temperature of all the samples are presented in Fig. 1(a). Our findings indicate that the x = 0 sample exhibits a single phase of BZT-BCT, which corresponds to a tetragonal structure. This is represented by a set of Miller indices (hkl), including (100), (110), (111), (002), (210), (211), and (220). In the XRD patterns of the other samples, we observed some peaks corresponding to the NFO phase, which has a cubic structure (denoted by asterisks *), coexisting with those of the BZT-BCT phase. Notably, there was no observable shift in the XRD peaks or any appearance of unusual peaks. This implies that the BZT-BCT and NFO phases can coexist in the samples, and the heat treatment did not result in the formation of a new phase. Raman spectroscopy is considered a powerful technique for identifying subtle structural distortions and symmetry in perovskite materials. The Raman spectra of the NFO/BZT-BCT material are shown in Fig. 1(b). The NFO/BZT-BCT material has a basic BaTiO3 (BTO) matrix with a perovskite structure and therefore exhibits the same Raman modes as pure BTO. The band assignments were performed using literature data for pure BTO. The resonance frequencies of [E(LO), A1(LO), E(TO)], [E(TO), A1(TO)], and [E(LO), A1(LO)] were reported to be located at 432.36, 519.1, and 725.54 cm−1, respectively, for all samples.33,34 This indicates that the material has a tetragonal phase. As the NFO content increases, the intensity of the spectral peaks corresponding to wavenumbers 519.1 and 725.54 cm−1 significantly decreases and shows a tendency to broaden gradually. When the NFO content gradually increases, the spectral peaks corresponding to wavenumbers 180.06, 519.1, and 725.54 cm−1 shift slightly to peaks corresponding to wavenumbers 171.39, 510.26, and 718.89 cm−1. This is due to fluctuations in the perovskite structure of the material. Although both the ferroelectric BZT-BCT phase and the ferromagnetic NFO phase are simultaneously present in the composite, there is no chemical reaction. However, electromagnetic interactions still occur at the interface between the two phases, causing a slight effect on the material's structure.
 |
| | Fig. 1 (a) XRD patterns and (b) Raman spectra of the powdered composites of xNiFe2O4/(1 − x)(0.5Ba(Zr0.2Ti0.8)O3-0.5(Ba0.7Ca0.3)TiO3). | |
The morphology and particle size of the samples were analyzed using scanning electron microscopy (SEM) images. Fig. 2 presents the SEM images of four samples of BZT-BCT, NBZ2, NBZ4, and NBZ8, (remaining sample has a similar form). The grains in all samples were not homogeneous, with sizes ranging from several tens to hundreds of nanometers. Smaller particles were observed adhering to the larger ones. The crystal orientation appeared random, likely due to various interactions. The average grain size (D) was determined using grain size analysis software integrated with field emission scanning electron microscopy (FE-SEM) equipment from Hitachi S4800. The particle size distribution was broad, with an average value of approximately 100 nm. Because of the sample's poor electrical conductivity, the grain boundaries were unclear, leading to the formation of clumps between the particles. Furthermore, the particle size remained consistent, regardless of the sample composition or the content of NFO.
 |
| | Fig. 2 SEM images of the (a) BZT-BCT, (b) NBZ2, (c) NBZ4, (d) NBZ8 samples. | |
To verify the presence and distribution of elements in the BZT-BCT sample, specifically Ba, Ca, Ti, Zr, and O, as well as Ba, Ca, Ti, Zr, Ni, Fe, and O in the composite samples, we conducted elemental mapping analysis, as shown in Fig. 3(a and b). The results indicate that all components are evenly distributed throughout the material. This finding confirms that the multiferroic composites have been fabricated, with the ferromagnetic and ferroelectric components thoroughly mixed and uniformly dispersed within the samples. The percentage rations of elements are quite close to those of the nominal values of the samples, no presence of any foreign elements, shown in Fig. 3(c and d), EDX spectra of BZT-BCT and NBZ4 samples. Fig. 4 shows hysteresis curves M(H) for all samples at room temperature. All samples demonstrate the ferromagnetic characteristics except the BZT-BCT sample, which is clearly identified as a paramagnetic compound exhibiting very low magnetization. The magnetization of the NFO/BZT-BCT composites increases significantly with higher concentrations of NFO, with saturation magnetization (Ms) rising from 13.6 to 57.7 emu g−1 and residual magnetization (Mr) increasing from 0.67 to 1.4 emu g−1 as NFO content (x) changing from 0.2 to 0.8. This is completely agreed with previous studies.2,3,5,10 The coercivity (Hc) value decreases with increasing NFO concentration, from Hc = 66 Oe at x = 0.2 to Hc = 49 Oe at x = 0.8, is also a trend that has been reported in some studies, although the relationship between ferrite content and coercivity can be more complex. A decrease in coercivity with increasing ferrite content might be explained by: (i) with a higher proportion of the magnetic phase, the composite might become easier to magnetize and demagnetize, leading to a lower coercive field,1 (ii) at lower ferrite concentrations, the non-magnetic ferroelectric grains might act as “pores” in the magnetic structure, hindering the movement of magnetic domain walls and thus increasing coercivity.2 The increase of saturation and residual magnetization with NFO content, and the decrease of coercive force, are generally consistent with the behaviour observed in similar multiferroic composite systems as described in the provided sources. The dominance of the ferrite phase's magnetic contribution explains the increase in Ms and Mr, while the decrease in Hc could be related to easier magnetization.10,11,13 This data is clearly presented in the inset of Fig. 4 and Table 1. Fig. 5(a) shows the ferroelectric hysteresis loops P(E) of NFO/BZT-BCT composites measured at room temperature under a maximum external voltage of 1 kV at a frequency of 50 Hz. It is clear that these P(E) hysteresis loops exhibit the ferroelectric characteristics. As the NFO concentration increasing, these P(E) curves are widened and the value of the electrical polarization increases significantly. When the ferrite phase content gradually increases from x = 0 to x = 0.8, the shape of the curve also changes quite significantly. The abnormal ferroelectric loops with rounded edges are due to the leakage current generated by the less resistive ferrite phase.7,11 The leakage current due to the incorporation of a less resistive ferrite phase compared to the higher resistive ferroelectric phase results in non-saturated, round P(E) loops, the non-saturated and rounded edges in P(E) loops are due to leakage currents in the composites.2,7 The remanent polarization is considered an indirect quantity used when evaluating the magnetoelectric coupling coefficient in multiferroic composites.35 Indeed, in these materials, the efficiency of magnetoelectric coupling largely depends on the ferroelectric phase's ability to generate strain when an electric field is applied. The greater value of the potential for a change in strain (ΔS) during ferroelectric switching will be occurred with higher value of the remanent polarization (Pr). This ΔS is then transferred to the magnetostrictive phase, altering its magnetic properties. Therefore, the magnitude of the polarization change (ΔP, from +Pr to −Pr or vice versa) directly determines the maximum strain transfer and the resulting magnetoelectric response.36 The piezoelectric coefficient, which indicates the strain generated per unit electric field, is inherently linked to the ferroelectric state and its Pr. A robust Pr signifies well-aligned ferroelectric domains, leading to a more effective piezoelectric response. Consequently, a larger ΔP (due to a stronger Pr) directly contributes to a greater induced strain, which is crucial for efficient strain-mediated magnetoelectric coupling.35,36 Besides, as x increases from x = 0 to x = 0.4, the value of Pr increases more than 3 times, from 0.02 to 0.064 μC cm−2. This enhancement has been attributed to the space charge effect that arises at the interface between the ferroelectric and ferrite phases due to differences in their conductivities and permittivities.10 As the amount of the ferrite phase increases, more space charges accumulate at these interfaces, contributing to a higher overall polarization.11 Additionally, the presence of the ferrite phase can induce stress on the ferroelectric phase, which, through magnetoelectric coupling, could potentially influence the polarization state and lead to an initial increase in Pr under certain conditions.12 However, beyond a certain concentration, the remanent polarization typically starts to decrease with further increases in the ferrite content x ≥ 0.4. This can be explained that: (i) the ferrite phase is generally not ferroelectric. As its proportion increases, it effectively dilutes the overall ferroelectric nature of the composite, leading to a reduction in the total polarization, including the remanent polarization;37 (ii) ferrite phases often have a lower electrical resistivity compared to ferroelectric phases. Introducing more of the ferrite phase31 creates more conductive pathways within the composite, resulting in a higher leakage current.38 This leakage of charge can hinder the retention of polarization, thus decreasing the measured remanent polarization.39 The rounded hysteresis loops observed in many studies with increasing ferrite content are indicative of this increased leakage;7 (iii) while the presence of the ferrite phase can lead to a pinning effect on the ferroelectric domains, which might initially contribute to an increase Ec and Pr, at higher concentrations, this pinning can become too dominant. It can impede the switching of ferroelectric domains and their alignment, ultimately leading to a decrease in the achievable remanent polarization.2 Beside, as x increases from x = 0 to x = 0.4, the Ec also tends to rise sharply, nearly 3 times, from 2.06 to 5.67 kV cm−1, these increases are attributed to the pinning effect that arises and relates to the presence of the FM phase in composites. It can be seen that, with the ferrite phase content reaching about x = 0.4, the Ec value reaches its maximum. This result indicates that, with the content x = 0.4, the pinning effect is most effective.14 This might occur at a specific concentration and distribution of the ferrite phase where the domain wall motion is optimally impeded.31 However, when the ferromagnetic phase content is higher than x = 0.4, the coercive force value Ec tends to decrease, which can be explained by: (i) at higher ferrite concentrations, the ferrite phase might become more interconnected, potentially leading to easier magnetic domain wall motion within the ferrite phase itself. This could, in turn, reduce the overall constraint on the ferroelectric domains;10 (ii) a higher content of the typically less resistive ferrite phase leads to a significant increase in leakage current. This leakage can effectively screen the applied electric field within the ferroelectric domains, making it easier to switch their polarization at lower applied fields, thus reducing Ec. The rounded P–E loops observed with higher ferrite content often indicate such increase leakage;14 (iii) at very high ferrite concentrations, the ferroelectric phase might become increasingly isolated, potentially altering
the collective domain switching behaviour and leading to a decrease in Ec.38 In this study, the ferromagnetic phase content has a value of x = 0.4, which is considered a more optimal content to improve the electromagnetic interaction occurring in multiferroic composites. The ferromagnetic phase content corresponding to x = 0.4 is optimal implies a balance between sufficient magnetic interaction for the pinning effect and maintaining good ferroelectric properties by having a dominant ferroelectric phase.40 Table 1 also lists the values of the characteristic parameters of NFO/BZT-BCT multiferroic nanocomposites, including Ms, Mr, Hc, Ps, Pr, and Ec. It shows that composites with x = 0.2–0.8 are multiferroics with rather small Hc (below 100 Oe).
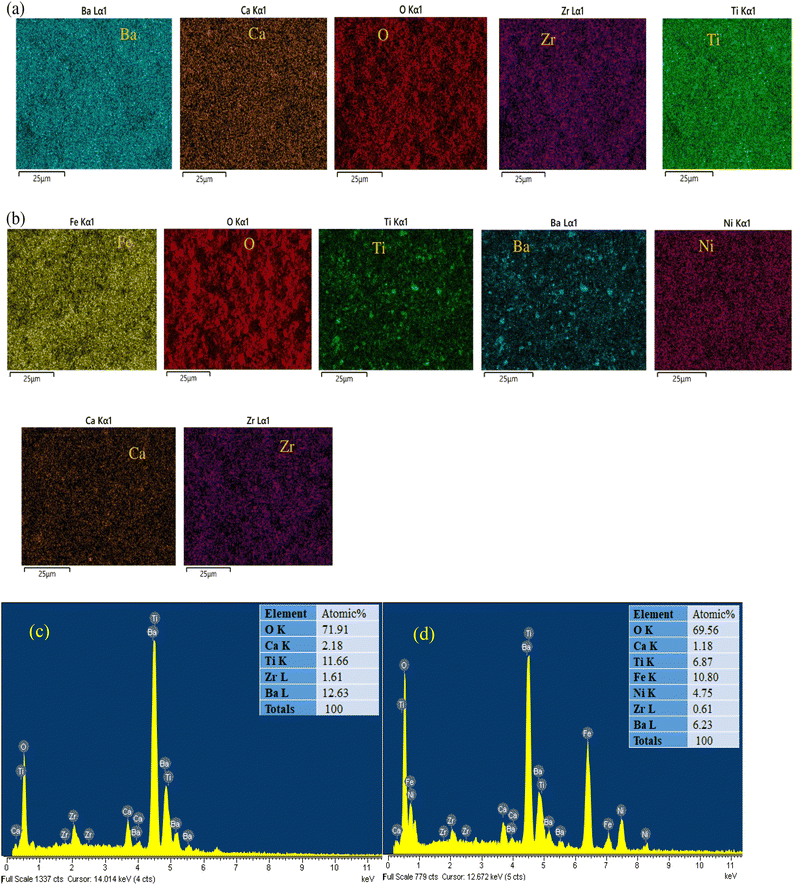 |
| | Fig. 3 (a and b) EDX element mapping images and (c and d) EDX spectra of BZT-BCT and NBZ4 samples, respectively. | |
 |
| | Fig. 4 M(H) loops measured at room temperature of NFO/BZT-BCT multiferroic. | |
Table 1 The values of the characteristic parameters of NFO/BZT-BCT multiferroic nanocomposite, including the remanent magnetization (Mr),the saturation magnetization (Ms), and the coercive force (Hc), the coercive field (Ec), the maximum electrical polarization (Pm) the residual polarization (Pr)
| Sample |
x |
Ms (emu g−1) |
Mr (emu g−1) |
Hc (Oe) |
Pm (μC cm−2) |
Pr (μC cm−2) |
Ec (kV cm−1) |
Ref. |
| xNFO/(1 − x)(BZT-BCT) |
0.0 |
— |
— |
— |
0.09 |
0.02 |
2.06 |
This work |
| 0.2 |
13.6 |
0.67 |
66 |
0.077 |
0.037 |
3.95 |
| 0.4 |
27.45 |
1.25 |
58 |
0.089 |
0.064 |
5.67 |
| 0.6 |
36.92 |
1.27 |
53 |
0.079 |
0.039 |
4.03 |
| 0.8 |
57.7 |
1.4 |
49 |
0.07 |
0.022 |
2.87 |
| xCNFO/(1 − x)(0.15BCT-0.85BZT) |
0 |
— |
— |
— |
5.51 |
0.72 |
4.91 |
28 |
| 0.1 |
3.38 |
0.35 |
91 |
6.79 |
1.77 |
7.72 |
| 0.2 |
10.89 |
1.24 |
96 |
9.34 |
5.15 |
7.58 |
| 0.3 |
22.2 |
3.09 |
120 |
11.11 |
6.36 |
6.18 |
| 0.4 |
29.08 |
4.29 |
130 |
10.37 |
5.78 |
8.98 |
| xNi0.7Zn0.3Fe2O4/(1− x)BaTiO3 |
0.1 |
4.1 |
0.48 |
48.67 |
0.21 |
0.14 |
7.6 |
12 |
| 0.3 |
20.8 |
3.43 |
54.47 |
0.44 |
0.55 |
7.6 |
| 0.5 |
37.6 |
7.21 |
68.03 |
0.3 |
0.52 |
5.1 |
| 0.7 |
55.5 |
5.04 |
39.17 |
0.75 |
0.25 |
4 |
| 0.9 |
67.6 |
4.44 |
31.55 |
0.95 |
0.2 |
2 |
| 1 |
78.7 |
2.64 |
0.018 |
— |
— |
— |
 |
| | Fig. 5 (a) P(E) curves, (b) the dependences of WUE, WLE, and ηP–E on NFO content for NFO/BZT-BCT composites. The insert in figure (a) shows the change of Pr, Pm, and Ec. | |
Determining magnetoelectric coupling in BZT-BCT/NFO multiferroic materials can be indirectly analyzed using Raman spectroscopy. This analysis focuses on observing changes (frequency shifts, linewidth broadening/narrowing) of the phonon peaks of one phase when the other phase is influenced by an external field (magnetic or electric field), indicating the mechanical transfer of strain between the two phases. Specifically, when an external magnetic field is applied to the ferromagnetic phase (NFO), it induces magnetostriction. This strain is then transferred to the ferroelectric phase (BZT-BCT) due to the mechanical coupling between the two phases, leading to a change in the electric polarization of BZT-BCT. Conversely, when an electric field is applied to BZT-BCT, it causes piezoelectric strain, which is then transferred to NFO, altering its magnetic properties. This transferred strain will affect BZT-BCT, modifying the interatomic interactions within its crystal lattice. These changes can result in a phonon frequency shift or linewidth broadening/narrowing of the Raman peaks of BZT-BCT. Such shifts serve as indirect evidence of magnetoelectric coupling occurring in the material, demonstrating the mechanical strain transfer from the magnetic to the ferroelectric phase. Qualitative assessments of the electromagnetic interactions occurring within the material are clearly demonstrated by the most significant shift in the spectral peaks corresponding to the sample with an NFO ferromagnetic phase content of x = 0.4 (i.e., sample NBZ4). Besides, to choose a material with high loss that has effective absorption and shielding of electromagnetic waves, in this study we perform some analyses and evaluation of the loss and energy storage capacity of the materials.41–48 Therefore, in the following contents, we will consider and have specific and relevant discussions. The useful recoverable energy storage density and the energy storage efficiency can be obtained from the expressions:42
| |
 | (1) |
| |
 | (2) |
where
Eapplied is the applied electric field,
Pinduced is the induced polarization,
ηP–E is the energy storage efficiency,
WUE and
WLE are the recoverable useful energy storage density and the lost energy density, respectively.
Fig. 5(b) shows the dependences of
WUE,
WLE, and
ηP–E on NFO content of samples measured at 10 kV cm
−1. As
x increases from
x = 0 to
x = 0.8, we see that the
P(
E) curve tends to expand gradually with increasing NFO content. It means that the energy loss could increase. Under an electric field of 10 kV cm
−1, the loss of energy density increases from 0.415 to 1.13 mJ cm
−3 and the stored energy density decreases from 52.3 to 27.6%, with NFO content increasing from 0 to 0.8, the value of the loss of energy density reaches its maximum value at the NFO ferrite content of
x = 0.4. This result has significant implications for the practice of conducting material-oriented studies in the field of microwave absorption. In this study, the dependence of dielectric constant and magnetic permeability on the frequency of NFO, BZT-BCT, and NBZ4 samples was investigated in detail. This is clearly shown in
Fig. 6(a–d). The results clearly show the influence of the investigated frequency on the real and imaginary parts of dielectric constant. The
ε′ values shows that electric energy's storage capability decreases with an increasing of frequency. The
ε′ values of BZT-BCT showed the peaks at ∼3.5; 12.5 GHz and 15.6 GHz; of NFO reaches the maximum values at 3.5; 12 and 15.1 GHz. For the NBZ4 sample, we see a shift of the peaks to positions corresponding to frequencies of 11.5 and 15.5 GHz. While in the frequency range from 4–10 GHz, the
ε′ values tend to decrease sharply, the
ε′′ values change quite specifically. Indeed, for all samples, in the frequency range of 4–12 GHz, the imaginary part of the dielectric constant as well as the dielectric loss reach larger values than in other frequency ranges, with multiple peaks appearing at different frequencies. The
ε′′ value reaches the maximum values at the frequencies of 5.8 GHz and 8.8 GHz corresponding to the BZT-BCT sample; meanwhile, this value reaches the maxima at frequencies of 4.2; 6.2 and 8.5 GHz for NFO sample and the maximum value of
ε′′ is achieved at a frequency of 6.5 GHz, for NBZ4 sample. The appearance of multiple peaks of the imaginary part of the dielectric constant with frequencies in the range of 4–12 GHz for the samples is explained by: (i) at low frequencies, space charges accumulate at interfaces within the material (grain boundaries, phase boundaries in composites, electrode-material interfaces) due to differences in conductivity and permittivity.
49
 |
| | Fig. 6 (a and c) Real permittivity and (b and d) complex permeability as a function of frequency for NFO, BZT-BCT and NBZ4 samples. | |
This accumulation contributes significantly to the high value of ε′. However, the movement and accumulation of these charges are not instantaneous and involve some lag with respect to the alternating electric field. This lag leads to energy dissipation, resulting in a higher ε′′. The frequency at which the maximum loss occurs is related to the relaxation time of these interfacial charges;31,47 (ii) the presence of defects and impurities in the crystal lattice can trap charge carriers, leading to polarisation at low frequencies.27,29 The movement of these trapped charges in response to the electric field is often associated with energy loss due to interactions with the surrounding lattice, contributing to ε′′.39 In the higher frequency range from 12–18 GHz, in all samples, the graph showing the dependence of the imaginary part value of the dielectric and imaginary permeability constant on frequency tends to increase with frequency and reaches a maximum at a specific frequency for each sample. Specifically, For the BZT-BCT sample, this maximum value is achieved at a frequency of about 17.2 GHz; the NFO sample is achieved at frequencies of 14.2 and 17.2 GHz; the NBZ4 sample reaches a maximum at a frequency of 14.2 GHz. This is also clearly shown in Fig. 7 (a) dielectric and (b) magnetic loss tangents as a function of frequency for NFO, BZT-BCT and NBZ4 samples. Especially at a frequency of 14.2 GHz, we can clearly see the role of the presence of the NFO ferromagnetic phase in the material; the loss value has increased significantly compared to the original NFO and BZT-BCT samples. The presence of a ferromagnetic phase in the materials increases the dielectric loss which can be explained: ferromagnetic materials often exhibit higher electrical conductivity compared to ferroelectric materials.50–52 At higher frequency range, this increased conductivity can lead to greater energy dissipation through conduction losses. As frequency increases, the contribution of these conductive charge carriers to the loss might become more significant relative to the decreasing contribution from slower polarization mechanisms.46,52 Besides, when analyzing the dependence of the real and imaginary permeability of the system on the data frequency, we see a similar trend as the survey results with the dielectric constant. The results show that: μ′′ has a maximum value at a lower frequency and then increases exponentially with increasing frequency. The magnetic loss value reaches a large value in the frequency range below 10 GHz. This loss peak in permeability is attributed to the lag of domain wall motion with respect to the applied field and lattice imperfections. This result is completely agreed with previous researches.10,11 When the ferromagnetic phase x = 0.4 is present in the material composition, the dependence of the real part of the dielectric constant does not change much, tending to decrease with frequency. In the low-frequency range, below 6 GHz, the real part of the dielectric constant of the sample is slightly reduced compared to when only the ferroelectric phase is present. This can be explained by: (i) ferrite materials typically exhibit a lower dielectric constant compared to ferroelectric materials. When a ferrite phase is introduced into a ferroelectric matrix, it effectively reduces the overall proportion of the high dielectric constant ferroelectric material within the composite.7–10
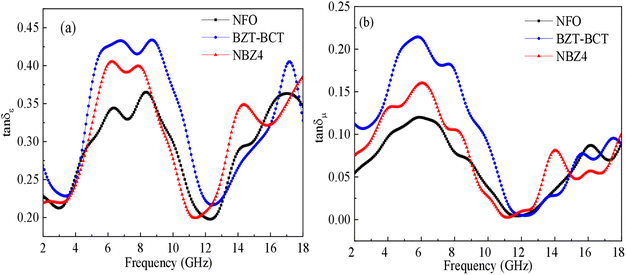 |
| | Fig. 7 (a) Dielectric and (b) magnetic loss tangents as a function of frequency for NFO, BZT-BCT and NBZ4 samples. | |
Consequently, the composite as a whole can exhibit a lower dielectric constant, especially if the ferrite content becomes significant. This result was also shown by Richa Sharma et al. and colleagues that the dielectric constant of their composites decreased with increasing CFO (ferrite) concentration,7 suggesting that the incorporation of CFO dilutes the dielectric properties of the ferroelectric phase. Similarly, Ajith S. Kumar et al. observed a decrease in the dielectric constant with an increase in ferrite content, attributing it to the lower dielectric constant of the ferrite phase compared to the ferroelectric phase;10 (ii) ferrite phases often possess a lower electrical resistivity (higher conductivity) than ferroelectric phases.12,29,40 The presence of a more conductive ferrite phase can lead to an increase in the overall conductivity and leakage current in the composite.12,14,26,37 This increased conductivity can hinder the effective build-up of charge in response to the applied electric field at low frequencies, potentially leading to a reduction in the measured capacitance and, consequently, the dielectric constant. Patil et al. noted that the resistivity of composites decreases with increasing ferrite content due to the lower resistivity of ferrites.40 Kumar et al. also mentioned that the leakage current decreases with an increasing concentration of the ferroelectric phase because the electrical resistivity of the magnetic phase is smaller than that of the ferroelectric phase;4 (iii) while the introduction of a second phase generally creates interfaces that can enhance polarisation through the Maxwell–Wagner effect, the specific properties of the ferrite phase and its interaction with the ferroelectric matrix can sometimes lead to a less effective contribution to low-frequency polarisation compared to the pure ferroelectric material.12 For instance, the conductivity difference might not be optimally suited for charge accumulation at the interfaces in the low-frequency regime in all material combinations. Although typically interfacial polarisation leads to a higher dielectric constant at low frequencies, the overall effect on the dielectric constant depends on the relative contributions of all polarisation mechanisms and the specific electrical properties of the constituent phases.51,52 We further analyze the absorption mechanism by means of the Cole–Cole plot. Fig. 8(a–c) shows relation curves of ε′ versus ε′′ of pure NFO, BZT-BCT, NBZ4 composites in 2–18 GHz. The Cole–Cole semicircles derived from the plots of ε′ versus ε′′ represent Debye relaxation process to confirm the polarization relaxation behaviors. On the basis of classical Debye theory, the relationship between ε′ and ε′′ may be described below:32
| |
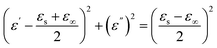 | (3) |
where
εs and
ε∞ represent the static dielectric constant and dielectric constant at the infinite frequency, respectively. Generally, a single semicircle denoted as Cole–Cole symbolizes one Debye polarization relax ation process. The abscissa of the Cole–Cole plots of NFO, BZT-BCT, NBZ4, parafin is the real part of the complex dielectric constant, and the ordinate is the imaginary part of the complex dielectric constant. The appearance of a semicircle in the curve in the Cole–Cole plots indicates the presence of a Debye relaxation process.
53 The more Debye semicircles, the stronger the polarization ability and dielectric loss of the material are.
54 Fig. 8 indicates that a certain amount of Debye semicircle exists in all three samples, which means that polarization relaxation exists in all three samples during wave absorption. When the microwave passes through these defects, it will form a polarization center and form a Debye semicircle. The polarization losses of NFO, BZT-BCT and NFO/BZT-BCT samples are present together, and they have a certain conductive loss, which is consistent with the previous analysis results.
 |
| | Fig. 8 The relation between the real part (ε′) and imaginary part (ε′′) of complex permittivity (Cole–Cole plot) of (a) the NFO-paraffin; (b) BZT-BCT-paraffin and (c) NBZ4-paraffin composites. | |
To investigate the ability of material to absorb and shield electromagnetic waves, in the next content we used xNFO/(1 − x)BZT-BCT multiferroic composites with x = 0, 0.4 and 1.0 (denoted as NFO; NBZ4; BZT-BCT samples, respective) as a filler in paraffin 40% to create NFO-Paraffin; NBZ4-paraffin and BZT-BCT-paraffin composites. The electromagnetic parameters of the material are tested in the frequency range of 2–18 GHz using vector network analyzer. The RL values are calculated according to the formula (4) and (5) and the graphs are plotted as below. Fig. 9(a–i) shows two-dimensional RL curves: (a) NFO-paraffin; (b) BZT-BCT-paraffin; (c) NBZ4-paraffin; three-dimensional RL curves: (d) NFO-paraffin; (e) BZT-BCT-paraffin; (f) NBZ4-paraffin; RL contour plots: (g) NFO-paraffin; (h) BZT-BCT-paraffin; (i) NBZ4-paraffin mixed at the mass ratio 40 wt% in paraffin. The horizontal axis is the frequency, and the vertical axis is the RL value. Based on the transmission line theory, the key index RL for evaluating the absorption characteristics of electromagnetic waves can be derived from the following formulas.43
| |
 | (4) |
| |
 | (5) |
where
Zin is the normalized input impedance of the absorbing material,
Z0 is the free space impedance,
εr is the complex permittivity,
μr is the complex permeability,
f is the frequency,
c is the speed of light in free space, and
d is the thickness of the absorber. As the effective absorption bandwidth (the RL value is below −15 dB), the electromagnetic wave absorption rate of the material can reach to 90%, which is effective absorption. The maximum bandwidth with RL value continuously less than 10 dB is the maximum effective absorption bandwidth. In order to better evaluate the microwave absorbing properties of the materials, we divide the 2–18 GHz band into four parts, which are S (2–4 GHz), C (4–8 GHz), X (8–12 GHz) and K
u (12–18 GHz) bands. According to the grey dashed reference line in
Fig. 9, we can see that the composites perform better overall in the range of 1.5–5.0 mm for samples thicknesses, with all RL
min values below −10 dB.
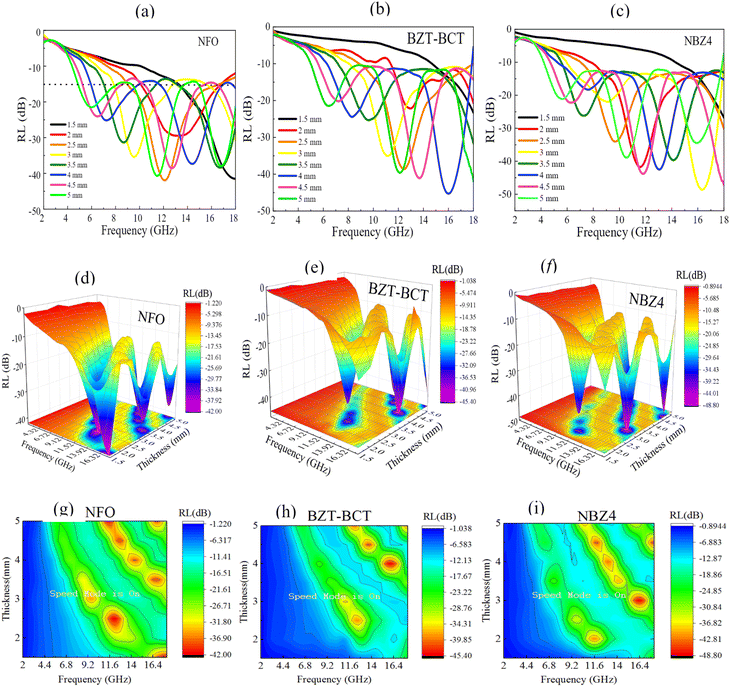 |
| | Fig. 9 Two-dimensional RL curves: (a) NFO-parafin; (b) BZT-BCT-parafin; (c) NBZ4-parafin; three-dimensional RL curves: (d) NFO-parafin; (e) BZT-BCT-parafin; (f) NBZ4-parafin; RL contour plots: (g) NFO-parafin; (h) BZT-BCT-parafin; (i) NBZ4-parafin. | |
Observing the RL(f) curve of all samples, we see that absorption peaks appear at specific frequencies corresponding to different thicknesses. For the NFO sample, except for the thickness of 1.5 mm, absorption peaks appear at other thicknesses with the minimum value of the smallest RL all being less than −20 dB. Corresponding to the sample with a thickness of 2.5 mm, the smallest RL value reaches −41.87 dB at a frequency of 13.06 GHz, with the effective absorption bandwidth (EAB) value greater than 10.3 GHz. When the thickness increases to 3.5 mm, the RLmin value reaches −38.51 dB corresponding to a frequency of 16.74 GHz; when the thickness increases, corresponding to 4 mm, 4.5 mm and 5 mm, the RLmin value does not change much, however, the resonance frequency is shifted to a smaller value, corresponding to 14.18; 12.69 and 11.51 GHz. For the BZT-BCT sample, as the sample thickness increases, the frequency of the resonance peaks tends to decrease. When the sample has a thickness of 2; 2.5; 3; 3.5 mm, the frequency of the resonance peak is achieved at frequencies of 12.95; 12.5; 11.74 and 9.68 mm GHz, respectively. For samples with larger thicknesses, the RLmin value increases significantly compared to thinner samples, corresponding to thicknesses of 4; 4.5 and 5 mm, the RLmin value reaches the smallest values of −45.2; −41.04 and −39.6, respectively, corresponding to frequencies of 16.06; 13.61 and 12.13 GHz. For the NBZ4 sample, the simultaneous presence of both ferroelectric and ferromagnetic phases changes the material's ability to absorb electromagnetic waves. For the sample with a thickness of 2 mm, the RLmin value reached −41.71 dB at a frequency of 11.6 GHz. When the frequency increased to 2.5 mm, the RLmin value tended to decrease, RLmin reached −33.91 dB. However, the frequency of the absorption peak at this time reached a value of about 9.62 GHz, tending to decrease in the range of 8–12 GHz. This means that, for the NBZ4 material, the ability to absorb electromagnetic waves in the X-band band is highly effective corresponding to a thickness of about 2.5 mm. This is a reasonable thickness for the development of applications of electromagnetic wave absorbing materials in the future. When the thickness of the NBZ4 material increased, the RLmin value changed quite significantly, reaching −48.83; −39.85; −42.36; −43.68 and −38.93 dB, correspond to frequencies 16.4; 14.11; 13.09; 11.79; 10.52 GHz at thicknesses of 3; 3.5; 4; 4.5; 5 mm, respectively. We can see that as the thickness of the sample increases, the frequency of the electromagnetic wave at the absorption peaks tends to shift to lower frequencies. This result is completely consistent with previous research results.51–53 The difference in the RLmin value as well as the absorption capacity of the electromagnetic wave at different thicknesses is due to the influence of the impedance matching of the sample during the sample measurement process. The results obtained are considered quite impressive compared to previous studies on BaTiO3-based multiferroic composites,5,6,26,55,56 as shown in Table 2.
Table 2 The parameters (RLmin, resonant frequency f and the EAB corresponding to the RL value at −10 dB) related to the microwave absorption of NFO/BZT-BCT composites with different thickness and comparison with some similar composites
| Sample |
x |
Filler loading (wt%) |
Thickness (mm) |
RLmin (dB) |
f (GHz) |
EAB (GHz) |
Ref. |
| NFO |
1 |
40 |
2.5 |
−41.87 |
13.06 |
≥10.3 |
This work |
| 3.0 |
−35.39 |
9.56 |
| 3.5 |
−38.51 |
16.74 |
| 4.0 |
−37.7 |
14.48 |
| 4.5 |
−38.63 |
12.69 |
| 5.0 |
−40.67 |
11.51 |
| BZT-BCT |
0 |
2.5 |
−38.51 |
12.5 |
≥11.5 |
| 3.0 |
−35.15 |
11.74 |
| 3.5 |
−25.66 |
9.68 |
| 4.0 |
−45.24 |
16.06 |
| 4.5 |
−41.04 |
13.6 |
| |
5.0 |
−39.6 |
12.13 |
| NBZ4 |
0.4 |
2.5 |
−33.91 |
9.62 |
≥12.1 |
| 3 |
−48.83 |
16.4 |
≥12.3 |
| 3.5 |
−39.85 |
14.11 |
≥12.7 |
| 4.0 |
−42.36 |
13.09 |
≥13.2 |
| 4.5 |
−43.68 |
11.79 |
≥13.5 |
| 5.0 |
−40.12 |
10.43 |
— |
|
| xCoFe2O4/(1 − x)BaTiO3 |
0 |
— |
— |
−13.338 |
10.04 |
— |
5 |
| 0.2 |
— |
— |
−33.39 |
11.32 |
— |
| 0.5 |
— |
— |
−40.11 |
10.98 |
— |
| 0.8 |
— |
— |
−20.44 |
11 |
— |
| 1.0 |
— |
— |
−29.29 |
11.32 |
— |
| xFe3O4/(1 − x)BTO |
0 |
— |
4.5 |
−20.7 |
17.7 |
0.7 |
6 |
| 0.25 |
— |
1.9 |
−29.5 |
12.1 |
2.4 |
| 0.5 |
— |
1.7 |
−49.5 |
14.6 |
4.0 |
| 0.75 |
— |
2.3 |
−42.5 |
10.2 |
2.6 |
| 0.8 |
— |
2.2 |
−47.4 |
12.26 |
5.0 |
| 1 |
— |
3 |
−16 |
9.6 |
2.4 |
| NCZFO/BTO |
— |
30 |
3 |
−30.7 |
— |
4.8–10.6 |
26 |
| — |
30 |
5 |
−65.6 |
— |
2.6–6.8; 13.7–17.3 |
| Co2Z/BaTiO3 |
— |
15 |
3 |
−31 |
— |
5.1–9.5 |
55 |
| NFO-BTO-AP |
0.3 |
— |
5 |
−16.5 |
17.5 |
2.6 |
56 |
| NiFe2O4@SiO2@MXene |
— |
— |
2 |
−52.8 |
11.6 |
7.2 |
57 |
It is clear that these parameters depend not only on the nature of the composites, but also on the thickness of the absorbing layers. For NBZ4 – parafin composite with thickness of 2.5 mm, the absorbing bandwidth value at RL = −10 dB is found to be over 12.1 GHz. This research result can be compared with the research results of Zainal et al.5 and Yue H et al.6 From the Fig. 9(a–i), it can be seen that the greater thickness corresponds to the lower frequency of the effective absorption band. The projection of the RL peak gradually moves to the direction of lower frequency as the thickness increases. This phenomenon can be explained by the quarter-wavelength theory with the following formula:
| |
 | (6) |
where
λ denotes the wavelength. From the formula, we can see that when other parameters keep unchanged, the thickness
tm is inversely proportional to the frequency
f. Thus, when the thickness
tm continuously increases, the frequency
f will gradually decrease. The theoretical derivation is consistent with the experimental results. As the test frequency increases and the thickness decreases, the RL value of all samples gradually decreases. For all samples, the full profile of the width of the maximum RL value could not be displayed as it exceeds the measurement range. However, the trend of the curves illustrates that the width is still large and has important application prospects at higher frequencies. The attenuation coefficient
α is also an important factor that influences the reflection loss and determines the attenuation characteristics of the material. According to the transmission line theory and electromagnetic wave propagation con stant, the derivation formula of the attenuation coefficient
α is as follows:
56| |
 | (7) |
In order to select a sample with a suitable thickness for practical application, we chose a sample with a thickness of 2.5 mm as the subject of the study. The larger the attenuation coefficient
α, the stronger the ability to attenuate electromagnetic waves.
Fig. 10(a) illustrates that the attenuation coefficient
α of BZT-BCT-paraffin is also greater than those of NFO and NBZ4 samples, in the frequency range from 2–8 GHz. However, in the frequency range from 13–15 GHz, the attenuation coefficient
α value of NBZ4 material is much higher than that of BZT-BCT and NFO samples. This shows that the presence of NFO ferromagnetic phase with
x = 0.4 content will enhance the ability to absorb electromagnetic waves of NBZ4 material in the frequency range from 12–15 GHz. For better quantitative evaluation of the impedance matching performance of 2.5 mm thick NFO, BZT-BCT and NBZ4 samples with frequency, we plotted all values of impedance matching ratio in the frequency range of 2–18 GHz. According to formula
(5),
54 when
Z = 1, the reflection coefficient is zero, indicating that the electromagnetic wave incident perpendicular from the free space to the interface of the microwave absorbing material can achieve zero reflection, which is complete impedance matching at this time. The impedance matching ratio in the range of 0.8–1.2 as good impedance matching performance. This is shown in
Fig. 10(b). Obviously, the figure shows that all samples have good impedance matching in the frequency range of 10–18 GHz. In the frequency range of 10–18 GHz, the curves representing the impedance matching ratio with frequency for the two samples NFO and NBZ4 are almost identical and approximately equal to 1, while the value for the BZT-BCT sample deviates more from the value
Z = 1. It can be seen that the NFO ferromagnetic phase plays an important role in enhancing the impedance matching in the frequency range of 10–18 GHz. NFO/BZT-BCT composites are excellent microwave absorbers due to a combination of magnetic and dielectric loss mechanisms.
58 This is also indicated in some recent research findings on perovskite-based composite.
59,60 Fig. 11 presents a detailed diagram illustrating the electromagnetic wave absorption mechanism of the NFO/BZT-BCT multiferroic composite material in the 2–18 GHz frequency range, with specific color annotations for each material and its contributions.
 |
| | Fig. 10 Frequency dependence of attenuation constant α (a) and impedance matching ratio (b) of all as prepared samples. | |
 |
| | Fig. 11 Diagram illustrating the electromagnetic wave absorption mechanism of NFO/BZT-BCT composites in the 2–18 GHz. | |
For NFO material (NiFe2O4 – ferromagnetic)
Represented by the color dark red/brown; primary contribution: magnetic loss; mechanism: when electromagnetic waves pass through NFO, the magnetic field component of the wave interacts with the magnetic moments within the material. The wave's energy is dissipated as heat through: (i) spin resonance: electron spins in NFO oscillate and resonate at specific frequencies. (ii) Domain wall resonance: the oscillation and movement of the boundaries between different magnetized regions (domains). (iii) Eddy current loss: induced currents generated in conductive or semiconductive materials (NFO can have some conductivity) due to a changing magnetic field, leading to energy dissipation.
For BZT-BCT material (lead-free piezoelectric)
Represented by the color light blue/green; primary contribution: dielectric loss; mechanism: the electric field component of the electromagnetic wave interacts with the electric dipoles within BZT-BCT. The wave's energy is dissipated as heat through: (i) dipole polarization: permanent or induced electric dipoles in BZT-BCT attempt to align with the alternating electric field, causing friction and energy dissipation; (ii) ion polarization: the relative displacement of charged ions within the crystal lattice under the influence of the electric field. For interfacial polarization: highlighted with a glowing, bright purple effect at the boundaries between the NFO and BZT-BCT phases; mechanism: as electromagnetic waves pass through the composite material, charge carriers (e.g., electrons, holes) can accumulate at the interfaces between the two materials with different electrical properties (NFO and BZT-BCT). This accumulation and release of charges create larger dipoles and cause significant energy dissipation, which is particularly effective across a broad frequency range.
For impedance matching: illustration
The incident electromagnetic wave (green arrow) enters the material with minimal reflection (dotted green arrow); mechanism: for an absorbing material to be effective, its impedance must closely match that of free space. When impedance is matched, most of the wave energy enters the material instead of being reflected, maximizing absorption capability. The combination of NFO and BZT-BCT with appropriate ratios and structures can help tune the impedance of the composite material to achieve optimal impedance matching in the 2–18 GHz range. Absorbed electromagnetic wave: represented by dark blue arrows inside the material, indicating that the wave energy has been converted.
The synergistic combination of all these mechanisms (dielectric loss, magnetic loss, interfacial polarization, and impedance matching) enables the NFO/BZT-BCT composites to achieve excellent electromagnetic wave absorption properties within the broad 2–18 GHz frequency band.
Conclusions
Multiferroic composites of xNiFe2O4/(1 − x)(0.5BaZr0.2Ti0.8O3-0.5Ba0.7Ca0.3TiO3) (NFO/BZT-BCT with x = 0, 0.2, 0.4, 0.6, 0.8 and 1.0) were prepared by high-energy ball milling combined with the thermal annealing methods. The presence of NFO ferromagnetic phase improved the ferroelectric and ferromagnetic properties of the materials. The values of saturation magnetization and remanence magnetization gradually increase with the ferromagnetic phase content. The values of residual electric polarization and loss electric energy density reach their maxima corresponding to the ferromagnetic phase content of x = 0.4. The material was capable of absorbing electromagnetic waves in the frequency range of 6–18 GHz with an efficiency of over 90%, especially for the NFO/BZT-BCT with x = 0.4 sample, at a thickness of 2.5 mm, the ability to absorb electromagnetic waves reached over 99.9% in the frequency range above 8 GHz, the minimum position of the reflection loss is shifted to a lower frequency range, reaching about 9.62 GHz. As the thickness of the sample for measuring electromagnetic wave absorption increases, the absorption efficiency is significantly improved, tending to shift towards shorter frequency waves. This research result shows the potential application of BZT-BCT multiferroic materials in the field of electromagnetic wave absorption.
Data availability
The data that support the findings of this study are available within the article.
Author contributions
Tran Dang Thanh: conceptualization (equal); writing – original draft (equal); writing – review & editing (equal). Bui Son Tung: formal analysis (equal); writing – review & editing (equal). Tran Quang Dat: formal analysis (equal); writing – review & editing (equal). Dinh Chi Linh: formal analysis (equal). Bui Xuan Khuyen: validation (equal), writing – original draft (equal); Le Thi Giang: formal analysis (equal). Phan Tien Danh: formal analysis (equal). Dao Son Lam: project administration (lead); conceptualization (equal); visualization (lead); formal analysis (equal); writing – original draft (lead); writing – review & editing (equal).
Conflicts of interest
The authors have no conflicts to disclose.
Acknowledgements
This work is supported by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under the code number 103.02-2021.145.
Notes and references
- C. W. Nan, M. I. Bichurin, S. Dong, D. Viehland and G. Srinivasan, Multiferroic magnetoelectric composites: historical perspective, status, and future directions, J. Appl. Phys. Rev., 2008, 103, 031101, DOI:10.1063/1.2836410.
- C. Binek and B. Doudin, Magnetoelectronics with magnetoelectrics, J. Phys.: Condens. Matter, 2005, 17, 39–44, DOI:10.1088/0953-8984/17/2/L06.
- L. Kozielski and F. Clemens, Multiferroics application – magnetic controlled piezoelectric transformer, Process. Appl. Ceram., 2012, 6, 15–20, DOI:10.1007/s12613-014-1003-9.
- M. Kumar, S. Shankar, A. Kumar, A. Anshul, M. Jayasimhadri and O. P. Thakur, Progress in multiferroic and magnetoelectric materials: applications, opportunities and challenges, J. Mater. Sci.: Mater. Electron., 2020, 31, 19487–19510, DOI:10.1088/2053-1591/ac7fe1.
- Y. B. Zainal, D. Dedi and A. Mana, Microstructure and microwave absorption characteristics of BaTiO3–CoFe2O4 composites, Key Eng. Mater., 2020, 855, 322–329, DOI:10.4028/www.scientific.net/KEM.855.322.
- H. Yue, J. Jindou, C. Yan, L. Xiang, H. Jun, C. Xingwang, H. Shuli, L. Ying and L. Jiping, Broadband microwave absorption of Fe3O4–BaTiO3 composites enhanced by interfacial polarization and impedance matching, Composites, Part B, 2019, 163, 598–605, DOI:10.1016/j.compositesb.2019.01.008.
- R. Sharma, P. Pahuja and R. P. Tandon, Structural, dielectric, ferromagnetic, ferroelectric and AC conductivity studies of the BaTiO3–CoFe1.8Zn0.2O4 multiferroic particulate composites, Ceram. Int., 2014, 40, 9027–9036, DOI:10.1016/j.ceramint.2014.01.115.
- H. Krir, F. Gadhoumi, N. Abdelmoul, M. Tabellout, H. Khemakhema and N. Randrianantoandro, Engineering 0.8BiFeO3–0.2BaTiO3 multiferroics with improved dielectric and magnetic properties via samarium doping, RSC Adv., 2025, 15, 2175–2183, 10.1039/D4RA08068H.
- A. Jalouli and S. Ren, Magnetoelectric interaction in molecular multiferroic nanocomposites, RSC Adv., 2022, 12, 24050–24054, 10.1039/D2RA04060C.
- A. S. Kumar, C. S. C. Lekha, S. Vivek, V. Saravanan, K. Nandakumar and S. S. Nair, Multiferroic and magnetoelectric properties of Ba0.85Ca0.15Zr0.1Ti0.9O3–CoFe2O4 core–shell nanocomposite, J. Magn. Magn. Mater., 2016, 418, 294–299, DOI:10.1016/j.jmmm.2016.02.065.
- M. J. Miah, M. N. I. Khan and A. K. M. A. Hossain, Weak ferromagnetism and magnetoelectric effect in multiferroic xBa0.95Sr0.05TiO3–(1−x)BiFe0.9Gd0.1O3 relaxors, J. Magn. Magn. Mater., 2016, 401, 600–611, DOI:10.1016/j.jmmm.2015.10.083.
- N. N. Jiang, Y. Yang, J. P. Zhou, J. Yang and P. Liu, Microstructure and microwave-frequency electromagnetic properties of Ni0.4Zn0.6Fe2O4/Ba0.6Sr0.4TiO3 composites, Ceram. Int., 2016, 42, 15585–15591, DOI:10.1016/j.ceramint.2016.07.007.
- H. Kaur, A. Marwaha, C. Singh, S. B. Narang, R. Jotania, S. Jacobo and P. Dhruv, Investigation of structural, hysteresis and electromagnetic parameters for microwave absorption application in doped Ba–Sr hexagonal ferrites at X-band, J. Alloys Compd., 2019, 806, 1220–1229, DOI:10.1016/j.jallcom.2019.07.032.
- A. S. Dzunuzovic, M. M. Vijatovic Petrovic, J. D. Bobic, N. I. Ilic, M. Ivanov, R. Grigalaitis and B. D. Stojanovic, Magneto-electric properties of xNi0.7Zn0.3Fe2O4/(1−x)BaTiO3 multiferroic composites, Ceram. Int., 2018, 44, 683–694, DOI:10.1016/j.ceramint.2017.09.229.
- S. G. Chavan, S. M. Mane, S. B. Kulkarni, M. E. Jayasingh, P. B. Joshi and D. J. Salunkhe, Micro-wave sintered nickel-doped cobalt ferrite nanoparticles prepared by hydrothermal method, J. Mater. Sci.: Mater. Electron., 2016, 27, 7105–7108, DOI:10.1007/s10854-016-4672-1.
- H. Kaddoussi, A. Lahmar, Y. Gagou, B. Manoun, J. N. Chotard, J. L. Dellis, Z. Kutnjak, H. Khemakhem, B. Elouadi and M. El Marssi, Sequence of structural transitions and electrocaloric properties in (Ba1-xCax)(Zr0.1Ti0.9)O3 ceramics, J. Alloys Compd., 2017, 713, 164–179, DOI:10.1016/j.jallcom.2017.04.148.
- S. M. Mane, P. M. Tirmali and S. B. Kulkarni, Hybrid microwave sintering and shifting of To in lead-free ferroelectric composition x(Ba0.7Ca0.3TiO3)/(1−x)(BaZr0.2TiO0.8O3), Mater. Chem. Phys., 2018, 213, 482–491, DOI:10.1016/j.matchemphys.2018.04.05.
- Z. Yun, G. Zheng and H. Dong, et al., The microwave absorption performance of NiFe2O4 prepared under the gradient magnetic field, J. Mater. Sci.: Mater. Electron., 2024, 35, 936, DOI:10.1007/s10854-024-12638-w.
- G. Liang, F. Han, X. Ye and X. Meng, Hierarchical 0D/2D NiFe2O4/Ti3C2Tx MXene composites for boosting microwave absorption, Mater. Sci. Eng., B, 2023, 289, 116224, DOI:10.1016/j.mseb.2022.116224.
- S. Golchinvafa, S. M. Masoudpanah and S. Alamolhoda, In-situ combustion synthesis of Ni1-xZnxFe2O4/FeNi3/ZnO composite powders for electromagnetic absorption, Ceram. Int., 2023, 49, 18134–18142, DOI:10.1016/j.ceramint.2023.02.182.
- W. Lin and Z. Wang, Fabrication of core-shell NiFe2O4@C@PPy composite microspheres with efficient microwave absorption properties, Mater. Lett., 2023, 352, 135212, DOI:10.1016/j.jallcom.2023.170132.
- R. S. Yadav and I. Kuřitka, Recent developments on nanocomposites based on spinel ferrite and carbon nanotubes for applications in electromagnetic interference shielding and microwave absorption, Crit. Rev. Solid State Mater. Sci., 2023, 49(3), 371–407, DOI:10.1080/10408436.2023.2214577.
- X. Meng, W. Xu, X. Ren and M. Zhu, Progress and Challenges of Ferrite Matrix Microwave Absorption Materials, Materials, 2024, 17(10), 2315, DOI:10.3390/ma17102315.
- R. S. Yadav, A. Anju and I. Kuitka, Spinel ferrite and MXene-based magnetic novel nanocomposites: an innovative high-performance electromagnetic interference shielding and microwave absorber, Crit. Rev. Solid State Mater. Sci., 2022, 48(4), 441–479, DOI:10.1080/10408436.2022.2067122.
- D. Mandal, B. Bhandari, S. V. Mullurkara and P. R. Ohodnicki, All-Around Electromagnetic Wave Absorber Based on Ni-Zn Ferrite, ACS Appl. Mater. Interfaces, 2024, 16(26), 33846–33854, DOI:10.1021/acsami.4c06498.
- J. Xiang, Z. Hou, X. Zhang, L. Gong, Z. Wu and J. Mi, Facile synthesis and enhanced microwave absorption properties of multiferroic Ni0.4Co0.2Zn0.4Fe2O4/BaTiO3 composite fibers, J. Alloys Compd., 2018, 737, 412–420, DOI:10.1016/j.jallcom.2017.12.047.
- D. Mao, Z. Zhang and M. Yang, et al., Constructing BaTiO3/TiO2@polypyrrole composites with hollow multishelled structure for enhanced electromagnetic wave absorbing properties, Int. J. Miner., Metall. Mater., 2023, 30, 581–590, DOI:10.1007/s12613-022-2556-7.
- A. N. Tarale, D. J. Salunkhe, P. B. Joshi, S. B. Kulkarni and V. R. Reddy, Magnetodielectric properties of nano-crystalline BaZr0.15Ti0.85O3/La0.67Sr0.33MnO3 thin film heterostructures, J. Mater. Sci.: Mater. Electron., 2013, 24, 4457–4463, DOI:10.1007/s10854-013-1425-6.
- C. E. Ciomaga, A. Guzu, M. Airimioaei, L. P. Curecheriu, V. A. Lukacs, O. G. Avadanei and L. Mitoseriu, Comparative study of magnetoelectric BaTiO3–Co0.8Zn0.2Fe2O4 bi-tunable ceramics sintered by Spark Plasma Sintering and classical method, Ceram. Int., 2019, 45, 12512–12522, DOI:10.1016/j.ceramint.2019.08.125.
- M. M. Sutar, A. N. Tarale, S. R. Jigajeni, S. B. Kulkarni, V. R. Reddy and P. B. Joshi, Magnetoelectric and magnetodielectric effect in Ba1-xSrxTiO3 and Co0.9Ni0.1Fe2-xMnxO4 composites, Solid State Sci., 2012, 14(8), 1064–1070, DOI:10.1016/j.solidstatesciences.2012.04.002.
- W. Liu and X. Ren, Large piezoelectric effect in Pb-free ceramics, Phys. Rev. Lett., 2009, 103(25), 257602, DOI:10.1103/PhysRevLett.103.257602.
- S. M. Mane, S. A. Pawar, D. S. Patil, S. B. Kulkarni, N. T. Tayade and J. C. Shin, Magnetoelectric, magnetodielectric effect and dielectric, magnetic properties of microwave-sintered lead-free x(Co0.9Ni0.1Fe2O4)–(1−x)[0.5(Ba0.7Ca0.3TiO3)–0.5(BaZr0.2Ti0.8O3)] particulate multiferroic composite, Ceram. Int., 2020, 46(3), 3311–3323, DOI:10.1016/j.ceramint.2019.10.038.
- I. Coondoo, N. Panwar, H. Amorín, V. Eskilla Ramana, M. Algueró and A. Kholkin, Enhanced piezoelectric properties of praseodymium-modified Lead Free (Ba0.85Ca0.15)(Ti0.90Zr0.10)O3 ceramics, J. Am. Ceram. Soc., 2015, 98(10), 3127–3135, DOI:10.1111/jace.13713.
- L. Huang, D. Ying, Y. Wu, X. Pei and C. Wen, Enhanced ferroelectric and piezoelectric properties of (1-x)BaZr0.2Ti0.8O3–xBa0.7Ca0.3TiO3 thin films by sol–gel process, Appl. Surf. Sci., 2016, 388, 35–39, DOI:10.1016/j.apsusc.2016.05.030.
- B. Zhao, Y. Du, Z. Yan, L. Rao, G. Chen, M. Yuan, L. Yang, J. Zhang and R. Che, Structural Defects in Phase-Regulated High-Entropy Oxides toward Superior Microwave Absorption Properties, Adv. Funct. Mater., 2023, 33, 2209924, DOI:10.1002/adfm.202209924.
- C.-W. Nan, G. Liu and Y. H. Lin, Multiferroic Magnetoelectric Composites: Historical Perspective, Status, and Future Directions, Prog. Mater. Sci., 2021, 119, 100788, DOI:10.1063/1.2836410.
- R. Gao, Z. Wang, G. Chen, X. Deng, W. Cai and C. Fu, Influence of core size on the multiferroic properties of CoFe2O4@BaTiO3 core-shell structured composites, Ceram. Int., 2018, 44, 23450–23457, DOI:10.1016/j.ceramint.2018.08.234.
- P. J. Praveen, V. R. Monaji, E. Chandrakala, S. Indla, S. Dinesh Kumar, V. Subramanian and D. Das, Enhanced magnetoelectric coupling in Ti and Ce substituted lead-free CFO–BCZT laminate composites, J. Alloys Compd., 2018, 750, 392–400, DOI:10.1016/j.jallcom.2018.04.026.
- S. A. Lokare, D. R. Patil, R. S. Devan, S. S. Chougule, Y. D. Kolekar and B. K. Chougule, Electrical conduction, dielectric behavior and magnetoelectric effect in (x)BaTiO3+(1−x)Ni0.94Co0.01Mn0.05Fe2O4 ME composites, Mater. Res. Bull., 2008, 43(2), 326–332, DOI:10.1016/j.materresbull.2007.03.020.
- D. R. Patil, S. S. Chougule, S. A. Lokare and B. K. Chougule, Electrical properties of xNiFe2O4+(1−x)Ba0.7Sr0.3TiO3 composites, J. Alloys Compd., 2008, 452(2), 414–418, DOI:10.1016/j.jallcom.2006.11.070.
- W. Ping, W. Liu and S. Li, Enhanced energy storage property in glass-added Ba(Zr0.2Ti0.8)O3–0.15(Ba0.7Ca0.3)TiO3 ceramics and the charge relaxation, Ceram. Int., 2019, 45(9), 11388–11394, DOI:10.1016/j.ceramint.2019.03.003.
- H. Bao, C. Zhou, D. Xue, J. Gao and X. Ren, A modified lead-free piezoelectric BZT–xBCT system with higher To, J. Phys. D: Appl. Phys., 2010, 43(46), 465401, DOI:10.1088/0022-3727/43/46/465401.
- Z. Dai, X. Jinglong, L. Weiguo, W. Xi, Z. Lin, Z. Zhijian, L. Jinglei and X. Ren, An effective strategy to achieve excellent energy storage properties in lead-free BaTiO3-based bulk ceramics, ACS Appl. Mater. Interfaces, 2020, 12, 27, DOI:10.1021/acsami.0c02832.
- Y. Letao, K. Xi, L. Fei, H. Hua, C. Zhenxiang, L. Hanxing, L. JingFeng and Z. Shujun, Perovskite lead-free dielectrics for energy storage applications, Prog. Mater. Sci., 2016, 102, 72–108, DOI:10.1016/j.pmatsci.2018.12.005.
- V. Veerapandiyan, F. Benes, T. Gindel and M. Deluca, Strategies to improve the energy storage properties of perovskite lead-free relaxor ferroelectrics: a review, Materials, 2020, 13, 5742, DOI:10.3390/ma13245742.
- Z. Shen, X. Wang, B. Luo and L. Li, BaTiO3–BiYbO3 perovskite materials for energy storage applications, J. Mater. Chem. A, 2015, 3, 18146–18153, 10.1039/C5TA03614C.
- B. C. Luo, X. H. Wang, E. Tian, H. M. Qu, Q. C. Zhao, Z. M. Cai, H. X. Wang, W. Feng, B. W. Li and L. T. Li, Chemical composition and temperature dependence of the energy storage properties of Ba1-xSrxTiO3 ferroelectrics, J. Am. Ceram. Soc., 2018, 101, 2976–2986, DOI:10.1111/jace.15429.
- V. S. Puli, D. K. Pradhan, B. C. Riggs, D. B. Chrisey and R. S. Katiyar, Investigations on structure, ferroelectric, piezoelectric and energy storage properties of barium calcium titanate (BCT) ceramics, J. Alloys Compd., 2014, 584, 369–373, DOI:10.1016/j.jallcom.2013.09.108.
- S. B. Li, C. B. Wang, Q. Shen and L. M. Zhang, Multiferroic properties of (1−x)BCZT–xLCMO laminated composites, Ceram. Int., 2018, 44(1), 231–235, DOI:10.1016/j.ceramint.2017.09.177.
- M. D. Rather, R. Samad and B. Want, Improved magnetoelectric effect in ytterbium doped BaTiO3–CoFe2O4 particulate multiferroic composites, J. Alloys Compd., 2018, 755, 89–99, DOI:10.1016/j.jallcom.2018.04.289.
- R. Xu, Z. Wang and R. Gao, et al., Effect of molar ratio on the microstructure, dielectric and multiferroic properties of Ni0.5Zn0.5Fe2O4–Pb0.8Zr0.2TiO3 nanocomposite, J. Mater. Sci.: Mater. Electron., 2018, 29, 16226–16237, DOI:10.1007/s10854-018-9712-x.
- R. Gao, Q. Zhang, Z. Xu, Z. Wang, G. Chen, X. Deng and W. Cai, A comparative study on the structural, dielectric and multiferroic properties of Co0.6Cu0.3Zn0.1Fe2O4/Ba0.9Sr0.1Zr0.1Ti0.9O3 composite ceramics, Composites, Part B, 2019, 166, 204–212, DOI:10.1016/j.compositesb.2018.12.001.
- C. M. Kanamadi, L. B. Pujari and B. K. Chougule, Dielectric behaviour and magnetoelectric effect in (x)Ni0.8Cu0.2Fe2O4+(1−x)Ba0.9Pb0.1Ti0.9Zr0.1O3 ME composites, J. Magn. Magn. Mater., 2005, 295(2), 139–144, DOI:10.1016/j.jmmm.2005.01.006.
- M. Lu, Y. Chang, X.-H. Guan and G.-S. Wang, The synthesis of CoxNi1−xFe2O4/multi-walled carbon nanotube nanocomposites and their photocatalytic performance, RSC Adv., 2019, 9(58), 33806–33813, 10.1039/c9ra06261k.
- X. Wang, Q. Li, Z. Su, W. Gong, R. Gong, Y. Chen and V. G. Harris, Enhanced microwave absorption of multiferroic Co2Z hexaferrite–BaTiO3 composites with tunable impedance matching, J. Alloys Compd., 2015, 643, 111–115, DOI:10.1016/j.jallcom.2015.04.012.
- D. S. Lam, N. N. Tung, D. D. Dung, B. X. Khuyen, V. D. Lam and T. D. Thanh, Electrical, magnetic and microwave absorption properties of multiferroic NiFe2O4–BaTiO3 nanocomposites, Mater. Res. Express, 2022, 9, 075004, DOI:10.1088/2053-1591/ac7fe1.
- Z. Yun, G. Zheng, H. Dong, M. Wang, C. Zhu, Z. Dai and W. Ding, The microwave absorption performance of NiFe2O4 prepared under the gradient magnetic field, J. Mater. Sci.: Mater. Electron., 2024, 35, 936, DOI:10.1007/s10854-024-12638-w.
- M. Yuan, M. Zhou and H. Fu, Synergistic microstructure of sandwich-like NiFe2O4@SiO2@MXene nanocomposites for enhancement of microwave absorption in the whole Ku-band, Composites, Part B, 2021, 224, 109178, DOI:10.1016/j.compositesb.2021.109178.
- B. Zhao, Z. Yan, Y. Du, L. Rao, G. Chen, Y. Wu, L. Yang, J. Zhang, L. Wu, D. W. Zhang and R. Che, High-Entropy Enhanced Microwave Attenuation in Titanate Perovskites, Adv. Mater., 2023, 35, 2210243, DOI:10.1002/adma.202210243.
- R. Ramesh and N. A. Spaldin, Multiferroics: Progress and prospects in thin films, Nat. Mater., 2007, 6(1), 21–29, DOI:10.1038/nmat1805.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Bui Son Tungb,
Tran Quang Datc,
Dinh Chi Linha,
Bui Xuan Khuyena,
Le Thi Giangd,
Phan Tien Danhe and
Dao Son Lam*ab
a,
Bui Son Tungb,
Tran Quang Datc,
Dinh Chi Linha,
Bui Xuan Khuyena,
Le Thi Giangd,
Phan Tien Danhe and
Dao Son Lam*ab
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60, and then were formed into toroidal devices using a punch, which had inner and outer diameters of 3.04 mm and 7 mm, respectively. After collecting the S-parameter data, we used the Nicolson–Ross–Weir (NRW) method to extract the complex permittivity and complex permeability of the samples. Finally, the microwave absorption performance was calculated using transmission line theory.
60, and then were formed into toroidal devices using a punch, which had inner and outer diameters of 3.04 mm and 7 mm, respectively. After collecting the S-parameter data, we used the Nicolson–Ross–Weir (NRW) method to extract the complex permittivity and complex permeability of the samples. Finally, the microwave absorption performance was calculated using transmission line theory.