Self-assembly and thermal conductivity of amphiphilic Janus nanoparticles under nanoslit confinement

Abstract

The interplay between nanoparticle (NP) interaction anisotropy and nanoscale confinement gives rise to diverse self-assembly behaviors and the resulting macroscopic thermal properties. In this study, we use molecular dynamics (MD) simulations to explore the relationship between the structural and thermal properties of nanofluids confined in nanoscale channels. The chemical surface design of NPs alters the dependence of thermal conductivity on channel width: homogeneous hydrophilic (HI) NPs maintain thermal conductivity by forming a stable adsorption layer around dispersed NPs, whereas diblock Janus NPs exhibit clustering effects due to interaction anisotropy. This clustering weakens adsorption layers, reducing thermal conductivity even under weak confinement. Under strong confinement, solvent molecules form more pronounced structured layers near the walls; however, NPs disrupt this ordering, resulting in lower thermal conductivity than in a confined purely solvent system. Diblock Janus NPs, in particular, disrupt these layers more due to their clustering, further hindering thermal conductivity. Although both NP types exhibit reduced Brownian motion as channel width decreases, we conclude that it does not significantly affect the thermal conductivity of nanofluids. For instance, Janus NPs, which exhibit greater Brownian motion in wider channels, still show lower thermal conductivity than HI NPs. While HI NPs form stable adsorption layers that enhance thermal transport, Janus NPs tend to self-assemble into micelles, weakening the adsorption layer and further reducing thermal conductivity. Our study provides molecular insight into the relationship between NP dynamics, surface properties, and adsorption layers in determining the thermal conductivity of confined nanofluids.

---

1 Introduction

Nanofluids, composed of conventional base fluids with suspended nanoparticles (NPs), have emerged as a promising solution for enhancing heat transfer in various industrial applications. These suspensions typically contain NPs less than 100 nm in diameter, dispersed in a base fluid at concentrations ranging from below 1% to 10%. The concept of nanofluids was first introduced by Choi et al.,¹ who proposed that incorporating NPs into conventional coolants could significantly enhance thermal conductivity. Since then, extensive research has focused on understanding the fundamental physics of nanofluids, particularly their heat transport mechanisms, stability, and performance in heat transfer applications.^2–6

One major finding in this field is that nanofluid thermal conductivity can be enhanced for various reasons. Sarker and Selvam⁷ used equilibrium molecular dynamics (MD) simulations of a Cu–Ar system and concluded that enhanced liquid atom mobility upon NP addition improves thermal conductivity. However, other studies^8,9 argue that Brownian motion is irrelevant because the self-diffusion of NPs is much lower than that of thermal diffusion. Several theoretical models have been proposed to explain the observed enhancement in thermal conductivity, including those based on the molecular layer effect.^10–13 These models suggest that molecular-scale interactions between the NPs and the fluid enhance thermal conductivity. Some studies have challenged the applicability of these models,¹⁴ arguing that thermal transport in multilayer liquids cannot fully explain the experimentally observed enhancement of thermal conductivity. This controversy highlights the need for a deeper exploration of the mechanisms underlying thermal conductivity enhancement in nanofluids.

In fine flow channels, such as lab-on-a-chip systems, spatial constraints and solid–liquid interface effects dominate. Consequently, fluids confined in nanoscale channels exhibit distinct phase and thermal behaviors not observed in bulk.^15–20 Even low-molecular-weight solutions like water display abnormal thermal behavior under nanoscale confinement.^21–24 For instance, Zhao et al.²² used MD simulations to study the thermal conductivity of monolayer water confined within graphene channels. Their findings revealed a non-intuitive relationship between thermal conductivity and factors such as water number density and channel height. Specifically, they identified density-dependent structural changes as the primary mechanism influencing the thermal conductivity of confined monolayer water. Additionally, the study identified significant effects of channel height on both the structure and thermal conductivity of monolayer water. In narrower channels, high channel wall pressure induces a more ordered, plane-like water structure, resulting in greater thermal conductivity. Conversely, in wider channels, fewer confined water molecules form a wrinkled structure, leading to lower thermal conductivity. These findings provide critical insights into the interplay between water structure and thermal transport at the nanoscale. When complex fluids, such as colloidal NP solutions, are confined in nanoscale channels, both dimensional constraints imposed by the nanochannel and distinctive chemical interactions between the channel wall, solvent, and NP surface can disrupt the existing force balance in free solution, affecting thermodynamic equilibrium.

The interplay between NP interaction anisotropy and nanoscale confinement leads to diverse self-assembly behaviors and macroscopic thermal properties. Janus NPs have gained considerable interest in recent years due to their unique properties and advances in synthesis.^25,26 Named after the two-faced Roman god, Janus particles have two distinct hemispheres with different physicochemical properties. Recent studies^6,27–30 have demonstrated that Janus particles offer significant advantages over conventional (homogeneous) NPs, including enhanced stability, improved dispersion, and more efficient heat transfer in nanofluids. Cui et al.²⁸ conducted MD simulations on nanofluids containing a single Janus NP with hemispheres of differing wetting properties. Their results showed that nanofluid thermal conductivity improves with stronger solid–liquid coupling on one side of the Janus particle and weaker coupling on the other, enhancing Brownian motion. Further research has highlighted the aggregation effects of Janus NPs,^27,29 where self-assembled structures, such as micelles or lamellae, form depending on NP volume fraction and fluid temperature.

In this work, we investigate the structural and thermal properties of nanofluids containing Janus NPs confined in nanoscale channels via MD simulations. The majority of previous studies have focused on bulk systems with single or multiple Janus NPs but have neglected nanoconfinement-induced changes in structural and thermal behaviors. Our simulation provides a fundamental guide for controlling the thermal properties of nanoconfined nanofluids through chemical patterns on NP surfaces, spatial constraints, solid–liquid interfaces, and self-assembled structures.

2 Model and methods

We employ the MD method to investigate the thermal conductivity of nanofluids confined between two solid walls in equilibrium. The solvent (labeled as S) is modeled as a monomer of diameter σ = 1 and mass m = 1. The spherical NP of radius R = 3.0 σ is composed of 459 constituent beads on a face-centered cubic (FCC) lattice with a lattice constant of ≈1.0 σ. As shown in Fig. 1(a and b), two types of NPs are considered: (i) homogeneous NPs, consisting entirely of hydrophilic (type A) beads, and (ii) diblock Janus NPs, composed of both hydrophilic (type A) and hydrophobic (type B) beads. Hereafter, we will refer to the homogeneous hydrophilic NP as “HI NP”. For the Janus NP, 199 and 260 beads are type A and type B, respectively. Note that the numbers are unequal because the FCC lattice cannot be evenly divided into two distinct bead types within the same plane. Based on previous studies,^30,31 all constituent beads in each NP are connected to their nearest neighbors via a finite extensible nonlinear elastic (FENE) potential^32,33 to maintain the spherical shape of the NPs:where k = 30 ε/σ² is the spring constant, and r_max = 1.5 σ is the maximum bond extension. ε is the pair interaction energy parameter. Each wall (labeled as W) is built from beads arranged in a FCC lattice with a lattice constant of ≈1.0 σ, and consists of four atomic layers. The outermost layer lies beyond the cutoff distance and does not contribute to direct wall–fluid interactions. This configuration ensures that a sufficient number of wall atoms participate in wall–fluid interactions while maintaining the shape of the wall throughout the simulation. The channel walls are fixed perpendicular to the z-direction (parallel to the xy-plane), with periodic boundary conditions applied along the x- and y-directions to simulate an infinitely extended channel. The dimensions in the x- and y- directions are L_x = L_y = 38 σ. To investigate the confinement effect, the surface separation H is systematically varied from 9 σ to 21 σ, with a solvent number density of ρ = 0.75 σ⁻³, resulting in a NP volume fraction ranging from 3.5% to 7.0%. We use structured walls with harmonically bound atoms instead of a structureless potential wall. This approach allows proper modeling of interactions and heat exchange at the wall–fluid interface.³⁴ To this end, we introduce a harmonic spring potential, U_w, between wall atoms:where k_w is the wall crystal bonding stiffness, and r_i − r₀ is the distance between the initial lattice position and current position of the wall beads. In this study, we use k_w = 500 ε/σ² based on the previous studies.^35–37 These studies have shown that this stiffness value ensures stable lattice vibrations of wall atoms while still enabling effective thermal exchange with the surrounding fluid. In the initial configuration, eight NPs are randomly placed between two parallel walls, with the remaining system volume filled with solvent beads.

Fig. 1 Simulation models of (a) HI NP and (b) Janus NP with radius R = 3 σ. (c) Representative snapshot of a nanofluid confined between two solid walls with channel height H. In all panels, hydrophilic beads are shown in blue, hydrophobic beads in orange, solvent beads in cyan, and wall beads in gray.

The interatomic interactions between any two beads are modelled by the standard Lennard-Jones (LJ) potential:

with particle distance r and cutoff radius r_cut = 2.5 σ. The interaction strength between particles of type i and j is controlled via ε_ij (see Table 1). These interaction parameters are mainly inspired by a previous study³⁸ on amphiphilic Janus NPs in solution, where similar parameter choices were shown to successfully reproduce self-assembled structures such as spherical micelles in systems of Janus NPs. Moreover, comparable interaction parameter ranges have been employed in previous simulation studies,^9,31 yielding results that are consistent with predictions from effective medium theory and with experimental findings on well-dispersed metal NP suspensions.

Table 1 Interaction parameters of U_LJ [see eqn (3)], ε_ij, between bead pairs. All values^a are given in units of ε

	A	B	S	W
a A: hydrophilic NP bead, B: hydrophobic NP bead, S: solvent bead, W: wall bead.
A	0.1	0.1	1.0	0.1
B		0.1	0.1	0.1
S			1.0	1.0
W				0.0

---

All the simulations are carried out using the large-scale atomic/molecular massively parallel simulator (LAMMPS).³⁹ For the confined systems, thermostat selection is a sensitive issue, for example, applying a thermostat to the liquid could potentially cause unrealistic dynamics.^40–44 In this study, the fluid temperature is controlled at T = 1.0 εk_B⁻¹ with Boltzmann constant k_B through the velocity scaling method to each layer of the walls separately, as proposed by Kim et al.³⁴ The equations of motion are integrated by the Velocity Verlet algorithm⁴⁵ with a time step of dt = 0.004τ (τ = √ε/mσ²). The systems are first equilibrated under the NVT ensemble for 10⁶ timesteps. After the system is equilibrated, we run the NVE simulations for 10⁶ timesteps to compute the thermal conductivity, λ. To improve the statistics, we perform 30 independent runs with different initial configurations. We determine λ from equilibrium simulations via Green–Kubo relations:^46,47

where V is the system volume, J is the heat current vector, and 〈⋯〉 denotes the ensemble average, i.e., the average over time. For a two-component system, the heat current J can be derived as^48,49where the subscripts α and β represent two different species in a nanofluid, N_α and N_β are the number of beads of species α and β, respectively. v_iα is the velocity of the i-th particle of specie α. r_iαjβ, and U(r_iαjβ) are the distance and the pair potential between the two particles i of specie α and j of specie β, respectively. I is the unit tensor, and h_α is the average enthalpy per particle of the species α, which is calculated as the sum of the average kinetic energy, potential energy, and average virial terms per particle of species α:where K_i and P_i are the kinetic and potential energy of each particle of species α, respectively. Here, thermal conductivity in nanochannels is anisotropic between directions parallel and normal to the channel walls.^36,50 The normal thermal conductivity is relatively well understood: as channel width increases, molecular diffusion also increases, leading to higher conductivity normal to the walls. Based on these findings,³⁷ we calculate only the thermal conductivity perpendicular to the xy-plane.

3 Results and discussion

We begin by comparing the self-assembled structures of Janus and HI NPs at different H, as shown in Fig. 2. From these snapshots, we observe that HI NPs are randomly distributed and remain unaggregated. In contrast, Janus NPs exhibit distinctive behavior, tending to cluster and self-assemble into dimers, trimers, or tetramers, depending on the width of the nanoconfined slit. As H increases, the enhanced mobility of Janus NPs perpendicular to the wall surface driven by entropic effects leads to the formation of larger aggregates, such as tetramers. To obtain detailed structural information, we computed the orientational distributions, P(cosθ), of the confined Janus NPs, where θ is the angle between the surface normal of the wall (along the z-direction) and the unit vector from the HI to the HO pole. A perpendicular orientation with the surface normal corresponds to cosθ = 0, while a parallel alignment corresponds to cosθ = 1. Fig. 3 shows the orientational distribution, P(cosθ), of the confined Janus NPs at different channel heights H. At H = 9 σ, P(cosθ) exhibits two peaks at cosθ ≈ 0.45 and ≈0.85. The peak at cosθ ≈ 0.85 originates from free Janus NPs orienting their HI hemispheres toward the solvent layering near the wall (see Fig. 6 for a quantitative analysis of the formation of solvent layers). The other peak at cosθ ≈ 0.45 is attributed to clusters such as dimers. In these configurations, the NPs retain their self-assembled structure while keeping their HI sides in contact with the surrounding solvent. These two preferred orientations reflect the combined influence of wall-induced layering of solvent and anisotropic interactions of NPs. At H = 12 σ and 15 σ, the peak at cosθ ≈ 0.85 disappears, and the distribution becomes broader for cosθ < 0.4 with increasing P(cosθ) at cosθ = 0. This indicates that Janus NPs more frequently adopt perpendicular orientations relative to the wall surface as the slit height increases, as a result of the formation of dimers and trimers that favor such alignment under weaker confinement. This reflects a regime in which the confinement is not sufficient to induce significant orientational ordering of the Janus NPs. Under relatively weak confinement, larger clusters such as tetramers are formed in nearly three dimensions without a preferred orientation, resembling the behavior observed in bulk-like systems.

Fig. 2 Representative snapshots of (a) homogeneous HI NPs and (b) Janus NPs at various channel heights, H, as indicated. In each panel, the top image shows the side view, while the bottom image presents the view along the direction normal to the wall surface.

Fig. 3 Orientational distributions, P(cosθ), of confined Janus NPs at various channel heights, H, as indicated. θ is defined as the angle between the surface normal of the wall (along the z-direction) and the unit vector from the hydrophilic to the hydrophobic pole.

We next discuss the thermal conductivity behavior in the equilibrium state. Fig. 4 shows the thermal conductivity as a function of the degree of confinement, C, defined as C = H/d, where d is the diameter of the NP. As a reference, the corresponding data for the confined pure solvent system are also included in Fig. 4. The thermal conductivity of the pure solvent increases as the confinement ratio C decreases. This behavior is qualitatively consistent with previous simulation results,³⁷ which demonstrated that thermal conductivity parallel to the wall surface increases as channel height decreases. Our results also show that the introduction of both HI and Janus NPs into the nanofluids does not enhance thermal conductivity at a system height of H = 9 σ; instead, it reduces it. However, as the channel height increases resulting in a lower volume fraction due to the fixed size of the NPs, the presence of HI NPs allows the thermal conductivity to be maintained. In contrast, for nanofluids containing Janus NPs, a slight decrease in thermal conductivity is observed as the channel height increases. To shed light on the mechanisms behind these results, the following subsection discusses the origin of thermal conductivity enhancement and explores why Janus particles exhibit lower thermal conductivity.

Fig. 4 Thermal conductivity, λ of nanofluids as functions of the confinement ratio C. Blue squares: hydrophilic NPs, orange triangles: Janus NPs, green diamonds: pure solvent (without NPs).

An ordered structure of fluid atoms, known as an interfacial molecular layer, could be responsible for the enhancement of thermal conductivity, primarily because heat transport through ordered liquids is more efficient than through disordered bulk liquids. Several studies^10–12 have reported that the thickness and density of the interfacial molecular layer affect the thermal conductivity of nanofluids and are closely related to the strength of the binding energy between liquid and solid atoms. Therefore, the structure of the liquid layer may account for the observed changes in the thermal conductivity of confined nanofluids. To examine the effect of the chemical nature of the NP surface on the liquid structure, we calculated the radial distribution function (RDF) between the center of mass of the NPs and solvent particles at various channel heights H, as shown in Fig. 5. The RDFs for both HI NPs and Janus NPs exhibit three distinct peaks at approximately r ≈ 3.1 σ, 4.3 σ, and 5.1 σ, respectively. Moreover, in both cases, increasing the channel height reduces the density of the solvent layer around the NPs, as indicated by the decreasing RDF peak intensities. For all investigated systems, the RDF peaks for HI NP fluids are consistently higher than those for Janus NP fluids, suggesting a more structured solvent layer around HI NPs. A similar relation between interfacial layer and NP wettability was also observed in our recent simulations of nanofluids in bulk systems.³⁰ Interestingly, as the channel height increases, the difference in RDF peak intensities between the two NP types becomes more pronounced. For confined liquids, decreasing the channel height leads to the formation of more densely structured solvent layers around the NPs, which likely contributes to the enhancement of thermal conductivity.³⁷ However, for both types of NPs, no significant increase in thermal conductivity is observed as the channel height decreases (see Fig. 4). This suggests that the resulting thermal conductivity of confined liquids arises from the concerted action of various factors.To gain a more detailed understanding of the combined effect of various factors, we also analyzed the solvent distributions to examine the interactions between the wall and solvents. According to a study by Frank and Drikakis,³⁷ the arrangement of solvent atoms into well-ordered, solid-like layers aligned parallel to the channel walls contributes to enhanced thermal conductivity in nanochannels. Fig. 6 shows the density profiles of solvent atoms along the direction normal to the wall surface to examine the formation of layered structures for both Janus NP and HI NP fluids at different confinement ratios C. Here, the pure solvent cases are not shown in Fig. 6, as the results were nearly identical to those of the nanofluid cases. We observed a nearly identical solvent distribution in the direction normal to the wall surface for both types of NPs. This indicates that the assembled or dispersed configurations of NPs confined in the nanochannels do not significantly affect the formation of solvent layers near the wall surface. To gain a deeper understanding of the arrangement of the layered structures, we also plotted the density distributions in the direction parallel to the wall surface, as shown in Fig. 7. From these plots, the solvent density profile in the pure solvent system appears evenly distributed and consistent, exhibiting clear periodic peaks regardless of the confinement ratio C. For nanofluids under strong confinement (C = 1.5), the solvent distributions become disrupted for both types of NPs, resulting in noticeable irregularities in the density profiles, as shown in Fig. 7(a). This is due to the NPs themselves occupy a substantial volume of the narrowly confines space. Thus, the introduction of NPs into the liquids under strong confinement causes disruption on the orderly arrangement of solvents in the direction parallel to the wall surface. As a result of the disruption in the orderly arrangement of solvent molecules parallel to the wall surface, we consider that the thermal conductivity of nanofluids containing either HI or Janus NPs at C = 1.5 is lower than that of the pure solvent system. Under weak confinement (C = 3.0), the system with Janus NPs still exhibits a broad peak in the range of −5.0 σ ≲ x ≲ 4.0 σ, attributed to the presence of relatively large clusters, such as tetramers, within the nanochannels, as shown in Fig. 7(b). However, compared to the case of C = 1.5 (cf. Fig. 7(a) and (b)), we can see a more uniform distribution for both types of NPs. In such systems, the influence of the layered structures near the wall surface becomes less significant, while the role of adsorption layers around the NPs becomes more pronounced. Thus, the system with a large confinement ratio C allows greater mobility of both the solvent and NPs, reducing the spatial constraints that facilitate phonon transport.³⁷ This increased mobility leads to a decrease in the thermal conductivity of the pure solvent system compared to that of nanofluids, as phonon modes become less long-range and the thermal behavior approaches that of the bulk liquid.

Fig. 5 Radial distribution function, g(r), between NP center of mass and solvents for two types of nanofluids at various confinement ratio C, as indicated.

Fig. 6 Density profiles of solvent, ρ_s, along the direction normal to the wall surface, z, for two types of nanofluids at various confinement ratio C, as indicated.

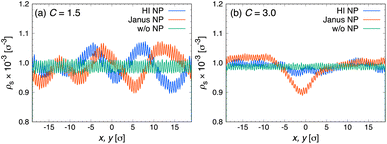Fig. 7 Density profiles of solvent, ρ_s, in the direction parallel to the wall surface, x, y, at (a) C = 1.5 and (b) C = 3.0. Blue: hydrophilic NPs, orange: Janus NPs, green: pure solvent (without NPs).

In addition to the solvent adsorption layer, Brownian motion of NPs has also been proposed as one of the mechanisms responsible for the enhancement of thermal conductivity in nanofluids. We determined the translational self-diffusion coefficient of the NPs, D, from the mean squared displacement of their centers of mass, defined as

ΔR²(t) = 〈[R_i(t₀ + t) − R_i(t₀)]²〉, (7)

as a function of time, in combination with the Einstein relation ΔR²(t) = 6Dt. We then calculated the ratio of the diffusion coefficient of Janus NPs (D_Janus) to that of the HI NPs (D_HI) and have plotted it as a function of confinement ratio C in Fig. 8. We found that dispersed HI NPs exhibit a higher diffusion coefficient than self-assembled Janus NPs under strong confinement (C ≤ 2.0). This result is somewhat unexpected, given the NP–solvent interaction strength, which is 1.0ε for the HI surface and 0.1 ε for the hydrophobic surface, as summarized in Table 1. Thus, the average NP–solvent coupling strength over the HI NP surface is higher than that over the Janus NP surface. The hydrophobic surfaces of the Janus NPs reduce interactions with the solvent, resulting in more dynamic movement of solvent particles around the NPs. This increased mobility leads to more frequent collisions, which would be expected to enhance Brownian motion.²⁸ The main reason for the lower diffusion of Janus NPs under strong confinement is the formation of clusters. Amphiphilic Janus NPs interact asymmetrically with the solvent due to their distinct surface properties, leading to self-assembly (see Fig. 2). Since the characteristic size of Janus NP clusters is larger than that of dispersed HI NPs, these clusters effectively increase the degree of confinement, thereby reducing the dynamics of Janus NPs due to spatial constraints. As the channel height increases, D_Janus/D_HI approaches unity at C = 2.5, and exceeds ≈1.0 at C = 3.0, indicating that Janus NPs exhibit higher diffusion than HI NPs under weak confinement. In such systems, the effect of spatial constraints becomes relatively weak; in other words, the role of solvent adsorption layers around the NPs becomes more pronounced. Looking again at Fig. 5, we observe that the solvent layer surrounding Janus NPs is more loosely structured than that around HI NPs, particularly under weak confinement (C = 3.0). The tetrahedral clusters observed under weak confinement exhibit high energetic stability;⁵¹ however, it is worth noting that smaller clusters, such as dimers and trimers, are also present. These small clusters (micelles) still expose some hydrophobic surfaces (see Fig. 2), resulting in higher diffusion of Janus NPs compared to HI NPs, which maintain stable and well-structured adsorption layers around them. Nevertheless, the obtained thermal conductivity is not strongly correlated with the diffusion behavior of the NPs. Based on the analysis of adsorption layers and Brownian motion, we conclude that adsorption layers play a more critical role in determining thermal conductivity in nanoconfined systems than collisions between NPs and surrounding solvent molecules induced by Brownian motion.

Fig. 8 Ratio of the self-diffusion coefficient of Janus NPs (D_Janus) to that of HI NPs (D_HI), as a function of the confinement ratio C.

4 Conclusions

In this study, we performed molecular dynamics simulations to investigate the structural and thermal properties of nanofluids containing Janus or hydrophilic (HI) nanoparticles (NPs) confined in a nanoslit. For the pure solvent, thermal conductivity clearly increases as the channel height decreases due to the formation of the adsorption solvent layer near the wall surface. For the nanofluids, we found that thermal conductivity in nanoconfined systems is governed by the concerted action of multiple factors. Under strong confinement, decreasing the channel height leads to the formation of more densely structured solvent layers around the NPs, which contributes to the enhancement of thermal conductivity. However, introducing NPs under strong confinement disrupts the orderly arrangement of solvents parallel to the wall surface, resulting in lower thermal conductivity in nanofluids containing either HI or Janus NPs compared to the pure solvent system. Under weak confinement, the influence of the layered structures near the wall surface becomes less significant, whereas the role of adsorption layers around the NPs becomes more pronounced. Thus, the thermal conductivity of nanofluids containing HI NPs, which maintain stable and well-structured adsorption layers, is higher than that of those containing Janus NPs. We also investigated the effect of Brownian motion of NPs on thermal conductivity. The formation of clusters of Janus NPs leads to confinement-induced slower dynamics compared to the HI NP case, particularly under strong confinement. As the degree of confinement decreases, the role of solvent adsorption layers around the NPs becomes more pronounced. As a result, Janus NPs exhibit higher diffusion than HI NPs. Importantly, we found that adsorption layers play a more critical role in determining thermal conductivity in nanoconfined systems than collisions between NPs and surrounding solvents induced by Brownian motion. Our research explored the complex interplay between heat transport mechanisms, the dynamic behavior of NPs, and anisotropic surface properties in nanofluid systems under confinement. Although our simulations were performed under constant volume conditions, experimental systems typically operate under constant pressure. Increased pressure could enhance fluid layering near the walls or modify the self-assembled structure of NPs. Investigating such pressure-dependent effects would be an important direction for future work. Future studies should also investigate the effects of NP volume fraction, more complex anisotropic NPs such as patchy particles, and other transport properties such as viscosity, to gain a deeper understanding of nanofluid behavior under nanoscale confinement.

Data availability

All data are presented in the paper in either figure or tabular form.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

A. H. Azhar acknowledges the Malaysian Government for his scholarship through Jabatan Perkhidmatan Awam (JPA) Malaysia. Y. K. acknowledges JSPS KAKENHI Grant No. JP24K17216 and the support of KIT Grants-in-Aid for Early-Career Scientists.

References

1. S. U. S. Choi, Z. G. Zhang, W. Yu, F. E. Lockwood and E. A. Grulke, Appl. Phys. Lett., 2001, 79, 2252–2254.
2. J. Dai, Y. Zhai, Z. Li and H. Wang, J. Mol. Liq., 2024, 400, 124518.
3. C. Peng, H. Chen, Y. Song, J. Deng and J. Wu, Int. J. Heat Mass Transfer, 2024, 233, 126023.
4. J. M. Gonçalves, A. R. N. Bastos, S. J. L. Ribeiro, L. D. Carlos, R. L. Longo, J. M. A. Caiut and R. A. S. Ferreira, Nanoscale Adv., 2024, 6, 1486–1496.
5. A. Singh, R. Lenin, N. K. Bari, C. Bakli and C. Bera, Nanoscale Adv., 2020, 2, 3507–3513.
6. Y. Yu, J. Du, J. Hou, X. Jin and R. Wang, Int. J. Heat Mass Transfer, 2024, 226, 125468.
7. S. Sarkar and R. P. Selvam, J. Appl. Phys., 2007, 102, 074302.
8. P. Keblinski, S. R. Phillpot, S. U. S. Choi and J. A. Eastman, Int. J. Heat Mass Transfer, 2002, 45, 855–863.
9. W. Evans, J. Fish and P. Keblinski, Appl. Phys. Lett., 2006, 88, 093116.
10. Z. Liang and H. L. Tsai, Phys. Rev. E, 2011, 83, 041602.
11. W. Cui, Z. Shen, J. Yang and S. Wu, Int. Commun. Heat Mass Transfer, 2016, 71, 75–85.
12. H. Guo and N. Zhao, J. Mol. Liq., 2018, 259, 40–47.
13. X. Wang and D. Jing, Int. J. Heat Mass Transfer, 2019, 128, 199–207.
14. L. Xue, P. Keblinski, S. R. Phillpot, S. U. S. Choi and J. Eastman, Int. J. Heat Mass Transfer, 2004, 47, 4277–4284.
15. T. Sato, Y. Kobayashi, T. Michioka and N. Arai, Soft Matter, 2021, 17, 4047–4058.
16. Y. Kobayashi, T. Inokuchi, A. Nishimoto and N. Arai, Mol. Syst. Des. Eng., 2019, 4, 122–132.
17. F. Leoni, C. Calero and G. Franzese, ACS Nano, 2021, 15, 19864–19876.
18. V. Kapil, C. Schran, A. Zen, J. Chen, C. J. Pickard and A. Michaelides, Nature, 2022, 609, 512–516.
19. T. Ikeda, Y. Kobayashi and M. Yamakawa, J. Chem. Phys., 2024, 161, 024901.
20. E. Zunzunegui-Bru, S. R. Alfarano, P. Zueblin, H. Vondracek, F. Piccirilli, L. Vaccari, S. Assenza and R. Mezzenga, ACS Nano, 2024, 18, 21376–21387.
21. Z. Zhao, R. Zhou and C. Sun, J. Chem. Phys., 2020, 153, 234701.
22. Z. Zhao, Y. Jin, R. Zhou, C. Sun and X. Huang, J. Phys. Chem. B, 2023, 127, 4090–4098.
23. S. Imamura, Y. Kobayashi and E. Yamamoto, J. Chem. Phys., 2024, 160, 184503.
24. Y. Gao, Z. Chen, Y. Zhang, Y. Wen, X. Yu, B. Shan, B. Xu and R. Chen, Nano Lett., 2024, 24, 5379–5386.
25. J. B. Fan, Y. Song, H. Liu, Z. Lu, F. Zhang, H. Liu, J. Meng, L. Gu, S. Wang and L. Jiang, Sci. Adv., 2017, 3, e1603203.
26. T. Zhang, D. Lyu, W. Xu, X. Feng, R. Ni and Y. Wang, Nat. Commun., 2023, 14, 8494.
27. Y. Kobayashi and N. Arai, J. Electrochem. Soc., 2019, 166, B3223.
28. X. Cui, J. Wang and G. Xia, Nanoscale, 2022, 14, 99–107.
29. J. Hou, C. Shao, L. Huang, J. Du and R. Wang, Powder Technol., 2023, 430, 119005.
30. T. Ikeda, Y. Kobayashi and M. Yamakawa, Chem. Phys. Lett., 2025, 867, 141969.
31. I. Topal and J. Servantie, Chem. Phys., 2019, 516, 147–151.
32. M. Bishop, M. H. Kalos and H. L. Frisch, J. Chem. Phys., 1979, 70, 1299–1304.
33. G. S. Grest and K. Kremer, Phys. Rev. A, 1986, 33, 3628–3631.
34. B. H. Kim, A. Beskok and T. Cagin, Microfluid. Nanofluid., 2008, 5, 551–559.
35. N. Asproulis and D. Drikakis, Phys. Rev. E, 2010, 81, 061503.
36. M. Frank, D. Drikakis and N. Asproulis, Microfluid. Nanofluid., 2015, 19, 1011–1017.
37. M. Frank and D. Drikakis, Microfluid. Nanofluid., 2017, 21, 148.
38. Y. L. Zhu, D. Wang, J. L. Guan, Z. Y. Sun and Z. Lu, Nanoscale, 2022, 14, 3554–3560.
39. S. Plimpton, J. Comp. Physiol., 1995, 117, 1–19.
40. R. Khare, J. de Pablo and A. Yethiraj, J. Chem. Phys., 2001, 114, 7593–7601.
41. S. Bernardi, B. D. Todd and D. J. Searles, J. Chem. Phys., 2010, 132, 244706.
42. X. Yong and L. T. Zhang, J. Chem. Phys., 2013, 138, 084503.
43. J. E. Basconi and M. R. Shirts, J. Chem. Theory Comput., 2013, 9, 2887–2899.
44. M. Thomas and B. Corry, Microfluid. Nanofluid., 2015, 18, 41–47.
45. W. C. Swope, H. C. Andersen, P. H. Berens and K. R. Wilson, J. Chem. Phys., 1982, 76, 637.
46. M. S. Green, J. Chem. Phys., 1954, 22, 398–413.
47. R. Kubo, J. Phys. Soc. Jpn., 1957, 12, 570–586.
48. J. Eapen, L. Ju and S. Yip, Phys. Rev. Lett., 2007, 98, 028302.
49. H. Babaei, P. Keblinski and J. M. Khodadadi, J. Appl. Phys., 2012, 112, 054310.
50. Y. Liu, Q. Wang, L. Zhang and T. Wu, Langmuir, 2005, 21, 12025–12030.
51. Y. Kobayashi, N. Arai and A. Nikoubashman, Soft Matter, 2020, 16, 476–486.

---