Open Access Article
Open Access ArticleA deep learning method for nanoparticle size measurement in SEM images
Tingwang Taoa,
Haining Ji *ab and
Bin Liu
*ab and
Bin Liu ab
ab
aSchool of Physics and Optoelectronics, Xiangtan University, Xiangtan, 411105, China
bHunan Engineering Laboratory for Microelectronics, Optoelectronics and System on a Chip, Xiangtan University, Xiangtan, 411105, China. E-mail: sdytjhn@126.com
First published on 13th June 2025
Abstract
Accurate characterization of nanoparticle size distribution is vital for performance modulation and practical applications. Nanoparticle size measurement in SEM images often requires manual operations, resulting in limited efficiency. Although existing semantic segmentation models enable automated measurement, challenges persist regarding small particle recognition, low-contrast region segmentation accuracy, and manual scalebar calibration needs. Therefore, we propose an improved U-Net model based on attention mechanisms and residual networks, combined with an automatic scalebar recognition algorithm, to enable accurate pixel-to-physical size conversion. The model employs ResNet50 as the backbone network and incorporates the convolutional block attention module (CBAM) module to enhance feature extraction for nanoparticles, especially small or low-contrast particles. The results show that the model achieved IoU and F1-score values of 87.79% and 93.50%, respectively, on the test set. The Spearman coefficient between the measured particle sizes and manual annotations was 0.91, with a mean relative error of 4.25%, confirming the accuracy and robustness of the method. This study presents a highly reliable automated method for nanoparticle size measurement, providing an effective tool for nanoparticle analysis and engineering applications.
1. Introduction
Nanomaterials have found widespread use across various fields due to their unique physical and chemical properties, including electrical, optical, and magnetic characteristics. These applications span medicine,1 environmental science,2 electronic devices,3 energy,4 and aerospace,5 where the size of nanoparticles plays a crucial role in determining their performance. Therefore, the advancement of nanoparticle size measurement techniques remains essential for both nanomaterials research and practical applications.In recent years, the researchers have developed a range of techniques for measuring nanoparticle size, including UV-visible spectrophotometry,6 X-ray diffraction (XRD) analysis,7 and laser diffraction.8 Although these techniques enable indirect measurement, they are frequently accompanied by systematic errors. In contrast, scanning electron microscopy (SEM) has become the preferred method due to its reliability and direct visual characterization. However, manual measurement of nanoparticle sizes from SEM images is a time-consuming and labor-intensive process.
To enable automated and accurate measurement of nanoparticle sizes in SEM images, precise identification and segmentation of particles must first be achieved. Traditional image segmentation methods, such as watershed transform (WST),9 clustering analysis,10 and thresholding analysis,11 are well-suited for images with high quality. However, when dealing with SEM images of poor quality (e.g., low-contrast between particles and background or very small particles), these methods often cause over-segmentation or image erosion, resulting in the loss of critical information. Additionally, these methods require manual parameter tuning when applied to different samples, which not only fails to meet the standards of measurement accuracy but also significantly increases human labor costs.
With advancements in deep learning algorithms and machine vision, deep learning-based image segmentation techniques have been widely applied across various scientific fields. To improve the accuracy of particle identification and segmentation, numerous efficient deep learning algorithms have been proposed.12–20 For instance, Wang et al.12 proposed a transformer-enhanced segmentation network (TESN) that integrates a hybrid CNN-transformer architecture, reducing the relative error of nanoparticle size measurement to within 3.52%. Kim et al.13 developed a method that uses machine vision and machine learning technologies to quantitatively extract particle size, distribution, and morphology from SEM images. It can achieve high-throughput, automated measurement even for overlapping or rod-shaped nanoparticles. Zhang et al.14 introduced HRU2-Net+ based on U2-Net+, which achieved a mean intersection over union (MIoU) of 87.31% and an accuracy above 97.31% on their dataset, significantly improving segmentation performance and accuracy. M. Frei et al.20 proposed DeepParticleNet based on Mask R-CNN and introduced a method for generating synthetic SEM images. By training the network on both synthetic and real SEM images, the model maintained adaptability while achieving high-precision particle segmentation.
Despite these advancements, two critical challenges remain: the accurate segmentation of nanoparticles, especially small or low-contrast particles; and the automatic recognition of scale bars in SEM images to ensure accurate nanoparticle size measurement.
To address these issues, we propose an improved semantic segmentation model based on the U-Net architecture, which employs ResNet50 as the backbone and integrates CBAM in the decoder to enhance feature extraction and segmentation accuracy. Furthermore, a scale recognition algorithm is introduced that enables accurate measurement of nanoparticle sizes by extracting and interpreting scale bar information.
2. Materials and methods
2.1 Data preparation
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio, resulting in 298 training images and 75 validation images. Additionally, to comprehensively evaluate the model's ability to identify small or low-contrast particles, we selected 42 additional images (containing approximately 1211 particles) from public datasets previously mentioned, most of which feature small particles or low-contrast particles, for testing the segmentation performance. The detailed dataset partitioning is shown in Table 1.
2 ratio, resulting in 298 training images and 75 validation images. Additionally, to comprehensively evaluate the model's ability to identify small or low-contrast particles, we selected 42 additional images (containing approximately 1211 particles) from public datasets previously mentioned, most of which feature small particles or low-contrast particles, for testing the segmentation performance. The detailed dataset partitioning is shown in Table 1.
| Number of images | Number of particles | |
|---|---|---|
| a “Ca.” stands for “containing approximately.” | ||
| Training set | 298 | Ca.5494 |
| Validation set | 75 | |
| Test set | 42 | Ca.1211 |
Through synchronized transformations of images and their corresponding masks, annotation consistency was preserved while data diversity was effectively enhanced, thereby improving the model's generalization and ensuring efficient training of the segmentation model.
2.2 Proposed network and training
To address several challenges in SEM image segmentation, including data scarcity and the difficulty of segmenting nanoparticles, especially small or low-contrast particles, we adopt a transfer learning strategy,23 and propose an improved U-Net architecture that integrates attention mechanisms and residual networks, as shown in Fig. 1a.The channel attention mechanism (CAM) first performs global average-pooling and global max-pooling on the input feature map separately. Then, the results are processed through shared fully connected layers (MLP). The processed feature vectors are added together and passed through the sigmoid activation function. This generates the channel weight coefficients (ranging from 0 to 1). Finally, the generated channel weights are multiplied with the original input feature map on a per-channel basis to complete the attention weighting along the channel dimension, σ represents the sigmoid function:
| Mc(F) = σ(MLP(AvgPool(F))) + MLP(MaxPool(F)) | (1) |
The spatial attention mechanism (SAM) first computes the maximum and average values across the channel dimension for each spatial location of the input feature map. Then, the results are concatenated along the channel dimension and passed through a 7 × 7 convolution to reduce the number of channels to one. The sigmoid activation function is applied to generate spatial attention weights ranging from 0 to 1. Finally, the spatial attention weights are multiplied with the original input feature map at each spatial position to perform spatial attention weighting:
| Ms(F′) = σ(f7×7([MaxPool(F′); AvgPool(F′)])) | (2) |
CBAM sequentially multiplies the outputs of the channel attention module and the spatial attention module to obtain the final attention-enhanced features:
 | (3) |
By weighting features in the channel and spatial dimensions, CBAM strengthens key feature representation while reducing redundant information, thus improving particle segmentation accuracy in complex scenarios while maintaining computational efficiency. At the same time, it expands the receptive field in feature extraction and captures multi-scale information of particles, enabling accurate recognition even in low-contrast regions, thereby enhancing the model's ability to detect small or low-contrast particles and improving its generalization capability.
2.3 Scalebar recognition and size measurement
Firstly, considering that the scale bar in SEM images is located within a white stripe region, contour detection is used to locate the white stripe. Secondly, as the scale bar typically resides on the left edge of the white stripe, and the numeric length value and its unit symbol are arranged adjacently. PaddleOCR is employed to recognize text starting from the leftmost part of the region, and regular expressions are used to precisely extract the numerical value and unit, thereby obtaining the pixel length of the scale bar Lr. Subsequently, to improve the accuracy of scale detection, the detection area is refined to the region located beneath the identified numerical label. And Canny edge detection30 combined with the probabilistic hough transform31 is used to automatically detect tick marks, calculating the pixel length Lp of the scale bar. Finally, the actual length per pixel L is computed using the following formula (4).
 | (4) |
3. Results and discussion
To comprehensively and objectively evaluate the effectiveness of the proposed method, the validation was conducted from both qualitative and quantitative perspectives on the test set.3.1 Qualitative analysis
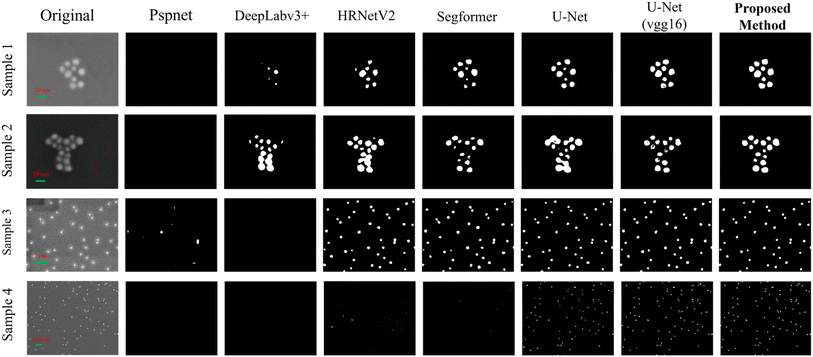
As can be visually observed in Fig. 5, the proposed model exhibits significant advantages over models such as U-Net and SegFormer. In low-contrast images (samples 1 and 2), it accurately segments particle contours. When segmenting dense particles in sample 3, the model shows high precision and preserves detailed particle features. For sample 4, which contains small particles, the proposed model demonstrates superior accuracy in identifying these features compared to the other models. These qualitative results demonstrate that the proposed model can provide more reliable outputs for downstream tasks such as particle counting and morphological analysis, demonstrating its superior segmentation performance and practical value in complex scenarios.
3.2 Quantitative analysis
To quantitatively evaluate the proposed model's segmentation performance for nanoparticles, we further adopt semantic segmentation evaluation metrics, including intersection over union (IoU), precision, recall, and F1-score, for quantitative analysis. The definitions of these metrics are provided in eqn (5)–(8).
 | (5) |
 | (6) |
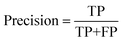 | (7) |
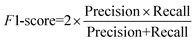 | (8) |
TP (true positive) indicates the number of particle pixels that are correctly identified by the model; FP (false positive) denotes the number of background pixels that are mistakenly classified as particle pixels; FN (false negative) refers to the number of pixels that actually belong to particle regions but are misclassified as background; TN (true negative) represents the number of background pixels that are correctly identified as background. IoU quantifies the overlap between the predicted particle segmentation and the ground truth annotated regions. Recall measures the proportion of true particle pixels correctly identified by the model, while precision evaluates the proportion of correctly predicted particle pixels among all pixels predicted as particles. The F1-score combines recall and precision using the harmonic mean, reflecting the balance between the two metrics.
| Dataset | IoU/% | Recall/% | Precision/% | F1-score/% |
|---|---|---|---|---|
| Val | 95.92 | 98.77 | 97.08 | 97.9 |
| Test | 87.79 | 91.79 | 95.27 | 93.50 |
Experimental results show that the performance on the validation set and the independent test set is consistently high and closely aligned, indicating that the model generalizes well without overfitting. Then we compare the proposed model with U-Net variants employing different backbone networks on the test set. The detailed results are presented in Table 3.
| Method | Backbone | IoU/% | Recall/% | Precision/% | F1-score/% |
|---|---|---|---|---|---|
| U-Net | — | 77.85 | 84.26 | 91.10 | 87.54 |
| U-Net | vgg16 | 84.39 | 87.68 | 95.74 | 91.53 |
| U-Net | ResNet50 | 86.37 | 89.68 | 95.90 | 92.69 |
| Our | ResNet50 | 87.79 | 91.79 | 95.27 | 93.50 |
Experimental results show that the U-Net model with a ResNet50 backbone outperforms architectures such as VGG16 in terms of IoU, F1-score, and other metrics. This quantitatively confirms that the residual connection structure enables effective retention of nanoparticle edge features through cross-layer feature reuse. It significantly reduces the particle miss detection rate and validates the architectural advantage of ResNet50 over other backbones. The proposed model achieves a 3.40% improvement in IoU compared to U-Net with a VGG16 backbone, with notable increases in other metrics as well. These results quantitatively validate the proposed model's superior segmentation performance. We also compare our model with other mainstream methods, as shown in Table 4.
| Method | IoU/% | Recall/% | Precision/% | F1-score/% |
|---|---|---|---|---|
| Pspnet | 34.30 | 34.61 | 97.43 | 54.12 |
| DeepLabv3+ | 62.30 | 63.71 | 96.57 | 76.69 |
| HRNetV2 | 75.60 | 78.99 | 94.63 | 86.09 |
| Segformer | 78.02 | 81.45 | 94.87 | 87.65 |
| Our | 87.79 | 91.79 | 95.27 | 93.50 |
Experimental results show that the proposed model achieves an IoU of 87.79%, representing an improvement of more than 9.77% compared to mainstream models such as Segformer. The F1-score improves by 5.85% and the recall by 10.34% compared to Segformer, indicating that the model exhibits better balance in suppressing both false positives and false negatives. In addition, the precision increases by 0.40%, reaching 95.27%, which outperforms Segformer (94.87%) and HRNetV2 (94.63%). Combined with the results in Fig. 5, these findings further confirm that the CRCRA module effectively suppresses background noise and improves segmentation precision for nanoparticles.
As shown in Fig. 4, the qualitative results have demonstrated that the absence of the CRCRA module leads to suppressed key feature regions, thereby reducing segmentation accuracy for particles. The quantitative results in Table 5 further validate this conclusion. The inclusion of the ResNet50 residual network alone improves the IoU by 8.52% and the F1-score by 5.51% compared to the baseline U-Net, with other evaluation metrics also showing significant gains. These results verify the strong feature extraction capability of the ResNet50 residual network for complex patterns. The introduction of the CRCRA module results in a modest IoU improvement of 1.04% compared to the baseline model. By enhancing key region features through channel and spatial attention mechanisms, it boosts precision by 4.98%, quantitatively demonstrating its effectiveness in suppressing background noise and improving focus on critical regions. In addition, the combination of both modules improves the IoU by 9.94% and the F1-score by 5.96% compared to the baseline, while the recall increases to 91.79%, outperforming all individual enhancement schemes. This demonstrates the synergistic effect of integrating the ResNet50 residual network with the CRCRA module, substantially enhancing the model's segmentation performance on complex SEM images.
| U-Net | ResNet50 | CRCRA | IoU/% | Recall/% | Precision/% | F1-score/% |
|---|---|---|---|---|---|---|
| √ | — | — | 77.85 | 84.26 | 91.10 | 87.54 |
| √ | √ | — | 86.37 | 89.68 | 95.90 | 92.69 |
| √ | — | √ | 78.89 | 81.41 | 96.08 | 88.11 |
| √ | √ | √ | 87.79 | 91.79 | 95.27 | 93.50 |
3.3 Particle size measurement
In the process of particle size measurement from SEM images, the average diameter of different particles is commonly used to represent the particle size. To evaluate the performance and effectiveness of our particle size measurement method, the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R-Acc (binary logistic regression-based accuracy), the Spearman coefficient and the mean relative error of the particle size measurement were used to evaluate the models. The formula for log
R-Acc (binary logistic regression-based accuracy), the Spearman coefficient and the mean relative error of the particle size measurement were used to evaluate the models. The formula for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R-Acc is given by (9):
R-Acc is given by (9):
 | (9) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R-Acc. Additionally, three images containing only a single particle were excluded from the calculation of log
R-Acc. Additionally, three images containing only a single particle were excluded from the calculation of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R-Acc due to the absence of standard deviation. Thus, the overall failure rate on the full test corpus is calculated as 1/42 and the log
R-Acc due to the absence of standard deviation. Thus, the overall failure rate on the full test corpus is calculated as 1/42 and the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R-Acc is calculated as 37/38.
R-Acc is calculated as 37/38.
For log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R-Acc, it can be seen from the formula that its value largely depends on the critical value of the particle size measurement results. So, this evaluation metric is insufficient to accurately assess the performance of the proposed method. When evaluating the effectiveness of the method, more attention should be paid to the Spearman coefficient and the mean relative error of the particle size measurement.
R-Acc, it can be seen from the formula that its value largely depends on the critical value of the particle size measurement results. So, this evaluation metric is insufficient to accurately assess the performance of the proposed method. When evaluating the effectiveness of the method, more attention should be paid to the Spearman coefficient and the mean relative error of the particle size measurement.
The Spearman coefficient is a non-parametric statistical measure used to assess the rank correlation between predicted particle sizes and manually measured values. It evaluates the method's ability to capture the particle size distribution trend by comparing the consistency of the rankings of two data sets (rather than their absolute numerical differences). The coefficient ranges from −1 to 1, with values closer to 1 indicating that the predicted relative particle size relationships (such as particle A being larger than particle B) are more consistent with the manual measurements. The statistical analysis shows that the statistical analysis reveals the Spearman coefficient is 0.91, indicating a strong correlation between the predicted and manually measured particle sizes. And the mean relative error of the mean particle size is 4.25%, indicating the good generalizability of the proposed method for particle size measurement on SEM images containing particles of various sizes.
To more intuitively demonstrate the accuracy of the model, six images were randomly selected from the test set to compare the particle sizes measured both by the model and manually. As shown in Fig. 6, the average particle sizes measured both by the proposed method for particles of various sizes are very close to the manually obtained results, intuitively confirming the effectiveness of the model proposed in this study.
4. Conclusions
A deep learning-based method for automated nanoparticle size measurement in SEM images is proposed in this study, enabling nanoparticle semantic segmentation and quantitative nanoparticle size measurement. This study adopts a transfer learning strategy and CBAM attention mechanism, combined with a staged parameter freezing strategy. This combination not only reduces hardware resource consumption but also significantly enhances nanoparticle segmentation and recognition accuracy in SEM images, achieving an IoU of 87.79% and an F1-score of 93.50%. Moreover, this study proposes an automatic image scale recognition algorithm based on machine vision technology. By integrating with particle segmentation results, it enables accurate quantitative calculation of nanoparticle size distribution, providing an innovative solution for complex SEM image analysis and exhibiting broad prospects for engineering applications.Although this study has achieved certain results, several areas still require improvement, including the accurate segmentation of densely overlapping particle boundaries in SEM images; the introduction of unsupervised learning methods to reduce the labor cost of dataset annotation; and the development of lightweight architectures to reduce computational cost and improve hardware resource utilization while maintaining segmentation effectiveness. At present, we are committed to integrating the latest research findings to iteratively improve the proposed method, focusing on overcoming the above technical bottlenecks and providing new research perspectives for related fields.
Data availability
The data are available from the corresponding author on reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (No. 51902276, 62005234), the Natural Science Foundation of Hunan Province (No. 2019JJ50583, 2023JJ30585), the Scientific Research Fund of Hunan Provincial Education Department (No. 21B0111), and the Hunan Provincial Innovation Foundation for Postgraduate (No. QL20220158).References
- R. Tenchov, K. J. Hughes, M. Ganesan, K. A. Iyer, K. Ralhan, L. M. Lotti Diaz, R. E. Bird, J. M. Ivanov and Q. A. Zhou, Transforming medicine: cutting-edge applications of nanoscale materials in drug delivery, ACS Nano, 2025, 19, 4011–4038, DOI:10.1021/acsnano.4c09566.
- S. F. Ahmed, M. Mofijur, N. Rafa, A. T. Chowdhury, S. Chowdhury, M. Nahrin, A. B. M. S. Islam and H. C. Ong, Green approaches in synthesising nanomaterials for environmental nanobioremediation: technological advancements, applications, benefits and challenges, Environ. Res., 2022, 204, 111967, DOI:10.1016/j.envres.2021.111967.
- A. Ahmed, S. Sharma, B. Adak, M. M. Hossain, A. M. LaChance, S. Mukhopadhyay and L. Sun, Two-dimensional MXenes: new frontier of wearable and flexible electronics, InfoMat, 2022, 4, e12295, DOI:10.1002/inf2.12295.
- G. Zhang, H. Yang, H. Zhou, T. Huang, Y. Yang, G. Zhu, Y. Zhang and H. Pang, MXene-mediated interfacial growth of 2D–2D heterostructured nanomaterials as cathodes for Zn-based aqueous batteries, Angew. Chem., Int. Ed., 2024, 63, e202401903, DOI:10.1002/anie.202401903.
- C. Marques, A. Leal-Júnior and S. Kumar, Multifunctional integration of optical fibers and nanomaterials for aircraft systems, Materials, 2023, 16, 1433, DOI:10.3390/ma16041433.
- W. Haiss, N. T. K. Thanh, J. Aveyard and D. G. Fernig, Determination of size and concentration of gold nanoparticles from UV–vis spectra, Anal. Chem., 2007, 79, 4215–4221, DOI:10.1021/ac0702084.
- H. Khan, A. S. Yerramilli, A. D'Oliveira, T. L. Alford, D. C. Boffito and G. S. Patience, Experimental methods in chemical engineering: X-ray diffraction spectroscopy—XRD, Can. J. Chem. Eng., 2020, 98, 1255–1266, DOI:10.1002/cjce.23747.
- M. Bittelli, Experimental evidence of laser diffraction accuracy for particle size analysis, Geoderma, 2022, 409, 115627, DOI:10.1016/j.geoderma.2021.115627.
- J. Cheng and J. C. Rajapakse, Segmentation of clustered nuclei with shape markers and marking function, IEEE Trans. Biomed. Eng., 2009, 56, 741–748, DOI:10.1109/TBME.2008.2008635.
- K. P. Sinaga and M.-S. Yang, Unsupervised K-means clustering algorithm, IEEE Access, 2020, 8, 80716–80727, DOI:10.1109/ACCESS.2020.2988796.
- J. Zheng, Y. Gao, H. Zhang, Y. Lei and J. Zhang, OTSU multi-threshold image segmentation based on improved particle swarm algorithm, Appl. Sci., 2022, 12, 11514, DOI:10.3390/app122211514.
- Z. Wang, L. Fan, Y. Lu, J. Mao, L. Huang and J. Zhou, TESN: transformers enhanced segmentation network for accurate nanoparticle size measurement of TEM images, Powder Technol., 2022, 407, 117673, DOI:10.1016/j.powtec.2022.117673.
- H. Kim, J. Han and T. Yong-Jin Han, Machine vision-driven automatic recognition of particle size and morphology in SEM images, Nanoscale, 2020, 12, 19461–19469, 10.1039/D0NR04140H.
- Y. Zhang, H. Zhang, F. Liang, G. Liu and J. Zhu, The segmentation of nanoparticles with a novel approach of HRU2-Net†, Sci. Rep., 2025, 15, 2177, DOI:10.1038/s41598-025-86085-w.
- C. Liang, Z. Jia and R. Chen, An automated particle size analysis method for SEM images of powder coating particles, Coatings, 2023, 13, 1547, DOI:10.3390/coatings13091547.
- G. A. A. Monteiro, B. A. A. Monteiro, J. A. dos Santos and A. Wittemann, Pre-trained artificial intelligence-aided analysis of nanoparticles using the segment anything model, Sci. Rep., 2025, 15, 2341, DOI:10.1038/s41598-025-86327-x.
- J. D. López Gutiérrez, I. M. Abundez Barrera and N. Torres Gómez, Nanoparticle detection on SEM images using a neural network and semi-synthetic training data, Nanomaterials, 2022, 12, 1818, DOI:10.3390/nano12111818.
- A. G. Okunev, M. Y. Mashukov, A. V. Nartova and A. V. Matveev, Nanoparticle recognition on scanning probe microscopy images using computer vision and deep learning, Nanomaterials, 2020, 10, 1285, DOI:10.3390/nano10071285.
- P. Monchot, L. Coquelin, K. Guerroudj, N. Feltin, A. Delvallée, L. Crouzier and N. Fischer, Deep learning based instance segmentation of titanium dioxide particles in the form of agglomerates in scanning electron microscopy, Nanomaterials, 2021, 11, 968, DOI:10.3390/nano11040968.
- M. Frei and F. E. Kruis, Image-based size analysis of agglomerated and partially sintered particles via convolutional neural networks, Powder Technol., 2020, 360, 324–336, DOI:10.1016/j.powtec.2019.10.020.
- R. Aversa, M. H. Modarres, S. Cozzini, R. Ciancio and A. Chiusole, The first annotated set of scanning electron microscopy images for nanoscience, Sci. Data, 2018, 5, 180172, DOI:10.1038/sdata.2018.172.
- B. C. Russell, A. Torralba, K. P. Murphy and W. T. Freeman, LabelMe: a database and web-based tool for image annotation, Int. J. Comput. Vis., 2008, 77, 157–173, DOI:10.1007/s11263-007-0090-8.23.
- M. Iman, H. R. Arabnia and K. Rasheed, A review of deep transfer learning and recent advancements, Technologies, 2023, 11, 40, DOI:10.3390/technologies11020040.
- M. Shafiq and Z. Gu, Deep residual learning for image recognition: a survey, Appl. Sci., 2022, 12, 8972, DOI:10.3390/app12188972.
- J. Deng; W. Dong; R. Socher; L.-J. Li; K. Li and Li Fei-Fei ImageNet, A large-scale hierarchical image database, in Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, 2009, pp. 248–255 Search PubMed.
- S. Woo, J. Park, J.-Y. Lee and I. S. Kweon. CBAM, convolutional block attention module, arXiv, 2018, preprint, arXiv:1807.06521, DOI:10.48550/arXiv.1807.06521.
- K. Goutam, S. Balasubramanian, D. Gera and R. R. Sarma, LayerOut: freezing layers in deep neural networks, SN Comput. Sci., 2020, 1, 295, DOI:10.1007/s42979-020-00312-x.
- D. P. Kingma, J. Ba Adam, a method for stochastic optimization, arXiv, 2017, preprint, arXiv:1412.6980, DOI:10.48550/arXiv.1412.6980.
- Y. Du, C. Li, R. Guo, X. Yin, W. Liu, J. Zhou, Y. Bai, Z. Yu, Y. Yang, Q. Dang, et al., PP-OCR: a practical ultra lightweight OCR System, arXiv, 2020, preprint, arXiv:2009.09941, DOI:10.48550/arXiv.2009.09941.
- L. Ding and A. Goshtasby, On the canny edge detector, Pattern Recognit., 2001, 34, 721–725, DOI:10.1016/S0031-3203(00)00023-6.
- J. Illingworth and J. Kittler, A survey of the hough transform, Comput. Vis. Graph. Image Process., 1988, 44, 87–116, DOI:10.1016/S0734-189X(88)80033-1.
- K. Harikrishna, M. Joseph Davidson, G. Dhanush Reddy and K. Veera Venkata Nagaraju, Overcoming optical image challenges in automatic grain size measurement using a novel computer vision algorithm applied to hot deformation of Al-Zn-Mg powder metallurgy alloy, Mater. Lett., 2024, 357, 135743, DOI:10.1016/j.matlet.2023.135743.
| This journal is © The Royal Society of Chemistry 2025 |