Mechanical performance analysis of a 3D printing-based transtibial prosthetic socket against the gait cycle using the finite element method

Abstract

In order to restore near-normal gait patterns and increase patients' mobility post-amputation, prosthetic sockets are crucial. Currently, few 3D-printed prosthetic sockets are available, and little research has been conducted on their mechanical performance. Thus, the purpose of this study is to assess and characterize the performance of polyethylene terephthalate (PET), polycarbonate (PC), and polyamide 6/Nylon 6 (PA6) materials in prosthetic sockets fabricated via 3D printing. The heel-strike phase was determined to be the most critical condition in this study, and finite element technique simulations were used to consider the loads caused during the gait cycle. Findings demonstrated the superior strength and durability of the PC material, with the highest safety factor of 1.697 and a maximum Von-Mises stress of 36.49 MPa. The PET material provides the finest balance between strength and cost-effectiveness, while the PA6 material delivers the best strength and flexibility with a total deformation of 16.01 mm. This study offers suggestions for choosing materials to improve the ultimate functionality of prosthetic sockets made using 3D printing technology in clinical applications.

---

1. Introduction

Amputation is a medical treatment that profoundly affects patients' quality of life. Globally, approximately 65 million people are living with amputations, with 1.5 million new cases occurring each year.¹ With an 83% amputation rate, lower extremity amputations continue to account for the majority of amputation procedures performed, far greater than the 17% rate for upper extremities.² Below-the-knee (transtibial) amputation procedures are the most frequently conducted among the various types of amputations, attributed to the elevated incidence of post-amputation problems.³ A rehabilitation program that includes support for prosthetic devices is crucial for enhancing patients' mobility and quality of life. In addition to enhancing mobility, prosthetic devices make daily tasks and personal hygiene easier for patients.⁴ Additionally, using prosthetics can lessen the severity of health issues, save medical expenses, and lessen the need for auxiliary aids, all of which can improve the patient's total recuperation.

The production of prosthetic devices in Indonesia continues to conventionally depend on gypsum-based techniques, which possess some notable disadvantages. A significant limitation is the prosthetic socket's incapacity to adapt to variations in residual amputation volume over time, resulting in patient discomfort.⁵ Furthermore, the conventional manufacturing procedure leads to comparatively expensive costs and extended production periods.⁶ Indonesia heavily relies on imports of prosthetic sockets owing to the lack of native prosthetic devices and subpar workmanship. China, Singapore, and Japan are the primary suppliers of medical device components needed to fulfill Indonesia's requirements.⁷ To mitigate this dependency, innovation and technological advancement are essential for creating prosthetic devices that are more efficient, cost-effective, and readily available to patients in Indonesia.

Freeman and Wontorick⁸ asserted that additive manufacturing presents numerous benefits, including eradicating manual procedures in fabricating positive moulds and providing freedom in developing intricate geometries with diverse wall thicknesses. Supplementary advantages include enhanced material characteristics and reduced production expenses, making additive manufacturing more efficient for fabricating prosthetic sockets for clinical applications. Additive manufacturing's capability to produce tailored, patient-specific geometries and reduced costs relative to traditional techniques establishes it as a viable option for prosthetic applications that necessitate high precision and production efficiency.^8–10

3D printing technology provides significant responses through rapid prototyping. This technology is advancing swiftly in the medical sector, becoming a vital instrument for creating complex products with remarkable accuracy and efficiency.¹¹ This method improves efficiency, accelerates production timelines, and is more cost-effective than traditional manufacturing processes.^12–14 Chen et al.⁹ illustrated that a range of materials, including polycarbonate, acrylic, duraform, nylon P301, duraform polyamide (Nylon 12), Nylon 11, plaster infused with polyurethane, and polycarbonate coated with unsaturated polyester resin, has been thoroughly investigated in various additive manufacturing processes, such as selective laser sintering, fused deposition modeling, and 3D printing, for the fabrication of prosthetic sockets. Furthermore, Kim et al.¹⁵ highlighted that carbon fiber, polypropylene (PP), and polylactic acid (PLA) are commonly employed in prosthetic sockets using 3D printing methods. Although evaluated under limited settings, the durability of 3D-printed sockets demonstrates significant potential for clinical use, particularly for those designed to withstand P5 loading. This is particularly relevant when the cost is critical or healthcare access is restricted, making 3D printing an appealing choice for prosthetic applications, especially in terms of cost efficiency and accessibility of care.

Extensive research indicates that fused filament fabrication (FFF) and fused deposition modelling (FDM) are prevalent in 3D printing due to their user-friendliness, rapidity, and affordability. Nevertheless, stereolithography (SLA) and selective saser sintering (SLS) provide unique benefits, including an exceptionally flawless surface, superior structural strength, and high accuracy. Despite these advantages, both SLS and SLA involve considerably elevated operational expenses. Consequently, the fabrication of economical prosthetic sockets by FDM/FFF technology is highly feasible, contingent upon selecting suitable materials that fulfil the structural criteria of the socket.^16,17 Research on polypropylene (PP) sockets fabricated by fused deposition modelling (FDM) technology has demonstrated favourable outcomes for prosthetic applications. The PP sockets, characterized by a double-wall construction reinforced via FDM, have exceptional static strength and endure cyclic testing up to 250 000 cycles without substantial deterioration. This indicates that sockets manufactured via FDM satisfy the strength and durability criteria for prolonged utilization.¹⁸ Clinical comparisons suggest that the performance of FDM-produced sockets is comparable to that of conventional sockets fabricated using traditional processes, such as casting or molding. The results demonstrate that, when employing 3D printing technology, FDM sockets provide functionality comparable to that of traditional methods.

The production time for FDM sockets is approximately 3.5 hours, considerably more efficient than older technologies that typically require longer periods. Consequently, FDM-produced PP sockets demonstrate considerable promise as a viable and efficient substitute for prosthesis manufacturing, delivering performance comparable to traditional sockets while ensuring expedited production times.^18–20

Materials like polylactic acid (PLA) remain popular in 3D printing technology.^21,22 PLA provides numerous unique benefits compared to materials like acrylonitrile butadiene styrene (ABS), polyethylene terephthalate glycol (PETG), and nylon. PLA exhibits strong layer adhesion, markedly improving the strength and longevity of the socket. Furthermore, PLA is recognized for its printing simplicity, attributed to its superior adhesion to the print surface and its ability to minimize warping, thereby reducing the likelihood of print faults. Additionally, PLA is comparatively affordable, which reduces production expenses and enhances the affordability of prosthetic sockets.²³ Lestari et al.²³ determined the optimal parameters for reducing socket weight and printing time in the production of prosthetic sockets with PLA filament using 3D printing technology. The ideal parameters comprise a nozzle temperature of 190 °C, a print speed of 80 mm s⁻¹, a layer height of 0.2 mm, an infill density of 100%, and a socket thickness of 3 mm. This arrangement enables efficient printing, yielding lighter sockets while preserving the necessary strength and durability vital for prosthetic applications.

Owen and DesJardins²⁴ employed carbon fiber, PETG thermoplastic, and 3D-printed polylactic acid (PLA) to fabricate prosthetic sockets of identical configurations. The International Standards Organisation (ISO) 10328 guidelines subsequently evaluated the socket system. The assessments encompassed evaluations of ultimate strength (US), peak deflection, and investigation of failure mechanisms. The findings demonstrated that carbon fiber-based sockets displayed superior ultimate strength values upon failure compared to thermoplastic and PLA 3D-printed sockets. Nonetheless, PLA 3D-printed sockets exhibited a superior strength-to-weight ratio. This indicates that PLA-based 3D-printed sockets offer benefits in material efficiency and strength-to-weight ratio, rendering them a more effective choice for prosthetic applications. Van der Stelt et al.²⁵ conducted an economical production study using CAD design and the FFF process with PLA material to create patellar tendon-bearing sockets. The findings demonstrated that the 3D-printed sockets were favorably welcomed by patients, providing improved comfort and mobility relative to traditional sockets.

Marinopoulos et al.²⁶ constructed above-the-knee prosthetic sockets from PLA and carbon fiber (CF)-reinforced nylon using a commercial 3D printer. All 3D-printed sockets successfully fulfilled the strength test criteria in compliance with ISO 10328 standards. Their research indicated that the mean maximum load-bearing capacity for the PLA socket was 6382.6 N, accompanied by an average compression deformation of 13.6 mm. Conversely, the CF nylon socket endured a stress of 10 000 N without failure, exhibiting a displacement of 15.9 mm. The results demonstrate that prosthetic sockets constructed from PLA and CF-reinforced nylon possess significant strength, with the CF-reinforced nylon exhibiting enhanced load-bearing capability prior to failure. Ramlee et al.²⁷ constructed prosthetic sockets using 3D printing equipment with PLA + filament. The study employed post-processing procedures to use carbon fibre, Kevlar, fiberglass, and cement as reinforcements for the 3D-printed sockets. Assessing the stress–strain curves for several socket reinforcement materials revealed considerable potential for enhancement in strength and durability. The cement-reinforced socket exhibited much greater yield strength and Young's modulus than the other specimens. The yield strength of the cement-reinforced socket exceeded that of other sockets by 89.57%. Furthermore, the Young's modulus of the cement-reinforced socket was 76.15% superior to that of the other sockets.

The utilization of 3D printing technology in the fabrication of prosthetic sockets has considerable issues related to material characteristics, structural integrity, and long-term durability.^15,28,29 Despite extensive research on PLA for prosthetic socket applications,²⁵ it demonstrates inferior strength, thermal resistance, chemical resistance, and impact resistance when compared to more established engineering plastics, including acrylonitrile butadiene styrene (ABS), polycarbonate, polyamide, and composite materials such as glass or carbon-reinforced plastics.³⁰ Although PLA has benefits like ease of printing and cost efficiency, its mechanical qualities and material durability deficiencies necessitate consideration, especially in applications demanding superior resistance, such as prosthetic sockets intended to endure substantial loads and intensive use. Therefore, this research aims to develop designs and perform finite element analysis (FEA) for 3D-printed prosthetic sockets using various materials, including polyethylene terephthalate (PET), polycarbonate (PC), and polyamide 6/Nylon 6 (PA6). Polyethylene terephthalate (PET) material can be a viable option, as it exhibits good dimensional stability and distributes pressure efficiently.³¹ In addition, polycarbonate (PC) material offers high impact strength and excellent thermal resistance,³² making it suitable for prosthetic socket applications. Meanwhile, polyamide 6 (PA6) is the solution when a material with high strength and flexibility is required.³³ This study conducted finite element analysis (FEA) under loading configurations that replicate the walking cycle to evaluate the strength of prosthetic sockets constructed from PET, PC, and PA6 materials. This examination is crucial, as transtibial prosthetic sockets must be tailored to meet the unique anatomical and functional needs of each user. The findings are expected to provide substantial recommendations for achieving optimal performance in prosthetic sockets produced by 3D printing for clinical use.

2. Materials and methods

2.1. Materials

This study utilized polyethylene terephthalate (PET), polycarbonate (PC), and polyamide 6/Nylon 6 (PA6) materials, selected for their optimal mechanical qualities, including strength, elasticity, durability, and ease of manufacturing. Given these properties, they are expected to provide performance materials that are the best in transtibial prosthetic sockets, particularly in guaranteeing user comfort and longevity. The material characteristics used in this study were obtained from the Material Property Data for Engineering Materials produced by ANSYS and are available in the Engineering Data.³⁴ Table 1 presents comprehensive data on the material properties of PET, PC, and PA6, emphasizing critical parameters pertinent to fabricating transtibial prosthetic sockets.

Table 1 Material properties of PET, PC, and PA6 (ref. 34)

Materials	Mechanical properties
	Density (kg m^−3)	Modulus of elasticity (GPa)	Yield strength (MPa)	Tensile strength (MPa)	Poisson's ratio
PET	1339	2.898	52.44	57.45	0.3887
PC	1160	2.180	61.93	62.82	0.4002
PA6	1140	1.111	43.13	71.89	0.3499

---

2.2. Transtibial prosthetic socket design

Custom-designed transtibial prosthetic sockets are created by analyzing the 3D geometry of the patient's residual limb to guarantee optimal functionality, comfort, and stability during daily use.

This study involves a 13-year-old male patient who underwent a below-knee amputation as a result of a traffic accident. The residual limb was assessed as mature and healthy following post-amputation recovery, with no issues that could impede prosthetic socket fabrication. To ensure design accuracy, a qualified prosthetist carefully conducted the residual limb measurements, as depicted in Fig. 1. A clinically driven strategy was deemed the most pragmatic and pertinent for achieving a socket shape that precisely matches the patient's anatomical condition. These data are the foundation for developing a socket that meets the patient's anatomical and biomechanical needs, ultimately enhancing their quality of life.

Fig. 1 Residual limb measurements by a qualified prosthetist.

The transtibial prosthetic socket design was 3D modeled at a scale of 1 : 1 using Solidworks 2019 software according to the patient's residual limb dimension. The socket was designed with a wall thickness of 6 mm, following the study by van der Stelt et al.,³⁵ who mentioned that this thickness is more suitable for active users. This thickness was chosen not only to support the patient's activity but also to maintain the strength and structural feasibility of a prosthetic socket that meets the standard of use. In addition, the design of the socket's bottom was changed from a square to a circular shape, aiming to reduce stress concentrations that can appear at the corners of the socket. The design geometry of the transtibial prosthetic socket, designed according to the patient's stump dimensions, is shown in Fig. 2.

Fig. 2 Transtibial prosthetic socket geometry design.

2.3. Finite element model

We then used ANSYS Workbench 2024 R2 software to analyze the modeled transtibial prosthetic socket design through meshing and structural simulation. These tests were conducted to study the load received by the prosthetic socket and analyze the stress distribution during the gait cycle. The finite element model represents the transtibial prosthetic socket design and the loads applied during testing. The testing process evaluates several parameters, such as the maximum Von-Mises stress, total deformation, and safety factor. This analysis is done to ensure that the socket design can withstand the load, provide optimal performance, and remain safe for use by the patient. With this approach, the simulation results are expected to provide in-depth insight into the strength and stability of the socket design before it enters the production stage.

In the meshing stage, the mesh elements are organized through an independent study approach by trying different element sizes and numbers to determine the optimal configuration. This process is carried out in stages to ensure that the distribution of elements remains homogeneous, resulting in accurate and reliable simulations. The quality of meshing results is viewed with the element quality mesh method to determine and evaluate element quality based on shape and size relative to the ideal shape by considering side lengths, angles, and aspect ratios.

The final mesh configuration is selected after achieving a stable mesh quality characterized by no significant changes in the simulation results, even though the element size is varied (mesh convergence).³⁶ Afterward, the meshing process is validated to ensure that the simulation results are representative of the actual conditions and can be trusted. This stage allows the prosthetic socket design to be virtually tested to identify and optimize aspects of strength, comfort, and durability before entering the production stage. This approach not only improves efficiency in the design process but also ensures the final product can meet the high-quality standards expected by users.

We used structural simulations to examine how well the transtibial prosthetic socket worked during the gait cycle, including the main steps like heel strike, mid-stance, and toe-off. In determining the boundary conditions, the placement of the fixed support is adjusted to the direction of loading during the walking activity, where it is placed on the distal (bottom) part of the socket, which is the connection area with the pylon or other prosthetic components. This represents when the body load is transmitted from top to bottom during the walking cycle. Meanwhile, the load is applied from the proximal (top of the socket) part, corresponding to the direction of the physiological force of the body during footing. This configuration allows the analysis of stress distribution and deformation to be more realistic to the conditions of use. The loading in this test follows the research of van der Stelt et al.,³⁵ which stipulates that the load case is applied during the most critical phase of the gait cycle, with applied loadings of 3360 N in the heel-strike phase and 3019 N in the toe-off phase.

Then, the direction of loading was adjusted to the direction of footwork to represent the force distribution during walking activities. The load angle variation was directed parallel to the plane of the foot motion, as shown in Fig. 3. This approach was based on realistic scenarios, as outlined in Table 2, the aim being to analyze the socket's response to changing stresses during walking phase transitions.

Fig. 3 Free-body diagram representation of the transtibial prosthetic socket according to force distribution in the gait cycle phase.

Table 2 Variation in loading direction angles across gait cycle phases

Position	Angle (◦)	F (N)	Fx (N)	Fz (N)
Heel-strike	15	3360	869.6	3245.5
	10	3360	583.5	3308.9
	5	3360	292.8	3347.2
Mid-stance	0	3360	0	3360
Toe-off	5	3019	263.1	3007.5
	12	3019	627.7	2953
	20	3019	1032.6	2836.9

---

With this approach, the aim is to represent the extreme conditions that a prosthetic socket may experience while identifying potential structural failures. This analysis enables optimization of the socket design to ensure maximum strength, durability, and safety. Thus, we expect the final product to meet the user's needs in accordance with high-quality standards.

3. Results and discussion

3.1. Mesh independent study

The finite element simulation of this transtibial prosthetic socket model uses 3D tetrahedral elements, which are commonly used for complex geometries. This type of element allows flexible mesh formation and accurately follows the contours of the socket surface. The mesh quality evaluation was performed using the Element Quality method, which has a value range of 0 to 1 (poor to excellent). The aim is to measure how ideal the element's shape is compared to its optimal shape. Based on the mesh evaluation image, most elements are in the range of 0.5 to 0.99 (green to blue color), indicating that the mesh quality is good to excellent. The maximum value of 0.99956 indicates the presence of elements very close to ideal shapes, while the minimum value of 0.032 is still tolerable because the distribution of low-quality elements is very small and scattered.

This shows that the discretization process is performed with high precision, and the resulting mesh is sufficient to ensure accuracy and numerical stability in the simulation (Fig. 4).

Fig. 4 Element quality visualization of the transtibial prosthetic socket mesh using the element quality method.

In addition, we also conducted mesh-independent studies to determine the optimal meshing configuration and element size, aiming to balance simulation accuracy and computational efficiency.^37,38 The mesh quality is categorized into fine mesh and coarse mesh, which regulates the variation of element size to affect the precision level of simulation results as well as the computational power requirements. Smaller element sizes tend to produce high accuracy but require more computational power. So, the right element size is chosen by finding the best balance between accuracy and efficiency. This way, the simulation can run at its best without using too many computer resources. If the difference in results between mesh variations is small, then the optimal mesh configuration can be used.

The mesh-independent study involved 16 experiments with various element sizes, as shown in Table 3, to evaluate their effect on simulation accuracy and computational efficiency. The results were validated to ensure that the mesh settings used can minimize potential simulation errors.

Table 3 Results of the mesh independence study for determining optimal mesh configuration in the simulation

Element size (mm)	Number of elements	Von-Mises stress (MPa)	Error calculation, % (Von Mises stresses)
20	1864	30.84	15.78%
19	2034	36.62	5.42%
18	2281	34.74	10.17%
17	2450	38.67	3.80%
16	2774	40.20	1.41%
15	3165	40.77	1.04%
14	3638	41.20	0.52%
13	4301	40.99	15.54%
12	4907	48.53	8.18%
11	5888	44.86	9.95%
10	7221	40.80	22.64%
9	9084	52.74	6.33%
8	11891	49.60	11.06%
7	16542	55.77	17.80%
6	26801	47.34	10.93%
5	52242	53.15

---

The calculation of the Von Mises stress errors in the present study utilizes the methods suggested by Jindal et al.³⁹ and Saad et al.⁴⁰ It was proposed that mesh convergence occurs when the error differential between two simulations with varying mesh sizes is below 1%, especially following further mesh refining.^39,40

Mesh convergence is an iterative procedure that involves the systematic application of loads and boundary conditions, incrementally modifying the element size until the analytical results demonstrate convergence, characterized by nearly equal outcomes for two different mesh sizes. This technique is crucial to guarantee that the numerical simulation outcomes are precise and stable, irrespective of the mesh element size employed.^39–41

According to Jindal et al.,³⁹ the maximum stress and total deformation parameters on prosthetic sockets did not significantly change when the mesh size was reduced from 0.75 mm to 0.5 mm; instead, deviations remained below 1%. This discovery indicates that even with finer meshes, the outcomes remained constant. Thus, the study determined that mesh convergence was achieved at a mesh size of 0.75 mm, as the slight variations in findings suggested that further mesh refinement would not yield significant enhancements. Furthermore, Saad et al.⁴⁰ demonstrated that a socket mesh consisting of 229 340 pieces and a mesh size of 3 mm had an inaccuracy of 0.75%. With a 1% error threshold established, the mesh analysis verified that convergence was attained. This indicates that, despite the increased mesh element size, the analysis results were adequately precise for the research aims, with the error remaining comfortably within the established limit.

Fig. 5 depicts the correlation between the number of mesh elements and the Von-Mises stress generated during the analysis. The results of this study show that a nearly linear Von Mises stress trend is obtained at mesh sizes of 16 mm, 15 mm, and 14 mm, with the corresponding numbers of elements being 2774, 3165, and 3638, respectively. The 14 mm mesh produces an error of 0.52%, indicating that convergence has been achieved, as the error is less than the required 1%. This specific mesh arrangement was chosen for the finite element analysis (FEA) because of its ideal balance between computational efficiency and excellent accuracy.

Fig. 5 Graph of mesh independent study with the relationship of the number of elements and Von-Mises stress to determine the optimal mesh configuration.

3.2. Finite element analysis of transtibial prosthetic socket design

Prosthetic sockets are designed to help patients achieve a nearly normal gait pattern, keeping in mind the balance between efficiency and comfort. The optimal design focuses not only on biomechanical functionality but also on the economic aspects that can be achieved through 3D printing fabrication methods and proper material selection. By considering all these aspects, prosthetic sockets can fulfill both biomechanical and economic needs simultaneously, significantly improving the patient's quality of life. This approach enables the production of high-quality, durable, and affordable sockets for users. The results of the finite element simulation in this study are shown in Fig. 6.

Fig. 6 Finite element simulation results of maximum Von-Mises stress: (a) PET, (b) PC, and (c) PA6.

Finite element simulation results identified the heel-strike phase with an inclination angle α = 15° as the most critical condition in prosthetic socket performance during the gait cycle. In this phase, the initial load from the body starts to be transmitted abruptly to the prosthetic socket, resulting in significant stress spikes. This leads to maximum stress concentration at the posterior and distal parts of the socket, thus increasing the risk of structural failure.^42,43

Without considering proper material selection and geometry, the risk of deformation or even structural failure can increase significantly. Therefore, an even stress distribution during the heel-strike phase is essential in the design of prosthetic sockets. The optimal socket should withstand the load while maintaining strength and stability and ensuring comfort for the user.⁴⁴ This approach not only supports a natural and efficient walking pattern but also ensures the socket can be used safely and durably, thus improving the patient's quality of life in the long run.

Based on the finite element simulation results shown in Fig. 6, the variation of maximum Von-Mises stress values received between the PET and PC materials against PA6 shows functionally relevant significance. In use, the PA6 material shows higher Von-Mises stress values than PET and PC. The PA6 material recorded the highest stress of 41.20 MPa, followed by the PET material with a stress of 37.65 MPa, and the PC material with the lowest stress of 36.49 MPa. This difference occurs due to the mechanical properties of the material; materials with a lower yield strength value tend to be more susceptible to stress concentration in critical areas.^45,46 This causes the material to enter the plastic deformation phase more quickly, especially when facing repeated loads during the gait cycle in prosthetic socket use. These findings show how important stress distribution analysis is in designing prosthetic sockets to make sure they are strong, reliable, and safe for the user so they can do their daily tasks well.

The Von Mises stress distribution resulting from the finite element analysis shows that the maximum stress occurs at the posterior-distal portion of the prosthetic socket, as shown in Fig. 7. This location is marked red to orange, indicating the peak stress value. The high stress in the area is due to the vertical force transmitted directly from the body to the socket during the heel-strike phase of the walking cycle. In addition, the shape of the socket geometry that accommodates the anatomy of the residuum also influences the stress concentration.^47,48 These findings indicate that the posterior-distal portion is a critical point that needs special attention in prosthetic socket design and material selection to avoid the risk of structural failure due to high-stress accumulation.

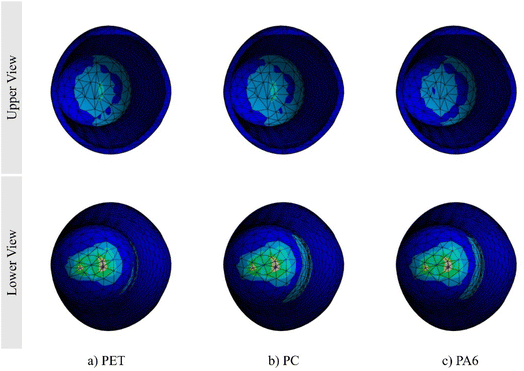Fig. 7 Von-Mises stress distribution in the transtibial prosthetic socket during the heel-strike phase: (a) PET, (b) PC, and (c) PA6.

The results of the finite element simulations of the maximum Von-Mises stress during the current force cycle show mechanically significant differences in stress values, particularly under repeated loading during the gait cycle, as shown in Fig. 8. When receiving stress, the PET and PC materials have more rigid and stable mechanical properties. Hence, they can distribute the load more evenly, and the Von Mises stress values tend to be lower.

Fig. 8 Graph of maximum Von Mises stress of the prosthetic socket at various gait cycle phases.

Meanwhile, the PA6 material, with its elastic properties, tends to create stress concentrations in certain areas, especially at the fulcrum or parts with force concentrations. Nonetheless, all three materials remain within acceptable safety limits and provide sufficient safety margins to avoid the risk of structural failure.

Prosthetic sockets change shape when given a load, which can be analyzed through the total deformation parameter. This parameter illustrates how overall shift or deformation occurs in the socket in response to load, especially in the most critical conditions. Based on the analysis results shown in Fig. 9, the PA6 material experiences a higher total deformation than the PET and PC materials, so the PA6 material tends to have good flexibility properties. PA6 shows a total deformation value of 16.01 mm, much higher than those of the PC material of 7.95 mm and PET material of 6.02 mm. The analysis also revealed the distribution pattern of displacement in the transtibial prosthetic socket, where the largest displacement occurred at the top of the socket close to the knee area, while the smallest displacement was found at the attachment site of the ear socket adapter.

Fig. 9 Finite element simulation results of total deformation: (a) PET, (b) PC, and (c) PA6.

Fig. 10 shows a comparison of the total deformation during the gait cycle. This significant difference confirms that the PA6 material is more flexible than the PET and PC materials. This flexibility is due to the lower elastic modulus value, which allows the material to deform more easily under load.⁴⁹ In contrast, materials with higher elastic modulus values tend to deform less due to their stiffer nature. Thus, PA6 materials may absorb greater deformation without increasing the risk of structural failure, although this property may be less suitable for designs that require higher dimensional stability. These findings suggest that it is important for prosthetic socket designers to select materials based on a balance between flexibility, stiffness, and user requirements to create sockets that are safe and comfortable in supporting daily activities.

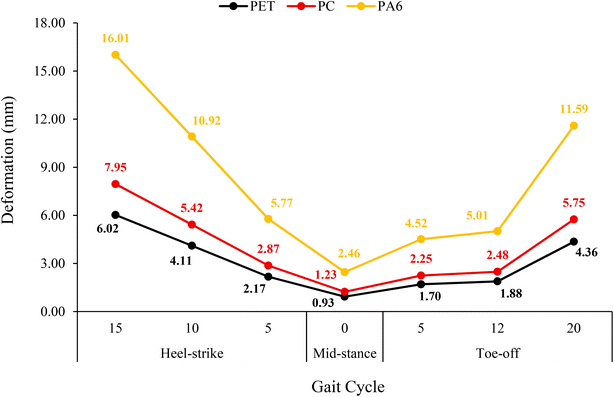Fig. 10 Graph of the total deformation of the prosthetic socket at various phases of the gait cycle.

Prosthetic sockets encounter significant repetitive compressive and flexural loads during their use, especially during the gait cycle. This repetitive loading can affect the strength and stability of the socket, potentially decreasing its level of safety. To ensure socket safety and reliability, it is important to understand and effectively replicate these loading conditions.^50,51 Material selection plays a crucial role, as the material used will determine the ability of the socket to withstand maximum stress and deformation.

The heel-strike phase was chosen as the test condition because it is the most critical condition in the gait cycle. In this phase, the initial load from the body starts to be transmitted abruptly to the prosthetic socket, resulting in significant stress spikes, making it a critical stage to evaluate the stability and comfort of the prosthetic socket.

Based on the safety factor analysis shown in Fig. 11, the PC material performed best with the highest value of 1.697, followed by the PET material at 1.393 and the PA6 material with the lowest value of 1.047. Nonetheless, all three materials still meet the minimum standard for static testing, as their safety values are greater than 1 (SF > 1), indicating reliability and safety during use.^52,53 However, the design will be considered safe against material fatigue if the factor of safety value reaches or exceeds 1.25, as suggested by various engineering standards and previous studies.^54–56 These findings are consistent with previous research, including the study by Jindal et al.,³⁹ which evaluated multiple materials and established a minimum safety factor threshold of 1.5 for assessing maximum static load-bearing capacity.

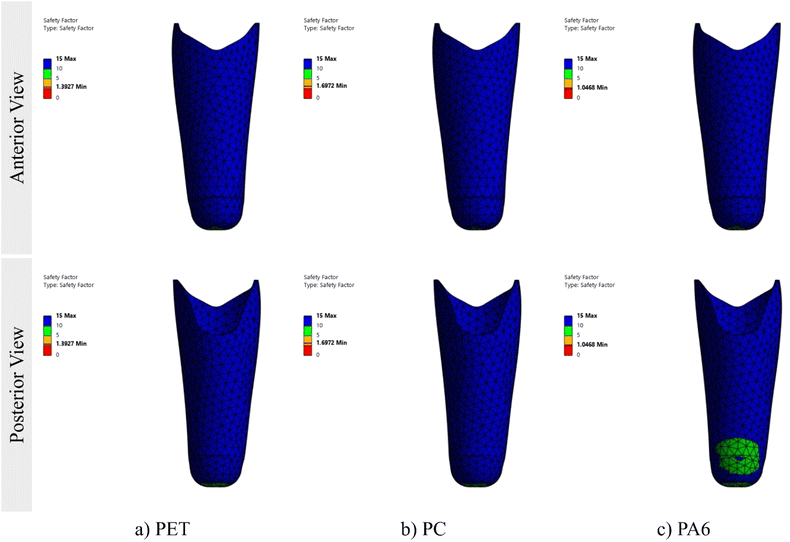Fig. 11 Finite element simulation results with respect to the factor of safety: (a) PET, (b) PC, and (c) PA6.

In the research of Plesec et al.,⁵⁷ a safety factor of more than 2 was obtained, and the 3D-printed socket made of PLA could withstand the stresses and strains during a normal gait cycle. However, it should be understood that differences in results between studies are very likely to occur, mainly due to factors such as patient-specific conditions and the type of loading received by the material during use. Thus, the margin of safety factor achieved still assures reliability and safety of use while demonstrating compatibility with theoretical references and previous research results, as long as it is applied in the context of patient loads and needs.

Fig. 12 compares the safety factors for the PET, PC, and PA6 materials during the gait cycle. During the gait cycle, the mid-stance phase shows a relatively higher safety margin as the stresses generated are still low. The heel-strike phase becomes the most critical condition, where the material experiences maximum stress and deformation, testing the socket's ability to withstand peak loads. Furthermore, in the toe-off phase, the safety margin again decreases due to stress concentration in the anterior-distal area of the socket. Although the total force is lower than in the heel-strike phase, the more focused force direction and smaller contact area cause the specific pressure to increase, decreasing the safety factor in this phase.

Fig. 12 Graph of the safety factor of the prosthetic socket at various phases of the gait cycle.

The analysis showed that the PC and PET materials obtained higher safety factors due to their superior elastic modulus and tensile strength characteristics, allowing them to withstand greater loads with more limited deformation. In contrast, although the PA6 material excels in flexibility and energy-absorbing capability, its margin of safety tends to be lower than those of PC and PET. These findings emphasize the importance of proper material selection to balance safety, flexibility, and the prosthetic socket's performance.

The research by Goh et al.¹⁸ suggests that, to ensure patient safety, prosthetic sockets produced via 3D printing technology should undergo thorough structural testing following ISO 10328 criteria. The tests consist of two main categories: static testing, which subjects the material to maximum loads usually experienced during diverse activities, and cyclic testing, which simulates the regular walking pattern over 3 million cycles, applying loads uniformly with each step. These tests aim to verify that the socket will not fail due to peak loads or material fatigue under standard usage conditions.¹⁸

The present study involved testing simulations of prosthetic sockets made from the PET, PC, and PA6 materials under loads of 3360 N at the heel-strike and mid-stance positions and 3019 N at the toe-off position. The load values employed in this study align with the ISO 10328 requirements, as indicated by the research conducted by Goh et al.¹⁸ and van der Stelt et al.³⁵ The static tests typically conform to three established loading levels defined by ISO 10328: A60, A80, and A100. The A60 standard mandates that the socket shall withstand a load of 3360 N at heel-strike and 3019 N at toe-off without failure. The results of this study demonstrate that the A60 load level does not induce failure in the tested socket model. This indicates that the socket design is resilient and can endure static testing criteria. Nonetheless, further design enhancements and supplementary testing are necessary to guarantee the socket's long-term safety and endurance.

Goh et al.¹⁸ also observed that cyclic testing is performed solely if the socket completes the static testing phase. According to their findings, cyclic testing of 3D-printed polypropylene prosthetic sockets showed no failures after 250 000 cycles. Mankai et al.⁵⁸ revealed that lower-limb prosthetic sockets reinforced with carbon fiber failed with a static stress of 3400 N. In contrast, sockets reinforced with alfa fibers (Stipa tenacissima) ruptured under a pressure of 2900 N. The cyclic testing indicated that the fatigue life of these sockets was approximately 2 325 000 cycles, which constituted only 77.5% of the 3 000 000 cycles required by the ISO 10328 standard.

The results of this study indicate that polycarbonate (PC) sockets offer a superior safety factor compared to those constructed from polyethylene terephthalate (PET) and polyamide 6 (PA6) across all loading scenarios. This result is primarily attributed to PC's enhanced yield strength of 61.93 MPa, which exceeds those of PET at 52.44 MPa and PA6 at 43.13 MPa.³⁴ The elevated yield strength of PC enables it to withstand greater applied loads before experiencing plastic deformation or mechanical failure.^59–61 As a result, PC exhibits superior structural integrity under stress, leading to a markedly increased safety factor. Conversely, sockets made from PA6 demonstrate the lowest safety factor of the three materials. This signifies an increased liability of PA6 to plastic deformation or structural failure under elevated stress conditions. Although PA6 exhibits commendable abrasion and wear resistance, its mechanical performance under stress is constrained since it tends to deform rapidly under substantial loads.

In addition, the mechanical properties of PC, PET, and PA6 are significantly affected by the monomers employed in their fabrication. Polycarbonate is a thermoplastic polymer produced from bisphenol A (BPA) and phosgene, creating carbonate bonds identical to ester bonds.^62,63 The aromatic rings in BPA substantially enhance the polymer's stiffness by limiting molecular chain motion, thus improving its strength and toughness. This molecular structure confers significant resistance to deformation, rendering PC highly durable and mechanically dependable. The unique combination of stiffness and toughness enables polycarbonate to withstand substantial mechanical stresses without irreversible deformation, making it a favored material for engineering applications that require both ductility and endurance. Consequently, polycarbonate is esteemed as a high-performance engineering resin owing to its superior mechanical properties.^62–64 In contrast, PET is a condensation polymer produced via the esterification of ethylene glycol (EG) with either terephthalic acid (TPA) or dimethyl terephthalate (DMT), leading to the creation of ester groups (–C(=O)–O–).^65–67 The inflexible aromatic ring of TPA enhances the material's rigidity, whereas the brief aliphatic chain of EG (–CH–CH₂–) restricts its toughness.^68,69

PET demonstrates commendable rigidity; however, its inferior toughness relative to PC renders it more susceptible to failure in high-stress or dynamic environments. Consequently, PET exhibits a diminished safety factor owing to its limited capacity to withstand deformation or fracture under stress. PA6, also known as nylon 6, is produced from ε-caprolactam and consists of extended aliphatic chains (–CH₂)₅– and amide functional groups (–NH–C(=O)–).⁶⁵

Additionally, PA6 exhibits exceptional molding capabilities, notable water absorption properties, and elevated thermal stability. The robust intermolecular hydrogen bonding in its molecular structure significantly contributes to its raised melting point, improving its performance at high temperatures.⁷⁰ The pliable aliphatic backbone results in less hydrogen bonding, which decreases intermolecular cohesion and increases vulnerability to plastic deformation. While PA6 offers moderate strength, its reduced toughness and increased flexibility render it more susceptible to mechanical failure under high-load conditions. Consequently, PA6 exhibits the lowest safety factor among the evaluated materials, signifying its restricted suitability in high-stress conditions.

This study found that the prosthetic socket designs using the PET, PC, and PA6 materials had respective masses of 905 g, 784 g, and 770 g. The 3D printing expenses per kg for the PET, PC, and PA6 filaments were $7.4,⁷¹ $95,⁷² and $95,⁷² respectively. Based on these findings, the fabrication costs for prosthetic sockets created from PET, PC, and PA6 materials were calculated to be $6.73, $74.48, and $73.15, respectively. PET is distinguished by its comparatively reduced filament cost relative to PC and PA6, making it more economical for prosthetic socket fabrication. PET offers a cost-effective alternative due to its reduced fabrication expenses, maintaining quality, and establishing itself as the ideal option for applications that highlight production cost-effectiveness.

Semi-aromatic synthetic polymers, such as polyethylene terephthalate (PET), possess exceptional physicochemical characteristics, including an elevated heat distortion temperature, excellent dimensional stability, outstanding mechanical strength, excellent chemical resistance, and effective electrical insulation. The increased glass transition temperature (T_g) and melting temperature (T_m) of PET indicate its capacity to maintain shape and structural integrity at high temperatures.^73–75 The remarkable properties of PET render it an ideal material for applications requiring thermal stability and substantial mechanical strength. PET is an exceptionally adaptable material, defined by numerous excellent properties that make it appropriate for various applications. Moreover, its recyclability improves its environmental sustainability, establishing it as an environmentally friendly material alternative.^74,76,77 The expense of 3D printing with PET filament is expected to decrease gradually as researchers focus on generating PET filament from recycled plastic bottles.^78–81 This trend is driven by PET plastic waste, a cost-effective alternative to virgin plastic in filament manufacturing.

The recycling process, which includes cleaning, shredding, and extrusion, enhances the economic viability of transforming plastic waste into usable filament. Using recycled PET bottles as the raw material significantly reduces the production cost of filament, hence decreasing the market price of PET filament. Furthermore, the recycling of post-consumer waste plastic helps alleviate environmental pollution by reducing the amount of plastic that accumulates in landfills or natural habitats.^78–83 The sustainability and effectiveness of turning plastic bottles into PET filaments will increase dramatically as recycling technology advances. These advancements are expected to lower production costs and improve the environmental efficacy of 3D printing methods.^{78–80,82–84} Ultimately, the decreasing expense and ecological advantages of recycled PET filament may render 3D printing more economical and accessible across diverse industries. As a result, industries including manufacturing, product design, and healthcare may adopt additive manufacturing technologies more quickly.^85–87

4. Conclusions

3D printing technology offers enormous potential for developing prosthetic sockets, particularly in enabling personalized, efficient, and cost-effective fabrication. Through finite element method analysis under gait cycle loading, the heel-strike phase was identified as the most critical due to the abrupt transmission of body load, resulting in peak stress concentrations at the posterior-distal region of the socket. Among the materials evaluated, polycarbonate (PC) demonstrated the highest structural integrity, making it ideal for applications requiring high strength and durability. Polyamide 6/Nylon 6 (PA6) exhibited excellent flexibility and deformation resistance, suitable for dynamic loading conditions. Meanwhile, polyethylene terephthalate (PET) provided a favorable compromise between mechanical performance and cost efficiency. Ultimately, the selection of prosthetic socket materials should align with the specific anatomical and functional needs of individual users. Careful material selection tailored to patient-specific conditions can significantly enhance the comfort, reliability, and long-term functionality of transtibial prosthetic sockets produced through additive manufacturing. Further research is necessary to examine the actual performance of these materials under various operational conditions, thereby facilitating future experimental validation. The mechanical properties of 3D-printed prosthetic socket prototypes will be carefully compared with the outcomes derived from finite element analysis (FEA) simulations to evaluate the accuracy and reliability of the computational predictions. This comparative assessment will also evaluate material selection and design parameters in relation to patient-specific requirements, thereby enhancing the clinical relevance of the study.

Data availability

Data will be made available on request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank the Universitas Negeri Semarang (UNNES), Semarang, Indonesia, for providing the financial support needed to complete this research through the Inovasi Lanjutan Research Grant in 2024 with contract number 388.26.2/UN37/PPK.10/2024. The authors extend their appreciation to the Deanship of Research and Graduate Studies at King Khalid University for funding this work through Large Research Project under grant number RGP2/531/45. This study was funded by Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2025R821), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

References

1. D. Z. M. Ramirez, B. Nakandi, R. Ssekitoleko, L. Ackers, E. Mwaka, L. Kenney, C. Holloway and M. Donovan-Hall, et al., The lived experience of people with upper limb absence living in Uganda: A qualitative study, Afr. J. Disabil., 2022, 11, 1–13,  DOI:10.4102/ajod.v11i0.890.
2. M. Caruso and S. Harrington, Prevalence of Limb Loss and Limb Difference in the United States: Implications for Public Policy, Avalere Amputation Coalit., 2024.
3. N. S. Tamfu, T. J. Gustave, E. N. Ngeh, N. B. Kwijirba and P. T. Christopher, Indications and complications of lower extremity amputations in two tertiary hospitals in the North West Region of Cameroon, Pan Afr. Med. J., 2023, 44, 196,  DOI:10.11604/pamj.2023.44.196.34969.
4. C. P. F. Pasquina, A. J. Carvalho and T. P. Sheehan, Ethics in rehabilitation: Access to prosthetics and quality care following amputation, AMA J. Ethics, 2015, 17(6), 535–546,  DOI:10.1001/journalofethics.2015.17.6.stas1-1506.
5. J.-H. Seo, et al., A Prosthetic Socket with Active Volume Compensation for Amputated Lower Limb, Sensors, 2021, 2(2), 407,  DOI:10.3390/s21020407.
6. Y. Wang, Q. Tan, F. Pu, D. Boone and M. Zhang, A Review of the Application of Additive Manufacturing in Prosthetic and Orthotic Clinics from a Biomechanical Perspective, Engineering, 2020, 6(11), 1258–1266,  DOI:10.1016/j.eng.2020.07.019.
7. D. D. Statistik, Buletin Statistik Perdagangan Luar Negeri Impor Desember 2023, BPS, 2024, 41(2), 1–422.
8. D. Freeman and L. Wontorcik, Stereolithography and Prosthetic Test Socket Manufacture: A Cost/Benefit Analysis, J. Prosthet. Orthot., 1998, 10(1), 17–20 , available: https://www.journals.lww.com/jpojournal/fulltext/1998/01010/stereolithography_and_prosthetic_test_socket.5.aspx.
9. R. K. Chen, Y. Jin, J. Wensman and A. Shih, Additive manufacturing of custom orthoses and prostheses—A review, Addit. Manuf., 2016, 12, 77–89,  DOI:10.1016/j.addma.2016.04.002.
10. A. M. Gómez-Amador, C. Pérez-Carrera, L. Prieto-Fernández and H. Rubio-Alonso, 3D-printed prosthetic foot design: Mechanical similarity and testing, Mater. Des., 2025, 253, 1–14,  DOI:10.1016/j.matdes.2025.113918.
11. Q. Hu, et al., Additive manufacture of complex 3D Au-containing nanocomposites by simultaneous two-photon polymerisation and photoreduction, Sci. Rep., 2017, 7(1), 17150,  DOI:10.1038/s41598-017-17391-1.
12. D. H. Ballard, P. Mills, R. Duszak, J. A. Weisman, F. J. Rybicki and P. K. Woodard, Medical 3D Printing Cost-Savings in Orthopedic and Maxillofacial Surgery: Cost Analysis of Operating Room Time Saved with 3D Printed Anatomic Models and Surgical Guides, Acad. Radiol., 2020, 27(8), 1103–1113,  DOI:10.1016/j.acra.2019.08.011.
13. S. H. Khajavi, et al., Additive Manufacturing in the Construction Industry: The Comparative Competitiveness of 3D Concrete Printing, Appl. Sci., 2021, 11(9), 3865,  DOI:10.3390/app11093865.
14. T. Tabassum and A. A. Mir, A review of 3d printing technology-the future of sustainable construction, Mater. Today: Proc., 2023, 93, 408–414,  DOI:10.1016/j.matpr.2023.08.013.
15. S. Kim, S. Yalla, S. Shetty and N. J. Rosenblatt, 3D printed transtibial prosthetic sockets: A systematic review, PLoS One, 2022, 17(10), 1–19.
16. A. Álvarez-trejo, E. Cuan-urquizo, D. Bhate and A. Roman-flores, Mechanical metamaterials with topologies based on curved elements : An overview of design , additive manufacturing and mechanical properties, Mater. Des., 2023, 233, 112190,  DOI:10.1016/j.matdes.2023.112190.
17. L. Zhou, et al., Additive Manufacturing : A Comprehensive Review, Sens. Rev., 2024, 24(9), 2668,  DOI:10.3390/s24092668.
18. J. C. H. Goh, P. V. S. Lee and P. Ng, Structural integrity of polypropylene prosthetic sockets manufactured using the polymer deposition technique, Proc. Inst. Mech. Eng., Part H, 2002, 216(6), 359–368,  DOI:10.1243/095441102321032157.
19. F. E. H. Tay, M. A. Manna and L. X. Liu, A CASD/CASM method for prosthetic socket fabrication using the FDM technology, Rapid Prototyp. J., 2002, 8(4), 258–262,  DOI:10.1108/13552540210441175.
20. Y. S. Fuh, J. Y. H. Feng and W. Wong, Modelling, Analysis and Fabrication of Below-knee Prosthetic Sockets Using Rapid Prototyping, in Advanced Manufacturing Technology for Medical Applications, ed. I. Gibson, John Wiley & Sons Ltd, 2005, pp. 207–226.  DOI:10.1002/0470033983.ch10.
21. K. Bagal and S. Rajesh, A review on PLA with different fillers used as a filament in 3D printing, Mater. Today: Proc., 2022, 50, 2057–2064,  DOI:10.1016/j.matpr.2021.09.413.
22. A. Sola and A. Trinchi, The need for fused deposition modeling of composite materials, Fused Depos. Model. Compos. Mater., Elsevier, 2023, pp. 39–89,  DOI:10.1016/B978-0-323-98823-0.00004-4.
23. W. D. Lestari, et al., Optimization of 3D printed parameters for socket prosthetic manufacturing using the taguchi method and response surface methodology, Results Eng., 2024, 21, 1–9,  DOI:10.1016/j.rineng.2024.101847.
24. M. K. Owen and J. D. DesJardins, Transtibial Prosthetic Socket Strength: The Use of ISO 10328 in the Comparison of Standard and 3D-Printed Sockets, J. Prosthet. Orthot., 2020, 32(2), 93–100 , available: https://www.journals.lww.com/jpojournal/fulltext/2020/04000/transtibial_prosthetic_socket_strength__the_use_of.4.aspx.
25. van der Stelt, et al., Design and Production of Low-Cost 3D-Printed Transtibial Prosthetic Sockets, J. Prosthet. Orthot., 2018, 35(1), 30–36,  DOI:10.33137/cpoj.v1i2.30843.
26. T. Marinopoulos, S. Li and V. V Silberschmidt, Structural integrity of 3D-printed prosthetic sockets: Experimental study for paediatric applications, J. Mater. Res. Technol., 2023, 24, 2734–2742,  DOI:10.1016/j.jmrt.2023.03.192.
27. M. H. Ramlee, M. I. Ammarullah, N. S. Mohd Sukri, N. S. Faidzul Hassan, M. H. Baharuddin and M. R. Abdul Kadir, Investigation on three-dimensional printed prosthetics leg sockets coated with different reinforcement materials: analysis on mechanical strength and microstructural, Sci. Rep., 2024, 14(1), 1–20,  DOI:10.1038/s41598-024-57454-8.
28. E. Stenvall, et al., Additive Manufacturing of Prostheses Using Forest-Based Composites, Bioeng. Artic., 2020, 7(3), 103,  DOI:10.3390/bioengineering7030103.
29. L. Campbell, A. Lau, B. Pousett, E. Janzen and S. U. Raschke, How Infill Percentage Affects The Ultimate Strength Of A 3d- Printed Transtibial Socket, Can. Prosthet. Orthot. J., 2018, 1(2), 2–3,  DOI:10.1586/17434440.2015.1059274.
30. V. Plesec, J. Humar, P. Dobnik-Dubrovski and G. Harih, Numerical Analysis of a Transtibial Prosthesis Socket Using 3D-Printed Bio-Based PLA, Materials, 2023, 16(5), 1–17,  DOI:10.3390/ma16051985.
31. T. Muringayil, S. Azat, Z. Ahmadi, O. Moini and S. Thomas, Polyethylene terephthalate (PET) recycling : A review, Case Stud. Chem. Environ. Eng., 2024, 9 DOI:10.1016/j.cscee.2024.100673.
32. A. Bahar, et al., Mechanical and Thermal Properties of 3D Printed Polycarbonate, Energies Artic, 2022, 15(10), 1–11,  DOI:10.3390/en15103686.
33. M. Kohutiar et al., Comprehensive Review : Technological Approaches , Properties , and Applications of Pure and Reinforced Polyamide 6 (PA6) and Polyamide 12 (PA12) Composite Materials, vol. 6, 2025.
34. M. Ashby, Material property data for engineering materials, in Department of Engineering, University of Cambridge , United Kingdom., 2021.
35. M. van der Stelt, F. Stenveld, T. Bitter, T. J. J. Maal and D. Janssen, Design Evaluation of FFF-Printed Transtibial Prosthetic Sockets Using Follow-Up and Finite Element Analysis, Prosthesis, 2020, 4(4), 589–599,  DOI:10.3390/prosthesis4040048.
36. K. Tlales, K. Eddine, O. Gerasimos, N. Gonzalo and E. Ferrer, Machine learning mesh - adaptation for laminar and turbulent flows : applications to high - order discontinuous Galerkin solvers, Eng. Comput., 2024, 40(5), 2947–2969,  DOI:10.1007/s00366-024-01950-y.
37. A. Seeni, P. Rajendran and H. Mamat, A CFD mesh independent solution technique for low reynolds number propeller, CFD Lett., 2019, 11(10), 15–30.
38. C. Wang, S. Sun, S. Sun and L. Li, Numerical analysis of propeller exciting force in oblique flow, J. Mar. Sci. Technol., 2017, 22(4), 602–619,  DOI:10.1007/s00773-017-0431-4.
39. P. Jindal, et al., Two-Material-Based Transtibial Socket Designs for Enhanced Load-Bearing Capacity Using FEA, Prothesis, 2025, 7(2), 1–17,  DOI:10.3390/prosthesis7020030.
40. H. Saad, M. Abdullah, H. Wasmi and H. Ansaripour, Finite Element Analysis and Modelling of Perlon-Fiberglass of a Prosthetic socket, Innov. Syst. Des. Eng., 2016, 7, 2222–2871 , available: https://www.iiste.org.
41. S. Anis, K. T. Romadhoni, D. F. Fitriyana, A. Bahatmaka, H. N. Firmansyah and N. F. da S. Guterres, The Effect of Perforated Plate Geometry on Thermofluid Characteristics of Briquette Drying Oven: A 3D Computational Fluid Dynamics (CFD) Study, CFD Lett, 2024, 16(11), 111–132,  DOI:10.37934/cfdl.16.11.111132.
42. F. Gariboldi, D. Pasquarelli and A. G. Cutti, Structural testing of lower-limb prosthetic sockets: A systematic review, Med Eng Phys, 2022, 99, 103742,  DOI:10.1016/j.medengphy.2021.103742.
43. V. Plesec, Development of a Generic Numerical Transtibial Model for Limb – Prosthesis System Evaluation, Appl. Sci., 2023, 13(4), 2339,  DOI:10.3390/app13042339.
44. M. Hazwan, M. Norli, A. Kamil, A. Sukimi and M. H. Ramlee, Static Structural Analysis on Different Topology Optimization Transtibial Prosthetic Socket Leg, Int. J. Technol., 2024, 15, 455–462,  DOI:10.14716/ijtech.v15i2.6711.
45. M. Gao, C. Wang, D. Yang, Y. Fu, B. Li and R. Guan, Effect of stress concentration and deformation temperature on the tensile property and damage behavior of a B 4 Cp/Al composite, J. Mater. Res. Technol., 2021, 15, 2601–2610,  DOI:10.1016/j.jmrt.2021.09.101.
46. A. Kaimkuriya, B. Sethuraman and M. Gupta, Effect of Physical Parameters on Fatigue Life of Materials and Alloys : A Critical Review, Technologies, 2024, 12, 1–31.
47. K. M. Devin, J. Tang and D. Moser, Assessing Socket Fit Effects on Pressure and Shear at a Transtibial Residuum/Socket Interface, Appl Bionics Biomech, 2023, 2023, 1–8,  DOI:10.1155/2023/3257059.
48. E. A. Al-fakih, N. Azuan, A. Osman, F. Rafiq and M. Adikan, Techniques for Interface Stress Measurements within Prosthetic Sockets of Transtibial Amputees : A Review of the Past 50 Years of Research, Sensors, 2016, 16(7), 1119,  DOI:10.3390/s16071119.
49. H. Tr and A. Barzycka, Mechanical Properties and Functions of Elastin : An Overview, Biomolecules, 2023, 13, 574.
50. M. P. McGrath, J. Gao, S. Zahedi and P. Laszczak, Development of a residuum/socket interface simulator for lower limb prosthetics, Proc. Inst. Mech. Eng., Part H, 2017, 231(3), 235–242.
51. M. A. Golovin, N. V. Marusin, M. V. Petrauskas, E. V. Fogt, and A. R. Sufelfa, 3D-printed BK and AK Prosthetic Socket Testing System, 2020 IEEE Conf. Russ. Young Res. Electr. Electron. Eng., 2020, pp. 124–126,  DOI:10.1109/EIConRus49466.2020.9039335.
52. A. K. González, J. Rodríguez-reséndiz, J. E. E. Gonzalez-durán, J. Manuel, O. Ramírez and A. A. Estévez-bén, Development of a Hip Joint Socket by Finite-Element-Based Analysis for Mechanical Assessment, Bioeng. Artic., 2023, 10(2), 1–268,  DOI:10.3390/bioengineering10020268.
53. R. Herdian, B. Ash, F. Hasan and R. Roespinoedji, Engineering , Environment , and Technology Safety Factor Analysis on the Stability of the Retaining Wall Structure in Cimahi City , Indonesia, J. Geosci. Eng. Environ. Technol., 2024, 9(3), 366–372,  DOI:10.25299/jgeet.2024.9.3.16368.
54. G. Djogo, J. Li, C. Yao, P. Pripatnanont, Y. Wang and S. Liu, An Investigation to the Effects of Impact Strength on Laminated Notched Composites used in Prosthetic Sockets Manufacturing An Investigation to the Effects of Impact Strength on Laminated Notched Composites used in Prosthetic Sockets Manufacturing, IOP Conf. Ser.:Mater. Sci. Eng., 2020, 928(2), 022081,  DOI:10.1088/1757-899X/928/2/022081.
55. F. M. Kadhim and M. S. Al-Din Tahir, Design and Analysis of Three-Point Pressure for Varus Foot Deformity, J. Biomimetics, Biomater. Biomed. Eng., 2020, 45, 1–11 , 10.4028/www.scientific.net/JBBBE.45.1.
56. F. M. Kadhim and M. S. Hayal, Analysis and Evaluating of Flexible Ankle Foot Orthosis for Drop Foot Deformity, Defect Diffus. Forum, 2020, 398, 41–47 , 10.4028/www.scientific.net/DDF.398.41.
57. B. Pla, Numerical Analysis of a Transtibial Prosthesis Socket Using, Materials, 2023, 16(5), 1985,  DOI:10.3390/ma16051985.
58. W. Mankai, S. Ben Brahim, B. Ben Smida, R. Ben Cheikh and M. Chafra, Mechanical behavior of a lower limb prosthetic socket made of natural fiber reinforced composite, J. Eng. Res., 2021, 9(2), 269–277,  DOI:10.36909/jer.v9i2.8699.
59. T. Boot, P. Kömmelt, R. W. A. Hendrikx, A. J. Böttger and V. Popovich, Effect of plastic deformation on the hydrogen embrittlement of ferritic high strength steel, npj Mater. Degrad., 2025, 9(39), 1–10,  DOI:10.1038/s41529-025-00592-9.
60. S. Sadeghi Esfahlani, Ballistic performance of Polycarbonate and Polymethyl methacrylate under normal and inclined dynamic impacts, Heliyon, 2021, 7(4), 1–10,  DOI:10.1016/j.heliyon.2021.e06856.
61. B.-A. Behrens, A. Bouguecha, I. Lüken, J. Mielke, and M. Bistron, 5.11 - Tribology in Hot Forging, in Reference Module in Materials Science and Materials Engineering Comprehensive Materials Processing, ed. S. Hashmi, G. F. Batalha, C. J. Van Tyne and B. Yilbas, Elsevier, Oxford, 2014, pp. 211–234.  DOI:10.1016/B978-0-08-096532-1.00538-0.
62. B. Love, Polymeric Biomaterials, in Biomaterials A Systems Approach to Engineering Concepts, ed. L. Overend and N. Welford, Chennai, India, Matthew Deans, 2017, pp. 205–238.  DOI:10.1007/978-3-319-58607-6_5.
63. J. Y. Q. Teo and J. Y. C. Lim, Sustainable chemical recycling of plastic waste, in Circularity of Plastics Sustainability, Emerging Materials, and Valorization of Waste Plastic, ed. Z. Li, J. Y. C. Lim, and C.-G. Wang, Elsevier, 2023, pp. 37–70,  DOI:10.1016/B978-0-323-91198-6.00004-8.
64. P. Xu, J. Ge, J. Mao and R. Bi, Polycarbonate resin powder production via steam precipitation process: Experiment and CFD simulation, Powder Technol., 2025, 449, 1–13,  DOI:10.1016/j.powtec.2024.120373.
65. G. L. Robertson, Food Packaging, in Encyclopedia of Agriculture and Food Systems, ed. N. K. Van Alfen, London-United Kingdom: Academic Press, 2014, pp. 232–249.  DOI:10.1016/B978-0-444-52512-3.00063-2.
66. Z. Jia, L. Gao, L. Qin and J. Yin, Chemical recycling of PET to value-added products, RSC Sustainability, 2023, 1(9), 2135–2147,  10.1039/d3su00311f.
67. Z. Guo, J. Wu and J. Wang, Chemical degradation and recycling of polyethylene terephthalate (PET): a review, RSC Sustainability, 2025, 3, 2111–2133,  10.1039/d4su00658e.
68. S. Bhagia, K. Bornani, S. Ozcan and A. J. Ragauskas, Terephthalic Acid Copolyesters Containing Tetramethylcyclobutanediol for High-Performance Plastics, ChemistryOpen, 2021, 10(8), 830–841,  DOI:10.1002/open.202100171.
69. V. D. Neelalochana, P. Scardi and N. Ataollahi, Polyethylene terephthalate (PET) waste in electrochemical applications, J. Environ. Chem. Eng., 2025, 13(3), 1–18,  DOI:10.1016/j.jece.2025.116823.
70. J. Wang, J. Qiu, S. Xu, J. Li and L. Shen, Electron beam irradiation influencing the mechanical properties and water absorption of polycaprolactam (PA6) and polyhexamethylene adipamide (PA66), RSC Adv., 2020, 10(36), 21481–21486,  10.1039/d0ra03673k.
71. G. E. Sosa Valenzuela and P. M. Pascua Cantarero, Feasibility Study for the Manufacturing of 3D Printing Filaments from Recycled PET: A Design of Experiments Approach, J. Fluid Flow, Heat Mass Transf., 2024, 11, 388–396,  DOI:10.11159/jffhmt.2024.038.
72. J. Flynt, How Much Does 3D Printing Filament Cost?, 3DInsider, 2017, https://www.3dinsider.com/3d-printing-filament-cost/, accessed Jun. 22, 2025.
73. P. G. C. Nayanathara Thathsarani Pilapitiya and A. S. Ratnayake, The world of plastic waste: A review, Clean. Mater., 2024, 11, 1–23,  DOI:10.1016/j.clema.2024.100220.
74. T. Muringayil Joseph, et al., Polyethylene terephthalate (PET) recycling: A review, Case Stud. Chem. Environ. Eng., 2024, 9, 1–16,  DOI:10.1016/j.cscee.2024.100673.
75. L. T. Sin and B. S. Tueen, 2 - Eco-profile of plastics, in Plastics and Sustainability: Practical Approaches, ed. L. T. Sin and B. S. Tueen, Elsevier, 2023, pp. 45–89,  DOI:10.1016/B978-0-12-824489-0.00010-6.
76. M. Alaghemandi, Sustainable Solutions Through Innovative Plastic Waste Recycling Technologies, Sustain, 2024, 16(23), 1–37,  DOI:10.3390/su162310401.
77. L. Umdagas, R. Orozco, K. Heeley, W. Thom and B. Al-Duri, Advances in chemical recycling of polyethylene terephthalate (PET) via hydrolysis: A comprehensive review, Polym. Degrad. Stab., 2025, 234, 1–23,  DOI:10.1016/j.polymdegradstab.2025.111246.
78. N. A. Elessawy, A. El Shakhs, M. Fahmy El-Saka, M. E. Youssef, B. A. B. Youssef and M. A. Malek Ali, Sustainable and eco-friendly 3D printing filament fabricated from different recycled solid wastes and evaluate its impact on interior and furniture design, Results Eng., 2024, 23, 1–8,  DOI:10.1016/j.rineng.2024.102428.
79. E. S. Pepek and J. C. Hanan, 3D Printing with Recycled PET as a Sustainable Thermoplastic Alternative Comparing Printed and Filament Material Properties, Polym. Technol. Mater., 2025, 1–15,  DOI:10.1080/25740881.2025.2501164.
80. M. Nikam, P. Pawar, A. Patil, A. Patil, K. Mokal and S. Jadhav, Sustainable fabrication of 3D printing filament from recycled PET plastic, Mater. Today Proc., 2023, XX, 1–11,  DOI:10.1016/j.matpr.2023.08.205.
81. R. P. Rimington, A. J. Capel, S. D. R. Christie and M. P. Lewis, Biocompatible 3D printed polymers: Via fused deposition modelling direct C2C12 cellular phenotype in vitro, Lab Chip, 2017, 17(17), 2982–2993,  10.1039/c7lc00577f.
82. G. Morales Méndez, A. del Cerro Pérez and F. del Cerro Velázquez, Prototype Pultrusion of Recycled Polyethylene Terephthalate Plastic Bottles into Filament for 3D Eco-Printing: Education for a Sustainable Development Project, Sustain, 2024, 16(19), 1–17,  DOI:10.3390/su16198347.
83. Y. K. P. Saleh, M. Zaenudin, M. M. Al Azzam, A. K. Bakar and A. N. Haryudiniarti, Filament maker design for Polyethylene Terephthalate(PET) plastic bottle recycling, AIP Conf. Proc., 2024, 3167(1), 60009,  DOI:10.1063/5.0218078.
84. M. Meraj, P. X. Ku, H. L. Choo and P. P. Aung, Design and Development of an Automated PET Plastic Bottle 3D Printer Filament Making Machine, J. Phys. Conf. Ser., 2024, 2923(1), 1–13,  DOI:10.1088/1742-6596/2923/1/012005.
85. M. Hassan, A. K. Mohanty and M. Misra, 3D printing in upcycling plastic and biomass waste to sustainable polymer blends and composites: A review, Mater. Des., 2024, 237, 112558,  DOI:10.1016/j.matdes.2023.112558.
86. A. Toghan, O. K. Alduaij, M. M. S. Sanad and N. A. Elessawy, Scalable Engineering of 3D Printing Filaments Derived from Recycling of Plastic Drinking Water Bottle and Glass Waste, Polymers, 2024, 16(22), 1–11,  DOI:10.3390/polym16223195.
87. A. Kassab, D. Al Nabhani, P. Mohanty, C. Pannier and G. Y. Ayoub, Advancing Plastic Recycling: Challenges and Opportunities in the Integration of 3D Printing and Distributed Recycling for a Circular Economy, Polymers, 2023, 15(19), 1–45,  DOI:10.3390/polym15193881.

---