 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Sodium hexafluorophosphate mediated enhancement of electrical and electrochemical properties of poly(vinyl alcohol)–chitosan solid polymer electrolytes for EDLCs†
Vipin Cyriac a,
Ismayil
a,
Ismayil *a,
Kuldeep Mishra
*a,
Kuldeep Mishra b,
Ankitha Rao
b,
Ankitha Rao c,
Riyadh Abdekadir Khelloufd,
Saraswati P. Masti
c,
Riyadh Abdekadir Khelloufd,
Saraswati P. Masti e and
I. M. Noor
e and
I. M. Noor fg
fg
aDepartment of Physics, Manipal Institute of Technology, Manipal Academy of Higher Education, Manipal 576104, Karnataka, India. E-mail: ismayil.mit@manipal.edu; ismayil.486@gmail.com; Tel: +91 98454 97546
bSymbiosis Institute of Technology (SIT), Symbiosis International (Deemed University) (SIU), Pune 412115, Maharashtra, India
cDepartment of Electronics and Communication, Manipal Institute of Technology, Manipal Academy of Higher Education, Manipal 576104, Karnataka, India
dCentre of Polymer Systems, University Institute, Tomas Bata University in Zlin, Tr. T. Bati 5678, 760 01 Zlin, Czech Republic
eDepartment of Chemistry, Karnataka University's Karnataka Science College, Dharwad, Karnataka 580001, India
fIonic Materials and Energy Devices Laboratory, Physics Department, Faculty of Science, Universiti Putra Malaysia, 43400 UPM Serdang, Selangor Darul Ehsan, Malaysia
gPhysics Division, Centre for Foundation Studies in Science of Universiti Putra Malaysia, Universiti Putra Malaysia, 43400 Serdang, Selangor Darul Ehsan, Malaysia
First published on 11th July 2025
Abstract
A free-standing, flexible and biodegradable biopolymer electrolyte (BPE) derived from a poly(vinyl alcohol) (PVA)–chitosan (CS) blend immobilizing sodium hexafluorophosphate (NaPF6) salt was fabricated via solution casting method. The effect of salt concentration on the structural, electrical, and electrochemical properties of the electrolyte was systematically investigated. X-ray diffraction (XRD) and Fourier-transform infrared (FTIR) spectroscopy were used to ascertain the microstructural changes in the polymer matrix including the complexation of PVA, CS, and NaPF6. Electrochemical impedance spectroscopy (EIS) measurements revealed that the BPE containing 40 wt% NaPF6 exhibited the highest conductivity (6.94 ± 0.04) × 10−5 S cm−1, which was three-order enhancement over the pristine system. The ion transport behaviour, interpreted through the Schütt and Gerdes (S–G) model, revealed that the ionic conductivity of the SPE system is strongly influenced by both the concentration of charge carriers and their mobility. The electrolyte displayed a predominant ionic nature with an electrochemical stability window of ∼3.25 V. When incorporated into an Na-ion EDLC, the optimized electrolyte sample provided a specific capacitance of 42.65 F g−1, energy density of 5.4 W h kg−1, and power density of 95 W kg−1, as determined by galvanostatic charge–discharge (GCD) tests performed at 0.05 mA g−1.
1 Introduction
Solid polymer electrolytes (SPEs) have emerged as valuable materials for use in modern electrochemical devices. They provide key benefits, such as enhanced safety, flexibility, and stability over traditional liquid electrolytes.1 These electrolytes are usually prepared by combining salts with polymers such as poly(ethylene oxide) or poly(ethylene imine).2 SPEs are used in various technologies including batteries, supercapacitors, fuel cells, and solar cells.3,4SPEs have notable benefits for lithium-ion batteries, such as enhanced safety, flexibility, and minimized leakage risk.5 They are characterized by low flammability, ease of processing, and high thermal stability.6 Additionally, SPEs can prevent dendrite growth and provide improved mechanical strength.7 Despite these advantages, challenges like low ionic conductivity and limited contact at the electrode/electrolyte interface remain.8 Researchers have addressed this issue through strategies such as polymer blending, the use of plasticizers, fillers, and the incorporation of ionic liquids.9 Polymer blending improves SPE performance in several ways. It increases the amorphous regions in the polymer matrix, allowing ions to move more freely.10 The addition of nanoparticles can boost both mechanical strength and ionic conductivity simultaneously.11 Furthermore, combining different polymers enhances both the dimensional and chemical stability, as demonstrated in SPEEK/SPAES blends designed for fuel cell applications.12
Polyvinyl alcohol (PVA) and chitosan (CS) have been widely explored for biomedical applications because of their complementary properties. PVA is known for its flexibility, hydrophilicity, and robust mechanical strength,13 whereas CS is biocompatible, biodegradable, and has antibacterial properties.14 Blending PVA with CS enhances mechanical properties such as tensile strength and flexibility under both dry and wet conditions.15 Chitosan also improves PVA's biocompatibility, encouraging cell attachment and growth.16,17 PVA–chitosan blends exhibit better hydrophilicity, moisture regain, and water uptake compared to pure chitosan.18 The blends also demonstrate good compatibility and miscibility due to intermolecular hydrogen bonding.19 Recent research highlights that optimizing chitosan levels in PVA/chitosan hydrogels significantly boosts mechanical and viscoelastic properties, making these materials ideal for tissue engineering and drug delivery applications.20 Polymer blend electrolytes composed of PVA and CS offer a flexible and effective alternative for solid polymer electrolytes. These blends exhibit improved ionic conductivity, thermal stability, and mechanical strength in comparison to single-polymer systems.21,22 PVA/CS blends are well-suited for applications such as lithium-ion and proton-conducting electrolytes.23,24 Structural studies indicate that blending and the addition of salts increases the amorphous regions, which improves the ionic conductivity. These materials also exhibit excellent electrochemical stability and energy storage potential, making them ideal for energy storage devices.25,26
Sodium salts, such as NaPF6, are integral to the development of solid polymer electrolytes for sodium-ion batteries. When combined with polymers like PEO, PVA and PVDF–HFP, NaPF6 enhances ionic conductivity.27,28 For instance, the PVA–NaPF6 (with PVA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NaPF6 weight ratio of 60
NaPF6 weight ratio of 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40) exhibits the highest room-temperature ionic conductivity, reaching 3.65 × 10−5 S cm−1.19 NaPF6 is the preferred electrolyte salt because of its high ionic conductivity, electrochemical stability, and compatibility with electrode materials. Research indicates NaPF6-based electrolytes achieve ionic conductivities of 5–7 mS cm−1 at room temperature and remain stable up to 4.5 V vs. Na/Na+.29 Additionally, NaPF6 facilitates favorable surface film formation and enhances cathode material reversibility.30 Compared with NaClO4, NaPF6 offers superior Na+ desolvation kinetics and better interfacial stability. These properties make NaPF6 a strong candidate for sodium-ion battery electrolytes, combining high performance, stability, and conductivity.
40) exhibits the highest room-temperature ionic conductivity, reaching 3.65 × 10−5 S cm−1.19 NaPF6 is the preferred electrolyte salt because of its high ionic conductivity, electrochemical stability, and compatibility with electrode materials. Research indicates NaPF6-based electrolytes achieve ionic conductivities of 5–7 mS cm−1 at room temperature and remain stable up to 4.5 V vs. Na/Na+.29 Additionally, NaPF6 facilitates favorable surface film formation and enhances cathode material reversibility.30 Compared with NaClO4, NaPF6 offers superior Na+ desolvation kinetics and better interfacial stability. These properties make NaPF6 a strong candidate for sodium-ion battery electrolytes, combining high performance, stability, and conductivity.
NaPF6-based polymer electrolytes also enhance the performance of electric double-layer capacitors (EDLCs) by expanding their voltage window beyond 3.5 V, leading to improved energy density.31 Compared to traditional quaternary ammonium salts, NaPF6 offers superior rate performance and reduced ionic resistance in EDLCs.32 Furthermore, NaPF6-based electrolytes demonstrate comparable or better capacitance and cycling stability than LiPF6 and KPF6 counterparts, making them excellent options for high-performance EDLCs.33
Fig. 1 compiles earlier reports on PVA/CS electrolytes doped with protons, Li+, Mg2+ and Na+, pinpointing the best conductivities achieved so far along with electrochemical stability window (ESW).21,34–40 Achieving higher room temperature ionic conductivity is crucial for efficient ion transport and optimal battery performance. ESW is the voltage range within which the electrolyte remains stable without degradation. For PVA/CS-based SPEs, the ESW usually ranges from 2.0 V to 4.0 V, depending on the composition and inclusion of additives like plasticizers or ceramic fillers. A wider ESW enables the electrolyte to operate with electrodes at higher voltages, expanding its applications in energy storage systems. Balancing ionic conductivity and electrochemical stability is essential for optimizing SPE formulations based on the PVA/CS matrix, guiding material selection for specific battery technologies. This study focused on the development and investigation of a novel SPE system composed of a PVA and CS blend doped with NaPF6. A thorough review of the literature reveals that this specific combination has not been previously explored in terms of its structural, electrical, electrochemical, and mechanical properties. By addressing this gap, this research aims to provide a deeper understanding of the potential of this material for energy storage applications. The optimized SPE was further employed in the fabrication of an EDLC, with a detailed analysis of its discharge profiles. The results demonstrate the capability of the developed system to contribute to environmentally friendly energy-storage solutions. By utilizing biodegradable materials like PVA and CS, this work emphasizes the potential of sustainable SPEs to meet the growing need for eco-conscious technologies in advanced energy storage systems.
 | ||
| Fig. 1 A bar graph depicting the peak conductivity along with electrochemical stability window of PVA/CS solid polymer electrolytes containing proton, lithium, magnesium and sodium ions. | ||
2 Experimental techniques
2.1 Materials used
Chitosan (CS; ≥75% deacetylated, 200 cPs viscosity in 1% solution; Loba Chemie), poly(vinyl alcohol) (PVA; Mw = 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1, 86% hydrolysed; SD Fine Pvt Ltd), and sodium hexafluorophosphate (NaPF6; 167.95 g mol−1; Sigma-Aldrich) were combined to form the PVA/CS–NaPF6 host matrix. The 1 vol% acetic acid solvent was prepared by diluting glacial acetic acid (60.05 g mol−1; Merck Life Science, Bangalore) with deionized water. For EDLC electrode fabrication, activated carbon (AC; 1602 m2 g−1; Kuraray, Japan), carbon black (CB), polyvinylidene fluoride (PVDF), and N-methyl-2-pyrrolidone (NMP) were all obtained from Alfa Aesar (Mumbai). All reagents were used as received without further purification.
000 g mol−1, 86% hydrolysed; SD Fine Pvt Ltd), and sodium hexafluorophosphate (NaPF6; 167.95 g mol−1; Sigma-Aldrich) were combined to form the PVA/CS–NaPF6 host matrix. The 1 vol% acetic acid solvent was prepared by diluting glacial acetic acid (60.05 g mol−1; Merck Life Science, Bangalore) with deionized water. For EDLC electrode fabrication, activated carbon (AC; 1602 m2 g−1; Kuraray, Japan), carbon black (CB), polyvinylidene fluoride (PVDF), and N-methyl-2-pyrrolidone (NMP) were all obtained from Alfa Aesar (Mumbai). All reagents were used as received without further purification.
2.2 Solid polymer electrolyte preparation
Electrolyte films were fabricated by solution casting with 1 vol% acetic acid serving as the common solvent. PVA and CS were blended in a 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 wt% ratio, selected based on previous study,41 which demonstrated that this specific composition exhibits the highest degree of amorphous character among the tested blends. Increased amorphousness is advantageous because it facilitates more efficient ion transport within the polymer matrix, which is essential for achieving better electrochemical performance in supercapacitor applications. This blend was doped with varying NaPF6 contents as listed in Table 1. The doping level was restricted to 40 wt% because higher concentrations caused the films to become unstable and lose their free-standing nature. Also, beyond this concentration, the system transitions into a polymer-in-salt regime, where the polymer becomes the minority component and ion transport is primarily governed by diffusion through ion clusters rather than polymer segmental motion. The polymer–salt mixture received 100 mL of the acetic-acid solution and was magnetically stirred at 60 °C for 4 h to ensure complete dissolution of PVA. After the mixture cooled to room temperature, stirring continued for a further 24 h to promote thorough homogenization. The resulting solution was filtered to remove any residual CS particulates, poured into polyethylene Petri dishes, and dried at 40 °C for three days. Once fully solvent-free, the films were carefully peeled and transferred to a silica-gel vacuum desiccator for storage prior to characterization, a step that helps minimize moisture uptake.
40 wt% ratio, selected based on previous study,41 which demonstrated that this specific composition exhibits the highest degree of amorphous character among the tested blends. Increased amorphousness is advantageous because it facilitates more efficient ion transport within the polymer matrix, which is essential for achieving better electrochemical performance in supercapacitor applications. This blend was doped with varying NaPF6 contents as listed in Table 1. The doping level was restricted to 40 wt% because higher concentrations caused the films to become unstable and lose their free-standing nature. Also, beyond this concentration, the system transitions into a polymer-in-salt regime, where the polymer becomes the minority component and ion transport is primarily governed by diffusion through ion clusters rather than polymer segmental motion. The polymer–salt mixture received 100 mL of the acetic-acid solution and was magnetically stirred at 60 °C for 4 h to ensure complete dissolution of PVA. After the mixture cooled to room temperature, stirring continued for a further 24 h to promote thorough homogenization. The resulting solution was filtered to remove any residual CS particulates, poured into polyethylene Petri dishes, and dried at 40 °C for three days. Once fully solvent-free, the films were carefully peeled and transferred to a silica-gel vacuum desiccator for storage prior to characterization, a step that helps minimize moisture uptake.
| Designation | PVA/CS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NaPF6 (wt% NaPF6 (wt%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) wt%) wt%) |
PVA/CS (g) | NaPF6 (g) |
|---|---|---|---|
| PCX0 | 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0 |
2.0 | 0 |
| PCX5 | 95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 5 |
1.9 | 0.1 |
| PCX10 | 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10 |
1.8 | 0.2 |
| PCX15 | 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 15 |
1.7 | 0.3 |
| PCX20 | 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 20 |
1.6 | 0.4 |
| PCX25 | 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 25 |
1.5 | 0.5 |
| PCX30 | 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 30 |
1.4 | 0.6 |
| PCX35 | 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35 35 |
1.3 | 0.7 |
| PCX40 | 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 40 |
1.2 | 0.8 |
2.3 Fabrication of EDLC device
An EDLC device was fabricated to evaluate the practical applicability of the polymer electrolytes studied. Electrodes were prepared by dry blending AC and CB in an 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 weight ratio. PVDF binder solution was separately prepared by dissolving 1 g PVDF into 30 mL NMP. Subsequently, the binder solution was added incrementally to the AC–CB mixture and homogenized using a mortar and pestle, yielding a uniform slurry. Approximately 1 mg of the active material slurry was deposited onto stainless-steel electrodes using doctor blade method, which were then dried at 60 °C in an oven until completely dry. The EDLC stack was completed by inserting the highest-conductivity polymer electrolyte between the AC–CB electrodes.
15 weight ratio. PVDF binder solution was separately prepared by dissolving 1 g PVDF into 30 mL NMP. Subsequently, the binder solution was added incrementally to the AC–CB mixture and homogenized using a mortar and pestle, yielding a uniform slurry. Approximately 1 mg of the active material slurry was deposited onto stainless-steel electrodes using doctor blade method, which were then dried at 60 °C in an oven until completely dry. The EDLC stack was completed by inserting the highest-conductivity polymer electrolyte between the AC–CB electrodes.
2.4 Solid polymer electrolyte characterisation
The ionic conductivity of the SPE was calculated using the following equation:
 | (1) |
Total ionic transference number (tion) was determined at 25 °C with a Keithley 2636B sourcemeter using a blocking-electrode stack (SS|SPE|SS). A constant bias of 100 mV was applied for 600 s, and current was logged every 0.01 s. The decay from the initial polarization current (I0) to the steady state value (Iss) was analyzed to extract (tion), providing insight into the ionic versus electronic transport within the SPE films. The high-resolution time step ensures that the early transient regime which is critical for accurate tion evaluation is fully captured.
The total ionic transference number (tion) was calculated using the following formula:
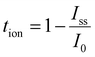 | (2) |
The ionic conductivity σion was determined from the bulk conductivity and ion transference numbers using these equations:
| σion = σbulk × tion | (3) |
2.5 EDLC characterisation
Electrochemical characterization was carried out on a Biologic SP-150e workstation, encompassing cyclic voltammetry (CV), galvanostatic charge–discharge (GCD), and electrochemical impedance spectroscopy (EIS). EIS spectra were recorded over 1 MHz to 0.01 Hz to capture the full frequency-dependent impedance response.The specific capacitance obtained from CV data is calculated from,
 | (4) |
The specific capacitance (Cs) obtained from GCD data is calculated from
 | (5) |
In this expression, m denotes the total mass of active material present on both electrodes. I is the discharge current (mA), Δt is the discharge time (s) and ΔV is the effective discharge voltage. The factor of 4 converts the measured cell capacitance to a per-electrode basis—recognizing that an EDLC effectively comprises two capacitors (one on each electrode) in series. This normalization facilitates direct comparison of specific capacitance values with those reported for single-electrode systems.43–47
The energy and power densities48 were calculated using,
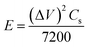 | (6) |
 | (7) |
2.6 Results and discussion
Fig. 2(a), compares the FTIR profiles of the electrolyte films and the NaPF6 salt over the 400–4000 cm−1 window, while Table 2 lists the primary vibrational bands identified for the PVA/CS matrix.
 | ||
| Fig. 2 (a) FTIR spectra of PVA/CS–NaPF6 SPEs and NaPF6 along with (b) XRD spectra of PVA/CS–NaPF6 SPEs along with XRD spectra of NaPF6 salt. | ||
| Bands | Samples along with wavenumbers associated with various functional groups (cm−1) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| PCX0 | PCX5 | PCX10 | PCX15 | PCX20 | PCX25 | PCX30 | PCX35 | PCX40 | |
| –OH stretch | 3262 | 3253 | 3274 | 3308 | 3348 | 3348 | 3367 | 3361 | 3366 |
| –CH asymmetric stretch | 2940 | 2943 | 2945 | 2948 | 2948 | 2946 | 2950 | 2946 | 2948 |
| –CH symmetric stretch | 2919 | 2923 | 2920 | 2917 | 2920 | 2919 | 2918 | 2919 | 2926 |
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretch of PVA O stretch of PVA |
1712 | 1714 | 1712 | 1712 | 1712 | 1712 | 1712 | 1712 | 1711 |
O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–NHR carboxamide C–NHR carboxamide |
1643 | 1641 | 1642 | 1642 | 1642 | 1641 | 1641 | 1632 | 1632 |
| –NH2 bending | 1555 | 1549 | 1553 | 1553 | 1548 | 1548 | 1548 | 1547 | 1547 |
| –CH stretch | 1412 | 1410 | 1413 | 1413 | 1413 | 1413 | 1414 | 1414 | 1414 |
| –OH bending | 1375 | 1379 | 1379 | 1379 | 1379 | 1379 | 1379 | 1379 | 1379 |
| C–H wagging | 1253 | 1262 | 1263 | 1264 | 1266 | 1266 | 1269 | 1270 | 1270 |
| C–O bending | 1074 | 1071 | 1073 | 1072 | 1073 | 1076 | 1075 | 1075 | 1077 |
| C–O stretch of CS | 1024 | 1024 | — | 1026 | 1026 | 1027 | 1026 | 1028 | 1028 |
| Skeletal vibrations of PVA | 946 | — | — | — | — | 949 | 949 | 948 | 947 |
| CH rocking | 826 | 846 | 842 | 841 | 840 | 839 | 837 | 836 | 839 |
The broad absorption centred between 3200 and 3550 cm−1 represents overlapping O–H and N–H stretching modes created by intra- and intermolecular hydrogen bonding in the PVA/CS matrix.52 In the NaPF6-doped films this composite band shifts from 3262 to 3366 cm−1, signalling coordination of Na+ ions with hydroxyl and/or amino sites. Earlier studies identify the –NH2 and –OH groups of chitosan as primary metal-ion anchoring centres; Na+ can bridge both groups simultaneously, disrupting the native –NH⋯OH hydrogen-bond network.53,54 A comparable effect occurs in PVA, where cation binding to –OH sites compete with existing inter-chain hydrogen bonds.55 The breaking and re-formation of these interactions suppress chain regularity, lower crystallinity, and thus hindering the reorganization of the polymer.
Furthermore, the introduction of salt induced significant shifts in multiple CH vibrational modes. Specifically, the CH rocking frequency shifted from 826 cm−1 to 839 cm−1, CH wagging moved from 1253 cm−1 to 1270 cm−1, CH symmetric stretching changed from 2919 cm−1 to 2926 cm−1 and CH asymmetric stretching shifted from 2940 cm−1 to 2948 cm−1. These observed variations suggest that the PF6− anion is interacting with the CH groups of the PVA/CS matrix via hydrogen bonding. Previous research explored the interaction between PF6− anions and the CH groups of the polymer, attributing it to weak hydrogen bonds and electrostatic forces. Specifically, studies indicate that the partially positive C–H hydrogen atoms can establish weak hydrogen bonds with the highly electronegative fluorine atoms in the PF6− anion, with bond energies ranging from approximately 2.8 to 3.1 kcal mol−1.56,57 The PF6− anion, being a large and symmetric anion, can exhibit weak electrostatic interactions with the hydrogen atoms of CH groups. These interactions are primarily due to the polarizability of the CH bonds, but they are not as strong as interactions with more electronegative atoms (like oxygen or nitrogen).58 While PF6− is not a classic hydrogen bond acceptor like some other anions (e.g., halides), there can be weak interactions between the fluorine atoms of PF6− and the hydrogen atoms of the CH groups. However, these interactions are generally weaker than traditional hydrogen bonds.59 Also, the asymmetry observed in the broad band in the IR spectra of NaPF6 salt within the 800–900 cm−1 range suggests the coexistence of a PF6− free anion peak, associated with the asymmetric P–F stretching band, and a peak corresponding to Na+⋯PF6− contact ions.60 Consequently, changes in the salt concentration led to noticeable variations in the intensity of the CH rocking band within the 800–900 cm−1 region further corroborating polymer–salt interactions. Similar observations were reported by Yong et al.19 where NaPF6 complexed PVA showed variations in –C–H and –OH stretching IR vibrations. A schematic of the proposed interaction is provided in Fig. S1 (ESI file†).
Incorporating salt caused a reduction in the intensity of the characteristic peak at 2θ = 19.6°, as well as a decrease in the halo portion associated with the PVA/CS membrane. Additionally, as the concentration of salt increases, the intensity of the diffraction peak at 2θ = 11.52° diminishes, indicating a reduction in the crystalline phase of the SPEs.67 Incorporating salt into polymer electrolytes initially hinders crystallinity by disrupting the arrangement of polymer chains and fostering amorphous areas.68 Salt ions form complexes with polymer chains, which change their shape and prevent crystallization.69 The primary factor contributing to the reduction in the crystalline phase within this system is the coordination and hydrogen bonding interactions between the PVA–CS polymer matrix and the Na-salt, as evidenced by FTIR studies. This interaction results in a modification of the microstructural characteristics of the blend composites, shifting from a crystalline to a more amorphous state as the salt concentration increases from 5% to 40% by weight. The suppression of crystallinity generally enhances ionic conductivity by increasing the mobility of the polymer chains.70
The degree of crystallinity (χ) in the polymer films was determined using the Hermans and Weidinger method,71 which allows for the quantitative separation of crystalline and amorphous contributions from the X-ray diffraction pattern. This approach involves fitting the deconvoluted XRD spectrum (shown in Fig. S2, ESI file†) into distinct crystalline and amorphous regions. Based on this separation, the crystallinity was calculated using eqn (8):
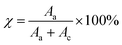 | (8) |
Fitting the Nyquist plot with a suitable electrical equivalent circuit (EEC) offers a straightforward yet powerful means of dissecting the system's electrochemical behavior. Through such EEC analyses, it is possible to directly determine the bulk resistance of the SPE, along with other components like interfacial resistances and capacitances, thus providing quantitative insights into ion transport and the interactions between electrodes and electrolytes.
Real SPE Nyquist patterns (Fig. 3(a)) rarely resemble an ideal Debye response. The high-frequency semicircle is depressed and the low-frequency spike tilts, because film thickness, morphology, and electrode roughness introduce heterogeneity.76 These non-idealities are handled by replacing the ideal capacitor in the equivalent circuit with a constant-phase element (CPE) whose impedance is 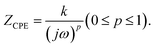 At p = 0 the CPE behaves as a resistor (k = R), at p = 1 it reduces to a pure capacitor (k−1 = C), and intermediate p values stand for the distributed, “leaky” interfacial response.77 The specific EECs adopted for fitting are shown in the Fig. 3(a) insets.
At p = 0 the CPE behaves as a resistor (k = R), at p = 1 it reduces to a pure capacitor (k−1 = C), and intermediate p values stand for the distributed, “leaky” interfacial response.77 The specific EECs adopted for fitting are shown in the Fig. 3(a) insets.
The complex impedance equation corresponding to EEC of PCX0 is given by
 | (9) |
Simplifying eqn (9) into real (Z′) and imaginary parts (Z′′) yields eqn (10) and (11)
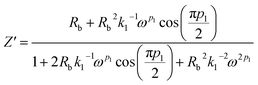 | (10) |
 | (11) |
The complex impedance equation corresponding to EEC of PCX5–PCX40 is given as
 | (12) |
Simplifying eqn (12) into real (Z′) and imaginary parts (Z′′) yields eqn (13) and (14)
 | (13) |
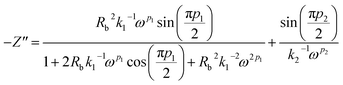 | (14) |
Non-linear least square fitting method was used to fit Nyquist plot data using the eqn (10), (11), (13) and (14) and the fitted parameter Rb and hence σ calculated from eqn (1) are listed in Table 3. According to the existing literature, a conductivity level of 10−3 to 10−5 S cm−1 is appropriate for use of electrolytes in energy storage systems. The conductivity of the SPEs increases (Table 3) with the salt concentration and reaches a maximum for PCX40 ((6.94 ± 0.04) × 10−5 S cm−1) which is three orders of magnitude higher than that of the pristine blend. The factors affecting the conductivity of the SPEs are now being discussed.
| Sample | Rb (Ω) | σ (S cm−1) at 25 °C | σdc (S cm−1) | s | (τ) (s) | R2 |
|---|---|---|---|---|---|---|
| PCX0 | 480![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 ± 7500 800 ± 7500 |
(1.43 ± 0.26) × 10−8 | (4.71 ± 1.11) × 10−8 | 0.90 ± 0.01 | — | 0.99 |
| PCX5 | 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 ± 1900 800 ± 1900 |
(1.72 ± 0.07) × 10−7 | (2.10 ± 0.16) × 10−7 | 0.82 ± 0.01 | — | 0.99 |
| PCX10 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 790 ± 200 790 ± 200 |
(3.83 ± 0.05) × 10−7 | (4.25 ± 0.17) × 10−7 | 0.79 ± 0.01 | 1.13 × 10−3 | 0.99 |
| PCX15 | 5755 ± 29 | (7.87 ± 0.03) × 10−7 | (8.06 ± 0.20) × 10−7 | 0.79 ± 0.01 | 4.49 × 10−4 | 0.99 |
| PCX20 | 4060 ± 110 | (1.84 ± 0.04) × 10−6 | (1.91 ± 0.02) × 10−6 | 0.75 ± 0.01 | 4.49 × 10−4 | 0.99 |
| PCX25 | 1176 ± 70 | (6.16 ± 0.35) × 10−6 | (5.80 ± 0.04) × 10−6 | 0.77 ± 0.01 | 2.52 × 10−4 | 0.99 |
| PCX30 | 508 ± 20 | (1.28 ± 0.04) × 10−5 | (1.25 ± 0.06) × 10−5 | 0.84 ± 0.01 | 3.99 × 10−5 | 0.99 |
| PCX35 | 80.9 ± 1.1 | (5.50 ± 0.07) × 10−5 | (6.84 ± 0.45) × 10−5 | 1 ± 0.03 | 2.00 × 10−5 | 0.99 |
| PCX40 | 52.46 ± 0.37 | (6.94 ± 0.04) × 10−5 | (7.21 ± 0.03) × 10−5 | 0.94 ± 0.02 | 2.24 × 10−6 | 0.99 |
To analyze the factors influencing conductivity, transport parameters were examined using the Schütt & Gerdes (S–G) model.78 According to the S–G model, the carrier concentration is given by
 | (15) |
In eqn (15), σ is the DC conductivity, kb is the Boltzmann constant, ε0 represents the permittivity in vacuum, and d signifies sample thickness. Here, ε∞ denotes the dielectric permittivity (real part) in the high-frequency region, ωx stands for angular frequency, where ε′(ωx) = 10ε∞. Fig. 3(b) compares the Schütt–Gerdes transport metrics with the measured bulk conductivity. While the real permittivity ε′ follows the same trend as the charge-carrier density n, the dc conductivity σdc diverges, confirming that σdc is controlled by the combined effects of n and the carrier mobility μ rather than by n alone. At the highest salt loadings (35 and 40 wt%), n decreases, yet μ rises accordingly, offsetting the loss in carriers and shaping the overall conductivity profile.
| σac(ω) = σdc + Aωs | (16) |
As the NaPF6 loading increases, the low-frequency tail in the σac spectrum broadens, signalling a larger pool of mobile charge carriers. Fig. S3(b) (ESI file†) tracks the σac spectra of optimized SPE membrane from 303 to 353 K where conductivity rises steadily with temperature, confirming thermally activated transport. Each curve shows a shallow maximum that shifts to higher frequency as T increases; beyond this point σac drops sharply, the fall-off being steeper at the upper temperatures. This apparent “peak” originates from high-frequency instrumental noise rather than a genuine dielectric relaxation, and the elevated thermal energy amplifies conduction losses that restrict ion motion in this range.80,81 Because the spectrum lacks a true high-frequency dispersion branch, Jonscher's power-law formalism cannot be applied and the fit diverges.
Fig. S3(c) (ESI file†) plots the loss tangent (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) against frequency for the NaPF6 doped SPEs. Every plot shows a single, asymmetric relaxation maximum that originates from conductivity relaxation within SPE films. As the salt fraction increases, this peak systematically moves to higher frequencies, signaling faster dipolar/ionic response.
δ) against frequency for the NaPF6 doped SPEs. Every plot shows a single, asymmetric relaxation maximum that originates from conductivity relaxation within SPE films. As the salt fraction increases, this peak systematically moves to higher frequencies, signaling faster dipolar/ionic response.
The corresponding relaxation time was extracted using
 | (17) |
 | (18) |
Fig. S4(c) and (d) (ESI file†) follow ε′ and ε′′ for PCX40 as temperature rises. Both increase because added thermal energy dissociates more Na+ and PF6− ions, boosting the pool of mobile charges. Although dielectric spectroscopy can reveal secondary dipolar relaxations, none appear in ε′′(f) for PCX40 over the temperature range studied, implying that only the primary ion-related processes are active.83
Fig. S6 (ESI file†) displays the 2D and 3D AFM images for selected samples, with a scanning area of 5 μm × 5 μm. The undoped film (PCX0) had a rough surface with a roughness of 6.16 nm. Adding salt made the surface smoother, reducing roughness to 5.11 nm. This smoother surface may help improve contact between the electrode and electrolyte, which can boost device performance.89 This improvement in surface morphology is supported by the reduction in surface height variation of PCX40 from 32.2 nm to 21.3 nm.
 | ||
| Fig. 4 (a) DSC thermogram illustrating glass transition region and thermal decomposition regions and (b) glass transition temperature variation in PVA/CS–NaPF6 SPEs. | ||
All SPEs display a single glass-transition temperature (Tg), confirming that polymer and salt are fully miscible. The non-linear shift of Tg and the lack of a melting peak shows that salt addition increases the amorphous fraction by fostering ion–dipole interactions between the ions and polar groups in the blend.90 The pronounced drop in Tg for the highest-conductivity sample, PCX40, compared with the undoped PCX0, illustrates the salt's plasticizing effect.91 TGA and DTG curves (Fig. S7†) reveal three mass-loss events for both doped and undoped SPEs. A 5–9% loss at 30–120 °C arises from residual acetic acid92 and loosely bound water attached to amine or hydroxyl sites.93 Between 180 and 237 °C the backbone undergoes chain scission and salt–polymer bonds break. The final stage, 350–500 °C, removes roughly 20% of the mass as the remaining char burns off. As shown in Table 4, the major decomposition temperature (Td) falls as dopant content rises, reflecting new salt–polymer complexes that alter the degradation pathway.94
| Sample | Major decomposition temperature Td (°C) | % weight loss |
|---|---|---|
| PCX0 | 237 | 57 |
| PCX5 | 229 | 61 |
| PCX10 | 216 | 61 |
| PCX15 | 205 | 65 |
| PCX20 | 198 | 62 |
| PCX25 | 192 | 70 |
| PCX30 | 186 | 68 |
| PCX35 | 181 | 72 |
| PCX40 | 180 | 72 |
Fig. S8 (ESI file†) presents the chronoamperometry plot for the all the salt doped samples, obtained using Wagner's DC polarization method.96 The rapid decline in polarization current over time confirms the ionic conductivity of the fabricated electrolytes. The ion transport numbers along with ionic conductivity are tabulated in Table S1 (ESI file†). The tion values for these SPE films were found to be close to unity (>0.98), confirming that the electrolytes are ionic conductors, with minimal electronic contribution. This shows that ion transport governs overall conductivity. The results in this study align well with earlier studies.97–99
2.7 EDLC characterization
Specific capacitance (Cs), calculated from the CV data with eqn (4) and summarized in Table 5, is highest at low scan rates and falls steadily as the scan rate rises. Slow scans allow ions enough time to build a thick diffuse layer and a stable electric double layer, producing a broad, nearly flat current plateau and lower ohmic resistance. At higher scan rates, ion transport toward the electrode surface occurs more rapidly, limiting the time available for complete double-layer formation. As a result, the development of a well-defined electric double layer becomes less efficient under these conditions.107 Cyclic voltammetry was also employed to assess the device's durability through repeated cycling. After 4000 charge–discharge cycles (Fig. 7(c)), the CV plot shows only a minor drop in Cs (Table 5), confirming that the EDLC retains its performance over prolonged cycling.
| Scan rate (mV s−1) | Cs before cycling (F g−1) | Cs after cycling (F g−1) |
|---|---|---|
| 100 | 6.4 | 5.8 |
| 50 | 10.4 | 8.8 |
| 20 | 18 | 14.9 |
| 10 | 24.6 | 18 |
| 5 | 28 | 24 |
| Current density (mA g−1) | Specific capacitance (F g−1) | Energy density (W h kg−1) | Power density (W kg−1) |
|---|---|---|---|
| 0.05 | 42.65 | 5.3 | 95 |
| 0.06 | 38.20 | 4.7 | 114 |
| 0.07 | 35.48 | 4.4 | 133 |
| 0.08 | 34.06 | 4.0 | 147 |
| 0.09 | 32.43 | 3.8 | 162 |
| 0.1 | 31.50 | 3.4 | 178 |
| 0.2 | 25.27 | 2.0 | 304 |
| Element | Cycling | Values |
|---|---|---|
| Rs | Before | 59.2 Ω |
| After | 59.1 Ω | |
| Rct | Before | 153.4 Ω |
| After | 211.3 Ω |
 | (19) |
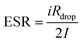 | (20) |
 | ||
| Fig. 8 (a) Efficiency and ESR and (b) energy and power density values of PCX40-based EDLC over 4000 charge–discharge cycles. | ||
Fig. 8(a) illustrates that ESR starts at about 575 Ω in the first cycle and then settles around 700 Ω by cycle 4000. This gradual increase in iRdrop and hence ESR can stem from slight degradation of the polymer electrolyte, whose conductivity here is about 10−5 S cm−1.109 Enhancing electrolyte conductivity with plasticizers or more mobile salts can lower ESR. The values observed align well with those reported for other EDLC systems.109–111
| Electrolyte system | Specific capacitance (F g−1) | Energy density (W h kg−1) | Power density (W kg−1) | Nature of electrolyte | Reference |
|---|---|---|---|---|---|
| Chitosan–PEO–LiClO4 | 6.88 @ 0.5 mA cm−2 | 1.07 | 321 | Solid electrolyte | 114 |
| PVA–CS–NaSCN–glycerol | 55.5 @ 20 mV s−1 | 12.96 | 2054 | Plasticized electrolyte | 115 |
CS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MgCl2–glycerol MgCl2–glycerol |
50 @ 10 mV s−1 | 13.1 | 550 | Plasticized electrolyte | 116 |
| PVA–CS–MgCl2 | 5.80 @ 5 mV s−1 | — | — | Solid electrolyte | 37 |
| PVA–CS–NaClO4·H2O | 38.45 @ 5 mV s−1 | 2.69 | 97 | Solid electrolyte | 117 |
| PVA–CS–PEG–Mg(NO3)2 | 4.24 @ 5 mV s−1 | 1.89 | 62.42 | Plasticized electrolyte | 118 |
| PVA–CS–NaPF6 | 28 @ 5 mV s−1 | 5.3 | 95 | Solid electrolyte | Present work |
3 Conclusions
SPEs based on CS and PVA were synthesized by incorporating varying amounts of NaPF6. The sample with the highest ionic conductivity was subsequently utilized to fabricate an EDLC. XRD analysis confirmed the predominantly amorphous nature of the SPEs, while FTIR spectroscopy underscored the strong interactions between the polymer matrix and the salt dopant. Furthermore, the relatively smooth surface morphology suggests good compatibility between the salt and the polymer phases. EEC model was applied to the prepared samples to obtain a comprehensive understanding of their electrical characteristics. The electrochemical performance of the EDLC cell was assessed under ambient conditions via impedance spectroscopy, CV, and GCD. The characteristic “leaf-shaped” CV curves, with no observable redox peaks, confirmed the non-faradaic, electric double-layer mechanism at the electrode–electrolyte interface. At a current density of 0.05 A g−1, the specific capacitance, energy density, and power density for the optimum electrolyte-based cell reached 42.65 F g−1, 5.3 W h kg−1, and 95 kW kg−1, respectively. Moreover, an EDLC with a polymer electrolyte containing 40 wt% NaPF6 retained good stability over 4000 charge–discharge cycles. These findings highlight the potential of bio-polymer blend electrolytes for constructing high-performance EDLC devices, with further conductivity enhancements achievable using various additives.Consent for publication
The authors hereby consent to publication of the present research work in this journal, if selected for publication.Data availability
Data will be made available on request upon contacting the corresponding author.Author contributions
Vipin Cyriac: conceptualization, data curation, formal analysis, investigation, methodology, writing – original draft. Ismayil: methodology, resources, supervision, validation, writing – review & editing. Kuldeep Mishra: resources, validation. Ankitha Rao: investigation, formal analysis. Riyadh Abdekadir Khellouf: formal analysis, validation. Saraswati P. Masti: formal analysis, resources, validation. I. M. Noor: validation, formal analysis, writing – review & editing.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
One of the co-authors, Vipin Cyriac, extends his gratitude to the Directorate of Minorities in Bengaluru, India for their support. VC is particularly thankful for the financial assistance provided in the form of a fellowship for minority students as per the sanction order DOM/Fellowship/CR-10/2019-20 dated June 29, 2020, which made this study possible.References
- L. P. Teo, M. H. Buraidah and A. K. Arof, Molecules, 2021, 26, 6499 CrossRef CAS PubMed
.
- M. M. Silva, V. de Zea Bermudez and A. Pawlicka, in Polymer Electrolytes, Wiley, 2020, pp. 113–136 Search PubMed
.
- N. A. Choudhury, S. Sampath and A. K. Shukla, Energy Environ. Sci., 2009, 2, 55–67 RSC
.
- R. C. Agrawal and G. P. Pandey, J. Phys. D Appl. Phys., 2008, 41, 223001 CrossRef
.
- S. Kalybekkyzy, A.-F. Kopzhassar, M. V. Kahraman, A. Mentbayeva and Z. Bakenov, Polymers, 2020, 13, 15 CrossRef PubMed
.
- B. Sun, J. Phys.: Conf. Ser., 2024, 2798, 012021 CrossRef CAS
.
- Y. Zhao, L. Wang, Y. Zhou, Z. Liang, N. Tavajohi, B. Li and T. Li, Adv. Sci., 2021, 8(7), 2003675 CrossRef CAS PubMed
.
- S. Hadad, M. A. Pope, M. Kamkar and K. C. Tam, Adv. Sustainable Syst., 2025, 9(1), 2400532 CrossRef CAS
.
- M. J. Park, I. Choi, J. Hong and O. Kim, J. Appl. Polym. Sci., 2013, 129, 2363–2376 CrossRef CAS
.
- S. K. Patla, R. Ray, K. Asokan and S. Karmakar, J. Appl. Phys., 2018, 123, 125102 CrossRef
.
- E. Glynos, P. Petropoulou, E. Mygiakis, A. D. Nega, W. Pan, L. Papoutsakis, E. P. Giannelis, G. Sakellariou and S. H. Anastasiadis, Macromolecules, 2018, 51, 2542–2550 CrossRef CAS
.
- A. Haragirimana, P. B. Ingabire, Y. Liu, N. Li, Z. Hu and S. Chen, Int. J. Hydrogen Energy, 2020, 45, 10017–10029 CrossRef CAS
.
- P.-Y. Zhuang, Y.-L. Li, L. Fan, J. Lin and Q.-L. Hu, Int. J. Biol. Macromol., 2012, 50, 658–663 CrossRef CAS PubMed
.
- A. Rafique, K. Mahmood Zia, M. Zuber, S. Tabasum and S. Rehman, Int. J. Biol. Macromol., 2016, 87, 141–154 CrossRef CAS PubMed
.
- S. B. Bahrami, S. S. Kordestani, H. Mirzadeh and P. Mansoori, Iran. Polym. J., 2003, 12(2), 139–146 CAS
.
- C. C. Huang, C. W. Lou, C. T. Lu, S. H. Huang, C. Y. Chao and J. H. Lin, Adv. Mater. Res., 2010, 123–125, 975–978 CAS
.
- Y. Liu, N. E. Vrana, P. A. Cahill and G. B. McGuinness, J. Biomed. Mater. Res., Part B, 2009, 90B, 492–502 CrossRef CAS PubMed
.
- A. Islam, T. Yasin, N. Gull, S. M. Khan, M. A. Munawar, M. Shafiq, A. Sabir and T. Jamil, Int. J. Biol. Macromol., 2016, 82, 551–556 CrossRef CAS PubMed
.
- J. Yong, Y.-C. Chen, S. B. Aziz, M. U. Khandaker and H. J. Woo, Electrochim. Acta, 2025, 513, 145610 CrossRef CAS
.
- K. Enoch, R. C. S and A. A. Somasundaram, Surf. Interfaces, 2023, 41, 103178 CrossRef CAS
.
- R. N. Sagar, R. Vasachar and S. Hegde, eXPRESS Polym. Lett., 2023, 17, 883–899 CrossRef CAS
.
- N. M. Sadiq, S. B. Aziz and M. F. Z. Kadir, Gels, 2022, 8, 153 CrossRef CAS PubMed
.
- A. Shahab Marf, R. M. Abdullah and S. B. Aziz, Membranes, 2020, 10, 71 CrossRef PubMed
.
- M. M. Nofal, S. B. Aziz, J. M. Hadi, R. T. Abdulwahid, E. M. A. Dannoun, A. S. Marif, S. Al-Zangana, Q. Zafar, M. A. Brza and M. F. Z. Kadir, Materials, 2020, 13, 4890 CrossRef CAS PubMed
.
- A. Shahab Marf, R. M. Abdullah and S. B. Aziz, Membranes, 2020, 10, 71 CrossRef PubMed
.
- M. M. Nofal, S. B. Aziz, J. M. Hadi, R. T. Abdulwahid, E. M. A. Dannoun, A. S. Marif, S. Al-Zangana, Q. Zafar, M. A. Brza and M. F. Z. Kadir, Materials, 2020, 13, 4890 CrossRef CAS PubMed
.
- I. S. Ravi Varma, K. Kumar Ganta, V. Ramana Jeedi and S. Ramesh, J. Phys.: Conf. Ser., 2024, 2778, 012008 CrossRef CAS
.
- A. Arya and A. L. Sharma, J. Solid State Electrochem., 2018, 22, 2725–2745 CrossRef CAS
.
- A. Bhide, J. Hofmann, A. Katharina Dürr, J. Janek and P. Adelhelm, Phys. Chem. Chem. Phys., 2014, 16, 1987–1998 RSC
.
- F. Cheng, M. Cao, Q. Li, C. Fang, J. Han and Y. Huang, ACS Nano, 2023, 17, 18608–18615 CrossRef CAS PubMed
.
- R. E. Ruther, C.-N. Sun, A. Holliday, S. Cheng, F. M. Delnick, T. A. Zawodzinski and J. Nanda, J. Electrochem. Soc., 2017, 164, A277–A283 CrossRef CAS
.
- S. Uchida and T. Masese, Batteries Supercaps, 2020, 3, 392–396 CrossRef CAS
.
- T. Thomberg, R. Väli, J. Eskusson, T. Romann and A. Jänes, J. Electrochem. Soc., 2018, 165, A3862–A3870 CrossRef CAS
.
- M. F. Z. Kadir, S. R. Majid and A. K. Arof, Electrochim. Acta, 2010, 55, 1475–1482 CrossRef CAS
.
- S. B. Aziz, J. M. Hadi, E. M. A. Dannoun, R. T. Abdulwahid, S. R. Saeed, A. Shahab Marf, W. O. Karim and M. F. Z. Kadir, Polymers, 2020, 12, 1938 CrossRef CAS PubMed
.
- M. H. Buraidah and A. K. Arof, J. Non-Cryst. Solids, 2011, 357, 3261–3266 CrossRef CAS
.
- P. Nayak, Ismayil and Y. N. Sudhakar, Int. J. Biol. Macromol., 2025, 297, 139797 CrossRef CAS PubMed
.
- S. B. Aziz, M. J. Ahmed, O. Gh. Abdullah, A. R. Murad, S. M. Hamad and J. M. Hadi, Electrochim. Acta, 2023, 461, 142659 CrossRef CAS
.
- M. Benítez, J.-E. Diosa and R. A. Vargas, Ionics, 2018, 24, 2029–2034 CrossRef
.
- D. C. Bharati, P. Rawat and A. L. Saroj, J. Solid State Electrochem., 2021, 25, 1727–1741 CrossRef CAS
.
- M. F. Z. Kadir, S. R. Majid and A. K. Arof, Electrochim. Acta, 2010, 55, 1475–1482 CrossRef CAS
.
- V. Cyriac, Ismayil, K. Mishra, Y. N. Sudhakar, Z. E. Rojudi, S. P. Masti and I. M. Noor, Solid State Ionics, 2024, 411, 116578 CrossRef CAS
.
- S. T. Senthilkumar, R. K. Selvan, Y. S. Lee and J. S. Melo, J. Mater. Chem. A, 2012, 1, 1086–1095 RSC
.
- D. Sun, X. Yan, J. Lang and Q. Xue, J. Power Sources, 2013, 222, 52–58 CrossRef CAS
.
- M. D. Stoller and R. S. Ruoff, Energy Environ. Sci., 2010, 3, 1294–1301 RSC
.
- A. Iakunkov, V. Skrypnychuk, A. Nordenström, E. A. Shilayeva, M. Korobov, M. Prodana, M. Enachescu, S. H. Larsson and A. Vtalyzin, Phys. Chem. Chem. Phys., 2019, 21, 17901–17912 RSC
.
- B. Andres, A. C. Engström, N. Blomquist, S. Forsberg, C. Dahlström and H. Olin, PLoS One, 2016, 11, e0163146 CrossRef PubMed
.
- M. F. Shukur, R. Ithnin and M. F. Z. Kadir, Electrochim. Acta, 2014, 136, 204–216 CrossRef CAS
.
- A. M. Stephan, Eur. Polym. J., 2006, 42, 21–42 CrossRef
.
- P. Sharma, G. Mathur, N. Goswami, S. K. Sharma, S. R. Dhakate, S. Chand and A. Mathur, e-Polym., 2015, 15, 237–243 CAS
.
- J. M. Yang, C. S. Fan, N. C. Wang and Y. H. Chang, Electrochim. Acta, 2018, 266, 332–340 CrossRef CAS
.
- X. Li, X. Zhu, J. Liang, H. Shi, B. Lan, C. Zhang, T. I. Alanazi and A. M. El Sayed, Phys. Scr., 2023, 98, 085946 CrossRef
.
- J. R. B. Gomes, M. Jorge and P. Gomes, J. Chem. Thermodyn., 2014, 73, 121–129 CrossRef CAS
.
- J. an Zhao and F. de Ren, J. Mol. Model., 2020, 26, 1–16 CrossRef PubMed
.
- A. Bhattacharya and P. Ray, J. Appl. Polym. Sci., 2004, 93, 122–130 CrossRef CAS
.
- S. A. Katsyuba, M. V. Vener, E. E. Zvereva, Z. Fei, R. Scopelliti, G. Laurenczy, N. Yan, E. Paunescu and P. J. Dyson, J. Phys. Chem. B, 2013, 117, 9094–9105 CrossRef CAS PubMed
.
- Y. Gao, L. Zhang, Y. Wang and H. Li, J. Phys. Chem. B, 2010, 114, 2828–2833 CrossRef CAS PubMed
.
- E. W. Castner, C. J. Margulis, M. Maroncelli and J. F. Wishart, Annu. Rev. Phys. Chem., 2011, 62, 85–105 CrossRef CAS PubMed
.
- M. M. Coleman and P. C. Painter, Prog. Polym. Sci., 1995, 20, 1–59 CrossRef CAS
.
- C. Chavan, R. F. Bhajantri, V. Cyriac, Ismayil, S. S. Bulla and K. Sakthipandi, Polym. Adv. Technol., 2023, 34(5), 1698–1715 CrossRef CAS
.
- J. H. Kim and Y. M. Lee, J. Membr. Sci., 2001, 193, 209–225 CrossRef CAS
.
- V. Cyriac, S. Molakalu Padre, Ismayil, G. Sangam Chandrashekar, C. Chavan, R. Fakeerappa Bhajantri and M. S. Murari, J. Appl. Polym. Sci., 2022, 139, e52525 CrossRef CAS
.
- C. Chavan, R. F. Bhajantri, S. Bulla, H. B. Ravikumar, M. Raghavendra, K. Sakthipandi, K. Yogesh Kumar and B. P. Prasanna, Ceram. Int., 2022, 48, 17864–17884 CrossRef CAS
.
- P. Nayak, Ismayil, V. Cyriac, S. Hegde, G. Sanjeev, M. S. Murari and Y. N. Sudhakar, J. Non-Cryst. Solids, 2022, 592, 121741 CrossRef CAS
.
- D. C. Bharati, P. Rawat and A. L. Saroj, J. Solid State Electrochem., 2021, 25, 1727–1741 CrossRef CAS
.
- X. Li, X. Zhu, J. Liang, H. Shi, B. Lan, C. Zhang, T. I. Alanazi and A. M. El Sayed, Phys. Scr., 2023, 98, 085946 CrossRef
.
- R. Muchakayala, S. Song, S. Gao, X. Wang and Y. Fan, Polym. Test., 2017, 58, 116–125 CrossRef CAS
.
- A. Bartolotta, G. Di Marco, M. Lanza and G. Carini, J. Non-Cryst. Solids, 1994, 172–174, 1195–1201 CrossRef CAS
.
- E. Metwalli, M. Rasool, S. Brunner and P. Müller-Buschbaum, ChemPhysChem, 2015, 16, 2882–2889 CrossRef CAS PubMed
.
- S. Bi, C. N. Sun, T. A. Zawodzinski, F. Ren, J. K. Keum, S. K. Ahn, D. Li and J. Chen, J. Polym. Sci., Part B: Polym. Phys., 2015, 53, 1450–1457 CrossRef CAS
.
- P. H. Hermans and A. Weidinger, J. Polym. Sci., 1949, 4, 709–723 CrossRef CAS
.
- V. Cyriac, Ismayil, I. M. Noor, K. Mishra, C. Chavan, R. F. Bhajantri and S. P. Masti, Cellulose, 2022, 29, 3271–3291 CrossRef CAS
.
- V. Cyriac, Ismayil, I. S. B. M. Noor, Z. E. Rojudi, Y. N. Sudhakar, C. Chavan, R. F. Bhajantri and M. S. Murari, Int. J. Energy Res., 2022, 46, 22845–22866 CrossRef CAS
.
- S. B. Aziz, M. A. Brza, E. M. A. Dannoun, M. H. Hamsan, J. M. Hadi, M. F. Z. Kadir and R. T. Abdulwahid, Molecules, 2020, 25, 4503 CrossRef CAS PubMed
.
- D. Golodnitsky, E. Strauss, E. Peled and S. Greenbaum, J. Electrochem. Soc., 2015, 162, A2551–A2566 CrossRef CAS
.
- G. J. Brug, A. L. G. van den Eeden, M. Sluyters-Rehbach and J. H. Sluyters, J. Electroanal. Chem. Interfacial Electrochem., 1984, 176, 275–295 CrossRef CAS
.
- T. Winie and A. K. Arof, Physical Chemistry of Macromolecules: Macro to Nanoscales, 2014, pp. 333–364 Search PubMed
.
- H. J. Schütt and E. Gerdes, J. Non-Cryst. Solids, 1992, 144, 14–20 CrossRef
.
- K. A. Mauritz, Macromolecules, 1989, 22, 4483–4488 CrossRef CAS
.
- B. Natesan, N. K. Karan and R. S. Katiyar, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 042801 CrossRef CAS PubMed
.
- J. Pan, K. Li, J. Li, T. Hsu and Q. Wang, Appl. Phys. Lett., 2009, 95, 022902 CrossRef
.
- A. Schönhals and F. Kremer, in Broadband Dielectric Spectroscopy, Springer Berlin Heidelberg, Berlin, Heidelberg, 2003, pp. 59–98 Search PubMed
.
- A. Rao, S. Bhat, S. De and V. Cyriac, J. Energy Storage, 2024, 102, 113965 CrossRef
.
- S. B. Aziz, M. H. Hamsan, R. M. Abdullah and M. F. Z. Kadir, Molecules, 2019, 24, 2503 CrossRef CAS PubMed
.
- S. K. S. Basha, G. S. Sundari, K. V. Kumar and M. C. Rao, Polym. Bull., 2018, 75, 925–945 CrossRef CAS
.
- S. A. M. Noor, A. Ahmad, I. A. Talib and M. Y. A. Rahman, Ionics, 2010, 16, 161–170 CrossRef CAS
.
- M. Vahini and M. Muthuvinayagam, J.
Mater. Sci.: Mater. Electron., 2019, 30, 5609–5619 CrossRef CAS
.
- B. Chatterjee, N. Kulshrestha and P. N. Gupta, Phys. Scr., 2015, 90, 025805 CrossRef
.
- P. K. Singh, B. Bhattacharya, R. M. Mehra and H. W. Rhee, Curr. Appl. Phys., 2011, 11, 616–619 CrossRef
.
- R. He and T. Kyu, Macromolecules, 2016, 49, 5637–5648 CrossRef CAS
.
- N. Vijaya, S. Selvasekarapandian, G. Hirankumar, S. Karthikeyan, H. Nithya, C. S. Ramya and M. Prabu, Ionics, 2012, 18, 91–99 CrossRef CAS
.
- Y. M. Yusof, H. A. Illias and M. F. Z. Kadir, Ionics, 2014, 20, 1235–1245 CrossRef CAS
.
- R. N. Sagar, R. Vasachar and S. Hegde, eXPRESS Polym. Lett., 2023, 17, 883–899 CrossRef CAS
.
- D. Bharati and A. Saroj, Polym.-Plast. Technol. Mater., 2023, 62, 989–1007 CAS
.
- Z. Xie, Q. Lai, Y. Dou, X. Chen and Y. Yang, Chem. Eng. J., 2024, 481, 148510 CrossRef CAS
.
- J. B. Wagner and C. Wagner, J. Chem. Phys., 1957, 26, 1597–1601 CrossRef CAS
.
- A. Rao, S. Bhat, S. De and V. Cyriac, J. Energy Storage, 2024, 102, 113965 CrossRef
.
- R. A. Khellouf, C. Bubulinca, V. Cyriac, J. Cisar, S. Durpekova and V. Sedlarik, J. Energy Storage, 2024, 101, 113769 CrossRef
.
- R. A. Khellouf, S. Durpekova, V. Cyriac, J. Cisar, C. Bubulinca, A. Lengalova, D. Skoda and V. Sedlarík, Solid State Ionics, 2023, 402, 116379 CrossRef CAS
.
- Z. Xie, B. Xiang, Y. Dou, Y. Cheng, X. Chen, Y. Jiang and Y. Yang, Chem. Eng. J., 2025, 503, 158474 CrossRef CAS
.
- C. S. Kim and S. M. Oh, Electrochim. Acta, 2001, 46, 1323–1331 CrossRef CAS
.
- S. Ramesh, T. Winie and A. K. Arof, Eur. Polym. J., 2007, 43, 1963–1968 CrossRef CAS
.
- D. Mohanty, S. Y. Chen and I. M. Hung, Batteries, 2022, 8, 173 CrossRef CAS
.
- S. B. Aziz, M. H. Hamsan, M. M. Nofal, W. O. Karim, I. Brevik, M. A. Brza, R. T. Abdulwahid, S. Al-Zangana and M. F. Z. Kadir, Polymers, 2020, 12, 1411 CrossRef CAS PubMed
.
- A. S. F. M. Asnawi, S. B. Aziz, M. M. Nofal, M. H. Hamsan, M. A. Brza, Y. M. Yusof, R. T. Abdilwahid, S. K. Muzakir and M. F. Z. Kadir, Polymers, 2020, 12, 1433 CrossRef CAS
.
- R. L. Lavall, R. S. Borges, H. D. R. Calado, C. Welter, J. P. C. Trigueiro, J. Rieumont, B. R. A. Neves and G. G. Silva, J. Power Sources, 2008, 177, 652–659 CrossRef CAS
.
- H. D. Yoo, J. H. Jang, J. H. Ryu, Y. Park and S. M. Oh, J. Power Sources, 2014, 267, 411–420 CrossRef CAS
.
- S. Aziz, E. Dannoun, R. Abdulwahid, M. Kadir, M. Nofal, S. Al-Saeedi and A. Murad, Membranes, 2022, 12, 139 CrossRef CAS PubMed
.
- M. Selva Kumar and D. K. Bhat, Phys. B, 2009, 404, 1143–1147 CrossRef CAS
.
- S. B. Aziz, M. A. Brza, M. H. Hamsan, M. F. Z. Kadir, S. K. Muzakir and R. T. Abdulwahid, J. Mater. Res. Technol., 2020, 9, 3734–3745 CrossRef CAS
.
- M. A. Brza, S. B. Aziz, H. Anuar, F. Ali, M. H. Hamsan, M. F. Z. Kadir and R. T. Abdulwahid, Arabian J. Chem., 2020, 13, 7247–7263 CrossRef CAS
.
- A. Shukur and M. Fadhlullah, Characterization of ion conducting solid biopolymer electrolytes based on starch-chitosan blend and application in electrochemical devices, PhD thesis, 2015
.
- M. H. Hamsan, N. Abdul Halim, S. Z. Ngah Demon, N. S. N. Sa'aya, M. F. Z. Kadir, S. B. Aziz and Z. H. Zainal Abidin, Arab J. Basic Appl. Sci., 2023, 30, 1–9 Search PubMed
.
- S. B. Aziz, M. H. Hamsan, M. A. Brza, M. F. Z. Kadir, R. T. Abdulwahid, H. O. Ghareeb and H. J. Woo, Results Phys., 2019, 15, 102584 CrossRef
.
- S. B. Aziz, P. O. Hama, D. M. Aziz, N. M. Sadiq, H. J. Woo, M. F. Z. Kadir, R. T. Abdulwahid, B. A. Al-Asbahi, A. A. A. Ahmed and J. Hassan, J. Energy Storage, 2025, 114, 115841 CrossRef
.
- M. H. Hamsan, S. B. Aziz, M. M. Nofal, M. A. Brza, R. T. Abdulwahid, J. M. Hadi, W. O. Karim and M. F. Z. Kadir, J. Mater. Res. Technol., 2020, 9, 10635–10646 CrossRef CAS
.
- V. Cyriac, Ismayil, K. Mishra, A. Rao, R. A. Khellouf, S. P. Masti and I. M. Noor, Mater Adv., 2025, 6, 3149–3170 RSC
.
- R. K. Prajapati, P. Rawat, H. Kumar and A. L. Saroj, Mater. Sci. Eng., B, 2025, 317, 118200 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ra02897c |
| This journal is © The Royal Society of Chemistry 2025 |




