 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The reaction of acetamiprid with OH radicals in the environment: a theoretical study†
Quan V. Vo *a,
Nguyen Thi Hoaa,
Nguyen Thanh Vinhb and
Adam Mechler
*a,
Nguyen Thi Hoaa,
Nguyen Thanh Vinhb and
Adam Mechler c
c
aThe University of Danang – University of Technology and Education, Danang 550000, Vietnam. E-mail: vvquan@ute.udn.vn
bFaculty of Pharmacy, University of Pécs, Pécs H-7624, Hungary
cDepartment of Biochemistry and Chemistry, La Trobe University, Victoria 3086, Australia
First published on 6th June 2025
Abstract
The chemical fate of acetamiprid (AMP), a neonicotinoid pesticide, is determined by photo-oxidation: a combination of radical degradation pathways driven by the action of hydroxyl radicals. This study utilizes quantum chemical calculations to investigate the reaction of AMP with hydroxyl radicals in atmospheric, lipidic, and aqueous media. It was shown that the degradation process has a steep temperature dependence with the overall rate constant decreasing from 9.04 × 109 to 5.01 × 109 M−1 s−1 in the temperature range of 253–323 K thus AMP lifetime in the gas phase varies from 17.26 to 41.37 hours. In lipid media, the AMP + HO˙ reaction exhibited an overall rate constant koverall of 1.63 × 108 M−1 s−1, while in water, it was 2.95 × 108 M−1 s−1, closely matching the experimentally measured rate constant (kexp = 7.59 × 108 M−1 s−1). In natural water, where hydroxyl radical concentrations range from 10−18 to 10−15 M, AMP degradation is predicted to occur over approximately 6.47 × 102 to 1.06 × 106 hours at 273–373 K, corresponding to a range of ∼27 days to ∼121 years. Across all examined media and temperature conditions, the AMP + HO˙ reaction followed primarily the hydrogen transfer mechanism, with a minor role also played by the radical adduct formation pathway.
1 Introduction
Neonicotinoid insecticides are frequently used as seed coatings to reduce crop losses. These compounds are neurotoxins, attacking the central nervous system. Ultimately, neonicotinoids cause paralysis by acting as selective agonists that bond to acetylcholine receptors (AChRs) and disrupt neural function through overstimulation. They are widely used in pest control due to their high potency to disrupt the nervous systems of insects.1,2 (E)-N-(6-Chloro-3-pyridylmethyl)-N′-cyano-N-methylacetamidine, commonly referred to as acetamiprid (AMP), shown in Fig. 1, is a pesticide classified within the neonicotinoid insecticide group. It is among the most widely used insecticides in modern agricultural practices.3–5 Due to its widespread application, this micropollutant has been detected in surface water6,7 as well as wastewater8,9 samples globally. The presence of AMP in the environment and thus long-term exposure may pose potential risks to human health such as through DNA/RNA damage.10Despite its low vapor pressure (∼1.7 × 10−6 Pa), acetamiprid exhibited the highest average atmospheric exposure concentration (0.05–3.0 μg m−3) among six commonly used pesticides, including acetamiprid, difenoconazole, thiazophos, isoprocarb, malathion, and pyridaben.11 In comparison to imidacloprid, acetamiprid demonstrated greater persistence in greenhouse air post-application, particularly under conditions of limited ventilation.12 Additionally, acetamiprid can be adsorbed and accumulated in airborne fine particulate matter.13 This particulate matter may serve as a significant carrier for the atmospheric transport of acetamiprid, thereby contributing to human exposure to airborne pesticides. Consequently, the prolonged persistence of acetamiprid in the greenhouse atmosphere may pose substantial long-term risks to the atmospheric systems and associated ecosystems; however, the degradation of AMP in the atmospheric environment has not been fully studied yet.
AMP persists at concentrations ranging from ng L−1 to μg L−1 across various organic waste matrices, including soils with high organic matter content,14,15 sewage sludge, and organic waste originating from wastewater treatment facilities.16,17 Furthermore, residual acetamiprid has been detected in agricultural organic waste, such as animal manure and plant residues.4,15 Despite its persistence, the degradation of AMP in such lipid-rich media remains underexplored, highlighting a critical knowledge gap that warrants further investigation.
Hydroxyl radical is a powerful oxidizing agent with high reactivity towards organic substrates. Hydroxyl radicals initiate the main natural breakdown pathways of organic molecules, even though their natural steady-state concentrations are modest, ranging from 10−18 to 10−15 M.18,19 Due to their potent oxidative properties, hydroxyl radicals are also used as primary oxidants in advanced oxidation processes for the destruction of neonicotinoid pesticides, including AMP, in industrial effluent.20–25
The HO˙ + AMP reaction rate constants in water were experimentally determined to fall in the range of 7.59 × 108 to 2.1 × 109 M−1 s−1.17,20,26 Previous studies concluded that the degradation of AMP by HO/O2 radicals can occur at the C7-H and C8-H bonds through a formal hydrogen transfer (FHT) reaction. This process results in the formation of (E)-N-(6-chloropyridin-3-yl(hydroxy)methyl)-N′-cyano-N-methylacetimidamide (MW 238.7), (E)-N-((6-chloropyridin-3-yl)methyl)-N′-cyano-N-(hydroxymethyl)-acetimidamide (MW 238.7),17,26–28 or (E)-6-chloro-N-(1-(cyanoimino)ethyl)-N-methylnicotinamide (MW 236.7) and (E)-N-((6-chloropyridin-3-yl)methyl)-N′-cyano-N-formylacetimidamide (MW 236.7).27 However, information regarding the formation of hydroxylated AMP (MW 238.7) and the branching ratios of its intermediates remains limited.
As part of a series of studies on pesticide degradation using quantum chemical calculations,29,30 this work aims to assess the environmental persistence of AMP and examine the thermodynamic and kinetic properties of its hydroxyl radical-initiated degradation.
2 Computational methods
The Gaussian 16 software package was employed to perform the calculations for this study at the M06-2X/6-311++G(d,p) level of theory.31 This method is a proven way for precise calculations of thermodynamics and kinetics in current computational studies.32–36 The solvent effects of water were simulated using the SMD methodology,32 which is a common way of evaluating the radical scavenging properties of antioxidants. The methodology was benchmarked repeatedly against experimental results with a kcalc/kexp ratio of 0.3 to 2.9.34,37–41 It was recently suggested that a more realistic treatment of intramolecular rotation could improve the accuracy.42 However, due to the size and complexity of the system, the QM-ORSA level of accuracy was accepted as a necessary compromise.Quantum Mechanics-based Overall Free Radical Scavenging Activity (QM-ORSA) method41 was used to perform the kinetic calculations.34,43 Under standard conditions of 1 M and varying ambient temperatures (253–323 K for the gas phase and 273–373 K for water), the rate constant (k) was determined using eqn (1) and transition state theory (TST) and details in Table S1, ESI.† 39,44–49
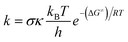 | (1) |
The Gibbs free energy of activation is denoted as ΔG≠, while kB and h represent the Boltzmann constant and Planck constant, respectively. Tunneling corrections (κ), were computed using the Eckart barrier model.50 σ stands for the reaction symmetry number.51,52
The radical adduct formation (RAF), or formal hydrogen transfer (FHT) pathways detailed in eqn (2) and (3) can provide the mechanistic underpinning of the reaction between AMP and HO˙, with consideration to the molecular structure:29,34,39,43,53–55
| RAF: AMP-H + HO˙ → [HO-AMP-H]˙ | (2) |
| FHT: AMP-H + HO˙ → AMP˙ + H2O | (3) |
3 Results and discussion
3.1 Reaction of hydroxyl radical with AMP in the gas phase
The standard Gibbs free energy change (ΔG°) for each potential AMP + HO˙ reaction in the gas phase was calculated based on the FHT, and RAF mechanisms, with the results summarized in Table 1. The findings indicated that this reaction is generally spontaneous, except for the RAF mechanism at the N1, N3, N6, and N11 positions, where ΔG° values were positive. Electron-withdrawing substituents such as Cl and C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N diminish the nitrogen atom's electron density, leading to instability of radical adducts at these positions. The higher energy cost of the addition reaction at N3/11 = C bonds is likely due to this effect. These results suggest that the AMP + HO˙ reaction in the gas phase can follow either FHT or RAF mechanisms (ΔG° < 0), highlighting the need for further kinetic analysis of these pathways.
N diminish the nitrogen atom's electron density, leading to instability of radical adducts at these positions. The higher energy cost of the addition reaction at N3/11 = C bonds is likely due to this effect. These results suggest that the AMP + HO˙ reaction in the gas phase can follow either FHT or RAF mechanisms (ΔG° < 0), highlighting the need for further kinetic analysis of these pathways.
| Mechanisms | Positions | ΔG° |
|---|---|---|
| FHT | C5-H | −22.0 |
| C7-H | −25.3 | |
| C8-H | −28.8 | |
| RAF | N1 | 25.0 |
| N3 | 30.5 | |
| N6 | 1.7 | |
| N11 | 21.5 | |
| C2 | −17.6 | |
| C4 | −8.1 | |
| C9 | −10.1 | |
| C10 | −14.1 | |
| C12 | −25.5 | |
| C13 | −10.0 | |
| C14 | −6.5 |
| Mechanism | ΔG≠ | κ | kEck | Γ | Products | |
|---|---|---|---|---|---|---|
| FHT | C5-H | 6.9 | 10.4 | 1.81 × 109 | 31.9 | P5 |
| C7-H | 5.4 | 1.8 | 3.79 × 109 | 66.9 | P7 | |
| C8-H | 9.3 | 1.8 | 3.61 × 106 | 0.1 | P8 | |
| RAF | C2 | 9.3 | 1.6 | 1.39 × 106 | 0.0 | P2 |
| C4 | 17.4 | 1.2 | 1.39 | 0.0 | P4 | |
| C9 | 7.3 | 1.2 | 3.61 × 107 | 0.6 | P9 | |
| C10 | 7.5 | 1.3 | 2.47 × 107 | 0.4 | P10 | |
| C12 | 15.1 | 1.5 | 7.83 × 101 | 0.0 | P12 | |
| C13 | 9.6 | 1.3 | 7.83 × 105 | 0.0 | P13 | |
| C14 | 11.2 | 1.4 | 5.06 × 104 | 0.0 | P14 | |
| koverall (AMP + HO˙) | 5.67 × 109 | |||||
 | ||
| Fig. 2 The potential energy surfaces of the AMP + HO˙ reaction at 0 K, in the gas phase (PC: post-complexes). | ||
The HO˙ radicals form intermediates P2-14 by abstracting hydrogen through the C–H bonds located at C5, C7, and C8, or alternatively through T2, T4, T9, T10, T11, T12, T13 and T14 within the RAF pathway. The FHT pathway has some variation in the reaction barrier ranging from 6.2 to 9.6 kcal mol−1. Conversely, the RAF barrier for reactions at positions T2, T4, T9, T10, T11, T12, T13, and T14 range from 6.5 to 16.1 kcal mol−1 towards the corresponding products P2, P4, and P9-14. The H-abstraction of C5 and C7 bonds exhibited the lowest observed reaction barriers at 6.2 and 6.8 kcal mol−1, respectively, whereas that of RAF was observed at the C9 position, which had a value of 6.5 kcal mol−1. Consequently, the abstraction of hydrogen of the C5 and C7 bonds is the dominant degradation of AMP against HO˙ radicals in the gas phase.
The findings summarized in Table 2 indicate that HO˙ and AMP engage in rapid gas-phase interactions, characterized by an overall rate constant of koverall = 5.67 × 109 M−1 s−1, in accordance with the H-abstraction mechanism. Under the studied media, the RAF pathway did not play a role in the degradation of AMP by HO˙ radicals. Despite the relatively low reaction barrier of 6.5 kcal mol−1 for the C9 position (Fig. 2), the RAF reaction at C9 accounted for only 0.6% of the koverall value. For the formation of the principal intermediates (as detailed in Table 2), the highest rate constants were recorded for C5 and C7, with values of kapp = 1.81 × 109 and 3.79 × 109 M−1 s−1, respectively. It is noteworthy that the tunneling correction (κ) for the FHT (C5-H) mechanism (κ = 10.4) is approximately 5.8 times greater than that for the C7/8−H mechanisms (κ = 1.8). This difference is attributed to the lower vibrational frequency of C5 (ν = −1482.54 cm−1) compared to C7 (ν = −744.10 cm−1) and C8 (ν = −741.06 cm−1), as detailed in Table S2 of the ESI file.† This resulted in the formation of P5 at a yield of 31.9% and P7 at a yield of 66.9%.
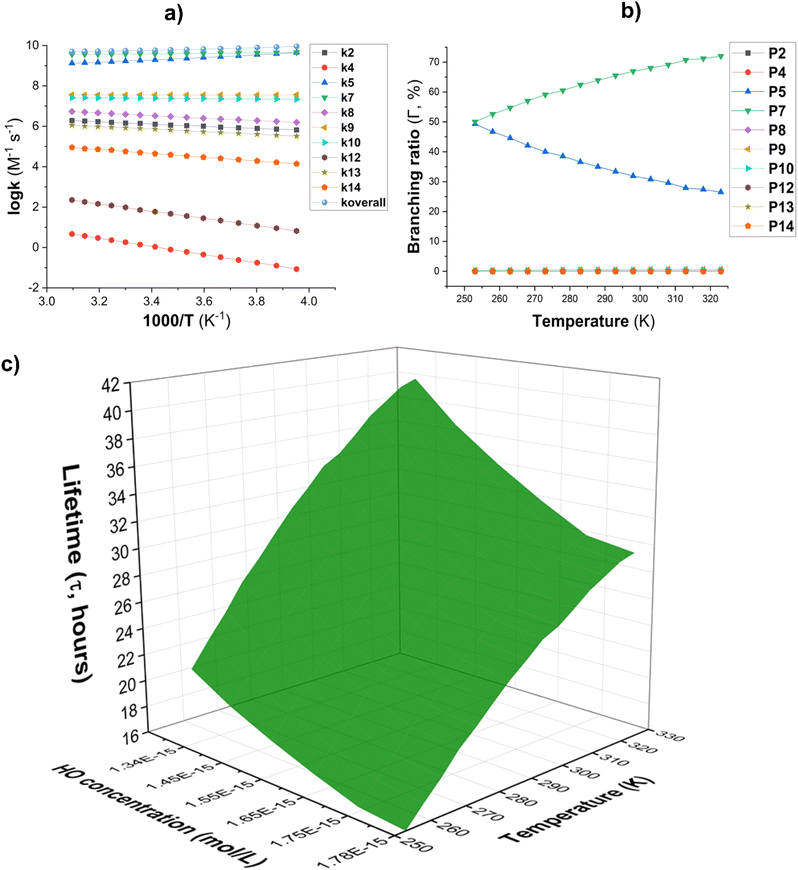 | ||
Fig. 3 (a) The temperature influence on apparent rate constants (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k); (b) Γ values (%); (c) lifetime (τ, s) at 253–323 K. k); (b) Γ values (%); (c) lifetime (τ, s) at 253–323 K. | ||
The lifetime (τ) of AMP was also investigated in the presence of HO˙ radicals at temperatures ranging from 253 to 323 K. The concentration of [HO˙] was [HO˙] = [1.34–1.78] × 10−15 M ([9.4 ± 1.3] × 105 molecule per cm3, Fig. 3C).59,60 The findings indicate that AMP can easily decompose in the gaseous state within 17.26–41.37 hours in the temperature range of 253 to 323 K. The atmospheric decomposition of AMP becomes increasingly efficient as the ambient temperature increases.
3.2 Reaction of hydroxyl radical with AMP in lipid environment
The FHT and RAF mechanisms were used to directly calculate the kinetics of the AMP + HO˙ reaction in the lipidic medium (i.e., pentyl ethanoate solvent) in all possible positions following the gas phase investigation. Table 3 shows the findings. It was determined that in the lipidic medium AMP can react with the hydroxyl radical at an overall rate constant of 1.63 × 108 M−1 s−1. The FHT reaction is the predominant pathway with a Γ value exceeding 95.1%. The RAF reactions contributed only 1.2% to the overall rate constant. The HO˙ + AMP reaction was only slightly enhanced by the other FHT reaction of C8-H, with a Γ value of 3.6%. It was noted that the rate of HO˙ + AMP reaction in the lipid medium was comparable to the radical decomposition of the lipid itself (koverall = 4.12 × 108 M−1 s−1). Thus in lipid media AMP might not decompose. Even if neglecting this competition effect, the degradation rate of AMP in the lipid medium was approximately 34.8 times lower than that of the gas phase (Table 2). Thus, nonpolar media are not suitable environments for the degradation of AMP by HO˙ radicals.| Mechanism | ΔG≠ | κ | kD | kapp | Γ | Products | |
|---|---|---|---|---|---|---|---|
| a koverall = Σkapp.b Γ = kapp × 100/koverall. | |||||||
| FHT | C5-H | 8.9 | 4.3 | 3.00 × 109 | 2.50 × 107 | 15.3 | P5 |
| C7-H | 7.4 | 1.8 | 3.10 × 109 | 1.30 × 108 | 79.8 | P7 | |
| C8-H | 9.2 | 1.9 | 3.10 × 109 | 5.90 × 106 | 3.6 | P8 | |
| RAF | C2 | 14.7 | 1.6 | 2.30 × 109 | 1.70 × 102 | 0.0 | P2 |
| C4 | 18.2 | 1.3 | 2.20 × 109 | 0.340 | 0.0 | P4 | |
| C9 | 9.0 | 1.2 | 2.40 × 109 | 1.80 × 106 | 1.1 | P9 | |
| C10 | 11.0 | 1.3 | 2.40 × 109 | 7.00 × 104 | 0.0 | P10 | |
| C12 | 15.1 | 1.5 | 2.30 × 109 | 8.30 × 101 | 0.0 | P12 | |
| C13 | 10.7 | 1.3 | 2.40 × 109 | 1.20 × 105 | 0.1 | P13 | |
| C14 | 12.4 | 1.4 | 2.30 × 109 | 7.50 × 103 | 0.0 | P14 | |
| koverall (AMP + HO˙) | 1.63 × 108 | ||||||
3.3 Reaction of hydroxyl radical with AMP in water
The interaction between AMP and HO˙ may proceed by RAF or FHT mechanisms. Thus, the kinetics of the AMP + HO˙ reaction in water were computed and are displayed in Table 4. The AMP + HO˙ reaction exhibited the koverall of 2.95 × 108 M−1 s−1. This aligns with the measured experimental rate constant (kexp = 7.59 × 108 M−1 s−1).26 The FHT mechanism dominated the reaction between AMP and HO˙ radicals, contributing 94.2% to the koverall. The primary contributors to the FHT reactions at the C8-H and C7-H positions exhibited Γ values of 57.6% and 30.5%, respectively. The two pathways together represented 88.1% of the total reactivity. The FHT reaction at C5-H contributed an additional 6.1% to the overall rate constant. The RAF mechanism contributed 5.8% to the overall rate constant, comprising 1.6% from the C9 position and 3.2% from the C10 position. Other RAF pathways (C2, C4, C12, C13, and C14) exhibited minimal contribution.
| Mechanism | ΔG≠ | κ | kD | kapp | Γ | ||
|---|---|---|---|---|---|---|---|
| a λ (the nuclear reorganization energy, kcal mol−1).b koverall = Σkapp.c Γ = kapp × 100/koverall. | |||||||
| FHT | C5-H | 9.2 | 5.2 | 2.90 × 109 | 1.80 × 107 | 6.1 | P5 |
| C7-H | 7.8 | 2.5 | 3.00 × 109 | 9.00 × 107 | 30.5 | P7 | |
| C8-H | 7.1 | 2.5 | 2.90 × 109 | 1.70 × 108 | 57.6 | P8 | |
| RAF | C2 | 12.0 | 1.5 | 2.20 × 109 | 1.40 × 104 | 0.0 | P2 |
| C4 | 16.3 | 1.3 | 2.10 × 109 | 8.30 | 0.0 | P4 | |
| C9 | 8.4 | 1.1 | 2.30 × 109 | 4.80 × 106 | 1.6 | P9 | |
| C10 | 8.1 | 1.3 | 2.30 × 109 | 9.50 × 106 | 3.2 | P10 | |
| C12 | 12.7 | 1.3 | 2.30 × 109 | 3.90 × 103 | 0.0 | P12 | |
| C13 | 8.7 | 1.2 | 2.30 × 109 | 3.00 × 106 | 1.0 | P13 | |
| C14 | 11.2 | 1.4 | 2.20 × 109 | 5.20 × 104 | 0.0 | P14 | |
| koverall (AMP + HO˙) | 2.95 × 108 | ||||||
The principal intermediates of the AMP + HO˙ reaction in the aqueous solution were P5 (6.1%), P7 (30.5%), and P8 (57.6%) as shown in Table 4, while those in the lipid medium (Table 3) were P5 (15.3%), P7 (79.8%) and P8 (3.6%).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M−1 s−1 at 273 K to 9.33 × 109
M−1 s−1 at 273 K to 9.33 × 109![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M−1 s−1 at 373 K while demonstrating a stable temperature dependency. Concerning the branching ratio (Fig. 5b), it was observed that with rising temperature, the principal intermediates for the AMP + HO˙ reaction were P8 (57.4–58.3%), P7 (31.0–28.0%), and P5 (5.7–7.7%). As the temperature increased, the fraction of intermediate P8 remained stable, although the proportion of P7 had a modest decline and P5 saw an increase. That could be well explained with the formation of (E)-N-(6-chloropyridin-3-yl(hydroxy)methyl)-N′-cyano-N-methylacetimidamide (MW 238.7), (E)-N-((6-chloropyridin-3-yl)methyl)-N′-cyano-N-(hydroxymethyl)-acetimidamide (MW 238.7), or (E)-6-chloro-N-(1-(cyanoimino)ethyl)-N-methylnicotinamide (MW 236.7) and (E)-N-((6-chloropyridin-3-yl)methyl)-N′-cyano-N-formylacetimidamide (MW 236.7) in the experimental studies.17,26–28
M−1 s−1 at 373 K while demonstrating a stable temperature dependency. Concerning the branching ratio (Fig. 5b), it was observed that with rising temperature, the principal intermediates for the AMP + HO˙ reaction were P8 (57.4–58.3%), P7 (31.0–28.0%), and P5 (5.7–7.7%). As the temperature increased, the fraction of intermediate P8 remained stable, although the proportion of P7 had a modest decline and P5 saw an increase. That could be well explained with the formation of (E)-N-(6-chloropyridin-3-yl(hydroxy)methyl)-N′-cyano-N-methylacetimidamide (MW 238.7), (E)-N-((6-chloropyridin-3-yl)methyl)-N′-cyano-N-(hydroxymethyl)-acetimidamide (MW 238.7), or (E)-6-chloro-N-(1-(cyanoimino)ethyl)-N-methylnicotinamide (MW 236.7) and (E)-N-((6-chloropyridin-3-yl)methyl)-N′-cyano-N-formylacetimidamide (MW 236.7) in the experimental studies.17,26–28Additional intermediates, namely P9 and P10, exhibited negligible contributions (1.4–2.2% and 2.6–3.5%, respectively) with small fluctuations throughout the studied temperature range. The results of the calculations indicated that the degradation of AMP by HO˙ radicals consistently generated the same primary intermediates (P8, P7, and P5) at all temperatures evaluated. Therefore, it is determined that the reaction mechanism remains substantially unchanged within the temperature range. The FHT pathways (represented by P7 and P8) are the primary mechanism of the reaction, while RAF pathways (such as P9 and P10) have a minor impact.
These findings emphasize the necessity of examining the AMP + HO˙ reaction mechanism in the aqueous phase in the context of multiple reaction pathways, such as FHT and RAF. Temperature-dependent data is essential for assessing the environmental fate of AMP under a variety of conditions.63
The lifetime (τ) of AMP in the presence of HO radicals in water at temperatures ranging from 273 to 383 K, with HO˙ concentrations of 10−18 to 10−15 M in natural water and 10−10 to 10−9 M in AOP-treated wastewater (Fig. 5c).18,19 It was found that the degradation of AMP in water takes place within a time frame of 6.47 × 10−4 to 1.06 × 106 hours. In wastewater treated with AOP ([HO˙] = 10−10 to 10−9 M), the degradation of AMP is achieved rapidly, within 2.83 to 38.3 seconds. The rate of degradation increases with increasing temperature from 273 to 373 K. Consequently, the AOP approach is a highly effective method for the removal of AMP from aqueous systems. In aqueous aerosol particles, the HO˙ concentration is approximately 10−11 to 10−13 M.64–66 The lifetime of AMP in these particles ranges from 0.07 to 6.47 hours (at temperatures between 273 and 373 K). These results show that the ˙OH concentration is sufficient to drive significant oxidative processes in remote aerosols. The degradation of AMP in remote aerosols occurs at a significantly faster rate compared to that in the atmosphere, where the half-life ranges from 17.26 to 41.37 hours. Consequently, this appears to suggest that AMP is predominantly removed within aerosols rather than in the gas phase in the atmospheric environment.
 | ||
Fig. 5 (a) Temperature-dependent apparent rate constants (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k); (b) branching ratio (Γ, %); (c) lifetime (log(τ), h, τ = 1/([HO] × k)) in water in the range of 273–373 K. k); (b) branching ratio (Γ, %); (c) lifetime (log(τ), h, τ = 1/([HO] × k)) in water in the range of 273–373 K. | ||
In the natural aqueous solution ([HO˙] = 10−18 to 10−15 M), the degradation of AMP takes 6.47 × 102 to 1.06 × 106 hours (i.e. 0.07 hours to 121.43 years). For a given [HO˙], the lifetime of AMP declines as the temperature rises. As a result, the lifetime of AMP in the environment is estimated to be between 1.06 × 103 to 1.06 × 106 hours at a low temperature of 273 K. This amount may, however, reduce to 6.47 × 102 to 6.47 × 105 hours at 373 K. The data shows that τ shortens from 121.43 years at 273 K to 73.90 years at 373 K when [HO˙] = 10−18 M which confirms Arrhenius-based kinetic models that demonstrate temperature increases the rate of radical-driven deterioration.67 This trend is continuous across all HO˙ concentrations, revealing the major impact of temperature on the persistence of AMP in water.
4 Conclusion
The degradation of the AMP with HO˙ radicals under aqueous, lipid, and atmospheric conditions was investigated using DFT calculation. The results revealed that the reaction between hydroxyl radicals and AMP exhibited a decrease in the overall rate constant from 9.04 × 109 to 5.01 × 109 M−1 s−1 within the temperature range of 253–323 K. The degradation of AMP by hydroxyl radicals proceeded rapidly in the gas phase, with an estimated lifetime ranging from 17.26 to 41.37 hours. The AMP + HO˙ reaction in the lipid medium exhibited the koverall of 1.63 × 108 M−1 s−1, whereas that in water was 2.95 × 108 M−1 s−1. This aligns with the measured experimental rate constant (kexp = 7.59 × 108 M−1 s−1). In natural water where the hydroxyl radical concentration ranges from 10−18 to 10−15 M, AMP degradation is expected to occur over a timescale of approximately 6.47 × 102 to 1.06 × 106 hours at 273–373 K, equivalent to 0.07 to 121.43 years. In all of the studied media and temperatures, the FHT reaction of C5, C7, and C8 defined the AMP + HO˙ reaction, whereas the RAF reaction contributed a minor role in the degradation, resulting in the main intermediates of P5, P7, and P8.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research is funded by the Vietnamese Ministry of Education and Training under project number B2024.DNA.09.References
- K. Matsuda, S. D. Buckingham, D. Kleier, J. J. Rauh, M. Grauso and D. B. Sattelle, Trends Pharmacol. Sci., 2001, 22, 573–580 Search PubMed.
- V. Christen, F. Mittner and K. Fent, Environ. Sci. Technol., 2016, 50, 4071–4081 Search PubMed.
- A. M. Cimino, A. L. Boyles, K. A. Thayer and M. J. Perry, Environ. Health Perspect., 2017, 125, 155–162 CrossRef CAS PubMed.
- A. Phogat, J. Singh, V. Kumar and V. Malik, Environ. Chem. Lett., 2022, 1–26 Search PubMed.
- X. Shao, Z. Liu, X. Xu, Z. Li and X. Qian, J. Pestic. Sci., 2013, 38, 1–9 Search PubMed.
- F. Sánchez-Bayo and R. V. Hyne, Chemosphere, 2014, 99, 143–151 CrossRef PubMed.
- J. Struger, J. Grabuski, S. Cagampan, E. Sverko, D. McGoldrick and C. H. Marvin, Chemosphere, 2017, 169, 516–523 Search PubMed.
- K. Licht, V. Kosar, V. Tomašić and M. Duplančić, Environ. Technol., 2023, 44, 1125–1134 Search PubMed.
- M. Sánchez, D. Ramos, M. Fernández, S. Aguilar, I. Ruiz, M. Canle and M. Soto, Sci. Total Environ., 2022, 842, 156750 CrossRef PubMed.
- H.-X. Zhang, D. Yu, J.-F. Sun, L. Zeng, C.-Y. Wang, L.-P. Bai, G.-Y. Zhu, Z.-H. Jiang and W. Zhang, Environ. Int., 2023, 178, 108038 CrossRef CAS PubMed.
- Y. Hu, S. Wu, W. Lyu, J. Ning and D. She, Sci. Rep., 2023, 13, 5138 CrossRef CAS PubMed.
- M. E. Badawy, A. M. Ismail and A. I. Ibrahim, J. Environ. Sci. Health, Part B, 2019, 54, 898–905 CrossRef CAS PubMed.
- K. Gao, S. Wang, R. Li, F. Dong, Y. Zheng and Y. Li, Environ. Sci. Technol., 2024, 58, 1680–1689 CrossRef CAS PubMed.
- S. Gupta and V. Gajbhiye, Bull. Environ. Contam. Toxicol., 2007, 78, 349–352 CrossRef CAS PubMed.
- J. Potts, D. L. Jones, A. Macdonald, Q. Ma and P. Cross, Sci. Total Environ., 2022, 842, 156711 CrossRef CAS PubMed.
- E. Nicol, Z. Varga, S. Vujovic and S. Bouchonnet, Chemosphere, 2020, 248, 126040 CrossRef CAS PubMed.
- A. Cruz-Alcalde, C. Sans and S. Esplugas, Sci. Total Environ., 2017, 599, 1454–1461 CrossRef PubMed.
- D. Vione, G. Falletti, V. Maurino, C. Minero, E. Pelizzetti, M. Malandrino, R. Ajassa, R.-I. Olariu and C. Arsene, Environ. Sci. Technol., 2006, 40, 3775–3781 CrossRef CAS.
- J. M. Burns, W. J. Cooper, J. L. Ferry, D. W. King, B. P. DiMento, K. McNeill, C. J. Miller, W. L. Miller, B. M. Peake and S. A. Rusak, Aquat. Sci., 2012, 74, 683–734 CrossRef CAS.
- F. J. Real, J. L. Acero, F. J. Benitez and E. Matamoros, Sep. Purif. Technol., 2022, 301, 121975 CrossRef CAS.
- J. L. Acero, F. J. Real, F. J. Benitez and E. Matamoros, Sep. Purif. Technol., 2019, 211, 218–226 CrossRef CAS.
- H. Yang, H. Wang, P. Wang and Q. Feng, ACS Appl. Mater. Interfaces, 2025, 17(2), 3052–3061 CrossRef CAS PubMed.
- S. Cui, J. Lv, R. Hough, Q. Fu, L. An, Z. Zhang, Y. Ke, Z. Liu and Y.-F. Li, Sci. Total Environ., 2024, 173509 CrossRef CAS PubMed.
- E. S. da Silva, M. C. V. M. Starling and C. C. Amorim, Environ. Sci. Pollut. Res., 2023, 1–23 Search PubMed.
- G. Aragay, F. Pino and A. Merkoçi, Chem. Rev., 2012, 112, 5317–5338 CrossRef CAS.
- L. Chen, T. Cai, C. Cheng, Z. Xiong and D. Ding, Chem. Eng. J., 2018, 351, 1137–1146 CrossRef CAS.
- X. Wang, W. Wang, L. M. Wingen, V. Perraud and B. J. Finlayson-Pitts, Proc. Natl. Acad. Sci. U. S. A., 2024, 121, e2312930121 CrossRef CAS PubMed.
- I. Carra, C. Sirtori, L. Ponce-Robles, J. A. S. Pérez, S. Malato and A. Agüera, Chemosphere, 2015, 130, 73–81 CrossRef CAS PubMed.
- N. T. Hoa and Q. V. Vo, Chemosphere, 2023, 314, 137682 CrossRef CAS PubMed.
- Q. V. Vo, B.-T. Truong-Le, N. T. Hoa and A. Mechler, J. Mol. Liq., 2024, 413, 126028 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, G. Z. J. Bloino, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 16, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- M. Carreon-Gonzalez, A. Vivier-Bunge and J. R. Alvarez-Idaboy, J. Comput. Chem., 2019, 15, 2103–2110 CrossRef PubMed.
- N. Mora-Diez, J. R. Alvarez-Idaboy and R. J. Boyd, J. Phys. Chem. A, 2001, 105, 9034–9039 CrossRef CAS.
- A. Galano and J. R. Alvarez-Idaboy, J. Comput. Chem., 2014, 35, 2019–2026 Search PubMed.
- C. Kalalian, G. El Dib, H. Singh, P. Rao, E. Roth and A. Chakir, Atmos. Environ., 2020, 223, 117306 CrossRef CAS.
- C. Kalalian, A. Grira, J. N. Illmann, I. Patroescu-Klotz, G. El Dib, P. Coddeville, A. Canosa, P. Wiesen, B. Aazaad and L. Senthilkumar, Atmosphere, 2022, 13, 291 CrossRef CAS.
- J. R. l. Alvarez-Idaboy and A. Galano, J. Phys. Chem. B, 2012, 116, 9316–9325 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- E. Dzib, J. L. Cabellos, F. Ortíz-Chi, S. Pan, A. Galano and G. Merino, Int. J. Quantum Chem., 2019, 119, e25686 CrossRef.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- M. E. Alberto, N. Russo, A. Grand and A. Galano, Phys. Chem. Chem. Phys., 2013, 15, 4642–4650 RSC.
- W. Li, Y. Shang, H. Ning, J. Li and S.-N. Luo, Phys. Chem. Chem. Phys., 2020, 22, 5797–5806 RSC.
- A. Galano, G. Mazzone, R. Alvarez-Diduk, T. Marino, J. R. Alvarez-Idaboy and N. Russo, Annu. Rev. Food Sci. Technol., 2016, 7, 335–352 CrossRef CAS PubMed.
- M. G. Evans and M. Polanyi, Trans. Faraday Soc., 1935, 31, 875–894 RSC.
- H. Eyring, J. Chem. Phys., 1935, 3, 107–115 CrossRef CAS.
- D. G. Truhlar, W. L. Hase and J. T. Hynes, J. Phys. Chem., 1983, 87, 2664–2682 CrossRef CAS.
- T. Furuncuoglu, I. Ugur, I. Degirmenci and V. Aviyente, Macromolecules, 2010, 43, 1823–1835 CrossRef CAS.
- E. Vélez, J. Quijano, R. Notario, E. Pabón, J. Murillo, J. Leal, E. Zapata and G. Alarcón, J. Phys. Org. Chem., 2009, 22, 971–977 Search PubMed.
- E. Dzib, J. L. Cabellos, F. Ortiz-Chi, S. Pan, A. Galano and G. Merino, Eyringpy 1.0.2, Cinvestav, Mérida, Yucatán, 2018 Search PubMed.
- C. Eckart, Phy. Rev., 1930, 35, 1303 Search PubMed.
- E. Pollak and P. Pechukas, J. Am. Chem. Soc., 1978, 100, 2984–2991 CrossRef CAS.
- A. Fernández-Ramos, B. A. Ellingson, R. Meana-Pañeda, J. M. Marques and D. G. Truhlar, Theor. Chem. Acc., 2007, 118, 813–826 Search PubMed.
- B. N. Ames, M. K. Shigenaga and T. M. Hagen, Proc. Natl. Acad. Sci. U. S. A., 1993, 90, 7915–7922 CrossRef CAS PubMed.
- A. Galano and J. Raúl Alvarez-Idaboy, Int. J. Quantum Chem., 2019, 119, e25665 CrossRef.
- M. Li, J. Sun, Q. Mei, B. Wei, Z. An, H. Cao, C. Zhang, J. Xie, J. Zhan and W. Wang, J. Hazard. Mater., 2021, 416, 126250 CrossRef CAS PubMed.
- W. Hehre, J. Yu, P. Klunzinger and L. Lou, Spartan Software, Wavefunction Inc., Irvine, 2000 Search PubMed.
- A. Galano and J. R. Alvarez-Idaboy, RSC Adv., 2011, 1, 1763–1771 Search PubMed.
- Q. V. Vo, N. M. Tam, M. Van Bay and A. Mechler, Chem. Phys. Lett., 2020, 739, 137004 CrossRef CAS.
- R. Prinn, J. Huang, R. Weiss, D. Cunnold, P. Fraser, P. Simmonds, A. McCulloch, C. Harth, S. Reimann and P. Salameh, Geophys. Res. Lett., 2005, 32, 1–4 CrossRef.
- R. Prinn, J. Huang, R. Weiss, D. Cunnold, P. Fraser, P. Simmonds, A. McCulloch, C. Harth, P. Salameh and S. O'doherty, Science, 2001, 292, 1882–1888 CrossRef CAS PubMed.
- C. Alister, M. Araya, K. Becerra, J. Saavedra and M. Kogan, Food Chem., 2017, 221, 548–554 CrossRef CAS PubMed.
- T. T. Radović, S. D. Grujić, S. R. Kovačević, M. D. Laušević and M. A. Dimkić, Environ. Sci. Pollut. Res., 2016, 23, 25232–25244 CrossRef PubMed.
- C. S. Miyashiro and S. Hamoudi, Water, Air, Soil Pollut., 2022, 233, 401 CrossRef CAS PubMed.
- A. Tilgner, P. Bräuer, R. Wolke and H. Herrmann, J. Atmos. Chem., 2013, 70, 221–256 CrossRef CAS.
- H. Herrmann, Chem. Rev., 2003, 103, 4691–4716 CrossRef CAS PubMed.
- A. Tilgner and H. Herrmann, Atmos. Environ., 2010, 44, 5415–5422 CrossRef CAS.
- E. E. Mitsika, C. Christophoridis and K. Fytianos, Chemosphere, 2013, 93, 1818–1825 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ra02754c |
| This journal is © The Royal Society of Chemistry 2025 |


