 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Perovskite-type hydrides ACaH3 (A = Li, Na): computational investigation on materials properties for hydrogen storage applications†
Sol-Hyang Ri‡
a,
Un-Gi Jong‡ *b,
Thae-Song Imc and
Un-Ryong Rim
*b,
Thae-Song Imc and
Un-Ryong Rim *d
*d
aFaculty of Distance Education, Kim Chaek University of Technology, Pyongyang, PO Box 76, Democratic People's Republic of Korea
bFaculty of Materials Science, Computational Materials Design (CMD), Kim Il Sung University, Pyongyang, PO Box 76, Democratic People's Republic of Korea. E-mail: ug.jong@ryongnamsan.edu.kp
cFaculty of Metal Engineering, Kim Chaek University of Technology, Pyongyang, PO Box 76, Democratic People's Republic of Korea
dInstitute of Ocean Engineering, Kim Chaek University of Technology, Pyongyang, PO Box 76, Democratic People's Republic of Korea. E-mail: lur8971@star-co.net.kp
First published on 6th June 2025
Abstract
Recently, perovskite materials have emerged as a multifunctional material for photovoltaics, luminescence, photocatalytics and hydrogen storage applications. This work reports a theoretical investigation on materials properties of hydride perovskite ACaH3 (A = Li, Na) with cubic phase of Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group for application of H2 storage material. Electronic structure calculations show that the cubic LiCaH3 and NaCaH3 have an indirect bandgaps of 2.1 and 2.3 eV with valence band maximum at R point and conduction band minimum at M point. Based on geometric factors, elastic constants and self-consistent phonon calculations, we reveal that ACaH3 can be dynamically stabilized in cubic phase at elevated temperatures, and the compounds are mechanically stable as well, satisfying Born's stability criteria. Finally, our calculations demonstrate that gravimetric (volumetric) H2 storage capacities are 5.99 and 4.54 wt% (63.77 and 60.93 g L−1), and dehydrogenation temperatures are 453.76 and 688.16 K with a consideration of quantum effect for A = Li and Na, respectively. This work highlights that cubic LiCaH3 is regarded as a potential H2 storage material due to its high H2 storage capacity, stability and suitable dehydrogenation temperature.
m space group for application of H2 storage material. Electronic structure calculations show that the cubic LiCaH3 and NaCaH3 have an indirect bandgaps of 2.1 and 2.3 eV with valence band maximum at R point and conduction band minimum at M point. Based on geometric factors, elastic constants and self-consistent phonon calculations, we reveal that ACaH3 can be dynamically stabilized in cubic phase at elevated temperatures, and the compounds are mechanically stable as well, satisfying Born's stability criteria. Finally, our calculations demonstrate that gravimetric (volumetric) H2 storage capacities are 5.99 and 4.54 wt% (63.77 and 60.93 g L−1), and dehydrogenation temperatures are 453.76 and 688.16 K with a consideration of quantum effect for A = Li and Na, respectively. This work highlights that cubic LiCaH3 is regarded as a potential H2 storage material due to its high H2 storage capacity, stability and suitable dehydrogenation temperature.
1 Introduction
Using hydrogen as a primary fuel in the long term would effectively reduce the world's dependence on fossil fuel without releasing any pollutant as by-products.1–3 In the quest for feasible hydrogen-fueled vehicles, one of the major challenges is to develop lightweight materials with high hydrogen densities (>5 wt%) which can absorb and release hydrogen in the range of 1–10 bar and 298–473 K.4 The U.S. Department of Energy (DOE) aims at developing a hydrogen storage material with a gravimetric capacity of 5.5 wt% and a volumetric capacity of 40 g L−1 by 2025 for a target driving range of 300 miles.5 Considerable research efforts have been concentrated on metal hydrides such as Mg(BH4)2,6–9 NaAlH4,10–13 LiBH4,14–16 MgH2 (ref. 17–19) and LiH2 (ref. 20) due to their relatively high hydrogen storage capacities and inexpensive production cost. However, most of these hydrides unfortunately suffer from poor kinetics and irreversibility of hydrogen absorption and desorption cycling. For example, it was demonstrated that LiBH4 (ref. 15) can be dehydrogenated and rehydrogenated above its melting point (∼550 K) because of its slow kinetics and unfavorable thermodynamics, and only when heating up to 770 K, most of the hydrogen stored in LiBH4 can be released from it. Moreover, some of them are likely to release toxic gas (e.g., ammonia, diborane) during the dehydrogenation reaction.21 Nevertheless, the complex metal hydrides containing alkali metals are expected to have great potential for enhancing kinetics and reversibility as well as inhibiting release of pollutant.In recent years, perovskite-type hydrides ABH3 where A and B are monovalent and divalent cations respectively have attracted great attention as a promising candidate for the future hydrogen storage materials.22–29 It was found that these compounds exhibit high thermodynamic stability, sufficient space to accommodate a large amount of hydrogen, catalytic effect on the hydrogen reversibility and high hydrogen storage capacity.30–33 Ikeda et al. first synthesized the perovskite-type hydride NaMgH3 by mechanically milling the binary hydrides of NaH and MgH2 at ambient temperature, explaining the formation ability of other hydride perovskite from Goldschmidt tolerance factors.23–26 They observed reversible hydrogenation and dehydrogenation with a hydrogen capacity of 5.9 wt% and rapid hydrogen motion at elevated temperature. On the other hand, Komiya et al. fabricated the perovskite-type hydrides AMgH3 (A = Na, K, Rb) by using ball-milling, reporting that the hydrides are dehydrogenated at temperatures between 673 and 723 K according to several ways depending on the type of A cation.33 Furthermore, it was revealed that the hydride perovskite ZrCoH3 can reversibly absorb and desorb hydrogen, but it suffers from the hydrogen-induced disproportionation (HID) phenomena.34 However, it was proved that the HID can be improved by partial substitution of Zr or Co cation with Ti cation.35
Trigger by the experimental studies,23–26 extensive theoretical investigations have been carried out to provide an in-depth understanding of materials properties for hydrogen storage applications of the perovskite-type hydrides.22,28,30–32,36,37 In 2007, Fornari et al.31 reported a density functional study on the structural and lattice dynamics properties for the perovskite hydrides AMgH3 (A = Na, K, Rb), revealing the compound's ionic bonding nature and dynamical stability. Based on density functional theory (DFT) calculations, Gencer et al.38 investigated the electronic and mechanical properties of the hydride perovskites LiNiH3, NaNiH3 and KNiH3 with hydrogen storage capacities of 4.4, 3.6 and 3.3 wt% respectively, illustrating their mechanical stability and metallic nature. Siddique et al.39,40 carried out DFT studies on the dynamical and mechanical stabilities of the hydride perovskites LiBH3 (B = Sc, Ti, V) and AVH3 (A = Be, Mg, Ca, Sr) with hydrogen storage capacities higher than 4.0 wt%, confirming their stabilities. Recently, Xu et al.36 reported the hydrogen storage capacities and structural, electronic, optical, mechanical, thermodynamic and dynamical properties for XAlH3 (X = Na, K) hydride perovskites. They concluded that the compounds show mechanical, dynamical and thermodynamical stabilities with metal-like electronic properties by ionic chemical bonding. Despite enormous researches on the hydride perovskites, little attention has been drawn to perovskite-type hydride ACaH3 (A = Li, Na) for application as a hydrogen storage material. The LiCaH3 and NaCaH3 have high hydrogen storage capacities of 6.0 and 4.5 wt%, respectively and contain nontoxic and earth-abundant elements. Thus, the hydride perovskites ACaH3 (A = Li, Na) can be regarded as a potential candidate for high-performance, low-cost and nontoxic hydrogen storage materials. In this work, we present a comprehensive and systematic investigation of the structural, electronic and lattice dynamic properties and thermodynamic and mechanical stabilities of the hydride perovskites ACaH3 for the application as the hydrogen storage material by using first-principles calculations.
2 Computational methods
Density functional theory (DFT) calculations were performed using the Vienna ab initio simulation package (VASP).44,45 The projector augmented wave (PAW) potentials46,47 were used to describe the interactions between ions and valence electrons. The valence electron configurations were given as Li–2s1, Na–3s1, Ca–3p64s2 and H–1s1. Convergence test revealed that the cutoff energy 800 eV for plane wave basis sets and k-point mesh 10 × 10 × 10 provided a total energy accuracy of 1 meV per atom (see Fig. S1, ESI†). The variable-cell structural optimizations were performed until the atomic forces were less than 10−3 eV Å−1 with the self-consistent convergence threshold of 10−8 eV. We utilized the Perdew–Burke–Ernerhof (PBE)48 and PBE-revised functionals for solid (PBEsol)49 within the generalized gradient approximation (GGA) and the Perdew–Wang (PW91)50 functional within the local density approximation (LDA) in order to account for the exchange-correlation (XC) interaction among the valence electrons. We computed the atomic forces for the 2 × 2 × 2 supercells, using the reduced cutoff energy of 600 eV and k-point mesh of 4 × 4 × 4 with the same convergence thresholds.As proposed by Ikeda,23 we considered the H2 decomposition reaction for the hydride perovskite ACaH3 as follows:
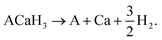 | (1) |
According to eqn (1), the H2 decomposition enthalpy ΔH was calculated as follows:
 | (2) |
| H = Etextele + Ezpe | (3) |
 | (4) |
| Tdes = −ΔH/ΔS | (5) |
Hydrogen storage materials are utilized to store and release hydrogen for the applications of the hydrogen-powered vehicles, fuel cells and energy storage medium. Thus, their mechanical stabilities are a crucial factor because they determine the hydrogen storage system's durability and safety under operation. In order to estimate the materials mechanical stability, we evaluated the elastic constants such as bulk (B), shear (G) and Young's (E) moduli, which represent linear response of lattice to small strain. The elastic stiffness (Cij) and compliance (Sij) constants were obtained from the density functional perturbation theory (DFPT)52 calculations using the PBEsol functional.
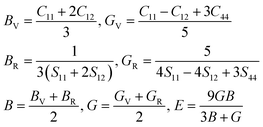 | (6) |
For the cubic phase, there exist three independent stiffness constants such as C11, C12 and C44. According to the Born's stability criteria,53 the cubic crystalline solids are mechanically stable when satisfying the following eqn (7):
| C11 > 0, C44 > 0, C11 + 2C12 > 0, C11 − C12 > 0 | (7) |
In order to calculate the phonon density of state (DOS) and the Ezpe, we computed the phonon dispersion curves for all the compounds involved in the H2 decomposition reaction eqn (1). The phonon dispersion curves and DOS calculations were carried out by using the finite displacement method, as implemented in the ALAMODE code.54,55 Using 2 × 2 × 2 supercells, we prepared 30 different configurations where all the atoms were randomly displaced by 0.01–0.06 Å from their equilibrium positions for the cubic ACaH3, A and Ca compounds, respectively. We then calculated the atomic forces for all the displaced configurations by performing precise DFT calculations, and harmonic and anharmonic interatomic force constants (IFCs) were extracted by using the compressive sensing lattice dynamics (CSLD),56 as implemented in the ALAMODE code. We ensure that for all the compounds, the IFCs can reproduce the atomic forces within the relative errors less than 2.4% when comparing to the DFT-calculated forces. The harmonic IFCs were extracted by considering all the possible harmonic terms, whereas the cubic and quartic anharmonic IFCs were extracted by setting the cutoff distance up to the 8th – and 5th – nearest neighbor for each type of atom. The self-consistent phonon (SCP) calculations57 were carried out to obtain temperature-dependent phonon dispersion curves and DOS by considering the anharmonic effects at finite temperatures.
3 Results and discussion
3.1 Crystal structures
Perovskite-type compounds are generally regarded to successively crystallize in orthorhombic, tetragonal and cubic phases upon increasing temperature. In fact, it was experimentally found that MMgH3 (M = Na, K, Rb) adopt the cubic and orthorhombic phases at different temperatures.21,23,33 As for the perovskite compounds ABH3, the stability of the perovskite structure can be empirically assessed by using the Goldschmidt tolerance factor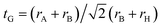 and octahedral factor to = rB/rH, where rA, rB and rH are the ionic radii for A+, B2+ and H− ions, respectively. The to can be used to assess whether the BH6 octahedron is stable, while the tG to check whether the A-site cation can fit between the BH6 octahedra. According to the empirical criteria,58,59 the perovskite compounds can adopt the stable cubic phase when satisfying 1.0 ≥ tG ≥ 0.8 and to ≥ 0.4. This criteria have been successfully applied to estimate the formability of cubic phase for the oxide, halide and fluoride perovskites.60,61 Table 1 lists the calculated geometric factors of tG and to for the hydride perovskites ACaH3 (A = Li, Na). Based on the analysis of geometric factors, it was found that the hydride perovskites LiCaH3 and NaCaH3 can stabilize in the cubic phase because of suitable geometric factors of tG = 0.8, 0.9 and to = 0.7. Therefore, it was supposed that the hydride perovskites ACaH3 can adopt the cubic phase with the Pm
and octahedral factor to = rB/rH, where rA, rB and rH are the ionic radii for A+, B2+ and H− ions, respectively. The to can be used to assess whether the BH6 octahedron is stable, while the tG to check whether the A-site cation can fit between the BH6 octahedra. According to the empirical criteria,58,59 the perovskite compounds can adopt the stable cubic phase when satisfying 1.0 ≥ tG ≥ 0.8 and to ≥ 0.4. This criteria have been successfully applied to estimate the formability of cubic phase for the oxide, halide and fluoride perovskites.60,61 Table 1 lists the calculated geometric factors of tG and to for the hydride perovskites ACaH3 (A = Li, Na). Based on the analysis of geometric factors, it was found that the hydride perovskites LiCaH3 and NaCaH3 can stabilize in the cubic phase because of suitable geometric factors of tG = 0.8, 0.9 and to = 0.7. Therefore, it was supposed that the hydride perovskites ACaH3 can adopt the cubic phase with the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group like the oxide, halide and fluoride perovskites (see Fig. 1). We note that even though the structural factors of tG and to can provide a qualitative estimation of the perovskite structure stability, a quantitative and detailed assessment of materials stability should be based on precise calculations of lattice dynamics properties and elastic constants.
m space group like the oxide, halide and fluoride perovskites (see Fig. 1). We note that even though the structural factors of tG and to can provide a qualitative estimation of the perovskite structure stability, a quantitative and detailed assessment of materials stability should be based on precise calculations of lattice dynamics properties and elastic constants.
| Compound | PW91 | PBE | PBEsol | Exp. | Geometric factor | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lattice constants (Å) | Atom | Position | Lattice constants (Å) | Position | Lattice constants (Å) | Position | Lattice constants (Å) | Position | |||||||||||
| x | y | z | x | y | z | x | y | z | x | y | z | tG | to | ||||||
| a Experiment.41b Experiment.42c Experiment.43 | |||||||||||||||||||
| LiCaH3 | a = 4.25 | Li | 0.5 | 0.5 | 0.5 | a = 4.29 | 0.5 | 0.5 | 0.5 | a = 4.28 | 0.5 | 0.5 | 0.5 | — | — | — | — | 0.8 | 0.7 |
| Ca | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | — | — | — | — | ||||||
| H1 | 0.5 | 0.0 | 0.0 | 0.5 | 0.0 | 0.0 | 0.5 | 0.0 | 0.0 | — | — | — | — | ||||||
| H2 | 0.0 | 0.5 | 0.0 | 0.0 | 0.5 | 0.0 | 0.0 | 0.5 | 0.0 | — | — | — | — | ||||||
| H3 | 0.0 | 0.0 | 0.5 | 0.0 | 0.0 | 0.5 | 0.0 | 0.0 | 0.5 | — | — | — | — | ||||||
| NaCaH3 | a = 4.31 | Na | 0.5 | 0.5 | 0.5 | a = 4.35 | 0.5 | 0.5 | 0.5 | a = 4.34 | 0.5 | 0.5 | 0.5 | — | — | — | — | 0.9 | 0.7 |
| Ca | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | — | — | — | — | ||||||
| H1 | 0.5 | 0.0 | 0.0 | 0.5 | 0.0 | 0.0 | 0.5 | 0.0 | 0.0 | — | — | — | — | ||||||
| H2 | 0.0 | 0.5 | 0.0 | 0.0 | 0.5 | 0.0 | 0.0 | 0.5 | 0.0 | — | — | — | — | ||||||
| H3 | 0.0 | 0.0 | 0.5 | 0.0 | 0.0 | 0.5 | 0.0 | 0.0 | 0.5 | — | — | — | — | ||||||
| Li | a = 3.44 | Li1 | 0.5 | 0.5 | 0.5 | a = 3.49 | 0.5 | 0.5 | 0.5 | a = 3.47 | 0.5 | 0.5 | 0.5 | a = 3.47a | 0.5 | 0.5 | 0.5 | ||
| Li2 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |||||||
| Na | a = 4.17 | Na1 | 0.5 | 0.5 | 0.5 | a = 4.25 | 0.5 | 0.5 | 0.5 | a = 4.23 | 0.5 | 0.5 | 0.5 | a = 4.22b | 0.5 | 0.5 | 0.5 | ||
| Na2 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |||||||
| Ca | a = 5.51 | Ca1 | 0.0 | 0.0 | 0.0 | a = 5.61 | 0.0 | 0.0 | 0.0 | a = 5.59 | 0.0 | 0.0 | 0.0 | a = 5.57c | 0.0 | 0.0 | 0.0 | ||
| Ca2 | 0.5 | 0.5 | 0.0 | 0.5 | 0.5 | 0.0 | 0.5 | 0.5 | 0.0 | 0.5 | 0.5 | 0.0 | |||||||
| Ca3 | 0.5 | 0.0 | 0.5 | 0.5 | 0.0 | 0.5 | 0.5 | 0.0 | 0.5 | 0.5 | 0.0 | 0.5 | |||||||
| Ca4 | 0.0 | 0.5 | 0.5 | 0.0 | 0.5 | 0.5 | 0.0 | 0.5 | 0.5 | 0.0 | 0.5 | 0.5 | |||||||
Through the variable-cell structural optimization by using the PW91, PBE and PBEsol functionals, we calculated the equilibrium lattice constants for the cubic ACaH3, Ca, Li and Na compounds. According to the previous experiments,41–43 we assume that the Ca and Li (Na) compounds adopt the cubic phases with the space group of Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and Im
m and Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, respectively (see Fig. S2, ESI†). The calculated lattice constants are listed in Table 1. The PBEsol-calculated lattice constant of LiCaH3 is a = 4.28 Å, which is slightly smaller than a = 4.34 Å of NaCaH3 because of the smaller ionic radius of Li cation than Na cation. To the best of our knowledge, there are no experimental and theoretical works of the hydride perovskites ACaH3 for comparison. However, the optimized lattice constants are in good agreement with the previous experiments41–43 for the cubic Ca, Li and Na. Especially, the PW91-calculated lattice constants of a = 5.51, 4.17 and 3.44 Å underestimate the experimental ones41–43 of a = 5.59, 4.23 and 3.47 Å for the cubic Ca, Na and Li respectively, whereas the PBE-calculated ones slightly overestimate the experimental ones. Moreover, the PBEsol-calculated lattice constants of a = 5.59, 4.23 and 3.47 Å are in excellent agreement with the experimental ones of a = 5.59, 4.23 and 3.47 Å, providing a relative error less than 0.5%. Hereby, we adopted the PBEsol functional for the calculations of lattice dynamics and electronic structure properties, mechanical stability and H2 decomposition energetics for the cubic ACaH3.
m, respectively (see Fig. S2, ESI†). The calculated lattice constants are listed in Table 1. The PBEsol-calculated lattice constant of LiCaH3 is a = 4.28 Å, which is slightly smaller than a = 4.34 Å of NaCaH3 because of the smaller ionic radius of Li cation than Na cation. To the best of our knowledge, there are no experimental and theoretical works of the hydride perovskites ACaH3 for comparison. However, the optimized lattice constants are in good agreement with the previous experiments41–43 for the cubic Ca, Li and Na. Especially, the PW91-calculated lattice constants of a = 5.51, 4.17 and 3.44 Å underestimate the experimental ones41–43 of a = 5.59, 4.23 and 3.47 Å for the cubic Ca, Na and Li respectively, whereas the PBE-calculated ones slightly overestimate the experimental ones. Moreover, the PBEsol-calculated lattice constants of a = 5.59, 4.23 and 3.47 Å are in excellent agreement with the experimental ones of a = 5.59, 4.23 and 3.47 Å, providing a relative error less than 0.5%. Hereby, we adopted the PBEsol functional for the calculations of lattice dynamics and electronic structure properties, mechanical stability and H2 decomposition energetics for the cubic ACaH3.
3.2 Lattice dynamics properties
In order to predict lattice dynamics properties, we calculated the phonon dispersion curves and density of states (DOS) at elevated temperatures for the cubic ACaH3 (A = Li, Na) with a space group of Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m by using the SCP theory. From the phonon dispersions and DOS (Fig. 2), we can directly estimate the material's dynamical stability and compute the zero-point Ezpe energy in consideration of quantum effect by using eqn (4). As calculated at 0 K, Fig. 2 shows the harmonic phonon dispersion curves (blue-colored lines in the left panel) computed along the high symmetry line of Γ–X–M–Γ–R in the phonon Brillouin zone (BZ). It was found that the relatively deep negative phonon eigenvalues reaching up to −70 meV, known as the soft mode, appear in the whole phonon BZ range for the cubic ACaH3. Such finding indicates that these compounds are dynamically unstable in the cubic phase at 0 K. From the phonon DOS at 0 K (middle panel in Fig. 2), we found that these soft phonon modes are mainly ascribed to the Ca- and Li-atomic (Na- and H-atomic) vibrations for the LiCaH3 (NaCaH3).The symmetry analysis of the phonon eigenvectors indicates that the soft phonon modes are responsible for symmetry breaking instabilities like in the halide and oxide perovskites.62,63 As shown in Fig. 3(a), the lowest soft mode at the Γ point induces the displacement of Li and Ca atoms from the ideal centers of the CaH3 inorganic framework and the CaH6 octahedron, respectively for the cubic LiCaH3. Moreover, the lowest soft modes causes collective displacements of the H and Na atoms with a larger magnitude of Na displacement for the cubic NaCaH3 (Fig. 3(b)). The presence of such soft modes suggests that the cubic hydride perovskites ACaH3 can undergo a phase transition to a lower symmetry structure such as tetragonal or orthorhombic phase upon decreasing temperature like the halide and oxide perovskites. The calculated phonon dispersion curves and DOS are plotted in Fig. S3–S5, ESI† for the cubic Li, Na and Ca without any soft phonon modes, implying their dynamical stabilities.
m by using the SCP theory. From the phonon dispersions and DOS (Fig. 2), we can directly estimate the material's dynamical stability and compute the zero-point Ezpe energy in consideration of quantum effect by using eqn (4). As calculated at 0 K, Fig. 2 shows the harmonic phonon dispersion curves (blue-colored lines in the left panel) computed along the high symmetry line of Γ–X–M–Γ–R in the phonon Brillouin zone (BZ). It was found that the relatively deep negative phonon eigenvalues reaching up to −70 meV, known as the soft mode, appear in the whole phonon BZ range for the cubic ACaH3. Such finding indicates that these compounds are dynamically unstable in the cubic phase at 0 K. From the phonon DOS at 0 K (middle panel in Fig. 2), we found that these soft phonon modes are mainly ascribed to the Ca- and Li-atomic (Na- and H-atomic) vibrations for the LiCaH3 (NaCaH3).The symmetry analysis of the phonon eigenvectors indicates that the soft phonon modes are responsible for symmetry breaking instabilities like in the halide and oxide perovskites.62,63 As shown in Fig. 3(a), the lowest soft mode at the Γ point induces the displacement of Li and Ca atoms from the ideal centers of the CaH3 inorganic framework and the CaH6 octahedron, respectively for the cubic LiCaH3. Moreover, the lowest soft modes causes collective displacements of the H and Na atoms with a larger magnitude of Na displacement for the cubic NaCaH3 (Fig. 3(b)). The presence of such soft modes suggests that the cubic hydride perovskites ACaH3 can undergo a phase transition to a lower symmetry structure such as tetragonal or orthorhombic phase upon decreasing temperature like the halide and oxide perovskites. The calculated phonon dispersion curves and DOS are plotted in Fig. S3–S5, ESI† for the cubic Li, Na and Ca without any soft phonon modes, implying their dynamical stabilities.
To clearly estimate the phase stability, we renormalized the phonon dispersion curves and DOS at elevated temperatures from 300 to 900 K with an interval of 200 K by using the SCP theory. From the SCP calculations, the negative phonon energies corresponding to the soft modes were renormalized to be real within the whole range of the phonon BZ (orange and red lines in the left panel of Fig. 2), which indicates that the cubic phase of ACaH3 is dynamically stable at elevated temperatures, as confirmed in experiment33 for the Mg-based hydride perovskites AMgH3 (A = Na, K, Rb). In particular, the negative phonon energies of −49 and −38 (−26) meV were renormalized at 900 K to 81 and 129 (40 and 125) meV at the Γ point for LiCaH3 (NaCaH3). Noticeable changes were observed for the phonon DOS as well (right panel in Fig. 2). For instance, at 300 K, the H and Ca atoms in both LiCaH3 and NaCaH3 play dominant roles in the high-lying optical phonon modes and the acoustic phonon modes coupled with the low-lying optical modes, respectively. However, in the case of LiCaH3, the Li atom makes a dominant contribution to the mid-lying phonon modes ranging from 40 to 115 meV, while in the case of NaCaH3, the Na atom significantly contributes to the acoustic and low-lying optical modes below 30 meV. Upon increasing temperature, the phonon dispersion curves and phonon DOS broaden towards higher energy due to stronger atomic vibrations (see Fig. S6 and S7, ESI†).
3.3 Electronic structure properties
Considering that the cubic phase can be stabilized at elevated temperatures, we calculated the electronic structure properties for the cubic hydride perovskite ACaH3 with the space group of Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m by using the PBEsol functional. Using the calculated energy band structures (Fig. 4(a)), we can directly estimate the energy band gap, and from the atom-projected electron DOS (Fig. 4(b)), we can understand which atom can play important role near the Fermi level Ef. It was established that the PBE or PBEsol functional within the GGA can describe electronic structure properties in good agreement with experiment for the halide and hydride perovskites. The spin–orbit coupling (SOC) effect was not considered as all the constituent atoms are very light for ACaH3. Fig. 4(a) shows the energy band structure calculated along the high symmetry line of R–Γ–X–R–X1–M–Γ–X1 in the BZ for the cubic LiCaH3. It was found that the compound has an indirect band gap of 2.1 eV with the valence band maximum (VBM) at the R point and the conduction band minimum (CBM) at the M point, and a direct band gap of 2.8 eV at the R point. Meanwhile, the cubic NaCaH3 provides an indirect (direct) band gap of 2.3 (3.2) eV with similar band structures to the LiCaH3 (see Fig. S8, ESI†). It is worth noting that the larger the ionic radii of A cation, the larger band gaps the hydride perovskites ACaH3 provide, being similar to the case of the halide and fluoride perovskites.60,61 Through the analysis of atom-projected partial DOS, it was revealed that the valence bands (VBs) are dominated by H-s state with a small contribution of Ca-s states, while the conduction bands (CBs) are dominated by Ca-s states coupled with Li- and H-s states (see Fig. 4 and S8, ESI†).Such analysis coincides with the isosurface plot of the electron charge density corresponding to the VBM and CBM, as shown in Fig. 5.
m by using the PBEsol functional. Using the calculated energy band structures (Fig. 4(a)), we can directly estimate the energy band gap, and from the atom-projected electron DOS (Fig. 4(b)), we can understand which atom can play important role near the Fermi level Ef. It was established that the PBE or PBEsol functional within the GGA can describe electronic structure properties in good agreement with experiment for the halide and hydride perovskites. The spin–orbit coupling (SOC) effect was not considered as all the constituent atoms are very light for ACaH3. Fig. 4(a) shows the energy band structure calculated along the high symmetry line of R–Γ–X–R–X1–M–Γ–X1 in the BZ for the cubic LiCaH3. It was found that the compound has an indirect band gap of 2.1 eV with the valence band maximum (VBM) at the R point and the conduction band minimum (CBM) at the M point, and a direct band gap of 2.8 eV at the R point. Meanwhile, the cubic NaCaH3 provides an indirect (direct) band gap of 2.3 (3.2) eV with similar band structures to the LiCaH3 (see Fig. S8, ESI†). It is worth noting that the larger the ionic radii of A cation, the larger band gaps the hydride perovskites ACaH3 provide, being similar to the case of the halide and fluoride perovskites.60,61 Through the analysis of atom-projected partial DOS, it was revealed that the valence bands (VBs) are dominated by H-s state with a small contribution of Ca-s states, while the conduction bands (CBs) are dominated by Ca-s states coupled with Li- and H-s states (see Fig. 4 and S8, ESI†).Such analysis coincides with the isosurface plot of the electron charge density corresponding to the VBM and CBM, as shown in Fig. 5.
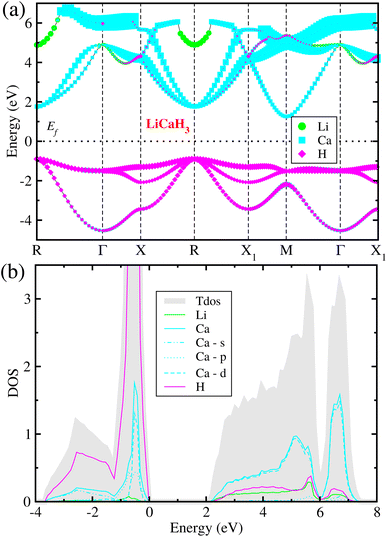 | ||
| Fig. 4 (a) Atom-resolved electronic band structure and (b) partial density of states (DOS) calculated with the PBEsol functional for the hydride perovskite LiCaH3 in the cubic phase. | ||
3.4 Mechanical stability and H2 decomposition energetics
In order to assess the mechanical stability of the compounds, we then estimated the elastic constants such as the stiffness constant (Cij), bulk modulus (B), shear modulus (G) and Young's modulus (E) by using the DFPT calculations. As listed in Table 2, the elastic stiffness constants of C11, C12 and C44 satisfy the Born's stability criteria for the cubic LiCaH3 and NaCaH3, expressed as eqn (7). Furthermore, we found that the cubic LiCaH3 (NaCaH3) is a ductile (brittle) material according to the Pugh's criteria64 because the Poisson's ratio ν and the Pugh's ratio B/G are larger (smaller) than the threshold values of 0.26 and 1.75, respectively (see Table 2). Based on such analysis, it was found that the cubic ACaH3 is mechanically as well as dynamically stable. Due to the larger B (smaller G and E), the LiCaH3 exhibits greater (smaller) hardness upon bulk (shear and tensile) deformation compared to the NaCaH3. On the other hand, both LiCaH3 and NaCaH3 are elastically anisotropic in nature because the anisotropic factor A = 2C44/(C11 − C12) is much smaller than unity.| Functional | Properties | LiCaH3 | NaCaH3 | Li | Na | Ca | H2 |
|---|---|---|---|---|---|---|---|
| ρg (wt%) | 5.99 | 4.54 | |||||
| ρv (g L−1) | 63.77 | 60.93 | |||||
| PW91 | H (eV) | −14.92 | −14.85 | −3.77 | −2.61 | −7.73 | −6.81 |
| ΔH (eV) | 0.89 | 1.39 | |||||
| Tdes (K) | 437.42 | 687.23 | |||||
| PBE | H (eV) | −14.73 | −14.64 | −3.81 | −2.62 | −7.73 | −6.77 |
| ΔH (eV) | 0.73 | 1.24 | |||||
| Tdes (K) | 361.68 | 612.46 | |||||
| PBEsol | H (eV) | −14.74 | −14.66 | −3.92 | −2.80 | −8.54 | −6.51 |
| ΔH (eV) | 0.87 | 1.35 | |||||
| Tdes (K) | 430.86 | 666.23 | |||||
| Ezpe (eV) | 0.37 | 0.37 | 0.34 | 0.02 | 0.01 | 0.27 | |
| Tqdes (K) | 453.76 | 688.16 | |||||
| C11 (GPa) | 661.99 | 631.11 | |||||
| C12 (GPa) | 83.89 | 95.43 | |||||
| C44 (GPa) | 90.46 | 122.79 | |||||
| B (GPa) | 276.59 | 273.99 | |||||
| G (GPa) | 147.32 | 168.78 | |||||
| E (GPa) | 375.33 | 420.09 | |||||
| B/G | 1.87 | 1.62 | |||||
| ν | 0.27 | 0.24 |
Finally, we investigated the H2 storage capacities and decomposition energetics for the hydride perovskites ACaH3 (A = Li, Na). The H2 gravimetric and volumetric storage capacities were calculated by using the formula of ρg = 3MH/(MA + MCa + 3MH) × 100% and ρv = 3MH/(NAVo), where MA, MCa and MH are the molar masses of A, Ca and H atoms, respectively while NA and Vo are the Avogadro number and PBEsol-optimized unit cell volume. As shown in Table 2, the LiCaH3 and NaCaH3 have ρg (ρv) of 5.99 and 4.54 wt% (63.77 and 60.93 g L−1), respectively, being larger or comparable to the targeted values of 5.5 wt% (40 g L−1) provided by the U.S. DOE.
The H2 decomposition temperature Tqdes (Tdes) with (without) a consideration of the quantum effect was estimated by employing the eqn (5). Ignoring the quantum effect, the PBEsol-calculated Tdes is 430.86 and 666.23 K for the cubic LiCaH3 and NaCaH3, respectively. With the calculated phonon energies and DOS, we calculated the zero-point energy Ezpe, finding that by considering the quantum effect, the Tqdes was slightly increased to 453.76 and 688.16 K for LiCaH3 and NaCaH3, respectively. To sum up, the hydride perovskite LiCaH3 can store 5.99 wt% and 63.77 g L−1 hydrogen with mechanical and dynamical stabilities and suitable H2 decomposition temperature of about 450 K, satisfying the U.S. DOE requirement.
4 Conclusions
In conclusion, by using the first-principles calculations, we have theoretically investigated the materials properties such as structural, electronic and lattice dynamics properties and mechanical and dynamical stabilities of the hydride perovskites ACaH3 (A = Li, Na) in cubic phase of Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group for the application of hydrogen storage material. From the calculations of Goldschmidt tolerance factor tG and octahedral factor to, it was suggested that the ACaH3 (A = Li, Na) can stabilize in the cubic phase of Pm
m space group for the application of hydrogen storage material. From the calculations of Goldschmidt tolerance factor tG and octahedral factor to, it was suggested that the ACaH3 (A = Li, Na) can stabilize in the cubic phase of Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group. We found that the PBEsol-calculated lattice constants and atomic positions are in good accordance with the available experimental data, while the PBE(PW91) functional slightly overestimate (underestimate) the structural properties for Li, Na and Ca metals. From the electronic structure calculations, it was found that the cubic LiCaH3 and NaCaH3 have an indirect (direct) bandgaps of 2.1 and 2.3 (2.8 and 3.2) eV with the VBM at the R point and the CBM at the M point (at the R point). The electron partial DOS indicated that the H-s and Ca-s states make significant contributions to the valence and conduction bands, respectively. The harmonic phonon dispersions and DOS calculations revealed that the cubic phase is dynamically unstable at 0 K with the negative phonon energies in the whole range of phonon BZ. However, the negative phonon energies were renormalized to be real by the SCP calculations, indicating that the ACaH3 can be dynamically stabilized in the cubic phase at elevated temperatures. Based on the DFPT calculations of elastic constants, it was demonstrated that the cubic phase of ACaH3 is mechanically stable in accordance with the Born's stability criteria. Finally, we investigated the H2 storage capacities and decomposition temperature by considering the quantum effect, finding that ρg (ρv) is 5.99 and 4.54 wt% (63.77 and 60.93 g L−1), and Tqdes is 453.76 and 688.16 K for A = Li and Na, respectively. Based on such calculations, it was concluded that the hydride perovskite LiCaH3 is a potential candidate for the onboard hydrogen storage application with the high gravimetric and volumetric capacities of 5.99 wt% and 63.77 g L−1 and a suitable dehydrogenation temperature of 453.76 K.
m space group. We found that the PBEsol-calculated lattice constants and atomic positions are in good accordance with the available experimental data, while the PBE(PW91) functional slightly overestimate (underestimate) the structural properties for Li, Na and Ca metals. From the electronic structure calculations, it was found that the cubic LiCaH3 and NaCaH3 have an indirect (direct) bandgaps of 2.1 and 2.3 (2.8 and 3.2) eV with the VBM at the R point and the CBM at the M point (at the R point). The electron partial DOS indicated that the H-s and Ca-s states make significant contributions to the valence and conduction bands, respectively. The harmonic phonon dispersions and DOS calculations revealed that the cubic phase is dynamically unstable at 0 K with the negative phonon energies in the whole range of phonon BZ. However, the negative phonon energies were renormalized to be real by the SCP calculations, indicating that the ACaH3 can be dynamically stabilized in the cubic phase at elevated temperatures. Based on the DFPT calculations of elastic constants, it was demonstrated that the cubic phase of ACaH3 is mechanically stable in accordance with the Born's stability criteria. Finally, we investigated the H2 storage capacities and decomposition temperature by considering the quantum effect, finding that ρg (ρv) is 5.99 and 4.54 wt% (63.77 and 60.93 g L−1), and Tqdes is 453.76 and 688.16 K for A = Li and Na, respectively. Based on such calculations, it was concluded that the hydride perovskite LiCaH3 is a potential candidate for the onboard hydrogen storage application with the high gravimetric and volumetric capacities of 5.99 wt% and 63.77 g L−1 and a suitable dehydrogenation temperature of 453.76 K.
Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
Sol-Hyang Ri and Un-Gi Jong developed the original project, performed the DFT calculations and drafted the first manuscript. Un-Gi Jong and Un-Ryong Rim supervised the work. All authors reviewed the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported as part of the basic research project “Design of New Energy Materials” (No. 2021-12) funded by the State Commission of Science and Technology, DPR Korea. Computations have been performed on the High-Performance Computer managed by Faculty of Materials Science and Technology, Kim Chaek University of Technology.References
- L. W. Jones, Science, 1971, 174, 367–370 CrossRef CAS PubMed.
- J. O. Bockris and M. A, Science, 1972, 176, 1323 CrossRef CAS PubMed.
- G. W. Crabtree, M. S. Dresselhaus and M. V. Buchanan, Phys. Today, 2004, 57, 39–44 CrossRef CAS.
- L. E. Klebanoff and J. O. Keller, Int. J. Hydrogen Energy, 2013, 38, 4533–4576 CrossRef CAS.
- https://www.energy.gov/eere/fuelcells/doe-technical-targetsonboard-hydrogen-storage-light-duty-vehicles, 2022.
- E. I. Epelle, K. S. Desongu, W. Obande, A. A. Adeleke, P. P. Ikubanni, J. A. Okolie and B. Gunes, Int. J. Hydrogen Energy, 2022, 47, 20398–20431 CrossRef CAS.
- J. Andersson and S. Gronkvist, Int. J. Hydrogen Energy, 2019, 44, 11901–11919 CrossRef CAS.
- J. Liu, L. Sun, J. Yang, D. Guo, D. Chen, L. Yang and P. Xiao, RSC Adv., 2022, 12, 35744–35755 RSC.
- X. Hu, J. Wang, S. Li, X. Hu, R. Ye, L. Zhou, P. Li and C. Chen, RSC Adv., 2023, 13, 14980–14990 RSC.
- Y. Liu, X. Zhang, K. Wang, Y. Yang, M. Gao and H. Pan, J. Mater. Chem., 2016, 4, 1087–1095 RSC.
- E. Arora, S. Saini, P. Basera, M. Kumar, A. Singh and S. Bhattacharya, J. Phys. Chem. C, 2019, 123, 62–69 CrossRef CAS.
- S. Zheng, F. Fang, G. Zhou, G. Chen, L. Ouyang, M. Zhu and D. Sun, Chem. Mater., 2008, 20, 3954–3958 CrossRef CAS.
- C. Milanese, S. Garroni, F. Gennari, A. Marini, T. Klassen, M. Dornheim and C. Pistidda, Metals, 2018, 8, 567–578 CrossRef.
- Y. Luo, L. Sun, F. Xu and Z. Liu, J. Mater. Chem. A, 2018, 6, 7293–7309 RSC.
- G. Xu, W. Zhang, Y. Zhang, X. Zhao, P. Wen and D. Ma, RSC Adv., 2018, 8, 19353–19361 RSC.
- M. V. Sofianos, D. A. Sheppard, M. R. Rowles, T. D. Humphries, S. Liu and C. E. Buckley, RSC Adv., 2017, 7, 36340–36350 RSC.
- M. Dornheim, S. Doppiu, G. Barkhordarian, U. Boesenberg, T. Klassen, O. Gutfleisch and R. Bormann, Scr. Mater., 2007, 56, 841–846 CrossRef CAS.
- S. Rivoirard, P. de Rango, D. Fruchart, J. Charbonnier and D. Vempaire, J. Alloys Compd., 2003, 356, 622–628 CrossRef.
- C. Pohlmann, L. Rontzsch, J. Hu, T. Weigarber, B. Kieback and M. Fichtner, J. Power Sources, 2012, 205, 173–179 CrossRef CAS.
- Y. Nakamori and S. i. Orimo, Appl. Phys. Lett., 2006, 88, 112104–112106 CrossRef.
- H. Wu, W. Zhou, T. J. Udovic, J. J. Rush and T. Yildirim, Chem. Mater., 2008, 20, 2335–2342 CrossRef CAS.
- M. M. Parvaiz, A. Khalil, M. B. Tahir, S. Ayub, T. E. Alic and H. T. Masoodd, RSC Adv., 2024, 14, 8385–8396 RSC.
- K. Ikeda, Y. Kogure, Y. Nakamori and S. Orimo, Scr. Mater., 2005, 53, 319–322 CrossRef CAS.
- K. Ikeda, S. Kato, Y. Shinzato, N. Okuda, Y. Nakamori, A. Kitano, H. Yukawa, M. Morinaga and S. Orimo, J. Alloys Compd., 2007, 446, 162–165 CrossRef.
- K. Ikeda, Y. Kogure, Y. Nakamori and S. Orimo, Prog. Solid State Chem., 2007, 35, 329–337 CrossRef CAS.
- K. Ikeda, Y. Nakamori and S. Orimo, Acta Mater., 2005, 53, 3453–3457 CrossRef CAS.
- H. Wang, J. Zhang, J. W. Liu, L. Z. Ouyang and M. Zhu, J. Alloys Compd., 2013, 580, 197–201 CrossRef.
- C. Kurkcu, S. Al and C. Yamcicier, Eur. Phys. J. B, 2022, 595, 180–190 CrossRef.
- T. Sato, D. Noreus, H. Takeshita and U. Haussermann, J. Solid State Chem., 2005, 178, 3381–3388 CrossRef CAS.
- W. Azeem, S. Hussain, F. A. Muhammad Khuram Shahzad, G. Khan, V. Tirth, H. Alqahtani, A. Algahtani, T. Al-Mughanam and Y. H. Wong, Int. J. Hydrogen Energy, 2024, 79, 514–524 CrossRef CAS.
- M. Fornari, A. Subedi and D. J. Singh, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 214118–214124 CrossRef.
- M. K. Masood, W. Khan, K. Chaoui, Z. Ashraf, S. Bibi, A. Kanwal, A. A. Alothman and J. Rehman, Int. J. Hydrogen Energy, 2024, 63, 1248–1257 CrossRef CAS.
- K. Komiya, N. Morisaku, R. Rong, Y. Takahashi, Y. Shinzato and H. Yukawa, J. Alloys Compd., 2008, 453, 157–160 CrossRef CAS.
- H. Q. Kou, H. He, W. H. Luo, T. Tang, Z. Y. Huang and G. Sang, Int. J. Hydrogen Energy, 2018, 43, 322–328 CrossRef CAS.
- G. H. Zhang, G. Sang, R. J. Xiong, H. Q. Kou, K. Z. Liu and W. H. Luo, Int. J. Hydrogen Energy, 2015, 40, 6582–6593 CrossRef CAS.
- N. Xu, R. Song, J. Zhang, Y. Chen, S. Chen, S. Li, Z. Jiang and W. Zhang, Int. J. Hydrogen Energy, 2024, 60, 434–440 CrossRef CAS.
- M. López, M. B. Torres and I. Cabria, Int. J. Hydrogen Energy, 2024, 71, 1363–1372 CrossRef.
- A. Gencer and G. Surucu, Int. J. Hydrogen Energy, 2019, 44, 15173–15182 CrossRef CAS.
- A. Siddique, A. Khalil, B. S. Almutairi, M. B. Tahir, T. Ahsan and A. Hannan, et al., Chem. Phys., 2023, 568, 111851–111859 CrossRef CAS.
- A. Siddique, A. Khalil, B. S. Almutairi, M. B. Tahir, M. Sagir and Z. Ullah, et al., Int. J. Hydrogen Energy, 2023, 48, 24401–24411 CrossRef CAS.
- A. P. Frolov and K. P. Rodionov, Science, 1983, 219, 1071–1072 CrossRef PubMed.
- R. Berliner, O. Fajen, H. G. Smith and R. L. Hitterman, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 12086–12097 CrossRef CAS PubMed.
- A. W. Hull, Science, 1920, 52, 227 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406–136411 CrossRef PubMed.
- J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244–13252 CrossRef PubMed.
- S. V. Alapati, J. K. Johnson and D. S. Sholl, J. Phys. Chem. B, 2006, 110, 8769–8776 CrossRef CAS PubMed.
- S. Sharma, J. K. Dewhurst and C. Ambrosch-Draxl, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 165332–165341 CrossRef.
- B. Max and H. Kun, Dynamical theory of crystal lattices, Clarendon, Oxford, UK, 1956 Search PubMed.
- T. Tadano, Y. Gohda and S. Tsuneyuki, J. Phys.: Condens. Matter, 2014, 26, 225402–225413 CrossRef CAS PubMed.
- T. Tadano and S. Tsuneyuki, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 054301–054311 CrossRef.
- Y. Xia, J. M. Hodges, M. G. Kanatzidis and M. K. Y. Chan, Appl. Phys. Lett., 2018, 112, 181906–181910 CrossRef.
- M. Simoncelli, N. Marzari and F. Mauri, Nat. Phys., 2019, 15, 809–816 Search PubMed.
- W. Travis, E. N. K. Glover, H. Bronstein, D. O. Scanlon and R. G. Palgrave, Chem. Sci., 2016, 7, 4548–4556 RSC.
- Z. Li, M. Yang, J. Park, S. Wei, J. J. Berry and K. Zhu, Chem. Mater., 2016, 28, 284–292 CrossRef CAS.
- U.-G. Jong, C.-J. Yu and Y.-H. Kye, RSC Adv., 2020, 10, 201–209 RSC.
- C.-J. Pak, U.-G. Jong, C.-J. Kang, Y.-S. Kim, Y.-H. Kye and C.-J. Yu, Mater. Adv., 2023, 4, 4528–4536 RSC.
- U.-G. Jong, C.-J. Yu, Y.-H. Kye, S.-N. Hong and H.-G. Kim, Phys. Rev. Mater., 2020, 4, 075403–075408 CrossRef CAS.
- U.-G. Jong, Y.-S. Kim, C.-H. Ri, Y.-H. Kye and C.-J. Yu, J. Phys. Chem. C, 2021, 125, 6013–6019 CrossRef CAS.
- S. F. Pugh, Philos. Mag., 1954, 45, 823–843 CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Total energy convergence tests according to the kinetic energy cutoff and k-point mesh, crystalline structures, phonon dispersion curves and phonon DOS for the cubic Ca, Li and Na compounds, total phonon DOS of the cubic ACaH3 at elevated temperatures, atom-projected energy band structure and DOS for NaCaH3. See DOI: https://doi.org/10.1039/d5ra01810b |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2025 |




