Optimization of the mechanical performance of TDI-based polyurethanes via orthogonal design and response surface methodology

Abstract

The mechanical properties of polyurethane elastomers are primarily determined by their formulations and synthetic processes. Here, we present an in-depth investigation into the optimization of the mechanical performance of a toluene diisocyanate (TDI)-based polyurethane using orthogonal design and response surface methodology (RSM). The utmost mechanical performance with a tensile strength of 14.67 MPa and an elongation at break of 1160% was achieved. The model reliability in predicting the mechanical strength was validated with a reasonable accuracy error of 2.2%. The correlation between mechanical properties of the TDI-based polyurethane and factors including NCO/OH ratio (R-value), chain extension coefficient, crosslinking coefficient, and curing temperature was elucidated through a combination of Fourier transform infrared (FTIR) and Raman spectroscopy with RSM. A net positive interactive effect among the R-value, chain extension coefficient, and curing temperature was observed. Additionally, a volcano-shaped relationship was identified between tensile strength and the crosslinking coefficient, while a similar non-monotonic trend was found between elongation at break and curing temperature. Through multiple characterization experiments including equilibrium swelling measurements, differential scanning calorimetry (DSC) and scanning electron microscopy (SEM), the relationship between elastomer crosslink density and mechanical properties was systematically examined. This work provides valuable insights for the rational design of high-performance polymer materials.

---

1. Introduction

Polyurethane elastomers are a kind of important polymer materials and widely used in multiple fields, including aerospace, biomaterials, and green chemistry, due to their excellent properties.^1–4 In particular, superior mechanical performance is highly desired for the development of polyurethane materials. Polyurethane elastomers are typically synthesized using polyester or polyether polyols, diisocyanatos, chain extenders, and crosslinkers.^5–7 To date, toluene diisocyanate (TDI)-based polyurethanes are among the most widely used polymer materials due to their excellent properties and facile synthesis process. Any changes in formulations or process conditions can significantly affect the performance of polyurethane elastomers, particularly their mechanical properties.⁸ Understanding the relationship between formulations, synthesis conditions, and the mechanical properties of polyurethane is crucial for designing new materials with enhanced performance. Recently, the influences of the NCO/OH ratio (R-value), chain extenders, and crosslinkers on mechanical properties of polyurethanes based on single factor experiments have been reported.^9–12 It has been found that the tensile strength of polyurethane increases with the R-value, while the elongation at break decreases as the R-value rises. Additionally, crosslinkers influence the mechanical properties of polyurethane elastomers by altering the morphology from a linear structure to a crosslinked network.

Despite the large number of reports on formulations and preparation conditions, the critical factors affecting the mechanical properties of polyurethane elastomers are still not fully understood. Conventional research on polyurethane preparation and formulations typically relies on single-factor experiments, where one factor is varied at a time while keeping the other variables fixed. However, the overall properties of polyurethanes depend on the combined effects of multiple elements related to formulations and synthesis process. Hence, gaining an in-depth understanding of the role of all parameters is challenging due to the extensive experiments required by traditional single-factor experimental designs, making the design and process optimization of high-performance polyurethane synthesis a complex task.

Design of experiments (DOE) plays a crucial role in saving time and cost by reducing the number of necessary experiments. Moreover, it can be effectively used for modelling, analyzing, and optimizing the responses of multiple factors. The orthogonal design is a statistical technique that allows for the screening of significant factors affecting the response from multiple variables. It provides optimized conditions to achieve the most desirable performance without the need for conducting full-factorial experiments.¹³ The interactive effects of processing parameters on the performance of polyurethane elastomers have been previously investigated using orthogonal design;^14–16 however, orthogonal design is limited in its ability to capture nonlinear relationships. Recently, Response Surface Methodology (RSM) has become a widely used mathematical and statistical experimental design for modelling and optimizing experimental conditions. Through the strategic allocation of additional experimental points in critical regions, RSM enables accurate characterization of underlying nonlinear relationships between factors and response variables, while also facilitating the identification of optimal process parameters. In addition, response surface plots derived from the regression model provide visual support for analyzing the interactive effects among factors. RSM designs, including Central Composite Design (CCD) and Box–Behnken Design (BBD), are widely applied in various fields such as agriculture, biology, and chemistry.^17–21 BBD, which is more efficient than CCD for experiments involving three or four factors, has been widely applied to optimize the processing conditions of polyurethane elastomers.^22–26 Its integration with orthogonal design is expected to provide novel insights for more efficient and systematic process optimization.

To bridge the gap between the mechanical properties of TDI-based polyurethane and critical factors related to formulations and the synthesis process, we employed orthogonal design and Box–Behnken design to systematically investigate the effects of polyether, isocyanate, chain extender, and crosslinker – components commonly used in solid propellants – on the mechanical performance of TDI-based polyurethane. Fourier transform infrared (FTIR) and Raman spectroscopy identified that the consumption of NCO by OH is the predominant reaction step in the synthesis of polyurethane, confirming the critical roles of R-value, chain extender content, crosslinker content, and curing temperature. These factors were selected as the control parameters, while tensile strength and elongation at break of the elastomers were chosen as responses to evaluate the mechanical properties. First, a standard L₁₆ orthogonal array was employed for the orthogonal design with four factors and four levels to investigate the effects of process parameters on the mechanical properties of elastomers. The optimized parameters obtained from the orthogonal range analysis, which maximize tensile strength and elongation at break separately, were used as inputs for BBD. Next, two BBDs were performed based on the results of the orthogonal experiment, and the regression models were developed, along with response surface plots. The interactive effects of these factors were analyzed using the response surface plots, and the optimal conditions for maximum tensile strength and elongation were determined using the regression models. Finally, verification tests were conducted, confirming the validity of the experimental design. The predicted maximum tensile strength and elongation at break of the polyurethane are 14.34 MPa and 1103%, respectively, while the corresponding measured values are 14.67 MPa and 1160%.

2. Materials and methods

2.1. Materials

The bis-azidomethyl oxetane (BAMO) and tetrahydrofuran (THF) copolyether (PBT), with a number average molecular weight of 5100 and a hydroxyl value of 20.44 mg_KOH g⁻¹, was purchased from Liming Research Institute of Chemical Industry, China. Diethylene glycol (DEG) was sourced from Solarbio, China, while TDI and trimethylolpropane (TMP) were sourced from TCI, Japan.

2.2. Design of experiments

An orthogonal design was first used to quantify the individual effects of parameters and optimize the experimental conditions. Subsequently, two BBDs were performed based on the results of the orthogonal experiment to analyze the interactive effects of the parameters on the mechanical properties and to determine the optimal conditions for maximum tensile strength and elongation at break, respectively. Four key factors, including the R-value (A) the chain extension coefficient (B), the crosslinking coefficient (C), and the curing temperature (D), were selected as the controlled variables in the orthogonal design. The chain extension coefficient represents the molar ratio of OH in chain extender to the total OH (including all OH groups in the macrodiol, chain extender, and crosslinker), while the crosslinking coefficient represents the molar ratio of OH in the crosslinker to the total OH. Four levels were selected for each parameter, as shown in Table 1. A standard L₁₆ orthogonal array (Table 2) was employed based on the selected factors and levels. In the chosen coordinate system, the codes 1, 2, 3, and 4 correspond to level 1, level 2, level 3, and level 4, respectively.

Table 1 The parameters for four levels of selected factors

Factors	Level 1	Level 2	Level 3	Level 4
R-value, A	1.0	1.2	1.4	1.6
Chain extension coefficient, B (%)	0	20	40	60
Crosslinking coefficient, C (%)	0	10	20	30
Curing temperature, D (°C)	50	55	60	65

---

Table 2 L₁₆ orthogonal array of designed experiments based on coded levels

Trial	A	B	C	D	Trial	A	B	C	D
1	1	1	1	1	9	3	1	3	4
2	1	2	2	2	10	3	2	4	3
3	1	3	3	3	11	3	3	1	2
4	1	4	4	4	12	3	4	2	1
5	2	1	2	3	13	4	1	4	2
6	2	2	1	4	14	4	2	3	1
7	2	3	4	1	15	4	3	2	4
8	2	4	3	2	16	4	4	1	3

---

2.3. Preparation of elastomers

The polyurethane films were prepared using a two-step method. First, a calculated amount of TDI was added to PBT and stirred for 5 minutes, followed by a reaction period of 30 minutes to form an NCO-terminated prepolymer. Next, the chain extender and crosslinker were added to the prepolymer and mixed intensively for an additional 5 minutes. After a 30-minute resting period, the product was cast into Teflon molds, and degassing was performed under vacuum at 60 °C for at least 60 minutes. Finally, the prepared polyurethane mixture was cured for 7 days at a specific curing temperature.

2.4. Method of testing and characterization

The FTIR spectra were collected over a wavelength range of 4000 cm⁻¹ to 1000 cm⁻¹, with 32 scans per spectrum and a resolution of 1 cm⁻¹. The measurements were conducted in transmission mode using a PerkinElmer Spectrum 3 FT-IR/FT-NIR Spectrometer (USA). A Renishaw InVia Series Laser Micro-Raman Spectrometer was used to monitor the polyurethane (PU) polymerization process. The laser wavelength employed was 785 nm. Data were collected at intervals of 1 cm⁻¹ across the spectral range of 200 cm⁻¹ to 4000 cm⁻¹.

The tensile properties measurements of the polyurethane elastomers were performed according to the ASTM standard 412a. The standard dumbbell specimens were tested using an RGM-2020 universal testing machine at a constant rate of 100 mm min⁻¹. All the tests were repeated at least three times at room temperature (23 ± 2 °C) to ensure the reproducibility. The stress–strain curves, tensile strength, and elongation at break were obtained from the tensile tests to evaluate the mechanical properties of polyurethane elastomers.

Swelling measurements were carried out in toluene. Elastomers samples were weighted and immersed in toluene at 25 °C for 24 hours. They were then removed from the toluene, blotted, and reweighted to calculate the swelling ratio. The crosslink density of the elastomer was determined based on the swelling ratio. Differential scanning calorimetry (DSC) analysis was performed using a DSC-8500 differential scanning calorimeter (PerkinElmer Inc.) at a heating rate of 15 °C min⁻¹, within a temperature range of −80 °C to 20 °C. Fracture surface observations of the elastomer samples were conducted using a Helios G4 UC field emission scanning electron microscope (Thermo Fisher Scientific Inc.).

2.5. Determination of crosslink density

Crosslink density, defined as the number of moles of effective network chains per cubic meter, was calculated from the swelling ratios of the elastomers.²⁷ The swelling ratio (Q) was calculated using the weights of swollen and deswollen specimens, along with the densities of toluene and polyurethane, according to the following equation:where W₀ and W₁ are the elastomer samples weights before and after swelling, respectively; ρ_t is the density of the toluene, and ρ_p is the density of polyurethane elastomers density. The volume fraction of the polymer in the swollen gel (V₂) is calculated using the following equation:

The crosslink density (V_e) were obtained from V₂ using Flory–Rehner equation:²⁸

V_e = −[ln(1 − V₂) + V₂ + χV₂²]/V₁(V₂^1/3 − V₂/2) (3)

where V₁ is the molar volume of the solvent, and χ is the Flory–Huggins polymer–solvent interaction parameter.

3. Results and discussion

3.1. Mechanism of the curing reaction

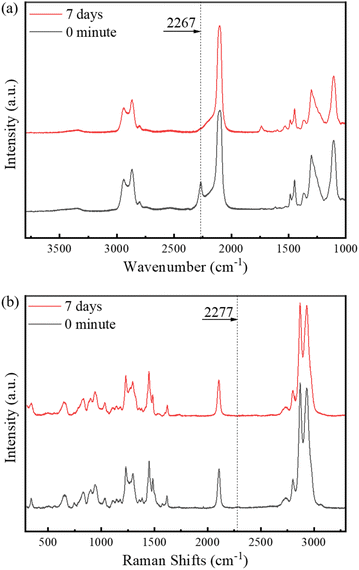
To explore the curing reaction mechanism of TDI-based polyurethane, we performed FTIR and Raman spectroscopy characterizations of the PBT-TDI reactant mixture before the reaction (denoted as 0 min) and the polyurethane product after curing at 60 °C for seven days (denoted as 7 days). The results are presented in Fig. 1. The peak at 2267 cm⁻¹ in the FTIR spectrum is attributed to the NCO functional group of TDI. As shown in Fig. 1a, after seven days of curing, the intensity of the NCO peak at 2267 cm⁻¹ significantly decreased compared to that at the reaction starting point. This observation indicates that the reaction between NCO and OH, which is predominantly influenced by the concentrations of NCO- and OH-containing chemicals as well as the reaction temperature, plays a pivotal role in the synthesis of TDI-based polyurethane. In Fig. 1b, the Raman peak at 2277 cm⁻¹ corresponds to the NCO functional group of TDI, and this peak almost completely disappears after seven days of curing, consistent with the FTIR results. Thus, we confirm that the NCO/OH ratio, reaction temperature, chain extension coefficient, and crosslinking coefficient that govern the reaction between NCO and OH are crucial factors influencing the performance of the polyurethane. Consequently, these parameters are identified as key targets for optimizing the synthesis process using orthogonal testing and RSM design.

Fig. 1 FTIR (a) and Raman (b) spectra of the samples with reaction time of 0 min and 7 days.

3.2. Orthogonal test results and range analysis

Based on FTIR and Raman results, R-value (A), the chain extension coefficient (B), the crosslinking coefficient (C), and the curing temperature (D) were selected as the controlled variables in the orthogonal design. Table 3 represents the results of orthogonal test and the corresponding range analysis. In the range analysis, two key parameters are considered: K_ji and R_j. K_ji is defined as the sum of the evaluate indexes of all levels (i = 1, 2, 3, 4) within each factor (j = A, B, C, D), while k_ji (the average value of K_ji) is used to determine the optimal level and combination of factors. The optimum level for each factor is identified when k_ji is at its maximum. R_j is defined as the range between the maximum and minimum values of k_ji, and it evaluates the relative influence sequence of each factor on the evaluate indexes. A larger R_j indicates a more significant impact of that factor. Based on the range analysis in Table 3, the influence sequence of the parameters and the optimized formula were determined.

Table 3 Orthogonal test and range analysis results^a

Trial	Tensile strength (MPa)	Elongation at break (%)	Range analysis	A	B	C	D
a A, B, C, D refer to R-value, the chain extension coefficient, the crosslinking coefficient, and curing temperature respectively. R, k are the range analysis parameters for tensile strength. R′, k′ are the range analysis parameters for elongation at break.
1	0.74	910	k1	3.06	0.77	2.24	1.93
2	0.78	557	k2	3.57	1.00	1.70	3.16
3	1.60	728	k3	1.75	1.88	3.21	2.52
4	9.12	547	k4	2.33	7.07	3.57	3.11
5	0.86	420	R	1.82	6.3	1.87	1.23
6	0.84	440		686	669	1025	1338
7	2.82	838		723	784	867	992
8	9.76	1193		1115	891	1041	731
9	0.70	581		1067	1246	657	528
10	1.59	478	R′	429	577	384	810
11	1.33	1454
12	3.37	1945
13	0.76	765
14	0.77	1660
15	1.77	545
16	6.03	1297

---

For the tensile strength of polyurethane elastomers, the sequence of R_j values is as follows: R_B (6.3) > R_C (1.87) > R_A (1.82) > R_D (1.23), indicating that the chain extension coefficient is the most influential factor, followed by the crosslinking coefficient, while the curing temperature has the least influence in the orthogonal test. Regarding the optimum levels for each factor, the sequences are as follows: k_A2 > k_A1 > k_A4 > k_A3, k_B4 > k_B3 > k_B2 > k_B1, k_C4 > k_C3 > k_C1 > k_C2, and k_D2 > k_D4 > k_D3 > k_D1. Based on these sequences, the optimum combination of parameters for achieving the maximum tensile strength would be A₂B₄C₄D₂, corresponding to an R-value of 1.2, a chain extension coefficient of 60%, a crosslinking coefficient of 30%, and a curing temperature of 55 °C.

To evaluate the reliability of the optimized parameters, a validation experiment was conducted. Tensile specimens were prepared under the optimal conditions for the maximum tensile strength identified in the orthogonal experiments (trail no. 8, A₂B₄C₃D₂) and the optimized parameter settings (A₂B₄C₄D₂). The corresponding stress–strain curves are shown in Fig. 2a. The results show that the tensile strength of the elastomer manufactured under the optimized conditions is higher than that produced under the conditions of trail no. 8. This confirms the validity of the orthogonal test results and the range analysis conducted in this study. Therefore, the optimum conditions for achieving maximum tensile strength is A₂B₄C₄D₂, corresponding to an R-value of 1.2, a chain extension coefficient of 60%, a crosslinking coefficient of 30%, and a curing temperature of 55 °C.

Fig. 2 Validation experiment results of the optimum conditions for maximum tensile strength (a) and maximum elongation at break (b).

For the elongation at break of polyurethane elastomers, the sequence of values is as follows: . Contrary to the findings for tensile strength, 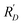is the largest, indicating that curing temperature is the most influential factor for elongation at break. The chain extension coefficient ranks as the second most important factor, followed by the R-value in third place, with the crosslinking coefficient being the least significant factor. Regarding the optimum levels, the sequences are as follows: , , , and . Therefore, the optimum combination of parameters for achieving the maximum elongation at break is A₃B₄D₁C₁ or C₃, corresponding to an R-value of 1.4, a chain extension coefficient of 60%, a crosslinking coefficient of 0 or 20%, and a curing temperature of 50 °C. Significantly, the values of 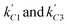are approximately equal, suggesting that the contributions of these two crosslinker concentrations to the elongation at break are similar. To refine the selection of the optimum conditions and verify the reliability of these optimized parameters, a supplementary experiment is necessary.

Elastomer specimens were prepared under the optimal condition for the maximum elongation at break in the orthogonal experiments (trail no. 12, A₃B₄C₂D₁) and the optimized parameter settings (A₃B₄C₁D₁ and A₃B₄C₃D₁). The difference between these three process parameters is the crosslinking coefficient, which is set at 0, 10%, and 20%, respectively. The stress–strain curves of these three different elastomers are compared in Fig. 2b. The elongation at break of the elastomer prepared under the conditions of A₃B₄C₁D₁ is higher than that of the others, implying that the introduction of the crosslinker reduces the elongation at break of the polyurethane elastomers. Therefore, the optimum conditions for maximum elongation at break is A₃B₄D₁C₁, corresponding to an R-value of 1.4, a chain extension coefficient of 60%, a crosslinking coefficient of 0, and a curing temperature of 50 °C.

3.3. Box–Behnken design for tensile strength

3.3.1. BBD results and regression model. After determining the optimized parameters for maximum tensile strength through the orthogonal design, a BBD was employed to investigate the effects of the independent variables, including the R-value (X₁), chain extension coefficient (X₂), crosslinking coefficient (X₃), and curing temperature (X₄), on the tensile strength of polyurethane elastomers. The experimental ranges and coded levels of the independent variables, selected based on the results of the orthogonal experiments for the maximum tensile strength, are listed in Table 4. “−1”, “0”, and “1” in this table represent the low, middle, and high levels of each factor, respectively. The experimental design and corresponding response data are presented in Table 5. The creation of the design matrix and analysis of the experimental data were performed using Design Experts 8.0.6 software. A quadratic regression model was developed using the software to identify optimal parameters for tensile strength optimization in polyurethane elastomers. The coded-variable model is mathematically expressed as:

Tensile strength = 9.54 + 1.85X₁ + 0.89X₂ + 0.51X₃ + 0.90X₄ + 0.45X₁X₂ − 0.92X₁X₃ + 0.52X₁X₄ − 0.45X₂X₃ − 0.24X₂X₄ − 0.027X₃X₄ − 0.15X₁² − 0.39X₂² − 0.52X₃² + 0.61X₄² (4)

Table 4 Factors and their levels in Box–Behnken design

Factors	Levels
	Low (−1)	Medium (0)	High (1)
X1	1.1	1.2	1.3
X2	57.5	60	62.5
X3	27.5	30	32.5
X4	52.5	55	57.5

---

Table 5 Box–Behnken design arrangement on ceded levels and the responses

Trail	X1	X2	X3	X4	Response tensile strength (MPa)
1	0	0	0	0	10.01
2	−1	−1	0	0	7.65
3	0	0	1	1	11.92
4	0	0	0	0	10.40
5	0	0	−1	−1	9.08
6	0	0	1	−1	10.04
7	0	0	0	0	10.37
8	1	−1	0	0	10.27
9	−1	1	0	0	8.63
10	1	1	0	0	13.04
11	0	0	−1	1	11.07
12	−1	0	0	−1	7.21
13	0	0	0	0	9.23
14	0	1	1	0	9.01
15	0	0	0	0	9.43
16	0	−1	−1	0	6.20
17	−1	0	0	1	8.04
18	0	−1	1	0	8.01
19	0	0	0	0	8.95
20	1	0	0	1	12.65
21	1	0	0	−1	9.76
22	0	1	−1	0	8.99
23	0	−1	0	1	9.67
24	1	0	−1	0	10.85
25	0	1	0	−1	9.66
26	0	0	0	0	8.84
27	0	0	0	0	9.76
28	−1	0	1	0	8.06
29	0	0	0	0	8.83
30	−1	0	−1	0	5.00
31	1	0	1	0	10.23
32	0	1	0	1	10.78
33	0	−1	0	−1	7.59

---

Analysis of variance (ANOVA) was employed to assess the goodness of fit for the regression models, with detailed results for tensile strength responses presented in Tables 6 and 7. The statistical significance of the response surface model is confirmed by both P-value and F-value in the ANOVA analysis. With the model's P-value less than 0.0001 (Table 6), it demonstrates high statistical significance, while the lack-of-fit P-value higher than 0.05 indicates acceptable model adequacy. Among the investigated variables, X₁ (R-value) emerges as the dominant factor affecting tensile strength, evidenced by its exceptionally high F-value (499.27) and statistically significant P-value (<0.0001). The coefficient of determination (R²) presented in Table 7 quantifies the proportion of variance in tensile strength explained by the model relative to the total variance, while also serving as an indicator of agreement between experimental measurements and model predictions. Higher R² values correspond to greater predictive accuracy, reflecting closer alignment between model outputs and actual experimental results. The R² in this work is 0.9830, indicating that 98.30% of the variance in the response variable is accounted for by the model. This demonstrates the model's high predictive reliability for tensile strength within the investigated experimental parameter range. An R_adj² value of 0.9681 demonstrates acceptable model goodness-of-fit. Combined with a low standard deviation (0.29) and coefficient of variation (CV = 3.06%), these statistical parameters collectively confirm the model's robust predictive capability and a high degree of experimental reproducibility.

Table 6 ANOVA results of Box–Behnken design for tensile strength

Source	DF	SS	MS	F-Value	P-Value
Block	2	12.2	6.1
Model	14	76.18	5.44	66.09	<0.0001
X1-R	1	41.11	41.11	499.27	<0.0001
X2-DEG%	1	9.58	9.58	116.31	<0.0001
X3-TMP%	1	3.08	3.08	37.42	<0.0001
X4-T	1	9.7	9.7	117.84	<0.0001
X1X2	1	0.8	0.8	9.73	0.0066
X1X3	1	3.39	3.39	41.12	<0.0001
X1X4	1	1.06	1.06	12.89	0.0025
X2X3	1	0.8	0.8	9.73	0.0066
X2X4	1	0.23	0.23	2.8	0.1138
X3X4	1	3.03 × 10^−3	3.03 × 10^−3	0.037	0.8504
X1^2	1	0.18	0.18	2.15	0.1621
X2^2	1	1.15	1.15	13.93	0.0018
X3^2	1	2.04	2.04	24.8	0.0001
X4^2	1	2.79	2.79	33.94	<0.0001
Residual	16	1.32	0.082
Lack of fit	10	0.54	0.054	0.41	0.8966
Pure error	6	0.78	0.13
Cor total	32	89.7

---

Table 7 Statistical parameters estimated from ANOVA

Statistical parameter	Value	Statistical parameter	Value
Std. dev	0.29	R^2	0.9830
Mean	9.37	Adj R^2	0.9681
CV%	3.06	Pred R^2	0.9432
Press	4.40	Adeq precision	37.874

---

Fig. 3 compares the predicted tensile strength from the quadratic response model with experimental measurements. The close alignment between predicted and experimental values demonstrates the model's accuracy in representing the relationship between processing parameters and tensile strength. This agreement confirms the model's reliability for predicting mechanical performance within the studied experimental ranges.

Fig. 3 Tensile strength of elastomers obtained in the experiment versus predicted by the model.

3.3.2. Analysis of response surface. Three-dimensional response surfaces were generated from the quadratic regression model to investigate the interaction among the variables. The regression model equation is visualized through three-dimensional plots of the response versus two factors, with the other two factors held constant. Fig. 4a illustrates the effects of the R-value and chain extension coefficient on tensile strength, with a constant crosslinking coefficient of 30% and curing temperature of 55 °C. Both the R-value and chain extension coefficient positively influence tensile strength, with an increase in either factor leading to higher tensile strength. The change in tensile strength due to variations in the R-value is greater than that observed for changes in the chain extension coefficient, indicating that the R-value has a more significant impact on strength.

Fig. 4 Three-dimensional response surface plots of the effect of process parameters on tensile strength of polyurethane elastomers: (a) R-value and chain extension coefficient (b) R-value and curing temperature (c) chain extension coefficient and curing temperature (d) R-value and crosslinking coefficient (e) chain extension coefficient and crosslinking coefficient (f) crosslinking coefficient and curing temperature.

Fig. 4b shows a three-dimensional plot illustrating the effect of R-value and curing temperature on tensile strength, with the chain extension coefficient held constant at 60% and the crosslinking coefficient at 30%. As shown in the graph, the tensile strength of the elastomer increases with increasing R-value and curing temperature. Similarly, Fig. 4c illustrates the interaction between the chain extension coefficient and curing temperature, with other conditions held constant. As shown, the tensile strength of the elastomer reaches its highest value when both the chain extension parameter and curing temperature are at their maximum values.

Fig. 4a–c clearly demonstrate a net positive interactive effect among the R-value, chain extension coefficient, and curing temperature when the crosslinking coefficient is held constant. Moreover, the impact of the R-value and chain extension coefficient on enhancing the elastomer's strength is more pronounced. This behavior can be attributed to the increased crosslink density and the higher content of hard segments in the polyurethane elastomers. The increase in R-value results in a higher concentration of free NCO groups, which react to form three-dimensional allophanate, thereby enhancing the crosslink density. Additionally, the increased crosslinking contributes to changes in morphology, which improves tensile strength. On the other hand, the hard segment, formed by the diisocyanate, chain extender, and crosslinker, increases with the rising R-value and chain extension coefficient. The hard segments strengthen intermolecular interactions, thereby improving the tensile strength of polyurethane elastomers.

Fig. 4d illustrates the interactive effect of R-value and crosslinking coefficient on tensile strength, with a constant chain extension coefficient of 60% and curing temperature of 55 °C. As shown in the figure, the influence of crosslinking coefficient on elastomer strength exhibits distinct variation trends under different R-values. When the R-value is 1.1, the elastomer strength increases with rising crosslinking coefficient. Conversely, at an R-value of 1.3, the strength shows a monotonic decrease with increasing crosslinking coefficient. For intermediate R-value between 1.1 and 1.3, the strength initially increases then subsequently decreases with crosslinking coefficient elevation. This pattern demonstrates that the synergistic enhancement effect through simultaneous increases in both R-value and crosslinking coefficient has limited effectiveness in strength improvement, highlighting the importance of optimizing both the R-value and crosslinking coefficient for enhanced material performance.

Fig. 4e illustrates the synergistic interaction between chain extension coefficient and crosslinking coefficient on tensile strength with other conditions held constant. The data demonstrate a positive correlation between chain extension coefficient elevation and enhanced tensile strength in polyurethane elastomers. Concurrently, crosslinking coefficient augmentation initially improves mechanical performance, but beyond optimal levels induces progressive strength deterioration. Fig. 4f reveals the interactive effects between crosslinking coefficient and curing temperature on tensile strength. Similarly, the tensile strength of the elastomer demonstrates an initial increase followed by a progressive decline with ascending crosslinking coefficient, suggesting that excessive crosslinkers incorporation would adversely affect the strength enhancement of elastomers.

Fig. 4d–f demonstrate the detrimental effects of excessive crosslinker on elastomer tensile strength, resulting from increased crosslinker dosage that elevates both crosslink density and hard segment content. While higher crosslinker content normally enhances the crosslinking network (improving tensile strength through structural rigidity), the concurrent reduction in soft segment content compromises the material's elastomeric character and ductility. Furthermore, the intensified crosslinking network restricts soft segment mobility, diminishing slip capability and reducing ductility. Consequently, when crosslinking exceeds a critical threshold, the decreased elongation and ductility progressively counteract tensile strength enhancement, eventually causing strength reduction. This fundamental trade-off between crosslinking reinforcement and flexibility loss dictates that excessive crosslinking induces brittleness, ultimately impairing mechanical performance.

3.3.3. Verification test. The BBD regression model identifies optimal processing parameters for maximizing polyurethane elastomer tensile strength as: an R-value of 1.3, a chain extension coefficient of 62.5%, a crosslinking coefficient of 27.67%, and a curing temperature of 57.5 °C. Specimens fabricated under these conditions yielded a measured tensile strength of 14.67 MPa, closely matching the model's prediction of 14.34 MPa with an error of 2.2%. This strong agreement between predicted and experimental values validates the regression model's accuracy and confirms the experimental design's reliability in forecasting tensile strength within the defined parameter ranges.

3.4. Box–Behnken design for elongation at break

3.4.1. BBD results and regression model. The second BBD employed in this study involved 15 experimental runs, with the R-value (Y₁), chain extension coefficient (Y₂), and curing temperature (Y₃) as the independent variables. The experimental ranges and coded levels of these variables were determined based on the results of the orthogonal experiments aimed at maximizing the elongation at break (Table 8). “−1”, “0”, and “1” in the table correspond to the low, middle, and high levels of the factors, respectively. The 15 experimental runs and the corresponding response data are provided in Table 9. The design matrix creation and subsequent analysis of the experimental data were performed using Design Expert 8.0.6 software. The quadratic regression model for elongation at break, expressed in terms of the coded parameters, is given by the following equation:

Elongation at break = 992.33 + 25Y₁ + 80.75Y₂ − 53.75Y₃ − 0.75Y₁Y₂ − 18.75Y₁Y₃ + 8.25Y₂Y₃ − 31.79Y₁² + 16.21Y₂² − 75.29Y₃² (5)

Table 8 Factors and their levels in Box–Behnken design

Factors	Levels
	Low (−1)	Medium (0)	High (1)
Y1	1.3	1.4	1.5
Y2	50	60	70
Y3	47.5	50	52.5

---

Table 9 Box–Behnken design arrangement on coded levels and the responses

Trail	Y1	Y2	Y3	Response elongation at break (%)
1	0	0	0	1004
2	−1	0	1	819
3	1	1	0	1083
4	−1	−1	0	869
5	0	−1	−1	902
6	0	0	0	957
7	−1	1	0	1027
8	0	0	0	1017
9	0	1	1	981
10	1	−1	0	928
11	0	−1	1	798
12	−1	0	−1	909
13	0	1	−1	1052
14	1	0	−1	989
15	1	0	1	824

---

The ANOVA analysis for elongation at break in Table 10 demonstrates statistical significance with a model P-value of 0.0022 (less than 0.05). Significant contributors include the Y₁, Y₂, Y₃, and Y₃² terms. The lack of fit test yielded an F-value of 0.31, indicating no significant deviation from pure error variation (82.07% probability of noise-induced variation). The regression model ANOVA results presented in Table 11 demonstrate an R² value of 0.9726, indicating that 97.26% total variation in elongation yield was attributed to the experimental variables. This strong correlation between experimental measurements and model predictions (Fig. 5) demonstrates adequate model fit. The close agreement between R_pred² (0.8187) and R_adj² (0.9233) further confirms appropriate model adjustment. Acceptable precision was evidenced by low standard deviation and coefficient of variation (CV%), confirming experimental reliability.

Table 10 ANOVA results of Box–Behnken design for elongation at break

Source	DF	SS	MS	F-Value	P-Value
Model	9	1.08 × 10^5	11 947.17	19.73	0.0022
Y1-R	1	5000	5000	8.26	0.0348
Y2-DEG%	1	52 164.5	52 164.5	86.16	0.0002
Y3-T	1	23 112.5	23 112.5	38.18	0.0016
Y1Y2	1	2.25	2.25	3.72 × 10^−3	0.9538
Y1Y3	1	1406.25	1406.25	2.32	0.188
Y2Y3	1	272.25	272.25	0.45	0.5322
Y1^2	1	3731.85	3731.85	6.16	0.0557
Y2^2	1	970.01	970.01	1.6	0.2614
Y3^2	1	20 931.08	20 931.08	34.57	0.002
Residual	5	3027.17	605.43
Lack of fit	3	962.5	320.83	0.31	0.8207
Pure error	2	2064.67	1032.33
Cor total	14	1.11 × 10^5

---

Table 11 Statistical parameters estimated from ANOVA

Statistical parameter	Value	Statistical parameter	Value
Std. dev	24.61	R^2	0.9726
Mean	943.87	Adj R^2	0.9233
CV%	2.61	Pred R^2	0.8187
Press	20 045.50	Adeq precision	14.497

---

Fig. 5 Elongation at break of elastomers obtained in the experiment versus predicted by the model.

3.4.2. Analysis of response surface. Three-dimensional response surfaces were generated to investigate the interaction among the variables and to determine the optimal conditions for maximizing elongation at break. Fig. 6a depicts the combined effects of R-value and chain extension coefficient on elongation at break at a fixed curing temperature of 50 °C. As shown in the figure, the elastomer's elongation at break initially increases then decreases with rising R-value, indicating excessive curing agent content. The surplus curing agent elevates crosslink density, thereby restricting molecular chain mobility and inducing material embrittlement. Conversely, elongation at break demonstrates continuous enhancement with increasing chain extender coefficient, attributed to the improved flexibility of soft segments through chain extender incorporation. Notably, variations in the chain extension coefficient induce greater elongation at break modifications compared to R-value adjustments, indicating that the chain extension coefficient has a more significant impact on elongation.

Fig. 6 Three-dimensional response surface plots of the effect of process parameters on elongation at break of polyurethane elastomers: (a) R-value and chain extension coefficient (b) R-value and curing temperature (c) chain extension coefficient and curing temperature.

Fig. 6b depicts the combined effects of R-value and curing temperature on elongation at break at a constant chain extender coefficient. The curing temperature demonstrates a volcano-shaped relationship with elastomer elongation at break, exhibiting maximum performance at 49 °C. Below this critical temperature, delayed curing kinetics lead to incomplete molecular chain alignment and heterogeneous hard segment distribution, causing localized fracture initiation. Controlled temperature elevation enhances phase-segregated structural uniformity, thereby optimizing ductility. Conversely, temperatures exceeding 49 °C induce detrimental over-crosslinking and hard segment crystallization that restrict molecular mobility, increasing brittleness. Fig. 6c delineates the synergistic interplay between chain extender coefficient and curing temperature governing elongation at break. Similarly, the elongation of the elastomer demonstrates an initial increase followed by a progressive decline with ascending curing temperature, highlighting the critical need for coordinated thermal-stoichiometric control in performance optimization.

3.4.3. Verification test. Through the BBD regression model, the optimal parameters for maximizing polyurethane elastomer elongation at break were identified as an R-value of 1.45, chain extension coefficient of 70%, and curing temperature of 49.09 °C. The specimens fabricated under optimized conditions exhibited an elongation at break of 1160%, showing excellent consistency with the predicted value of 1103% (error of 4.9%). This close agreement validates the model's predictive accuracy and experimental design efficacy.

3.5. Correlation of crosslink density with mechanical properties

The crosslink density of the polyurethane elastomers was determined through equilibrium swelling experiments. Fig. 7a demonstrates a strong correlation between crosslink density and the mechanical properties of the elastomers prepared in the BBD experiment of tensile strength. The results indicate that as crosslink density increases, tensile strength rises while elongation at break decreases. This strength enhancement can be attributed to the increasing complexity of the crosslinking network, which enhances the elastomer's ability to withstand larger loads. The DSC curves show that elastomers with higher crosslink density exhibit a higher glass transition temperature, indicating a reduction in internal free volume and decreased polymer chain segment mobility (Fig. 7b). This suggests that the inclusion of crosslinkers restricts the mobility of the soft segments, thereby reducing the elongation at break. SEM results further reveal that as crosslink density increases, numerous cracks appear on the fracture surface of the sample, indicating that a higher crosslink density makes the film more rigid and brittle (Fig. 8). These observations suggest that while increased crosslink density significantly improves the strength of the material, it also reduces its toughness, which explains the observed decrease in elongation at break.

Fig. 7 Relationship of crosslink density and mechanical properties of elastomers prepared in the BBD experiment of tensile strength (a) and the DSC curves of the elastomers with the lowest and highest crosslink densities (b).

Fig. 8 SEM images of the sample with crosslink density of 723.1 mol m⁻³ (a) and 2293.5 mol m⁻³ (b).

The correlation between the crosslink density and the mechanical properties of the elastomers prepared in the BBD experiment with respect to elongation at break is illustrated in Fig. 9a. The tensile strength increases with increasing crosslink density, while the elongation at break remains constant, exhibiting no apparent dependence on crosslink density. This behaviour can be attributed to variations in the hard segment content within the polyurethane elastomer, as the mechanical properties of linear polyurethane are significantly influenced by the proportion of hard segments. Fig. 9b illustrates the relationship between the elastomer's mechanical properties and its hard segment content. A clear linear increase in tensile strength is observed with rising hard segment content, while the elongation at break shows no consistent trend. In linear polyurethane systems, hard segment microdomains serve as anchor points. Increasing the hard segment content facilitates the formation of these microdomains, and a sufficiently high content can further promote hard segment crystallization, thereby enhancing the elastomer's resistance to deformation. Within the elastomer, the hard segment microdomains along with hydrogen-bonding interactions create a physical crosslinking network. Unlike chemical crosslinking, this physical network has limited influence on the elastomer's extensibility. Consequently, the elongation at break remains largely unaffected by changes in crosslink density.

Fig. 9 Correlation of mechanical properties with (a) crosslink density and (b) hard segment content in elastomers prepared in the BBD experiment of elongation at break.

4. Conclusions

In this work, a combined approach utilizing orthogonal design and response surface methodology (RSM) was employed to optimize the synthesis process and mechanical performance for polyurethane elastomers. Using FTIR and Raman spectroscopy, we confirm that the NCO/OH ratio, reaction temperature, chain extension coefficient, and crosslinking coefficient that govern the reaction between NCO and OH are crucial factors influencing the performance of the polyurethane, and these parameters are identified as key targets for optimizing the synthesis process. A standard L₁₆ orthogonal design with range analysis was employed to conduct preliminary screening of optimized process combinations for polyurethane mechanical properties across a broad range of process conditions. The results revealed that the chain extension coefficient had the most significant impact on tensile strength, while curing temperature predominantly influenced the elongation at break. Based on the orthogonal design results, two more refined BBDs were employed to analyze the interactive effects of the parameters on the mechanical properties and to obtain the optimal conditions for maximum tensile strength and elongation at break. Three-dimensional response surface plots indicated a net positive interaction between the R-value, chain extension coefficient, and curing temperature on tensile strength. Furthermore, tensile strength initially increased and then decreased as the crosslinking coefficient increased. The optimal conditions for the predicted maximum tensile strength (14.34 MPa) are determined to be an R-value of 1.3, chain extension coefficient of 62.5%, crosslinking coefficient of 27.67%, and curing temperature of 57.5 °C. For the predicted highest elongation at break (1103%), the optimal conditions are an R-value of 1.45, chain extension coefficient of 70%, and curing temperature of 49.09 °C. Verification tests showed that high-performance polyurethanes with a tensile strength of 14.67 MPa and an elongation at break of 1160% were experimentally achieved using the optimal conditions. The experimental values (14.67 MPa and 1160%) are in close agreement with the predicted values (14.34 MPa and 1103%, error of 2.2% and 4.9%, respectively), confirming the accuracy of the regression model and the appropriateness of the experimental design. Thus, this combined approach of orthogonal design and RSM enables efficient and precise optimization of processing conditions to enhance the mechanical performance of polyurethane. Finally, the structure–performance relationship of the polyurethane was revealed through swelling measurements, DSC analysis, and SEM characterization. The volcano-shaped relationship observed between tensile strength and the crosslinking coefficient suggests an inherent limitation in the ability of crosslinkers to enhance the performance of polyurethane. This work provides an efficient and reliable strategy for optimizing the synthesis process of TDI-based polyurethane elastomers. The formation of the polyurethane network structure in polyol-isocyanate systems is fundamentally governed by the reaction between OH and NCO groups. Accordingly, the formulation/processing-structure–property relationships established in this study for the PBT-TDI polyurethane system can offer valuable insights for understanding other polyol-isocyanate systems. Furthermore, the mechanical performance optimization strategy proposed here can serve as a general framework for the rational design of high-performance polyurethane materials.

Data availability

All the data that support the findings of this study are included in the manuscript.

Author contributions

Tian-Jiao Hong: data curation, formal analysis, investigation, methodology, writing – original draft. Yan Kang: conceptualization, data curation. Peng-Fei Tian: methodology, supervision, writing – review and editing. Fu-Zhen Xuan: funding acquisition, project administration, supervision.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

The authors are grateful to the support from the Basic Research Program of Science and Technology Commission of Shanghai Municipality (22JC1400600), the National Natural Science Foundation of China (22178110), and the Shanghai Rising-Star Program (23QA1402400).

References

1. Y. Jia, L. Zhang, M. Qin, Y. Li, S. Gu, Q. Guan and Z. You, Chem. Eng. J., 2022, 430, 133081.
2. L. Wan, C. Deng, H. Chen, Z.-Y. Zhao, S.-C. Huang, W.-C. Wei, A.-H. Yang, H.-B. Zhao and Y.-Z. Wang, Chem. Eng. J., 2021, 417, 129314.
3. S.-J. Wang, C.-Y. Lu, S.-H. Huang and D. S.-H. Wong, Chem. Eng. Process., 2020, 149, 107827.
4. G. Rossignolo, G. Malucelli and A. Lorenzetti, Green Chem., 2024, 26, 1132–1152.
5. J. Ma, B. Deng, Y. Fan, X. Huang, D. Chen, Y. Ma, H. Chen, A. L. Grzesiak and S. Feng, Polym. Chem., 2022, 13, 5159–5168.
6. P. K. Behera, K. Usha, P. Guchhait, D. Jehnichen, A. Das, B. Voit and N. K. Singha, RSC Adv., 2016, 6, 99404–99413.
7. H. Shi, W. Zhou, Z. Wen, W. Wang, X. Zeng, R. Sun and L. Ren, Mater. Horiz., 2023, 10, 928–937.
8. V. Sekkar, S. Gopalakrishnan and K. Ambika Devi, Eur. Polym. J., 2003, 39, 1281–1290.
9. S. B. Haska, E. Bayramli, F. Pekel and S. Özkar, J. Appl. Polym. Sci., 1997, 64, 2347–2354.
10. N. Akram, S. Saleem, K. M. Zia, M. Saeed, M. Usman, S. Maqsood, N. Mumtaz and W. G. Khan, J. Polym. Res., 2021, 28, 1–15.
11. M. Yarmohammadi, S. Komeili and M. Shahidzadeh, Propellants, Explos., Pyrotech., 2018, 43, 156–161.
12. J. Hu, R. Yang, L. Zhang, Y. Chen, X. Sheng and X. Zhang, Polymer, 2021, 222, 123674.
13. M. Joulazadeh and A. H. Navarchian, Polym. Adv. Technol., 2010, 21, 263–271.
14. H.-Y. Mi, X. Jing, J. Peng, L.-S. Turng and X.-F. Peng, J. Cell. Plast., 2013, 49, 439–458.
15. Y. El-Shekeil, S. Sapuan, M. Azaman and M. Jawaid, Adv. Mater. Sci. Eng., 2013, 2013.
16. X. Guo, L. Wang, S. Li, X. Tang and J. Hao, J. Mater. Cycles Waste Manage., 2015, 17, 560–565.
17. A. Karadag, X. Yang, B. Ozcelik and Q. Huang, J. Agric. Food Chem., 2013, 61, 2130–2139.
18. A. Khodaei, R. Bagheri, H. R. M. Hosseini and E. Bagherzadeh, Eur. Polym. J., 2019, 120, 109197.
19. A. Abbasi, M. M. Nasef, W. Z. N. Yahya, M. Moniruzzaman and A. S. M. Ghumman, Eur. Polym. J., 2021, 143, 110202.
20. A. Hosseinzadeh, A. Altaee, I. Ibra and J. L. Zhou, Chem. Eng. Process., 2024, 110140.
21. X. Xiao, C.-Z. Wang, J. Bian and R.-C. Sun, RSC Adv., 2015, 5, 106219–106226.
22. D. Zhao, G. Wang and M. Wang, J. Appl. Polym. Sci., 2018, 135, 46327.
23. M. Fittipaldi, L. A. Rodriguez, A. Damley-Strnad and L. R. Grace, Mater. Des., 2015, 86, 6–13.
24. A. Agić and E. G. Bajsić, J. Appl. Polym. Sci., 2007, 103, 764–772.
25. R. Hasanzadeh, P. Mojaver, A. Chitsaz, M. Mojaver and M. A. Rosen, Chem. Eng. Process., 2022, 176, 108961.
26. C. Aseibichin, W. C. Ulakpa, I. Omenogor, E. Doyah, A. A. Olaseinde, O. C. Anakpoha, M. Keke and S. Karuppannan, RSC Adv., 2024, 14, 11784–11796.
27. H. Oikawa and K. Murakami, Rubber Chem. Technol., 1987, 60, 579–590.
28. P. J. Flory and J. Rehner, J. Chem. Phys., 1943, 11, 521–526.

---