Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Shape-directed modification of truncated octahedral to coffin-like cobalt-doped ferrite particles by changing the hydrothermal reaction conditions†
Maria Weißpflog *a,
Dietmar Eberbeckb and
Birgit Hankiewicz
*a,
Dietmar Eberbeckb and
Birgit Hankiewicz *a
*a
aInstitute of Physical Chemistry, University of Hamburg, Grindelallee 117, 20146 Hamburg, Germany. E-mail: maria.weisspflog@uni-hamburg.de; birgit.hankiewicz@uni-hamburg.de
bPhysikalisch-Technische Bundesanstalt (PTB), Abbestraße 2-12, 10587 Berlin, Germany
First published on 7th July 2025
Abstract
Truncated octahedral cobalt ferrite-based nanoparticles were synthesised using a precursor-derived coprecipitation reaction followed by a hydrothermal step. The nanoparticles were characterised regarding their shape anisotropy and size distribution as a function of reaction parameters such as time, temperature, metal salt concentration, base molarity, pressure, and reactor filling volume. Notably, temperature and molarity serve as critical synthesis factors that reduce the polydispersity of the particles to values below 0.1, which is an exceptionally favourable result compared to aqueous coprecipitation reactions. Furthermore, an increase in filling volume resulted in higher proportions of coffin-like nanoparticles due to alterations in flow velocity. The crystallographic assignment of the nanoparticle facets was analysed using high-resolution transmission electron microscopy, selected area diffraction, and angle-resolved scanning electron microscopy measurements. This analysis revealed that the {222} facet exhibited preferential growth in the coffin-like particles. By elucidating the significant reaction parameters for enhanced shape anisotropy, it is possible to increase the magnetic anisotropy constants by assuming a prolate spheroid structure with uniaxial shape combined with cubic magnetocrystalline anisotropy. Contributions of the strain and surface anisotropy are discussed briefly to ensure a comprehensive overview.
1 Introduction
Cobalt ferrite (CoxFe3−xO4, CF) is extensively studied for its unique physical, chemical, and magnetic properties, e.g., high chemical stability, remarkable catalytic activity, and large magneto-crystalline anisotropy.1–4 Consequently, CF exhibits a wide range of applications as gas sensors,5 adsorbent materials for dyes and metal ions,6–8 ferrofluid components in electronic devices,9 heating elements for magnetic hyperthermia,10,11 and particle systems for magnetic imaging and drug delivery.12,13 In conjunction with the characteristics of CF within the single-domain regime (critical diameter <100 nm),14 dependencies on heating capacity have emerged, especially in the context of medical applications. Notably, the heating capacity of these materials is influenced by the crystallinity, morphology, size, and size distribution of the CF nanoparticles (NPs).15–17 Particularly, the magnetic anisotropy (expressed by its constant K), which is comprised of surface, shape, magneto-crystalline, and strain contributions, can be altered in this manner.14,18 Hence, these parameters affect the Brownian motion as a consequence of thermal fluctuations through viscous drag, as well as the Néel relaxation, which is influenced by the magnetic anisotropy energy barrier.15,16 According to Néel's theory, it can be postulated that surface anisotropy becomes negligible for particle diameters exceeding approximately 10 nm.18 This is due to the fact that the volume of the particle increases relative to its surface area, resulting in the surface effects becoming relatively insignificant.19 Furthermore, Durhuus et al. simplified the dependency of K on the shape and the magneto-crystalline contributions, resulting in K ≠ 0 for elongated and flattened shapes.17 It is further assumed that the system consists of single-domain NP exhibiting uniform magnetisation M in a liquid suspension at constant viscosity η.20,21 The NPs were described as prolate spheroids with uniaxial anisotropy.22,23 Thus, the representation of the shape anisotropy constant KS can be simplified as a function of the aspect ratio AR of the particles.17 Due to the dependence of the AR and the associated changes in KS, it is, therefore, feasible to derive predictions concerning the heating capacity through determinations of the distributions of the particle elongations as predicted by Clarke et al.22 and McGhie et al.23 It can be stated that with an increasing anisotropy constant, the average size of the particles decreases at which maximum heat is generated.24 However, the size distribution should be considered as well, as magnetic and hyperthermal properties are dependent on the particles' volume and, hence, K.16,25–27Numerous approaches, such as decomposition, solvothermal, microemulsion, and template-assisted methods, facilitate the production of shape-anisotropic CF particles in various morphologies, including cubes, stars, octahedrons, nanowires, and plate-like structures.26,28–33 However, these techniques often involve toxic precursors or surfactant additives. To achieve shape anisotropy in combination with a green approach, a simple and environmentally friendly method is being developed for this work, enabling future hyperthermia applications. Previous studies have demonstrated that cubic CoxFe3−xO4 nanoparticles with a cobalt content of x < 0.5 can be synthesised via an aqueous co-precipitation method using significantly reduced cobalt salt concentrations, followed by a hydrothermal step.34 Parameters, such as reagent concentration and pressure, notably influence the morphology of CF particles. Additional shape-altering factors that arise from the use of a hydrothermal reactor include, e.g., the temperature T, the reaction time t, the stirring speed v, and the filling volume V. Variations in T, V, and v lead to significant differences in the flow dynamics between laminar and turbulent flow states, thus affecting the assumed ideal biphasic system composed of particles and solution.35–37 Especially, the liquid volume within the reactor serves as a critical factor that influences various aspects of the reaction dynamics.38,39 It dictates the mixing efficiency, which is essential for achieving homogeneity and uniform distribution of reactants, as forced convection leads to a more homogeneous reaction.37 Furthermore, the filling volume affects the frequency of particle collisions with the reactor walls while keeping the stirring speed constant. The interactions among particles and between particles and walls are crucial for the formation of unique morphologies, resulting in varying particle shapes through processes such as coalescence, fragmentation, and aggregation.40 Moreover, the heat transfer efficiency within the solution is closely linked to the filling volume. For example, Ma et al. simulated the batch hydrothermal fluid behaviour in dependency on the temperature ranging from 393 K to 473 K. A higher temperature ensures an axisymmetric heat transfer and flow field, resulting in higher velocity and viscous force.37 An insufficient liquid volume can lead to localised overheating, which is also connected to an inhomogeneous heating process. Therefore, it is essential to consider the filling volume as a multifaceted parameter that influences both particle morphology and the efficacy of the reaction process. A systematic determination of reactor configuration and characterisation parameters is crucial to receive valuable insights into the optimisation of the reactor synthesis methods with regard to the enhancement of shape anisotropy of the CF nanoparticles.
Additionally, in this work, the aforementioned hydrothermal synthesis for the production of CF was scaled up by a factor of 3. The upscaling of the synthesis and identification of synthesis-altering reactor parameters aim to enhance particle mass yield for future applications while minimising impacts on size distribution. Notably, this discussion is frequently overlooked in fundamental syntheses performed in small autoclaves at scales not exceeding 20 mL of reaction solutions. Given that modifications in reactor dimensions lead to alterations in parameters such as flow velocity and thermal transfer, this discourse is imperative for the advancement of innovative applications.
In this work, the formation of CF particles was mechanistically described in part 1. In part 2, the synthesised particles were examined in terms of their size, size distribution, and shape anisotropy to verify the parameters for a high shape anisotropy combined with a small size distribution. A systematic study was conducted based on reaction and reactor parameters, utilizing techniques such as transmission electron microscopy (TEM) and high-resolution transmission electron microscopy (HR-TEM). The crystallite structure was confirmed by X-ray diffraction (XRD) measurements, and the crystallite sizes as well as strains were obtained using Williamson–Hall (WH) and Halder–Wagner (HW) plots. We want to highlight the investigation of the influence of the filling volume on the particle morphology in part 3, which partially led to coffin-like structures, which were analysed using angle-dependent scanning electron microscopy (SEM) and selected area electron diffraction (SAED) analysis. These particle samples were discussed in part 4 with respect to their anisotropy constants as a function of their shape anisotropy (expressed by the aspect ratio) and size distribution.
2 Experimental methods
2.1 Materials
All chemicals were used as received without further purification. Iron(III) chloride hexahydrate (97%), iron(II) chloride tetrahydrate (97%), and cobalt(II) chloride hexahydrate (97%) were acquired from Sigma-Aldrich (St. Louis, MO, USA). Disodium hydrogen phosphate dihydrate (99.5%) and sodium hydroxide (99%) were obtained from Merck (Darmstadt, Germany) and Grüssing (Filsum, Germany), respectively. For the stabilisation step, tetramethylammonium hydroxide solution (25 wt%, VWR LLC., Radnor, PA, USA), citric acid (Grüssing, Filsum, Germany), and trisodium citrate dihydrate (Fluka Inc., Buchs, Switzerland) were used. Ultrapure water (Milli-Q quality, resistivity >18.2 MΩ cm) was obtained from a Millipore Milli-Q water purification system from Merck (Darmstadt, Germany). A system manufactured by Berghof Instruments (Eningen unter Achalm, Germany) was used for the hydrothermal treatments. The stainless-steel autoclave features a Teflon liner with internal volumes of 150 mL and adapters to degas the system. The pressure reached a maximum of approximately 5 bar throughout the reaction process. A photograph of the hydrothermal reactor, including the heating block and Teflon inlet, is shown in Fig. S1.†2.2 Preparation of cobalt-doped magnetic particles
An up-scaled protocol for the preparation of the akaganeite precursor solution (2.4 L) was used as described in previous literature, resulting in a nanorod mass concentration of 1.12 wt% in aqueous solution.34 For the coprecipitation and hydrothermal step, we utilise the synthesis method demonstrated in prior work.34 However, the procedure was scaled up threefold, and reaction parameters like temperature and filling volume were varied. The metal chloride salts of Fe(III), Fe(II), and Co(II) were dissolved in 35.25 mL Milli-Q water and stirred with a magnetic bar (length × width = 30 mm × 8 mm) for around 2 minutes. The precursor solution (27.27 mL solution, 3.39 mmol particle amount, 0.3 g particle mass, respectively) was added to the aqueous metal salt solution and stirred at 1000 rpm for 2 minutes. The solution's final concentration of sodium hydroxide (NaOH) was maintained at 0.5 mol L−1. For this purpose, 12.5 mL of a 3 M NaOH solution was injected within 5 seconds using a syringe. By percentage adjustment of the total reaction solution at 25%, 50%, or 100%, the filling volume of the Teflon inlet ranged from ∼17% to 50%. The specific conditions are outlined in Tables S1 and S2.† The hydrothermal reactor was sealed and degassed for 1 minute with nitrogen before being closed through the needle valves at the gas connections. Two distinct temperature profiles were employed for the hydrothermal synthesis. The first profile involved maintaining a temperature of 160 °C for 24 hours. The second profile consisted of a temperature ramp of 120 minutes to achieve 190 °C, followed by isothermal heating at 160 °C for an additional 22 hours. Throughout this thermal treatment, the stirring speed was consistently maintained at 500 rpm. After the reaction, the particles were separated from the solution with a magnet. The particles were washed magnetically three times with Milli-Q water. Subsequently, the nanoparticles were stabilised to obtain negatively charged surfaces according to a process described in Section S1.† Each experiment was conducted once, as the same precursor solution should be used for all experiments to ensure comparability. To address the issue of sample repetition, a statistical analysis of the data and their mean differences was conducted. The significance of these differences was examined at a 5% significance level (p = 0.05).2.3 Characterisation methods
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(θ) versus 4
cos(θ) versus 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ), where β describes the line broadening at half of the maximum intensity of the reflex and ε is the intrinsic crystalline strain. Using k as a dimensionless shape factor fixed at 0.9 for cubic crystallites, the relationship can be expressed as follows (eqn (1)):41
sin(θ), where β describes the line broadening at half of the maximum intensity of the reflex and ε is the intrinsic crystalline strain. Using k as a dimensionless shape factor fixed at 0.9 for cubic crystallites, the relationship can be expressed as follows (eqn (1)):41
 | (1) |
Including the reciprocal lattice point and interplanar spacing, the alternative formula by the HW plot can be adapted, where the crystallite size dHW was calculated from the slope and the strain from the intercept (eqn (2)).41 The analysis is summarised in Section S2.†
 | (2) |
3 Results and discussion
3.1 Formation of cobalt-doped ferrite particles using akaganeite nanorods as precursors
In this section, the general synthesis route will be described first, followed by an explanation of the particle morphology and an outline of the proposed reaction mechanism illustrated in Fig. 1.In the initial step of the foundational synthesis of CF1, akaganeite (β-FeOOH) nanorods with lengths of (30 ± 9) nm (σ = 30%) by widths of (6 ± 1) nm (σ = 17%) were prepared using a hydrolysis mechanism of Fe(III) chloride at a moderate temperature of 80 °C. The crystalline phase of β-FeOOH was found to be consistent with reference to the Joint Committee on Powder Diffraction Standard (JCPDS) no. 00-034-1266. The analysis of this system was intensively described in previous work.34,42 In the second step, Co(II), Fe(II), and Fe(III) chloride salts of a defined ratio to β-FeOOH were filled into the Teflon liner, and the base NaOH was added. The reaction mixture was then processed in the hydrothermal reactor at various parameters (see Section S1†), resulting in non-stoichiometric CF nanoparticles of different morphologies, sizes, and aspect ratios. The crystal phase of the CF particles was confirmed in reference to the JCPDS PDF no. 00-022-1086 for cobalt ferrite, demonstrating a high degree of concordance regarding the diffraction angles and intensities of all reflexes (see Section S2†). As the reaction is performed under a N2 atmosphere, hematite and maghemite impurities should be prevented.43
To verify the initial mechanism of the coprecipitation at room temperature, TEM and diffraction images of the reaction solutions were taken at 0 s, 60 s, and 300 s after NaOH addition (Fig. S6†), presenting small spheres. Surface tension is the dominant factor influencing the growth of small nanoparticles in the initial phase, as it tends to form spherical shapes, which minimise their surface area and the corresponding surface energy. When the particle size increases to around 20 nm, the shape gradually changes from spherical to cubic, where the surface tension effects and the 〈100〉 direction growth balance. With further increase in diameter, the shape change is due to a higher growth rate along the 〈100〉 directions compared to the 〈111〉 directions, resulting in octahedral particles. This is also due to the lower energy of the {111} surface. This size-dependent morphology behaviour was also demonstrated by López-Ortega et al.44,45 Additionally, the size and crystallinity of the particles increase with increasing reaction temperature using a hydrothermal step. Fig. S7† illustrates the change of the diffraction rings to dots as well as the spherical to octahedral shape of the particle sample heated to 90 °C after the coprecipitation reaction. Due to the high temperatures and the increased reactivity of the nanoparticle edges, the Ostwald ripening process preferentially occurs at these edges.46,47 As a result, rounded octahedral shapes are truncated by the {100} facets, which predominantly appear as rounded rhombuses, rounded rectangles, and spheres in 2D images, as visualised in Fig. 1 (right).
The illustrated reactions in Fig. 1 (left) represent the proposed reaction mechanisms that are likely to occur. First of all, it should be noted that the precursor is needed to form the non-stoichiometric cobalt-ferrite particles as presented in our previous work.34 Performing the reaction with the same amount of Fe(III) chloride instead of precursor nanorods, we obtain mixtures of different particle phases and sizes. This includes goethite rods or stars (length × width ≈ 1000–2000 nm × 200–500 nm), goethite needles (length × width ≈ 1000–2000 nm × 20–100 nm), cobalt ferrite spheres (diameter ≈ 2–6 nm), and/or magnetite cubes (diameter ≈ 15–25 nm or 500–800 nm). Furthermore, the hindering of the akaganeite transformation due to a protective shell around these nanorods leads to the formation of truncated cubic particles instead of truncated octahedra. Performing the reaction without additional Fe(II) and Fe(III) salts leads to cobalt oxide and cobalt oxyhydroxide phases, which means that akaganeite cannot be reacted with cobalt chloride under the given reaction conditions to obtain cobalt-doped ferrite particles.
Reaction I depicts the conversion of the nanorods with Fe(II) hydroxide into magnetite. Due to the phase transformation of akaganeite resulting in magnetite, the elongated form is completely dissolved. Blesa et al. reported that β-FeOOH is transformed into Fe3O4 through dissolution–recrystallisation with hydrazine at pH 9–11.5 and 100 °C under hydrothermal conditions. Even though NaOH is a much stronger base than hydrazine, only dissolution to Fe(OH)4− would be observed in the case of NaOH as used in our system.48 Ishikawa et al. demonstrated in ageing experiments that akaganeite can be converted into magnetite using NaOH in the presence of Fe(II) at temperatures from 25 °C to 100 °C with an increasing trend.49 At room temperature, this phase conversion needs long reaction times of 720 h. However, this process preferentially requires OH−/Fe(II) ratios of 2. At ratios of 2.5, the formation of magnetite takes place from dissolved akaganeite (Fe(OH4)−) at pH > 11.84 but is reduced or combined with the presence of goethite phases at much higher ratios. As our system is performed at much higher levels of NaOH, the magnetite production will be reduced. The presence of the akaganeite phase after 24 hours of stirring at room temperature confirms this assumption, where NaOH solution was added, but the hydrothermal treatment was not performed (Fig. S6†).34
We further assume that the nanorods dissolve at higher temperatures below a certain Fe(III) ion concentration of 0.01 mol L−1.50 This is achieved through the consumption of Fe(III) hydroxides during the formation of octahedral magnetite particles from the coprecipitation reaction of Fe(II) and Fe(III) hydroxides (reaction II, Fig. S7a†). At the time, as the nucleation sites are produced from the Massart reaction, the Fe(III) concentration should be lowered due to the consumption during coprecipitation, reaching the solubility limit of akaganeite. The presence of magnetic material before the hydrothermal step (but also with the presence of the akaganeite phase) indicates that this dissolution process could be reasonable at the used OH−/Fe(II) ratios.34 Additionally, the nanorods can act as a heterogeneous surface to form the crystallisation nuclei of magnetite from the Massart reaction. Mao et al.51 and LaGrow et al.52 have each resolved the mechanisms of magnetite formation precipitated with the strong base NaOH and the weak base Na2CO3 (to slow down the precipitation reaction), respectively, with intermediates such as ferrihydrite and goethite or iron hydroxide carbonate [Fe6(OH)12CO3] being formed and promptly agglomerating. In LaGrow's work, amorphous ferrihydrite nanoparticles grow to sizes of up to 2 nm before converting to magnetite and/or maghemite within a period of 3 to 4 minutes. Ferrihydrite acts here as a nucleation seed, while the carbonates serve as feedstock. In contrast, in Mao's study, primary magnetite cores are already present after just 3 seconds using a pH value above 10 (as in our case), which grow to 9.6 nm in size over 2.5 minutes. The growth phase is primarily explained by the agglomeration of periodically occurring intermediates with magnetic cores and magnetite nuclei amongst themselves. The addition of sodium hydroxide in this work ceases after 5 seconds, which should conclude the process of magnetite nuclei formation from Fe(II) and Fe(III), as verified by TEM images shown in Fig. S6.† The akaganeite rods would thereafter also be available as ‘feedstocks’ through their dissolution to enable a constant particle growth over time, even at room temperature after 300 s. The parallel integration of Co(II) ions in exchange for Fe(II) ions at high temperatures would release Fe(II) ions that would be available for growth. This allows for the assumption of a constant supply of Fe(III) and Fe(II) ions during the growth process, which would lead to a focusing of the size distribution. In some literature, this possibility of continuous provision of precursors or intermediates after the nucleation phase is referred to as an “extended” LaMer process.53,54 Furthermore, the Ostwald ripening process would lead to the growth of the already larger particles at the expense of the smaller ones, resulting in a focusing of the size distribution.
It is also noteworthy that Fe(III) ions and Co(II) ions have the potential to directly facilitate the formation of cobalt ferrite (reaction III) due to the direct crystal growth mechanism.55,56 However, this reaction typically occurs only at temperatures of 70 °C or higher and is not expected at the onset of the reaction at room temperature.57 In contrast, Kim et al. coprecipitated CF nanoparticles at lower temperatures, showing a clear transition in size and crystallinity between 40 °C and 60 °C.58 A mixture of nanocrystalline and crystalline CF phases of 47% and 53%, respectively, was synthesised at a comparable pH value of 12 at moderate temperatures of 60 °C by Thomas et al.59 This mixture could only be converted into a homogenous sample by calcination at 600 °C, as shown for a sample at pH 11.
Lastly, the hydrothermal step results in the formation of cobalt-doped ferrite through an ion exchange between Fe(II) ions and Co(II) ions. This process was also demonstrated by Mitra et al., who showed an ion exchange of Fe(II) with Co(II) ions in magnetite nanorods.60
The influences of the varied reactor and reaction parameters on the size and size distributions of the obtained particles in comparison to CF1 will be explained based on the models for the preparation of monodisperse particles, as explained by Sugimoto et al.61,62 Monodisperse nanoparticles with a size distribution coefficient of less than 10% are preferably formed through a three-step process involving initiation, nucleation, and growth, where the nucleation and growth phases are separated. Specifically, a high nucleation rate must be followed by a slow growth phase to achieve this uniformity. During the subsequent growth phase according to LaMer, metal atoms diffuse from the surrounding medium to the nucleation sites, depositing and contributing to particle growth. This growth is thus contingent upon the number of nucleation sites, the concentration of metal atoms, and the diffusion coefficient. The diffusion-controlled Ostwald ripening process would result in an increase in the diameter of the big particles through the dissolution of small nanoparticles. Including most metal oxide growth processes, the mode is mainly reaction-controlled so that the size distribution is sharpened by the initially restricted nucleation phase. Furthermore, the use of a heterogeneous system, where a solid precursor acts as a reservoir, could lead to recrystallization processes during these phases. To establish the actual particle formation mechanism, the reaction kinetics of the mechanisms outlined in Fig. 1 would need to be investigated in a highly time-resolved manner. The mechanistic resolution is also challenging to implement due to the design of the hydrothermal reactors with reaction pressures up to 5 bar, which is difficult to carry out in known setups for, e.g., ultrafast small-angle X-ray scattering measurements in combination with synchrotron X-ray diffraction due to the existing reaction pressure in combination with the high temperatures. However, many studies on iron oxides and ferrites predict the applicability of spontaneous nucleation and/or diffusion-controlled growing processes to their systems, primarily involving thermal decomposition or solvothermal processes.53,63–65 Additionally, attention is drawn to the critical examination of the applicability of the LaMer mechanism to various nanoparticle syntheses of, e.g., metal oxides, by Whitehead et al.66
3.2 Influence of the hydrothermal conditions on the morphology
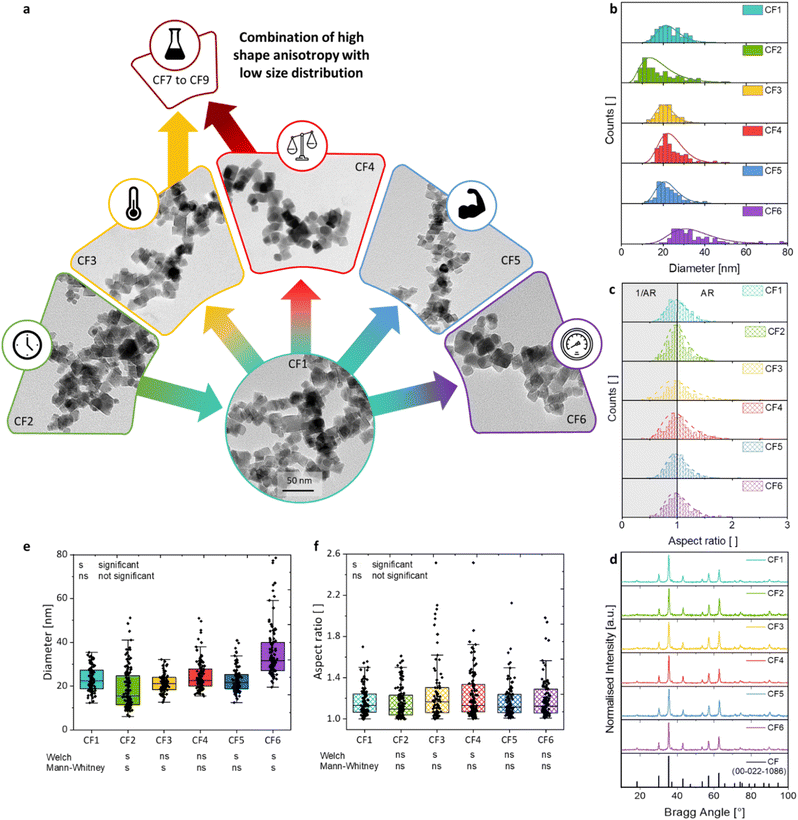
The morphologies (Fig. 2a), sizes (Fig. 2b), and aspect ratios (Fig. 2c) of the synthesised particles in dependence on the changed reaction parameters are presented compared to the reference sample CF1. This includes the reaction time t, the reaction temperature T, the precursor-to-metal salt ratio r, the molarity of the base cNAOH, and the pressure p. The size di of each particle was obtained from the measured lengths li and widths wi of the particle (i = 100), which is shown for samples CF1 to CF6 (see Section S4†). The particle diameter di was assessed based on certain assumptions. The first assumption was made that the particles are truncated octahedral, which primarily form rhombuses, squares, and slightly rounded shapes in the 2D projection (Fig. 1). Then, the width of the particles is comparable to the particle images, regardless of the orientation of the crystal surfaces in the 2D projection. The diameter di of the measured particles was calculated using eqn (3) based on the assumption that it approximately corresponds to the diagonal of a square with
 | (3) |
This assumption deviates from rhombuses with an edge angle of less than 90° but applies to the other 2D projections and can be considered as an approximation. The mean size values of w, l, and d, and the corresponding absolute and relative size deviations σ, were calculated from the log-normal distribution curves (Section S4†). Based on these size values and the standard deviations, the polydispersity indices (PDI) can be calculated with (σ/size)2, assuming a Gaussian distribution (Table S3†).
The aspect ratio (AR) of the samples was determined as the mean average value of the individual ARi of each measured nanoparticle length and width, where ARi was observed through eqn (4) as follows:
| ARi = li/wi. | (4) |
The extension of the ARi values by their reciprocal values 1/ARi (highlighted in grey) leads to Fig. 2c, where a log-normal distribution curve has been fitted to the measured values. This curve is included solely for visual purposes to assess the anisotropy of the particles and was not used for the calculation of the average AR value. A wide, gently declining curve indicates a broad distribution of aspect ratios, suggesting an increased presence of shape-anisotropic particles. Additionally, the representation of the 1/ARi values makes it easier to identify any secondary maxima that may occur.
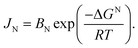 | (5) |
It is demonstrated that an increase in the heating rate affects the NP dispersity and size as the amount of nucleation sites decreases. Therefore, the presence of larger NPs with a higher dispersity is expected with the increase in pressure or heating rate, as demonstrated for sample CF6.
3.3 Influence of the hydrothermal conditions on the crystallite size and crystallinity
A brief comparison of the crystallite sizes obtained from the Williamson–Hall (WH) and Halder–Wagner (HW) plots (see Section S2†) with the TEM data is addressed in this section. This alignment further supports the reliability of the crystallite size determinations derived from different analytical techniques. The crystallite sizes exhibit a strong correlation with the widths of the particle samples, especially for the values obtained from the HW plots. The linear fits of HW plot demonstrate notably high coefficients of determination, ranging from R2 = 0.9945 to 0.9998, which indicates that the HW model nearly completely explains the variability in the variables with respect to the mean. It is well-documented that particle sizes determined through XRD tend to be slightly smaller than those measured via TEM.63,64,71 This difference is primarily attributed to the presence of crystallite defects, particularly at the surface of the particles, which reduces the measured crystallite size. Furthermore, it is essential to acknowledge that the statistics of the XRD analyses are significantly higher than those of the TEM measurements, which were limited to a sample size of only 100 particles in this study. It should also be noted that the comparison of the dWH values of different samples with regard to the absolute particle sizes could be prone to error if the crystallinity is also changed by the change in the respective reaction parameter. Therefore, the crystallinity index (CI) was calculated from the ratio of the integrals of the crystalline peaks and the total area of all peaks (see Table 1 and Fig. S5†).72 The relatively sharp reflections indicate a high degree of crystallinity in the samples of 83% to 96% in dependence on the reaction conditions. The change in the crystallinity can result in differences in the crystal sizes, which may vary from the particle sizes observed via TEM. However, a similar trend is observed between the TEM data and the XRD results, indicating consistent findings across both methods.| No. | w ± σw [nm] ([%]) | l ± σl [nm] ([%]) | d ± σd [nm] ([%]) | AR ± σAR [ ] ([%]) | dWH ± σd,WH [nm] ([%]) | dHW ± σd,HW [nm] ([%]) | CI [%] |
|---|---|---|---|---|---|---|---|
| CF1 | 15.1 ± 3.6 (24) | 17.6 ± 4.5 (26) | 23.3 ± 5.7 (24) | 1.17 ± 0.11 (9) | 15.2 ± 0.3 (2) | 14.5 ± 0.2 (1) | 87 |
| CF2 | 12.4 ± 6.3 (51) | 14.1 ± 6.8 (48) | 18.8 ± 9.2 (49) | 1.16 ± 0.12 (10) | 17.1 ± 0.7 (4) | 16.0 ± 0.3 (2) | 88 |
| CF3 | 13.6 ± 3.1 (23) | 16.8 ± 4.4 (26) | 21.4 ± 4.4 (21) | 1.26 ± 0.21 (17) | 14.3 ± 0.8 (6) | 14.2 ± 0.3 (2) | 83 |
| CF4 | 15.4 ± 3.6 (23) | 18.9 ± 5.4 (29) | 24.5 ± 6.2 (25) | 1.23 ± 0.17 (14) | 17.6 ± 0.4 (2) | 16.4 ± 0.2 (1) | 95 |
| CF5 | 14.6 ± 3.4 (23) | 17.1 ± 4.5 (26) | 22.6 ± 5.5 (24) | 1.17 ± 0.12 (10) | 14.6 ± 0.7 (5) | 13.9 ± 0.3 (2) | 96 |
| CF6 | 22.5 ± 6.4 (28) | 26.8 ± 8.8 (33) | 35.1 ± 10.7 (30) | 1.19 ± 0.13 (11) | 20.6 ± 2.1 (10) | 18.6 ± 0.8 (4) | 91 |
| CF7 | 15.6 ± 3.5 (22) | 18.5 ± 4.5 (24) | 24.3 ± 5.4 (22) | 1.19 ± 0.13 (11) | 18.4 ± 1.6 (7) | 17.0 ± 0.6 (4) | 96 |
| CF8 | 16.6 ± 4.2 (25) | 19.6 ± 5.5 (28) | 25.8 ± 6.7 (26) | 1.18 ± 0.13 (11) | 18.6 ± 1.9 (10) | 16.9 ± 0.6 (4) | 93 |
| CF9 | 16.3 ± 3.8 (23) | 19.9 ± 5.0 (25) | 25.8 ± 6.0 (23) | 1.23 ± 0.16 (13) | 17.8 ± 0.4 (2) | 16.6 ± 0.1 (1) | 85 |
3.4 Evaluation of the reaction parameters for a high shape anisotropy combined with a low size distribution
Since the significance of nanoparticle-descriptive parameters is often not assessed, this study will address this aspect (Fig. 2e and f). The considered parameters of this work are the size and aspect ratios, as well as the differences between various particle suspensions. The aim is to provide insights into the challenges of evaluating particle suspensions. The parameters should be identified that do not exhibit a significant change compared to CF1 in terms of the size combined with a low size distribution, while simultaneously showing a significant increase in shape anisotropy. These reaction parameters should then be combined and further studied with alterations in the filling volume. In terms of size and aspect ratios, Welch t-tests and Mann–Whitney U-tests were conducted.73–76 Both methods enable the assessment of the significance of the means of two datasets, which are assumed to be normally distributed in one case and non-normally distributed in the other, respectively. Furthermore, different variances are assumed in both cases, which is often overlooked in most significance tests, yet is considered meaningful when evaluating the size distribution of two different nanoparticle suspensions. A significance level of 0.05 was adopted.The size distributions indicate that samples CF3 and CF4 do not show a significant difference in means compared to sample CF1 when a normal distribution is assumed. The non-normally distributed testing shows a lack of significance for CF4 and CF5 in comparison to CF1. This implies that the differences in the mean sizes of the samples CF1 and CF3 to CF5 can be regarded as not significant. Consequently, these reaction parameters are suitable if no significant differences in mean sizes are desired. Interestingly, CF3 and CF4 represent the samples that demonstrate a significant difference in aspect ratio compared to the mean of CF1. All other samples, along with changes in the reaction parameters time, base strength, and pressure, exhibit comparable aspect ratios to CF1.
In summary, the following reaction parameters can be identified in comparison to CF1 concerning a narrow particle size distribution combined with a high shape anisotropy (or shape distribution): a high reaction temperature of 190 °C (CF3) and a low molar ratio of precursor to metal salt of 1 (CF4). The temperature was not raised above 190 °C, as this may lead to higher induced strain values and the formation of crystal defects, as demonstrated by the decreased crystallinity and by Fayazzadeh et al.67 An enhancement in anisotropy may be achieved by further reducing the precursor-to-metal salt ratio.
3.5 Coffin-like nanoparticles due to changes in the filling volume
To enhance the shape anisotropy of the truncated octahedral nanoparticles with narrow size distribution, a controlled reactor reaction strategy was employed based on the findings of Sections 3.2 to 3.4. This involves a low metal salt concentration (ratio of 0.5) and elevated heating rates through higher reaction temperatures. In this context, the influence of the filling volume on the particle morphology was investigated (Fig. 3). The liquid volume within the reactor is a crucial parameter that profoundly influences various aspects of the reaction process. It governs the efficiency of mixing, the frequency of collisions between wall and particle interfaces, inter-particle interactions, and particle-wall interactions, as well as the dynamics of laminar and turbulent flow velocities, and other related parameters such as the heating efficiency of the solution volume. Under a constant heating rate, a reduced volume of solution exhibits a higher temperature increase compared to a larger volume. The observed effect indicates that as the filling volume increases, the time required to reach the target temperature of 190 °C also increases. At 17% of the maximum filling volume (CF7), this target temperature can be attained in approximately 1 hour, likely due to the resulting vapour pressure established in the reactor, a condition not achieved at a fill level of 25% (CF8). After 2 hours of heating, maximum temperatures of 180 °C and 170 °C are reached at filling volumes of 25% (CF8) and 50% (CF9), respectively. When the target temperature is set to 160 °C afterwards, and the power input is subsequently reduced, the system achieves this temperature after 30 minutes for CF7 and after 1 hour for both CF8 and CF9.The exemplary TEM images of the resulting NP samples are depicted in Fig. 3. In addition to the analysis of the TEM data in histograms (Fig. S12a–d†), box plots were also calculated for the samples CF7 to CF9 (Fig. S12†). The advantage of representing the data as a box plot resides in its independence from the selection of the number and width of the bins, which may influence the histogram representations and the log-normal distribution curves. The diameter of the sample CF9 is increased in comparison to CF1 and CF4 due to the further enhancement of the amounts of metal salts introduced (Table 1). The standard deviation does not change significantly and reaches comparable values of 22% to 26%, similar to those of CF1 and CF4. The polydispersity indices are below 0.07 (Table S4†). This phenomenon is elucidated by the altered mechanism of the initiation phase being shortened and the supersaturation being reached more rapidly, as previously described. In terms of a comparison of the calculated size values obtained as the expected value from a log-normal distribution curve and a boxplot, the mean diameters are ranked in the order of CF7 < CF8 ≈ CF9 in the range of 24.3 to 25.8 nm. Considering the median values, the sizes increase in the sequence of 23.0 nm < 23.5 nm < 23.6 nm, respectively CF7 < CF8 < CF9. Taking both analyses into account, a slight increase in the diameters can thus be observed due to the increase in filling volume. Nevertheless, this increase is not significant due to the variations observed in the TEM analysis. The edge width of the particle samples CF7 to CF9 exhibits no significant differences as well. However, the lengths of the NP show a modest increase. As a result, the mean AR increases from 1.19 to 1.23 for the solution volume of 25% to 100%, corresponding to a percentage deviation of 11 to 13%. These values are comparable with the median aspect ratios for CF7 (1.14), CF8 (1.13), and CF9 (1.17), depicted in Fig. S12e.† The increased AR is likely associated with the pronounced differences in the vertical flow behaviour within the reactor vessel. Differences in flow velocities within the profile arise, which consequently impact the Reynolds number. Thus, the flow regime becomes alterable, categorising it into laminar and turbulent flow. With a higher fill level in a cylindrical vessel, the variance of the stirrer flow perpendicular to the stirrer increases. As a result, the previously mentioned parameters related to the filling volume, such as the number of collisions and the temperature profile, are significantly altered within the reactor. In either case, an increased filling volume results in a rise in the aspect ratios of the particles.
The increase in the aspect ratio can be attributed to a higher proportion of distorted parallelograms (2D representation) observed in sample CF9 (marked area in Fig. 4). HR-TEM images further indicate the formation of elongated honeycomb-like projections. When a foundational octahedral 3D structure is considered (see CF1 and CF7), this truncated octahedron structure appears to undergo additional distortion. The elucidation of the 3D structure was achieved through angle-dependent SEM measurements (Fig. 4 and Section S6†), which demonstrate a pronounced representation of the coffins (highlighted circle) in sample CF9 as a function of the angle, ranging from 0° to 85°. The characterisation of crystal planes in the HR-TEM images, facilitated by inverse fast Fourier transformation (Section S7†), suggests that the preferential growth of the {222} plane is responsible for this elongated distortion. The width of the coffins is defined by the growth of the {111} plane. A visually higher proportion of these elongated octahedral nanoparticles is observed as a result of the increase in the filling volume. This is accompanied by an elevation in the liquid level within the thin Teflon vessel, decreasing the frequency of particle-wall collisions. Additionally, there is an alteration in the flow pattern generated by the stirrer within the reactor vessel, which is anticipated to exert an influence on both the particle morphology and anisotropy. The flow velocity and mixing along the reactor axis diminish with increasing fill height from 25% to 100% while maintaining a constant cross-flow rate. Due to the preferred growth of the {222} crystal facet of the particles, there must be an influence on the particle growth along this specific crystal plane, or alternatively, the other crystal planes must be blocked. Since no crystal-blocking agents are added during synthesis, this effect is likely resulting from the significantly higher variability in flow and temperature profiles within the reactor at higher fill levels. In combination with this, the further increased metal salt concentration in the reactor syntheses from CF7 to CF9 could also influence the growth phase, as more metal ions are available. We therefore hypothesise that the particle growth phase is being affected to obtain coffin-like particles.
The crystallographic analysis of the SAED images enables the assignment of the inverse spinel structure to the NP. The same crystalline phases are determined via HR-TEM and SAED analysis. The observation of bright spots in the diffraction pattern indicates the presence of larger crystallites within all samples. This aligns with the particle size distribution data illustrated in Fig. S12.† Furthermore, lattice patterns can be observed in the TEM images of the larger particles, with enhanced evidence in the HR-TEM images for almost all particles depicted. In certain instances, these patterns do not extend to the particle edges, indicating the presence of amorphous regions in these areas. This would result in a reduction of the magneto-crystalline anisotropy, particularly pronounced in CF7. Upon examining the particle morphology of the octahedrons and their shape irregularities, a certain uniaxial anisotropy can be assumed for all samples from CF7 to CF9.77
3.6 Determination of the magnetic anisotropy constants
The assessment of the magnetic anisotropy in this study is especially conducted through the combination of magneto-crystalline and shape anisotropies, respectively, KC and KS. In this context, the approaches of the theoretical and experimental works by Faílde, Clarke, McGhie, and Durhuus et al. are applied.17,22,23,78 The illustration of the approximations made is depicted in Fig. 5a, where the sum of KC and KS is considered to obtain the magnetic anisotropy constant K. Additionally, an experimental approach for evaluating K was determined to enable a comparison with the calculated anisotropy values, which is summarised in Section S8.†If the magnetisation M of a single-domain particle is uniformly distributed above the particle volume VP, the magnetic energy E can be written as
E = KVP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2 sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ
| (6) |
| No. | MS [A m2 kg−1] | dmag [nm] | KC,LAS [104 J m−3] | KS [103 J m−3] | KS,r [103 J m−3] | Kε [104 J m−3] | KO [10−4 J m−2] |
|---|---|---|---|---|---|---|---|
| CF7 | 14.3 ± 0.2 | 23.4 ± 0.3 | 3.2 ± 0.4 | 0.2 ± 0.2 | 0.2 ± 0.1 | −0.6 ± 0.6 | 1.3 ± 0.2 |
| CF8 | 26.7 ± 0.4 | 18.1 ± 0.2 | 5.9 ± 0.7 | 0.8 ± 0.6 | 0.8 ± 0.3 | −1.5 ± 0.7 | 1.8 ± 0.2 |
| CF9 | 37.8 ± 0.2 | 16.7 ± 0.1 | 4.9 ± 1.1 | 1.9 ± 1.4 | 1.7 ± 0.8 | −1.1 ± 0.2 | 1.4 ± 0.3 |
The experimental verification of the magneto-crystalline magnetic anisotropy KC was conducted by VSM measurements and plotting the mass magnetisation M in A m2 kg−1 versus the magnetic field strength μ0H in Tesla (Fig. 5b). There is no significant opening of the hysteresis loops because the particles within the suspension may align along the external field. It is evident that no saturation is reached at high magnetic field strengths due to the slight increase in the curve. Therefore, a modified LAS approach was used, as described in eqn (7):80,81
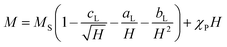 | (7) |
The saturation region can be described by eqn (8), where the terms with aL and cL can be neglected due to the linearity shown in Fig. 5c:80
| M = MS(1 − bL/H2). | (8) |
Thus, the saturation magnetisation values MS were calculated from the y-intercepts by linear fitting of the M vs. 1/(μ0H)2 representation in the high-field range (Fig. 5c). The MS values increase from (14.3 ± 0.2) A m2 kg−1 to (37.8 ± 0.2) A m2 kg−1 with the filling volume used. Then, KC,LAS was determined by fitting the M(μ0H) curves from 0.4 T to 2.5 T (Fig. 5d), using the relationship of bL with the magneto-crystalline anisotropy constant described via eqn (9):80
 | (9) |
All samples exhibited an R2 value of >0.994 (Fig. 5d). The KC,LAS values of (3.2 ± 0.4) × 104 J m−3 to (5.9 ± 0.7) × 104 J m−3 fall within the range discussed above. KC,LAS follows the trend of the strain (see Fig. S4†). The decreased values compared to CF (KC = 1.1 × 105 J m−3) can be explained by the lower cobalt content. The fitting, which was performed over a broader range using the LAS method compared to the linear fitting, served as the basis for the KC values to enable comparison with the K constants. Note that the LAS approach regards the rotation of the vector of the magnetic moment from the direction of the easy axis towards the external field direction.84 This means that the particles should be fixed during the measurement. Here, the measurements were performed on suspensions and partially on immobilised magnetic NP. However, the magnetic NP were aggregated and precipitated due to an interaction. Thus, we presume that the MNP rotation is hindered and that the assumption of eqn (8) with eqn (9) is valid. While the alternating current susceptibility (ACS) data show that almost all magnetic NP of CF7 are immobilised, only 65% of CF8 are so (Table S7†). In case of CF9, even more NP appear not fixed and are partially organised in large clusters (Section S8†). Therefore, the calculated values for the crystal anisotropy should be interpreted with caution. Furthermore, due to possible interactions between the magnetic NP, the KC values should be interpreted as effective values. Nevertheless, the ratio of the corresponding K values between CF7 and CF8 obtained from analysis of the data of ACS (Table S7†) matches the ratio of the related KC values obtained from the modified LAS approach (Table 2).
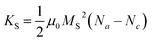 | (10) |
Na and Nc describe the dimensionless demagnetisation coefficients parallel to the short symmetry axis a and along the long symmetry axis c represented by
 | (11) |
 | (12) |
The particle elongation was determined by measuring the long semiaxis c and the short semiaxis a (Fig. 5a). These values approximately correspond to the measurements obtained from the width and length assessments used to calculate the AR of the octahedrons discussed in this work.
All KS values were then plotted similarly to the size distribution histograms (Fig. 5e). The log-normal distribution curves are only inserted for visual orientation. A determination of KS with the help of the lognormal distribution function is not meaningful, as the error values exceed the mean values. The average values and standard deviations of normal distributions were calculated, which are presented in Table 2. The average values follow the trend CF7 < CF8 < CF9, which is consistent with the observed AR. It is evident that the calculation of the mean provides limited information, as it likewise exhibits large error values. However, it is obtained that the distribution of the KS values in sample CF9 exhibits a notably higher variability compared to the other samples, indicating a broader dispersion of the data points. A significant second increase in frequencies is observed in sample CF9 beginning at a KS of 2.5 × 103 J m−3, which corresponds to an AR > 1.25. We assume that the higher variance and the second maxima in the histogram can be attributed to the higher variance in the flow and temperature profiles during the synthesis, resulting in a larger proportion of shape-anisotropic particles.
The visualisation of eqn (10) in Fig. 5f depicts the dependence of KS on AR, revealing a marked increase in KS with increasing AR. From eqn (10)–(12), it is evident that for an AR = 1 (i.e., a sphere or symmetric octahedron), Nc equals 1/3, leading to KS = 0. In contrast, the curve should approach KS,max at 0.25μ0MS2 as the AR receives infinite values. This results in approximately 1.3 × 104 J m−3 for sample CF9 with the highest MS, and in values of 6.3 × 103 J m−3 and 1.8 × 103 J m−3 for CF8 and CF7. The obtained maxima of KS in this work are 0.8, 2.9, and 6.2 × 103 J m−3 for CF7, CF8, and CF9, respectively. The highest value of KS corresponds to an AR of approximately 2.0, observed in the CF9 sample. Although no clear correlation with the mean sizes obtained via TEM is discernible (Fig. 5g), only the previously mentioned broader distribution of the sizes can be observed. As we cannot obtain a cross-section between KS and KC in both diagrams, the magneto-crystalline anisotropy is expected to dominate for all AR and sizes.
To assess the impact of the particle size distribution on AR and KS, the sizes used for calculations of the shape anisotropy and the aspect ratios were divided into ranges corresponding to a width interval of 2 nm (indexed by “r”). A linear increasing trend from diameter to width is clearly observable (Fig. S19a†). In contrast, the ARr values exhibit a decreasing trend in dependence on the widths (Fig. 5j) as the ARi for each particle size decreases with the width of the particles for each filling volume (Fig. S19b†). The distribution of the KS,r values is shown in the histograms in Fig. 5h. In contrast to the distribution in Fig. 5e, the mean values can be determined using the logarithmic distribution curve in the interval representation, which are presented in Table 2. The shift in the mean values with the filling volume is clearly noticeable. Additionally, a more pronounced second peak in the distribution can be observed for sample CF9, located at approximately 2.5 × 103 J m−3. This corresponds to an AR > 1.3, as determined from the AR-dependent representation of the data in Fig. 5i. KS,r demonstrates an increasing trend with ARr in the interval representation with a good agreement in linear dependency (R2 ≥ 0.990). Furthermore, the ARr distribution increases with the filling volume. Hence, the particle elongation does not seem to correlate with the ARr distribution. It is apparent that the KS,r distribution increases within the intervals that coincide with the region of particle distribution characterised by the highest frequency. This phenomenon can be attributed to the larger number of measurable particles within this range. Conversely, at the boundaries of the particle size distribution, there are considerably fewer particles available for measurement, resulting in a diminished distribution of KS,r and ARr values. Considering the mean widths derived from the TEM analysis, the average KS,r values calculated with the linear fits are in good agreement with the mean values obtained from the histograms of KS,r. KS,r is directly proportional to the AR and the size trend obtained by the WH plot is inversely proportional. As the mean size differences between CF7 to CF9 are not significant, the size effect was considered as a non-justifiable fact for the trend of KS.
In summary, the presentation using size intervals allows for a more accurate visualisation of the KS values in relation to the size distribution. Such features, like possible secondary maxima in KS, would not be as clearly evident using the approach based on eqn (10) (Fig. 5e), but rather through the interval-based representation. However, this has little influence on the calculation of the mean. When considering the standard deviation, it becomes evident that the particle size distribution has a significant effect on KS and therefore cannot be neglected within a particle suspension. This is especially important for precipitation reactions or syntheses in aqueous media, which typically exhibit broader size distributions of 10–30%.
 | (13) |
It is essential to consider that amorphous regions are evident at the edges of the particles (Fig. 3 and S15†), which may be associated with dead layers at the surface. Assuming a layer thickness of two atoms, or 0.3 nm, this affiliation would correlate with a change in the surface anisotropy KO.22,23 Furthermore, the different sizes associated with the size distribution can be attributed to a change in KO previously reported by other workers.90 The effective magnetic anisotropy K increases with decreasing sizes of the NPs due to a higher contribution of KO to K.90 However, we do not identify significant contributions from surface anisotropy KO, which was calculated using the magnetic core volume (see Section S10† and Table 2).91,92 The magnetic domain size, dmag, can vary significantly from the particle diameter. This discrepancy is most likely due to a magnetically dead layer present on the surface of the nanoparticles. An increase in the nanoparticle diameter may amplify the effect of surface-spin misalignment, leading to a greater non-magnetic volume and, consequently, a stronger influence on the surface anisotropy constant. As the obtained values for KO are seven to eight magnitudes lower than KC and KS, the contribution can be neglected.
4 Conclusions
This study systematically investigates the synthesis of CFNPs through a coprecipitation reaction combined with a hydrothermal process, utilising akaganeite nanorods as precursors. By carefully adjusting reaction parameters such as temperature, precursor-to-metal salt ratio, and sodium hydroxide concentration, various morphologies from truncated octahedral shapes were successfully obtained. An increase in temperature and a lower precursor-to-metal salt ratio significantly enhanced the shape anisotropy to mean values of up to 1.26 and allowed for a more focused size distribution. The comparison of crystallite sizes from the WH and the HW plot further confirms the consistency and reliability of these findings, where the HW fitting allows R2 values of up to 0.9998. Additionally, the estimated crystallinity of the synthesised particles indicates that the reaction conditions can be optimised to achieve high degrees of crystalline structures of up to 96% by setting a low precursor-to-metal salt ratio or a high molarity of the base.Secondly, this work focuses on enhancing the shape anisotropy of truncated octahedral NPs by changing the filling volume of the reactor. Specifically, higher filling volumes correlate with an increase in the proportion of elongated octahedral 3D shapes and elongated honeycomb 2D projections. The HR-TEM and SAED analysis confirmed the nanoparticles' inverse spinel structure and the elongation of the octahedra along the {222} facet.
Furthermore, shape anisotropy constants were determined by assuming a prolate spheroid model, which allowed for an accurate assessment of both magneto-crystalline and shape anisotropy contributions. The results revealed that the anisotropy constant KS varies significantly with increasing AR. As expected, shape anisotropy becomes dominant in more elongated particles with a notable increase in KS observed as AR exceeds 1.3. The distributions of AR and KS also increase with the size distribution. A more precise calculation of the KS values through a combination of M(H) and ACS measurements would be associated with optimising the stabilisation of the particle suspension. This could be achieved through additional stabilisation steps, which would not rely solely on electrostatic stabilisation via citrate but could also involve spatial stabilisation using, e.g., inorganic ligands, polymers, and silica shells.
As SAR is inversely proportional to the polydispersity of a sample within the examined single-domain diameter range, it is essential to explore synthetic approaches that result in monodisperse samples with high AR values. Understanding these interdependencies, future studies should aim to enhance the contribution of coffin-like particles with high anisotropy, as these shapes have the potential to significantly improve the performance of magnetic hyperthermia. Extending the experiments to flow reactors could be particularly beneficial, since flow profiles in such systems may positively influence the anisotropy of the particles. Additionally, an experimental investigation of the dependency of the anisotropy of coffin-like particles on hyperthermia efficiency is crucial. This requires more precise magnetic separation of the octahedral and coffin-like morphologies as well as their improved fluidic stabilisation in future studies. Addressing these current limitations and exploring these future perspectives will be essential to enhance the applicability of CFNPs in various biotechnological applications that require optimised magnetic and hyperthermia properties.
Data availability
The data supporting the results of this study can be found in the article and its ESI.† Should raw data be necessary, it can be made available by the corresponding author upon reasonable request.Author contributions
Maria Weißpflog: data curation, analysis, conceptualising, methodology, investigation, roles/writing – original draft, writing – review & editing. Dietmar Eberbeck: analysis, writing – review & editing. Birgit Hankiewicz: supervision, project administration, roles/writing – original draft, writing – review & editing.Conflicts of interest
There are no conflicts of interest.Acknowledgements
This work is supported by the German Research Foundation (Deutsche Forschungsgemeinschaft, DFG) for funding under Germany's excellence strategy within the project “nanohybrid” (RTG 2536). The authors gratefully acknowledge Stefan Werner for measuring the TEM samples and Andrea Köppen for examining the HR-TEM and SAED measurements. Furthermore, the authors would like to thank Robert Schön for conducting the SEM measurements.References
- L. Ajroudi, N. Mliki, L. Bessais, V. Madigou, S. Villain and C. Leroux, Mater. Res. Bull., 2014, 59, 49–58 CrossRef CAS.
- R. Jasrotia, J. Prakash, Y. B. Saddeek, A. H. Alluhayb, A. M. Younis, N. Lakshmaiya, C. Prakash, K. A. Aly, M. Sillanpää, Y. A. Ismail, A. Kandwal and P. Sharma, Coord. Chem. Rev., 2025, 522, 216198 CrossRef CAS.
- T. Tatarchuk, Nanomaterials, 2024, 14, 1640 CrossRef CAS PubMed.
- R. Perthel, G. Elbinger and W. Keilig, Phys. Status Solidi B, 1966, 17, 151–154 CrossRef CAS.
- C. Xiangfeng, J. Dongli, G. Yu and Z. Chenmou, Sens. Actuators, B, 2006, 120, 177–181 CrossRef.
- J. C. Almeida, C. E. D. Cardoso, D. S. Tavares, T. Trindade, C. Vale, R. Freitas and E. Pereira, Environ. Sci. Pollut. Res., 2024, 31, 28789–28802 CrossRef CAS PubMed.
- R. Jayalakshmi, J. Jeyanthi and K. R. Aswin Sidhaarth, Environ. Nanotechnol., Monit. Manage., 2022, 17, 100659 CAS.
- L. Wang, J. Li, Y. Wang, L. Zhao and Q. Jiang, Chem. Eng. J., 2012, 181–182, 72–79 CrossRef CAS.
- H. Kwon, Y. Yang, G. Kim, D. Gim and M. Ha, Anisotropy in magnetic materials for sensors and actuators in soft robotic systems, Nanoscale, 2024, 16, 6778–6819 RSC.
- A. Zeleňáková, Ľ. Nagy, P. Hrubovčák, M. Barutiak, M. Lisnichuk, V. Huntošová, A. Mrakovič, M. Gerina and D. Zákutná, J. Alloys Compd., 2024, 989, 174415 CrossRef.
- M. A. Medina, G. Oza, A. Ángeles-Pascual, M. González M, R. Antaño-López, A. Vera, L. Leija, E. Reguera, L. G. Arriaga, J. M. Hernández Hernández and J. T. Ramírez, Molecules, 2020, 25, 4428 CrossRef CAS PubMed.
- Y. Teng, S. Yuan, J. Shi and P. W. T. Pong, Adv. NanoBiomed Res., 2022, 2, 2200044 CrossRef CAS.
- J. Muhamad Arshad, W. Raza, N. Amin, K. Nadeem, M. Imran Arshad and M. Azhar Khan, Mater. Today: Proc., 2021, 47, S50–S54 Search PubMed.
- S. Bedanta, O. Petracic and W. Kleemann, Handbook of Magnetic Materials: Chapter 10 – Supermagnetism, Elsevier B. V., The Netherlands, 2015, pp. 1–83 Search PubMed.
- G. Nijhawan, S. S. Nijhawan and M. Sethi, Noble Metal-Metal Oxide Hybrid Nanoparticles: Chapter 12 – Hyperthermia Treatments, Elsevier Inc., Woodhead Publishing, United Kingdom, 2019, pp. 241–263 Search PubMed.
- R. E. Rosensweig, J. Magn. Magn. Mater., 2002, 252, 370–374 CrossRef CAS.
- F. L. Durhuus, M. Beleggia and C. Frandsen, Phys. Rev. B, 2024, 110, 144425 CrossRef CAS.
- S. Mørup, M. F. Hansen and C. Frandsen, Magnetic Nanoparticles, Elsevier B.V., The Netherlands, 2019, pp. 98–140 Search PubMed.
- G. Laufersky and T. Nann, Physical Chemistry of Nanoparticle Syntheses, Elsevier B.V., The Netherlands, 2019, pp. 1–16 Search PubMed.
- M. Beleggia, M. de Graef and Y. Millev, Philos. Mag., 2006, 86, 2451–2466 CrossRef CAS.
- B. D. Cullity and C. D. Graham, Introduction to Magnetic Materials, John Wiley & Sons, Inc., New Jersey, 2009 Search PubMed.
- D. M. Clarke, C. Marquina, D. C. Lloyd and G. Vallejo-Fernandez, J. Magn. Magn. Mater., 2022, 559, 169543 CrossRef CAS.
- A. A. McGhie, C. Marquina, K. O'Grady and G. Vallejo-Fernandez, J. Phys. D: Appl. Phys., 2017, 50, 455003 CrossRef.
- A. H. Habib, C. L. Ondeck, P. Chaudhary, M. R. Bockstaller and M. E. McHenry, J. Appl. Phys., 2008, 103, 07A307 CrossRef.
- G. Vallejo-Fernandez and K. O'Grady, Appl. Phys. Lett., 2013, 103, 142417 CrossRef.
- N. A. Wibowo, S. Pranoto, C. A. Riyanto and A. Setiawan, J. Phys. Theor. Appl., 2020, 4, 16 CrossRef.
- H. M. Joshi, Y. P. Lin, M. Aslam, P. V. Prasad, E. A. Schultz-Sikma, R. Edelman, T. Meade and V. P. Dravid, J. Phys. Chem. C, 2009, 113, 17761–17767 CrossRef CAS PubMed.
- A. L. Lopes-Moriyama, V. Madigou, C. P. de Souza and C. Leroux, Powder Technol., 2014, 256, 482–489 CrossRef CAS.
- Ž. Fabriciová, A. Zeleňáková, Ľ. Nagy, P. Hrubovčák, M. Barutiak, D. Zákutná and M. Lisnichuk, IEEE Trans. Magn., 2024, 61, 6500204 Search PubMed.
- R. Valdez, A. Olivas, D. B. Grotjahn, E. Barrios, N. Arjona, R. Antaño and M. T. Oropeza-Guzman, Appl. Surf. Sci., 2017, 426, 980–986 CrossRef CAS.
- C. L. Londoño-Calderón, A. Londoño-Calderón, S. Menchaca-Nal, N. A. Salazar-Henao, A. Rosales-Rivera, L. G. Pampillo and R. Martínez-García, J. Magn. Magn. Mater., 2020, 495, 165899 CrossRef.
- D. Lisjak, P. Jenuš and A. Mertelj, Langmuir, 2014, 30, 6588–6595 CrossRef CAS PubMed.
- D. Carlier and J.-P. Ansermet, J. Electrochem. Soc., 2006, 153, C277 CrossRef CAS.
- M. Weißpflog, N. Nguyen, N. Sobania and B. Hankiewicz, J. Phys. Chem. C, 2024, 128, 15598–15612 CrossRef.
- J. Li, Q. Wu and J. Wu, Handbook of Nanoparticles, Springer International Publishing, Switzerland, 2015, pp. 1–28 Search PubMed.
- M. Safaei, R. Sarraf-Mamoory, M. Rashidzadeh and M. Manteghian, J. Porous Mater., 2010, 17, 719–726 CrossRef CAS.
- Z.-Y. Ma, Z.-L. Yu, Z.-L. Xu, L.-F. Bu, H.-R. Liu, Y.-B. Zhu, B. Qin, T. Ma, H.-J. Zhan, L. Xu, H.-A. Wu, H. Ding and S.-H. Yu, Matter, 2020, 2, 1270–1282 CrossRef.
- N. K. V. Nadimpalli, R. Bandyopadhyaya and V. Runkana, Fluid Phase Equilib., 2018, 456, 33–45 CrossRef CAS.
- M. Sanna Angotzi, V. Mameli, C. Cara, D. Peddis, H. L. Xin, C. Sangregorio, M. L. Mercuri and C. Cannas, Nanoscale Adv., 2021, 3, 1612–1623 RSC.
- Y. Wang, K. Hu, J. He and Y. Zhang, RSC Adv., 2019, 9, 24783–24790 RSC.
- M. Basak, M. L. Rahman, M. F. Ahmed, B. Biswas and N. Sharmin, J. Alloys Compd., 2022, 895, 162694 CrossRef CAS.
- J. Scheck, T. Lemke and D. Gebauer, Minerals, 2015, 5, 778–787 CrossRef CAS.
- S. Alibeigi and M. R. Vaezi, Chem. Eng. Technol., 2008, 31, 1591–1596 CrossRef CAS.
- A. López-Ortega, E. Lottini, C. d. J. Fernández and C. Sangregorio, Chem. Mater., 2015, 27, 4048–4056 CrossRef.
- Z. L. Wang and X. Feng, J. Phys. Chem. B, 2003, 107, 13563–13566 CrossRef CAS.
- N. T. K. Thanh, N. Maclean and S. Mahiddine, Chem. Rev., 2014, 114, 7610–7630 CrossRef CAS PubMed.
- B. Muzzi, E. Lottini, N. Yaacoub, D. Peddis, G. Bertoni, C. de Julián Fernández, C. Sangregorio and A. López-Ortega, ACS Appl. Nano Mater., 2022, 5, 14871–14881 CrossRef CAS PubMed.
- M. A. Blesa, M. Mijalchik, M. Villegas and G. Rigotti, React. Solids, 1986, 2, 85–94 CrossRef CAS.
- T. Ishikawa, Y. Kondo, A. Yasukawa and K. Kandori, Corros. Sci., 1998, 40, 1239–1251 CrossRef CAS.
- F. Jones, M. I. Ogden, A. Oliveira, G. M. Parkinson and W. R. Richmond, CrystEngComm, 2003, 5, 159 RSC.
- Y. Mao, Y. Li, Z. Guo, B. Chen, Z. Qin, Z. Zhang, J. Sun and N. Gu, Colloids Surf., A, 2022, 647, 129107 CrossRef CAS.
- A. P. LaGrow, M. O. Besenhard, A. Hodzic, A. Sergides, L. K. Bogart, A. Gavriilidis and N. T. K. Thanh, Nanoscale, 2019, 11, 6620–6628 RSC.
- E. C. Vreeland, J. Watt, G. B. Schober, B. G. Hance, M. J. Austin, A. D. Price, B. D. Fellows, T. C. Monson, N. S. Hudak, L. Maldonado-Camargo, A. C. Bohorquez, C. Rinaldi and D. L. Huber, Chem. Mater., 2015, 27, 6059–6066 CrossRef CAS.
- B. D. Fellows, S. Sandler, J. Livingston, K. Fuller, L. Nwandu, S. Timmins, K. A. Lantz, M. Stefik and O. T. Mefford, IEEE Magn. Lett., 2018, 9, 1–5 Search PubMed.
- C. N. Chinnasamy, M. Senoue, B. Jeyadevan, O. Perales-Perez, K. Shinoda and K. Tohji, J. Colloid Interface Sci., 2003, 263, 80–83 CrossRef CAS PubMed.
- H. Tamura and E. Matijevic, J. Colloid Interface Sci., 1982, 90, 100–109 CrossRef CAS.
- S. Kakati, M. K. Rendale and S. N. Mathad, Int. J. Self-Propag. High-Temp. Synth., 2021, 30, 189–219 CrossRef CAS.
- Y. I. Kim, D. Kim and C. S. Lee, Phys. B, 2003, 337, 42–51 CrossRef CAS.
- J. Thomas, N. Thomas, F. Girgsdies, M. Beherns, X. Huang, V. D. Sudheesh and V. Sebastian, New J. Chem., 2017, 41, 7356–7363 RSC.
- A. Mitra, J. Mohapatra, H. Sharma and M. Aslam, Phys. Status Solidi A, 2017, 214, 1700505 CrossRef.
- T. Sugimoto, Monodispersed Particles: Part 1 – Fundamentals, Elsevier, Amsterdam, 2019, pp. 1–85 Search PubMed.
- T. Sugimoto, Monodispersed Particles: Part 2 – General Principles for the Formation of Monodispersed Particles, Elsevier, Amsterdam, 2019, pp. 187–207 Search PubMed.
- N. M. Refat, M. Y. Nassar and S. A. Sadeek, RSC Adv., 2022, 12, 25081–25095 RSC.
- P. Tancredi, P. C. Rivas-Rojas, O. Moscoso-Londoño, D. Muraca, M. Knobel and L. M. Socolovsky, J. Alloys Compd., 2022, 894, 162432 CrossRef CAS.
- J. Park, J. Joo, S. G. Kwon, Y. Jang and T. Hyeon, Angew. Chem., 2007, 119, 4714–4745 CrossRef.
- C. B. Whitehead, S. Özkar and R. G. Finke, Mater. Adv., 2021, 2, 186–235 RSC.
- S. Fayazzadeh, M. Khodaei, M. Arani, S. R. Mahdavi, T. Nizamov and A. Majouga, J. Supercond. Novel Magn., 2020, 33, 2227–2233 CrossRef CAS.
- C. R. Stein, M. T. S. Bezerra, G. H. A. Holanda, J. André-Filho and P. C. Morais, AIP Adv., 2018, 8, 056303 CrossRef.
- Suharyana, R. R. Febriani, N. P. Prasetya, Utari, N. A. Wibowo, Suharno, A. Supriyanto, A. H. Ramelan and B. Purnama, Kuwait J. Sci., 2023, 50, 575–579 CrossRef.
- D. V. Talapin, A. L. Rogach, M. Haase and H. Weller, J. Phys. Chem. B, 2001, 105, 12278–12285 CrossRef CAS.
- M. Goodarz Naseri, E. B. Saion, H. Abbastabar Ahangar, A. H. Shaari and M. Hashim, J. Nanomater., 2010,(1), 907686 CrossRef.
- A. Khan, A. M. Toufiq, F. Tariq, Y. Khan, R. Hussain, N. Akhtar and S. u. Rahman, Mater. Res. Express, 2019, 6, 65043 CrossRef CAS.
- G. E. P. Box, Biometrika, 1953, 40, 318 CrossRef.
- P. E. McKnight and J. Najab, The Corsini Encyclopedia of Psychology: Mann-Whitney U Test, John Wiley & Sons, Inc., New Jersey, 2010 Search PubMed.
- B. L. Welch, Biometrika, 1947, 34, 28 CAS.
- B. L. Welch, Biometrika, 1951, 38, 330 CrossRef.
- A. Virden, S. Wells and K. O'Grady, J. Magn. Magn. Mater., 2007, 316, e768–e771 CrossRef CAS.
- D. Faílde, V. Ocampo-Zalvide, D. Serantes and Ò. Iglesias, Nanoscale, 2024, 16, 14319–14329 RSC.
- A. Mandziak, J. E. Prieto, J. Dávalos, P. Prieto, M. Foerster, L. Aballe and J. de La Figuera, Appl. Surf. Sci., 2025, 689, 162408 CrossRef CAS.
- A. Aftabi, A. Babakhani and R. Khoshlahni, Sci. Rep., 2025, 15, 10039 CrossRef CAS PubMed.
- K. S. Sivaranjani, G. A. Jacob and R. J. Joseyphus, Phys. Status Solidi B, 2022, 259, 2200050 CrossRef CAS.
- H. Zhang, D. Zeng and Z. Liu, J. Magn. Magn. Mater., 2010, 322, 2375 CrossRef CAS.
- J. C. R. Araújo, C. A. M. Iglesias, J. Xavier, R. Pinto, R. B. da Silva, J. M. Soares, D. L. Mariano, M. d. A. V. Heringer, E. Baggio-Saitovitch, C. C. Plá Cid, S. N. de Medeiros, M. A. Morales, E. F. Silva, M. A. Correa and F. Bohn, J. Phys. Chem. Solids, 2025 DOI:10.2139/ssrn.5173441.
- N. S. Akulov, Z. Phys., 1931, 69, 822 CrossRef.
- D. Gandia, L. Gandarias, L. Marcano, I. Orue, D. Gil-Cartón, J. Alonso, A. García-Arribas, A. Muela and M. L. Fdez-Gubieda, Nanoscale, 2020, 12, 16081–16090 RSC.
- E. C. Stoner and E. P. Wohlfahrt, Philos. Trans. R. Soc. London, Ser. A, 1948, 240, 599–642 CrossRef.
- I. Volkov, M. Chukharkin, O. Snigirev, A. Volkov, S. Tanaka and C. Fourie, J. Nanopart. Res., 2008, 10, 487–497 CrossRef CAS.
- D. Bonvin, A. Arakcheeva, A. Millán, R. Piñol, H. Hofmann and M. Mionić Ebersold, RSC Adv., 2017, 7, 13159–13170 RSC.
- K. V. Chandekar and K. M. Kant, Superlattices Microstruct., 2017, 111, 610–627 CrossRef CAS.
- L. Lartigue, C. Innocenti, T. Kalaivani, A. Awwad, M. M. Del Sanchez Duque, Y. Guari, J. Larionova, C. Guérin, J.-L. G. Montero, V. Barragan-Montero, P. Arosio, A. Lascialfari, D. Gatteschi and C. Sangregorio, J. Am. Chem. Soc., 2011, 133, 10459–10472 CrossRef CAS PubMed.
- M. Gerina, M. Sanna Angotzi, V. Mameli, M. Mazur, N. Rusta, E. Balica, P. Hrubovcak, C. Cannas, D. Honecker and D. Zákutná, ACS Appl. Nano Mater., 2024, 7, 27210–27216 CrossRef CAS PubMed.
- D. Zákutná, D. Nižňanský, L. C. Barnsley, E. Babcock, Z. Salhi, A. Feoktystov, D. Honecker and S. Disch, Phys. Rev. X, 2020, 10, 031019 Search PubMed.
- S. Geng, H. Yang, X. Ren, Y. Liu, S. He, J. Zhou, N. Su, Y. Li, C. Xu, X. Zhang and Z. Cheng, Chemistry, 2016, 11, 2996–3000 CAS.
- N. A. Usov, M. S. Nesmeyanov and V. P. Tarasov, Sci. Rep., 2018, 8, 1224 CrossRef CAS PubMed.
- A. Ramzannezhad, P. Gill and A. Bahari, BioNanoMaterials, 2017, 18, 20170008 Search PubMed.
- J. S. Anandhi, T. Arun and R. J. Joseyphus, Phys. B, 2020, 598, 412429 CrossRef CAS.
- H. Mamiya, H. Fukumoto, J. L. Cuya Huaman, K. Suzuki, H. Miyamura and J. Balachandran, ACS Nano, 2020, 14, 8421–8432 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Specific conditions for the preparation and stabilisation of the nanoparticles. Analysis of the crystal phases, crystallite sizes, and strains. TEM images of the initial reaction. Analysis of the size and aspect ratios using TEM measurements. Additional angle-dependent SEM measurements. Determination of the crystal planes and d-spacings using HR-TEM and SAED measurements. Alternating current susceptibility measurements. Distribution of the shape anisotropy constants by implementing size intervals. Determination of the surface anisotropy constants. See DOI: https://doi.org/10.1039/d5ra02233a |
| This journal is © The Royal Society of Chemistry 2025 |