DOI:
10.1039/D5RA02081F
(Paper)
RSC Adv., 2025,
15, 16901-16920
A novel Araucaria gum/carrageenan/Mg–Fe LDH nanocomposite for advanced batch and fixed-bed adsorption of mercuric ions from aqueous medium
Received
24th March 2025
, Accepted 8th May 2025
First published on 20th May 2025
Abstract
In the present work, several meticulously planned batch and fixed-bed adsorption experiments were performed to compare the adsorption capacities of the synthesized magnesium-ferric layered double hydroxide (Mg–Fe LDH, MFL), carrageenan/Mg–Fe LDH nanocomposite (MFC), and Araucaria gum/carrageenan/Mg–Fe LDH nanocomposite (MFAC) for mercuric ion removal from aqueous medium. Various physicochemical approaches were conducted to characterize the fabricated adsorbents, proving the successful incorporation of potassium κ-carrageenan and Araucaria gum on the LDH surface. The relatively greater particle size (130 nm), irregular pore distribution, average pore radius (3.2086 nm), and pHPZC (6.25) of MFAC were mainly responsible for its superior Hg2+ adsorption. Through a series of batch adsorption tests, Hg2+ adsorption on the MFAC nanocomposite exhibited a maximum adsorption capacity of 505.74 mg g−1 at 20 °C, pH 6, and a solid dosage of 2 g L−1 after 30 min. Several kinetics and isotherms were well-fitted for the adsorption process. Fixed-bed column tests proved that MFAC achieved 550.50 mg g−1 at a bed height of 1 cm, a Hg2+ solution concentration of 80 mg L−1, and a flow rate of 30 mL min−1 at 20 °C and pH 6 over 300 min. Thus, MFAC can be efficiently applied in wastewater treatment, offering major support for further research into practical applications.
1. Introduction
Water contamination is one of the most essential environmental challenges that motivates researchers worldwide to take action due to the existence of heavy metal ions in groundwater, wastewater, and industrial effluents. Environmental heavy metal pollution is pervasive and primarily caused by industrial activities. Because of their biomagnification and bioaccumulation in the food chain and organisms, heavy metals have a major impact on animal health as well as the ecosystem.1 Even in trace amounts, heavy metal ions are highly toxic to living cells, are highly stable, require advanced techniques for detection, are highly soluble in water, and can destroy freshwater supplies.2 As a result, heavy metal ions (Mn+) can cause several human health issues. Wastewater containing dangerous Mn+ ions such as lead, mercury, arsenic, cadmium, or chromium can cause acute or chronic heavy metal poisoning. These poisoning symptoms include kidney pathologies, gastrointestinal difficulties, an elevated risk of cancer, neurological disorders, developmental abnormalities in children, respiratory illnesses, and organ damage.3,4 Mercuric ions (Hg2+) are regarded as one of the most hazardous metals ions after arsenic (As5+). Its negative effect multiplies after Hg2+ is converted to more toxic methylmercury because it can attach to enzymes and proteins.4 The primary sources of Hg2+ ions in aqueous environments include various industries such as the production of paper and pulp, oil refineries, chlor-alkali wastewater, gold extraction, and indirect mercury emission from fossil fuels burning, particularly coal.2 However, numerous disorders and diseases result from the environmental release of these metallic ions. People who are exposed to mercury on a long-term basis can develop many illnesses that impact their immune, neurological, and cardiovascular systems.5 Consequently, the European Union (EU) and United States (US) Environmental Protection Agencies (EPA) have set maximum contamination levels (MCLs) for Hg2+ in drinking water at 1.0 and 0.2 μg L−1, respectively.1 Additionally, US EPA declared that the level of wastewater discharged with mercuric ions must not exceed 5 μg L−1.6 Because of the flowability and refractory nature of mercury ions, the development of technologies and materials for eliminating mercuric ions from aqueous solutions is critically needed to prevent its negative effects on the human population and ecosystems.
Until now, there have been various techniques to remove Hg2+ from wastewater, including coagulation, flocculation, chemical precipitation,7 chemical reduction,8 ion exchange,9 biological treatment,10 reverse osmosis, membrane separation,11 and other methods. The main problems with applying these methods to remove Hg2+ are related to their demanding elimination process of waste products and high cost. Hence, researchers have focused on adsorption technology because of its high performance, adsorbent regeneration, insensitivity to toxic materials, affordability, low cost, simplicity, versatility, mature technical means, and ability to use in both batch and column modes. Adsorbent properties are fundamental for heavy metal removal so determining preparation conditions is essential to optimize functional groups, pore size distribution, and surface area for enhancing the adsorption capacity.12 There is a wide group of adsorbents from chemical and biological sources such as magnetic nanocomposites, metal–organic frameworks,5 graphene oxide composites,13 microorganisms, biochar,14 waste biomass,15 and polymer-based and carbon-based materials that are effective and inexpensive in removing Hg2+ from aqueous media. Nevertheless, layered double hydroxide materials have emerged as a promising popular topic for researchers due to their special benefits.
Layered double hydroxides (LDHs) are anion-exchange materials formed of layers with the formula: [M1−x2+ Mx3+ (OH)2]x+ [Ax/mm−]·nH2O, where Am− is the interlayer anion (SO42−, OH−, CO32−, NO3−, Cl−, etc.), and M2+ and M3+ are divalent and trivalent metal cations. X is an M2+/M3+ molar ratio ranging from 2 to 4.16 The LDH structure is similar to brucite, in which M2+ is surrounded by six hydroxide ions, forming an octahedral array linking together and producing an infinite 2D nanostructure. In the primary hydrotalcite layer, trivalent metal cations replace divalent metal cations, preserving the original structure and producing a positively charged layer. To neutralize the charge of these layers, anions are present in the interlayer spaces, balancing this layer. The presence of water molecules in the interlayer spaces can also aid in the stabilization of the structure.17 LDHs have attracted significant attention because of their unique features in biomedical science, magnetization, polymerization, electrochemistry, photochemistry, catalysis, and environmental applications. Moreover, LDHs are easy to synthesize in the lab using common chemicals by deposition/precipitation reactions, precursor LDH anion exchange, structural reconstruction, electrochemical techniques, co-precipitation, sol–gel, urea hydrolysis, and hydrothermal synthesis.18 Recently, calcined layered double hydroxides have been extensively employed as promising adsorbents for the treatment of contaminants like organic dyes,19 pharmaceutics, insecticides, CO2,20 and especially heavy metals in wastewater. This is because of their unique physicochemical characteristics such as high specific surface area, modification possibility, strong hydrophobicity, cost-effectiveness, tunable architecture, high negative interlayer spaces (high porosity), high efficiency, and “memory effect” recovering the original LDH by calcined LDHs' rehydration.17,21 Moreover, LDHs tend to adsorb heavy metals by many mechanisms, including isomorphous substitution, ion exchange, surface complexation, and electrostatic interactions.22 Nevertheless, pristine LDHs have some drawbacks, including multilayered stacking, high discharge rates, and time-consuming recovery from aqueous solutions. Therefore, it is necessary to functionalize LDHs with various compounds such as polymers to multiply their functions and improve the adsorption capacity.
One of the cheap natural hydrophilic polysaccharides, κ-carrageenan derived from specific marine red algae species is widely utilized as a gelling agent in the food and biomedical industries and as a biocatalyst.23 It is an anionic sulfated polysaccharide with interesting characteristics such as nontoxicity, mucoadhesion, biodegradability, and biocompatibility. The ionic groups in this hydrogel provide an extra benefit for eliminating positively charged contaminants from wastewater. Though these advantages, carrageenan ability to adsorb Mn+ still has some drawbacks, including unstable composition, weak gel strength, and high-water solubility. Hence, its adsorption properties can be improved via chemical and physical modifications through crosslinking, grafting, composite creation with clays, carbon-based materials, magnetic nanoparticles, and other polymers.24 This leads to the development of nanocomposite materials with a high adsorption capacity, a high surface area/volume ratio, and effective functional groups. Rahmani et al. fabricated magnetic κ-carrageenan with a maximum adsorption capacity for Cu2+, Hg2+, Pb2+, and Cd2+ reached 107.6, 99.2, 114.6, and 94.2 mg g−1, respectively.23 Omer et al. showed that the Pb2+ was removed by GO@Fe3O4-i.Carr with a removal percent of 93.68% within a fast equilibrium of nearly 30 min.24 Additionally, a class of naturally occurring hydrophilic polysaccharides is gum. The low cost, environmental friendliness, nontoxicity, and availability of gum make it a valuable pharmaceutical excipient with reported antibacterial, anti-ulcerogenic, anticytotoxic, anticancer, antioxidant, and bioactive effects.25 Araucaria gum is made from the bark exudates of the Araucaria heterophylla plant, and the genus Araucaria has about 14 species. The physical and chemical characteristics of Araucaria gum are large, brittle, unevenly shaped, hard by nature, and rich with hydroxyl groups.26 However, Araucaria gum without modifications lacks selectivity and needs to be functionalized to be more effective in wastewater treatment. Araucaria gum was used in environmental applications for the first time in our previous work and wasn't used yet. Where Khoj et al. prepared Araucaria gum/calcium alginate composite beads for the Pb2+ ions adsorption, attaining an adsorption capacity of 149.95 mg g−1.27 Nevertheless, to our knowledge, Araucaria gum/carrageenan/Mg–Fe LDH nanocomposite hasn't been reported for Hg2+ removal from aqueous medium.
In the present study, we intended to synthesize efficient adsorbents with a high adsorption capacity, stability in water, high physical strength, and large surface area for the toxic Hg2+ removal from wastewater. For this goal, magnesium-ferric layered double hydroxide (Mg–Fe LDH, MFL) was synthesized and then functionalized with potassium κ-carrageenan (KG) and with the naturally fabricated Araucaria gum (AR), creating carrageenan/Mg–Fe LDH nanocomposite (MFC) and Araucaria gum/carrageenan/Mg–Fe LDH nanocomposite (MFAC). The prepared materials were characterized using various methods such as ATR-FTIR, TGA, XRD, N2 adsorption–desorption, SEM, TEM, and zeta potential. The experimental conditions’ effects such as pH, temperature, adsorbent dosage, shaking time, and initial Hg2+ ions concentration was investigated for the batch adsorption. The adsorption kinetics, isotherms, and thermodynamics parameters for the batch adsorption process were evaluated. Column adsorption was also studied under different application conditions such as bed height, flow rate, and initial Hg2+ concentration.
2. Materials and methods
2.1. Materials
Magnesium nitrate hexahydrate (Mg (NO3)2·6H2O, 99%), ferric nitrate nonahydrate (Fe (NO3)2·9H2O, ≥98.0%), hydrochloric acid (37%), sodium hydroxide (NaOH, ≥98.0%), κ-carrageenan, potassium chloride (KCl, ≥99.0%), mercuric chloride (HgCl2, ≥99.5%), and acetone (≥99.5%) were obtained from Sigma Aldrich. Bark exudates from Araucaria heterophylla trees were gathered from trees in special gardens in New Damietta City, Egypt.
2.2. Synthesis of adsorbents
2.2.1. Synthesis of magnesium-ferric layered double hydroxide nanoparticles (MFL). Mg–Fe LDH was synthesized by co-precipitation of solutions of magnesium nitrate hexahydrate and ferric nitrate nonahydrate (Mg/Fe molar ratio = 3) at constant pH in the existence of NaOH. Firstly, 300 mL of a solution containing Mg (NO3)2·6H2O (0.400 M) and Fe (NO3)2·9H2O (0.133 M) were prepared under continuous stirring for 1 h. Next, a solution of sodium hydroxide (1 M) was dripped slowly into the previous solution through titration while keeping the mixture pH 8.7–12.5 to precipitate Mg–Fe LDH under vigorous magnetic stirring, regarding the precipitation of Fe(OH)3 at pH > 4.5. The resulting mixture was magnetically stirred at 60 °C for 3 h and aged for 24 h. Then, the precipitate was filtered, rinsed with distilled water, and dried at 85 °C. Finally, the material was calcined for 3 h at 400 °C to break the weak hydrogen bonds in LDH and partially eliminating the interlayer water molecules and intercalated anions.28
2.2.2. Extraction of Araucaria gum (AR). The bark exudates from Araucaria heterophylla tree were gathered in October, dried, and ground. Using an impeller, the powder was combined with demineralized water for 4 h. Next, filtration removed the impurities through a muslin cloth. Precipitating the gum was done by treating the extract with aliquots of acetone. In a vacuum desiccator, the precipitate was detached and dried at 60 °C for 48 h. After being pulverized in a lab blender and passing through an 80 mesh sieve to obtain uniformly sized particles, the dried gum was stocked in an airtight container.29
2.2.3. Synthesis of carrageenan/Mg–Fe LDH nanocomposite (MFC). Carrageenan/Mg–Fe LDH nanocomposite was fabricated by in situ co-precipitation technique. Firstly, 100 mL of κ-carrageenan solution (1% w/v) was prepared at 80 °C under continuous stirring. Next, 1 g of Mg–Fe LDH was dispersed in 50 mL of distilled water, treated ultrasonically, and then added to the carrageenan solution under magnetic stirring for 1 h till homogeneity. Using a syringe, the resulting mixture was added dropwise into 200 mL of KCl (1.3 mol L−1) under stirring for 1 h. Eventually, the product was centrifuged, cleaned with distilled water several times, and dried at 80 °C.
2.2.4. Synthesis of Araucaria gum/carrageenan/Mg–Fe LDH nanocomposite (MFAC). Two separate solutions of κ-carrageenan (1 g, 50 mL H2O) and Araucaria gum (1 g, 50 mL H2O) were prepared under stirring at 70 °C and then mixed. After that, 1 g of Mg–Fe LDH was dispersed in 50 mL of distilled water, treated ultrasonically, and then added to the previous mixture with stirring for 1 h till homogeneity. To prepare nanocomposite beads, the resulting solution was dropped gradually by a syringe into 200 mL of KCl (1.3 mol L−1) under stirring for 1 h. Finally, the resulting beads were treated as the above-prepared nanocomposite.30
2.3. Physicochemical characterization of the solid adsorbents
Various analytical techniques were used in this study to characterize the prepared materials. Setaram–Labsys–Evo S60 thermogravimetric analyzer was employed to perform thermogravimetric analysis (TGA), heating materials from ambient temperature up to 850 °C with 10 °C min−1 as heating rate. The crystal structure of the samples was recorded by X-ray diffraction (XRD, Bruker D2 Phaser 2nd Gen) utilizing a Cu Kα radiation source. XRD patterns were determined using a scan period of 132 s and a step size of 0.04° per step from 10 to 80°. Gas sorption analyzer (BELSORP MAX X, MicrotracBEL Corp., Japan) measured the textural parameters and pore structure of the materials by the standard N2 adsorption technology at 77 K. ATR-FTIR spectroscopy (ZnSe crystal on Nicolet Impact 400 D) was employed with a resolution of 4.0 cm−1 and a scan range from 4000–400 cm−1 to analyze the functional groups of the prepared adsorbents before and after mercuric adsorption. Zeta potential changes are completed by determining the point of zero charge (pHPZC) of adsorbents (Zetasizer, Nano S, Malvern Instrument, UK). The surface morphology was characterized by scanning electron microscopy (SEM, JEOL JSM-6510LV, Japan) and transmission electron microscopy (TEM, JEOL-JEM-2100 model, Japan).
2.4. Batch adsorption experiments of mercuric ions
Adsorption of Hg2+ onto MFL, MFC, and MFAC in a batch system was investigated as follows: 0.05 g adsorbent was soaked into 25 mL of 900 mg L−1 of Hg2+ concentration and shaken for 60 min at pH 6 and 20 °C. Moreover, several tests were conducted to study the adsorption performance according to different effects as initial Hg2+ concentration (30–900 mg L−1), shaking time (1–70 min), pH (1–8), adsorbent dose (0.4–3.0 g L−1), and temperature (20–45 °C). Each experiment was carried out 3 times to obtain average value and the error bars were depicted in the related figures. The unadsorbed Hg2+ concentration was centrifuged and then measured by iCAP Q ICP-MS, Thermo Fisher, Germany. The maximum adsorption capacity of the solid adsorbents (Qe, mg g−1, eqn (1)) and Hg2+ removal percent (R%, eqn (2)) were computed as follows:| |
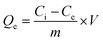 | (1) |
| |
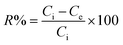 | (2) |
where, Ci and Ce denote the initial and final Hg2+ concentration (mg L−1), respectively. m is the adsorbent mass (g) and V is the aqueous Hg2+ solution volume (L).
2.4.1. Adsorption kinetics. The nonlinear kinetic models as pseudo-first-order (PFO, eqn (4)), pseudo-second-order (PSO, eqn (5)), Avrami (eqn (6)), Elovich (eqn (7)), Bangham's pore diffusion (eqn (8)), intra-particle diffusion (eqn (9)), and linear Boyd (eqn (10)) scrutinized the experimental data of the Hg2+ uptake.27,31| |
 | (3) |
| |
 | (5) |
| | |
Qt = [1 − e−(KAVt)nAV] × QAV
| (6) |
| |
 | (7) |
| |
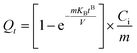 | (8) |
| |
 | (10) |
Herein, the residual Hg2+ concentration at time t is expressed by Ct (mg L−1). The adsorbed Hg2+ quantity at time t (min) and equilibrium is represented by Qt (eqn (3)) and Qexp (mg g−1), respectively. k1 (min−1) and k2 (g mg−1 min−1) are PFO and PSO models' rate constants, successively. nAV, KAV (min−1), and QAV (mg g−1) correlate to the order, rate constant, and adsorption capacity of Avrami model, respectively. The initial Hg2+ adsorption rate and surface coverage quantity are symbolized by α (mg g−1 min−1) and β (g mg−1), respectively. Bangham's constants are signified by KB (mL L g−1) and B (<1). k0 (mg g−1 min1/2), C, and Bt are the intra-particle diffusion rate constant, boundary layer thickness, and Boyd constant, respectively.
2.4.2. Adsorption isotherms. The nonlinear adsorption isotherm models: Langmuir (eqn (11)), Freundlich (eqn (13)), Temkin (eqn (14)), Dubinin–Radushkevich (DR, eqn (15)), Redlich–Peterson (eqn (17)), Sips (eqn (18)), and Toth (eqn (19)) determine the capacity of the synthesized adsorbents for Hg2+ adsorption from the aqueous solution.31,32| |
 | (11) |
| |
 | (12) |
| |
 | (13) |
| |
 | (14) |
| |
 | (16) |
| |
 | (17) |
| |
 | (18) |
| |
 | (19) |
where, the equilibrium Langmuir constant attributed to bond formation energy, and maximum adsorption capacity are described by b (L mg−1) and Qm (mg g−1), respectively. The dimensionless constant values of 0 < KL < 1, KL > 1, KL = 1, and KL = 0 reflect that the adsorption nature which may be favorable, unfavorable, linear, and irreversible, respectively as calculated by eqn (12). KF (L1/n mg1−1/n g−1) is Freundlich constant and n is the surface heterogeneity factor correlated to adsorption intensity. Temkin constants are expressed by KT (L g−1) and bT (J mol−1). T (K) is the temperature in Kelvin and R (8.314 J mol−1 K−1) is the gas adsorption constant. EDR (kJ mol−1, eqn (16)), KDR (mol2 kJ−2), and ε denote the mean adsorption-free energy, DR constant, and Polanyi potential, successively. DR, Sips, and Toth adsorption capacity are symbolized by QDR, Qs, and Qth (mg g−1), successively. Redlich–Peterson, Sips, and Toth isotherm constants and exponents are represented by ((KRP (L g−1) and αRP (mg L−1)−g), g), (Ks (L g−1), ns), and (Kth (L mg−1), nth), respectively.
2.4.3. Adsorption thermodynamic parameters. The adsorption feasibility of Hg2+ onto MFL, MFC, and MFAC was explained using thermodynamic parameters like enthalpy (ΔH°, kJ mol−1), entropy (ΔS°, kJ mol−1 K−1), and Gibbs free energy (ΔG°, kJ mol−1) changes. The previous thermodynamic parameters were calculated by applying different equations as distribution coefficient (Kd, eqn (20)), Gibbs–Helmholtz equation (eqn (21)), and van't Hoff equation (eqn (22)).30,33| |
 | (20) |
| |
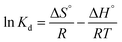 | (22) |
2.4.4. Hg2+ desorption and solid adsorbent reusability. The batch desorption study of mercuric ions was conducted by agitating 0.1 mol L−1 of several desorbing agents (KCl, thiourea, EDTA, ethylene diamine, and HCl) with Hg2+-pre-loaded adsorbent for 30 min at 20 °C. Then, the desorbed Hg2+ concentration was measured as stated above. The desorption percent (D.E.%) was calculated as follows.| |
 | (23) |
Herein, V (L), Q (mg g−1), m (g), and Cdes (mg L−1) are the eluent volume, maximum adsorption capacity, adsorbent mass, and desorbed Hg2+ concentration after the desorption process, respectively.The reusability of solid adsorbents was examined by repeating the Hg2+ adsorption/desorption cycles eight times. Hg2+ adsorption was achieved at a concentration of 900 mg L−1, an adsorbent dosage of 2 g L−1, pH 6, 20 °C, and 30 min as a shaking time. To remove the pre-absorbed Hg2+, the adsorbent was filtered and rinsed with 50 mL of 0.1 mol L−1 EDTA after each run. It was then cleaned with deionized water and dried at 70 °C so that it could be used in the next adsorption cycle.
2.5. Column adsorption experiments of mercuric ions
MFAC was chosen as packing material in a fixed-bed column during continuous tests to remove Hg2+ from aqueous solutions according to its maximum batch adsorption capacity. A plexiglass column with a 2 cm inner diameter and a 20 cm height was packed with pure dried sand. A known quantity of MFAC composite at different bed heights was filled into the column. Glass beads were placed into the two column ends to keep the sample from falling off the column and to maintain a constant flow rate at the water input and outlet. Firstly, distilled water was poured through the adsorbent bed to eliminate air trapped and impurities, and to ensure additional dense packing. Utilizing a peristaltic pump, a solution with a known initial Hg2+ concentration was fed through the column at a certain flow rate at 20 °C and pH 6. In the present study, the factors varied are the bed height (BH, 1. 2, and 3 cm), inlet flow rate (μ, 15, 20, 30 mL min−1), and initial Hg2+ concentration (Ci, 40, 80, 150 mg L−1), which were studied by graphing Ct/Ci against t (min) to produce breakthrough curve (BTC). Later, the effluent concentration of Hg2+ from the outlet was measured at regular intervals (up to 300 min) and Hg2+ concentrations were measured as discussed before.
Calculating the parameters of the breakthrough curve is a crucial step in analyzing and assessing the column adsorption performance. The exhaustion time (te, min) was computed as the period when the effluent Hg2+ concentration reached roughly 95% of the influent concentration (Ci, mg L−1) (i.e., Ct/Ci = 0.95), while the breakthrough time (tb, min) is the time at which the effluent Hg2+ concentration (Ct, mg L−1) equaled 5% of the influent concentration (i.e., Ct/Ci = 0.05).
The integrated area above the breakthrough curve represented by the adsorbed concentration as a time function at specific adsorption settings was utilized to estimate the total adsorbed quantity of Hg2+ (Qtotal, mg) as followed in eqn (24). Qtotal was determined at nearly 80% of column saturation (i.e., Ct = 0.8 × Ci) to prevent experimental procedures from being misinformed. The maximum adsorbed Hg2+ amount (Q0, mg g−1) was measured by eqn (25), where the packed bed weight in the column is symbolized by m (g).27
| |
 | (24) |
| |
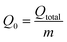 | (25) |
The solution flow rate (μ, mL min−1) (eqn (26)) was estimated by the ratio of total effluent volumes (Veff): total flow time (ttotal) as follows:
| |
 | (26) |
The mass transfer zone (MTZ), where the adsorption takes place, was evaluated as follows:34
| |
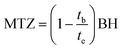 | (27) |
Various nonlinear kinetic column models including Yoon-Nelson (eqn (28)), Thomas (eqn (29)), Clark (eqn (30)), and Yan (eqn (31)) are valuable tools for assessing and predicting the column adsorption efficiency of mercuric ions onto MFAC.35
| |
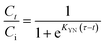 | (28) |
| |
 | (29) |
| |
 | (30) |
| |
 | (31) |
where,
τ is the time (min) at
Ct/
Ci = 0.5.
KYN (min
−1),
KTh (L mg
−1 min),
r (min
−1), and
KY (L mg
−1 min
−1) = Yoon–Nelson, Thomas, Clark, and Yan rate constants, respectively.
Veff = the effluent Hg
2+ solution volume (L).
QTh and
QY denote to Thomas and Yan column adsorption capacities (mg g
−1).
A is Clark parameter and
n is related to Freundlich isotherm exponent.
3. Results and discussion
3.1. Characterization of the fabricated adsorbents
The thermal treatment of MFL, MFC, and MFAC under temperatures from room temperature up to 850 °C is demonstrated in Fig. 1a. The overall loss of MFL, MFC, and MFAC mass was 13.2, 40.2, and 25.8%, respectively. TGA curve of MFL is divided into three stages. The mass loss of the first stage from the beginning to 245 °C was 3.1%, resulting from the removal of physisorbed water molecules. In the second stage between 245 and 420 °C, the mass loss was 6.0%, mostly related to the intercalated anions being removed and the dehydroxylation linked to the interlayer water removal.19 The final weight loss observed over a temperature from 420 to 545 °C was 4.1%, corresponding to the continual release of strongly bound nitrate anions and hydroxide layers breaking down due to the ensuing metal oxides from dehydroxylation. As a result, small MgO domains linking Fe3+ were formed, and this process is considered as one of the main causes of porosity development. Lastly, Mg–Fe LDH showed high thermal stability above 545 °C, where the mass remained constant, evolving a thermodynamically stable spinel phase (MgFe2O4).36 TGA curves of MFC and MFAC displayed an initial mass loss of 6.9 and 3.4%, respectively up to 210 °C, resulting from the adsorbed water evaporation. The significant second loss of 22.4 and 17.3 wt% of MFC and MFAC from 210 to 450 °C was caused by the polysaccharide backbone degradation or breaking down of the glycosidic bonds between units.23 The 10.9 and 5.1% third weight loss for MFC and MFAC, respectively up to 800 °C, included destroying the remaining organic materials, containing the sulfate groups, and remaining the inorganic residue. These previous three decomposition stages were besides those of MFL. Furthermore, the addition of AR to MFC composite strengthened the structure of MFAC nanocomposite with higher thermal stability. The better dispersion of Mg–Fe LDH in the samples' structure was correlated to the thermal stability enhancement, favoring the shielding effect.37
 |
| | Fig. 1 TGA (a), XRD (b), N2 adsorption (c), ATR-FTIR (d), zeta potential (e) curves for MFL, MFC, and MFAC, additionally, XRD for AR gum and ATR-FTIR curve of MFAC after Hg2+ adsorption. | |
XRD diffraction patterns of the synthesized samples (MFL, AR, MFC, and MFAC) are depicted in Fig. 1b. The analysis of XRD curve of MFL exhibited reflections at 2θ of 35.6, 42.9, and 62.0° with broad peaks of (111), (200), and (220) planes, respectively (JCPDS Card No. 01-1157), indicating the removal of some water and interlayer anions as well as a partial breakdown of the original LDH after the sample calcination at 400 °C for 3 h.38 This resulted in the creation of a periclase (MgO) phase in a major amount, showing the successful synthesis of Mg–Fe LDH.39 These wide peaks suggested an amorphous phase or a nanocrystalline substance with very small nanoparticles. The curve showed no additional impurity peaks, suggesting that the synthesized LDH only had one crystal orientation. The segregated phases weren't detected, suggesting that the oxides of transition metal were uniformly dispersed in Mg2+ and Fe3+ oxide matrix.40 XRD graph of Araucaria gum was highly amorphous with a broad peak around 2θ of 20°, revealing the disordered gum structure.27 In terms of MFC and MFAC, the crystalline nature of potassium κ-carrageenan dominated MFC and MFAC nanocomposites, resulting from the crosslinking of SO42− groups of the amorphous κ-carrageenan with K+ ions, yielding an ordered double helical structure and increasing the crystallinity of Mg–Fe LDH. Where very sharp peaks demonstrated at 2θ values of 28.4, 40.5, 50.2, 58.6, 66.4, and 73.7° related to the planes of (200), (220), (222), (400), (420), and (422), respectively (JCPDS No. 41-1476), which were characteristic to the crystalline diffraction of potassium chloride.32 The reflection peaks of MFL considerably disappeared during the composites' preparation, implying that MFL was positively restructured with dispersed and loaded KG and AR. The peaks' intensity of MFAC is sharper than that of MFC, indicating the successful intercalation of MFL with KG and AR, and enhancing the adsorption characteristics of MFAC.
The surface area and pore architectures of MFL, MFC, and MFAC were investigated by applying N2 adsorption–desorption isotherm, and Table 1 records their corresponding pore parameters. The study found that N2 desorption and adsorption patterns differed, with a characteristic hysteresis loop forming, causing pore filling through capillary condensation during adsorption, and pore emptying through evaporation during desorption. As depicted in Fig. 2c, based on IUPAC standards, the adsorbents manifested type IV adsorption–desorption isotherm and H3 type of hysteresis loop; which suggested the coexistence of slit-shaped well-ordered mesopores of filling plate-like particles.41 Where the mesoporosity produced by the linked stacking structure of LDH and biopolymers accounted for the porosity majority. The exhibited hysteresis loops ranged from relative pressure (P/P0) of 0.99 to 0.43, 0.51, and 0.49 in the case of MFL, MFC, and MFAC, respectively. These findings demonstrated the lamellar architecture of the materials and multilayered physical adsorption of nitrogen between platelet particle aggregates. The findings in Table 1 reveal that MFL demonstrated a great specific surface area (SBET) of 185.90 m2 g−1 and total pore volume (VT) of 0.1552 cm3 g−1. This was related to the partial elimination of intercalation ions and interlayer water from the interlayer space, which promoted ease of access into the interlayer space and unobstructed the LDH's porous structure. Moreover, when LDH was being calcined, its layered structure became more disorganized. This led to a large number of surface-active sites, which improved Hg2+ ion adsorption and made it easier for ions to diffuse into adsorbent interiors. However, MFC and MFAC nanocomposites have significantly decreased surface areas of 3.65 and 7.48 m2 g−1, respectively in comparison with MFL, as proved in the measured total pore volumes. This was illustrated that during the preparation of MFC and MFAC nanocomposites, the dissolved biopolymers were stirred with LDH and entered between layers and pores of Mg–Fe LDH. Also, with the addition of potassium ions as a crosslinking agent, the formed crystalline potassium κ-carrageenan biopolymer may sharply diminish the surface area of the formed composite, which mainly originated from the pores and layered function of MFL. These results aligned with those of related studies.42–44 Furthermore, the mesoporosity of the materials was shown from the average pore radius (![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ) values ranging from 3.0685–3.3425 nm.
) values ranging from 3.0685–3.3425 nm.
Table 1 Characterization parameters for the synthesized solid adsorbents
| Sample |
pHPZC |
SBET (m2 g−1) |
VT (cm3 g−1) |
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (nm) (nm) |
| MFL |
6.53 |
185.90 |
0.1552 |
3.3425 |
| MFC |
5.98 |
3.65 |
0.0028 |
3.0685 |
| MFAC |
6.25 |
7.48 |
0.0060 |
3.2086 |
 |
| | Fig. 2 SEM (a–c) and TEM (d–f) images for MFL, MFC, and MFAC, respectively. | |
ATR-FTIR spectra of all the prepared materials in addition to MFAC after the adsorption of Hg2+ (Hg2+/MFAC) are displayed in Fig. 1d ranging from 400 to 4000 cm−1. MFL spectrum is similar to other phases with counter anions that resemble hydrotalcite. A broad and strong absorption band around 3445 cm−1 was linked to the hydroxyl stretching formed by hydrogen-bonded interlayer water molecules and metal-hydroxyl groups in LDH. Other absorption peaks at 1383 and 1626 cm−1 corresponded to the stretching vibration of interlayer nitrate anions and water deformation.38 The distinctive stretching vibrations of the crystal lattice of magnesium and iron oxides (Mg–O or M–O–M) were superposed in bands between 462 and 660 cm−1.45 FTIR spectrum of MFC maintained the characteristic bands of MFL in addition to the appearance of bands of KG. Whereas, strong broadband around 3456 cm−1 and bands at 2915, 1644, 1393, 1259, 1073, 931, and 854 cm−1 referred to O–H stretching vibration, C–H stretching, O–H bending vibration, sulfate group, symmetric stretching vibration of (O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S
S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) sulfate ester, glycosidic linkage or C–OH stretching, C–O–C in 3,6-anhydrogalactose stretching vibration, and C–O–S stretching vibration, respectively.32 In the case of MFAC curve, the bands were shifted only compared to MFC, asserting the successful intercalation of KG and AR into the LDH structure. There was also a minor weakening of the intensity of some absorption bands with a slight shift in MFAC spectrum following the adsorption of Hg2+ ions. This may result from the surface complexation of functional groups (–OH and M–O), electrostatic interaction of OSO3−, and isomorphic displacement of Mg2+ with Hg2+ ions, reducing the vibration intensity of Mg–O bond, showing the dominant role of these functional groups in the Hg2+ removal.46
O) sulfate ester, glycosidic linkage or C–OH stretching, C–O–C in 3,6-anhydrogalactose stretching vibration, and C–O–S stretching vibration, respectively.32 In the case of MFAC curve, the bands were shifted only compared to MFC, asserting the successful intercalation of KG and AR into the LDH structure. There was also a minor weakening of the intensity of some absorption bands with a slight shift in MFAC spectrum following the adsorption of Hg2+ ions. This may result from the surface complexation of functional groups (–OH and M–O), electrostatic interaction of OSO3−, and isomorphic displacement of Mg2+ with Hg2+ ions, reducing the vibration intensity of Mg–O bond, showing the dominant role of these functional groups in the Hg2+ removal.46
Fig. 1e shows that as pH rose zeta potential levels have been dropped for all the investigated solid adsorbents from (+1.24) to (−1.98) mV. It is well recognized that a variety of parameters, including variations in surface functional groups, porosity, surface area, material composition, and the extent of solid material defects, can influence the pHPZC of the solid materials under investigation. The pHPZC values for MFL, MFC, and MFAC were evaluated to be 6.53, 5.98, and 6.25, respectively (Table 1), which verified that the adsorbents demonstrated positively charged surface at pH < pHPZC, but they had negatively charged surface at pH > pHPZC. Therefore, it can be concluded that electrostatic attraction was not the primary mechanism involved in the removal of Hg2+ as can be observed in Fig. 3b. The point is pHPZC at which the surface charge of the adsorbent is zero.47
 |
| | Fig. 3 Effect of adsorbent dose (a) and pH (b) for Hg2+ adsorption onto MFL, MFC, and MFAC at 20 °C, Hg2+ concentration of 900 mg L−1, and 60 min of shaking duration. | |
The morphological changes, particle sizes, and pores' network formed by the synthesized solid adsorbents were investigated using SEM and TEM techniques. Fig. 2a–c shows SEM micrographs of studied MFL, MFC, and MFAC. Fig. 2a shows small particles' agglomerates of Mg–Fe LDH with heterogeneous sizes. It was made up of many stacked nanosheets with irregular, porous, and rough surface. It can be observed slit-shaped pores in a collection of plate-like particles based on the N2 adsorption isotherm technique results.28 The morphological characteristics of Mg–Fe LDH adsorbent pointed to a developed degree of porosity that would be advantageous for adsorbing Hg2+. SEM images (Fig. 2b and c) exhibit heterogeneous and porous surfaces of MFC and MFAC nanocomposites due to the incorporation of potassium κ-carrageenan and Araucaria gum with Mg–Fe LDH, which increased the surface heterogeneity. The samples' microstructure at a much larger magnification was investigated by TEM images (Fig. 2d–f). The morphology of MFL showed a layered structure, and it was easy to observe the lattice fringes. TEM micrographs (Fig. 2e and f) of MFC and MFAC display that the particles of Mg–Fe LDH were effectively dispersed inside the matrix of two biopolymers (KG and AR), which caused an increase in the particle size from about 52 nm of MFL to 120 nm of MFC and 130 nm of MFAC.
3.2. Batch adsorption of Hg2+ ions
3.2.1. Adsorbent dosage optimization. A variation of adsorbent dosage in a range of 0.4 to 3.0 g L−1 was investigated to analyze the influence on Hg2+ removal percent (R%, eqn (2)) at a 25 mL of 900 mg L−1 as initial Hg2+ concentration at pH 6 and 20 °C for 60 min of shaking duration (Fig. 3a). It was evident that the mercuric ions removal rate increased gradually with rising the adsorbent dose due to more accessible active adsorption sites and increasing availability of free bonds of adsorbents in solutions. About 10.0, 30.0, and 22.5% of mercuric ions were adsorbed by MFL, MFC, and MFAC at the lowest adsorbent dosage of 0.4 g L−1, and thereafter, R% augmented with the dosage, attaining maximum values of 80, 92, and 100% at 2.0 g L−1 for the previous adsorbent trend, respectively. At small dosages, the surplus Hg2+ moieties were inefficiently adsorbed in the solution due to fewer available sites. After 2.0 g L−1, the removal rate was constant and reached equilibrium by MFL because of surplus adsorption sites at fixed Hg2+ concentration in the aqueous medium, reducing the driving force of the concentration gradient between the adsorbent–adsorbate species.3,48 It was noted that the adsorption rate declined to 76 and 82% after exceeding MFC and MFAC dosage of 2.0 g L−1 due to the aggregation of adsorption sites onto the surface, restricting the Hg2+ adsorption.49 The removal efficiency of Hg2+ was maximum for MFAC, reflecting the beneficial effect of the functionalization of Mg–Fe LDH on boosting the MFAC capacity to adsorb Hg2+ and the synergistic effect between LDH, KG, and Araucaria gum in creating an effective nanocomposite with superior capacity. As a result, 2.0 g L−1 was chosen as the ideal adsorbent dose for all ensuing experimental investigations.
3.2.2. Adsorbate pH optimization. Batch adsorption tests under various pH values are required to investigate the relationship between the adsorbent's adsorption performance and the pH value. Hg2+ uptake performance of MFL, MFC, and MFAC at several solution pH tuning from 1 to 8 is shown in Fig. 3b, using 25 mL of Hg2+ concentration of 900 mg L−1 along with an optimal adsorbent dosage of 2 g L−1 at 20 °C for 60 min of shaking duration. According to Fig. 3b, as pH rose, the adsorbents generally displayed a trend where removal first increased and subsequently declined. A low removal efficiency of 20, 11, and 30% was observed at pH 2 which gradually increased to 78, 88, and 98% at pH 6, and then decreased by 23.1, 43.2, and 20.4% at pH 8 for MFL, MFC, and MFAC, respectively. This was because Hg2+ and H3O+ competed for the adsorption surface sites at a lower pH, leading to inadequate removal rates. Furthermore, the point of zero charge (pHPZC) was 6.53 (MFL), 5.98 (MFC), and 6.25 (MFAC), indicating that when pH < pHPZC, the positively charged adsorbent surface created electrostatic repulsion with mercuric ions in the solution. The concentration of H3O+ steadily dropped as pH rose, making the competitive advantage of Hg2+ clear. Additionally, the Lewis-base functional groups onto the adsorbent surface were more well-matched with Lewis-acidic Hg2+, enhancing the adsorption rate.5 On the other hand, the solution pH affects the speciation of Hg2+. At pH < 3, Hg2+ is only present while within the pH range of 3 to 6, mercuric ions existed in two forms concurrently: Hg(OH)2 and Hg2+ with a trace quantity of Hg(OH)+. At higher pH levels (>6), Hg(OH)2, Hg(OH)3−, and Hg(OH)42− were formed and exhibited a difficulty of adsorption onto the solid active sites, making them harder to be captured by adsorbents.48 Thus, pH 6 was the best choice for further examination.
3.2.3. Adsorption kinetic analysis. The practicality of adsorbents is largely dependent on their adsorption rate for large-scale applications. The influence of shaking time on the performance of MFL, MFC, and MFAC for Hg2+ adsorption was studied by the kinetics of adsorption with 25 mL of initial Hg2+ concentration of 900 mg L−1 over 1–70 min at pH 6, 20 °C, and adsorbent dosage of 2 g L−1 as depicted in Fig. 4a–e spots. There was a fast increase of Hg2+ uptake in the first adsorption period (<20 min) by 5.9, 2.9, and 2.2 times for MFL, MFC, and MFAC, respectively. When the adsorption time surpassed 20 min, the adsorption rate decelerated and eventually reached a dynamic equilibrium after 30 min. The previous data illustrated that the initial increase was related to the abundance of vacant adsorption sites onto the surface of adsorbents and the plentiful availability of mercuric ions in the solution, establishing a concentration gradient and facilitating the adsorption process. Furthermore, the functional groups of adsorbents contributed to the capture of mercuric ions. Subsequently, the Hg2+ concentration in the solution decreased as the adsorption process went on and more adsorption sites were occupied. The result was a decrease in the adsorption driving force, which allowed the adsorption capacity to stabilize.
 |
| | Fig. 4 The nonlinear plots of PFO and PSO (a), Avrami (b), Elovich (c), Bangham's pore diffusion (d), intra-particle diffusion (e), and linear Boyd (f) for the adsorption of Hg2+ onto MFL, MFC, and MFAC (at 20 °C, pH 6, initial Hg2+ concentration of 900 mg L−1, and adsorbent dosage of 2 g L−1). | |
To better understand the adsorption mechanism, several linear and nonlinear kinetic models: pseudo-first-order (PFO) (eqn (4), Fig. 4a), pseudo-second-order (PSO) (eqn (5), Fig. 4a), Avrami (eqn (6), Fig. 4b), Elovich (eqn (7), Fig. 4c), Bangham's pore diffusion (eqn (8), Fig. 4d), intra-particle diffusion (eqn (9), Fig. 4e), and linear-Boyd (eqn (10), Fig. 4f) were applied. The parameters of these models are listed in Table 2. The results showed that some models demonstrated higher correlation coefficient values (0.9100–0.9881) for PSO and (0.9695–0.9983) for Avrami kinetics than those of PFO (0.7881–0.9577), in addition to the lower reduced chi-square (χ2) of PSO (1.1156–6.5290) and Avrami (0.1587–2.2122) than those of PFO (0.9237–15.3811). Moreover, a high analogy was noted between the values of the Langmuir adsorption capacity (Qm) and the estimated values (Qexp, QAV) from PSO and Avrami models with low differences of 0.2–2.8% and 4.1–13.6%, respectively, but a low similarity between Qexp of PFO and Qm was observed with a large variance of 14.2–16.5%. Hence, it was evident that PSO and Avrami kinetics presented excellent fitness for the adsorption data of Hg2+ by MFL, MFC, and MFAC. PSO model assumed that the adsorption process was controlled by the active sites of adsorbent.50 The values of PSO rate constants (K2) of MFAC > MFC > MFL by 36.8 and 58.2%, and the rate constant values (KAV) of Avrami model followed the previous trend by 1.4 and 1.8 times, respectively, compared to MFAC, representing the rapid saturation of active binding sites of MFAC by Hg2+. The time exponent values of Avrami (nAV) (0.4952–0.9067) of MFL > MFC > MFAC related to the potential shift in the adsorption mechanism, displayed that there were many kinetic orders in the adsorption.51 The great R2 (0.9375–0.9642) and acceptable χ2 (4.1258–5.2234) values of Elovich kinetic verified its validity in describing the experimental adsorption results. The greater initial adsorption rate and quicker surface coverage of MFAC with Hg2+ were confirmed by α and β values of MFAC > MFC > MFL, which matched with K2 and KAV values of PSO and Avrami. The effectiveness of Bangham's pore diffusion model in depicting the mercuric ions adsorption onto the produced adsorbents was evident from B (<1) values (0.5516–0.5851) and the elevated R2 values (≥0.9442) in conjunction with low χ2, corroborating the dominance of pore diffusion in the uptake of Hg2+.52 The order of KB values confirmed the highest adsorption capacity and rate of MFAC, which matched with α, K2, and KAV values of Elovich, PSO, and Avrami. Besides, intra-particle diffusion model provided an accurate prediction of Hg2+ adsorption kinetics with proper R2 (≥0.9304) and satisfactory χ2 values. As revealed from C values (27.173–174.072), the lines did not cross the origin point, suggesting the adsorption process may involve numerous mechanisms, and the rate of adsorption was limited by various factors, including the intraparticle diffusion process.50 Since the Boyd model's linear plot provided with R2 ≥ 0.9656 didn't cross through the origin, it can be concluded that film diffusion or extra-particular transport can affect the Hg2+ adsorption onto the generated adsorbents, revealing the complexity of the adsorption process.53
Table 2 PFO, PSO, Avrami, Elovich, Bangham's pore diffusion, intra-particle diffusion, and Boyd parameters for the adsorption of Hg2+ onto MFL, MFC, and MFAC at 20 °C
| Models |
Parameters |
MFL |
MFC |
MFAC |
| PFO |
Qm (mg g−1) |
417.18 |
474.29 |
505.74 |
| Qexp (mg g−1) |
350.88 |
395.89 |
433.76 |
| k1 (min−1) |
0.1150 |
0.1544 |
0.2079 |
| R2 |
0.9577 |
0.9202 |
0.7881 |
| χ2 |
0.9237 |
6.6413 |
15.3811 |
| PSO |
Qexp (mg g−1) |
417.92 |
460.73 |
492.30 |
| k2 (g mg−1 min−1) × 10−4 |
3.5088 |
5.3139 |
8.4063 |
| R2 |
0.9881 |
0.9610 |
0.9100 |
| χ2 |
1.1156 |
3.2480 |
6.5290 |
| Avrami |
QAV (mg g−1) |
360.32 |
442.47 |
484.86 |
| KAV (min−1) |
0.1129 |
0.1465 |
0.2082 |
| nAV |
0.9067 |
0.6164 |
0.4952 |
| R2 |
0.9983 |
0.9846 |
0.9695 |
| χ2 |
0.1587 |
1.2809 |
2.2122 |
| Elovich |
α (mg g−1 min−1) |
124.9 |
392.4 |
1233.0 |
| β (g mg−1) |
0.0118 |
0.0131 |
0.0144 |
| R2 |
0.9642 |
0.9504 |
0.9375 |
| χ2 |
5.2234 |
4.1258 |
4.5356 |
| Bangham's pore diffusion |
KB (mL L−1 g−1) |
2.5260 |
3.9500 |
5.8576 |
| B |
0.5516 |
0.5592 |
0.5851 |
| R2 |
0.9468 |
0.9827 |
0.9442 |
| χ2 |
4.9785 |
1.4416 |
4.0521 |
| Intra-particle diffusion |
k0 (mg g−1 min1/2) |
60.0889 |
57.1687 |
53.6962 |
| C |
27.173 |
104.357 |
174.072 |
| R2 |
0.9359 |
0.9486 |
0.9304 |
| χ2 |
6.3980 |
4.5927 |
5.5764 |
| Boyd |
R2 |
0.9954 |
0.9656 |
0.9899 |
3.2.4. Adsorption isotherm analysis. The adsorption isotherm test is imperative to evaluate the maximum adsorption capacity of nanoadsorbents toward the target pollutant. The adsorption performance of the prepared MFL, MFC, and MFAC at several initial concentrations (30–900 mg L−1) was evaluated along with an adsorbent dosage of 2 g L−1 at 20 °C and pH 6 for 30 min of shaking duration. The plots of equilibrium adsorption capacity (Qe) vs. equilibrium mercuric ions concentration (Ce) are shown in Fig. 5a–d and 6a–c spots. All the isotherms were concave, positive, and regular along the concentration axis. These characteristics belonged to L2-type isotherms of Giles classification, corresponding to the favorable adsorption process in a liquid phase.54 As displayed in Fig. 5a–d and 6a–c spots, as feed concentration rose, the adsorption capacity increased and finally reached a constant value as defined by the curves' plateau region. For a fixed adsorbent dosage (2 g L−1), the number of active sites in the solution doesn't change. The excess quantity of active sites effectively adsorbed the Hg2+ species on the surface at lesser feed concentrations, which caused the adsorption capacity to rise rapidly. At greater pollutant concentrations, the excess Hg2+ ions began competing for the limited sites that were still available, reaching saturation. As a result, the capacity was reduced to a constant value that corresponded to a zero slope in the profiles due to an effective impediment caused by competing Hg2+ species for saturation sites.48
 |
| | Fig. 5 The nonlinear plots of Langmuir (a), Freundlich (b), Temkin (c), and DR (d) for the adsorption of Hg2+ onto MFL, MFC, and MFAC at 20 °C, an adsorbent dosage of 2 g L−1, and pH 6 for 30 min of shaking duration. | |
 |
| | Fig. 6 The nonlinear plots of Redlich–Peterson (a), Sips (b), and Toth (c) models, and van't Hoff plot (d) for the adsorption of Hg2+ onto MFL, MFC, and MFAC at 20 °C. | |
Several adsorption isotherm models including Langmuir (eqn (11)), Freundlich (eqn (13)), Temkin (eqn (14)), Dubinin–Radushkevich (DR, eqn (15)), Redlich–Peterson (eqn (17)), Sips (eqn (18)), and Toth (eqn (19)) were investigated to study the adsorption mechanism as shown in the nonlinear fitting of Fig. 5a–d and 6a–c, respectively. The obtained isothermal parameters are listed in Table 3. Regarding the results in Table 3, it was evident that both Langmuir (R2 = 0.9945–0.9973) (χ2 = 0.3418–0.5928) and Freundlich (R2 = 0.9248–0.9479) (χ2 = 4.8403–9.6744) isotherms provided an accepted fitting with experimental outcomes. It can be expected that the dominating adsorption trend happened as a monolayer on a homogenous surface without any attraction between the adsorbate ions through Langmuir model.55 On the other hand, multilayer adsorption with a heterogeneous distribution of active adsorption sites aided by adsorbed ions' interaction was presented by Freundlich model. Interestingly, the experimental findings were correlated with Langmuir isotherm model. The estimated maximum uptake capacity (Qm) of Hg2+ ions was 417.18, 474.29, and 505.74 mg g−1 for MFL, MFC, and MFAC, respectively. Thus, Araucaria gum and potassium κ-carrageenan functionalized Mg–Fe LDH possessed nearly 1.1 and 1.2 times higher improved adsorption capacity than potassium κ-carrageenan modified Mg–Fe LDH and Mg–Fe LDH, showcasing the superior adsorption capacity of MFAC. The b parameter depending on bond formation energy for mercuric ions adsorption with values of MFAC > MFC > MFL represented the robust affinity of mercuric ions towards MFAC surface.2 The values of KL lied between 0 and 1 (0.0518–0.1552), highlighting a favorable and feasible capture of mercuric ions by all the adsorbents.55 Freundlich model attested to an ideal, favorable, and physical adsorption mechanism with values of the heterogeneity factor (1/n) below 1 for all materials ranging from 0.3402 to 0.4728.12 According to the high R2 values (≥0.9384) and low χ2 values (0.9630–5.7176) of Temkin model, and great R2 (≥0.9778) and low χ2 (0.0406–0.0550) of Dubinin–Radushkevich isotherm, the Hg2+ uptake process through MFL, MFC, and MFAC was well described by these models. Where the adsorption mechanism in Temkin and DR models was typically explained by the energy distribution on heterogeneous surfaces. Temkin demonstrated how the physical interaction on the mercuric ions adsorption process was controlled when the bT values were less than 80 kJ mol−1, indicating MFAC needed the lowest heat amount for the Hg2+ adsorption.12 DR model showed a similar fitting performance to Langmuir isotherm through the values of Qm and QDR with a difference of 9.9–15.7% between them. Notably, the adsorption energy (EDR) values spanning from 0.0147 to 0.0234 kJ mol−1 (<8 kJ mol−1) were determined from DR isotherm to suggest that the adsorption process was physisorption. Besides, Redlich–Peterson, Sips, and Toth isotherm models showed a good match to the experimental data of pollutant adsorption onto the investigated adsorbents. Whereas, they appeared with high R2 values, which reached equal or above 0.9972, 0.9973, and 0.9964, and low χ2 values ranging from 0.1020 to 0.3615, 0.0626 to 0.3469, and 0.1507 to 0.4337, respectively for all the previous three models. As demonstrated by Langmuir model, the best-fitted Redlich–Peterson isotherm assumed that the adsorbents' surface textures were uniform and homogenous.56 It was noted that the constants of KF (L1/n mg1−1/n g−1), KRP (L g−1), αRP (mg L−1)−g, Ks (L g−1), and Kth (L mg−1) obeyed the similar order of Langmuir constant (b) values (MFAC > MFC > MFL), asserting the great adsorption strength of mercuric ions with MFAC. The values of theoretical exponent of g (0.9900–1.2033), ns (0.8230–1.0024), and nth (1.0044–1.4246) approached and exceeded unity, representing a homogenous and heterogenous monolayer and multilayer adsorption mechanism.56 It was observed that the theoretical exponent values of MFAC were nearly equal one, indicating the possible dominance of the uniform monolayer adsorption mechanism onto its surface. The satisfied correlation between the adsorption amounts (Qm) of Langmuir and (Qs and Qth) of Sips and Toth models with low differences ranging from 0.3 to 7.9% and 1.1 to 8.9%, respectively suggested their excellent application. The nuances of Hg2+ adsorption phenomena can be better understood by the studied non-linear isotherms, which also help us comprehend the interactions that control adsorbate–adsorbent systems.
Table 3 Langmuir, Freundlich, Temkin, Dubinin–Radushkevich, Redlich-Peterson, Sips, and Toth parameters for the adsorption of Hg2+ onto MFL, MFC, and MFAC at 20 °C, in addition to the thermodynamic parameters
| Models |
Parameters |
Temp. |
MFL |
MFC |
MFAC |
| Langmuir |
Qm (mg g−1) |
|
417.18 |
474.29 |
505.74 |
| b (L mg−1) |
|
0.0173 |
0.0210 |
0.0405 |
| KL |
|
0.1552 |
0.1131 |
0.0518 |
| R2 |
|
0.9945 |
0.9945 |
0.9973 |
| χ2 |
|
0.5113 |
0.5928 |
0.3418 |
| Freundlich |
1/n |
|
0.4728 |
0.4283 |
0.3402 |
| KF (L1/n mg1−1/n g−1) |
|
36.1868 |
42.4911 |
79.7434 |
| R2 |
|
0.9479 |
0.9331 |
0.9248 |
| χ2 |
|
4.8403 |
7.1657 |
9.6744 |
| Temkin |
bT (J mol−1) |
|
33.4892 |
22.9799 |
22.6076 |
| KT (L g−1) |
|
0.4076 |
0.1915 |
0.4449 |
| R2 |
|
0.9384 |
0.9910 |
0.9891 |
| χ2 |
|
5.7176 |
0.9630 |
1.3962 |
| Dubinin–Radushkevich |
QDR (mg g−1) |
|
351.70 |
405.74 |
455.78 |
| EDR (kJ mol−1) |
|
0.0147 |
0.0164 |
0.0234 |
| R2 |
|
0.9778 |
0.9843 |
0.9946 |
| χ2 |
|
0.0406 |
0.0550 |
0.0456 |
| Redlich–Peterson |
KRP (L g−1) |
|
5.6135 |
8.4978 |
19.6812 |
| αRP (mg L−1)−g |
|
0.0031 |
0.0069 |
0.0348 |
| g |
|
1.2033 |
1.1320 |
0.9900 |
| R2 |
|
0.9989 |
0.9985 |
0.9972 |
| χ2 |
|
0.1020 |
0.1565 |
0.3615 |
| Sips |
Qs (mg g−1) |
|
392.82 |
436.90 |
507.26 |
| Ks (L g−1) |
|
0.0217 |
0.0275 |
0.0424 |
| ns |
|
0.8374 |
0.8230 |
1.0024 |
| R2 |
|
0.9974 |
0.9994 |
0.9973 |
| χ2 |
|
0.2422 |
0.0626 |
0.3469 |
| Toth |
Qth (mg g−1) |
|
380.13 |
433.59 |
511.22 |
| Kth (L mg−1) |
|
0.0144 |
0.0190 |
0.0392 |
| nth |
|
1.4246 |
1.3512 |
1.0044 |
| R2 |
|
0.9983 |
0.9986 |
0.9964 |
| χ2 |
|
0.1614 |
0.1507 |
0.4337 |
| Thermodynamic parameters |
R2 |
|
0.9660 |
0.9256 |
0.9798 |
| ΔH° (kJ mol−1) |
|
19.0864 |
15.8549 |
14.0645 |
| ΔS° (kJ mol−1 K−1) |
|
0.0798 |
0.0626 |
0.0576 |
| −ΔG° (kJ mol−1) |
20 °C |
1.9913 |
2.4869 |
2.8123 |
| 27 °C |
2.5499 |
2.9251 |
3.2155 |
| 34 °C |
3.1085 |
3.3633 |
3.6187 |
| 45 °C |
3.9863 |
4.0519 |
4.2523 |
3.2.5. Adsorption thermodynamic analysis. During the adsorption process, the temperature effect on Hg2+ removal by the prepared materials was drawn as a linear plot of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kd vs. 1/T shown in Fig. 6d over a range of 20–45 °C, using 25 mL of Hg2+ concentration of 900 mg L−1 with an adsorbent dose of 2 g L−1 for 30 min of shaking time. Table 3 also includes correlation coefficients and computed thermodynamic factors. ΔG° showed negative values, suggesting the spontaneous proceeding of mercuric ions adsorption onto MFL, MFC, and MFAC in the forward direction and more energetically advantageous as the solution temperature rose. On the other side, ΔG° values (−1.9913 to −4.2523 kJ mol−1) varied between 0 and −20 kJ mol−1, relating to physical adsorption. Moreover, the Hg2+ adsorption was an endothermic process with positive estimated enthalpy values (14.0645–19.0864 kJ mol−1), indicating that heat was absorbed throughout all steps included in the adsorption process. Whereas the positive ΔS° values pointed to an increment in randomness at the boundary between the mercuric ions and the adsorbent surface. In addition, van't Hoff graph (Fig. 6d) possessed high R2 values (≥0.9256), reflecting its good fitting for Hg2+ adsorption.
Kd vs. 1/T shown in Fig. 6d over a range of 20–45 °C, using 25 mL of Hg2+ concentration of 900 mg L−1 with an adsorbent dose of 2 g L−1 for 30 min of shaking time. Table 3 also includes correlation coefficients and computed thermodynamic factors. ΔG° showed negative values, suggesting the spontaneous proceeding of mercuric ions adsorption onto MFL, MFC, and MFAC in the forward direction and more energetically advantageous as the solution temperature rose. On the other side, ΔG° values (−1.9913 to −4.2523 kJ mol−1) varied between 0 and −20 kJ mol−1, relating to physical adsorption. Moreover, the Hg2+ adsorption was an endothermic process with positive estimated enthalpy values (14.0645–19.0864 kJ mol−1), indicating that heat was absorbed throughout all steps included in the adsorption process. Whereas the positive ΔS° values pointed to an increment in randomness at the boundary between the mercuric ions and the adsorbent surface. In addition, van't Hoff graph (Fig. 6d) possessed high R2 values (≥0.9256), reflecting its good fitting for Hg2+ adsorption.
3.3. Column adsorption study
3.3.1. Effect of adsorbent bed height. In the initial step of continuous tests in a column packed with MFAC adsorbent, the effect of bed heights (BH) on the adsorption of Hg2+ was studied at varying heights from 1, 2, and 3 cm at a fixed inlet Hg2+ solution concentration of 80 mg L−1 and flow rate of 30 mL min−1 at 20 °C and pH 6 through 300 min. The dots in Fig. 7a display the produced breakthrough curves and Table 4 lists the evaluated column parameters. Initially, Hg2+ adsorption was high until the breakthrough time (tb) was reached, after which the effluent Hg2+ concentration began to rise quickly. Throughout the dynamic process, the breakthrough curve slope was higher for a smaller bed height (1 cm) and the bed column was exhausted faster, indicating that the mass transfer zone was reduced since adsorption saturation was soon achieved after the breakthrough point. It can be noted that the increase in bed height from 1 to 3 cm rose both the breakthrough times from 94.00 to 127.72 min by 35.9% and exhaustion or saturation times (te) from 193.22 to 249.09 min by 28.9%. As the bed depth augmented, the zone of mass transfer between the residence or contact time of ions in MFAC bed and the two column ends improved from 0.51 to 1.46 cm, which permitted more efficient interaction between MFAC adsorbent and Hg2+ ions. Furthermore, as bed height increased, more binding sites became available for Hg2+ adsorption and the mercuric diffusion increased onto the adsorbent.57 Conversely, columns with a low bed height can attain adsorption saturation more quickly because of fewer adsorbent and reactive groups, thereby it is not recommended to have a very large bed height since this may result in flow resistance.34,58 Correspondingly, the adsorption capacity (Q0, eqn (25)) declined from 550.50 to 231.48 mg g−1 by 58% by raising the bed height from 1 to 3 cm.
 |
| | Fig. 7 Effect of bed height (a) at μ = 30 mL min−1 and Ci = 80 mg L−1, flow rate (b) at BH = 2 cm and Ci = 80 mg L−1, and initial Hg2+ concentration (c) at BH = 2 cm and μ = 30 mL min−1, represented in the dots, for Hg2+ adsorption onto MFAC with the nonlinear fitting of Yoon–Nelson, Thomas, Clark, and Yan column models at 20 °C and pH 6. | |
Table 4 Column adsorption data, Yoon–Nelson, Thomas, Clark, and Yan model parameters for the removal of Hg2+ by MFAC at different application conditions
| Parameters |
BH (cm) |
μ (mL min−1) |
Ci (mg L−1) |
| 1 |
2 |
3 |
10 |
20 |
30 |
40 |
80 |
150 |
| tb (min) |
94.00 |
118.93 |
127.72 |
151.12 |
143.86 |
118.93 |
134.04 |
118.93 |
89.43 |
| te (min) |
193.22 |
223.99 |
249.09 |
273.77 |
250.95 |
223.99 |
248.55 |
223.99 |
199.79 |
| MTZ (cm) |
0.51 |
0.94 |
1.46 |
0.90 |
0.85 |
0.94 |
0.92 |
0.94 |
1.10 |
| Qo (mg g−1) |
550.50 |
333.31 |
231.48 |
130.01 |
251.95 |
333.31 |
173.32 |
333.31 |
491.47 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| Yoon–Nelson model |
| τexp (min) |
147.37 |
170.19 |
184.71 |
196.60 |
189.34 |
174.82 |
188.14 |
174.66 |
140.42 |
| τcal (min) |
147.39 |
170.21 |
184.42 |
198.02 |
190.31 |
174.39 |
188.19 |
173.95 |
141.10 |
| KYN (min−1) |
0.0628 |
0.0602 |
0.0594 |
0.0561 |
0.0595 |
0.0608 |
0.0518 |
0.0542 |
0.0558 |
| R2 |
0.9988 |
0.9992 |
0.9978 |
0.9968 |
0.9990 |
0.9985 |
0.9990 |
0.9990 |
0.9991 |
| χ2 × 10−4 |
2.3864 |
1.4919 |
3.9832 |
5.4587 |
1.8691 |
2.9370 |
1.8207 |
1.9062 |
1.6300 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| Thomas model |
| QTh (mg g−1) |
520.19 |
315.22 |
220.34 |
123.21 |
242.10 |
320.56 |
161.76 |
319.47 |
483.98 |
| KTh (L mg−1 min−1) × 10−4 |
7.9075 |
7.7862 |
7.7188 |
6.5438 |
7.3650 |
7.6700 |
12.9675 |
6.7462 |
3.7373 |
| R2 |
0.9978 |
0.9982 |
0.9970 |
0.9960 |
0.9980 |
0.9905 |
0.9980 |
0.9790 |
0.9890 |
| χ2 × 10−4 |
2.3865 |
1.4921 |
3.9909 |
5.4599 |
1.8692 |
2.9372 |
1.8208 |
1.9071 |
1.6302 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| Clark model |
| A × 106 |
0.4773 |
3.5339 |
29.3510 |
46.4808 |
39.6828 |
2.3246 |
2.2383 |
1.6474 |
0.0937 |
| r (min−1) |
0.0843 |
0.0838 |
0.0821 |
0.0782 |
0.0809 |
0.0823 |
0.0714 |
0.0756 |
0.0767 |
| R2 |
0.9986 |
0.9990 |
0.9976 |
0.9926 |
0.9977 |
0.9971 |
0.9972 |
0.9980 |
0.9973 |
| χ2 × 10−4 |
2.6870 |
1.8589 |
4.4105 |
12.7000 |
4.1990 |
5.5102 |
4.8346 |
3.7633 |
5.0467 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| Yan model |
| QY (mg g−1) |
510.22 |
310.43 |
210.77 |
120.15 |
235.00 |
315.43 |
156.23 |
310.87 |
476.23 |
| KY (L mg−1 min−1) × 10−3 |
4.2208 |
3.8244 |
3.5611 |
1.3574 |
2.8607 |
3.8347 |
7.1737 |
3.6303 |
1.5460 |
| R2 |
0.9974 |
0.9979 |
0.9971 |
0.9985 |
0.9990 |
0.9983 |
0.9988 |
0.9982 |
0.9991 |
| χ2 × 10−4 |
4.9941 |
3.9519 |
5.2432 |
2.5314 |
1.7668 |
3.2636 |
2.1092 |
3.4269 |
1.7015 |
3.3.2. Effect of flow rate. This continuous research on mercuric ions adsorption is highly dependent on flow rate. As a result, various tests were conducted to examine the impact of flow rate on the Hg2+ uptake by MFAC nanocomposite at 15, 20, and 30 mL min−1, while maintaining a constant initial Hg2+ concentration of 80 mg L−1 and a bed height of 2 cm at 20 °C and pH 6. The results are shown in the breakthrough curves form in Fig. 7b spots. According to the findings, there was a negative correlation between the flow rate and both the breakthrough and saturation times. There is a shortage in tb from 151.12 to 118.93 min by 21.3% and te from 273.77 to 223.99 min by 18.2% (Table 4) as a result of the breakthrough threshold being reached faster with an improvement in flow rate from 10 to 30 mL min−1. This is because there may be more Hg2+ ions available for adsorption. The curve slope was greater at a higher flow rate (30 mL min−1). The alterations in the breakthrough curves can be related to the quick mass transfer of Hg2+ to the bulk surface and therefore, subsequent rapid occupancy of the active sites of the MFAC composite. At the beginning, a significant load of mercuric ions into the column, which complexed with the functional groups onto MFAC adsorbent surface, increased at a great flow rate due to the improved mass transfer rate, speeding up the column bed saturation. Rising flow rates from 10 to 30 mL min−1 caused a rise in the maximum adsorption capacity from 130.01 to 333.31 mg g−1 by 2.6 folds due to the possible contact of more mercuric ions with the adsorbent at a higher flow rate, causing the higher loading of metal ions and increasing adsorption.59 Consequently, it follows that running a column at a high flow rate (30 mL min−1) improved process efficiency.
3.3.3. Effect of inlet Hg2+ concentration. During the dynamic adsorption, the mercuric ions accumulation is primarily dependent on the influent concentration. The impact of the inlet concentration on the adsorption capacity and breakthrough curves are shown in Fig. 7c dots. The studies were executed at a concentration range of 40 to 150 mg L−1 at 20 °C and pH 6 with a fixed flow rate of 30 mL min−1 and a bed height of 2 cm. With the elevation in influent Hg2+ concentration, the breakthrough curves gradually altered from gentle to sharp in profile, showing that the driving force of the higher mass transfer zone under the higher concentration gradient made it easier to penetrate the fixed-bed column and caused it to attain saturation or exhaustion more quickly. As the initial Hg2+ concentration rose from 40 to 150 mg L−1, the values of tb and te decreased from 134.04 to 89.43 min and 248.55 to 199.79 min, respectively (Table 4). This is because the diffusion of adsorbed ions increased and a large influent Hg2+ concentration occupied the majority of the active sites, increasing the treated effluent volume. The outcomes indicated that the column adsorption capacity inevitably ascended from 173.32 to 491.47 mg g−1 by 183.6% by raising the initial Hg2+ concentration. That was due to strengthening the complex contact between the active sites and Hg2+ ions, high mercuric ions transportation from the film layer to MFAC surface, and amplification of adsorption driving force, increasing the MTZ height.58
3.3.4. Column adsorption data modeling. The breakthrough curves were analyzed through the nonlinearized form of Yoon-nelson (eqn (28)), Thomas (eqn (29)), Clark (eqn (30)), and Yan (eqn (31)) as shown in Fig. 7. Table 4 displays the model parameters for each experimental breakthrough curve (bed height, flow rate, and initial Hg2+ concentration) that were found using curve fitting. The results in Table 4 showed that Yoon–Nelson, Thomas, Clark, and Yan kinetic models fitted well with the experimental breakthrough curves of fixed-bed column. Whereas correlation coefficient values (R2) appeared high, ranging from 0.9968 to 0.9992, 0.9790 to 0.9982, 0.9926 to 0.9990, and 0.9971 to 0.9991, in addition to reduced low chi-square values (χ2) for all the applied models, respectively. Moreover, a high analogy was noted between the experimental τexp and the calculated τcal values from Yoon–Nelson model with low variance (0.01–0.7%) between them. This might result from the restriction of Yoon–Nelson model, which holds that time is the only variable that influences breakthrough curves.60 The 50% breakthrough curve values increased from 147.39 to 184.42 min by 1.2 folds with increasing the bed height, besides this the 50% BTC curves also decreased from 198.02 to 174.39 min by 11.9% as well as 188.19 to 141.10 min by 25.0% when the flow rate and initial Hg2+ concentration raised, respectively. The sequence and illustration of τexp and τcal values are the same as those of tb and te. This research demonstrated that increasing BH (cm) declined the Yoon–Nelson and Clark rate constants (KYN, r) from 0.0628 to 0.0594 min−1 by 5.4% and from 0.0843 to 0.0821 min−1 by 2.6%. Additionally, KYN and r values increased from 0.0561 to 0.0608 min−1 by 1.1 times and 0.0782 to 0.0823 min−1 by 1.0 times when rising μ (mL min−1) and also rose from 0.0518 to 0.0558 min−1 by 7.7% and 0.0714 to 0.0767 min−1 by 7.4% with enhancing Ci (mg L−1), respectively. It indicated the improvement of adsorption rate at lower bed height, and higher flow rate and inlet Hg2+ concentration. This trend agreed with the experimental adsorption capacity (Q0) and showed a reverse trend with the times’ values. It was noticed that Thomas and Yan rate constants (KTh, KY) were reduced by 2.4 and 15.6% with improving BH (cm), but improved by 1.2 and 2.8 folds with rising μ (mL min−1) and also, decreased by 3.5 and 4.6 times when enhancing Ci (mg L−1), respectively because the difference in concentration acted as a driving force for improved adsorption.59 For instance, the calculated adsorption capacities (QTh and QY) from Thomas and Yan models coincided precisely with the experimental values (Q0) with slight differences of 1.5–6.7% and 3.1–9.9%, respectively due to the optimum use of active sites.34 Furthermore, there was a decrement in QTh and QY values from 520.19 to 220.34 mg g−1 by 57.6% and 510.22 to 210.77 by 58.7% at the intensification of bed height from 1 to 3 cm. However, they were amplified from 123.21 to 320.56 mg g−1 by 2.6 times and 120.15 to 315.43 mg g−1 by 2.6 folds at the growth of flow rate from 10 to 30 mL min−1 and upsurged from 161.76 to 483.98 mg g−1 by 3.0 folds and 156.23 to 476.23 by 3.0 folds at the augment of initial Hg2+ concentration from 40 to 150 mg L−1, successively. Additionally, these values were greatly positively correlated with the adsorption rate for BH and μ effects. This may be owing to the increased mercuric ions loading at lower bed height and greater flow rate and initial concentration. It can be seen that Clark parameter (A) was directly proportional to bed height and inversely proportional to flow rate and influent concentration. The previous findings illustrated the success of the applied dynamic models in a fair description of the experimental data of Hg2+ ions adsorption onto MFAC surface. The mid-range of BTCs demonstrated a strong correlation between the column models studied. This could be explained by either internal diffusion occurring more slowly or by the initial pore diffusion adsorption occurring quickly, depending on the size of the pores and mercuric ions.60
3.4. Adsorption mechanism
Fig. 8a displays the possible Hg2+ adsorption mechanism on MFAC nanocomposite. The mechanism was a complex process that involved multiple physisorption mechanisms. Chemical interaction may occur when Hg2+ ions were combined with hydroxyl ions in the interlayer structure of MFAC, generating mercuric hydroxide, which easily adsorbed onto MFAC surfaces.61 The surface functional groups like –OH, Mg2+, OSO3−, and Mg–O groups in MFAC composite reacted with Hg2+ through isomorphic substitution, electrostatic interactions, and surface complexation process.62 By isomorphic substitution, Hg2+ ions in the solution could be exchanged with Mg2+ cations in MFAC. The hydroxyl and metal oxide groups on MFAC surface interacted with Hg2+, subsequently leading to surface complexation. Besides, Hg2+ ions may be adsorbed onto the porous MFAC structure through van der Waals forces and pore-filling.47,61
 |
| | Fig. 8 Expected adsorption mechanism of Hg2+ ions onto MFAC (a), Hg2+ desorption (b), and reusability of the studied adsorbents (c). | |
3.5. Desorption and reusability studies
The suitability of Hg2+ removal in water treatment was examined by performing tests to investigate the batch desorption rates of Hg2+. Desorption tests were performed on Hg2+-loaded MFL, MFC, and MFAC in different desorbing agents (KCl, thiourea, EDTA, ethylene diamine, and HCl) to determine which eluent produces the highest recovery ratio. Fig. 8b shows that ethylene diamine was used to obtain the lowest desorption percentages (73.8, 81.0, and 89.6%) onto MFL, MFC, and MFAC loaded with Hg2+, respectively. When using EDTA on the same prior adsorbent trend, the Hg2+ desorption rose to 100.0, 99.4, and 99.9%, indicating almost total mercury recovery from the surfaces. The higher desorption percent of Hg2+ by EDTA compared to other eluents (EDTA > HCl > thiourea > KCl > ethylene diamine) can be explained based on chelation strength, complex stability, and binding affinity to Hg2+. Where EDTA is a strong chelating agent, which forms highly stable, soluble, and multidentate complexes with metal ions due to its hexadentate nature.63 HCl desorbs Hg2+ mainly by protonating binding sites and forming weak chloride complexes, and thiourea binds Hg2+ (soft metal ion) through soft sulfur atoms, forming moderately stable soft–soft complexes. KCl supplies Cl− ions, which form weak complexes with Hg2+ (HgCl2, HgCl42−), but lacks chelating power, and ethylene diamine is a bidentate N-donor ligand, forming moderately weak complexes with Hg2+.
The reusability was displayed in Fig. 8c after eight runs of the Hg2+ adsorption/desorption process, where the efficiency of MFL, MFC, and MFAC decreased by 1.9, 1.7, and 9.9%. This can be attributed to the reduction in surface area due to the coagulation of adsorbent particles, loss of some active surface sites, and the potential negative impact of eluent on the reduced adsorption sites.64
3.6. Efficacy comparison
Table 5 displays the highest batch and column adsorption capacity of MFAC through its comparison with other adsorbents.1,2,34,55,65–67 Overall, MFAC seemed like a promising adsorbent for treating wastewater contaminated with mercuric ions.
Table 5 Comparison of the maximum adsorption capacity of MFAC with other materials for Hg2+ removal. (Note: g L−1 is a unit of adsorbent dosage)
| Adsorbents |
Available conditions |
Type of adsorption |
Adsorption capacity (mg g−1) |
References |
| AC |
pH 5, 30 °C, 240 min |
Batch |
74.40 |
1 |
| WPF-AC |
pH 5, 30 °C, 240 min |
Batch |
54.70 |
1 |
| GO/Fe3O4–Si-Pr-SH |
pH 7, 25 °C, 0.2 g L−1, 60 min |
Batch |
129.70 |
2 |
| PANF-TU |
pH 6, 25 °C, 1.0 g L−1, 150 min |
Batch |
227.00 |
34 |
| CB-50% |
pH 5, 25 °C, 1.0 g L−1, 240 min |
Batch |
290.70 |
55 |
| AC-S |
pH 6, 25 °C, 0.5 g L−1, 120 min |
Batch |
120.87 |
65 |
| AC-H1.5 |
pH 6, 25 °C, 0.5 g L−1, 120 min |
Batch |
105.55 |
65 |
| CP12 |
pH 7, 25 °C, 1.0 g L−1, 40 min |
Batch |
111.60 |
66 |
| Hydrochar |
NA |
Batch |
39.80 |
67 |
| MFAC |
pH 6, 20 °C, 2.0 g L−1, 30 min |
Batch |
505.74 |
[This work] |
| PANF-TU |
BH = 2.5 cm, μ = 5 mL min−1, Ci = 100 mg L−1, pH 6, 25 °C, 500 min |
Column |
169.54 |
34 |
| AC-H |
BH = 2.0 cm, μ = 1 mL min−1, Ci = 50 mg L−1, 160 min |
Column |
528.42 |
65 |
| CP12 |
BH = 4.0, μ = 2 mL min−1, Ci = 300 mg L−1, 35 h |
Column |
132.10 |
66 |
| Hydrochar |
NA |
Column |
111.50 |
67 |
| MFAC |
BH = 1.0 cm, μ = 30 mL min−1, Ci = 80 mg L−1,20 °C, pH 6, 300 min |
Column |
550.50 |
[This work] |
4. Conclusion
Mercuric ions removal from water utilizing inexpensive and environmentally benign materials through adsorption is a main concern. This work was considered to assemble and synthesize magnesium-ferric layered double hydroxide (Mg–Fe LDH, MFL) (Mg/Fe molar ratio = 3) at constant pH by co-precipitation method. It was followed by functionalization with potassium κ-carrageenan (KG) only and with Araucaria gum (AR), creating carrageenan/Mg–Fe LDH nanocomposite (MFC) and Araucaria gum/carrageenan/Mg–Fe LDH nanocomposite (MFAC). Their structural and compositional characteristics were rigorously investigated by various techniques such as SEM, TEM, ATR-FTIR, zeta potential, TGA, XRD, and nitrogen adsorption–desorption analysis. These analyses asserted that MFAC nanocomposite had a porous structure, high thermal stability, great crystallinity, and high dominance of new functional groups. In the batch adsorption, the ideal adsorption conditions were at 6 pH, 30 min contact time, and 2.0 g L−1 adsorbent dosage. The adsorption isotherms, kinetics, and thermodynamics were also investigated, revealing that the adsorption mechanism followed monolayer and multilayer physical adsorption through the application of Langmuir and Freundlich models. It was also well fitted with Avrami, Bangham's pore diffusion, and PSO kinetics with an endothermic and spontaneous process based on thermodynamic studies. MFAC composite demonstrated a high potential for Hg2+ elimination from wastewater, resulting from the surface complexation of functional groups (–OH and M–O), electrostatic interaction of OSO3−, and isomorphic displacement of Mg2+ with Hg2+ ions. Studies using column mode also demonstrated the applicability of MFAC. In column mode, the bed height, flow rate, and initial Hg2+ concentration were optimized. The experimental data was also effectively fitted with Yoon–nelson, Thomas, Clark, and Yan kinetic models. Overall, it was found that MFAC exhibited great capability for adsorbing Mn+ from contaminated water.
Data availability
Data will be made available on request.
Author contributions
Asaad F. Hassan: conceptualization and methodology, Walaa A. Shaltout: formal analysis and investigation, H. Hafez and Maha S. Elsayed: writing – original draft preparation, data handling, and analysis of data.
Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this work.
References
- L. C. Ramírez-Rodríguez, D. I. Mendoza-Castillo, A. Bonilla-Petriciolet and C. Jiménez-Junca, Environ. Nanotechnology, Monit. Manag., 2023, 20, 100826 CrossRef.
- E. Mohammadnia, M. Hadavifar and H. Veisi, Polyhedron, 2019, 173, 114139 CrossRef CAS.
- G. A. A. M. Al-Hazmi, A. A. A. Alayyafi, M. G. El-Desouky and A. A. El-Bindary, Int. J. Biol. Macromol., 2024, 261, 129769 CrossRef CAS PubMed.
- V. Algieri, A. Tursi, P. Costanzo, L. Maiuolo, A. De Nino, A. Nucera, M. Castriota, O. De Luca, M. Papagno, T. Caruso, S. Ciurciù, G. A. Corrente and A. Beneduci, Chemosphere, 2024, 355, 141891 CrossRef CAS.
- J. Li, G. Lin, F. Tan, L. Fu, B. Zeng, S. Wang, T. Hu and L. Zhang, J. Colloid Interface Sci., 2023, 651, 659–668 CrossRef CAS PubMed.
- R. Bhatt and P. Padmaj, Carbohydr. Polym., 2019, 207, 663–674 CrossRef CAS.
- L. Wang, M. Wang, Z. Li and Y. Gong, Chem. Eng. J., 2020, 393, 124635 CrossRef CAS.
- L. Si, B. A. Branfireun and J. Fierro, Water, 2022, 14(12), 1891 CrossRef CAS.
- E. A. Eparina and M. A. Sinyakova, Russ. J. Gen. Chem., 2018, 88, 2837–2842 CrossRef CAS.
- L. Rani, A. L. Srivastav and J. Kaushal, Chemosphere, 2021, 280, 130654 CrossRef CAS PubMed.
- N. Traiwongsa, S. Suren, U. Pancharoen, K. Nootong, K. Maneeintr, W. Punyain and A. W. Lothongkum, J. Ind. Eng. Chem., 2023, 117, 522–537 CrossRef CAS.
- A. S. Eltaweil, H. A. Mohamed, E. M. Abd El-Monaem and G. M. El-Subruiti, J. Mol. Liq., 2024, 125275 CrossRef CAS.
- F. S. Awad, K. M. AbouZied, W. M. Abou El-Maaty, A. M. El-Wakil and M. Samy El-Shall, Arab. J. Chem., 2020, 13, 2659–2670 CrossRef CAS.
- Y. Zhang, B. Fan, L. Jia, X. Qiao and Z. Li, Chem. Eng. J. Adv., 2022, 10, 100259 CrossRef CAS.
- M. Kumar, A. K. Singh and M. Sikandar, Heliyon, 2020, 6, e03321 CrossRef CAS PubMed.
- C. Dai, X. Wu, Q. Wang, Y. Bai, D. Zhao, J. Fu, B. Fu and H. Ding, Sep. Purif. Technol., 2025, 352, 128277 CrossRef CAS.
- M. A. Ahmed and A. A. Mohamed, Inorg. Chem. Commun., 2023, 148, 110325 CrossRef CAS.
- X. Wu, R. Li and J. Lin, Chemosphere, 2024, 346, 140643 CrossRef CAS.
- H. Djezar, K. Rida and M. Salhi, Inorg. Nano-Metal Chem., 2022, 52, 161–172 CrossRef CAS.
- L. Santamaría, S. A. Korili and A. Gil, Chem. Eng. J., 2023, 455, 140551 CrossRef.
- D. Zhang, Z. Zhong, Z. Liu, S. He, J. Lin, Y. Lv, T. Lü, Y. Pan, H. Shi and H. Zhao, Chemosphere, 2024, 352, 141399 CrossRef CAS.
- R. Hameed, A. Abbas, J. Lou, W. A. Khattak, B. Roha, B. Iqbal, G. Li, Q. Zhang and X. Zhao, J. Environ. Chem. Eng., 2024, 12, 112687 CrossRef CAS.
- Z. Rahmani, M. Ghaemy and A. Olad, Hydrometallurgy, 2022, 213, 105915 CrossRef CAS.
- A. M. Omer, M. El-Sayed, E. M. Abd El-Monaem, G. M. El-Subruiti and A. S. Eltaweil, Int. J. Biol. Macromol., 2023, 253, 127437 CrossRef CAS PubMed.
- A. V. Samrot, J. L. A. Angalene, S. M. Roshini, S. M. Stefi, R. Preethi, P. Raji, A. M. Kumar, P. Paulraj and S. S. Kumar, Int. J. Biol. Macromol., 2019, 140, 393–400 CrossRef CAS PubMed.
- A. V. Samrot, T. Kudaiyappan, U. Bisyarah, A. Mirarmandi, E. Faradjeva, A. Abubakar, J. A. Selvarani and S. K. Subbiah, Int. J. Nanomedicine, 2020, 15, 7097–7115 CrossRef CAS.
- M. A. Khoj, A. F. Hassan, N. S. Awwad, H. A. Ibrahium and W. A. Shaltout, Int. J. Biol. Macromol., 2024, 255, 128234 CrossRef CAS PubMed.
- L. A. Cano, D. Barrera, J. Villarroel-Rocha and K. Sapag, Catal. Today, 2023, 422, 114222 CrossRef CAS.
- R. Gayathri and R. Sundaraganapathy, Der Pharmacia Lettre, 2019, 11(1), 42–50 CAS.
- A. F. Hassan, G. A. El-Naggar, G. Esmail and W. A. Shaltout, Appl. Surf. Sci. Adv., 2023, 13, 100388 CrossRef.
- M. Benjelloun, Y. Miyah, G. Akdemir Evrendilek, F. Zerrouq and S. Lairini, Arab. J. Chem., 2021, 14, 103031 CrossRef CAS.
- A. F. Hassan, A. Elhassanein, M. A. Khoj and W. A. Shaltout, Int. J. Biol. Macromol., 2024, 276, 133999 CrossRef CAS.
- B. Liu, J. Cao, Y. Jiang, S. Yan, H. He, Y. Shi, S. Xu, J. Liang and X. Ren, RSC Adv., 2022, 12, 25623–25632 RSC.
- C. Chen, Z. Chen, J. Shen, J. Kang, S. Zhao, B. Wang, Q. Chen and X. Li, J. Cleaner Prod., 2021, 310, 127511 CrossRef CAS.
- M. Hanbali, H. Holail and H. Hammud, Green Chem. Lett. Rev., 2014, 7, 342–358 CrossRef.
- S. Bin Lee, E. H. Ko, J. Y. Park and J. M. Oh, Nanomaterials, 2021, 11, 1–19 Search PubMed.
- Z. Li, J. Wang, D. F. Expósito, J. Zhang, C. Fu, D. Shi and D. Y. Wang, Compos. Commun., 2018, 9, 1–5 CrossRef.
- Y. Zhu, R. Zhu, Q. Chen, M. Laipan, J. Zhu, Y. Xi and H. He, Appl. Clay Sci., 2018, 151, 66–72 CrossRef CAS.
- W. Xu, M. Mertens, T. Kenis, E. Derveaux, P. Adriaensens and V. Meynen, Mater. Chem. Phys., 2023, 295, 127113 CrossRef CAS.
- A. Dalma, B. Nancy, E. Griselda and C. Mónica, Front. Chem. Eng., 2022, 4, 1–10 Search PubMed.
- T. Sadeghi Rad, E. S. Yazici, A. Khataee, E. Gengec and M. Kobya, Surf. Interfac., 2023, 36, 102628 CrossRef CAS.
- M. Pavlovic, A. Szerlauth, S. Muráth, G. Varga and I. Szilagyi, Adv. Drug Deliv. Rev., 2022, 191, 114590 CrossRef CAS.
- N. Ghanbari and H. Ghafuri, Environ. Technol. Innov., 2022, 26, 102377 CrossRef CAS.
- A. M. Aldawsari, I. Alsohaimi, H. M. A. Hassan, Z. E. A. Abdalla, I. Hassan and M. R. Berber, J. Alloys Compd., 2021, 857, 157551 CrossRef CAS.
- R. Elmoubarki, F. Z. Mahjoubi, A. Elhalil, H. Tounsadi, M. Abdennouri, M. Sadiq, S. Qourzal, A. Zouhri and N. Barka, J. Mater. Res. Technol., 2017, 6, 271–283 CrossRef CAS.
- Q. Wang, Y. Peng, M. Chen, M. Xu, J. Ding, Q. Yao and S. Lu, Sci. Total Environ., 2024, 912, 169482 CrossRef CAS PubMed.
- G. S. dos Reis, G. L. Dotto, J. Vieillard, M. L. S. Oliveira, S. F. Lütke, A. Grimm, L. F. O. Silva, É. C. Lima, M. Naushad and U. Lassi, J. Alloys Compd., 2023, 960, 170530 CrossRef CAS.
- S. Saha Chowdhury, B. Bera, A. Thakare and S. De, Sep. Purif. Technol., 2023, 325, 124646 CrossRef CAS.
- S. M. Waly, A. M. El-Wakil, W. M. Abou El-Maaty and F. S. Awad, RSC Adv., 2024, 14, 15281–15292 RSC.
- M. Zhao, Y. Wang, H. Zhao, Z. Zhang, J. Su, X. Ma, F. Kong, Y. Xie, Z. Ma, Q. Zhang and Z. Meng, Sep. Purif. Technol., 2023, 327, 124886 CrossRef CAS.
- I.-H. T. Kuete, D. R. T. Tchuifon, G. N. Ndifor-Angwafor, A. T. Kamdem, S. G. Anagho and J. Encapsulation Adsorpt, Science, 2020, 10, 1–27 CrossRef CAS.
- A. A. Inyinbor, F. A. Adekola and G. A. Olatunji, Water Resour. Ind., 2016, 15, 14–27 CrossRef.
- J. S. Calisto, I. S. Pacheco, L. L. Freitas, L. K. Santana, W. S. Fagundes, F. A. Amaral and S. C. Canobre, Heliyon, 2019, 5, 0–8 CrossRef.
- C. H. Giles, T. H. MacEwan, S. N. Nakhwa and D. Smith, J. Chem. Soc., 1960, 3973–3993 RSC.
- M. Li, P. Zhang, J. Mao, J. Li, Y. Zhang, B. Xu, J. Zhou, Q. Cao and H. Xiao, J. Environ. Manage., 2024, 359, 121076 CrossRef CAS PubMed.
- J. O. Ighalo, V. E. Ojukwu, C. T. Umeh, C. O. Aniagor, C. E. Chinyelu, O. J. Ajala, K. Dulta, A. O. Adeola and S. Rangabhashiyam, J. Water Process Eng., 2023, 56, 104514 CrossRef.
- A. H. Nordin, N. Ngadi, M. L. Nordin, N. A. Noralidin, W. Nabgan, A. Y. Osman and R. Shaari, Int. J. Biol. Macromol., 2023, 253, 126501 CrossRef CAS.
- C. Yang, Z. Li, Z. Hu, Y. Sun, F. Chen, T. Guo and J. Hu, Process Saf. Environ. Prot., 2023, 177, 496–506 CrossRef CAS.
- M. Basu, A. K. Guha and L. Ray, Bioresour. Technol., 2019, 283, 86–95 CrossRef CAS PubMed.
- M. A. Islam, T. K. Dada, M. I. Parvin, A. K. Vuppaladadiyam, R. Kumar and E. Antunes, J. Water Process Eng., 2022, 48, 102935 CrossRef.
- A. K. A. Khalil, I. W. Almanassra, A. Chatla, I. Ihsanullah, T. Laoui and M. Ali, Chem. Eng. Sci., 2023, 281, 119192 CrossRef CAS.
- Y. Huang, C. Liu, L. Qin, M. Xie, Z. Xu and Y. Yu, Molecules, 2023, 28(11), 4538 CrossRef CAS.
- R. Ghubayra, I. Mousa, H. A. Althikrallah, A. N. M. A. Alaghaz, A. F. Hassan and W. A. Shaltout, Int. J. Biol. Macromol., 2025, 305, 141021 CrossRef CAS.
- A. F. Hassan, A. Elhassanein, W. A. Shaltout and G. H. G. Ahmed, Int. J. Biol. Macromol., 2025, 294, 139465 CrossRef CAS PubMed.
- F. Kazemi, H. Younesi, A. A. Ghoreyshi, N. Bahramifar and A. Heidari, Process Saf. Environ. Prot., 2016, 100, 22–35 CrossRef CAS.
- A. F. Hassan and R. Hrdina, Int. J. Biol. Macromol., 2018, 109, 507–516 CrossRef CAS.
- K. Szostak, G. Hodacka, O. Długosz, J. Pulit-Prociak and M. Banach, Processes, 2022, 10(10), 2114 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
H. Hafezb,
Maha S. Elsayedc and
Asaad F. Hassan
*a,
H. Hafezb,
Maha S. Elsayedc and
Asaad F. Hassan d
d
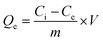
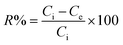



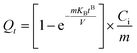










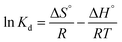


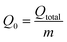

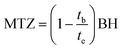
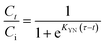




![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ) values ranging from 3.0685–3.3425 nm.
) values ranging from 3.0685–3.3425 nm.![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (nm)
(nm)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S
S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) sulfate ester, glycosidic linkage or C–OH stretching, C–O–C in 3,6-anhydrogalactose stretching vibration, and C–O–S stretching vibration, respectively.32 In the case of MFAC curve, the bands were shifted only compared to MFC, asserting the successful intercalation of KG and AR into the LDH structure. There was also a minor weakening of the intensity of some absorption bands with a slight shift in MFAC spectrum following the adsorption of Hg2+ ions. This may result from the surface complexation of functional groups (–OH and M–O), electrostatic interaction of OSO3−, and isomorphic displacement of Mg2+ with Hg2+ ions, reducing the vibration intensity of Mg–O bond, showing the dominant role of these functional groups in the Hg2+ removal.46
O) sulfate ester, glycosidic linkage or C–OH stretching, C–O–C in 3,6-anhydrogalactose stretching vibration, and C–O–S stretching vibration, respectively.32 In the case of MFAC curve, the bands were shifted only compared to MFC, asserting the successful intercalation of KG and AR into the LDH structure. There was also a minor weakening of the intensity of some absorption bands with a slight shift in MFAC spectrum following the adsorption of Hg2+ ions. This may result from the surface complexation of functional groups (–OH and M–O), electrostatic interaction of OSO3−, and isomorphic displacement of Mg2+ with Hg2+ ions, reducing the vibration intensity of Mg–O bond, showing the dominant role of these functional groups in the Hg2+ removal.46

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kd vs. 1/T shown in Fig. 6d over a range of 20–45 °C, using 25 mL of Hg2+ concentration of 900 mg L−1 with an adsorbent dose of 2 g L−1 for 30 min of shaking time. Table 3 also includes correlation coefficients and computed thermodynamic factors. ΔG° showed negative values, suggesting the spontaneous proceeding of mercuric ions adsorption onto MFL, MFC, and MFAC in the forward direction and more energetically advantageous as the solution temperature rose. On the other side, ΔG° values (−1.9913 to −4.2523 kJ mol−1) varied between 0 and −20 kJ mol−1, relating to physical adsorption. Moreover, the Hg2+ adsorption was an endothermic process with positive estimated enthalpy values (14.0645–19.0864 kJ mol−1), indicating that heat was absorbed throughout all steps included in the adsorption process. Whereas the positive ΔS° values pointed to an increment in randomness at the boundary between the mercuric ions and the adsorbent surface. In addition, van't Hoff graph (Fig. 6d) possessed high R2 values (≥0.9256), reflecting its good fitting for Hg2+ adsorption.
Kd vs. 1/T shown in Fig. 6d over a range of 20–45 °C, using 25 mL of Hg2+ concentration of 900 mg L−1 with an adsorbent dose of 2 g L−1 for 30 min of shaking time. Table 3 also includes correlation coefficients and computed thermodynamic factors. ΔG° showed negative values, suggesting the spontaneous proceeding of mercuric ions adsorption onto MFL, MFC, and MFAC in the forward direction and more energetically advantageous as the solution temperature rose. On the other side, ΔG° values (−1.9913 to −4.2523 kJ mol−1) varied between 0 and −20 kJ mol−1, relating to physical adsorption. Moreover, the Hg2+ adsorption was an endothermic process with positive estimated enthalpy values (14.0645–19.0864 kJ mol−1), indicating that heat was absorbed throughout all steps included in the adsorption process. Whereas the positive ΔS° values pointed to an increment in randomness at the boundary between the mercuric ions and the adsorbent surface. In addition, van't Hoff graph (Fig. 6d) possessed high R2 values (≥0.9256), reflecting its good fitting for Hg2+ adsorption.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)





