Spin-scaled double hybrids with long-range correction solve the TD-DFT overestimation problem in BODIPY dyes: benchmarking and experimental validation

Abstract

It has been established in the literature that time-dependent density functional theory (TD-DFT) methods systematically overestimate the electronic excitation energies in boron-dipyrromethene (BODIPY) dyes. Herein, we present the new SBYD31 benchmark set for BODIPY absorption energies and assess 28 different TD-DFT methods, most of which have not been tested on BODIPY dyes before. We show how functionals belonging to the class of recently developed spin-scaled double hybrids with long-range correction (J. Chem. Theory Comput., 2021, 17, 5165) overcome the overestimation problem and provide more robust results that have met the chemical accuracy threshold of 0.1 eV. To our knowledge, these are the most accurate absorption energies for BODIPY dyes reported for TD-DFT methods. In passing, we also point out how previous recommendations of “DSD” double hybrids, incl. one published in this journal (RSC. Adv., 2022, 12, 1704; Comput. Theor. Chem., 2022, 1207, 113531), were based on incorrect interpretations of the results. Our top-three recommended methods are SOS-ωB2GP-PLYP, SCS-ωB2GP-PLYP and SOS-ωB88PP86 and we verify our recommendations by making predictions, which we confirm with experimental measurements of newly synthesised BODIPY dyes. Our results add to existing evidence how time-dependent double hybrids with spin-component scaling and long-range correction solve notoriously hard cases for conventional TD-DFT methods and we are confident that our recommendations will assist in future developments of BODIPY dyes.

---

1 Introduction

Boron-dipyrromethene (BODIPY) dyes have emerged as versatile agents in photophysics and sensing applications. They have tunable emission profiles, high quantum yields, and possess multiple spectroscopic advantages.¹ They have found their use as laser dyes, biomolecular labels, and fluorescent switches, to name a few of their many applications.^2,3 There are continued efforts to tailor the properties of BODIPY dyes, with synthetic chemists pursuing new systems that exhibit improved photophysical properties. In particular, solvatochromic BODIPY dyes have garnered significant interest. This is largely attributed to their ability in exhibiting exceptional sensitivity to both macro- and micro-environmental polarity. This phenomenon described as solvatofluorochromism,⁴ has enabled their application in polarity mapping,^5,6 probing cellular processes,⁷ developing novel sensors, and imaging live cells and tissues.^8–10 Solvatofluorochromism in BODIPY dyes, arises from the incorporation of donor–acceptor groups onto the BODIPY core where these functional groups are electronically coupled through conjugation to induce intramolecular charge transfer (ICT) following excitation.⁶ This ICT state involves a sizable redistribution of electron density, with the interaction between the excited-state dipole moment and that of the solvent governing the extent of spectral shifts.⁴

Considering the significance of BODIPY dyes, it is important that computational chemistry techniques can accurately model their excited states to aid experimentalists in making new dyes with desired properties. Time-dependent density functional theory (TD-DFT)^11–13 remains the most popular methodology to model excited state properties. Indeed, many researchers use TD-DFT as default for the computational study of BODIPY dyes.^14,15 However, benchmarking studies to date have shown that it is difficult to match calculated results with experimental absorption data.

Jacquemin and coworkers pioneered the area of TD-DFT benchmarking for BODIPY dyes.¹⁶ In that initial work, they computed excitation energies of eight BODIPY dyes with 15 TD-DFT methods mainly belonging to the categories of General Gradient Approximations (GGAs), meta-GGAs, global hybrids (GHs) and long-range corrected hybrids (LCHs). They concluded the global hybrid BMK¹⁷ to be the best performing functional. That study relied on the common approach to compare vertical excitation energies directly with experimental λ_max values. This work showed a problem specific to BODIPY systems, namely that TD-DFT methods characteristically overestimate (blueshift) excitation energies of BODIPYs. In an attempt to understand the systematic blueshift when TD-DFT methods are applied to BODIPYs, Momeni and Brown, carried out a benchmarking study involving 17 BODIPY dyes and nine density functionals belonging to the GGA, GH and LCH classes.¹⁸ They also tested some ab initio methods and concluded the insufficient treatment of electron correlation to be one of the causes for the previously reported overestimation trend;¹⁸ for a detailed study by the same group involving coupled cluster approaches, see ref. 19.

Helal and co-workers followed up on Momeni and Brown's work with two separate TD-DFT benchmarking studies.^20,21 Both studies combined tested 31 TD-DFT methods on 25 BODIPYs. The importance of those studies is that also the highest rung of Jacob's Ladder²² was assessed with the inclusion of seven time-dependent double-hybrid (DH)^23,24 methods. A significant reduction of errors was reported for DHs, particularly for the two methods DSD-BLYP²⁵ and DSD-PBEP86 (ref. 26) with mean absolute errors (MAEs) of about 0.1 eV, which was an important level of accuracy compared to the aforementioned previous TD-DFT findings. However, after a close inspection of Helal and co-workers’ works, we conclude that the reported DSD-type numbers cannot be correct as the ORCA version used in their work did not have the capability to calculate excitation energies with those functionals, as we will briefly address in a later section of this present article. This means reliable double-hybrid studies on BODIPYs remain scarce, with other studies using such approaches being quite limited in scope.^27,28

From suggesting the usage of molecular mechanics,²⁹ to utilising the ΔSCF procedure,³⁰ numerous theoretical works have emerged trying to improve the accuracy of calculated excitation energies in BODIPY dyes.^31–40 However, in these works, authors often talked down the TD-DFT regime and advised users to rely on alternative approaches, such as applying a “fudge factor”.³⁷ To our knowledge, no one has yet reported reliable solutions and answers for accurate prediction of excitation energies in BODIPYs within the pure TD-DFT regime without empirical corrections, and the blue-shifting problem remains unsolved. Nevertheless, finding a solution is worthwhile because using vertical excitation energies to estimate λ_max values remains the preferred approach among computational chemists.

In the present study, we intend to revisit the application of time-dependent double hybrids to BODIPYs to address the blue-shifting problem. Compared to other studies, the current study presents results on a larger selection of double hybrids and involves the utilization of relatively more modern concepts in the area of TD-DFT. Time-dependent double hybrids in general, have been shown to be superior for treating excitation energies in organic molecules,^41–55 including cases that are notoriously difficult for TD-DFT methods. This includes treatment of exciton coupling,^55,56 polycyclic aromatic hydrocarbons^46,50,57 and open-shell systems;⁵⁸ see ref. 59 for a review. In 2021, the Goerigk group developed fourteen spin-scaled double hybrids,⁵⁰ some of which are also long-range corrected—or range-separated—to better describe long-range excitations. These functionals were specifically parametrised for excitation energies in small molecules with localised and Rydberg excitations, and cross-validation studies have reported the best TD-DFT results for excitation energies and excited state interaction energies in organic molecules and dimers.^50,54,55,58 Long-range corrected double hybrids were shown to significantly improve the description of long-range excitations, such as Rydberg, intra- and intermolecular CT.^{46,49,50,52,55} Studies by a different group showed a mixed picture for intermolecular CT, but spin-scaled double hybrids with a long-range correction also worked well for the therein investigated intramolecular CT cases.⁵² Very recently two of these spin-scaled DHs, SOS-PBE-QIDH and SOS-ωPBEPP86, were used on a smaller set of three BODIPY dyes.⁶⁰ However, a thorough assessment of these methods for applications on BODIPYs is still lacking and our present study aims to close this gap.

Herein, we present the first thorough TD-DFT benchmarking study on BODIPY dyes that includes an assessment on time-dependent double hybrids with spin scaling. Our study is based on a new compilation of 23 synthesised BODIPY dyes with 31 excitation energies measured in different solvents (SBYD31) set, as described in the next section. In Section 3, we elaborate on technical details and briefly revisit the proper definition of time-dependent double hybrids with spin-component scaling. We also briefly address the problem the previous studies that claimed to have assessed two older spin-scaled functionals (DSD-BLYP and DSD-PBEP86) on BODIPY dyes. In our current study, we provide numbers for the correct implementation. In Section 4 we discuss the calculation results of 28 density functionals for our SBYD31 set and provide recommendations, which we cross-validate in Section 5 by making predictions on synthesised BODIPYs, two of which are synthesised for the first time.

2 The SBYD31 set

We present our new benchmark set SBYD31 for Synthetic BODIPY Dyes containing 31 experimental λ_max values for 23 BODIPY dyes (see Fig. 1). BODIPYs B1, B2, B3, B4 and B11 possess more than one experimental reference value due to experimental measurements carried out in different solvent environments, thus contributing to more than 23 reference values. The inclusion of these cases is helpful, as some BODIPYs are more susceptible to solvatochromism, which should be captured by computational methods. All 31 experimental reference values are given in Section 1 of the ESI.† The 23 BODIPYs were chosen to incorporate the vast diversity of BODIPY analogues found in the literature. Furthermore, all 23 of them have been synthesized with their spectroscopic properties measured.

Fig. 1 The SBYD31 set.

It is also to be noted here that some of the 23 structures, especially BODIPYs B5–B23 have been used in previous benchmarking studies.^18,20 However, our SBYD31 set can be understood as novel in the consideration of following aspects: some of the BODIPY structures used before were not the exact same structures synthesized, as some alkyl chains had been replaced with methyl groups, or only wave function references were available. We compiled SBYD31 such that all the BODIPY dyes and their λ_max values we refer to are exactly the same ones used in experiments, which makes the set more appealing due to its synthetic relevance.

B11 is the fully unsubstituted parent BODIPY system (difluoroborodiaza-s-indacene). BODIPYs B10 and B17 are altered versions of the parent BODIPY in a sense that the s-indacene core is replaced with different cores. In B10, an imidazole and a pyridinium group are fused with difluoroboron moiety instead of the s-indacene group and in B17, the s-indacene group is replaced with an anthracene-like core (B17 is often referred to as aza-BODIPY). The other molecules are variations that show a large variety of substituents and functional groups, as shown in Fig. 1.

3 Technical and experimental details

3.1 Computational details

All calculations were carried out with ORCA 5.0.4.⁶¹ Geometry optimisations were performed at the B3LYP^62,63-D3(BJ)^64,65/def2-TZVP⁶⁶ level of theory. Vertical excitation energies for all 28 TD-DFT methods were calculated without reoptimisation. The Ahlrichs def2-TZVP basis set⁶⁶ was used for these single point calculations. The conductor-like polarizable continuum solvent model (CPCM)⁶⁷ was employed both during geometry optimisations and subsequent calculations; see Section 1 of ESI† for information on the specific solvents. PCM-based solvent models were shown before to work well for BODIPYs^20,21,38 and are available in multiple programs. The self consistent field (SCF) convergence criterion was set to 10⁻⁷ E_h, the geometry convergence criterion to ORCA's default setting, which includes a change of total energy less than 5 × 10⁻⁶ E_h.

The resolution-of-the-identity (RI) approximation for Coulomb integrals⁶⁸ paired with the chain of spheres approximation for exchange integrals (RIJCOSX)⁶⁹ was used in all calculations. The RI approximation⁷⁰ was also used in all perturbative steps for double-hybrid DFT calculations. Appropriate auxiliary basis sets were applied for the RI approximations.^71,72 The def2-type effective core potential was applied to iodine.⁶⁶ The default numerical quadrature grid (DEFGRID2) was used in all calculations.

Excitation energies were calculated with the full TD^11–13 algorithm and the Tamm–Dancoff approximation (TDA).⁷³ The same 28 functionals were used for both the TD and TDA-DFT treatments with all methods belonging to the top two rungs of the Jacob's ladder, as previous works have established that lower-rung methods produce inaccurate excitation energies in organic molecules.^42,59,74 As outlined in the Introduction, previous benchmark studies have tested sufficient functionals to conclude that they have a systematic blue shift. As such, we limit our analysis of rung-4 functionals to just a handful of popular examples. This will allow us to put the results for double hybrids that have never been tested before on BODIPYs into better context. In the present study, we categorise our 28 DFT methods in the following order: Global Hybrids (GHs)—BHLYP⁷⁵ and B3LYP;^62,63 Long-Range Corrected Hybrids (LCHs)—ωB97X⁷⁶ and CAM-B3LYP;⁷⁷ Global Double Hybrids (GDHs)—B2PLYP,²³ B2GP-PLYP,⁷⁸ and PBE-QIDH;⁷⁹ Long-Range Corrected Double Hybrids (LCDHs)—ωB2PLYP,⁸⁰ ωB2GP-PLYP,⁸⁰ RSX-QIDH,⁸¹ ωB88PP8,⁵⁰ and ωPBEPP86;⁵⁰ Spin-Scaled Global Double Hybrids (SCS/SOS-GDHs)—DSD-BLYP,²⁵ DSD-PBEP86,²⁶ SOS-B2PLYP,⁵⁰ SCS-B2GP-PLYP,⁵⁰ SOS-B2GP-PLYP,⁵⁰ SCS-PBE-QIDH,⁵⁰ and SOS-PBE-QIDH;⁵⁰ Spin-Scaled Long-Range Corrected Double Hybrids (SCS/SOS-LCDHs)—SCS-RSX-QIDH,⁵⁰ SOS-RSX-QIDH,⁵⁰ SOS-ωB2PLYP,⁵⁰ SCS-ωB2GP-PLYP,⁵⁰ SOS-ωB2GP-PLYP, SCS-ωB88PP86,⁵⁰ SOS-ωB88PP86,⁵⁰ SCS-ωPBEPP86,⁵⁰ and SOS-ωPBEPP86.⁵⁰

Time-dependent double hybrids (TD-DHs) mentioned in this study follow the idea established by Grimme and Neese,²⁴ where the first calculation step obtains a hybrid-type TD-DFT excitation energy, which is perturbatively corrected by configuration interaction singles with perturbative doubles [CIS(D)].⁸² Time-dependent long-range corrected double hybrids (TD-LCDHs) were introduced in 2019 and they include the concept of long-range correction in the exchange component of the functionals.⁸⁰ The SCS/SOS-GDHs and SCS/SOS-LCDHs mentioned above follow the protocol introduced by Goerigk and co-workers^45,50 based on the SCS/SOS-CIS(D) idea by Rhee and Head-Gordon,⁸³ where the “SCS” and “SOS” acronyms describe the well-established spin-component⁸⁴ and spin-opposite scaling⁸⁵ techniques for electron correlation energies, as reviewed in detail in ref. 86. For a fair comparison, we also carried out CIS(D) and SCS-CIS(D) calculations. As we preferred to stick to the same program for like-to-like comparisons, we were unable to test the SOS-CIS(D)⁸³ method, as it requires a specific method-inherent parameter to be switched off, which cannot be done in ORCA through the input file. Note that SOS-CIS(D) and SCS-CIS(D) have been found to perform very similarly for large organic dyes.⁴³ The scaling parameters used in our SCS-CIS(D) tests are shown in Table S10 in the ESI;† for more details on the different versions of SCS-CIS(D) and more details on SOS-CIS(D), see ref. 43 and 87.

Readers unfamiliar with (TD-)DHs are advised that they formally have a higher scaling with system size than conventional DFT methods due to the second-order perturbative steps. RI approximations can reduce the pre-factor for such calculations.⁸⁸ SOS techniques can bring down the formal scaling behaviour depending on the available code.^83,85,86 It has been demonstrated how TD-DHs do require the calculation of fewer states compared to other functionals that can produce artificial ghost states.^56,59 While each individual state might require more time for a double hybrid, the total number of states calculated might be fewer, making them overall competitive again. Memory and storage requirements of the perturbative part can be controlled based on the program. ORCA provides four different algorithms for the CIS(D) correction and we refer the interested reader to ref. 24 and the ORCA manual for more information.

Values for the Λ CT descriptor⁸⁹ were calculated with Multiwfn Version 3.8 (ref. 90 and 91) based on TD-CAM-B3LYP calculations; note that we found little functional dependence on the values.

3.2 A comment on previously published results with DSD-type double hybrids

Having briefly summarised the steps that need to be taken to obtain excitation energies with an SCS/SOS-DH, we take this opportunity to briefly address previous BODIPY studies, which recommended the two double hybrids DSD-BYLP and DSD-PBEP86.^20,21 DSD-type double hybrids include spin-component scaling and were originally developed for ground state properties. They can be used without any problem in the ORCA program. However, when SCS-DHs are used for excitation energies, the SCS technique also needs to be applied to the CIS(D)-type correction. This has been possible since the first version of ORCA 5.0 after the developments published in ref. 50. However, the authors of ref. 20 and 21 used ORCA 4.2.0, which means that their reported excitation energies for the DSD-type functionals cannot be correct. Instead, the perturbative components of the excitation energies reported in their studies were not spin scaled. Note that this was most likely due to an oversight, as ORCA4.2.0 does not give a warning that spin scaling cannot be applied in the excited state treatment. That being said, the first TD-DFT treatments with DSD functionals date back to 2017 where the necessity for applying spin scaling was clearly stated.⁴⁵

Herein, we assess the same functionals in their proper implementation. The established ground state scaling parameters for same and opposite spin contributions were applied to the SCS-CIS(D) component. In ORCA 5.0 and beyond, additional keywords are required when calculating excitation energies with DSD functionals, as just using the DSD functional keyword alone will not ensure the correct treatment of excitation energies. This is documented in detail in the ORCA manual and a sample input is provided in Section 2 of the ESI.† In our current study, we discuss results from the correct DSD implementations in Section 4.

The impact of using the wrong implementation is shown in Tables S6 and S7 in the ESI.† Differences in excitation energies between the incorrect and correct implementations are significant, for instance for B1 they amount to 0.276 eV for TD-DSD-BLYP and 0.309 eV TD-DSD-PBEP86. MAEs for the entire benchmark set are 0.175 eV for the correct DSD-BLYP and 0.196 eV for the incorrect version. For DSD-PBEP86 the MAEs are 0.171 eV and 0.229 eV respectively. Mean signed errors (MSEs) for the incorrect versions are negative, whereas they are positive for the correct implementations (see ESI† for more details). While the incorrectly implemented version seems to give the best results in the aforementioned studies by Helal and co-workers, we do not recommend it as a valid approach. Clearly, the electron-correlation contributions to ground and excited states are not treated in the same way, and as such the seemingly good results that were reported were due to fortuitous error compensation.

We hope that this section will serve as a reminder on how DSD methods are to be applied for excited state problems, thus preventing the publication of future incorrect results.

3.3 Experimental details

3.3.1 Synthesis of BODIPYs. Reagents were purchased from Sigma-Aldrich and Combiblocks while organic solvents were purchased from Merck and Ajax and were used without further purification. All reactions were monitored using thin layer chromatography, with plates precoated with Merck Silica Gel 60 F254 and analyzed by exposure to ultraviolet (UV) light. Silica gel column chromatography was carried out using silica gel SiliaFlash F60 (230–400 mesh). NMR experiments were performed in deuterated chloroform, DCM or dimethyl sulfoxide (CDCl₃, CD₂Cl₂ or DMSO-d₆). ¹H, ¹³C{¹H}, ¹⁹F and ¹¹B NMR spectra were recorded at 298 K on either a Bruker Avance III or Bruker Avance III nanobay NMR spectrometer equipped with a 9.4 T magnet and 5 mm BBFO probe, operating at 400 MHz (¹H), 101 MHz (¹³C{¹H}), 377 MHz (¹⁹F) and 128 MHz (¹¹B). Chemical shifts (δ) are reported in ppm and were referenced to the residual solvent signals (¹H, ¹³C{¹H}). Bruker software and Mnova 14.2.3 were used for data acquisition and processing. Mass spectrometry experiments were performed on an Agilent Q-TOF 6540 mass spectrometer, using the electrospray ionization technique and controlled via the Mass Hunter software package. The precursor molecule 1 and its derivative B3 are known dyes and were synthesized using methods previously reported in literature with slight modifications.^92,93 while compounds 2 and 3 are previously unreported. Our synthesis scheme is shown in Scheme 1. All additional information and spectral data are provided in Section 8.1 of the ESI.†

Scheme 1 Synthesis of BODIPYs 1, B3, 2 and 3. Reaction conditions: (a) (i) CH₂Cl₂/TFA, 18 h, N₂, rt, (ii) DDQ, (iii) Et₃N/BF₃–OEt₂; (b) toluene, AcOH, piperidine, p-N,N-dimethylaminobenzaldehyde, MW, 20 min; (c) CH₂Cl₂/MeOH (9 : 1), NaOH, rt; (d) DMF, NHS, EDC, N₂, rt.

3.3.2 UV-Vis spectroscopy. UV-Vis spectroscopy experiments of compounds 1, 2 and 3 (10 μM) were performed on an Agilent Technologies Cary 60 UV-Vis spectrophotometer using Agilent Technologies standard quartz cuvettes of 1 cm path length. Baseline corrections were applied over the entire wavelength range collected for each solvent. See Section 8.2 of the ESI† for all the UV-Vis data.

4 Results and discussion

In this work, we compare experimental λ_max values directly with the calculated vertical excitation energies, which are expected to be S₀ → S₁ transition energies. More specifically we take the differences between calculated and reference values, which means that a positive error indicates an overestimation by the given method. As also pointed out by others,^18,20,94 doing such a comparison is common practice even though vertical excitation energies do not include any vibronic effects. In the case of BODIPYs it was discussed how this “vertical approximation” is appropriate.^18,94

We are aware that DFT methods in lower-rungs of the Jacob's ladder (here GHs) often show ‘ghost states’ that have no experimental counterpart.⁵⁹ We witnessed the same for B3LYP, which often had one or two ghost states lying lower than the actual state of interest for B5–B9, B12 and B13. No other assessed functional showed this problem thanks to their high amounts of Fock exchange. Also note that the description of the relevant transition is not always one from the highest occupied molecular orbital (HOMO) to the lowest unoccupied molecular orbital (LUMO). This is functional dependent and often transitions from the HOMO−1 were observed, which is a known problem but often still overlooked in discussions of similar nature. While we refrain from discussing orbital contributions, they can be found in Tables S6 (for full TD-DFT) and S7 (for TDA-DFT) in the ESI† alongside information on the relevant state for a given functional and the oscillator strength.

We assess the overall performance of every functional in terms of MAE, MSE, root mean squared error (RMSE), error range (Δ_err), i.e. the difference between most positive and most negative error, and the squared correlation coefficient R². Those metrics for both TD-and TDA-DFT are shown in Table 1. In addition, Fig. 2 shows the TD statistics in the form of a chart (a-MAE, b-MSE and c-error range). The main focus of our subsequent discussion will focus on full TD-DFT followed by a short summary of TDA-DFT results. Some excitations are reported for different solvents but the same molecules. Even when removing those states and running analyses on just 23 excitation energies, our recommendations reported below were the same.

Table 1 Metrics for each assessed functional for both full TD- and TDA-DFT: MAE, MSE, RMSE, Δ_err (all in eV) and R². The top-three for each metric are highlighted in bold

	TD-DFT					TDA-DFT
	MAE	MSE	RMSE	Δerr	R^2	MAE	MSE	RMSE	Δerr	R^2
a GH—global hybrids, LCH—long-range corrected hybrids, GDH—global double hybrids, LCDH—long-range corrected double hybrids, SCS/SOS—spin-scaled; averaged MAEs per TD-DFT category (in eV): GH = 0.289, LCH = 0.344, GDH = 0.193, LCDH = 0.258, SCS/SOS-GDH = 0.202, SCS/SOS-LCDH = 0.111.
GH^a
BHLYP	0.362	0.337	0.385	0.993	0.882	0.511	0.498	0.538	1.060	0.864
B3LYP	0.216	0.103	0.281	1.345	0.778	0.319	0.238	0.384	1.470	0.725
LCH^a
ωB97X	0.363	0.353	0.384	0.781	0.921	0.524	0.524	0.546	0.816	0.920
CAM-B3LYP	0.324	0.297	0.343	0.970	0.895	0.473	0.457	0.493	1.031	0.880
GDH^a
PBE-QIDH	0.241	0.209	0.262	0.903	0.912	0.342	0.320	0.361	0.931	0.903
B2GP-PLYP	0.188	0.146	0.219	0.959	0.906	0.274	0.241	0.297	0.988	0.893
B2PLYP	0.150	0.096	0.212	1.080	0.873	0.223	0.179	0.277	1.123	0.846
LCDH^a
RSX-QIDH	0.299	0.287	0.320	0.713	0.931	0.439	0.439	0.462	0.729	0.931
ωB2PLYP	0.286	0.270	0.304	0.737	0.932	0.424	0.421	0.443	0.755	0.932
ωB2GP-PLYP	0.266	0.248	0.284	0.734	0.934	0.397	0.392	0.416	0.750	0.933
ωB88PP86	0.228	0.202	0.246	0.806	0.931	0.340	0.324	0.354	0.824	0.927
ωPBEPP86	0.211	0.183	0.230	0.806	0.932	0.317	0.299	0.331	0.822	0.928
SCS/SOS-GDH^a
SOS-B2PLYP	0.405	0.378	0.415	1.001	0.896	0.518	0.501	0.535	1.054	0.875
SCS-B2GP-PLYP	0.253	0.218	0.266	0.896	0.920	0.357	0.332	0.369	0.920	0.911
SOS-B2GP-PLYP	0.208	0.169	0.227	0.898	0.919	0.310	0.281	0.323	0.921	0.911
DSD-BLYP	0.175	0.138	0.203	0.887	0.922	0.256	0.227	0.276	0.905	0.913
DSD-PBEP86	0.171	0.131	0.198	0.885	0.922	0.257	0.226	0.275	0.904	0.914
SCS-PBE-QIDH	0.112	0.067	0.164	0.876	0.921	0.212	0.177	0.236	0.894	0.914
SOS-PBE-QIDH	0.088	0.038	0.152	0.863	0.924	0.188	0.151	0.214	0.877	0.918
SCS/SOS-LCDH^a
SOS-RSX-QIDH	0.175	−0.153	0.199	0.674	0.943	0.075	0.022	0.126	0.681	0.945
SOS-ωB2PLYP	0.141	0.113	0.173	0.704	0.939	0.291	0.276	0.305	0.716	0.941
SCS-RSX-QIDH	0.118	−0.049	0.155	0.737	0.929	0.130	0.098	0.177	0.752	0.928
SCS-ωPBEPP86	0.116	−0.063	0.156	0.782	0.929	0.113	0.073	0.162	0.794	0.927
SCS-ωB88PP86	0.113	0.078	0.157	0.764	0.935	0.242	0.219	0.258	0.777	0.934
SOS-ωPBEPP86	0.094	−0.049	0.141	0.748	0.938	0.132	0.099	0.165	0.756	0.938
SCS-ωB2GP-PLYP	0.087	0.006	0.132	0.706	0.939	0.187	0.163	0.209	0.715	0.940
SOS-ωB2GP-PLYP	0.080	0.029	0.131	0.692	0.942	0.214	0.193	0.230	0.700	0.944
SOS-ωB88PP86	0.078	0.026	0.136	0.755	0.937	0.200	0.172	0.218	0.765	0.937

---

Fig. 2 TD-DFT results in the form of a bar chart; (a) MAE, (b) MSE and (c) error range (all in eV).

4.1 TD-DFT results

Fig. 2a and Table 1 reveal how MAEs on average decrease when moving from hybrids to double hybrids. However, within a given rung of Jacob's ladder, long-range correction leads to an increase in the MAEs. For instance, the average MAE for GHs is 0.289 eV and increases to 0.344 eV for LCHs. The increase for unscaled GDHs to LCDHs is similar (from 0.193 eV to 0.258 eV, respectively). While the average MAE for spin-scaled global double hybrids does not look like an improvement (0.202 eV) this is mainly due to SOS-B2PLYP being an outlier in this category, with an MAE of 0.405 eV. The combination of long-range correction with spin scaling leads to the best results with an average MAE of 0.111 eV for this category. The smallest MAEs of all 28 tested methods belong to this category, and they are SOS-ωB88PP86 (0.078 eV), SOS-ωB2GPLYP (0.080 eV), and SCS-ωB2GPLYP (0.087 eV). This trend is in excellent agreement with the original development study performed in our group,⁵⁰ as well as with Helal's recent study on cyanine dyes.⁹⁵ In addition to those three methods, the remaining functionals in the top 10 for MAEs are exclusively spin-scaled double hybrids: SOS-PBE-QIDH (0.088 eV), SOS-ωPBEPP86 (0.094 eV), SCS-PBE-QIDH (0.112 eV), SCS-ωB88PP86 (0.113 eV), SCS-ωPBEPP86 (0.116 eV), SCS-RSX-QIDH (0.118 eV) and SOS-ωB2PLYP (0.141 eV). This finding aligns with studies on other organic single chromophores and non-covalent interactions between chromophores, which demonstrated the robust and superior behaviour of SCS/SOS-DHs.^54,55,58

The MAEs of popular methods are significantly higher: CAM-B3LYP (0.324 eV), ωB97X (0.363 eV) and B3LYP (0.216 eV). The DSD-type double hybrids discussed in Section 3.2 no longer stand out when properly applied with MAEs between 0.17 and 0.18 eV. Methods with MAEs below 0.1 eV are considered to fall within the chemical accuracy threshold. In total, five methods satisfy this criterion—SOS-ωPBEPP86, SOS-PBE-QIDH, SCS-ωB2GPLYP, SOS-ωB2GPLYP and SOS-ωB88PP86. However, to develop recommendations for method users, more than one metric should be considered and we continue our discussion by looking at MSEs next.

The systematic blueshift observed for many TD-DFT methods applied to BODIPYs can be seen in Fig. 2b, with all hybrids and unscaled DHs having positive MSEs. To our knowledge, our study presents the first double-hybrid results where the systematic blueshift is overcome and, instead, a tendency to underestimate excitation energies is found. This is the case for SOS-RSX-QIDH (MSE = −0.153 eV), SCS-RSX-QIDH (−0.049 eV), SCS-ωPBEPP86 (−0.063 eV), and SOS-ωPBEPP86 (−0.049 eV). Again, all these methods combine long-range correction with spin scaling. This is an important result in the context of TD-DFT modelling of BODIPYs, as we show a solution to the systemic blueshift while merely relying on vertical excitation energies instead of more complicated approaches mentioned in the Introduction.

The best MSEs, i.e. those that are the closest to a perfect value of 0 eV, are observed for SCS-ωB2GP-PLYP (0.006 eV), SOS-ωB88PP86 (0.026 eV), and SOS-ωB2GP-PLYP (0.029 eV). Spin-scaled long-range corrected double hybrids, thus emerge again as the best-performing also for the MSE metric.

RMSEs follow the same trends as MAEs and are not discussed in detail, see Table 1 and Fig. S1 for details.†

Section 10 in the ESI† shows results for CIS(D) and SCS-CIS(D). It has already been demonstrated in 2010 that those methods are outperformed by global, spin-unscaled double hybrids for the description of large organic dyes.⁴³ When comparing the newer SCS/SOS-LCDHs with (SCS)-CIS(D), we see again that the latter cannot compete with them. For instance the MAE for CIS(D) is 0.169 eV and for SCS-CIS(D) 0.147 eV. SCS introduces a strong red shift leading to an MSE of −0.126 eV (Table S10†).

Before continuing our results analysis, we can rationalise our findings thus far. We have seen how long-range correction by itself leads to a blueshift in BODIPYs, as it usually does for other chromophores, resulting in worse MAEs and MSEs. Applying spin scaling to DHs, on the other hand has led to a redshift, as evidenced from our results. This clarifies that the excitation energies in BODIPYs are sensitive to how the underlying method treats electron correlation. Momeni and Brown also pointed out the same sensitivity to the treatment of electron correlation based on their analysis of wave function approaches applied to BODIPYs.¹⁸ We know that SCS/SOS-DHs include less electron correlation than their parent functional. Ultimately, it is the interplay between long-range correction and spin scaling that has lead to a more balanced result. Stener and co-workers attributed the inability of TD-DFT methods to properly address double excitations to their poor performance for BODIPYs.³⁰ However, we do not see any validation for this, as it is well established how time-dependent double hybrids cannot properly describe double excitations.^42,50,58 And yet our time-dependent double hybrids have accurately captured the excitation energies in BODIPYs. Henceforth, we conclude that the lack of double excitations in TD-DFT calculations could not have been the cause for the positive MSEs.

Furthermore, ICT can occur in some BODIPY dyes, as mentioned in the Introduction, which is why we carried out an additional analysis with Helgaker, Tozer and co-workers’ Λ metric, which allows characterising the long-range character of an excitation with values close to zero being typical for CT and values closer to 1 being typical for localised excitations.⁸⁹ Λ values for all 31 excitations are shown in Table S9 in the ESI.† The results indicate that none of the investigated excitations have strong CT character with the lowest value being 0.504 (B12) and the largest being 0.747 (B14). In comparison, the original Λ study reported values of 0.44 for some localised excitations; a considerable CT is expected to have lower values than that.⁸⁹ Even an influence of partial CT character on the herein reported functional errors can be ruled out, as correlation plots between Λ and calculated errors do not show the expected behaviour of systematic red shifts for transitions with CT character, nor an improvement with long-range corrections (Fig. S18–S23†). As such, the good performance of the best functionals in our study is not due to a better description of CT character, but due to the aforementioned better description of electron-correlation effects.

We continue our analysis by pointing out how all methods show significant Δ_err values (Fig. 2c and Table 1). The smallest value is 0.674 eV (SOS-RSX-QIDH), but many spin-scaled and unscaled DHs have similar error ranges between 0.7 and 0.9 eV that are not too different from the ωB97X long-range corrected hybrid (0.781 eV). Contrary to the MAE trend, the long-range corrected double hybrids ωB2PLYP and ωB2GP-PLYP have smaller error ranges than their parent double hybrid (B2PLYP; 1.080 eV, B2GP-PLYP; 0.959 eV). Thus, the error ranges give rise to a different overall ranking. Another noteworthy aspect is the error range for the popular B3LYP functional, which is the highest of all tested functionals with a value of 1.345 eV, indicating overall poorer robustness. This aspect of B3LYP is not evident upon analysing the MAEs or MSEs alone. The different trends for error ranges are motivation to consider one additional metric in our analysis, namely the R² value.

R² is a measure of how well the calculated values correlate with the reference, with a value of 1 meaning perfect correlation. SOS-RSX-QIDH emerges as the functional with the best correlation (R² = 0.943), very closely followed by SOS-ωB2GP-PLYP (0.942), SOS-ωB2PLYP (0.939) and SCS-ωB2GP-PLYP (0.939). In fact, with the exception of SOS-B2PLYP, all spin-scaled DHs have R² values above 0.900. Fig. 3a compares the two extremes, namely B3LYP with the worst R² value of 0.778 and SOS-RSX-QIDH. While the figure shows the tendency of SOS-RSX-QIDH to underestimate excitation energies, it also demonstrates that the results are less spread compared to B3LYP, which indicates the overall higher robustness of SOS-RSX-QIDH, and of spin-scaled double hybrids with similar R² values in general.

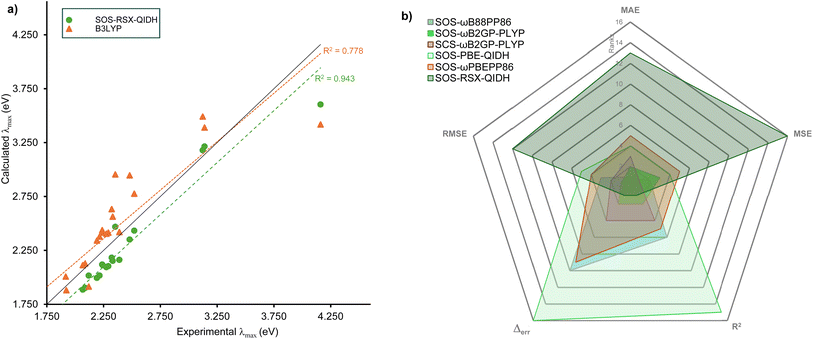Fig. 3 (a) Comparison between the methods with best (SOS-RSX-QIDH) and worst R² values (B3LYP). (b) Radar chart showing the overall performance of select functionals.

In order to provide recommendations for future treatment of electronic excitations in BODIPYs, we need to consider all five metrics to ensure that the recommended methods are not only accurate without any systemic shifts, but also more robust. For this purpose, we ranked all 28 functionals for each of the five metrics (MAE, MSE, RMSE, Δ_err and R²). Whenever values were identical up to three decimal places, we based the ranking on the fourth decimal place to simplify the procedure and avoid ties. The resulting detailed rankings for all functionals and metrics are shown in Table S2 in the ESI.† The results were then analysed in the form of a radar chart to identify the best performers. A radar chart for six functionals is shown in Fig. 3b; for better visibility, the best six functionals are shown. The chart makes it very clear that SOS-ωB2GP-PLYP emerges as the best-performing functional covering the smallest area in comparison to other functionals. However, as we saw in the detailed analysis of the five metrics, often functionals are close to one another. Therefore, we decided to recommend the top-three functionals when using the full TD-DFT algorithm, which are all spin-scaled double hybrids with long-range correction:

(1) SOS-ωB2GP-PLYP,

(2) SCS-ωB2GP-PLYP,

(3) SOS-ωB88PP86.

4.2 TDA-DFT results

The Tamm–Dancoff approximation is a popular alternative to full TD-DFT, the default option in some programs, and it is popular for larger chromophores. For completeness reasons we repeat the same analysis as in the previous section, but keep the discussion brief. The same five metrics as discussed before for each of the 28 assessed TDA-DFT methods are shown in Table 1. MAEs are displayed in Fig. 4, while MSEs, RMSEs and error ranges are shown in Fig. S3 in the ESI.†

Fig. 4 MAEs (in eV) for the assessed TDA-DFT methods.

Almost all MAEs are larger than for the TD-DFT formalism. Increases are between around 0.1 to about 0.15 eV. In general, no functional has an MAE below the chemical accuracy threshold of 0.1 eV. The only exception is SOS-RSX-QIDH whose MAE improves by 0.1 eV from 0.175 eV to 0.075 eV.

The observed trends for the MAEs, including that for SOS-RSX-QIDH, can be understood with the help of MSEs. It is well-established how the TDA induces a blueshift to electronic excitation energies.^{45,48,73,96,97} The same can be seen here with the MSEs for all 28 functionals increasing. None of the functionals possess a negative MSE. SOS-RSX-QIDH's better MAE for the TDA approach can be explained by the fact that its MSE for the full TD formalism was strongly negative (−0.153 eV) whereas for the TDA it gives the best of all 28 MSEs with a value of 0.022 eV. The overall blueshift induced by TDA explains the higher MAEs for the remaining 27 functionals.

Unsurprisingly, RMSEs also increased. The same is also true for the error ranges. The MAEs, MSEs, RMSEs and the error ranges mostly indicate larger inaccuracies when using the TDA formalism. However, as the TDA is still popular, or also necessary, for instance when calculating triplet excitation energies due to the triplet instability problem,^48,98,99 we decided to carry out a ranking of all 28 functionals analogous to full TD-DFT. The rankings and the radar chart are provided in Section 4 of the ESI.† Based on the radar chart, we rank the top-three functionals when using TDA-DFT as follows:

(1) SOS-RSX-QIDH,

(2) SCS-RSX-QIDH,

(3) SOS-ωB2GP-PLYP.

However, when only singlet excitations are considered we strongly advise DFT users to use the full TD-DFT formalism for computational treatment of BODIPY dyes.

5 Cross validation of recommendations

In this section we cross-validate our recommendations for the full TD-DFT regime to demonstrate the usefulness of spin-scaled, long-range corrected double hybrids for making predictions prior to synthesis. The cross validation is carried out for three solvatochromic BODIPY dyes shown in Scheme 1. Dye 1 has been synthesised before and was used by us as an intermediate to synthesise the novel dyes 2 and 3. Table 2 shows both calculated and measured λ_max values in different solvents. The ESI provides more details on nature of electronic transitions and experimentally measured spectra.† All three methods predicted the measured λ_max values within the chemical accuracy threshold of 0.1 eV. In fact, some results for SOS-ωB2GP-PLYP and SOS-ωB88PP86 show negligible deviations below 0.01 eV (2 and 3 for the solvents toluene and DCM). Relatively larger absolute deviations are found in some conditions, but these do not exceed 0.063 eV for SOS-ωB2GP-PLYP and 0.038 eV for SOS-ωB88PP86. That being said, the results for SCS-ωB2GP-PLYP are also still in excellent agreement for all three dyes and in their various solvents with absolute deviations ranging from 0.023 to 0.074 eV.

Table 2 Comparison between our predicted (Pred.) and experimental (Exp.) values for compounds in the synthetic scheme (all in eV)

Compound	Solvent^a	Pred.	Exp.	Pred. − Exp.
a Tol—toluene, DCM—dichloromethane, Acet—acetone, MeOH—methanol, MeCN—acetonitrile.
TD-SOS-ωB2GP-PLYP
1	Tol	2.392	2.455	−0.063
	DCM	2.424	2.465	−0.041
2	Tol	2.022	2.023	−0.001
	DCM	2.027	2.026	−0.001
	Acet	2.045	2.070	−0.025
	MeOH	2.054	2.070	−0.016
	MeCN	2.049	2.080	−0.031
3	Tol	2.016	2.009	0.007
	DCM	2.021	2.016	0.005
	Acet	2.038	2.043	−0.005
	MeOH	2.048	2.053	−0.005
	MeCN	2.042	2.049	−0.007
TD-SCS-ωB2GP-PLYP
1	Tol	2.381	2.455	−0.074
	DCM	2.414	2.465	−0.051
2	Tol	1.992	2.023	−0.031
	DCM	1.996	2.026	−0.030
	Acet	2.014	2.070	−0.056
	MeOH	2.023	2.070	−0.047
	MeCN	2.018	2.080	−0.062
3	Tol	1.986	2.009	−0.023
	DCM	1.990	2.016	−0.026
	Acet	2.007	2.043	−0.036
	MeOH	2.017	2.053	−0.036
	MeCN	2.011	2.049	−0.038
TD-SOS-ωB88PP86
1	Tol	2.417	2.455	−0.038
	DCM	2.448	2.465	−0.017
2	Tol	2.020	2.023	−0.003
	DCM	2.022	2.026	−0.004
	Acet	2.038	2.070	−0.032
	MeOH	2.047	2.070	−0.023
	MeCN	2.042	2.080	−0.038
3	Tol	2.015	2.009	0.006
	DCM	2.015	2.016	−0.001
	Acet	2.031	2.043	−0.012
	MeOH	2.041	2.053	−0.012
	MeCN	2.035	2.049	−0.014

---

In summary, the herein discussed findings verify our benchmarking study.

6 Summary and conclusion

We presented a new benchmark set called SBYD31, to assess vertical excitation energies of BODIPY dyes. SBYD31 includes 31 experimental excitation energies for 23 different systems, measured in different solvents.

With the help of SBYD31, we carried out the first thorough assessment of time-dependent double-hybrid functionals for the calculation of electronic excitations in BODIPYs. Our results for 28 density functionals, some of which were popular hybrids or older double hybrids, show that modern spin-scaled, long-range corrected double hybrids by far outperform older methods with the top ten of our tested functionals belonging to this category. Five of those had average errors below the chemical accuracy threshold of 0.1 eV. We also point out how previous assessments of the spin-scaled class of DSD functionals were based on erroneous inputs and how those functionals do not particularly stand out for the treatment of BODIPYs.

The most important finding of our study is that many of the tested spin-scaled, long-range corrected double hybrids offer a solution to a notorious, long-standing problem reported in the literature, namely that TD-DFT methods systematically overestimate excitation energies in BODIPYs when vertical excitation energies are compared to experimental λ_max values.

We compared results for the full TD-DFT algorithm with that of the Tamm–Dancoff approximation. Unsurprisingly, the latter leads to a blueshift in the results and we recommend relying on the full TD-DFT algorithm when possible. A combined analysis of five different error metrics allowed us to particularly recommend three density functionals to be used with full TD-DFT, as they have shown higher robustness, accuracy and only negligible systematic shifts in excitation energies. These are: SOS-ωB2GP-PLYP, SCS-ωB2GP-PLYP, and SOS-ωB88PP86.

The three recommended methods were then successfully cross-validated against three BODIPY dyes, two of which were newly synthesised. Different solvent environments were considered. All three methods predicted excitation energies well within the chemical accuracy threshold. In fact in some cases, our calculated numbers were within experimental uncertainties.

Our findings complement earlier reports on the superiority of spin-scaled, long-range corrected double hybrids for the calculation of excitation energies in organic molecules, including difficult cases. Our recommended methods have shown the capability to be used in theoretical predictions, and as such we hope that they can be of use for the future development of novel BODIPY dyes and related chromophores. A study on fluorescence in BODIPYs is underway to further enhance the computational chemist's toolbox.

Data availability

The data supporting this article have been included as part of the ESI.† Any raw data can be obtained from the corresponding authors upon request.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

S. S. acknowledges a Melbourne Research Scholarship. We acknowledge funding by the Australian Research Council within the Discovery Project scheme (DP230102664). L. G. is grateful for generous allocations of computational resources from the National Computational Infrastructure (NCI) Facility within the National Computational Merit Allocation Scheme (project fk5) and Research Platform Services (ResPlat) at The University of Melbourne (project punim0094). This research was additionally supported by the Research Computing Services NCI Access scheme at The University of Melbourne.

References

1. X. Qin, X. Yang, L. Du and M. Li, RSC Med. Chem., 2021, 12, 1826–1838.
2. R. Ziessel, G. Ulrich and A. Harriman, New J. Chem., 2007, 31, 496–501.
3. A. Loudet and K. Burgess, Chem. Rev., 2007, 107, 4891–4932.
4. G. Köhler, P. Wolschann and K. Rotkiewicz, Proceedings of the Indian Academy of Sciences-Chemical Sciences, 1992, pp. 197–207.
5. K. Pal, T. Dutta and A. L. Koner, ACS Omega, 2020, 6, 28–37.
6. F. Y. Telegin, V. S. Karpova, A. O. Makshanova, R. G. Astrakhantsev and Y. S. Marfin, Int. J. Mol. Sci., 2023, 24, 1217.
7. X. Duan, P. Li, P. Li, T. Xie, F. Yu and B. Tang, Dyes Pigm., 2011, 89, 217–222.
8. T. Kowada, H. Maeda and K. Kikuchi, Chem. Soc. Rev., 2015, 44, 4953–4972.
9. E. V. Antina, N. A. Bumagina, A. I. V’yugin and A. V. Solomonov, Dyes Pigm., 2017, 136, 368–381.
10. H. T. Bui, D. K. Mai, B. Kim, K.-H. Choi, B. J. Park, H.-J. Kim and S. Cho, J. Phys. Chem. B, 2019, 123, 5601–5607.
11. E. Gross and W. Kohn, in Adv. Quantum Chem., Elsevier, 1990, vol. 21, pp. 255–291.
12. M. E. Casida, in Recent Advances in Density Functional Methods: (Part I), World Scientific, 1995, pp. 155–192.
13. R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Lett., 1996, 256, 454–464.
14. S. Bakalova, F. Mendicuti, O. Castaño and J. Kaneti, Chem. Phys. Lett., 2009, 478, 206–210.
15. A. D. Quartarolo, N. Russo and E. Sicilia, Chem. - Eur. J., 2006, 12, 6797–6803.
16. B. Le Guennic, O. Maury and D. Jacquemin, Phys. Chem. Chem. Phys., 2012, 14, 157–164.
17. A. D. Boese and J. M. Martin, J. Chem. Phys., 2004, 121, 3405–3416.
18. M. R. Momeni and A. Brown, J. Chem. Theory Comput., 2015, 11, 2619–2632.
19. M. Feldt and A. Brown, J. Comput. Chem., 2021, 42, 144–155.
20. Q. Alkhatib, W. Helal and A. Marashdeh, RSC Adv., 2022, 12, 1704–1717.
21. W. Helal, Q. Alkhatib and M. Gharaibeh, Comput. Theor. Chem., 2022, 1207, 113531.
22. J. P. Perdew and K. Schmidt, AIP Conf. Proc., 2001, 577, 1–20.
23. S. Grimme, J. Chem. Phys., 2006, 124, 034108.
24. S. Grimme and F. Neese, J. Chem. Phys., 2007, 127, 154116.
25. S. Kozuch, D. Gruzman and J. M. Martin, J. Phys. Chem. C, 2010, 114, 20801–20808.
26. S. Kozuch and J. M. Martin, Phys. Chem. Chem. Phys., 2011, 13, 20104–20107.
27. W. Helal, A. Marashdeh, Q. Alkhatib, H. Qashmar, M. Gharaibeh and A. T. Afaneh, Int. J. Quantum Chem., 2022, 122, e27000.
28. M. R. Momeni and A. Brown, J. Phys. Chem. A, 2016, 120, 2550–2560.
29. F. de Jong, M. Feldt, J. Feldt and J. N. Harvey, Phys. Chem. Chem. Phys., 2018, 20, 14537–14544.
30. D. Toffoli, M. Quarin, G. Fronzoni and M. Stener, J. Phys. Chem. A, 2022, 126, 7137–7146.
31. A. Charaf-Eddin, B. Le Guennic and D. Jacquemin, RSC Adv., 2014, 4, 49449–49456.
32. A. Rose, S. V. Kumar, S. Swavey and J. Erb, Comput. Theor. Chem., 2017, 1118, 107–114.
33. V. E. Matulis, E. G. Ragoyja and O. A. Ivashkevich, Int. J. Quantum Chem., 2020, 120, e26159.
34. J.-N. Wang, J.-L. Jin, Y. Geng, S.-L. Sun, H.-L. Xu, Y.-H. Lu and Z.-M. Su, J. Comput. Chem., 2013, 34, 566–575.
35. A. Nykanen, L. Thiessen, E.-M. Borrelli, V. Krishna, S. Knecht and P. Fabijan, J. Phys. Chem. Lett., 2024, 15, 7111–7117.
36. R. Berraud-Pache, F. Neese, G. Bistoni and R. Izsak, J. Chem. Theory Comput., 2019, 16, 564–575.
37. A. Schlachter, A. Fleury, K. Tanner, A. Soldera, B. Habermeyer, R. Guilard and P. D. Harvey, Molecules, 2021, 26, 1780.
38. S. Chibani, B. Le Guennic, A. Charaf-Eddin, O. Maury, C. Andraud and D. Jacquemin, J. Chem. Theory Comput., 2012, 8, 3303–3313.
39. S. Chibani, A. D. Laurent, B. Le Guennic and D. Jacquemin, J. Chem. Theory Comput., 2014, 10, 4574–4582.
40. P. Boulanger, S. Chibani, B. Le Guennic, I. Duchemin, X. Blase and D. Jacquemin, J. Chem. Theory Comput., 2014, 10, 4548–4556.
41. L. Goerigk and S. Grimme, J. Phys. Chem. A, 2009, 113, 767–776.
42. L. Goerigk, J. Moellmann and S. Grimme, Phys. Chem. Chem. Phys., 2009, 11, 4611–4620.
43. L. Goerigk and S. Grimme, J. Chem. Phys., 2010, 132, 184103.
44. F. D. Meo, P. Troiullasa, C. Adamo and J. C. Sancho-García, J. Chem. Phys., 2013, 139, 164104.
45. T. Schwabe and L. Goerigk, J. Chem. Theory Comput., 2017, 13, 4307–4323.
46. M. Casanova-Páez, M. B. Dardis and L. Goerigk, J. Chem. Theory Comput., 2019, 15, 4735–4744.
47. D. Mester and M. Kállay, J. Chem. Theory Comput., 2021, 17, 927–942.
48. M. Casanova-Páez and L. Goerigk, J. Chem. Phys., 2020, 153, 064106.
49. M. Casanova-Páez and L. Goerigk, J. Comput. Chem., 2021, 42, 528–533.
50. M. Casanova-Páez and L. Goerigk, J. Chem. Theory Comput., 2021, 17, 5165–5186.
51. D. Mester and M. Kállay, J. Chem. Theory Comput., 2021, 17, 4211–4224.
52. D. Mester and M. Kállay, J. Chem. Theory Comput., 2022, 18, 1646–1662.
53. A. C. Hancock and L. Goerigk, RSC Adv., 2023, 13, 35964–35984.
54. A. C. Hancock, E. Giudici and L. Goerigk, J. Comput. Chem., 2024, 45, 1667–1681.
55. A. C. Jones and L. Goerigk, Phys. Chem. Chem. Phys., 2024, 26, 25192–25207.
56. L. Goerigk, H. Kruse and S. Grimme, in Theoretical Electronic Circular Dichroism Spectroscopy of Large Organic and Supramolecular Systems, Wiley-Blackwell, 2012, ch. 22, pp. 643–673.
57. L. Goerigk and S. Grimme, J. Chem. Theory Comput., 2011, 7, 3272–3277.
58. J. Van Dijk, M. Casanova-Páez and L. Goerigk, ACS Phys. Chem. Au, 2022, 2, 407–416.
59. L. Goerigk and M. Casanova-Paéz, Aust. J. Chem., 2020, 74, 3–15.
60. A. Sbai and J. Guthmuller, Phys. Chem. Chem. Phys., 2024, 26, 25925–25935.
61. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108.
62. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
63. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
64. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
65. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
66. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
67. V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001.
68. K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 242, 652–660.
69. R. Izsák and F. Neese, J. Chem. Phys., 2011, 135, 144105.
70. F. Weigend and M. Häser, Theor. Chem. Acc., 1997, 97, 331–340.
71. K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chem. Acc., 1997, 97, 119–124.
72. F. Weigend, M. Häser, H. Patzelt and R. Ahlrichs, Chem. Phys. Lett., 1998, 294, 143–152.
73. S. Hirata and M. Head-Gordon, Chem. Phys. Lett., 1999, 314, 291–299.
74. J. Liang, X. Feng, D. Hait and M. Head-Gordon, J. Chem. Theory Comput., 2022, 18, 3460–3473.
75. A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377.
76. J.-D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106.
77. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
78. A. Karton, A. Tarnopolsky, J.-F. Lamére, G. C. Schatz and J. M. Martin, J. Phys. Chem. A, 2008, 112, 12868–12886.
79. É. Brémond, J. C. Sancho-García, Á. J. Pérez-Jiménez and C. Adamo, J. Chem. Phys., 2014, 141, 031101.
80. M. Casanova-Páez, M. B. Dardis and L. Goerigk, J. Chem. Theory Comput., 2019, 15, 4735–4744.
81. E. Bremond, M. Savarese, Á. J. Pérez-Jiménez, J. C. Sancho-García and C. Adamo, J. Chem. Theory Comput., 2018, 14, 4052–4062.
82. M. Head-Gordon, R. J. Rico, M. Oumi and T. J. Lee, Chem. Phys. Lett., 1994, 219, 21–29.
83. Y. M. Rhee and M. Head-Gordon, J. Phys. Chem. A, 2007, 111, 5314–5326.
84. S. Grimme, J. Chem. Phys., 2003, 118, 9095–9102.
85. Y. Jung, R. C. Lochan, A. D. Dutoi and M. Head-Gordon, J. Chem. Phys., 2004, 121, 9793–9802.
86. S. Grimme, L. Goerigk and R. F. Fink, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 886–906.
87. L. Goerigk and S. Grimme, ChemPhysChem, 2008, 9, 2467–2470.
88. L. Goerigk and S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 576–600.
89. M. J. Peach, P. Benfield, T. Helgaker and D. J. Tozer, J. Chem. Phys., 2008, 128, 044118.
90. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
91. T. Lu, J. Chem. Phys., 2024, 161, 082503.
92. X. Xia, Y. Qian and B. Shen, J. Mater. Chem. B, 2018, 6, 3023–3029.
93. A. Filarowski, M. Kluba, K. Cieślik-Boczula, A. Koll, A. Kochel, L. Pandey, W. M. De Borggraeve, M. Van der Auweraer, J. Catalán and N. Boens, Photochem. Photobiol. Sci., 2010, 9, 996–1008.
94. S. Chibani, B. Le Guennic, A. Charaf-Eddin, A. D. Laurent and D. Jacquemin, Chem. Sci., 2013, 4, 1950–1963.
95. W. Helal, J. Phys. Chem. A, 2022, 127, 131–141.
96. T. Lettmann and M. Rohlfing, J. Chem. Theory Comput., 2019, 15, 4547–4554.
97. B. Baumeier, D. Andrienko, Y. Ma and M. Rohlfing, J. Chem. Theory Comput., 2012, 8, 997–1002.
98. M. J. G. Peach and D. J. Tozer, J. Phys. Chem. A, 2012, 116, 9783–9789.
99. M. J. Peach, N. Warner and D. J. Tozer, Mol. Phys., 2013, 111, 1271–1274.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ra01408e

---