Open Access Article
Open Access ArticleInsights into anti-tuberculosis drug design on the scaffold of nitroimidazole derivatives using structure-based computer-aided approaches†
Wei Yang abc,
Hui Zhao‡
ab,
Ziting Zhao‡ab,
Shaojun Peidef,
Zheng Zhug,
Zhen Huangab,
Yao Zhao*ab,
Shuihua Lu*ab,
Fangfang Wang
abc,
Hui Zhao‡
ab,
Ziting Zhao‡ab,
Shaojun Peidef,
Zheng Zhug,
Zhen Huangab,
Yao Zhao*ab,
Shuihua Lu*ab,
Fangfang Wang *h and
Yanlin Zhao*abef
*h and
Yanlin Zhao*abef
aNational Clinical Research Center for Infectious Diseases, Shenzhen Third People's Hospital, Shenzhen, 518112, China
bShenzhen Clinical Research Center for Tuberculosis, Shenzhen, People's Republic of China
cWarshel Institute for Computational Biology, School of Science and Engineering, The Chinese University of Hong Kong, Shenzhen, 518172, China
dDepartment of Global Health, School of Public Health, Peking University, Beijing, 100191, China
eNational Center for TB Control and Prevention, Chinese Center for Disease Control and Prevention, Beijing, 102206, China. E-mail: zhaoyl@chinacdc.cn
fChinese Center for Disease Control and Prevention, Beijing, 102206, China
gDepartment of Urology, Xijing Hospital, Air Force Military Medical University, Xi'an, China
hSchool of Life Science, Linyi University, Linyi, 276000, China
First published on 3rd July 2025
Abstract
Deazaflavin-dependent nitroreductase (Ddn) is a crucial enzyme involved in mycolic acid biosynthesis, a vital component of the cell wall in Mycobacterium tuberculosis (MTB)—the bacterial pathogen responsible for tuberculosis. Over the past two decades, nitroimidazole oxazine scaffold (NOS) derivatives have been investigated as potential therapeutic agents targeting Ddn in MTB, with a focus on enhancing drug efficacy, minimizing toxicity, and combating drug resistance. In this study, we performed an extensive theoretical investigation combining three-dimensional quantitative structure–activity relationship (3D-QSAR) studies, all-atom molecular docking, and atomic-level molecular dynamics (MD) simulations. Additionally, we analyzed the binding free energies and their decomposed terms between inhibitors and Ddn to elucidate the structure–activity relationships (SARs) and mechanisms of a series of NOS derivatives developed for MTB inhibition. The CoMFA and CoMSIA models demonstrated strong performance, with cross-validation coefficients (Rcv2) of 0.591 and 0.629, respectively, and prediction coefficients (Rpred2) of 0.7698 and 0.6848 for CoMFA and CoMSIA, respectively. These models effectively predicted the minimum inhibitory concentration (MIC) values of the compounds against MTB based on the NOS scaffold. Molecular docking followed by MD simulations was employed to validate the binding modes of these derivatives at the active site of Ddn, providing detailed insights into their interaction patterns. Notably, our analysis revealed that residues Tyr65, Ser78, Tyr130, Tyr133, and Tyr136 played critical roles in determining the potency of the compounds by contributing significantly to their binding energies. These findings provide valuable guidance for the rational design of novel NOS inhibitors with enhanced potential as effective anti-tuberculosis agents.
1. Introduction
Mycobacterium tuberculosis (MTB) is reported as the third most significant infectious disease with respect to global morbidity and mortality caused by a single infectious agent.1,2 Despite the availability of multiple chemotherapy treatments,3,4 the global rise of multidrug-resistant tuberculosis (MDR-TB) and extensively drug-resistant (XDR) strains presents an urgent and pressing challenge.5 In response, the BpaL strategy, comprising the combination of Bedaquiline (BDQ), Pretomanid (PA-824), and linezolid, has been proposed for the treatment of MDR- and XDR-TB.6–8 Notably, FDA-approved nitroimidazole drugs such as PA-824 (ref. 6) and delamanid (OPC-67683),8 exhibit significant therapeutic efficacy. However, their widespread use raises concerns about the development of potential drug resistance, particularly concerning the target protein, deazaflavin-dependent nitroreductase (Ddn).9,10 Consequently, the development of novel drugs to tackle these challenges is imperative, especially considering that BpaL and DLM currently constitute the final line of defense against M/XDR-TB.In response to these challenges, three drugs, namely PA-824,6 OPC-67683,8 and CGI-17341 (CGI),11 have demonstrated the capacity to inhibit drug-resistant MTB growth. These drugs, which share a common NOS (Fig. 1A), primarily target Ddn in MTB; however, it was believed that NOS inhibitors also target the F420H2-dependent quinone reductase (FQR) family of enzymes, such as F420-dependent glucose-6-phosphate dehydrogenase 1 (FGD1) and FGD2 enzymes, thereby disrupting the redox cycle of cofactor deazaflavin F420 (F420) and interfering with cell-wall formation metabolism pathways in MTB.12,13 For instance, both the shortage of F420 caused by PA-824 inhibiting Ddn and the direct inhibition of FGD2 by PA-824 would disrupt the keto mycolic acid synthesis.6,8,14 Recently, both Batt15 and Abrahams16 reported that the activated form of PA-824 and OPC-67683 processed initially by Ddn might directly interact with the decaprenylphosphoryl-2-keto-β-D-erythro-pentose reductase (DprE2) enzyme, with the latter being responsible for generating arabinogalactan (AG) or lipoarabinomannan (LAM) for the cell wall in MTB (Fig. 1B), although Abrahams also reported that the overexpression of DprE2 would exhaust the dose of PA-824 and result in anti-PA-824 activity. Notably, under anaerobic conditions, MTB relies on Ddn to catalyze menaquinone, producing oxygen gas and free radicals (O2 or O˙), which are essential for ATP synthesis.14 These drugs swiftly convert NOS into several products, including nitrogen oxides (NO products) upon binding with the Ddn and F420H2.17,18 The NO captures the O2 and O˙, and further inhibits mycobacterial growth,14 suggesting the potential of NOS inhibitors to enhance the sensitivity of other drugs. Consequently, NOS-based drugs hold considerable promise for the treatment of drug-resistant MTB.19,20
While structural biology techniques,21 have provided insights into the crystal structure of Ddn with its cofactor F420 (Fig. 1C), challenges remain in studying NOS-drug interactions due to compound instability during catalysis. Despite theoretical studies21–23 identifying key residues such as Tyr65, Tyr130, Tyr133, Tyr136, and Ser78 (Fig. 1D) involved in binding PA-824, the structural basis for the structure–activity relationship (SAR) of these drugs remains elusive. Furthermore, while NOS derivatives have been synthesized and studied,19,20 their general medical applicability is hindered because of their systemic toxicity, specific binding mode, and unresolved capability of drug catalysis with Ddn. Developing better inhibitors based on NOS derivatives is currently a key direction for treating MDR and XDR-TB patients.24 On one hand, these typical patients would face the dilemma of no new drugs becoming available if the current NOS drugs failed; on the other hand, developing completely new inhibitors is significantly time-consuming work. Accordingly, the critical need to develop a robust quantitative structure–activity relationship (QSAR) profiles that can be used to predict the drug efficiency of NOS inhibitors, particularly towards Ddn, is emphasized for the design of potent and selective NOS-based MTB drugs.
Traditionally, SAR studies have relied on labor-intensive compound synthesis and biological assays.25 However, the adoption of computational approaches offers an efficient means to predict SAR while minimizing the physical costs involved.26 Recently, several NOS inhibitors have emerged as potential anti-MTB agents. In this study, we leverage three-dimensional QSAR (3D-QSAR) techniques, including comparative molecular field analysis (CoMFA) together with the comparative molecular similarity indices analysis (CoMSIA) methods27,28 to examine the intrinsic relationship underlying the structures and the drug efficiencies as determined by the minimum inhibition concentration (MIC) experiments.24,29–34 Beyond the 3D-QSAR approach, we further employ atomic molecular docking, the key results of which were further examined in all-atom molecular dynamics (MD) simulations to anticipate stable binding conformations of Ddn-NOS inhibitors and discern the functions of the pivotal key amino acid residues in terms of governing the binding process and initiating drug catalysis. Ultimately, this study not only enhances our understanding of NOS-based inhibitors but also provides a valuable toolset for predicting and designing more effective anti-tuberculosis drugs. By integrating 2D and 3D QSAR modeling with molecular dynamics simulations and binding free energy analyses, our study provides structural and energetic insights that may facilitate the rational design of more effective inhibitors against drug-resistant strains of Mycobacterium tuberculosis, particularly in regions burdened by MDR-TB and XDR-TB.
2. Materials and methods
2.1. Data sets and biological activity
The dataset of antitubercular compounds was taken from available sources.29–31,33 The antitubercular activity MIC against H37Rv was converted into pMIC values (pMIC = −logMIC). The range of pMIC values was from 3.0216 to 7.4089, indicating that a broad dataset with uniform density was employed that was suitable for 3D-QSAR investigations. The entire dataset was partitioned into a training set consisting of 43 compounds to generate the model and a separate test set comprised of 15 compounds for model validation. The selection of compounds for the test set was based on their similarity to the compounds in the training set, in terms of both structure and activity. The structures and biological activities of these compounds are listed in Table 1.| Structure | Compound | R1 | R2 | R3 | pMIC |
|---|---|---|---|---|---|
| a Selected as the test set. | |||||
 |
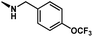
1 | CH2(4-OCF3-Ph) | H | H | 5.8508 |
| 2 | CH2(4-CH3-Ph) | H | H | 6.3565 | |
| 3a | CH2(4-F-Ph) | H | H | 5.4595 | |
| 4a | CH2(3-OCF3-Ph) | H | H | 6.4522 | |
| 5 | CH2(3-CH3-Ph) | H | H | 6.6753 | |
| 6 | CH2(3-CF3-Ph) | H | H | 6.7508 | |
| 7 | CH2(2-OCF3-Ph) | H | H | 5.5491 | |
| 8 | CHMe(4-F-Ph) | H | H | 5.7812 | |
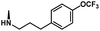
| 9 | CH2CH2(4-OCF3-Ph) | H | H | 4.6629 | |
| 10 | CH2CH2(4-CH3-Ph) | H | H | 4.8722 | |
| 11a | CH2(4-OCF3-Ph) | CH3 | CH3 | 5.5817 | |
| 12 | CH2(4-CH3-Ph) | CH3 | CH3 | 5.1931 | |
| 13 | CH2(3-OCF3-Ph) | CH3 | CH3 | 5.5817 | |
| Structure | Compound | R7 | R8 | pMIC |
|---|---|---|---|---|
 |
41a | 2,4-Dichloro | H | 3.9734 |
| 42a | 2,4-Dichloro | Br | 5.2775 | |
| 43 | 2,4-Difluoro | H | 3.0216 | |
| 44 | 2,4-Difluoro | Br | 3.7341 | |
| 45 | 4-F | Br | 3.4100 | |
| 46a | 4-Cl | Br | 3.7316 | |
| 47 | 4-NO2 | Br | 3.7452 | |
| 48 | H | Br | 3.9876 | |
| 49 | 2,4-Dimethyl | Br | 3.4230 | |
| 50 | 2,4-Dichloro | Ome | 5.8209 | |
| 51 | 2,4-Difluoro | Ome | 4.8737 | |
| 52 | 4-F | Ome | 4.2447 | |
| 53 | 4-Cl | Ome | 4.2687 | |
| 54a | 4-NO2 | Ome | 4.2845 | |
| 55 | 4-Phenyl | Ome | 5.8314 | |
| 56 | 2,4-Dichloro | SMe | 4.3157 | |
| 57a | H | Ome | 4.5170 | |
| 58 | 2,4-Dimethyl | Ome | 4.2600 |
2.2. The in silico molecular preparations of NOS inhibitors
All the molecular preparations of NOS inhibitors were conducted with Sybyl-X 1.1 (Tripos Associates, St. Louis, MO). Initially, the compounds were assigned the Gasteiger–Huckel charges,35 then the structural conformation was minimized by the Tripos molecular force field (FF) with 0.05 kcal mol−1 Å−1 by the Powell method for the criterion of energy gradient convergence.36 Lastly, with the lowest energies, the 3D conformations of the compound were prepared for construction of the 3D-QSAR models.2.3. Molecular alignment for NOS inhibitors
Constructing a suitable 3D-QSAR model relies greatly on the molecular alignment and template selection process.37 Two alignment rules were employed in the current study to derive rational models: template ligand-based alignment and docking-based alignment. The template ligand-based alignment refers to selecting the most potent compound (Cp28, PA-824, pretomanid) as the template for the alignment, and all the other 52 compounds were aligned to the common part of the molecule (Fig. 2A, blue parts) by the use of the “database alignment” module; the superimposed structures of the aligned molecules are depicted in Fig. 2B. In the docking-based alignment, the diverse models were derived from the best docking conformations that were ranked by total scores (described in molecular docking method). Fig. S1† shows the result of docking-based alignment.2.4. 3D-QSAR on the NOS inhibitors by CoMFA and CoMSIA
To build the 3D-QSAR models on the NOS inhibitors, the ideal methods such as CoMFA and CoMSIA were performed in this work.28,38 CoMFA analysis involves computing the biochemical properties in terms of steric fields, electrostatic fields hydrophobicity, and hydrogen bond donor and acceptor fields. The compounds that were aligned were initially positioned within a 3D cubic container, with a grid spacing of 2.0 Å. To calculate the steric (Lennard-Jones 6-12 potential) and electrostatic (Coulomb potential) field energies, an sp3 hybridized carbon atom with a +1.0 charge and a van der Waals radius of 1.52 Å was utilized as the probe. To enhance analysis and minimize noise, the default cutoff energy and column filtering were adjusted to 30 kcal mol−1 and 2.0 kcal mol−1, respectively. The CoMFA-STD technique was subsequently employed to rescale the CoMFA fields.In the CoMSIA analysis, five similarity fields were computed: steric, electrostatic, hydrophobic and hydrogen bond donor and acceptor fields. These fields were calculated using a probe atom with a radius of 1 Å, a charge of +1, a hydrophobicity of +1, a hydrogen bonding donor of +1, and a hydrogen bond acceptor of +1. Furthermore, an attenuation factor of 0.3 was applied.
The partial least-squares (PLS) method39 was utilized for the generation of valid CoMFA and CoMSIA models. Initially, a leave-one-out (LOO) approach was employed to determine the optimal number of components (Nc) and the cross-validation correlation coefficient (Rcv2). Subsequently, the non-cross validation was performed using the determined Nc, yielding the non-cross validation correlation coefficient (Rncv2), standard error of estimate (SEE), and F statistical values. Furthermore, the robustness of the derived CoMFA and CoMSIA models was assessed through external validation using a test set of compounds. Generally, the selection of the best model is based on high values of Rcv2, Rncv2, and Rpred2 (Rcv2 > 0.5, Rncv2 > 0.6, and Rpred2 > 0.6), as well as a low SEE value.40,41
2.5. Molecular docking
Molecular docking procedures were conducted by using AutoDock software 4.0.2 (The Scripps Research Institute, La Jolla, USA).42 The initial conformation of Ddn was obtained from the crystal structure (PDB entry: 3R5W) deposited in the Protein Data Bank. The receptor preparations involved the removal of water molecules from the PDB file, repair of missing atoms in the receptor (including Ddn and the reductive form of the cofactor F420), and addition of hydrogen atoms with Kollman charges43 for all atoms. For the inhibitors, hydrogen atoms were added to neutralize the ligands and Gasteiger partial charges35 were assigned to all atoms. All single sp3 bonds were allowed to move freely, whereas the aromatic rings were set rigidly. The docking box was defined with dimensions of 80 × 58 × 83 Å and a grid spacing of 0.375 Å to adequately cover the docking space. Other docking parameters were consistent with our previous works.44 The final docking pose of each compound from the 58 NOS inhibitors was selected based on the lowest binding free energy (total score, Table S2†) and the appropriate positioning of the nitroimidazodiazine moiety. The redock of PA-824 was used as the docking parameter validation, in which the criterion is to reproduce the docked pose of the nitroimidazodiazine moiety of PA-824, similar to the previous theoretical studies.21,322.6. MD method
Herein, only the representative compounds (Cp28, Cp38, Cp39, and Cp43) bound with Ddn and F420 systems, namely Ddn–F420–Cp28, Ddn–F420–Cp38, Ddn + F420–Cp39, Ddn + F420–Cp43, were performed with MD calculations to save computational power. Each of the final docking poses from the four docking processes was further put forward to MD simulations to study the binding stabilities and the most stable binding states, which were obtained for further calculations of the binding free energies in between Ddn + F420 and the ligands.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms).
000 atoms).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps of minimization were carried out on each system before the system equilibration stage. The equilibration stages consisted of 500 ps heating, 500 ps of density equilibration process, and 5 ns of constant pressure at 1 atm at room temperature (300 K). The SHAKE algorithm53 was applied to constrain the hydrogen atoms in a reasonable sphere of moving. The constraints (10 kcal mol−1 Å−2, 8 kcal mol−1 Å−2, 5 kcal mol−1 Å−2) were set to all the receptor and ligand atoms along the three stages of the equilibration. Lastly, the production phase was performed for 200 ns by 3 replicates, and the sampling pools for MD analysis were saved as every conformation per 10 ps.
000 steps of minimization were carried out on each system before the system equilibration stage. The equilibration stages consisted of 500 ps heating, 500 ps of density equilibration process, and 5 ns of constant pressure at 1 atm at room temperature (300 K). The SHAKE algorithm53 was applied to constrain the hydrogen atoms in a reasonable sphere of moving. The constraints (10 kcal mol−1 Å−2, 8 kcal mol−1 Å−2, 5 kcal mol−1 Å−2) were set to all the receptor and ligand atoms along the three stages of the equilibration. Lastly, the production phase was performed for 200 ns by 3 replicates, and the sampling pools for MD analysis were saved as every conformation per 10 ps.
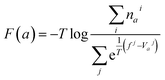 | (1) |
 | (2) |
The total production simulation time denoted as tsim is the duration of the MD simulation. On the other hand, teq represents the final frame of the equilibrium phase, which signifies the point at which the bias potentials reached stability. Consequently, the 2D scattered map was transformed into a 2D free energy enumerations of microstates (FEEM) heat map and also 3D LFEL surface map by the use of Gromacs v5.11 (ref. 54) and Mathematica v11.3.57
| ΔGb = ΔGcom − (ΔGrec + ΔGlig) | (3) |
| ΔGcom/rec/lig = ΔH − TΔS | (4) |
| ΔH = ΔEgas + ΔGsol | (5) |
| ΔEgas = ΔEint + ΔEvdw + ΔEele | (6) |
| ΔGsol = ΔGPB/GB + ΔGNP | (7) |
| ΔGNP = γSASA + β | (8) |
3. Results and discussion
3.1. 3D-QSAR statistical results
In this study, different combinations of steric, electrostatic, hydrophobic and hydrogen bond donor and acceptor fields were computed to generate diverse models. A summary of these combinations is provided in Tables S1 and S3.† Our statistical analyses reveal that the models derived from template ligand-based alignment outperform those based on docking-based alignment. Consequently, we focus on those models derived from template ligand-based alignment for the subsequent discussions.The CoMFA statistical results are presented in Table 2. The model exhibits strong internal validation performance, as indicated by a high Rcv2 value of 0.732 for the training set with Nc (components) of 6, a non-cross-validation coefficient Rncv2 of 0.991, a high F value of 654.454, and a low SEE of 0.122. These results suggest that the generated CoMFA model is reliable. Additionally, the model demonstrates outstanding predictive ability, with an Rpred2 value of 0.7212, highlighting the robustness of the CoMFA model. A graphical representation of the observed versus predicted pMIC values for the entire dataset is presented in Fig. 3A. The data points closely align with the straight line of the derived optimal CoMSIA model (steric + electrostatic + hydrogen bond donor fields), detailed in Table 2, which demonstrates an Rcv2 value of 0.809 (ten optimal components), a high non-cross-validated coefficient Rncv2 of 0.9930, an SEE of 0.113, and a significant F value of 456.734, collectively validating the reliability of the CoMSIA model and confirming that the experimental values are consistent with the predicted values, with small variance. The field contributions are 38.1%, 25.4%, and 36.5% for steric, electrostatic, and hydrogen bond donor fields, respectively. This distribution underscores the prominent roles played by the steric and hydrogen bond donor fields in Ddn binding. Additionally, the CoMSIA model displays excellent predictive capability, with an Rpred2 value of 0.7597. A plot of the observed values vs. and predicted values is depicted in Fig. 3B. The blue squares and red triangles are distributed on both sides of the line Y = X, and it is evident that more points lie either on the best fit line or are very close to it, confirming that the experimental values closely align with the predicted values with small variance, reaffirming the superior predictive ability of the CoMSIA model.
| Parameters | CoMFA | CoMSIA |
|---|---|---|
| Rcv2 | 0.732 | 0.809 |
| Rncv2 | 0.991 | 0.993 |
| SEE | 0.122 | 0.113 |
| F | 654.454 | 456.734 |
| Rpred2 | 0.7212 | 0.7597 |
| SEP | 0.660 | 0.591 |
| Nc | 6 | 10 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| Field contribution | ||
| S | 0.899 | 0.381 |
| E | 0.101 | 0.254 |
| H | — | — |
| D | — | 0.365 |
| A | — | — |
 | ||
| Fig. 3 Correlation plots of the actual pMIC versus the predicted values calculated from the optimal CoMFA (A) and CoMSIA (B) models. | ||
3.2. 3D-QSAR contour maps
In this study, 3D-QSAR contour maps were utilized to elucidate the structural requirements for optimizing and designing novel compounds. The well-known, highly potent compound Cp28 (PA-824, pretomanid) served as the template for contour map analysis. To validate the model rigorously, we analyzed the most potent compounds separately within other structural series.3.2.1.1 Cp28 (Fig. 4A). A conspicuous green contour at the R4 position suggested the necessity of bulky groups, explaining why Cp17 (–CHO) exhibited higher activity than Cp9 (–CH3) at this site. Interestingly, the absence of a corresponding substituent in the most active Cp28 at the same location implied a potential for structural modification based on steric field information to enhance its activity. Notably, a large yellow contour adjacent to the –NH–C–C group in the R5 substituent foretells increased potency with smaller substituents, as exemplified by Cp26 surpassing Cp25. Similarly, a substantial green contour at the R5 substituent indicated higher potency with larger groups, reflecting the higher activity of Cp24 compared to Cp23.
3.2.1.2 Cp6 (Fig. 4B). A substantial green region near the R1 substituent advocated for the introduction of bulky groups, correlating with enhanced activity in Cp2 (CH2(4-CH3-Ph)) compared to Cp3 (CH2(4-F-Ph)). Yellow contour maps enveloping R1 and R2 substituents suggested the affinity for smaller substituents in these regions. The reduced activity of Cp1 relative to Cp11 was attributed to the higher steric effect of CH3 compared to H in this region. This trend was consistent with Cps2 and 12, as well as Cps4 and 13.
3.2.1.3 Cp39 (Fig. 4C). No effective contour map information was available for the R6 substituent in this skeletal series, precluding detailed discussion.
3.2.1.4 Cp55 (Fig. 4D). The prominent yellow contour around the R7 substituent implied a preference for smaller groups at this position, explaining why Cp48 (H) exhibits higher activity than Cp47 (4-NO2). Additionally, an irregular contour in the R8 substituent suggested a preference for larger substituents, providing insight into the higher activity of Cp50 (–OMe) compared to Cp42 (Br).
3.2.2.1 Cp28 (Fig. 5A). Two red contours near the R4 substituent indicate that electronegative groups in these regions enhance activities. In contrast, the most potent Cp28 lacked negative groups at this position, suggesting the potential introduction of negatively charged groups for improved activity. A small blue contour near the end of the R5 substituent illustrated that electropositive groups contribute to higher activity, explaining why Cp24 stays in the pocket better than Cp25.
3.2.2.2 Cp6 (Fig. 5B). A blue area near the 4′ position of the R1 substitution suggested that increasing the electropositive property improves activity. Consistent with this, Cps2 (4-CH3) and 3 (4-F) validate the phenomenon. Another small blue contour around the 3′ position of R1 substitution and near R2 and R3 substituents implies a preference for electropositive atoms in these regions.
3.2.2.3 Cp39 (Fig. 5C). A blue contour around the –NO2 group suggests a favorable region for electropositive groups, allowing modifications to enhance activity based on charge characteristics.
3.2.2.4 Cp55 (Fig. 5D). A small blue contour near the 4′ position of R7 indicates acceptability for electropositive groups, providing insights into the activity order of ligands. Additionally, a red contour near the R8 substituent suggests improved activities with electronegative groups, explaining why Cp42 (Br) outperforms Cp41 (H).
3.2.4.1 Cp28 (Fig. 7A). A cyan contour map is close to the NH group of R5 substituent, indicating that hydrogen bond donor substituents at this position can increase the activity, which explains why Cp26 (with an NH group) exhibits better activity than Cp20 (with group O). In addition, the purple contour located at the NH end of the R5 substituent suggests that hydrogen bond donor groups were unfavorable. Consequently, modifications were needed at this position for the most potent Cp28.
3.2.4.2 Cp6 (Fig. 7B). Purple contours observed near R2 and R3 substituents are indicators that hydrogen bond acceptor groups are necessary for better activity. By analyzing this series of compounds, we found that no hydrogen bond receptor groups were located at the two substituents, thus future modifications could be applied according to the purple contour map. Additionally, a purple contour is observed over the 6′ position of the R1 substituent, illustrating that hydrogen bond acceptor groups will increase the activities.
3.2.4.3 Cp39 (Fig. 7C). A cyan contour map was positioned at the –NH substituent for this series of compounds, which reveals that the hydrogen bond donor group is advantageous to the activity. Meanwhile, a purple contour map observed around the COO group indicates that a hydrogen bond acceptor group would enhance the activity. Additionally, there were no hydrogen bond donor groups distributed around the R6 substituent, implying that the hydrogen bond interaction has little effect on its activity.
3.2.4.4 Cp55 (Fig. 6D). A purple contour was identified near the R7 position, suggesting that hydrogen bond acceptor groups would be favorable for the activity. This may explain why Cp54 (4-NO2) showed higher activity than Cp53 (4-Cl). In addition, a cyan contour was observed around the R8 substituent, which indicates that the addition of hydrogen bond donor groups in this area would increase the activity. However, the substituent of Cp55 at this site is –OMe, thus further structural modification was expected for the improvement.
3.3. MD simulations detected dynamics of the compound binding systems
Following the construction of CoMFA and CoMSIA models, we performed molecular docking of all compounds into the Ddn + F420 binding site to gain 3D insights into ligand binding. The majority of compounds adopted a binding conformation in which the NOS moiety was positioned within the catalytic pocket in the S-conformation, except for Cp39. Notably, the R-conformation of NOS, as exhibited by Cp39, is known to have no effect on pathogen killing, rendering Cp39 less effective in this docked conformation. Subsequently, we conducted molecular dynamics (MD) simulations for the four ligand-binding systems (Cp28/38/39/43) to sample the dynamic behavior of the systems and identify the most stable binding states, which could provide valuable information for the 3D-QSAR analysis.Fig. 9 illustrates the root mean square fluctuation (RMSF) on the Ddn in the four MD systems, showing that the first 30 amino acids displayed significant fluctuations, consistent with predictions from previous theoretical studies.22,71,72 This phenomenon may explain why the N-terminal helix remains unresolved in crystallography studies. In contrast, the inhibitor and F420 binding domains (residues 60–70, 76–90, and 125–140) exhibited relatively low fluctuations.
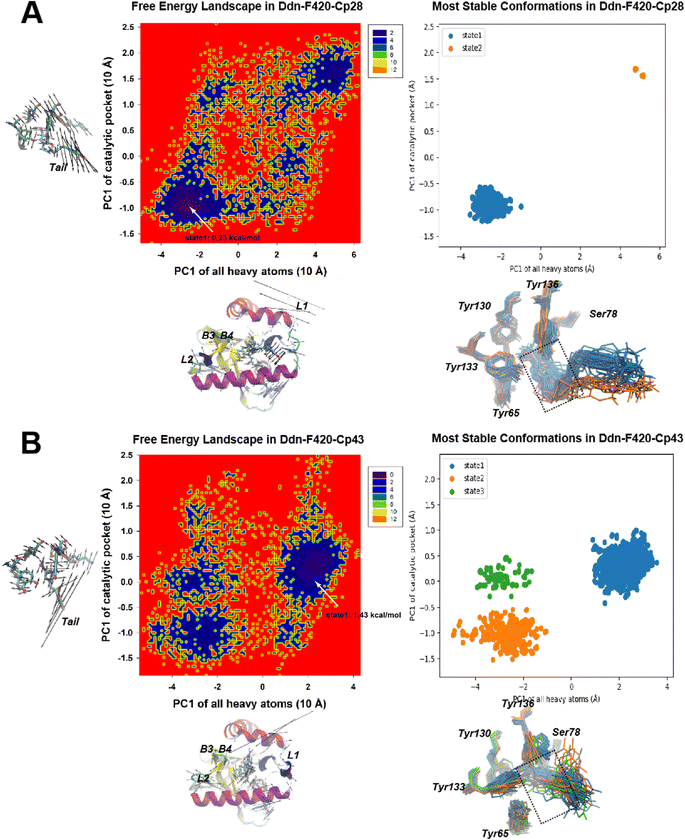
In contrast, Cp43 exhibited three major microstates, with considerable variations observed in the NOS moiety among them. State 1 of Cp43, characterized by a free energy difference of 1.24 kcal mol−1, closely resembled the NOS moiety positioning observed in Cp28. However, states 2 and 3 each lost a hydrogen bond with either Tyr65 or Ser78. It was deduced that this variation in NOS interaction could be attributed to the relatively small R group of Cp43, which might not be long enough to effectively insert into the kink groove formed by helix 1 and 2. Therefore, we deduced that this is why Cp43 is less effective than PA-824. Thus, the length and chemical composition of the tail were identified as critical factors for stabilizing the compound within Ddn.
For the recently developed Ddn inhibitors, Cp38 and Cp39 (Fig. 11), our investigation revealed distinct dynamics. In the Cp38-containing system, we identified only two stable microstates. Both of these states correctly positioned the NOS segment within the Ddn pocket, similar to what was observed in the Cp28-containing system. Nevertheless, we observed some minor protrusions beyond the Ddn pocket in the Cp38-containing system, suggesting potential off-target interactions (Fig. 10A). This observation raises questions about the specificity of Cp38 in its binding to Ddn. Conversely, the Cp39-containing system presented a more intricate scenario with six metastable states. Among these states, Cp39 exhibited notable flipping (states 1 and 2, and states 5 and 6) and significant movement (states 3 and 4) in comparison to the other compounds. This high molecular dynamic variability of Cp39 may suggest that its inhibitory efficiency is less robust than that of the other three compounds (Cpd28, Cpd43, and Cpd38) (Fig. 12).
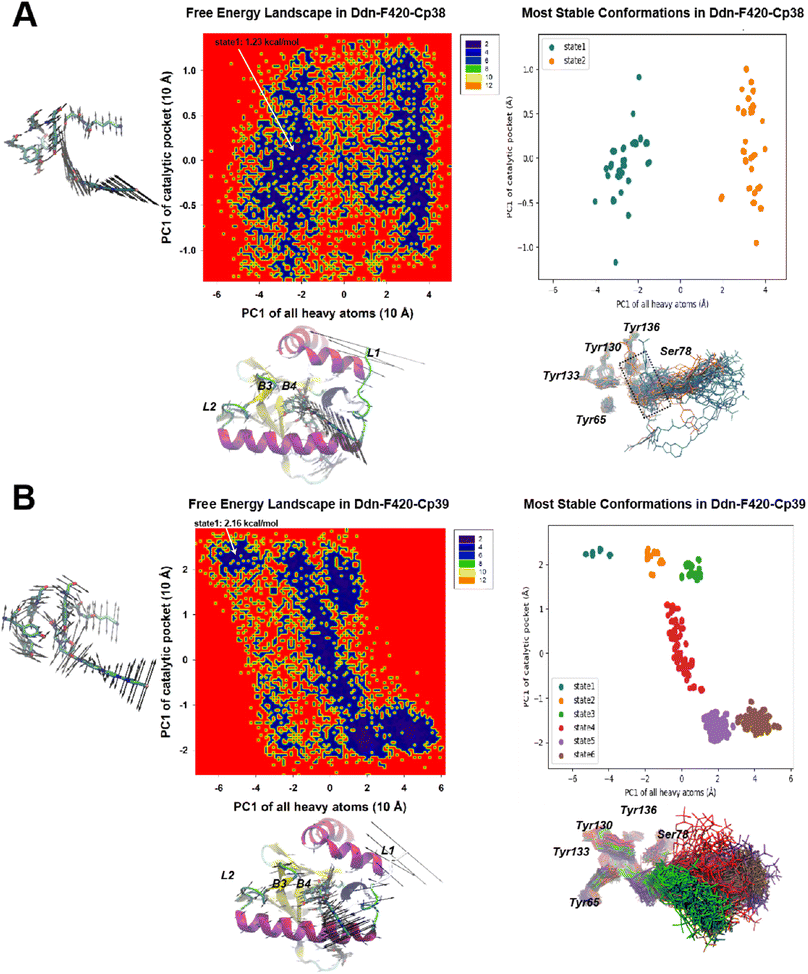 | ||
| Fig. 11 The CPCA analysis on Cp38 (A) and Cp39 (B) systems. The descriptions are the same as in Fig. 10. | ||
Binding free energies of the newly developed ligands, Cp38 and Cp39, were also calculated (−6.82 kcal mol−1 and −4.64 kcal mol−1). However, the binding affinity of Cp39 did not align with the results of a previous minimum inhibition concentration (MIC) study.30 We speculate that Cp39 might perform less effectively than the other ligands in inhibiting Ddn, possibly due to challenges in either initiating the first step of drug catalysis or mitigating the entropy contributions (29.14 kcal mol−1) in the Ddn binding process. An alternative explanation could be that Cp39 possesses inhibitory capabilities when interacting with other NOS-favorable targets, such as DPRE2(16), in its activated form, similar to the active form of PA-824, thereby resulting in an overall inhibitory effectiveness akin to that of Cp38. Regarding the contributions of key residues to the binding process, our analysis indicated that the four conserved tyrosine residues (Tyr65, Tyr130, Tyr133, and Tyr136) did play a role in inhibitor binding. These might be the reason why mutants such as Tyr133Phe, Tyr136Phe73 are the highly drug-resistance types against PA-824. However, the most substantial contributions to the binding energies involved Phe8, Leu9, Phe17, ILE18, and Met21, located in L1 and H1. These residues also serve as key driving forces in enhancing the unfavorable entropy of smaller NOS inhibitors, as identified from the metastable states of the free energy landscape in CPCA. Thus, the free energy decomposition analysis underscores the significance of the inhibitor moiety in L1 and H1 for designing efficient Ddn-targeting drugs. As part of the L1 was missing in the crystal structure,21 it is generally a difficult task to develop an optimized compartment structure binding with L1, nevertheless targeting the identified key residues (Phe8, Leu9, Phe17, ILE18, and Met21) in L1 might provide a hint for advancing this task. Surprisingly, we observed that Ser78 and Lys79 appeared to hinder inhibitor binding, despite their interactions with NOS and the F420 tail (rich in hydroxy chain groups), respectively. This could be attributed to the frequent oscillations of NOS and the random swinging motion of F420 tail atoms, as observed in our MD trajectories.
4. Conclusion
Our study employed a comprehensive approach, encompassing CoMFA and CoMSIA models, molecular docking, together with molecular dynamics simulations, to provide vital insights into the quantitative structure–activity relationships of the compounds under investigation. Our results underscore the efficacy of employing template ligand-based alignment for model generation. The CoMFA and CoMSIA models showed strong statistical performance, with a notable focus on the steric field and hydrogen bond donor field. The contour maps derived from 3D-QSAR models provided indispensable information regarding the structural prerequisites essential for augmenting compound activity (large, electronegative groups at R4 substituent, minor, electropositive and hydrogen bond donor groups at R5 substituent for Cp28 are favorable for the activity). Through molecular dynamics simulations, we revealed stable binding states of the compounds, with Cp28 emerging as the most stable, while Cp39 displayed certain degrees of instability, which may influence its inhibitory effectiveness. Furthermore, our analysis of the results from the four MD systems revealed that the R groups of the NOS-based inhibitors demonstrated a predilection for insertion into the kink area formed by L1 and H2, thereby conferring stability to the entire inhibitor within Ddn. This positioning also promotes the NOS plane's alignment for subsequent drug catalysis. As a consequence, we anticipate that future refinements in the design of R4 and R5 groups for NOS inhibitors, such as elongating the R chain and incorporating positively charged groups to facilitate interactions and hydrogen bonding with Lys79, will be instrumental in enhancing the binding affinity of NOS inhibitors to Ddn. An additional noteworthy observation pertains to the NO2 component of the NOS, which exhibited an unfavorable tendency to bind with the conserved Ser78. The persistent breaking of the hydrogen bond pair (Ser78-NO2@O) across all MD systems, along with negative contributions to inhibitor binding as revealed by energy decomposition, suggests the potential for an upgrade of the NOS structure itself in future drug design for combating anti-MTB. Ideally, the future NOS derivatives based on our prediction model might serve as an alternative or secondary treatment option to PA-824 or delamanid, when drug-resistance mutants of Ddn develop. However, we are aware of the limitations of the project, including pure bio-informatics predictions, and have not considered the difficulty of synthesizing the novel NOS inhibitors. Future NOS development will rely on the wet-lab experimental work to solve these problems. In summary, our study offers a solid foundation for designing potent Ddn-targeting inhibitors based on the NOS scaffold. The insights gained from this work provide actionable guidance for ongoing efforts in anti-tuberculosis drug development and pave the way to addressing the challenges posed by drug-resistant MTB strains.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
The authors declare that they have no competing interests.Acknowledgements
This work was supported by the National Key Research and Development Program of China (2022YFC2305200) and the Shenzhen Clinical Research Center for Tuberculosis (20210617141509001). We gave our thanks to Dr Minghe Zhu from the Chinese University of Hong Kong, Shenzhen, for his contributions in helping us select snapshots from given metastable states by creating in-house python scripts.References
- S. Bagcchi, WHO's Global Tuberculosis Report 2022, Lancet Microbe, 2023, 4(1), e20 CrossRef PubMed.
- World Health Organization, Global Tuberculosis Report 2024, World Health Organization, 2024 Search PubMed.
- A. H. Diacon, A. Pym, M. Grobusch, R. Patientia, R. Rustomjee and L. Page-Shipp, et al., The diarylquinoline TMC207 for multidrug-resistant tuberculosis, N. Engl. J. Med., 2009, 360(23), 2397–2405 CrossRef CAS PubMed.
- R. Gupta, L. J. Geiter, C. D. Wells, M. Gao, A. Cirule and H. Xiao, Delamanid for Extensively Drug-Resistant Tuberculosis, N. Engl. J. Med., 2015, 373(3), 291–292 CrossRef CAS PubMed.
- A. Matteelli, S. Lovatti, B. Rossi and L. Rossi, Update on MDR-TB preventive therapy towards the global TB elimination, Int. J. Infect. Dis., 2025, 107849 CrossRef CAS PubMed.
- C. K. Stover, P. Warrener, D. R. VanDevanter, D. R. Sherman, T. M. Arain and M. H. Langhorne, et al., A small-molecule nitroimidazopyran drug candidate for the treatment of tuberculosis, Nature, 2000, 405(6789), 962–966 CrossRef CAS PubMed.
- S. E. Mudde, A. M. Upton, A. Lenaerts, H. I. Bax and J. E. M. De Steenwinkel, Delamanid or pretomanid? A Solomonic judgement, J. Antimicrob. Chemother., 2022, 77(4), 880–902 CrossRef CAS PubMed.
- M. Matsumoto, H. Hashizume, T. Tomishige, M. Kawasaki, H. Tsubouchi and H. Sasaki, et al., OPC-67683, a nitro-dihydro-imidazooxazole derivative with promising action against tuberculosis in vitro and in mice, PLoS Med., 2006, 3(11), e466 CrossRef PubMed.
- H. Li, J. Yuan, S. Duan and Y. Pang, Resistance and tolerance of Mycobacterium tuberculosis to antimicrobial agents-How M. tuberculosis can escape antibiotics, WIREs Mech. Dis., 2022, 14(6), e1573 CrossRef CAS PubMed.
- H. L. Haver, A. Chua, P. Ghode, S. B. Lakshminarayana, A. Singhal and B. Mathema, et al., Mutations in genes for the F420 biosynthetic pathway and a nitroreductase enzyme are the primary resistance determinants in spontaneous in vitro-selected PA-824-resistant mutants of Mycobacterium tuberculosis, Antimicrob. Agents Chemother., 2015, 59(9), 5316–5323 CrossRef CAS PubMed.
- D. R. Ashtekar, R. Costa-Perira, K. Nagrajan, N. Vishvanathan, A. D. Bhatt and W. Rittel, In vitro and in vivo activities of the nitroimidazole CGI 17341 against Mycobacterium tuberculosis, Antimicrob. Agents Chemother., 1993, 37(2), 183–186 CrossRef CAS PubMed.
- G. Bashiri, C. J. Squire, N. J. Moreland and E. N. Baker, Crystal structures of F420-dependent glucose-6-phosphate dehydrogenase FGD1 involved in the activation of the anti-tuberculosis drug candidate PA-824 reveal the basis of coenzyme and substrate binding, J. Biol. Chem., 2008, 283(25), 17531–17541 CrossRef CAS PubMed.
- M. Gurumurthy, M. Rao, T. Mukherjee, S. P. S. Rao, H. I. Boshoff and T. Dick, et al., A novel F420-dependent anti-oxidant mechanism protects Mycobacterium tuberculosis against oxidative stress and bactericidal agents, Mol. Microbiol., 2013, 87(4), 744–755 CrossRef CAS PubMed.
- E. Purwantini and B. Mukhopadhyay, Rv0132c of Mycobacterium tuberculosis encodes a coenzyme F420-dependent hydroxymycolic acid dehydrogenase, PLoS One, 2013, 8(12), e81985 CrossRef PubMed.
- S. M. Batt, S. Toth, B. Rodriguez, K. A. Abrahams, N. Veerapen and G. Chiodarelli, et al., Assay development and inhibition of the Mt-DprE2 essential reductase from Mycobacterium tuberculosis, Microbiology, 2023, 169(1), 001288 CrossRef CAS PubMed.
- K. A. Abrahams, S. M. Batt, S. S. Gurcha, N. Veerapen, G. Bashiri and G. S. Besra, DprE2 is a molecular target of the anti-tubercular nitroimidazole compounds pretomanid and delamanid, Nat. Commun., 2023, 14(1), 3828 CrossRef CAS PubMed.
- R. Singh, U. Manjunatha, H. I. Boshoff, Y. H. Ha, P. Niyomrattanakit and R. Ledwidge, et al., PA-824 kills nonreplicating Mycobacterium tuberculosis by intracellular NO release, Science, 2008, 322(5906), 1392–1395 CrossRef CAS PubMed.
- F. H. Ahmed, P. D. Carr, B. M. Lee, L. Afriat-Jurnou, A. E. Mohamed and N. S. Hong, et al., Sequence-Structure-Function Classification of a Catalytically Diverse Oxidoreductase Superfamily in Mycobacteria, J. Mol. Biol., 2015, 427(22), 3554–3571 CrossRef CAS PubMed.
- T. Burki, BPaL approved for multidrug-resistant tuberculosis, Lancet Infect. Dis., 2019, 19(10), 1063–1064 CrossRef PubMed.
- G. Fekadu, T. Tolossa, E. Turi, F. Bekele and G. Fetensa, Pretomanid development and its clinical roles in treating tuberculosis, J. Global Antimicrob. Resist., 2022, 31, 175–184 CrossRef CAS PubMed.
- S. E. Cellitti, J. Shaffer, D. H. Jones, T. Mukherjee, M. Gurumurthy and B. Bursulaya, et al., Structure of Ddn, the deazaflavin-dependent nitroreductase from Mycobacterium tuberculosis involved in bioreductive activation of PA-824, Structure, 2012, 20(1), 101–112 CrossRef CAS PubMed.
- R. Singh, M. Shaheer and M. E. Sobhia, Molecular dynamic assisted investigation on impact of mutations in deazaflavin dependent nitroreductase against pretomanid: a computational study, J. Biomol. Struct. Dyn., 2023, 41(10), 4421–4443 CrossRef CAS PubMed.
- B. M. Lee, L. K. Harold, D. V. Almeida, L. Afriat-Jurnou, H. L. Aung and B. M. Forde, et al., Predicting nitroimidazole antibiotic resistance mutations in Mycobacterium tuberculosis with protein engineering, PLoS Pathog., 2020, 16(2), e1008287 CrossRef CAS PubMed.
- R. Gupta, S. Sharma, R. Singh, R. A. Vishwakarma, S. Mignani and P. P. Singh, Functionalized Nitroimidazole Scaffold Construction and Their Pharmaceutical Applications: A 1950-2021 Comprehensive Overview, Pharmaceuticals, 2022, 15(5), 561 CrossRef CAS PubMed.
- J. Verma, V. M. Khedkar and E. C. Coutinho, 3D-QSAR in drug design--a review, Curr. Top. Med. Chem., 2010, 10(1), 95–115 CrossRef CAS PubMed.
- E. N. Muratov, J. Bajorath, R. P. Sheridan, I. V. Tetko, D. Filimonov and V. Poroikov, et al., QSAR without borders, Chem. Soc. Rev., 2020, 49(11), 3525–3564 RSC.
- H. Hong, H. Fang, Q. Xie, R. Perkins, D. M. Sheehan and W. Tong, Comparative molecular field analysis (CoMFA) model using a large diverse set of natural, synthetic and environmental chemicals for binding to the androgen receptor, SAR QSAR Environ. Res., 2003, 14(5–6), 373–388 CrossRef CAS PubMed.
- G. Klebe, U. Abraham and T. Mietzner, Molecular similarity indices in a comparative analysis (CoMSIA) of drug molecules to correlate and predict their biological activity, J. Med. Chem., 1994, 37(24), 4130–4146 CrossRef CAS PubMed.
- S. H. Lee, S. Kim, M. H. Yun, Y. S. Lee, S. N. Cho and T. Oh, et al., Synthesis and antitubercular activity of monocyclic nitroimidazoles: insights from econazole, Bioorg. Med. Chem. Lett., 2011, 21(5), 1515–1518 CrossRef CAS PubMed.
- G. F. S. Fernandes, K. F. Manieri, A. F. Bonjorno, D. L. Campos, C. M. Ribeiro and F. M. Demarqui, et al., Synthesis and Anti-Mycobacterium tuberculosis Activity of Imidazo[2,1-b][1,3]oxazine Derivatives against Multidrug-Resistant Strains, ChemMedChem, 2023, 18(12), e202300015 CrossRef CAS PubMed.
- P. Kim, S. Kang, H. I. Boshoff, J. Jiricek, M. Collins and R. Singh, et al., Structure-activity relationships of antitubercular nitroimidazoles. 2. Determinants of aerobic activity and quantitative structure-activity relationships, J. Med. Chem., 2009, 52(5), 1329–1344 CrossRef CAS PubMed.
- M. Gurumurthy, T. Mukherjee, C. S. Dowd, R. Singh, P. Niyomrattanakit and J. A. Tay, et al., Substrate specificity of the deazaflavin-dependent nitroreductase from Mycobacterium tuberculosis responsible for the bioreductive activation of bicyclic nitroimidazoles, FEBS J., 2012, 279(1), 113–125 CrossRef CAS PubMed.
- A. M. Jarrad, C. W. Ang, A. Debnath, H. J. Hahn, K. Woods and L. Tan, et al., Design, Synthesis, and Biological Evaluation of 2-Nitroimidazopyrazin-one/-es with Antitubercular and Antiparasitic Activity, J. Med. Chem., 2018, 61(24), 11349–11371 CrossRef CAS PubMed.
- A. M. Thompson, M. Bonnet, H. H. Lee, S. G. Franzblau, B. Wan and G. S. Wong, et al., Antitubercular Nitroimidazoles Revisited: Synthesis and Activity of the Authentic 3-Nitro Isomer of Pretomanid, ACS Med. Chem. Lett., 2017, 8(12), 1275–1280 CrossRef CAS PubMed.
- J. Gasteiger and M. Marsili, Iterative partial equalization of orbital electronegativity—a rapid access to atomic charges, Tetrahedron, 1980, 36(22), 3219–3228 CrossRef CAS.
- M. Clark, R. D. Cramer and N. Van Opdenbosch, Validation of the general purpose tripos 5.2 force field, J. Comput. Chem., 2004, 10(8), 982–1012 CrossRef.
- Z. Zhang, P. Cheng, Y. Z. Zhu, Q. Xia and S. P. Zhang, 3D-QSAR Analysis of a Series of 1,2,3-Triazole-chromenone Derivatives as an Acetylcholinesterase Inhibitor against Alzheimer's Disease, Chin. J. Struct. Chem., 2020, 39(7), 1235–1242 CAS.
- R. D. Cramer, D. E. Patterson and J. D. Bunce, Comparative molecular field analysis (CoMFA). 1. Effect of shape on binding of steroids to carrier proteins, J. Am. Chem. Soc., 1988, 110(18), 5959–5967 CrossRef CAS PubMed.
- S. Wold, A. Ruhe, H. Wold and I. W. J. Dunn, The Collinearity Problem in Linear Regression. The Partial Least Squares (PLS) Approach to Generalized Inverses, SIAM J. Sci. Stat. Comput., 1984, 5(3), 735–743 CrossRef.
- A. Tropsha, P. Gramatica and V. K. Gombar, The importance of being earnest: Validation is the absolute essential for successful application and interpretation of QSPR models, QSAR Comb. Sci., 2003, 22(1), 69–77 CrossRef CAS.
- M. Baroni, S. Clementi, G. Cruciani, G. Costantino, D. Riganelli and E. Oberrauch, Predictive ability of regression models. Part II: Selection of the best predictive PLS model, J. Chemom., 1992, 6(6), 347–356 CrossRef CAS.
- G. M. Morris, D. S. Goodsell, R. S. Halliday, R. Huey, W. E. Hart and R. K. Belew, et al., Automated docking using a Lamarckian genetic algorithm and an empirical binding free energy function, J. Comput. Chem., 1998, 19(14), 1639–1662 CrossRef CAS.
- S. J. Weiner, P. A. Kollman, D. A. Case, U. C. Singh, C. Ghio and G. Alagona, et al., A new force field for molecular mechanical simulation of nucleic acids and proteins, J. Am. Chem. Soc., 2002, 106(3), 765–784 CrossRef.
- F. F. Wang, W. Yang and B. Zhou, Studies on the antibacterial activities and molecular mechanism of GyrB inhibitors by 3D-QSAR, molecular docking and molecular dynamics simulation, Arabian J. Chem., 2022, 15(6), 103872 CrossRef CAS.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, Development and testing of a general amber force field, J. Comput. Chem., 2004, 25(9), 1157–1174 CrossRef CAS PubMed.
- D. A. Case, H. M. Aktulga, K. Belfon, D. S. Cerutti, G. A. Cisneros and V. W. D. Cruzeiro, et al., AmberTools, J. Chem. Inf. Model., 2023, 63(20), 6183–6191 CrossRef CAS PubMed.
- C. I. Bayly, P. Cieplak, W. Cornell and P. A. Kollman, A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges: the RESP model, J. Phys. Chem., 2002, 97(40), 10269–10280 CrossRef.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields, J. Phys. Chem., 2002, 98(45), 11623–11627 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb and J. R. Cheeseman, et al., Gaussian 09, Gaussian, Inc., Wallingford, CT, USA, 2009 Search PubMed.
- J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser and C. Simmerling, ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters from ff99SB, J. Chem. Theory Comput., 2015, 11(8), 3696–3713 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, Comparison of simple potential functions for simulating liquid water, J. Chem. Phys., 1983, 79(2), 926–935 CrossRef CAS.
- D. A. Case, H. M. Aktulga, K. Belfon, I. Y. Ben-Shalom, S. R. Brozell, D. S. Cerutti, T. E. Cheatham III, G. A. Cisneros, V. W. D. Cruzeiro, T. A. Darden, R. E. Duke, G. Giambasu, M. K. Gilson, H. Gohlke, A. W. Goetz, R. Harris, S. Izadi, S. A. Izmailov, C. Jin, K. Kasavajhala, M. C. Kaymak, E. King, A. Kovalenko, T. Kurtzman, T. S. Lee, S. LeGrand, P. Li, C. Lin, J. Liu, T. Luchko, R. Luo, M. Machado, V. Man, M. Manathunga, K. M. Merz, Y. Miao, O. Mikhailovskii, G. Monard, H. Nguyen, K. A. O'Hearn, A. Onufriev, F. Pan, S. Pantano, R. Qi, A. Rahnamoun, D. R. Roe, A. Roitberg, C. Sagui, S. Schott-Verdugo, J. Shen, C. L. Simmerling, N. R. Skrynnikov, J. Smith, J. Swails, R. C. Walker, J. Wang, H. Wei, R. M. Wolf, X. Wu, Y. Xue, D. M. York, S. Zhao and P. A. Kollman, Amber 2021, University of California, San Francisco, 2021 Search PubMed.
- J.-P. Ryckaert, G. Ciccotti and H. J. Berendsen, Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes, J. Comput. Phys., 1977, 23(3), 327–341 CrossRef CAS.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith and B. Hess, et al., GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers, SoftwareX, 2015, 1, 19–25 CrossRef.
- S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, The weighted histogram analysis method for free-energy calculations on biomolecules. I. The method, J. Comput. Chem., 1992, 13(8), 1011–1021 CrossRef CAS.
- F. Marinelli, F. Pietrucci, A. Laio and S. Piana, A kinetic model of trp-cage folding from multiple biased molecular dynamics simulations, PLoS Comput. Biol., 2009, 5(8), e1000452 CrossRef PubMed.
- Wolfram Research, Inc., Mathematica, Wolfram Research, Inc., Champaign, Illinois, 2018 Search PubMed.
- P. A. Kollman, I. Massova, C. Reyes, B. Kuhn, S. Huo and L. Chong, et al., Calculating structures and free energies of complex molecules: combining molecular mechanics and continuum models, Acc. Chem. Res., 2000, 33(12), 889–897 CrossRef CAS PubMed.
- J. Wang, P. Morin, W. Wang and P. A. Kollman, Use of MM-PBSA in reproducing the binding free energies to HIV-1 RT of TIBO derivatives and predicting the binding mode to HIV-1 RT of efavirenz by docking and MM-PBSA, J. Am. Chem. Soc., 2001, 123(22), 5221–5230 Search PubMed.
- B. R. Miller III, T. D. McGee Jr, J. M. Swails, N. Homeyer, H. Gohlke and A. E. Roitberg, MMPBSA. py: an efficient program for end-state free energy calculations, J. Chem. Theory Comput., 2012, 8(9), 3314–3321 CrossRef PubMed.
- F. Wang, W. Yang, H. Liu and B. Zhou, Identification of the structural features of quinazoline derivatives as EGFR inhibitors using 3D-QSAR modeling, molecular docking, molecular dynamics simulations and free energy calculations, J. Biomol. Struct. Dyn., 2022, 40(21), 11125–11140 CrossRef CAS PubMed.
- F. F. Wang, W. Yang, Y. H. Shi, X. R. Cheng and G. W. Le, Structure-based approach for the study of thyroid hormone receptor binding affinity and subtype selectivity, J. Biomol. Struct. Dyn., 2016, 34(10), 2251–2267 CrossRef CAS PubMed.
- F. Wang, W. Yang and X. Hu, Discovery of High Affinity Receptors for Dityrosine through Inverse Virtual Screening and Docking and Molecular Dynamics, Int. J. Mol. Sci., 2018, 20(1), 115 CrossRef PubMed.
- G. D. Hawkins, C. J. Cramer and D. G. Truhlar, Parametrized Models of Aqueous Free Energies of Solvation Based on Pairwise Descreening of Solute Atomic Charges from a Dielectric Medium, J. Phys. Chem., 1996, 100(51), 19824–19839 Search PubMed.
- T. Hou, K. Chen, W. A. McLaughlin, B. Lu and W. Wang, Computational analysis and prediction of the binding motif and protein interacting partners of the Abl SH3 domain, PLoS Comput. Biol., 2006, 2(1), e1 CrossRef PubMed.
- V. Tsui and D. A. Case, Molecular dynamics simulations of nucleic acids with a generalized born solvation model, J. Am. Chem. Soc., 2000, 122(11), 2489–2498 CrossRef CAS.
- A. Onufriev, D. Bashford and D. A. Case, Modification of the generalized Born model suitable for macromolecules, J. Phys. Chem. B, 2000, 104(15), 3712–3720 CrossRef CAS.
- J. Weiser, P. S. Shenkin and W. C. Still, Approximate atomic surfaces from linear combinations of pairwise overlaps (LCPO), J. Comput. Chem., 1999, 20(2), 217–230 CrossRef CAS.
- R. B. Hermann, Theory of hydrophobic bonding. II. Correlation of hydrocarbon solubility in water with solvent cavity surface area, J. Phys. Chem. B, 1972, 76(19), 2754–2759 CrossRef CAS.
- D. Sitkoff, K. A. Sharp and B. Honig, Accurate Calculation of Hydration Free Energies Using Macroscopic Solvent Models, J. Phys. Chem., 2002, 98(7), 1978–1988 Search PubMed.
- H. K. Chaudhari and A. Pahelkar, 3D QSAR, Docking, Molecular Dynamics Simulations and MM-GBSA studies of Extended Side Chain of the Antitubercular Drug (6S) 2-Nitro-6- [4-(trifluoromethoxy) benzyl] oxy-6,7-dihydro-5H-imidazo[2,1-b] [1,3] oxazine, Infect. Disord.:Drug Targets, 2019, 19(2), 145–166 CAS.
- A. E. Mohamed, K. Condic-Jurkic, F. H. Ahmed, P. Yuan, M. L. O'Mara and C. J. Jackson, et al., Hydrophobic Shielding Drives Catalysis of Hydride Transfer in a Family of F(420)H(2)-Dependent Enzymes, Biochemistry, 2016, 55(49), 6908–6918 CrossRef CAS PubMed.
- F. Zhang, S. Li, S. Wen, T. Zhang, Y. Shang and F. Huo, et al., Comparison of in vitro Susceptibility of Mycobacteria Against PA-824 to Identify Key Residues of Ddn, the Deazoflavin-Dependent Nitroreductase from Mycobacterium tuberculosis, Infect. Drug Resist., 2020, 13, 815–822 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ra01362c |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2025 |