Competition among weak C–H⋯O/S/H interactions in the crystal structure of {(C₂H₅O)₂P(S)}₂N₂C₄H₈ bis(thiophosphoramide): experimental/computational studies

Abstract

Supramolecular assembly driven by weak C–H⋯S=P/O and CH⋯HC contacts was studied in a new bis(thiophosphoramide) structure, {(C₂H₅O)₂P(S)}₂N₂C₄H₈, using X-ray crystallography and DFT computational methods. Combined QTAIM/noncovalent interaction (NCI) and natural bond orbital (NBO) analyses were used to gain deeper insights into the nature, energy and strengths of these contacts. The C–H⋯O hydrogen bond was found to be the strongest interaction, followed by two H⋯H and then H⋯S contacts. Crystal lattice energy calculations were performed, and the components contributing to the intermolecular interactions were investigated and discussed (electrostatic, polarization, dispersion and repulsion). The dispersion forces were found to be the most prominent in the network energy. The relative contributions of the intermolecular contacts were visualized by Hirshfeld surfaces and two-dimensional fingerprint diagrams. Some topics related to geometry and conformation were also studied.

---

1 Introduction

Hydrogen bonds have been extensively studied in supramolecular assemblies of numerous materials,¹ including small molecules,^2,3 macromolecules,^4,5 minerals,⁶ organic frameworks⁷ and nanomaterials.⁸ Absence of strong and moderate hydrogen bonds allows for a better study of the competition/cooperation between weaker contacts,^9,10 typically C–H⋯O/S and CH⋯HC, in the crystal-packing features.^11,12

CH⋯HC dispersion contacts, despite their weakness, were found to be effective in the conformational changes and physical properties of some materials containing organic groups.¹³ In alkanes, the additive and unsaturated nature of these contacts were confirmed through calculation/measurement of the sum of the energy values that arise in analogous structures with different numbers of CH bonds. A direct correlation was found between the sizes of hydrocarbons and certain characteristics, such as melting point and vaporization enthalpy.^14–17 CH⋯HC contacts appear in the distance range of 1.7–2.4 Å ¹⁷ and have been proposed as a means to interpret the stability of bulky phosphatetrahedrane¹⁸ and the DNA helix, particularly through stacking interactions.¹⁹ Generally, these interactions lead to structures with optimized energy and thermodynamic stability.¹⁴

C–H⋯S/C–H⋯O hydrogen bonds are common in molecular biology, catalysis, the primary coordination sphere of inorganic and bioorganic molecules, and supramolecular systems.²⁰ Compared to oxygen, the sulfur atom, due to its large size, is prone to forming more contacts with neighbors in the structure, with a tendency toward bent angles. These interactions were found to have a higher dispersion component than classical hydrogen-bonding elements.²¹

Wide applications have been reported for thiophosphoramides in pharmaceutical formulations,^22–24 agriculture,^25,26 designing suitable ligands for coordination,^27,28 and pure scientific studies related to hydrogen bond patterns/strengths.^29,30 Furthermore, some phosphorus-nitrogen-based materials, including those with the S–P–N moiety, are known as flame-retardant (FR) additives in many polymer systems and cotton fabrics.^31,32

The title thiophosphoramide compound has been theoretically studied as a promising cholinesterase inhibitor.³³ The flame-retardant properties of a closely related analogue compound, i.e. {(CH₃O)₂P(S)}₂N₂C₄H₈, and the phosphoramide resemblance of the title compound, i.e. {(C₂H₅O)₂P(O)}₂N₂C₄H₈, have also been investigated, and the former was found to present greater effectiveness and a lower degradation onset than the latter at additive levels.³⁴

The abundances of NH⋯S and NH⋯O hydrogen bonds in (CO)₂P(S)(NH)-based structures retrieved from the Cambridge Structural Database (CSD) indicate the better hydrogen-bond-acceptor capability of the sulfur atom with respect to the ester oxygen atom (in P=S and P–O–C moieties).³⁵ In continuation of this work, we investigated a new crystal structure, {(C₂H₅O)₂P(S)}₂N₂C₄H₈ thiophosphoramide (Scheme 1), which possesses a similar O₂P(S)(N) skeleton but lacks NH groups, to examine C–H⋯O, C–H⋯S and H⋯H contacts. Crystal lattice energy calculations, QTAIM/NCI analysis, and Hirshfeld (HS) surface analysis (including 2D fingerprint characteristics) were studied.

Scheme 1 Chemical structure of (C₂H₅O)₂P(S)NC₄H₈NP(S)(OC₂H₅)₂.

2 Experimental section

2.1. Synthesis of (C₂H₅O)₂P(S)NC₄H₈NP(S)(OC₂H₅)₂

All the reagents used in this study were obtained from commercial sources and used as received. IR spectrum was recorded on an AVATAR 370 FT-IR Thermo Nicolet spectrometer using a KBr pellet. The title compound was prepared according to a published method from the reaction between O,O′-diethyl chlorothiophosphate, piperazine and triethylamine (2 : 1 : 2 molar ratio) in dry acetonitrile at 273 K. After 5 h stirring, the solvent was removed, and the obtained solid was washed with distilled water. Single crystals were obtained in an unsuccessful attempt to prepare a Cd complex (in CH₃OH under reflux conditions). The data related to the ³¹P, ¹H, and ¹³C NMR spectra (in DMSO-d₆) and IR spectrum were previously reported,³⁶ while here X-ray crystallography experiment was performed. The IR spectrum of the title compound was re-investigated for the single-crystal sample in order to further discuss the band assignment (Table S1†).

3 Results and discussion

3.1. Refinement

Diffraction data were collected on a Rigaku Synergy-DW rotating anode X-ray source diffractometer with a hybrid pixel array detector and Kappa goniometer using Mo Kα radiation at 120 K. The structure was solved by intrinsic phasing and refined by full-matrix least-squares methods on F² using SHELXT³⁷ and SHELXL.³⁸ All the non-hydrogen atoms were refined anisotropically, and the hydrogen atoms were refined as riding on their carrier atoms.

3.2. Description of the crystal structure

The compound O,O,O′,O′-tetraethyl piperazine-1,4-diyldiphosphonothioate crystallizes in the triclinic crystal system and space group P1̄. The asymmetric unit consists of one-half of the molecule (Fig. 1), and the complete molecule is organized around an inversion element located in the center of the piperazine ring. The nitrogen atoms of piperazine are linked to the P(S)(OC₂H₅)₂ moieties. The crystal data, X-ray/theoretical values of selected bond lengths and angles and geometrical parameters of the hydrogen bonds are given in Tables 1, 2 and 3, respectively.

Fig. 1 Title structure with labelling of the non-hydrogen atoms of the asymmetric unit. Displacement ellipsoids are drawn at the 50% probability level.

Table 1 Crystallographic parameters for the title compound

Crystal data
Chemical formula	C12H28N2O4P2S2
Mr	390.42
Crystal system, space group	Triclinic, P1̄
Temperature (K)	120
a, b, c (Å)	6.8399 (4), 8.3288 (6), 8.5473 (5)
α, β, γ (°)	84.974 (5), 77.633 (5), 87.946 (5)
V (Å^3)	473.72 (5)
Z	1
Radiation type	Mo Kα
μ (mm^−1)	0.47
Crystal size (mm)	0.20 × 0.15 × 0.15
Tmin, Tmax	0.565, 1.000
No. of measured, independent, and observed reflections [I > 2.0σ(I)]	4327, 1725, 1493
Rint	0.026
(sin θ/λ)max (Å^−1)	0.602
R[F^2 > 2σ(F^2)]	0.031
wR(F^2)	0.086
S	1.09
No. of reflections	1725
No. of parameters	102
Δρmax, Δρmin (e Å^−3)	0.41, −0.29

---

Table 2 Selected experimental and optimized geometrical parameters at the B3LYP/6-311++G(d,p) level of the title molecule^a

Parameter	Experimental	Theoretical
a Symmetry code: (i) −x, −y + 1, −z + 1.
Bond distances (Å)
S1–P1	1.9285 (7)	1.949
P1–O1	1.5860 (13)	1.617
P1–O2	1.5922 (14)	1.625
P1–N1	1.6374 (16)	1.670
O1–C1	1.459 (2)	1.451
O2–C3	1.464 (2)	1.450
N1–C5	1.454 (2)	1.469
N1–C6	1.468 (2)	1.475
C1–C2	1.503 (3)	1.515
C3–C4	1.502 (3)	1.515
C5–C6^i	1.515 (3)	1.526
Bond angles (°)
O1–P1–O2	99.15 (7)	98.84
O1–P1–N1	104.66 (8)	103.25
O2–P1–N1	105.34 (8)	104.39
O1–P1–S1	116.11 (5)	116.81
O2–P1–S1	115.95 (6)	115.72
N1–P1–S1	113.88 (6)	115.59
C1–O1–P1	120.09 (11)	122.03
C3–O2–P1	118.37 (12)	121.58
C5–N1–C6	112.99 (15)	112.65
C5–N1–P1	124.92 (13)	121.67
C6–N1–P1	121.36 (13)	119.54
O1–C1–C2	107.78 (15)	107.91
O2–C3–C4	108.53 (17)	107.92
N1–C5–C6^i	109.88 (15)	109.79
N1–C6–C5^i	109.88 (16)	110.00

---

Table 3 Experimental and calculated hydrogen-bond geometry parameters (Å and °). Calculated values are given in parentheses^a

D–H⋯A	D–H	H⋯A	D⋯A	D–H⋯A
a Symmetry codes: (ii) −x + 1, −y + 1, −z, (iii) x − 1, y, z.
C2–H2B⋯O1^ii	0.98 (1.092)	2.70 (3.090)	3.596 (4.108)	152.0 (155.475)
C2–H2A⋯S1^iii	0.98 (1.093)	3.13 (3.546)	3.791 (4.283)	126.3 (126.213)

---

In general, the bond lengths and angles are within the expected values of compounds with a (CO)₂P(S)(N) skeleton.³⁹ Typical examples are P1=S1, P1–N1 and P1–O1/P–O2 bond lengths of 1.9285 (7) Å, 1.6374 (16) Å and 1.5860 (13)/1.5922 (14) Å, respectively. The closest phosphoramide structure to the title thiophosphoramide compound is (C₆H₅O)₂P(O)NC₄H₈NP(O)(OC₆H₅)₂, which has a P–N bond length shorter than (1.6275 (10) Å ³⁵) that of the P–N bond length of the title compound. The phosphoramide resemblance of title compound was only studied from the view of the spectroscopic features.

The P–N bond length of the title compound is smaller than a typical phosphorus-nitrogen single bond length (1.77 Å),⁴⁰ and was estimated to have slightly more than 30% π-character, according to a previously calculated analogous structure. The phosphorus atom displays a distorted tetrahedral O₂P(S)N environment, and the smallest and largest bond angles around the phosphorus atom are the O1–P1–O2 and O1–P1–S1 angles (99.15 (7)° and 116.11 (5)°). The N atom exhibits a practically planar (sp²) geometry based on the bond-angle sum with a deviation of less than 1° from the ideal value of 360°.

The “N2C4” piperazine ring (N1/C5/C6ⁱ/N1ⁱ/C5ⁱ/C6) of the title molecule adopts a near chair conformation based on the puckering parameters [Q = −0.5592 (19), θ = 177.67 (1)°, Φ = 0°] calculated according to Cremer and Pople.⁴¹

The P–O–C bond angles, 120.09 (11)° (P1–O1–C1) and 118.37 (12)° (P1–O2–C3) are within the range reported based on the CSD P(S)(O–C)₂(N) structures (106–140° with the maximum population within 120–122°), and in accordance with a nearly sp² hybridization state for these O atoms.⁴²

The conformation of the [CH₃CH₂OPOCH₂CH₃] segment was considered based on the C–C–O–P, C–O–P–O, O–P–O–C, and P–O–C–C torsion angles, and the values of 147.86°, −178.60°, −77.97°, and −171.54° show the +ac−ap−sc−ap conformations (ac = anticlinal, ap = antiperiplanar, sc = synclinal). The conformations, due to the presence of flexible OC₂H₅ groups, deviate from the ideal zigzag pattern for a chain sequence of saturated systems. Typically, more usual conformations of ±ap±ap±ap±ap in the (CH₃CH₂CH₂)₂NH₂⁺ cations were observed in the structures retrieved from the CSD,⁴³ based on the C–C–C–N/C–C–N–C/C–N–C–C/N–C–C–C torsion angles. The gas phase optimized structure of the title molecule shows the −ap−ap+ap+ap conformations, and the related torsion angles are −175.47°, −170.01°, 175.47° and 170.01°. A superposition of the theoretical and experimental structure is shown in Fig. S1.†

A new conformer was also created in solution (in CH₃OH) for the chemical calculations, and after optimization, the values, 175.98°, −178.01°, −174.89° and 179.36°, +ap−ap−ap+ap, showed significant differences in two dihedral angles. The deviations were related to the effect of the different phases in the DFT and experimental structures (gas/solution and single crystal). The optimized XYZ coordinates of this conformer are given in Table S2 (ESI†).

The supramolecular assembly was considered based on the interactions with D–H⋯A angles greater than 120°, in accordance with the methodology reported by Wood and co-workers.⁴⁴ Furthermore, the hydrogen-bonded dimers used for the chemical calculations were constructed applying this criterion.

The C1–O1 and C3–O2 bond lengths are 1.459 (2) Å and 1.464 (2) Å, respectively, and the O1 atom takes part in an intermolecular C2–H2B⋯O1 hydrogen bond to form a one-dimensional arrangement in the direction perpendicular to the (−102) plane. This assembly includes an R₂²(8) ring motif (Fig. 2).

Fig. 2 View of the one-dimensional array of the title structure in the direction perpendicular to the (−102) plane, mediated by non-classical C2–H2B⋯O1 hydrogen bonds forming an R₂²(8) graph set motif.

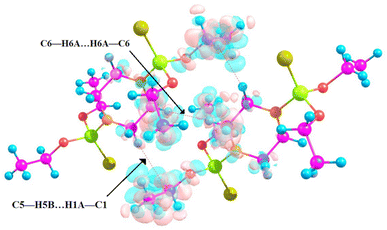
The three-dimensional supramolecular network includes the C5–H5B⋯H1A–C1, C6–H6A⋯H6A–C6 and C2–H2A⋯S1 contacts, and an R₂²(12) ring motif is formed through a pair of C2–H2A⋯S1 contacts (see Fig. 3).

Fig. 3 C5–H5B⋯H1A–C1, C6–H6A⋯H6A–C6, and C2–H2A⋯S1 interactions in the 3D supramolecular assembly of the title structure.

3.3. Hirshfeld surface analysis and fingerprint plots

3D Hirshfeld surface (HS) maps and 2D fingerprint plots were generated using Crystal Explorer 21.5.^45–47 The Hirshfeld surface mapped with d_norm shows the crystal structure interactions based on contacts at distances closer than the sum of the vdW radii with red areas, and contacts around the vdW separation and longer contacts with white and blue areas, respectively.

In the HS map (Fig. 4), the large and bright red areas correspond to the H6A⋯H6A and H5B⋯H1A contacts, which are formed between the two piperazine rings for the former and between the OC₂H₅ group and the piperazine ring for the latter. No other pronounced interaction was observed.

Fig. 4 Hirshfeld surface mapped with d_norm for visualizing the H6A⋯H6A (I) and H5B⋯H1A (II) contacts in the title structure. One adjacent molecule outside the surface is shown to illustrate the interactions with the molecule within the surface.

In the X-ray crystallography analysis, the H6A⋯H6A distance was 2.219 Å, and the normalized Hirshfeld distance was 2.034 Å. For the C–H bond, the neutron-normalized distance in Hirshfeld was 1.083 Å, compared to 0.980 Å, 0.979 Å, and 0.990 Å in the X-ray analysis.

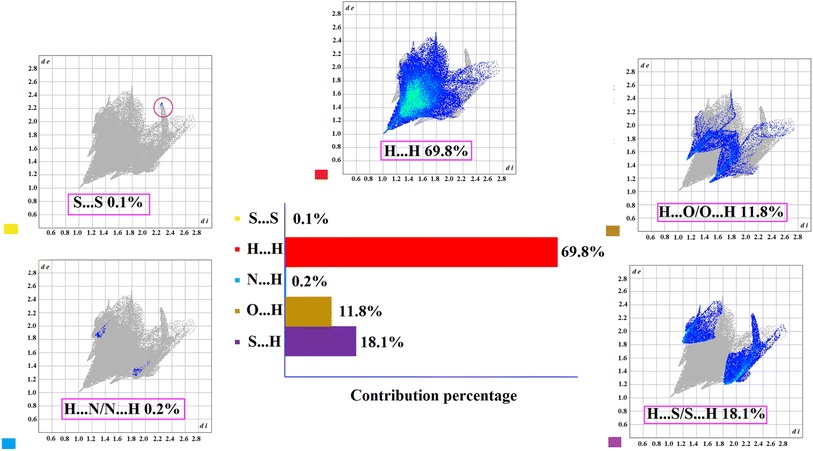
Fig. 5 shows the 2D fingerprint plots and the percentages of different intermolecular contacts. Each point in the fingerprint plot represents the distances from each point on the Hirshfeld surface to the internal nearest atom (d_i) and the external nearest atom (d_e). Therefore, the term d_i + d_e can be used as a measure to evaluate the bond strength.

Fig. 5 Contribution percentages of the contacts participating in the title structure.

In this figure, the highest contribution percentage (69.8%) belonged to the H⋯H contacts with the lowest d_i + d_e ≈ 2 Å. There are four O and two S atoms in the molecule, but the sulfur atoms, due to larger size, exhibited greater participation in the crystal contacts (H⋯O, 11.8%, and H⋯S, 18.1%). Two spikes and two wings on the plot correspond to these contacts with the shortest d_i + d_e ≈ 2.6 and 3 Å, respectively (Fig. 5, top/bottom-right). The S⋯S and N⋯H contacts had a negligible contribution of 0.3% in total (Fig. 5, top/bottom-left).

3.4. Theoretical methods

Crystal lattice energy calculations were performed using Crystal Explorer 21.5 software at the B3LYP/6-31G(d,p) level of theory,⁴⁸ considering the first spherical surface of adjacent molecules. According to previously published articles, the total energy of intermolecular interactions for each molecular pair (E_tot) is expressed as the sum of four terms: electrostatic (E_ele), polarization (E_pol), dispersion (E_dis) and repulsion (E_rep).

E_tot = k_eleE_ele + k_polE_pol + k_disE_dis + k_repE_rep

The E_ele term is the classical Coulomb interaction energy between two unperturbed molecular charge distributions. The E_pol term refers to the perturbation of the electron density caused by the distortion of the electron cloud of a molecule by other nearby charge distributions. The E_dis term comes from the effects of non-classical attraction caused by temporary fluctuations in the electron distribution of a molecule. The E_rep term is the energy required to overcome the forces that prevent two molecules from occupying the same space.

As shown in the above noted formula, the k constants are scale factors and are determined by calibration against the results of quantum mechanics: k_ele = 1.057 for electrostatic interactions, k_pol = 0.740 for polarization, k_dis = 0.871 for dispersion, and k_rep = 0.618 for repulsion.^48–50

The crystal lattice energy (E_latt) is calculated using the equation E_latt = 1/2ΣNE_tot, where N is the number of equivalent pairs with the same energy values in the molecular shell. Similar formulas are used to calculate the sum of each energy component⁵⁰ (, where X = electrostatic, dispersion, polarization, and repulsion components).

Density functional theory (DFT) calculations were performed using the Gaussian 09 program.⁵¹ Harmonic vibrational frequencies were calculated by diagonalization of the Hessian matrix of the potential energy surface (PES). The CIF file was used as the input for the calculations and geometry optimization. The QTAIM parameters were obtained using the Multiwfn 3.8 program⁵² (for dimers constructed from X-ray data including target contacts). Details of the geometry parameters for the DFT structure and the X-ray crystallography are given in Table 2. The regression coefficients of the bond lengths (0.9917) and bond angles (0.9533) showed the good agreement of the theoretical and experimental structures (Fig. S2†).

Natural Bond Orbital (NBO) analysis was done using the NBO 5.0 package.⁵³ Visualization of the natural orbitals was achieved using the ChemCraft program.⁵⁴ Optimization of the molecular geometry, QTAIM, and NBO analyses were carried out at the B3LYP/6-311++G(d,p) level of theory.

The optimized molecular structure is presented in Fig. S3.† The labels of the atoms in the calculations were done according to the labels from the X-ray analysis. The optimized XYZ coordinates of the title molecule and three hydrogen-bonded dimers are listed in Tables S3–S6 (ESI†).

3.4.1. Energy framework calculations. The energies of the crystal lattice, including electrostatic, polarization, dispersion and repulsion components, were calculated for molecular pairs constructed by noncovalent interactions and are summarized in Table S7.† The sums of the electrostatic, polarization, dispersion, and repulsion interaction energies (Σ1/2NE) were equal to −68.9, −19.4, −192.9, and +113.8 kJ mol⁻¹, respectively, and the sum of the total energies was −185.1 kJ mol⁻¹. Molecular pairs with E_tot < −20 kJ mol⁻¹ were considered, and the contributions of the energy components in the total energy for each molecular pair are shown in the diagram in Fig. 6.

Fig. 6 Total energy and energy components for different molecular pairs of the title structure. The red, yellow, green, black, and blue columns represent electrostatic, polarization, dispersion, repulsion (components), and total energy, respectively. The diagram is sorted based on the total energy.

3.4.2. QTAIM analysis. The topological parameters were obtained from the critical points within the dimeric inputs created by the X-ray structure for the calculations. The total electron density, ρ(r), Laplacian, ∇²ρ(r), and the hydrogen bond energy (IHBE), estimated by the E = V_BCP/2 equation,⁵⁵ for C2–H2B⋯O1, C2–H2A⋯S1, homopolar H6A⋯H6A and heteropolar H5B⋯H1A contacts (Table 4) and for all intermolecular contacts are presented (Table S8, ESI†). The positive total electronic densities, ρ(r), for all the interactions are characteristic of a closed-shell situation. The two H⋯H contacts noted are typical examples of such contacts in the structure, which had the highest energy values, and were formed between piperazine⋯piperazine and piperazine⋯ethyl. There were two other H⋯S interactions with approximately equal energy to C2–H2A⋯S1, with angles slightly less than 120°.

Table 4 Estimated energies (E_ESP) for C–H⋯O/S and CH⋯HC contacts

Hydrogen bonds/contacts	ρ(r) (e au^−3)	∇^2ρ(r) (e au^−5)	G(r)	V(r)	EESP (kJ mol^−1)
a There are two equivalent such interactions in the molecular pair.
C2–H2B⋯O1^a	0.0071	0.0225	0.0049	−0.0042	−5.5
C2–H2A⋯S1^a	0.0063	0.0201	0.0041	−0.0032	−4.2
H6A⋯H6A	0.0079	0.0222	0.0046	−0.0037	−4.9
H5B⋯H1A^a	0.0070	0.0217	0.0045	−0.0036	−4.7

---

The hydrogen bond energy (in kJ mol⁻¹) of C2–H2B⋯O1 (5.5) was greater than that of H6A⋯H6A (4.9) and H5B⋯H1A (4.7), and the C2–H2A⋯S1, C1–H1B⋯S1, and C3–H3A⋯S1 hydrogen bonds with the hydrogen bond angles of 126.29°, 115.18°, and 112.88° had energies of 4.2, 4.6, and 4.7, respectively. The low angles C–H⋯S contacts were in accordance with the reported nonlinear character of C–H⋯S contacts, based on a CSD survey that considered the angles within 90° to 180°, with the most common contacts between 121°−126° and 3.12–3.25 Å.²¹ The following discussion focuses on a comparison between the crystal lattice energy calculations and the QTAIM analysis results.

3.4.3. Integrating QTAIM/NCI methods with lattice energy analysis. Combined QTAIM/NCI molecular graphs for different molecular pairs were constructed, and the results of the lattice energy calculations were included (Fig. 7). In these pictures, the total energy framework is represented using blue cylinders.

Fig. 7 Combined QTAIM/NCI plots of the molecular pairs with E_tot < −20 kJ mol⁻¹ in the title structure (atom color codes: P = orange, S = yellow, O = red, N = blue, C = light beige, and H = light pink). The total energy and their components are listed (left). The energy framework is displayed by blue cylinders with a scale factor of 50, along the a, b and c axes (right). Small orange spheres and yellow lines represent critical points and bond paths, respectively. The NCI-isosurface value was 0.65.

The pair Ia had the highest total energy of −48.4 kJ mol⁻¹, and comprised H6A⋯H6A, 2 × H5B⋯H1A contacts and some other weak contacts (H⋯S, H⋯H and H⋯O). In this pair, the highest energy value was related to H6A⋯H6A/2 × H5B⋯H1A contacts (ΣE_ESP = −14.3 kJ mol⁻¹), with V(r) values of −0.0037 and −0.0036 a.u., respectively. The 2 × C2–H2A⋯S1 hydrogen bonds were the most pronounced contacts in pair Ib with a V(r) value of −0.0032 a.u., besides H⋯H and other H⋯S contacts (E_tot of −33.0 kJ mol⁻¹).

The pairs Ic, Id, and If (with E_tot values of −30.1, −24.1, and −21.4 kJ mol⁻¹, respectively) were characterized by various intermolecular interactions: C–H⋯S and H⋯H in Ic and If and C–H⋯S, C–H⋯O, and H⋯H in Id (Fig. S4†). The pair Ie, with an E_tot of −23.8 kJ mol⁻¹, included 2 × C2–H2B⋯O1 hydrogen bonds (V(r) = −0.0042 a.u.) and some other H⋯H contacts. The total energy framework was viewed along the a, b and c axes.

In the title structure, the major part of the attractive energy was due to dispersion forces, with the total dispersion energy of −192.9 kJ mol⁻¹, while the total electrostatic energy was equal to −68.9 kJ mol⁻¹. A large part of the total attractive energy (−281.2 kJ mol⁻¹) was compensated by a repulsive component of +113.8 kJ mol⁻¹. On the other hand, in all the pairs, the electrostatic components contributed less to lattice energy than the dispersion forces, and the highest electrostatic interactions corresponded to pair Ic. The greatest proximity of the dispersion and electrostatic forces was found in pair Ib (−17.5/−13.8 kJ mol⁻¹), while the greatest difference was observed in pair Ia (−62.6/−14.9 kJ mol⁻¹), Table S7.†

In the NCI plots of title compound, the red–green mixed regions within the weak C–H⋯O/S and CH⋯HC contacts illustrate weak repulsion forces, compared with the blue region demonstrating strong repulsive forces, where electron-rich atoms are close to each other, such as HB acceptors in strong and moderate hydrogen bonds.⁵⁶ The highest repulsive energy (+40.1 kJ mol⁻¹) was associated with the molecular pair Ia, which also had the largest total energy (−48.4 kJ mol⁻¹) and the smallest distance (6.84 Å) compared to the other pairs. In pair Ib, the repulsive force reached zero due to the significantly increased distance (12.48 Å).

3.4.4. Electron delocalization. An estimation of the IHB strength was made based on the second-order perturbation theory. Thus, the second-order interaction energies E⁽²⁾ were calculated for noncovalent interactions, considering occupied Lewis type (lone pair) NBO orbitals and unoccupied (antibonding) non-Lewis NBO orbitals participating in target intermolecular interactions (donor–acceptor interactions).⁵⁷

For these calculations, three dimers including C2–H2B⋯O1, C2–H2A⋯S1, and H⋯H contacts were created, and the associated E⁽²⁾ energies are listed in Tables 5 and S9 (ESI†).

Table 5 E⁽²⁾ interaction energies (kJ mol⁻¹) obtained from NBO analysis at the B3LYP/6-311++G(d,p) level. The data were obtained from three dimers

Donor MO	Acceptor MO	E^(2) (kJ mol^−1)
LP(1)O(1)	σ*(1)C2–H2B	1.0042
LP(2)O(1)	σ*(1)C2–H2B	0.4184
σ(1)C5–H5B	σ*(1)C1–H1A	0.4602
σ(1)C6–H6A	σ*(1)C6–H6A	1.0878
LP(1)S(1)	σ*(1)C2–H2A	0.5858
LP(2)S(1)	σ*(1)C2–H2A	0.5858

---

The second-order energies of the C–H⋯O/S and H⋯H contacts were related to LP(1,2)O1 to σ*(1)C2–H2B, and LP(1,2)S1 to σ*(1)C2–H2A, σ(1)C5–H5B to σ*(1)C1–H1A and σ(1)C6–H6A to σ*(1)C6–H6A with values of 1.0042/0.4184, 0.5858/0.5858, 0.4602 and 1.0878 kJ mol⁻¹, respectively. Fig. 8 shows the hyper conjugations of two H⋯H contacts in the related dimer.

Fig. 8 Depiction of hyper conjugation for the H6A⋯H6A and H5B⋯H1A contacts.

The energy gap between the frontier molecular orbitals, highest occupied molecular orbital (HOMO), and lowest unoccupied molecular orbital (LUMO) can be used to describe electron charge transfer and to predict molecular reactivity.¹⁷ The HOMO and LUMO orbitals of the title molecule and associated charge transfer energy are depicted in Fig. 9.

Fig. 9 HOMO and LUMO of the title molecule and the associated band gap.

The HOMO was mainly localized on the P=S groups and the O atoms, with a small share of the N atoms, and the LUMO was mainly located on the –CH₃/–CH₂ moieties.

The electrostatic potential (ESP) surface displays the charge distribution in a molecule and provides an important analysis in molecular modeling to predict intermolecular interactions.⁵⁸ The ESP surface of the title molecule and the atomic vdW radius, obtained from the optimized geometry using the B3LYP/6-311++G(d,p) level, are given in Fig. S5.†

A negative potential and high electron density were observed around the C–O and P=S bonds (orange and red areas, respectively). A region with electron deficiency and positive potential was observed for the CH₂ units of the piperazine moiety and the CH₂/CH₃ units of –OEt groups (blue and green areas, respectively). The green color of ESP for N atom shows that it is not accessible for interaction.

3.4.5. Reduced density gradient (RDG). RDG analysis is used to illustrate intra and inter non-bonding interactions in a crystal structure.⁵⁹ The RDG scatter graph is produced by plotting RDG versus sign(λ₂)ρ. Here, sign(λ₂)ρ is the 2^nd eigenvalue of the electron density and its value and sign describe the nature of the bond. Also, sign(λ₂)ρ > 0 and sign(λ₂)ρ < 0 are related to repulsive and attractive interactions and sign(λ₂)ρ values of about zero area indicate van der Waals interactions. A color-filled RDG isosurface map with relevant identified contacts and RDG scatter graph of the dimer created based on the H⋯H contacts of the title molecule are presented in Fig. 10 and 11. This dimer was the most energetically important possible dimer that may be constructed for the parent molecule with neighbors in the structure. The color-filled RDG isosurface map and RDG scatter graph of the dimer created based on a pair of H2B⋯O1 interactions of the title molecule are shown in Fig. S6 and S7.†

Fig. 10 Color-filled RDG isosurface map for the dimer created based on the H6A⋯H6A and H5B⋯H1A contacts of the title structure.

Fig. 11 RDG scatter graph for the dimer created based on the H6A⋯H6A and H5B⋯H1A contacts of the title structure.

In the isosurface map, the red areas indicate steric contacts with the highest repulsive forces (piperazine ring). The red–green mixed regions show week repulsive forces that are accompanied by the attractions of C2–H2B⋯O1/C2–H2A⋯S1 interactions, and the green areas correspond to the van der Waals interactions for H⋯H.

A theoretical analysis of the vibrational frequencies, along with a detailed description and discussion of the IR spectroscopic features, is provided in the ESI (Fig. S8 and Table S1†).

4 Conclusion

The strengths of H⋯H contacts and C–H⋯O/C–H⋯S hydrogen bonds were studied in the P(S)(OC₂H₅)₂NC₄H₈NP(S)(OC₂H₅)₂ thiophosphoramide structure by a combination of X-ray crystallography and computational methods. The C–H⋯O hydrogen bond was calculated to be stronger than the H⋯H contacts and C–H⋯S hydrogen bonds. The lattice energy calculations showed the most pronounced contribution of dispersion forces in the attractive energy of the molecular architecture with respect to the electrostatic and polarization components. The highest repulsive energy was seen in the molecular pair, which also had the highest total energy and dispersion component.

Data availability

The data supporting this article have been included as part of the ESI.† Crystallographic data for the title compound have been deposited at the CCDC (2426091) and can be obtained from https://www.ccdc.cam.ac.uk/structures.

Author contributions

Maliheh Khorramaki: synthesis, writing, and formal analysis. Mehrdad Pourayoubi: supervision of experimental section, project administration, formal analysis, and writing-review & editing. Vahidreza Darugar: writing and chemical calculation. Mohammad Vakili: supervision of chemical calculation, project administration, and editing. Marek Nečas: X-ray crystallography and editing. Mahmood Akbari: chemical calculation and editing. Malik Maaza: chemical calculation.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

Support of this investigation by Ferdowsi University of Mashhad (3/53938) is gratefully acknowledged. The authors also gratefully acknowledge the Centre for High Performance Computing (CHPC), South Africa, for providing computational resources and facilities that supported this research project.

References

1. D. I. Ugwu and J. Conradie, J. Mol. Struct., 2023, 1293, 136275.
2. M. Khorramaki, M. Pourayoubi, V. R. Yazdan-Abad, V. Darugar, M. Vakili, V. Eigner and M. Dušek, J. Mol. Struct., 2025, 1321, 140068.
3. V. Darugar, M. Vakili, S. F. Tayyari, P. E. Hansen and F. S. Kamounah, J. Mol. Liq., 2021, 334, 116035.
4. J. Wang, H. Li and B. Xu, RSC Chem. Biol., 2021, 2, 289–305.
5. E. N. Baker, International Tables for Crystallography, ed. M. G. Rossmann and E. Arnold, Springer, Dordrecht, 2006, ch. 22.2, vol. F, pp. 546–552.
6. F. Colmenero, J. Plášil, J. Cobos, J. Sejkora, V. Timón, J. Čejka and L. J. Bonales, RSC Adv., 2019, 9, 15323–15334.
7. Z.-J. Lin, S. A. R. Mahammed, T.-F. Liu and R. Cao, ACS Cent. Sci., 2022, 8, 1589–1608.
8. Y. Cai, W. Peng and P. Vana, Nanoscale Adv., 2022, 4, 2787–2793.
9. S. C. C. van der Lubbe and C. Fonseca Guerra, Chem.–Asian J., 2019, 14, 2760–2769.
10. S. Hosseinpoor, M. Pourayoubi, M. Dušek and E. Skořepová, Phosphorus, Sulfur Silicon Relat. Elem., 2022, 197, 747–757.
11. C. E. Galvez, O. E. Piro, G. A. Echeverría, N. L. Robles, J. O. G. Lezama, S. V. Sankaran, S. Thamotharan, M. B. Villecco, M. del H. Loandos and D. M. Gil, New J. Chem., 2022, 46, 5690–5704.
12. L. R. de Almeida, P. S. Carvalho, H. B. Napolitano, S. S. Oliveira, A. J. Camargo, A. S. Figueredo, G. L. B. de Aquino and V. H. Carvalho-Silva, Cryst. Growth Des., 2017, 17, 5145–5153.
13. S. N. Britvin, A. M. Rumyantsev, A. A. Silyutina and M. V. Padkina, ChemistrySelect, 2017, 2, 8721–8725.
14. J. P. Wagner and P. R. Schreiner, J. Chem. Theory Comput., 2016, 12, 231–237.
15. J. Echeverría, G. Aullón, D. Danovich, S. Shaik and S. Alvarez, Nat. Chem., 2011, 3, 323–330.
16. A. M. Reilly and A. Tkatchenko, Chem. Sci., 2015, 6, 3289–3301.
17. D. Danovich, S. Shaik, F. Neese, J. Echeverría, G. Aullón and S. Alvarez, J. Chem. Theory Comput., 2013, 9, 1977–1991.
18. M. L. Y. Riu, G. Bistoni and C. C. Cummins, J. Phys. Chem. A, 2021, 125, 6151–6157.
19. J. P. Wagner and P. R. Schreiner, Angew. Chem., Int. Ed., 2015, 54, 12274–12296.
20. S. Ghosh, P. Chopra and S. Wategaonkar, Phys. Chem. Chem. Phys., 2020, 22, 17482–17493.
21. H. A. Fargher, T. J. Sherbow, M. M. Haley, D. W. Johnson and M. D. Pluth, Chem. Soc. Rev., 2022, 51, 1454–1469.
22. W. Liu, L. Zhang, H. Zhou, C. Yang, Z. Miao and Y. Zhao, Nucleosides, Nucleotides Nucleic Acids, 2013, 32, 161–173.
23. R. Penchovsky, A. V. Georgieva, V. Dyakova, M. Traykovska and N. Pavlova, Antibiotics, 2024, 13, 221.
24. H. K. Langner, K. Jastrzebska and M. H. Caruthers, J. Am. Chem. Soc., 2020, 142, 16240–16253.
25. K. Gholivand, A. A. Ebrahimi Valmoozi and M. Bonsaii, Pestic. Biochem. Physiol., 2014, 112, 40–50.
26. H. Cantarella, R. Otto, J. R. Soares and A. G. de. B. Silva, J. Adv. Res., 2018, 13, 19–27.
27. D. A. Safin, M. G. Babashkina, M. Bolte and Y. Garcia, CrystEngComm, 2012, 14, 774–778.
28. M. Khorramaki, M. Abad, V. Darugar, M. Pourayoubi, M. Vakili, M. Nečas, D. Choquesillo-Lazarte, P. V. Andreev and E. S. Shchegravina, Polyhedron, 2022, 228, 116157.
29. D. A. Safin, M. G. Babashkina, A. Klein, H. Nöth, M. Bolte and D. B. Krivolapov, Polyhedron, 2010, 29, 1837–1841.
30. M. P. Mitoraj, F. Sagan, M. G. Babashkina, A. Y. Isaev, Y. M. Chichigina and D. A. Safin, Eur. J. Org. Chem., 2019, 2019, 493–503.
31. R. Nazir and S. Gaan, J. Appl. Polym. Sci., 2020, 137, 1–27.
32. S. Chang, M. Nguyen, B. Condon and J. Smith, Fibers Polym., 2017, 18, 666–674.
33. K. Gholivand, A. A. Ebrahimi Valmoozi and M. Bonsaii, J. Agric. Food Chem., 2014, 62, 5761–5771.
34. T.-M. Nguyen, S. Chang, B. Condon and J. Smith, Mater. Sci. Appl., 2014, 5, 789–802.
35. B. Vahdani Alviri, M. Pourayoubi, A. Farhadipour, M. Nečas and V. Bertolasi, Acta Crystallogr., Sect. C: Struct. Chem., 2018, 74, 1610–1621.
36. E. Torabi Farkhani, M. Pourayoubi, M. Izadyar, P. V. Andreev and E. S. Shchegravina, Dalton Trans., 2019, 48, 17908–17918.
37. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8.
38. G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8.
39. M. Pourayoubi, M. Abrishami, V. Eigner, M. Nečas, M. Dušek and M. Delavar, Acta Crystallogr., Sect. C: Struct. Chem., 2014, 70, 1147–1152.
40. F. H. Allen and I. J. Bruno, Acta Crystallogr., Sect. B: Struct. Sci., 2010, 66, 380–386.
41. D. Cremer and J. A. Pople, J. Am. Chem. Soc., 1975, 97, 1354–1358.
42. F. Sabbaghi, M. Pourayoubi, M. Dušek, V. Eigner, S. Bayat, K. Damodaran, M. Nečas and M. Kučeráková, Struct. Chem., 2016, 27, 1831–1844.
43. F. Sabbaghi, A. As’habi, A. Saneei, M. Pourayoubi, A. A. Abdul Salam, M. Nečas, M. Dušek, M. Kučeráková and S. Acharya, Acta Crystallogr., Sect. C: Struct. Chem., 2021, 77, 68–80.
44. P. A. Wood, F. H. Allen and E. Pidcock, CrystEngComm, 2009, 11, 1563–1571.
45. M. A. Spackman and D. Jayatilaka, CrystEngComm, 2009, 11, 19–32.
46. M. A. Spackman and J. J. McKinnon, CrystEngComm, 2002, 4, 378–392.
47. P. R. Spackman, M. J. Turner, J. J. McKinnon, S. K. Wolff, D. J. Grimwood, D. Jayatilaka and M. A. Spackman, J. Appl. Crystallogr., 2021, 54, 1006–1011.
48. C. F. Mackenzie, P. R. Spackman, D. Jayatilaka and M. A. Spackman, IUCrJ, 2017, 4, 575–587.
49. M. A. Spackman, CrystEngComm, 2018, 20, 5340–5347.
50. M. J. Turner, S. Grabowsky, D. Jayatilaka and M. A. Spackman, J. Phys. Chem. Lett., 2014, 5, 4249–4255.
51. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian Inc, Wallingford, CT, USA, 2009, https://www.gaussian.com.
52. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
53. F. Weinhold. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann and C. M. Morales, NBO 5.0, Theor. Chem. Institute, Univ. Wisconsin, Madison, WI.
54. G. A. Zhurko and D. A. Zhurko, ChemCraft, Version 1.8, https://www.chemcraftprog.com.
55. E. Espinosa, E. Molins and C. Lecomte, Chem. Phys. Lett., 1998, 285, 170–173.
56. J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632.
57. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926.
58. N. Kaya Kınaytürk, T. Kalaycı and B. Tunalı, Spectrosc. Lett., 2021, 54, 693–706.
59. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.

---

Footnote

† Electronic supplementary information (ESI) available: Tables and figures related to quantum chemical calculations. CCDC 2426091. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d5ra01306b

---