First-principles study of Ga₂Ge₂S₃Se₃ monolayer: a promising photocatalyst for water splitting

Abstract

Recently, the quaternary Janus monolayers with the formula A₂B₂X₃Y₃ have been shown to be promising candidates for optoelectronic applications, especially in the photocatalytic water splitting reaction. Therefore, first-principles calculations were employed to investigate the photocatalytic properties of Ga₂Ge₂X₃Y₃ (X and Y represent S, Se or Te atoms) monolayers. The Ga₂Ge₂S₃Se₃ and Ga₂Ge₂Se₃Te₃ monolayers exhibit dynamic and thermal stability, supported by high cohesive energies (3.78–4.20 eV) and positive phonon dispersion. With a moderate Young's modulus (50.02–65.31 N m⁻¹) and high Poisson's ratio (0.39–0.41), these monolayers offer a balance of stiffness and flexibility, making them suitable for flexible electronic applications. Especially, the difference in work function of 0.27 eV induces an intrinsic electric field in the Ga₂Ge₂S₃Se₃ monolayer, making the electronic structure of this material be suitable for the photocatalytic water splitting process. With light irradiation, the oxygen evolution reaction (OER) happened simultaneously, producing electrons and H⁺ protons for the hydrogen evolution reaction (HER) to happen at a low potential barrier. Moreover, the Ga₂Ge₂S₃Se₃ monolayer has a high absorption rate α(ω) of 10⁵–10⁶ cm⁻¹ and a high electron mobility of 430.82–461.50 cm² V⁻¹ s⁻¹. These characteristics result in a good solar-to-hydrogen of the Ga₂Ge₂S₃Se₃ monolayer (14.80%) which is promising for use in photon-driven water splitting.

---

1 Introduction

Water splitting, the process of decomposing water into hydrogen and oxygen through electrolysis, offers a potential solution to the global energy crisis. This technology holds the promise of a clean, sustainable, and efficient energy future. A variety of materials have been explored as photocatalysts for water splitting, each with its unique properties and potential advantages. Inorganic semiconductors, such as metal oxides (TiO₂, ZnO, Fe₂O₃),^1–3 metal sulfides (CdS, ZnS),^4,5 and metal nitrides (TiN),⁶ have been extensively studied. While these materials offer stability and high catalytic activity, their performance is often limited by factors like wide bandgaps and rapid charge carrier recombination. Organic semiconductors, including graphitic carbon nitride (g-C₃N₄) and organic dyes,^7,8 offer advantages such as low cost and tunable bandgaps. However, their stability and efficiency can be compromised. Hybrid materials, combining the best of both inorganic and organic worlds, have emerged as promising candidates.⁹ These materials often exhibit enhanced light absorption, charge separation, and stability.

To further enhance the efficiency of photocatalytic water splitting, researchers are exploring various strategies. Bandgap engineering, which involves modifying the bandgap of materials to better match the solar spectrum, is a key approach. Additionally, strategies to prevent electron–hole recombination, such as introducing co-catalysts or forming heterojunctions, are being investigated.^3,10 Surface modification techniques are employed to improve light absorption and charge transfer, while nanostructuring is used to increase surface area and light harvesting efficiency.^4,5 These advancements hold the potential to significantly improve the performance of photocatalytic water splitting systems.

Among 2D materials, ternary 2D chalcogenides have emerged as promising materials for photocatalytic water splitting due to their unique electronic and optical properties.¹¹ Compounds like ZnIn₂S₄ and AgInS₂ have garnered significant attention.¹² These materials often exhibit suitable bandgap energies for visible light absorption, efficient charge carrier separation, and enhanced stability compared to their binary counterparts.¹³ However, challenges such as photocorrosion and low carrier mobility still need to be addressed. Ongoing research focuses on optimizing synthesis techniques, incorporating co-catalysts, and developing heterostructures to further improve the photocatalytic performance of these materials.

Two-dimensional (2D) layered transition metal phosphorus trichalcogenides (MPX₃, where M represents transition metals and X = S, Se) exhibit high in-plane stiffness and lower cleavage energies than graphite.^14–17 This allows them to be exfoliated down to atomic thickness. Recently, these materials have attracted renewed attention due to their unique structural and electronic properties. Notably, chemically exfoliated monolayer FePS₃ has demonstrated efficient photocatalytic hydrogen evolution.¹⁸ Inspired by these findings, monolayers such as AsGeC₃, SbSnC₃, and BiPbC₃ have been investigated, revealing strong stability and excellent optical properties.¹⁹ Additionally, CoGeSe₃, GaSnS₃, and InSnS₃ monolayers show promise as visible-light photocatalysts with high carrier mobility.^20,21 The GaGeSe₃ monolayer, in particular, exhibits a solar-to-hydrogen conversion efficiency of 11.33% and a charge carrier mobility of 790.65 cm² V⁻¹ s⁻¹.²² Substitution is an effective strategy for tuning the electronic properties of monolayers, as demonstrated experimentally. For instance, the MoSSe monolayer was synthesized by replacing the top-layer S atoms with Se atoms.²³ Building on this concept, many quaternary monolayers have been theoretically designed based on the aforementioned ternary structures. The Zn₂P₂S₃Se₃ and Cd₂P₂S₃Se₃ monolayers are predicted to exhibit exceptionally high charge carrier mobility of 2772 cm² V⁻¹ s⁻¹.²⁴ Meanwhile, Janus-type monolayers such as In₂Ge₂Te₃Se₃, In₂Ge₂Se₆, and In₂Ge₂S₃Se₃ have emerged as promising candidates for thermoelectric applications in high-temperature environments. In this study, the Ga₂Ge₂S₃Se₃ and Ga₂Ge₂Se₃Te₃ monolayers were constructed based on the atomic structures of GaGeS₃ and GaGeSe₃ monolayers, respectively. The structural, electronic and transport properties of the two new monolayers are studied using first-principles calculation.

2 Methodology

All calculations were performed using the Quantum-ESPRESSO package.²⁵ The Perdew–Burke–Ernzerhof (PBE) functional²⁶ within the generalized gradient approximation (GGA) and the hybrid functional HSE06 (ref. 27) were employed to describe exchange–correlation effects. Projector augmented-wave (PAW) pseudopotentials²⁸ were used to represent core-valence electron interactions. An energy cutoff of 520 eV was chosen for effective convergence of the total energies. In addition, a density cutoff, four times the energy cutoff, was used in the calculations. The geometry was fully relaxed until the forces on all of the atoms decreased to less than 0.01 eV Å⁻¹ and the total energy change was smaller than 10⁻⁶ eV. A 15 × 15 × 1 Monkhorst–Pack k-point mesh was used to sample the Brillouin zone. The initial structural models of Ga₂Ge₂S₃Se₃ and Ga₂Ge₂Se₃Te₃ monolayers were constructed based on the known structures of GaGeS₃ and GaGeSe₃, respectively. The 20 Å vacuum layers were added to avoid interactions between periodic images. The structural asymmetry of Ga₂Ge₂X₃Y₃ monolayers induces significant dipole moments, leading to notable van der Waals (vdW) interactions. To accurately account for these vdW interactions, DFT-D3 corrections²⁹ were incorporated into the DFT functionals. The dynamic stability of the monolayers was assessed by calculating phonon dispersion curves using the functional perturbation method implemented in the PHONOPY code.³⁰ Transport properties, including carrier mobility, were estimated using the deformation potential method.³¹

3 Results and discussion

3.1 Structural characteristics

The equilibrium configurations of Ga₂Ge₂X₃Y₃, shown in Fig. 1, were achieved by optimizing their lattice structures for the lowest energy. The top view of Ga₂Ge₂X₃Y₃, as shown in Fig. 1(a), has a hexagonal pattern constructed based on the rhombus unit-cell, which contains 10 constituent atoms including two Ga (green balls), two Ge (purple balls), three S/Se (red balls), and three Se/Te (brown) atoms. As illustrated in Fig. 1(b), these atoms are arranged in five sublayers of S/Se, Ge, Ga, Ge, and Se/Te atoms that are stacked on top of one another. On the right-hand side, Fig. 1(c) shows the dynamic characteristics of these structures in form of phonon dispersions. While Ga₂Ge₂S₃Se₃ and Ga₂Ge₂Se₃Te₃ monolayers are dynamically stable with positive phonons, the Ga₂Ge₂S₃Te₃ monolayer is predicted to be unstable due to the negative frequencies of some acoustic phonons.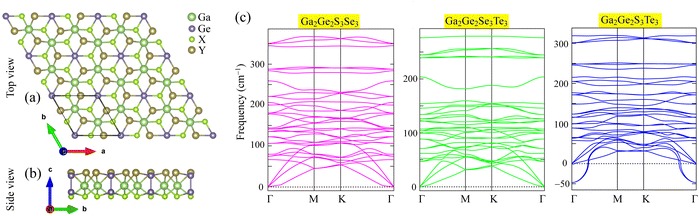

Fig. 1 Optimized atomic structure of Ga₂Ge₂X₃Y₃ (X/Y = S, Se, Te; X ≠ Y) monolayers shown in (a) top view and (b) site view together with (c) their phonon dispersions.

It is worth noting that the Ga₂Ge₂S₃Se₃ and Ga₂Ge₂Se₃Te₃ monolayers are formed by modifying the atomic structures of GaGeS₃ and GaGeSe₃ monolayers,²² respectively, where heavier atoms Se/Te are substituted for lighter host atoms S/Se. Such substitutions cause lattice enlargement, as shown in Table 1, the lattice constants (a = b) of Ga₂Ge₂S₃Se₃ and Ga₂Ge₂Se₃Te₃ monolayers are 6.29 Å and 6.74 Å, respectively. These lattice constants are about 0.17–0.28 Å longer than the corresponding values of GaGeS₃ or GaGeSe₃ monolayer.²² Due to the stacking of sublayer of identical elements, the substitution of Se atoms for S atoms replaces the whole S-sublayer in the GaGeS₃ monolayer²² (S–Ge–Ga–Ge–S) with the Se-sublayer in the Ga₂Ge₂S₃Se₃ monolayer (S–Ge–Ga–Ge–Se). Such a significant change causes noticeable enlargement of all bond-lengths as GaGeS₃ monolayer²² transforms into Ga₂Ge₂S₃Se₃ monolayer. As shown in Table 1, the Ge–S, Ga–S, and Ge–Ge bond lengths increase by 0.3–0.13 Å. Consequently, the monolayer thickness, which is defined as the distance between the two edge sublayers, also increases by about 0.08 Å. Similarly, the data listed in Table 1 shows that the replacement of Se-sublayer in GaGeSe₃ monolayer²² with the Te-sublayer in Ga₂Ge₂Se₃Te₃ monolayer results in some increase in the Ge–Se, Ga–Se, and Ge–Ge bond lengths by about 0.04–0.22 Å. Meanwhile, the thickness of Ga₂Ge₂Se₃Te₃ monolayer is 0.12 eV.

Table 1 Lattice constant a, thickness h, and interatomic distance d, cohesive energy E_coh, PBE/HSE06 bandgap E_g, elastic coefficient C_ij, Young's modulus Y_2D and Poisson's ratio ν_2D of Ga₂Ge₂S₃Se₃, Ga₂Ge₂Se₃Te₃ monolayers

	a (Å)	h (Å)	dGe–X (Å)	dGa–X (Å)	dGe–Ge (Å)	dGe–Y (Å)	dGa–Y (Å)	Ecoh (eV per atom)	E^PBEg (eV)	E^HSE06g (eV)	C11 (N m^−1)	C12 (N m^−1)	C66 (N m^−1)	Y2D (N m^−1)	ν2D
Ga2Ge2S3Se3	6.29	3.28	2.37	2.66	2.37			4.20	1.02	1.83	76.69	29.55	23.57	65.31	0.39
Ga2Ge2Se3Te3	6.74	3.50			2.42	2.57	2.87	3.78	0.06	0.63	59.82	24.21	17.81	50.02	0.41

---

The significant change in the structural characteristics of the two new monolayers requires further study on their stability. From an energy perspective, a new system is considered stable if its total energy is less than the combined energies of its individual components. Such energetic difference is called cohesive energy E_coh, which can be calculated for the Ga₂Ge₂X₃Y₃ monolayers as follows:

where, E_tot represents the total energy of the Ga₂Ge₂S₃Se₃ and Ga₂Ge₂Se₃Te₃ monolayers. E_Ga, E_Ge, E_X, E_Y represents the total energy of isolated Ga, Ge, S, or Se atom. The cohesive energies of Ga₂Ge₂S₃Se₃ and Ga₂Ge₂Se₃Te₃ monolayers are 4.20 eV and 3.78 eV, respectively. These values indicate that the formations of the two monolayers are energetically favorable. Such cohesive energies can also be regarded to be typical values for the A₂B₂X₃Y₃ family, as other members, namely Al₂Ge₂S₃Se₃ and Al₂Ge₂Se₃Te₃ monolayers, have similar cohesive energies (4.10–4.59 eV).³² The thermal stabilities of the two monolayers are evaluated by analyzing the changes in their total energies at 300 K (room temperature) and at 500 K during an ab initio molecular dynamics (AIMD) simulation. As shown in Fig. 2(a) and (b), respectively, the total energies of Ga₂Ge₂S₃Se₃ and Ga₂Ge₂Se₃Te₃ monolayers vary within a very small deviation ranging from 0.8 to 1.0 eV. This slight energy fluctuation quickly decreases after the first 1–2 picoseconds. This result rules out the possibility of heat-induced structural damage, confirming that Ga₂Ge₂S₃Se₃ and Ga₂Ge₂Se₃Te₃ monolayers are stable at room temperature and at higher temperature of 500 K.

Fig. 2 (a and b) Total energy variation of Ga₂Ge₂S₃Se₃ and Ga₂Ge₂Se₃Te₃ monolayers at 300 K and 500 K; angular functions of (c) Young's modulus and (d) Poisson's ratio of Ga₂Ge₂S₃Se₃ (pink circles) and Ga₂Ge₂Se₃Te₃ (green circles) monolayers.

The mechanical stability, stiffness and deformation behavior of 2D materials, such as graphene, transition metal dichalcogenides, and MXenes, etc.,^33–35 can be analyzed using Born's stability criteria, Young's modulus (Y) and Poisson's ratio (ν), respectively. These properties are determined from the elastic constants C₁₁, C₁₂, and C₆₆, which are derived by calculating the second partial derivatives of the total energy of the system with respect to the corresponding components of strain, thereby linking the material's atomic-level interactions to its macroscopic mechanical properties.³⁶

For 2D hexagonal materials such Ga₂Ge₂S₃Se₃ and Ga₂Ge₂Se₃Te₃ monolayers, the Born's mechanical stability criteria are simplified due to their symmetry and two-dimensional nature as follows: C₁₁ > 0, C₆₆ > 0, and C₁₁ − C₁₂ > 0.^37,38 As reported in Table 1, the calculated C₁₁, C₁₂ and C₆₆ moduli of Ga₂Ge₂S₃Se₃ and Ga₂Ge₂Se₃Te₃ monolayers comply these criteria. These findings are crucial, as the Born criteria ensure the strength of materials under small deformations and indicate the absence of lattice instabilities. Furthermore, the Young's modulus and Poisson's ratio as angular functions were calculated in the xy plane. As plotted in Fig. 2(c) and (d) for Ga₂Ge₂S₃Se₃ and Ga₂Ge₂Se₃Te₃ monolayers, respectively, the graphs of these functions are nearly perfect circles. This angular dependence directly correlates with the structural isotropy and uniformity of these monolayers, underscoring their potential for applications where uniform mechanical properties are essential.^39,40 The calculated Young's modulus values are 65.31 N m⁻¹ for Ga₂Ge₂S₃Se₃ and 50.02 N m⁻¹ for Ga₂Ge₂Se₃Te₃, placing them among 2D materials with moderate stiffness such as GaGeSe₃, GaGeS₃, Al₂Ge₂S₃Se₃, Al₂Ge₂Se₃Te₃, tinselenidene and bismuth telluride nanosheets.^22,32,41,42 Meanwhile, Ga₂Ge₂S₃Se₃ and Ga₂Ge₂Se₃Te₃ monolayers are more flexible than phosphorene, graphene, black phosphorus (BP), hexagonal boron nitride and MoS₂ monolayer.^43–45 The reduced modulus compared to graphene can be attributed to the buckled structure and the chemical composition of these monolayers, which result in lower in-plane bonding strength. This intermediate stiffness makes Ga₂Ge₂S₃Se₃ and Ga₂Ge₂Se₃Te₃ suitable for applications requiring flexibility without significant loss of mechanical stability. In addition, the Poisson's ratios of Ga₂Ge₂S₃Se₃ and Ga₂Ge₂Se₃Te₃ range from 0.39 to 0.41, exceeding those observed in many ternary and quaternary monolayers of similar atomic structures, including GaGeS₃, GaGeSe₃, and Al₂Ge₂Se₃Te₃.^22,32 A high Poisson's ratio indicates the material's ability to undergo lateral expansion when stretched, which is a desirable trait for enhancing toughness and ductility. For comparison, the Poisson's ratios of typical 2D transition metal dichalcogenides MoS₂ and WS₂, tin chalcogenides, boron nitride (h-BN)^46–48 hover around 0.3, making Ga₂Ge₂S₃Se₃ and Ga₂Ge₂Se₃Te₃ superior in terms of toughness and deformation resilience.

This combination of moderate stiffness and high Poisson's ratio suggests that Ga₂Ge₂S₃Se₃ and Ga₂Ge₂Se₃Te₃ monolayers can endure significant deformation without losing their structural integrity. The demonstration of FeClF, MnSeTe, and MnSTe monolayers as promising materials for a wide range of electronic applications, particularly due to their favorable elastic properties,^49,50 provides strong support for considering Ga₂Ge₂S₃Se₃ and Ga₂Ge₂Se₃Te₃ as potential candidates for flexible electronic devices, such as foldable displays, wearable sensors, and stretchable photovoltaics, where both mechanical resilience and flexibility are required.^51–53 Furthermore, their structural and mechanical characteristics could enable their integration into composite materials to enhance performance under mechanical stress.

3.2 Electronic characteristics of Ga₂Ge₂S₃Se₃ and Ga₂Ge₂Se₃Te₃ monolayers

Fig. 3 presents the band structures of Ga₂Ge₂S₃Se₃ and Ga₂Ge₂Se₃Te₃ monolayers, calculated using both HSE06 (solid pink curves) and GGA-PBE (dashed blue curves) functionals. Both monolayers exhibit analogous band structure patterns, characterized by a high density of electronic states due to the large number of atoms in their unit cells. Notably, both materials possess direct band gaps, with the valence band maximum (VBM) and conduction band minimum (CBM) situated at the Γ – point. The HSE06 method offers a more accurate treatment of the exchange–correlation interaction, effectively suppressing the unphysical overestimation of electron energies in the valence bands. As a result, the calculated band gap between the valence and conduction bands is significantly larger in the HSE06 approach compared to the values calculated by the GGA-PBE method. For the Ga₂Ge₂S₃Se₃ monolayer, the HSE06 calculation yields a band gap of 1.83 eV, which is 0.81 eV larger than the value calculated by the GGA-PBE method. In the case of the Ga₂Ge₂Se₃Te₃ monolayer, the GGA-PBE method predicts an extremely narrow band gap of 0.06 eV. However, the HSE06 approach provides a significantly improved result, revealing a band gap of 0.63 eV.

Fig. 3 Electronic band structures and projected density of states (PDOS) ofGa₂Ge₂S₃Se₃ and Ga₂Ge₂Se₃Te₃ monolayers. The band structures were calculated using PBE functional (dash blue lines) and HSE06 hybrid functional (solid pink lines).

Compared to the HSE06 band gaps of GaGeS₃ (2.51 eV) and GaGeSe₃ (1.91 eV) monolayers,²² replacing the S sublayer with a Se sublayer or the Se sublayer with a Te sublayer reduces the band gaps of the original monolayers. These results highlight that substituting heavier element provides an efficient strategy for narrowing the band gaps of monolayers. This effect results from the increased spin–orbit coupling (SOC) induced by heavier atoms, which brings the conduction and valence band edges closer together.^54,55 In two-dimensional materials, the impact of SOC is further amplified by quantum confinement,^56,57 leading to more pronounced band gap reductions and tunable electronic properties. The band gap of Ga₂Ge₂Se₃Te₃ is below 1.23 eV, rendering it unsuitable as a photocatalyst for water splitting due to insufficient energy for driving the reaction.⁵⁸ In contrast, the Ga₂Ge₂S₃Se₃ monolayer is well-suited for this application. Additionally, it represents an advancement over the GaGeS₃ monolayer,²² as its narrower band gap enables greater absorption of visible light, which makes up a significant portion of the solar energy spectrum. In the Ga₂Ge₂S₃Se₃ monolayer, the PDOS reveals that p-orbitals from Ga, Ge, S, and Se dominate both the valence and conduction bands across a wide energy range. Strong hybridization is observed, particularly between the s- and p-orbitals of Ga and Ge. The direct bandgap is formed by the valence band maximum (VBM) dominated by Se-p orbitals and the conduction band minimum (CBM) dominated by Ga-s orbitals. A similar PDOS profile is observed in the Ga₂Ge₂Se₃Te₃ monolayer, with p-orbitals from the constituent atoms dominating at all energy levels. The VBM is primarily composed of Te-p orbitals, while the CBM is dominated by Se-s, p orbitals and p-orbitals from the other atoms.

To gain deeper insights into the orbital contributions of each constituent element to the electronic band structure, we analyzed the projected band structures of Ga₂Ge₂S₃Se₃ and Ga₂Ge₂Se₃Te₃ monolayers, as depicted in Fig. 4. In these plots, the s, p_x, p_y, and p_z orbitals are depicted in blue, pink, red, and green, and their relative contributions are visualized by the size of the corresponding spheres. By examining these projected band structures, we can identify the specific orbitals of each element that dominate the formation of the valence band maximum and conduction band minimum, providing valuable information about the electronic and hole transport properties of these materials. It is obvious that the highest valence bands are mainly occupied by Se-p orbitals in Ga₂Ge₂S₃Se₃ monolayer and by Te-p orbitals in Ga₂Ge₂Se₃Te₃ monolayer. Consequently, the width of the band gap is partially determined by the substituted Se or Te element. It is worth noting that the lowest conduction bands, on the other hand, are mainly constructed by the Ga-s orbitals, making them another important factor in creating the band gap.

Fig. 4 Orbital-projected band structures of Ga₂Ge₂S₃Se₃ and Ga₂Ge₂Se₃Te₃ monolayers.

In Al₂Ge₂S₃Se₃ and Al₂Ge₂Se₃Te₃ monolayers, the bandgaps range from 1.07 to 2.38 eV.³² These values are smaller than those observed in Ga₂Ge₂S₃Se₃ and Ga₂Ge₂Se₃Te₃ monolayers. This reduction in bandgap can be attributed to the lighter atomic mass of Al compared to Ga, resulting in weaker SOC effects in the Al-containing compounds. When analyzing the bandgaps of In₂Ge₂S₃Se₃, In₂Ge₂S₃Te₃, Al₂Ge₂S₃Se₃, and Al₂Ge₂Se₃Te₃ monolayers^32,59 within the A₂B₂X₃Y₃ family, it is observed that the Y atoms (Se or Te) play a significant role in determining the bandgap width. Specifically, heavier Y atoms result in narrower bandgaps. These findings confirm the mechanism discussed in the previous section, which emphasizes the significant influence of SOC on bandgap values. At lower valence bands, ranging from −2 to −1 eV, orbital hybridization is observed to happen between p_z orbitals from Ge, S, and Se elements in Ga₂Ge₂S₃Se₃ monolayer or Ge, Se, and Te elements in Ga₂Ge₂Se₃Te₃ monolayer. The hybridization of other orbitals happens in the deeper energy levels. Meanwhile, the p_y orbitals from Se or Te atoms participate in the hybridization with other orbitals at almost all valence energy bands, showing the important role of Se and Te elements in the formation of covalent bonds in Al₂Ge₂S₃Se₃ and Al₂Ge₂Se₃Te₃ monolayers.

3.3 Photocatalytic performance of Ga₂Ge₂S₃Se₃ monolayer

Fig. 5(a) illustrates the variation in electrostatic potential across both sides of the Ga₂Ge₂S₃Se₃ monolayer. To move an elementary charge away from the monolayer's surface, work must be done against the electrostatic potential. The horizontal blue line in the diagram represents the vacuum level, where a free electron is no longer influenced by the material's potential. The work function (Φ) is defined as the energy required to move an electron from the Fermi level to the vacuum level. Due to the higher electronegativity of S compared to Se, the S-side of the monolayer exhibits a higher electrostatic potential. This results in a difference in work function (ΔΦ) of 0.27 eV between the two sides of the monolayer. As a result, an internal electric field E is induced,⁶⁰ pointing from the lower-potential Se-side to the higher-potential S-side. This field facilitates the movement of photoexcited electrons from the S-side to the Se-side, while photoexcited holes move in the opposite direction. This promotes effective electron–hole separation, which not only enhances the material's photocatalytic efficiency but also influences the band edge alignment relative to the redox potential.⁶⁰ The energies of the conduction band edge E_CBE and valence band edge E_VBE can be defined by formula proposed by Toroker et al.^61,62 based on the energy at vacuum level E_V and the energies of the unshifted conduction band minimum E_CBM and valence band maximum E_VBM as E_CBE/VBE = E_CBM − E^S/Se-side_V. In Fig. 5(a), the positions of E_VBE and E_CBE are denoted with green and red solid rectangles, respectively. It is obvious that the E_VBE is located below the oxidation potential O₂/H₂O and the E_CBE is above the H⁺/H₂ reduction potential. Therefore, it is expected that the Ga₂Ge₂S₃Se₃ monolayer can induce the separation of water to release oxygen and hydrogen gases if the energetic requirements are met. In Fig. 5(a), the positions of E_VBE and E_CBE are denoted by green and red solid rectangles, respectively. The diagram shows that the E_VBE is positioned below the oxidation potential of water (O₂/H₂O), while the E_CBE lies above the reduction potential of protons (H⁺/H₂). This band alignment is typical for water splitting photocatalyst.

Fig. 5 (a) Electrostatic potential with intrinsic electric field (red arrow) of Ga₂Ge₂S₃Se₃ monolayer and (b) the variation of bandgap and band edge alignment relative to the redox potential of water splitting reaction.

Strain engineering emerges as a powerful tool for enhancing the photocatalytic activity of two-dimensional materials, particularly Janus structures like Ga₂Ge₂S₃Se₃. By applying strain, precise control over the bandgap and band alignment becomes possible. This allows for optimization of light absorption and efficient charge carrier transport, crucial for driving photocatalytic reactions.^63–66 Furthermore, strain can effectively align the band edges with the redox potentials of water splitting reactions. This alignment facilitates efficient charge transfer and improves the overall catalytic efficiency.^67,68 Most of 2D materials can withstand substantial strains, typically up to around 10%,⁶⁹ before significant deformation or failure. This high flexibility stems from their unique atomic structure. However, it's crucial to recognize that this value is not universal and depends strongly on the specific material and the nature of the applied strain. For example, reported strain limits for 2D GeP range from 12.9% to 26.2%,⁷⁰ and MoS₂ monolayers have been shown to maintain stability above 10% strain.⁷¹ The Ga₂Ge₂S₃Se₃ and Ga₂Ge₂Se₃Te₃ monolayers, with their moderate Young's moduli (50.02–65.31 N m⁻¹) and high Poisson's ratios (0.39–0.41), are predicted to be relatively flexible. Therefore, the compressive and tensile strains ranging from −8% to 8% were applied on these two monolayers. Our investigation delves into the impact of strain on the bandgap and band edge alignment of the Ga₂Ge₂S₃Se₃ monolayer (Fig. 5(b)). Compressive strains ranging from −2% to −4% lead to a bandgap widening of approximately 2.0 eV. Beyond this range, both further compression and tensile strains result in a bandgap reduction. Notably, the band edges of the Ga₂Ge₂S₃Se₃ monolayer remain suitable for water redox reactions when subjected to compressive strains between −6% and −8% or tensile strains below 4%.

Strain engineering offers a versatile approach to fine-tune the electronic and optical properties of 2D materials, including their bandgap, band edge positions, and light absorption characteristics. These tunable properties hold significant potential for enhancing photocatalytic performance in applications such as water splitting.^72–74 Given the promising photocatalytic potential of Ga₂Ge₂S₃Se₃ monolayer, we investigated the effects of strain ranging from −8% to 8%. The resulting changes in band structure and light absorption rate are illustrated in Fig. 6, respectively.

Fig. 6 (a) Impact of strain on the band structure and (b) the light absorption rate of the Ga₂Ge₂S₃Se₃ monolayer.

Fig. 6(a) presents the band structures with the valence band maximum (VBM) aligned to the Fermi level, allowing us to focus on the shifts in the conduction band minimum (CBM). Previous studies on black phosphorus, transition metal dichalcogenides, and ternary Janus monolayers have demonstrated that strain can induce significant band structure modifications, such as direct-to-indirect bandgap transitions, bandgap tuning, and changes in band curvature.^75,76 In contrast, the Ga₂Ge₂S₃Se₃ monolayer maintains a direct bandgap configuration under both compressive and tensile strain, with the VBM and CBM remaining at the Γ – point. Notably, the curvature of the conduction bands increases significantly under strain compared to the unstrained monolayer (Fig. 3). This increased curvature suggests a reduced effective mass of electrons, potentially leading to enhanced electron mobility.

The variation in electronic structure, particularly the changes in bandgap discussed above, significantly influences the optical properties of Ga₂Ge₂S₃Se₃ monolayers. Fig. 6(b) presents the calculated absorption rates, α(ω), for the monolayer under strains ranging from −8% to 8%. The unstrained Ga₂Ge₂S₃Se₃ monolayer exhibits a relatively high absorption rate (black curve), exceeding 10⁵ cm⁻¹ in the infrared region and increasing further in the visible region. In the ultraviolet region, the absorption rate surpasses 10⁶ cm⁻¹. This strong absorption across a broad spectral range, including the infrared and visible regions, makes Ga₂Ge₂S₃Se₃ a promising candidate for solar energy applications, as these regions contain the majority of solar energy reaching Earth. Compressive strains (−4% and −8%) lead to a widening of the bandgap, resulting in a reduced absorption of infrared and visible light. However, these larger bandgaps enable the absorption of higher-energy ultraviolet photons. Conversely, tensile strains (4% and 8%) narrow the bandgap, enhancing the absorption of infrared and visible light.

A critical step in water splitting involves the adsorption of hydrogen atoms onto the catalyst surface, facilitating electron transfer. This adsorption process induces a change in the system's total energy, which can be analyzed through Gibbs free energy calculations. To calculate the change in Gibbs free energy for the Ga₂Ge₂S₃Se₃ monolayer, it is necessary to determine the total energies of hydrogen-adsorbed system E_{Ga2Ge2S3Se3+H}, pristine Ga₂Ge₂S₃Se₃ monolayer E_Ga2Ge2S3Se3, and isolated hydrogen molecule E_H2. Then the change in energy ΔE_H is calculated as ΔE_H = E_{Ga2Ge2S3Se3+H} − E_Ga2Ge2S3Se3 − 0.5E_H2, and the Gibbs free energy ΔG_H is defined as ΔG_H = ΔE_H + 0.24 eV.^77–79 Fig. 7(a) and (b) depicts the Gibbs free energy diagram of the Ga₂Ge₂S₃Se₃ monolayer, wherein the bottom and top surfaces are designated as the S-side and Se-side, respectively. The calculated ΔG_H values at the Ga, Ge, and Se sites exhibit negative values, ranging from −0.95 to −2.01 eV. The negative ΔG_H suggests that the adsorption of hydrogen atoms at these specific sites is thermodynamically favorable.

Fig. 7 (a and b) Gibbs free energy change as hydrogen atom is connected to the Ga, Se, or Ge atoms on the S-side and Se-side of in Ga₂Ge₂S₃Se₃ monolayer; (c and d) photocatalytic reaction steps of HER and OER half-reactions.

The Ga₂Ge₂S₃Se₃ monolayer's capacity for photocatalytic water splitting can be assessed by examining the thermodynamic feasibility of both the Hydrogen Evolution Reaction (HER) and the Oxygen Evolution Reaction (OER).^59,80 The Gibbs free energy changes (ΔG) associated with each of these half-reactions at pH = 0 are shown in Fig. 7(c) and (d). The OER half-reaction on the Ga₂Ge₂S₃Se₃ monolayer involves a series of steps. Initially, energy is required to break the O–H bond in water to form an adsorbed hydroxyl ion (OH*). Subsequently, this hydroxyl ion undergoes further oxidation to generate an adsorbed oxygen atom (O*). The adsorbed oxygen atom then reacts with another water molecule to form a hydroperoxide intermediate (OOH*), which finally decomposes to release molecular oxygen (O₂). In the absence of light irradiation (U = 0 eV), the calculated ΔG values for these four steps are 1.38 eV, 3.71 eV, 4.64 eV, and 4.92 eV, respectively. The highest energy barrier, and thus the potential-determining step, is the transformation from OOH* to O₂. As mentioned in previous sections, the electronic characteristics of Ga₂Ge₂S₃Se₃ monolayer is favorable for the generation of photoexcited electron–hole pairs. The photogenerated holes in the valence bands can effectively interact with the intermediate species formed during the OER half-reactions, thereby facilitating the subsequent oxidation steps. Upon illumination, the energy barriers for the OER steps are modified. The calculation method of energy barriers of the illuminated material is presented in ESI.† As shown in Fig. 7(d), these effective barriers are reduced to negative or near-zero values, indicating that the OER steps become spontaneous or require minimal activation energy. These results strongly suggest that light irradiation can effectively trigger the OER half reactions on the Ga₂Ge₂S₃Se₃ monolayer spontaneously.

In water splitting, the OER oxidizes water to produce oxygen O₂, protons H⁺, and electrons. These products are subsequently utilized by the HER to generate hydrogen gas H₂. However, the thermodynamic feasibility of this process is governed by the change in Gibbs free energy ΔG. Fig. 7(c) illustrates the ΔG for the HER process on the Ga₂Ge₂S₃Se₃ monolayer. Without light irradiation, the formation of adsorbed hydrogen atoms H* requires an energy input of 1.36 eV. Under light irradiation, photogenerated electrons contribute an external potential of U = 0.47 eV, effectively reducing the HER reaction barrier on the Janus Ga₂Ge₂S₃Se₃ to 0.89 eV. Many promising photocatalysts exhibit positive HER reaction barriers, which can be mitigated through various strategies such as adsorbing alkali and transition metals,⁸¹ constructing heterojunctions,⁸² and introducing point defects like vacancies.⁸³ In practice, applying an external bias voltage can significantly enhance the separation of photogenerated electron–hole pairs, thereby improving the overall photocatalytic efficiency. For example, studies have demonstrated that combining a TiO₂ photoanode with an organo-photocathode enables stoichiometric water decomposition at bias voltages below the theoretical minimum of 1.23 V. This exemplifies the effectiveness of external voltage in lowering the energy barrier for water splitting reactions and boosting photocatalytic activity. However, the wide bandgap of TiO₂ (approximately 3.2 eV) restricts its activity to the ultraviolet region of the solar spectrum, which constitutes a relatively small portion of solar energy.⁸⁴ Therefore, the Ga₂Ge₂S₃Se₃ monolayer, with its moderate bandgap and low HER energy barrier, emerges as a promising candidate for efficient hydrogen generation through photocatalytic water splitting.

To calculate the charge carrier mobility, it is necessary to establish the dependence of the system total energy E_total and band edges E_edge (the positions of VBM and CBM) as functions of the uniaxial strains ε_uni. As shown in Fig. 8(a), the E_total values are calculated at 5 discrete values of the ε_uni, which ranges from −1% to 1%. The E_edge values, as shown in Fig. 8(b), are also determined at these discrete values of uniaxial strains. Therefore, an interpolation model was applied to construct the continuous functions E_total and E_edge, making it possible to the determine the elastic modulus C_2D by taking the second derivative of the total energy function and divided by the area of the unit-cell. Meanwhile, the deformation energy E_def is derived from the Laplacian of E_edge the edge energy function. The charge carrier mobility in 2D material, μ_2D, is then defined as μ_2D = eℏ³C_2D/k_BTm*m̄*E_def², where e, ℏ, k_B, and T represent charge of a free electron, the temperature in kelvin, the reduced Planck constant, and the Boltzman constant, respectively. The symbol m̄* is the average value of the effective masses m*, which is defined based on the energy function of k – point E(k) as m* = (ℏ²∂²E_k/∂²k)⁻¹.

Fig. 8 (a) Total energy E_total and (b) band edge energy E_edge as functions of uniaxial strains ε_uni applied on the Ga₂Ge₂S₃Se₃ monolayer.

The Ga₂Ge₂S₃Se₃ monolayer exhibits nearly isotropic electron mobility in the range of 430.82–461.50 cm² V⁻¹ s⁻¹, enabling efficient charge transport in all directions. This isotropic mobility minimizes anisotropic losses that can hinder device performance in complex architectures.^85,86 Moreover, the Ga₂Ge₂S₃Se₃'s electron mobility is comparable to well-established 2D photocatalysts like MoS₂, PdS₂, PdSe₂, SnP₂S₆, and As₂S₃,^87–91 facilitating rapid electron transport to the reduction site for reactions such as hydrogen evolution. The Ga₂Ge₂S₃Se₃ monolayer exhibit significantly higher electron mobility compared to their hole mobility (19.55–33.47 cm² V⁻¹ s⁻¹). This disparity can suppress electron–hole recombination, a major loss mechanism in photocatalytic processes.

The previous sections have established Ga₂Ge₂S₃Se₃ monolayer as a promising material for photocatalytic applications. Its 1.83 eV bandgap aligns well with the solar spectrum, making it an ideal candidate for sunlight-driven water splitting. To further explore its potential, additional calculations were performed to assess its performance in this process. The solar-to-hydrogen efficiency η_STH of Ga₂Ge₂S₃Se₃ monolayer, a measure for its ability to convert solar energy into hydrogen, is determined by two primary factors: light absorption efficiency η_abs and carrier utilization efficiency η_cu. As outlined in equations η_STH = η_abs × η_cu,⁹² η_abs, which quantifies the photocatalyst's ability to absorb sunlight, is primarily governed by the semiconductor's bandgap E_g. The Ga₂Ge₂S₃Se₃ monolayer exhibits a high light absorption rate α(ω) of 10⁵–10⁶ cm⁻¹ across a broad spectral range from infrared to ultraviolet, leading to the η_abs of 32.18%. Carrier utilization efficiency η_cu, on the other hand, reflects the efficiency of converting absorbed sunlight into usable charge carriers. As shown in the supplementary, this parameter is influenced the bandgap E_g. The calculated value of η_cu is 47.54%. Based on the values of η_abs and η_cu, the η_STH of Ga₂Ge₂S₃Se₃ monolayer is predicted to be 15.30%. However, this value must be corrected⁹² because in the Janus monolayers with difference in vacuum level (ΔE_V), the intrinsic electric field can do positive work W_in in separating the electron–hole pair. As defined in the discussion regarding to Fig. 5(a), the ΔE_V equals to the difference in work function ΔΦ, which is 0.27 eV. With P(ℏω) is the AM1.5G solar energy flux, the work W_in is determined as . Therefore, the total work for photocatalytic process becomes 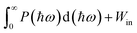. The actual efficiency is . Applying this correction, the efficiency of Ga₂Ge₂S₃Se₃ monolayer becomes 14.80%, making this monolayer a promising candidate for photon-driven water splitting photocatalysis. As mentioned above, a water splitting photocatalyst must meet many strict requirements. Therefore, to achieve the 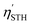in the range of 3.33–16%, a monolayer is usually modified by elemental substitution, phase transitions, or the application of strain.^{22,59,62,93,94} The Ga₂Ge₂S₃Se₃ monolayer offers several advantages over its parent GaGeS₃ monolayer.²² Notably, its solar-to-hydrogen conversion efficiency (14.80%) surpasses that of GaGeS₃ (11.33%). The transition from an indirect to a direct bandgap in Ga₂Ge₂S₃Se₃ enhances light absorption and facilitates faster charge separation. While direct bandgap materials are often susceptible to rapid electron–hole recombination, this effect is mitigated in Ga₂Ge₂S₃Se₃ due to an intrinsic electric field that promotes charge separation. Consequently, the substitution of Se for S results in a monolayer with demonstrably improved photocatalytic properties.

4 Conclusion

This work employed first-principles calculations to explore potential photocatalytic water splitting materials within the A₂B₂X₃Y₃ family. Structural investigations revealed that Ga₂Ge₂Se₃Te₃ monolayer is unstable, while Ga₂Ge₂S₃Se₃ and Ga₂Ge₂Se₃Te₃ monolayers exhibit both dynamic and thermal stability. Furthermore, elastic parameter analysis demonstrates a favorable balance between flexibility and stiffness in these monolayers, making them suitable for flexible applications. Electronic structure analysis of Ga₂Ge₂S₃Se₃ and Ga₂Ge₂Se₃Te₃ monolayers indicates that orbital contributions from Ga and Y atoms within the Ga₂Ge₂X₃Y₃ formula play a crucial role in determining the bandgap values. This finding suggests a straightforward approach to tune the bandgap of Ga₂Ge₂X₃Y₃ materials, enabling a broader range of applications. While the bandgap of Ga₂Ge₂Se₃Te₃ monolayer (0.63 eV) is too narrow for efficient photocatalytic water splitting, the bandgap of Ga₂Ge₂S₃Se₃ monolayer (1.83 eV) positions it as a promising candidate. Further investigations reveal several key advantages of Ga₂Ge₂S₃Se₃ monolayer for photocatalytic water splitting applications. A significant difference of 0.27 eV in the work functions between the S-side and Se-side of the monolayer induces an intrinsic electric field, effectively driving photoexcited electrons from the Se-side to the S-side and facilitating efficient charge separation. The band edge alignment of Ga₂Ge₂S₃Se₃ monolayer is well-suited for triggering the photoexcited redox reactions involved in water splitting. This photocatalytic activity is maintained under moderate compressive strains (−6% to −8%) and tensile strains below 4%. Moreover, the Ga₂Ge₂S₃Se₃ monolayer demonstrates the capability to initiate the oxygen evolution reaction (OER) under light irradiation, releasing electrons and protons (H⁺) for the hydrogen evolution reaction (HER) to occur at low overpotential. The Ga₂Ge₂S₃Se₃ monolayer, even with a moderate solar-to-hydrogen efficiency of 14.80%, holds significant potential as a photocatalyst for water splitting, particularly when considering its other advantageous properties.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of interest

There are no conflicts of interest to declare.

References

1. R. Li, Y. Weng, X. Zhou, X. Wang, Y. Mi, R. Chong, H. Han and C. Li, Energy Environ. Sci., 2015, 8, 2377–2382.
2. Y. Li, C. Liao and S. C. Tjong, Int. J. Mol. Sci., 2020, 21, 8836.
3. N. Arif, M. N. Zafar, M. Batool, M. Humayun, M. A. Iqbal, M. Younis, L. Li, K. Li and Y.-J. Zeng, J. Mater. Chem. C, 2024, 12, 12653–12691.
4. Z. Chang, J. Zhang, W. Dong, X. Meng, H. Wang, D. Wei and Y. Ren, RSC Adv., 2020, 10, 37820–37825.
5. H. Yu, X. Huang, P. Wang and J. Yu, J. Phys. Chem. C, 2016, 120, 3722–3730.
6. M. Jothibas, S. Johnson Jeyakumar, C. Manoharan, I. Kartharinal Punithavathy, P. Praveen and J. Prince Richard, J. Mater. Sci.: Mater. Electron., 2017, 28, 1889–1894.
7. J. Pan, X. Shao, X. Xu, J. Zhong, J. Hu and L. Ma, J. Phys. Chem. C, 2020, 124, 6580–6587.
8. D. Bhanderi, P. Lakhani and C. K. Modi, RSC Sustainability, 2024, 2, 265–287.
9. P. Gomez-Romero, A. Pokhriyal, D. Rueda-García, L. N. Bengoa and R. M. González-Gil, Chem. Mater., 2023, 36, 8–27.
10. V. Kumar, G. Prasad Singh, M. Kumar, A. Kumar, P. Singh, A. K. Ansu, A. Sharma, T. Alam, A. S. Yadav and D. Dobrotă, ACS Omega, 2024, 9, 6147–6164.
11. W. Xu, R. Wang, B. Zheng, X. Wu and H. Xu, J. Phys. Chem. Lett., 2019, 10, 6061–6066.
12. P. Ganguly, S. Mathew, L. Clarizia, S. Kumar R, A. Akande, S. J. Hinder, A. Breen and S. C. Pillai, ACS Omega, 2019, 5, 406–421.
13. M. M. Khan and A. Rahman, Catalysts, 2022, 12, 1338.
14. M. A. Susner, M. Chyasnavichyus, M. A. McGuire, P. Ganesh and P. Maksymovych, Adv. Mater., 2017, 29, 1602852.
15. F. Wang, T. A. Shifa, P. Yu, P. He, Y. Liu, F. Wang, Z. Wang, X. Zhan, X. Lou and F. Xia, et al., Adv. Funct. Mater., 2018, 28, 1802151.
16. R. Samal, G. Sanyal, B. Chakraborty and C. S. Rout, J. Mater. Chem. A, 2021, 9, 2560–2591.
17. Y. Dedkov, M. Yan and E. Voloshina, Chem. Phys. Lett., 2020, 754, 137627.
18. Z. Cheng, T. A. Shifa, F. Wang, Y. Gao, P. He, K. Zhang, C. Jiang, Q. Liu and J. He, Adv. Mater., 2018, 30, 1707433.
19. V. Kumar, K. Rajput and D. R. Roy, Carbon, 2021, 172, 791–803.
20. M. Naseri, D. R. Salahub, T. V. Vu and H. Zakaryae, J. Mater. Chem. C, 2022, 10, 11412–11423.
21. A. Jalil, S. Z. Ilyas, S. Agathopoulos, A. Qureshi, I. Ahmed and T. Zhao, Appl. Surf. Sci., 2021, 565, 150588.
22. P. D. Trung and H. D. Tong, RSC Adv., 2024, 14, 15979–15986.
23. A.-Y. Lu, H. Zhu, J. Xiao, C.-P. Chuu, Y. Han, M.-H. Chiu, C.-C. Cheng, C.-W. Yang, K.-H. Wei and Y. Yang, et al., Nat. Nanotechnol., 2017, 12, 744–749.
24. Z. Feng, Y. Huang, S. Lin, H. Yuan and H. Chen, J. Chem. Phys., 2023, 159, 044115.
25. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni and I. Dabo, J. Phys.:Condens. Matter, 2009, 21, 395502.
26. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
27. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215.
28. G. Kresse and D. Joubert, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 59, 1758.
29. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
30. A. Togo, L. Chaput and I. Tanaka, Phys. Rev. B:Condens. Matter Mater. Phys., 2015, 91, 094306.
31. J. Bardeen and W. Shockley, Phys. Rev., 1950, 80, 72.
32. T. V. Vu, A. Kartamyshev, M. D. Nguyen, K. D. Pham, T. T. Trinh, N. P. Nhuan and N. D. Hien, Mater. Sci. Semicond. Process., 2024, 181, 108590.
33. F. A. Rasmussen and K. S. Thygesen, J. Phys. Chem. C, 2015, 119, 13169–13183.
34. I. Khan and J. Hong, Nanotechnology, 2020, 31, 195704.
35. M. K. Mohanta and A. De Sarkar, ACS Appl. Mater. Interfaces, 2020, 12, 18123–18137.
36. Y. Guo, S. Zhou, Y. Bai and J. Zhao, Appl. Phys. Lett., 2017, 110, 163102.
37. M. Born and K. Huang, Dynamical Theory of Crystal Lattices, Oxford University Press, 1996.
38. E. Cadelano, P. L. Palla, S. Giordano and L. Colombo, Phys. Rev. B:Condens. Matter Mater. Phys., 2010, 82, 235414.
39. J. Guo, R. Peng, X. Zhang, Z. Xin, E. Wang, Y. Wu, C. Li, S. Fan, R. Shi and K. Liu, Small, 2023, 19, 2300766.
40. P. V. Sarma, R. Nadarajan, R. Kumar, R. M. Patinharayil, N. Biju, S. Narayanan, G. Gao, C. S. Tiwary, M. Thalakulam and R. N. Kini, et al., 2D Mater., 2022, 9, 045004.
41. L.-C. Zhang, G. Qin, W.-Z. Fang, H.-J. Cui, Q.-R. Zheng, Q.-B. Yan and G. Su, Sci. Rep., 2016, 6, 19830.
42. L. Guo, H. Yan, Q. Moore, M. Buettner, J. Song, L. Li, P. T. Araujo and H.-T. Wang, Nanoscale, 2015, 7, 11915–11921.
43. J. Tao, W. Shen, S. Wu, L. Liu, Z. Feng, C. Wang, C. Hu, P. Yao, H. Zhang and W. Pang, et al., ACS Nano, 2015, 9, 11362–11370.
44. A. Falin, Q. Cai, E. J. Santos, D. Scullion, D. Qian, R. Zhang, Z. Yang, S. Huang, K. Watanabe and T. Taniguchi, et al., Nat. Commun., 2017, 8, 15815.
45. J. W. Christopher, M. Vutukuru, D. Lloyd, J. S. Bunch, B. B. Goldberg, D. J. Bishop and A. K. Swan, J. Microelectromech. Syst., 2019, 28, 254–263.
46. L. Yu, Q. Yan and A. Ruzsinszky, Nat. Commun., 2017, 8, 1–8.
47. H. Yi, P. Solís-Fernández, H. Hibino and H. Ago, Nanoscale Adv., 2022, 4, 3786–3792.
48. B. Dong, Z. Wang, N. T. Hung, A. R. Oganov, T. Yang, R. Saito and Z. Zhang, Phys. Rev. Mater., 2019, 3, 013405.
49. L. Zhang, Y. Zhao, Y. Liu and G. Gao, Nanoscale, 2023, 15, 18910–18919.
50. L. Zhang, Y. Liu, M. Wu and G. Gao, Adv. Funct. Mater., 2024, 2417857.
51. A. K. Geim and I. V. Grigorieva, Nature, 2013, 499, 419–425.
52. M. Sledzinska, G. Jumbert, M. Placidi, A. Arrighi, P. Xiao, F. Alzina and C. M. Sotomayor Torres, ACS Appl. Electron. Mater., 2020, 2, 1169–1175.
53. A. K. Katiyar, A. T. Hoang, D. Xu, J. Hong, B. J. Kim, S. Ji and J.-H. Ahn, Chem. Rev., 2023, 124, 318–419.
54. L. Yang, Q. Fu, W. Wang, J. Huang, J. Huang, J. Zhang and B. Xiang, Nanoscale, 2015, 7, 10490–10497.
55. C. Gao, X. Yang, M. Jiang, L. Chen, Z. Chen and C. V. Singh, Phys. Chem. Chem. Phys., 2022, 24, 4653–4665.
56. G. Wei, D. A. Czaplewski, E. J. Lenferink, T. K. Stanev, I. W. Jung and N. P. Stern, Sci. Rep., 2017, 7, 3324.
57. F. Zhou, Y. Liu, Z. Lai, M. Liao, Y. Zhou, Y. Huang and J. Zhu, RSC Adv., 2018, 8, 20477–20482.
58. A. Fujishima and K. Honda, Nature, 1972, 238, 37–38.
59. M. K. Mohanta and P. Jena, J. Mater. Chem. C, 2024, 12, 1888–1896.
60. D. Er, H. Ye, N. C. Frey, H. Kumar, J. Lou and V. B. Shenoy, Nano Lett., 2018, 18, 3943–3949.
61. M. C. Toroker, D. K. Kanan, N. Alidoust, L. Y. Isseroff, P. Liao and E. A. Carter, Phys. Chem. Chem. Phys., 2011, 13, 16644–16654.
62. Q.-W. He, J.-H. Wang, D.-Y. Zhu, D.-S. Tang, Z. Lv, F. Guo and X.-C. Wang, Nano Lett., 2024, 24, 8979–8987.
63. Z. Wang and G. Zhou, J. Phys. Chem. C, 2019, 124, 167–174.
64. S. Singh, P. Anees, S. Chandra and T. K. Ghanty, J. Phys. Chem. C, 2022, 126, 8436–8449.
65. Z. Liu, B. Wang and C. Cazorla, ACS Sustain. Chem. Eng., 2022, 10, 16924–16934.
66. X.-H. Li, B.-J. Wang, X.-L. Cai, W.-Y. Yu, L.-W. Zhang, G.-D. Wang and S.-H. Ke, RSC Adv., 2017, 7, 44394–44400.
67. L. Ju, J. Shang, X. Tang and L. Kou, J. Am. Chem. Soc., 2019, 142, 1492–1500.
68. N. Vonrüti and U. Aschauer, Phys. Rev. Mater., 2018, 2, 105401.
69. M. Pandey, C. Pandey, R. Ahuja and R. Kumar, Nano Energy, 2023, 109, 108278.
70. L.-B. Shi, S. Cao and M. Yang, Phys. E, 2019, 107, 124–130.
71. R. Roldán, A. Castellanos-Gomez, E. Cappelluti and F. Guinea, J. Phys.: Condens. Matter, 2015, 27, 313201.
72. Y. Jiao, F. Ma, G. Gao, J. Bell, T. Frauenheim and A. Du, J. Phys. Chem. Lett., 2015, 6, 2682–2687.
73. X. Zhang, X. Zhang, P. M. Ajayan, J. Wen and H. D. Espinosa, Small, 2022, 18, 2105194.
74. E. Blundo, E. Cappelluti, M. Felici, G. Pettinari and A. Polimeni, Appl. Phys. Rev., 2021, 8, 021318.
75. X. Peng, Q. Wei and A. Copple, Phys. Rev. B:Condens. Matter Mater. Phys., 2014, 90, 085402.
76. D. D. Vo, T. V. Vu, A. Kartamyshev, T. H. Ho and N. N. Hieu, Nanoscale Adv., 2024, 6, 6019–6028.
77. J. K. Nørskov, T. Bligaard, A. Logadottir, J. Kitchin, J. G. Chen, S. Pandelov and U. Stimming, J. Electrochem. Soc., 2005, 152, J23.
78. C. Quan, S. Ji, R. Yao, W. Liu, J. Yang and X. Li, Int. J. Hydrogen Energy, 2024, 56, 1227–1234.
79. T. V. Vu, N. N. Hieu, D. D. Vo, A. Kartamyshev, H. D. Tong, T. T. Trinh, V. Khuong Dien, Z. Haman, P. Dey and N. Khossossi, J. Phys. Chem. C, 2024, 128, 4245–4257.
80. L. Ju, M. Bie, X. Tang, J. Shang and L. Kou, ACS Appl. Mater. Interfaces, 2020, 12, 29335–29343.
81. Y. Sun, A. Huang and Z. Wang, RSC Adv., 2019, 9, 26321–26326.
82. Q. Cai, W. Hong, C. Jian, X. He and W. Liu, Adv. Energy Sustainability Res., 2023, 4, 2200178.
83. D. W. Boukhvalov, S. Nappini, M. Vorokhta, T. O. Menteş, L. Piliai, M. Panahi, F. Genuzio, J. De Santis, C.-N. Kuo and C. S. Lue, et al., Adv. Funct. Mater., 2021, 31, 2106228.
84. Y. Chen, X. Fu and Z. Peng, Metals, 2023, 13, 1163.
85. L. M. Herz, ACS Energy Lett., 2017, 2, 1539–1548.
86. D. Shi, V. Adinolfi, R. Comin, M. Yuan, E. Alarousu, A. Buin, Y. Chen, S. Hoogland, A. Rothenberger and K. Katsiev, et al., Science, 2015, 347, 519–522.
87. Y. Cai, G. Zhang and Y.-W. Zhang, J. Am. Chem. Soc., 2014, 136, 6269–6275.
88. Y. Wang, Y. Li and Z. Chen, J. Mater. Chem. C, 2015, 3, 9603–9608.
89. C. Long, Y. Liang, H. Jin, B. Huang and Y. Dai, ACS Appl. Energy Mater., 2018, 2, 513–520.
90. Y. Jing, Z. Zhou, J. Zhang, C. Huang, Y. Li and F. Wang, Phys. Chem. Chem. Phys., 2019, 21, 21064–21069.
91. X. Liu, Z. Zhang, Z. Ding, B. Lv, Z. Luo, J.-S. Wang and Z. Gao, Appl. Surf. Sci., 2021, 542, 148665.
92. X. Liu, W. Kang, J. Zhao, Y. Wang, W. Wang, L. Wang, L. Fang, Q. Chen and M. Zhou, Phys. Status Solidi RRL, 2022, 16, 2100417.
93. P. Jamdagni, A. Kumar, S. Srivastava, R. Pandey and K. Tankeshwar, Phys. Chem. Chem. Phys., 2022, 24, 22289–22297.
94. K. Chaoui, W. Elaggoune and K. Zanat, Int. J. Hydrogen Energy, 2024, 91, 1221–1231.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ra00812c

---