Neutron, X-ray diffraction, DSC, Raman, Mössbauer and leaching studies of iron phosphate glasses and crystalline phases

Abstract

xFe₂O₃–(100 − x)P₂O₅ glasses were synthesized by melt quenching and structure–property correlation studies were carried. Glasses containing 25 to 40 mol% Fe₂O₃ were prepared while the sample with 50 mol% Fe₂O₃ formed a crystalline sample containing Fe₃²⁺Fe₄³⁺[PO₄]₆³⁻ and Fe₂²⁺[P₂O₇]⁴⁻ phases on melt-quenching. Glass density increases from 2.98 to 3.20 g cm⁻³, ionic packing fraction is in the range of 0.63–0.65 and the glass transition temperature decreases from 500 °C to 493 °C on increasing Fe₂O₃ concentration from 25 to 40 mol%. Pair distribution function analysis and Reverse Monte Carlo simulations of neutron diffraction datasets were used to calculate the atomic pair distributions, interatomic distances and co-ordination environments. The P–O co-ordination is essentially tetrahedral and is in the range: 3.9–3.7 (±0.1), the Fe–O co-ordination number decreases steadily from 4.8 to 4.2 (±0.1) with an increase in Fe₂O₃ concentration in the phosphate network, while O–O co-ordination is in the range: 6.6–6.3(±0.1), the decrease in these co-ordination numbers are due to an increase in oxygen deficiency in the glass network with an increase in Fe₂O₃ mol%. Fe–O and P–O pair distributions are asymmetrical indicating short-range disorder due to the existence of a wide range of bond-lengths with maxima at 1.79 Å and in the range: 1.45–1.51 Å respectively. Mössbauer studies carried out at room temperature and 80 K found that Fe exists in 2+ and 3+ valence states, and the glass and crystalline samples contained Fe²⁺ at least at three different sites. Raman studies found that the meta and pyrophosphate structural units are dominant species up to 35 mol% Fe₂O₃ concentration, while the orthophosphate units are in majority at 40 mol% of Fe₂O₃. The crystalline sample is a two phase material and contained both orthophosphate and pyrophosphate units with the former being the dominant species. Leaching studies on two iron phosphate glasses carried out in purified water at 90 °C found that dissolution of glasses decreases and the chemical durability increases drastically with an increase in Fe₂O₃ mol%.

---

1. Introduction

Nuclear waste management is an end stage of the nuclear fuel cycle and it is important to find matrices or materials that can be used to incorporate and immobilize high level radioactive waste.^1,2 Borosilicate glasses have been widely used for high-level nuclear waste immobilization.^3–6 However, the high-level waste containing halide and Mo ions, P and noble metal atoms are only sparingly soluble in borosilicate glasses, and this limits the waste loading, and increases the cost and time of vitrification.⁷ Iron phosphate and lead iron phosphate glasses are functional materials that are considered to be economical alternatives to borosilicate glasses for nuclear waste immobilization,^8–12 because these are good solvents for heavy metal ions and possess excellent leaching resistance in acidic and neutral medium.¹³ Moreover, the addition of MoO₃ enhances the thermal stability and water durability of iron phosphate glasses.¹⁴ The iron phosphate glasses are chemically more durable than alkali and alkaline-earth phosphate glasses due to the existence of Fe–O–P linkages, the Fe²⁺/Fe³⁺ in the phosphate glass network strengthens the cross-linking between the polyphosphate chains and enhances the chemical and thermal durability of glasses.^15,16 The open structure and voids in iron phosphate glass network promotes the incorporation of large concentration of actinides and nuclear waste.¹⁷

The basic building blocks of the glassy and crystalline phosphates are the P–O tetrahedral structural units that are connected by covalently bonded oxygens and that form various phosphate anions. The tetrahedra are categorized using the Qⁱ terminology where i represents the number of bridging oxygens per tetrahedron. The three phosphate polyhedral units are: Q⁰, Q¹ and Q² respectively.¹⁸ The number of tetrahedral linkages through bridging oxygens between neighbouring P-tetrahedra can be classified by the oxygen to-phosphorus (O/P) ratio. Glass systems with O/P = 4, 3.5 and 3 are represented as Q⁰, Q¹ and Q² polyhedra and termed as orthophosphate, pyrophosphate and metaphosphate units respectively. The metaphosphates possess long chains of P-tetrahedra linked through two bridging oxygens, the pyrophosphates with single bridging oxygen terminates these chains and forms (P₂O₇)⁴⁻ anions while the orthophosphates without any bridging oxygens are similar to isolated phosphate groups that exist in the crystalline phosphate compounds.^18–20

The chemical durability of phosphate glasses can be enhanced considerably by adding Al₂O₃ and Fe₂O₃ in the glass network; the addition of these metal oxides replaces the easily hydrated –P–O–P– bonds by more hydrate resistant –M–O–P– bonds, where M are the metal cations.^15,16 The glass formation range of xFe₂O₃–(100 − x)P₂O₅ system is reported to be 10 to 45 mol% of Fe₂O₃.²¹ The 40Fe₂O₃–60P₂O₅ glass is reported to exhibit the best chemical durability or lowest leaching rate among all the iron phosphate glasses,^22–26 leaching is an important property of glasses/matrices that needs to be evaluated for their application in nuclear waste immobilization.

As the concentration of Fe₂O₃ increases in the phosphate network, the number of Fe–O–P linkages increases at the expense of P–O–P bonds and, the chain-like metaphosphate network breaks into dimeric pyrophosphate and finally into isolated orthophosphate groups.^19,20 Iron phosphate glasses are reported to contain both Fe²⁺ and Fe³⁺ in the network, and the valence state of Fe is reported to depend on the use of either FeO or Fe₂O₃ as starting material in the synthesis of iron phosphate glasses.²¹ Molecular dynamics (MD) studies using Buckingham potential were carried out on both xFeO–(100 − x)P₂O₅ and xFe₂O₃–(100 − x)P₂O₅ glass systems, and Fe–O, P–O and O–O atomic pair correlations were determined.²⁷ The experimental studies in which iron phosphate glasses were synthesized by melt-quenching have also reported large effects of melting temperature and melting time on relative concentration of Fe²⁺ and Fe³⁺ in the structure,¹⁹ however several of these experimental results can be erroneous as the investigators employed alumina or silica crucibles instead of more durable platinum crucibles for the synthesis of glasses.^19,21,28,29 It is well established that alumina and silica crucibles can introduce significant concentration of Al³⁺ and Si⁴⁺ impurities in the oxide glass melt and give rise to the impurity Al–O and Si–O peaks in the total pair correlation functions and consequently give incorrect results on Fe–O and P–O co-ordination numbers and bond lengths since the Fe–O and P–O peaks exist at almost the same positions as Al–O and Si–O peaks respectively.

It is therefore important that iron phosphate glasses are prepared by melting the batch materials in more durable platinum crucible for the accurate determination of glass structure and properties. In the present study series of iron phosphate glasses were prepared by melting the starting materials in platinum crucibles and subsequently characterized by density measurements, X-ray diffraction, differential scanning calorimetry (DSC), Raman and Mössbauer spectroscopy, neutron diffraction, pair distribution function and Reverse Monte Carlo (RMC) simulations and leaching tests. The RMC analysis was used to calculate the partial atomic pair distributions, the cation–oxygen bond lengths and Fe–O and P–O co-ordination numbers; RMC simulations give accurate and reliable values of glass short-range structural properties since it does not suffer from the disadvantages of overlapping atomic pair correlation peaks in the total pair distribution function,^30–34 that are difficult to deconvolute unambiguously when different atomic pairs exist at same or very similar distances. The chemical durability of two iron phosphate glasses were studied by measuring their leaching characteristics in MQ water at 90 °C for a period of 10 days.

2. Experimental

2.1 Glass synthesis

Disk shaped samples of the system: xFe₂O₃–(100 − x)P₂O₅ (x = 25, 30, 35, 40 and 50 mol%) were prepared by the melt-quenching (hereafter referred as 25FeP, 30FeP, 35FeP, 40FeP and 50FeP respectively). The starting materials for glass preparation were Fe₂O₃ (Aldrich India, 99%) and NH₆PO₄ (99%, Otto Kemi, India). The net weight of the batch mixture for all the samples was about 10 g. Appropriate amounts of materials were weighed and ground in an agate mortar-pestle for about 30 min. The batch mixture was then transferred into a platinum crucible. It was first heated in an electric furnace at 200 °C for 1 h and subsequently the temperature of the furnace was slowly increased to 550 °C to remove the residual gases (NH₃ and H₂O). The material was kept at this temperature for ∼1 h. Afterwards, the mixture was melted in another furnace and heated to 1300 °C, the melt was kept at this temperature for 1 h. The melt was then poured onto a brass block to get the final disk-shaped glass samples. All the glass samples were shining black in color. Samples upto 40 mol% Fe₂O₃ formed glasses, however the sample with 50 mol% Fe₂O₃ in the starting batch mixture did not produce a glass but solidified into a crystalline material on melt-quenching as confirmed by X-ray and neutron diffraction studies discussed below.

2.2 Density measurements

The density, ρ of the disk-shaped glasses was measured by the Archimedes method using dibutylphatalate (DBP) as the immersion fluid on an electronic balance of sensitivity 10⁻⁴ g at laboratory temperature by using the following relation:where ρ_L is the density of the DBP oil at the laboratory temperature, w_A and w_L are the weight of the glass sample in air and the liquid, respectively. The maximum error in density was in the range of ± 0.01 to 0.07 g cm⁻³. The density values were used to calculate molar volume, (where x_i is the mol% of ith component and M_i is its molecular weight). The packing fraction, PF, of glasses is the ratio of ionic volume to molar volume and calculated by using the following formula:³⁵where x_i and r_i are mole fraction and the ionic radius of the ith ion in one formula unit of glass sample. The values of ionic radii were taken as: r_Fe³⁺ = 0.55 Å, r_O²⁻ = 1.40 Å and r_P⁵⁺ = 0.38 Å.³⁶

2.3 X-ray diffraction experiments

X-ray diffraction (XRD) studies were carried out on powdered samples on Bruker D8 Focus XRD system with Cu K_α1,2 radiation in the 2θ range of 10–90°. The X-ray tube was operated at 40 kV and 30 mA and the scattered X-ray intensity was measured with a scintillation detector using step size of 0.02° and scan rate of 0.5° per min.

2.4 Differential scanning calorimetry

The thermal parameters such as glass transition temperature, T_g, crystallization temperature, T_c and the melting temperature, T_m were determined on SETARAM Labsys Evo DSC system. About 50 mg powder sample was taken in a platinum pan and the differential heat flow scan was recorded at a heating rate of 10 °C min⁻¹ in the temperature range of 200–1200 °C under argon flow conditions (10 ml min⁻¹). The glass transition temperature was taken as the mid-point value. The peak values of exothermic crystallization and endothermic melting peaks were taken as the crystallization and melting temperatures respectively. The maximum uncertainty in the measurement of T_g, T_c and T_m is ± 1 °C.

2.5 Raman spectroscopy

Raman scattering studies were performed at room temperature on the iron phosphate samples on Renishaw In-Via Reflex micro-Raman spectrometer in the Raman shift range of 30–1500 cm⁻¹ at a spectral resolution of 0.5 cm⁻¹. The Stokes spectra were recorded by using a 514.5 nm argon-ion excitation laser, an edge filter, diffraction grating with 2400 lines per mm and a CCD detector.

2.6 Neutron diffraction experiments

The neutron diffraction studies were carried out on powdered iron phosphate samples at the 2-axis Position Sensitive Detector (PSD) diffractometer, of Budapest Neutron Centre (BNC), Hungary, using monochromatic thermal neutrons of de Broglie wavelength, λ = 1.069 Å in the scattering vector or momentum transfer function (Q) range of 0.45 to 9.8 Å⁻¹. The pulverized samples of mass 4 to 5 g were placed in thin-walled cylindrical vanadium can of diameter of 8 mm and the diffraction data was recorded for 24 h each. The raw neutron diffraction data of four glass samples was corrected for background, absorption and multiple scattering and normalized with vanadium rod standard. The structure factors, S(Q)'s were calculated from the raw diffraction data using the programme package available at the BNC facility.

2.7 Pair distribution function (PDF) by Fourier transformation

The atomic pair distribution function, g(r) of each sample was calculated by the Fourier sine transformation of the neutron interference function amplified with Q i.e. F(Q)= Q(S(Q) − 1) by using the following formula:^30–34where, ρ_o is the atomic number density of the sample and M(Q) is the Lorch modification function defined as below:
and
Q_max was selected around 9.8 Å⁻¹ for calculating g(r) by (3).

2.8 Reverse Monte Carlo (RMC) simulations

The experimental neutron structure factors, S(Q) were simulated by the RMC technique using the RMC++ Version 1.5.1 software package.^37–40 During the RMC simulation runs, the partial structure factors, S_ij(Q) were calculated from the pair distribution functions g_ij(r) by Fourier transformation. If k is the total number of elements in the sample (k = 3 in the present glass system), then k(k + 1)/2 = 6 different atom pairs exist in its glass structure. The RMC technique minimizes the squared difference between the experimental S(Q) and the simulated one from a 3-dimensional atomic configuration by using the following equationswhere c_i, b_i are the molar fraction and coherent neutron scattering length for atoms of type i, the S_ij(Q) is the partial structure factors and w_ij are the neutron scattering weight factors for the 6 atomic pairs: Fe–Fe, Fe–P, Fe–O, P–P, P–O and O–O of the glass system. g_ij(r) are the partial pair correlation functions for the above mentioned 6 atomic pairs and these give the measure of the probability of finding the jth atom at a distance, r from the ith atom.

The RMC simulations were started by building an initial random atomic configuration in a simulation box that was populated with 10 000 atoms of Fe, P and O. The atomic number densities, ρ_o were 0.0799, 0.0818, 0.0813 and 0.0802 atoms per Å⁻³ (corresponding to box edges of 26.79, 24.81, 24.86 and 24.97 Å) for the glass samples 25FeP, 30FeP, 35FeP and 40FeP respectively. The atoms inside the box were constrained to move apart by certain minimum interatomic distances (cut-off distances) that were provided in the RMC input program. No other constraints (such as Fe–O or P–O co-ordination constraints) were imposed on the atomic pairs during the RMC simulations. Repeated RMC runs were performed by varying the cut-off distances slightly, to produce reliable data with good stability and statistics. About 20 atomic configurations were obtained from the RMC calculations of each sample corresponding to more than 1 100 000 accepted atomic displacements inside the simulation box. After multiple runs, the experimental and the RMC simulated structure factor, S(Q) matched well and the atomic pair-correlation functions, g_ij(r), coordination number distributions, N_ij, and bond angle distribution were calculated from the RMC simulated data.

2.9 Mössbauer spectroscopy

⁵⁷Fe Mössbauer spectra were recorded at room temperature (298–300 K) in transmission geometry by using a standard WissEl Mössbauer spectrometer setup along with a ⁵⁷Co(Rh) radioactive source with an activity of ∼2.2 mCi. The source movement followed a sinusoidal velocity signal. Unfolded spectra were recorded in 2048 channels and were subsequently folded into 1024 channels for analysis. Isomer shift (δ) values are quoted with respect to that of α-Fe at room temperature. Circular absorbers were prepared with a diameter of 15.5 mm by using sample amounts that were expected to result in comparable (∼12 mg cm⁻²) Fe surface densities of the resulting samples based on the nominal sample stoichiometries. The powdered samples were in addition mixed in each case with 200 mg of cellulose in order to achieve a uniform absorber surface density. For the low temperature (T ≈ 80 K) measurements the samples were kept in a bath type cryostat (SVT-400-MOSS, Janis, Woburn, MA, USA) filled with liquid nitrogen, while the spectrometer operated with a triangular velocity waveform, in constant acceleration mode, recording spectra in 512 channels before folding. Unless explicitly noted otherwise, the resulting spectra were fitted to symmetrical quadrupole doublets by using version 4.0i of the MossWinn program.⁴¹

2.10 Leaching tests

The chemical durability of the two disk shaped bulk glass samples: 30FeP (weight = 1.772 g) and 40FeP (1.919 g) and the chemical evolution of the leaching solution in water purified with Millipore Milli-Q lab water system (Merck, USA). This purified water is referred to as MQ-water in the manuscript.

MQ-water at 90 ± 1 °C were analyzed by calculating the normalized release and glass dissolution rate of P and Fe using the equations specified in the ASTM C1285-21 protocol.⁴² The procedure used for the leaching analysis is described elsewhere⁴³ and leaching tests were carried over a total period of 10 days. After 1, 2, 3, 7, and 10 days, the containers were opened, and the leachates were filtered through a 0.45 μm syringe filter. Subsequently, the leachates were acidified with cc. HNO₃ for inductively coupled plasma optical emission spectroscopy (ICP-OES) measurements to measure the concentration of P and Fe concentration (in the units of mg l⁻¹) that leached out in MQ-water using a PerkinElmer Avio 200 ICP-OES apparatus.⁴³

3. Results and discussion

3.1 X-ray diffraction (XRD)

The XRD patterns of all iron phosphate samples are shown in Fig. 1 and it is found that samples containing 25, 30, 35 and 40 mol% of Fe₂O₃ show only broad humps in the 2θ range of 15° to 35°, which confirmed their amorphous nature.

Fig. 1 XRD patterns of iron phosphate samples. The sharp peaks in the sample 50FeP are due to the coexisting Fe₇(PO₄)₆ (#) and Fe₂P₂O₇ ($) crystalline phases.

The sample: 50FeP prepared using 50 mol% Fe₂O₃ in the batch mixture, shows several sharp peaks; this sample is crystalline and its XRD peaks match with those of Fe(II)₃Fe(III)₄[PO₄]₆ and Fe(II)₂[P₂O₇] phases both of which possess triclinic crystal structure (powder diffraction files # 72-2446 and 76-1762 respectively).

3.2 Density, molar volume and packing fraction

The density data of the iron phosphate samples prepared with 25, 30, 35, 40 and 50 mol% Fe₂O₃ is given in Table 1. Density increases from 2.98 g cm⁻³ to 3.59 ± 0.05 g cm⁻³ as the concentration of Fe₂O₃ is increased from 25 to 50 mol%, it may be noted that sample prepared with 50 mol% Fe₂O₃ in the starting batch mixture, is not a glass but is crystalline.

Table 1 Composition, mass density, molar volume, packing fraction and atomic number densities of iron phosphate glasses (25FeP–40FeP) and crystalline sample (50FeP)

Sample code	Composition [mol%]		Density, ρ [g cm^−3]	Molar mass (amu)	Molar volume VM [cm^3 mol^−1]	Packing fraction (PF)	Atomic number density ρo [Å^−3]
	Fe2O3	P2O5
25FeP	25	75	2.98	146.38	49.1	0.64	0.0799
30FeP	30	70	3.13	147.26	47.0	0.65	0.0818
35FeP	35	65	3.18	148.15	46.6	0.64	0.0813
40FeP	40	60	3.20	149.04	46.5	0.63	0.0802
50FeP	50	50	3.59	150.82	42.0	0.67	0.0861

---

The molar masses of Fe₂O₃ and P₂O₅ are 159.6 u and 141.9 u respectively; therefore, the replacement of lighter P₂O₅ by the heavier Fe₂O₃ molecules in the glass network produces a steady enhancement in the density. Al-Hasni et al.⁴⁴ reported density of 3.03 g cm⁻³ for the 40Fe₂O₃–60P₂O₅ glass which is lower than the density of 3.20 ± 0.05 g cm⁻³ of the glass of equal composition prepared and characterized in the present study.

The molar volume, V_M defined as the volume occupied by 1 mole of glass molecules decreases from a value of 49.1 to 42.0 cm³, on increasing Fe₂O₃ concentration from 25 to 50 mol%. V_M of iron phosphate glasses is found to be significantly higher than that of other oxide glasses such as borate and borosilicate glasses, for instance lead borate,⁴⁵ lead borosilicate,⁴⁵ lead aluminoborosilicate,⁴⁶ bismuth borate⁴⁷ and bismuth borosilicate⁴⁸ have molar volume in the range of 24.2 to 42.7 cm³, the alkali and alkaline-earth silicate and aluminosilicate glasses have lower V_M in the range of 16 to 30 cm³.⁴⁹

The PF in iron phosphate glasses is in the range of 0.63–0.65 and it shows only a small variation with an increase in Fe₂O₃ concentration from 25 to 40 mol%, both V_M and PF are important structural parameters of glasses that are used as matrices for radioactive waste immobilization. A larger V_M and a smaller value of PF indicates greater concentration of voids that can incorporate other ions in the glass structure.

3.3 Thermal properties

DSC thermographs of the 4 iron phosphate glasses and one crystalline sample are displayed on Fig. 2. The glass transition temperature, T_g decreases steadily from 500 °C to 493 °C as Fe₂O₃ concentration is increased from 25 to 40 mol% (Table 2). This is because the weaker Fe–O (E_Fe–O = 409 kJ mol⁻¹) bonds replace the significantly stronger P–O (E_P–O = 597 kJ mol⁻¹) bonds in the phosphate network,³⁶ and this lowers the glass transition temperature. The value of T_g (493 ± 1 °C) in 40Fe₂O₃–60P₂O₅ glass is in good agreement with the value of T_g of 498 ± 5 °C reported for the same glass by Al-Hasni et al.⁴⁴

Fig. 2 DSC curves of iron phosphate samples. The dotted line indicates the midpoint of glass transition. The sample 50FeP is crystalline and exhibits only endothermic liquidus peak.

Table 2 Thermal properties of iron phosphate glasses

Sample	Tg [^oC]	Tc [^oC]			Tm [^oC]		EB [kJ mol^−1]
		Tc1	Tc2	Tc3	Tm1	Tm2
25FeP	500	588	775	—	875	944	550
30FeP	491	617	812	—	884	943	540
35FeP	493	594	630	897	887	942	531
40FeP	493	587	643	899	948	990	521

---

The average single bond enthalpy, E_B in four glasses was calculated by using the following formula:⁵⁰

where x = 25, 30, 35 and 40 mol%. It is found that the E_B decreases (Table 2) with an increase in Fe₂O₃ content and this decreases T_g from 500 to 491 °C on increasing Fe₂O₃ concentration from 25 to 30 mol%, however with further increase in Fe₂O₃ content to 35 and 40 mol%, T_g again increases slightly to 493 °C. This indicates cross linking of phosphate chains by Fe³⁺ ions through non bridging oxygens of P–O tetrahedra at high Fe₂O₃ content which strengthens the glass network. The intensity of exothermic crystallization peaks increases which indicates that the crystallization tendency increases or the glass forming ability decreases with an increase in Fe₂O₃ concentration from 25 to 50 mol%. The DSC results are consistent with X-ray and neutron diffraction findings; the latter studies confirm that the sample with 50 mol% Fe₂O₃ is not a glass but is crystalline containing coexisting Fe₇(PO₄)₆ and Fe₂P₂O₇ phases, therefore its DSC scan did not exhibit glass transition or crystallization peaks but an endothermic melting peak at 1041 °C. Table 2 gives the thermal properties data of all the glass samples.

3.4 Vibrational spectra

The Raman spectra of iron phosphate samples are shown in Fig. 3. The sharp peak at low frequency of ∼65 cm⁻¹ is the boson peak which is a universal feature of the disordered materials and glasses.^51–55 This peak is not prominent in the 50FeP sample as it is crystalline and not glassy. Fig. 4 shows the Raman spectra of glassy samples; 25FeP, 30FeP, 35FeP and 40FeP deconvoluted using 11 independent Gaussian peaks in range 400–1500 cm⁻¹ using peak positions at approximately same positions as reported in the earlier study by Stoch et al.⁵⁶

Fig. 3 Raman spectra of four iron phosphate glasses and one crystalline sample.

Fig. 4 Decomposition of Raman spectrum for (a) 25FeP (b) 30FeP (c) 35FeP (d) 40FeP into Gaussian peaks.

All the peaks in the mid-frequency region below 400 cm⁻¹ are due to the bending vibration modes of Fe–O and P–O bonds.^19,20 In this frequency range, glassy samples show a broad band centred at ∼340 cm⁻¹ while the Raman spectra of 50FeP glass-ceramic sample shows several sharp peaks at 109, 132, 179, 197, 230, 246, 277, 336, 367 and 391 cm⁻¹.²⁰ In 50FeP glass ceramic sample, peaks were observed at 447 and 460 cm⁻¹ which are due to O–P–O bending modes of Q⁰ units.^19,20 The Raman band in glasses in the range of 664–823 cm⁻¹ is due to the symmetric stretching vibrations of P–O–P bonds that contain bridging oxygens. Relative intensity of this band decreases with decrease in concentration of P₂O₅. The broad band in the Raman shift range: 869–1376 cm⁻¹ in glasses is due to symmetric and asymmetric stretching vibration modes of bridging and non-bridging oxygens associated with different phosphate tetrahedra i.e., orthophosphate (Q⁰), pyrophosphate (Q¹) and metaphosphate (Q²), respectively. The shoulder at ∼950 cm⁻¹ is due to the symmetric stretching vibration of (PO₄)³⁻ anions or the orthophosphate groups. In case of 50FeP sample, two sharp peaks are observed at 950 and 971 cm⁻¹ and these are due to vibrations of orthophosphate, (PO₄)³⁻ anions. The band at 1160 cm⁻¹ is due to the asymmetric stretching vibrations of pyrophosphate, (P₂O₇)⁴⁻ units of the Q¹ groups.^19,20

In the glass samples: 25FeP, 30FeP and 35FeP, the maximum intensity is of the Raman band at 1169 cm⁻¹ and this indicates that pyrophosphate groups are the dominant short-range structural units in the glasses containing 25 to 35 mol% of Fe₂O₃, the pyrophosphate units are linked by Fe–O units.^19,20 The Raman spectra of the glass sample 40FeP shows some differences, it has peak intensity at ∼1002 cm⁻¹ instead at 1169 cm⁻¹, the crystalline sample 50FeP also shows maximum intensity at ∼1002 cm⁻¹. The peak at 1002 cm⁻¹ is due to P–O⁻ stretching vibrations of non-bridging oxygens in Q⁰ units in orthophosphate groups. Finally, the shoulder at 1293 cm⁻¹ is due to the bond vibrations of metaphosphate (PO₃)⁻ units.^19,20 The analysis of the area of the deconvoluted peaks of Raman spectra provides more information about the short-range structural transformation occurring in the iron phosphate glasses as a function of Fe₂O₃ concentration. The variation of area of the 11 peaks in the glass samples is shown in Fig. 5. It is found that the maximum area is of the peak at ∼1087 cm⁻¹ and the area of this peak decreases significantly from 48 to 24% with an increase in Fe₂O₃ concentration from 25 to 40 mol%. This peak is due to symmetric stretching P–O vibrations in Q¹-FeO₆ units. Similarly, the areas of the peak at 472 cm⁻¹ is due to bending vibrations of P–O bonds in Q¹-FeO₆ units, the area under this peak also decreases steadily. On the other hand, the area under the peaks at 1185 cm⁻¹ (symmetric stretching P–O vibrations in Q¹-FeO₅ units), 1234 cm⁻¹ (symmetric stretching P–O stretching vibrations in Q¹-FeO₄ units) and at 1293 cm⁻¹ (asymmetric stretching P–O vibrations in Q¹-FeO₄) increases steadily (Fig. 5). These results reveal that the average Fe–O co-ordination number decreases with an increase in Fe₂O₃ content, a decrease in octahedral co-ordination of Fe with O indicates that the oxidation state of Fe must be decreasing simultaneously from +3 to +2, and this is indeed confirmed from the neutron diffraction and Mössbauer studies discussed below.

Fig. 5 Area (%) vs. concentration of Fe₂O₃ (mol%).

Finally, on comparing the Raman spectra of glasses (samples 25FeP, 30FeP, 35FeP and 40FeP) with that of crystalline sample (50FeP), it is found that broad Raman bands in glasses occur at almost same positions as the sharp peaks in the crystalline sample, and hence it is concluded that the short-range structures of iron phosphate glass and crystalline samples are very similar, further the relative concentration of different short-range structural units i.e. meta, pyro and ortho units varies with an increase in Fe₂O₃ concentration.^19,20

3.5 Short-range structure by neutron diffraction PDF and RMC analysis

The neutron scattering weight factors of all the six atomic pairs of glass samples are given in the Table 3. The neutron scattering weight factors of Fe–Fe, Fe–P and P–P atomic pairs are small while that of Fe–O, P–O and O–O atomic pair correlations have significantly higher values; therefore, the coordination number were calculated for the latter three atomic pair correlations.

Table 3 Neutron diffraction weighting factors, w_ij (%) of the interatomic correlations in iron phosphate glasses

Atomic pair	Weight factors, wij (%)
	25FeP	30FeP	35FeP	40FeP
Fe–Fe	1.506	2.193	2.987	3.938
Fe–P	4.907	5.547	6.018	6.430
Fe–O	16.628	19.684	22.573	25.383
P–P	3.995	3.507	3.031	2.624
P–O	27.08	24.895	22.742	20.722
O–O	45.882	44.171	42.646	40.901

---

Fig. 6 shows the experimental neutron diffraction (S(Q) − 1) factors of 4 glass samples together with those calculated by the RMC technique. The experimental structure factors, (S(Q) − 1) of all the iron phosphate glass samples match well with the calculated structure factors. The neutron diffraction structure factor of the crystalline sample (50FeP) is shown in Fig. 7. The structure factors were used to calculate the pair distribution function, g(r) by Fourier transformation (eqn (3)) and these are displayed for all samples on Fig. 8a and b.

Fig. 6 Experimental and RMC calculated neutron structure factors (S(Q) − 1) of 4 iron phosphate glasses. Curves are displaced by 1 unit successively for clarity.

Fig. 7 Neutron structure factor, S(Q) of crystalline iron phosphate sample.

Fig. 8 Pair distribution function, g(r) of iron phosphate glasses (a) 25FeP to 40FeP and (b) crystalline sample (50FeP) calculated by Fourier transformation of S(Q) with Lorch modification function.

The first peak in g(r) of the sample 25FeP is centered at 1.58 Å, this peak shifts to higher values of 1.62–1.65 Å in the samples 30FeP, 35FeP and 40FeP and it is centered at a significantly higher position of 1.84 Å in the crystalline sample 50FeP. This peak is due to superposition of P–O and Fe–O atomic pair correlations, and shifting of its position to longer distances with an increase in Fe₂O₃ concentration is due to a rise in the relative concentration of Fe–O atomic pairs in the glass network and also due to enhancement in the relative concentration of Fe²⁺ at the expense of Fe³⁺ (as found by Mössbauer studies discussed later). It is known that Fe²⁺–O bond lengths are longer than those of Fe³⁺–O linkages.^21,28 The second peak in g(r) at ∼2.5 Å is due to O–O and P–P correlations and its intensity decreases with a decrease in the concentration of P₂O₅ in the samples. The third peak at ∼3.5 Å is due to Fe–Fe atomic pairs and its intensity grows significantly with an increase in Fe₂O₃ concentration. The pair distribution function of the sample 50FeP shows oscillations at distances, r > 6 Å due to long-range atomic order that exists in the crystalline sample (Fig. 8b). In the case of the crystalline sample 50FeP, the structure factor shows the sharp and intense peak at ∼2 Å⁻¹ (Fig. 7), the First Sharp Diffraction Peak is due to medium range order of Fe–Fe and Fe–P atomic pairs. The higher medium range ordering is manifested in g(r) of the sample 50FeP (Fig. 8b) in which the intensity of the first peak at 1.84 Å is significantly less than that of the second peak at 3.4 Å. It is therefore concluded that Fe–Fe and Fe–P atomic pairs are dominant scattering species in the crystalline sample, whereas in case of glasses, the short range structural features of P–O and Fe–O atomic pairs are the dominant scattering species (Fig. 8a).

The P–O and Fe–O pair correlations strongly overlap in g(r) distributions, however the neutron data modelling by RMC technique provided the partial atomic pair distribution functions, g_ij(r) and the coordination numbers, N_ij. The partial pair correlation functions of all the six atomic pairs i.e. g_Fe–O(r),g_Fe–P(r), g_Fe–O(r), g_P–P(r),g_P–O(r) and g_O–O(r) are displayed in Fig. 9a–c and 10a–c.

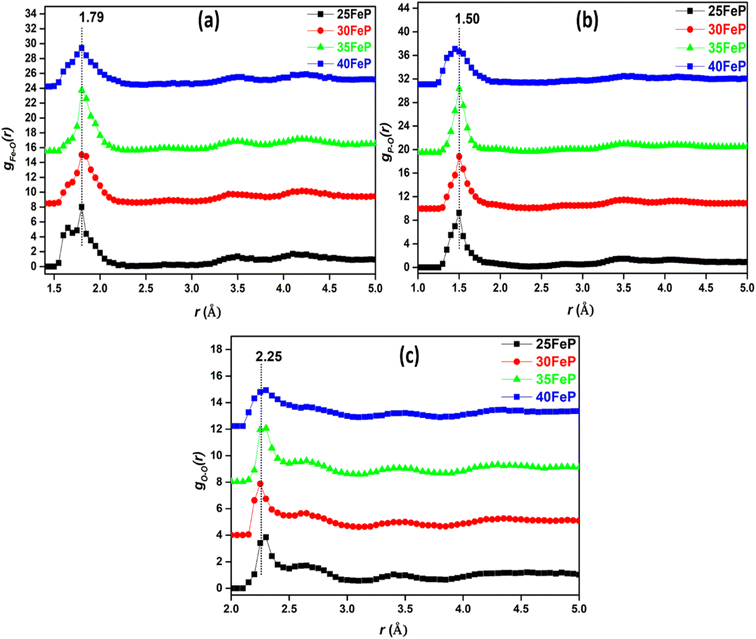Fig. 9 Partial atomic pair correlations of (a) Fe–O (g_Fe–O(r)), (b) P–O (g_P–O(r)) and (c) O–O (g_O–O(r)), in glass samples (curves are shifted successively along the y axis by 2.5 units for clarity).

Fig. 10 Partial atomic pair correlations of (a) Fe–Fe (g_Fe–Fe(r)), (b) P–P (g_P–P(r)) and (c) Fe–P (g_Fe–P(r)) in glass samples (curves are shifted successively along the y-axis by 2.5 units for clarity).

The g_Fe–O(r) has a peak at 1.79 ± 0.05 Å in 25FeP glass sample (Fig. 9a). On increasing the Fe₂O₃ concentration from 25 to 40 mol%, the peak position in Fe–O pair correlation remains constant at 1.79 Å (Fig. 9a and Table 4). It is reported that the peaks in the range of 1.80–1.87 Å are due to Fe³⁺–O bonds,^21,28 and further it is observed that the g_Fe–O is asymmetrical towards its tail end which indicates that there is significant peak due to Fe²⁺–O bonds, that are reported to show peaks at a longer distance of 2.12 Å in the iron phosphate glass network.^21,28 Zhang et al. found from titration analysis that Fe²⁺/Fe³⁺ concentration ratio in glasses increases with melting time and temperature and with an increase in Fe₂O₃ concentration,¹⁹ these investigators used alumina instead of a more durable platinum crucible for glass melting, the alumina crucibles can introduce Al³⁺ impurities in the final glasses and Al³⁺ can reduce some of Fe³⁺ into Fe²⁺ and produce erroneous results on iron phosphate glass structure and properties. The reported results of increase in Fe²⁺ concentration by Zhang et al. in iron phosphate glasses with increase in melting time and temperature can also be due to steady increase in leaching of alumina crucible by iron phosphate melt that will introduce large concentration of Al³⁺ impurities and Al–O correlations in the phosphate network that have bond lengths very close to that of Fe–O linkages.¹⁹

Table 4 Nearest neighbour atomic distances for atomic pairs in iron phosphate glasses. The maximum uncertainty is ±0.05 Å for interatomic distances

Sample code	Interatomic distances, gij(r) [Å]
	Fe–Fe	Fe–P	Fe–O	P–P	P–O	O–O
25FeP	3.50	3.08	1.79	2.70	1.50	2.29, 2.75
30FeP	3.41	3.05	1.79	2.76	1.50	2.25, 2.75
35FeP	3.45	3.13	1.79	2.74	1.50	2.29, 2.75
40FeP	3.45	3.10	1.79	2.70	1.48	2.29, 2.70

---

Hoppe et al. found from high energy X-ray diffraction studies that iron phosphate glasses prepared using FeO as a starting material (in the batch mixture) contained mostly Fe²⁺ while the glasses prepared from Fe₂O₃ contained mostly Fe³⁺ in the network, it is noteworthy that Hoppe et al. used alumina crucible for the synthesis of iron phosphate glasses.²¹ In the present study, Pt crucible, melting temperature of 1300 °C and melting time of ∼1 h has been used for glass synthesis, however large concentration of Fe²⁺ has been found in all samples (from Mössbauer studies discussed below) although Fe₂O₃ has been used as the starting material. It is therefore concluded that oxidation state of Fe in the final iron phosphate glass network doesn't seem to depend on the oxidation state of Fe in the starting materials.

The g_P–O(r) and g_O–O(r) distributions are shown in Fig. 9b and (c) respectively. The P–O partial pair correlation distributions are asymmetrical, and the most probable P–O bond length is in the range: 1.48–1.50 ± 0.05 Å in glasses. The O–O pair distribution is asymmetrical and there are at least two O–O distances of 2.27 ± 0.05 Å and 2.6 ± 0.05 Å in the phosphate network (Table 4). The Fe–Fe, Fe–P and P–P partial correlation functions are shown in Fig. 10a–c. The Fe–Fe partial pair distribution function, g_Fe–Fe(r), shows peak at 3.45 ± 0.05 Å (Fig. 10a). The P–P and Fe–P atomic pair correlation distributions shows the first peaks in the ranges: 2.70–2.90 ± 0.05 Å and 3.10–3.30 ± 0.05 Å, respectively. Within the sample series, the shape of the atomic pair distributions are quite similar to each other.

The cation-oxygen co-ordination numbers were calculated from the g_ij(r) plots and the corresponding r_min and r_max values that were used to calculate co-ordination number data are given in Table 5. The average co-ordination number of iron with oxygen (N_Fe–O) is 4.8 ± 0.1 in the 25FeP sample, it decreases steadily to a value of 4.2 in the glass sample 40FeP (Fig. 11a). Earlier Stoch et al.²⁸ found from ab initio simulations studies on 40Fe₂O₃–60P₂O₅ glass that the short-range structure of this glass is very similar to that of crystalline FePO₄ and basic building blocks are tetrahedral FeO₄ and PO₄ units.

Table 5 Co-ordination numbers in iron phosphate glasses. The values of r_min and r_max used to calculate the coordination numbers in glasses are given in brackets

Sample code	Co-ordination number, Nij (±0.1)
	Fe–O	P–O	O–O
25FeP	4.8 (1.30–2.40)	3.8 (1.30–2.35)	6.6 (2.10–3.10)
30FeP	4.6 (1.40–2.35)	3.9 (1.20–2.30)	6.5 (2.00–3.10)
35FeP	4.3 (1.40–2.35)	3.8 (1.30–2.35)	6.4 (2.10–3.10)
40FeP	4.2 (1.40–2.35)	3.7 (1.30–2.35)	6.3 (2.00–3.10)

---

Fig. 11 (a) Fe–O (b) P–O and (c) O–O co-ordination distributions in iron phosphate glasses.

The P–O coordination (N_P–O) is in the range of 3.8–3.7(±0.1) (Fig. 11b), therefore it is concluded that the P is essentially tetrahedrally co-ordinated with oxygens in the iron phosphate network. Finally, in case of O–O correlations, the average coordination number (Fig. 11c) is found to be in the range of 6.6–6.3 (±0.1). A steady decrease in Fe–O co-ordination number with an increase in Fe₂O₃ mol% is due to increasing oxygen deficiency in the glass network which also slightly lowers the P–O and O–O co-ordination numbers.

3.6 Fe oxidation states

The ⁵⁷Fe Mössbauer spectra of the four glass samples (i.e. those with x = 25, 30, 35, 40) recorded at room temperature are displayed on Fig. 12. The spectra allowed us to distinguish one Fe³⁺ along with three different main Fe²⁺ iron microenvironments, each contributing to the spectra with a distinct quadrupole doublet component. The spectral shape indicates that the individual absorption peaks belonging to the doublet components are subject to non-Lorentzian broadening. This is due to a distribution in the isomer shift (δ) and/or in the quadrupole splitting (Δ) Mössbauer parameters, reflecting the presence of a high number of slightly different iron microenvironments associated with the different Fe²⁺ and Fe³⁺ species, which is indeed a typical trait of glasses. The spectra were fitted successfully with Voigt-based fitting⁵⁷ by assuming a Gaussian distribution to be present only in the quadrupole splitting values of the doublets, except in the case of component Fe²⁺(C) (Fig. 12), for which the peaks' profile was better modelled by pure Lorentzian broadening. The Mössbauer parameters obtained from the fits are listed in Table 6.

Fig. 12 Room temperature ⁵⁷Fe Mössbauer spectra (dots) of amorphous 25FeP, 30FeP, 35FeP and 40FeP samples, along with their fit envelope and decomposition of the resonant absorption peaks into subcomponents (solid line). For the sample 25FeP the subcomponents are shifted upwards for clarity. The fit residual is shown below the spectra. See Table 6 for the associated fit parameter values.

Table 6 Room temperature ⁵⁷Fe Mössbauer parameters of xFe₂O₃·(100 − x)P₂O₅ (x = 25, 30, 35 and 40) glass samples obtained by fitting the spectra to four quadrupole doublets with a possible Gaussian distribution in the quadrupole splitting parameters being taken into account via Voigt-based fitting.⁵⁷ Numbers between parentheses denote the statistical error (1σ) in the last digit(s), whereas (F) refers to fixed parameter values. RA stands for the relative area fraction, δ denotes the ⁵⁷Fe isomer shift (wrt. α-Fe at room temperature), 〈Δ〉 denotes the mean and σ(Δ) denotes the standard deviation of the Gaussian distribution assumed to be present in the quadrupole splitting values, and W is the Lorentzian FWHM width of the individual peaks of the doublets. χ_n² denotes the normalized chi-square of the fits

Sample code	25FeP	30FeP	35FeP	40FeP
x	25	30	35	40
χn^2	1.20	1.07	1.04	1.10
Quadrupole doublet Fe^2+(A)
RA, %	29.2(2.3)	28.6(3.5)	25.1(2.7)	24.3(2.4)
δ, mm s^−1	1.19(3)	1.20(5)	1.20(1)	1.21(1)
〈Δ〉, mm s^−1	2.52(6)	2.6(1)	2.59(4)	2.60(4)
σ(Δ), mm s^−1	0.35(1)	0.36(2)	0.36(1)	0.35(1)
W, mm s^−1	0.256(6)	0.255(9)	0.245(6)	0.249(5)
Quadrupole doublet Fe^2+(B)
RA, %	20.4(2.3)	25.5(3.5)	30.2(2.8)	30.1(2.4)
δ, mm s^−1	1.03(5)	1.04(7)	1.06(2)	1.06(2)
〈Δ〉, mm s^−1	2.18(8)	2.2(1)	2.24(3)	2.25(3)
σ(Δ), mm s^−1	0.37(2)	0.38(2)	0.42(1)	0.41(1)
W, mm s^−1	0.256(6)	0.255(9)	0.245(6)	0.249(5)
Quadrupole doublet Fe^2+(C)
RA, %	7.4(3)	8.7(5)	7.9(4)	7.5(3)
δ, mm s^−1	0.872(6)	0.87(1)	0.877(9)	0.875(7)
〈Δ〉, mm s^−1	0.40(1)	0.34(2)	0.36(2)	0.41(2)
σ(Δ), mm s^−1	0(F)	0(F)	0(F)	0(F)
W, mm s^−1	0.41(1)	0.49(3)	0.49(2)	0.47(2)
Quadrupole doublet Fe^3+
RA, %	43.0(2)	37.1(4)	36.9(3)	38.2(3)
δ, mm s^−1	0.470(2)	0.467(4)	0.464(3)	0.466(3)
〈Δ〉, mm s^−1	0.640(4)	0.673(7)	0.693(8)	0.693(6)
σ(Δ), mm s^−1	0.286(5)	0.298(8)	0.310(6)	0.298(5)
W, mm s^−1	0.256(6)	0.255(9)	0.245(6)	0.249(5)

---

Around 40% of the spectral area is associated with iron in the high-spin (HS) Fe³⁺ state in each case. With increasing Fe₂O₃ mol% the relative area fraction of the Fe³⁺ component drops by ca. 6% (from ∼43% to ∼37%) as the Fe₂O₃ concentration increases from 25% to 30% and above, which can refer to a simultaneously increased level of oxygen deficiency in the glass structure. The Fe³⁺ isomer shift and mean quadrupole splitting Mössbauer parameters, δ ≈ 0.47 mm s ⁻¹ and 〈Δ〉 ≈ 0.64–0.69 mm s ⁻¹ (Table 6), are consistent with octahedral oxygen coordination of high-spin Fe³⁺.

For the assignment of the obtained Fe³⁺ and Fe²⁺ doublet components it is informative to compare the corresponding Mössbauer parameters with those obtained for Fe₇(PO₄)₆ in the crystalline sample 50FeP (Table 7). The ⁵⁷Fe Mössbauer spectra of the latter sample measured at room temperature and at T = 80 K are shown in Fig. 13. Based on the associated X-ray diffractometry results (see Fig. 1) we assumed paramagnetic components of Fe₇(PO₄)₆ and Fe₂P₂O₇ to contribute to the spectra. The spectral decomposition was carried out accordingly, by taking into account the results of previous studies concerning Fe₇(PO₄)₆ (ref. 58) and Fe₂P₂O₇,⁵⁹ and applying suitable constraints among others regarding the relative area fractions of the individual subcomponents. To fit these spectra properly in the thin absorber approximation limit, a minor asymmetry in the peak areas associated with the individual doublets had to be assumed (Table 7), which may be the consequence of thickness effects. The results indicate that in the sample 50FeP ca. 79% of iron is incorporated in the lattice of Fe₇(PO₄)₆, and ca. 16% in Fe₂P₂O₇ (Table 7), while a further ca. 5% contributes to a minor Fe²⁺ species (denoted with Fe²⁺(*) on Fig. 13) that remains unassigned. On the basis of the relatively low quadrupole splitting of the latter component, it may originate from Fe²⁺ species situated in a non-regular, distorted oxygen coordination environment. In the lattice of Fe₇(PO₄)₆, Fe²⁺ occur with 6-fold (octahedral) and 5-fold (pyramidal) oxygen coordination⁶⁰ with a relative occurrence of 2 : 1 in favor of the 5-fold coordination. On the basis of its higher relative area fraction and lower isomer shift value, among the Fe²⁺ components associated with Fe₇(PO₄)₆ (i.e. Fe²⁺(a) and Fe²⁺(b) in Table 7) in the spectra of 50FeP it is the Fe²⁺(b) component that can be associated with the 5-fold coordinated Fe²⁺ species. In addition to the Fe²⁺ sites, the structure of Fe₇(PO₄)₆ also includes two distinct Fe³⁺ sites.⁶⁰ In both of these Fe³⁺ sites, the iron atoms exhibit a distorted octahedral oxygen coordination. The Mössbauer parameters we obtained for these sites are given under the names Fe₇(PO₄)₆–Fe³⁺(a) and Fe³⁺(b) in Table 7.

Table 7 ⁵⁷Fe Mössbauer parameters of the crystalline 50FeP sample measured at room temperature (RT) as well as at T ≈ 80 K. The quadrupole doublets fitted to these spectra were asymmetric, A₊/A₋ denoting the ratio of the areas of the higher- and lower-velocity absorption peaks of the doublets. (For a given spectrum the same ratio was applied to all the fitted doublets.) Relative area fractions of Fe₇(PO₄)₆ components were constrained (at both temperatures) in accordance with the results of Millet et al.⁵⁸ On the basis of the work by Ericsson et al.,⁵⁹ the area fractions of Fe₂P₂O₇ components were assumed to be equal, and an isomer shift difference of 0.07 mm s⁻¹ was assumed between the two doublets. Furthermore, in the room-temperature spectrum the quadrupole splitting of the two Fe₂P₂O₇ doublets were constrained in such a way that ensured that the higher-velocity absorption peaks of the doublets coincide with each other.⁵⁹ See Table 6 for notations

Sample code	50FeP
T, K	RT	80
χn^2	1.15	1.08
A+/A−	1.08(1)	1.10(1)
Fe7(PO4)6–Fe^2+(a)
RA, %	11.1(1)	11.0(1)
δ, mm s^−1	1.258(3)	1.45(4)
〈Δ〉, mm s^−1	2.874(6)	2.97(8)
σ(Δ), mm s^−1	0(F)	0(F)
W, mm s^−1	0.261(4)	0.309(6)
Fe7(PO4)6–Fe^2+(b)
RA, %	23.0(2)	22.8(2)
δ, mm s^−1	1.151(3)	1.298(3)
〈Δ〉, mm s^−1	2.529(4)	2.939(5)
σ(Δ), mm s^−1	0(F)	0(F)
W, mm s^−1	0.261(4)	0.309(6)
Fe7(PO4)6–Fe^3+(a)
RA, %	23.0(2)	22.8(2)
δ, mm s^−1	0.50(1)	0.60(1)
〈Δ〉, mm s^−1	0.74(1)	0.73(1)
σ(Δ), mm s^−1	0.10(1)	0.14(3)
W, mm s^−1	0.261(4)	0.309(6)
Fe7(PO4)6–Fe^3+(b)
RA, %	22.2(2)	22.0(2)
δ, mm s^−1	0.37(1)	0.42(3)
〈Δ〉, mm s^−1	0.71(1)	0.80(7)
σ(Δ), mm s^−1	0.09(1)	0.14(3)
W, mm s^−1	0.261(4)	0.309(6)
Fe2P2O7–Fe^2+(1)
RA, %	7.9(3)	8.2(2)
δ, mm s^−1	1.31(2)	1.35(5)
〈Δ〉, mm s^−1	2.33(4)	2.6(1)
σ(Δ), mm s^−1	0.15(2)	0(F)
W, mm s^−1	0.261(4)	0.309(6)
Fe2P2O7–Fe^2+(2)
RA, %	7.9(3)	8.2(2)
δ, mm s^−1	1.24(2)	1.28(5)
〈Δ〉, mm s^−1	2.47(4)	2.7(2)
σ(Δ), mm s^−1	0.15(2)	0(F)
W, mm s^−1	0.261(4)	0.309(6)
Fe^2+(*)
RA, %	5(1)	5(F)
δ, mm s^−1	1.35(5)	1.36(3)
〈Δ〉, mm s^−1	1.4(1)	2.32(5)
σ(Δ), mm s^−1	0(F)	0(F)
W, mm s^−1	0.7(1)	0.28(5)

---

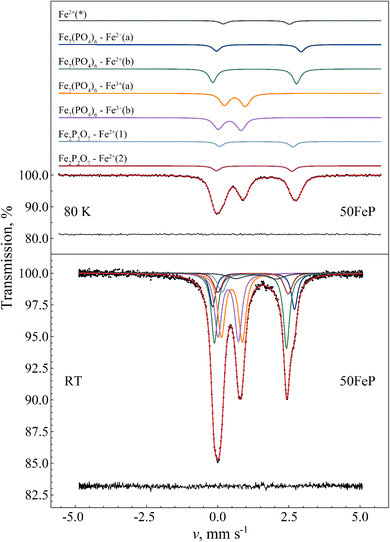Fig. 13 ⁵⁷Fe Mössbauer spectrum (dots) of 50Fe₂O₃·50P₂O₅ (50FeP) crystalline sample measured at 80 K (top) and at room temperature (bottom), along with the indication of the fit envelope and the subcomponents (solid line). For the measurement performed at 80 K, the fitted subcomponents are shifted upwards for clarity. Below the spectra the fit residual is displayed. See Table 7 for the associated fit parameter values.

The Fe³⁺ isomer shift and mean quadrupole splitting Mössbauer parameters obtained for the glass samples are δ ≈ 0.47 mm s⁻¹ and 〈Δ〉 ≈ 0.64–0.69 mm s⁻¹ (Table 6). These values are consistent with octahedral oxygen coordination of high-spin Fe³⁺. They are also similar to the parameters of the Fe³⁺(a) and Fe³⁺(b) species of Fe₇(PO₄)₆ (Table 7), with a closer match to the Fe³⁺(a) component. This corroborates that Fe³⁺ ions have distorted octahedral oxygen coordination in these glasses. The distortion of the oxygen octahedra appears to have a wide range of variability in the glass, as reflected by the considerable standard deviation of the distribution of quadrupole splitting values (Table 6). Note that some of the Gaussian broadening, which we modeled as a distribution in the quadrupole splitting values, may also be the result of a distribution in the isomer shift values.

Similarity between the δ and 〈Δ〉 values of Fe²⁺(b) in Fe₇(PO₄)₆ and Fe²⁺(A) in the glass samples (Table 6) then suggests that Fe²⁺(A) may be associated mainly with 5-fold coordinated high-spin Fe²⁺ species in the glass. At the same time, contribution of Fe²⁺ species with 6-fold (octahedral) oxygen coordination to the Fe²⁺(A) component cannot be fully excluded, as such a species may also display similar δ and 〈Δ〉 Mössbauer parameter values; one such example is the Fe²⁺(2) species in Fe₂P₂O₇ (Table 7) where iron has octahedral oxygen coordination.⁵⁹

Considering the Fe–O coordination distribution function displayed in Fig. 11a, component Fe²⁺(B) in Table 6 needs then to be attributed mainly to 4-fold (e.g. tetrahedral) coordinated Fe²⁺ species in the glass. The latter attribution is further corroborated by the increasing tendency in the relative area fraction of Fe²⁺(B) with increasing Fe₂O₃ mol% (Table 6), which is in qualitative agreement with a similar tendency reflected by the Fe–O coordination distribution function (Fig. 11a).

The isomer shift (δ ≈ 0.87 mm s⁻¹) and quadrupole splitting (Δ ≈ 0.4 mm s⁻¹) of the Fe²⁺(C) component found in the spectra of the amorphous samples (Fig. 12) are considerably lower (Table 6) than respective values of Fe²⁺(A) and Fe²⁺(B), and may be attributed to e.g., 4-fold coordinated Fe²⁺ with square-planar oxygen coordination environment. This assignment is also supported by similar isomer shift and quadrupole splitting values observed for square-planar coordinated high-spin Fe²⁺ in the mineral gillespite (δ ≈ 0.75 mm s⁻¹ wrt. α-Fe, Δ ≈ 0.51 mm s⁻¹).⁶¹

Fig. 14 displays the sum of the relative area fractions of the Fe²⁺(B) and Fe²⁺(C) doublet components that were attributed to Fe²⁺ species with 4-fold oxygen coordination. Clearly, from 25FeP to 35FeP the relative weight of 4-fold coordinated Fe²⁺ environments increases. On the basis of Table 6, this increase occurs at the expense of both the 5- and 6-coordinated iron species. In line with the model of Hoppe,⁶² the gradual reduction of the coordination number of iron indicates that in the studied samples the concentration of iron already exceeded the limit where the available terminal oxygen ions of PO₄ tetrahedra could ensure maximum (5–6) coordination number for all the iron ions. Based on the outstanding chemical durability of the 40FeP composition (see Table 9), the development of the glass structure leading to 40FeP must play a decisive role in shaping the advantageous material properties associated with this composition. Based on Fig. 14, from 35FeP to 40FeP the iron coordination numbers seem to be stationary. However, as calculated from atomic pair distribution functions, the concentration of iron atoms with 4-fold oxygen coordination increases further even in this range (Fig. 11a).

Fig. 14 Mössbauer-spectrum relative area fractions associated with 4-coordinated Fe species calculated based on the spectral decomposition of the room-temperature Mössbauer spectra of the 25FeP, 30FeP, 35FeP and 40FeP glass samples (Fig. 12). Among the identified components (Table 6), Fe²⁺ (B) and Fe²⁺ (C) were evaluated to be 4-coordinated species; the figure displays the sum of the relative area fractions of these components as a function of the Fe atomic concentration wrt. the total number of Fe and P atoms in the structure. See Table 6 for the associated Mössbauer parameters. Note that the depicted values were not corrected for possible differences in the recoilless fractions of Fe²⁺ and Fe³⁺ ions.

Due to possible differences in the temperature dependence of the f(Fe²⁺) and f(Fe³⁺) recoilless fractions associated with Fe²⁺ and Fe³⁺ species respectively, the Fe²⁺/Fe³⁺ ratio in the glass may not be faithfully reflected by the corresponding relative spectral area ratios characteristic to the room temperature Mössbauer spectra of the glass samples (Fig. 12 and Table 6). In order to find a more reliable value of the Fe²⁺/Fe³⁺ ratio, the sample 30FeP was also measured at T = 80 K. The obtained spectrum and the associated fit parameters are shown in Fig. 15 and Table 8. On the basis of the isomer shift and mean quadrupole splitting (〈Δ〉) parameters (Table 8), in the latter spectrum (Fig. 15) one can clearly identify the components associated with the iron species Fe²⁺(A), Fe²⁺(B), Fe²⁺(C) and Fe³⁺. In contrast with the spectra of glasses recorded at room temperature (Fig. 12), which reflect an Fe²⁺/Fe³⁺ spectral area ratio of approximately 1.3–1.7 (Table 6), the relative area fractions of the Fe²⁺ and Fe³⁺ components derived on the basis of the spectrum in Fig. 15 indicate that the Fe²⁺/Fe³⁺ ratio is closer to 2 in these glasses, and hence Fe²⁺ species are clearly in majority concentration in the glass samples (Table 8). Concerning the sample 30FeP in particular, the Fe²⁺/(Fe²⁺+Fe³⁺) ratio changes from 62.9(4)% (at room temperature) to 66.0(4)% (at 80 K), i.e. roughly by a factor of q ≈ 1.05. However, at 80 K the recoilless fraction of Fe²⁺ may still be smaller than that of Fe³⁺. Indeed, by assuming that at room temperature the f(Fe³⁺)/f(Fe²⁺) ratio of the recoilless fractions is ca. 1.3 as given, e.g., in ⁶³, the associated factor turns out to be q ≈ 1.09, meaning that in the sample 30FeP the real Fe²⁺/(Fe²⁺ + Fe³⁺) ratio could reach 68–69%.

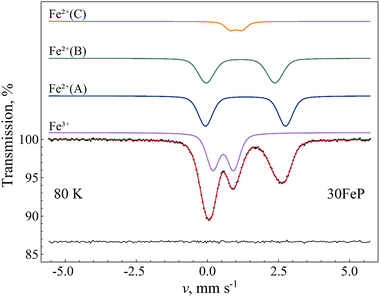Fig. 15 ⁵⁷Fe Mössbauer spectrum (dots) of 30Fe₂O₃-70P₂O₅ (30FeP) glass measured at 80 K, along with the indication of the fit envelope and the subcomponents (solid line). The subcomponents are shifted upwards for clarity. Below the spectrum the fit residual is displayed. See Table 8 for the associated fit parameter values.

Table 8 ⁵⁷Fe Mössbauer parameters of amorphous 30FeP sample measured at T ≈ 80 K. Internal Lorentzian FWHM line width values (W) were constrained to be the same for all the subcomponents. See Table 6 for the corresponding room temperature data and further notations

Sample code	30FeP
χn^2	1.43
Quadrupole doublet Fe^2+(A)
RA, %	31.4(3.9)
δ, mm s^−1	1.34(2)
〈Δ〉, mm s^−1	2.82(5)
σ(Δ), mm s^−1	0.38(2)
W, mm s^−1	0.26(1)
Quadrupole doublet Fe^2+(B)
RA, %	28.2(3.9)
δ, mm s^−1	1.17(4)
〈Δ〉, mm s^−1	2.42(6)
σ(Δ), mm s^−1	0.44(3)
W, mm s^−1	0.26(1)
Quadrupole doublet Fe^2+(C)
RA, %	6.4(3)
δ, mm s^−1	1.01(2)
〈Δ〉, mm s^−1	0.41(3)
σ(Δ), mm s^−1	0.23(2)
W, mm s^−1	0.26(1)
Quadrupole doublet Fe^3+
RA, %	34.0(4)
δ, mm s^−1	0.556(7)
〈Δ〉, mm s^−1	0.73(1)
σ(Δ), mm s^−1	0.31(1)
W, mm s^−1	0.26(1)

---

The theoretical model we applied for the decomposition of the iron phosphate glass Mössbauer spectra was chosen on account of being the simplest model providing reasonable and consistent results along with excellent mathematical fits (Table 6 and Fig. 12). Nevertheless, the model we applied appears to be rather uncommon in related literature, making it pertinent to compare our results with those obtained using other approaches to the decomposition of Mössbauer spectra of iron phosphate glasses. One of the main difficulties in analyzing the spectra of these glasses is that the absorption peaks are non-Lorentzian, making traditional spectrum analysis techniques based on a few Lorentzian doublets inaccurate. Therefore, different solutions have been developed to address this problem and to extract information from the Mössbauer spectra of such glasses.

The most straightforward approach is to fit glass spectra, akin to those in Fig. 12, with one broadened Lorentzian doublet for Fe²⁺ and one for Fe³⁺,^29,64–66 which will provide approximate average Mössbauer parameter values for the two different iron oxidation states. While not suitable to extract fine details from spectra of iron phosphate glass where Fe²⁺ or Fe³⁺ ions exist with multiple oxygen coordination environments, this method may be justified especially when the signal-to-noise ratio of the spectrum is not high enough to reveal deviations from the Lorentzian line profile. It also has the advantage of being easily reproducible in different laboratories, facilitating the comparison of associated results. However, even in this simple case two different solutions may be found reasonable regarding the Mössbauer parameters: one in which Fe³⁺ has a higher quadrupole splitting (QS), and therefore the left-most absorption peak belongs to Fe³⁺ in the fit model, and another in which Fe³⁺ has a lower QS, and the left-most Lorentzian of the model belongs to Fe²⁺ (similarly to the cases shown in Fig. 12). Usually, the former model provides the better fit, leading to room temperature Fe³⁺ quadrupole splitting values around 0.8–0.9 mm s⁻¹,^29,64,65 in contrast with the lower mean Fe³⁺ quadrupole splitting values of 0.64–0.70 mm s⁻¹ we obtained (Table 6). However, when we apply the same model to the spectrum of 40FeP shown in Fig. 12 (which composition is also studied for example in ref. 22, 29, 63 and 66–68), we also find the larger QS solution to provide the better fit with main Mössbauer parameters of δ (Fe³⁺) ≈ 0.38 mm s⁻¹, Δ(Fe³⁺) ≈ 0.89 mm s⁻¹, δ(Fe²⁺) ≈ 1.23 mm s⁻¹, Δ(Fe²⁺) ≈ 2.23 mm s⁻¹. At the same time, the more accurate multi-component fits, displayed in Fig. 12, already favor the solution with the lower QS values of Fe³⁺ given in Table 6.

Another common method is the formal fit of the Fe²⁺ and Fe³⁺ spectrum parts with multiple (usually 3–4 for each oxidation state) broadened Lorentzian quadrupole doublets, without associating specific iron species with the individual components. The number of doublets is chosen to be high enough to achieve an acceptable fit of the spectra. The results are then reported as weighted averages of the isomer shift (IS) and quadrupole splitting values obtained for the individual oxidation states.^{22,63,67–71} An advantage of this method over the previous one is that due to the better fit of the spectra the obtained averages can reflect minor changes in the spectral shape more sensitively than by using only a single doublet for each oxidation state.

The main limitation of the two methods mentioned above is that they provide only a single average isomer shift and quadrupole splitting value for each oxidation state. This means that they cannot distinguish between different Fe²⁺ (or Fe³⁺) oxygen coordination environments that are simultaneously present in the sample. The average IS and QS values resulting from such analyses of Mössbauer spectra of iron phosphate glasses are typically found to refer mainly to 6-fold (octahedral or distorted octahedral) oxygen coordination for both Fe²⁺ and Fe³⁺ ions.^{22,29,63,66,68–71}

A third method applied to decompose Mössbauer spectra of iron phosphate glasses utilizes the VBF (Voigt based fitting,⁷²) or xVBF (extended Voigt based fitting⁵⁷) method to fit quadrupole doublets by assuming correlated Gaussian distributions of the QS and IS Mössbauer parameter values of the individual doublets.^28,73–75 This is the same method we also apply in the present work, with the significant difference that we have assumed the distributions of IS and QS values to be uncorrelated (or that of IS values being negligible). In the presence of IS-QS correlation the VBF and xVBF models can produce a wide variety of doublet peak profiles, where the amplitudes and the widths of the individual (Voigt-profile) peaks contributing to the doublet can differ from each other. By adjusting the parameter of correlation between distributions of IS and QS values of individual doublets of a fit model, iron phosphate glass spectra could be accounted for with high accuracy with only three main VBF or xVBF components and associated three main iron positions, two assumed for Fe³⁺ and one for Fe²⁺.^28,73–75 By using this method, in different iron phosphate glass samples Fe³⁺ and Fe²⁺ ions were associated with positions having 6-, 5- and 4-fold and 6- and 5-fold oxygen coordination, respectively. As we see it, currently it is unclear whether correlation between distributions of IS and QS values of iron species should indeed be taken into account in the interpretation of iron phosphate glass Mössbauer spectra. Our results indicate (Fig. 12 and Table 6) that excellent fits can be achieved by assuming only four main iron species, even without considering the possibility of IS-QS distribution correlations. In comparison with previous reports, a novel component in our decomposition of the iron phosphate glass Mössbauer spectra (Fig. 12) is the minor doublet Fe²⁺(C) (Table 6) that displays Mössbauer parameters referring to Fe²⁺ in a square-planar oxygen coordination environment. The inclusion of this component into our model played a decisive role in the achievement of high-accuracy spectrum fits with a limited number of spectrum components.

3.7 Chemical durability of iron phosphate glasses

The chemical stability of two bulk glasses of composition 30Fe₂O₃–70P₂O₅ (sample code 30FeP) and 40Fe₂O₃–60P₂O₅ (sample code 40FeP) were analyzed over a period of 10 days in MQ-water kept at 90 °C and the concentration of dissolved Fe and P was measured after 1, 2, 3, 7 and 10 days and the experimental data are presented in Table 9. In case of glass sample 30FeP, the concentration of P in MQ-water increases from a value of 1.014 ± 0.100 to 15.855 ± 0.253 mg l⁻¹ while that of Fe increases from a value of 0.092 ± 0.006 to 0.747 ± 0.049 mg l⁻¹ over a time period of 10 days. In case of 40FeP glass, the concentration of P increases from a value of 0.337 ± 0.039 to 1.231 ± 0.195 mg l⁻¹ while that of Fe remains nearly constant in the range: 0.078 ± 0.003 to 0.053 ± 0.013 mg l⁻¹. It is found that the chemical stability of 40FeP glass is drastically higher than that of 30FeP glass and further the concentration of dissolved P is significantly higher than that of Fe. These findings are in agreement with the earlier reports that 40Fe₂O₃–60P₂O₅ glass has maximum chemical durability.^22–26

Table 9 Concentration of P and Fe leached from 30FeP and 40FeP glass samples kept in MQ-water at 90 °C over a period of 10 days

Sample code & number of days	P (mg l^−1)	Fe (mg l^−1)
30FeP	1.014 ± 0.100	0.092 ± 0.006
1 Day
40FeP	0.337 ± 0.039	0.078 ± 0.003
1 Day
30FeP	6.699 ± 0.100	0.343 ± 0.008
2 Days
40FeP	0.552 ± 0.074	0.086 ± 0.015
2 Days
30FeP	11.755 ± 0.188	0.506 ± 0.019
3 Days
40FeP	0.958 ± 0.033	0.069±±0.010
3 Days
30Fe	12.807 ± 0.358	0.579 ± 0.0139
7 Days
40FeP	1.163 ± 0.060	0.069 ± 0.006
7 Days
30FeP	15.855 ± 0.253	0.747 ± 0.049
10 days
40FeP	1.231 ± 0.195	0.053 ± 0.013
10 Days

---

4. Conclusions

Iron phosphate glasses with 25 to 40 mol% Fe₂O₃ were produced by melt quenching. The sample with a higher concentration of 50 mol% Fe₂O₃ has poor glass-forming ability and it produces crystalline sample containing Fe₇[PO₄]₆ and Fe₂P₂O₇ phases on melt-quenching. The glass transition, crystallization and liquidus temperatures were determined by DSC analysis. The ionic packing fraction show a small variation while the glass forming tendency decreases significantly with an increase in Fe₂O₃ concentration in the phosphate network. The RMC analysis of neutron diffraction datasets were used to calculate the partial atomic pair distributions and coordination environments in iron phosphate glasses. The most probable P–O and Fe–O bond distances in glasses are 1.50 Å and 1.79 ± 0.05 Å respectively. Mössbauer studies revealed that Fe exists in both 3+ and 2+ oxidation states in the glasses, with a Fe²⁺/Fe³⁺ occurrence ratio of ca. 2. Fe³⁺ ions were identified as having distorted octahedral oxygen coordination, while Fe²⁺ ions in the glass were found to have 4-fold and 5-fold oxygen coordination environments. The relative fraction of Fe²⁺ increases significantly with an increase in Fe₂O₃ concentration in the starting bath mixture, which also lowers the glass forming ability of the system. Iron coordination numbers from partial atomic pair distribution functions and Mössbauer results indicated that the occurrence of Fe²⁺ with 4-fold oxygen coordination increases with the concentration of Fe₂O₃. Neutron diffraction and Raman studies found that the short-range structure of iron phosphate glasses and crystalline phases are similar. Leaching experiments on iron phosphate glasses in purified water kept at 90 °C confirmed that chemical durability is enhanced considerably with an increase in iron concentration in the glass and that P dissolution is higher than that of Fe.

Data availability

All data reported in the manuscript is available with the authors and will be provided on request to the corresponding author.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Atul Khanna, acknowledges UGC-DAE-CSR, Mumbai Centre, India for research grants (CRS-M-547) and the Central European Research Infrastructure (CERIC-20212041) for financial support to carry out the neutron diffraction experiments at Budapest Neutron Centre, Centre for Energy Research, Budapest, Hungary. Kajal Dadwal and Suruchi Sharma acknowledge UGC –DAE-CSR Mumbai Centre, India for PhD research fellowships. Maria Gracheva and Zoltán Klencsár express thanks to Gábor Benyács for the preparation of Mössbauer sample holders.

References

1. J. D. Vienna, Nuclear waste vitrification in the United States: recent developments and future options, Int. J. Appl. Glass Sci., 2010, 1, 309–321.
2. C. Corkhill and N. Hyatt, Nuclear Waste Management, IOP Publishing, Bristol, UK, 2018.
3. C. P. Kaushik, R. K. Mishra, P. Sengupta, A. Kumar, D. Das, G. B. Kale and K. Raj, barium borosilicate glass – a potential matrix for immobilization of sulfate bearing high-level radioactive liquid waste, J. Nucl. Mater., 2006, 358, 129–138.
4. M. J. Plodinec, Borosilicate Glasses for Nuclear Waste Imobilisation, Glass Technology, vol. 41, 2000, pp. 186–192.
5. M. Fábián, F. Pinakidou, I. Tolnai, O. Czompoly and J. Osan, Lanthanide (Ce, Nd, Eu) environments and leaching behavior in borosilicate glasses, Sci. Rep., 2021, 11, 13272–13286.
6. M. Fábián, F. Gergely, J. Osan, T. Cendak, S. Kesari and R. Rao, Structural investigation of borosilicate glasses containing lanthanide ions, Sci. Rep., 2020, 10, 7835–7848.
7. I. Pegg and I. Joseph, Hazardous and Radioactive Waste Treatment Technologies Handbook, ed. H. Chang, Boca Raton, CRC Press, 2001, ch. 4.2.
8. P. A. Bingham, S. D. Forder, R. J. Hand and A. Lavaysierre, Mössbauer studies of phosphate glasses for the immobilisation of toxic and nuclear wastes, Hyperfine Interact., 2005, 165, 135–140.
9. R. C. Ewing and L. Wang, Phosphates as nuclear waste forms, Rev. Mineral. Geochem., 2002, 48, 673–699.
10. D. Day, C. Ray and C. Kim, Final Report: Iron Phosphate Glasses: an Alternative for Vitrifying Certain Nuclear Wastes, Project No, DEFG07 e96ER45618, 2004.
11. B. C Sales and L. A. Boatner, Lead iron phosphate glass – a stable storage medium for high level nuclear waste, Science, 1984, 226, 45–48.
12. B. C. Sales and L. A. Boatner, Physical and chemical characteristics of lead iron phosphate nuclear waste glasses, J. Non-Cryst. Solids, 1986, 79, 83–116.
13. L. Na Maa, Dissolution Behaviour of Phosphate Glasses, Doctoral Dissertation, Missouri University Rolla, 2014.
14. H. Takebe, M. Fujisawa, Y. Maeda and A. Saitoh, Effect of molybdenum oxide addition on the durability and structure of iron phosphate glasses, J. Ceram. Soc. Jpn., 2021, 129, 105–110.
15. S. T. Reis, A. Mogus-Milankovic, V. Licina, J. B. Yang, M. Karabulut, D. E. Day and R. K. Brow, Iron redox equilibrium, structure and properties of zinc iron phosphate glasses, J. Non-Cryst. Solids, 2007, 353, 151–158.
16. S. T. Reis, D. L. A. Faria, J. R. Martinelli, W. M. Pontuschka, D. E. Day and C. S. M. Partiti, Structural features of lead iron phosphate glasses, J. Non-Cryst. Solids, 2002, 304, 188–194.
17. X. Zhang, L. Zhang, H. Liu, B. Cao, L. Liu and W. Gong, Structure, morphology, size and application of iron phosphate, Rev. Adv. Mater. Sci., 2020, 59, 538–552.
18. R. K. Brow, Review: structure of simple phosphate glasses, J. Non-Cryst. Solids, 2000, 263&264, 1–28.
19. L. Zhang and R. K. Brow, A Raman study of iron–phosphate crystalline compounds and glasses, J. Am. Ceram. Soc., 2011, 94, 3123–3130.
20. L. Zhang, R. K. Brow, M. E. Schlesinger, L. Ghussn and E. D. Zanotto, Glass formation from iron-rich phosphate melts, J. Non-Cryst. Solids, 2010, 356, 1252–1257.
21. U. Hoppe, M. Karabulut, E. Metwalli, R. K. Brow and P. Jóvári, The Fe–O coordination in iron phosphate glasses by x-ray diffraction with high energy photons, J. Phys.: Condens. Matter, 2003, 15, 6143–6153.
22. G. K. Marasinghe, M. Karabulut, C. S. Ray, D. E. Day, M. G. Shumsky, W. B. Yelon, C. H. Booth, P. G. Allen and D. K. Shuh, Structural features of iron phosphate glasses, J. Non-Cryst. Solids, 1997, 222, 144–152.
23. C. H. Booth, P. G. Allen and D. K. Shuh, Structural features of iron phosphate glasses, J. Non-Cryst. Solids, 1997, 222, 144–152.
24. M. G. Mesko and D. E. Day, Immobilization of spent nuclear fuel in iron phosphate glass, J. Nucl. Mater., 1997, 273, 27–36.
25. M. Karabulut, G. K. Marasinghe, C. S. Ray, D. E. Day, O. Ozturk and G. D. Waddill, X-ray photoelectron and Mössbauer spectroscopic studies of iron phosphate glasses containing U, Cs and Bi, J. Non-Cryst. Solids, 1999, 249, 106–116.
26. B. Qian, X. Liang, S. Yang, S. He and L. Gao, Effects of lanthanum addition on the structure and properties of iron phosphate glasses, J. Mol. Struct., 2012, 1027, 31–35.
27. B. Al-Hasni and G. Mountjoy, Structural investigation of iron phosphate glasses using molecular dynamics simulation, J. Non-Cryst. Solids, 2011, 357, 2775–2779.
28. P. Stoch, W. Szczerba, W. Bodnar, M. Ciecinska, A. Stoch and E. Burkel, Structural properties of iron-phosphate glasses: spectroscopic studies and ab initio simulations, Phys. Chem. Chem. Phys., 2014, 16, 19917–19927.
29. S. T. Reis, W. M. Pontuschka, A. Moguš-Milanković and C. S. Partiti, Structural features of iron phosphate glass, J. Am. Ceram. Soc., 2017, 100, 1976–1981.
30. N. Kaur, A. Khanna and A. C. Hannon, Neutron diffraction investigation of copper tellurite glasses with high real-space resolution, J. Appl. Crystallogr., 2021, 54, 1647–1655.
31. A. Khanna, M. Fábián, Hirdesh, P. S. R. Krishna, C. J. Benmore, A. Kaur, A. Kaur, A. B. Shinde, P. Rajput and S. N. Jha, Structural analysis of WO₃-TeO₂ glasses by neutron, high energy X-ray diffraction, reverse Monte Carlo simulations and XANES, J. Non-Cryst. Solids, 2018, 495, 27–34.
32. A. Kaur, A. K. Hirdesh, M. Fábián, P. S. R. Krishna and A. B. Shinde, Structure of lead tellurite glasses and its relationship with stress-optic properties, Mater. Res. Bull., 2019, 110, 239–246.
33. A. Khanna, A. Kaur, M. Fábián, Hirdesh and A. Kaur, Structure of lead silicate glasses and its corelation with photoelastic properties, Indian J. Phys., 2021, 95, 2187–2199.
34. R. Kaur, A. Khanna and M. Fábián, Neutron diffraction investigation of strontium tellurite glass, anti-glass and crystalline phases, Phase Transitions, 2020, 93, 1016–1029.
35. S. Bista, A. O. Donovan-Zavada, M. Tyler, M. Franke, M. Affatigato and S. Feller, Packing in alkali and alkaline earth borosilicate glass systems, Eur. J. Glasses Sci. Technol. B Phys. Chem. Glasses, 2009, 50, 224–228.
36. J. A. Dean, Lange's Handbook of Chemistry, McGraw-Hill, 1992.
37. O. Gereben, P. Jóvári, L. Temleitner and L. Pusztai, A new version of the RMC++ Reverse Monte Carlo programme, aimed at investigating the structure of covalent glasses, J. Optoelectron. Adv. Mater., 2007, 9, 3021–3027.
38. G. Evrard and L. Pusztai, Reverse Monte Carlo modelling of the structure of disordered materials with RMC++: a new implementation of the algorithm in C++, J. Phys.: Condens. Matter, 2005, 17, S1–S13.
39. M. Fábián, E. Svab and K. Krezhov, Network structure with mixed bond-angle linkages in MoO₃–ZnO–B₂O₃ glasses: neutron diffraction and reverse Monte Carlo modelling, J. Non-Cryst. Solids, 2016, 433, 6–13.
40. R. Kaur, A. Khanna, A.-C. Dippel, O. Gutowski, F. González and M. González-Barriuso, Structure of strontium tellurite glass, anti-glass and crystalline phases by high-energy X-ray diffraction, reverse Monte Carlo and Rietveld analysis, Acta Crystallographica Section B: Structural ScienceCrystal Engineering and Materials, 2020, 76, 108–121.
41. Z. Klencsár, E. Kuzmann and A. Vértes, User-friendly software for Mössbauer spectrum analysis, J. Radioanal. Nucl. Chem., 1996, 210(1), 105–118.
42. Standard Test Methods for Determining Chemical Durability of Nuclear, Hazardous, and Mixed Waste Glasses and Multiphase Glass Ceramics: the Product Consistency Test (PCT), 2021.  DOI:10.1520/C1285-21.
43. I. Tolnai, J. Osan, F. Pinakidou, Zs. Kovacs and M. Fabian, Effects of UO3 on the structure, thermal and chemical stability of borosilicate glass matrix, J. Non-Cryst. Solids, 2024, 637, 123054.
44. B. M. Al-Hasni, G. Mountjoy and E. Barney, Atomic structure of iron phosphate glasses, Int. J. Appl. Glass Sci., 2021, 12, 245–258.
45. A. Saini, A. Khanna, V. K. Michaelis, S. Kroeker, F. González and D. Hernandez, Structure property correlations in lead borate and borosilicate glasses doped with aluminium oxide, J. Non-Cryst. Solids, 2009, 355, 2323–2332.
46. A. Khanna, A. Saini, B. Chen, F. González and B. Ortiz, Structural characterization of PbO–B₂O₃–SiO₂ Glasses, J. Optoelectron. Adv. Mater., 2014, 55(2), 65–73.
47. A. Bajaj, A. Khanna, B. Chen, J. G. Longstaffe, U. Werner Zwanziger, J. W. Zwanziger, Y. Gómez and F. González, Structural investigation of bismuth borate glasses and crystalline phases, J. Non-Cryst. Solids, 2009, 355, 45–53.
48. A. Khanna, A. Saini, B. Chen, F. González and C. Pesquera, Structural study of bismuth borosilicate, aluminoborate and aluminoborosilicate glasses by ¹¹B and ²⁷Al MAS NMR spectroscopy and thermal analysis, J. Non-Cryst. Solids, 2013, 373–374, 34–41.
49. D. R. Neuville and C. Le Losq, Link between Medium and Long-range Order and Macroscopic Properties of Silicate Glasses and Melts, Rev. Mineral. Geochem., 2022, 87, 105–162.
50. N. Kaur, A. Khanna, M. Gónzález-Barriuso, F. González and B. Chen, Effects of Al³⁺, W⁶⁺, Nb⁵⁺ and Pb²⁺ on the structure and properties of borotellurite glasses, J. Non-Cryst. Solids, 2015, 429, 151–163.
51. G. D'Angelo, G. Carini, 1 C. Crupi, M. Koza, G. Tripodo and C. Vasi, Boson peak in alkaline borate glasses: Raman spectroscopy, neutron scattering, and specific-heat Measurements, Phys. Rev. B:Condens. Matter Mater. Phys., 2009, 79, 014206.
52. C. Mclntosh, J. Toulouse and P. Tick, The Boson peak in alkali silicate glasses, J. Non-Cryst. Solids, 1997, 222, 335.
53. A. I. Chumakov, G. Monaco, A. Monaco, W. A. Crichton, A. Bosak, R. Rüffer, A. Meyer, F. Kargl, L. Comez, D. Fioretto, H. Giefers, S. Roitsch, G. Wortmann, M. H. Manghnani, A. Hushur, Q. Williams, J. Balogh, K. Parlinski, P. Jochym and P. Piekarz, Equivalence of the Boson Peak in Glasses to the Transverse Acoustic van Hove Singularity in Crystals, Phys. Rev. Lett., 2011, 106, 225501.
54. E. Stavrou, C. Tsiantos, R. D. Tsopouridou, S. Kripotou, A. G. Kontos, C. Raptis, B. Capoen and M. Bouazaoui, S Turrell and S Khatir, Raman scattering boson peak and differential scanning calorimetry studies of the glass transition in tellurium–zinc oxide glasses, J. Phys.: Condens. Matter, 2010, 22, 195103.
55. M. González-Jiménez, T. Barnard, B. A. Russell, N. V. Tukachev, U. Javornik, L.-A. Hayes, A. J. Farrell, S. Guinane, H. M. Senn, A. J. Smith, M. Wilding, G. Mali, M. Nakano, Y. Miyazaki, McM. Paul, G. C. Sosso and K. Wynne, Understanding the emergence of the boson peak in molecular glasses, Nat. Commun., 2023, 14, 215.
56. P. Stoch, A. Stoch, M. Ciecinska, I. Krakowiak and M. Sitarz, Structure of phosphate and iron-phosphate glasses by DFT calculations and FTIR/Raman spectroscopy, J. Non-Cryst. Solids, 2016, 450, 48–60.
57. K. Lagarec and D. G. Rancourt, Extended Voigt-based analytic lineshape method for determining N-dimensional correlated hyperfine parameter distributions in Mössbauer spectroscopy, Nucl. Instrum. Methods Phys. Res., B, 1997, 129, 266.
58. J. M. Millet, C. Virely, M. Forissier, P. Bussière and J. C. Vedrine, Mössbauer spectroscopic study of iron phosphate catalysts used in selective oxidation, Hyperfine Interact., 1989, 46, 619–628.
59. T. Ericsson, A. G. Nord, M. M. O. Ahmed, A. Gismelseed and F. Khangi, Fe₂P₂O₇ and Fe₂P₄O₁₂ Studied Between 5 - 800 K, Hyperfine Interact., 1990, 57, 2179–2186.
60. E. Kozlyakova, I. Danilovich, A. Volkov, K. Zakharov, O. Dimitrova, E. Belokoneva, L. Shvanskaya, E. Zvereva, D. Chareev, O. Volkova and A. Vasiliev, Tuning of physical properties of Fe₇(PO₄)₆ by sodium intercalation, J. Alloys Compd., 2018, 744, 600–605.
61. G. M. Bancroft, A. G. Maddock and R. G. Burns, Applications of the Mössbauer Effect to silicate mineralogy–I. Iron silicates of known crystal structure, Geochim. Cosmochim. Acta, 1967, 31, 2219–2246.
62. U. Hoppe, A structural model for phosphate glasses, J. Non-Cryst. Solids, 1996, 195, 138–147.
63. P. A. Bingham, R. J. Hand, S. D. Forder, A. Lavaysierre, S. H. Kilcoyne and I. Yasin, Preliminary studies of sulphate solubility and redox in 60P₂O₅-40Fe₂O₃ glasses, Mater. Lett., 2006, 60(2), 844–847.
64. H. Bińczycka and J. A. Sawicki, Conversion Electron Mossbauer Spectroscopy Study of Iron Oxidation in Phosphate Glasses, J. Phys. D: Appl. Phys., 1983, 16, 197–201.
65. K. Joseph, R. Asuvathraman, R. V. Krishnan, T. R. Ravindran, R. Govindaraj, K. V. G. Kutty and P. R. V. Rao, Iron phosphate glass containing simulated fast reactor waste: Characterization and comparison with pristine iron phosphate glass, J. Nucl. Mater., 2014, 452(1–3), 273–280.
66. I. Khan, K. Sunakawa, R. Higashinaka, T. D. Matsuda, Y. Aoki, K. Nomura, E. Kuzmann, Z. Homonnay, K. Sinkó, T. Naka, T. Nakane, S. Krehula, S. Music and S. Kubuki, Structural characterization and magnetic properties of iron-phosphate glass prepared by sol-gel method, J. Non-Cryst. Solids, 2020, 543, 120158.
67. D. L. Griscom, C. I. Merzbacher, N. E. Bibler, H. Imagawa, S. Uchiyama, A. Namiki, G. K. Marasinghe, M. Mesko and M. Karabulut, On the structure and radiation chemistry of iron phosphate glasses: New insights from electron spin resonance, Mössbauer, and evolved-gas mass spectroscopy, Nucl. Instrum. Methods Phys. Res., Sect. B, 1998, 141(1–4), 600–615.
68. C. S. Ray, X. Fang, M. Karabulut, G. K. Marasinghe and D. E. Day, Effect of melting temperature and time on iron valence and crystallization of iron phosphate glasses, J. Non-Cryst. Solids, 1999, 249, 1–16.
69. X. Y. Yu, D. E. Day, G. J. Long and R. K. Brow, Properties and structure of sodium-iron phosphate glasses, J. Non-Cryst. Solids, 1997, 215(1), 21–31.
70. M. Karabulut, E. Metwalli, D. E. Day and R. K. Brow, Mössbauer and IR investigations of iron ultraphosphate glasses, J. Non-Cryst. Solids, 2003, 328(1–3), 199–206.
71. P. A. Bingham, R. J. Hand, S. D. Forder and A. Lavaysierre, Vitrified metal finishing wastes. II. Thermal and structural characterisation, J. Hazard. Mater., 2005, 122(1–2), 129–138.
72. D. G. Rancourt and J. Y. Ping, Voigt-based methods for arbitrary-shape static hyperfine parameter distributions in Mössbauer spectroscopy, Nucl. Instrum. Methods Phys. Res., B, 1991, 58, 85–97.
73. M. Karabulut, G. K. Marasinghe, C. S. Ray, D. E. Day, G. D. Waddill, C. H. Booth, P. G. Allen, J. J. Bucher, D. L. Caulder and D. K. Shuh, An investigation of the local iron environment in iron phosphate glasses having different Fe(II) concentrations, J. Non-Cryst. Solids, 2002, 306(2), 182–192.
74. P. Stoch, M. Ciecińska, P. Zachariasz, J. Suwalski, L. Górski and T. Wójcik, Mössbauer spectroscopy study of 60P₂O₅-40Fe₂O₃ glass, Nukleonika, 2013, 58(1), 63–66.
75. P. Stoch and A. Stoch, Mössbauer spectroscopy study of 60P₂O₅-40Fe₂O₃ glass crystallization, Nukleonika, 2015, 60(1), 133–136.

---