Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Computational screening of appealing perspectives of indium-based halide double perovskites In2AgSbX6 (X = Cl, Br, and I) for energy harvesting technologies
Ahmad Ayyaz *a,
M. Zaman
*a,
M. Zaman b,
Hanof Dawas Alkhaldic,
H. Irfan Alia,
Imed Boukhrisd,
S. Bouzgarrouef,
Murefah mana Al-Anazyg and
Q. Mahmood
b,
Hanof Dawas Alkhaldic,
H. Irfan Alia,
Imed Boukhrisd,
S. Bouzgarrouef,
Murefah mana Al-Anazyg and
Q. Mahmood *hi
*hi
aCentre for Advanced Studies in Physics, GC University, Lahore 54000, Pakistan. E-mail: raiayyaz23@gmail.com
bDepartment of Physics, GC University, Lahore 54000, Pakistan
cDepartment of Science and Technology, University College at Nairiyah, University of Hafr Al Batin (UHB), Nairiyah 31981, Saudi Arabia
dDepartment of Physics, Faculty of Science, King Khalid University, P.O. Box 960, Abha, Saudi Arabia
eDepartment of Physics, College of Science, Qassim University, Buraidah 51452, Al-Qassim, Saudi Arabia
fLaboratoire de Microélectronique et Instrumentation (UR03/13-04), Faculté des Sciences de Monastir, Avenue de l'Environnement, 5000 Monastir, Tunisia
gDepartment of Chemistry, College of Sciences, Princess Nourah bint Abdulrahman University (PNU), P.O. Box 84428, Riyadh 11671, Saudi Arabia
hDepartment of Physics, College of Science, Imam Abdulrahman Bin Faisal University, P.O. Box 1982, Dammam 31441, Saudi Arabia
iBasic and Applied Scientific Research Center, Imam Abdulrahman Bin Faisal University, P.O. Box 1982, Dammam 31441, Saudi Arabia. E-mail: qmmustafa@iau.edu.sa
First published on 9th April 2025
Abstract
Halide double perovskites have attracted considerable attention for their potential use in solar cells and thermoelectric devices, as they are ecologically benign and possess band gap tunability. Herein, the stability, optoelectronic, and thermal transport characteristics of In2AgSbX6 (X = Cl, Br, and I) were examined using density functional theory (DFT). Ab initio molecular dynamics (AIMD) analysis was conducted, which verified the dynamic stability of In2AgSbX6 up to 700 K. The estimated elastic parameters further confirmed their mechanical stability. Through mechanical analysis, the asymmetric characteristics of In2AgSbX6 were revealed. The above-mentioned materials were ductile, validating their utilization in flexible or foldable technologies. Analyses of the electrical properties of In2AgSbCl6, In2AgSbBr6, and In2AgSbI6 showed indirect band gaps (Eg) of 1.95 eV, 1.35 eV, and 0.78 eV, respectively. These electronic Eg values were ideal for solar cell applications. The lower effective masses and binding energies of excitons of In2AgSbCl6, In2AgSbBr6, and In2AgSbI6 than those of the perspective solar cell candidates CsPbI3 and Cs2AgBiBr6 provided evidence for their effectiveness as absorber layer materials. The optical analysis of the dielectric constant, absorption, reflection, and loss demonstrated higher absorption, lower reflection, and minimal energy loss within the visible and ultraviolet spectra. The thermal transport features were analyzed for various temperatures up to 600 K and chemical potentials. In2AgSbCl6, In2AgSbBr6, and In2AgSbI6 demonstrated p-type nature, higher Seebeck coefficient, and ZT values of 0.75, 0.77, and 0.76, respectively. Thus, In2AgSbCl6, In2AgSbBr6, and In2AgSbI6 possessed feasible characteristics for applications in solar cells and thermal energy transformation, demonstrating that they can be utilized in future energy harvesting technologies.
1. Introduction
Energy is an essential aspect for the sustenance of contemporary civilization, and it facilitates the ongoing socioeconomic and commercial improvement and evolution of future generations.1 The rapid exhaustion of fossil resources and escalating energy needs threaten the occurrence of a global energy calamity. Considering this possible energy shortage, scientists are compelled to identify cost-effective and environmentally sustainable renewable energy sources. Photovoltaics is a promising method for addressing future energy requirements.2,3 In recent times, perovskite solar cells (PSCs) containing a lead halide in an organic/inorganic mixture have garnered significant interest and attained a power conversion efficiency (PCE) of over 26.1%.4 Nevertheless, the inadequate chemical stability of these halides and the poisonous nature of lead are hindering the technological advancement of these photovoltaic cells. Inorganic-only PSCs exhibit excellent stability at elevated temperatures and moist conditions, effectively capturing light throughout the visible range of the spectrum.Currently, emphasis is placed on compounds with formulations of A2M+M3+X6, which have garnered significant interest owing to their tremendous stability and superior solar energy generation capacity.5,6 The PCE of double perovskite (DP) solar cells has achieved an incredible theoretical value of approximately 30% in the recent past,7 suggesting that they are viable alternatives to silicon cells, which are currently used in commercial applications.8 Moreover, halide replacement in DPs has led to substantial progress in materials discovery, and accordingly, DPs are recognized as a compelling technology for the future development of renewable energy technologies.9 A wide variety of experiments and computational studies have been conducted to elucidate the physical and inherent defect characteristics of DP derivatives. Zhang et al. studied hydrogenated Cs2AgBiBr6, revealing a band gap (Eg) reduction from 2.18 eV to 1.64 eV, high carrier mobility, and 6.37% ECE.10 Moreover, Cs2SnI6, which exhibits remarkable performance and an appropriate bandgap of 1.6 eV, is an extremely promising light-harvesting material. The power conversion efficiency of Cs2SnI6 was 8%.11 García-Espejo et al. synthesized Cs2AgSbBr6, which showed greater stability and an Eg of 1.93 eV.12 Bhorde et al. investigated Rb2AgBiI6 and revealed its semiconductor nature with a 1.98 eV band gap.13 These limited studies on halide DPs have motivated computational scientists to predict DPs and suggest materials with exceptional characteristics to experimentalists.
Therefore, density functional theory (DFT) is a key computational tool for predicting the crystal structure and physical properties of semiconductor materials.14 Alotaibi et al. estimated the energy harvesting potential of Cs2AgBi(Cl/Br/I)6.15 Hnuna et al. examined the band gap and optical performance of DPs Rb2AgIn(Cl/Br/I)6, which showed visible absorption and p-type semiconductors.16 In addition, Cs2NaInBr6 and Cs2NaInI6 exhibit superior stability and are suitable for wasted thermal energy.17 Rb2InSb(F/Cl/Br/I)6 has been used to elucidate direct Eg and has shown exceptional optical attributes for Br and I-based compounds.18 Moreover, several other combinations based on DFT explorations19–22 require further validation by experimental researchers. In addition, recent studies on indium-based DP combinations have shown their significance and effectiveness.23,24 Recently, new single perovskites InGeF3, InGeCl3, and InGeI3 are efficient for photovoltaics and thermal energy conversion applications.25 Consequently, this study motivated us to predict the photovoltaic and thermoelectric potentials of innovative indium-based DP combinations.
The present investigation focused on the performance analysis of DP In2AgSbX6 (X = Cl, Br, and I) combinations based on optical and thermoelectric analysis. The stability under cubic arrangement and under mechanical conditions was also investigated, which is crucial for various technological applications. To the best of our knowledge, there has been no written research on the studied In2AgSbX6 (X = Cl, Br, and I) DP combinations in literature. This report presents a comprehensive DFT-based examination of In2AgSbCl6, In2AgSbBr6, and In2AgSbI6, accompanied by a full explanation of the relevant DP compounds, highlighting the significance of the analyzed DP combinations for future applications in photovoltaics and various other power generation technologies.
2. Computational methodology
This work employed DFT by deploying the WIEN2k code26 to assess the optical and thermoelectric analysis of In2AgSbCl6, In2AgSbBr6, and In2AgSbI6. This code employs the full potential linearized augmented plane wave (FP-LAPW) method.27 The optimization procedure was conducted for the simulated cubic frameworks to obtain the optimal lattice constants (a0) and structural parameters. Following the verification of the structural characteristics, self-consistent-field (SCF) computations were conducted to determine the electronic characteristics and associated aspects. The Generalized Gradient Approximation (GGA) established by Perdew, Burke, and Ernzerhof (PBE)28 was employed to address compositional considerations. To rectify the recognized band gap underestimation, the Tran–Blaha–modified Becke–Johnson technique (TB-mBJ) was employed.29 The maximum angular momentum value, lmax, is established at 10 and Gmax was fixed at 14. The muffin tin radii (RMT) values (in atomic units) for the specified components are as follows: 2.1 for In, 2.0 for Ag, 2.0 for Sb, and 2.0 for Cl or Br. The RMT × Kmax = 8 was selected, accompanied by a binding energy value of −6 Ry, where RMT is the muffin-tin radius of the smallest constituent of the examined DP compounds. The optical and thermoelectric aspects were determined using TB-mBJ with a dense k-mesh of 10 × 10 × 10. Additionally, some thermoelectric (TE) characteristics have been calculated using the BoltzTraP code, which uses semiclassical Boltzmann theory to understand TE aspects and the relationship with temperature and chemical potential of the TE properties. The constant relaxation time approximation (CRTA) was employed to compute the TE parameters, with constant relaxation time (τ) set at 10−14 s.3. Results and discussion
3.1. Structural properties and stability
The structural characteristics were analyzed to determine the specifics of the arrangement and to evaluate the operational variations in the features of the examined substances. The compounds In2AgSbX6 (X = Cl, Br, and I) possess an A2M+M3+X6 crystalline structure and are classified under the space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, with a space group number of 225. The structural configuration of the In2AgSbX6 perovskite with the cubical framework is illustrated in Fig. 1. The total energy of In2AgSbX6 was reduced by optimizing the changes in the unit cell volume, as shown in Fig. 2. This facilitates the identification of ground state characteristics. In proximity to the volume at the ground state (V0), the framework exhibits stability in the equilibrium or ground state. Significantly expanding the volume beyond V0 may decrease energy as the structure moves toward greater stability. As the substance approaches equilibrium, the potential energy (PE) decreases, and the volume slightly increases. At equilibrium volume, the energy reaches its minimum value (E0), which reflects the most stable configuration of the DP compound under scrutiny. When the volume exceeds V0, the energy starts to increase once more because the substance has been elongated beyond its stable configuration, resulting in a heightened PE due to increased atomic separation. The obtained lattice constant (a0) and equilibrium parameters (V0 and E0) are presented in Table 1. A notable difference in a0, V0, and E0 is observed when In2AgSbCl6 is interchanged with In2AgSbBr6 and In2AgSbI6, which are replaced in the compounds. The variation in the dimensions of the halides results in a regular shift in the lattice parameters (a0), exemplifying the “octahedral impact,” which dramatically affects the volume of the unit cell.30 The a0 values for In2AgSbX6 (X = Cl, Br, and I) are consistent with those of similar materials such as Rb2AgSbX6 (X = Cl, Br) and Cs2AgSbX6 (X = Cl, Br, and I), as displayed in Table 1. The ionic radius of In is 0.8 Å, which is less than that of Rb (1.52 Å) and Cs (1.67 Å). Therefore, In2AgSbX6 had relatively lower a0 values than Rb2AgSbX6 and Cs2AgSbX6. This examination emphasizes the correlation between halide substitution and structural alterations, illustrating the significant implications of Cl/Br/I size on the entire crystal framework and the long-term stability of these substances.
m, with a space group number of 225. The structural configuration of the In2AgSbX6 perovskite with the cubical framework is illustrated in Fig. 1. The total energy of In2AgSbX6 was reduced by optimizing the changes in the unit cell volume, as shown in Fig. 2. This facilitates the identification of ground state characteristics. In proximity to the volume at the ground state (V0), the framework exhibits stability in the equilibrium or ground state. Significantly expanding the volume beyond V0 may decrease energy as the structure moves toward greater stability. As the substance approaches equilibrium, the potential energy (PE) decreases, and the volume slightly increases. At equilibrium volume, the energy reaches its minimum value (E0), which reflects the most stable configuration of the DP compound under scrutiny. When the volume exceeds V0, the energy starts to increase once more because the substance has been elongated beyond its stable configuration, resulting in a heightened PE due to increased atomic separation. The obtained lattice constant (a0) and equilibrium parameters (V0 and E0) are presented in Table 1. A notable difference in a0, V0, and E0 is observed when In2AgSbCl6 is interchanged with In2AgSbBr6 and In2AgSbI6, which are replaced in the compounds. The variation in the dimensions of the halides results in a regular shift in the lattice parameters (a0), exemplifying the “octahedral impact,” which dramatically affects the volume of the unit cell.30 The a0 values for In2AgSbX6 (X = Cl, Br, and I) are consistent with those of similar materials such as Rb2AgSbX6 (X = Cl, Br) and Cs2AgSbX6 (X = Cl, Br, and I), as displayed in Table 1. The ionic radius of In is 0.8 Å, which is less than that of Rb (1.52 Å) and Cs (1.67 Å). Therefore, In2AgSbX6 had relatively lower a0 values than Rb2AgSbX6 and Cs2AgSbX6. This examination emphasizes the correlation between halide substitution and structural alterations, illustrating the significant implications of Cl/Br/I size on the entire crystal framework and the long-term stability of these substances.
 | ||
| Fig. 1 Atomic visualization of the cubic structure for DP compounds of In2AgSbX6 in 2D and 3D polyhedral view. | ||
 | ||
| Fig. 2 Varying energy versus volume curve obtained by optimizing the structures of (a) In2AgSbCl6, (b) In2AgSbCl6, and (c) In2AgSbI6. | ||
| Compounds | a0 (Å) this work | a0 (Å) other works | V0, (a.u.)3 | E0 (Ry) | B (GPa) | τ | Ef (eV per atom) |
|---|---|---|---|---|---|---|---|
| In2AgSbCl6 | 10.64 | 10.71 (ref. 33), 10.77 (ref. 34) | 2036.9395 | −52673.0561 | 29.73 | 0.94 | −1.97 |
| In2AgSbBr6 | 11.18 | 11.26 (ref. 33), 11.12 (ref. 34) | 2359.4342 | −78414.6102 | 25.13 | 0.94 | −1.55 |
| In2AgSbI6 | 11.93 | 11.99 (ref. 34) | 2865.6652 | −132563.1825 | 19.02 | 0.95 | −1.32 |
The calculation of the tolerance factor confirms the integrity or stability of cubic DP compounds, which can be calculated from the ionic radii as follows:
 | (1) |
The resulting values (Table 1) vary from 0.81 to 1.11 for the designated materials, confirming that they remain stable in the cubic framework.31 Furthermore, to computationally assess the feasibility of synthesis and evaluate the resilience of these DP substances against spontaneous disintegration into alternative binary or elemental segments, the formation energy (Ef) is determined from the enthalpy, as described in ref. 32:
| Ef = EIn2AgSbX6 − (2EIn + EAg + ESb + 6EX) | (2) |
The ascertained Ef values are shown in Table 1. The negative values signify that In2AgSbX6 (X = Cl, Br, and I) is chemically stable, indicating that these compounds can be synthesized practically under atmospheric circumstances.
In addition, we executed ab initio molecular dynamics (AIMD) calculations at 300 K, 500 K, and 700 K to confirm the stability of In2AgSbCl6, In2AgSbBr6, and In2AgSbI6. The canonical ensemble (NVT) with an interval period of 1.0 femtosecond (fs) and the Nosé thermostat were employed to perform the computations. The results are shown in Fig. 3(a–c)3, and the computation time was up to 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 picoseconds. The material's stability is demonstrated by the fact that, while considering both the total energy and the simulation duration, the AIMD research revealed energy variations around an equilibrium average value. However, suppose the total energy levels are consistently rising or falling. In this case, the results might indicate that the material is unstable because of an abrupt shift in phase or a change in its chemical structure. In addition, due to thermal vibrations within the structure, a small loss of energy occurs due to temperature variations between 300 K and 700 K. Regardless, In2AgSbCl6, In2AgSbBr6, and In2AgSbI6 show a stable mean total energy value for temperature fluctuations. The fact that these halides remain stable indicates that neither phase nor structural breakdown has evolved significantly. Thus, the double perovskites In2AgSbCl6, In2AgSbBr6, and In2AgSbI6 exhibit dynamic stability and may be used for future technological applications.
000 picoseconds. The material's stability is demonstrated by the fact that, while considering both the total energy and the simulation duration, the AIMD research revealed energy variations around an equilibrium average value. However, suppose the total energy levels are consistently rising or falling. In this case, the results might indicate that the material is unstable because of an abrupt shift in phase or a change in its chemical structure. In addition, due to thermal vibrations within the structure, a small loss of energy occurs due to temperature variations between 300 K and 700 K. Regardless, In2AgSbCl6, In2AgSbBr6, and In2AgSbI6 show a stable mean total energy value for temperature fluctuations. The fact that these halides remain stable indicates that neither phase nor structural breakdown has evolved significantly. Thus, the double perovskites In2AgSbCl6, In2AgSbBr6, and In2AgSbI6 exhibit dynamic stability and may be used for future technological applications.
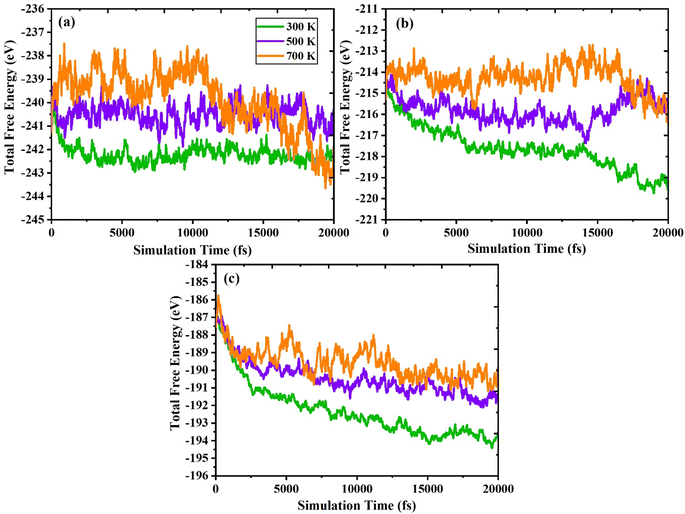 | ||
| Fig. 3 AIMD plots showing total free energy (eV) versus simulation time (fs) for (a) In2AgSbCl6, (b) In2AgSbBr6, and (c) In2AgSbI6. | ||
3.2. Elastic properties
A thorough analysis of the structure-related characteristics yields an understanding of the mechanical behavior of substances.35 The atomic configuration inside the framework is crucial for estimating the framework's susceptibility to external pressures and thus determines its mechanical stability. The evaluation of this characteristic is essential for device manufacturing and engineering applications. We determined the elastic constants (Cij) of the specified DP materials using the volume and energy method while preserving deformation tetrahedrally and rhombohedrally inside the cubic flexible framework.36,37 The estimated Cij (C11, C12, and C44) for In2AgSbCl6, In2AgSbBr6, and In2AgSbI6 halide DP materials (Fig. 4) were positive and uphold the Born stability criteria.38 The computed Cij offers perspectives on the stability under mechanical forces and enables the examination of diverse elastic properties. Several other factors, including bulk (B), shear (G), and Young's (Y) elastic moduli, are obtained from Cij using mathematical relationships documented in previous studies,39 with the results presented in Fig. 5(a–c).Young's modulus indicates the degree of rigidity of DP compounds, indicating their capacity to hold up to distortion during horizontal stretching or compressive stresses. In contrast to Young's modulus, which pertains to rigidity or hardness, the bulk modulus emphasizes the ability to compress a material, with elevated values signifying increased resistance to volumetric changes. The shear modulus (G), which denotes the ability to endure plastic deformation, suggests that lower G-values enable less endurance against plastic deformation in DP compounds.40 According to the data presented in Fig. 5(a), In2AgSbCl6 exhibited a higher B value of 32.06, which is considerably greater than the B values of In2AgSbBr6 (26.01) and In2AgSbI6 (21.5). Although In2AgSbCl6, In2AgSbBr6, and In2AgSbI6 reveal fewer values than 40 GPa (for hard materials)41 and show a flexible nature, In2AgSbCl6 is superior in withstanding volumetric changes than In2AgSbBr6 and In2AgSbI6. Because of these characteristics, In2AgSbCl6 is a promising option for use in thin-film solar cell manufacturing, where flexibility and stress resilience are crucial.42 Moreover, In2AgSbCl6 shows higher values of G (9.56) and Y (26.08) than In2AgSbBr6 and In2AgSbI6, as demonstrated in Fig. 5(b) and (c), respectively, indicating higher endurance against plastic deformation and hardness. This higher plasticity indicates that In2AgSbCl6 is comparatively more resistant to plastic deformation than In2AgSbBr6 and In2AgSbI6, making it suitable for foldable devices. Additionally, the higher rigidity of In2AgSbCl6 is suitable for systems requiring higher structural stability, such as resistance to fracture under applied pressure.
Furthermore, the analysis of the ductile nature of materials further confirms their suitability for use in flexible optoelectronics and foldable thin films for solar cell applications, which can be determined by elastic features.43 Poisson's ratio (ν) showcases insights into a material's ductility and flexibility, which is elucidated by values ranging from 0.26 to 0.42, below which materials are referred to as brittle. The values of ν for In2AgSbCl6, In2AgSbBr6, and In2AgSbI6 were 0.36, 0.41, and 0.40, respectively, as shown in Fig. 5(d). Moreover, the ductile or brittle features of In2AgSbCl6, In2AgSbBr6, and In2AgSbI6 may be evaluated more thoroughly using Pugh's ratio, which is represented as B/G. Fig. 5(e) indicates that the Pugh ratio for In2AgSbCl6, In2AgSbBr6, and In2AgSbI6 exceeds the crucial value of 1.75, thereby affirming the ductile characteristics of these perovskites. This ductility is essential for systems that require materials capable of enduring mechanical stresses without breaking, such as flexible technologies like solar cells.
3.3. Mechanical anisotropy
Mechanical anisotropy is a crucial characteristic that significantly affects several physical characteristics. It significantly influences phenomena such as permanent deformation and fracture formation in crystals, as well as the mechanical characteristics of materials, especially their texture. The relevance of these consequences is significant in the field of engineering because comprehending the influence of mechanical anisotropy on the functionality of a substance is crucial for the creation of efficient and lasting structures. Diverse anisotropy indexes are employed to determine the orientation dependency of a material's characteristics. A commonly used metric for purposes such as the anisotropic parameter (A) quantifies the disparity in binding strength among atoms situated in different crystalline axes. This allows scientists and technologists to modify the layout and functionality to meet particular requirements. A comprehensive understanding of these anisotropic features can enhance material effectiveness, improve structural durability, and ensure the longevity and safety of materials. Due to the symmetry of In2AgSbCl6, In2AgSbBr6, and In2AgSbI6 in cubical configuration, A was determined using the following relation:
 | (3) |
Fig. 5(f) presents the A values, which are below the isotropic line (A = 1), indicating that In2AgSbCl6, In2AgSbBr6, and In2AgSbI6 are anisotropic DP compounds.44 The A values indicate that In2AgSbCl6 is highly anisotropic compared to In2AgSbBr6 and In2AgSbI6, affirming that In2AgSbCl6 is more durable and long-lasting.
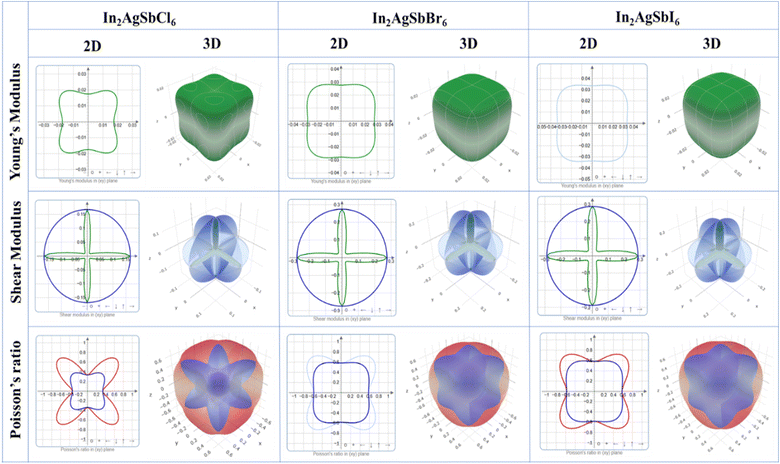
To illustrate the degree of anisotropy of elastic moduli in In2AgSbCl6, In2AgSbBr6, and In2AgSbI6 DP compounds, three-dimensional surface designs (3D contours) and their two-dimensional figures (2D contours) were generated. The graphic representations were generated using the ELATE tool,45 which uses the estimated Cij values. In an isotropic crystallized material, such representations are often shown to be exact spheres in three-dimensional space. Nonetheless, for anisotropic substances like In2AgSbCl6, In2AgSbBr6, and In2AgSbI6, the three-dimensional surfaces diverge from a sphere-like configuration, signifying varying mechanical qualities along distinct crystalline orientations.46 Fig. 6 shows the 2D and 3D anisotropic visualizations for Y and G (in GPa) and ν of the In2AgSbCl6, In2AgSbBr6, and In2AgSbI6 compositions, illustrating the degree of mechanical anisotropy. Anisotropy is evident in the irregular shape of the 3D surfaces, demonstrating the directional sensitivity of the elastic characteristics inside the crystalline structure.
This investigation entails the computation and graphical representation of the lowest and highest estimated values of Y and G (in GPa) and ν of the In2AgSbCl6, In2AgSbBr6, and In2AgSbI6 in various orientations, as shown in Table 2. The descending order of anisotropy for these parameters is In2AgSbCl6 > In2AgSbBr6 > In2AgSbI6. Hence, the hierarchy of the values indicates that In2AgSbCl6 has the greatest degree of anisotropy, followed by In2AgSbBr6, and finally In2AgSbI6. Graphical and numerical assessments are essential for understanding the elastic characteristics of In2AgSbCl6, In2AgSbBr6, and In2AgSbI6 with different crystal lattice orientations. These findings are crucial in technology and development for the customization and enhancement of materials' mechanical characteristics in particular applications, thereby assuring their dependability and reliability under diverse stress circumstances.
| Parameters | In2AgSbCl6 | In2AgSbBr6 | In2AgSbI6 | |
|---|---|---|---|---|
| Y (Gpa) | Ymin | 0.017431 | 0.027755 | 0.033557 |
| Ymax | 0.029366 | 0.036733 | 0.044137 | |
| A | 1.685 | 1.323 | 1.315 | |
| G (Gpa) | Gmin | 0.013172 | 0.033267 | 0.040161 |
| Gmax | 0.1675 | 0.27473 | 0.28818 | |
| A | 12.72 | 8.258 | 7.176 | |
| ν | νmin | −0.95706 | −0.95433 | −0.94429 |
| νmax | −0.33833 | −0.58285 | −0.58221 | |
| A | 0.3535 | 0.6107 | 0.6166 | |
3.4. Electronic properties
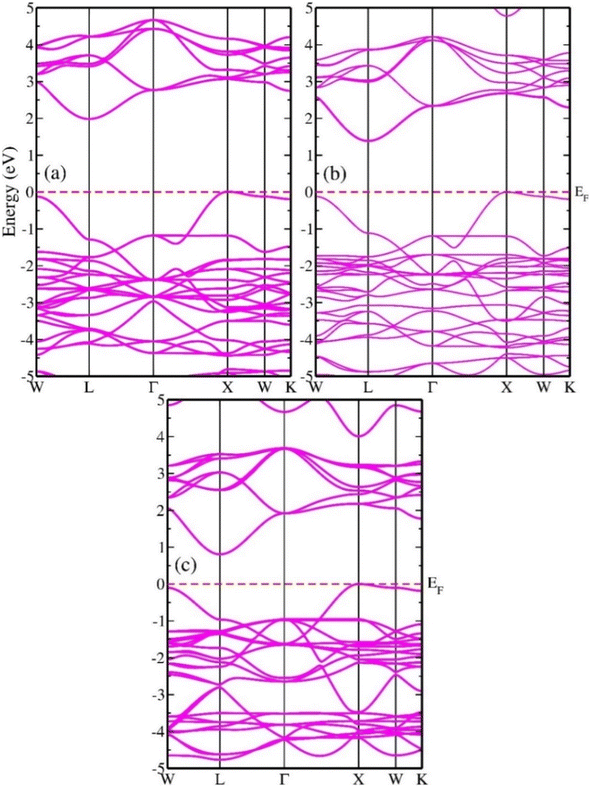
In the analysis of electronic properties, estimation of the band structure (BS) is essential because it provides information on the distribution of the energy concentrations of electrons inside a substance. Before substances can be used in different technologies, their energy BS must be assessed to obtain a more comprehensive understanding of the materials. Thus, insulating substances, semiconductor components, and metallic compounds can be categorized according to their energy BS.47 Fig. 7(a–c) show the band profiles of In2AgSbCl6, In2AgSbBr6, and In2AgSbI6, respectively, obtained using the mBJ approximation. There is a separation between the conduction and valence bands (CB and VB) because their energies are shifted from the Fermi level (EF), as visualized from the BS shown in Fig. 7. Additionally, Fig. 7 indicates that In2AgSbCl6, In2AgSbBr6, and In2AgSbI6 are semiconductors because their energy band gaps (Eg) range from 0.7 to 2.0 eV. In2AgSbCl6 exhibits an indirect (L–X) Eg of 1.95 eV, and In2AgSbBr6 exhibits an indirect (L–X) Eg of 1.35 eV. For In2AgSbI6, the value of Eg was further reduced to 0.78 eV (L–X). The bandgap decreased when the halogen atom size increased from In2AgSbCl6 to In2AgSbI6, as shown in Fig. 7. As the lattice constant rises, the spacing between atoms will broaden. It follows that the coulombic interaction between the electrons in VB and the nucleus would become weaker, resulting in adjustments in the electronic states in CB closer to EF. Therefore, the minimal amount of energy needed to transform the constrained electrons in VB into electrons in CB allows them to move unhindered inside the material. The energy required to excite valence electrons from the VB to CB decreases as the separation between atoms increases, which is the primary requirement for efficient electronic transitions.48Furthermore, the extracted BS and tunability of Eg indicate that In2AgSbCl6, In2AgSbBr6, and In2AgSbI6 can be used in innovative optical technologies such as photovoltaic and thermal energy conversion systems. The band structure configurations of materials with respect to the Fermi level may establish their characteristics exactly based on semiconducting theory. The chemicals included in this investigation have electrical band gap values similar to those of other perovskite-based substances that have been demonstrated in the literature; these values are shown in Table 3.
The predicted densities of states of the atoms are shown in Fig. 8 to evaluate the contribution of atoms to the formation of VB and CB. Fig. 8 shows the orbital projected density of states (PDOS) and total density of states (TDOS) of In2AgSbCl6, In2AgSbBr6, and In2AgSbI6. From this analysis, it can be seen that the transition metal Ag's d-orbital occupies the states in the VB, whereas the p-states of Sb atoms characterize the CB. The EF was located close to the VB, the highest point indicating the p-type nature of the materials. PDOS discovered that at EF, the d-orbital of the Ag atom at the maximum VB states and the p-states of Sb atoms at the CB minimum contributed the most. Due to the modification of In2AgSbCl6 with In2AgSbBr6 and In2AgSbI6, there is a shift in the electronic states in the CB above EF. Therefore, the substitution of halogen atoms causes a shift in the electronic states, thereby facilitating electronic transitions. The p-orbitals of the In also contribute to the generation of the CB in the compounds under study, with the contribution being slightly distant from EF compared to the Sb-p. Moreover, the VB is also contributed by the p-orbital of Cl/Br/I, which is less than the Ag-d states. For all configurations, no hybridization was observed in the creation of energy levels at the EF due to the energy gap. Therefore, the contributing atomic states in the VB and CB will have greater significance in assessing the electronic transitions for technological applications.
In addition, the effective mass is a crucial measure for assessing the optical and electrical features of substances, such as conductance and mobility. The movement of carriers is inversely proportional to the effective mass values of holes and electrons, which decrease with increasing effective mass values.49 Eqn (4) facilitates the calculation of the effective masses by non-linear fitting of the BS curve.
 | (4) |
Additionally, the exciton binding energy (Eexb) was evaluated by utilizing the effective masses and dielectric constant at zero frequency ε1(0) by the given eqn (5). Additionally, the exciton binding energy is the amount of energy required to separate an exciton, which consists of two electrons and a hole, into free carriers of energy. In photovoltaic technologies, effective absorption and carrier collection are made possible by materials with low binding energies.
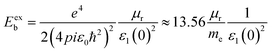 | (5) |
The effective masses and binding energies are listed in Table 3. The electrons and holes in In2AgSbCl6 have a higher effective mass than the electrons in In2AgSbBr6 and In2AgSbI6, suggesting that In2AgSbCl6 electrons are more inert or face greater movement resistance.49 Additionally, the values of Eexb have shown that In2AgSbCl6, In2AgSbBr6, and In2AgSbI6 have lower exciton binding energies than CsPbI3 (0.068 eV),50 Cs2AgBiBr6 (0.268 eV),51 and Cs2AgBiBr6 (0.227 eV).52 This indicates that In2AgSbCl6, In2AgSbBr6, and In2AgSbI6 can serve as absorber layer materials in solar cell applications.
3.5. Optical properties
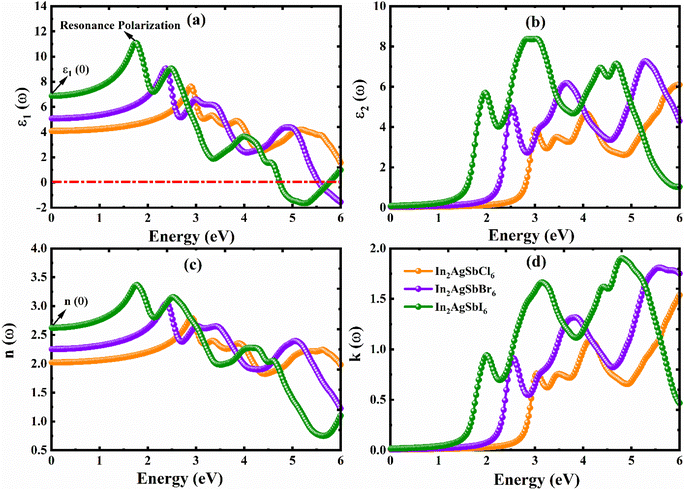
We can better comprehend materials' possible use in optoelectronics and photovoltaics by examining their optical characteristics, which offer important insights into how they respond to light. A thorough comprehension of a material's optical characteristics is necessary to maximize its capability in optoelectronics and solar cells. This work has thoroughly examined the optical characteristics of In2AgSbCl6, In2AgSbBr6, and In2AgSbI6. A medium's interaction with the incoming electromagnetic radiation is described by the dielectric function, ε(ω), which is defined ε(ω) = ε1(ω) + iε2(ω). The ε(ω) can be used to determine optical characteristics by applying well-established mathematical concepts.53–55 All the optical parameters of In2AgSbCl6, In2AgSbBr6, and In2AgSbI6 were obtained between 0 and 6 eV, as shown in Fig. 9(a–d) and 10(a–d). The polarization behavior of a dielectric material is defined by the real part, ε1(ω). The absorptivity of halides can be described by the imaginary component, ε2(ω).56 To comprehensively understand the material's optoelectronic characteristics, ε1(ω) and ε2(ω) were computed as functions of photon energy in this DFT investigation. The ε1(ω), was calculated via the Kramers–Kronig transformation, and ε2(ω), was obtained by calculating the momentum matrix elements. All other optical characteristics were calculated using the ε1(ω) and ε2(ω) values of the dielectric function, as described in ref. 57 and 58.Fig. 9(a) and (b) show the ε1(ω) and ε2(ω) values for In2AgSbX6 (X = Cl, Br, and I) under incident photon energies, respectively. The ε1(ω) curve starts at a static value, ε1(0), which is 4.08 for In2AgSbCl6, 4.67 for In2AgSbBr6, and 6.88 for In2AgSbI6, as shown in Fig. 9(a). The value of ε1(0) is important for determining the exciton binding energy (Eexb) required to separate electron–hole pairs. The materials with higher ε1(0) results in less Eexb, as In2AgSbI6 has higher ε1(0) among the studied substances and showed the lowest Eexb, as listed in Table 3. Moreover, the listed values for In2AgSbCl6, In2AgSbBr6, and In2AgSbI6 are considerably lower than those of CsPbI3 (0.068 eV),50 Cs2AgBiBr6 (0.268 eV),51 and Cs2AgBiBr6 (0.227 eV).52 These characteristics render In2AgSbCl6, In2AgSbBr6, and In2AgSbI6 for solar cells with an exceptional tendency. Then, with the increase in the photon energy, it climbs to its highest value, with an amplitude of 7.6 for In2AgSbCl6 at 2.90 eV, 9.1 for In2AgSbBr6 at 2.35 eV, and 11.1 for In2AgSbI6 at 1.75 eV. In the presence of photons with energies ranging from 4.7 to 6 eV, the halide DPs In2AgSbBr6 and In2AgSbI6 show negative values for ε1(ω), suggesting that both halides demonstrate total internal reflection of light in this region. According to this behavior, these materials appear to have significant reflectivity and low light transmission under photon energy settings.59 The fluctuating transformation rates of the incoming photons due to interaction with the DPs are responsible for the observed variations in ε1(ω).
Furthermore, inter-band transitions and intra-band transitions are two categories of transitions that determine a material's optical behavior. The metallic behavior of materials is characterized by intra-band transitions; thus, since the materials under study are semiconductors, only inter-band transitions were considered while determining the optical characteristics.60 The thresholds of ε2(ω) for In2AgSbCl6, In2AgSbBr6, and In2AgSbI6 correspond to electronic Eg (see Table 2), indicating that these DPs are semiconductors. All materials ε2(ω) start to rise as soon as their photon energy reaches the value of their individual electronic Eg. In the electronic properties discussed above, the bandgap is correlated with the first absorption peak. The BS and DOS plots suggest the presence of deep energy states responsible for the secondary absorption peaks. These states result from orbital hybridization, as explained in ref. 61. For every material, the value of ε2(ω) increased with increasing photon energy until it reached its highest peak value (see Fig. 9(b)). According to the ε1(ω) and ε2(ω) results, the peak values for all materials were in the visible and UV areas.
The extinction coefficient, k(ω), and refractive index, n(ω), are two other significant optical characteristics that are crucial for assessing the energy gain and loss in materials during the manufacturing of optoelectronic memory devices.57 Through the following formulae,61 ε(ω) is theoretically connected to n(ω), and k(ω):
| ε1(ω) = n2 − k2 | (6) |
| ε2(ω) = 2nk | (7) |
Fig. 9(c and d) show the n(ω) and k(ω) values for In2AgSbX6 (X = Cl, Br, and I) under incident photon energies, respectively. The optical spectra of the materials under investigation are not well-documented either experimentally or theoretically. The n(ω) shows properties that are comparable to those of ε1(ω). The static n(0) values are 2, 2.3, and 2.6 for In2AgSbCl6, In2AgSbBr6, and In2AgSbI6. At photon energies of approximately 2.90 eV, 2.45, and 1.75 eV, the maximum recorded values of n(ω) for In2AgSbCl6, In2AgSbBr6, and In2AgSbI6 are 3.7, 3.1, and 3.4, respectively. The n(ω) graph shows a decreasing tendency with increasing photon energy after these peaks. The peak values for In2AgSbCl6, In2AgSbBr6, and In2AgSbI6 are 1.6, 1.7, and 1.9, respectively, at photon energies of 6 eV, 5.6 eV, and 4.9 eV. These k(ω) values are comparable to those of ε2(ω). According to n(ω) and k(ω) results, the peak values of all materials were in visible as well as UV areas.
The amount of light absorbed by a substance per unit length of propagation is measured by the absorption coefficient, α(ω).62 A restricted photon absorbing capacity is indicated by the transparency of materials with low α(ω). Materials with high α(ω), on the other hand, have efficient light absorbance capabilities. Consequently, α(ω) is a thorough indicator of how a material reacts to light. Fig. 10(a) demonstrates that no absorption occurs prior to the absorption edge; absorption only starts when the energy of the incident photons enters the visible spectrum. After the absorption edge, the α(ω) of these materials shows a notable increase, reaching peak magnitudes (×104 cm) at energies of 3.08/4.1/6.0 eV for In2AgSbCl6, 2.5/3.9/5.9 eV for In2AgSbBr6, and 2.03/3.25/4.9 eV for In2AgSbI6. In the IR spectrum, they are transparent, whereas in the visible and UV regions, they efficiently absorb light. The intensities of the peaks in the vis-to-UV region were observed because more states were available for electronic transitions due to absorption.
The ability of a material to conduct electricity when exposed to light is referred to as photoconductivity or optical conductivity, σ(ω).63 This characteristic is essential for comprehending and creating optoelectronic devices. Fig. 10(b) shows the σ(ω) of In2AgSbX6 (X = Cl/Br/I) against photon energy. The peak values of all materials were observed at energies corresponding to α(ω). These variations in σ(ω) can be explained by stronger interactions between photons and the electronic structure of the material, as well as increased photon absorption. The increased photoconductive characteristics of In2AgSbX6 (X = Cl/Br/I) make it suitable for optoelectronic applications.
The capability of a material to bounce back light photons is measured by its optical reflectivity coefficient, R(ω).64 Fig. 10(c) plots R(ω) against the photon energies of In2AgSbCl6, In2AgSbBr6, and In2AgSbI6. The static R(0) values were 0.12, 0.15, and 0.2 for In2AgSbCl6, In2AgSbBr6, and In2AgSbI6, respectively. The peak R(ω) values for In2AgSbCl6, In2AgSbBr6, and In2AgSbI6 were 0.24 at 3 eV, 0.36 at 5.5 eV, and 0.42 at 5.3 eV. These energy levels are within the ultraviolet (UV) range. These materials could therefore be very effective UV radiation shielding. Nevertheless, it is noted that for In2AgSbI6, R(ω) falls below 0.1 in the 5.5–6 eV energy range. The effective transparency of the incoming photons is indicated by low In2AgSbI6 R(ω) within the range of the observed spectrum.
The loss function L(ω) measures the energy gained or lost during reflection and represents the energy loss in the medium.63 A material's energy loss function L(ω) is intimately related to α(ω) and R(ω). Since L(ω) is quite lower in magnitude for In2AgSbCl6, In2AgSbBr6, and In2AgSbI6 in the visible range of the energy spectrum; these halides exhibit high absorption. The L(ω) of In2AgSbCl6, In2AgSbBr6, and In2AgSbI6 are plotted in Fig. 10(d). In the energy range of 5.5–6 eV, the L(ω) value of In2AgSbI6 is approximately 0.89. In contrast, In2AgSbCl6 and In2AgSbBr6 exhibited a smaller increase in peak height. The higher L(ω) values suggest improved absorption capacities.
Consequently, the above discussion on parameters ε(ω), α(ω), and σ(ω) higher polarizability, absorption, and optical conduction in the visible regions for In2AgSbCl6, In2AgSbBr6, and In2AgSbI6. Moreover, R(ω) and L(ω) validates the effectiveness of these halides in visible regions with low reflective (<0.32) and optical losses (<0.2). Hence, In2AgSbCl6, In2AgSbBr6, and In2AgSbI6 are favorable materials as absorber layer materials in solar cells.
3.6. Thermoelectric (TE) properties
 | ||
| Fig. 11 Plot of TE features varying with temperature: (a) S (b) σ/τ (c) κe/τ (d) S2 σ/τ for In2AgSbCl6, In2AgSbBr6, and In2AgSbI6. | ||
The potential difference caused by a temperature gradient across the material is measured by S, which is an important parameter.66 The predominant charge carrier is determined by the Seebeck coefficient (S), which also helps determine the voltage generated by temperature fluctuations. Charge carriers are classified according to their sign, where positive and negative S denote holes and electrons, respectively. The p-type semiconductor nature of these materials is indicated by the positive values of S (see Fig. 11(a)), which confirms that the majority of charge carriers in In2AgSbX6 (X = Cl/Br/I) are holes. When T was increased to 600 K, the S values of all materials decreased. S decreased from 0.254, 0.259, and 0.254 (in mV K−1) at 300 K to 0.248, 0.247, and 0.240 (in mV K−1) for In2AgSbCl6, In2AgSbBr6, and In2AgSbI6, respectively.
The electrical conductivity (σ/τ) is another crucial TE characteristic that quantifies how the electric current flows as temperature changes.67 Due to increased mobility and carrier concentration at higher temperatures, electrons can move through the material more readily, as seen by the σ/τ (see Fig. 11(b)), increasing linearly with temperature. Due to Ag's lower electronegativity than Sb, a notable improvement in σ/τ is shown. Higher carrier concentration, enhanced charge mobility, and decreased power consumption are the outcomes of Ge's lower electronegativity, which causes valence electrons to be bound loosely. The σ/τ demonstrates the maximum intensities (×1019 Ω−1 m−1 s−1) of 0.44, 0.45, and 0.46 for In2AgSbCl6, In2AgSbBr6, and In2AgSbI6, respectively.
The material's heat capacity is indicated by its thermal conductivity (κe/τ).67 A greater density of states (DOS) close to the Fermi level is linked to higher κe/τ, which enhances σ/τ by offering additional energy levels for electron mobility. To sustain a high-temperature gradient and achieve the best TE capability, low κe/τ is necessary (see Fig. 11(c)). According to the theoretical predictions, all materials exhibit an increase in κe/τ as the temperature rises, indicating efficient heat transport. Similar to σ/τ, κe/τ rises with temperature, and for In2AgSbCl6, In2AgSbBr6, and In2AgSbI6 have κe/τ of 1.24, 1.27, and 1.35 × 1014 W m−1 K−1 s−1 at 200 K, whereas they are 2.11, 2.08, and 2.02 × 1014 W m−1 K−1 s−1 at 600 K, respectively.
The power factor (PF) of a material, which is crucial for assessing TE capability, is computed as PF = S2σ/τ, where σ/τ is the electrical conductivity and S is the Seebeck coefficient.64 At 200 K, the PF starts at 0.46, 0.48, and 0.51 × 1011 W m−1 K−2 s−1 for In2AgSbCl6, In2AgSbBr6, and In2AgSbI6, respectively. At 600 K, the values reached 2.76, 2.71, and 2.65 × 1011 W m−1 K−2 s−1, respectively (Fig. 11(d)). These results indicate that all materials are suitable for high-temperature applications because their PFs steadily increase with temperature.
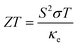 | (8) |
For the practical application of substances in TE technologies, parameters S and σ should be increased because these features directly affect the TE performance. The thermal conductivity (κe/τ) impacts inversely on the TE performance and should be lower than the S and σ. At 300 K (room temperature), the ZT values of In2AgSbCl6, In2AgSbBr6, and In2AgSbI6 were 0.75, 0.77, and 0.76, respectively. Fig. 13 shows similar plots for In2AgSbCl6, In2AgSbBr6, and In2AgSbI6, with ZT increasing from 200 K to 600 K. The highest values for these DP compounds were 0.785 for In2AgSbCl6, In2AgSbBr6, and 0.780 for In2AgSbI6. These values demonstrate efficient thermal energy conversion into useful power at room temperature and higher temperatures.
Additionally, these substances offer higher ZT values than several reported similar halides, such as Cs2AgBiCl6 (0.72), Cs2AgBiBr6 (0.71),72 Cs2AgSbCl6 (0.72), and Cs2AgSbBr6 (0.73),73 at 300 K. Consequently, the elevated ZT measurements for In2AgSbCl6, In2AgSbBr6, and In2AgSbI6 indicate that it is capable of effectively converting thermal radiation into electricity, rendering it an appealing choice for thermal energy recovery devices and the production of thermal electricity. The prospective use of the substance in TE devices is further supported by the substantial Seebeck coefficient, which measures the voltage produced in reaction to a difference in temperature across the material, demonstrating a robust TE effect. In2AgSbCl6, In2AgSbBr6, and In2AgSbI6 are advantageous materials for the development of thermoelectric systems for a variety of manufacturing purposes due to their elevated ZT and S values. These results suggest that TEs can achieve superior performance. Therefore, it provides noteworthy energy transmission features.
4. Conclusion
Briefly, the stability, optoelectronic, and thermal transport characteristics of In2AgSb(Cl/Br/I)6 were investigated by comprehensive DFT exploration. A tolerance factor ranging between 0.94 and 0.95 suggests cubic stability and a formation energy ranging between −1.97 and −1.32 eV per atom ensured thermal stability. The AIMD analysis confirmed the dynamic stability of In2AgSb(Cl/Br/I)6 up to 700 K. The mechanical stability and asymmetric and ductile characteristics validated suitability in foldable technologies. The electrical properties revealed indirect band gaps (Eg) of 1.95 eV, 1.35 eV, and 0.78 eV for In2AgSbCl6, In2AgSbBr6, and In2AgSbI6, respectively, which lie in the acceptable region for solar cell applications. The lower binding energies of excitons for In2AgSbCl6, In2AgSbBr6, and In2AgSbI6 compared with the efficient solar cell materials CsPbI3 and Cs2AgBiBr6 confirmed their effectiveness as absorber layer materials. The optical analysis revealed a higher dielectric constant and absorption, whereas low reflection and loss of photons during interaction in the visible and ultraviolet spectrum. The thermal transport response exhibited a p-type nature, with higher S and ZT values of 0.75, 0.77, and 0.76, respectively. These characteristics demonstrate that In2AgSbCl6, In2AgSbBr6, and In2AgSbI6 are effective options for future energy harvesting technologies.Data availability
The data will be made available on request.Conflicts of interest
The authors declare no competing interests.Acknowledgements
This research was funded by Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2025R7), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. The authors thank the Deanship Research and Graduate Studies at King Khalid University, Saudi Arabia for funding this work through the Large Groups Project under Grant Number (RGP2/447/45).References
- M. Ali, Q. Ain, M. Alkadi, J. Munir, Z. Bibi and M. W. Younis, et al., First-principles evaluation of LiCaF3-αHα as an effective material for solid-state hydrogen storage, J. Energy Storage, 2024, 83, 110731 CrossRef.
- N. S. Lewis, Toward cost-effective solar energy use, Science, 2007, 315(5813), 798–801 CrossRef CAS PubMed.
- T. Li, J. Xu, R. Lin, S. Teale, H. Li and Z. Liu, et al., Inorganic wide-bandgap perovskite subcells with dipole bridge for all-perovskite tandems, Nat. Energy, 2023, 8(6), 610–620 CrossRef CAS.
- M. Yang, T. Tian, Y. Fang, W. G. Li, G. Liu and W. Feng, et al., Reducing lead toxicity of perovskite solar cells with a built-in supramolecular complex, Nat. Sustain., 2023, 6(11), 1455–1464 CrossRef.
- M. A. Green, A. Ho-Baillie and H. J. Snaith, The emergence of perovskite solar cells, Nat. Photonics, 2014, 8(7), 506–514 CrossRef CAS.
- P. Singh and A. Kumar, Device engineering of double perovskite based solar cells towards high-performance, eco-friendly solar cells, Opt. Quantum Electron., 2023, 55(4), 304 CrossRef CAS.
- S. Bimli, V. Manjunath, S. R. Mulani, A. Miglani, O. S. Game and R. S. Devan, Theoretical investigations of all inorganic Cs2SnI6 double perovskite solar cells for efficiency ∼30%, Sol. Energy, 2023, 256, 76–87 CrossRef CAS.
- S. F. Hoefler, G. Trimmel and T. Rath, Progress on lead-free metal halide perovskites for photovoltaic applications: a review, Monatsh. fur Chem., 2017, 148, 795–826 CrossRef CAS PubMed.
- A. Natik, Y. Abid, R. Moubah, M. Abid and H. Lassri, Ab-initio investigation of the structural, electronic and optical properties of lead-free halide Cs2TiI6 double perovskites, Solid State Commun., 2020, 319, 114006 CrossRef CAS.
- Z. Zhang, Q. Sun, Y. Lu, F. Lu, X. Mu, S. H. Wei and M. Sui, Hydrogenated Cs2AgBiBr6 for significantly improved efficiency of lead-free inorganic double perovskite solar cell, Nat. Commun., 2022, 13(1), 3397 CrossRef CAS PubMed.
- B. Lee, C. C. Stoumpos, N. Zhou, F. Hao, C. Malliakas, C. Y. Yeh, T. J. Marks, M. G. Kanatzidis and R. P. Chang, Air-stable molecular semiconducting iodosalts for solar cell applications: Cs2SnI6 as a hole conductor, J. Am. Chem. Soc., 2014, 136(43), 15379–15385 CrossRef CAS PubMed.
- G. García-Espejo, D. Rodríguez-Padrón, R. Luque, L. Camacho and G. de Miguel, Mechanochemical synthesis of three double perovskites: Cs2AgBiBr6,(CH3NH3)2TlBiBr6 and Cs2AgSbBr6, Nanoscale, 2019, 11(35), 16650–16657 RSC.
- A. Bhorde, R. Waykar, S. R. Rondiya, S. Nair, G. Lonkar, A. Funde and N. Y. Dzade, Structural, electronic, and optical properties of lead-free halide double perovskite Rb2AgBiI6: a combined experimental and DFT study, ES Mater. Manuf., 2021, 12, 43–52 CAS.
- A. Jain, Y. Shin and K. A. Persson, Computational predictions of energy materials using density functional theory, Nat. Rev. Mater., 2016, 1(1), 1–13 Search PubMed.
- N. H. Alotaibi, G. M. Mustafa, N. A. Kattan, Q. Mahmood, H. Albalawi and M. Morsi, et al., DFT study of double perovskites Cs2AgBiX6 (X= Cl, Br): an alternative of hybrid perovskites, J. Solid State Chem., 2022, 313, 123353 CrossRef CAS.
- L. Hnuna and Z. Pachuau, Electronic, optical and thermoelectric properties of halide double perovskites Rb2AgInX6 (X= Cl, Br, I), Phys. Scr., 2023, 98(3), 035814 CrossRef CAS.
- T. Atsue and O. E. Oyewande, First-principles study of the structural, mechanical, dynamical, and transport properties of Cs2NaInX6 [X= Br, I] for thermoelectric applications, Curr. Appl. Phys., 2024, 57, 70–78 CrossRef.
- T. Ou, Q. Zhuang, H. Yan, S. Feng, P. Li and X. Ma, Lead-free halide double perovskites Rb2InSbX6 (X= F, Cl, Br, I): A first-principles study of structural and optoelectrical properties, Chem. Phys., 2023, 573, 112015 CrossRef CAS.
- S. H. Shah, T. Huang, S. Shakeel, S. Khan, M. W. Ashraf and G. Murtaza, Comprehensive study of structural, elastic, electronic, optical, and thermoelectric properties of Rb2NaTlZ6 (Z= Cl, Br, and I) by DFT, Mater. Sci. Semicond. Process., 2024, 178, 108400 CrossRef CAS.
- M. A. Razzaq, Mechanical, electronic, optical, and thermoelectric properties of Rb2TlGaX6 (X= F, I) lead-free double perovskites: a first-principles study, Phys. Scr., 2024, 100(1), 015906 CrossRef.
- T. Tang, D. Hu, X. Zhao, L. Li and Y. Tang, First-principles study on the mechanical, electronic and optical properties of double halide perovskite Cs2TlSbX6 (X= Cl, Br, I), Phys. Scr., 2022, 97(12), 125821 CrossRef CAS.
- A. Mera, M. A. Rehman, Z. ur Rehman, Z. Sarfraz, M. Sohaib, J. Fatima and M. Usman, Exploring the physical properties of Rb2TlSbM6 (M= Cl, Br) inorganic halide perovskites for solar cell applications: A DFT study, Inorg. Chem. Commun., 2024, 165, 112528 CrossRef CAS.
- W. Lee, S. Hong and S. Kim, Colloidal synthesis of lead-free silver–indium double-perovskite Cs2AgInCl6 nanocrystals and their doping with lanthanide ions, J. Phys. Chem. C, 2019, 123(4), 2665–2672 CrossRef CAS.
- S. Z. Shah and S. Niaz, Lead-free indium-silver based double perovskites for thermoelectric applications: Structural, electronic and thermoelectric properties using first-principles approach, Mater. Today Commun., 2021, 28, 102609 CrossRef CAS.
- A. Nazir, E. A. Khera, M. Manzoor, B. A. Al-Asbahi, Y. A. Kumar and R. Sharma, A density functional theory study of the structural, mechanical, optoelectronics and thermoelectric properties of InGeX3 (X= F, Cl) perovskites, Polyhedron, 2024, 257, 117009 CrossRef CAS.
- K. Schwarz and P. Blaha, Solid state calculations using WIEN2k, Comput. Mater. Sci., 2003, 28(2), 259–273 CrossRef CAS.
- P. Blaha, K. Schwarz, P. Sorantin and S. B. Trickey, Full-potential, linearized augmented plane wave programs for crystalline systems, Comput. Phys. Commun., 1990, 59(2), 399–415 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865 CrossRef CAS PubMed.
- D. J. Singh, Electronic structure calculations with the Tran-Blaha modified Becke-Johnson density functional, Phys. Rev. B:Condens. Matter Mater. Phys., 2010, 82(20), 205102 CrossRef.
- M. S. Khan, B. Gul, A. S. Mohamed and F. Abbas, First-principles study of electronic, optical, and thermoelectric properties of KMCuS3 (M= Th and Sm) quaternary chalcogenides, RSC Adv., 2024, 14(37), 27332–27342 RSC.
- C. J. Bartel, C. Sutton, B. R. Goldsmith, R. Ouyang, C. B. Musgrave, L. M. Ghiringhelli and M. Scheffler, New tolerance factor to predict the stability of perovskite oxides and halides, Sci. Adv., 2019, 5(2), eaav0693 CrossRef CAS PubMed.
- N. H. Alotaibi, G. M. Mustafa, N. A. Kattan, Q. Mahmood, H. Albalawi, M. Morsi, H. H. Somaily, M. A. Hafez, H. I. Mahmoud and M. A. Amin, DFT study of double perovskites Cs2AgBiX6 (X= Cl, Br): an alternative of hybrid perovskites, J. Solid State Chem., 2022, 313, 123353 CrossRef CAS.
- M. Asghar, M. W. Iqbal, M. Manzoor, N. A. Noor, M. Zanib, R. Sharma, H. Ullah, S. Aftab and T. Zahid, A computational insight of the lead-free double perovskites Rb2AgSbCl6 and Rb2AgSbBr6 for optoelectronic and thermoelectric applications, Int. J. Energy Res., 2022, 46(15), 24273–24285 CrossRef CAS.
- M. Babaei, V. Ahmadi and G. Darvish, Opto-electro-mechanical properties of lead-free hybrid double perovskites Cs2AgSbX6 (X= Cl, Br, I) for solar cells: A first-principles study, J. Phys. Chem. Solids, 2022, 169, 110880 CrossRef CAS.
- G. García-Espejo, D. Rodríguez-Padrón, R. Luque, L. Camacho and G. de Miguel, Mechanochemical synthesis of three double perovskites: Cs2AgBiBr6,(CH3NH3)2TlBiBr6 and Cs2AgSbBr6, Nanoscale, 2019, 11(35), 16650–16657 RSC.
- D. Y. Hu, X. H. Zhao, T. Y. Tang, L. M. Lu, L. Li, L. K. Gao and Y. L. Tang, Study on the structural, electronic and optical properties of double-perovskite halides Cs2AgSbX6 (X= I, Br, Cl) based on first-principles, Mater. Sci. Semicond. Process., 2022, 152, 107077 CrossRef CAS.
- T. Charpin, A package for calculating elastic tensors of cubic phase using WIEN. Lab. Geometrix, Paris, 2001 Search PubMed.
- M. Born, On the stability of crystal lattices. I, Math. Proc. Cambridge Philos. Soc., 1940, 36(2), 160–172 CrossRef CAS.
- M. Y. Sofi and D. C. Gupta, Scrutinized the inherent spin half-metallicity and thermoelectric response of f-electron-based RbMO3 (M= Np, Pu) perovskites: a computational assessment, Sci. Rep., 2022, 12(1), 19476 CrossRef CAS PubMed.
- K. Radja, B. L. Farah, A. Ibrahim, D. Lamia, I. Fatima, B. Nabil, A. Mohamed, Y. Al-Douri and A. F. Abd El-Rehim, Investigation of structural, magneto-electronic, elastic, mechanical and thermoelectric properties of novel lead-free halide double perovskite Cs2AgFeCl6: First-principles calcuations, J. Phys. Chem. Solids, 2022, 167, 110795 CrossRef CAS.
- S. T. Ahams, A. Shaari, R. Ahmed, N. A. Pattah, M. C. Idris and B. U. Haq, Ab initio study of the structure, elastic, and electronic properties of Ti3(Al1− nSin)C2 layered ternary compounds, Sci. Rep., 2021, 11(1), 4980 CrossRef CAS PubMed.
- N. Hasan, M. Arifuzzaman and A. Kabir, Structural, elastic and optoelectronic properties of inorganic cubic FrBX3 (B= Ge, Sn; X= Cl, Br, I) perovskite: the density functional theory approach, RSC Adv., 2022, 12(13), 7961–7972 RSC.
- R. R. Reddy, K. R. Gopal, K. Narasimhulu, L. S. Reddy, K. R. Kumar, G. Balakrishnaiah and M. R. Kumar, Interrelationship between structural, optical, electronic and elastic properties of materials, J. Alloys Compd., 2009, 473(1–2), 28–35 CrossRef CAS.
- B. Shafiro and M. Kachanov, Anisotropic effective conductivity of materials with nonrandomly oriented inclusions of diverse ellipsoidal shapes, J. Appl. Phys., 2000, 87(12), 8561–8569 CrossRef CAS.
- R. Gaillac, P. Pullumbi and F. X. Coudert, ELATE: an open-source online application for analysis and visualization of elastic tensors, J. Phys.:Condens. Matter, 2016, 28(27), 275201 CrossRef PubMed.
- M. Z. Hasan, K. M. Hossain, S. K. Mitro, M. Rasheduzzaman, J. K. Modak and M. A. Rayhan, Structural, mechanical, electronic, and anisotropic properties of niobium-doped strontium ferrite: first-principle calculations, Appl. Phys. A, 2021, 127, 1–9 CrossRef.
- S. K. Singh, J. A. Abraham, A. S. Alofi, A. Srivastava, K. L. Meena, B. Alshahrani, R. Sharma and A. J. Moayad, Physical, optoelectronic and thermoelectric characteristics of double perovskite (Sr2ScBiO6) for green energy technology using ab initio computations, RSC Adv., 2023, 13(50), 35145–35160 RSC.
- N. Hasan, M. Arifuzzaman and A. Kabir, Structural, elastic and optoelectronic properties of inorganic cubic FrBX3 (B= Ge, Sn; X= Cl, Br, I) perovskite: the density functional theory approach, RSC Adv., 2022, 12(13), 7961–7972 RSC.
- N. Rahman, M. Husain, V. Tirth, A. Algahtani, H. Alqahtani, T. Al-Mughanam, A. H. Alghtani, R. Khan, M. Sohail, A. A. Khan and A. Azzouz-Rached, Appealing perspectives of the structural, electronic, elastic and optical properties of LiRCl3 (R= Be and Mg) halide perovskites: a DFT study, RSC Adv., 2023, 13(27), 18934–18945 RSC.
- M. A. Fadla, B. Bentria, T. Dahame and A. Benghia, First-principles investigation on the stability and material properties of all-inorganic cesium lead iodide perovskites CsPbI3 polymorphs, Phys. B, 2020, 585, 412118 CrossRef CAS.
- R. Kentsch, M. Scholz, J. Horn, D. Schlettwein, K. Oum and T. Lenzer, Exciton dynamics and electron–phonon coupling affect the photovoltaic performance of the Cs2AgBiBr6 double perovskite, J. Phys. Chem. C, 2018, 122(45), 25940–25947 CrossRef CAS.
- H. Chen, C. R. Zhang, Z. J. Liu, J. J. Gong, W. Wang, Y. Z. Wu and H. S. Chen, Vacancy defects on optoelectronic properties of double perovskite Cs2AgBiBr6, Mater. Sci. Semicond. Process., 2021, 123, 105541 CrossRef CAS.
- G. K. Madsen and D. J. Singh, BoltzTraP. A code for calculating band-structure dependent quantities, Comput. Phys. Commun., 2006, 175(1), 67–71 CrossRef CAS.
- M. M. Hossain, First-principles study on the structural, elastic, electronic and optical properties of LiNbO3, Heliyon, 2019, 5(4), e01478 CrossRef PubMed.
- F. Hamioud and A. A. Mubarak, Structural, elastic and optoelectronic properties of the hydrogen based perovskite compounds: ab-initio study, Chin. J. Phys., 2018, 56(1), 1–9 CrossRef CAS.
- D. Y. Hu, X. H. Zhao, T. Y. Tang, L. M. Lu, L. Li, L. K. Gao and Y. L. Tang, Revealing structural, elastic, electronic and optical properties of potential perovskites K2CuBiX6 (X= Br, Cl) based on first-principles, J. Solid State Chem., 2022, 310, 123046 CrossRef CAS.
- M. Nesa, M. A. Momin, M. Sharmin and A. H. Bhuiyan, Structural, optical and electronic properties of CuO and Zn doped CuO: DFT based First-principles calculations, Chem. Phys., 2020, 528, 110536 CrossRef CAS.
- A. R. Benrekia, N. Benkhettou, A. Nassour, M. Driz, M. Sahnoun and S. Lebègue, Structural, electronic and optical properties of cubic SrTiO3 and KTaO3: Ab initio and GW calculations, Phys. B, 2012, 407(13), 2632–2636 CrossRef CAS.
- M. I. Hussain, R. A. Khalil, F. Hussain, M. Imran, A. M. Rana and S. Kim, Investigations of structural, electronic and optical properties of TM-GaO3 (TM= Sc, Ti, Ag) perovskite oxides for optoelectronic applications: a first principles study, Mater. Res. Express, 2020, 7(1), 015906 CrossRef.
- M. Dadsetani and R. Beiranvand, First principles study of the optical properties of alkaline-earth metal nitrides, Comput. Mater. Sci., 2010, 49(2), 400–406 CrossRef CAS.
- X. Rocquefelte, F. Goubin, H. J. Koo, M. H. Whangbo and S. Jobic, Investigation of the origin of the empirical relationship between refractive index and density on the basis of first principles calculations for the refractive indices of various TiO2 phases, Inorg. Chem., 2004, 43(7), 2246–2251 CrossRef CAS PubMed.
- M. D. Ratul Hasan, I. A. Apon, I. Ahmed Ovi and F. T. Zahra, Impact of applied pressure on tin-based cubic halide perovskite ASnX3 (A= Li, Na and X= Cl, Br, and I) in reference to their optoelectronic applications, Int. J. Energy Res., 2024, 2024(1), 8213804 CrossRef.
- M. R. Hasan, I. A. Apon, M. M. Islam, A. U. Azad, M. Aminuzzman and M. S. Haque, DFT based analysis of pressure driven mechanical, opto-electronic, and thermoelectric properties in lead-free InGeX3 (X= Cl, Br) perovskites for solar energy applications, AIP Adv., 2024, 14(11), 115109 CrossRef CAS.
- S. C. Mouna, M. Radjai, A. Bouhemadou, M. A. Rahman, H. Kara, D. Houatis, D. Allali, S. S. Essaoud and H. Allaf, Structural, electronic, and optical characteristics of BaXCl3 (X= Li, Na) perovskites, Mater. Sci. Eng., B, 2024, 308, 117578 CrossRef.
- C. Wood, Materials for thermoelectric energy conversion, Rep. Prog. Phys., 1988, 51(4), 459 CrossRef CAS.
- U. Mumtaz, S. Kiran, S. Ahmad, F. Hussain, S. A. Rouf, R. M. Khalil, M. Alam, R. Wahab and M. F. Ehsan, Exploring the role of Germanium on the optoelectronic and thermoelectric response in making ductile lead-free perovskite halide using DFT, Mater. Res. Express, 2024, 11(12), 125506 CrossRef CAS.
- A. Ayyaz, G. Murtaza, S. Ali, N. Naeem, A. Mahmood, S. M. Ramay, M. Q. Shah and M. Irfan, Pressure influenced electronic phase transition, mechanical, optoelectronic, and transport characteristics of double perovskite Rb2AgSbCl6: A first-principles investigation, Chem. Phys. Lett., 2024, 847, 141342 CrossRef CAS.
- A. Nazir, E. A. Khera, M. Manzoor, K. Althubeiti, S. Al Otaibi, M. Soliyeva, N. Elboughdiri, H. Ullah and R. Sharma, DFT insights for thermoelectric characteristics of Sr3AsI3 for energy harvesting applications by TB-mBJ studies, Inorg. Chem. Commun., 2024, 169, 113112 CrossRef CAS.
- S. K. Singh, J. A. Abraham, A. Srivastava, K. L. Meena, R. Almeer, M. Manzoor and R. Sharma, Unveiling the energy driven potential Sc-based double perovskite through comprehensive DFT screening on physical, optoelectronic and transport characteristic of Sr2ScAsO6 compound, Solid State Commun., 2024, 394, 115676 CrossRef CAS.
- M. Manzoor, J. A. Abraham, R. Sharma, M. Aslam, A. Kumar, F. N. Almutairi, M. Jeridi and H. Ullah, Probing the Optoelectronic and Thermoelectric Performance of Inorganic Halide Perovskite Rb2KInI6 for Renewable Energy Applications via DFT Computations, J. Inorg. Organomet. Polym. Mater., 2024, 1–7 Search PubMed.
- M. A. Ali, S. A. Dar, A. A. AlObaid, T. I. Al-Muhimeed, H. H. Hegazy, G. Nazir and G. Murtaza, Appealing perspectives of structural, electronic, mechanical, and thermoelectric properties of Tl2(Se, Te)Cl6 vacancy-ordered double perovskites, J. Phys. Chem. Solids, 2021, 159, 110258 CrossRef CAS.
- N. H. Alotaibi, G. M. Mustafa, N. A. Kattan, Q. Mahmood, H. Albalawi, M. Morsi, H. H. Somaily, M. A. Hafez, H. I. Mahmoud and M. A. Amin, DFT study of double perovskites Cs2AgBiX6 (X= Cl, Br): an alternative of hybrid perovskites, J. Solid State Chem., 2022, 313, 123353 CrossRef CAS.
- A. Sajjad, M. Faizan, T. A. Alrebdi, G. Murtaza, J. Rehman, X. Shen, Y. Dong, K. Shaheen and S. H. Khan, Exploring double perovskites Cs2AgSbX6 (X= Cl, Br, and I) as promising optoelectronic and thermoelectric materials: a first-principles study, Phys. Chem. Chem. Phys., 2025, 27(9), 4880–4891 RSC.
| This journal is © The Royal Society of Chemistry 2025 |