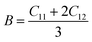First-principles investigation of thermoelectric performance in KMnZ (Z = Sn, Pb) half-Heusler alloys

Abstract

In this study, we performed an in-depth analysis of the structure stability, elasto-mechanical properties, thermophysical characteristics, and thermoelectric behavior of the KMnZ half-Heusler alloy using density functional theory (DFT) implemented through the WIEN2k simulation package. We examined the structural stability across phase types I, II, and III by optimizing their energy configurations. Our results demonstrate that the compound achieves optimal stability in the spin-polarized state of phase type II. Subsequently, we employ density functional perturbation theory (DFPT) to forecast the dynamic behavior of these structured systems. The electronic band structure analysis, conducted using the local spin density approximation (LDA), Perdew–Burke Generalized Gradient Approximation (PBE-GGA), and Tran–Blaha modified Becke–Johnson (TB-mBJ) schemes, reveals that the Heusler alloy exhibits half-metallic properties. Additionally, the calculated second-order elastic parameters confirm the material's ductile nature. To evaluate the thermodynamic and thermoelectric stability under various temperature and pressure conditions, we utilized the Quasi-Harmonic Debye model. The computed magnetic moment is consistent with the Slater-Pauling rule. These findings indicate that the KMnZ half-Heusler alloy is a promising candidate for applications in spintronics and thermoelectrics.

---

1. Introduction

In recent years, spintronic materials have garnered significant global attention due to their broad applicability across various advanced devices.^1–4 As a rapidly evolving field, spintronics canters on the manipulation of electron spin properties to facilitate high-speed information processing and enhanced data storage capabilities.⁵ The integration of spintronic technology is increasingly becoming vital to the development of modern solid-state devices, which exploit both the spin and charge carrier mobility.^6–9 Among the forefront of these technologies is the integration of spin injection and single-electron spin sources, which has emerged as a critical area of research. Spin-polarized charge carriers are fundamental to the advancement of contemporary spintronic devices.^10–13 Heusler compounds, distinguished by their superior spin-polarized characteristics,^14–17 have established themselves as leading candidates in this domain, enabling the creation of novel devices. The spin-polarized nature of these materials is essential for the efficient processing of large data sets and reliable information storage, underscoring their importance in the ongoing evolution of spintronic technologies.^18–21 Heusler compounds are distinguished by their spin-dependent electronic properties, most notably their half-metallic behavior. This unique characteristic is defined by the material's metallic conduction in one spin channel (either spin-up or spin-down) while acting as a semiconductor in the opposite spin channel, resulting in 100% spin polarization.^22,23 The extent of this spin polarization is typically determined by analyzing the density of states at the Fermi level (EF) for both spin channels.²⁴

Thermoelectricity (TE) represents a cutting-edge technology that harnesses the thermoelectric effect to convert heat into electric current and vice versa, providing an environmentally friendly energy solution. TE technology is particularly effective in capturing and repurposing waste heat from sources such as automobiles, refineries, and various industrial processes, thereby playing a crucial role in efforts to achieve zero carbon emissions. Heusler compounds have emerged as promising candidates for thermoelectric applications due to their cost-efficiency, ease of synthesis, environmental compatibility, and stable crystal structures. These characteristics position them at the forefront of thermoelectric materials research. Heusler compounds are generally categorized into three primary types based on their structural stoichiometry: half-Heusler (HH), full-Heusler (FH), and quaternary Heusler (QH) compounds.

Over the years, a substantial body of research, encompassing both theoretical and experimental approaches, has focused on unravelling the spintronic and thermoelectric properties of Heusler compounds.^25–30 These materials have garnered significant attention due to their versatile electronic and magnetic characteristics, which are highly tunable through compositional and structural modifications. The pioneering work by Groot et al.³¹ marked a critical milestone in this field by experimentally confirming the half-metallic behavior of the NiMnSb half-Heusler compound. This discovery laid the foundation for subsequent investigations into similar materials. Shortly after, Fe₂TiSb and Fe₂TiAs were reported as half-metallic full Heusler compounds, further expanding the scope of research in this domain.³² The exploration of half-metallicity continued with Luo and colleagues, who conducted extensive theoretical studies on a series of full Heusler compounds, including Mn₂FeGa, Mn₂FeAl, Mn₂FeGe, and Mn₂FeSe.³³ These studies provided deeper insights into the electronic structures and magnetic properties of these materials, highlighting their potential for spintronic applications. Among the broad spectrum of Heusler compounds, half-Heusler alloys have emerged as a particularly promising class of materials, distinguished by their unique structural attributes and exceptional performance in various applications.³⁴ Transitioning from full Heusler (FH) to half-Heusler (HH) compounds introduces a shift in structural composition and chemical flexibility. Half-Heusler compounds typically adopt the formula XYZ, where X and Y are metallic atoms, often selected from transition metals or the alkaline earth metal family, while Z is typically an element from the sp-block. This structural configuration results in a C_1b crystal structure, characterized by three interpenetrating face-centered cubic (FCC) lattices. The key distinction between half-Heusler and full Heusler compounds lies in the presence of a vacant site within the lattice of half-Heuslers, which significantly influences their electronic and magnetic properties. This structural feature not only differentiates them from their full Heusler counterparts but also contributes to their distinct physical properties, making them highly suitable for spintronic and thermoelectric applications.

With the multifaceted growth in spintronic applications, half-Heusler (HH) alloys have emerged as a versatile class of materials, offering significant potential for both spintronic and thermoelectric applications. Numerous HH alloys have been reported in the literature, including XCrSb (X = Fe, Ni),³⁵ KCrZ (Z = Si, Ge),³⁶ KCrZ (Z = S, Se, Te),³⁷ NaZrZ (Z = P, Sb, As),³⁸ LiMnZ (Z = N, Si, P),³⁹ RhCrZ (Z = Ge, Si),⁴⁰ PtXBi (X = Co, Fe, Mn, Ni),⁴¹ IrCrZ (Z = Ge, Sn, As, Sb),⁴² and VCoSb.⁴³ These compounds are distinguished by their ability to achieve 100% spin polarization, classifying them as half-metallic ferromagnets (HMFs).⁴⁴ HMFs are particularly valued for their wide-ranging applications in spintronic technologies, including spin injection,⁴⁵ magnetic tunnel junctions (MTJs),⁴⁶ spin valve devices,⁴⁷ tunnelling magnetoresistance (TMR),⁴⁸ magnetic random-access memory (MRAM),⁴⁹ and permanent magnets.⁵⁰ The appeal of HH alloys lies in their unique electronic structures, which enable them to exhibit half-metallic behavior, where one spin channel is metallic while the other is insulating. This characteristic makes them ideal candidates for spintronic devices that rely on high spin polarization. Despite the considerable progress made in identifying and synthesizing HH alloys with desirable properties, the ongoing quest for new half-metallic materials remains critical to advancing the efficiency and performance of spintronic and thermoelectric devices.

In particular, potassium (K)-based half-Heusler compounds have attracted attention due to their structural robustness and potential to exhibit half-metallic ferromagnetism. These materials offer a promising avenue for the fabrication of next-generation spintronic and thermoelectric devices. Their ability to maintain structural integrity while delivering high spin polarization and favorable thermoelectric properties positions them as strong candidates for further research and development. The exploration of these K-based HH compounds could lead to significant breakthroughs in the design and optimization of materials for advanced technological applications, reinforcing their role as a cornerstone in the evolution of spintronic and thermoelectric device technologies.

This research aims to provide a detailed analysis of the physical properties of KMnZ (Z = Sn, Pb) half-Heusler compounds, employing density functional theory (DFT) models integrated with the WIEN2k simulation package. The study emphasizes a multifaceted exploration of these compounds, including structural phase stability, half-metallic ferromagnetism (HMF), mechanical stability, magnetic properties, and thermodynamic behavior. The research objectives include determining the most stable magnetic configuration, evaluating half-metallic ferromagnetism, calculating second-order elastic constants, magnetic moments, and Curie temperatures, as well as investigating electronic properties using the PBE-GGA approximation within the DFT framework. Furthermore, the thermodynamic performance of the KMnZ compounds under varying temperature and pressure conditions will be rigorously analyzed using the BoltzTraP code and quasi-harmonic Debye approximation. This work seeks to deliver a comprehensive computational assessment of the fundamental properties of these half-Heusler compounds, with a particular focus on their potential applications in sustainable spintronics, electronics, thermoelectrics, and other emerging technologies.

2. Computational parameters and convergence criteria

In this study, density functional theory (DFT) was employed to conduct a comprehensive investigation into the structural stability, half-metallic behavior, magnetic properties, and thermodynamic response of the alkaline earth metal-based half-Heusler compound KMnZ. DFT, recognized for its precision and accuracy, was implemented using the full-potential linearized augmented plane wave (FP-LAPW) basis set within the WIEN2k simulation package.^51–55 To analyze phonon dispersions and evaluate dynamical stability, we utilized density functional perturbation theory (DFPT) within the Quantum Espresso simulation framework.³⁴ Electron–electron interactions were managed through the generalized gradient approximation with the Perdew–Burke–Ernzerhof (PBE) exchange-correlation potential.⁵⁶ For a more detailed analysis of the electronic structure, the modified Becke–Johnson (mBJ) potential⁵⁷ was utilized. Structural stability and magnetic properties of KMnZ were rigorously examined. The simulations involved partitioning the KMnZ unit cell into two distinct regions: the muffin-tin sphere and the interstitial space. The muffin-tin approximation, a well-established method for estimating electron energy states within the crystal lattice, was applied with muffin-tin radii (R_MT) of 2.28, 2.31, 2.34, and 2.25 for K, Mn, Sn, and Pb atoms, respectively. Outside the muffin-tin spheres, electron wave functions were represented by plane waves with a cutoff defined as R_MT × K_max = 7, where K_max denotes the reciprocal lattice vector. A fixed energy of −7.0 Ry was used to differentiate between core and valence electrons, and self-consistent field (SCF) convergence was achieved with a precision of 10⁻⁵ Ry. The Brillouin zone was sampled using the Monkhorst–Pack technique⁵⁸ with a (14 × 14 × 14) k-point mesh. The elastic parameters of KMnZ were analyzed using the IRElast module within the WIEN2k package, and thermodynamic properties were investigated using the BoltzTrap2 code⁵⁹ with the classical Boltzmann approximation.

3. Result and discussions

In this section, we present a detailed analysis of the distinctive properties exhibited by KMnZ half-Heusler compounds, (Z = Sn, Pb).

3.1 Crystal structure and optimised lattice parameter

To accurately predict the properties of any material, a thorough understanding of its crystal structure is essential, as the arrangement of atoms within a crystal lattice fundamentally influences its physical, electronic, and mechanical properties. Half-Heusler compounds, such as KMnZ, are particularly notable for their C_1b-type crystal structure, which can stabilize in three distinct atomic configurations. These configurations are crucial because they dictate the material's behavior under various conditions, including temperature, pressure, and magnetic fields. The C_1b-type structure of these half-Heusler compounds consists of three interpenetrating face-centered cubic (FCC) sublattices, where each sublattice is occupied by different atomic species. The three possible configurations, each defined by specific atomic coordinates and Wyckoff positions, represent different ways in which the constituent atoms (K, Mn, Sn and Pb) can be arranged within the crystal lattice. These variations in atomic positioning not only impact the stability of the crystal structure but also influence the electronic band structure, magnetic properties, and elastic characteristics of the material. Understanding these configurations allows researchers to predict and tailor the material's properties for specific applications, such as in spintronics, thermoelectrics, and other advanced technologies.

The specific Wyckoff positions for these three configurations of the KMnZ half-Heusler compound are detailed in Table 1, providing a precise map of atomic locations within the lattice represented in Fig. 1, which is critical for further computational and experimental analysis.

Table 1 Wyckoff positions in three atomic configurations of KMnZ (Z = Sn, Pb) half Heusler alloys

Alloys	Phase	K	Mn	Z = Sn, Pb
KMnZ	Type 1	(0.25,0.25,0.25)	(0.50,0.50,0.50)	(0,0,0)
	Type 2	(0,0,0)	(0.25,0.25,0.25)	(0.50,0.50,0.50)
	Type 3	(0.50,0.50,0.50)	(0,0,0)	(0.25,0.25,0.25)

---

Fig. 1 Crystallographic structures of the KMnZ (Z = Sn, Pb) half-Heusler alloys, illustrating three distinct phase configurations: type I, type II, and type III respectively.

The structure stability of the proposed half-Heusler (HH) compound is contingent upon its atomic arrangement within the crystal lattice. Consequently, identifying the most energetically favorable phase among the existing configurations is imperative. Our computational analysis and Fig. 2 reveals that the type I structure of KMnZ HH exhibits the lowest energy relative to types II and III. Subsequently, we determined that KMnZ with the F4̄3m (#216) space group is more stable in the spin-polarized (SP) phase than in the non-magnetic (NM) phase as reported in Fig. 3. The antiferromagnetic (AFM) configuration of the KMnZ Heusler alloy was thoroughly analyzed to better understand its magnetic and structural properties. As part of this investigation, the relationship between the unit cell volume and the total energy for the AFM state was calculated and graphically represented, as shown in Fig. 4. This plot provides crucial insights into the stability of the material in its antiferromagnetic phase, indicating how energy varies with changes in lattice volume. To ascertain the equilibrium lattice parameters and minimum energy for cubic KMnZ with the stable type-I crystal structure, we employed the Murnaghan equation of state,⁶⁰ as expressed in equation for volume optimization in the SP phase:

Here, E₀ denotes the minimum total energy, V₀ represents the unit cell volume at zero pressure, B₀ is the bulk modulus, and B′ is the derivative of the bulk modulus. As presented in Table 2, the calculated lattice constant (a₀) for KMnSn and KMnPb HH at the given symmetry, obtained using GGA, is 7.14 Å and 7.28 Å. The remaining parameters V₀, B₀, and B′ are reported for the first time for KMnZ (Z = Sn, Pb) HH alloys. A comprehensive energy minimization analysis was conducted to identify the most energetically favorable magnetic configuration for the KMnZ half-Heusler compounds. By calculating the volume-energy relationship, we determined that the spin-polarized (SP) state in phase II is energetically superior to the non-magnetic (NM) and antiferromagnetic (AFM) state. The energy–volume data were fitted to the Murnaghan equation of state, as depicted in equation. The lattice constants for all three states were computed within the scope of this investigation.

Fig. 2 Optimized energy–volume curve for the spin-polarized cubic KMnZ (Z = Sn, Pb) half-Heusler alloys in the type I, type II, and type III configuration.

Fig. 3 Optimized energy–volume curve for the spin-polarized cubic KMnZ (Z = Sn, Pb) half-Heusler alloys in the spin-polarised (SP) and non-magnetic (NM) configuration.

Fig. 4 Optimized energy–volume curve for the spin-polarized cubic KMnZ (Z = Sn, Pb) half-Heusler alloys in the anti-spin-polarised (antiferromagnetic AFM) configuration.

Table 2 Calculated structural parameters for the half Heusler KMnZ determined in three distinct types and in both magnetic phase, spin polarized (SP), non-magnetic (NM), and antiferromagnetic (AFM) phases, including lattice constant (a in Å), volume (V in a.u.³), bulk modulus (B in GPa) and energy (E₀ in Ry)

Alloys	Phase	a	V	B		E0
KMnSn	Type I	7.49	542.43	27.80	4.37	−15 879.57
	Type II	7.14	614.07	24.45	4.99	−15 879.69
	Type III	7.35	554.62	26.73	4.74	−15 879.66
	NM	6.69	507.18	38.99	4.57	−15 879.54
	AFM	7.23	635.47	40.58	4.69	−15 879.67
KMnPb	Type I	7.58	739.65	23.98	4.72	−45 378.63
	Type II	7.28	651.94	25.97	5.17	−45 378.73
	Type III	7.48	707.06	29.57	5.03	−45 378.71
	NM	7.12	711.56	29.12	5.31	−45 378.56
	AFM	7.35	706.78	28.92	5.12	−45 378.64

---

3.1.1 Cohesive energy. The analyses were conducted to evaluate the stability of the compounds using specific relationships developed for this purpose. Cohesive energy (E_coh) is defined as:

E_coh = E^KMnZ_total − (E^K_atom + E^Mn_atom + E^Z_atom)

Cohesive energy represents the amount of energy necessary to separate the KMnZ (Z = Sn, Pb) crystal into its individual atoms, providing an indication of the material's bonding strength. From the data in Table 3, it is evident that all cohesive energy values are positive. This suggests that the bonds in both alloys are sufficiently robust to maintain the integrity of their atomic structures, emphasizing their structural stability. In summary, the positive cohesive energy values confirm the strong molecular structure and the cohesive forces that hold the atoms together in the KMnZ compounds.

Table 3 Calculated values for cohesive energy (E_coh in eV per atom), formation energy (E_For in eV per atom), and enthalpy (ΔH in eV) for KMnSn and KMnPb HH alloys

Alloys	ECoh	EFor	ΔH
KMnSn	2.38	−0.64	−4.59
KMnPb	2.76	−0.43	−3.87

---

3.1.2 Formation energy. Furthermore, the formation energy of the KMnZ (Z = Sn, Pb) alloys was calculated to further validate their structural stability, using the following equation:

E_For = E^KMnZ_total − (E^K_bulk + E^Mn_bulk + E^Z_bulk)

The formation energy, represented as ΔE_For, quantifies the difference between the total energy of a crystal E^KMnZ_bulk and the summed energies of its elemental components E^K_bulk, E^Mn_bulk, and E^Z_bulk under standard conditions of 300 K temperature and 0 GPa pressure. A negative formation energy value indicates that the compound is thermodynamically stable. As shown in Table 3, both compounds exhibit negative formation energy values, demonstrating their potential for experimental synthesis. This highlights their favorable energetic properties and supports the possibility of synthesizing these materials under standard laboratory conditions.

3.1.3 Enthalpy. The cohesive energy observed in these compounds highlights the significant strength of interatomic bonds, providing further evidence of the chemical stability of KMnSn and KMnPb. This stability reflects the strong bonding interactions among the constituent atoms. To thoroughly evaluate the stability of these compounds, the enthalpy of formation (ΔH) is analyzed, calculated using the following equation:

ΔH = E_Total − aE_A − bE_B − dE_X

In this equation, E_Total represents the total energy of the KMnSn and KMnPb compounds, while E_A, E_B, and E_X, denote the individual atomic energies of K, Mn, Sn, and Pb, respectively. The computed enthalpy values for KMnSn and KMnPb are −4.59 eV and −3.87 eV, respectively. These negative values of formation energy provide clear evidence of the thermodynamic stability of these compounds. A comprehensive summary of the calculated energies, including cohesive, formation, and enthalpy energies, is presented in Table 3.

3.1.4 Phonon dispersion. Analyzing the complex dynamics, thermodynamic properties, and vibrational characteristics of crystalline solids requires a thorough investigation of phonon dispersion. In this study, we employ Density Functional Perturbation Theory (DFPT) within the pseudopotential framework of Quantum Espresso to evaluate the dynamical stability of the half-Heusler alloys KMnSn and KMnPb in their primitive unit cells as reported in Fig. 5. Dynamical stability is indicated by the presence of three acoustic phonon branches exhibiting zero frequency at the Γ-point, while optical phonons exhibit non-zero frequencies. The three acoustic branches consist of one longitudinal acoustic (LA) mode and two transverse acoustic (TA) modes, accompanied by 3N – 3 optical modes in a unit cell containing N atoms.³⁹ Our analysis delves into the nine phonon branches arising from the interactions of the constituent atoms, tracing their evolution along the high-symmetry directions of the irreducible Brillouin zone. Of these, three branches intersect at the Γ-point and are classified as acoustic, while the remaining six are identified as optical modes. The lower-frequency branches primarily result from the vibrations of heavier atoms, whereas the higher-frequency optical branches are attributed to lighter atoms. Factor group theory further categorizes the optical modes into Raman-active, infrared-active, or silent, depending on their frequency ranges. The absence of negative or imaginary frequencies in the phonon band structure confirms the dynamical stability of the investigated systems.

Fig. 5 Phonon dispersion curves were calculated for KMnSn and KMnPb along the high-symmetry direction of their respective Brillouin zones.

3.2 Mechanical and elastic properties

Elastic and mechanical properties of a material are characterized by its elastic parameters, which quantify the relationship between stress and strain. These parameters determine the material's deformation under external forces and its subsequent return to its original state. For assessing mechanical stability, elastic constants are crucial, particularly at optimized conditions. The mechanical attributes of solids, which underlie their practical applications, are directly linked to these elastic constants.⁴⁹ Given that the KMnZ half-Heusler is stable in the cubic type II symmetry, we calculated the values of three independent elastic parameters: C₁₁, C₁₂, and C₄₄. C₁₁ measures longitudinal expansion, while C₁₂ measures transverse deformation. To ensure mechanical stability, these independent elastic constants must satisfy the Born stability criteria for cubic symmetry, which are as follows:

C₁₁ + 2C₁₂ > 0; C₁₁ − C₁₂ > 0; C₁₂ > 0; C₁₁ > 0 and C₄₄ > 0.

As shown in Table 4, the KMnZ half-Heusler compound unequivocally satisfies the Born stability criteria, thereby confirming its robust mechanical stability. Furthermore, the table presents other pertinent parameters, including the shear modulus (G) and bulk modulus (B), which respectively characterize compressibility and stiffness. The resistance to plastic deformation, a measure of the opposing force to fracture, can be quantified by the G and B parameters. These values are calculated using the following equations:

Table 4 Computed values of elastic parameters (C₁₁, C₁₂, C_44, C_P, E, B, G in GPa), Pugh's ratio (B/G), Poisson's ratio (σ), Anisotropy factor (A), sound velocities, and Debye temperature (θ_D in K)

Parameters	KMnSn	KMnPb
C11	32.39	41.94
C12	21.44	17.65
C44	2.02	9.17
B	25.09	25.74
GV	3.40	10.36
GR	2.70	10.16
G	3.05	10.26
E	8.79	27.17
CP	19.42	8.48
B/G	8.22	2.50
σ	0.44	0.32
A	0.36	0.75
Vl (m s^−1)	3.16	10.07
Vt (m s^−1)	1.02	5.14
Vm (m s^−1)	1.16	5.76
θD	121.18	232

---

The subscripts R and V in above equation denote the Reuss and Voigt bounds, respectively. The values of G_R and B_V can be determined using the equations below:

Table 4 summarizes the calculated values of these elastic parameters. The calculated results not only confirm the mechanical stability of the KMnZ compound but also provide valuable insights into its resistance to deformation and its potential applications in various structural and engineering contexts. The bulk modulus (B) value derived from above bulk modulus eqn, as presented in Table 4, is consistent with the values obtained through our calculations. Young's modulus (E), which defines the material's stiffness and is the ratio of stress to strain, was determined using the following relationship:

This relation connects the bulk modulus (B) and shear modulus (G) to provide insight into the material's elastic properties. To evaluate the material's brittleness or ductility, the Cauchy pressure (C_P) is a crucial factor. The Cauchy pressure is calculated using the following relation:

C_P = C₁₁ − C₁₂

In this context, C₁₂ and C₄₄ are elastic constants. If the calculated Cauchy pressure is positive, the material is considered ductile, meaning it can undergo significant plastic deformation before fracture. Conversely, a positive Cauchy pressure suggests that the material is ductile and prone to fracture under stress without significant deformation. Our findings reveal that the KMnZ half-Heusler compound has a positive Cauchy pressure, confirming its ductile nature. Additionally, the Pugh ratio (B/G) is another critical parameter for assessing ductility versus brittleness. This ratio is calculated by dividing the bulk modulus (B) by the shear modulus (G). Generally, a Pugh ratio less than 1.75 indicates a brittle material, while a ratio greater than 1.75 suggests ductility. The computed Pugh ratio for the KMnZ HH compound, as shown in Table 4, further confirms its brittleness. The Poisson's ratio (σ) is another important parameter that helps determine the compressibility of a material. This ratio, which is defined as the positive ratio of transverse to axial strain, also sheds light on the nature of bonding forces within the material. It is calculated using the following formula:

A higher Poisson's ratio typically indicates a material that is more compressible and has more ductile behavior. However, for the KMnZ alloy, the Poisson's ratio suggests that the material is relatively incompressible, supporting the conclusion that it is mechanically stable and ductile. From the exploration of these elastic properties, it can be concluded that the KMnZ HH alloy exhibits brittleness and incompressibility, characteristics that affirm its mechanical stability. These properties are essential for the practical use of the alloy, particularly in applications requiring high structural integrity under stress. Given the growing interest in half-Heusler (HH) alloys for potential spintronic applications, a thorough understanding of their mechanical stability is crucial during the device fabrication process.

The Debye temperature (θ_D) is a fundamental property of solid materials, representing the temperature at which the vibrational energy of atoms within the material equals their thermal energy. It is calculated using the average sound velocity (v_m)⁴²

where h is Planck's constant, k is Boltzmann's constant, n is the number of atoms per formula unit, V is the unit cell volume, and v_m is the average sound velocity calculated as:

Utilizing Navier's equation⁴¹ and the calculated bulk and shear moduli, we determined the longitudinal velocity (v_l) and shear velocity (v_s). The resulting values are tabulated in Table 4.

The Debye temperatures for KMnSn and KMnPb alloys were found to be 121.18 K and 232 K, respectively. When a material's Debye temperature exceeds room temperature, it signifies that the vibrational energy of its constituent atoms surpasses its thermal energy.

Another significant physical property is the anisotropic factor (A), which characterizes the nature of bonding in different crystallographic directions and is defined by:

A value of A = 1 indicates an isotropic crystal, while values less than one suggest elastic anisotropy. The computed data in Table 4 reveals that both half-Heusler compounds exhibit anisotropic behavior.

3.3 Electronic properties

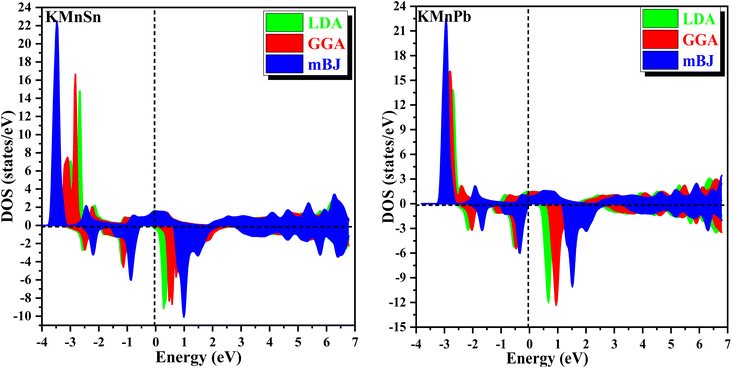
To investigate the electronic properties of half-Heusler alloys KMnZ (Z = Sn, Pb), we calculated spin-polarized electronic band structures at the equilibrium lattice constant in the ferromagnetic (FM) phase. These calculations, performed along the high-symmetry directions of the first Brillouin zone (BZ), used LDA, GGA-PBE, and TB-mBJ, approximations at 0 K and 0 GPa. The spin-resolved band structures (BS) and density of states (DOS), shown in Fig. 6–10, provide essential insights into the electronic behavior. These results reveal how spin-up and spin-down states contribute to the electronic structure, highlighting the material's half-metallic and semiconducting characteristics. Such findings are crucial for spintronic applications, where controlling spin-polarized currents is key.

Fig. 6 Spin polarised band structure for KMnSn and KMnPb in LDA approximation.

Fig. 7 Spin polarised band structure for KMnSn and KMnPb in GGA approximation.

Fig. 8 Spin polarised band structure for KMnSn and KMnPb in mBJ approximation.

Fig. 9 Spin-polarized TDOS of KMnZ (Z = Sn, Pb) HH alloys by LDA, GGA, and mBJ approximation.

Fig. 10 Spin-polarized PDOS of KMnZ (Z = Sn, Pb) HH alloys by mBJ approximation.

3.3.1 Band structure (BS). To understand the electronic behavior of KMnZ (Z = Sn, Pb) half-Heusler (HH) alloys, it is essential to analyze both the band structure and density of states (DOS). The band gap (E_g) derived from these analyses plays a crucial role in determining the thermoelectric properties of these materials. We have meticulously studied the band gap using three computational schemes: LDA, GGA-PBE, and TB-mBJ. Fig. 6–8 presents the electronic structure for the spin-up configuration, showing that all three methods consistently reveal a metallic nature for the spin-up channel. This metallic behavior arises from the overlap between the valence and conduction bands at the Fermi level (E_F). In contrast, Fig. 6–8 demonstrates that the spin-down configuration exhibits a semiconducting nature due to a distinct band gap separating the valence and conduction bands. The conduction band reaches its minimum at the (X) symmetry point, while the valence band reaches its maximum at the Gamma (Γ) point, confirming an indirect band gap (E_g) for the alloys. For KMnSn, the band gap values are 0.56 eV, 0.73 eV, and 1.10 eV in the LDA, GGA-PBE, and mBJ schemes, respectively. Similarly, for KMnPb, the band gap values are 0.56 eV, 0.72 eV, and 1.24 eV. These results suggest that the semiconducting nature in the spin-down channel could significantly impact the thermoelectric response, as the presence of a band gap enhances carrier mobility and energy conversion efficiency.

3.3.2 Density of states. The Total Density of States (DOS) and Partial Density of States (PDOS) for KMnZ alloys (Z = Sn, Pb) were rigorously computed and are presented in Fig. 9 and 10 to provide a comprehensive understanding of their electronic structure. Fig. 9 illustrates the total DOS for KMnSn and KMnPb using the LDA, GGA, and mBJ exchange–correlation approximations, highlighting variations across different methodologies. Fig. 10 focuses on the PDOS under the mBJ potential, offering a detailed analysis of the orbital contributions. The results reveal that the spin-up (majority) channel in both alloys exhibits a finite band gap, indicative of metallic behavior in this channel. Conversely, the spin-down (minority) channel shows a clear band gap with the Fermi level positioned within it, confirming the semiconducting nature of this state and affirming the half-metallic (HM) characteristics of KMnSn and KMnPb. The observed 100% spin polarization is attributed to this distinctive electronic configuration, aligning with HM behavior where only one spin channel contributes to conduction. The bonding and anti-bonding states within the DOS and PDOS plots further elucidate the electronic structure: in the minority spin channel, the bonding states predominantly derive from the p-orbitals of the Sn and Pb atoms, contributing significantly to the electronic states near the Fermi level. In contrast, the bonding region in the majority spin channel is primarily influenced by the Mn d-orbitals, which play a crucial role in band formation and band gap development. The Mn d-orbitals hybridization with p-orbitals of Sn and Pb atoms is essential for understanding the origin of the band gap observed in these half-metallic systems. This hybridization and the subsequent electron distribution demonstrate the intricate interplay between transition metal d-states and main group element p-states, underpinning the electronic and magnetic properties that define KMnSn and KMnPb as half-metallic materials.

3.4 Magnetic properties

According to the Galanakis model⁴² the spin magnetic moment of half-Heusler compounds is defined as the difference between the occupied energy bands corresponding to the up and down spin states. This relationship is particularly pertinent for ternary 1 : 1 : 1 half-Heusler compounds characterized by a C_1b crystal structure, such as the prototype Cu₂MnAl. Kubler was notably the first to establish the Slater-Pauling 18-electron rule, which articulates that the total magnetic moment (M_Tot) is given by the equation:

M_Tot = 8 − Z_Tot

In these half-Heusler materials, the C_1b structure is defined by the presence of three atoms per unit cell, and the Slater-Pauling rule is instrumental in predicting their magnetic characteristics. Here, M_Tot represents the total spin magnetic moment, while Z_Tot indicates the total number of valence electrons within the system. This rule is crucial as it dictates that the number of occupied states in the spin bands is fixed at 18. In our present study focusing on ternary 1 : 1 : 1 half-Heusler alloys, we have determined a total magnetic moment (M_Tot) of approximately 4 μB. Our findings are summarized in Table 5, which outlines the total magnetic moment alongside contributions from atomic resolved and interstitial magnetic moments specific to the compounds KMnZ (Z = Sn, Pb). Significantly, our analysis reveals that the predominant contributions to the total magnetic moment arise from the manganese (Mn) atom in these half-Heusler compounds. This observation underscores the critical influence of the Mn atom in shaping the magnetic properties of the material, aligning well with the predictions made by the Slater-Pauling rule.

Table 5 The magnetic moments of atomic, total magnetic moment, interstitial magnetic moments (all in μB) and band gap (in eV) are investigated for the KMnZ (Z = Sn, Pb) HH alloys in three different methods

Alloys	Methods	K	Mn	Sn/Pb	Int.	Total	Band gap
KMnSn	LDA	0.05	3.79	−0.10	0.17	3.91	0.55
	GGA	0.05	3.91	−0.13	0.15	3.98	0.72
	mBJ	0.04	4.06	−0.19	0.08	4.00	1.09
KMnPb	LDA	0.01	4.11	−0.14	0.01	4.00	0.56
	GGA	0.01	4.21	−0.17	−0.05	4.00	0.73
	mBJ	0.01	4.33	−0.20	−0.13	3.99	1.25

---

3.5 Curie temperature

The Curie temperature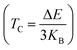 for the alloys KCrSi and KCrGe was determined using a well-established equation derived from the Heisenberg model,.⁴³ In this context, ΔE represents the energy difference between E_NM (the total energy of the nonmagnetic state) and E_FM (the total energy of the ferromagnetic state). This parameter captures the energy gap associated with the stability of magnetic ordering in the material. The calculation also incorporates the Boltzmann constant (K_B), which connects the energy to the thermal properties of the system. The parameter ΔE is a fundamental quantity that reflects the minimum energy barrier required for a system to transition between states, such as magnetic phases or other physical transformations. This energy difference provides significant insights into the thermodynamic stability and kinetic feasibility of these transitions. Specifically, it quantifies the degree of stability of the ferromagnetic state relative to the nonmagnetic state. At the Curie temperature (T_C), the thermal energy in the material becomes comparable to ΔE, enabling the disruption of the ferromagnetic spin alignment. This marks a critical point where the material undergoes a phase transition from a ferromagnetic to a paramagnetic state. Consequently, ΔE plays a central role in determining the Curie temperature and, by extension, the thermal stability of the magnetic ordering. It defines the threshold energy at which magnetic interactions are overcome by thermal agitation, providing an essential parameter for evaluating the magnetic behavior of the material under varying thermal conditions. The Curie temperature not only indicates the temperature at which a material loses its magnetic ordering but also serves as a benchmark for the thermal stability of ferromagnetic phases. For the alloys studied, the predicted values of T_C are 814.89 K for KMnSn and 821.42 K for KMnPb. These results highlight the robustness of the ferromagnetic state in these materials and emphasize the influence of ΔE on their magnetic and thermal properties. Furthermore, this analysis underscores the significance of understanding the interplay between the energy states of a material and its magnetic behavior. The ability to estimate T_C from first principles, using the Heisenberg model and energy state calculations, offers a reliable framework for predicting and analyzing the performance of magnetic materials in applications requiring thermal stability, such as spintronics and thermoelectric devices. By correlating ΔE with T_C, this approach provides valuable insights into the material's ability to maintain ferromagnetic order under varying temperature conditions.

3.6 Thermodynamics properties

The calculation of thermodynamic properties is essential for understanding the behavior of materials under conditions of pressure and temperature that differ from their standard state. This enables the prediction of thermal, mechanical, and chemical stability across a range of environments. Theoretical modeling of these properties provides critical insights, serving as key indicators for assessing the potential industrial scalability of such compounds. In this study, the quasi-harmonic Debye model, as implemented in the Gibbs2 program,²⁵ is employed to predict the thermodynamic behavior of Heusler KMnZ (Z: Sn and Pb) alloys as a function of temperature. The properties are evaluated over a temperature range of 0–900 K and at pressures of 0, 5, 10, and 15 GPa, within the framework of the GGA approximation.

The heat capacity at constant volume (C_v) is a fundamental thermodynamic property that measures a material's ability to absorb heat without experiencing changes in volume. This property is deeply linked to the vibrational behavior of a material's atomic structure, influencing its thermal, mechanical, and electronic characteristics. A thorough understanding of these vibrational properties is essential for optimizing materials used in a wide range of applications, including thermoelectric devices, superconductors, and high-temperature technologies. Fig. 11(a) illustrates the evolution of C_V with temperature for KMnSn and KMnPb alloys, highlighting key trends in their thermal responses. At temperatures below 300 K, C_V exhibits a strong dependence on both temperature and pressure, following a T³ relationship in accordance with the Debye T³ law.³⁷ This behavior, typical of low-temperature crystalline solids, suggests that the heat capacity is primarily governed by acoustic phonon vibrations. As temperature rises above 300 K, C_V increases more slowly, approaching the Dulong–Petit limit,³⁸ which represents the maximum possible contribution of atomic vibrations to heat capacity at high temperatures. Furthermore, an inverse relationship between C_V and pressure is observed at constant temperatures, indicating that increasing pressure reduces the material's ability to absorb thermal energy. This suggests that pressure restricts atomic vibrations, diminishing the overall heat capacity. The results also indicate that temperature has a more significant influence on C_V than pressure, highlighting the dominant role of thermal excitations in determining a material's thermal behavior. Understanding these interactions is crucial for predicting the performance of KMnSn and KMnPb alloys under various operational conditions in industrial applications.

Fig. 11 (a) Specific heat as a function of temperature for different pressure values for KMnZ (Z = Sn, Pb). (b) Bulk modulus as a function of temperature for different pressure values for KMnZ (Z = Sn, Pb). (c) Thermal expansion coefficient as a function of temperature for different pressure values for KMnZ (Z = Sn, Pb). (d) Thermal expansion coefficient as a function of temperature for different pressure values for KMnZ (Z = Sin, Pb).

The variation of the bulk modulus (B) with temperature exhibits a nearly identical trend for both KMnSn and KMnPb alloys, as depicted in Fig. 11(b). The data consistently show that B decreases linearly with increasing temperature, a pattern observed across all applied pressure conditions. This linear reduction indicates that the material becomes more compressible as temperature rises, a behavior typically associated with thermal expansion and the weakening of atomic bonds at elevated temperatures. Moreover, the results demonstrate that at any specific temperature, the bulk modulus increases proportionally with pressure, signifying reduced compressibility as pressure rises. This suggests that higher pressures enhance the material's resistance to deformation by reinforcing atomic cohesion, while increasing temperature has the opposite effect, making the material more compressible. The contrasting influence of temperature and pressure on the bulk modulus underscores their opposing roles in shaping the material's mechanical properties—pressure strengthens atomic interactions, whereas temperature diminishes them. The values of the bulk modulus at 0 K and 0 GPa closely match those obtained from the Birch–Murnaghan equation of state and are consistent with those derived from the elastic constants. This alignment confirms the accuracy of the theoretical modeling employed in the study, reinforcing confidence in the calculated mechanical properties. The findings highlight the significance of comprehending the combined effects of temperature and pressure when assessing the mechanical stability and compressibility of these alloys, which is crucial for their potential industrial and technological applications.

The thermal expansion coefficient (α) characterizes how a material's dimensions respond to temperature fluctuations, providing critical insight into its structural stability under thermal stress. Fig. 11(c) illustrates the variation of α as a function of temperature and pressure for the half-Heusler (HH) alloys KMnZ (Z = Sn, Pb) within a temperature range of 0 to 1000 K and pressure levels of 0, 5, 10, and 15 GPa. The data show that at lower temperatures, particularly below 300 K, α increases sharply as temperature rises, indicating rapid dimensional expansion driven by intensified atomic vibrations as thermal energy accumulates. As the temperature exceeds 300 K, the rate of increase in α becomes more gradual, suggesting that the material approaches a thermal equilibrium where expansion is less pronounced. This behavior is characteristic of many solids, as the thermal expansion rate tends to stabilize at higher temperatures once atomic vibrations reach a maximum amplitude. The shift from rapid to moderate growth in α reflects the material's nuanced response to temperature changes across different thermal regimes, with the lower range displaying more dynamic expansion behavior. Additionally, at constant temperatures, α exhibits a linear decrease as pressure increases, highlighting an inverse relationship between thermal expansion and pressure. This suggests that increasing pressure suppresses atomic vibrations, thereby limiting the material's capacity to expand under thermal stress. The reduction in α with rising pressure underscores the stabilizing effect of compressive forces on material dimensions. Understanding the combined impact of temperature and pressure on α is crucial for predicting the behavior of KMnSn and KMnPb alloys in applications requiring high-dimensional stability across varied operational environments.

The Grüneisen parameter (γ) is a key thermodynamic quantity that provides critical insight into the behavior of phonon frequencies in response to variations in crystal volume. It is instrumental in assessing the anharmonic properties of a material, as it directly correlates with the degree of anharmonicity inherent in the system. Specifically, γ serves to quantify how phonons—quanta of lattice vibrations—are influenced by changes in both temperature and pressure. In this work, the dependence of the Grüneisen parameter on temperature and pressure is illustrated in Fig. 11(d). At lower temperatures, the alloys exhibit an exponentially decreasing trend in γ, indicating a significant sensitivity of phonon frequencies to anharmonic effects as temperature increases from low values. This decline in γ suggests that as temperature rises, anharmonic interactions grow stronger, leading to a reduction in phonon stability. However, at higher temperatures, the Grüneisen parameter plateaus, reflecting a stabilization of anharmonicity where further increases in temperature have little to no impact on phonon behavior. Conversely, the influence of pressure on the Grüneisen parameter is markedly subdued. As depicted in Fig. 11(d), γ shows minimal variation under increasing pressure, suggesting that pressure has a negligible effect on the phonon dynamics of these alloys when compared to temperature. This contrast highlights the dominance of thermal effects over pressure in governing the anharmonic behavior of the material. Thus, the temperature effect far outweighs the pressure effect, indicating that thermal expansion and vibrational properties are more strongly governed by temperature variations.

3.7 Thermoelectric properties

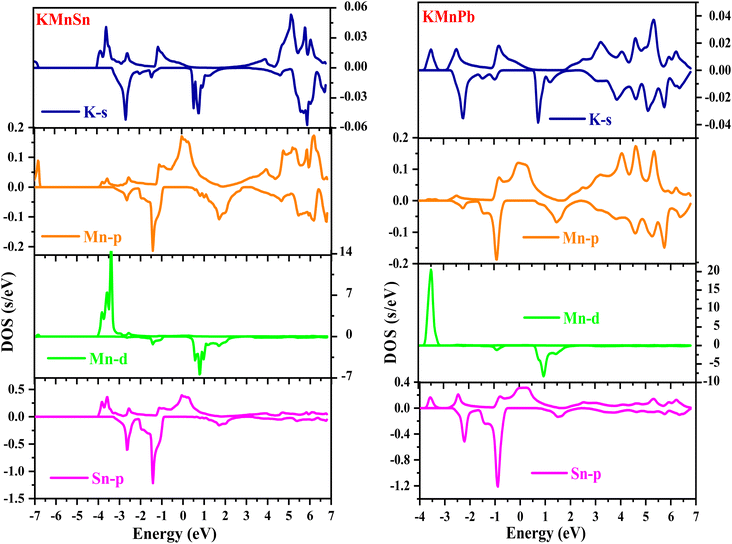
Utilizing the WIEN2k software and the BoltzTrap code, we conducted a comprehensive analysis of the thermoelectric properties of KMnZ (Z = Sn, Pb) compounds. BoltzTrap enabled the accurate calculation of the Seebeck coefficient (S), electrical conductivity (σ), power factor (PF), thermal conductivity (κ), and figure of merit (ZT), for both spin-up and spin-down channels over a temperature range of 50 K to 900 K. To ensure computational accuracy, a dense k-mesh grid of 50 × 50 × 50 was employed in conjunction with the mBJ approximation. This rigorous approach provides a solid foundation for understanding the thermoelectric performance of these alloys and their potential applications.

3.7.1 Seeback coefficient (S). The Seebeck coefficient, a crucial parameter for thermoelectric materials, quantifies their ability to generate an electromotive force in response to a temperature gradient, it is calculated by the following equation:

This property is intimately linked to the material's electronic structure near the Fermi level. As depicted in Fig. 12(a), KMnZ (Z = Sn, Pb) alloys exhibit a pronounced positive Seebeck coefficient in the spin-up state at room temperature, characteristic of p-type semiconductors. Specifically, KMnSn and KMnPb display Seebeck coefficients of 163.20 μV K⁻¹ and 159.09 μV K⁻¹, respectively. Conversely, the spin-down channel of these alloys demonstrates a decreasing Seebeck coefficient with increasing temperature, indicative of semiconductor behavior. At room temperature, KMnSn and KMnPb in the spin-down state exhibit Seebeck coefficients of 396.17 μV K⁻¹ and 452.76 μV K⁻¹, respectively. These findings underscore the distinct thermoelectric properties of these alloys and their potential for applications in energy conversion and management.

Fig. 12 (a) Variation of the Seebeck coefficient with temperature for KMnZ (Z = Sn, Pb) half-Heusler alloys in both spin channels. (b) Variation of the electrical conductivity with temperature for KMnZ (Z = Sn, Pb) half-Heusler alloys in both spin channels. (c) Variation of the thermal conductivity (κ) with temperature for KMnZ (Z = Sn, Pb) half-Heusler alloys. (d) Variation of the Power factor (PF) and figure of merit (ZT) with temperature for KMnZ (Z = Sn, Pb) half-Heusler alloys.

3.7.2 Electrical conductivity (σ/τ). Fig. 12(b) illustrates the temperature-dependent variation of electrical conductivity per relaxation time (σ/τ) for KMnZ (Z = Sn, Pb) alloys. In the spin-up state, the electrical conductivity exhibits a negative temperature coefficient, characteristic of metallic behavior. This implies that as the temperature increases, the electrical conductivity decreases. This trend is consistent with the metallic nature of the spin-up channel, as evidenced by the band structure and density of states calculations. At room temperature, KMnSn and KMnPb possess electrical conductivities of approximately 5.36 × 10²⁰ and 5.65 × 10²⁰ Ω⁻¹ m⁻¹ s⁻¹, respectively. These values suggest that the spin-up channel of these alloys exhibits relatively high electrical conductivity at room temperature. Conversely, the spin-down channel demonstrates a positive temperature coefficient, indicative of semiconducting behavior, as anticipated by band structure and density of states calculations. This means that the electrical conductivity increases with increasing temperature, which is a typical characteristic of semiconductors. The electrical conductivities of KMnSn and KMnPb in the spin-down state at room temperature are approximately 0.73 × 10²⁰ and 1.27 × 10²⁰ Ω⁻¹ m⁻¹ s⁻¹, respectively. These values highlight the significant difference in electrical conductivity between the spin-up and spin-down channels of these alloys. The spin-down channel of KMnSn exhibits a relatively high electrical conductivity at room temperature, while the spin-down channel of KMnPb exhibits a very low electrical conductivity. Overall, the electrical conductivity of KMnZ (Z = Sn, Pb) alloys is highly anisotropic, with the spin-up channel exhibiting metallic behavior and the spin-down channel exhibiting semiconducting behavior. These findings underscore the distinct electronic transport properties of these alloys and their potential for diverse applications.

3.7.3 Thermal conductivity (κ). Thermal conductivity (κ) measures a material's ability to transfer heat energy. This transfer is primarily driven by the continuous motion of atoms, which can involve rotational, translational, and vibrational motions. These atomic vibrations generate thermal energy through various mechanisms, such as electron–phonon interactions and the vibration of atoms at specific frequencies. Both electronic and lattice vibrations contribute to the overall thermal conductivity, which can be expressed as the sum of the electronic thermal conductivity (κ_electronic) and the lattice thermal conductivity (κ_lattice). Materials with high electrical conductivity are generally good thermal conductors due to the efficient movement of electrons. The lattice thermal conductivity can be estimated using the Slacks equation, which takes into account the properties of the material's crystal structure and atomic vibrations. As shown in Fig. 12(c), the electronic thermal conductivity (κ_e) of KMnSn and KMnPb increases with temperature. This means that these materials become more efficient at conducting heat through the movement of electrons as the temperature rises. At 300 K, the electronic thermal conductivity (κ_e) of KMnSn and KMnPb are 1.55 W mK⁻¹ and 3.42 W mK⁻¹, respectively. In this section, we investigate the thermoelectric properties of the materials under study by analyzing their lattice thermal conductivity (κ_L). Understanding lattice thermal conductivity is essential for assessing a material's efficiency in heat conduction, as it is influenced by atomic vibrations and electrical conductivity, both of which significantly affect thermoelectric performance. The lattice thermal conductivity (κ_L) of both half-Heusler materials demonstrates an exponential decrease with increasing temperature, indicating that the materials' ability to conduct heat through atomic lattice vibrations diminishes rapidly at higher temperatures. At 300 K, the calculated lattice thermal conductivities of KMnSn and KMnPb are 3.73 W mK⁻¹ and 3.22 W mK⁻¹, respectively. At 900 K, these values decrease to 1.14 W mK⁻¹ for KMnSn and 0.97 W mK⁻¹ for KMnPb.

To achieve reduced thermal conductivity, we employ Slack's model, which emphasizes the critical role of acoustic phonon modes in heat transport in semiconductors.⁵² Slack's model is mathematically represented as:⁶⁰

In this equation, A stands as a constant with a precise value of 3.04 × 10⁻⁸. M signifies the average molar mass, θ_D denotes the Debye temperature, V represents the average volume, γ pertains to the Grüneisen parameter, n indicates the number of atoms within the primitive unit cell (where n = 3 for half-Heuslers and n = 4 for full/quaternary Heuslers), and T denotes the temperature.

3.7.4 Power factor (PF). The power factor (PF) is a key metric for evaluating the efficiency of thermoelectric materials. It represents the ability of a material to generate power from a given temperature difference. A higher power factor indicates that a material can more effectively convert thermal energy into electrical energy. As depicted in Fig. 12(d), the power factor of KMnZ (Z = Sn, Pb) alloys increases with temperature, suggesting that their thermoelectric efficiency improves as the temperature rises. This is a promising trend, as it indicates that these materials can be effectively used in applications where high temperatures are encountered, such as waste heat recovery and power generation. The power factor is calculated by considering the contributions of both the Seebeck coefficient and electrical conductivity. The recorded power factors of KMnSn and KMnPb at room temperature are 31.27 W mK⁻² and 32.97 W mK⁻², respectively. And the value of power factor at 900 K is 128.11 W mK⁻² and 132.90 W mK⁻² for KMnSn and KMnPb respectively. These values demonstrate the competitive thermoelectric performance of these alloys. In particular, the power factor of KMnPb is relatively high, suggesting that it may be a promising candidate for thermoelectric applications. The increasing trend in power factor with temperature is a positive sign for the future of these materials. It suggests that they can be further optimized for thermoelectric applications by operating them at higher temperatures. Additionally, further research and development may lead to improvements in the power factor of these materials, making them even more attractive for practical use.

3.7.5 Figure of merit (ZT). The figure of merit (ZT) is the most important metric for evaluating the thermoelectric efficiency of a material. A high ZT value, ideally close to unity, is essential for a thermoelectric power generator (TEG) to achieve optimal performance. The ZT values of KMnZ (Z = Sn, Pb) alloys at various temperatures are shown in Fig. 12(d). These results demonstrate that KMnZ alloys are promising candidates for thermoelectric applications. As illustrated in Fig. 10(d), the ZT values of KMnSn and KMnPb increase with temperature. This is a positive trend, as it indicates that the thermoelectric efficiency of these alloys improves at higher temperatures. At 900 K, the ZT values of KMnSn and KMnPb are 0.70 and 0.76, respectively. These values are particularly noteworthy, as they approach unity, which is the ideal ZT value for a thermoelectric material. The high ZT values of KMnSn and KMnPb highlight their potential for use in thermoelectric power generation. These alloys can effectively convert waste heat into electricity, which can be used to power various devices and systems. Further research and development may lead to even higher ZT values for these materials, making them even more attractive for practical applications.

4. Conclusion

In this work, we employ the FP-LAPW method within the density functional theory (DFT) framework to conduct an in-depth analysis of the half-Heusler (HH) alloys KMnZ (Z = Sn, Pb). Our results identify the type II configuration as the most energetically favorable, with these alloys exhibiting half-metallic ferromagnetic (HM-FM) characteristics and band gaps of 1.09 eV for KMnSn and 1.25 eV for KMnPb. The half-metallic nature and complete spin polarization, as evidenced by DOS and band structure analyses, underscore their suitability for spintronic applications. The calculated total magnetic moments (MM) of the KMnZ alloys align closely with established theoretical values, validating the accuracy of our approach. Mechanical property assessments confirm the alloys' stability and ductility, making them viable for engineering and industrial purposes. Furthermore, transport property evaluations indicate a ZT value of 1, highlighting their potential for thermoelectric applications, specifically in converting waste heat to electricity. Thermal stability analyses also confirm their robustness under extreme conditions, supporting their applicability in practical scenarios. Collectively, these findings position HH KMnZ alloys as promising materials for advanced technological applications, particularly in spintronic heterostructures, energy harvesting, and other next-generation devices, given their comprehensive electronic, mechanical, and thermal attributes.

Data availability

Data will be made are available from the corresponding author upon reasonable request.

Author contributions

Bharti Gurunani: writing – review & editing, writing – original draft, methodology. Dinesh C. Gupta: supervision, software, writing – review & editing.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

Any agency does not fund the research work.

References

1. T. Ghellab, H. Baaziz, Z. Charifi, H. Latelli, M. J. Ahmad, M. Telfah, A. Alsaad, A. Telfah, R. Hergenröder and R. Sabirianov, First-principles calculations of the high-pressure behavior, electronic, magnetic, and elastic properties of praseodymium pnictides: PrX (X= P, As and Bi), J. Magn. Magn. Mater., 2022, 546, 168919.
2. X. P. Wei, Y. D. Chu, X. W. Sun, J. B. Deng and Y. Z. Xing, Stability, electronic, magnetic and pressure effect of half-Heusler alloys CNaCa and SiNaCa: a first-principles study, Superlattices Microstruct., 2014, 74, 70–77.
3. J. F. Gregg, R. P. Borges, E. Jouguelet, C. L. Dennis, I. Petej, S. M. Thompson and K. Ounadjela, Spin injection efficiency in spin electronic devices, J. Magn. Magn. Mater., 2003, 265(3), 274–289.
4. A. Kumar, S. Singh, S. A. Sofi, T. Chandel and N. Thakur, Robustness in half-metallicity, thermophysical and structural properties of Co2YAl (Y= Pd, Ag) Heuslers: a first-principles perspective, Mol. Phys., 2022, 120(18), e2120839.
5. Z. Bai, L. E. Shen, G. Han and Y. P. Feng, Data storage: review of Heusler compounds, Spin, 2012, 2, 1230006.
6. V. Mishra, V. Barwal, L. Pandey, N. K. Gupta, S. Hait, A. Kumar, N. Sharma, N. Kumar and S. Chaudhary, Investigation of spin gapless semiconducting behaviour in quaternary CoFeMnSi Heusler alloy thin films on Si (1 0 0), J. Magn. Magn. Mater., 2022, 547, 168837.
7. S. Dubey, K. Dubey, V. Sahu, A. Modi, R. A. Parry, G. Pagare and N. K. Gaur, Structural, electronic and elastic properties of FeCrAs Half-metallic ferromagnetic Half-Heusler Alloy: A First-Principles study, Mater. Today: Proc., 2022, 67, 12–19.
8. I. Galanakis and P. Mavropoulos, Spin-polarization and electronic properties of half-metallic Heusler alloys calculated from first principles, J. Phys.: Condens. Matter, 2007, 19(31), 315213.
9. N. A. Ganie, S. A. Mir and D. C. Gupta, Tantalum half-Heusler alloys RbTaSi and RbTaGe: potential candidates for desirable thermoelectric and spintronic applications, RSC Adv., 2023, 13(11), 7087–7101.
10. E. Gürbüz, M. Tas, E. Şaşıoğlu, I. Mertig, B. Sanyal and I. Galanakis, First-principles prediction of energy bandgaps in 18-valence electron semiconducting half-Heusler compounds: Exploring the role of exchange and correlation, J. Appl. Phys., 2023, 134(20), 1–10.
11. A. O. Moghaddam, R. Fereidonnejad, M. Naseri, N. Shaburova, D. Mikhailov, S. Uporov and E. Trofimov, Synthesis and characterization of novel high entropy Heusler intermetallics, Intermetallics, 2023, 159, 107917.
12. M. Salaheldeen, A. Wederni, M. Ipatov, V. Zhukova and A. Zhukov, Preparation and Magneto-Structural Investigation of High-Ordered (L21 Structure) Co2MnGe Microwires, Processes, 2023, 11(4), 1138.
13. A. Kumar, T. Chandel and T. N. Diwaker, Predicting the magnetism, structural, thermodynamic and electronic properties of new co-based Heuslers: first principle perspective, Philos. Mag., 2020, 100(21), 2721–2734.
14. K. Elphick, W. Frost, M. Samiepour, T. Kubota, K. Takanashi, H. Sukegawa, S. Mitani and A. Hirohata, Heusler alloys for spintronic devices: review on recent development and future perspectives, Sci. Technol. Adv. Mater., 2021, 22(1), 235–271.
15. S. Kumar, S. L. Gupta, D. Kumar and K. S. Vinayak, Structural properties of novel potential spintronic material and Full-Heusler alloy Co₂NbGe: First Principles investigation, Mater. Today: Proc., 2022, 1–12.
16. J. D. D. Enamullah, K. G. Suresh and A. Alam, Half-metallic Co-based quaternary Heusler alloys for spintronics: Defect-and pressure-induced transitions and properties, Phys. Rev. B, 2016, 94(18), 184102.
17. C. J. Palmstrøm, Heusler compounds and spintronics, Prog. Cryst. Growth Charact. Mater., 2016, 62(2), 371–397.
18. A. Candan, A study on magnetic, electronic, elastic and vibrational properties of Ir₂MnAl Heusler alloy for spintronic applications, Mater. Res. Express, 2019, 6(9), 096571.
19. K. Hu, R. Xie, C. Shen, H. Peng, H. Liu and H. Zhang, High-throughput design of Co-based magnetic Heusler compounds, Acta Mater., 2023, 259, 119255.
20. S. Tavares, K. Yang and M. A. Meyers, Heusler alloys: Past, properties, new alloys, and prospects, Prog. Mater. Sci., 2023, 132, 101017.
21. S. Parkin, Magnetic Race-Track—a Novel Storage Class Spintronic Memory, Int. J. Mod. Phys. B, 2008, 22(01n02), 117–118.
22. S. Yousuf and D. C. Gupta, Insight into half-metallicity, spin-polarization and mechanical properties of L21 structured MnY₂Z (Z= Al, Si, Ga, Ge, Sn, Sb) Heusler alloys, J. Alloys Compd., 2018, 735, 1245–1252.
23. B. Hillebrands and C. Felser, High-spin polarization of Heusler alloys, J. Phys. D: Appl. Phys., 2006, 39(5), E01.
24. A. Kumar, T. Chandel and N. Thakur, Robust stability, half metallic Ferromagnetism and structural properties of Co2RhSi, and Co2RuSi Heusler compounds-A first principles approach, Mater. Today: Proc., 2022, 66, 3292–3297.
25. S. L. Gupta, S. Kumar, T. S. S. Anupam and S. Panwar, Diwaker. A newly proposed full Heusler alloy Ir₂VZ (Z= Sn, In) suitable for high-temperature thermoelectric applications: A DFT approach, Mod. Phys. Lett. B, 2024, 38(09), 2450030.
26. Q. Gao, I. Opahle and H. Zhang, High-throughput screening for spin-gapless semiconductors in quaternary Heusler compounds, Phys. Rev. Mater., 2019, 3(2), 024410.
27. B. Gurunani and D. C. Gupta, Tailoring the intrinsic magneto-electronic, mechanical, thermo-physical and thermoelectric response of cobalt-based Heusler alloys: an ab initio insight, RSC Adv., 2023, 13(43), 29959–29974.
28. A. A. Santos and P. D. Borges, Ab initio investigation of Co–Ta–Sn Heusler alloys for thermoelectric applications, Comput. Theor. Chem., 2023, 1229, 114301.
29. H. Alam and S. Ramakrishna, A, review on the enhancement of figure of merit from bulk to nano-thermoelectric materials, Nano energy, 2013, 2(2), 190–212.
30. S. A. Khandy, I. Islam, D. C. Gupta and A. Laref, Full Heusler alloys (Co₂TaSi and Co₂TaGe) as potential spintronic materials with tunable band profiles, J. Solid State Chem., 2019, 270, 173–179.
31. R. A. De Groot, F. M. Mueller, P. V. van Engen and K. H. Buschow, New class of materials: half-metallic ferromagnets, Phys. Rev. Lett., 1983, 50(25), 2024.
32. H. Luo, G. Liu, F. Meng, J. Li, E. Liu and G. Wu, Half-metallicity in Fe-based Heusler alloys Fe₂TiZ (Z= Ga, Ge, As, In, Sn and Sb), J. Magn. Magn. Mater., 2012, 324(20), 3295–3299.
33. H. Z. Luo, H. W. Zhang, Z. Y. Zhu, L. Ma, S. F. Xu, G. H. Wu, X. X. Zhu, C. B. Jiang and H. B. Xu, Half-metallic properties for the Mn₂FeZ (Z= Al, Ga, Si, Ge, Sb) Heusler alloys: A first-principles study, J. Appl. Phys., 2008, 103(8), 1–9.
34. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo and A. Dal Corso, QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials, J. Phys.:Condens. Matter, 2009, 21(39), 395502.
35. N. O. Nenuwe and E. Omugbe, Electronic properties of half-Heusler compounds XCrSb (X= Fe, Ru, Os): Potential applications as spintronics and high-performance thermoelectric materials, Curr. Appl. Phys., 2023, 49, 70–77.
36. B. Gurunani, S. Ghosh and D. C. Gupta, Comprehensive investigation of half Heusler alloy: Unveiling structural, electronic, magnetic, mechanical, thermodynamic, and transport properties, Intermetallics, 2024, 170, 108311.
37. A. Kumar, S. L. Gupta, S. Kumar and V. Kumar, Spin-polarized DFT calculations for physical properties of novel KVSb half-Heusler compound for spintronic and thermodynamic applicability, arXiv, 2024, preprint, arXiv:2406.06656,  DOI:10.48550/arXiv.2406.06656.
38. M. Moradi, N. Taheri and M. Rostami, Structural, electronic, magnetic and vibrational properties of half-Heusler NaZrZ (Z= P, As, Sb) compounds, Phys. Lett. A, 2018, 382(41), 3004–3011.
39. L. Damewood, B. Busemeyer, M. Shaughnessy, C. Y. Fong, L. H. Yang and C. Felser, Stabilizing and increasing the magnetic moment of half-metals: The role of Li in half-Heusler LiMn Z (Z= N, P, Si), Phys. Rev. B, 2015, 91(6), 064409.
40. R. Ahmad and N. Mehmood, Investigation of Half-Heusler Compounds RhCrZ (Z= P, As, Sb, Sn): A First Principle Study, J. Supercond. Novel Magn., 2018, 31, 2637–2645.
41. W. Huang, X. Wang, X. Chen, W. Lu, L. Damewood and C. Y. Fong, Structural and electronic properties of half-Heusler alloys PtXBi (with X= Mn, Fe, Co and Ni) calculated from first principles, J. Magn. Magn. Mater., 2015, 377, 252–258.
42. M. A. Behbahani, M. Moradi, M. Rostami and S. Davatolhagh, First principle study of structural, electronic and magnetic properties of half-Heusler IrCrZ (Z= Ge, As, sn and sb) compounds, J. Phys. Chem. Solids, 2016, 92, 85–93.
43. Y. Xue, Z. Shen, Z. Wu and C. Song, Theoretical prediction of Curie temperature in two-dimensional ferromagnetic monolayer, J. Appl. Phys., 2022, 132(5), 1–8.
44. V. V. Marchenkov and V. Y. Irkhin, Half-metallic ferromagnets, spin gapless semiconductors, and topological semimetals based on Heusler alloys: Theory and experiment, Phys. Met. Metallogr., 2021, 122, 1133–1157.
45. G. Saravanan, V. Asvini, R. K. Kalaiezhily, I. M. Parveen, and K. Ravichandran. Structural and magnetic characterization of Fe2CrSi Heusler alloy nanoparticles as spin injectors and spin based sensors, in AIP Conference Proceedings, AIP Publishing, 2018, vol. 1953, No. 1.
46. K. V. Larionov, J. J. Pais Pereda, S. Li, S. Sakai and P. B. Sorokin, Half-metallic Heusler alloy/MoS₂ based magnetic tunnel junction, ACS Appl. Mater. Interfaces, 2022, 14(49), 55167–55173.
47. Y. Kawasugi, T. Ujino and H. Tada, Room-temperature magnetoresistance in organic spin-valves based on a Co₂MnSi Heusler alloy, Org. Electron., 2013, 14(12), 3186–3189.
48. M. Saleem and M. Shakil, Determination of tunnelling magneto resistance of magnetic tunnel junction designed using Co₂TiAl Heusler alloy with MgO spacer layer, Phys. B, 2023, 649, 414458.
49. A. Hirohata, W. Frost, M. Samiepour and J. Y. Kim, Perpendicular magnetic anisotropy in Heusler alloy films and their magnetoresistive junctions, Materials, 2018, 11(1), 105.
50. M. Marathe and H. C. Herper, Exploration of all-3 d Heusler alloys for permanent magnets: Ab initio based high-throughput study, Phys. Rev. B, 2023, 107(17), 174402.
51. P. Blaha, K. Schwarz, F. Tran, R. Laskowski, G. K. Madsen and L. D. Marks, WIEN2k: An APW+ lo program for calculating the properties of solids, J. Chem. Phys., 2020, 152(7), 1–6.
52. P. Blaha, K. Schwarz, G. K. H. Medsen, D. Kvasnicka and J. Luitz, WIEN2k, An Augmented Plane Wave Plus Local Orbitals Program for Calculating Crystal Properties, Vienna University of Technology, Vienna, Austria, 2001.
53. P. Nayak and D. C. Gupta, Exploring the multifaceted properties: electronic, magnetic, Curie temperature, elastic, thermal, and thermoelectric characteristics of gadolinium-filled PtSb₃ skutterudite, RSC Adv., 2024, 14(25), 17364–17379.
54. B. Gurunani and D. C. Gupta, Half-metallicity and thermoelectric performance: A multifaceted investigation of Zr-based half-Heusler alloys, Mater. Sci. Eng., B, 2025, 311, 117783.
55. K. Schwarz and P. Blaha, Solid state calculations using WIEN2k, Comput. Mater. Sci., 2003, 28(2), 259–273.
56. B. Gurunani and D. C. Gupta, A holistic approach to understanding structural, magneto-electronic, thermoelectric, and thermodynamic properties of RhMnZ (Z= Si, Ge) half Heusler alloys, Phys. Chem. Chem. Phys., 2024, 26(48), 30002–30017.
57. K. Schwarz, P. Blaha and S. B. Trickey, Electronic structure of solids with WIEN2k, Mol. Phys., 2010, 108(21–23), 3147–3166.
58. G. K. Madsen, P. Blaha, K. Schwarz, E. Sjöstedt and L. Nordström, Efficient linearization of the augmented plane-wave method, Phys. Rev. B, 2001, 64(19), 195134.
59. H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B, 1976, 13(12), 5188.
60. T. Lin, Q. Gao, J. Zhong, S. Yu and G. Liu, Structural, Mechanical, and Thermoelectric Properties of Quaternary Heusler Compounds CuCoZrZ (Z= Sn, Pb): A First-Principles Investigation, Phys. Status Solidi B, 2025, 2400278.

---