DOI:
10.1039/D5RA00199D
(Paper)
RSC Adv., 2025,
15, 6833-6846
Validation and optimization of a Prussian blue nanoparticle-based method for efficient detection and removal of lead ions in environmental samples
Received
8th January 2025
, Accepted 26th February 2025
First published on 3rd March 2025
Abstract
Lead (Pb2+) poisoning in water is now a more serious environmental concern than any other, due to its potential toxicity and accumulation in the human body. The Prussian blue nanoparticles (PBNPs) effectively removed organic and inorganic pollutants from aqueous solution. This study comprehensively investigates the adsorption properties of PBNPs for Pb2+ removal, optimizing experimental conditions through various analytical techniques. Key validation parameters—linearity, precision, accuracy, the limit of detection (LOD), the limit of quantification (LOQ), and the method detection limit (MDL)—were assessed. We investigate a comprehensive study focused on the adsorption properties of Prussian blue nanoparticles (PBNPs) for Pb2+ removal from aqueous solutions. The adsorption process was most effective at pH 7.5, achieving an adsorption capacity of 190 mg g−1. Kinetic analysis revealed that the adsorption follows a pseudo-second-order model with a chemisorption mechanism, while isothermal studies confirmed monolayer adsorption consistent with the Langmuir model. Thermodynamic analysis indicated that the process is spontaneous and endothermic. The Pb2+ concentration was precisely measured using graphite furnace atomic absorption spectroscopy (GFAAS) and flame atomic absorption spectroscopy (FAAS), with strong linearity (R2 = 0.997), LOQ = 0.179 mg L−1, and LOD = 0.056 mg L−1 for FAAS. These findings show that the PBNPs have a significant potential for effective Pb2+ removal and are reusable, making them suitable for eco-friendly remediation applications. Validation parameters confirmed that trace Pb2+ levels in environmental samples were accurately and precisely detected. The study emphasizes the high absorption capacity of PBNPs for lead, which was evaluated using different experimental approaches and methodologies.
Introduction
Heavy metals are a group of metals with a density at least five times higher than water. Additionally, even in small amounts, they can be quite detrimental and pose a serious hazard as environmental pollutants, and they can harm the surroundings and human health.1–5 Typical heavy metals observed in environmental pollutants include arsenic (As), cadmium (Cd), chromium (Cr), lead (Pb), and mercury (Hg).6,7 The health of humans and ecosystems can be at risk from these metals, which can accumulate in soil, water, and the air and enter the food chain. Like man-made materials, natural products can release Pb2+ and other heavy metals into the environment. Many natural processes such as soil erosion, volcanic activity, dissolution of rocks and minerals, and biological processes can lead to the accumulation of heavy metals in the environment. However, human activities such as mining operations, chemical and pharmaceutical industries, kitchenware production, and paper manufacturing also play a significant role. The quantity of heavy metals released due to human activities exceeds that from natural sources. Annually, synthetic sources contribute approximately 23 to 54 kilotons, whereas natural sources release around 20 to 51 kilotons.8 One of the most extensively researched hazardous materials is Pb2+. When ingested through drinking water, it has a detrimental impact on practically every vertebrate system as well as human health.9–11 Due to the associated risks,12,13 Italian legislation sets different limits for lead in water. Groundwater must contain less than 0.01 mg L−1. Water discharged to surfaces can contain up to 0.2 mg L−1. A solution of 0.3 mg L−1 is added to sewage to prevent Pb2+ and other heavy metals from spreading, and various methods have been developed to reduce or limit their presence in soil and water. The World Health Organization has set a maximum allowable amount of Pb2+ in drinking water at 0.01 mg L−1.14–16 There are different methods for metal removal such as ion exchange,17–19 adsorption,20–22 coagulation,23 electrocoagulation,24–26 and biological processes.27 Adsorption is one of the most effective methods for water remediation. The term “adsorption” refers to the mass transfer process of substances from the liquid to the surface of the solid phase, where they are attached by chemical or physical interactions.28 Adsorption processes utilize adsorbents derived from natural sources, industrial by-products, or low-impact waste products.29–34 According to Davarnejad and Panhi,35 adsorption is widely used to remove various metal ions from industrial wastewater.22
However, numerous low-cost adsorbents have been developed to eliminate Pb2+ from metal-contaminated wastewater.36–38 Natural materials, modified biopolymers, biological wastes, industrial byproducts, and nanomaterials are the sources of these adsorbents. Nanoparticles have garnered attention as potential adsorbents for heavy metals due to their unique properties. Their small size results in a larger surface area, enhancing their chemical activity and adsorption capacity for metal ions.39 According to Khajeh et al.,40 factors such as high specific surface area, strong adsorption and chemical activity, atomic arrangement on the surface, absence of internal diffusion barriers, and high surface binding energy play crucial roles in the adsorption process in aqueous environments. Several important properties are necessary for nanoparticles to be effective adsorbents for heavy metal removal. They must be safe, have strong adsorption capacity, absorb trace amounts of pollutants (μg L−1), easily remove surface contaminants, and be reusable with no apparent degradation in effort. Iron(III) hexacyanoferrate(II) (Fe4[Fe(CN)6]3) is the chemical name for Prussian blue nanoparticles (PBNPs), which might be great in getting rid of both organic and inorganic contaminants because of their high surface area, porous shape, and strong adsorption capacity.41,42 In addition to supporting the detection of harmful compounds like aflatoxin B1,43 they can trap hydrocarbons and tiny gaseous molecules, which are used as Fenton catalysts for dye removal.44 Since PBNPs effectively adsorb radioactive elements and heavy metals such as cobalt (Co2+), strontium (Sr2+), and cesium (Cs+),45 they may be useful for treating nuclear waste46,47 and purifying water.45–47 Ammonium (NH4+), sodium (Na+), and potassium (K+) can be captured through their selective ion changeability,48 and adhesion to metal oxides increases their catalytic balance.49 The FDA has also certified Prussian blue as an antidote for heavy metal toxicity,50 especially from exposure to cesium and thallium.51 Due to their proven biocompatibility and biosafety, PBNPs are versatile materials suitable for medical and environmental remediation applications.
The environment and human health are at serious risk due to the rising incidence of heavy metal contamination, especially lead (Pb2+). Because of its toxic nature and propensity to bioaccumulate within biological systems, lead poisoning is still a serious problem. Conventional techniques for removing lead from water, like ion exchange and chemical precipitation, frequently lack environmental sustainability, cost-effectiveness, and efficiency. Therefore, creative and effective methods to reduce lead pollution in aquatic ecosystems are desperately needed. This work presents an entirely novel approach for effectively detecting and eliminating lead ions from environmental samples using Prussian blue nanoparticles (PBNPs). A validated method for the determination of Pb2+ was developed using atomic absorption spectroscopy (graphite and flame detector) regarding linearity, accuracy, precision, limit of quantification (LOQ), limit of detection (LOD), and method detection limit (MDL). The proposed method is expected to be more sensitive and allow monitoring of Pb2+ at trace and high levels using graphite furnace atomic absorption spectroscopy (GFAAS) and flame atomic absorption spectroscopy (FAAS) respectively, with satisfactory accuracy and precision. This study is motivated by the unique properties of PBNPs, including their high surface area, strong adsorption capacity, and potential for reusability. By harnessing these characteristics, this research aims to provide a more effective solution for lead remediation compared to conventional methods. To maximize the adsorption capacity of PBNPs, the study also highlights the importance of optimizing experimental conditions like pH, adsorbent dose, and temperature. This study addresses gaps in the existing literature regarding adsorption mechanisms and lead removal efficiency through the examination of several parameters, including kinetic and thermodynamic analyses. In conclusion, this study is innovative because it combines cutting-edge nanomaterials with an emphasis on sustainable methods, with the dual goals of successfully removing lead ions and creating a foundation for remediation technologies of the future. This supports international initiatives to find eco-friendly solutions, highlighting the study's importance and urgency regarding environmental preservation and public health.
Materials and methods
Chemicals
Tetraethyl orthosilicate (TEOS, 99.9%). Pluronic F-127, aluminum nitrate, ethanol, ferric chloride, sodium citrate, potassium ferrocyanide, phosphoric acid, and sodium hydroxide were purchased from Sigma-Aldrich, Germany, with an assay ≥99%. HNO3 69% Supelco, made in Germany. Lead standard for AAS (Sigma-Aldrich Part#16595), stock solutions at 1000 mg L−1 were used as adsorbents, and the stock was diluted with distilled water to create different concentrations. All chemicals used were of analytical reagent grade.
Synthesis of Prussian blue/silica monolith (HOM) nanocomposites
The PB/silica HOM nanocomposite sorbent was synthesized using the traditional sol–gel method. Initially, 11.07 g of Pluronic F-127 and 16.06 g of TEOS were mixed in a flask. The mixture was then dissolved and homogenized using a rotary evaporator. Separately, 2.5 g of FeCl3, 5.28 g of potassium ferrocyanide, and 1.62 g of sodium citrate were dissolved in 40 mL of distilled water. Subsequently, 20 mL of each prepared solution was added to the main mixture and processed in the rotary evaporator for 15 minutes. Afterward, approximately 10 mL of H3PO4 (adjusted to pH 1.6) was introduced, ensuring complete dissolution, and the mixture was left in the rotary evaporator for another 15 minutes. The solution was then heated to 80 °C to evaporate water and ethanol. The resulting material was washed with ethanol, followed by distilled water, and dried at 60 °C overnight.52
Characterization of PB/silica HOM
The size of the PB/silica HOM nanocomposites was determined via high-resolution transmission electron microscopy (HR-TEM) using an FEI TECNAI G2 Spirit TWIN (Model No. 9432 050 18111, Czech Republic), operated with a VELETA camera at an accelerating voltage of 120 kV. The surface morphology was examined through scanning electron microscopy (SEM) using a JEOL JSM-5400 LV (Japan). A gold film was applied to the samples at room temperature using a JEOL JTC-1100E fine-coat ion sputtering apparatus (Japan). The textural properties of the nanocomposites were assessed using a BELSORP MIN-II analyzer based on nitrogen adsorption at 77 K (MicrotracBEL Corp., Osaka, Japan). The FTIR spectrum was recorded using a nicolet 6700 spectrophotometer (USA) with KBr pellets, covering the range of 4000–400 cm−1 at a resolution of 4 cm−1 with 16 scans. The particle size distribution in the 4–90° range was analyzed using a Philips PW 1710 X-ray diffractometer with nickel-filtered CuKα radiation (λ = 1.54060 Å) at 40 kV and 40 mA.
Adsorption experiment
Two sets of Pb2+ adsorption experiments were carried out in the batch method. The adsorption experiment was carried out using PBNPs dissolved in 10 mL Pb2+ solution with continuous stirring at 180 rpm the effect of experimental parameters such as pH, adsorbent concentration, and temperature ranging from pH 3.0 to 9.0 was studied. Furthermore, the effects of adsorbent concentration were studied with doses ranging from 0.1 g to 2.0 g at an initial Pb2+ concentration of 10 mg L−1, a temperature of 25 °C, and a contact time of 24 hours. To get the appropriate pH, HNO3 (0.1 N), or NaOH (0.1 N) were added to the solutions, and 22 mg of PBNPs were fully dissolved in 50 mL of Pb2+ solution, which initially contained 100 mg, to investigate the desorption capacity of the produced PBNPs. After adsorption, the PBNPs saturated with Pb2+ were separated and washed with deionized water to remove unabsorbed traces. Subsequently, 50 mL of HNO3 (0.01 N) was used as the optimal method to agitate the PBNP samples one by one.53,54 The desiccant was cleaned several times with distilled water to remove excess acid beforehand and used in the next desorption cycle. The adsorption cycle was repeated five times with the same spent adsorbent. FAAS and GFAA spectroscopy techniques were used to determine the residual Pb2+ concentration in the samples in both cases. Flame type: C2H2–air at measurement line wavelength 217 nm ContrAA 700 analytikjena (Germany). Table 1 presents the GFAAS furnace setup. Dried samples were placed in vials for the autosampler. The autosampler was configured to give a signal over background absorbance when using 20 μL. Measurements were made, and each standard and reference solution was tested at least twice. When the relative standard deviation (%RSD) exceeds 7%, additional measurements will be performed. Aspect CS 2.2.2.0 (analytikjena, made in Germany) software will average the dimensions where acceptable. The software produced a linear graph with Pb2+ concentration on the x-axis and the corresponding signal values on the y-axis.
Table 1 Graphite furnace program
| Metal |
Temperature (°C)/ramp-hold (s) |
Cleaning out step (°C) |
| Ashing step |
Atomization step |
| Pb2+ |
800 |
1500 |
2500 |
Using eqn (1) and (2), respectively, the adsorption capacity, qe (mg g−1), and adsorption removal percentage (%R) were determined.55,56
| |
 | (1) |
| |
 | (2) |
The Pb2+ initial and equilibrium concentrations are expressed in mg L−1 as Ci and Ce, respectively. V represents the reaction mixture's volume, and m denotes the adsorbent's mass.
Response surface methodology
The experimental design involved three levels (low, medium, and high, coded as −1, 0, and +1) as shown in Table 2, with 13 runs repeated to optimize variables like adsorbent dosage and pH. For statistical analysis, these two-factor variables were denoted as X1 and X2. Based on the preliminary experiments the ranges and levels listed in Table 2 were selected. The primary effects and interplay among the variables were identified. The experimental design matrix followed the central composite design (CCD) as tabulated in Table 3, and corresponding experiments were conducted. Results were analyzed using response plots and analysis of variance (ANOVA). In response surface methodology (RSM), a commonly used second-order polynomial (eqn (3)) was developed to fit the experimental data:| |
 | (3) |
where K is the number of experimental factors, ε is the model error, Y is the expected response, β0 is constant, βi is the linear coefficient of the input factor Xi, βii is the quadratic coefficient of the input factor Xi, βij is the different interaction coefficients between input factors Xi and Xj.57,58 This equation helps in understanding the relationship between variables and optimizing conditions for maximum efficiency in Pb2+ removal.
Table 2 Factors and levels used in the factorial design
| Factor |
Low level (−1) |
Medium level (0) |
High level (+1) |
| PBNPs dose (X1) |
0.10 g |
1.05 g |
2.00 g |
| pH (X2) |
3.00 |
6.50 |
9.00 |
Table 3 CCD and results for the study of two experimental variables
| No. |
Coded value |
Real value |
Lead ion (Pb2+) |
| pH |
Dose (g L−1) |
pH |
Dose (g L−1) |
Removal (%) |
Qe (mgPb/gPBNPs) |
| 1 |
−1 |
+1 |
3 |
2 |
53.92 |
5.09 |
| 2 |
+1 |
+1 |
9 |
2 |
100.00 |
4.96 |
| 3 |
0 |
−1 |
6 |
0.1 |
16.15 |
16.02 |
| 4 |
0 |
+1 |
6 |
2 |
95.17 |
4.73 |
| 5 |
−1 |
0 |
3 |
1.05 |
53.92 |
5.09 |
| 6 |
+1 |
0 |
9 |
1.05 |
100.00 |
9.45 |
| 7 |
+1 |
−1 |
9 |
0.1 |
100.00 |
99.20 |
| 8 |
−1 |
−1 |
3 |
0.1 |
16.15 |
16.02 |
| 9 |
0 |
0 |
6 |
1.05 |
100.00 |
9.45 |
| 10 |
0 |
0 |
6 |
1.05 |
100.00 |
9.45 |
| 11 |
0 |
0 |
6 |
1.05 |
99.40 |
2.66 |
| 12 |
0 |
0 |
6 |
1.05 |
99.44 |
4.73 |
| 13 |
0 |
0 |
6 |
1.05 |
99.66 |
4.96 |
Method validation
Method validation is performed to verify that the method is suitable for its intended use. Numerous global conferences and institutions have released recommendations and procedures on the validation of an analytical method in a single laboratory.59 The method's reliability was evaluated by calculating various analytical performance parameters specified by the International Conference on Harmonization.60 Our work evaluated various validation parameters such as linearity, limits of detection, limits of quantification, accuracy, precision, and sensitivity indicated by the method detection limit.
Linearity. Absorbance versus concentration data for metal concentrations was used to construct a calibration curve by linear regression, y = axe + b, where y is the predicted value, a is the slope, and b is the intercept linearity is typically achieved at a minimum of four concentration levels for most standards, although six levels are generally preferred.60 In this work, FAAS was established using nine concentration levels; while GFAAS was established using six concentration levels for high and low Pb2+ concentrations, respectively. The linearity of the calibration curves was assessed via the calculation of the correlation coefficients (R2).61–63
Method detection limits (MDL). The method detection limit is the lowest Pb2+ concentration that can be reliably reported as greater than zero and the method results can be distinguished with 99% confidence. In this study, MDLs were evaluated by analyzing seven spike concentrations and blanks generated in deionized water. MDLs were determined by multiplying the standard deviation (SD) by the Student's t-value, as shown in eqn (4) at (n − 1 = 6) degrees of freedom at the 99% confidence limit.64,65
Limit of detection (LOD) and limit of quantification (LOQ). The efficiency of an instrument or analytical system is evaluated based on LOD and LOQ. Several methods can be used to determine the LOD and LOQ that match the lowest reliable analyte concentration and the lowest detectable analyte concentration consistently and accurately, respectively.62,64,65 Detection and quantification limits require at least 7 blank samples to be analyzed to establish them. The LOD and LOQ values were calculated numerically using the slope of the linear calibration curve (slope) and the standard deviation (SD) of the ten blank solution absorbance values eqn (5) and (6),66| |
 | (5) |
| |
 | (6) |
Accuracy and precision. Studying the accuracy and precision of the method allowed the researchers to account for systematic and random errors, respectively. This study was performed through three levels of concentrations, 0.3, 2, and 5 mg L−1 samples for FAAS and two levels, 0.010 and 0.040 mg L−1 for GFAAS, with each level repeated three times (n = 3) to calculate their average. The percentage recovery of known metal concentrations added to the water samples was used to gauge the method's accuracy, and the added standard solutions were compared to the spiked samples. Accuracy values between 90% to 110% were considered acceptable.59,67 The precision of the method was determined by evaluating the consistency of the instrument response to the assay in a single run (intra-run precision) and multiple runs (inter-run precision). Repeatability is represented by the relative standard deviation (%RSD), as in eqn (7). Inter-run precision (reproducibility) is the accuracy over an extended period within a single laboratory.68 In our case, it was two weeks, measured as %RPD as in eqn (8), where C1 and C2 are the larger and smaller values of the two observed measurements.| |
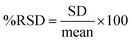 | (7) |
| |
 | (8) |
Results and discussion
Prussian blue/silica HOM nanocomposite characteristic analysis
HR-TEM and SEM were used to examine the surface morphology and nanostructure of PB/silica HOM nanocomposites (Fig. 1a and b). HR-TEM confirmed their hollow, spherical, and porous shape (Fig. 1a), while SEM revealed a combination of microscale and nanoscale particles, suggesting a hierarchical structure with smaller nanoparticles positioned on larger microparticles (Fig. 1b). The textural characteristics of PB/silica HOM nanocomposites were assessed using Brunauer–Emmett–Teller (BET) surface area analysis and Barrett–Joyner–Halenda (BJH) pore volume measurements (Fig. 1c).52 A surface area of 167.246 m2 g−1 and a pore volume of 0.082 cm3 g−1 were determined by the Langmuir model. Micropores were indicated by the nitrogen adsorption–desorption isotherm's type IV profile with hysteresis. Larger interspherical holes measuring 24 nm were seen in TEM, which improved porosity and adsorption. The principal pore diameter was 1.54 nm. These findings demonstrate that the linked hollow microsphere structure is the source of the large surface area and porosity. The functional groups present in the nanocomposite were examined using FTIR spectroscopy (Fig. 1d). The PB phase within the silica matrix was confirmed by a peak at 2081.92 cm−1, which corresponds to the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N stretching in potassium ferricyanide. Hydrogen bonding was shown by broad absorption bands at 3358.71 cm−1 and 1606.51 cm−1. Furthermore, a peak at 606.78 cm−1 confirmed the structural integrity of the PB/silica HOM nanocomposites by validating the Fe2+–C
N stretching in potassium ferricyanide. Hydrogen bonding was shown by broad absorption bands at 3358.71 cm−1 and 1606.51 cm−1. Furthermore, a peak at 606.78 cm−1 confirmed the structural integrity of the PB/silica HOM nanocomposites by validating the Fe2+–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N–Fe3+ connection.69,70 X-ray diffraction (XRD) was used to examine the nanocomposite's crystalline structure, as seen in (Fig. 1e).52 The characteristic crystal planes of Prussian blue (200), (220), (222), (420), and (442), respectively are represented by the distinct peaks in the diffraction pattern at 17.200°, 25.519°, 35.260°, 39.460°, and 53.680°. These peaks further validate the effective synthesis of PB/silica HOM nanocomposites by confirming the presence of a face-centered cubic (FCC) structure with an Fm
N–Fe3+ connection.69,70 X-ray diffraction (XRD) was used to examine the nanocomposite's crystalline structure, as seen in (Fig. 1e).52 The characteristic crystal planes of Prussian blue (200), (220), (222), (420), and (442), respectively are represented by the distinct peaks in the diffraction pattern at 17.200°, 25.519°, 35.260°, 39.460°, and 53.680°. These peaks further validate the effective synthesis of PB/silica HOM nanocomposites by confirming the presence of a face-centered cubic (FCC) structure with an Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group.52
m space group.52
 |
| | Fig. 1 PB/silica HOM nanocomposites' physical characteristics. (a)TEM image, (b) SEM image, (c) N2 sorption/desorption isotherms,52 (d) FT-IR spectrum and (e) XRD Pattern.52 | |
Method validation
Linearity. Standard solutions were used to evaluate the linearity of the calibration curves for FAAS and GFAAS. Nine concentration levels, ranging from 0.01 to 0.20 mg L−1, were utilized to generate the calibration curve for GFAAS, and six concentration levels, ranging from 0.20 to 5.00 mg L−1, were used for FAAS (Fig. 2). Then, the linear ranges for Pb2+ were determined based on the correlation coefficients (R2). A strong linearity of Pb2+ was observed with coefficients of determination (R2) of 0.997 for FAAS and 0.997 for GFAAS, as shown in Table 4. As described by Magnusson et al.,71 a linear analytical response is obtained over a certain concentration range when the value of R2 exceeds 0.995.
 |
| | Fig. 2 The scatter plot for the relationship between the Pb2+ concentrations and the corresponding absorbance values (a) by GFAAS and (b) by FAAS. (b) Method detection limits (MDL), limit of detection (LOD) and limit of quantification (LOQ). | |
Table 4 Linear regression for Pb2+ using GFAAS and FAAS analysis
| Detector |
Linear range (mg L−1) |
Slope |
Intercept |
R2 |
| GFAAS |
0.01–0.20 |
3.1205 |
0.0927 |
0.997 |
| FAAS |
0.20–5.00 |
0.0378 |
0.0039 |
0.997 |
Method detection limits (MDL), limit of detection (LOD) and limit of quantification (LOQ). The MDL, LOD, and LOQ values are presented in Table 5. According to EPA regulations at 40 CFR Part 141 Subpart I,72 the permissible Pb2+ level is 0.01 mg L−1 and the action level is 0.015 mg L−1. The quantification limit for Pb2+ must also be less than or equal to the maximum limit (ML) by commission regulation (EU) 2016/582. Our validated method for estimating Pb2+ in water exhibits higher sensitivity, enabling trace-level monitoring, as confirmed by the GFAAS results presented in Table 5.
Table 5 MDL, LOD, and LOQ for the calibration curves of Pb2+ using GFAAS and FAAS
| Detector |
MDL (mg L−1) |
LOD (mg L−1) |
LOQ (mg L−1) |
| FAAS |
0.058 |
0.056 |
0.179 |
| GFAAS |
0.008 |
0.003 |
0.010 |
Accuracy and precision. Accuracy was estimated by calculating the recovery of Pb2+ at three concentration levels, i.e., 0.3, 2, and 5 mg L−1 for FAAS, and two concentration levels, i.e., 0.010 and 0.040 mg L−1 for GFAAS. The recoveries for FAAS and GFAAS were in the acceptable range of 87.02% to 106.93% and 95.69% to 104.79%, for Pb2+, respectively (Fig. 3a and b). Typical Pb2+ recovery for the EPA method73 is between 70 and 130%. The Pb2+ recoveries in this study were within acceptable limits, demonstrating the accuracy of the validated method. The repeatability (RSD) and the reproducibility (RPD) were evaluated to determine the precision of the developed method over two weeks. The repeatability varied, as shown in Fig. 3c, with values such as 2.994% and 3.290% across different weeks. This suggests that the method has good repeatability. GFAAS exhibited a more consistent precision, with %RSD values generally lower than those of FAAS. The values ranged from 1.211% to 7.737%, indicating that GFAAS may be a more reliable choice for applications requiring high precision, especially at trace levels of Pb2+. On the other hand, reproducibility showed variability with %RPD values that reflect the consistency and robustness of results when different runs over two weeks are applied. The %RPD values varied between 3.804% and 5.440% using FAAS and for GFAAS the values varied between 3.129% and 5.376% as in Fig. 3d. This demonstrates that our validated approach is robust, meaning it is more resistant to fluctuations over an extended period, making it a superior alternative for analyses requiring high reproducibility across various experimental runs. According to EPA methodology,73 a 15% maximum RSD value is considered appropriate for the same set amount of analyte. Hence, it can be concluded that the proposed method exhibited satisfactory precision, according to the obtained RSD values.
 |
| | Fig. 3 Accuracy and precision analysis for Pb2+. The acceptable recovery range was set between 70% and 130%, with a %RSD threshold of 15%. (a) and (b) Illustrate the percent recovery for FAAS and GFAAS, respectively, while (c) and (d) depict the percent RSD for FAAS and GFAAS, respectively. | |
Adsorption result
Effect of pH on Pb2+ adsorption. pH is a crucial factor in the absorption process because it influences the chemistry of the solution and the surface interactions of the adsorbent.74 Due to the changes in dissolved species caused by metal ion precipitation and hydrolysis,75,76 the level of absorption significantly fluctuates with variations in pH. The influence of pH on Pb2+ adsorption onto PBNPs was investigated to assess this impact; the results are presented in Fig. 4. The data indicates that the adsorption capacity of Pb2+ reached its highest point at pH 7.5 and rose with higher pH levels. Beyond this point, insoluble Pb2+ precipitates such as Pb(OH)2, Pb(OH)+, and Pb(OH)3 (ref. 77 and 78) were formed, reducing the adsorption capacity. The optimal pH for further studies on Pb2+ absorption was found to be 7.5, which also exhibited the greatest adsorption capacity.
 |
| | Fig. 4 Effect of pH [pH: 2.0–9.0, time = 24 h, Co = 10 mg L−1, and T = 25 °C]. | |
Statistical analysis. The optimal conditions for Pb2+ adsorption on the surface of PBNPs were determined using the central composite design (CCD) of the reaction surface method (RSM) and were identified using Design-Expert® version 6.0 (DX6). The relationship between Pb2+ uptake and the adsorption capacity of PBNPs is described by the following equations.
| Y(Qe) = 19.78697 + 8.08666X1 + 10.12283X2 − 0.742225X1X2 − 1.11068X22X12 − 0.615745X229 |
| Y(removal) = −96.93846 + 36.64701X1 + 48.52338X2 − 3.3744214.560X1X2 − 5.64404X12 ± 2.84591X1210 |
The statistical analysis by ANOVA reveals the significant factors affecting the adsorption capacity and Pb2+ removal efficiency with the given adsorbent is tabulated in Table 6. The p-values of the model 0.0002 for removal efficiency and 0.0006 for adsorption capacity indicate that the model is statistically significant, indicating that the selected variables have a significant effect on the reaction variables pH level emerged as the most important factor affecting Pb2+ removal efficiency and adsorption capacity. The pH plays a significant role in the adsorption process with p-values of <0.0001 for separation efficiency and 0.0001 for adsorption capacity. This suggests that pH influences the adsorbent surface charge, degree of ionization, and metal ion speciation, which affects the adsorption mechanism with F-values of 91.28 for removal efficiency and 56.41 for adsorption capacity. In contrast to pH, the dose (A) is not statistically significant in terms of adsorption capacity or removal efficiency (p-values of 0.2445 and 0.1574, respectively) indicating that increasing the Pb2+ dose does not significantly improve the adsorption process. The insignificant effect of dose may be due to saturation, where increasing adsorbent doses does not provide additional surface area for adsorption beyond a certain point. The interaction between dose and pH (AB) shows marginal significance for extraction efficiency, with a p-value of 0.0542.
Table 6 Analysis of variance for the response of the adsorption capacity for Pb2+
| Source Pb2+ |
Removal efficiency (%) |
Adsorption capacity (mg g−1) |
| Sum of squares |
df |
Mean square |
F-Value |
P-Value |
Sum of squares |
df |
Mean square |
F-Value |
P-Value |
| A: for dose, and B: for pH. |
| Model |
9339.2 |
5 |
1867.84 |
26.92 |
0.0002 |
349.49 |
5 |
69.9 |
19.11 |
0.0006 |
| Aa |
112 |
1 |
112 |
1.61 |
0.2445 |
9.16 |
1 |
9.16 |
2.51 |
0.1574 |
| Ba |
6332.76 |
1 |
6332.76 |
91.28 |
<0.0001 |
206.29 |
1 |
206.29 |
56.41 |
0.0001 |
| AB |
369.95 |
1 |
369.95 |
5.33 |
0.0542 |
17.9 |
1 |
17.9 |
4.89 |
0.0626 |
| A2 |
71.66 |
1 |
71.66 |
1.03 |
0.3433 |
2.78 |
1 |
2.78 |
0.7588 |
0.4126 |
| B2 |
1811.91 |
1 |
1811.91 |
26.12 |
0.0014 |
84.82 |
1 |
84.82 |
23.19 |
0.0019 |
| Residual |
485.63 |
7 |
69.38 |
|
|
25.6 |
7 |
3.66 |
|
|
| Lack of fit |
450.63 |
3 |
150.21 |
17.17 |
0.0095 |
18.75 |
3 |
6.25 |
3.65 |
0.1214 |
| Pure error |
35 |
4 |
8.75 |
|
|
6.84 |
4 |
1.71 |
|
|
| Cor total |
9824.82 |
12 |
|
|
|
375.09 |
12 |
|
|
|
This may indicate a small overlapping effect, with some combinations of concentration and pH improving Pb2+ adsorption slightly more than each factor individually but an interaction effect (p = 0.0626) for the adsorption capacity being smaller, and possibly with the support is not so great. The quadratic term for pH (B2) was significant for both adsorption capacity (p = 0.0019) and removal efficiency (p = 0.0014). This indicates that the relationship between pH and Pb2+ adsorption is not strictly linear, and there is an optimal pH range where the adsorption process is large. Conversely, the quadratic term of dose (A2) is not significant, indicating that the dose modification is insignificant in affecting the stability of the adsorption process. The residuals for adsorption capacity and removal efficiency exhibit least squares (69.38 and 3.66, respectively), indicating low unexplained variability. However, the (lack of fit) for removal efficiency is insignificant (p = 0.1214), suggesting that the model accurately represents the experimental data for removal efficiency.
The 3D response surface plot. The 3D response surface plots are valuable for examining both the main and interaction effects of the factors,79–81 shown in Fig. 5. The surface plot in Fig. 5a shows the effect of dose (A) and pH (B) on Pb2+ removal efficiency. The red region above the plot corresponds to increasing removal, indicating that the higher pH and lower adsorbent concentration achieve optimal results. The increase in surface area shows a strong nonlinear relationship, on the pH axis. As pH increases, the removal rate becomes more effective, reaching a maximum around pH 6–7. After this point, further increases in pH appear to reach equilibrium in terms of their effect on removal efficiency. Increasing pH values enhance Pb2+ removal, consistent with the main impact of pH observed in the ANOVA results (Table 6). The lack of dramatic improvement with increasing rates suggests that as the optimal rates are achieved, further increases result in diminishing returns. Surface plot Fig. 5b shows the effect of dose (A) and pH (B) on adsorption capacity in mg g−1. The increasing trend of plots up to low pH and low dose indicates that these conditions result in low adsorption capacity. While the optimum is obtained at mid-dose levels and high pH values a significant decrease in adsorption capacity is observed at very high doses. The surface plot supports the ANOVA analysis, showing that pH has a greater effect than dose, especially at pH 7.56. The significant effect of pH in the ANOVA is reflected here in the nonlinear trend above, which demonstrates that the adsorption capacity is maximized at intermediate levels of the two variables.
 |
| | Fig. 5 Response surface plots of: (a) removal efficiency and (b) adsorption capacity versus the effect of two variables. | |
Adsorption kinetics. To understand the underlying mechanism and rate-limiting steps governing the adsorption process, the adsorption kinetics of Prussian blue nanoparticles (PBNPs) were analyzed based on pseudo-first-order, pseudo-second-order, and intra-particle diffusion models. The adsorption kinetics equations are expressed by eqn (11)–(13), respectively.82–84 Table 7 shows the kinetic parameters and experimental adsorption capacities for the removal of Pb2+ using PBNPs using three kinetics models. The pseudo-first-order kinetic model and the experimental data (Fig. 6a) showed a significant correlation with an R2 value of (0.992). However, the slope of the plot against the rate constant was relatively small (−0.0051), revealing that the process is more intricate in systems where adsorption is inconsistent. On the other hand, a pseudo-second-order kinetic model (Fig. 6b) displayed an exceptional fit to the experimental data, evidenced by a very high R2 value of (0.999). This suggests that the adsorption process may be chemisorption, where the limiting step involves coupling forces by electron sharing or exchange. The Pb2+ interface is highly dependent on concentration, and the adsorption sites gradually become occupied over time. Extra information about the diffusion mechanism can be obtained from the intra-particle diffusion model (Fig. 6c). The plot demonstrates that the adsorption process can take place in multiple steps, which is typical for intra-particle diffusion. While the R2 value of 0.866 is lower than the pseudo-second-order, it indicates that inter-particle diffusion plays a role but isn't a rate-limiting step.85 The effect of contact time on the adsorption capacity (Fig. 6d) shows that adsorption increased rapidly in the early part of the reaction and then slowly reached equilibrium. This behavior is typical for adsorption processes, where active site availability decreases in time during inhabitation. The first strong increase in the adsorption capacity indicates the presence of a strong PBNP-Pb2+ relationship, where equilibrium is reached after a certain time, indicating the saturation of the adsorption sites. Kinetic analysis shows that the pseudo-second-order model describes the adsorption process well, indicating that chemisorption is the main mechanism the intra-particle diffusion model again reflects the complexity of the adsorbent system, indicating that diffusion in PBNPs pores also consumes the main role making it promising for practical applications to remove Pb2+ from solutions. The adsorption capacity of Pb2+ in this study was reached at less than 60 min at 25 °C, compared to its adsorption on other adsorbents, which reaches 100% at 80 min86 and 120 min87 depending on the kind of adsorbent.
Table 7 Kinetic parameters and experimental adsorption capacities for Pb2+ onto PBNPsa
| Kinetic models |
Equations |
Rate constant |
Calculated Qe |
Experimental Qe |
R2 |
| Where: Qe and Qt (mg g−1): the amounts of Pb2+ absorbed at equilibrium and at the time (min) respectively. K1 (L min−1): the first-order adsorption rate constant. K2 (g mg−1 min−1): the rate constant for pseudo-second-order chemisorption Kid, (mg g−1 min−1/2): the intra-particle diffusion rate constant (mg g−1 min). |
| Pseudo-first order |
ln(Qe − Qt) = lnQe − K1t (11) |
K1 (min−1) −0.0117 |
66.696 |
188.09 |
0.992 |
| Pseudo-second order |
 (12) (12) |
K2 (g mg−1 min−1) 0.0005 |
192.308 |
0.999 |
| Intra-particle diffusion |
Qt = (Kidt1/2) + Q (13) |
Kid (mg g−1 min−1/2) 4.1256 |
118.910 |
0.866 |
 |
| | Fig. 6 Kinetic model (a) pseudo-first-order (b) pseudo-second-order (c) intra-particle diffusion and (d) the effects of solution/adsorbent contact time (tc) on the adsorption capacity of the adsorbent. | |
Adsorption isotherm. We assessed the PBNPs adsorption capacity and removal effectiveness at a range of initial Pb2+ concentrations, from 1 to 200 mg L−1, with 7.56 pH and 25 °C temperature using 0.44 g of PBNPs (Fig. 7), plots of the given provided valuable insight into the adsorption behavior of a system. Fig. 7a shows how the adsorption capacity of PBNPs varied from 2.273 mg g−1 to 190.000 mg g−1 as a function of Pb2+ concentration, ranging from 1 to 200 mg L−1. Adsorption capacity increases with increasing Pb2+ concentration, but the rate of increase slows at higher concentrations. This indicates that the adsorbent has a good ability to remove Pb2+ over a wide range of concentrations, but at the higher end of the concentration range, it begins to reach equilibrium. The number of electrons shared increases at higher concentrations, resulting in strong interactions between Pb2+ and PBNPs.88 The increase in adsorption capacity with broad Pb2+ concentration indicates that PBNPs exhibit higher adsorption capacity compared to other adsorbent materials reported in previous studies, such as rubber tree sawdust, hazelnut husk, and binary compounds.89–91 Fig. 7b shows the removal efficiency of the PBNPs as a function of the same Pb2+ range. Removal efficiency is an important parameter that determines the efficiency of the adsorption process in removing Pb2+ from the solution. The removal rate is very high (almost 100%), at low concentrations equal to 1.5 and 10 mg L−1, but then decreases gradually from 100% to 80.00% time with increasing concentration of Pb2+. This indicates the PBNPs are extremely effective at removing the Pb2+ in low concentrations, but their relative efficiency drops as the concentration increases. This may be because there are not enough adsorption sites available, requiring a higher concentration of PBNPs to obtain a better removal efficiency. The data indicates a trade-off between maintaining high removal efficiency and making use of adsorption capacity. At low Pb2+ concentrations, the PBNPs can realize very high removal rates, which could be favorable for finalizing applications. However, the overall capacity may be limited. As the concentration increases, the PBNPs can continue to adsorb more Pb2+, resulting in higher overall removal, but the removal efficiency decreases.
 |
| | Fig. 7 A plot of (a) the adsorption capacity with the Pb2+ concentration from 1 to 200 mg L−1, and (b) the removal efficiency with the same Pb2+ concentration. | |
The adsorption behavior of Prussian blue nanoparticles (PBNPs) was analyzed using the Langmuir, Freundlich, and Temkin isotherm models (Fig. 8). These models were utilized to validate the experimental results for the adsorption of Pb2+ onto PBNPs. The Langmuir, Freundlich, and Temkin adsorption isotherms equations are expressed by eqn (14)–(16) respectively.29,92,93 Table 8 shows the equations and adsorption constants for the removal of Pb2+ using PBNPs using three isotherm models. In (Fig. 8a) the Langmuir model and the results of the experiment illustrate a significant relationship with an R2 equal to 0.992. This high R2 indicates that the adsorption of Pb2+ on PBNPs takes place in a homogeneous system with similar limited areas, being monolayer adsorption.
 |
| | Fig. 8 Isotherm models (a) Langmuir (b) Freundlich (c) Temkin (d) the effects of solution concentration (Co) on the adsorption capacity of the adsorbent. | |
Table 8 Langmuir, Freundlich, and Temkin isotherm equations and constants for adsorption of Pb2+ using PBNPsa
| Isotherm models |
Equations |
Constants |
R2 |
| Where: KL, KF, B1, KT: Langmuir, Freundlich,and Temkin constants; n: heterogeneity coefficient; Qm: maximum adsorption capacity of Prussian blue (mg g−1); Qe: uptake at equilibrium; Ce: Pb2+ amount (mg g−1); B: activity coefficient related to mean sorption energy. |
| Langmuir |
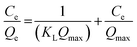 (14) (14) |
Qmax (mg g−1) 212.766 |
KL (L mg−1) 0.232 |
0.992 |
| Freundlich |
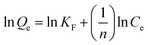 (15) (15) |
KF (mg L g−1) 54.949 |
N 3.350 |
0.766 |
| Temkin |
Qe = B1lnKT + B1lnCe (16) |
KT (L mg−1) 5.240 |
B1 31.616 |
0.825 |
On the contrary (Fig. 8b), Freundlich model had a low R2 value of 0.766. It is often applied to heterogeneous surfaces, where adsorption sites have different affinities for the adsorbent. The low correlations specify that although some heterogeneity exists, it is not significant in the PBNPs adsorption process, which is supported by other studies that found the Langmuir model to be more suitable for nanoparticle-based adsorbents. The Temkin model with R2 of 0.825 (Fig. 8c) provides insight into adsorbate–adsorbent interactions by considering the effects of indirect adsorbent/adsorbate interactions. The data incorporated into the Temkin model show that adsorption strength decreases linearly with adsorbate surface coverage. This trend helps identify the chemisorption mechanism, which is a common characteristic of heavy metal adsorption in various nanoparticle adsorbents. The effect of initial Pb2+ concentration on the adsorption capacity of PBNPs is shown in (Fig. 8d). Adsorption capacity (Qe) increases with increasing initial Pb2+ concentration (Co), which is a common adsorption mechanism because higher concentrations provide a greater driving force for mass transfer. The saturation point detected at high Pb2+ concentrations specifies the maximum adsorption capacity, which is consistent with the saturation concept described by the Langmuir isotherm. Saturation behavior was observed with increasing initial Pb2+ concentration. Furthermore, the Langmuir model assumes that there is no interaction between the adsorbed molecules. Overall, a good correlation with the Langmuir model supports the idea that PBNPs function as effective heavy metal adsorbents, primarily through monolayer adsorption mechanisms.
Therdynamic analysis. The thermodynamic behavior of Pb2+ adsorption onto PBNPs was analyzed by evaluating the Gibbs free energy change (ΔG) and the distribution ratio (D) across different temperatures, as depicted in Fig. 9. The thermodynamic parameters were calculated using the following eqn (17):where:
 |
| | Fig. 9 A plot of (a) Gibbs free energy change vs. temperature for Pb2+ adsorption onto PB NPs and (b) distribution ratio vs. temperature for Pb2+ adsorption onto PB NPs. | |
ΔG Gibbs free energy change.
R is the universal gas constant (8.314 J mol−1 K−1)
T is the temperature in Kelvin (K)
Kd is the distribution ratio, defined as eqn (18):
| |
 | (18) |
where
Cads is the concentration of metal in the adsorbent,
Ce is the concentration of metal in the solution.
Gibbs free energy changes in terms of enthalpy (ΔH) and entropy (ΔS) as in eqn (19):
To reveal crucial insights into the adsorption process of Pb2+ on PBNPs, which is illustrated in Fig. 9a, showing the relation between the Gibbs free energy ranging from −2315.84 to −5553.35 kJ mol−1 and temperature range of 293 to 323 K. The negative values of ΔG indicate a spontaneous process at all measured temperatures. Similarly, the fact that ΔG decreases with increasing temperature indicates that the drying process occurs spontaneously with increasing temperature. Such behavior is characteristic of endothermic adsorption processes, as seen in the increase of ΔG values. Changes in the free energy in the range of 0–20 kJ mol−1 suggest a physical adsorption reaction, while higher values in the range of 80–400 kJ mol−1 suggest a chemisorption process. Furthermore, a positive value of ΔH indicates that the adsorption was endothermic and the adsorption mechanism is considered to be physical.89 Besides, the thermodynamic model, the distribution coefficient (D), and the temperature diagram shown in Fig. 9b supported an increase of D with increasing temperature, indicating that PBNPs can adsorb Pb2+ more efficiently at higher temperatures. This feature indicates that the adsorption is endothermic, as higher temperatures provide the energy required to overcome the activation barrier for Pb2+ adsorption on the adsorbent surface. The thermodynamic evaluation indicated that the adsorption of Pb2+ on the surface of PBNPs is spontaneous and endothermic. This thermodynamic parameter stated the potential of PBNP as a useful adsorbent for Pb2+ removal under real-world conditions of varying temperatures.
Reusability and regeneration. Reusability and regeneration absorbents should be considered for sustainable development. This is because recyclability analysis typically uses physicochemical methods that preserve the adsorbent's integrity. Microstructure and remove heavy metal ions sorbet from the absorbent during desorption and regeneration for information on usable conditions without any change.The removal efficacy of Pb2+ was studied for five recycling methods using a dose of 10 mg L−1 as in Fig. 10. PBNPs passing through the regeneration process maintained an efficiency of about 99% in five cycles. The minimal reduction in activity indicates effective regeneration and maintains the adsorption properties of PBNPs over five cycles. This stability highlights their durability and long-term reusability, which are essential for practical environmental remediation. In contrast, recycled PBNPs without regeneration showed a significant decrease in removal. The removal efficiency decreased remarkably starting from about 99% in the first cycle to about 90% in the fifth cycle. The initial sharp decline and continuous decrease indicate that without regeneration, the active sites in PBNPs become progressively occupied by impurities, leading to reduced adsorption efficiency. This confirms the impaired ability of the adsorbent to bind the pollution over time repetition emphasis.
 |
| | Fig. 10 Reusability and regeneration of PBNPs through five cycles. | |
After five cycles, there was a significant difference in the removal efficiencies of reusability with and without regeneration of PBNPs; regenerated PBNPs exhibited approximately 9% higher efficiency than non-regenerated ones. According to these results, PBNP regeneration is not only beneficial but also necessary to maintain efficient heavy metal removal in drinking water role over a long period.
Conclusions
Recent studies have validated the superior performance of Prussian blue/silica HOM nanocomposites for Pb2+ removal from water, aligning with our previous findings. The adsorption kinetics were in accord with the pseudo-second-order model (R2 = 0.999). The adsorption isotherm results indicated that Pb2+ adsorption on PBNPs followed the Langmuir mode (R2 = 0.992), indicating that monolayer adsorption on uniform surface PBNPs showed high efficiency in removing Pb2+ with adsorption capacity a maximum of 212.766 mg g−1. The Freundlich and Temkin isotherm models displayed low correlation coefficients, suggesting that Pb2+ adsorption is governed by a homogeneous surface mechanism instead of heterogeneous adsorption. Overall, pH was identified as the primary factor influencing adsorption capacity, with optimal removal efficiency achieved for Pb2+ at 0.44 g of adsorbent. The most effective pH range for maximum adsorption was determined to be around 7.56, with a maximum of 0.44 g. The precipitation of metal ions and competition with H+ ions causes a decrease in performance. Kinetic isotherm analysis shows that pH changes can significantly improve chemisorption-driven adsorption, increasing its efficiency for real-world applications. The thermodynamic evaluation showed that adsorption is an endothermic and spontaneous process, confirmed by negative Gibbs free energy values as adsorption Prussian physical properties. The recycled blue/silica HOM nanocomposites proved cost-effective and environmentally friendly when removing Pb2+ from water, especially when exposed to HNO3 (0.01 N). Alternatively, the present study sought to enhance the removal of Pb2+ ions from an aqueous solution by an adsorption process, specific to the effect of pH and adsorbent dosage. Furthermore, methods adopted to measure Pb2+, such as flame atomic absorption spectroscopy (FAAS) and graphite furnace atomic absorption spectroscopy (GFAAS), have been validated for linearity, accuracy, precision, and detection limit. Strong linearity for FAAS in validation results linearity (R2 = 0.997), limit of detection (LOD = 0.056), method detection limit (MDL = 0.058), and quantification limit (LOQ = 0.179). In contrast, for GFAAS, linearity (R2 = 0.997) and acceptable limits of detection (LOD = 0.003), method detection limit (MDL = 0.008), and quantification (LOQ = 0.010), and ensured that trace levels were measured accurately and sensitively with low energy recovery at acceptable levels for both methods, with FAAS revealing values ranging from 87.02% to 106.93%, and GFAAS ranges from 95.69% to 104.79%, indicating high accuracy and precision. In summary, these parameters perform very well for Pb2+ removal, highlighting the effectiveness of Prussian blue/silica HOM nanocomposites as recyclable, cost-effective, and adsorbents, offering significant advantages.
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
Author contributions
Asmaa Y. Wahman: writing – review & editing, writing – original draft, visualization, conceptualization, methodology, formal analysis, software, data curation, validation, conceptualization. Nagwa Abo El-Maali: writing – review & editing, writing – original draft, project administration, software, funding acquisition, visualization, conceptualization, methodology, formal analysis, data curation, validation. Kawthar Abd El-Hameed: validation, funding acquisition, data curation, writing – review & editing, writing – original draft, visualization, formal analysis, data curation, validation, conceptualization. Ahmad Abo Markeb: visualization, conceptualization, software, validation, writing – original draft. Waleed El-Said: visualization, conceptualization, software, validation, writing – review & editing, writing – original draft.
Conflicts of interest
The authors declare that “there are no conflicts to declare”.
Acknowledgements
The authors acknowledge the support of the Analytical Chemistry Unit, for the experimental support throughout this research work.
References
- N. T. M. Ngoc, N. V. Chuyen, N. T. T. Thao, N. Q. Duc, N. T. T. Trang, N. T. T. Binh, H. C. Sa, N. B. Tran, N. V. Ba, N. V. Khai, H. A. Son, P. V. Han, E. V. Wattenberg, H. Nakamura and P. V. Thuc, Environ. Health Insights, 2020, 14, 1178630220921410 CrossRef PubMed.
- H. Ali, E. Khan and I. Ilahi, J. Chem., 2019, 2019, 1–14 Search PubMed.
- G. Yu, X. Wang, J. Liu, P. Jiang, S. You, N. Ding, Q. Guo and F. Lin, Sustainability, 2021, 13, 713 CrossRef.
- S. Shara, S. Moersidik and T. Soesilo, IOP Conf. Ser.: Earth Environ. Sci., 2021, 623, 012061 CrossRef.
- J. Briffa, E. Sinagra and R. Blundell, Heliyon, 2020, 6, e04691 CrossRef.
- G. Li, X. Qi, G. Zhang, S. Wang, K. Li, J. Wu, X. Wan, Y. Liu and Q. Li, Microchem. J., 2022, 179, 107515 CrossRef.
- G. Li, X. Qi, Y. Xiao, Y. Zhao, K. Li, Y. Xia, X. Wan, J. Wu and C. Yang, Nanomaterials, 2022, 12, 3317 CrossRef.
- J. O. Nriagu, Nature, 1989, 338, 47–49 CrossRef CAS.
- H. Abadin, A. Ashizawa, F. Llados and Y.-W. Stevens, 2007.
- G. Flora, D. Gupta and A. Tiwari, Interdiscip. Toxicol., 2012, 5, 47–58 CAS.
- A. L. Wani, A. Ara and J. A. Usmani, Interdiscip. Toxicol., 2015, 8, 55–64 CrossRef CAS PubMed.
- S. Cobbina, J. Toxicol. Environ. Health Sci., 2013, 5, 29–36 CrossRef CAS.
- M. Hanna-Attisha, J. LaChance, R. C. Sadler and A. Champney Schnepp, Am. J. Public Health, 2016, 106, 283–290 CrossRef.
- H. Aydin, Y. Bulut and C. Yerlikaya, J. Environ. Manage., 2008, 87, 37–45 Search PubMed.
- E. S. Z. El Ashtoukhy, N. K. Amin and O. Abdelwahab, Desalination, 2008, 223, 162–173 CrossRef CAS.
- E. Eren, J. Hazardous Mater., 2008, 159, 235–244 CrossRef CAS.
- K. Ibrahim, N. Ed-Deen and H. Khoury, Environ. Geol., 2002, 41, 547–551 CrossRef CAS.
- A. D
![[a with combining cedilla]](https://www.rsc.org/images/entities/char_0061_0327.gif) browski, Z. Hubicki, P. Podkościelny and E. Robens, Chemosphere, 2004, 56, 91–106 CrossRef PubMed.
browski, Z. Hubicki, P. Podkościelny and E. Robens, Chemosphere, 2004, 56, 91–106 CrossRef PubMed. - R. Al Dwairi, H. Khoury and K. Ibrahim, Environ. Earth Sci., 2014, 71, 5071–5078 CrossRef CAS.
- S. Mnasri-Ghnimi and N. Frini-Srasra, Appl. Clay Sci., 2019, 179, 105151 CrossRef CAS.
- A. H. Hawari and C. N. Mulligan, Bioresour. Technol., 2006, 97, 692–700 CrossRef CAS.
- M. Ince and O. Kaplan Ince, Int. J. Pure Appl. Sci., 2017, 3, 10–19 CrossRef.
- X. Tang, H. Zheng, H. Teng, Y. Sun, J.-S. Guo, W. Xie, Q. Yang and W. Chen, Desalin. Water Treat., 2014, 57, 1–16 Search PubMed.
- D. Sharma, P. K. Chaudhari and A. K. Prajapati, Sep. Sci. Technol., 2020, 55, 321–331 CrossRef CAS.
- L. S. Thakur, R. Baghel, A. Sharma, S. Sharma, H. Parmar, A. K. Varma and P. Mondal, Mater. Today: Proc., 2023, 72, 2697–2704 Search PubMed.
- U. Tezcan Un and S. n. Öcal, Int. J. Environ. Sci. Dev., 2015, 6, 425–429 CrossRef.
- S. A. Razzak, M. O. Faruque, Z. Alsheikh, L. Alsheikhmohamad, D. Alkuroud, A. Alfayez, S. Z. Hossain and M. M. Hossain, Environ. Adv., 2022, 7, 100168 CrossRef CAS.
- T. Kurniawan and S. Babel, in Proceedings of the 2nd International Conference on Energy Technology towards a Clean Environment (RCETE), 2003, vol. 2, pp. 9–18 Search PubMed.
- E. Heraldy, Y. Hidayat, M. Firdaus and Patiha, IOP Conf. Ser.: Mater. Sci. Eng., 2016, 107, 012067 Search PubMed.
- R. Bisht, M. Agarwal and K. Singh, J. Water Reuse Desalin., 2016, 7, 387–419 Search PubMed.
- S. De Gisi, G. Lofrano, M. Grassi and M. Notarnicola, Sustainable Mater. Technol., 2016, 9, 10–40 CrossRef CAS.
- J. Carvalho, J. Araújo and F. Castro, Waste Biomass Valorization, 2011, 2, 157–167 CrossRef.
- N. Khai, B. Nguyen, H. Nguyen and N. Hoang Ha, Appl. Sci., 2019, 9, 619 CrossRef.
- H. Hegazi, HBRC J., 2013, 9, 276–282 CrossRef.
- R. Davarnejad and P. Panahi, Sep. Purif. Technol., 2016, 158, 286–292 CrossRef CAS.
- X. Wang and C. Wang, Colloids Surf., A, 2016, 500, 186–194 CrossRef CAS.
- S. N. A. Abas, M. H. S. Ismail, M. L. Kamal and S. Izhar, World Appl. Sci. J., 2013, 28, 1518–1530 CAS.
- A. Maleki, B. Hayati, F. Najafi, F. Gharibi and S. W. Joo, J. Mol. Liq., 2016, 224, 95–104 CrossRef CAS.
- D. Shirsath and V. Shirivastava, Appl. Nanosci., 2015, 5, 927–935 CrossRef CAS.
- M. Khajeh, S. Laurent and K. Dastafkan, Chem. Rev., 2013, 113, 7728–7768 CrossRef CAS.
- D. Li, M. Liu, W. Li, Q. Fu, L. Wang, E. Lai, W. Zhao and K. Zhang, Pharmaceuticals, 2022, 15, 769 CrossRef CAS PubMed.
- A. Simonov, T. De Baerdemaeker, H. L. Boström, M. L. Rios Gomez, H. J. Gray, D. Chernyshov, A. Bosak, H.-B. Bürgi and A. L. Goodwin, Nature, 2020, 578, 256–260 CrossRef CAS.
- Z. Fu, J. Huang, W. Wei, Z. Wu and X. Shi, Anal. Methods, 2024, 16, 3088–3098 RSC.
- L. Doumic, G. Salierno, M. Cassanello, P. Haure and M. Ayude, Catal. Today, 2015, 240, 67–72 CrossRef CAS.
- W. Wang, Y. Gang, J. Peng, Z. Hu, Z. Yan, W. Lai, Y. Zhu, D. Appadoo, M. Ye and Y. Cao, Adv. Funct. Mater., 2022, 32, 2111727 CrossRef CAS.
- N. Song, S. Ren, Y. Zhang, C. Wang and X. Lu, Adv. Funct. Mater., 2022, 32, 2204751 CrossRef CAS.
- C. Xu, Z. Yang, X. Zhang, M. Xia, H. Yan, J. Li, H. Yu, L. Zhang and J. Shu, Nano-Micro Lett., 2021, 13, 1–36 CrossRef CAS.
- C. Dagan-Jaldety, P. Nativ, Y. S. Cristal and O. Lahav, Water Res., 2023, 247, 120757 CrossRef CAS PubMed.
- F. Scholz, D. Schwudke, R. Stösser and J. Boháček, Ecotoxicol. Environ. Saf., 2001, 49, 245–254 CrossRef CAS.
- P. Wang, S. Sun, G. Bai, R. Zhang, F. Liang and Y. Zhang, Acta Biomater., 2024, 77–98 CrossRef CAS.
- V. Kumar, R. Mahar and N. Sandal, J. Radioanal. Nucl. Chem., 2025, 1–12 Search PubMed.
- A. Markeb, K. Abdelhameed, W. El-Said and N. El-Maali, Int. J. Environ. Sci. Technol., 2024, 21, 7615–7630 CrossRef CAS.
- B. Kocadagistan and K. Oksuz, Adsorpt. Sci. Technol., 2022, 2022, 7195777 CrossRef.
- J. Bayuo, M. J. Rwiza, J. W. Choi, K. M. Mtei, A. Hosseini-Bandegharaei and M. Sillanpää, Adv. Colloid Interface Sci., 2024, 103196 CrossRef CAS.
- M. Long, H. Jiang and X. Li, Sci. Rep., 2021, 11, 11527 CrossRef CAS PubMed.
- L. Liu, X.-B. Luo, L. Ding and S.-L. Luo, in Nanomaterials for the Removal of Pollutants and Resource Reutilization, 2019, pp. 83–147, DOI:10.1016/B978-0-12-814837-2.00004-4.
- A. Fakhri and S. Adami, J. Chem. Eng. Process Technol., 2013, 4, 1–6 Search PubMed.
- S. Ye, S. Zhao, S. Shao, L. Chen, Y. Zheng, J. Liu, V. Sedov, S. Mandal, C. Li and J. Wei, Opt. Laser. Technol., 2025, 180, 111509 CrossRef.
- H. A. Sabzkoohi, V. Dodier and G. Kolliopoulos, RSC Adv., 2023, 13, 14887–14898 RSC.
- ICH Harmonised Tripartite Guideline, Q2(R1) Validation of Analytical Procedures: Text and Methodology, 2005 Search PubMed.
- M. Thompson, S. L. Ellison and R. Wood, Pure Appl. Chem., 2002, 74, 835–855 Search PubMed.
- S. M. Moosavi and S. Ghassabian, Calibration and Validation of Analytical Methods-A Sampling of Current Approaches, 2018, 109–127 Search PubMed.
- A. Kruve, R. Rebane, K. Kipper, M.-L. Oldekop, H. Evard, K. Herodes, P. Ravio and I. Leito, Anal. Chim. Acta, 2015, 870, 8–28 CrossRef CAS.
- C. J. O. Childress, W. T. Foreman, B. F. Connor and T. J. Maloney, New Reporting Procedures Based on Long-Term Method Detection Levels and Some Considerations for Interpretations of Water-Quality Data provided by the US Geological Survey National Water Quality Laboratory, Report 2331-1258, US Dept. of the Interior, US Geological Survey; Information Services, 1999 Search PubMed.
- N. J. Chowdhury, M. A. Akbor, A. Nahar and M. A. A. Shaikh, Heliyon, 2024, 10, 14 Search PubMed.
- S. Bratinova, B. Raffael and C. Simoneau, Guidelines for performance criteria and validation procedures of analytical methods used in controls of food contact materials. EUR 24105 EN, Publication office of the European Union, 2009 Search PubMed.
- A. R. Surana and P. R. Dighe, J. Sci. Technol. Res. Pharm., 2023, 3, 45–59 Search PubMed.
- K. B. S. Perelonia, K. C. D. Benitez, R. J. S. Banicod, G. C. Tadifa, F. D. Cambia and U. M. Montojo, Food Control, 2021, 130, 108363 CrossRef CAS.
- A. Kumar and I. Xagoraraki, Sci. Total Environ., 2010, 408, 5972–5989 CrossRef CAS PubMed.
- D. Water, Technical Fact, 2019 Search PubMed.
- B. Magnusson, The Fitness for Purpose of Analytical Methods: A Laboratory Guide to Method Validation and Related Topics, Eurachem, 2014 Search PubMed.
- Code of Federal Regulation (CFR), title 40 part 141 subpart I—Control of Lead and Copper Source 56 FR 26548, June 7, 1991, unless otherwise noted Search PubMed.
- J. Creed, T. Martin and J. O'Dell, Environmental Monitoring Systems Laboratory, Research and Development US Environmental Protection Agency, Cincinnati, OH, 1994, p. 45268 Search PubMed.
- M. E.-S. Abdel-Raouf, R. K. Farag, A. A. Farag, M. Keshawy, A. Abdel-Aziz and A. Hasan, ACS Omega, 2023, 8, 10086–10099 CrossRef CAS PubMed.
- M. A. Islam, M. J. Angove, D. W. Morton, B. K. Pramanik and M. R. Awual, J. Environ. Chem. Eng., 2020, 8, 103515 CrossRef CAS.
- M. A. Islam, M. J. Angove and D. W. Morton, J. Water Process Eng., 2019, 32, 100964 CrossRef.
- B. U. Maheswari, V. Sivakumar and M. Thirumarimurugan, Environ. Nanotechnol. Monitor. Manage., 2022, 18, 100680 CrossRef.
- R. El KaimBillah, M. A. Islam, M. Agunaou and A. Soufiane, Arab. J. Geosci., 2021, 14, 1134 CrossRef CAS.
- C. Cojocaru and G. Zakrzewska-Trznadel, J. Membr. Sci., 2007, 298, 56–70 CrossRef CAS.
- I. P. Arbizu and C. L. Perez, J. Mater. Process. Technol., 2003, 143, 390–396 CrossRef.
- Y. Yang, X. Li, Y. Gu, H. Lin, B. Jie, Q. Zhang and X. Zhang, Surf. Interfaces, 2022, 28, 101649 CrossRef CAS.
- H. Yuh-Shan, Scientometrics, 2004, 59, 171–177 CrossRef.
- N. Gandhi, D. Sirisha and K. C. Sekhar, Int. J. Environ. Biorem. Biodegrad., 2016, 4, 55–67 CAS.
- M. Alkan, Ö. Demirbaş and M. Doğan, Microporous Mesoporous Mater., 2007, 101, 388–396 CrossRef CAS.
- V. Gupta, P. I. Ali and V. Saini, Water Res., 2007, 41, 3307–3316 CrossRef CAS.
- S. A. Shahin, M. Mossad and M. Fouad, Water Sci. Eng., 2019, 12, 37–44 CrossRef.
- M. A. Zenasni, S. Benfarhi, A. Merlin, S. Molina, B. George and B. Meroufel, Nat. Sci., 2012, 4, 856–868 Search PubMed.
- R. I. Masel, Principles of Adsorption and Reaction on Solid Surfaces, John Wiley & Sons, 1996 Search PubMed.
- A. Kongsuwan, P. Patnukao and P. Pavasant, J. Ind. Eng. Chem., 2009, 15, 465–470 CrossRef CAS.
- M. Imamoglu and O. Tekir, Desalination, 2008, 228, 108–113 CrossRef CAS.
- M. H. Kalavathy, T. Karthikeyan, S. Rajgopal and L. R. Miranda, J. Colloid Interface Sci., 2005, 292, 354–362 CrossRef CAS PubMed.
- H. K. Boparai, M. Joseph and D. M. O'Carroll, J. Hazard. Mater., 2011, 186, 458–465 CrossRef CAS PubMed.
- K. Vijayaraghavan, T. Padmesh, K. Palanivelu and M. Velan, J. Hazard. Mater., 2006, 133, 304–308 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Kawthar Abd El-Hameedb,
Ahmad Abo Markeb
*a,
Kawthar Abd El-Hameedb,
Ahmad Abo Markeb c,
Waleed El-Said
c,
Waleed El-Said c and
Nagwa Abo El-Maali*c
c and
Nagwa Abo El-Maali*c






![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N stretching in potassium ferricyanide. Hydrogen bonding was shown by broad absorption bands at 3358.71 cm−1 and 1606.51 cm−1. Furthermore, a peak at 606.78 cm−1 confirmed the structural integrity of the PB/silica HOM nanocomposites by validating the Fe2+–C
N stretching in potassium ferricyanide. Hydrogen bonding was shown by broad absorption bands at 3358.71 cm−1 and 1606.51 cm−1. Furthermore, a peak at 606.78 cm−1 confirmed the structural integrity of the PB/silica HOM nanocomposites by validating the Fe2+–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N–Fe3+ connection.69,70 X-ray diffraction (XRD) was used to examine the nanocomposite's crystalline structure, as seen in (Fig. 1e).52 The characteristic crystal planes of Prussian blue (200), (220), (222), (420), and (442), respectively are represented by the distinct peaks in the diffraction pattern at 17.200°, 25.519°, 35.260°, 39.460°, and 53.680°. These peaks further validate the effective synthesis of PB/silica HOM nanocomposites by confirming the presence of a face-centered cubic (FCC) structure with an Fm
N–Fe3+ connection.69,70 X-ray diffraction (XRD) was used to examine the nanocomposite's crystalline structure, as seen in (Fig. 1e).52 The characteristic crystal planes of Prussian blue (200), (220), (222), (420), and (442), respectively are represented by the distinct peaks in the diffraction pattern at 17.200°, 25.519°, 35.260°, 39.460°, and 53.680°. These peaks further validate the effective synthesis of PB/silica HOM nanocomposites by confirming the presence of a face-centered cubic (FCC) structure with an Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group.52
m space group.52

 (12)
(12)

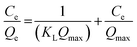 (14)
(14)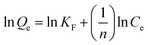 (15)
(15)

![[a with combining cedilla]](https://www.rsc.org/images/entities/char_0061_0327.gif) browski, Z. Hubicki, P. Podkościelny and E. Robens, Chemosphere, 2004, 56, 91–106 CrossRef PubMed.
browski, Z. Hubicki, P. Podkościelny and E. Robens, Chemosphere, 2004, 56, 91–106 CrossRef PubMed.





