Synthesis, characterization, and luminescence thermometry investigation of LiSrGd(WO₄)₃:Pr³⁺ phosphors

Abstract

In this study, LiSrGd(WO₄)₃ (LSGW) phosphors doped with different concentrations of Pr³⁺ were synthesized via the traditional solid–solid method to explore their suitability for luminescence thermometry applications. Structural and morphological analyses using X-ray powder diffraction and scanning electron microscopy offered comprehensive insights. The energy gap value of LSGW, calculated at E_g = 3.69 eV for x = 5 at% Pr³⁺, suggested minimal alteration in the bandgap energy upon incorporation of Pr³⁺ ions into the LSGW host. The empirical energy levels for the free ion Pr³⁺ were derived from absorption and emission data are gathered from LSGW:Pr³⁺. The theoretical energy diagram and corresponding eigenstates for Pr³⁺ were calculated using block diagonalization of the Hamiltonian's matrix in the basis set of coupled states 〈4f²〉〈4f²τSLJ〉, considering intermediate coupling. Thermometric parameters were calculated using the luminescence intensity ratio strategy based on Pr³⁺ emission spectra for thermal coupled levels. Our findings revealed that the LIR1 (I₅₃₁/I₅₅₇) exhibited maximum absolute and relative sensitivities of 31.5 10⁻⁴ K⁻¹ and 0.65% K⁻¹, respectively, at 300 K, accompanied by remarkably low-temperature uncertainty (δT) values ranging from 0.031 to 0.037 K in the 300–440 K temperature range. These results show the importance of LiSrGd(WO₄)₃:Pr³⁺ phosphors for optical applications.

---

1. Introduction

Optical temperature sensors have recently received significant attention due to their potential applications in inaccessible, harsh, or hazardous environments.^1–3 Recently, considerable focus has been given to contactless luminescence thermometry, which represents a new technique enabling temperature measurement with submicron spatial resolution and sub degree thermal precision.^4–6 The luminescence (fluorescence) intensity ratio technique, known as LIR (FIR), is widely employed for optical temperature detection due to its quick measurement capability, high thermal resolution, and excellent precision.^7,8 The LIR method exploits the temperature-induced variations in the intensity ratio of emission bands linked to the thermally-coupled levels (TCLs) of various lanthanide (Ln) ions. The energy separation (ΔE) between their TCLs ranges approximately from 200 to 2000 cm⁻¹.^9,10

Trivalent praseodymium (Pr³⁺) stands out among activator Ln ions for its fluorescence spanning from the ultraviolet, to the visible and near-infrared wavelengths. Its emission characteristics include green-bluish and red light, attributed to transitions within the ³P_0,1 and ¹D₂ multiplets.^11–13 The incorporation of Pr³⁺ into phosphors has demonstrated notable sensing capabilities, enabled by cross relaxation (CR) processes between the ³P₀ and ¹D₂ levels or between the thermally coupled levels (TCLs) ³P₀ and ³P₁. Additionally, researchers have investigated the interference of the metal–metal intervalence charge transfer (IVCT) state with Pr³⁺ luminescence as an innovative strategy for designing high-performance FIR-based thermometers. Previous studies have harnessed different Pr³⁺ transitions for FIR calculations based on their temperature-dependent intensity variations.^14–22

For the design of highly efficient luminescent materials and sensors, the choice of a suitable host material is crucial. Specially, tungstate has a strong and broad charge transfer band in the near-ultraviolet region due to the (WO₄)₂ group. This allows it to enhance the luminescence of the fluorescent activation centre by absorbing near-ultraviolet energy and transferring it to the light emitting centre.^23–25 Furthermore, tungstate compounds serve as excellent hosts for photoactive lanthanide ions, with potential applications in phosphors, lasers, photocatalysis, and negative thermal expansion.^26,27 Numerous reports exist in the literature on tungstates, particularly those involving rare earth ions such as Sm, Ce, and Tm, there is a noticeable gap in research focused specifically on LiSrGd(WO₄)₃ hosts. This particular compound remains relatively understudied compared to its counterparts. The LiSrGd(WO₄)₃ structure is intriguing as it exhibits two polymorphic forms, transitioning between a monoclinic structure at low temperatures and an orthorhombic structure at higher temperatures, influenced primarily by the electronegativity of the rare earth ion.²⁸ Gd₂(WO₄)₃, a member of the rare earth tungstate family, holds particular significance due to its versatility and applications in various fields including optical fibers, sensors, scintillators, light-emitting diodes, and solid-state lasers.²⁹ While Gd₂(WO₄)₃ and its substitutions have been extensively investigated for their optical properties, including self-luminescence in the visible spectrum, there is a notable gap in research specifically addressing the LiSrGd(WO₄) host.

This paper focuses on the synthesis and characterizations of LiSrGd(WO₄)₃:Pr³⁺ phosphors, with a notable emphasis on luminescent thermometry investigation. It begins with a detailed account of the synthesis process, followed by comprehensive characterizations including structural, morphological, and spectroscopic analyses. Results and discussions delve into various aspects such as structural and morphological characteristics, FTIR, UV-visible spectrum, photoluminescence, theoretical simulations of energy levels of free Pr³⁺ ion, and luminescence thermal stability with a specific focus on CIE changes in UC with temperature.

The study of luminescent thermometry explores the feasibility and accuracy of using luminophores for temperature sensing, highlighting their potential applications in advanced temperature measurement technologies.

2. Experimental section and characterizations

LiSrGd_1−x(WO₄)₃:x% Pr³⁺ (x = 1, 3, 5, and 7 at%) were synthesized though the traditional solid-state reaction method. High-purity precursors (≥99%) including lithium carbonate (Li₂CO₃), strontium carbonate (SrCO₃), praseodymium oxide (Pr₆O₁₁), gadolinium oxide (Gd₂O₃) and tungsten oxide (WO₃) were mixed in stoichiometric proportions and ground into fine powders. The mixture was then placed in a crucible and heated up to 350 °C for 10 hours. After cooling, the resulting product was then weighed, manually crushed, and pressed into pellets. These pellets were sintered at 800 °C for 5 hours. The particle agglomeration was observed during the sintering process at 800 °C, where increased atomic diffusion promotes grain growth and particle coalescence. The synthesis of the LiSrGd_1−xPr_x(WO₄)₃ compound can be described by the following reaction:

3Li₂CO₃ + 6SrCO₃ + 3(1 − x)Gd₂O₃ + xPr₆O₁₁ + 9W₂O₃ + (18 − 4x)O₂ → 6LiSrGd_1−xPr_x(WO₄)₃ + 9CO₂

A Siemens-D8-θ/2θ diffractometer with a Cu Kα X-ray source (λ = 0.15418 nm) was employed for X-ray diffraction (XRD) measurements under grazing incidence. A Thermo Scientific Apreo 2 S LoVac field emission scanning electron microscope (FE-SEM) is used to study the morphology of the samples. The Fourier transform infrared (FT-IR) spectra of the material were obtained at room temperature within the 400–4000 cm⁻¹ range using a PerkinElmer 1000 FTIR spectrometer. UV-vis-NIR absorption was measured using a PerkinElmer Lambda 365 UV-vis-NIR spectrometer. Photoluminescence spectra were measured using a Fluoromax 4P model Horiba spectrometer with a xenon arc lamp as the excitation source. Temperature-dependent DC emission was examined using a JOBIN YVON HR 320 spectrometer fitted with a temperature controller and a 450 nm laser excitation source.

3. Results and discussion

3.1. XRD and SEM

The XRD patterns of praseodymium doped LSGW synthesized in this work are shown in Fig. 1. All samples are crystalline. Most of the peaks can be assigned to the tetragonal scheelite crystalline phase, with the space group I4₁/a (no. 88).³⁰ Small diffraction peaks can be observed at 2θ = 13.39° and 2θ = 14.4°, which should belong to the oxide precursors. In this crystal, Li, Sr, Gd and Pr³⁺ are distributed randomly in the S₄ site that in CaWO₄ occupies Ca²⁺; which is surrounded by 8 oxygens. It was possible to clearly observe the shift of the peak located at around 18°, corresponding to the (101) reflection and shown in the inset of Fig. 1, when the Pr³⁺ concentration increased.

Fig. 1 XRD patterns of the obtained products, LiSrGd(WO₄)₃:x at% Pr³⁺ (x = 1, 3, 5, and 7). Inset: angle shift of the (101) reflection related to the Pr concentration.

Table 1 summarizes the unit cell parameters refined by using the Le Bail methodology using the TOPAS software. The introduction of Pr³⁺ in the crystalline structure affects the unit cell parameters, showing first a slight decrease in size for the two parameters a and c, that for Pr³⁺ concentrations of 5 at% or higher, increased again. This compression/stress should be expected when substituting Gd³⁺ or Sr²⁺ by Pr³⁺ because of the difference in ionic radii in a coordination environment of 8, that is Gd³⁺ = 1.05 Å, Pr³⁺ = 0.99 Å and Sr²⁺ = 1.18 Å. According to these data, a hypothesis that can be established is that Pr³⁺ tends to substitute first Sr²⁺ in the structure at low concentrations (below 5 at%), but then, as the concentration increases, it tends to substitute also Gd³⁺. However, no experiments have been done to confirm this.^31,32

Table 1 Evolution of the unit cell parameters as a function of the doping level

% Pr	a (Å)	c (Å)	Volume (Å^3)	Rexp/Rwp
1	5.28683	11.53198	322.326	5.43/24.96
3	5.28671	11.52927	322.235	5.14/19.50
5	5.28710	11.53043	322.314	5.10/15.70
7	5.28845	11.53205	322.525	5.10/11.73

---

The observed shift of diffraction peaks toward higher 2θ angles compared to the standard JCPDS data can be attributed to the substitution of Gd³⁺ and/or Sr²⁺ by Pr³⁺ in the LiSrGd(WO₄)₃ lattice. This substitution induces a slight contraction of the unit cell, leading to peak shifts according to Bragg's law. Additionally, minor structural strain introduced during the solid-state synthesis process could further contribute to these shifts. Such peak displacements are commonly observed in doped phosphor systems and reflect changes in lattice parameters due to ionic substitution.

Fig. 2 shows the microstructure of LSGW particles doped with (1, 3, 5)% Pr³⁺ obtained at two different sizes (30 and 100 μm). Irregularly shaped particles, approximately 10 μm in size, are observed. Moreover, high-temperature heat treatments result in significant particle agglomeration.

Fig. 2 SEM micrographs of LSGW:x at% Pr³⁺ (x = 1, 3, and 5) recorded at two different sizes.

3.2. FTIR spectroscopy

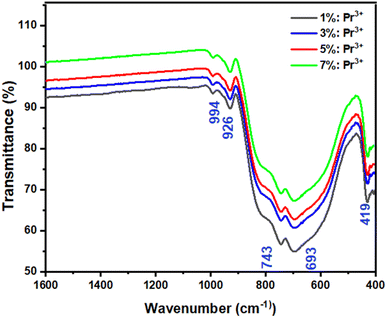
Fig. 3 shows the FTIR spectra of LSGW:3 at% Pr³⁺ and LSGW:5 at% Pr³⁺ phosphors. The set of vibrational bands below 1000 cm⁻¹ belong to the characteristic absorption of WO₄²⁻ group.³³ The absorption peaks at 994 cm⁻¹ and 926 cm⁻¹ are ascribed to the stretching mode of the W=O and W–O bands, respectively.^34,35 The peaks at 820 and 419 cm⁻¹ is attributed to the stretching and bending modes of single WOW bridge, while the absorption peaks at 743 and 693 cm⁻¹ are related to the stretching mode of the double WOOW bridge.³⁴ Thus, the results of FTIR analysis further prove the formation of LSGW.

Fig. 3 FTIR spectra of LSGW:x at% Pr³⁺ (x = 1, 3, 5, and 7).

3.3. Optical characterization

UV-visible spectroscopy. Fig. 4 shows the UV-visible reflectance spectra of LSGW:x at% Pr³⁺ in the 200–1000 nm range. In all the spectra, there's a broad absorption band in the UV range (200–400 nm) which is assigned to the W–O charge transfer band (CTB), involves electron transitions from the 2p oxygen orbital to the 4d tungsten orbital.³⁶ The 4f–4f intrinsic transitions of the Pr³⁺ ion are located around 448 nm, 475 nm, 488 nm and 595 nm which correspond to the ³H₄ → ³P₂, ³H₄ → ³P₁ + ¹I₆, ³H₄ → ³P₀ and ³H₄ → ¹D₂ electronic transitions, respectively.^37,38

Fig. 4 Reflectance spectra of LSGW:x at% Pr³⁺ (x = 1, 3, 5, and 7).

The Kubelka–Munk function is used to calculate the band gap of LSGW phosphors from diffuse reflectance spectra. The remission function establishes a link between the sample's diffuse reflectance (R), the absorption coefficient (K), and the diffusion coefficient (S) through the well known equation:³⁹

Within the parabolic band structure, the energy band gap (E_g) can be obtained using the Tauc's relation given by the following equation:^39,40

(F(R)hν)² = C(hν − E_g) (2)

The value of E_g, which is approximately 3.69 eV, is calculated by extrapolating the right portion of the curve (αhν)² from the hν to zero curve. The allowable direct transition is characterized by nonlinear and linear sections in the plot of [F(R)hν]² as a function of hν. The linear portion describes the fundamental absorption, while the nonlinear section refers to a residual absorption involving states of impurities.

The energy gap values of LSGW:x at% Pr³⁺, as illustrated in Fig. 5, were calculated to be: (a) E_g = 3.94 eV, (b) E_g = 3.93 eV, (c) E_g = 3.69 eV, and (d) E_g = 3.67 eV, for x = 1, 3, 5, and 7, respectively. The obtained results suggest that the incorporation of Pr³⁺ ions into the LSGW host induces a maximal variation of approximately 23 meV.

Fig. 5 The plot of [F(R)hν]² versus hν of LSGW:x% Pr ³⁺ (a) x = 1 at%, (b) x = 3 at%, (c) x = at. 5%, and (d) x = 7 at%.

Theoretical simulation of Pr³ free ion energy levels. Empirical energy levels for the free ion Pr³⁺ were derived from absorption and emission data gathered from LSGW:Pr³⁺. These observed energy levels are summarized in Table 2. In addition, a theoretical energy diagram and corresponding eigenstates for Pr³⁺ were calculated using block diagonalization of the Hamiltonian's matrix in the basis set of coupled states 〈4f²〉〈4f²τSLJ〉, considering intermediate coupling.

Table 2 Experimental and theoretical energy level multiplets of free Pr³⁺ ion

	EExp (cm^−1)	EThe (cm^−1)		EExp	EThe
^3H4	0	225.7	^1D2	—	17 207.4
^3H5	2320	2310.8	^3P0	—	21 085.9
^3H6	4492	4493.4	^3P1	—	21 629.1
^3F2	5131	5120.6	^1I6	—	21 676.7
^3F3	6494	6495.9	^3P2	—	22 839.5
^3F4	6966	6974.2	Conduction band: 29 842
^1G4	9962	9956.3	^0S0	—	47 124.5

---

To optimize the model parameters, a MATLAB program implementing the Nelder–Mead simplex method⁴¹ was used. The quality of the fit was assessed by the root mean square deviation (r.m.s.),^42,43 calculated using eqn (3):

where N represents the total number of experimental data points and P indicates the number of free ion parameters. Key parameters such as Slater parameters F₂, F₄, and F₆, the spin–orbit coupling parameter ζ, and linear configuration interaction parameters α, β, and γ were obtained by fitting the theoretical and experimental energy levels for Pr³⁺. These parameter values are presented in Table 3.

Table 3 Pr³⁺ free ion parameters^a

	F2	F4	F6	α	β	γ	ζ
a F4 = 0.729248954 × F2 and F6 = 0.477047309 × F2.
	69 361	50 581	33 088	14.65	−423	1321	740.3

---

The agreement between the theoretical and experimental energy levels for Pr³⁺ was good, with a root mean square deviation of approximately 20 cm⁻¹. Table 3 shows the experimental and theoretical energy levels for Pr³⁺. These results confirm that the theoretical model is consistent with the known energy levels of the 4f² configuration for free Pr³⁺ ions, as well as ions embedded in various crystal lattices.⁴⁴

The wave functions or the eigenstates are represented in the form:

These eigenvectors associated with the praseodymium multiplets along with their intermediate coupling coefficients are calculated and presented in Table 4.

Table 4 Eigenstates of the Pr³⁺ ion in the LSGW host

	^3H	^3F	^1G	^1D	^3P	^1I	^0S
^3H4	0.98618	−0.03002	0.16295
^3H5	1
^3H6	0.99857					−0.05351
^3F2		−0.98894		−0.14769	0.01330
^3F3		1
^3F4	−0.11858	−0.81478	0.56752
^1G4	0.11573	−0.57900	−0.80707
^1D2		0.14534		−0.94750	0.28481
^3P0					0.99539		0.09586
^3P1					1
^1I6	0.05351					0.99857
^3P2		0.02946		−0.28360	−0.95849
^0S0					−0.09586		0.99539

---

The free ion energy multiplets of rare-earth ions like Pr³⁺ determine the luminescence properties and their dependence on temperature. The way these energy levels are populated at different temperatures affects the intensity ratios used for temperature measurement and hence the sensitivity and accuracy of the luminescent thermometry. Understanding this relationship allows for the design of more effective phosphors for specific thermometric applications.

Photoluminescence spectroscopy.
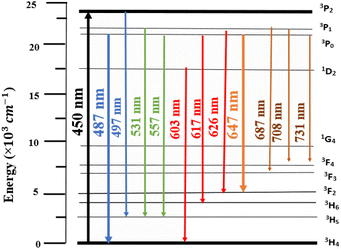
Luminescence of LSGW:Pr³⁺. The excitation spectrum (PLE) of LSGW:Pr³⁺ phosphors monitored at the 648 nm emission band shown in Fig. 6a is in accordance with the results in UV-vis diffuse reflectance spectra. It exhibits two distinct regions: a relatively wide charge transfer band (CTB) in the 200–400 nm range, originating from the (WO₄)²⁻ group,³⁶ and the 4f–4f intra-configurational transition bands specific to the Pr³⁺ ion, occurring between 450 and 486 nm. These peaks are attributed to the internal transitions of the 4f² configuration of the Pr³⁺ ion, with the most intense emission observed at 450 nm attributed to the ³H₄ → ³P₂ transition. Additionally, two other peaks are observed at 473 nm and 486 nm, corresponding to the ³H₄ → ³P₁ + ¹I₆ and ³H₄ → ³P₀ transitions, respectively.⁴⁵ Fig. 6b displays the emission spectrum (PL) of LSGW:5 at% Pr³⁺ excited at 450 nm. The spectra exhibit several intense peaks resulting from intra-4f transitions. The most intense peak, appearing at 647 nm, is attributed to the ³P₀ → ³F₂ transition. Other less intense peaks are observed at 487 nm, 531 nm, 557 nm, 603 nm, and 617 nm, 687, 708, and 731 corresponding to the transitions ³P₀ → ³H₄, ³P₁ → ³H₅, ³P₀ → ³H₅, ¹D₂ → ³H₄, ³P₀ → ³H₆, ³P₁ → ³H_5, ³P₁ → ³F₄ and ³P₀ → ³F₄ respectively.^20,46,47 The energy level diagram and the possible optical transitions of Pr³⁺ ions in the LSGW host material are presented in Fig. 7.

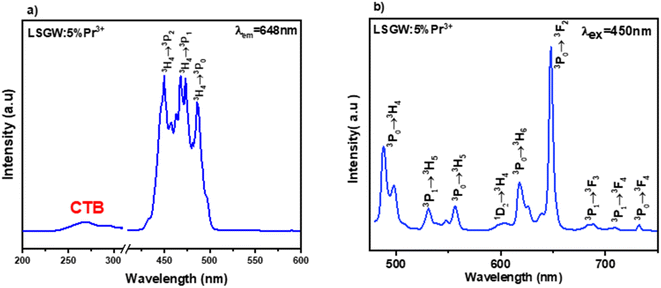Fig. 6 (a) Excitation spectrum measured by monitoring the 648 nm emission band, and (b) emission spectrum excited at 450 nm of LSGW:5% Pr³⁺.

Fig. 7 Energy level diagram and the possible optical transitions of Pr³⁺ ion.

To investigate the impact of Pr³⁺ doping concentration on LSGW in optical properties, we prepared a series of samples with different doping concentrations (x = 1, 3, 5, and 7 at%) under consistent conditions. Emission spectra of these samples were then recorded within the visible range of 450–750 nm under blue excitation (450 nm), as depicted in Fig. 8a. All emission spectra present the same shape with a variation of their intensities when increasing the Pr³⁺ concentration. It is clearly seen that the emission intensity of ³P₀ → ³F₂ is more intense than that of ³P₀ → ³H₄ at x = 1 at%. At a concentration of 3 at%, both transitions, ³P₀ → ³H₄ and ³P₀ → ³F₂ exhibit nearly identical emission intensities. However, with an increase in concentration to 5 at%, the emission intensity of the ³P₀ → ³H₄ transition decreases while that of the ³P₀ → ³F₂ transition increases. This result can be explained by the radiative energy transfer between neighbouring luminescent centres of Pr³⁺ ions.¹⁸ The highest intensity emission spectrum was attained at a doping concentration of 5 at%. Beyond this concentration, the emission intensity decreases due to the phenomenon of luminescence quenching or self-extinction. Generally, this quenching process is due to the short average distance between the Pr³⁺ ions. To investigate the main cause of concentration quenching, we use the eqn (5) provided by Blasse to estimate the critical distance between Pr³⁺ activator ions.⁴⁸

where V is the volume of one-unit cell, N is the number of cationic sites for the dopant in a unit cell, and x_c is the critical concentration of the activator ion. In this case, V = 322.31, N = 4, and x_c = 0.05. Thus, the R_c value for energy transfer was calculated to be about 14.54 Å. This value is far greater than 5 Å for the exchange interaction. The concentration quenching mechanism of Pr³⁺ can be attributed to the electric multipole–multipole interactions. The energy transfer mechanism can be controlled by multipolar interactions according to Dexter theory⁴⁹ using the following formula:where k and β are constants, x value of dopant ion concentration greater than or equal to critical concentration, I is the emission intensity, and Q is multipolar interaction i.e., 3 (exchange interaction), 6 (dipole–dipole), 8 (dipole–quadrupole), 10 (quadrupole–quadrupole). The variation of log(I/x) as a function of log(x) was presented in Fig. 8b, where I/x is the emission intensity per activator concentration. A linear line is obtained with a slope of −1.15 indicating that dipole–dipole interaction was responsible for the concentration quenching in LSGW:Pr³⁺ phosphors.

Fig. 8 (a) Emission spectra of LSGW:x at% Pr³⁺(x = 1, 3, 5, and 7) excited at 450 nm, (b) plot of log(I/x) as a function of log(x).

4. CIE chromaticity parameters

Fig. 9 shows the CIE chromaticity diagram for LSGW:x at% Pr³⁺ phosphors. It is clearly seen that the chromaticity coordinates of the compounds range from yellow to orange, with variation of the Pr³⁺ ions concentration. In order to find the practical utility of synthesized phosphors, the parameter Correlated Color Temperature (CCT) was calculated using the following formula proposed by McCamy:⁵⁰

CCT = −449n³ + 3525n² − 6823n + 5520.33 (7)

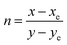With representing the convergence epicentre, which is located at point (x_e = 0.3320 and y_e = 0.1858) on the chromaticity diagram. The chromaticity coordinates as well as the CCT values are listed in Table 5. The obtained CCT values are all below 5000 K, indicating that the LSGW:Pr³⁺ phosphor can be used in white light-emitting diodes.

Fig. 9 CIE chromaticity diagram of LSGW:x% Pr³⁺ under 450 nm excitation.

Table 5 Chromaticity coordinates and TCC for LSGW:x% Pr³⁺

Doping rate	x	y	CCT (K)
1 at%	0.41	0.39	3460
3 at%	0.41	0.41	3498
5 at%	0.43	0.41	3267
7 at%	0.44	0.42	3010

---

5. Luminescent thermometry

In order to investigate the temperature effect, the temperature-dependent PL spectra of LSGW:5% Pr³⁺ were recorded from 300 to 440 K, under 450 nm excitation, as shown in Fig. 10. Notably, all emission spectra exhibit consistent spectral shapes, with no discernible shifts in peak position or full-width at half-maximum, indicating uniform distribution of crystal field. However, it is found that temperature has varying effects on emission-line intensity. Particular emphasis should be placed on transitions from thermally coupled ³P₀(I₁) and ³P₁(I₂) excited levels. In Fig. 11, the integrated intensities of ³P₁ → ³H₅ (531 nm), ³P₀ → ³H₅ (557 nm) and ³P₀ → ³H₆ (617 nm) are depicted against temperature variation. Notably, the emission intensity of the higher energy transition (³P₁ → ³H₅) increases, while the intensities of the lower-energy transitions (³P₀ → ³H₅ and ³P₀ → ³H₆) decrease as temperature increased, following a Boltzmann type distribution:²¹where LIR is the luminescence intensity ratio of the emission bands, T is the absolute temperature, B is a constant, k_B = 0.695 cm⁻¹ K⁻¹ is the Boltzmann constant, and ΔE is the energy gap between the two thermally coupled levels ³P₀ and ³P₁.

Fig. 10 Emission spectra of LSGW:5% Pr³⁺ in the 300–440 K range upon 450 nm excitation.

Fig. 11 Histogram displaying the integrated intensity of (a) ³P₁ → ³H₅ (531 nm) and ³P₀ → ³H₅ (557 nm) and (b) ³P₁ → ³H₅ (531 nm) and ³P₀ → ³H₆ (617 nm) emissions in the range of temperature from 300 to 440 K.

The temperature dependence of LIR between (I₅₃₁ and I₅₅₇) and (I₅₃₁ and I₆₁₇) relative to the temperature range 300–440 K are plotted in Fig. 12a and b, respectively. The experimental data are well fitted using eqn (1). The effective energy difference between the thermally coupled levels obtained from the fitting for LIR1 (I₅₃₁/I₅₅₇) is 403 cm⁻¹, and for LIR2 (I₅₃₁/I₆₁₇), it is 324 cm⁻¹. These values closely match the ΔE between the ³P₁ and ³P₀ states, which is approximately 500 cm⁻¹.¹⁹ The most important parameters for temperature sensing applications are the absolute (S_a) and the relative thermal sensitivities (S_r) defined as follows:⁵¹

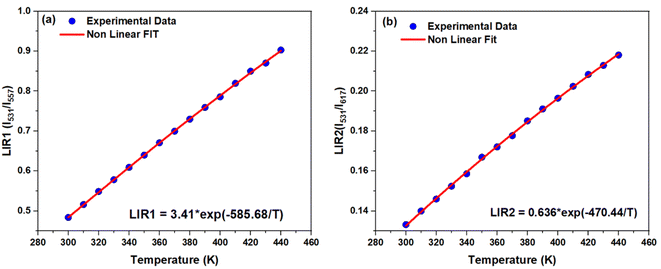Fig. 12 (a) The temperature dependent LIR1 (I₅₃₁/I₅₅₇) and (b) LIR2 (I₅₃₁/I₆₁₇) in 300–440 K temperature range.

Fig. 13 shows the variation of S_a and S_r of the LSGW:Pr³⁺ phosphor as a function of temperature from 300 to 440 K. For LIR1 and LIR2 the S_a and S_r values decrease with temperature, and they take the maximum value at room temperature (300 K). The maximal absolute and relative thermal sensitivities were found to be 0.00315 K⁻¹, and 0.65% K⁻¹ for LIR1 and 0.0007 K⁻¹ and 0.52% K⁻¹ for LIR2. Table 6 shows the comparison of the S_r values for different materials doped with Pr³⁺ ions in different temperature ranges.

Fig. 13 S_a and S_r values in the 300–440 K temperature range corresponding to (a) LIR1 (I₅₃₁/I₅₅₇) and (b) LIR2 (I₅₃₁/I₆₁₇).

Table 6 Maximum relative thermal sensitivity of Pr³⁺ based luminescent thermometers using the luminescence intensity ratio

Phosphors	Sr (% K^−1)	Temperature range (K)	References
SrMoO4:Pr^3+	0.45 (I486/I601)	298–498	17
Na2La2Ti3O10:Pr^3	1.96 (I611/I491)	303–543	52
Lu2GeO5:Pr^3+	1.12 (I490/I608)	150–550	53
CaSc2O4:Pr^3+	2.49 (I360/I630)	275–490	55
Gd2ZnTiO6:Pr^3+	1.67 (I617/I492)	293–433	56
YVO4:Pr^3+	0.78 (I595/I618)	303–323	57
CaMoO4:Pr^3+	0.96 (I605/I490)	303–573	58
LiSrGd(WO4)3:Pr^3+	0.65 (I531/I557)	300–440	This work
	0.52 (I531/I617)

---

In the field of luminescent thermometry, LiSrGd(WO₄)₃:Pr³⁺ phosphors present a balanced performance in comparison to several other notable hosts. With a relative sensitivity (S_r) of 0.65% K⁻¹ (I₅₃₁/I₅₅₇) and 0.52% K⁻¹ (I₅₃₁/I₆₁₇), LiSrGd(WO₄)₃:Pr³⁺ exhibits moderate sensitivity values, outperforming SrMoO₄:Pr³⁺ (S_r = 0.45% K⁻¹)¹⁷ but falling behind more sensitive hosts like Na₂La₂Ti₃O₁₀:Pr³⁺ (S_r = 1.96% K⁻¹).⁵²

The temperature range of 300–440 K for LiSrGd(WO₄)₃:Pr³⁺ is narrower than that of Lu₂GeO₅:Pr³⁺ (150–550 K),⁵³ yet it remains sufficient for various practical applications. These applications include biomedical diagnostics where the physiological temperature range is critical, microelectronics for real-time temperature monitoring of components, industrial processes requiring precise temperature control, environmental monitoring, household appliances for enhanced safety and efficiency, and energy systems such as battery management in electric vehicles and thermal management in solar panels.^5,17,54 Additionally, the specific intensity ratios (I₅₃₁/I₅₅₇ and I₅₃₁/I₆₁₇) used by LiSrGd(WO₄)₃:Pr³⁺ offer unique advantages for precise temperature sensing, similar to the specialized ratios utilized by other phosphors. Although CaSc₂O₄:Pr³⁺ (S_r = 2.49% K⁻¹)⁵⁵ and Gd₂ZnTiO₆:Pr³⁺ (S_r = 1.67% K⁻¹)⁵⁶ demonstrate higher sensitivities, LiSrGd(WO₄)₃:Pr³⁺ provides a reliable alternative with its balanced sensitivity and adequate temperature range. This makes it a valuable candidate for luminescent thermometry applications, offering a practical solution with moderate sensitivity and a suitable operational temperature range.

In addition to having high sensing sensitivity, the performance of a thermometer must also be assessed based on its temperature resolution, which determines the precision of the temperature measurements. The temperature uncertainty (δT) value can be determined through various experimental methods: by measuring a series of emission spectra at the same temperature, using the temperature calibration curve, or monitoring the cooling of the sample.⁵⁹ In this work, δT was obtained using the first method with the following expression:⁶⁰

where ∂LIR/LIR is the sensitivity of the detection system. In this case, ∂LIR signifies the standard deviation of the LIR data obtained from multiple measurements at a constant temperature, while LIR refers to the mean value of these measurements. To evaluate the sensitivity of the detection system, we performed 20 LIR measurements of our phosphor at room temperature, as depicted in the histograms in Fig. 14a and b. The estimated δT values increase with temperature and still below 1 K (Fig. 14c and d) which confirms the good thermometric performance of the LSGW:Pr³⁺ phosphor.

Fig. 14 Value of ∂LIR/LIR obtained using 20 measurements at 298 K of (a) LIR1 and (b) LIR2 and (c and d) temperature uncertainty values δT.

6. Conclusion

This study successfully synthesized LiSrGd(WO₄)₃ (LSGW) phosphors doped with Pr³⁺ using the solid-state method, confirming their potential for optical thermometry. Structural analyses verified Pr³⁺ incorporation with minimal bandgap alteration. Optimal doping (5 at%) yielded the highest emission intensity, while quenching effects at higher concentrations were attributed to dipole–dipole interactions. The LIR method demonstrated high sensitivity (S_a = 31.5 10⁻⁴ K⁻¹, S_r = 0.65% K⁻¹ at 300 K) and low temperature uncertainty (δT < 1 K) across 300–440 K, highlighting the competitive performance of LSGW:Pr³⁺ compared to similar materials. These findings establish LSGW:Pr³⁺ phosphors as promising candidates for precise and reliable optical temperature sensing.

Data availability

All data underlying the results are available as part of the article and no additional source data are required.

Conflicts of interest

There are no conflicts to declare.

References

1. V. Lojpur, M. G. Nikolić, D. Jovanović, M. Medić, Ž. Antić and M. D. Dramićanin, Appl. Phys. Lett., 2013, 103, 141912.
2. K. Li, M. Shang, H. Lian and J. Lin, J. Mater. Chem. C, 2016, 4, 5507–5530.
3. X. Wang, Q. Liu, Y. Bu, C. S. Liu, T. Liu and X. Yan, RSC Adv., 2015, 5, 86219–86236.
4. I. E. Kolesnikov, A. A. Kalinichev, M. A. Kurochkin and E. Y. Kolesnikov, Mater. Des., 2019, 184, 108188.
5. M. Runowski, P. Wozny, I. R. Martín, V. Lavín and S. Lis, J. Lumin., 2019, 214, 116571.
6. B. del Rosal, D. Ruiz, I. Chaves-Coira, B. H. Juarez, L. Monge, G. Hong, N. Fernandez and D. Jaque, Adv. Funct. Mater., 2018, 28, 1806088.
7. D. Jaque and F. Vetrone, Nanoscale, 2012, 4, 4301–4326.
8. E. C. Ximendes, U. Rocha, T. O. Sales, N. Fernández, F. Sanz-Rodríguez, I. R. Martín, C. Jacinto and D. Jaque, Adv. Funct. Mater., 2017, 27, 1702249.
9. M. Runowski, A. Shyichuk, A. Tymiński, T. Grzyb, V. Lavín and S. Lis, ACS Appl. Mater. Interfaces, 2018, 10, 172691–177279.
10. S. F. León-Luis, U. R. Rodríguez-Mendoza, E. Lalla and V. Lavín, Sens. Actuators, B, 2011, 158, 208–213.
11. Z. Liu and R. X. Wang, Chalcogenide Lett., 2022, 19, 471–481.
12. W. Ye, C. Ma, Y. Li, C. Zhao, Y. Wang, C. Zuo, Z. Wen, Y. Li, X. Yuan and Y. Cao, J. Mater. Chem. C, 2021, 9, 15201–15211.
13. C. D. S. Brites, K. Fiaczyk, J. F. C. B. Ramalho, M. Sójka, L. D. Carlos and E. Zych, Adv. Opt. Mater., 2018, 6, 1701318.
14. S. S. Zhou, G. C. Jiang, X. T. Wei, C. K. Duan, Y. H. Chen and M. Yin, J. Nanosci. Nanotechnol., 2014, 14, 3739–3742.
15. Y. Huang, L. Luo, J. Wang, Q. Zuo, Y. Yao and W. Li, J. Appl. Phys., 2015, 118, 044101.
16. M. S. Pudovkin, S. L. Korableva, D. A. Koryakovtseva, E. V. Lukinova, A. V. Lovchev, O. A. Morozov and V. V. Semashko, J. Nanopart. Res., 2019, 21, 2–14.
17. L. Li, P. Yang, W. Xia, Y. Wang, F. Ling, Z. Cao, S. Jiang, G. Xiang, X. Zhou and Y. Wang, Ceram. Int., 2021, 47, 769–775.
18. X. Tian, J. Li, H. Sheng, T. Li, L. Guo, C. Ji, Z. Huang, J. Wen, X. Liu, C. Li, J. Li and Y. Peng, Ceram. Int., 2022, 48, 3860–3868.
19. M. S. Pudovkin, O. A. Morozov, V. V. Pavlov, S. L. Korableva, E. V. Lukinova, Y. N. Osin, V. G. Evtugyn, R. A. Safiullin and V. V. Semashko, J. Nanomater., 2017, 2017, 3108586.
20. S. Jana, A. Mondal, J. Manam and S. Das, J. Alloys Compd., 2020, 821, 153342.
21. M. Runowski, P. Woźny, I. R. Martín, V. Lavín and S. Lis, J. Lumin., 2019, 214, 116571.
22. H. Zhang, Z. Gao, G. Li, Y. Zhu, S. Liu, K. Li and Y. Liang, Chem. Eng. J., 2020, 380, 122491.
23. B. Han, Y. Dai, J. Zhang, B. Liu and H. Sh, Ceram. Int., 2018, 44, 3734–3740.
24. K. Zhong, H. Ye, X. Wang, Y. Li and X. Yao, J. Mater. Sci.: Mater. Electron., 2021, 32, 17170–17181.
25. Q. Liu, X. Li, B. Zhang, L. Wang, Q. Zhang and L. Zhang, Ceram. Int., 2016, 42, 15294–15300.
26. L. Fan, Y. X. Fan, Y. H. Duan, Q. Wang, H. T. Wang, G. H. Jia and C. Y. Tu, Appl. Phys. B, 2009, 94, 553–557.
27. A. K. Parchur and R. S. Ningthoujam, Dalton Trans., 2011, 40, 7590–7594.
28. J. Bi, L. Wu, Y. Zhang, Z. Li, J. Li and X. Fu, Appl. Catal., B, 2009, 91, 135–143.
29. J. Yu, L. Qi, B. Cheng and X. Zhao, J. Hazard. Mater., 2008, 160, 621–628.
30. F. Ayachi, K. Saidi, M. Dammak, J. J. Carvajal and M. Cinta Pujol, RSC Adv., 2024, 14, 13494–13504.
31. S. Ward, M. A. Isaacs, G. Gupta, M. Mamlouk and S. S. Pramana, Sustainable Energy Fuels, 2021, 5, 154–165.
32. M. P. Selvam and K. J. Rao, Adv. Mater., 2000, 12, 1621–1624.
33. M. Song, W. Zhao, W. Ran, J. Xue, Y. Liu and J. H. Jeong, J. Alloys Compd., 2019, 803, 1063–1074.
34. L. Macalik, J. Hanuza and A. A. Kaminskii, J. Raman Spectrosc., 2002, 33, 92–103.
35. A. H. Ahmad and A. K. Arof, lonics, 2004, 10, 200–205.
36. P. F. S. Pereira, I. C. Nogueira, E. Longo, E. J. Nassar, I. L. V. Rosa and L. S. Cavalcante, J. Rare Earths, 2015, 33, 113.
37. P. Nemec, B. Frumarová and M. Frumar, J. Non-Cryst. Solids, 2000, 270, 137.
38. M. Laroche, A. Braud, S. Girard, J. L. Doualan, R. Moncorge, M. Thuau and L. D. Merkle, J. Opt. Soc. Am. B, 1999, 16, 2269.
39. A. E. Morales, E. S. Mora and U. Pal, Rev. Mex. Fis. S, 2007, 53, 18.
40. L. L. Noto, M. L. Chitambo, O. M. Ntwaeaborwa and H. C. Swart, Powder Technol., 2013, 247, 147–150.
41. J. A. Nelder and R. Mead, Comput. J., 1965, 7, 308.
42. K. Rajnak, J. Chem. Phys., 1965, 43, 847.
43. K. M. Murdoch, N. M. Edelstein, L. A. Boatner and M. M. Abraham, J. Chem. Phys., 1996, 105, 2539.
44. M. L. Duan, X. F. Yang and J. H. Li, Adv. Mater. Res., 2011, 418–420, 665–669.
45. C. Basavapoornima, T. Maheswari, C. R. Kesavulu, W. Pecharapa, J. Kaewkhao and C. K. Jayasankar, AIP Conf. Proc., 2020, 2279, 060002.
46. M. Runowskia, P. Woznya, I. R. Martínb, V. Lavínb and S. Lisa, J. Lumin., 2019, 214, 116571.
47. M. Fhoula, K. Saidi and M. Dammak, J. Alloys Compd., 2024, 979(5), 173537.
48. G. Blasse and B. C. Grabmaier, Luminescent Materials, Springer-Verlag, 1994.
49. D. L. Dexter and J. H. Schulman, J. Chem. Phys., 1954, 22, 1063–1070.
50. C. S. McCamy, Color Res. Appl., 1992, 17, 142–144.
51. I. E. Kolesnikov, A. A. Kalinichev, M. A. Kurochkin, D. V. Mamonova, E. Y. Kolesnikov and E. Lahderanta, J. Phys. Chem. C, 2019, 123, 5136–5143.
52. Y. Gao, F. Huang, H. Lin, J. Xu and Y. Wang, Sens. Actuators, B, 2017, 243, 137–143.
53. M. Sójka, C. D. S. Brites, L. D. Carlos and E. Zych, J. Mater. Chem. C, 2020, 8, 10086–10097.
54. S. Kaur, H. Kaur, A. S. Rao and G. V. Prakash, Phys. B, 2024, 690, 416224.
55. S. Wang, S. Ma, G. Zhang, Z. Ye and X. Cheng, ACS Appl. Mater. Interfaces, 2019, 11, 42330–42338.
56. Y. Gao, Y. Cheng, T. Hu, Z. Ji, H. Lin, J. Xu and Y. Wang, J. Mater. Chem. C, 2018, 6, 11178–11183.
57. H. Zhou, W. Gao, P. Cai, B. Zhang and S. Li, Solid State Sci., 2020, 104, 106283.
58. X. Tian, S. Xu, J. Wen, L. Zhu, C. Ji, Z. Huang, X. Wang, F. Luo, X. Liu, Y. Lu, J. Li, C. Li, Y. Peng, J. Cao and Z. He, Ceram. Int., 2023, 49, 27126–27137.
59. I. E. Kolesnikov, D. V. Mamonova, M. A. Kurochkin, E. Y. Kolesnikov and E. Lahderanta, ACS Appl. Nano Mater., 2021, 4, 1959–1966.
60. J. Stefanska and L. Marciniak, Adv. Photonics Res., 2021, 2, 2100070.

---