Open Access Article
Open Access ArticleNewly predicted halide perovskites Mg3AB3 (A = N, Bi; B = F, Br, I) for next-generation photovoltaic applications: a first-principles study
Mayeen Uddin Khandaker *abc,
Hamid Osman
*abc,
Hamid Osman d,
Shams A. M. Issae,
M. M. Uddin*f,
Md. Habib Ullahg,
Hajir Wahbih and
M. Y. Hanfiij
d,
Shams A. M. Issae,
M. M. Uddin*f,
Md. Habib Ullahg,
Hajir Wahbih and
M. Y. Hanfiij
aApplied Physics Radiation Technologies Group, CCDCU, School of Engineering and Technology, Sunway University, 47500 Bandar Sunway, Selangor, Malaysia
bFaculty of Graduate Studies, Daffodil International University, Daffodil Smart City, Birulia, Savar, Dhaka 1216, Bangladesh. E-mail: mayeenk@diu.edu.bd
cDepartment of Physics, College of Science, Korea University, 145 Anam-ro, Seongbuk-gu, Seoul, 02841, Republic of Korea
dDepartment of Radiological Sciences, College of Applied Medical Sciences, Taif University, P. O. Box 2425, Taif 21944, Saudi Arabia. E-mail: ha.osman@tu.edu.sa
ePhysics Department, Faculty of Science, University of Tabuk, Tabuk, Saudi Arabia. E-mail: sh_issa@ut.edu.sa
fDepartment of Physics, Chittagong University of Engineering and Technology, Chattogram 4349, Bangladesh. E-mail: mohi@cuet.ac.bd
gDepartment of Physics, American International University-Bangladesh, 408/1, Kuratoli, Khilkhet, Dhaka 1229, Bangladesh. E-mail: habib583@aiub.edu
hDepartment of Chemistry, Faculty of Science, Northern Border University, Arar, 91431, Saudi Arabia. E-mail: hajir.wahbi@nbu.edu.sa
iUral Federal University, Ekaterinburg 620002, Russia. E-mail: mokhamed.khanfi@urfu.ru
jNuclear Materials Authority, P. O. Box 530, El-Maadi, Cairo, Egypt
First published on 20th February 2025
Abstract
The research examines the exceptional physical characteristics of Mg3AB3 (A = N, Bi; B = F, Br, I) perovskite compounds through density functional theory to assess their feasibility for photovoltaic applications. Mechanical characterization further supports their stability where out of all the compounds, Mg3BiI3 demonstrates high ductility, while Mg3NF3 and Mg3BiBr3 possess a brittle nature. The calculated elastic constants and anisotropy factors also substantiate their mechanical stability, while there is an observed declining trend in Debye temperature with increase in atomic number. From the electronic point of view, Mg3NF3 can be considered as a wide-bandgap insulator with the bandgap of 6.789 eV, whereas Mg3BiBr3 and Mg3BiI3 can be classified as semiconductors suitable for photovoltaic applications bandgaps of 1.626 eV and 0.867 eV, respectively. The optical characteristics of such materials are excellent and pronounced by high absorption coefficients, low reflectivity, and good dielectrics, which are very important in the collection of solar energy. Among them, Mg3BiBr3 and Mg3BiI3 possess high light absorption coefficient, moderate reflectivity, and good electrical conductivity, indicating that they are quite suitable for applying the photoelectric conversion materials for solar cells. In addition, thermal analysis shows that Mg3NF3 is a good heat sink material, Mg3BiBr3 and Mg3BiI3 are favorable for thermal barrier coating materials. Due to their high absorption coefficients, low reflectance and suitable conductivity, both Mg3BiBr3 and Mg3BiI3 could be regarded as the most appropriate materials for the creation of the next generation of photovoltaic converters.
1 Introduction
Photovoltaic (PV) technology plays a crucial role in reducing environmental pollution and decreasing reliance on fossil fuels, positioning it as a key solution for sustainable energy production.1 Materials like silicon (Si), GaAs, CdTe, and Cu(In,Ga)(S,Se)2 (CIGS) have achieved remarkable advancements in PV applications, with crystalline silicon dominating commercialization due to its high power conversion efficiency (PCE), stability, and radiation resistance.2,3 However, the non-ideal, indirect bandgap of silicon and high fabrication costs limit further development.4 Since 2009,5 halide perovskites have emerged as transformative materials in solar energy, characterized by optimal bandgaps, high absorption coefficients, exceptional charge carrier mobility, and defect tolerance.6,7 These features have driven their PCE from 3.8% to 25.5% within a decade.8 However, challenges such as the toxicity and instability of lead-based perovskites hinder their scalability. Addressing these issues has led to intensive research into lead-free alternatives, though their efficiency and stability often lag behind traditional perovskites.9,10Among lead-free candidates, the A3MX3 perovskite family, featuring elements like A = Mg2+, Ba2+, Sr2+, Ca2+, and M = Sb3−, As3−, P3−, and halides (X = F−, Cl−, Br−, I−), has garnered attention. These compounds, with a cubic structure in the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group, exhibit direct bandgaps, high stability, and strong optoelectronic properties, making them ideal for PV applications.11–15 Notably, the Shockley–Queisser theory predicts a maximum PCE of 33% for materials with bandgaps between 1.2 and 1.4 eV, aligning well with the characteristics of A3MX3 perovskites.16–18 Inorganic lead halide perovskites (ILHPs) are particularly suited for optoelectronic and photovoltaic uses. However, their relatively large bandgaps pose challenges to achieving optimal PCE.19,20 Recent research highlights the necessity of tuning the bandgap to optimize efficiency. Promising approaches include strain engineering and compositional size tampering, both of which have been shown to effectively reduce the bandgap and enhance PV performance.21–26 For example, the band structure of lead halide perovskites can fragment, resulting in a significant reduction of approximately 1 eV in the bandgap when spin–orbit coupling (SOC) effects are considered.27
m space group, exhibit direct bandgaps, high stability, and strong optoelectronic properties, making them ideal for PV applications.11–15 Notably, the Shockley–Queisser theory predicts a maximum PCE of 33% for materials with bandgaps between 1.2 and 1.4 eV, aligning well with the characteristics of A3MX3 perovskites.16–18 Inorganic lead halide perovskites (ILHPs) are particularly suited for optoelectronic and photovoltaic uses. However, their relatively large bandgaps pose challenges to achieving optimal PCE.19,20 Recent research highlights the necessity of tuning the bandgap to optimize efficiency. Promising approaches include strain engineering and compositional size tampering, both of which have been shown to effectively reduce the bandgap and enhance PV performance.21–26 For example, the band structure of lead halide perovskites can fragment, resulting in a significant reduction of approximately 1 eV in the bandgap when spin–orbit coupling (SOC) effects are considered.27
Recent studies have demonstrated significant advancements in lead-free perovskite solar cells. For instance, He et al. achieved a PCE of 6.53% using novel MAPbBr3/CsPbBr3 dual absorbers,28 while Baruah et al. developed an inorganic La2NiMnO6/Cs3Bi2I9 graded absorber architecture with a remarkable PCE of 26.02%.29 Rahman et al. designed a CdTe/FeSi3-based device model, attaining a PCE of 27.35%.30 In addition to these innovations, tin-halide perovskites have emerged as promising alternatives, offering higher theoretical efficiencies and enhanced carrier mobility.31 Materials like NaZnBr3 and its variants, such as NaZn0.7Cu0.3Br3, have shown improvements in both stability and efficiency.32 Furthermore, Ca3NCl3 has demonstrated a PCE exceeding 24.73% as an absorber, offering advantages like visible-spectrum absorption, high chemical stability, and environmental friendliness.33 Although efficiency data for CaRbCl3 remains unreported, both materials show potential for durable, efficient, and scalable solar cell applications, supported by their tunable bandgaps and compatibility with low-temperature manufacturing processes.33 Recent studies have also emphasized Mg3SbX6 (X = I, Br, Cl, F) for its structural stability and direct bandgap, further establishing its potential as a promising material for photovoltaic applications.34
First-principles calculations have been extensively utilized to investigate the physical properties of perovskite materials.35,36 These properties can be tailored by substituting elements,37 introducing dopants,38 or applying hydrostatic pressure.39–41 Linh et al.42 demonstrated that replacing alkali metals with larger ionic radii (e.g., Li, Na, K) in (Bi0.5M0.5)TiO3 increased the electronic bandgap. Similarly, Gillani et al.38 showed that doping alkaline earth elements (Mg, Ca, Ba) into SrZrO3 shifted the bandgap from indirect to direct. Hydrostatic pressure is particularly effective in tuning the structural and electronic attributes of A3BX3 and ABX3 perovskites, enabling precise adjustments to their properties for technological applications. This clean and non-invasive approach modifies the crystal structure and electronic characteristics without altering the chemical composition.43,44 Additionally, the optoelectronic properties of perovskites under varying pressure have been explored,45,46 highlighting their suitability for p–n junctions, quantum wells, heterostructures, and photovoltaic or optoelectronic devices.47–50 For instance, Babu et al.51 observed a reduction in the bandgap of CsSnCl3 under compressive pressure, which led to a phase transition from semiconducting to metallic behavior.
Using density functional theory (DFT), this study investigates the physical and optoelectronic properties of novel A3MX3 perovskite compounds, specifically Mg3AB3 (A = N, Bi; B = F, Cl), for photovoltaic applications. These materials are characterized by their cubic crystal structures, direct bandgaps, and exceptional stability, making them highly promising for next-generation solar cell technologies. The objective of this work is to evaluate their structural, electronic, and optical properties to understand their potential for efficient solar energy conversion. By leveraging first-principles calculations, this study aims to provide insights into the design and optimization of environmentally friendly, lead-free perovskite materials, contributing to sustainable and scalable photovoltaic solutions.
2 Computational technique
In this work first-principles electronic structure calculations were performed using Quantum ESPRESSO software package to gain insights into the structure of Mg3AB3 (A = N, Bi; B = F, Br, I) materials. The calculated structure was based on plane-wave pseudopotential method with ultrasoft pseudopotentials were chosen to ensure both the efficiency and the accuracy of the method.52,53 Exchange-correlation interactions were described within the GGA-PBE approximation, while structural, mechanical, thermal, and vibrational characteristics were investigated in detail. There was a quantitative optimization of the k-point sampling, k-point mesh of Monkhorst–Pack 10 × 10 × 8 and plane-wave energy respectively 60 Ry to find the best results of all the compounds. For more reliable estimation of energy band and electronic and optical property calculations, the HSE06 hybrid functional was used.54 Phonon dispersion was investigated using density functional perturbation theory – implemented in the PHONOPY55 suite for detailed analysis of dynamical stability. The ineffective vibration was studied by employing a supercell (2 × 2 × 2) for the atomic movements of 0.01 Å along the lattice directions. The mechanical stability was estimated by calculating the elastic constants using the energy-strain approach available in the thermo_pw package, implemented within Quantum ESPRESSO.56,57 These advanced computational methodologies allowed for the detailed study of the structural, mechanical and physical properties of the Mg3AB3 (A = N, Bi; B = F, Br, I) compounds to understand if they have the potential for use in state-of-the-art technological applications.3 Results and discussion
3.1 Structural and thermodynamic stability
The revealed halide perovskite presents the Mg3AB3 (A = N, Bi; B = F, Br, I) compounds with the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m cubic structure.58 The unit cell comprises seven atoms: While Mg and A atoms form a face centered cubic cell, the B atoms are situated at the octahedral holes, shown in Fig. 1. The atomic coordinates of these ions are Mg (0.5, 0, 0.5), A (0.5, 0.5, 0.5), B (0, 0, 0.5), which are corresponding to the 3c, 1b, and 3d Wyckoff sites. The variable-cell relaxation (vc-relax) algorithm in Quantum ESPRESSO with projector-augmented wave (PAW) pseudopotentials and the Perdew–Burke–Ernzerhof (PBE) functional showed that the replacement of smaller atoms (N, F) with larger ones (Bi, Br, I) produced uniform lattice expansion through steric effects. The calculated lattice parameters, and the relevant structural information such as lattice constant (a), unit cell volume (V), and formation energy (Ef) are provided in Table 1.
m cubic structure.58 The unit cell comprises seven atoms: While Mg and A atoms form a face centered cubic cell, the B atoms are situated at the octahedral holes, shown in Fig. 1. The atomic coordinates of these ions are Mg (0.5, 0, 0.5), A (0.5, 0.5, 0.5), B (0, 0, 0.5), which are corresponding to the 3c, 1b, and 3d Wyckoff sites. The variable-cell relaxation (vc-relax) algorithm in Quantum ESPRESSO with projector-augmented wave (PAW) pseudopotentials and the Perdew–Burke–Ernzerhof (PBE) functional showed that the replacement of smaller atoms (N, F) with larger ones (Bi, Br, I) produced uniform lattice expansion through steric effects. The calculated lattice parameters, and the relevant structural information such as lattice constant (a), unit cell volume (V), and formation energy (Ef) are provided in Table 1.
| Compounds | a (Å) | V (Å3) | Ef | Ereac | Ref. | |
|---|---|---|---|---|---|---|
| Mg3NF3 | 4.269this work | 77.81this work | −1.6589 | 3.221 | −0.437 | 59 |
| 4.212exp | 74.75exp | |||||
| Mg3BiBr3 | 5.767 | 191.83 | −2.4468 | 2.109 | −1.258 | |
| Mg3BiI3 | 6.069 | 223.59 | −1.9767 | 1.875 | −1.047 |
The negative formation energies highlighted that these compounds are thermodynamically stable and energetically favorable for synthesis. The enthalpy of formation (Ef) was computed using the relation:60
 | (1) |
Our simulation confirms the phase stability by connecting cohesive energy analysis with thermodynamic stability. Materials science defines cohesive energy as the amount of energy needed to separate substances into atomic or molecular components.61,62 This has been determined using the following eqn (1):
 | (2) |
 is the cohesive energy of the Mg3AB3 phases, and xEMgsolid, yEAsolid, and zEBsolid are the sum of the energies of the individual isolated atoms, namely Mg, N/Bi, and F/Br/I, respectively. In this calculation, we isolated one atom from a cubic unit cell with edge length 16 Å, k sampled the gamma point, and relaxed. Table 1 listed the values of cohesive energies to assess thermodynamic stability. These results are strongly indicated that the predicted compounds XIn2C2 should be thermodynamically stable and possibly synthesizable.
is the cohesive energy of the Mg3AB3 phases, and xEMgsolid, yEAsolid, and zEBsolid are the sum of the energies of the individual isolated atoms, namely Mg, N/Bi, and F/Br/I, respectively. In this calculation, we isolated one atom from a cubic unit cell with edge length 16 Å, k sampled the gamma point, and relaxed. Table 1 listed the values of cohesive energies to assess thermodynamic stability. These results are strongly indicated that the predicted compounds XIn2C2 should be thermodynamically stable and possibly synthesizable.
We applied the eqn (3)–(6) to calculate the reaction energy to address the limited experimental data on the chemical stability of the Mg3AB3 (A = N, Bi; B = F, Br, I) compounds and the synthesized Mg3NF3 compound. As reference phases we use Mg3N2,63 MgF2,64 Mg3Bi2,65 MgBr2,66 and MgI2,67 and assume plausible chemical reactions similar to those carried out in preparing the original compound Mg3NF3.68 Based on that, we calculate the formation enthalpies of Mg3N2, MgF2, Mg3Bi2, MgBr2 and MgI2, −0.114, −0.922, −0.11, −0.175, and −0.932, respectively. In Table 1, we summarize the final reaction energies of the compounds. We then calculate the stability of Mg3NF3 to compare the computed result to the synthesized and stable Mg3NF3. All these values show the thermodynamic stability of these compounds and there is no competing phase more stable than this.
 | (3) |
| Mg3N2 + 3MgF2 = 2Mg3NF3 | (4) |
| Mg3Bi2 + 3MgBr2 = 2Mg3BiBr3 | (5) |
| Mg3Bi2 + 3MgI2 = 2Mg3BiI3 | (6) |
The computed, crystallographic data are summarized in Table 1 and compared with the previous experimental values. A good correlation with the experimental values shows that our calculations are provided with quite a reliable estimation. The replacement of two elements with larger atomic radii in Mg3NF3: Bi for N and Br or I for F, led to an increase in the values of the lattice constants and the unit cell volume. Geometrical optimization has been carried out with Quantum ESPRESSO. Furthermore, the negative formation energy, negative reaction energy, and positive cohesive energy values, as tabulated in Table 1, strongly indicate the thermodynamic stability of Mg3AB3.
Phonon dispersion analysis was used to assess dynamic stability by the finite displacement method69 using the PHONOPY program.70 Structural relaxation was done on a 2 × 2 × 2 supercell with an atomic displacement of 0.01 Å were used perform the relevant calculations. In Fig. 2, the phonon dispersion curves (PDCs) along high symmetrical points (Γ–X–M–Γ–R–X) excluded the negative values of the phonon frequencies for all calculated compounds, thus proving the dynamical stability. With seven atoms per unit cell, the compounds exhibit 21 vibrational modes: 3 acoustic and 18 optical. Acoustic modes with zero frequencies for Γ-point are linear (ω = vk) in the small Q-vector limit. Optical modes can be described as out-of-phase motion of the atomic planes, as opposed to the cooperatively in-phase motion of the planes in acoustic modes. There was not a phonon band gap between the acoustic and lower optical modes as expected from the stability of the vibration. These results give the theoretic foundation for the synthesis of Mg3AB3 (A = N, Bi; B = F, Br, I) compounds owing to their structural, and thermodynamically favorable characteristics.
 | ||
| Fig. 2 Phonon dispersion curve with phonon density of state of (a) Mg3NF3 (b) Mg3BiBr3 (c) Mg3BiI3 compounds. | ||
3.2 Mechanical properties
The elastic behavior of a crystal depends expressly on the elastic coefficients that characterize the response of the crystal to applied forces. Knowledge of these properties is necessary when it comes to comprehending mechanical characteristics of the compound. In this research, the mechanical aspect and the elastically related properties of the different compounds were examined using C11, C12, and C44 constants. Perovskite compound's mechanical stability was verified based on the criteria: C11 − C12 > 0, C11 + 2C12 > 0 and C44 > 0. One of the basic properties that determine the character of the material is its strength.71 Table 2 characterizes the individual elastic coefficients of the investigated compounds.| Compounds | Mg3NF3 | Mg3BiBr3 | Mg3BiI3 |
|---|---|---|---|
| C11 | 252.51 | 76.36 | 65.09 |
| C12 | 63.36 | 18.58 | 21.42 |
| C44 | 92.10 | 22.49 | 15.81 |
| A | 0.265 | 0.213 | 0.181 |
| B | 126.41 | 37.84 | 35.98 |
| G | 93.08 | 24.86 | 18.00 |
| Y | 224.22 | 61.19 | 46.28 |
| B/G | 1.358 | 1.522 | 1.999 |
| ν | 0.204 | 0.230 | 0.285 |
| B/C44 | 1.372 | 1.682 | 2.274 |
| Hmacro | 16.830 | 5.016 | 1.824 |
| Hmicro | 18.374 | 4.477 | 2.581 |
Thus, for Mg3AB3 (A = N, Bi; B = F, B, I) mechanical properties such as bulk modulus (B), shear modulus (G), Young's modulus (Y), Pugh's ratio (B/G), and Poisson's ratio (ν) were predicted. The bulk modulus may be taken to demonstrate the resistance to change in volume at the application of pressure, and the shear modulus describes the connection between shear stress and strain. Yong's modulus calculated from stress-to-strain ratio during uniaxial deformation gives the measure of elasticity of the material.72,73 The corresponding formulas are given as follows eqn (7)–(11):
 | (7) |
 | (8) |
 | (9) |
 | (10) |
 | (11) |
A bulk modulus (B) is a measure of material hardness; a higher value of B of Mg3NF3 consistently defines a stronger and harder material than Mg3BiBr3 and Mg3BiI3. Also, the values of Young's Modulus (Y) and, shear modulus (G) provide information about hardness of materials. In our calculation, we found that both Y and G values are significantly high for Mg3NF3, which also indicates its greater hardness compared to the other two compounds.
For determination of ductility/brittleness, absolute Poisson's ratio (ν) is used and for it value more than 0.26 suggests ductile material. Among the compounds, Mg3NF3 and Mg3BiBr3 exhibit brittle nature, whereas Mg3BiI3 shows ductile behavior (Table 2).75 The B/G ratio is also used in the classification of malleability or brittleness. A ratio higher than 1.75 is indicative of ductility as opposed to brittleness for a lesser value of that ratio. According to the B/G ratios, Mg3NF3 and Mg3BiBr3 materials are brittle in nature while Mg3BiI3 is ductile in nature.76,77
The machinability index, obtained as B/C44, is a major factor in mechanical performance.78 Low shear resistance and a smaller C44 rating usually equate to enhanced machinability. For example, Mg3BiI3 has better machinability properties as compared to the other compounds.
To evaluate hardness, parameters HMiao and HChen were computed using the following formulas:79,80
 | (12) |
 | (13) |
The Debye temperature (ΘD) in the lattice vibration theory corresponds to Fermi's temperature in the metal electronic theory.81 This essential parameter is closely associated with many thermal and physical properties of materials including elastic coefficients, specific heat and melting point. It is therefore important to understand ΘD to evaluate how suitable material is for electronic applications.
One widely used method to calculate the Debye temperature involves elastic constant data, with ΘD determined by averaging the sound velocity, vm, as expressed by the eqn (14):82
 | (14) |
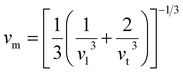 | (15) |
| vl = [(3B + 4G)/3ρ]1/2 | (16) |
| vt = [G/ρ]1/2 | (17) |
With these relations, the Debye temperature, sound velocities (vt, vl, vm), and density (ρ) were computed for Mg3AB3 and the data is presented in Table 3. From the above result, the longitudinal velocity is invariably higher than other velocities because it is associated to particle displacements along the direction of wave travel for longitudinal waves. For our calculated compounds Mg3NF3, Mg3BiBr3, and Mg3BiI3, it is ascertained that with an increase in atomic mass the calculated values of Debye temperature are getting down in the range of 804.67 K to 200.09 K. These changes in ΘD are as a result of differences in the elastic stiffness and bonding strength of the materials used. Debye temperature is very much related to hardness of the material which in turn supports the earlier hardness calculations.84 The Debye temperature measures the vibrational behavior of lattices in materials. The materials with lower Debye temperatures present softer lattice structures that contribute to enhanced stress tolerance which enables better accommodation of thermal expansion and contraction strains. Materials with lower Debye temperature tend to exhibit reduced thermal conductivity. Heat transport becomes an issue when materials exhibit lower Debye temperature values despite having better mechanical strain accommodation.85 Mg3NF3 showing high Debye temperature characterize high hardness while Mg3BiI3 showing low Debye temperature characterizes low hardness. The low Debye temperatures of Mg3BiBr3 and Mg3BiI3 suggest enhanced lattice flexibility, enabling better resistance to thermal stress and reducing the risk of microcracks during thermal cycling. This property, along with potentially lower thermal conductivity, could improve the device reliability and stability under prolonged operational conditions. Due to the lack of experimental data of these compounds, computational outcomes are anticipated to be further validated via experimental analysis.
| Compounds | ρ (kg m−3) | vm (m s−1) | vt (m s−1) | vl (m s−1) | ΘD (K) |
|---|---|---|---|---|---|
| Mg3NF3 | 3070.62 | 5935.77 | 5374.16 | 8816.48 | 804.67 |
| Mg3BiBr3 | 4436.64 | 2599.41 | 2346.66 | 3965.44 | 256.69 |
| Mg3BiI3 | 4920.20 | 2132.41 | 1912.53 | 3491.27 | 200.09 |
3.3 Electronic properties
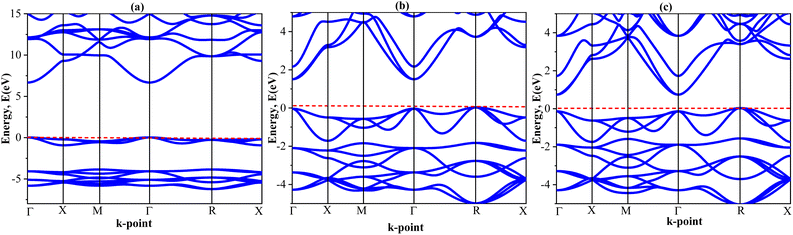
The fundamental electronic structures, including band structures, charge density and density of states (DOS) gives an insight to the electrical behavior of materials.86 In the present research, analysis of the electronic band structure along high-symmetry directions of the Mg3AB3 (A = N, Bi; B = F, Br, I) perovskite structures have been carried out. The band structure plots presented in Fig. 3(a)–(c) are referenced with the Fermi level set to 0 V, enabling a precise comparison of the bandgaps. The band structure is shown along the high symmetry directions of the Brillouin zone for Mg3AB3, including the Γ → X → M → Γ → R → X paths for the cubic structure. As seen in Fig. 3(a), Mg3NF3 shows the direct bandgap where the CBM and VBM are at Γ-point. On the other hand, Fig. 3(b) and (c) depicts that for Mg3BiBr3 and Mg3BiI3, the CBM is situated at Γ point but the VBM of both materials is slightly lower than that of Γ than R. This arrangement results in an indirect bandgap that is very close to a direct bandgap character for these compounds.The GGA predicted bandgap for Mg3NF3, Mg3BiBr3 and Mg3BiI3 compounds are presented in Table 4. The band structure calculated using HSE06 is displayed in Fig. 3. From the above compounds, the HSE06 yielded bandgaps of 6.789 eV, 1.626 eV, and 0.867 eV respectively. Semiconductor have band gap rang 0.5–3 eV, while the material with band gap >4 eV is typically classified as strong insulators. By sorting these compounds according to these classifications, the HSE06-calculated bandgap suggests that Mg3NF3 is an insulator, while Mg3BiBr3 and Mg3BiI3 are semiconductors. The omission of SOC may slightly affect the bandgap values, and its inclusion in future studies would provide more precise insights into these properties.
| Compounds | Approach | Nature | Bandgap (eV) | Ref. |
|---|---|---|---|---|
| Mg3NF3 | GGA | Direct | 3.738 | This study |
| HSE06 | Direct | 6.789 | This study | |
| Mg3BiBr3 | GGA | Indirect | 1.071 | This study |
| HSE06 | Indirect | 1.626 | This study | |
| Mg3BiI3 | GGA | Indirect | 0.224 | This study |
| HSE06 | Indirect | 0.867 | This study |
In the analysis of the contribution of specific atomic states on the electronic characteristics of Mg3AB3 (A = N, Bi; B = F, Br, I) perovskite structures, the PDOS is quite informative. Note that in Fig. 4(a)–(c) the PDOS distribution is plotted for Mg3NF3 in the range of −10 to +15 eV, while for Mg3BiBr3 and Mg3BiI3, this range is −5 to +8 eV. The total density of states (TDOS) gives general information of the electronic characteristics; the Fermi level (EF) is revealed by the vertical red dashed line at 0 eV. It is seen that for Mg3NF3, the valence band mainly has N-p and F-p orbitals, and the conduction band has Mg-s, p, N-s, p and F-s, p states as depicted in Fig. 4(a). Lack of any kind of electronic states near the Fermi level supports the view of having a large bandgap which defines this material as an insulator. For Mg3BiBr3, the valence band is mostly Bi-p and Br-p composition which suggests the substantial mixing between these states (Fig. 4(b)). Mg-p, Bi-p, d and I-p, d orbitals play vital roles in the conduction band and all the three bands are significantly influenced in the conduction band by the electronic transitions. In the case of Mg3BiI3 (Fig. 4(c)), the valence band comprises the I-p and Bi-p states with visible mixing between these two bands. It is also clear that Mg-p, Bi-p, d and I-p, d orbitals have contributions to the conduction band implying their relevance for the electronic transitions. These features are characteristic of semiconductors and particularly are suitable for optoelectronics. These analyses demonstrate that the atomic states and the orbital hybridization of electrons are significant for the electronic characteristic of Mg3AB3 compounds.
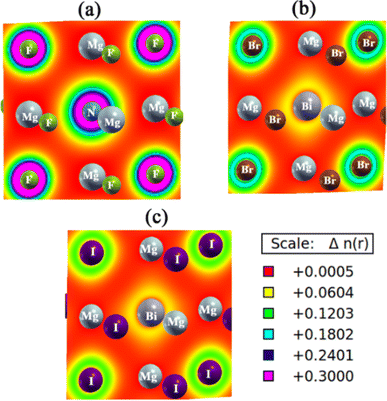
In Fig. 5, the electronic charge density maps of Mg3AB3 (A = N, Bi; B = F, Br, I) perovskite compounds are displayed to witness the charge distribution. The shades of colour in the maps correspond to the charge density as pointed out by the scale bar at the bottom of each map.
Bonds in Mg3AB3 perovskites are ionic and partially covalent depending on charge states of ions (Mg2+, N3− or Bi3+ and halogen anions). In turn, magnesium ionized in solution as Mg2+, was participating in bond formation of both nitrogen and bismuth with the valence halogen anion. In compounds of Mg3BiBr3 and Mg3BiI3, the halide ions have significant contribution for the ionic environment with strong electrostatic interaction with Mg2+, similarly bismuth (Bi3+) also has got very close coordination with Mg2+ as it has got high net positive charge.
Bonding characteristics are much influenced by the halogens. Fluorine (F−) being one of the highest electronegative elements ions very strongly localize electron density around itself, forming dominantly ionic bonds with Mg2+. The ionic radii are larger for bromine (Br−) and iodine (I−), which have lower electronegativity and a slightly weaker ionic bond due to more diffuse electron density distribution. But these halides are essential for stabilizing the perovskite structure.
The bonding also includes partial covalent character for compounds that contain bismuth and heavier halogens such as bromine and iodine because of orbital overlap. Iodine is an outcry concern because of its larger size and greater polarizability, which makes it an especially strong covalent interaction. Charge density maps show high electron density around halogens identifying them as ionic, and diffuse charge density around Mg2+ because of its role in stabilizing this complex. Stability and electronic properties of these materials arise from the balance of ionic and covalent interactions.
3.4 Optical properties
The optoelectronic properties of the Mg3AB3 structures (A = N, Bi; B = F, Br, I) are investigated to understand their light absorption, reflectivity, loss function, dielectric properties, and other related properties. The dielectric function ε(ω) consists of two components: the real part is denoted by ε1(ω), while the imaginary part is denoted by ε2(ω), and can be represented by eqn (18):| ε(ω) = ε1(ω) + iε2(ω) | (18) |
It has been calculated by the Kramers–Kronig transformation from the real part and from the momentum matrix elements for the imaginary part.87
The calculated ε1(0) values are outlined in the Table 5 below. From Fig. 6(c) it is clear that Mg3NF3 has a nearly constant response across the full range of photon energy implying weak electronic transitions and case of which is consistent with the insulating property of the compound. On the other hand, Mg3BiBr3 and Mg3BiI3 exhibit distinct peaks in ε1(ω) indicating significant electronic polarization and moderate interband transition. The first peak of Mg3BiI3 occurs around 3.47 eV, slightly higher than that of Mg3BiBr3, due to iodine occupying more space and being more polarized than bromine ions. Compared with the halogen parent compound, these results show the differences in dielectric responses owing to halogen substitution. Although Mg3NF3 is non-conductive and demonstrates a low level of optical activity, Mg3BiBr3 and Mg3BiI3 have high levels of optical activity that make them suitable for optoelectronic applications.
| Compounds | Mg3NF3 | Mg3BiBr3 | Mg3BiI3 |
|---|---|---|---|
| ε1(0) | 2.029 | 5.713 | 6.889 |
| ε2max(ω) | 3.01 (13.16 eV) | 7.56 (4.30 eV) | 8.706 (3.74 eV) |
| α(0) | 6.69 eV | 1.65 eV | 0.98 eV |
| αmax(ω) | 13.25 eV | 11.44 eV | 9.25 eV |
| L(0) | 7.13 eV | 3.67 eV | 1.45 eV |
| R(0) | 2% | 16% | 20% |
| Rmax(ω) | 18% | 37% | 44% |
| σmax(ω) | 4.68 (13.14 eV) | 4.62 (8.73 eV) | 4.95 (7.54 eV) |
| n(0) | 1.41 | 2.39 | 2.63 |
ε2(ω), the second component of the dielectric function, is an essential factor in evaluating the ability of light absorption and the energy gain capability. The ε2(ω) for the Mg3AB3 structures are presented in Fig. 6(d) where the values corresponding to the highest peak are also given in the Table 5. By observing the imaginary part, it is seen that the particular materials under consideration react to electromagnetic radiation. The imaginary part of dielectric function ε2(ω) indicate that Mg3NF3 has low absorption with no major electronic transitions, while Mg3BiBr3 and Mg3BiI3 exhibit higher absorption levels and a noticeable peak, indicating significant interband absorption. These results demonstrate that Mg3BiBr3 and Mg3BiI3 are more optically lively compounds that are suitable for potential optoelectronic uses.
The absorption coefficient α(ω) follows the dependence of ε2(ω). The absorption coefficient of the Mg3AB3 compounds is displayed in Fig. 6(a), which is in the range of 105 to 106 cm−1 near the absorption edges, while the static and peak values are given in Table 5, the result showed that Mg3NF3 exhibits significantly a lower absorption coefficient, and this is attributed to the insulating nature of Mg3NF3. On the other hand, Mg3BiBr3 and Mg3BiI3 show absorptivity values higher than the previous compounds, which would make them ideal for use in optoelectronic and photovoltaic devices.
The optical conductivity of these compounds, shown in Fig. 6(b), does not take any action below the energy band gap owing to the lack of electronic transitions. However, at higher energy levels above the band gap, the conductance rises drastically owing to photon stimulated excitation of the electrons and mainly due to interband transition. All these calculated compounds exhibit high optical conductivity, with Mg3BiBr3 and Mg3BiI3 showing comparatively lower conductivity than Mg3BiI3.
The reflectivity spectra R(ω) of the Mg3AB3 compounds in Fig. 6(e) indicates different behavior within the photon energies. The low reflectivity of Mg3NF3 is in concordance with the insulating nature, whereas Mg3BiBr3 and Mg3BiI3, which are semiconductors by behavior, have higher reflectivity than Mg3NF3, but quite perfect for absorbing materials in solar cell. The static values of optical reflectivity of Mg3AB3 compounds are summarized in Table 5 and the highest value is 20% for Mg3BiI3. The reflectivity values in the visible spectrum follow the trend: Mg3NF3 > Mg3BiBr3 > Mg3BiI3. The static values of optical reflectivity of Mg3AB3 compounds are summarized in Table 5.
In Fig. 6(f) and (h) are depicted the extinction coefficient k(ω) and the refractive index n(ω) which describes the amount of incident photons that are absorbed and velocity of light in the material. Static and optical values of the refractive index for Mg3AB3 compounds are similar to the real part of the dielectric tensor, which are shown in Table 5. The extinction coefficient persists to be zero at within the energy band gap while the k(ω) values are high at the higher photon energies representing interband transitions.
The last one, depicted in Fig. 6(g), characterizes the energy loss L(ω) over the course of the interaction of the electromagnetic radiation with the material. Local maxima of L(ω) are found to be at 18.49 eV for Mg3NF3, at 19.49 eV for Mg3BiBr3, and 16.40 eV for Mg3BiI3, which are the points of peak energy losses in view of interaction with electrons.
In summary, the properties of the calculated compounds are comparable to those of well-known materials such as CH3NH3PbCl3, CsPbI3, and MAPbCl3,88–90 highlighting their potential as highly efficient materials for photovoltaic energy conversion. Optoelectronic performance in the order of Mg3BiBr3 and Mg3BiI3 is shown to be excellent, including a high light absorption coefficient and optical conductivity, low optical reflectivity, and a suitable band gap. Finally, their properties make them highly attractive for photovoltaic applications. Overall, the non-toxicity, thermal stability, and mechanical stability of Mg3AB3 compounds offer significant advantages, highlighting their potential for use in environmentally friendly optoelectronic devices. In future studies, we recommend exploring the light absorption spectra of these materials using advanced methods, such as the Bethe–Salpeter Equation (BSE) combined with the GW method, to achieve more precise results.91–93
3.5 Thermal properties
The thermal properties of Mg3AB3 (A = N, Bi; B = F, Br, I), such as lattice thermal conductivity, melting temperature, minimum of thermal conductivity, and Grüneisen parameters are investigated, which give a clear understanding of thermal characteristics. In cubic crystals like the perovskite structure, the melting temperature can be predicted using the empirical formula developed by Fine et al.,94 which depends on the single crystal elastic constant:| Tm(K) = 553 + (5.911)C11 | (19) |
The calculated melting temperatures for Mg3AB3 (A = N, Bi; B = F, Br, I) are given in Table 6 below where it is observed that all the compounds exhibit a decreasing trend in their melting temperatures as the composition varies. The thermal conductivity of a system depends on atomic interactions, and the minimum thermal conductivity represents the theoretical lower limit of intrinsic thermal conductivity, calculated using the formula:95
 | (20) |
| Compounds | γ | Cp (J mol−1 K−1) | Cv (J mol−1 K−1) | Kmin (W m−1 K−1) | Kph (W m−1 K−1) | Tm (K) |
|---|---|---|---|---|---|---|
| Mg3NF3 | 1.301 | 89.45 | 89.22 | 1.64 | 75.51 | 2045.633 |
| Mg3BiBr3 | 1.408 | 120.86 | 120.21 | 0.39 | 9.92 | 1004.421 |
| Mg3BiI3 | 1.683 | 123.83 | 121.87 | 0.29 | 4.36 | 937.761 |
We have obtained that the minimum of the thermal conductivity of Mg3BiB3 and Mg3BiI3 is lower than that of Mg3NF3. Thermal conductivity is another material property that has to be low when it comes to application in coatings for thermal protection which are called thermal barrier coatings (TBC).
For perovskite materials, knowledge of the lattice thermal conductivity Kph is critical because it is implicated in heat dissipation and device efficiency. The empirical Slack model, which is valid for applications involving crystalline materials where phonon edge scattering controls thermal conduction, is used to determine Kph. The formula is:96
 | (21) |
As seen in Table 6, the Grüneisen parameter for all Mg3AB3 compounds is moderate. The estimates of lattice thermal conductivity of Mg3AB3 perovskite phases at 300 K are presented in Table 6, whereas the dependence on T is shown in Fig. 7.
 | ||
| Fig. 7 The temperature-dependent specific heats (a) Cv at constant volume (b) Cp at constant pressure and (c) lattice thermal conductivity of Mg3AB3 (A = N, Bi; B = F, Br, I) perovskite compounds. | ||
The lattice thermal conductivity of all three compound decreases with increasing temperature; however, Kph for Mg3NF3 starts at a much higher value and decreases slowly with temperature; Mg3BiBr3 and Mg3BiI3, on the other hand, experience a relatively steeper drop at low temperatures. As for the Kph, it is increased with the increasing of temperature but not as much as the initial values of Mg3NF3.
A thermal property of metal is specific heat whereby variation has a profound effect on casting and heat treatment among other operations as it defines the heat needed. Heat capacity is a thermodynamic property that quantifies the amount of heat required to change the temperature of a material by a given amount. When heat is supplied to a substance, the temperature of the material rises to levels corresponding to the heat. Fig. 7(b) and (c) depicts the Cv and Cp of states at the temperature range of 0 to 1200 K. The result of the increase in certain heat with temperature is thermal softening. Like for Mg3BiBr3 and Mg3BiI3, the Cv and Cp rise steeply in the 0–100 K range and for Mg3NF3 at the 0–900 K range. The high-temperature values are close to Dulong Petit (DP) limit but lower than Dulong Petit limit at all temperatures with the exception of the lowest one. Compared with Cp, the DP model97,98 predicts slightly lower Cp at high temperatures by 2.9–3.9% at 1200 K. Such behavior associates this material with conventional solids, were anharmonic effects impact Cp at elevated temperatures. The heat capacity values at 300 K are given in the Table 6. Based on the computations we did, Mg3NF3 has relatively low phonon mean free path and substantial lattice thermal conductivity and a high melting temperature meaning that it can effectively be used as heat sink material. These properties are similar to those of Ti2BC,99 another material that is believed to act as a good heat sink. On the other hand, while the minimum thermal conductivity (Kmin) values of the Mg3BiI3 and Mg3BiBr3 are low, they can be apt for use as thermal barrier coating (TBC) materials, however further experimental and details study need to fully understand these applications. The obtained Kmin values correlate well with the Kmin of other reference TBC materials, Y4Al2O9 (ref. 100) and Yb2SiO5.101 This similarity further highlights their usefulness in the high-temperature systems where effective thermal protection is needed.
4 Conclusion
The structural, mechanic, electrical, optical, and thermal characteristics of Mg3AB3 (A = N, Bi; B = F, Br, I) perovskite have been investigated employing density functional theory (DFT). Both structural and thermodynamic studies substantiate the stability of these materials. Mechanical characterization from analysis shows that Mg3BiI3 is very ductile and easy to work while, Mg3BiBr3 and Mg3BiI3 are more brittle with moderate hardness. Band structure electronic calculations show that Mg3NF3 has a wide direct band gap that qualifies it as an insulator whereas Mg3BiBr3 and Mg3BiI3 possess indirect bandgaps suitable for semiconductor optoelectronic devices. While indirect bandgaps can result in slightly lower absorption efficiency compared to direct bandgap materials, many successful photovoltaic materials, like silicon, also have indirect bandgaps and perform well. The bandgaps of Mg3BiI3 (0.867 eV) and Mg3BiBr3 (1.626 eV) fall outside the ideal range for single-junction solar cells (1.1–1.4 eV) but still allow for efficient photon absorption and energy conversion, with Mg3BiBr3 being closer to the optimal range. These bandgaps make Mg3BiI3 a potential bottom cell material in tandem solar cells, while Mg3BiBr3, being near the ideal limit, could contribute to enhanced efficiency. The optical analysis for Mg3NF3 shows low conductivity because of the insulating properties, in contrast, Mg3BiBr3 and Mg3BiI3 exhibit significant light-harvesting capabilities due to their pronounced interband transitions, high absorption coefficient, moderate reflectivity, relatively high conductivity and reduced optical losses, which underscoring their suitability for optoelectronic devices, particularly solar cells. Thermal characterization studies place Mg3NF3 as a candidate for heat sink applications while Mg3BiBr3 and Mg3BiI3 with low thermal conductivity are suitable for thermal barrier coatings. These compounds appear to offer high optical activity, suitable electronic band gaps and chemical stability. Unlike traditional lead-based perovskites, Mg3AB3 compounds are environmentally friendly and renewable which makes their usage more suitable in the future generations of solar cells. This work highly recommends the use of Mg3BiB3 and Mg3BiI3 in photovoltaic technologies due to their high absorption, low reflectivity, and closeness to the ideal bandgap incurred in photovoltaic applications. Therefore, further research is needed to validate such techniques and to explore how the applicability of these techniques might be promoted.Consent for publication
All authors of this work have agreed and are ready to sign the transfer of copyright which empowers the publisher to protect the work against unauthorized use and to maintain the integrity of the work from a bibliographical and archival standpoint.Data availability
All data are available in the manuscript.Author contributions
Mayeen Uddin Khandaker and M. M. Uddin: conceptualization, writing of original draft, and reviewing and editing of the manuscript; Hamid Osman and Shams Issa: simulation, software and validation, and writing of original draft, Md. Habib Ullah, Hajir Wahbi and M. Y. Hanfi: model calculation, discussion and validation, and reviewing of the manuscript.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
The authors extend their appreciation to the Deanship of Scientific Research at Northern Border University, Arar, KSA for funding this research work through project number “NBU-FFR-2025-2916-04”. During the preparation of this work, the authors used some online services (Gemini, Grammarly) to improve language and readability. After using this tool/service, the authors reviewed and edited the content as needed and took full responsibility for the content of the publication.References
- K. Liu, B. Chen, Z. J. Yu, Y. Wu, Z. Huang and X. Jia, et al., Reducing sputter induced stress and damage for efficient perovskite/silicon tandem solar cells, J. Mater. Chem. A, 2022, 10, 1343–1349, 10.1039/D1TA09143C.
- J. P. Thomas and K. T. Leung, Defect-Minimized PEDOT:PSS/Planar-Si Solar Cell with Very High Efficiency, Adv. Funct. Mater., 2014, 24, 4978–4985, DOI:10.1002/adfm.201400380.
- A. Hossain, M. A. Ali, M. M. Uddin, S. H. Naqib and M. M. Hossain, Theoretical studies on phase stability, electronic, optical, mechanical and thermal properties of chalcopyrite semiconductors HgXN2 (X=Si, Ge and Sn): A comprehensive DFT analysis, Mater. Sci. Semicond. Process., 2024, 172, 108092, DOI:10.1016/j.mssp.2023.108092.
- J. P. Wilcoxon, G. A. Samara and P. N. Provencio, Optical and electronic properties of Si nanoclusters synthesized in inverse micelles, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 60, 2704–2714, DOI:10.1103/PhysRevB.60.2704.
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, Organometal Halide Perovskites as Visible-Light Sensitizers for Photovoltaic Cells, J. Am. Chem. Soc., 2009, 131, 6050–6051, DOI:10.1021/ja809598r.
- S. D. Stranks, G. E. Eperon, G. Grancini, C. Menelaou, M. J. P. Alcocer and T. Leijtens, et al., Electron-Hole Diffusion Lengths Exceeding 1 Micrometer in an Organometal Trihalide Perovskite Absorber, Science, 2013, 342, 341–344, DOI:10.1126/science.1243982.
- G. E. Eperon, S. D. Stranks, C. Menelaou, M. B. Johnston, L. M. Herz and H. J. Snaith, Formamidinium lead trihalide: a broadly tunable perovskite for efficient planar heterojunction solar cells, Energy Environ. Sci., 2014, 7, 982–988, 10.1039/C3EE43822H.
- M. R. Sabour, M. A. Jafari and S. M. Hosseini Gohar, Si-based Solar Cells' Conversion Efficiency Related Publications Bibliometric Review During 2000-2017, Silicon, 2020, 12, 2705–2720, DOI:10.1007/s12633-019-00366-4.
- F. Hao, C. C. Stoumpos, D. H. Cao, R. P. H. Chang and M. G. Kanatzidis, Lead-free solid-state organic–inorganic halide perovskite solar cells, Nat. Photonics, 2014, 8, 489–494, DOI:10.1038/nphoton.2014.82.
- S. Niu, H. Huyan, Y. Liu, M. Yeung, K. Ye, L. Blankemeier, T. Orvis, D. Sarkar, D. J. Singh, R. Kapadia and J. Ravichandran, Band-Gap Control via Structural and Chemical Tuning of Transition Metal Perovskite Chalcogenides, Adv. Mater., 2017, 29, 1604733, DOI:10.1002/adma.201604733.
- A. Ghosh, M. F. Rahman, M. R. Islam, M. S. Islam, M. Amami, M. K. Hossain and A. B. M. Ismail, Heliyon, 2023, 9(8), e19271, DOI:10.1016/j.heliyon.2023.e19271.
- Md. S. Islam, Md. F. Rahman, Md. R. Islam, A. Ghosh, Md. A. Monnaf and Md. S. Reza, et al., An in-depth analysis of how strain impacts the electronic, optical, and output performance of the Ca3NI3 novel inorganic halide perovskite, J. Phys. Chem. Solids, 2024, 185, 111791, DOI:10.1016/j.jpcs.2023.111791.
- Md. F. Rahman, Md. H. Rahman, Md. R. Islam, M. K. Hossain, A. Ghosh and Md. S. Islam, et al., The optical and electronic properties of inorganic halide perovskite Sr3NCl3 under applied biaxial strain, J. Mater. Sci., 2023, 58, 13100–13117, DOI:10.1007/s10853-023-08825-5.
- Md. S. Islam, Md. F. Rahman, Md. R. Islam, Q. Mahmood, M. m. Al-Anazy and Md. Z. Hasan, et al., Investigation strain effects on the electronic, optical, and output performance of the novel inorganic halide perovskite Sr3SbI3 solar cell, Chin. J. Phys., 2024, 88, 270–286, DOI:10.1016/j.cjph.2024.01.011.
- M. A. B. Shanto, M. F. Rahman, M. R. Islam, A. Ghosh, A. Azzouz-Rached and H. Albalawi, et al., Investigating how the electronic and optical properties of a novel cubic inorganic halide perovskite, Sr3NI3 are affected by strain, F1000Research, 2023, 12, 1005, DOI:10.12688/f1000research.137044.1.
- A. Ghosh, Md. Ferdous Rahman, A. Kuddus, M. K. A. Mohammed, Md. Rasidul Islam and S. Bhattarai, et al., Investigating of novel inorganic cubic perovskites of A3BX3 (A=Ca, Sr, BP, As, X=I, Br) and their photovoltaic performance with efficiency over 28%, J. Alloys Compd., 2024, 986, 174097, DOI:10.1016/j.jallcom.2024.174097.
- A. Ghosh, M. F. Rahman, M. R. Islam, M. S. Islam, M. K. Hossain and S. Bhattarai, et al., Structural, electronic and optical characteristics of inorganic cubic perovskite Sr3AsI3, Opt. Continuum, 2023, 2, 2144–2153, DOI:10.1364/OPTCON.495816.
- M. F. Rahman, M. Harun-Or-Rashid, M. R. Islam, A. Ghosh, M. K. Hossain and S. Bhattarai, et al., Exploring the impact of strain on the electronic and optical properties of inorganic novel cubic perovskite Sr3PI3, Phys. Scr., 2023, 98, 115105, DOI:10.1088/1402-4896/acfce9.
- M. A. Green, Y. Jiang, A. M. Soufiani and A. Ho-Baillie, Optical Properties of Photovoltaic Organic–Inorganic Lead Halide Perovskites, J. Phys. Chem. Lett., 2015, 6, 4774–4785, DOI:10.1021/acs.jpclett.5b01865.
- J. Deng, J. Li, Z. Yang and M. Wang, All-inorganic lead halide perovskites: a promising choice for photovoltaics and detectors, J. Mater. Chem. C, 2019, 7, 12415–12440, 10.1039/C9TC04164H.
- S. Bouhmaidi, R. K. Pingak and L. Setti, First-principles investigation of electronic, elastic, optical and thermoelectric properties of strontium-based anti-perovskite Sr3MN (M= P and As) for potential applications in optoelectronic and thermoelectric devices, Moroccan J. Chem., 2023, 11(4), 1254–1265, DOI:10.48317/IMIST.PRSM/morjchem-v11i04.41366.
- A. Sedky, A. Hakamy, N. Afify, S. Bouhmaidi, L. Setti and D. Hamad, et al., Comparative investigation of structural, photoluminescence, and magnetic characteristics of MxSn1−xOy nanocomposites, Appl. Phys. A, 2023, 129, 669, DOI:10.1007/s00339-023-06941-2.
- J. Qian, B. Xu and W. Tian, A comprehensive theoretical study of halide perovskites ABX3, Org. Electron., 2016, 37, 61–73, DOI:10.1016/j.orgel.2016.05.046.
- P. Ramasamy, D.-H. Lim, B. Kim, S.-H. Lee, M.-S. Lee and J.-S. Lee, All-inorganic cesium lead halide perovskite nanocrystals for photodetector applications, Chem. Commun., 2016, 52, 2067–2070, 10.1039/C5CC08643D.
- G. Nawab, A. U. Rahman, I. U. Haq, A. Ali, A. Abdelkader and A. H. Ismail, et al., Structural and optoelectronic properties of 2D halide perovskites Cs2MBr4 (M = Zn, Cd, Hg): a first principle study, Opt. Quantum Electron., 2024, 56, 871, DOI:10.1007/s11082-024-06710-2.
- I. U. Haq, A. Ali, A. AbdelKader, A. H. Ismail, M. Alomar and I. Khan, Ground state structure and optoelectronic properties of novel quasi-2D layered halide perovskites CsPb2X5 (X= Cl, Br, I) via first principle calculations, Mater. Sci. Semicond. Process., 2024, 176, 108326, DOI:10.1016/j.mssp.2024.108326.
- M. Pandey, K. W. Jacobsen and K. S. Thygesen, Band Gap Tuning and Defect Tolerance of Atomically Thin Two-Dimensional Organic–Inorganic Halide Perovskites, J. Phys. Chem. Lett., 2016, 7, 4346–4352, DOI:10.1021/acs.jpclett.6b01998.
- B. He, L. Liu, J. Hu, S. Nie, Y. Chen and Y. Chen, The properties of perovskite solar cells with novel MAPbBr3/CsPbBr3 double absorber, J. Phys. D: Appl. Phys., 2022, 56, 015107, DOI:10.1088/1361-6463/ac9ce5.
- S. Baruah, J. Borah, B. Vandana, S. Simran, M. Nagendra and S. Rajasekaran, Improvement of photovoltaic response in perovskite solar cell via all inorganic lead free cubic double La2NiMnO6/Cs3Bi2I9 based graded absorber architecture, Opt. Quantum Electron., 2024, 56, 1321, DOI:10.1007/s11082-024-07239-0.
- Md. F. Rahman, M. J. A. Habib, Md. H. Ali, M. H. K. Rubel, Md. R. Islam and A. B. Md. Ismail, et al., Design and numerical investigation of cadmium telluride (CdTe) and iron silicide (FeSi2) based double absorber solar cells to enhance power conversion efficiency, AIP Adv., 2022, 12, 105317, DOI:10.1063/5.0108459.
- M. Roknuzzaman, K. Ostrikov and H. Wang, et al., Towards lead-free perovskite photovoltaics and optoelectronics by ab-initio simulations, Sci. Rep., 2017, 7, 14025 CrossRef PubMed , https://www.nature.com/articles/s41598-017-13172-y.
- M. E. Emetere, O. O. Bello and S. A. Afolalu, Enhancement of novel NaZnBr3 perovskite for solar cells application, Energy Rep., 2022, 8, 4453–4460, DOI:10.1016/j.egyr.2022.03.087.
- M. Sadia Islam Ria, A. Ghosh, Md. Azizur Rahman, J. Y. Al-Humaidi, N. S. Awwad and H. A. Ibrahium, et al., Examining anion influence on the physical properties and performance analysis of lead-free calcium-based Ca3NX3 (X=F, Cl, Br and I) perovskite, Mater. Sci. Eng., B, 2024, 310, 117674, DOI:10.1016/j.mseb.2024.117674.
- I. K. G. G. Apurba, M. R. Islam, M. S. Rahman, M. F. Rahman and S. Ahmad, Exploring the inorganic perovskite materials Mg3SbX3 (Where, X=I, Br, Cl and F) through the perspective of density functional theory: Adjustment of physical characteristics as consequence of strain, Heliyon, 2024, 10(20), e39218, DOI:10.1016/j.heliyon.2024.e39218.
- A. Hosen, Md. A. Hossain, M. S. Abu-Jafar, R. K. Pingak and A. A. Mousa, Unraveling lead-free Fr-based perovskites FrQCl3 (Q = Ca, Sr) and their pressure induced physical properties: DFT analysis for advancing optoelectronic performance, J. Phys. Chem. Solids, 2024, 193, 112211, DOI:10.1016/j.jpcs.2024.112211.
- H. Akter, M. A. Ali, M. M. Hossain, M. M. Uddin and S. H. Naqib, Oxysulfide perovskites: reduction of the electronic band gap of RbTaO3 by sulfur substitution, Phys. Scr., 2024, 99, 045950, DOI:10.1088/1402-4896/ad31f3.
- S. Tariq, O. Alsalmi, A. O. Alrashdi, A. A. Mubarak and B. Kanwal, Investigating the influence of pressure on SrFeO3 and SrMnO3 ferromagnets for high-pressure spintronic devices: a comparative DFT overview, Appl. Phys. A, 2021, 127, 902, DOI:10.1007/s00339-021-05052-0.
- S. S. A. Gillani, R. Ahmad, M. Rizwan, M. Rafique, G. Ullah and C. B. Cao, et al., Effect of magnesium doping on band gap and optical properties of SrZrO3 perovskite: A first-principles study, Optik, 2019, 191, 132–138, DOI:10.1016/j.ijleo.2019.05.099.
- A. Hosen, Investigating the effects of hydrostatic pressure on the physical properties of cubic Sr3BCl3 (B = As, Sb) for improved optoelectronic applications: A DFT study, Heliyon, 2024, 10(16), e35855, DOI:10.1016/j.heliyon.2024.e35855.
- A. Hosen, M. R. Islam and J. Park, Pressure-Induced Band Gap Shifting from Ultra-violet to Visible Spectrum of Non-toxic RbCaBr3 Cubic Perovskite for Enhancing Optoelectronic Applications, J. Inorg. Organomet. Polym. Mater., 2024, 34, 2378–2387, DOI:10.1007/s10904-023-02970-9.
- A. A. Mubarak and S. Tariq, Elucidating the effect of Pb and Ba substitution in SrTcO3 for advanced radioactive semiconducting applications, Opt. Quantum Electron., 2023, 55, 614, DOI:10.1007/s11082-023-04891-w.
- N. H. Linh, N. H. Tuan, D. D. Dung, P. Q. Bao, B. T. Cong and L. T. H. Thanh, Alkali metal-substituted bismuth-based perovskite compounds: A DFT study, J. Sci.:Adv. Mater. Devices, 2019, 4, 492–498, DOI:10.1016/j.jsamd.2019.06.005.
- Y. Shi, Z. Ma, D. Zhao, Y. Chen, Y. Cao, K. Wang, G. Xiao and B. Zou, Pressure-Induced Emission (PIE) of One-Dimensional Organic Tin Bromide Perovskites, J. Am. Chem. Soc., 2019, 141(16), 6504–6508, DOI:10.1021/jacs.9b02568.
- Z. Ma, Z. Liu, S. Lu, L. Wang, X. Feng and D. Yang, et al., Pressure-induced emission of cesium lead halide perovskite nanocrystals, Nat. Commun., 2018, 9, 4506, DOI:10.1038/s41467-018-06840-8.
- Y. Fang, L. Zhang, L. Wu, J. Yan, Y. Lin and K. Wang, et al., Pressure-Induced Emission (PIE) and Phase Transition of a Two-dimensional Halide Double Perovskite (BA)4AgBiBr8 (BA=CH3(CH2)3NH3+), Angew. Chem., Int. Ed., 2019, 58, 15249–15253, DOI:10.1002/anie.201906311.
- Y. Wang, X. Lü, W. Yang, T. Wen, L. Yang and X. Ren, et al., Pressure-Induced Phase Transformation, Reversible Amorphization, and Anomalous Visible Light Response in Organolead Bromide Perovskite, J. Am. Chem. Soc., 2015, 137, 11144–11149, DOI:10.1021/jacs.5b06346.
- M. Saeed, M. A. Ali, S. Murad, R. Ullah, T. Alshahrani and A. Laref, et al., Pressure induced structural, electronic, optical and thermal properties of CsYbBr3, a theoretical investigation, J. Mater. Res. Technol., 2021, 10, 687–696, DOI:10.1016/j.jmrt.2020.12.052.
- Q. Ou, X. Bao, Y. Zhang, H. Shao, G. Xing and X. Li, et al., Band structure engineering in metal halide perovskite nanostructures for optoelectronic applications, Nano Mater. Sci., 2019, 1, 268–287, DOI:10.1016/j.nanoms.2019.10.004.
- Md. A. Rahman, R. Khatun, R. Ferdous, D. Chandra Roy, Md. Z. Hasan and A. Irfan, et al., First-principles calculations to investigate structural, elastic, electronic, optical and thermal properties of La-based ternary intermetallic superconductors LaM2Si2 (M=Co, Cu, Rh, Pd, Ag, Ir, Pt, Au), J. Mater. Res. Technol., 2023, 26, 3840–3862, DOI:10.1016/j.jmrt.2023.08.177.
- M. Atikur Rahman, M. Hasan, J. F. Lubna, R. Khatun, S. Sarker and M. Z. Hasan, et al., Comparative study of the structural, mechanical, electronic, optical and thermodynamic properties of superconducting disilicide YT2Si2 (T=Co, Ni, Ru, Rh, Pd, Ir) by DFT simulation, J. Phys. Chem. Solids, 2023, 178, 111342, DOI:10.1016/j.jpcs.2023.111342.
- M. M. H. Babu, T. Saha, J. Podder, P. Roy, A. Barik and E. Haque, Electronic structure transition of cubic CsSnCl3 under pressure: effect of rPBE and PBEsol functionals and GW method, Heliyon, 2021, 7(8), e07796, DOI:10.1016/j.heliyon.2021.e07796.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli and M. Calandra, et al., Advanced capabilities for materials modelling with Quantum ESPRESSO, J. Phys.: Condens. Matter, 2017, 29, 465901, DOI:10.1088/1361-648X/aa8f79.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car and C. Cavazzoni, et al., QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21, 395502, DOI:10.1088/0953-8984/21/39/395502.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, Hybrid functionals based on a screened Coulomb potential, J. Chem. Phys., 2003, 118, 8207–8215, DOI:10.1063/1.1564060.
- A. Togo and I. Tanaka, First principles phonon calculations in materials science, Scr. Mater., 2015, 108, 1–5, DOI:10.1016/j.scriptamat.2015.07.021.
- A. D. Corso, Thermo Pw Driver v.1.7.0, 2023, Welcome to Thermo_pw, https://dalcorso.github.io/thermo_pw/, accessed February 23, 2024 Search PubMed.
- O. H. Nielsen and R. M. Martin, First-Principles Calculation of Stress, Phys. Rev. Lett., 1983, 50, 697–700, DOI:10.1103/PhysRevLett.50.697.
- H.-J. Feng and Q. Zhang, Predicting efficiencies >25% A3MX3 photovoltaic materials and Cu ion implantation modification, Appl. Phys. Lett., 2021, 118, 111902, DOI:10.1063/5.0039936.
- M. A. Brogan, R. W. Hughes, R. I. Smith and D. H. Gregory, Structural studies of magnesium nitride fluorides by powder neutron diffraction, J. Solid State Chem., 2012, 185, 213–218, DOI:10.1016/j.jssc.2011.11.008.
- M. W. Qureshi, X. Ma, G. Tang and R. Paudel, Ab initio predictions of structure and physical properties of the Zr2GaC and Hf2GaC MAX phases under pressure, Sci. Rep., 2021, 11, 3260, DOI:10.1038/s41598-021-82402-1.
- W. Shangguan, C. Yan and J. Cai, Quasi-Planar tetracoordiante carbon Networks with tunable electronic properties combined with Ultra-High carrier mobility and optical absorption Coefficient: Two-dimensional Be2C, Appl. Surf. Sci., 2022, 604, 154644, DOI:10.1016/j.apsusc.2022.154644.
- L. Liu, C. Yan, L. Gao, W. Shangguan, J. Dai and J. Cai, Structural stabilities, electronic structures, photocatalysis and optical properties of γ-GeN and α-SnP monolayers: a first-principles study, Mater. Res. Express, 2021, 8, 125010, DOI:10.1088/2053-1591/ac3fdc.
- O. Reckeweg and F. J. DiSalvo, About Binary and Ternary Alkaline Earth Metal Nitrides, Z. Anorg. Allg. Chem., 2001, 627, 371–377, DOI:10.1002/1521-3749(200103)627:3<371::AID-ZAAC371>3.0.CO;2-A.
- A. Bach, D. Fischer, X. Mu, W. Sigle, P. A. van Aken and M. Jansen, Structural evolution of magnesium difluoride: from an amorphous deposit to a new polymorph, Inorg. Chem., 2011, 50, 1563–1569, DOI:10.1021/ic1021615.
- E. Zintl and E. Husemann, Bindungsart und Gitterbau binärer Magnesiumverbindungen, Z. Phys. Chem., 1933, 21, 138–155, DOI:10.1515/zpch-1933-2112.
- C. M. Widdifield and D. L. Bryce, Crystallographic structure refinement with quadrupolar nuclei: a combined solid-state NMR and GIPAW DFT example using MgBr2, Phys. Chem. Chem. Phys., 2009, 11, 7120–7122, 10.1039/B911448N.
- M. A. Brogan, A. J. Blake, C. Wilson and D. H. Gregory, Magnesium diiodide, MgI2, Acta Crystallogr., Sect. C:Cryst. Struct. Commun., 2003, 59, i136–i138, DOI:10.1107/S0108270103025769.
- M. A. Brogan, R. W. Hughes, R. I. Smith and D. H. Gregory, Structural studies of magnesium nitride fluorides by powder neutron diffraction, J. Solid State Chem., 2012, 185, 213–218, DOI:10.1016/j.jssc.2011.11.008.
- S. Baroni, S. de Gironcoli, A. Dal Corso and P. Giannozzi, Phonons and related crystal properties from density-functional perturbation theory, Rev. Mod. Phys., 2001, 73, 515–562, DOI:10.1103/RevModPhys.73.515.
- A. Togo and I. Tanaka, First principles phonon calculations in materials science, Scr. Mater., 2015, 108, 1–5, DOI:10.1016/j.scriptamat.2015.07.021.
- N. T. Mahmoud, A. A. Mousa and J. M. Khalifeh, First principles investigation of thermoelectric and mechanical properties of VScO3 semiconductor perovskite for sustainable and renewable energy, Results Phys., 2020, 18, 103331, DOI:10.1016/j.rinp.2020.103331.
- H. Liu, J. Yang, Y. Jia, Z. Wang, M. Jiang and K. Shen, et al., Significant Improvement of Catalytic Performance for Chlorinated Volatile Organic Compound Oxidation over RuOx Supported on Acid-Etched Co3O4, Environ. Sci. Technol., 2021, 55, 10734–10743, DOI:10.1021/acs.est.1c02970.
- J. Liu, Y. Yin, K. Wang, P. Wei, H. Lu and C. Song, et al., Domain size control in all-polymer solar cells, iScience, 2022, 25, 104090, DOI:10.1016/j.isci.2022.104090.
- C. M. Zener and S. Siegel, Elasticity and Anelasticity of Metals, ACS Publications, 2002, DOI:10.1021/j150474a017.
- W. Azeem, S. Hussain, M. K. Shahzad, F. Azad, G. Khan and V. Tirth, et al., Computational insights of double perovskite X2CaCdH6 (X = Rb and Cs) hydride materials for hydrogen storage applications: A DFT analysis, Int. J. Hydrogen Energy, 2024, 79, 514–524, DOI:10.1016/j.ijhydene.2024.07.044.
- M. Caid, D. Rached, Y. Rached and H. Rached, Comprehensive exploration of halide double perovskites Cs2B′GeCl6 (B′: Zn, Cd) for affordable energy technologies: a high-throughput investigation, Opt. Quantum Electron., 2024, 56, 980, DOI:10.1007/s11082-024-06721-z.
- S. Hussain and J. U. Rehman, First-principles calculation to investigate structural, electronic, optical, and thermodynamics properties of perovskite KXO3 (KTa and Zn) alloys for photovoltaic and smart window applications, Phys. B, 2024, 687, 416116, DOI:10.1016/j.physb.2024.416116.
- D. Music, Z. Sun, R. Ahuja and J. M. Schneider, Electronic structure of M2AlC(0001) surfaces (M = Ti,V,Cr), J. Phys.: Condens. Matter, 2006, 18, 8877, DOI:10.1088/0953-8984/18/39/017.
- N. Miao, B. Sa, J. Zhou and Z. Sun, Theoretical investigation on the transition-metal borides with Ta3B4-type structure: A class of hard and refractory materials, Comput. Mater. Sci., 2011, 50, 1559–1566, DOI:10.1016/j.commatsci.2010.12.015.
- X.-Q. Chen, H. Niu, D. Li and Y. Li, Modeling hardness of polycrystalline materials and bulk metallic glasses, Intermetallics, 2011, 19, 1275–1281, DOI:10.1016/j.intermet.2011.03.026.
- C. Jasiukiewicz and V. Karpus, Debye temperature of cubic crystals, Solid State Commun., 2003, 128, 167–169, DOI:10.1016/j.ssc.2003.08.008.
- O. L. Anderson, A simplified method for calculating the debye temperature from elastic constants, J. Phys. Chem. Solids, 1963, 24, 909–917, DOI:10.1016/0022-3697(63)90067-2.
- E. Schreiber, O. L. Anderson, N. Soga and J. F. Bell, Elastic Constants and Their Measurement, J. Appl. Mech., 1975, 42, 747–748, DOI:10.1115/1.3423687.
- P. Deus and H. A. Schneider, Estimation of the debye temperature of diamond-like semiconducting compounds from bulk modul and microhardness, Cryst. Res. Technol., 1983, 18, 491–500, DOI:10.1002/crat.2170180410.
- Y. Zhang, First-principles Debye–Callaway approach to lattice thermal conductivity, Journal of Materiomics, 2016, 2, 237–247, DOI:10.1016/j.jmat.2016.06.004.
- M. Khalid Hossain, A. A. Arnab, R. C. Das, K. M. Hossain, M. H. K. Rubel and M. Ferdous Rahman, et al., Combined DFT, SCAPS-1D, and wxAMPS frameworks for design optimization of efficient CsBiAgI6-based perovskite solar cells with different charge transport layers, RSC Adv., 2022, 12, 35002–35025, 10.1039/D2RA06734J.
- K.-E. Peiponen, V. Lucarini, E. M. Vartiainen and J. J. Saarinen, Kramers-Kronig relations and sum rules of negative refractive index media, Eur. Phys. J. B, 2004, 41, 61–65, DOI:10.1140/epjb/e2004-00294-6.
- A. Hossain, M. A. Ali, M. M. Uddin, S. H. Naqib and M. M. Hossain, Theoretical studies on phase stability, electronic, optical, mechanical and thermal properties of chalcopyrite semiconductors HgXN2 (X=Si, Ge and Sn): A comprehensive DFT analysis, Mater. Sci. Semicond. Process., 2024, 172, 108092, DOI:10.1016/j.mssp.2023.108092.
- T. Baikie, N. S. Barrow, Y. Fang, P. J. Keenan, P. R. Slater and R. O. Piltz, et al., A combined single crystal neutron/X-ray diffraction and solid-state nuclear magnetic resonance study of the hybrid perovskites CH3NH3PbX3 (X = I, Br and Cl), J. Mater. Chem. A, 2015, 3, 9298–9307, 10.1039/C5TA01125F.
- E. Mosconi, P. Umari and F. D. Angelis, Electronic and optical properties of MAPbX3 perovskites (X = I, Br, Cl): a unified DFT and GW theoretical analysis, Phys. Chem. Chem. Phys., 2016, 18, 27158–27164, 10.1039/C6CP03969C.
- T. Yang, C. Yan, S. Qiu, Y. Tang, A. Du and J. Cai, First-Principles Study of Penta-PtXY (X = Se, Te; Y = S, Te; X ≠ Y) Monolayer with Highly Anisotropic Electronic and Optical Properties, ACS Omega, 2024, 9, 32502–32512, DOI:10.1021/acsomega.4c00803.
- W. Shangguan, C. Yan, W. Li, C. Long, L. Liu and C. Qi, et al., Two-dimensional semiconductor materials with high stability and electron mobility in group-11 chalcogenide compounds: MNX (M = Cu, Ag, Au; N = Cu, Ag, Au; X = S, Se, Te; M ≠ N), Nanoscale, 2022, 14, 4271–4280, 10.1039/D1NR06971C.
- C. Qi, C. Yan, Q. Li, T. Yang, S. Qiu and J. Cai, Two-dimensional Janus chalcogenides: candidates for efficient photocatalysts and piezoelectric materials, J. Mater. Chem. A, 2024, 12, 3542–3556, 10.1039/D3TA06340B.
- M. E. Fine, L. D. Brown and H. L. Marcus, Elastic constants versus melting temperature in metals, Scr. Metall., 1984, 18, 951–956, DOI:10.1016/0036-9748(84)90267-9.
- D. R. Clarke, Materials selection guidelines for low thermal conductivity thermal barrier coatings, Surf. Coat. Technol., 2003, 163–164, 67–74, DOI:10.1016/S0257-8972(02)00593-5.
- G. A. Slack, The Thermal Conductivity of Nonmetallic Crystals, in Solid State Physics, ed. Ehrenreich H., Seitz F. and Turnbull D., Academic Press, 1979, vol. 34, pp. 1–71, DOI:10.1016/S0081-1947(08)60359-8.
- M. Sarwan, V. A. Shukoor, M. F. Shareef and S. Singh, A first principle study of structural, elastic, electronic and thermodynamic properties of Half-Heusler compounds; YNiPn (Pn=As, sb, and bi), Solid State Sci., 2021, 112, 106507, DOI:10.1016/j.solidstatesciences.2020.106507.
- H. Akter, M. M. Hossain, M. M. Uddin, S. H. Naqib and M. A. Ali, Effects of S substitution on the structural, optoelectronic, and thermomechanical properties of KTaO3 through density functional theory, J. Phys. Chem. Solids, 2024, 190, 112021, DOI:10.1016/j.jpcs.2024.112021.
- R. Islam, M. M. Hossain, M. A. Ali, M. M. Uddin and S. H. Naqib, Metallic boro-carbides of A2BC (A = Ti, Zr, Hf and W): a comprehensive theoretical study for thermo-mechanical and optoelectronic applications, RSC Adv., 2022, 12, 32994–33007, 10.1039/D2RA05448E.
- P. Debye, Zur Theorie der spezifischen Wärmen, Ann. Phys., 1912, 344, 789–839, DOI:10.1002/andp.19123441404.
- R. Fox, The Background to the Discovery of Dulong and Petit's Law, Br. J. Hist. Sci., 1968, 4, 1–22, DOI:10.1017/S0007087400003150.
| This journal is © The Royal Society of Chemistry 2025 |