DOI:
10.1039/D4RA08946D
(Paper)
RSC Adv., 2025,
15, 24639-24647
Enhancement of electrocaloric response and elevated energy-storage characteristics in lead-free BCTZ-ZN ceramics
Received
21st December 2024
, Accepted 28th June 2025
First published on 14th July 2025
Abstract
Recently, considerable focus has been on exploring the electrocaloric effect in environmentally friendly, lead-free ferroelectric materials. In this study, lead-free (Ba0.95Ca0.05)(Ti0.95Zr0.05)1−x(Zn1/3Nb2/3)xO3 (BCTZ-xZN) ceramics were investigated. X-ray diffraction (XRD) analysis confirmed the formation of a pure perovskite structure with a structural phase transition depending on ZN substitution. Dielectric measurements revealed a diffuse phase transition and a shift in Curie temperature with increasing x. The electrical energy storage density (Wrec) was found to be 150 mJ cm−3 with an efficiency of η = 83% for BCTZ-2.5ZN. At an electric field strength of 25 kV cm−1, a peak electrocaloric response of 0.68 K at 340 K was attained, with a corresponding electrocaloric responsivity of 0.27 K mm kV−1 observed at 340 K for BCTZ-2.5ZN. The electrocaloric effect, combined with a calculated coefficient of performance (COP) of 2, demonstrates the material's potential for both cooling and energy storage. These findings underscore BCTZ-xZN as a promising material for applications in cooling systems and energy storage for electronic devices, offering versatile properties conducive to cooling operations via an external electric field across various operating temperatures.
1. Introduction
Electrocaloric refrigeration, renowned for its cost-effectiveness, high efficiency, and eco-friendly nature, has gained notable attention as an emerging alternative technology for refrigeration and power generation for micro-electromechanical and micro-electronic systems.1–3 The electrocaloric effect (ECE) is defined as the adiabatic temperature/entropy change (ΔT/ΔS) of a ferroelectric material under an external electric field.4,5 ECE characterizes the correlation between electrical and thermal attributes within ferroelectric materials. It peaks at the critical point, where the compound undergoes a structural transition, primarily caused by compositional irregularities leading to structural instability and external factors such as the electric field and temperature.6 Extensive research has been conducted on thin films of lead zirconate titanate (PbZrTiO3)7 and ferroelectric polymers,8 showing an increase in ECE since the finding of a great ECE of ΔT = 12 K. P(VDF-TrFE) polymers exhibit an electrocaloric response at temperatures above 70 °C, and PbZr0.95Ti0.05O3 thin films operate at temperatures close to 222 °C, which limits their practical cooling applications. Various categories of ferroelectric materials, including ceramics, thin or thick films, single crystals, and polymers, were investigated for ECE research.9 The most significant ECE was noted in thin film samples,10,11 although they exhibit restricted heat extraction capability.12 Due to the greater cooling capacity of bulk ceramics compared to thin films, bulk materials represent a notable advancement over thin films for functional cooling applications.13,14 Furthermore, bulk ceramics have a higher electrocaloric responsivity (ξ = ΔT/ΔE) than polymers, thin films, and single crystals.15 Since in the ABO3 structure, hybridization between the B-site atom and the oxygen atom is one of the reasons for exhibiting a favorable electrocaloric effect, a compound with a smaller ion and greater charge exhibits a good ECE.16 Within the domain of ferroelectric materials, lead-based ceramics exhibit significant electrocaloric responsivity and an extensive temperature range for ΔT owing to the existence of the morphotropic phase region.17,18 Nonetheless, the utilization of lead-containing electrocaloric materials is limited due to concerns about lead toxicity. Thus, numerous lead-free ferroelectric ceramics based on BaTiO3, (Ba, Ca)TiO3,19 Ba(Ti, Zr)O3,20 and (Ba, Ca)(Ti, Sn)O3,21 have been studied to examine their electrocaloric response. Recently, Hana et al. investigated the incorporation of Sn ceramics and reported an electrocaloric responsivity of ΔT = 0.36 K, which was the highest value among all the studied compositions.22 Among all, lead-free ceramics such as (Ba1−xCax)(Zr0.05Ti0.95)O3 have exhibited the best electrocaloric effects, demonstrating remarkable energy storage properties, excellent piezoelectric characteristics, and higher polarization values compared to ceramics such as BaTiO3.23,24
H. Kaddoussi25 showed that increasing the Ca substitution reduces the electrocaloric effect, which highlights the advantage of a low Ca doping level (x = 0.05). More precisely, Ba0.95Ca0.05Ti0.95Zr0.05O3 (BCTZ) is a potential ferroelectric material with high remanent polarization and a low coercive field. In this regard, Tossaporn et al. documented that Ba0.95Ca0.05Zr0.05Ti0.95O3 ceramics demonstrate significant spontaneous polarization (Pr = 6.25 μC cm−2) and minimal coercive strength (Ec = 2.6 kV cm−1).26 Singh et al.27 reported a ΔT of 0.31 K under a 15 kV cm−1 electric field in BCTZ ceramics. Furthermore, owing to adjustable breakdown strength and their low remnant polarization diminished coercive field, relaxor ferroelectrics (RFEs)28,29 hold considerable potential in the realm of dielectric energy. Their electric polarization response can also be transformed into recoverable electrostatic energy. Moreover, by varying the applied electric field, various properties of BCTZ can be elicited. K. Xu et al. reported that BCTZ had a uniform microstructure and energy storage properties at 20 kV cm−1 (Wrec = 0.06 J cm−3 and η = 87.4%).30 Moreover, BCTZ ceramics possess significant electrical and energy storage properties at 60 kV cm−1 (Wrec = 0.12 J cm−3 and η = 51.3%) as evaluated by W. Cai et al.31 To improve ferroelectric and electrocaloric characteristics, the introduction of dopants into the atomic positions of the ABO3 framework is a potent method, enhancing chemical stability by alleviating localized strain and adjusting oxygen valence concentration through the balance of ionic charges. Additionally, dopants are added to improve the energy storage capabilities of ferroelectric materials. Recently, materials with remarkable thermal, frequency, and cycling stabilities such as BNT-25BT-Zn1/3Nb2/3 have shown promise as high-performance energy storage options.32
In this study, we have empirically investigated the electrocaloric reaction in eco-friendly (Ba0.95Ca0.05)(Ti0.95Zr0.05)1−x(Zn1/3Nb2/3)xO3 (BCTZ-xZN) (x = 0%, x = 2.5% and x = 5%) ceramics employing Maxwell's equations. Notably, values of positive electrocaloric effects, elevated electrocaloric sensitivity, coefficient of performance (COP), and energy retention were noted, underscoring its suitability for solid-state cooling and high-capacity energy retention storage.
2. Experimental details
Ceramic samples of BCTZ-xZN with x values of 0%, 2.5% and 5% were synthesized through the conventional solid-state reaction method. High-purity precursors, namely BaCO3 (99.99%; Alpha aesar), CaCO3 (99.99%; Alpha aesar), TiO2 (99.99%; Alpha aesar), ZrO2 (99.99%; Alpha aesar), ZnO (99.99%; Alpha aesar), and Nb2O5 (99.99%; Alpha aesar), were selected and weighed based on the specified formula. Subsequently, the materials were ground using ethanol (Merck, India) in an agate mortar, followed by calcination at 1100 °C for 10 hours. Further, 1 wt% polyvinyl alcohol (PVA) was introduced as a binder into the homogenized powder, which was then moulded into circular discs measuring approximately 8 mm in diameter and 1 mm in thickness. The compressed pellets were sintered in a furnace at a temperature of 1400 °C for 3 hours. The two sides of the pellets were covered with material containing silver and then dried at a temperature of 200 °C for 2 hours. The samples were designated with the labels BCTZ, BCTZ-2.5ZN and BCTZ-5ZN, which stand for x values of 0%, 2.5%, and 5%, respectively. The hysteresis loops (P–E) were obtained utilizing a Keithley 428 current amplifier coupled with a high-voltage power source (TREK Model 20/20C). The electrocaloric investigation was conducted through an indirect approach, utilizing the temperature-dependent (P–E) hysteresis loops recorded at a frequency of 10 Hz.
3. Results and discussion
3.1. X-ray diffraction analysis
Fig. 1 displays the room temperature X-ray diffraction pattern of BCTZ-xZN (x = 0%, x = 2.5% and x = 5%) for 2θ of 20–80°. It is evident from Fig. 1 that all specimens exhibit a perovskite structure of the ABO3 type. The diffraction peaks exhibit high intensity, reflecting the excellent crystallinity of the samples, which is compared with the standard reference patterns from PDF#81-2200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 33 and PDF# 05-062.34 The composition with x = 0% corresponds to the mixed phase of orthorhombic and tetragonal structures, while the composition with x = 2.5% retains the mixed phase with peak broadening around 44–46°. As the ZN concentration increases further, the doublet peak near 45° transforms into a single peak, indicating a transition to a purely tetragonal structure at x = 5%, as illustrated in the inset of Fig. 1. As x increases, there is a tendency for the diffraction peaks to shift towards larger angles, possibly indicating lattice contraction. In our previous study,35 we thoroughly examined the crystal structures of the x = 2.5% and x = 5% compositions. We performed refinement using the FullProf program on the XRD patterns of the different BCTZ-xZN ceramics. The two samples, x = 0% and x = 2.5%, exhibit the coexistence of both the orthorhombic Pmm2 and tetragonal P4mm phases, with the orthorhombic phase being dominant (62.92% for x = 0 and 67.90% for x = 2.5%). In contrast, for x = 5%, only the tetragonal phase is present (see Fig. 2). Table 1 lists the atomic positions, bond angles, and bond distances for the BCTZ-xZN ceramics.
33 and PDF# 05-062.34 The composition with x = 0% corresponds to the mixed phase of orthorhombic and tetragonal structures, while the composition with x = 2.5% retains the mixed phase with peak broadening around 44–46°. As the ZN concentration increases further, the doublet peak near 45° transforms into a single peak, indicating a transition to a purely tetragonal structure at x = 5%, as illustrated in the inset of Fig. 1. As x increases, there is a tendency for the diffraction peaks to shift towards larger angles, possibly indicating lattice contraction. In our previous study,35 we thoroughly examined the crystal structures of the x = 2.5% and x = 5% compositions. We performed refinement using the FullProf program on the XRD patterns of the different BCTZ-xZN ceramics. The two samples, x = 0% and x = 2.5%, exhibit the coexistence of both the orthorhombic Pmm2 and tetragonal P4mm phases, with the orthorhombic phase being dominant (62.92% for x = 0 and 67.90% for x = 2.5%). In contrast, for x = 5%, only the tetragonal phase is present (see Fig. 2). Table 1 lists the atomic positions, bond angles, and bond distances for the BCTZ-xZN ceramics.
 |
| | Fig. 1 X-ray diffraction (XRD) patterns of BCTZ-xZN ceramics. The inset shows the peak located at 45°. | |
 |
| | Fig. 2 Rietveld refinement of BCTZxZN ceramic.35 | |
Table 1 Rietveld refinement results BCTZ-xZN ceramics
| Samples |
Compositions BCTZ-xZN |
| Cell parameters |
X = 0% |
X = 2.5% |
X = 5% |
| Orthorhombic (Pmm2) |
62.92% |
67.90% |
|
| a = 4.039(4), b = 4.012(0), c = 4.014(2) |
a = 4.0208(5), b = 4.0015(3), c = 4.0110(6)35 |
| Tetragonal, (P4mm) |
37.08% |
32.09% |
| a = b = 4.022(6), c = 4.060(0) |
a = b = 4.0214(3), c = 4.0442(8)35 |
a = b = 4.0143(4), c = 4.0153(6)35 |
| Samples |
X = 0% |
X = 2.5% |
X = 5% |
| Atomic positions (x; y; z) |
| Ba/Ca |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| Ti/Zr/Zn/Nb |
0.5 |
0.5 |
0.479(0) |
0.5 |
0.5 |
0.482(3) |
0.5 |
0.5 |
0.533(7) |
| O1 |
0.5 |
0 |
0.461(0) |
0.5 |
0 |
0.560(0) |
0.5 |
0 |
0.476(2) |
| O2 |
0.5 |
0.5 |
−0.059(0) |
0.5 |
0.5 |
−0.022(6) |
0.5 |
0.5 |
0.012(3) |
| O3 |
0 |
0.5 |
0.536(0) |
0 |
0.5 |
0.514(9) |
|
|
|
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| Bond angles (°) |
| [O1–Ti–O2] |
87.930(4) |
83.142(8) |
83.454(1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| Bond distances (Å) |
| O1–Ti |
2.005(1) |
2.024(1) |
2.013(0) |
| Ti–O2 |
1.859(2) |
1.985(6) |
1.868(3) |
| O3–Ti |
2.0312(0) |
2.014(1) |
|
BCTZ ceramics exhibit a perovskite structure with ABO3 composition. The A site is typically occupied by Ba2+ ions (1.61 Å) and Ca2+ ions (1.34 Å) in BCTZ-xZN based materials, while Nb5+ ions (0.64 Å) and Zn2+ ions (0.74 Å) occupy the B site in the perovskite structure.36 The crystalline characteristics of the ceramics can be confirmed using Scherrer's equation, where  with (d), (λ) and (β) representing the average crystallite size, the wavelength, and the full width at half maximum (FWHM) value, respectively. With a wavelength of 1.54 Å for Cu Kα radiation, the calculated average crystallite sizes are approximately 22 nm, 20 nm, and 19 nm for BCTZ-xZN with x = 0%, 2.5%, and 5%, respectively. The substitution of Zn2+ and Nb5+ leads to a gradual decrease in the average crystallite size, indicating that incorporating these elements affects the crystal growth and structure of the material.
with (d), (λ) and (β) representing the average crystallite size, the wavelength, and the full width at half maximum (FWHM) value, respectively. With a wavelength of 1.54 Å for Cu Kα radiation, the calculated average crystallite sizes are approximately 22 nm, 20 nm, and 19 nm for BCTZ-xZN with x = 0%, 2.5%, and 5%, respectively. The substitution of Zn2+ and Nb5+ leads to a gradual decrease in the average crystallite size, indicating that incorporating these elements affects the crystal growth and structure of the material.
3.2. Dielectric study
Fig. 3 shows the temperature-dependent change in the real part of the dielectric constant 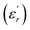 and the loss tangent (tan
and the loss tangent (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) for BCTZ-xZN ceramics with x = 0%, 2.5%, and 5%, at a fixed frequency of 1 kHz. In literature, the BCTZ ceramics are recognized by the presence of three distinct dielectric peaks, indicating phase transitions occurring approximately at 260 K, 290 K, and 381 K, corresponding to the transitions rhombohedral-orthorhombic (TR/O), orthorhombic-tetragonal (TO/T) and tetragonal-cubic (TT/C), respectively, as previously documented.24 In the case of BCTZ-xZN ceramics, the phase transitions occur at temperatures: 252 K, 302 K, and 393 K for x = 0%; 245 K, 302 K, and 356 K for x = 2.5%, respectively, as depicted in Fig. 3. For x = 5%, a single transition corresponding to the tetragonal-cubic phase is observed at 302 K. The analysis from XRD aligns well with these observations. As highlighted by Kaddoussi and Djemel,37,38 this kind of dielectric behavior marked by frequency dependence and diffuse phase transition is characteristic of classical ferroelectrics that exhibit diffuse phase transition features.39,40 With the increased ZN concentration, the transition temperature shifts towards the lower temperature range and exhibits a broader profile. These alterations may be attributed to local distortions within the crystal structure, as suggested by previous studies.41 However, since Zn2+, Nb5+, and Zr4+ have larger ionic radii than Ti4+, their incorporation induces structural distortions, leading to localized electric fields and charge imbalances. In Fig. 3, there is a slight increase in loss as the percentage of Zn and Nb increases, with the minimal value observed for x = 5% around the tetragonal-cubic transition temperature. The BCTZ5ZN composition exhibits the best permittivity and low-loss dielectric (Tc = 302 K,
δ) for BCTZ-xZN ceramics with x = 0%, 2.5%, and 5%, at a fixed frequency of 1 kHz. In literature, the BCTZ ceramics are recognized by the presence of three distinct dielectric peaks, indicating phase transitions occurring approximately at 260 K, 290 K, and 381 K, corresponding to the transitions rhombohedral-orthorhombic (TR/O), orthorhombic-tetragonal (TO/T) and tetragonal-cubic (TT/C), respectively, as previously documented.24 In the case of BCTZ-xZN ceramics, the phase transitions occur at temperatures: 252 K, 302 K, and 393 K for x = 0%; 245 K, 302 K, and 356 K for x = 2.5%, respectively, as depicted in Fig. 3. For x = 5%, a single transition corresponding to the tetragonal-cubic phase is observed at 302 K. The analysis from XRD aligns well with these observations. As highlighted by Kaddoussi and Djemel,37,38 this kind of dielectric behavior marked by frequency dependence and diffuse phase transition is characteristic of classical ferroelectrics that exhibit diffuse phase transition features.39,40 With the increased ZN concentration, the transition temperature shifts towards the lower temperature range and exhibits a broader profile. These alterations may be attributed to local distortions within the crystal structure, as suggested by previous studies.41 However, since Zn2+, Nb5+, and Zr4+ have larger ionic radii than Ti4+, their incorporation induces structural distortions, leading to localized electric fields and charge imbalances. In Fig. 3, there is a slight increase in loss as the percentage of Zn and Nb increases, with the minimal value observed for x = 5% around the tetragonal-cubic transition temperature. The BCTZ5ZN composition exhibits the best permittivity and low-loss dielectric (Tc = 302 K, 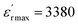 and tan(δ) ≈ 0.006 at Tc), indicating excellent dielectric properties which may be attributed to space charge polarization.35 The low dielectric losses are attributed to the sample's high density and uniform microstructure, which minimize interfacial defects and leakage currents.42 Because of its Tc, which is around ambient temperature, this ceramic is beneficial for room temperature applications. Moreover, the substitution of Zn2+ and Nb5+ improves the dielectric properties compared to pure BCTZ. The similarity in ionic radii between the composite cationic group (Zn1/3Nb2/3)4+ and Ti4+ facilitates their diffusion within the crystal lattice, enabling substitution at Ti4+ sites. This substitution contributes to the observed modifications in the material's properties.43 However, it's noteworthy that the loss values for all compositions remain relatively low. It is evident from the data that the loss tangent (tan
and tan(δ) ≈ 0.006 at Tc), indicating excellent dielectric properties which may be attributed to space charge polarization.35 The low dielectric losses are attributed to the sample's high density and uniform microstructure, which minimize interfacial defects and leakage currents.42 Because of its Tc, which is around ambient temperature, this ceramic is beneficial for room temperature applications. Moreover, the substitution of Zn2+ and Nb5+ improves the dielectric properties compared to pure BCTZ. The similarity in ionic radii between the composite cationic group (Zn1/3Nb2/3)4+ and Ti4+ facilitates their diffusion within the crystal lattice, enabling substitution at Ti4+ sites. This substitution contributes to the observed modifications in the material's properties.43 However, it's noteworthy that the loss values for all compositions remain relatively low. It is evident from the data that the loss tangent (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) increases notably above 500 K, particularly in the high-temperature range, due to thermally activated conductivity within the material. The rise in conductivity loss is the cause of this phenomena.
δ) increases notably above 500 K, particularly in the high-temperature range, due to thermally activated conductivity within the material. The rise in conductivity loss is the cause of this phenomena.
 |
| | Fig. 3 Temperature dependence of the real part of the dielectric constant  and the dielectric loss (tan and the dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) for BCTZ-xZN ceramics. δ) for BCTZ-xZN ceramics. | |
3.3. Ferroelectric properties
The P–E hysteresis loops at ambient temperature with applied electric fields ranging from 5 kV cm−1 to 30 kV cm−1 are depicted in Fig. 4a–c for varying compositions of x = 0%, 2.5%, and 5%. In contrast, Fig. 4d–f illustrates the behavior at different temperatures for fixed electric fields, focusing on the BCTZ-xZN solid solution. All loops exhibit ferroelectric characteristics within the studied temperature range. The P–E loops symmetrical form indicates that there aren't any pinning defect dipoles present. But if the composition changes, the loop's structure can also vary, most likely as a result of shifting internal field distributions and space-charge polarization.44 An increase in the electric field (E) results in a rise in the maximum of the polarization (Pmax) because a stronger electric field provides a greater driving force for ferroelectric domain switching. Consequently, the domain volume and overall polarization, including hysteresis characteristics, grow with the amplified driving force. The unsaturated loop observed at lower fields, which saturates at higher fields, indicates a higher energy density, alongside the material's elevated dielectric constant. For the composition with x = 0%, the maximum polarization (P) rises from 1.5 to 11.7 μC cm−2 whereas for x = 2.5%, it rises from 5.1 to 17.6 μC cm−2. In the case of x = 5%, it is from 3.4 to 15.8 μC cm−2 for the applied electric field range of 5 to 30 kV cm−1. The maximum polarization strongly depends on ceramic densification, with higher density reducing defects and enhancing dipole alignment. Doped samples (x = 2.5%, 5%) show similar polarization enhancement versus (x = 0%), confirming improved ferroelectric performance. In the instances of x = 0%, the P–E loops appear broader and shorter, attributed to the induced depolarization fields and defects hindering domain switching, thus diminishing the material's field. This increment signifies a higher energy density, accompanied by an improvement in the dielectric strength of the ceramic. The impact of temperature on the P–E hysteresis curve is depicted in Fig. 4d–f. The maximum polarization P decreases with increasing temperature for x = 0%, x = 2.5%, and x = 5%, as observed in the P–E loops. For x = 0%, the polarization decreases from 10 μC cm−2 to 8.05 μC cm−2; from 23.46 μC cm−2 to 18.83 μC cm−2 for x = 2.5%; and from 14.96 μC cm−2 to 10.63 μC cm−2 for x = 5% as a function a temperature. Dielectric materials exhibit electric energy storage characteristics and can be derived from the P–E loops depicted in the inset of Fig. 5. Prior research has connected this decrease in ferroelectric characteristics to material losses brought on by random charge effects and local compositional changes, which weaken ferroelectric order and break tetragonal symmetry.45
 |
| | Fig. 4 Polarization–electric field (P–E) hysteresis loops of BCTZ-xZNNb ceramics: (a–c); (d–f) at different temperatures for BCTZ-xZN, respectively. | |
 |
| | Fig. 5 Variation of the recoverable energy density (Wrec) (black) and energy storage efficiency (η)(red). The inset method for calculating energy storage efficiency from P–E loops. | |
3.4. Energy storage performances
Ferroelectric materials exhibit stable charge responses under varying electric fields, making them ideal for high-power energy storage. Due to their temperature-dependent polarization, they allow for efficient charge–discharge cycles and a high energy density. Polarization is affected by several factors, including doping, the crystal structure, domain configuration, and dipolar interactions. Standard equations46,47 can be used to estimate the total energy density (Wtot), recoverable energy (Wrec), and energy storage efficiency (η).| |
 | (1) |
| |
 | (2) |
| |
 | (3) |
Fig. 5 illustrates the variation in Wrec and η (%) with diverse compositions of BCTZ-xZN under 25 kV cm−1 at 353 K. These parameters exhibit consistent characteristics across both field and temperature variations, without significant impact. For x = 2.5%, the Wrec reaches 150.17 mJ cm−3, surpassing the values observed for other compositions. The efficiency calculated for x = 2.5% is η = 83%, while for x = 5% it is even higher, at η = 87%, due to the lower Wtotal associated with this composition. The achieved value surpasses that of other lead-free ceramics under this low applied electric field; for instance, in Ba0.85Ca0.15Zr0.10Ti0.90O3,48 it is below Wrec = 65 mJ cm−3, BaTi0.89Sn0.11O3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 49 exhibits less than Wrec = 75 mJ cm−3, in BaCe0.15Ti0.85O3
49 exhibits less than Wrec = 75 mJ cm−3, in BaCe0.15Ti0.85O3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 ceramics, it's approximately Wrec = 120 mJ cm−3, and in Ba0.90Ca0.10Zr0.15Ti0.85O3
9 ceramics, it's approximately Wrec = 120 mJ cm−3, and in Ba0.90Ca0.10Zr0.15Ti0.85O3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 ceramics, it's Wrec = 92.8 mJ cm−3 and so forth. Recently, an energy storage capacity for Pr doped Ba0.85Ca0.15Ti0.9Zr0.1O3 has been documented, reaching Wrec = 81.9 mJ cm−3 and energy storage efficiency of η = 76.4%,51 further demonstrating the improved energy storage performance of the presently investigated materials. Moreover, the compositions with x = 2.5% and x = 5% maintain an efficiency of around 80%, highlighting their strong potential for practical applications.
50 ceramics, it's Wrec = 92.8 mJ cm−3 and so forth. Recently, an energy storage capacity for Pr doped Ba0.85Ca0.15Ti0.9Zr0.1O3 has been documented, reaching Wrec = 81.9 mJ cm−3 and energy storage efficiency of η = 76.4%,51 further demonstrating the improved energy storage performance of the presently investigated materials. Moreover, the compositions with x = 2.5% and x = 5% maintain an efficiency of around 80%, highlighting their strong potential for practical applications.
3.5. Electrocaloric investigations
The electrocaloric effect (ECE) refers to the reversible change in both entropy and temperature when an electric field is applied or removed. To measure this effect, the isothermal change in entropy (ΔS) and the adiabatic change in temperature (ΔT) are calculated using Maxwell's relations and are expressed as follows:52| |
 | (4) |
| |
 | (5) |
where P represents saturation polarization, T signifies temperature, S denotes entropy, r stands for density, Cp indicates specific heat capacity, and E1, and E2 denote initial and final applied external electric fields, correspondingly. If E1 is set to zero, E2 will represent the final applied field value.
The polarization decreases with temperature, which is modeled using a first-order polynomial fit to estimate the electrocaloric effect (ECE),27,53,54 as shown in Fig. 6a–c. The derivative ∂P/∂T is calculated by first-order differentiating the saturation polarization for temperature to determine ΔT. The entropy change (ΔS), calculated using eqn (5), reaches peak values of 0.12 J kg−1 K−1, 1.14 J kg−1 K−1, and 0.47 J kg−1 K−1 at 384 K, 340 K, and 309 K, respectively. The highest entropy change of 1.14 J kg−1 K−1 was observed in the BCTZ-2.5ZN sample at 340 K under an applied electric field of 25 kV cm−1. This demonstrates that the substitution improves the electrocaloric response by increasing the entropy change. This enhancement in material performance is attributed to the orthorhombic–tetragonal phase transition occurring at room temperature.55 Using eqn (4), ΔT was calculated, giving a peak value of 0.68 K for the BCTZ-2.5ZN material. This ΔT value exceeds those of many other non-lead ceramics, as shown in Table 2.
 |
| | Fig. 6 (a–c) Polarization change (ΔP) and entropy change (ΔS) in BCTZ-xZN ceramics. (d) Maximum value of the coefficient of performance (COP) and electrocaloric responsivity (ΔT/ΔE) for BCTZ-xZN ceramics. | |
Table 2 Comparison of ECE properties for BCTZ-xZN ceramic with other lead-free ferroelectric ceramics
| Composition |
T (K) |
ΔT (K) |
E (kV cm−1) |
ξ = ΔT/ΔE (K mm kV−1) |
Measurement method |
Ref. |
| BCTZ |
384 |
0.13 |
26 |
0.05 |
Indirect |
This work |
| BCTZ-2.5ZN |
340 |
0.68 |
25 |
0.272 |
Indirect |
This work |
| BCTZ-5ZN |
309 |
0.25 |
25 |
0.1 |
Indirect |
This work |
| B0.85Ca0.15Zr0.1Ti0.9O3 |
363 |
0.115 |
6.65 |
0.164 |
Indirect |
56 |
| BZT-30BCT |
333 |
0.30 |
20 |
0.15 |
Indirect |
57 |
| B0.9Ca0.1Zr0.05Ti0.95O3 |
392 |
0.465 |
25 |
0.186 |
Indirect |
58 |
| Ba(Zr0.029Ti0.823)Sn0.075O3 |
303 |
0.19 |
8.7 |
0.22 |
Indirect |
59 |
| Ba0.80Ca0.20TiO3 |
398 |
0.12 |
7.95 |
0.15 |
Indirect |
60 |
The increased electrocaloric temperature change (ΔT) occurs near the phase transition temperature (Tc), with several studies confirming the electrocaloric effect (ECE) peak around this temperature.7,61 Ponomareva and Lisenkov62 suggested that this peak is due to configuration disorder at the transition points. As the applied field increases, the ECE also rises, reaching a threshold due to the breakdown of the field in BCTZ-2.5ZN. The peak corresponds to the full polarization state of the material. In ferroelectric materials, the electric dipoles transition from disorder to order under an external electric field, reducing the polarization entropy. This leads to an increase in lattice entropy with temperature to balance the changes. The conversion of lattice entropy into polar contributions during structural shifts is key to enhancing the ECE. The improved ΔT in BCTZ-2.5ZN ceramics results from better ferroelectric properties after Zn incorporation. Since entropy variation is proportional to P2,49 the increase in polarization has a significant impact on the ECE. Additionally, the random orientation of polar nano-domains and their multiple possible orientations further contribute to the ECE peak near the phase transition.63 These findings suggest that ferroelectric materials, with their higher polarization changes, are ideal candidates for the electrocaloric effect.64 In particular, the highest electrocaloric response is observed in the composition exhibiting an orthorhombic-to-tetragonal phase transition at room temperature, highlighting the strong coupling between phase transition and entropy variation.
Fig. 6d illustrates the electrocaloric responsivity (ΔT/ΔE)65,66 over the applied field for various compositions of BCTZ-xZN, which explains ΔT change concerning the applied electric field. The maximum value recorded was 0.27 K mm kV−1 at 340 K with an applied field of 25 kV cm−1 for BCTZ-2.5ZN, surpassing that of other lead-based or lead-free ceramic materials like for Ba0.975La0.017(Zr0.05Ti0.9)Sn0.05O3 ceramics it is 0.2 K mm kV−1,67 0.043 K mm kV−1 for (Pb0.88Sr0.08)(Nb0.08(Zr0.53Ti0.47)0.92)O3,68 0.21 K mm kV−1 for (Pb0.97La0.02) (Zr0.66Sn0.27Ti0.07)O3 (ref. 69) and 0.207 K mm kV−1 for 0.05BCBT-7.5%.70 To assess the cooling efficiency, the Coefficients of Performance (COP) for BCTZ-2.5ZN were determined. COP is calculated as the absolute value of Q divided by the absolute value of Wtotal,71,72 where W represents the total electrical energy input and Q represents the isothermal heat extracted. The computed COP values for BCTZ-xZN with x = 0%, 2.5%, and 5% are 0.33, 2 and 1.03, respectively. Notably, BCTZ-2.5ZN exhibits the highest COP, as depicted in Fig. 6d. This value is higher than that of Pb0.85Ba0.05La0.10(Zr0.90Ti0.10)O3 thick films (COP = 1.7, ΔE = 80 kV cm−1),73 as well as Ba0.85Ca0.15Zr0.1Ti0.9 ceramics (COP of 1.5 at 350 K under ΔE = 55 kV cm−1).74 Additionally, our ceramics outperformed 0.9 (K0.5Na0.5)NbO3–0.1 (SrZrO3) ceramics, which reached a COP of 0.62 under 35 kV cm−1.75 The results of BCTZ-2.5ZN show excellent electrocaloric performance, with ΔS = 1.14 J kg−1 K−1, a responsivity of 0.27 K mm kV−1, and a COP of 2, demonstrating its potential for energy-efficient cooling applications.
4. Conclusion
In this study, lead-free BCTZ-xZN (x = 0%, 2.5%, 5%) ceramics were investigated. X-ray diffraction (XRD) analysis confirmed the formation of a pure perovskite structure. Dielectric measurements revealed a diffuse phase transition. The electrical energy storage (Wrec) was calculated to be 150 mJ cm−3, with an efficiency of η = 83% for BCTZ-2.5ZN. An extensive examination of the electrocaloric properties was conducted using Maxwell's approach (indirect thermodynamic method). Among these compositions, BCTZ-2.5ZN exhibits an electrocaloric effect of 0.68 K at 340 K under an applied electric field of 25 kV cm−1, along with an electrocaloric responsivity (ΔT/ΔE) of 0.27 K mm kV−1 at the same temperature. The coefficient of performance (COP) is measured as 2. These findings underscore BCTZ-xZN as a promising material for applications in cooling systems and energy storage for electronic devices, offering versatile properties conducive to cooling operations via an external electric field across various operating temperatures.
Data availability
The data supporting the findings of this study were generated during the experimental work conducted in our laboratory (LaMMa), a multifunctional materials and applications laboratory, in collaboration with the Electrical Engineering and Ferroelectricity Laboratory (INSA-Lyon, LGEF). All relevant data are included in the manuscript. Additional information can be made available upon reasonable request from the corresponding author. Interested researchers may contact us at: E-mail: abdmouleh.hanen@gmail.com.
Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- S.-G. Lu and Q. Zhang, Adv. Mater., 2009, 21, 1983–1987 CrossRef CAS.
- M. Ožbolt, A. Kitanovski, J. Tušek and A. Poredoš, Int. J. Refrig., 2014, 40, 174–188 CrossRef.
- Y. Bai, X. Han, K. Ding and L. Qiao, Energy Tech, 2017, 5, 703–707 CrossRef CAS.
- A.-K. Axelsson, F. Le Goupil, M. Valant and N. M. Alford, Acta Mater., 2017, 124, 120–126 CrossRef CAS.
- M. E. Lines and A. M. Glass, Principles and Applications of Ferroelectrics and Related Materials, OUP Oxford, 2001 Search PubMed.
- F. Weyland, M. Acosta, J. Koruza, P. Breckner, J. Rödel and N. Novak, Adv. Funct. Mater., 2016, 26, 7326–7333 CrossRef CAS.
- A. S. Mischenko, Science, 2006, 311, 1270–1271 CrossRef CAS PubMed.
- B. Neese, B. Chu, S.-G. Lu, Y. Wang, E. Furman and Q. M. Zhang, Science, 2008, 321, 821–823 CrossRef CAS PubMed.
- K. S. Srikanth and R. Vaish, J. Eur. Ceram. Soc., 2017, 37, 3927–3933 CrossRef CAS.
- Z. Xu, Z. Fan, X. Liu and X. Tan, Appl. Phys. Lett., 2017, 110, 082901 CrossRef.
- H. Gao, X. Hao, Q. Zhang, S. An and L. B. Kong, J. Alloys Compd., 2017, 690, 131–138 CrossRef CAS.
- Z. Fan, X. Liu and X. Tan, J. Am. Ceram. Soc., 2017, 100, 2088–2097 CrossRef CAS.
- G. Ramesh, M. S. Ramachandra Rao, V. Sivasubramanian and V. Subramanian, J. Alloys Compd., 2016, 663, 444–448 CrossRef CAS.
- J. F. Scott, Annu. Rev. Mater. Res., 2011, 41, 229–240 CrossRef CAS.
- M. Valant, Prog. Mater. Sci., 2012, 57, 980–1009 CrossRef CAS.
- K. C. Kao, Dielectric Phenomena in Solids, Elsevier, 2004 Search PubMed.
- L. Luo, H. Chen, Y. Zhu, W. Li, H. Luo and Y. Zhang, J. Alloys Compd., 2011, 509, 8149–8152 CrossRef CAS.
- R. Chukka, J. W. Cheah, Z. Chen, P. Yang, S. Shannigrahi, J. Wang and L. Chen, Appl. Phys. Lett., 2011, 98, 242902 CrossRef.
- X. M. Chen, T. Wang and J. Li, Mater. Sci. Eng., B, 2004, 113, 117–120 CrossRef.
- T. Badapanda, S. Chaterjee, A. Mishra, R. Ranjan and S. Anwar, Phys. B, 2017, 521, 264–269 CrossRef CAS.
- D. Xue, Y. Zhou, H. Bao, J. Gao, C. Zhou and X. Ren, Appl. Phys. Lett., 2011, 99, 122901 CrossRef.
- H. Kaddoussi, Y. Gagou, A. Lahmar, B. Allouche, J. L. Dellis, M. Courty, H. Khemakhem and M. El Marssi, J. Mater. Sci., 2016, 51, 3454–3462 CrossRef CAS.
- W. Li, Z. Xu, R. Chu, P. Fu and G. Zang, J. Am. Ceram. Soc., 2010, 93, 2942–2944 CrossRef CAS.
- G. Singh, V. S. Tiwari and P. K. Gupta, J. Appl. Crystallogr., 2013, 46, 324–331 CrossRef CAS.
- H. Kaddoussi, A. Lahmar, Y. Gagou, B. Asbani, J.-L. Dellis, G. Cordoyiannis, B. Allouche, H. Khemakhem, Z. Kutnjak and M. El Marssi, J. Alloys Compd., 2016, 667, 198–203 CrossRef CAS.
- T. Chullaphan, S. Phokha, S. Hunpratub, P. Chindaprasirt and P. Kidkhunthod, Integr. Ferroelectr., 2019, 195, 70–80 CrossRef CAS.
- G. Singh, V. S. Tiwari and P. K. Gupta, Appl. Phys. Lett., 2013, 103, 202903 CrossRef.
- H. Liu, Z. Sun, J. Zhang, H. Luo, Q. Zhang, Y. Yao, S. Deng, H. Qi, J. Liu, L. C. Gallington, J. C. Neuefeind and J. Chen, J. Am. Chem. Soc., 2023, 145, 11764–11772 CrossRef CAS PubMed.
- H. Liu, Z. Sun, J. Zhang, H. Luo, Y. Zhang, A. Sanson, M. Hinterstein, L. Liu, J. C. Neuefeind and J. Chen, J. Am. Chem. Soc., 2024, 146, 3498–3507 CrossRef CAS PubMed.
- K. Xu, P. Yang, W. Peng and L. Li, J. Alloys Compd., 2020, 829, 154516 CrossRef CAS.
- W. Cai, Q. Zhang, C. Zhou, R. Gao, S. Zhang, Z. Li, R. Xu, G. Chen, X. Deng, Z. Wang and C. Fu, J. Mater. Sci.: Mater. Electron., 2020, 31, 9167–9175 CrossRef CAS.
- Z. Sun, H. Liu, J. Zhang, H. Luo, Y. Yao, Y. Zhang, L. Liu, J. C. Neuefeind and J. Chen, J. Am. Chem. Soc., 2024, 146, 13467–13476 CrossRef CAS PubMed.
- S. Su, R. Zuo, D. Lv and J. Fu, Powder Technol., 2012, 217, 11–15 CrossRef CAS.
- B. G. Baraskar, P. S. Kadhane, T. C. Darvade, A. R. James, R. C. Kambale, B. G. Baraskar, P. S. Kadhane, T. C. Darvade, A. R. James and R. C. Kambale, in Ferroelectrics and Their Applications, IntechOpen, 2018 Search PubMed.
- H. Abdmouleh, I. Kriaa, N. Abdelmoula and H. Khemakhem, Ceram. Int., 2024, 50, 32505–32512 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A, 1976, 32, 751–767 CrossRef.
- H. Kaddoussi, A. Lahmar, Y. Gagou, J.-L. Dellis, H. Khemakhem and M. E. Marssi, Ceram. Int., 2015, 41, 15103–15110 CrossRef CAS.
- I. Djemel, I. Kriaa, N. Abdelmoula and H. Khemakhem, J. Alloys Compd., 2017, 720, 284–288 CrossRef CAS.
- H. Kaddoussi, A. Lahmar, Y. Gagou, B. Manoun, J. N. Chotard, J.-L. Dellis, Z. Kutnjak, H. Khemakhem, B. Elouadi and M. El Marssi, J. Alloys Compd., 2017, 713, 164–179 CrossRef CAS.
- H. Abdmouleh, I. Kriaa, N. Abdelmoula, Z. Sassi and H. Khemakhem, J. Alloys Compd., 2021, 878, 160355 CrossRef CAS.
- Z. Liu, H. Fan, S. Lei, X. Ren and C. Long, J. Eur. Ceram. Soc., 2017, 37, 115–122 CrossRef CAS.
- Y. Gu, F. Zhang, W. Wu and Z. Liu, J. Adv. Dielect., 2023, 13, 2350002 CrossRef CAS.
- Y. Yang, K. Liu, X. Liu, G. Liu, C. Xia, Z. He and Y. Yan, Ceram. Int., 2016, 42, 7877–7882 CrossRef CAS.
- L. Jin, F. Li and S. Zhang, J. Am. Ceram. Soc., 2014, 97, 1–27 CrossRef CAS.
- H. I. Humburg, M. Acosta, W. Jo, K. G. Webber and J. Rödel, J. Eur. Ceram. Soc., 2015, 35, 1209–1217 CrossRef CAS.
- V. S. Puli, D. K. Pradhan, I. Coondoo, N. Panwar, S. Adireddy, S. Luo, R. S. Katiyar and D. B. Chrisey, J. Phys. D: Appl. Phys., 2019, 52, 255304 CrossRef CAS.
- H. Kacem, A. Dhahri, Z. Sassi, L. Seveyrat, L. Lebrun, V. Perrin and J. Dhahri, J. Alloys Compd., 2021, 872, 159699 CrossRef CAS.
- S. Merselmiz, Z. Hanani, D. Mezzane, A. G. Razumnaya, M. Amjoud, L. Hajji, S. Terenchuk, B. Rožič, I. A. Luk’yanchuk and Z. Kutnjak, RSC Adv., 2021, 11, 9459–9468 RSC.
- S. Merselmiz, Z. Hanani, D. Mezzane, M. Spreitzer, A. Bradeško, D. Fabijan, D. Vengust, M. Amjoud, L. Hajji, Z. Abkhar, A. G. Razumnaya, B. Rožič, I. A. Luk’yanchuk and Z. Kutnjak, Ceram. Int., 2020, 46, 23867–23876 CrossRef CAS.
- A. Dahri, Y. Gagou, N. Abdelmoula, H. Khemakhem and M. El Marssi, Ceram. Int., 2022, 48, 3157–3171 CrossRef CAS.
- J. Kaarthik, C. Kaushiga, G. Sradha, R. Nayak, S. G. Reddy, K. C. Sekhar and V. Annapureddy, J. Alloys Compd., 2023, 943, 169069 CrossRef CAS.
- F. Zhuo, Q. Li, H. Qiao, Q. Yan, Y. Zhang, X. Xi, X. Chu, X. Long and W. Cao, Appl. Phys. Lett., 2018, 112, 133901 CrossRef.
- Y. Bai, X. Han and L. Qiao, Appl. Phys. Lett., 2013, 102, 252904 CrossRef.
- G. Singh, I. Bhaumik, S. Ganesamoorthy, R. Bhatt, A. K. Karnal, V. S. Tiwari and P. K. Gupta, Appl. Phys. Lett., 2013, 102, 082902 CrossRef.
- Y. Zhang, J. Glaum, C. Groh, M. C. Ehmke, J. E. Blendell, K. J. Bowman and M. J. Hoffman, J. Am. Ceram. Soc., 2014, 97, 2885–2891 CrossRef CAS.
- S. Merselmiz, Z. Hanani, D. Mezzane, A. G. Razumnaya, M. Amjoud, L. Hajji, S. Terenchuk, B. Rožič, I. A. Luk’yanchuk and Z. Kutnjak, RSC Adv., 2021, 11, 9459–9468 RSC.
- Y. Bai, X. Han and L. Qiao, Appl. Phys. Lett., 2013, 102, 252904 CrossRef.
- M. ben Abdessalem, I. Kriaa, A. Aydi and N. Abdelmoula, Ceram. Int., 2018, 44, 13595–13601 CrossRef CAS.
- H. Kaddoussi, Y. Gagou, A. Lahmar, J. Belhadi, B. Allouche, J.-L. Dellis, M. Courty, H. Khemakhem and M. El Marssi, Solid State Commun., 2015, 201, 64–67 CrossRef CAS.
- B. Asbani, Y. Gagou, J.-L. Dellis, A. Lahmar, M. Amjoud, D. Mezzane, Z. Kutnjak and M. EL Marssi, Structural, dielectric and electrocaloric properties in lead-free Zr-doped Ba0.8Ca0.2TiO3 solid solution, Solid State Commun., 2016, 237-238, 49–54 CrossRef CAS.
- P. Hansen, D. Hennings and H. Schreinemacher, J. Am. Ceram. Soc., 1998, 81, 1369–1373 CrossRef CAS.
- I. Ponomareva and S. Lisenkov, Phys. Rev. Lett., 2012, 108, 167604 CrossRef CAS PubMed.
- R. Pirc, Z. Kutnjak, R. Blinc and Q. M. Zhang, J. Appl. Phys., 2011, 110, 074113 CrossRef.
- X. Hao, J. Zhai, L. B. Kong and Z. Xu, Prog. Mater. Sci., 2014, 63, 1–57 CrossRef CAS.
- B. Lu, P. Li, Z. Tang, Y. Yao, X. Gao, W. Kleemann and S.-G. Lu, Sci. Rep., 2017, 7, 45335 CrossRef CAS PubMed.
- S. G. Lu, B. Rožič, Q. M. Zhang, Z. Kutnjak, X. Li, E. Furman, L. J. Gorny, M. Lin, B. Malič, M. Kosec, R. Blinc and R. Pirc, Appl. Phys. Lett., 2010, 97, 162904 CrossRef.
- S. Smail, M. Benyoussef, K. Taïbi, N. Bensemma, B. Manoun, M. El Marssi and A. Lahmar, Mater. Chem. Phys., 2020, 252, 123462 CrossRef CAS.
- C. Chen, R. Liang, Z. Liu, S. Yan, X. Nie, Z. Zhou and X. Dong, Mater. Lett., 2017, 189, 303–306 CrossRef CAS.
- Y. Zhou, Y. Qiao, Y. Tian, K. Wang, G. Li and Y. Chai, J. Eur. Ceram. Soc., 2017, 37, 995–999 CrossRef CAS.
- H. Zaghouene, I. Kriaa and H. Khemakhem, Mater. Sci. Eng., B, 2018, 227, 110–115 CrossRef CAS.
- Y. Liu, J. F. Scott and B. Dkhil, APL Mater., 2016, 4, 064109 CrossRef.
- H. Gao, X. Hao, Q. Zhang, S. An and L. B. Kong, J. Mater. Sci.: Mater. Electron., 2016, 27, 10309–10319 CrossRef CAS.
- H. Gao, X. Hao, Q. Zhang, S. An and L. B. Kong, J. Mater. Sci.: Mater. Electron., 2016, 27, 10309–10319 CrossRef CAS.
- A. Lakouader, H. Mezzourh, D. Mezzane, M. Amjoud, L. Hajji, E. H. Choukri, I. A. Luk’yanchuk, Z. Kutnjak and M. El Marssi, J. Mater. Sci.: Mater. Electron., 2022, 33, 14381–14396 CrossRef CAS.
- R. Kumar and S. Singh, J. Alloys Compd., 2018, 764, 289–294 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Issa Kriaa
*a,
Issa Kriaa a,
Najmeddine Abdelmoulaa,
Zina Sassib and
Hamadi Khemakhema
a,
Najmeddine Abdelmoulaa,
Zina Sassib and
Hamadi Khemakhema
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 33 and PDF# 05-062.34 The composition with x = 0% corresponds to the mixed phase of orthorhombic and tetragonal structures, while the composition with x = 2.5% retains the mixed phase with peak broadening around 44–46°. As the ZN concentration increases further, the doublet peak near 45° transforms into a single peak, indicating a transition to a purely tetragonal structure at x = 5%, as illustrated in the inset of Fig. 1. As x increases, there is a tendency for the diffraction peaks to shift towards larger angles, possibly indicating lattice contraction. In our previous study,35 we thoroughly examined the crystal structures of the x = 2.5% and x = 5% compositions. We performed refinement using the FullProf program on the XRD patterns of the different BCTZ-xZN ceramics. The two samples, x = 0% and x = 2.5%, exhibit the coexistence of both the orthorhombic Pmm2 and tetragonal P4mm phases, with the orthorhombic phase being dominant (62.92% for x = 0 and 67.90% for x = 2.5%). In contrast, for x = 5%, only the tetragonal phase is present (see Fig. 2). Table 1 lists the atomic positions, bond angles, and bond distances for the BCTZ-xZN ceramics.
33 and PDF# 05-062.34 The composition with x = 0% corresponds to the mixed phase of orthorhombic and tetragonal structures, while the composition with x = 2.5% retains the mixed phase with peak broadening around 44–46°. As the ZN concentration increases further, the doublet peak near 45° transforms into a single peak, indicating a transition to a purely tetragonal structure at x = 5%, as illustrated in the inset of Fig. 1. As x increases, there is a tendency for the diffraction peaks to shift towards larger angles, possibly indicating lattice contraction. In our previous study,35 we thoroughly examined the crystal structures of the x = 2.5% and x = 5% compositions. We performed refinement using the FullProf program on the XRD patterns of the different BCTZ-xZN ceramics. The two samples, x = 0% and x = 2.5%, exhibit the coexistence of both the orthorhombic Pmm2 and tetragonal P4mm phases, with the orthorhombic phase being dominant (62.92% for x = 0 and 67.90% for x = 2.5%). In contrast, for x = 5%, only the tetragonal phase is present (see Fig. 2). Table 1 lists the atomic positions, bond angles, and bond distances for the BCTZ-xZN ceramics.


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
 with (d), (λ) and (β) representing the average crystallite size, the wavelength, and the full width at half maximum (FWHM) value, respectively. With a wavelength of 1.54 Å for Cu Kα radiation, the calculated average crystallite sizes are approximately 22 nm, 20 nm, and 19 nm for BCTZ-xZN with x = 0%, 2.5%, and 5%, respectively. The substitution of Zn2+ and Nb5+ leads to a gradual decrease in the average crystallite size, indicating that incorporating these elements affects the crystal growth and structure of the material.
with (d), (λ) and (β) representing the average crystallite size, the wavelength, and the full width at half maximum (FWHM) value, respectively. With a wavelength of 1.54 Å for Cu Kα radiation, the calculated average crystallite sizes are approximately 22 nm, 20 nm, and 19 nm for BCTZ-xZN with x = 0%, 2.5%, and 5%, respectively. The substitution of Zn2+ and Nb5+ leads to a gradual decrease in the average crystallite size, indicating that incorporating these elements affects the crystal growth and structure of the material.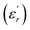 and the loss tangent (tan
and the loss tangent (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) for BCTZ-xZN ceramics with x = 0%, 2.5%, and 5%, at a fixed frequency of 1 kHz. In literature, the BCTZ ceramics are recognized by the presence of three distinct dielectric peaks, indicating phase transitions occurring approximately at 260 K, 290 K, and 381 K, corresponding to the transitions rhombohedral-orthorhombic (TR/O), orthorhombic-tetragonal (TO/T) and tetragonal-cubic (TT/C), respectively, as previously documented.24 In the case of BCTZ-xZN ceramics, the phase transitions occur at temperatures: 252 K, 302 K, and 393 K for x = 0%; 245 K, 302 K, and 356 K for x = 2.5%, respectively, as depicted in Fig. 3. For x = 5%, a single transition corresponding to the tetragonal-cubic phase is observed at 302 K. The analysis from XRD aligns well with these observations. As highlighted by Kaddoussi and Djemel,37,38 this kind of dielectric behavior marked by frequency dependence and diffuse phase transition is characteristic of classical ferroelectrics that exhibit diffuse phase transition features.39,40 With the increased ZN concentration, the transition temperature shifts towards the lower temperature range and exhibits a broader profile. These alterations may be attributed to local distortions within the crystal structure, as suggested by previous studies.41 However, since Zn2+, Nb5+, and Zr4+ have larger ionic radii than Ti4+, their incorporation induces structural distortions, leading to localized electric fields and charge imbalances. In Fig. 3, there is a slight increase in loss as the percentage of Zn and Nb increases, with the minimal value observed for x = 5% around the tetragonal-cubic transition temperature. The BCTZ5ZN composition exhibits the best permittivity and low-loss dielectric (Tc = 302 K,
δ) for BCTZ-xZN ceramics with x = 0%, 2.5%, and 5%, at a fixed frequency of 1 kHz. In literature, the BCTZ ceramics are recognized by the presence of three distinct dielectric peaks, indicating phase transitions occurring approximately at 260 K, 290 K, and 381 K, corresponding to the transitions rhombohedral-orthorhombic (TR/O), orthorhombic-tetragonal (TO/T) and tetragonal-cubic (TT/C), respectively, as previously documented.24 In the case of BCTZ-xZN ceramics, the phase transitions occur at temperatures: 252 K, 302 K, and 393 K for x = 0%; 245 K, 302 K, and 356 K for x = 2.5%, respectively, as depicted in Fig. 3. For x = 5%, a single transition corresponding to the tetragonal-cubic phase is observed at 302 K. The analysis from XRD aligns well with these observations. As highlighted by Kaddoussi and Djemel,37,38 this kind of dielectric behavior marked by frequency dependence and diffuse phase transition is characteristic of classical ferroelectrics that exhibit diffuse phase transition features.39,40 With the increased ZN concentration, the transition temperature shifts towards the lower temperature range and exhibits a broader profile. These alterations may be attributed to local distortions within the crystal structure, as suggested by previous studies.41 However, since Zn2+, Nb5+, and Zr4+ have larger ionic radii than Ti4+, their incorporation induces structural distortions, leading to localized electric fields and charge imbalances. In Fig. 3, there is a slight increase in loss as the percentage of Zn and Nb increases, with the minimal value observed for x = 5% around the tetragonal-cubic transition temperature. The BCTZ5ZN composition exhibits the best permittivity and low-loss dielectric (Tc = 302 K, 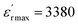 and tan(δ) ≈ 0.006 at Tc), indicating excellent dielectric properties which may be attributed to space charge polarization.35 The low dielectric losses are attributed to the sample's high density and uniform microstructure, which minimize interfacial defects and leakage currents.42 Because of its Tc, which is around ambient temperature, this ceramic is beneficial for room temperature applications. Moreover, the substitution of Zn2+ and Nb5+ improves the dielectric properties compared to pure BCTZ. The similarity in ionic radii between the composite cationic group (Zn1/3Nb2/3)4+ and Ti4+ facilitates their diffusion within the crystal lattice, enabling substitution at Ti4+ sites. This substitution contributes to the observed modifications in the material's properties.43 However, it's noteworthy that the loss values for all compositions remain relatively low. It is evident from the data that the loss tangent (tan
and tan(δ) ≈ 0.006 at Tc), indicating excellent dielectric properties which may be attributed to space charge polarization.35 The low dielectric losses are attributed to the sample's high density and uniform microstructure, which minimize interfacial defects and leakage currents.42 Because of its Tc, which is around ambient temperature, this ceramic is beneficial for room temperature applications. Moreover, the substitution of Zn2+ and Nb5+ improves the dielectric properties compared to pure BCTZ. The similarity in ionic radii between the composite cationic group (Zn1/3Nb2/3)4+ and Ti4+ facilitates their diffusion within the crystal lattice, enabling substitution at Ti4+ sites. This substitution contributes to the observed modifications in the material's properties.43 However, it's noteworthy that the loss values for all compositions remain relatively low. It is evident from the data that the loss tangent (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) increases notably above 500 K, particularly in the high-temperature range, due to thermally activated conductivity within the material. The rise in conductivity loss is the cause of this phenomena.
δ) increases notably above 500 K, particularly in the high-temperature range, due to thermally activated conductivity within the material. The rise in conductivity loss is the cause of this phenomena.

 and the dielectric loss (tan
and the dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) for BCTZ-xZN ceramics.
δ) for BCTZ-xZN ceramics.




![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 49 exhibits less than Wrec = 75 mJ cm−3, in BaCe0.15Ti0.85O3
49 exhibits less than Wrec = 75 mJ cm−3, in BaCe0.15Ti0.85O3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 ceramics, it's approximately Wrec = 120 mJ cm−3, and in Ba0.90Ca0.10Zr0.15Ti0.85O3
9 ceramics, it's approximately Wrec = 120 mJ cm−3, and in Ba0.90Ca0.10Zr0.15Ti0.85O3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 ceramics, it's Wrec = 92.8 mJ cm−3 and so forth. Recently, an energy storage capacity for Pr doped Ba0.85Ca0.15Ti0.9Zr0.1O3 has been documented, reaching Wrec = 81.9 mJ cm−3 and energy storage efficiency of η = 76.4%,51 further demonstrating the improved energy storage performance of the presently investigated materials. Moreover, the compositions with x = 2.5% and x = 5% maintain an efficiency of around 80%, highlighting their strong potential for practical applications.
50 ceramics, it's Wrec = 92.8 mJ cm−3 and so forth. Recently, an energy storage capacity for Pr doped Ba0.85Ca0.15Ti0.9Zr0.1O3 has been documented, reaching Wrec = 81.9 mJ cm−3 and energy storage efficiency of η = 76.4%,51 further demonstrating the improved energy storage performance of the presently investigated materials. Moreover, the compositions with x = 2.5% and x = 5% maintain an efficiency of around 80%, highlighting their strong potential for practical applications.


