 Open Access Article
Open Access ArticleTuning diffusion coefficient, ionic conductivity, and transference number in rGO/BaCoO3 electrode material for optimized supercapacitor energy storage†
Mohsin Shahzada,
Farooq Ahmad *ab,
M. Ibraheema,
Abdul Shakoora,
Shahid M. Ramayc,
M. Rafi Razad and
Shahid Atiq
*ab,
M. Ibraheema,
Abdul Shakoora,
Shahid M. Ramayc,
M. Rafi Razad and
Shahid Atiq *a
*a
aCentre of Excellence in Solid State Physics, University of the Punjab, Lahore 54590, Pakistan. E-mail: satiq.cssp@pu.edu.pk
bInstitute of Molecular Physics Polish Academy of Sciences Poznan, Poznan, Poland. E-mail: farooq.ahmad@ifmpan.poznan.pl
cDepartment of Physics and Astronomy, King Saud University (KSU), Riyadh, Saudi Arabia
dDepartment of Mechanical Engineering, COMSATS University Islamabad, Sahiwal Campus, Sahiwal, Pakistan
First published on 25th February 2025
Abstract
Due to their remarkable cycle stability and outstanding capacitance, ABO3-type perovskite materials have emerged as highly effective electrode materials, delivering remarkable electrochemical performance. In this study, BaCoO3/rGO composites with varying rGO content (0, 5, 10, and 15%), designated as PBCO, BCO-I, BCO-II, and BCO-III, were synthesized using a solvothermal process. These composites were evaluated for their potential as electrode materials in supercapacitor (SC) applications. X-ray diffraction analysis confirmed the presence of well-crystallized samples with a hexagonal phase structure. Field emission scanning electron microscopy revealed the desired level of porosity, well-defined morphologies, and uniformly distributed grains, which are beneficial for electrochemical applications. Elemental analysis verified the stoichiometric composition of the samples. Comprehensive electrochemical characterization was performed using cyclic voltammetry in a 2 M KOH solution, revealing a transition from diffusive control (EDLC) to hybrid capacitor behavior. Additionally, galvanostatic charge–discharge experiments demonstrated that the BCO-III composite exhibited a specific capacity of 90.15 C g−1, an energy density of 21.28 W h kg−1, and a power density of 531.25 W kg−1. The transference number (t+) is found to be 0.2, which means that higher current will be driven through the anion. Further, the sample BCO-III, exhibiting the highest specific capacity, was evaluated for stability and demonstrated a remarkable retention rate of 90% after 5k GCD cycles and a remarkable coulombic efficiency of 94%, with an excellent diffusion rate and ionic conductivity of about 4.51 × 10−14 cm2 s−1, 0.128 S cm−1, respectively, highlighting its significant potential for SC applications.
1. Introduction
Extensive usage of fossil fuels results in excessive greenhouse gas emissions such as methane (CH4) and carbon dioxide (CO2), escalating the threat of world conflict and climate change and its effects on the planet. Therefore, it is essential to advance renewable energy technologies and decarbonize fuel. The sporadic nature of these sources, like solar and wind, continues to be the primary obstacle to increasing the efficiency of renewable energy systems (RESs).1 The only way to solve these challenges is to build a community free of carbon and dependent on clean and renewable energy resources. To meet energy and environmental requirements, the world has been forced to reevaluate its power strategy.2 This rising need has made developing energy storage systems (ESS) with more extensive and better capacities possible. From this perspective, energy from numerous irregular renewable sources, such as wind, waves, and sun, might be considered beneficial sources.3 Therefore, the energy produced from these sources must be stored to be made available wherever required.4 For this purpose, effective energy storage technologies, including batteries and electrochemical SCs, have been explored.5 Over the last two decades, SCs have steadily replaced batteries thanks to their remarkable operating voltage and specific capacitance (Csp).6–10SCs are supposed to be one of the emerging energy storage devices (ESDs) due to their tremendous power density (PD) (105 W kg−1), long cyclic stability (>106 charge–discharge cycle), and low maintenance requirements.11 Unfortunately, because of their energy density (ED), SCs can only be used in systems that require a quick power supply, such as bullet trains and backup power sources.12 There are two categories of SCs based on the energy storage mode. These categories are electric double-layer capacitors (EDLCs) and pseudo-capacitors (PCs).13 The EDLCs store charges through the adsorption/desorption of ions into porous materials (commonly carbon-based).14 They possess exceptional PD but low ED.15 On the other hand, in PCs, the energy storage is governed by fast reversible redox reactions.16 The electrode material for such capacitors is composed of transition metal oxide (TMOs), conducting polymers (CPs), and metal hydroxides.17 These electrode materials exhibit excellent capacitance but poor ED.18
The features of electrode materials will significantly impact the electrochemical behavior of SCs.18 The selected electrode should have strong conductivity and an elevated specific surface area (SSA) to achieve an excellent specific capacity.19 A few years ago, pseudocapacitive materials attracted considerable interest because their energy storage was more than that of EDLCs.20 However, ABO3-type perovskite materials, compared to TMOs and TMDs, are captivating candidates as electrode materials for SCs. Due to their extraordinary electrochemical performance, ABO3-type perovskite materials, such as BaCoO3, SrCoO3, and MnFeO3 have been widely used as electrode materials for SCs for a long time. Such 2D materials have restricted commercial production because of their toxicity and prohibitive costs. In addition to perovskite materials, it is essential to note that cobalt oxide (Co3O4) is inexpensive and easy to make.21–24 Unfortunately, the perovskite materials suffer from low-rate capacitance and limited reversibility; some are uncommon and expensive. Contrarily, carbon-based materials like carbon nanotubes (CNTs) have gained interest as electrode materials for SCs because of their significant electrical conductivity and chemical stability.25
Graphene consists of a continuous thin sheet of carbon with sp2 bonds. Geim and Novoselov identified graphene in 2004 via the ‘scotch tape’ approach, and as a result, graphene is now widely used in many industries. Similarly, derivatives of graphene or functionalized graphene, such as GO and rGO, are assembled using different reduction techniques and are equally favorable.26 Compared to many other carbon compounds, GO, with its exceptional electrical conductivity, mechanical flexibility, and SSA (∼2630 m2 g−1), has become an advanced electrode material for SCs. Electrodes made of Graphene have been found to have good reversibility, minimum intrinsic electrical resistivity, and initial solid discharge capacity.27 Besides these features of rGO, it suffers from agglomeration of layers. To address such challenges, it has been integrated with ABO3-type perovskite oxides like LaCo1−xZnxO3, SrxNi1−xCoO3, etc. Therefore, the effectiveness of perovskite-based and rGO-based composite electrode materials for SC applications should be evaluated compared to other materials.
Sr1−xBaxCoO3 is an important ABO3-type perovskite material among the 2D materials family. Herein, Sr and Ba belong to alkaline earth metals occupying the A-site. In contrast, Co belongs to transition metal occupying the B-site as a cation. This type of perovskite has garnered significant attention for its potential applications in SCs due to its favorable electrochemical properties.28 This material exhibits high electrical conductivity and a rich redox chemistry, which enhances its capacitance performance. Incorporating barium into the strontium cobalt oxide matrix allows for tunable properties, enabling optimization of ionic conductivity and structural stability. Additionally, the layered perovskite structure of Sr1−xBaxCoO3 facilitates efficient ion transport, which is crucial for energy storage applications. Previous research has shown that this material can achieve high specific capacitance and good cycling stability, making it a promising candidate for advanced energy storage technologies. Furthermore, modifying its composition allows researchers to tailor its properties for specific applications in SCs, thus highlighting its significance in energy storage.10,29
In this context, Hadji et al. synthesized LaCo1−xZnxO3 perovskite-type oxides using the sol–gel method where LaCo0.95Zn0.05O3 exhibits a specific capacitance of 300.47 F g−1, which is around fourfold more significant than that of undoped LaCoO3. Additionally, it demonstrates excellent cycle stability, with 85.73% retention after 5000 cycles. The LaCo0.95Zn0.05O3/activated carbon hybrid device has an ED of 36.12 W h kg−1 and retains 81% of its capacitance after 5000 cycles.30 Shafi et al. prepared LaMnO3 perovskite oxides for SCs in one more study. Conventional synthesis methods conducted at temperatures above 500 °C result in the formation of clumped and deformed structures, which diminish the number of active sites. A sustainable method utilizing natural lemon juice as a surfactant is employed to create three-dimensional polyhedron-structured LaMnO3 nanoparticles (NPs). These NPs exhibit improved specific capacitance and can achieve an ED of up to 52.5 W h kg−1 in a symmetric cell arrangement.31 In another study, Coa et al. prepared La1−xSrxCoO3 nanofibers to improve the electrochemical performance of electrode materials for SC. They designed a symmetric and asymmetric device and achieved energy and power densities of about 38 W h kg−1 and 400 W kg−1, respectively. Such novel approaches provide a hopeful pathway for developing high-performance SC materials.32
This study investigates ABO3-type perovskite composites, specifically focusing on the Sr1−xBaxCoO3 series, with particular emphasis on the BaCoO3 (BCO) variant, which was modified by integrating varying concentrations of reduced graphene oxide (rGO). We employed solvothermal synthesis, a method chosen for its environmental sustainability and effectiveness in yielding composites with robust structural integrity and favorable morphological characteristics. This research primarily explores the transition of capacitor behavior from a basic electric double-layer capacitor (EDLC) to a more complex hybrid capacitor with increasing rGO contents. The BCO-III composites with 15% rGO demonstrated superior electrochemical performance in specific capacity, energy, power densities, and remarkable retention capabilities. Additionally, we quantified diffusion coefficients, transference numbers, ionic conductivity, and relaxation times, providing a comprehensive electrochemical profile of these composites. These results contribute valuable understandings of these materials' scalability and practical applicability for advanced energy storage systems, highlighting their potential in SC applications.
2. Experimental
2.1 Synthesis of the Sr1−xBaxCoO3 by sol–gel auto combustion method
The chemical material required to prepare the complete series of the Sr1−xBaxCoO3 (at x = 0.0, x = 0.33, x = 0.67, and x = 1.0) were Sr(NO3)2, Ba(NO3)2, Co(NO3)2, CH4N2O, and NH2CH2COOH. The appropriate quantities of Sr(NO3)2 (2.94 g) and Ba(NO3)2 (2.05 g) were dissolved in 40 mL of deionized water (DIW) in a small beaker. In a separate beaker, 1.315 g of urea and 1.69 g of glycine, serving as fuel agents, were also dissolved in 40 mL of DIW. The molar ratio of the precursor to fuel was adjusted to 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3. After this, all solutions were poured into a beaker to form the collective solution known as a sol. Then, the beaker and the magnetic stirrer were shifted towards the hot plate and stirred for 2 h. As the temperature rose to 95 °C, the beaker began to emit bubbles, indicating the gel formation. The gel continued to thicken due to evaporation and pierced the spin of the magnetic stirrer. When the stirrer was withdrawn, the temperature of the gel had risen to 250 °C, which resulted in self-ignition. After that, the gel-like solution turned into ash. This ash was ground using mortar and pestle to get a fine powder. Then, it underwent calcination at 750 °C for 2 h.
3. After this, all solutions were poured into a beaker to form the collective solution known as a sol. Then, the beaker and the magnetic stirrer were shifted towards the hot plate and stirred for 2 h. As the temperature rose to 95 °C, the beaker began to emit bubbles, indicating the gel formation. The gel continued to thicken due to evaporation and pierced the spin of the magnetic stirrer. When the stirrer was withdrawn, the temperature of the gel had risen to 250 °C, which resulted in self-ignition. After that, the gel-like solution turned into ash. This ash was ground using mortar and pestle to get a fine powder. Then, it underwent calcination at 750 °C for 2 h.
2.2. Preparation of graphene oxide (GO)
A modified Hummers' method was adopted to prepare the GO by oxidizing pure graphite powder. Typically, 25 mL of H2SO4 and 4 mL of NaNO3 (volume ratios 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6) were placed into a 200 mL beaker in an ice bath to stir for one h. The mixing solution was then supplemented with 1.0 g of graphite powder while aggressively stirring. The solution turned black because of the graphite powder. Then, 1.32 g of potassium permanganate (KMnO4) was subsequently added to the suspension by keeping the temperature below 20 °C and stirring for 3 h. After stirring, 25 mL of DIW was added dropwise to the reaction system at a temperature lower than 50 °C to start the oxidation. The color of the solution changed to dark brown, which indicated the formation of GO. An additional 100 mL of DIW was added to the solution to further dissolve the graphite and ensure any insoluble material's dispersion. 5 mL of 30% H2O2 was steadily added to the solution to remove the unrestricted amount of KMnO4. The solution was washed with 5% HCL to eliminate metal ions and then centrifuged at 450 rpm for 10 min. Conclusively, it was dried in an oven to procure the powder of GO.
6) were placed into a 200 mL beaker in an ice bath to stir for one h. The mixing solution was then supplemented with 1.0 g of graphite powder while aggressively stirring. The solution turned black because of the graphite powder. Then, 1.32 g of potassium permanganate (KMnO4) was subsequently added to the suspension by keeping the temperature below 20 °C and stirring for 3 h. After stirring, 25 mL of DIW was added dropwise to the reaction system at a temperature lower than 50 °C to start the oxidation. The color of the solution changed to dark brown, which indicated the formation of GO. An additional 100 mL of DIW was added to the solution to further dissolve the graphite and ensure any insoluble material's dispersion. 5 mL of 30% H2O2 was steadily added to the solution to remove the unrestricted amount of KMnO4. The solution was washed with 5% HCL to eliminate metal ions and then centrifuged at 450 rpm for 10 min. Conclusively, it was dried in an oven to procure the powder of GO.
2.3 Synthesis of rGO
The solvothermal technique was employed aiming to reduce the GO sheets into rGO. Initially, a precise quantity of 50 mL of undiluted ethanol was wholly combined with a specified amount of GO, which had previously been evenly distributed in water at a 2 mg mL−1 concentration. The mixture underwent heating at 70 °C for 3 h and subjected to sonicate for 2 h, followed by 3 h. The mixture was swirled using a magnetic stirrer while maintaining a temperature of approximately 70 °C. Subsequently, the mixture was put into a 100 mL autoclave coated with Teflon. The mixture was then heated for 3 h at 70 °C. The elevated pressure and temperature within the autoclave aided the decrease of GO. After the autoclave reached ambient temperature, the resultant product was gathered. A high-quality, deep-brown powder was acquired after the washing and drying process.2.4 Synthesis of the PBCoO3/rGO composites
Four samples were synthesized using a solvothermal method: pure BaCoO3 (PBCO) and BaCoO3 with varying percentages of rGO (5%, 10%, 15%). These samples were labeled PBCO, BCO-I, BCO-II, and BCO-III, respectively. First, PBCO and rGO were united in ethanol and sonicated for 1 h to ensure complete mixing. The solution was stirred using a magnetic stirrer for 4 h. The solution was carefully moved toward a Teflon-lined autoclave after the stirring process. This autoclave was placed inside a muffle furnace and heated at 140 °C for 5 h. After heating, the samples were removed from the autoclave, thoroughly washed to eliminate impurities, and then dried in an oven. This method effectively generates samples.2.5 Fabrication of electrode
The electrode preparation involved three key steps. Initially, nickel foam (NF) pieces, each measuring 1 × 2 cm, underwent an etching process. This process required immersing the NF in a 50 mL acidic solution, prepared by mixing 13 mL of concentrated H2SO4 with 37 mL of distilled water. Following the etching, the NFs were thoroughly rinsed with distilled water and subsequently dried. To create the binder solution, 10 mL of DMF was combined with 200 mg of PVDF. This mixture was stirred on a hot plate at 150 rpm for 30 min to ensure complete dissolution and uniform mixing. The slurry preparation involved maintaining a precise mass ratio of 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 among the active material, the binder solution, and activated carbon. Specifically, the mass of the active material used was 2 mg. The slurry mixture was heated on a hot plate at 450 rpm for 8 h to achieve a homogeneous consistency. Once synthesized, the slurry was uniformly applied to the etched NF. The coated NFs were then transferred to an oven and dried for 30 min to ensure thorough drying and adherence of the slurry to the NFs substrate. These coated NF pieces were then employed as electrodes for further electrochemical analysis in SC applications. The complete procedure of synthesizing the active substance and fabricating the electrode is illustrated in Fig. 1.
1 among the active material, the binder solution, and activated carbon. Specifically, the mass of the active material used was 2 mg. The slurry mixture was heated on a hot plate at 450 rpm for 8 h to achieve a homogeneous consistency. Once synthesized, the slurry was uniformly applied to the etched NF. The coated NFs were then transferred to an oven and dried for 30 min to ensure thorough drying and adherence of the slurry to the NFs substrate. These coated NF pieces were then employed as electrodes for further electrochemical analysis in SC applications. The complete procedure of synthesizing the active substance and fabricating the electrode is illustrated in Fig. 1.
3. Results and discussions
In this work, we examined the crystalline structure of the materials using XRD patterns produced by a Bruker D8 advanced X-ray diffractometer using CuKα radiation (λ = 1.54 Å). We installed a Nova Nano SEM-450 FESEM for a detailed surface study. Additionally, compositional analysis of the samples was done using EDX spectroscopy with an instrument from Oxford. Textural features of prepared samples were revealed via Braunauer–Emmett–Teller (BET) analysis. All electrochemical parameters of the prepared electrodes were tested using a 3-electrode cell system. The experimental setup contained a reference electrode (Ag/AgCl) and a counter electrode (Pt wire) submerged in a 2 M KOH electrolyte. Cyclic voltammetry (CV) curves, electrochemical impedance spectroscopy (EIS), and galvanostatic charge–discharge (GCD) curves were acquired using an electrochemical workstation (CHI 660E).3.1 Structural analysis
Fig. 2(a) upper panel depicts the standard diffraction patterns along with the experimental XRD pattern of Sr1−xBaxCoO3 samples with compositions x = 0.0, x = 0.33, x = 0.67, and x = 1.0. The distinct peaks observed in these XRD patterns confirm the crystalline nature of the samples. For the sample with x = 0 (SrCoO3), diffraction peaks are present at 2θ values of 33.10°, 40.70°, 47.43°, 59.01°, and 69.34° corresponding to the crystallographic planes (400), (402), (440), (622) and (800), respectively. This pattern aligns with the tetragonal crystal structure, consistent with the ICSD card no. 00-039-1084, which describes SrCoO3 in the P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) mbm space group (221). The samples with x = 0.33 (Sr0.67Ba0.33CoO3) and x = 0.67 (Sr0.33Ba0.67CoO3) exhibit diffraction peaks at nearly identical angles to SrCoO3. For the sample with x = 1.0 (BaCoO3), diffraction peaks are observed at 2θ values of 25.92°, 31.76°, 41.43°, 42.18°, 53.48°, 56.85° corresponding to the Miller planes (101), (110), (201), (102), (202), and (300) respectively. This pattern confirms a hexagonal crystal structure, in agreement with the ICSD card no. 00-052-1612. The complete substitution of Sr by Ba leads to the transformation from a tetragonal to a hexagonal structure. The XRD patterns of Sr1−xBaxCoO3 thus reveal the crystalline nature of these materials. The SrCoO3 sample exhibits a tetragonal structure, while the BaCoO3 sample demonstrates a hexagonal structure. With the addition of Ba (x = 0.33 and x = 0.67), peaks of the pure phase (SrCoO3) started to disappear gradually. Upon complete substitution, the crystal structure transitions to a hexagonal phase (x = 1.0). The crystal structures of pure samples are shown in Fig. 2(b) and (c).
mbm space group (221). The samples with x = 0.33 (Sr0.67Ba0.33CoO3) and x = 0.67 (Sr0.33Ba0.67CoO3) exhibit diffraction peaks at nearly identical angles to SrCoO3. For the sample with x = 1.0 (BaCoO3), diffraction peaks are observed at 2θ values of 25.92°, 31.76°, 41.43°, 42.18°, 53.48°, 56.85° corresponding to the Miller planes (101), (110), (201), (102), (202), and (300) respectively. This pattern confirms a hexagonal crystal structure, in agreement with the ICSD card no. 00-052-1612. The complete substitution of Sr by Ba leads to the transformation from a tetragonal to a hexagonal structure. The XRD patterns of Sr1−xBaxCoO3 thus reveal the crystalline nature of these materials. The SrCoO3 sample exhibits a tetragonal structure, while the BaCoO3 sample demonstrates a hexagonal structure. With the addition of Ba (x = 0.33 and x = 0.67), peaks of the pure phase (SrCoO3) started to disappear gradually. Upon complete substitution, the crystal structure transitions to a hexagonal phase (x = 1.0). The crystal structures of pure samples are shown in Fig. 2(b) and (c).
 | ||
| Fig. 2 (a) Standard diffraction and XRD patterns of Sr1−xBaxCoO3 and (b and c) crystal structures of SrCoO3 and BaCoO3. | ||
3.2 Morphological analysis
The morphological features of Sr1−xBaxCoO3 at the substitution of x = 0, x = 0.33, x = 0.67, and x = 1.0 were analyzed from SEM images obtained through FESEM, as depicted in Fig. 3(a–d). The images were captured at 105× magnification. These analyses were carried out to find the shape and size of the grains present in the samples. Fig. 3(a) shows that at x = 0, the sample is SrCoO3. It is noted that a large number of spherical-size grains with a tiny uniform distribution are present. The sample's average grain size is measured to be 0.52 μm. There are some visible gaps can also be seen. It reveals the small uniform pattern through which ions can easily penetrate. At x = 0.33, the sample is Sr0.67Ba0.33CoO3, as shown in Fig. 3(b). It shows that substituting a small amount of Barium (Ba) has transferred its morphology. As the substitution amount is raised, bigger non-uniform grains with clear grain boundaries and an average grain size of 0.5 μm are observed. Some pores can also be seen where the grains are loosely connected. At x = 0.67, the sample is Sr0.33Ba0.67CoO3, as represented in Fig. 3(c). By increasing the further substitution of Ba, the grains are closely packed with each other, and the average grain size is found to be 0.53 μm. The porosity and voids have also increased, proving that this sample shows good electrochemical behavior.9,29 For x = 1.0, Fig. 3(d) shows the sample of BaCoO3. The small agglomeration and the presence of voids can also be observed. The average particle size is found to be 0.58 μm. All the microstructures are good porous. Ions can easily be transferred into the electrode's internal structure during the charging and discharging. | ||
| Fig. 3 (a–d) FESEM images of Sr1−xBaxCoO3 (x = 0.00, 0.33, 0.67, and 1.00) and (e) EDX spectra of Sr1−xBaxCoO3 (x = 0.00, 0.33, 0.67, and 1.00). | ||
3.3. Elemental analysis
EDX spectroscopy was conducted using a Nova Nano SEM 450 scanning electron microscope to ensure the elemental composition of the prepared samples. The EDX analysis verified the presence of Co, O, C, Ba, Sr, and Au, with the detected elemental ratios aligning with the predetermined stoichiometric values. Fig. 3(e) illustrates the EDX spectrum for the composite of SrCoO3 (x = 0). In this sample, peaks for Sr and Co are observed, indicating their significant presence. A minor peak for C is also detected, attributed to the carbon adhesive tape used to mount the sample on the aluminum holder. For the sample with x = 0.33 (Sr0.67Ba0.33CoO3), the substitution of barium introduces multiple intensity peaks for Ba and O. This diversity arises due to the different characteristic X-rays emitted by a single element.33 Ba peaks' intensity increases while Sr peaks' intensity decreases, indicating successful barium substitution. The presence of Au results from the gold coating applied to enhance sample conductivity and improve contrast during SEM analysis. As the barium content increases to x = 0.67 (Sr0.33Ba0.67CoO3), the EDX spectrum shows further enhancement in the intensity of Ba peaks and a corresponding reduction in Sr peak intensity. Finally, for the sample with x = 1.0 (BaCoO3), Ba exhibits the major peaks while Sr peaks are absent, confirming the complete replacement of Sr by Ba. The elements' mol percentage (wt%) values (C, O, Co, Sr, Ba, and Au) were quantified using EDX, as presented in Table S1.† The data indicate a progressive decrease in the mol% of Sr and an associated increase in the mol% of Ba with increasing barium substitution. This corroborates the successful incorporation of Ba into the SrCoO3 lattice and corresponding changes in elemental composition.3.4. Braunauer–Emmett–Teller (BET) analysis
The textural characteristics of prepared samples were revealed by nitrogen adsorption/desorption isotherms at 77 K, acquired through BET analysis in order to highlight the availability of active sites from specific surface area (SSA), pore size, and volume. Where N2 gas, due to its inert nature, cost-effectiveness, and high sensitivity (more helpful in the detection of small-sized pores), was used as an adsorbate. According to the IUPAC classification, the displayed N2 adsorption/desorption isotherms in Fig. 4 are encountered as type IV isotherms, which are characteristics of mesoporous structures and are associated with PBCO, BCO-I, BCO-II, and BCO-III-based samples. Moreover, the low relative pressure region (P/P0 < 0.1) suggests the monolayer coverage that indicates the occupancy of gas molecules to be adsorbed at available surfaces, while the relative pressure region below the 0.9 shows the multilayer coverage of gas molecules due to subsequent layers by Van-der Wall forces. The region right after the multilayer coverage comes the plateau region, indicating the saturation point of multilayer coverage with restricted relative pressure of P/P0 > 0.9 to 1. From Fig. 4, it can be seen that isotherms of BCO-I, BCO-II, and BCO-III showed a clear upward shift due to an increase in SSA attributed 5, 10, and 15% rGO content compared to PBCO at the plateau region. The highest upward shift of BCO-III towards the y-axis suggested the highest adsorbed quantity of nitrogen gas compared to others due to enhanced SSA. Furthermore, the BJH approach opted to calculate the SSA from N2 adsorption/desorption isotherms for PBCO (4.97 m2 g−1), BCO-I (9.37 m2 g−1), BCO-II (8.61 m2 g−1), and BCO-III (11.64 m2 g−1), as shown in Table S2.† This analysis confirmed that BCO-III demonstrated fascinating textural features, evidencing its potential as the best electrode material. | ||
| Fig. 4 Illustration of nitrogen adsorption/desorption isotherms for PBCO, BCO-I, BCO-II, and BCO-III. | ||
3.5 Electrochemical analysis
CV is a fundamental technique employed to investigate the electrochemical characteristics of materials. It enables researchers to comprehend the reactions of substances when the voltage is altered at varying rates, yielding valuable insights into redox mechanisms, electron transport, and capacitive characteristics. During charging, the BaCoO3 undergoes oxidation by transitioning Co3+ to Co4+ with the loss of an electron transferred through an external circuit. Using KOH as an electrolyte, the OH− ions participate,| BaCoO3 + OH(aq)− ↔ BaCoO3(4+) + e− + H2O |
While upon discharging, the transitioning of Co3+ to Co4+ demonstrates the reversibility by receiving an electron and undergoing the reduction through absorption of OH− ions from the electrolyte as,
| BaCoO3(4+) + e− + H2O ↔ BaCoO3 + OH(aq)− |
After receiving an electron, BaCoO3(4+) returns to its original state. BaCoO3 and OH− ions are released back into the electrolyte, consuming the water.
Fig. 5(a–d) presents the results of CV studies, which comprehensively analyze the charge storage dynamics and capacities of PBCO and its composites. The CV curves, acquired with scan rates ranging from 5 to 100 mV s−1, exhibit clear redox peaks in each cycle. These peaks indicate that the main capacities arise from pseudo-capacitive (PC) and electrical double-layer capacitance (EDLC) behavior, which are associated with faradaic and non-faradaic redox reactions. Even when the scan rates are increased, the continuous symmetrical patterns of the peaks suggest that the charge storage dynamics maintain exceptional cycle reversibility and stability.34 While minor changes have been observed in the anodic and cathodic peaks, these shifts are caused by polarization effects and do not substantially impact the overall shape of the peaks. The voltammograms obtained for PBCO display voltammograms with rectangular shapes, which are distinctive features of electrochemical behavior beyond simple EDLC. EDLC refers to the storage of charge through electrostatic processes at the electrode surface, resulting in the transfer of non-faradaic charge. In this context, the distinct peaks observed in the voltammograms of PBCO indicate the material's oxidation and reduction processes. The presence of these peaks suggests that the material undergoes reversible redox reactions, contributing to efficient charge storage. However, the CV curves for BCO-I, BCO-II, and BCO-III, depicted in Fig. 5(b–d), demonstrate different characteristics with narrow and low-intensity peaks. This suggests that although both PC and EDLC play a role in the charge/discharge processes, the influence of redox reactions is insignificant, with EDLC being the primary mechanism. The behavior of EDLCs is determined by the aggregation of charges at the interface between the electrode and electrolyte, resulting in the formation of an EDLC. This process is entirely physical, devoid of any chemical processes, and leads to the formation of a bilayer of ions on the surface of the electrode. Materials that demonstrate EDLC often produce a CV curve with a more rectangular form and fewer noticeable peaks than materials with assertive PC behavior. When integrating rGO content into PBCO, a transition from traditional EDLC behavior to hybrid capacitor behavior is observed. This shift is indicated by the combination of capacitive behavior observed in the resultant material. The increased conductivity and significant SSA of rGO play a crucial role in this transition. Consequently, the composite displays attributes resembling EDLCs and PCs, demonstrating hybrid or battery-like properties.
 | ||
| Fig. 5 CV curves at different scan rates for (a) PBCO, (b) BCO-I, (c) BCO-II, (d) BCO-III, and (e) comparison of all samples at 5 mV s−1, and (f) scan rate vs. specific capacity. | ||
The hybrid nature of rGO arises from its capacity to expedite electron movement and offer an extensive SSA for charge storage, enhancing overall performance and emulating the attributes of battery-type storage.35,36
The specific capacity, measured in coulombs per gram (C g−1), quantifies the charge an electrode can store. Eqn (1) performs the calculation.
 | (1) |
Table 1 shows that BCO-III has the largest Qs compared to all other samples, regardless of the scan rates. When the scan rate is set to 5 mV s−1, Qs reaches its highest value at 143.48 C g−1. The outstanding performance of this material can be due to its highly porous and evenly distributed nanostructure, as evidenced by the FESEM image in Fig. 3(d). The particular Qs values for each scan rate are shown in Fig. 5(f). As the scan rates increase, there is an evident and expected reduction in the Qs values. The decrease in performance is attributed to the diminished ability of electrolytic ions to penetrate the electrode material at faster scanning speeds. At higher scanning speeds, only the easily reachable surface sites participate in the transfer of charges, reducing the overall efficiency of the electrochemical process. This occurs because the internal active sites, which contribute substantially to the capacitance at lower scan rates, are not fully utilized.37 The relationship between scan rates and Qs highlights the significance of optimizing the electrode's structure and morphology to promote ion accessibility and enhance Qs, particularly at higher operational speeds. The permeable configuration of BCO-III enables effective ion migration and rapid charge–discharge cycles, which enhances its exceptional efficiency. Nevertheless, decreasing Qs at higher scan rates emphasizes achieving an optimal SSA and pore structure combination to maximize the material's electrochemical consumption.15,37
| Specific capacity (C g−1) | ||||
|---|---|---|---|---|
| Scan rate (mV s−1) | PBCO | BCO-I | BCO-II | BCO-III |
| 5 | 68.559 | 109.676 | 137.020 | 143.448 |
| 10 | 49.598 | 78.932 | 89.781 | 101.792 |
| 20 | 33.560 | 54.111 | 56.013 | 67.755 |
| 30 | 25.263 | 42.233 | 40.920 | 57.213 |
| 40 | 20.782 | 34.980 | 30.556 | 40.790 |
| 50 | 17.420 | 29.916 | 25.721 | 34.062 |
| 70 | 13.585 | 23.659 | 19.255 | 25.857 |
| 100 | 8.858 | 17.916 | 13.672 | 18.877 |
Based on the transitions mentioned above, the theoretical capacity of a material used in electrochemical cells (such as a battery or hybrid capacitor) is a measure of its potential to store electrical charge, which is governed by the number of charge carriers (electrons or ions) involved in the electrochemical reaction. In this case, we are focusing on the theoretical capacity of BaCoO3 when used in an electrochemical cell in the presence of KOH (potassium hydroxide) as the electrolyte. The theoretical capacity can be determined using Faraday's Law, which relates the total charge Q (in coulombs) transferred during a reaction to the amount of substance that undergoes electrochemical change. The formula for the theoretical capacity is given by,
 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485 C mol−1, and Mw = 244.26 g mol−1 is the theoretical capacity in C g−1. Thus, the theoretical capacity of BaCoO3 is approximately 394.77 C g−1.
485 C mol−1, and Mw = 244.26 g mol−1 is the theoretical capacity in C g−1. Thus, the theoretical capacity of BaCoO3 is approximately 394.77 C g−1.
The experimental capacity of a material is typically lower than its theoretical capacity due to limitations in the electrochemical process, particularly in the ability to fully extract the charge carriers (in this case, potassium ions, K+) from the lattice of the host material. While the theoretical capacity assumes complete extraction of K+ ions, a portion of these ions remains trapped within the lattice structure at higher voltages, significantly above the cutoff potential. This occurs because, as the voltage increases, the interaction between the K+ ions and the host material strengthens, making removing these ions more difficult. The electrochemical reaction slows down, and above a particular potential, the energy required to desolvate further and extract the remaining K+ ions exceeds the applied voltage. As a result, these K+ ions are not accessible for the charge–discharge cycle, limiting the actual capacity of the material. Thus, the difference between theoretical and practical capacity can be attributed to this partial extraction of ions, which is often further exacerbated by side reactions, structural degradation of the material, or inefficient ion transport at higher voltages. Consequently, while the theoretical capacity provides an idealized estimate, the practical capacity reflects the real-world performance of the material, influenced by these electrochemical constraints.
The theoretical framework has been employed to investigate further how electric charge is stored within the gadget to confirm its behavior and contribution. In electrochemical studies, the b-value calculated from Power's law is used to find a sample's charge storage mechanism, as shown in the equation below.
ipeak = avb or log(ipeak) = b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(v) + log(a) log(v) + log(a)
| (3) |
Herein, a and b are adjustable parameters, representing the intercept and slopes of redox peaks at specific scan rates upon linear fitting using Origin software. Specifically, a, b-value of 0.5 indicates a diffusion-controlled process, while a, b-value of 1 shows a capacitive process. However, a, b-value between 0.5 and 1 suggests that the sample has a hybrid storage mechanism, combining diffusion-controlled and capacitive process elements.38,39 This mixed behavior indicates that the material can store charge through both faradaic reactions and non-faradaic processes, and this is what we have seen in Fig. 6(a–d). The overall Qs of energy storage devices are composed of two components: capacitive and diffusive contributions. These components are analyzed via Dunn's model, which is applied to the CV graphs.
| I(v) = k1v + k2v1/2 | (4) |
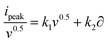 | (5) |
 | ||
| Fig. 6 (a–d) Values of b calculated from the CV curves and (e–h) values of k1 and k2 for PBCO, BCO-I, BCO-II, and BCO-III, respectively. | ||
However, Fig. 7 (a–d) shows the samples' combined capacitive and diffusive contributions at multiple scan rates obtained after putting k1 and k2 stand for slop and intercept values acquired from the linear fitting of v1/2 vs. ipeak/v1/2 in eqn (5) at different scan rates, as shown in Fig. 7(a–d) and S2–S5.† The linear graphs Fig. 6(a) and related b-values suggest that the charge storage mechanism is solely controlled by diffusion-controlled processes, with almost 100% contribution at all scan rates and absence of capacitive behavior. This suggests a robust, non-faradaic process, which is common in materials where the movement of ions plays a crucial role in storing charges. However, Fig. 7 (a–d) exhibits a combination of diffusion-controlled and capacitive processes that collectively contribute to the overall charge storage. At lower scan speeds (where v = 5 mV s−1), the diffusion-controlled contribution accounts for 80% of the total charge storage, while the capacitive contribution makes up 20%. This dominance of diffusion-controlled processes at low scan rates can be attributed to the effective diffusion of ions in the electrolyte, allowing them to interact with the electrode surface fully. With the scan rate increasing, the capacitive contribution reaches 44% when v = 50 mV s−1, while the diffusion-controlled contribution decreases to 56%. This shift implies that at higher scan speeds, the rapid charge–discharge cycles limit the time available for ion diffusion, thus enhancing the contribution of capacitive processes. The faster capacitive processes are favored as they rely on the immediate response of the electrode material to the applied voltage rather than the slower diffusion of ions. Including rGO further influences the observed behavior in Fig. 7(b); due to its excellent electrical conductivity, rGO facilitates rapid electron transfer, thereby enhancing the capacitive response of the electrode. This conductive nature of rGO and its high SSA and porous structure contribute to the hybrid capacitor behavior, as observed in Fig. 7(a–d). The Fig. 7(c) shows a notable rise in capacitive behavior with increasing scan rates. Initially, at v = 5 mV s−1, the diffusion-controlled contribution is 74%, and the capacitive contribution is 26%. At v = 50 mV s−1, these contributions shift to 47% and 53%, respectively, indicating a near equilibrium. This shows the enhanced capacitive response at higher scan rates and the importance of ion diffusion at lower rates, showcasing the system's efficient charge storage capabilities across varying conditions. Fig. 7(d) shows the highest capacitive contributions among the figures. At v = 5 mV s−1, the diffusion-controlled contribution is 60%, and the capacitive contribution is 40%. As the scan rate increases to v = 50 mV s−1, the capacitive contribution surges to 68%, while the diffusion-controlled contribution drops to 32%. This significantly shifts towards capacitive storage mechanisms at higher scan rates, emphasizing the material's ability to transition from non-faradaic to faradaic behavior.
 | ||
| Fig. 7 (a–d) Ratios of capacitive and diffusive controlled process, (e) capacitive vs. scan rate, and (f) diffusive vs. scan rate, for PBCO, BCO-I, BCO-II, and BCO-III, respectively. | ||
Fig. 7 confirms that faradaic and non-faradaic processes affect the device's electrochemical performance. It concisely depicts the capacitive and diffusive control elements included in the device. Fig. 7(e) shows that the capacitive-controlled division significantly increases with the increase in scan rate. In contrast, Fig. 7(f) shows a significant decrease in the diffusive-controlled fraction under comparable conditions.37
In a nutshell, PBCO exhibits prominent EDLC behavior due to its substantial redox activity. In contrast, BCO-I, BCO-II, and BCO-III predominantly display hybrid behavior, encompassing EDLC and PC behaviors. As the concentration of rGO increases, the materials shift towards a more hybrid capacitive behavior. It can be observed by modifying peaks and alterations in their electrochemical behavior while maintaining a restricted amount of redox activity. The variability in the behavior of these materials directly impacts the performance and utilization of these materials in energy storage devices.
An electrode material's electrochemical surface area (ECSA) describes the active sites facilitating redox activity. It is usually measured through double-layer capacitance (Cdl) from the non-faradaic mechanism region, where no current change due to potential variation is observed. In our case, this region is observed between 0.01 V and 0.08 V, as depicted in Fig. S1(a–d)† for all samples, indicating the values of Cdl from the slope after linear fitting of scan rate vs. current densities (ΔJ = (Ja − Jc)/2) at multiple scan rates.40 The eqn (6) has been used to quantify the ESCA.
 | (6) |
Eqn (6) helps calculate the ECSA of PBCO, BCO-I, BCO-II, and BCO-III-based electrode materials to be 7.45, 3.80, 7.10, and 10.10 cm2, respectively.
GCD testing, also known as constant current charge–discharge, is a fundamental electrochemical technique employed to characterize the performance of energy storage devices, such as SCs and batteries. Fig. 8(a–d) depicts the GCD profiles of PBCO3 and its composites obtained at 5 to 50 mA. Each graph illustrates the voltage response over time for both the charging and discharging cycles. The curves demonstrate a notable level of symmetry, suggesting exceptional electrochemical reversibility and stability. The duration of both charging and discharging cycles reduces with increased current density, indicating a faster rate of electrochemical reactions at higher currents. Fig. 8(e) depicts the correlation between Qs in C g−1 and current density (A g−1) for PBCO and its composites. It has been noted that the value of Qs falls as the current density increases in all samples. This is a common occurrence caused by the shorter time for ion diffusion at higher current densities. However, adding rGO greatly improves the conductivity at all electric current levels.41 BCO-III exhibits the highest Qs, followed by samples BCO-I and BCO-II. To calculate Qs, PD, and ED following equations were used;
 | (7) |
 | (8) |
 | (9) |
 | ||
| Fig. 8 GCD curves at different current densities for (a) PBCO, (b) BCO-I, (c) BCO-II, (d) BCO-III, and (e) current density vs. specific capacity, and (f) power density vs. energy density. | ||
| Sample | Current density (A g−1) | Discharging time (s) | Specific capacity (C g−1) | Energy density (W h kg−1) | Power density (W kg−1) |
|---|---|---|---|---|---|
| PBCO | 0.62 | 50.27 | 31.41 | 7.41 | 531.25 |
| 1.25 | 18.60 | 23.25 | 5.49 | 1062.5 | |
| 2.50 | 5.24 | 13.10 | 3.09 | 2125 | |
| 3.75 | 2.04 | 7.65 | 1.29 | 3187.5 | |
| 5.00 | 1.09 | 5.48 | 1.80 | 4250 | |
| BCO-I | 6.25 | 0.59 | 3.68 | 0.87 | 5312.5 |
| 0.62 | 85.61 | 53.50 | 12.63 | 531.25 | |
| 1.25 | 33.03 | 41.29 | 9.75 | 1062.5 | |
| 2.50 | 10.58 | 26.45 | 6.24 | 2125 | |
| 3.75 | 4.88 | 18.29 | 4.32 | 3187.5 | |
| 5.00 | 2.91 | 14.55 | 3.43 | 4250 | |
| 6.25 | 1.89 | 11.85 | 2.79 | 5312.5 | |
| BCO-II | 0.62 | 115.30 | 72.06 | 17.01 | 531.25 |
| 1.25 | 44.87 | 56.08 | 13.24 | 1062.5 | |
| 2.50 | 13.47 | 33.67 | 7.95 | 2125 | |
| 3.75 | 6.35 | 23.81 | 5.62 | 3187.5 | |
| 5.00 | 6.80 | 34.01 | 8.02 | 4250 | |
| 6.25 | 3.30 | 20.62 | 4.87 | 5312.5 | |
| BCO-III | 0.62 | 144.25 | 90.15 | 21.28 | 531.25 |
| 1.25 | 53.49 | 66.86 | 15.78 | 1062.5 | |
| 2.50 | 17.50 | 43.75 | 10.33 | 2125 | |
| 3.75 | 8.58 | 32.17 | 7.59 | 3187.5 | |
| 5.00 | 5.32 | 26.60 | 6.28 | 4250 | |
| 6.25 | 3.45 | 21.56 | 5.91 | 5312.5 |
| Sample | Specific capacitance (F g−1) | Energy density (W h kg−1) | Power density (W kg−1) | Cyclability (%) | References |
|---|---|---|---|---|---|
| CoO3/MWCNTs | 202 | 25 | 900 | — | 42 |
| LaCoO3/rGO | 317 | — | — | 75% after 5k cycles | 43 |
| SrCoO3 | 303 | — | — | 50% after 10k cycles | 44 |
| NiO/rGO | 171.3 | — | — | 20% after 2k cycles | 45 |
| CuS/rGO | 235 C g−1 | 43 | 1426 | 95% after 2k cycles | 46 |
| Ta substituted SrCoO3 | 227.91 C g−1 | 22.82 | 775.09 | 90% after 5k cycles | 47 |
| Fe substituted SrCoO3 | 526.6 | 26.2 | 800 | 86% after 5k cycles | 48 |
| rGO/TiO2 | 15.02 | 2.58 | 4000 | — | 49 |
| BaCoO3/rGO | 90.15 C g−1 | 21.28 | 531 | 90% after 5k cycles | This work |
Fig. 8(f) displays the Ragone plot, illustrating the correlation between ED and PD for the samples. The plot demonstrates that the addition of rGO not only increases the Qs but also enhances the ED of the materials. To evaluate the performance of the electrode, we conducted an extensive cyclic stability test on BCO-III, performing 5000 charge–discharge cycles at a current of 5 mA. The result in Fig. 9 indicates that BCO3-III has an impressive lifespan, retaining 90% of its initial capacity after 5000 cycles and demonstrating a remarkable coulombic efficiency of 94%. This excellent retention can be attributed to the inclusion of rGO within the BCO-III matrix and the practical synthesis achieved through the solvothermal process. The presence of rGO enhances the structural integrity and electrical conductivity of BCO-III, thereby improving its durability and performance during repeated cycling. Additionally, the solvothermal synthesis method ensures a homogeneous distribution of rGO within the matrix, contributing to the overall stability and efficiency of the electrode. This stability under prolonged cycling demonstrates the potential of BCO-III for use in high-performance energy storage devices.50
EIS measurements were performed across a frequency spectrum of 10−2 to 105 Hz to elucidate the ion diffusion and electron transfer characteristics. Fig. 10 depicts the resultant Nyquist plots and the equivalent circuit model derived from the EIS data. The Nyquist plots depict the correlation between the imaginary component of impedance (Z′′) and the fundamental element of impedance (Z′). They provide insights into the resistance and capacitive properties of the electrode materials.51
The Nyquist plot of PBCO, as seen in Fig. 10(a), displays a prominent semicircle, which signifies a higher charge transfer resistance (Rct). This indicates that PBCO has a poorer conductivity and lacks sufficient charge transfer at the contact between the electrode/electrolyte interface. When rGO is added at a low concentration (BCO-I), as depicted in Fig. 10(b), the diameter of the semicircle reduces slightly, suggesting a moderate decrease in Rct. This may be attributed to enhanced conductivity optimization arising from the effective dispersion of rGO. When the concentration of rGO reaches a moderate level (BCO-II), as seen in Fig. 10(c), the diameter of the semicircle shrinks even further. This indicates a lower Rct compared to BCO-I. At modest quantities of rGO, the material is likely to be well dispersed, which improves the mobility of electrons and reduces resistance. Fig. 10(d) represents the highest concentration of rGO (BCO-III). At this concentration, the semicircle is the shortest, which suggests the most favorable Rct. The notable reduction in Rct is due to the elevated concentration of rGO, which results in enhanced conductivity and charge transfer efficiency.52
The linear segments observed at low frequencies in the Nyquist plots indicate the Warburg impedance, which is linked to the diffusion of ions in the electrolyte. The significant reduction in the slope seen in the BCO-III linear zone indicates remarkable ion transport, providing additional proof of rGO's enhancement of electrochemical performance.53 Biologic EC Lab V11.6 was used to measure all EIS parameters, as listed in Table 5.
Moreover, we calculated the relaxation time for different materials based on the Bode plot of the frequency phase relationship, as depicted in Fig. 10(e). This relaxation time indicates how long a SC returns to normal after distraction. It measures energy dissipation and is linked to the SC's internal resistance. A longer relaxation time means elevated internal resistance, which can reduce the SC's ability to deliver power efficiently. For the BCO-III composite, the relaxation time is 0.055 s, which is significantly lower than that of PBCO, BCO-I, and BCO-II.54 Table 4 presents the calculated values of relaxation time from the Bode plot.
3.6. Diffusion coefficient
To evaluate the electrochemical behavior of the prepared samples with KOH as the electrolyte, their diffusion coefficients were determined using eqn (10).
 | (10) |
 | (11) |
The Nernst equation can be generalized into eqn (12).
 | (12) |
The diffusion coefficient plays a vital role in the electrochemical performance of materials. A higher diffusion coefficient typically correlates with better electrochemical performance, implying faster ion transport within the electrolyte, leading to more efficient redox reactions at the electrode surface. This efficiency is crucial for applications such as batteries, supercapacitors, and fuel cells, where the rate of ion transport can significantly affect the overall device performance. For instance, BCO-III, with the highest diffusion coefficient, would likely exhibit the best electrochemical performance among the samples studied, making it a promising candidate for applications where rapid ion transport is necessary. On the other hand, BCO-II, with the lowest diffusion coefficient, may suffer from slower reaction kinetics, potentially limiting its performance in similar applications. Fig. 10(f) shows the linear relationship between ω−1/2 and Z′ in the low-frequency region of the Nyquist plots, resulting in the Warburg coefficient (δ) obtained from slop for all prepared samples listed in Table 5. Moreover, the more significant value of δ is indicative of poorer diffusion, and lower reflects the efficient ion diffusion; that's what we have estimated for PBCO to be approximately 238.40 Ω s−1/2 and for BCO-III to be 44.36 Ω s−1/2, suggesting that BCO-III proved to be a potential candidate for good electrochemical performance.55–58
| Sample | Rs (Ω) | Rct (Ω) | C3 (F) | DK1+ (cm2 s−1) | δ (Ω s−1/2) | σ (S cm−1) | Transference number (t+) |
|---|---|---|---|---|---|---|---|
| PBCO | 0.94 | 0.0116 | 0.17 | 1.56 × 10−15 | 238.40 | 0.0841 | 0.20 |
| BCO-I | 0.73 | 0.0114 | 0.023 | 5.16 × 10−15 | 130.93 | 0.110 | 0.22 |
| BCO-II | 0.68 | 0.007 | 0.0051 | 1.53 × 10−14 | 76.01 | 0.118 | 0.22 |
| BCO-III | 0.62 | 0.003 | 0.0048 | 4.51 × 10−14 | 44.36 | 0.129 | 0.20 |
3.7. Ionic conductivity (σ)
In supercapacitor technology, ionic conductivity is a crucial parameter that helps us determine a material's electrochemical efficiency. Table 5 lists the estimated ionic conductivity values for PBCO, BCO-I, BCO-II, and BCO-III. The values of ionic conductivities for all samples have been determined using eqn (13).
 | (13) |
3.8. Transference number (t+)
From the transference number, we can deduce the contributions of the cation and anion to the overall current within the system. In ionic conduction, not all ions may contribute equally to the current. The transference number allows us to quantify the fraction of the current carried by each ion type. For this purpose, the following equation has been used as,
 | (14) |
4. Conclusion
The synthesis of BaCoO3/rGO composites (specifically PBCO, BCO-I, BCO-II, and BCO-III) via a solvothermal technique, followed by Ni foam etching, cleansing, and slurry creation, has shown substantial promise in addressing global energy challenges. Phase development was verified using XRD, with Bragg's plane (hkl) values aligning with the provided data and ICSD ID # 00-052-1612. FESEM analysis revealed nanoscale structures that were uniformly distributed and exhibited high porosity. Electrochemical analysis indicated a transition from electric double-layer capacitance (EDLC) to a combination of capacitive behaviors, with the BCO-III composite achieving an impressive specific capacity of 142.44 C g−1 at a scan rate of 5 mV s−1. Although the presence of surface species leads to a decline in specific capacity at higher scan rates, BCO-III demonstrates excellent discharge rates, power density (531.25 W kg−1), and energy density (21.28 W h kg−1). The sample BCO-III, which had the highest specific capacity, was tested for stability and showed an impressive retention rate of 90%. Further, excellent ionic conductivity confirmed the highlighted features of BCO-III. The cation's transference number is determined to be 0.2, indicating that the anion will undergo a large current. These properties highlight its potential as a high-performance electrode material for SCs and other energy storage applications.Data availability
The data will be made available upon request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to acknowledge the Researchers Supporting Project number (RSP2025R71), King Saud University, Riyadh, Saudi Arabia.References
- M. Hasan, S. Zawar, G. M. Mustafa, A. Ghaffar, A. Razaq and S. Atiq, Porous Architecture of Ni substituted ZnMn2O4 nanospheres as an electrode material for supercapacitor applications, Phys. B, 2022, 633, 413767 CrossRef CAS.
- M. Walter, M. V. Kovalenko and K. V. Kravchyk, Challenges and benefits of post-lithium-ion batteries, New J. Chem., 2020, 44(5), 1677–1683 RSC.
- A. P. Tiwari, T. Mukhiya, A. Muthurasu, K. Chhetri, M. Lee and B. Dahal, et al., A review of electrospun carbon nanofiber-based negative electrode materials for supercapacitors, Electrochem, 2021, 2(2), 236–250 CrossRef CAS.
- B. Talluri, K. Yoo and J. Kim, High entropy spinel metal oxide (CoCrFeMnNi)3O4 nanoparticles as novel efficient electrocatalyst for methanol oxidation and oxygen evolution reactions, J. Environ. Chem. Eng., 2022, 10(1), 106932 CrossRef CAS.
- Q. Ma, H. Liu, S. An, X. Han, J. Cui and Y. Zhang, et al., Layered double metal hydroxide coated nickel oxide embedded carbon fiber to form open petal-shaped nanosheet arrays as electrode materials for high-performance supercapacitors, J. Energy Storage, 2021, 44, 103455 CrossRef.
- Y. Niu, H. Su, X. Li, J. Li and Y. Qi, Synthesis of porous α-MoO3 microspheres as electrode materials for supercapacitors, J. Alloys Compd., 2022, 898, 162863 CrossRef CAS.
- X. Mao, Y. Zou, F. Xu, L. Sun, H. Chu and H. Zhang, et al., Three-dimensional self-supporting Ti3C2 with MoS2 and Cu2O nanocrystals for high-performance flexible supercapacitors, ACS Appl. Mater. Interfaces, 2021, 13(19), 22664–22675 CrossRef CAS PubMed.
- S. Wang, Y. Zou, F. Xu, C. Xiang, H. Peng and J. Zhang, et al., Morphological control and electrochemical performance of NiCo2O4@ NiCo layered double hydroxide as an electrode for supercapacitors, J. Energy Storage, 2021, 41, 102862 CrossRef.
- Z. Yu, S. Wang, Y. Huang, Y. Zou, F. Xu and C. Xiang, et al., Bi2O3 nanosheet-coated NiCo2O4 nanoneedle arrays for high-performance supercapacitor electrodes, J. Energy Storage, 2022, 55, 105486 CrossRef.
- X. Yang, C. Xiang, Y. Zou, J. Liang, H. Zhang and E. Yan, et al., Low-temperature synthesis of sea urchin-like Co-Ni oxide on graphene oxide for supercapacitor electrodes, J. Mater. Sci. Technol., 2020, 55, 223–230 CrossRef CAS.
- L. Tan, D. Guo, J. Liu, X. Song, Q. Liu and R. Chen, et al., In-situ calcination of polyoxometallate-based metal organic framework/reduced graphene oxide composites towards supercapacitor electrode with enhanced performance, J. Electroanal. Chem., 2019, 836, 112–117 CrossRef CAS.
- W. Song, X. Ma, L. Qiu, R. Guo, X. Lu and B. Sun, Anchoring polyaniline nanofibers on liquefied wood carbon aerogel for high-performance hybrid supercapacitors, Ind. Crops Prod., 2024, 215, 118645 CrossRef CAS.
- Y. Wang, Nanowire materials for supercapacitor electrode: Preparation, performance and prospects, J. Energy Storage, 2024, 97, 112848 CrossRef.
- J. Wang, X. Zhang, Z. Li, Y. Ma and L. Ma, Recent progress of biomass-derived carbon materials for supercapacitors, J. Power Sources, 2020, 451, 227794 CrossRef CAS.
- T. N. Myasoedova, O. V. Nedoedkova, R. Kalusulingam, Y. V. Popov, A. S. Mikheykin and A. S. Konstantinov, et al., Fabrication of Ni-Polyaniline/Graphene Oxide Composite Electrode with High Capacitance and Water Splitting Activity, ChemPhysChem, 2024, 25(15), e202300795 CrossRef CAS PubMed.
- F. Yang, H. Guo, J. Zhang, Y. Cao, Y. Chen and J. Xu, et al., Heterostructure of MnCo2O4 intercalated graphene oxide coated with Ni–V–Se nanoparticles for supercapacitors with high rate capability, J. Alloys Compd., 2022, 926, 166762 CrossRef CAS.
- P. K. Sahoo, N. Kumar, A. Jena, S. Mishra, C. P. Lee and S. Y. Lee, et al., Recent progress in graphene and its derived hybrid materials for high-performance supercapacitor electrode applications, RSC Adv., 2024, 14(2), 1284–1303 RSC.
- R. Kumar, R. Thangappan, F. Ran, S. Sambasivam, M. D. Albaqami and S. Mohammad, Enriched performance of practical device assisted asymmetric supercapacitor: NiO/Co3O4 intercalated with rGO nanocomposite electrodes, J. Energy Storage, 2024, 85, 111075 CrossRef.
- S. A. Thomas, J. Cherusseri and D. N. Rajendran, Recent advancements on carbon fibers-based sustainable electrodes for flexible and wearable supercapacitors, RSC Sustainability, 2024, 2, 2403–2443 RSC.
- K. Mariappan, D. D. F. Packiaraj, T. W. Chen, S. M. Chen, S. Sakthinathan and S. Alagarsamy, et al., The electrochemical performances of porous niobium pentoxide with multi-walled carbon nanotubes nanocomposite incorporated with glassy carbon electrode for the sensing of chloramphenicol, Colloids Surf., A, 2024, 691, 133840 CrossRef CAS.
- S. S. Shah and M. A. Aziz, Properties of Electrode Materials and Electrolytes in Supercapacitor Technology, J. Chem. Environ., 2024, 3(1), 1–45 Search PubMed.
- J. Duan, J. Li, G. Divitini, D. Cortecchia, F. Yuan and J. You, et al., 2D hybrid perovskites: from static and dynamic structures to potential applications, Adv. Mater., 2024, 36(30), 2403455 CrossRef CAS PubMed.
- S. Ali, A. Shakoor, M. Raza and A. Ahmad, Facile Synthesis of Zinc Cobalt Sulfide and Composite with Graphitic Carbon Nitride (ZCS@ GCN) for Photocatalysis and Electrode for Energy Storage Applications, Mater. Chem. Phys., 2025, 130431 CrossRef CAS.
- P. J. Sephra, T. Chandrapagasam, A. Sachdev and M. Esakkimuthu, Bifunctional properties of Ag/α-Fe2O3/rGO nanocomposite for supercapacitor and electrochemical nitrate sensing using tetradodecyl ammonium nitrate as ion-selective membrane, Environ. Sci. Pollut. Res., 2024, 31(40), 52886–52904 CrossRef CAS PubMed.
- X. T. Yin, E. M. You, R. Y. Zhou, L. H. Zhu, W. W. Wang and K. X. Li, et al., Unraveling the energy storage mechanism in graphene-based nonaqueous electrochemical capacitors by gap-enhanced Raman spectroscopy, Nat. Commun., 2024, 15(1), 5624 CrossRef CAS PubMed.
- M. Peplow, Coming of age, Science, 2024, 386, 138–143 CrossRef CAS PubMed.
- J. B. Falqueto, N. Hales, T. J. Schimidt and E. Fabbri, Recent Advances in Nickel-Based Perovskite Oxides for the Electrocatalytic Oxygen Evolution Reaction in Alkaline Electrolytes, ACS Mater. Lett., 2024, 6(12), 5227–5241 CrossRef CAS.
- M. Bilal, F. Ahmad, S. Zawar, U. Waqas, M. A. Khan and S. M. Ramay, et al., Optimized Charge Dynamics of Sr2Fe2O5/rGO Composite Electrodes: Redefining Supercapacitor Efficiency, ECS J. Solid State Sci. Technol., 2024, 13(2), 21001 CrossRef CAS.
- D. Tang, C. Shao, S. Jiang, C. Sun and S. Song, Graphitic C2N3: an allotrope of g-C3N4 containing active azide pentagons as metal-free photocatalyst for abundant H2 bubble evolution, ACS Nano, 2021, 15(4), 7208–7215 CrossRef CAS PubMed.
- F. Hadji, M. Omari, M. Mebarki, N. Gabouze and A. Layadi, Zinc doping effect on the structural and electrochemical properties of LaCoO3 perovskite as a material for hybrid supercapacitor electrodes, J. Alloys Compd., 2023, 942, 169047 CrossRef CAS.
- P. M. Shafi, N. Joseph, A. Thirumurugan and A. C. Bose, Enhanced electrochemical performances of agglomeration-free LaMnO3 perovskite nanoparticles and achieving high energy and power densities with symmetric supercapacitor design, Chem. Eng. J., 2018, 338, 147–156 CrossRef CAS.
- Y. Cao, B. Lin, Y. Sun, H. Yang and X. Zhang, Symmetric/asymmetric supercapacitor based on the perovskite-type lanthanum cobaltate nanofibers with Sr-SUBSTITUTION, Electrochim. Acta, 2015, 178, 398–406 CrossRef CAS.
- S. Venkateshalu, G. Subashini, P. Bhardwaj, G. Jacob, R. Sellappan and V. Raghavan, et al., Phosphorene, antimonene, silicene and siloxene based novel 2D electrode materials for supercapacitors-A brief review, J. Energy Storage, 2022, 48, 104027 CrossRef.
- S. Pappu, S. Anandan, T. N. Rao, S. K. Martha and S. V. Bulusu, High-performance hybrid supercapacitor with electrochemically exfoliated graphene oxide incorporated NiCo2O4 in aqueous and non-aqueous electrolytes, J. Energy Storage, 2022, 50, 104598 CrossRef.
- L. Li, Y. Jiang, C. Guo, K. Han, X. Cui and C. He, et al., Mechanochemical production of graphene/amorphous carbon/Mn3O4 nanocomposites for asymmetric supercapacitor, Appl. Surf. Sci., 2024, 653, 159388 CrossRef CAS.
- M. B. Askari, P. Salarizadeh, A. Di Bartolomeo and F. Şen, Enhanced electrochemical performance of MnNi2O4/rGO nanocomposite as pseudocapacitor electrode material and methanol electro-oxidation catalyst, Nanotechnology, 2021, 32(32), 325707 CrossRef CAS PubMed.
- F. Ahmad, M. A. Khan, U. Waqas, S. M. Ramay and S. Atiq, Elucidating an efficient super-capacitive response of a Sr2Ni2O5/rGO composite as an electrode material in supercapacitors, RSC Adv., 2023, 13(36), 25316–25326 RSC.
- A. Tariq, G. Ali, U. Waqas, K. J. Ahmad, S. M. Ramay and F. Afzal, et al., Synergistic integration of rGO into cobalt oxide matrix for efficient electrochemical performance mediated by structural stability, J. Energy Storage, 2024, 80, 110346, DOI:10.1016/j.est.2023.110346.
- A. Qayyum, M. O. ur Rehman, F. Ahmad, M. A. Khan, S. M. Ramay and S. Atiq, Performance optimization of Nd-doped LaNiO3 as an electrode material in supercapacitors, Solid State Ionics, 2023, 395, 116227 CrossRef CAS.
- N. Bano, S. I. A. Shah, A. Sami, M. Ali, R. A. Alshgari and S. Mohammad, et al., Development of binder–free Ni3S2/CoS2 nano–composite as electrode material for energy storage application, Ceram. Int., 2024, 50(23), 49880–49888 CrossRef CAS.
- Z. Shi, G. Sun, R. Yuan, W. Chen, Z. Wang and L. Zhang, et al., Scalable fabrication of NiCo2O4/reduced graphene oxide composites by ultrasonic spray as binder-free electrodes for supercapacitors with ultralong lifetime, J. Mater. Sci. Technol., 2022, 99, 260–269 CrossRef CAS.
- C. Bathula, I. Rabani, S. Ramesh, S. H. Lee, R. R. Palem and A. T. A. Ahmed, et al., Highly efficient solid-state synthesis of Co3O4 on multiwalled carbon nanotubes for supercapacitors, J. Alloys Compd., 2021, 887, 161307 CrossRef CAS.
- A. K. Vats, A. Kumar, P. Rajput and A. Kumar, Engineered perovskite LaCoO3/rGO nanocomposites for asymmetrical electrochemical supercapacitor application, J. Mater. Sci.:Mater. Electron., 2022, 1–17 Search PubMed.
- I. Ajin, R. Balamurugan, S. S. Shalini, and A. C. Bose. Investigation on SrCoO3 perovskites for supercapacitor applications, in AIP Conference Proceedings, AIP Publishing, 2024 Search PubMed.
- J. Xu, L. Wu, Y. Liu, J. Zhang, J. Liu and S. Shu, et al., NiO-rGO composite for supercapacitor electrode, Surf. Interfaces, 2020, 18, 100420 CrossRef CAS.
- S. I. El-Hout, S. G. Mohamed, A. Gaber, S. Y. Attia, A. Shawky and S. M. El-Sheikh, High electrochemical performance of rGO anchored CuS nanospheres for supercapacitor applications, J. Energy Storage, 2021, 34, 102001 CrossRef.
- G. Liu, L. Liu, G. Li, S. Wu, J. He and Y. Zhou, et al., Temperature-Dependent Electrochemical Performance of Ta-Substituted SrCoO3 Perovskite for Supercapacitors, Chem.–Eur. J., 2024, 30(14), e202303267 CrossRef CAS PubMed.
- L. Liu, G. Liu, S. Wu, J. He, Y. Zhou and M. Demir, et al., Fe-substituted SrCoO3 perovskites as electrode materials for wide temperature-tolerant supercapacitors, Ceram. Int., 2024, 50(1), 1970–1980 CrossRef CAS.
- S. M. Vidhi, A. K. Singh and O. P. Thakur, Synthesis of rGO/TiO2 composite electrode material for enhanced electrochemical activity and its applications in supercapacitors, Ionics, 2024, 1–13 Search PubMed.
- J. Huang, K. Jiang, D. Tranca, C. Ke, L. Zhang and J. Li, et al., Perovskite oxide and polyazulene–based heterostructure for high–performance supercapacitors, J. Appl. Polym. Sci., 2021, 138(41), 51198 CrossRef CAS.
- Z. M. Riyas and M. R. Prabhu, Microwave irradiation effect of La2O3–CeO2 nanocomposites as a potential electrode material for asymmetric supercapacitor, Ionics, 2024, 30(9), 5737–5754 CrossRef CAS.
- J. He, L. Cao, J. Cui, G. Fu, R. Jiang and X. Xu, et al., Flexible energy storage devices to power the future, Adv. Mater., 2024, 36(4), 2306090 CrossRef CAS PubMed.
- J. Singh, A. Kumar and A. Kumar, Facile solvothermal synthesis of nano-assembled mesoporous rods of cobalt free–La2NiFeO6 for electrochemical behaviour, Mater. Sci. Eng., B, 2020, 261, 114664 CrossRef CAS.
- D. Khalafallah, Y. Zhang, H. Dai, C. Liu and Q. Zhang, Manipulating the overall capacitance of hierarchical porous carbons via structure-and pore-tailoring approach, Carbon, 2024, 227, 119250 CrossRef CAS.
- B. A. Khan, R. Hussain, A. Shah, A. Mahmood, M. Z. U. Shah and J. Ismail, et al., NiSe2 nanocrystals intercalated rGO sheets as a high-performance asymmetric supercapacitor electrode, Ceram. Int., 2022, 48(4), 5509–5517 CrossRef CAS.
- A. M. Idris, T. Liu, J. Hussain Shah, H. Han and C. Li, Sr2CoTaO6 double perovskite oxide as a novel visible-light-absorbing bifunctional photocatalyst for photocatalytic oxygen and hydrogen evolution reactions, ACS Sustain. Chem. Eng., 2020, 8(37), 14190–14197 CrossRef CAS.
- Z. Wei, Q. Wang, M. Qu and H. Zhang, Rational Design of Nanosheet Array-Like Layered-Double-Hydroxide-Derived NiCo2O4 In Situ Grown on Reduced-Graphene-Oxide-Coated Nickel Foam for High-Performance Solid-State Supercapacitors, ACS Appl. Mater. Interfaces, 2024, 16(15), 18734–18744 CrossRef CAS PubMed.
- V. Lazarenko, R. Meija, Y. Rublova, A. Kons, V. Voikiva and J. Andzane, et al., Bi2Se3@ SWCNT heterostructures with beyond theoretical capacity as perspective binder-free anodes for lithium-ion batteries, J. Power Sources, 2024, 593, 233964 CrossRef CAS.
- P. R. Sørensen and T. Jacobsen, Conductivity, charge transfer and transport number—an ac-investigation of the polymer electrolyte LiSCN-poly (ethyleneoxide), Electrochim. Acta, 1982, 27(12), 1671–1675 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra08894h |
| This journal is © The Royal Society of Chemistry 2025 |




