Atomic structures and electronic properties of different contact surfaces for C_xF_y–SiO₂ triboelectric nanogenerator based on first-principles investigations

Abstract

Modification of the dielectric friction layer materials is an ideal way to enhance the output performance of a triboelectric nanogenerator (TENG), but current research mostly focuses on the metal–polymer or metal–SiO₂ materials. In this work, we constructed different TENG models based on polymer C_xF_y–SiO₂ electret materials, and the electronic properties of the different contact surfaces were investigated using first principles. We found that the charge transfer in C_xF_y–SiO₂ materials occurred only at the contact interface, and it was partially affected by the terminal atoms near the SiO₂ interface. The charge transfer of the polymer C_xF_y that was in contact with the O-terminated SiO₂ achieved a more satisfactory effect. Among them, the II-C₃F₆–O model exhibited the highest amount of charge transfer because of the better hybridization of II-C₃F₆ with the O atoms of SiO₂ layer. Our study showed that instead of adding different types of dielectric friction layers, varying the configurations of the same types of dielectric friction layers is an alternative way to regulate charge transfer. Furthermore, this strategy could provide new ideas for enhancing the performance of TENGs.

---

Introduction

With the continuous advancement of technology, microelectronic devices are increasingly being applied in the fields of self-powered flexible electronics and sensing. However, improving the energy efficiency of these devices to meet the demands of long-term use remains a pressing issue that needs to be addressed.^1–7 The invention of triboelectric nanogenerators (TENG) marked a significant milestone in the field of self-powered systems, such as multimodal sensors, wearable electronic devices, and real-time human health monitoring, offering a novel approach to efficiently harvest mechanical energy.^8–10 Current triboelectric nanogenerators still face issues such as insufficient output performance and low energy conversion efficiency,^11–14 which limit their application in high-power energy generation because the dielectric friction layers cannot store charge for extended periods.^15–25

In recent years, the performance enhancement of TENG has been focused on the modification of its dielectric friction layers.^26–31 Owing to their excellent ability to store charge for long periods, electret materials have become emerging materials for dielectric friction layers. Common electret materials mainly include inorganic electret materials, such as silicon dioxide, and organic electret materials, such as various polymers. In 2018, Wu et al.³² first investigated the mechanism of metal–polymer contact charging electrification via first-principles calculations and found that the stress on the contact region has a significant effect on the charge transfer. Further, Wu et al.³³ investigated the charge transfer mechanism between metal and amorphous polymers and found that the modification of contact materials is an important method to improve the output power of TENG. Subsequently, Al–PE polymer,²⁶ Cu–PVDF polymer,³⁴ Au–PTFE polymer³⁵ and Au–Nylon polymer³⁵ have attracted widespread attention from researchers through first-principles investigations. In 2021, Antony et al.³⁶ studied the electronic charge transfer of the hydroxylated metal/SiO₂ interface using density functional theory and found that the separation distance between the contact surfaces must be small enough to produce electronic states within the apparent insulating bandgap. Owing to the unique physicochemical properties of metals, researchers have also paid significant attention to metal–SiO₂ materials,^37,38 such as Cu–SiO₂, Au–SiO₂, Pd–SiO₂, Al–SiO₂ and Ag–SiO₂. In summary, current research on dielectric friction layers mainly focus on single electret materials, such as metal–polymer and metal–SiO₂ materials; however, few studies are reported on polymer–SiO₂ composite electret materials, indicating that there is still room for enhancing the output performance of TENG0073.

On this basis, we constructed polymer–SiO₂ composite electret materials and modified the dielectric friction layers by changing the contact atoms and further altering the charge transfer. In this paper, interface models consisting of polymer C_xF_y (x = 2, y = 4; x = 3, y = 6) and SiO₂ layer were considered, and the effect of different contact atoms on the electron transfer was investigated by first-principles calculations. The II-C₃F₆–O model, which consists of II-C₃F₆ and O-terminated SiO₂, shows the best performance of electron transfer because II-C₃F₆ can hybridize more significantly with the O atoms of the SiO₂ layer. Our study suggests that for the design of TENG, in addition to considering the different types of dielectric friction layers, different configurations of the same types can also be considered to enhance the performance of TENG.

Computational details

All the calculations in this paper are based on the Density Functional Theory (DFT) and were performed using the Vienna ab initio Simulation Package (VASP) software.^39,40 Density Functional Theory is a first principles-based theoretical method that can achieve rigorous transformation from many-body problems into single-body problems. The Projector Augmented Wave (PAW) method⁴¹ was used to describe the interactions between the core electrons and the remaining valence electrons. The Perdew–Burke–Ernzerhof (PBE) functional within the generalized gradient approximation (GGA)⁴² was used to describe the exchange correlations of the electrons.

VASP software was used to optimize the atomic structures and calculate the electronic properties of different contact models. The input energy was chosen to be 400 eV to ensure accuracy of calculations. For geometry optimization, all atomic positions and lattice structures were fully relaxed until convergence criteria were reached, with forces less than 0.05 eV per Å per atom and a total energy convergence criterion of 1.0 × 10⁻⁵ eV. For electronic properties, the same computational accuracy was used to obtain reliable results. According to previous studies,^43,44 a vacuum layer of 20 Å was added to the z-axis to eliminate periodicity and avoid interaction between the two periodic units. In addition, considering the large contact models, we used a 10 × 10 × 1 K-point mesh around the gamma point in reciprocal space. The interlayer interaction of all interface models was carried out using Grimme's D3 correction^45,46 to address the deficiencies in van der Waals forces.

Results and discussion

To better study the microscopic properties of triboelectric nanogenerators, we constructed interface models consisting of polymer C_xF_y (where x = 2, y = 4; x = 3, y = 6) and SiO₂ materials.^47,48 For the C₃F₆ polymer, according to the different atoms of the main and branched chains of the carbon chain, there are three conformations at the contact interface: CF₂, CF₃ and C₂F₂ atoms, respectively. We constructed three types of contact surface models, which were named I-C₃F₆, II-C₃F₆, and III-C₃F₆, as shown in Fig. 1(a–c), respectively. For the C₂F₄ polymer, on the other hand, the main and branched chains of the carbon chain are the same and there is only one conformation of CF₂ atoms at the contact interface. Therefore, only one C₂F₄ contact surface model was constructed, as shown in Fig. 1(d). Similarly, based on the type of terminal atoms of SiO₂ at the contact interface, we divided them into three configurations, and the atoms at the contact interface were O, Si, and SiO atoms, which were named as SiO₂–O, SiO₂–Si and SiO₂–SiO, as shown in Fig. 1(e–g), respectively. Consequently, considering the different conformations of dielectric friction layers between the polymer C_xF_y and SiO₂ materials, we considered a total of 12 different contact surface structures to investigate related microscopic properties for the nanogenerators.

Fig. 1 Side-view geometries of the C_xF_y–SiO₂ interface model: (a–d) I-C₃F₆, II-C₃F₆, III-C₃F₆, and C₂F₄, respectively, and (e–g) O, Si, and SiO termination configurations of SiO₂, respectively. The red, blue, brown, gray, and orange spheres in the figure represent O, Si, C, F, and H atoms, respectively.

To determine the stability of the structure and the nature of interaction force between the two dielectric friction layers, the binding energies of interface models with different configurations were calculated as follows

E_b = (E_CxFy–SiO2 − E_CxFy − E_SiO2)/A (1)

where E_CxFy–SiO2, E_CxFy and E_SiO2 denote the total energies of the interfacial model, C_xF_y is the dielectric friction layer and the SiO₂ dielectric friction layer, respectively. A denotes the interface area between the C_xF_y layer and SiO₂ layer of the metal–SiO₂ interface model. Table 1 demonstrates the number of atoms, lattice parameters, layer spacing, and binding energy of the different C_xF_y–SiO₂ interface models.

Table 1 Number of atoms, lattice parameters (a, b), layer spacing, and binding energies for the interfacial configurations of C₂F₄, I-C₃F₆, II-C₃F₆, and III-C₃F₆ terminated with different atoms of SiO₂, respectively

Material	Atomic number	a/Å	b/Å	Interlayer thickness/Å^2	Binding energy eV Å^−2
C2F4–SiO2–O	45	5.46	4.87	2.719	0.034
C2F4–SiO2–Si	43	5.46	4.87	2.740	0.011
C2F4–SiO2–SiO	44	5.46	4.87	2.369	0.053
I-C3F6–O	54	6.37	4.89	2.024	0.038
I-C3F6–Si	52	6.37	4.89	2.093	0.032
I-C3F6–SiO	53	6.37	4.89	2.362	0.008
II-C3F6–O	57	6.37	4.89	1.568	0.046
II-C3F6–Si	55	6.37	4.89	1.378	0.024
II-C3F6–SiO	56	6.37	4.89	2.038	0.012
III-C3F6–O	56	6.37	4.89	1.118	0.019
III-C3F6–Si	54	6.37	4.89	1.426	0.002
III-C3F6–SiO	55	6.37	4.89	1.356	0.002

---

Analysis of the values in Table 1 indicates that when C₂F₄ and C₃F₆ are combined with SiO₂, the contact area of C₂F₄ is smaller than that of C₃F₆ while the interlayer thickness is larger than that of C₃F₆. Consequently, it is easier for C₃F₆ to form a contact interface model with SiO₂ than C₂F₄. Among the interface models consisting of SiO₂ with different C₃F₆ configurations, the I-C₃F₆ model always has the largest interlayer thickness, whereas the II-C₃F₆ model has a suitable interlayer thickness. For the interface models consisting of C₃F₆ with different SiO₂ configurations, the binding energies of the C₃F₆–O configurations are consistently larger than those of the C₃F₆–Si configurations and larger than those of the C₃F₆–SiO configurations. Based on previous studies,^49,50 we screened the interface models with van der Waals interactions using 20–40 meV Å⁻¹ as the range of binding energies. When the polymer C₃F₆ layer contacted with SiO-terminated SiO₂, the binding energy is less than 0.02 eV Å⁻². When the SiO₂ layer contacted with II-C₃F₆, the formed configuration has the largest binding energy, of which the II-C₃F₆–O configuration has the most suitable binding energy of 0.046 eV Å⁻².

In order to better understand the output performance, we analyzed the plane-averaged charge density difference of these 12 interface models and attempted a preliminary screening based on the amount and direction of charge transfer between the contact surfaces. It can be inferred from Fig. 2 that when the polymer C_xF_y is contacted with O-terminated SiO₂ to form the C_xF_y–O interface model, the values of average charge density difference all reach up to 6 × 10⁻³ e Å⁻¹. In contrast, when it is contacted with Si-terminated and SiO-terminated SiO₂ to form the C_xF_y–Si and C_xF_y–SiO interface models, respectively, the values are much less likely to reach the same level in both dielectric friction layers.

Fig. 2 Plane-averaged charge density difference at the interface of C_xF_y and SiO₂: (a, e and i) C₂F₄ (b, f and j) I-C₃F₆, (c, g and k) II-C₃F₆, and (d, h and i) III-C₃F₆, where (a–d) denote O-contacting surfaces, (e–h) denote Si-contacting surfaces, and (i–l) denote SiO-contacting surfaces.

For the C_xF_y–O, I-C₃F₆–SiO, and II-C₃F₆–SiO configurations, as shown in Fig. 2(a)–(d), (j) and (k), the six configurations have similar charge transfer modes. The difference values between the C_xF_y and SiO₂ layers are almost equal, indicating a nearly unidirectional electron transfer. The configurations terminated with O atoms show a significantly larger charge transfer than those terminated with SiO atoms. In particular, the II-C₃F₆–O configuration has better charge transfer capacity with a larger amount of charge transfer, and the values of the average charge density difference reach up to 7.6 × 10⁻³ e Å⁻¹, which represents an increase of 26.7% compared to the previously mentioned average value. For the C_xF_y–Si and C₂F₄–SiO configurations, as shown in Fig. 2(e)–(i), the frequent charge transfer at the interface implies that the electrons of these models do not simply transfer between the C_xF_y and SiO₂ layers; some electrons accumulate near the interface instead of moving unidirectionally. For the III-C₃F₆–Si and III-C₃F₆–SiO configurations, as shown in Fig. 2(h) and (i), the charge transfers are too small and not considered in the subsequent calculations. In summary, among the above 12 interface conformations, the II-C₃F₆–O model has the most charge transfer and unidirectional electrons transfer.

In order to understand the effect of different polymer friction layers on the interfacial properties, the charge density difference Δρ at the interfaces was computed to further investigate the charge transfer and charge redistribution between the C_xF_y and SiO₂ interfaces.⁵¹

Δρ = ρ_CxFy–SiO2 − ρ_CxFy − ρ_SiO2 (2)

where ρ_CxFy–SiO2 is the total charge density of the C_xF_y–SiO₂ interfacial system while ρ_CxFy and ρ_SiO2 are the charge densities of the individual C_xF_y and SiO₂ layers, respectively. Δρ denotes the change in charge density due to the formation of chemical bonds between the C_xF_y and SiO₂ layers. Based on the analysis of the plane-averaged charge density difference, we identified 6 correlated structures with superior charge transfer properties, namely, C₂F₄–O, I-C₃F₆–O, II-C₃F₆–O, III-C₃F₆–O, II-C₃F₆–Si, II-C₃F₆–SiO, and further analyzed the charge transfer at the contact surfaces by the differential charge densities.

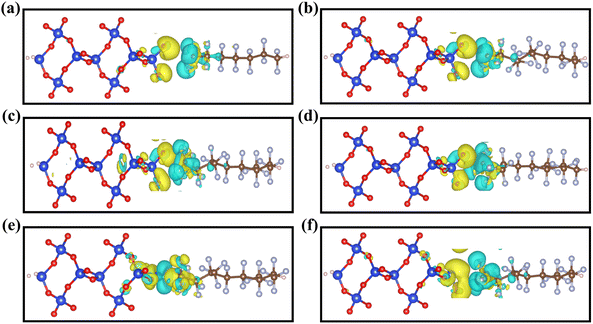
It can be inferred from Fig. 3 that the yellow area indicates the charge depletion region and the blue area indicates the charge aggregation region. Charge transfer at the contact interface can be visualized more intuitively through the differential charge density map. We can judge the level of charge density based on the size of the area where the charge accumulates. The charge aggregation and depletion mainly occur at the contact interface between the polymer C_xF_y and SiO₂ electret materials. There is more charge transfer occurring between the C_xF_y and O-terminated SiO₂, no significant charge transfer between the C_xF_y and Si-terminated SiO₂, and less charge transfer between the C_xF_y and SiO-terminated SiO₂. For the polymer C_xF_y contacting the SiO₂–O interface, as shown in Fig. 3(a–d), C_xF_y acquires electrons from the SiO₂ interface, forming a charge depletion region at the SiO₂ layer and a charge aggregation region at the C_xF_y layer. As shown in Fig. 3(c), II-C₃F₆ contact with the SiO₂–O interface has a greater charge density. This indicates that the II-C₃F₆–O model has a strong charge transfer capability as the electret materials of the triboelectric nanogenerator. For the polymer II-C₃F₆ contacting different termination atoms of SiO₂, as shown in Fig. 3(c, e and f), based on the different contact surfaces as well as the different sizes of the charge transfer region, it can be further judged that the II-C₃F₆–O structure has a better charge transfer ability and is more suitable to be the electret material for triboelectric nanogenerator.

Fig. 3 Differential charge density of (a) C₂F₄–O, (b) I-C₃F₆–O, (c) II-C₃F₆–O, (d) III-C₃F₆–O, (e) II-C₃F₆–Si, and (f) II-C₃F₆–SiO. The blue and yellow regions indicate the electron depletion and accumulation regions, respectively. The size of the isosurface was set to 0.001 e Å⁻³.

The electrostatic potential difference between the two dielectric friction layers can be used to understand the amount of charge transfer and the time of storing charge. All configurations were analyzed by the value of differential charge density, and the variation of electrostatic potential along the z-direction was plotted, as shown in Fig. 4.⁵² The electrostatic potential differences between C_xF_y and SiO₂–O, II-C₃F₆ and SiO₂–Si, II-C₃F₆ and SiO₂–SiO configurations were investigated. The electrostatic potential of the SiO₂ layer is shown on the left side of the figure and that of the polymer layer is on the right side. By quantitatively analyzing the electrostatic potential, for the configurations of the C_xF_y contacting the O-terminated SiO₂, as shown in Fig. 4(a–d), the difference in electrostatic potentials of the C₃F₆–O interface is significantly larger than that of the C₂F₄–O interface, which indicated that the charge transfer between the dielectric friction layers of the C₃F₆ and SiO₂–O interfaces is closer, among which the II-C₃F₆ configuration performs optimally. For the configurations of II-C₃F₆ contacting different termination atoms of SiO₂, as shown in Fig. 4(c, e and f), they possess almost the same trend of electrostatic potential change at the same distance. However, the difference in the electrostatic potential between the II-C₃F₆ and SiO₂–O interfaces is the largest, as shown in Fig. 4(c), which indicates that the II-C₃F₆–O model possesses more charge transfer and has better power generation performance.

Fig. 4 Electrostatic potential plots of (a) C₂F₄–O, (b) I-C₃F₆–O, (c) II-C₃F₆–O, (d) III-C₃F₆–O, (e) II-C₃F₆–Si, and (f) II-C₃F₆–SiO, with the horizontal coordinates denoting the distances in the z-direction, and the vertical coordinates denoting the electrostatic potentials. The blue area in the figure indicates the SiO₂ layer and the brown area indicates the C_xF_y layer.

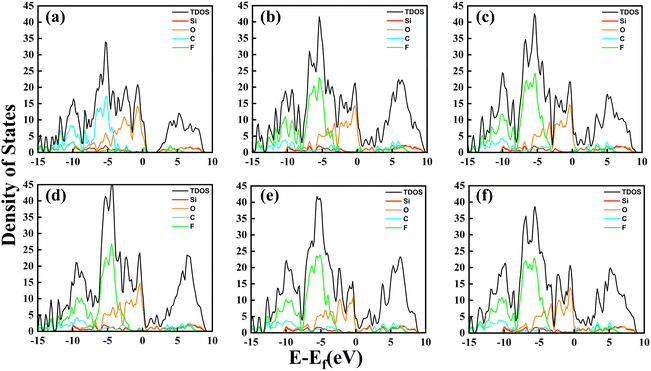
In order to gain insight into the nature of charge transfer between the dielectric friction layers composed of polymer C_xF_y and SiO₂ electret materials, we calculated the total density of states (TDOS) and the projected density of states (PDOS) of the atoms for these interface models, as shown in Fig. 5. Due to the difference in the C₂F₄ and C₃F₆ extra-nuclear electronic structures, the TDOS peaks of the C₂F₄ structure in Fig. 5(a) are smaller than those of the other C₃F₆ structures. Also, there is a region with no density of states near 1 eV that is also different from the other C₃F₆ structures, a characteristic that is not conducive to electron transfer between dielectric friction layers.

Fig. 5 PDOS plots of (a) C₂F₄–O, (b) I-C₃F₆–O, (c) II-C₃F₆–O, (d) III-C₃F₆–O, (e) II-C₃F₆–Si, and (f) II-C₃F₆–SiO. The black, red, orange, blue, and green colors in the plots indicate the orbital occupancy of TDOS, Si, O, C, and F, respectively.

In the interface models, as shown in Fig. 5(b)–(d), one layer of the dielectric friction layers is O-terminated SiO₂ and the other layer contacts different C₃F₆ structures. It can be seen that above the Fermi energy level, for the I-C₃F₆ structure, the first peak of the O atom is close to the C and F atoms and shows hybridization in both contour and value. For the II-C₃F₆ structure, the hybridization of the O atom with C and F atom also changes obviously, and the change in the O atom is more obvious than that of the Si atom, which makes it reasonable to assume that the II-C₃F₆–O structure has better orbital hybridization and charge transfer. However, for the III-C₃F₆ structure, the first peak does not show significant hybridization with O atoms, which shows that the charge transfer of the III-structure is not as good as that of the I- and II-structures.

In the interface models, as shown in Fig. 5(c), (e) and (f), one layer of dielectric friction layers is the polymer II-C₃F₆ material, the other layer contacts different termination atoms of SiO₂. For the SiO₂–O model, the first peak on the O, C and F atoms shows obvious hybridization above the Fermi energy level. For the SiO₂–Si model, the first peak also shows obvious hybridization but is numerically smaller than the O-terminated SiO₂ model. For the SiO₂–SiO model, the first peak has no obvious orbital hybridization compared with the other two models. Therefore, it is considered that the II-C₃F₆–O interface model, constituted by II-C₃F₆ in contact with the O-terminated SiO₂, has better output performance, which also explains the charge transfer phenomenon between the dielectric friction layers.

Conclusions

In this study, considering the different contact surfaces between polymer C_xF_y and SiO₂ electret materials, we constructed C₃F₆(C₂F₄)–SiO₂ interface models as the dielectric friction layers. The charge transfer between the contact surfaces was investigated through first principles to study the intrinsic reasons of TENG modification. It was found that a better charge transfer effect was achieved when the polymer C_xF_y was in contact with the O-terminated SiO₂. Among the interface models, the II-C₃F₆ configuration was likely to contact with the O atoms of the SiO₂ layer, which not only had the largest amount of charge transfer but also possessed unidirectional charge transfer. Notably, the II-C₃F₆–O model possesses the largest electrostatic potential difference, indicating that this TENG structure has the best output performance. By calculating and analyzing the density of states, we found that the II-C₃F₆ configuration will hybridize more significantly with the O atoms of SiO₂ compared to the other polymer configurations. This study reveals the intrinsic properties of TENG composed of polymer C_xF_y and SiO₂ electret materials and provides theoretical guidance for modifying dielectric friction layers through the different configurations of the same materials. How to improve the charge storage capability of the dielectric friction layers through material composition design is currently a hot topic of concern. In future, dielectric friction layers composed of composite electret materials need to be expanded.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Author contributions

Baonan Jia: writing – original draft, investigation, methodology, formal analysis. Jingming Gao: investigation, data curation, software. Jiaxiang Zhao: investigation, data curation, software. Guoying Qin: investigation, data curation, software. Xiaoning Guan: writing – review & editing, formal analysis. Xinhui Zhang: investigation, formal analysis. Wendong Xiao: writing – review & editing, conceptualization. Pengfei Lu: investigation, conceptualization.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Fundamental Research Funds for the Central Universities (No. 00007845), Foundation of Laboratory of Computational Physics (No. 6142A05QN22017) and project funded by China Postdoctoral Science Foundation (No. 2022M720516). We thank for the helpful discussion with Prof. Pengfei Guan and the computational support from the Beijing Computational Science Research Center (CSRC).

Notes and references

1. G. Ruhl, S. Wittmann, M. Koenig and D. Neumaier, Beilstein J. Nanotechnol., 2017, 8, 1056–1064.
2. J. Yang, K. Liu, X. Chen and D. Shen, Prog. Polym. Sci., 2022, 83, 100397.
3. A. I. Inamdar, S. Kamal, M. Usman, M.-H. Chiang and K.-L. Lu, Coord. Chem. Rev., 2024, 502, 215596.
4. X. Cao, Y. Xiong, J. Sun, X. Xie, Q. Sun and Z. L. Wang, Nano-Micro Lett., 2023, 15, 14.
5. X. Tao, X. Chen and Z. L. Wang, Energy Environ. Sci., 2023, 16, 3654–3678.
6. H. Xiang, L. Peng, Q. Yang, Z. L. Wang and X. Cao, Sci. Adv., 2024, 10, eads2291.
7. Y. Jiang, X. Liang, T. Jiang and Z. L. Wang, Engineering, 2024, 33, 204–225.
8. F.-R. Fan, Z.-Q. Tian and Z. L. Wang, Nano Energy, 2012, 1, 328–334.
9. J. Luo and Z. L. Wang, EcoMat, 2020, 2, e12059.
10. J. Tao, L. Wang, K. Kong, M. Hu and Z. Dai, Biomimetics, 2022, 7, 216.
11. Y. Li, Y. Luo, H. Deng, S. Shi, S. Tian, H. Wu, J. Tang, C. Zhang, X. Zhang and J. W. Zha, Adv. Mater., 2024, 36, 2314380.
12. X. Zhu, Y. Hao, J. Yang, W. Su, H. Zhang, Y. Qin, C. Zhang and X. Li, Appl. Mater. Today, 2024, 41, 102492.
13. K. Xiao, W. Wang, K. Wang, H. Zhang, S. Dong and J. Li, Adv. Funct. Mater., 2024, 34, 2404744.
14. W. Peng and S. Du, IEEE Trans. Circuits Syst. I Regul. Pap., 2023, 70, 3049–3062.
15. W. Sun, G. Ji, J. Chen, D. Sui, J. Zhou and J. Huber, Nano Energy, 2023, 108, 108248.
16. H. Zhang, P. Zhang, P. Li, L. Deng, W. Zhang, B. Liu and Z. Yang, Nano Res., 2022, 15, 7163–7171.
17. Q. M. Saqib, M. Y. Chougale, M. U. Khan, R. A. Shaukat, J. Kim, J. Bae, H. W. Lee, J.-I. Park, M. S. Kim and B. G. Lee, Nano Energy, 2021, 89, 106458.
18. Y. Zhu, Y. Zhao, L. Hou and P. Zhang, Micromachines, 2022, 13, 2053.
19. P. Zhang, Y. Ma, H. Zhang and L. Deng, ACS Appl. Energy Mater., 2023, 6, 6598–6606.
20. L. Shooshtari, N. Rafiefard, M. Barzegar, S. Fardindoost, A. Irajizad and R. Mohammadpour, ACS Appl. Nano Mater., 2022, 5, 17123–17132.
21. X. Liu, Y. Wang, G. Wang, Y. Ma, Z. Zheng, K. Fan, J. Liu, B. Zhou, G. Wang and Z. You, Matter, 2022, 5, 4315–4331.
22. W. Liu and J. Shi, Nano Energy, 2021, 89, 106479.
23. S.-N. Lai, C.-K. Chang, C.-S. Yang, C.-W. Su, C.-M. Leu, Y.-H. Chu, P.-W. Sha and J.-M. Wu, Nano Energy, 2019, 60, 715–723.
24. Y. Liu, G. Liu, T. Bu and C. Zhang, Mater. Today Energy, 2021, 20, 100686.
25. K. Xia and Z. Xu, Smart Mater. Struct., 2020, 29, 095016.
26. L. Li, X. Wang, P. Zhu, H. Li, F. Wang and J. Wu, Nano Energy, 2020, 70, 104476.
27. X. Chen, F. Wang, Y. Zhao, P. Wu, L. Gao, C. Ouyang, Y. Yang and X. Mu, Research, 2022, 2022, 9765634.
28. G. Yinben, C. Zixi, W. Hongzhi and Z. Qinghong, J. Inorg. Mater., 2021, 36, 919–928.
29. C. Xu, B. Zhang, A. C. Wang, W. Cai, Y. Zi, P. Feng and Z. L. Wang, Adv. Funct. Mater., 2019, 29, 1903142.
30. G. Khandelwal, A. Chandrasekhar, N. P. Maria Joseph Raj and S.-J. Kim, Adv. Energy Mater., 2019, 9, 1803581.
31. G. Khandelwal, M. K. Ediriweera, N. Kumari, N. P. Maria Joseph Raj, S. K. Cho and S.-J. Kim, ACS Appl. Mater. Interfaces, 2021, 13, 18887–18896.
32. J. Wu, X. Wang, H. Li, F. Wang, W. Yang and Y. Hu, Nano Energy, 2018, 48, 607–616.
33. J. Wu, X. Wang, H. Li, F. Wang and Y. Hu, Nano Energy, 2019, 63, 103864.
34. L. Li, X. Wang, Y. Hu, Z. Li, C. Wang and Z. Zhao, Adv. Funct. Mater., 2022, 32, 2109949.
35. D. Kang, J.-H. Hwang, Y.-J. Kim, P. Zhao, H. Y. Lee, J. Kim, M. S. Shin, S. Jeon, S. Kim and S.-W. Kim, Mater. Today, 2024, 72, 109–116.
36. A. C. Antony, D. Thelen, N. Zhelev, K. Adib and R. G. Manley, J. Appl. Phys., 2021, 129, 065304.
37. T.-R. Shan, B. D. Devine, S. R. Phillpot and S. B. Sinnott, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 115327.
38. J. Huang, E. Tea, G. Li and C. Hin, Appl. Surf. Sci., 2017, 406, 128–135.
39. V. Wang, N. Xu, J.-C. Liu, G. Tang and W.-T. Geng, Comput. Phys. Commun., 2021, 267, 108033.
40. Y. Y. Liang, D. M. Chen and J. F. Tong, Key Eng. Mater., 2012, 512, 490–493.
41. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
42. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
43. F. Withers, O. Del Pozo-Zamudio, A. Mishchenko, A. P. Rooney, A. Gholinia, K. Watanabe, T. Taniguchi, S. J. Haigh, A. Geim and A. Tartakovskii, Nat. Mater., 2015, 14, 301–306.
44. A. K. Geim and I. V. Grigorieva, Nature, 2013, 499, 419–425.
45. W. Liu, C.-L. Yang, Y.-T. Zhu and M.-S. Wang, J. Phys. Chem. C, 2008, 112, 1803–1811.
46. R. Chawla and S. Sharma, Compos. Sci. Technol., 2017, 144, 169–177.
47. K. Zhao, W. Sun, S. Li, Z. Song, M. Zhong, D. Zhang, B.-N. Gu, M.-J. Liu, H. Fu and H. Liu, Discover Nano, 2023, 18, 69.
48. D. L. Vu, C. D. Le and K. K. Ahn, Polymers, 2022, 14, 960.
49. T. Björkman, A. Gulans, A. V. Krasheninnikov and R. M. Nieminen, Phys. Rev. Lett., 2012, 108, 235502.
50. Y. Chen, X. Guan, L. Yang, B. Jia, H. Zhao, L. Han, P. Guan and P. Lu, Appl. Surf. Sci., 2023, 611, 155679.
51. M. T. As-Samee, M. S. Hasan Khan, K. Kubra, M. R. Islam and M. T. Hasan, AIP Adv., 2023, 13, 065004.
52. Q. Campbell, J. Electrochem. Soc., 2023, 170, 031506.

---