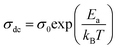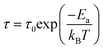DOI:
10.1039/D4RA07931K
(Paper)
RSC Adv., 2025,
15, 10022-10036
Effect of the in situ synthesis of vanadium oxide nanowires on the electrical properties of hybrid nanocomposites based on synthetic carbon matrices
Received
7th November 2024
, Accepted 23rd February 2025
First published on 1st April 2025
Abstract
Organic–inorganic nanocomposites (RF/VOX) were prepared by sol–gel method coupled with pyrolysis treatment using a resorcinol–formaldehyde carbon matrix enriched with vanadium nanoparticles. The structural properties of the final product were characterised using X-ray diffraction, revealing the transformation of the incorporated vanadium oxide from the V2O5 phase to V2O3 due to the pyrolysis temperature in a reductive atmosphere, alongside the formation of vanadium carbide (V8C7) in the sample treated at 1000 °C. The X-ray analysis also indicated the presence of a graphite phase across all samples. Microscopic examinations showed macroporous carbon structures enriched with vanadium oxide in the form of nanowires. These structural features significantly influenced the materials' electrical properties. At low frequencies, the AC conductance indicated a thermally activated process in the RF/VOX-625 and RF/VOX-650 samples pyrolysed y at 625 °C and 650 °C, respectively. RF/VOX-625 displayed semiconductor behaviour at high frequencies, while RF/VOX-650 transited from semiconductor behaviour to metal one at 200 K. The changes in the exponent s suggested that the CBH model effectively describes the AC conduction mechanism. Impedance analysis highlighted a relaxation phenomenon, and Nyquist plots illustrated the contribution of grain and grain boundaries in RF/VOX-625 and RF/VOX-650 at low temperatures. Furthermore, these plots indicated that in RF/VOX-650, the grain effect became predominant beyond 200 K. Incorporating vanadium oxide nanoparticles into the polymer matrix resulted in distinct physical properties and behaviours compared to the original organic matrix, allowing this material to be tested in various applications including negatronic devices and electronic components.
1. Introduction
Organic–inorganic hybrid materials represent a creative alternative to design new materials and compounds for academic research, and their improved or unusual characteristics allow the development of innovative industrial applications. Some hybrids come from the polymer and paint industries, in which fillers or inorganic particles are dispersed in organic materials (polymers, solvents, and surfactants) to improve their physicochemical properties. In fact, the term “organic–inorganic” hybrid materials was known only with the birth of soft chemistry in the 80s.1 This discovery allowed transferring research to nanocomposites of original and more refined structures. In this context, the development of “organic–inorganic” hybrid composites for advanced applications is involved, taking advantage of the benefits of the different constituents. This new generation of materials is applicable in various fields including optoelectronics,2 catalytic systems,3 medical and biological devices,4 functional smart coatings,5 solar cells,6 and sensors.7 The main interest of these composite materials lies in the combination of the properties of the polymer matrix and those of the inorganic element (filler). However, the good dispersion of these inorganic materials in the polymer matrix cannot be achieved by simple incorporation. To overcome these drawbacks, in recent years, continuous efforts by researchers have succeeded in establishing covalent bonds between polymer chains and inorganic particles. Indeed, an excellent synergy of the properties of these various elements results from this covalent association. For example, it is possible to combine the physicochemical properties of the polymer matrix and the optical,8–10 thermal9,11 and electrical9–12 properties of inorganic pigments while reducing dispersion problems. Generally, polymers are recognized by their electrical insulation criteria. For example, conventional polymers such as polystyrene and polyethylene have very low electronic conductivities ranging from 10−9 to 10−18 S cm−1.13 However, this insulating property of polymers has been widely exploited in various fields such as the insulation of some electronic devices and the coating of electronic wires. Despite their insulating nature, it is also known that polymers exhibit remarkable electronic and optical properties under certain conditions. These materials can transport electronic charges when they are composed of a system of conjugated bonds; they are called conductive polymers. In this context, different organic–inorganic materials have been prepared in our previous research, based on resorcinol–formaldehyde and pyrogallol–formaldehyde matrices incorporated with various metal oxide nanoparticles such as V2O5,14 ZrO2,15 SiO2,16 NiO2 (ref. 17 and 18) and MnO2.19 This work focuses on the synthesis of organic–inorganic nanocomposites by a sol–gel method following the incorporation of vanadium oxide nanoparticles into a resorcinol–formaldehyde matrix. The effect of pyrolysis temperature on the structural, morphological and electrical properties of the prepared nanocomposites was investigated. Vanadium pentoxide was chosen due to its unique properties, namely, high abundance, low cost, ease of synthesis, and the presence of multiple redox states.20–22 In addition, a variety of V2O5 nanostructures have been synthesized in previous works, such as nanowires,23 nanospheres,24 nanobelts,25 nanosheets,26 and nanoribbons.27 Therefore, this diverse nanostructure and vast properties enable vanadium pentoxide to be used in different applications. Indeed, carbon-based composites containing vanadium pentoxide have been shown to be promising materials for electrochemical devices. Du et al.28 reported that V2O5·nH2O@GO composites were used as negative electrode materials for sustainable lithium-ion batteries, and they exhibited extremely high capacity and good cycling stability. Ihsan et al.29 synthesized V2O5/mesoporous carbon composites, which performed well as positive electrode materials for lithium-ion batteries. Kong and et al.30 showed that sulfur/carbon/porous nanostructured V2O5 (S/C/PN-V2O5) composites prepared by wet ball milling and subsequent annealing are promising positive electrode materials for lithium–sulfur batteries. Fu et al.31 synthesized V2O5/graphene composites as electrode materials for supercapacitors by microwave synthesis, which exhibited excellent energy and power density characteristics. Hu et al.32 reported carbon nanotube-V2O5-chitosan nanocomposites used as electrochemical aptasensors for the detection of ciprofloxacin. Sekar et al.33 developed graphene carbon (GC-V2O5)-encapsulated vanadium pentoxide nanocomposites as photocatalysts for the degradation of crystal violet.
2. Experimental
2.1. Sample preparation
The sample preparation involved three key stages. Initially, the method established by El Mir et al.34,35 was used to synthesise vanadium nanopowder. In this process, ammonium metavanadate (NH4VO3) was dissolved in methanol. Following 15 minutes of magnetic stirring, the mixture underwent a drying phase in an autoclave under supercritical conditions of ethyl alcohol (Tc = 250 °C, Pc = 7 MPa). The resulting powder was then annealed at 350 °C for 24 hours in air to achieve the V2O5 phase. The second stage focused on forming a carbon matrix by blending formaldehyde (CH2O, 99% Bio pharm) with resorcinol R (C6H4(OH)2, 99%, Fisher Scientific) dissolved in acetone A (CH3COCH3, 99.8%, Prolabo), using picric acid (C6H3N3O7, 99% Scharlau) as a catalyst. A specified quantity of the prepared vanadium nanoparticles were incorporated into the carbon matrix at a V2O5/RF mass ratio of 5%, with continuous magnetic stirring until a wet gel was formed. This moist gel was then dried at room temperature in a humid environment for two weeks, and then placed in an incubator at 50 °C for 24 hours. The temperature was subsequently increased gradually by 10 °C every 24 hours until reaching 150 °C. In the final stage, the xerogels were subjected to pyrolysis at temperatures ranging from 600 °C to 1000 °C in a tubular furnace in an inert atmosphere for two hours. The resulting samples will be designated as RF/VOX-Tp, where RF stands for resorcinol–formaldehyde, VOX represents vanadium oxide, and Tp indicates the pyrolysis temperature.
2.2. Characterization
The crystal structures of the synthesized samples were analysed through X-ray diffraction (XRD) patterns acquired using a Bruker D8 powder diffractometer equipped with a CuKα X-ray source set at 40 kV and 40 mA. Morphological assessments were conducted using a JEOL-100C transmission electron microscope (TEM). A Zeiss-Gemini 2 Scanning Electron Microscopy operating at 15 kV and equipped with a Bruker Quantax EDX spectrometer was used for the SEM and elemental point analysis. Thermogravimetric analysis (TGA) was performed using a TAQ500 instrument (TA Instruments) under argon flow at a flow rate of 100 mL min−1 and a heating rate of 10 °C min−1 from RT to 1000 °C. For electrical property evaluation, the monoliths were formed into parallelepiped shapes with uniform thickness. To achieve ohmic contacts, thin layers of silver were applied to two opposing surfaces of the monoliths. Electrical measurements were carried out using a Keithley 487 pico-ammeter per voltage source and an Agilent 4156C semiconductor parameter analyser. Temperature-dependent experiments were conducted using an Advanced Research Systems liquid helium closed cycle at temperatures spanning from 80 to 320 K.
3. Results and discussion
Fig. 1 displays the X-ray diffraction (XRD) patterns of V2O5 nanopowder and carbon/vanadium nanocomposites annealed at 650 °C and 1000 °C. The XRD analysis of V2O5 nanoparticles reveals distinct peaks that indicate the presence of orthorhombic V2O5 (space group: Pmmn (no. 59), with parameters a = 3.5640 nm, b = 11.5190 nm, c = 4.3730 nm, referenced in JCPDS card no. 85-0601).36 Following the addition of V2O5 nanoparticles and the pyrolysis process, a transition in the crystalline structure was identified. The XRD patterns for samples RF/VOX-650 and RF/VOX-1000 show clear peaks at 2θ values of 30.9°, 47.4°, 57.6°, and 61.8°, corresponding to the (301), (060), (221), and (170) planes of orthorhombic V2O5. Additionally, peaks at 24.41°, 33.14°, 36.32°, 38.96°, 41.24°, 50.4°, 53.9°, 63.2°, 65.5°, and 71.02° are identified as belonging to the (012), (104), (110), (006), (113), (024), (116), (214), (300), and (119) planes of rhombohedral V2O3, as referenced in JCPDS card no. 34-0187.37,38 An intense peak at 22.58° for the RF/VOX-650 sample, associated with the (011) plane of orthorhombic V2O5, is absent in the RF/VOX-1000 sample. Furthermore, the XRD patterns for both RF/VOX-650 and RF/VOX-1000 exhibit a sharp peak at 26°, indicative of the graphite (C) phase, aligned with the (111) lattice plane according to JCPDS card no. 01-075-2078. The increase in pyrolysis temperature enhances the crystallinity of graphite, with the RF/VOX-1000 sample showing a peak around 43° associated with the (200) plane of cubic vanadium carbide (V8C7), as noted in JCPDS card no. 00-035-0786.39 The crystallite sizes were calculated using Scherrer's equation (eqn (1)):| |
 | (1) |
where D is the mean size of the crystallite, K is the dimensionless space factor having a value of 0.9 for spherical particles, λ is the X-ray wavelength, β is the full width at half maximum and θ is the Bragg angle. For the RF/VOX-650 °C sample, the average size of V2O5 was approximately 5 nm, while for RF/VOX-1000 °C, it was around 10 nm. The average sizes for V2O3 were found to be 12 nm and 25 nm for RF/VOX-650 °C and RF/VOX-1000 °C, respectively, while graphite crystallite sizes averaged 5 nm for RF/VOX-650 °C and 8 nm for RF/VOX-1000 °C. The average crystallite size for vanadium carbide was determined to be 33 nm.
 |
| | Fig. 1 XRD pattern of the V2O5 nanopowder and the nanocomposite RF/VOX pyrolyzed at 650 °C and 1000 °C. | |
Fig. 2(a–d) display the transmission electron microscopic (TEM) images of the RF/VOX samples prepared at 650 °C and 1000 °C. The images reveal that vanadium nanoparticles form an interconnected, nanowire-like structure dispersed within a carbon matrix, with variations in both length and diameter. The highlighted regions in Fig. 2(b and d) distinctly show the lattice fringes of the vanadium nanowires. For the RF/VOX-675 °C sample, a lattice fringe spacing of 0.526 nm is observed, corresponding to the (020) crystal plane of the orthorhombic phase of V2O5.36,40 In contrast, the RF/VOX-1000 sample displays an interplanar distance of 0.368 nm, which is related to the (012) crystal plane of the rhombohedral phase of V2O3.38 These findings are in good accordance with the X-ray diffraction results, indicating a phase transition of vanadium influenced by pyrolysis temperature.
 |
| | Fig. 2 TEM micrographs of the nanocomposites: (a and b) RF/VOX-650 and (c and d) RF/VOX-1000. | |
The scanning electron microscopic (SEM) images of RF/VOX-650 and RF/VOX-1000 are illustrated in Fig. 3(a–d). These micrographs show that the vanadium nanoparticles are well dispersed in the carbon matrix, indicating that the incorporation of V2O5 nanoparticles was successful. The presence of agglomerated carbon nanoparticles was also observed. In addition, it is easy to see that the vanadium nanoparticles are interconnected in the form of nanowires. The in situ developed nanowire-like structure can improve the electrical properties and extend the application field of the resulting material.
 |
| | Fig. 3 SEM micrographs of the nanocomposites: (a and b) RF/VOX-650 and (c and d) RF/VOX-1000. | |
The composition of the carbon/vanadium nanocomposites was confirmed using EDX analysis. The peaks corresponding to different percentages of C, O, and V elements can be clearly seen in Fig. 4 and 5 for RF/VOX-650 and RF/VOX-1000, respectively.
 |
| | Fig. 4 EDX point analysis of the nanocomposite RF/VOX-650. | |
 |
| | Fig. 5 EDX point analysis of the nanocomposite RF/VOX-1000. | |
As shown in Fig. 6, the thermogravimetric analysis of the RF/VOX nanocomposite showed a total weight loss of about 82% under argon flow at a flow rate of 100 mL min−1 and a heating rate of 10 °C min−1 from RT to 1000 °C. Three significant weight reductions were distinguished in the TGA curve: an initial weight loss of 6% occurred in the 50–100 °C range, 27% occurred in the 100–400 °C range, and 49% occurred in the 400–800 °C range. The first weight loss could be due to the desorption of water, while the second weight loss was due to the desorption of residual precursors. The third weight loss was assigned to the decomposition reactions involved in the carbonization process, probably due to the breaking of C–H and C–O bonds at the expense of C–C bond formation.17,41 However, no peak corresponding to the vanadium oxide phases appeared in the TGA plot. This result can be explained by the small quantity of vanadium oxide incorporated in the carbon matrix.
 |
| | Fig. 6 TGA curve of the RF/VOX nanocomposite. | |
To study the electrical properties of RF/VOX nanocomposites, we performed impedance spectroscopy measurements in the temperature range from 80 to 300 K and in the frequency range from 40 to 10 MHz. The variation in conductivity as a function of frequency at different temperatures for the RF/VOX-625 and RF/VOX-650 samples is illustrated in Fig. 7. Generally, the total conductivity is the contribution of two parts represented by the following relation (eqn (2)):
where the parameters
T and
ω = 2π
f denote the temperature and angular frequency, respectively. From
Fig. 7, it is clear that the conductivity depends on the temperature and frequency of both samples. These spectra follow Jonscher's law, which is described by the expression given in
eqn (3):
42where
Aωs is the response to the alternating current that occurs at high frequency,
A and
σdc are two constants and
s is the frequency exponent. The first term of the conductivity corresponding to the conductivity in continuous mode depends on the temperature and it follows the Arrhenius law given by
eqn (4):
43| |
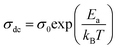 | (4) |
where
σ0 is the pre-exponential factor,
Ea is the thermal activation energy of electrical conduction and
kB is the Boltzmann constant. The second term depends on temperature and frequency and is linked to the relaxation mechanism caused by localized electric charge carriers. In addition, the shape of the spectra is influenced by the pyrolysis temperature. Indeed, for the sample treated at 625 °C, we notice that, whatever the measurement temperature, the spectra present a plateau independent of the frequency in the low frequency range (
σ =
σdc). In addition, the conductivity increases with the measurement temperature, which indicates the presence of a thermal activation process. While at high frequency, the conductivity increases with frequency and follows the universal Jonscher law, which is applicable for polymeric and semiconductor materials, and exhibits semiconductor behaviour. For the sample treated at 650 °C, we observe the same behaviours as those of the sample treated at 625 °C. In addition, we notice that the plateau extends more towards high frequencies when the pyrolysis temperature increases. However, at high frequencies and for measurement temperatures above 200 K, we notice that the conductivity decreases as the measurement temperature increases. This feature indicates that the metallic behaviour is dominant in this region. Indeed, in the case of metallic behaviour, Drude's law given in
eqn (5) describes the conductivity:
44| |
 | (5) |
where
τ is the relaxation time. At the measurement temperature of 200 K, the RF/VOX-650 sample undergoes a sudden transition where the transport mechanism changes trend from a character of semiconductor origin to a metallic behaviour. This variation in high-frequency conductivity was also found by Guadria
et al.16,45 in carbon–silica nanocomposites treated at 700 °C and by Ben Mansour
et al.46,47 in carbon–nickel oxide nanocomposites treated at 700 °C prepared by the sol–gel method after the incorporation of the nanoparticles into the carbon matrix; this work showed that the AC conductivity is attributed to different origins, such as the hopping conduction mechanism and the small polaron hopping model. In our work, the same conductivity behaviour is manifested at a lower pyrolysis temperature (650 °C), suggesting a higher effect of vanadium oxide nanoparticles on the conductivity of the carbon matrix. It appears from the preceding result that a change in the electrical attitude of the material as a function of frequency has been established, which is governed by the pyrolysis temperature. This can be linked to the nano-structuring of the material and also to the percolation phenomenon, which is well studied in our previous work.
14,15
 |
| | Fig. 7 Variation of conductivity as a function of frequency at different temperatures for (a) RF/VOX-625 and (b) RF/VOX-650 nanocomposites. | |
The variation of the exponent s with temperature can provide information on the conduction mechanisms involved. As shown in Fig. 8, the angular exponent s depends on temperature; this behaviour indicates that the type of hopping and carriers can be applied in transportation. In our study, the variation in the exponent s as a function of the measurement temperature is presented in Fig. 8. In this case, the exponent s is deduced from the isotherms of the variation in the conductance as a function of frequency, exploiting the linear part in the high frequency range based on equation eqn (6):48
| |
 | (6) |
 |
| | Fig. 8 Variation of exponent s with temperature for (a) RF/VOX-625 and (b) RF/VOX-650 nanocomposites. | |
For all samples, we notice that the value of s is always less than 1 and decreases with the increase in temperature. Furthermore, for sample RF/VOX-625, the value of s is close to zero at higher temperatures, indicating that DC conductivity dominates in this case. Eqn (7) shows that the model is based on the jump of charge carriers over the barrier, which is manifested by a decrease in the value of the angular exponent with the increase in temperature; this is therefore in agreement with the experimental results. Then, the conduction in the material can be attributed to the jump of charge carriers. In addition, the results show that the conduction mechanism is thermally activated. Indeed, the correlated barrier hopping (CBH) conduction model is the appropriate conduction model to describe carrier transfer in our samples.47,49 According to this model, the frequency exponent is given by eqn (7):50
| |
 | (7) |
where
Wm is the energy required to remove an electron from a site (activation energy) and
τ0 is the relaxation time.
Fig. 9 illustrates the linear variation of the exponent s as a function of temperature for samples RF/VOX-625 and RF/VOX-650. In this case, the expression of the exponent s is reduced to eqn (8):
| |
 | (8) |
where
Wm is calculated using the best fit of the experimental data shown in
Fig. 9, giving
Wm = 75 meV for RF/VOX-625 and
Wm = 61 meV for RF/VOX-650. This result is compatible with the hypothesis of electronic jumps between localized sites.
51,52 In addition, the value of
Wm decreases as the pyrolysis temperature increases.
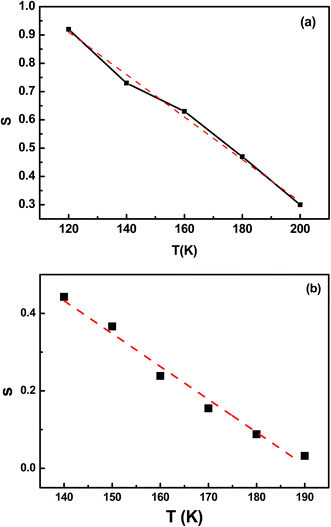 |
| | Fig. 9 Linear part of the exponent s as a function of the measurement temperature for the nanocomposites (a) RF/VOX-625 and (b) RF/VOX-650. | |
Fig. 10 illustrates the variation in conductivity as a function of 1000/T for samples RF/VOX-625 and RF/VOX-650. The obtained curves show temperature dependence following eqn (4). We observe that the direct current conductivity decreases with the decrease in measurement temperature, which reveals the presence of a thermally activated process. The activation energy is obtained from the slope of the curve in the Arrhenius diagram and is equal to 97 and 67 meV for samples RF/VOX-625 and RF/VOX-650, respectively. Thus, the activation energy Ea decreases with the increase in the pyrolysis temperature, which can be explained by the fact that the density of the state increases as a function of this temperature. The impedance measurements were carried out in the temperature range of 120 to 300 K and the frequency domain of 50 Hz to 1 MHz.
 |
| | Fig. 10 Variation of AC conductance as a function of temperature for samples (a) RF/VOX-625 and (b) RF/VOX-650. | |
Fig. 11 illustrates the variation of the real part of the impedance Z′ as a function of frequency at different measurement temperatures for samples RF/VOX-625 and RF/VOX-650. The overall appearance of these spectra is made up of two parts. At low frequencies, Z′ has a higher value (∼6 MΩ), while at higher frequencies, the value of the real part of the impedance Z′ decreases and merges for all measurement temperatures. These two characteristics are signs of the presence of space charge polarization.53,54 We also notice that the relaxation frequency, where Z′ starts to decrease, shifts towards the high-frequency side, which can be attributed to the release of space charge and the reduction of potential barriers.55 The decrease in Z′ values at low frequencies can be attributed to the improvement in the mobility of charge carriers and the decrease in the density of trapped charges.56,57 According to Fig. 11, we can also observe the decrease in Z′ as the measurement temperature increases. Such behaviour reveals an increase in conductivity. This result confirms the increase in conductivity observed in Fig. 7. In addition, the pyrolysis temperature influences the values of the real part of the impedance Z′. Indeed, the amplitudes of Z are higher for the RF/VOX-625 sample, as well as the plateaus at low frequencies are more pronounced for the RF/VOX-650 sample; consequently, the relaxation frequencies are higher for the RF/VOX-650 sample (from 104 Hz) than for the RF/VOX-625 sample (from 102 Hz).
 |
| | Fig. 11 Evolution of the real part of the impedance Z′ as a function of frequency at different temperatures for the samples (a) RF/VOX-625 and (b) RF/VOX-650. | |
We plotted the variation of the imaginary part of the impedance Z′′ as a function of frequency at different measurement temperatures for the samples RF/VOX-625 and RF/VOX-650 in Fig. 12. The spectra are characterized by the appearance of broad peaks in the frequency range between 102 and 104 Hz for the RF/VOX-625 sample and in the range between 104 and 106 Hz for the RF/VOX-650 sample. These peaks represent a good sign for the presence of relaxation phenomena in our material.58 Each peak corresponds to a well-defined frequency, called the relaxation frequency (fr). Furthermore, we notice that these peaks move towards a higher frequency region with the increase in the measurement temperature, which is a sign of the presence of a relaxation phenomenon in this material. The centres of these peaks are located at different frequency values, which shows the presence of non-Debye-type relaxation in the sample.59 This characteristic proves the involvement of thermally activated charge carriers in electrical conduction.57 The peaks appearing in the imaginary part of the Z′′ impedance curves are well defined. This observation indicates that electrical relaxation begins in the nanocomposite. Furthermore, the intensity of the relaxation peaks decreases as the temperature increases. This behaviour is a strong indication of the decline in the resistive properties of the sample.60
 |
| | Fig. 12 Frequency dependence of the imaginary part of impedance Z′′ at different temperatures for samples (a) RF/VOX-625 and (b) RF/VOX-650. | |
The relaxation time (τ) as a function of temperature is represented by the Arrhenius expression given by eqn (9):
| |
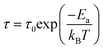 | (9) |
where
Ea is the activation energy of the relaxation time
τ. Generally, the relaxation time is determined by the relationship 2π
frτ = 1. The variation of the relaxation time
τ as a function of temperature is plotted in
Fig. 13, where the values of
τ are calculated from the plot of the position of the peaks in
Z′′ as a function of frequency using the relation 2π
frτ = 1. From
Fig. 13, the activation energy is calculated for all temperature domains and is approximately 102 and 82 meV for samples RF/VOX-625 and RF/VOX-650, respectively. This attitude indicates the presence of a single conduction mechanism in the studied materials. We also note that the values of the activation energy estimated from the continuous conductivity are of the same order as those obtained for the relaxation phenomenon. Taking into account the uncertainties of measurements and calculations, we can conclude that the conduction mechanism and the relaxation phenomenon are associated with the same process.
 |
| | Fig. 13 Evolution of the relaxation time according to the Arrhenius law of the nanocomposites (a) RF/VOX-625 and (b) RF/VOX-650. | |
The variation of the imaginary part of the impedance Z′′ as a function of the real part Z′ for different measurement temperatures representative of the RF/VOX-625 and RF/VOX-650 samples is shown in Fig. 14. Arcs of circles and passers-by in the vicinity of the origin are observed for the two samples for the entire range of measurement temperatures. This shows the presence of a distribution of relaxation times in the different mechanisms, and it suggests that the conduction process in the sample does not follow the Debye model but it follows the Cole–Cole model.61,62 Generally, the appearance of an ideal semi-circle in the complex plane (Cole–Cole) indicates the presence of Debye-type dispersion, which is not the case in our material. Furthermore, these arcs shift towards higher frequencies as the measurement temperature increases. The impedance spectra show that the radius decreases as the measurement temperatures increase. This indicates that the classical thermal behaviour of resistance is present in our nanocomposite and that the resistance decreases with the increase in temperature. Therefore, this confirms the thermal activation of the conduction mechanism and proves that the semiconductor behaviour is dominant in the samples.63
 |
| | Fig. 14 Nyquist diagram of (a) RF/VOX-625 and (b) RF/VOX-650 nanocomposites. | |
To obtain the electrical data from the Nyquist diagrams, we used software to adjust these parameters. These diagrams are modelled with an equivalent electrical circuit, as illustrated in Fig. 15. These arcs represent capacitive and resistive behaviours. For the nanocomposite treated at 625 °C (Fig. 13(a)), we modelled the results by two series circuits which consist of a resistor R and a constant phase element (CPE) connected in parallel, over the entire temperature range. The same modelling is attributed to the nanocomposite treated at 650 °C (Fig. 15(b)) in the low temperature range (between 140 and 190 K), whereas the equivalent electrical circuit consists of resistance R in parallel with the constant phase element CPE in the high temperature range (Fig. 15(c)). In our case, the capacitive element was replaced by a CPE because of the non-Debye behaviour nature of our compound.
 |
| | Fig. 15 Fitting of the Nyquist diagrams using the Zview software for samples (a) RF/VOX-625 at T = 300 K, (b) RF/VOX-650 at T = 140 K and (c) RF/VOX-650 at T = 300 K. | |
Our main goal is to identify the origins of each curve. To solve this challenge, we focused on the values of the resistance R or the fractal capacitance CPE. Regarding this electric parameter, scientists generally conclude that grain resistance is low compared to that of grain boundary;64,65 however, they have sometimes found that grain is less conductive than intragrain. Therefore, comparing resistance values is not sufficient. Regarding capacitance, the magnitude of the grain capacitance value is generally smaller than that of the grain boundary. Considering these facts, for samples RF/VOX-625 and RF/VOX-650 (Fig. 15(a and b)), the equivalent circuits represent the effect of grain boundary and grain at low and high frequencies, respectively. However, the curve in Fig. 15(c) is attributed to the grain effect. The fractal capacitance values at low and high frequencies belong to the typical grain boundary and grain capacitance ranges, respectively.66 It is a good signature to assign the low-frequency curve to the grain boundary and the high-frequency curve to the grain. We note that beyond 200 K, the grain contribution is dominant in the electrical conduction for the RF/VOX-650 sample. This result is in good agreement with the electrical conductivity measurements, which showed the presence of a transition from semiconductor behaviour to metallic behaviour at 200 K.
Complex modulus is a complementary study of impedance, giving a clear picture of the different physical processes occurring in the material. In our case, neither relaxation frequencies nor peak maxima are useful for determining the correct microstructures, due to the presence of only one peak. The best clue to clarify the ambiguity produced concerning the presence of a grain or grain boundary effect is to combine the spectra of the imaginary part of the electrical modulus M′′ and the imaginary part of the impedance Z′′.67 Fig. 16 illustrates the variation of M′′ and Z′′ as a function of frequency at 140 and 300 K. Fig. 16(a and b) show three relaxation peaks appearing at distinct frequencies, while Fig. 16(c) indicates that the peak of electrical modulus and that of impedance coincide at the same frequency. From this figure, we can decide that the main peak on each subfigure of Fig. 16(a–c) is due to the grain effect. In addition, we validate that the active microstructures in the RF/VOX-625 sample are grains and grain boundaries. Additionally, the contributing microstructures in sample RF/VOX-650 are grains and grain boundaries at low temperatures (140 to 190 K), while at high temperatures (200 to 300 K), the microstructure is associated with the grain effect only. This observation confirms the results obtained by the Nyquist diagram.
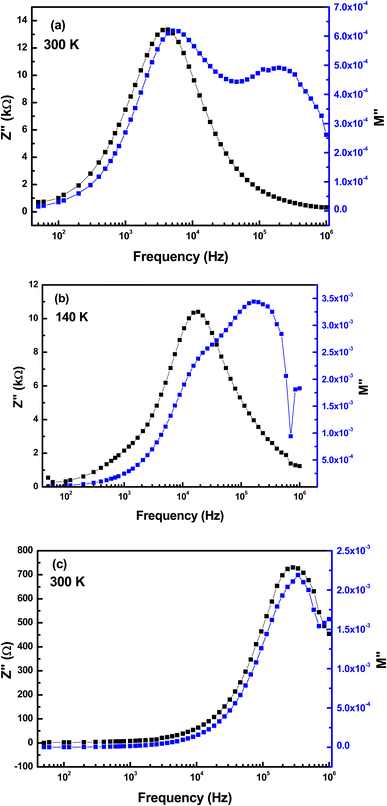 |
| | Fig. 16 Variation of combined M′′ and Z′′ as a function of frequency for the nanocomposites (a) RF/VOX-625 at T = 300 K, (b) RF/VOX-650 at T = 140 K and (c) RF/VOX-650 at T = 300 K. | |
4. Conclusion
In this work, we studied the effect of the pyrolysis temperature on the electrical properties of nanocomposites based on a resorcinol–formaldehyde matrix enriched with vanadium oxide nanoparticles. XRD analysis revealed that increasing the pyrolysis temperature enhanced the crystallinity of the sample. Microscopic examination confirmed that the V2O5 nanoparticles were observed to have a nanowire morphology dispersed in the carbon matrix. Indeed, at low frequencies, the ac conductance showed a thermally activated process for samples RF/VOX-625 and RF/VOX-650. At high frequencies, the RF/VOX-625 sample exhibits semiconductor behaviour, while the RF/VOX-650 sample undergoes a transition from a semiconductor attitude to a metallic one at 200 K. The variation of the exponent s demonstrated that the CBH model describes the mechanism of AC conduction. The impedance spectra revealed the presence of a relaxation phenomenon in the sample. Nyquist plots of the complex impedance spectra reveal the presence of grain and grain boundary contributions in samples RF/VOX-625 and RF/VOX-650 at low temperatures. In addition, these diagrams show the dominance of the grain effect in the RF/VOX-650 sample beyond 200 K. The incorporation of vanadium nanoparticles to the polymer matrix endows it with new physical properties and behaviours that are interesting compared to the original organic matrix, suggesting the potential for testing the resulting material in several applications, such as negatronic devices, gas storage devices and gas sensors.
Data availability
The datasets generated during the current study are available from the corresponding author upon reasonable request.
Author contributions
All the authors conceived the study design. H. J. and W. A. contributed to conceptualization, methodology, synthesis, data analysis, and original draft preparation. I. N. and M. E. contributed to the conceptualization and electrical characterizations. M. C. and G. N. contributed to the thermogravimetric and SEM-EDX characterizations. H. L. G. and L. E. M. performed the supervision, reviewing, and editing of the manuscript.
Conflicts of interest
The authors declare no conflict of interest in preparing this article.
Acknowledgements
This work was financially supported by the Tunisian Ministry of Higher Education and Scientific Research through the budget of the Tunisian Laboratories.
References
- R. G. Pearson, Coord. Chem. Rev., 1990, 100, 403–425 CrossRef CAS.
- L. El Mir, Z. Ben Ayadi, M. Saadoun, H. J. von Bardeleben, K. Djessas and A. Zeinert, Phys. Status Solidi, 2007, 204, 3266–3277 CrossRef CAS.
- R. Slama, J. El Ghoul, K. Omri, A. Houas, L. El Mir and F. Launay, J. Mater. Sci.: Mater. Electron., 2016, 27, 7939–7946 CAS.
- S. Amara, I. Ben Slama, I. Mrad, N. Rihane, W. Khemissi, L. El Mir, K. Ben Rhouma, H. Abdelmelek and M. Sakly, Hum. Exp. Toxicol., 2014, 33, 1150–1157 CAS.
- K. C. Krogman, T. Druffel and M. K. Sunkara, Nanotechnology, 2005, 16, S338 Search PubMed.
- Z. Ben Ayadi, H. Mahdhi, K. Djessas, J. L. Gauffier, L. El Mir and S. Alaya, Thin Solid Films, 2014, 553, 123–126 CAS.
- S. Jaballah, M. Benamara, H. Dahman, D. Lahem, M. Debliquy and L. El Mir, J. Mater. Sci.: Mater. Electron., 2020, 31, 8230–8239 CAS.
- J. L. Knutson, J. D. Martin and D. B. Mitzi, Inorg. Chem., 2005, 44, 4699–4705 CAS.
- C. Aruta, F. Licci, A. Zappettini, F. Bolzoni, F. Rastelli, P. Ferro and T. Besagni, Appl. Phys. A, 2005, 81, 963–968 CrossRef CAS.
- D. B. Mitzi, C. D. Dimitrakopoulos and L. L. Kosbar, Chem. Mater., 2001, 13, 3728–3740 CAS.
- Y. Tominaga and H. Ohno, Electrochim. Acta, 2000, 45, 3081–3086 CAS.
- K. Chondroudis and D. B. Mitzi, Chem. Mater., 1999, 11, 3028–3030 CAS.
- B. G. Soares, F. Gubbels, R. Jéro^me, E. Vanlathem and R. Deltour, Rubber Chem. Technol., 1997, 70, 60–70 CAS.
- H. Jeidi, W. Ahmed, L. Chouiref, H. L. Gomes, I. Najeh and L. El Mir, J. Inorg. Organomet. Polym. Mater., 2024, 34, 5153–5163 Search PubMed.
- W. Ahmed, H. Jeidi, L. Chouiref, H. L. Gomes, H. Dahman and L. El Mir, Appl. Phys. A, 2023, 129, 1–9 CrossRef.
- S. Gouadria, Z. M. Elqahtani, F. F. Alharbi and K. Omri, J. Inorg. Organomet. Polym. Mater., 2020, 30, 3317–3324 CAS.
- N. Ben Mansour, W. Djeridi and L. El Mir, J. Inorg. Organomet. Polym. Mater., 2021, 31, 4360–4371 Search PubMed.
- F. Sayari, N. Ben Mansour, M. Kraini, M. A. Wederni, M. Hjiri, F. Aouaini, A. Sharma and L. El Mir, J. Inorg. Organomet. Polym. Mater., 2024, 35(1), 98–108 Search PubMed.
- W. Ahmed, H. Jeidi, I. Najeh, H. Dahman, J. P. B. Silva, J. A. Moreira, M. Pereira, M. J. M. Gomes and L. El Mir, J. Mater. Sci.: Mater. Electron., 2022, 33, 25846–25860 CAS.
- T. Chirayil, P. Y. Zavalij and M. S. Whittingham, Chem. Mater., 1998, 10(10), 26292640 Search PubMed.
- Y. Yue and H. Liang, Adv. Energy Mater., 2017, 7(17), 1602545 Search PubMed.
- L. Q. Mai, Q. Y. An, Q. L. Wei, J. Y. Fei, P. F. Zhang, X. Xu, Y. L. Zhao, M. Y. Yan, W. Wen and L. Xu, Small, 2014, 10(15), 3032–3037 CAS.
- Z. Chen, V. Augustyn, J. Wen, Y. Zhang, M. Shen, B. Dunn and Y. Lu, Adv. Mater., 2011, 23(6), 791–795 CAS.
- H. L. Fei, H. J. Zhou, J. G. Wang, P. C. Sun, D. T. Ding and T. H. Chen, Solid State Sci., 2008, 10(10), 1276–1284 CAS.
- Q. T. Qu, Y. Shi, L. L. Li, W. L. Guo, Y. P. Wu, H. P. Zhang, S. Y. Guan and R. Holze, Electrochem. Commun., 2009, 11(6), 1325–1328 CrossRef CAS.
- Z. L. Wang, D. Xu, L. M. Wang and X. B. Zhang, ChemPlusChem, 2012, 77(2), 124–128 CrossRef CAS.
- Y. P. Liu, W. W. Zhong, Y. X. Du, Q. X. Yuan, X. Wang and R. X. Jia, J. Alloys Compd., 2015, 633, 353–358 CrossRef CAS.
- L. Du, H. Lin, Z. Ma, Q. Wang, D. Li, Y. Shen, W. Zhang, K. Rui, J. Zhu and W. Huang, J. Power Sources, 2019, 424, 158–164 CAS.
- M. Ihsan, Q. Meng, L. Li, D. Li, H. Wang, K. H. Seng, Z. Chen, S. J. Kennedy, Z. Guo and H. K. Liu, Electrochim. Acta, 2015, 173, 172–177 CAS.
- L. Kong and I. Taniguchi, Adv. Powder Technol., 2017, 28(17), 1411–1417 CAS.
- M. Fu, Q. Zhuang, Z. Zhu, Z. Zhang, W. Chen, Q. Liu and H. Yu, J. Alloys Compd., 2020, 862, 158006 Search PubMed.
- X. Hu, K. Y. Goud, V. S. Kumar, G. Catanante, Z. Li, Z. Zhu and J. L. Marty, Sens. Actuators, B, 2018, 268, 278 CAS.
- S. Sekar, I. Rabani, C. Bathula, S. Kumar, S. Govindaraju, K. Yun, Y. S. Seo, D. Y. Kim and S. Lee, Environ. Res., 2021, 205, 112201 Search PubMed.
- L. El Mir, A. Amlouk and C. Barthou, J. Phys. Chem. Solids, 2006, 67, 2395–2399 CrossRef CAS.
- L. El Mir, Z. Ben Ayadi, H. Rahmouni, J. El Ghoul, K. Djessas and H. J. von Bardeleben, Thin Solid Films, 2009, 517, 6007–6011 CrossRef CAS.
- W. Bi, J. Huang, M. Wang, E. P. Jahrman, G. T. Seidler, J. Wang, Y. Wu, G. Gao, G. Wu and G. Cao, J. Mater. Chem. A, 2019, 7, 17966–17973 RSC.
- N. Hassan, J. Riaz, M. T. Qureshi, A. Razaq, M. Rahim, A. M. Toufiq and A. Shakoor, J. Mater. Sci.: Mater. Electron., 2018, 29, 16021–16026 CAS.
- H. Zhang, Z. Yao, D. Lan, Y. Liu, L. Ma and J. Cui, J. Alloys Compd., 2021, 861, 158560 CAS.
- Z. Zhao, Y. Liu, H. Cao, S. Gao and M. Tu, Vacuum, 2008, 82, 852–855 CAS.
- S. Sekar, I. Rabani, C. Bathula, S. Kumar, S. Govindaraju, K. Yun, Y.-S. Seo, D. Y. Kim and S. Lee, Environ. Res., 2022, 205, 112201 CAS.
- L. El Mir, S. Kraiem, M. Bengagi, E. Elaloui, A. Ouederni and S. Alaya, Phys. B, 2007, 395, 104–110 CAS.
- A. K. Jonscher, J. Mater. Sci., 1981, 16, 2037–2060 CAS.
- S. Ilican, Y. Caglar, M. Caglar and F. Yakuphanoglu, Phys. E Low Dimens. Syst. Nanostruct., 2006, 35, 131–138 CAS.
- D. C. Tsui, S. J. Allen, R. A. Logan, A. Kamgar and S. N. Coppersmith, Surf. Sci., 1978, 73, 419–433 CAS.
- S. Gouadria, H. Dahman, I. Najeh, A. Alyamani and L. El Mir, J. Mater. Sci.:Mater. Electron., 2015, 26, 7397–7406 CrossRef CAS.
- N. Ben Mansour and L. El Mir, Appl. Surf. Sci., 2014, 308, 10–16 CrossRef CAS.
- N. Ben Mansour and L. El Mir, J. Phys. Chem. Solids, 2019, 127, 1–10 CrossRef CAS.
- D. K. Pradhan, R. N. P. Choudhary and B. K. Samantaray, Mater. Chem. Phys., 2009, 115, 557–561 CAS.
- I. Najeh, N. Ben Mansour, H. Dahman, A. Alyamani and L. El Mir, J. Phys. Chem. Solids, 2012, 73, 707–712 CAS.
- R. Dhahri, M. Hjiri, L. E. Mir, A. Bonavita, D. Iannazzo, S. G. Leonardi and G. Neri, Appl. Surf. Sci., 2015, 355, 1321–1326 CAS.
- D. K. Pradhan, B. K. Samantaray, R. N. P. Choudhary and A. K. Thakur, Mater. Sci. Eng. B., 2005, 116, 7–13 CrossRef.
- H. Radscheit and K. G. Breitschwerdt, Solid State Commun., 1983, 47, 157–161 CAS.
- J. Suchanicz, Mater. Sci. Eng. B., 1998, 55, 114–118 Search PubMed.
- M. Smari, H. Rahmouni, N. Elghoul, I. Walha, E. Dhahri and K. Khirouni, RSC Adv., 2015, 5, 2177–2184 RSC.
- K. Omri, A. Bettaibi, K. Khirouni and L. El Mir, Phys. B Condens. Matter, 2018, 537, 167–175 CAS.
- J. Hu and H. Qin, J. Magn. Magn. Mater., 2001, 231, 1–3 Search PubMed.
- H. Rahmouni, M. Smari, B. Cherif, E. Dhahri and K. Khirouni, Dalton Trans., 2015, 44, 10457–10466 CAS.
- M. Ram, Solid State Sci., 2010, 12, 350–354 CAS.
- P. S. Anantha and K. Hariharan, Mater. Chem. Phys., 2005, 89, 428–437 CAS.
- M. Younas, M. Nadeem, M. Atif and R. Grossinger, J. Appl. Phys., 2011, 109, 93704 Search PubMed.
- K. S. Cole and R. H. Cole, J. Chem. Phys., 1941, 9, 341–351 CrossRef CAS.
- Z. Aloui, V. Ferretti, S. Abid, M. Rzaigui, F. Lefebvre and C. Ben Nasr, J. Mol. Struct., 2015, 1087, 26–32 CrossRef CAS.
- L. H. Omari, R. Moubah, A. Boutahar, L. Hajji and R. El Ouatib, J. Electroceram., 2020, 44, 23–31 CAS.
- I. Ahmad, M. J. Akhtar, M. Younas, M. Siddique and M. M. Hasan, J. Appl. Phys., 2012, 112, 74105 Search PubMed.
- M. Nadeem, M. J. Akhtar, A. Y. Khan, R. Shaheen and M. N. Haque, Chem. Phys. Lett., 2002, 366, 433–439 CAS.
- I. Ahmad, M. J. Akhtar and M. M. Hasan, Mater. Res. Bull., 2014, 60, 474–484 CAS.
- P. Nayak, T. Badapanda, A. K. Singh and S. Panigrahi, Ceram. Int., 2017, 43, 4527–4535 CAS.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
W. Ahmeda,
I. Najeha,
M. Erouela,
H. L. Gomesb,
M. Chellyc,
G. Neri
*a,
W. Ahmeda,
I. Najeha,
M. Erouela,
H. L. Gomesb,
M. Chellyc,
G. Neri c and
L. El Mira
c and
L. El Mira