 Open Access Article
Open Access ArticleA minimalistic approach to broad band emission modeling, and automated configurational diagram construction†
Andrii Shyichuk * and
Eugeniusz Zych
* and
Eugeniusz Zych
University of Wrocław, Faculty of Chemistry, 14 F. Joliot-Curie, 50-506 Wrocław, Poland. E-mail: andrii.shyichuk@uwr.edu.pl
First published on 27th May 2025
Abstract
In this paper, we propose a novel approach to broad emission band modeling. The ground state and the excited state of the emitter are represented as two continuous parabolic manifolds, where energy is proportional to the square of a certain geometrical coordinate (E = kx2). The emitting level population is described by Boltzmann distribution, with absolute temperature as a parameter. Depending on the offset between the two parabolas and their curvatures (force constants) both symmetric and asymmetric Gaussian-like band shapes can be produced. Also proposed is a simple algebra that maps the input energy axis values of the experimental spectrum to the values of the geometrical (configurational) coordinate. The resulting band shape can be compared to the experimental one via least-squares fitting of the model parameters. Its usefulness in spectrum decomposition (deconvolution) is demonstrated using a few examples (doped inorganic phosphors; d–d, f–d and charge transfer transitions). Presence of absolute temperature in the definition of the model provides a potential for its use in primary luminescence thermometry.
1 Introduction
Transition metal cations are an essential part of many photoluminescent materials. Those include complexes with organic ligands, metal–organic frameworks, inorganic (crystalline powder) phosphors, and laser crystals. In all of them, several kinds of electronic transitions occur. Characteristic narrow bands, often called lines, originate from spin-forbidden transitions: 4f ↔ 4f in most lanthanide (3+) or (2+) cations and d ↔ d in d-block metals. Along the narrow features, different types of broad bands can occur. Those include intraconfigurational d ↔ f transitions in lanthanides (Ce3+, Pr3+, Tb3+ Eu2+, and Sm3+ likely being the most classic examples), spin-allowed d ↔ d bands, as well as charge transfer bands (typical cases are O2− → Eu3+, O2− → Ce4+, O2− → V5+, O2− → Mn7+, O2− → Mn4+ but also others). The width of the latter is highly sensitive to the coordination surrounding chemistry and geometry, as well as to temperature.The broad bands can be quite different in both shapes and widths and are referred to simply as “broad” in the literature. If the specific origin of such a band is known – these bands are referred to as (ligand to metal) charge-transfer (CT, LMCT),1–3 f–d transitions,2,3 metal-to-metal charge transfer (MMCT),4 intervalence charge transfer,5–7 etc. General terminology for these bands, such as “log-normal”8 and “asymmetric Gaussian”9 is used, and this already shows that the community has not established precise and accurate terminology for such absorption, excitation or luminescent components of spectra. This is surprising as transitions generating such broad bands play a vital role in tailoring the overall properties of luminescent materials and compounds.
A typical approach to band shape analysis involves separating the band into constituent components. Each component of a band shape is thought to originate from an individual and distinct spectroscopic entity (for inorganic phosphors – a crystallographic site). The number of constituents of the analyzed band is taken to correspond to the number of sites. Often, the components are taken to be of Gaussian shape. The traditional name for this process is deconvolution, although it does not involve a convolution (a very well defined term in mathematics) of components but a mere sum. Convolution is defined as the integral of the product of the two functions after one is reflected about the y-axis and shifted. The integral is evaluated for all values of the shift, producing the convolution function. The “decomposition” term is used in, e.g. ref. 8.
The use of Gaussian bands contains several fundamental problems. Firstly (as will be shown below), a Gaussian band with its vertical symmetry axis is not a good fit for an asymmetric band (with different slopes in its high- and low-energy sides). Secondly, the Gaussian band shape is used with no regard for it being physically justified. Gaussian band shape corresponds to specific mechanisms of atomic line broadening10 – natural broadening due to Heisenberg uncertainty of the transition energy, Doppler broadening, and pressure/proximity broadening. At low temperatures of several kelvins, lanthanide(III) 4f ↔ 4f transitions in inorganic matrices (e.g. ref. 11 and 12) are characterized by band widths in the order of tens of GHz, or several cm−1, or hundreds of μeV. However, bands typically occurring in phosphors are usually much broader – sometimes as broad as hundreds of nanometers or several eVs. Any model for such bands must also include geometrical (chemical) broadening mechanisms. The emitters in phosphors are subjected to deformations by lattice vibrations that constantly change the geometry of the emitter surround. What occurs as a single broad band in a spectrum originates in fact from an ensemble of sites (quantum oscillators/emitters) of multiple different (albeit similar) geometries. The resulting distribution of transition energies in such an ensemble may or may not follow a normal distribution and thus does not have to result in a Gaussian band shape.
This paper addresses these problems and provides a mathematical description of broad bands of any kind in electronic spectra that is still relatively simple and physically much less simplified than routinely used decomposition. The shape of symmetric, slightly asymmetric, and strongly asymmetric broad bands can be achieved in terms of the same basic algebra. Moreover, several important features can be extracted from the experimental data by fitting the experimental band using our approach. This method can be applied to both broad and narrow bands and appears superior to Gaussian decomposition (commonly called deconvolution). Correspondingly, a general term for the band shape is proposed: a biparabolic band.
With the proposed methodology, for any experimental absorption, excitation, or emission spectrum, the corresponding energy level diagram (a configuration coordinate diagram) can be constructed, taking advantage of the few parameters provided by the fit. Although the examples in this paper are all focused on emission bands, most of the conclusions would also be valid for independent analysis of absorption or excitation spectra. Basically, as long as a transition can be described by a single parabolic manifold of initial states with the corresponding populations, and a single parabolic manifold of final states – this approach will work. Hence, there is no need to specifically address absorption analysis. However, in order to fully utilize the potential of biparabolic decomposition, one should use multispectral fitting. For example, the optimization process must look for a set of levels that satisfy both the excitation and emission spectra in question. Such analysis is an interesting topic on its own and deserves a dedicated paper.
2 The approach fundamentals
Let us consider a model system consisting (for simplicity) of an atom in a solid. The atom is treated explicitly, while the solid is represented by a certain embedding environment (e.g., point charges; the particular kind is irrelevant). Any lattice vibrations in such a system distort the surroundings of the atom, resulting in some changes in its energy levels. Commonly, the surround would be deformed by a fully symmetric (breathing) vibrational mode. Here, no particular mode is assumed; merely an arbitrary deformation is considered. In more physical terms, the deformation can be viewed as a certain average of multiple vibrations of a lattice that contains this particular impurity/atom and is thus not completely symmetric (in respect to the symmetry of the perfect host crystal). The atom and its ligands are not viewed as a harmonically oscillating system but rather as an ensemble of geometries the lattice oscillations generate. The geometries change into each other slowly enough for the electrons to occupy the respective equilibrium states at every particular geometry (i.e. adiabatic approximation is assumed). The atoms are thus considered not moving at any given configuration coordinate point.Then, let us assume that the total energy E1 of the model system in its ground state is a quadratic function of a configurational coordinate x. The intention of this paper was not to answer the question of “Why is that dependence quadratic?”, but to show that a quadratic dependence, in particular, allows the reproduction of a certain band shape. Nevertheless, chemical bond energies exhibit quadratic dependence on the bond lengths at the proximity of the equilibrium length. The deformations of the model atom surround can be viewed as simultaneous deformations of all of the atom bonds.
To reduce the number of parameters, E1 minimum can be at x = 0, while E1(x = 0) can be zero as well. Then:
| E1(x) = ax2 | (1) |
Consequently, let us assume that the total energy E2 of the model system in a certain excited state is another quadratic function of the same configurational coordinate. Its minimum may or may not be at x = 0, while its minimum energy is necessarily not the same as E1 minimum. The coefficient at x2 for E2 may differ from that of E1. Thus:
| E2(x) = b(x − c)2 + d | (2) |
With these four parameters defining two parabolae, the 2 → 1 transition (emission) energy as a function of x is given by:
| Eem(x) = E2(x) − E1(x) = b(x − c)2 + d − ax2 = b(x2 − 2cx + c2) + d − ax2 = (b − a)x2 − 2bcx + bc2 + d | (3) |
Thus, the final version of eqn (3) describes the energy difference (the transition energy) between the two energy levels as a function of the configuration coordinate x and four parameters defining both parabolas (Fig. 1). While eqn (3) provides a dependence of the energy difference on an arbitrary x, any experimental spectrum comes with a defined set of energy values at which the respective intensity is measured. In other words, every spectrum has its own abscissa values. Thus, to reproduce an experimental band using eqn (3), a set of x values must be found that produce energy differences corresponding to the experimental data points – for a given set of parameters a, b, c, d. In other words, the Eem = f(x) function must be transformed into the corresponding x = g(Eem) function.
 | ||
| Fig. 1 An example of two parabolae with the visualizations of the underlying parameters (as used in eqn (4) and (8)). The scales were selected to emphasize the Gaussian-like shape at the E2 parabola representing the Boltzmann probabilities from eqn (12). | ||
Using the Wolfram Alpha online engine, the inverse function is found to be:
 | (4) |
The ± sign in eqn (4) indicates the existence of two x = g(Eem) functions – the one with the plus and the one with the minus. Due to the shape of the parabolas, the same energy difference can occur at two different values of x, and eqn (4) reflects this property. Consequently, the following spectrum generation uses both x = g(Eem) functions.
Eqn (4) will not work for all possible values of a, b, and c. In the (a = b, c = 0) case, the parabolas have identical curvatures and are not offset in respect to each other along x. The corresponding energy difference will thus always be equal to d, and the respective spectrum is a Dirac's delta function, the purest idealized spectral line. With (a = b, c ≠ 0), eqn (4) will still not work due to division by zero in the a − b part. The whole calculation must be adapted for this particular case:
| Eema=b(x) = E2(x) − E1(x) = b(x − c)2 + d − ax2 = b(x2 −2cx + c2) + d − ax2 = (b − a)x2 − 2bcx + bc2 + d = −2bcx + bc2 + d | (5) |
| Eema=b(x) − bc2 − d = −2bcx | (6) |
 | (7) |
Thus, the complete procedure for mapping Eem to x involves three different solvers that conditionally depend on the values of a, b, and c: Dirac's delta if (a = b, c = 0); eqn (7) if (a = b, c ≠ 0); eqn (4) otherwise.
In eqn (7), the configurational coordinate x is a linear function of the transition energy Eem of the spectrum (provided that a = b). The resulting band is defined solely by the distribution shape of the excited manifold populations. In the case of Boltzmann distribution, the shape is Gaussian.
Now, eqn (4) and (7) can be relabeled so that the parameters gain physical meanings. The parameter a is the ground state parabola curvature and is double the value of the second derivative of E1 with respect to x. In the physical–chemical sense, parameter x should correspond to some deformation of the central atom bonds. Then, parameter a is double the value of the collective force constant of the deformation corresponding to x. The same goes for b and E2. Thus, a and b can be relabeled k1 and k2, respectively. The factor of two is ignored for simplicity, as the x coordinate value is arbitrary: its sole purpose is to generate two parabolic manifolds. The parameter c is the excited state parabola abscissa offset in the units of x and is relabeled to xO, (similarly to the classical Pekarian formula13 from vibrational analysis), and d is a minimum-to-minimum energy difference between the two states, ΔEmm.
With the given Eem vector (a sequence, a set) of experimental spectrum energy values, x (as produced by x = g(Eem) function) is a vector of the same size. Eqn (4) and (7) now read:
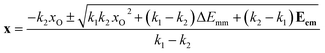 | (8) |
 | (9) |
The x = g(Eem) function is essential as it allows mapping any experimental emission spectrum energy axis to the values of x – given the four parameters that define the parabolas. In other words, for any experimental spectrum with arbitrary values of the energy axis – those values can be mapped analytically to the transition energies between the two sets of energy levels represented by the parabolas. With no need to interpolate, the equations can be wrapped into an efficient fitting function, producing a spectrum from the input parameters and the given energy axis. Such a function can be used as any other band-shape function in spectrum decomposition (deconvolution) into principal components.
Noteworthy, parabolas are also present in the classical vibrational analysis, where they represent potential energy of a harmonic oscillator. Due to the quantum nature of the oscillator, it can only assume certain (discrete) vibrational energy levels that give rise to vibronic progression. I.e. only selected points on the parabola correspond to the observed transitions. Such an approach assumes that electronic oscillations and mechanical oscillations of atom positions are coupled. On the contrary, we presume Born–Oppenheimer approximation: lattice vibrations merely produce a set of geometries and do it slowly enough for the electrons to comply with the geometries as if the latter were static. In other words, each parabola represents a certain continuous manifold of (infinitely many) states.
To simulate an emission spectrum, both the transition energies and emitting level population are required. The latter corresponds to emission intensities (photon counts) via multiplication by a constant. Let us assume that after a single electron is excited from the ground to the excited state, the excited state manifold lives long enough to achieve thermal equilibrium within its space of states. The said space energy levels are, by construction, described by a parabola. The less-energetic levels thermally populate the more energetic ones. The integral population of the levels in the excited state manifold is unity – due to a single electron being excited. To simulate the thermal population of the particular levels, Boltzmann distribution is used (Fig. 1). It is justified here due to the assumed thermal equilibrium condition. Other options are possible, and the band shape would change accordingly. The selection of the population distribution model does not affect the overall conclusions (below) regarding the biparabolic band shape and will not be analyzed in this work.
Note that the parabola states are not vibronic states in the classical (Pekarian) sense. When vibronic states are considered, the continuous parabola represents a harmonic potential, while the vibronic levels are discrete states on the said potential. In the spectroscopically relevant range of energies and x values, there is (typically) no more than a dozen vibrational levels that give rise to vibronic progressions. In biparabolic band, the distribution of states within manifolds is assumed to be (quasi) continuous. In other words, the spacing between energy levels is infinitesimal, and there can be a huge number of them – giving rise to a smooth band and no vibronic progression. The population of i-th state (within the excited manifold) is given by:
 | (10) |
 iterates over all of the values of the manifold, E or x. A particular ΔEi value is the energy difference between E2 minimum (E2(x = xO) = ΔEmm) and E2(xi) (Fig. 1, eqn (10)):
iterates over all of the values of the manifold, E or x. A particular ΔEi value is the energy difference between E2 minimum (E2(x = xO) = ΔEmm) and E2(xi) (Fig. 1, eqn (10)):| ΔEi = E2(xi) − E2(x = xO) = k2(xi − xO)2 + ΔEmm − ΔEmm = k2(xi − xO)2 | (11) |
 | (12) |
Substituting the values from eqn (8) into eqn (12) (and given the parameters k1, k2, xO, ΔEmm), it is possible to predict the intensity of the emission, assuming that Ii = pi. This assumption is quite crude, as the spontaneous emission intensity has (by Fermi's golden rule) a power dependence on the transition frequency. That dependence can be taken into account via spectrum processing. Typically, spectra are measured as a function of wavelength. Such spectra must be converted into intensity as a function of transition energy via the Jacobian transformation.14 In order to obtain actual line shapes, the next conversion step is to divide the emission spectrum by transition frequency to the third power. With such a form of the spectrum, the Ii = pi assumption is legit.
Summarizing, eqn (8)–(12) provide a simple and straightforward routine to fit any luminescence broad band peak with the minimum of five fit parameters plus temperature. The parabolae are defined by four parameters as above, and the resulting band shape must be multiplied by another parameter to match the experimental spectrum amplitude/intensity. The temperature can either be frozen (set to the experimental value for the spectrum at hand) or allowed to be a fit parameter. The second option might be helpful as a temporary measure in establishing the guess values for the other parameters. I.e., we found it is much simpler to achieve a fit with variable temperature and then change the temperature to the experimental value – as compared to setting the experimental temperature from the beginning. If needed, the resulting band shape can be convoluted with a Gaussian or a Voigt function to account for additional (non-thermal) broadening. The broadening parameters can be either fixed or fitted, as suits the particular purpose and experimental case.
3 Properties of the biparabolic peak
In Fig. 2, two examples of the biparabolic peaks are shown. Both peaks integrate to unity. The two differ in the value of xO: in panel (d), the upper curve is more shifted to the larger x values, its xO is larger. As the result of this shift, the peak in panel (c) is lower in its maximal amplitude, more broad, and is located at lower energies in respect to the peak in panel (a). Note the big difference between the maximum position (13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 in panel (a) and 9000 cm−1 in panel (c)). Both peak maxima do not correspond to the minimum-to-minimum energy difference between the curves (14
000 cm−1 in panel (a) and 9000 cm−1 in panel (c)). Both peak maxima do not correspond to the minimum-to-minimum energy difference between the curves (14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1). In other words, unlike traditional “ladder-like” Jabloński diagrams, the spectral peak maximum does not map directly to the corresponding energy level difference. The energy level difference between the two parabolas is not a single value but a set of values. In principle, one can safely map spectral band maxima to energy levels only if the bands are narrow (atomic-like) – or rather, if the bandwidth in the units of energy is much smaller than the corresponding transition energy. Typical configuration coordinate diagrams with offset parabolas (that actually date back to the paper by Pekar13,15) illustrate this very clearly. Nevertheless, the ladder-like diagrams are still commonly used for spectroscopic bands of any widths. With the example in Fig. 2, we illustrate potential inconsistencies that can be introduced by mapping broad band peaks to energy differences of discrete levels that are, technically speaking, infinitely narrow. The Pekarian/Huang–Rhys approach, however, does not work if the vibronic structure is not visible.
000 cm−1). In other words, unlike traditional “ladder-like” Jabloński diagrams, the spectral peak maximum does not map directly to the corresponding energy level difference. The energy level difference between the two parabolas is not a single value but a set of values. In principle, one can safely map spectral band maxima to energy levels only if the bands are narrow (atomic-like) – or rather, if the bandwidth in the units of energy is much smaller than the corresponding transition energy. Typical configuration coordinate diagrams with offset parabolas (that actually date back to the paper by Pekar13,15) illustrate this very clearly. Nevertheless, the ladder-like diagrams are still commonly used for spectroscopic bands of any widths. With the example in Fig. 2, we illustrate potential inconsistencies that can be introduced by mapping broad band peaks to energy differences of discrete levels that are, technically speaking, infinitely narrow. The Pekarian/Huang–Rhys approach, however, does not work if the vibronic structure is not visible.
 | ||
| Fig. 2 Two examples of the biparabolic peak with different offsets (a and c) and the corresponding configuration diagrams (b and d). Vertical lines in panels (b and d) are darkened proportionally to the corresponding emitting (upper) level population. Parameters correspond to eqn (8)–(12). | ||
The dark vertical lines in panels (b) and (d) of Fig. 2 shade the area where the energy differences between the two curves map to the emission band. The darker the line, the larger is the corresponding population of the initial state, which relates to higher intensity of the transition. (The lines actually blur together and for the visible gradient.) The minimum of the excited state curve corresponds to the maximum of population (and maximum of the intensity), but not to the maximum energy difference of the resulting emission band.
In Fig. 3, the dependence of the biparabolic peak on the values of k2 (the excited state curvature) is visualized. In panels (a) and (b), the extreme case is analyzed, where the offset value is very small (xO = 0.001), and the upper level curvature is smaller than the lower level curvature (k2 < k1). In such cases, the maximum of transition (E2 − E1) energy difference is located at almost the same value of x as is the upper level energy minimum. Both the increase and decrease of x correspond to the reduction of the transition energy in respect to the maximum. Correspondingly, the band extends to the lower-energy side. The higher-energy side of the emission band exhibits an abrupt stop. In the real system, that would have been the position of a zero-phonon line, likely of a Gaussian or a Voigt shape. A smaller value of k2 (“softer” excited state dependence on x, panel (a) in Fig. 3) corresponds to a broader band, but the abrupt edge is present anyway.
 | ||
| Fig. 3 Selected examples of the biparabolic peak with different offsets (a and c) and the corresponding configuration diagrams (b and d). Parameters correspond to eqn (8)–(12). | ||
Asymmetric side bands with one side much steeper than the other one can be seen in e.g. Fig. 6c and 7 of the work by Wigger et al.,16 as well as in the work by Feldman et al.17 However, those experimental spectra also contain zero-phonon lines, and it is quite hard to tell if the abrupt stop is present there or not. On the other hand, the decomposition of spectrum of Fe3+ in Ca8Mg(SiO4)4Cl2 (CASI) (Section 4.4) does exhibit a biparabolic band with an abrupt stop. The abrupt-edge biparabolic bands shown in Fig. 4 do look very confusing, but one must remember that zero-phonon lines are not shown in that figure. In a real spectrum, zero-phonon line will hide the edge.
 | ||
| Fig. 4 Selected examples of the biparabolic peak with different offsets and curvatures (a and c) and the corresponding configuration diagrams (b and d). Parameters correspond to eqn (8)–(12). | ||
With the larger offset of parabolas (xO = 0.03, panels (c) and (d) in Fig. 3), the band may become smooth and Gaussian-like on both sides – depending on the broadening caused by the excited parabola's curvature. The total emission band is far from Gaussian shape, however. Lower values of k2 (broader bands) might correspond to a certain presence of the abrupt edge in the high-energy side of the band (panel c in Fig. 3). As the difference between k2 and k1 becomes smaller, the band becomes less asymmetric and narrower, resembling a Gaussian band. Noteworthy, the Gaussian character in this case stems from the use of the Boltzmann distribution, which in itself corresponds to the iconic bell-shaped curve. Changing the distribution would change the character of the biparabolic band slopes, but the band would still exhibit the asymmetry originating from the parabolas' mutual offset.
In Fig. 4, panels (a) and (b), the dependence of the biparabolic peak on the x offset (xO = 0.03–0.09) is visualized for several characteristic examples. The increase in xO from 0.03 to 0.09 results in a broader and more symmetric band with a lower peak intensity, while the parabola curvatures undergo no change. Yet again, the curves integrate to unity. Alternatively, as the value of k2 approaches the value of k1 (Fig. 4, panels (c) and (d)), the increase in k2 (with the fixed offset) also results in a narrower and more symmetric band. Clearly, the parameters in the biparabolic curve provide a wide range of flexibility in terms of the band shape. Noteworthy, as in earlier cases, the relative change in the peak-intensity in Fig. 4a is associated with the change of the bands' width – as the integral intensity remains unity. Any non-radiative relaxation must increase with increasing xO as the crossover barrier to the ground state decreases. This type of deexcitation would obviously increase with growing temperature. In other words, in a real material at temperatures at which the competing non-radiative relaxation starts playing its role, peak amplitude would further decrease.
When analyzing photoemission band shapes, it is typical to use decomposition into Gaussian bands.8,14 In Fig. 5, a theoretical (simulated) biparabolic band (k1 = 1 × 106, k2 = 2 × 105, xO = 0.08, ΔEmm = 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, T = 300) is approximated with 1, 2, 3 or 4 Gaussian bands. One component does not provide a satisfactory fit (panel (a)), and the discrepancy between the symmetric Gaussian band and the asymmetric biparabolic band is obvious. Two Gaussians, panel (b), are still not enough for the same reasons. With three (c) and four (d) components, the fit looks good, or at least good enough for most purposes. However, the result of such a decomposition – if it was an experimental spectrum being fitted – would most likely be (incorrectly) interpreted as the presence of several emitting species. Here, by construction, there is only one chromophore – albeit with variable (deformation-dependent) transition energies. Thus, the use of a biparabolic band would eliminate the seeming multiplicity of the emission components. As it is known, a simpler theory that provides the correct fit to the data is a better theory. Thus, a decomposition of an experimental spectrum into a single biparabolic band (6 parameters including amplitude, interpreted as one chromophore) is superior to the decomposition of the same spectrum into three Gaussian bands (9 parameters including amplitudes, interpreted as three chromophores). We will yet deal with this by analyzing recorded spectra.
000, T = 300) is approximated with 1, 2, 3 or 4 Gaussian bands. One component does not provide a satisfactory fit (panel (a)), and the discrepancy between the symmetric Gaussian band and the asymmetric biparabolic band is obvious. Two Gaussians, panel (b), are still not enough for the same reasons. With three (c) and four (d) components, the fit looks good, or at least good enough for most purposes. However, the result of such a decomposition – if it was an experimental spectrum being fitted – would most likely be (incorrectly) interpreted as the presence of several emitting species. Here, by construction, there is only one chromophore – albeit with variable (deformation-dependent) transition energies. Thus, the use of a biparabolic band would eliminate the seeming multiplicity of the emission components. As it is known, a simpler theory that provides the correct fit to the data is a better theory. Thus, a decomposition of an experimental spectrum into a single biparabolic band (6 parameters including amplitude, interpreted as one chromophore) is superior to the decomposition of the same spectrum into three Gaussian bands (9 parameters including amplitudes, interpreted as three chromophores). We will yet deal with this by analyzing recorded spectra.
 | ||
| Fig. 5 Decomposition of a biparabolic band (black line) into 1, 2, 3 and 4 Gaussian components. Residuals (red dashed) are scaled by the specified factors. | ||
One also needs to consider the situation, where multiple chromophores are erroneously interpreted as one. It is possible in principle, but it actually seems rather dubious. For it to happen with even two chromophores, the parameters for the corresponding biparabolic bands must be identical, which would mean the same chemical surround, the same bond length, same transitions. All this factors added up make the supposed two emitters the same emitter. The resolution requires additional experiments, e.g., measure decay times at several wavelengths within band, do a temperature-dependent series of spectra and decay times.
The need for the several Gaussian components to approximate a biparabolic band is simple: Gaussian band has a mirror symmetry at its maximum and cannot, in principle, be a good match for any band lacking such symmetry. An asymmetric function can be approximated with a sum of symmetric functions, but the number of the required components can technically be infinite – the classical examples being the Fourier transform (that maps an arbitrary signal into a sum of sine waves) and the Tailor series expansion. As a counter-example, a special case of a symmetric biparabolic band that is exactly a Gaussian band will be shown below. Consequently, the biparabolic band is more general.
As addition to the spectrum decomposition feature(s), the biparabolic band always comes with a corresponding configuration coordinate diagram. The approach, however, has a drawback. It is very likely that a biparabolic fit does not provide a unique solution for a given spectrum. Potentially, many bands with different parameters might correspond to equally good fits. Thus, it is an open question of whether the resulting configuration diagrams are physically feasible. On the other hand, the same problem is with the decomposition of a spectrum into a sum of Gaussian or Voigt profiles. Depending on the initial guess and the number of components, multiple equally good, mathematically, solutions can be obtained. The problem is not unsolvable – it just lies outside the scope of this particular paper. Unlike Gaussian decomposition, however, the biparabolic one always comes with a corresponding configurational diagram that can be tested for correspondence to reality via additional experiments and criteria. For instance, ab initio calculations might provide insight into the expected values of the k1 and k2 force constants. Chemical intuition and experience should also be helpful in selecting a more reasonable result.
4 Experimental examples
4.1 A single biparabolic band decomposition example
In Fig. 6, an experimental emission spectrum of HfGeO4: 0.2% Ti recorded with a 320 nm excitation at 100 K, data from ref. 18 is fitted using the biparabolic approach (eqn (8)–(12)). It is noteworthy that the achieved fitted temperature (99.929 K) is very close to the experimental one. The whole spectrum is reproduced by a single biparabolic peak with impressive accuracy. The corresponding configurational coordinate diagram features a rather large x offset (see panel b) and a “soft” excited state (k2 < k1) – both typical for charge transfer bands, in line with the conclusion in the source paper.18 Excited states of d-block metals are expected to be more spatially spread (in terms of the corresponding electron density) compared to their ground states. The overlap integral between such states and the ligand orbitals is larger than in the latter case. This aspect is addressed explicitly in the last section of this paper. The larger is the overlap integral, the less sensitive it would be to the thermal changes in bond length. Consequently, the excited state energies are expected to be less sensitive to the changes in bond length than the ground state energy. In other words, the excited state parabola having smaller force constant is perfectly in line with the general physical–chemical reasoning.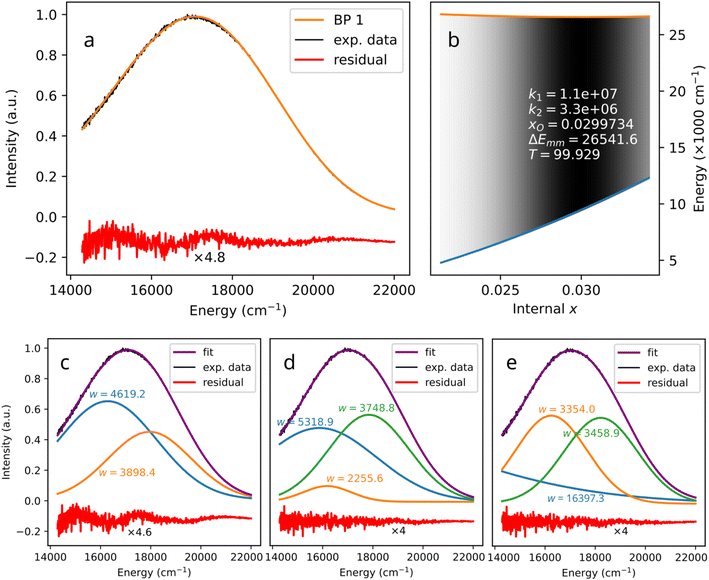 | ||
| Fig. 6 A biparabolic band fitted to an experimental emission spectrum of HfGeO4: 0.2% Ti at 100 K (a), data from ref. 18, and the corresponding configuration diagram (b). The same data fitted with two (c) and three (d and e) Gaussian bands is shown as well, with the corresponding widths of the components. In panel (b), only the part of diagram corresponding to the shown spectrum is displayed. | ||
The residual in Fig. 6a is a bit wavy, meaning that the fit might be somehow incomplete. On the other hand, the magnitude of the wavy pattern is comparable to the noise, indicating that the overall fit quality is high. With Gaussian decomposition (panels (c–e)), such a residual would result in the temptation of adding another Gaussian to the decomposition in order to get a numerically better fit. Indeed, as Fig. 6 panels (d) and (e) illustrate, a fit with three Gaussian bands does result in a flatter residual. However, even two, not to say three, Gaussian bands are unjustified in the case of luminescence of HfGeO4: 0.2% Ti. The chemistry of the materias does not support the presence of two or three emissions related to the dopant. With a biparabolic band, such a temptation is balanced out by the clarity of the fit result. The fitted curve sits well on the experimental data, and the solution is simple, elegant, and physically sound. The biparabolic fit requires six independent parameters to optimize (amplitude, temperature, k1, k2, xO and ΔEmm) and so does the two-Gaussian fit (midpoint, amplitude and width for both components). Being numerically similar, the biparabolic fit is also more physical. It assumes a certain model and shows its feasibility, while the Gaussian bands are quite abstract.
In the mentioned biparabolic band fit, the temperature was a variable parameter. While it was possible to simply freeze it at the experimental value, keeping it as a variable parameter has some benefits. Another degree of freedom improves fit stability: the fit is less sensitive to the guess (i.e. the initial values can be less accurate) and the result is achieved in fewer steps. Variable temperature is also a sanity control. The experimental value of the temperature showing up naturally in the fit procedure argues that the underlying model is realistic – or at least more realistic than the one requiring frozen temperature.
The three Gaussian decompositions shown in Fig. 6c–e introduce another ambiguity. The result depends strongly on the number of components and the use of a vertical (y, intensity) offset. The same y = f(x) band shape can be decomposed in two ways: either as the sum of Gaussian bands or as the sum of Gaussian bands plus a single parameter – the offset, which shifts the whole function vertically. Suppose the offset degree of freedom is absent. In that case, there is a tendency for some of the Gaussian bands to become very broad (much broader than the whole fitted experimental band) and thus act similarly to the offset by shifting the entire curve upwards. In principle, the intensity offset should always be included – the presence of experimental noise results in the zero-intensity background being measured above zero on the intensity axis. In particular, with vertical (y, intensity) offset and two components, one gets band positions of 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 285.9 and 17
285.9 and 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 955.7 cm−1 (Fig. 6c), while with three components the bands are centered at 15
955.7 cm−1 (Fig. 6c), while with three components the bands are centered at 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 873.3, 16
873.3, 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 174.4, and 17
174.4, and 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 842.1 cm−1 (Fig. 6d). Without the vertical offset, the three-component fit results in bands at 2988.3, 16
842.1 cm−1 (Fig. 6d). Without the vertical offset, the three-component fit results in bands at 2988.3, 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 246.7, and 18
246.7, and 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 220.0 cm−1 (Fig. 6e). The only common property of the fits in Fig. 6c–e is the presence of two main bands, while it is not clear which band positions to accept as “correct”.
220.0 cm−1 (Fig. 6e). The only common property of the fits in Fig. 6c–e is the presence of two main bands, while it is not clear which band positions to accept as “correct”.
4.2 A two biparabolic band decomposition example
In Fig. 7a, another broad emission band (Al2O3: 0.1% Eu2+ at 300 K, 440 nm excitation, data from ref. 19) is fitted with two biparabolic peaks, as just one was distinctly not enough. In general, two biparabolic peaks can have independent parameters. However, here it was assumed that emission can originate from two different excited states of the same emitter. In that case, the bands share the ground state curvature (the k1 parameter) and the temperature. The two excited state parameters and the two x offsets were varied. The result is a perfect match with a physically sane picture of the excited states – the higher one is more “soft” (less sensitive to geometry distortions), in line with the nature of Eu2+ 5d → 4f emission. Higher excited states can be expected to be more spatially diffuse (somewhat less localized). The total number of parameters in such a model is 10: A1, A2, k1, k21, k22, xO1, xO2, ΔE1, ΔE2, T. A fit of a slightly lower quality can be achieved with 2 Gaussians (total of 6 parameters). The wavy pattern in the residual clearly indicates an incomplete fit (Fig. 7c). The higher quality fit is achievable with 3 Gaussians (9 parameters), one of which has to have a negative amplitude, which is unphysical. | ||
| Fig. 7 Two biparabolic bands fitted to an experimental emission spectrum of Al2O3: 0.1% Eu2+ at 300 K (a), data from ref. 19, and the corresponding configuration diagram (b). Gaussian fit of the same band with three (c) and four (d) components. In panel (b), only the part of diagram corresponding to the shown spectrum is displayed. | ||
4.3 An example of decomposition with both biparabolic and Gaussian bands
In Fig. 8a, a more complicated example of a broad band is shown. In the emission spectrum of Ga2O3: 1% Cr3+ at room temperature (excited at 442 nm, data from ref. 20), sharp peaks overlap with the broad bands. The latter was fitted with two biparabolic bands that again shared k1 and T. The sharp peaks were fitted with Gaussians, resulting in a very satisfactory agreement with the measured narrow features. The task could have been considered complete: the Gaussians represent “narrow, atomic-like” bands that underwent the same broadening as the levels corresponding to the broad bands. That, however, poses the question of how to show the “narrow peaks” in the configuration coordinate diagram. Would flat lines do? If so, and given a non-linear ground state in the diagram – at which energy? The answer can be brought by the smart use of biparabolic peak, which is reversely compatible with Gaussian bands. Setting k2 = k1 and varying the offset and energy difference, any Gaussian band can be reproduced exactly (due to the use of Boltzmann distribution in the band generation). Such fits produce curves that are slightly offset copies of the ground state shape – these are shown as the grey lines in Fig. 8b. From the diagram, it is very clear that the orange curve and the grey curves correspond to the same chromophore. The narrow bands are single-phonon (Pekarian) vibronic bands, while the broad band comes from a different broadening mechanism. As the two lines share many overlapping points, they can populate each other in many ways. The green band in Fig. 8b corresponds to an excited state of a different nature. In particular, given the similarities between the k2 values of the two bands, and basically the same ΔEmm, Cr3+2 E → 4A2 spin-forbidden transition likely corresponds to the less-offset orange parabola, and Cr3+ spin-allowed 4T2 → 4A2 corresponds to the more offset green parabola. This conclusion comes from the distinct pressure (i.e. bond length) sensitivity of the position of the broad band, as observed in the source paper. All of the mentioned bands share the ground state and thus originate from the same emitter. In other words, despite the clear two-component nature of the broad band, both constituents can be reasonably attributed to the same chromophore (Cr3+). | ||
| Fig. 8 Two biparabolic bands and a set of Gaussian peaks fitted to an experimental emission spectrum of Ga2O3: 1% Cr3+ at room temperature, data from ref. 20, and the corresponding configuration diagram. The grey lines in panel (b) correspond to the Gaussian peaks from panel (a), see text. Two kinds of Gaussian fit (c and d) of the same band, see text. | ||
It is worth noting that in the process described above, Gaussian bands were fitted to the narrow peaks, and then biparabolic bands where fitted to the Gaussian bands. Is if of course possible to fit the biparabolic bands to the narrow peaks directly. However, as more parameters must be varied at the same time, such an option is computationally heavier and more prone to errors and overfitting. Fitting a Gaussian first clears out a lot of experimental noise, while fitting a biparabolic band to a noise-free Gaussian is always very rigid, unambiguous and fast.
A traditional Gaussian decomposition was also attempted in this case, using the narrow bands from the biparabolic fit as the starting point. Several broad Gaussian peaks were added. The resulting decomposition contains a very broad component centered at 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 634 cm−1, i.e., at the edge of the energy scale (Fig. 8c). Given its width, the component is likely artificial and acts as a vertical offset. However, this solution is very stable. Trying to remove this component or replace it with something more sensible results in changes in the narrow component part – some of the narrow components become broad at the cost of certain small features not being reproduced anymore (Fig. 8d). On the other hand, adding components to the decomposition seen in Fig. 8d results in the decomposition from Fig. 8c. In other words, the 10
634 cm−1, i.e., at the edge of the energy scale (Fig. 8c). Given its width, the component is likely artificial and acts as a vertical offset. However, this solution is very stable. Trying to remove this component or replace it with something more sensible results in changes in the narrow component part – some of the narrow components become broad at the cost of certain small features not being reproduced anymore (Fig. 8d). On the other hand, adding components to the decomposition seen in Fig. 8d results in the decomposition from Fig. 8c. In other words, the 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 634 cm−1 broad component must be present to achieve a good fit.
634 cm−1 broad component must be present to achieve a good fit.
All three decompositions indicate the presence of narrow bands around 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1, as well as a semi-broad band at about 14
500 cm−1, as well as a semi-broad band at about 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. However, both Gaussian decompositions result in overestimation of the number of components of the primary broad band. With biparabolic bands, there is clearly only one main broadband chromophore (emission site). From the Gaussian decompositions, the number of chromophores appears to be either two or three, depending on the interpretation of the first component on the lower-energy side. With the use of biparabolic bands, such ambiguity is not present. The bands in the presented biparabolic interpretation have a “hardness” parameter k2 that can be compared to calculations (either ab initio or some sort of crystal/ligand field theory). One only needs to do the calculations for a set of geometries simulating a deformation.4–7,21 With such calculations, band nature can be identified exactly.
000 cm−1. However, both Gaussian decompositions result in overestimation of the number of components of the primary broad band. With biparabolic bands, there is clearly only one main broadband chromophore (emission site). From the Gaussian decompositions, the number of chromophores appears to be either two or three, depending on the interpretation of the first component on the lower-energy side. With the use of biparabolic bands, such ambiguity is not present. The bands in the presented biparabolic interpretation have a “hardness” parameter k2 that can be compared to calculations (either ab initio or some sort of crystal/ligand field theory). One only needs to do the calculations for a set of geometries simulating a deformation.4–7,21 With such calculations, band nature can be identified exactly.
4.4 A biparabolic band photoemission at very low temperature (12 K)
The experimental examples shown in Fig. 6–8 are characterized by temperatures quite far from 0 K. In all of them, one can speculate that broad bands are formed by strong thermal broadening of vibronic bands,22 or that many thermally excited vibrational modes are acting on the activator simultaneously. Fig. 9 shows the emission spectrum of Fe3+ in Ca8Mg(SiO4)4Cl2 (CASI) at 12 K. With such a low temperature, one cannot explain the broad band (more than 1000 cm−1 width) by thermal broadening of a single line. In particular, the E2 range, which is produced by Boltzmann distribution at 12 K, eqn (12), and the one corresponding to the biparabolic curve in Fig. 9, is only 175 cm−1. Correspondingly, the E2 parabola in Fig. 9b looks like a flat line, while the curvature of the ground state parabola is mostly responsible for the broadening of the band.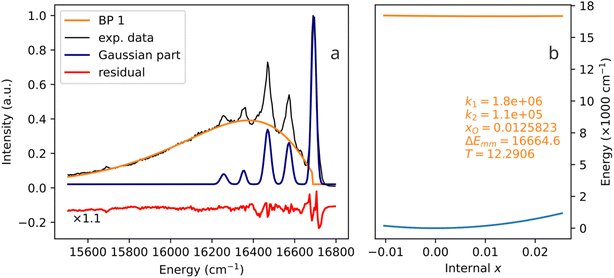 | ||
| Fig. 9 A biparabolic band and a set of Gaussian peaks fitted to an experimental emission spectrum of Fe3+ in Ca8Mg(SiO4)4Cl2 (CASI) at 12 K (a), data from ref. 23, and the corresponding configuration diagram (b). | ||
The spectrum in Fig. 9 is a very noteworthy case. On the one hand, the vibronic progression is clearly visible. On the other hand, so is the biparabolic component. Despite the relatively low temperature, two emission mechanisms are active simultaneously. During some of the emission events, the electron transition in question exhibits coupling to lattice vibrations, and the vibronic sidebands are produced. However, during other emission events, the coupling is not present, and the emission seemingly occurs between two parabolic manifolds, giving rise to the broad band. Undoubtedly, only one chromophore is present: the biparabolic band breaks abruptly right at the zero-phonon line position.
The authors of the referenced paper23 do not interpret the sidebands as originating from different vibrational levels of the same oscillator. On the contrary, they attribute each sideband to a different Raman mode. In other words, the traditional Huang–Rhys vibronic coupling (a single coupled electron-phonon system, multiple emission lines) is not assumed in the interpretation of this spectrum. Rather, independent couplings of the chromophore to several vibrations are assumed,23 in line with the multi-mechanism single-chromophore interpretation presented here.
4.5 The role of orbital overlap in the parabola curvature
With the configurational diagrams produced by the biparabolic fitting, several questions arise. Why is the emission manifold parabola shifted, and why is it shifted towards larger x? Why are the excited manifold parabolas characterized by lower force constants than the ground state manifold parabolas, i.e., why is k2 < k1? The nature of x shift between the parabolas can be deduced as follows. In Eu2+, the 5d orbital is empty and can thus accept electron pairs from ligand O. The 4f–5d excitation results in additional electrons in 5d orbitals that repel the ligand electron density. Consequently, the optimal bond length for such an excited state is larger compared to the ground state. In Ti4+, the excited state involves electron transfer from oxygen to titanium, causing an increase in both 3d orbital population and bond length. In Cr3+ and Fe3+, excitation from lower 3d orbitals, which experience a weaker crystal field, to higher 3d orbitals, which experience a stronger crystal field, also increases ligand repulsion and leads to bond elongation. Thus, for all of the cases above, the excited state parabola minimum is expected to correspond to larger bond lengths (larger x) than the ground state parabola minimum.The answer to the k2 < k1 question can be provided by analyzing overlap integrals between oxygen 2p atomic orbitals and the 4f, 5d, and 3d orbitals of the activator cations. To perform the analysis, PySCF Python code24–26 and atomic natural orbitals relativistic core-corrected (ANO-RCC27–29) large basis sets were used. The test system contained the activator ion at the origin and the oxygen atom on the z-axis, some distance r away from the activator. The distance was changed, and the overlap integral (designated int1e_ovlp in PySCF) was calculated at each r. The orbitals of interest were O 2pz, Ti/Cr/Fe 3dz2, Eu 5dz2, and Eu 4fz3.
In Fig. 10, two sets of data are presented. The data on the right are the relative sensitivities of the integrals with respect to r, calculated as |dS/dr|/S. The latter parameter shows how much (as a fraction of S) the S changes (at a given r) as a function of r. The relative rate of change is the defining property, not the absolute rate of change (the derivative). Let us consider an example. Under a certain deformation, orbital overlap 1 changed by 1%, while orbital overlap 2 changed by 10%. Clearly, the latter difference would result in more pronounced changes in the respective orbital energies. The overlap integral is largest for Eu 5d (in its chemically relevant range of r above 2.2 Å), and gets lower in the Ti 3d, Cr 3d, Fe 3d, Eu 4f sequence. The sensitivities clearly exhibit a trend opposite to that of the overlap integrals. In other words, the larger is the overlap integral, the less sensitive it is to the changes in the bond length. This conclusion is made by comparing the five orbitals, but it also holds true for each of them: smaller values of the overlap correspond to the larger values of the sensitivity.
A broader excited state parabola indicates a smaller sensitivity of the respective state to geometrical changes (i.e. smaller k). From Fig. 10b, it can be concluded that Eu 4f orbitals are the most sensitive (more narrow parabolas, narrow bands), 3d metals are less sensitive (broader parabolas, wider peaks), and Eu 5d orbitals are the least sensitive in this group (even broader parabolas, even wider peaks). Note that this observation correlates well with the spatial spread of the orbitals. The 4f orbitals are the most localized, the 3d orbitals have a larger effective radius, and the 5d orbitals are even larger. Within the 3d group, in the Fe–Cr–Ti series, the sensitivity decreases, the overlap integral increases, and the orbital/atomic/ionic radii increase. Summarizing, a larger overlap integral between the activator ion excited state orbitals and the ligand orbitals results in lower sensitivity of the activator excited state properties to changes in ligand distance (bond length) – hence, the respective parabola is broader.
5 Conclusions
In this paper, we present a method to decompose complex broad emission bands using simple algebra. Provided is a rigorous band shape (biparabolic band) that can be used in decomposition/deconvolution using least-squares fitting. An addition to every biparabolic band is, by construction, a configuration coordinate diagram that matches the band. Both symmetric (Gaussian, atomic-like, f–f, d–d) and asymmetric (f–d, charge-transfer, organic chromophore) spectral bands can be reproduced. The algebra intrinsically contains temperature and is thus potentially useful for primary luminescence thermometry. It is also shown that traditional decomposition with Gaussians is prone to errors due to potential misinterpretation and false data creation. The biparabolic band is more intuitive and safer in interpretation, as it provides a visual aid: the corresponding configuration diagram. The latter can be easily linked to theoretical calculation of any sort: multiconfigurational, density functional theory, crystal/ligand field theory, etc.. The only requirement for the theory is to provide a set of energy levels as a function of a coordination geometry – which typical physical–chemical theories do.A crucial strong side of the biparabolic band model is that it directly makes experimentally testable assessments. It connects macroscopic spectral properties (band shape, width, and position) to microscopic properties – temperature (explicitly) and sensitivity to bond length changes (via force constants k). Experimentally, the respective data can be collected via high-pressure spectroscopy at different pressure and temperature values. The connection to theoretical calculation is straightforward.
Data availability
The data supporting this article have been included as part of the ESI.† In particular, data corresponding to Fig. 5–9 are included. Note that the experimental spectra are published here with the permission of the respective corresponding authors of the papers that originally feature the data.18–20,23 Any further reuse of the said data must be agreed upon with those authors. The ESI† also contains Python scripts relevant to this paper. All of them contain the function (subroutine) mentioned in the text, the one that produces the biparabolic band shape. The respective code can be used as is, modified, refactored and adapted as needed, as long as the source paper (this paper) is properly cited in all products and publications that use (or rely upon) the presented idea.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The following people are acknowledged for sharing the spectral data used in this paper: Joanna Jedoń (University of Wrocław, Poland; Chalmers University of Technology in Gothenburg, Sweden), Paulina Bukowska (nee Bolek, University of Wrocław, Poland), Natalia Majewska (University of Gdańsk, Poland), Alok M. Srivastava (Current Chemicals, Cleveland, OH, USA). This work is supported by University of Wrocław via the internal grant BPIDUB.21.2024. Open source software was used in preparation of this article, in particular: Python, Matplotlib, SciPy, NumPy, PySCF, Inkscape, LibreOffice, Zotero, DOI2Bib.References
- J. Balasurendran, A. Balhara, M. Jafar, K. Sudarshan, J. Bahadur and S. K. Gupta, Contrasting role of Ca2+ on the Gd2TiO5: Eu3+ light emission under charge transfer and f-f band excitation: interplay of oxygen vacancies and structural distortion, J. Mol. Struct., 2024, 1318, 139296, DOI:10.1016/j.molstruc.2024.139296.
- R. E. López, G. P. Oscar, F. J. Davila, E. L. Martínez, G. González-García and D. Y. Medina, et al., Ligand-to-metal energy transfer in terbium and europium oxalate heptahydrate crystals: understanding the influence of oxalate ligand on the photoluminescent properties, J. Lumin., 2025, 277, 120925, DOI:10.1016/j.jlumin.2024.120925.
- V. Wessels, S. Kügle and H. A. Höppe, Crystal structure, optical properties and thermal properties of M2[W2O3(SO4)6] (M = Y, Eu, Tb, Lu, Bi), Dalton Trans., 2024, 53(37), 15703–15712, 10.1039/d4dt02259a.
- J. J. Joos, I. Neefjes, L. Seijo and Z. Barandiarán, Charge transfer from Eu2+ to trivalent lanthanide co-dopants: systematic behavior across the series, J. Chem. Phys., 2021, 154(6), 064704, DOI:10.1063/5.0037992.
- J. J. Joos, D. Van der Heggen, L. Amidani, L. Seijo and Z. Barandiarán, Elucidation of the electron transfer mechanism in Eu2+ and Sm2+ codoped CaF2: a step towards better understanding of trapping and detrapping in luminescent materials, Phys. Rev. B: Condens. Matter Mater. Phys., 2021, 104(20), L201108, DOI:10.1103/PhysRevB.104.L201108.
- Z. Barandiarán and L. Seijo, Intervalence charge transfer luminescence: interplay between anomalous and 5d-4f emissions in Yb-doped fluorite-type crystals, J. Chem. Phys., 2014, 141(23), 234704, DOI:10.1063/1.4902759.
- L. Seijo and Z. Barandiarán, Intervalence charge transfer luminescence: the anomalous luminescence of cerium-doped Cs2LiLuCl6 elpasolite, J. Chem. Phys., 2014, 141(21), 214706, DOI:10.1063/1.4902384.
- M. Bacalum, B. Zorilă and M. Radu, Fluorescence spectra decomposition by asymmetric functions: Laurdan spectrum revisited, Anal. Biochem., 2013, 440(2), 123–129, DOI:10.1016/j.ab.2013.05.031.
- A. R. Pietros, K. Rebeszko, J. R. Rosenbaum, M. P. Stone, A. Brasovs and K. G. Kornev, et al., (INVITED) Investigation of intense visible defect luminescence from visible and infrared pumped barium fluorosilicate glass-core fiber, Opt. Mater.: X, 2023, 19, 100231, DOI:10.1016/j.omx.2023.100231.
- J. M. Hollas, Modern Spectroscopy, John Wiley & Sons, Chichester, England, 4th edn, 2003 Search PubMed.
- S. Mothkuri, M. F. Reid, J. P. R. Wells, E. Lafitte-Houssat, A. Ferrier and P. Goldner, Laser site-selective spectroscopy and magnetic hyperfine splittings of Ho3+ doped Y2SiO5, J. Lumin., 2024, 275, 120705, DOI:10.1016/j.jlumin.2024.120705.
- M. K. Alqedra, C. Deshmukh, S. Liu, D. Serrano, S. P. Horvath and S. Rafie-Zinedine, et al., Optical coherence properties of Kramers’ rare-earth ions at the nanoscale for quantum applications, Phys. Rev. B, 2023, 108(7), 075107, DOI:10.1103/PhysRevB.108.075107.
- A. E. Hughes, Zero-Phonon Transitions and Vibrational Structure, J. Phys. Colloques, 1967, 28(C4), C455–C465 Search PubMed.
- J. Mooney and P. Kambhampati, Get the Basics Right: Jacobian Conversion of Wavelength and Energy Scales for Quantitative Analysis of Emission Spectra, J. Phys. Chem. Lett., 2013, 4(19), 3316–3318, DOI:10.1021/jz401508t.
- W. H. Fonger and C. W. Struck, Relation between the Huang-Rhys-Pekar and the single-configurational-coordinate models of localized centers, J. Lumin., 1974, 8(6), 452–456, DOI:10.1016/0022-2313(74)90010-6.
- D. Wigger, R. Schmidt, O. Del Pozo-Zamudio, J. A. Preuß, P. Tonndorf and R. Schneider, et al., Phonon-assisted emission and absorption of individual color centers in hexagonal boron nitride, 2D Mater., 2019, 6(3), 035006, DOI:10.1088/2053-1583/ab1188.
- M. A. Feldman, A. Puretzky, L. Lindsay, E. Tucker, D. P. Briggs and P. G. Evans, et al., Phonon-induced multicolor correlations in hBN single-photon emitters, Phys. Rev. B, 2019, 99(2), 020101(R), DOI:10.1103/PhysRevB.99.020101.
- J. Jedoń, D. Pasiński and E. Zych, On the luminescence of HfGeO4:Ti4+ X-ray phosphor and luminescence thermometer, ECS J. Solid State Sci. Technol., 2023, 12(7), 076011 CrossRef.
- P. Bolek, Y. Wu, Y. Yang and E. Zych, Photo- Radio- and Thermoluminescence of Sintered Transparent Al2O3:Eu2+ in the Range 15–800 K, Opt. Mater., 2020, 105, 109877 CrossRef CAS.
- N. Majewska, A. Muñoz, R. S. Liu and S. Mahlik, Influence of Chemical and Mechanical Pressure on the Luminescence Properties of Near-Infrared Phosphors, Chem. Mater., 2023, 35(12), 4680–4690 CrossRef CAS.
- Z. Barandiarán and L. Seijo, Metal-to-metal charge transfer between dopant and host ions: photoconductivity of Yb-doped CaF2 and SrF2 crystals, J. Chem. Phys., 2015, 143(14), 144702, DOI:10.1063/1.4932388.
- M. de Jong, L. Seijo, A. Meijerink and F. T. Rabouw, Resolving the ambiguity in the relation between Stokes shift and Huang–Rhys parameter, Phys. Chem. Chem. Phys., 2015, 17(26), 16959–16969, 10.1039/c5cp02093j.
- A. M. Srivastava, A. Suchocki, L. I. Bulyk, Y. Zhydachevskyy, M. G. Brik and W. W. Beers, et al., Narrowband red luminescence of tetrahedral-site Fe3+ in Ca8Mg(SiO4)4Cl2, Opt. Mater., 2024, 150, 115290, DOI:10.1016/j.optmat.2024.115290.
- Q. Sun, X. Zhang, S. Banerjee, P. Bao, M. Barbry and N. S. Blunt, et al., Recent developments in the PySCF program package, J. Chem. Phys., 2020, 153(2), 024109, DOI:10.1063/5.0006074.
- Q. Sun, T. C. Berkelbach, N. S. Blunt, G. H. Booth, S. Guo and Z. Li, et al., PySCF: the Python-based simulations of chemistry framework, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 8(1), e1340, DOI:10.1002/wcms.1340.
- Q. Sun, Libcint: an efficient general integral library for Gaussian basis functions, J. Comput. Chem., 2015, 36(22), 1664–1671, DOI:10.1002/jcc.23981.
- B. O. Roos, R. Lindh, P. A. Malmqvist, V. Veryazov and P. O. Widmark, Main Group Atoms and Dimers Studied with a New Relativistic ANO Basis Set, J. Phys. Chem. A, 2003, 108(15), 2851–2858, DOI:10.1021/jp031064.
- B. O. Roos, R. Lindh, P. A. Malmqvist, V. Veryazov and P. O. Widmark, New Relativistic ANO Basis Sets for Transition Metal Atoms, J. Phys. Chem. A, 2005, 109(29), 6575–6579, DOI:10.1021/jp0581126.
- B. O. Roos, R. Lindh, P. A. Malmqvist, V. Veryazov, P. O. Widmark and A. C. Borin, New Relativistic Atomic Natural Orbital Basis Sets for Lanthanide Atoms with Applications to the Ce Diatom and LuF3, J. Phys. Chem. A, 2008, 112(45), 11431–11435, DOI:10.1021/jp803213j.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra07885c |
| This journal is © The Royal Society of Chemistry 2025 |

