Open Access Article
Open Access ArticleOptical properties of BaTiO3 at room temperature: DFT modelling
Talgat M. Inerbaevab,
David R. Graupner c,
Aisulu U. Abuovaa,
Fatima U. Abuova*a and
Dmitri S. Kilin
c,
Aisulu U. Abuovaa,
Fatima U. Abuova*a and
Dmitri S. Kilin *c
*c
aL.N. Gumilyov Eurasian National University, Astana 010000, Kazakhstan. E-mail: fatika_82@mail.ru
bVernadsky Institute of Geochemistry and Analytical Chemistry, Russian Academy of Science, 119991 Moscow, Russia
cNorth Dakota State University, Fargo, North Dakota 58108, USA. E-mail: dmitri.kilin@ndsu.edu
First published on 18th February 2025
Abstract
The optical properties of the tetragonal phase of BaTiO3 have been studied using the density functional method. In the study of a static lattice, we employed the generalized gradient approximation functional combined with on-site Hubbard correlation (GGA + U) and a hybrid functional. To account for the thermal motion of the atoms, we performed ab initio molecular dynamics calculations using the GGA + U method. We calculated the optical absorption spectra both for the static lattice and along the molecular dynamics trajectory. The results show that considering the motion of atoms leads to a significant decrease in the calculated value of the threshold energy for optical absorption. This effect occurs for two main reasons. First, changes in the atomic configuration due to thermal motion make electronic transitions that were previously dark for a static lattice become bright. Second, the optical absorption threshold decreases due to fluctuations in the energy of electronic transitions caused by the motion of atoms. The calculations were performed separately for different k-points of the Brillouin zone. The dispersion of electron energy in the reciprocal space may explain some features observed in the photoluminescence spectra.
1 Introduction
Barium titanate (BaTiO3) has been thoroughly studied as a ferroelectric,1–3 high-k dielectric,4,5 and photorefractive material6,7 among the perovskite oxides, both in experimental and theoretical research. BaTiO3 shows promise for various technological applications, including gate dielectrics,8 holographic storage,9 photocatalysts,10,11 and multi-layer ceramic capacitors,12 due to its unique properties.In order of increasing temperature, BaTiO3 has five distinct structures: rhombohedral, orthorhombic, tetragonal, cubic, and hexagonal. The ferroelectric and optical properties of the tetragonal phase at 290–390 K render it significant.
The PL response can be significantly enhanced by external influences, such as temperature,13 applied electric field,14–16 or mechanical stress,17 especially when the host matrix is a ferroelectric material that is highly susceptible to these excitations. Ferroelectrics are materials that are inherently characterized by a spontaneous polarization that can be switched in response to an electric field. They are highly responsive to any structural changes induced by electrical, thermal, or mechanical means, and polarization is also dependent on the temperature and strain.
A broad PL spectrum is observed in BaTiO3, which is highly crystalline and exhibits weak PL properties at room temperature.18,19 The PL spectra are enhanced by structural deficiencies and reduced band gaps.18,20,21 BaTiO3 that is non-crystalline and/or disordered exhibits PL at approximately 550 nm when excited at 488 nm.
It was found experimentally that highly crystalline BaTiO3 exhibits a small broad peak at approximately 500 nm, acute peaks at 540 and 610 nm, and a large broad peak above 800 nm in its PL spectra.19 Emission peaks were observed in the visible-light region, particularly at 300 K, and they dissipated as the temperature increased. The quantum yields for the emission peaks are less than 1% and demonstrated a significant decrease as the temperature increased. At room temperature, as the wavelength of the exciting radiation decreases, the intensities of the radiation peaks at 540 and 610 nm increase.
In this paper, we simulate the optical absorption and photoluminescence spectra at room temperature, taking into account the contribution of each k-point of the Brillouin zone. The thermal motion of atoms significantly influences the optical absorption of BaTiO3. The displacement of atoms from equilibrium positions results in the brightening of previously dark optical transitions in the static lattice, and the motion of atoms causes fluctuations in the transition energies. By figuring out the quantum yield of photoluminescence, it was found that BaTiO3 doesn't have many luminescent properties. It is likely that structure defects are responsible for the photoluminescence observed in the experiment.
2 Methods
2.1 Theoretical approaches
Computational characterization of materials' properties is accomplished through five distinct methods: ground-state electronic structure, linear optical absorption, thermal motion of nuclei, nonradiative transitions, and photoluminescence.| Dij(k) = e〈ψKSi(k)|r|ψKSj(k)〉 | (1) |
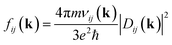 | (2) |

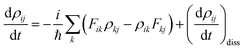 | (3) |
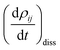 represents the electronic dissipative transitions caused by nonadiabatic electron–ion interaction. Nonadiabatic couplings (NAC) can be computed according to the on-the-fly procedure along the nuclear trajectory as a measure of violation of KS orbital orthogonality due to nuclear motion
represents the electronic dissipative transitions caused by nonadiabatic electron–ion interaction. Nonadiabatic couplings (NAC) can be computed according to the on-the-fly procedure along the nuclear trajectory as a measure of violation of KS orbital orthogonality due to nuclear motion
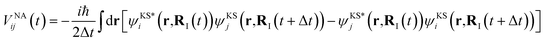 | (4) |
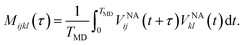 A Fourier transform of the autocorrelation function provides elements of Redfield tensor, which control the dissipative dynamics of the density matrix
A Fourier transform of the autocorrelation function provides elements of Redfield tensor, which control the dissipative dynamics of the density matrix
 | (5) |
The nonequilibrium distribution of charge as a function of time and energy reads  where (a,b) is corresponding to the initial photoexcitation from state a to b. The change in population from the equilibrium distribution is
where (a,b) is corresponding to the initial photoexcitation from state a to b. The change in population from the equilibrium distribution is
| Δn(a,b)(ε,t) = n(a,b)(ε,t) − neq(ε,t) | (6) |
 | (7) |
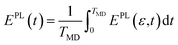 | (8) |
An emission event between a pair of orbitals may occur if inverse population conditions are satisfied where ρjj > ρii, εj > εi. The technique for calculating nonequilibrium electron dynamics and photoluminescence spectra is described in more detail in our previous publications.23–27
2.2 Computational details
The electronic structures, which encompass Coulomb, correlation, and exchange electron–electron interactions, as well as interactions between electrons and ions, were determined using density functional theory (DFT) through the self-consistent solution of the Kohn–Sham equations, as implemented in the Vienna ab initio simulation package (VASP).28,29 The hybrid functional Heyd–Scuseria–Ernzerhof (HSE06)30 and the Perdew–Burke–Ernzerhof (PBE)31 exchange–correlation functional under the generalized gradient approximation were employed. The precise Hartree–Fock exchange was determined by the mixing parameter of 0.25 for HSE06 functional. The Dudarev parametrization32 was used to account for the on-site Coulomb correlation of Ti-3d electrons, with a U–J value of 2.6 eV in the case of PBE functional.33 The projector augmented-wave formalism,34 which was devised using the concept of pseudopotentials in the plane-wave basis, was employed to perform the calculations. All MD simulations were performed with PBE + U functional at T = 300 K. The temperature was controlled using the Nosé–Hoover thermostat.35The modeling conducted in this study employed the tetragonal BaTiO3 phase (P4mm, #99), which is not energetically favorable at zero and exists at ambient temperature. The Ba atom has a coordination number of six with oxygen anions, while the Ti atom has a coordination number of twelve. The TiO6 octahedra form a skeletal structure by sharing their corners, as illustrated in Fig. 1. Additionally, Ti cation is located at the center of this structure.
The initial crystal structure was obtained from the Materials Project database.36 Used was a 3 × 3 × 3 supercell of the primitive cell, which contained 135 atoms. The calculations were conducted using a 500 eV basis and a 2 × 2 × 2 k-point mesh centered on the Γ-point. The analysis of the nature of chemical bonds was carried out using the electron localization function (ELF).37,38 We used the VASPKIT code to postprocess the calculated data from VASP.39
The original methodology24,40,41 was developed for monitoring excited state dynamics in nanostructures with surfaces exposed to (disordered) liquid solvent. While applying this methodology to a periodic crystal one may find interesting observations related to dynamic change of the symmetry. One may introduce tolerance limit for coordinates retaining certain symmetry within allowed error bar. However such exploration would go beyond the scope of this work.
3 Results and discussion
3.1 Electronic properties of static lattice
The results presented here were obtained using PBE + U calculations of the optimized BaTiO3 supercell geometry. Table 1 displays the band gap values (Eg) at all irreducible points in the Brillouin zone. We found these numbers in two ways: by calculating the difference between the energies of the conduction band minimum (CBM) and valence band maximum (VBM) (ECBM–VBM = E(CBM) − E(VBM)), and by calculating the smallest value of the optical transition energy with a nonzero oscillator strength (Eoptic). We performed the calculations using the PBE + U and HSE06 functionals.| k-Point | ECBM–VBM, eV | Eoptic, eV | ||
|---|---|---|---|---|
| PBE + U | HSE06 | PBE + U | HSE06 | |
| Γ = (0 0 0) | 2.40 | 3.56 | 2.58 | 3.70 |
| Z = (0 0 ½) | 2.46 | 3.62 | 2.67 | 3.79 |
| X = (½ 0 0) | 2.69 | 3.89 | 3.23 | 4.33 |
| M = (½ ½ 0) | 2.51 | 3.73 | 3.11 | 4.34 |
| R = (0 ½ ½) | 2.77 | 3.97 | 3.38 | 4.47 |
| A = (½ ½ ½) | 2.72 | 3.95 | 3.42 | 4.67 |
The valence band maximum of BaTiO3 is located at the M point, whereas the conduction band minimum is found at the Γ point. Consequently, BaTiO3 is classified as a semiconductor with an indirect bandgap, in line with results reported in the literature based on PBE calculations.42 The calculated PBE + U indirect bandgap for BaTiO3 is 1.94 eV, while the direct bandgap is 2.48 eV.
In Section 3.4, we reexamine the character of Ti–O bonding and find that it is rather ionic and indirect optical transitions are not expected. The electronic structure of the ground state of BaTiO3 was simulated while considering the effects of spin–orbit coupling. The calculations indicated a slight reduction in the direct bandgap value, which was found to be 2.44 eV. The value of the indirect bandgap remained unchanged. Due to its minimal influence, spin–orbit coupling was not considered further.
The Eg values calculated using the PBE + U functional are significantly smaller than the corresponding values obtained using the HSE06 hybrid functional. The results for ECBM–VBM calculated at the Γ-point using the HSE06 functional are close to the analogous value of 3.66 eV obtained using the B3LYP functional18 and differ greatly from the results of PBE0 calculations, which give 4.1 eV.43 At the same time, the ECBM–VBM and Eoptic values differ from each other. The minimum Eoptic value significantly exceeds the experimental value of the optical absorption threshold, equal to 3.2 eV.18,44 The reasons for such a large difference between the theoretical and experimental data are discussed below in Section 3.2.
The PBE + U calculated element-projected band structure of BaTiO3 is presented in Fig. 2. Near the Fermi level, the valence band (VB) is formed by the O-2p states, while the conduction band (CB) is formed by the Ti-3d states. The top of the VB is at the A-point and is very close to the M-point. The bottom of CB is at the Γ-point and is close to the Z-point. In this paper, we consider only direct optical transitions, although the possibility of indirect optical transitions was predicted theoretically due to the presence of a covalent Ti–O bond in the compound.45
 | ||
| Fig. 2 Element-projected band structure of BaTiO3 supercell. Red and blue symbols correspond to O and Ti atoms, respectively. | ||
The PBE + U calculations of the electron density of states (DOS) at all the irreducible points in Table 1's Brillouin zone are shown in Fig. 3(a). At all considered k-points in VB and CB, there are sub-bands in which electron states are absent. This leads to energy intervals in the optical absorption spectrum in which electrons with a given value of the wave vector do not absorb electromagnetic radiation (Fig. 3(b), dotted lines). Considering all k values, the total optical absorption indicates that BaTiO3 absorbs in the entire energy range above Eoptic (Fig. 4(a)). Similar data for the static lattice calculated using the HSE06 functional are presented in Fig. 4(b).
 | ||
| Fig. 3 (a) DOS (b) absorption static (dotted lines) and at T = 300 K (solid lines) calculated at different k-points. | ||
3.2 Optical properties at T = 300 K
The above theoretical values of the band gap, calculated using hybrid functionals, differ significantly from the corresponding experimental values. To explain this contradiction, it is necessary to remember that the theoretical data indicated were obtained for static lattices without considering the motion of atoms at a finite temperature.The oscillator strengths and energies of electron transitions along the MD trajectories were calculated at T = 300 K for all k-points in the Brillouin zone to consider the effect of atomic motion. The comparison of the results of static calculations using the optimized structure of the model supercell and the results of calculations along the MD trajectory at 300 K is carried out using the PBE + U functional since calculations using the hybrid HSE06 functional along the MD trajectory are too expensive. The optical absorption values averaged along the MD trajectory are shown in Fig. 3(b) compared to similar data for the static lattice. At all k-points, a significant (up to 0.8 eV in X-point) red shift in the optical absorption energy threshold value is observed.
To explain this effect, Fig. 5 shows the calculated values of the oscillator strengths and energies of electron transitions at the Γ- and Z-points. For the remaining points in k-space, the data are qualitatively the same. The selected k-points correspond to the lowest-energy electron transitions for the static lattice. The results shown in Fig. 5 represent data for two types of electron transitions – bright and dark transitions when considering the static crystal lattice. Thus, a change in the atomic configuration at a finite temperature enhances optical absorption by involving a more significant number of states in the process. Due to the thermal motion of atoms, some transitions that are dark in a static lattice become bright. While transitions that are bright in a static lattice do not turn dark, their oscillator strengths may decrease. For comparison, Fig. 5(a and c) displays the oscillator strengths for a static lattice as horizontal red dashed lines.
The transition of optical characteristics from dark to bright occurs due to changes in lattice symmetry caused by the thermal motion of atoms, where the interatomic distances experience contractions and elongations at the frequency of activated normal modes. The analysis reveals that throughout all structures along the MD trajectory, the lattice symmetry is P1. This change in symmetry is a result of a decrease in point symmetry due to atomic movement. One should note that the NVE molecular dynamics starts with equipartitioned activation of all nuclear degrees of freedom (normal modes). There is an expectation for independent contraction/elongation of all internuclear distances, bonds, dihedrals as function of time. The amplitude of these contractions/elongations is small, but phase is random. Strictly speaking, it will distort any absolute symmetry; there will be no rotation, or inversion that will reproduce the same structure, except translation by the lattice vector. Distortion of symmetry during ab initio MD is referred to as dynamical disorder. For analysis of keeping or breaking crystalline structure one may explore RDF as function of time, catching transitions from crystalline to amorphous phase or keeping “approximate” symmetry. Alternatively, one may “cool down” the model after the dynamics (optimization) and then analyze new equilibrium geometry, in a spirit of simulated annealing, for retention or change of original symmetry.
The reduction of symmetry leads to change in selection rules for matrix elements, eqn (1), and affects the absorption spectrum. Superimposed oscillations of all normal modes make these trajectories quasiperiodic; in a large enough model, the trajectories would gain a random nature.
Some of the optical transitions that are dark for the static lattice become bright as the system evolves along the MD trajectory. Such changes concern transitions with energies both below and above the value of Eoptic. For transitions with energies below Eoptic, the oscillator strengths decrease as the ECBM–VBM transition energy is approached. The oscillator strengths for ECBM–VBM transitions are less than 10−4. The second reason for the decrease in the optical absorption energy is thermal fluctuations in the energies of electronic transitions.
It is necessary to figure out the oscillator strengths and energies of electron transitions along the MD trajectory using the hybrid HSE06 functional to get a good idea of the optical absorption threshold. This task requires lengthy calculations. However, based on PBE + U calculations, one can assume that since the lowest energy of the optical absorption threshold corresponds to absorption at the Γ-point of the Brillouin zone. The shift in the onset of optical absorption due to the thermal motion of atoms is approximately 0.5 eV. After applying this value to the HSE06 results for a static lattice, we get 3.2 eV as the expected value of the optical absorption threshold. This value is consistent with the results of the experiments.
3.3 Nonradiative charge relaxation and photoluminescence
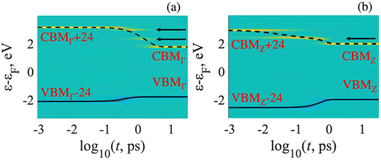
Fig. 6 illustrates the supercell calculated excited-state dynamics of electron–hole pairs. The results were obtained by processing NACs from adiabatic MD trajectories using spin-restricted DFT for the in the different k-points. As mentioned in eqn (6), the blue and yellow colors represent the gain in population of electrons and holes, respectively. The green color indicates no change, which corresponds to the ground-state charge density. The energy expectation values for electrons and holes in the excited states are shown by solid and dashed lines, respectively.Each panel shows how electronic populations are distributed based on energy and time. When each panel starts, there is an immediate excitation that moves electrons to the CBMK + y (y-th orbital above the CBM) in the conduction band and introduces holes to the VBMK − x (x-th orbital below the VBM) orbital in the valence band. The index K denotes a point in the Brillouin zone. These excitations, VBMK − x → CBMK + y, indicate optical transitions with very high oscillator strengths. After the excitation, a nonradiative process called vibrational relaxation converts the excited electrons to the CBMK and the holes to the VBMK. It's important to note that the electron–hole pairs stay in the frontier orbitals for a specific period of time before returning to the ground electronic state. Arrows in Fig. 6 depict intermediate states that trap excited electrons during relaxation. As a result, a radiative transition from these intermediate states is also possible, leading to the appearance of peaks in the PL spectrum. Upon including noncollinear spin basis and spin–orbit coupling effect into account one expects some modification of transition energies, relaxation rates, recombination rates, and intensity of optical transitions. Such comparison was reported for lead halide perovskites.46
The most probable transitions can be identified by analyzing the time-integrated PL spectra of excited-state trajectories in Fig. 7. Nevertheless, this approach uses transition energies obtained from HSE06 calculations, which results in the generation of PL features with narrow line widths. In order to achieve a more accurate match with experimental PL spectra, it is necessary to consider the impact of thermal broadening. This has been reported through the method known as molecular dynamics photoluminescence (MDPL).25
 | ||
| Fig. 7 Time-integrated PL spectra computed along the excited-state dynamics trajectories for all irreducible k-points in the reciprocal space. | ||
The MDPL spectrum, which considers the contribution from the states at each k-point, is displayed in Fig. 8. The PL spectra for each k-point are within the energy range ≤ Eoptic. The minimum energy is determined by the fluctuations of the KS orbitals along the MD trajectory. The PL spectrum exhibits a wide energy extension, with several PL peaks present at all k-points. This is due to the fact that electronic excitations relax to states at the edges of the bandgap, and excited states occupy orbitals with transition energies below Eoptic. Fluctuating oscillator strengths of optical transitions are attributed to instantaneous atomic configurations at each point of the MD trajectory. As excited electrons and holes approach the CBM and VBM, the oscillator strengths decrease in absolute value. Despite this it remains a relatively high probability of a radiative transition occurring before the excitations have reached the band gap edge. This effect results in a wide PL range and multiple emission peaks.
 | ||
| Fig. 8 MDPL spectra computed at different k-points of Brillouin zone. Total spectrum is a sum of contribution from each k-point. | ||
The calculated PL spectrum qualitatively matches the measured spectrum.19 This range spans from 1.8 to 2.8 eV (440–690 nm) and shows the existence of multiple peaks, though not as clearly as observed in the experiment. However, the theoretical PL quantum yield (PLQY) is ∼10−8, while the experimental PLQY value is ∼10−3. This difference can be explained by the fact that experimentally it was shown that the PL peak decreases as oxygen-deficient BaTiO3 samples are annealed in an oxygen flow.18 This finding is supported by theoretical modeling.18 Since our simulations were carried out using a perfect lattice, the observed difference between calculated and experimental data suggests that even a small concentration of defects greatly improves the PL properties of BaTiO3 compared to the ideal lattice. Therefore, the complete PL behavior in BaTiO3 is influenced by both defects and fluctuations in electron transitions near the band gap edge.
This significant difference suggests that even a small concentration of defects greatly improves the PL properties of BaTiO3 compared to the ideal lattice. Therefore, the complete PL behavior in BaTiO3 is influenced by both defects and fluctuations in electron transitions near the band gap edge.
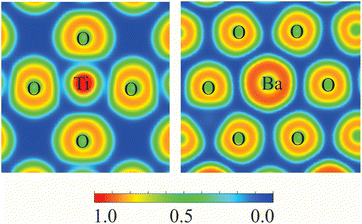
3.4 Chemical bonding in BaTiO3
In Gao et al.,45 the analysis of chemical bonds between atoms in the BaTiO3 lattice was based on the examination of charge density in the interatomic space. However, to fully understand the nature of these chemical bonds, we must consider the formation of electron pairs, which we can achieve through Electron Localization Function (ELF) analysis.The ELF value ranges from 0 to 1, with a value of 0.5 indicating a homogeneous electron gas. An ELF of 1.0 signifies perfect localization of electrons, while a value of 0.5 denotes perfect delocalization. Additionally, ELF readings below 0.5 suggest areas with minimal electron pair density.
The calculated ELF projections for the Ti–O and Ba–O bonds are shown in Fig. 9. A narrow region of minimum ELF separating the valence shells of Ti and O indicates the presence of ionic bonding. The minimal ELF values in the regions between Ti and O ions range from 0.12 to 0.22. In contrast, the minimal ELF value between Ba and O ions is 0.08. This analysis suggests that BaTiO3 behaves primarily as a purely ionic crystal, with no covalent bonds present.
4 Conclusions
We have employed the density functional method to investigate the optical properties of the tetragonal phase of BaTiO3. We conducted the calculations for both a static lattice and one that takes into account the thermal motion of atoms at ambient temperature. The results show a significant reduction in the calculated threshold energy for optical absorption when accounting for atom motion. There are two primary causes for this phenomenon. Initially, electronic transitions that were previously dark for a static lattice become luminous as a result of changes in the atomic configuration caused by thermal motion. Secondly, fluctuations in the energy of electronic transitions induced by atoms' motion lead to a decrease in the optical absorption threshold. The dispersion of electron energy in the reciprocal space may account for certain characteristics observed in the photoluminescence spectra.Data availability
Atomistic models of the considered materials are available upon request.Author contributions
Conceptualization, D. S. K. and T. M. I.; methodology, D. R. G. and T. M. I.; software, T. M. I. and D. S. K.; validation, D. S. K. and T. M. I.; formal analysis, D. R. G., A. U. A. and F. U. A.; investigation, A. U. A., D. R. G., F. U. A., T. M. I. and D. S. K.; resources, T. M. I. and D. S. K.; writing—original draft preparation, T. M. I.; writing—review and editing, T. M. I., D. R. G. and D. S. K.; visualization, A. U. A.; supervision, T. M. I.; project administration, F. U. A.; funding acquisition, T. M. I. All authors have read and agreed to the published version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was carried out with the financial support of the Ministry of Science and Higher Education of the Republic of Kazakhstan: AP14869492 “Development of nanocrystalline metal oxide catalysts for hydrogen production”. The work by T. M. I. was performed under the state assignment of GEOKHI RAS. D. R. G. acknowledges support of NSF 1944921 for developing methods of quantum dynamics. D. S. K. acknowledges partial support from the U.S. Department of Energy DE-SC0022239 for computational exploration of photoluminescence of earth abundant metal compounds.Notes and references
- K. J. Choi, M. Biegalski, Y. L. Li, A. Sharan, J. Schubert, R. Uecker, P. Reiche, Y. B. Chen, X. Q. Pan, V. Gopalan, L.-Q. Chen, D. G. Schlom and C. B. Eom, Science, 2004, 306, 1005–1009 CrossRef CAS PubMed.
- V. Buscaglia, M. T. Buscaglia and G. Canu, in Encyclopedia of Materials: Technical Ceramics and Glasses, ed. M. Pomeroy, Elsevier, Oxford, 2021, pp. 311–344, DOI:10.1016/B978-0-12-803581-8.12132-0.
- M. E. Lines and A. M. Glass, Principles and Applications of Ferroelectrics and Related Materials, Oxford University Press, 2001 Search PubMed.
- M. T. Buscaglia, M. Viviani, V. Buscaglia, L. Mitoseriu, A. Testino, P. Nanni, Z. Zhao, M. Nygren, C. Harnagea, D. Piazza and C. Galassi, Phys. Rev. B:Condens. Matter Mater. Phys., 2006, 73, 064114 CrossRef.
- S. S. Parizi, D. Caruntu, A. Rotaru and G. Caruntu, Mater. Adv., 2022, 3, 6474–6484 RSC.
- D. Kip, Appl. Phys. B:Lasers Opt., 1998, 67, 131–150 CrossRef CAS.
- Z. Hasan, M. A. Rahman, D. K. Das and H. K. Rouf, Sci. Rep., 2023, 13, 10487 CrossRef CAS PubMed.
- H. Lee, J. F. McGlone, S. I. Rahman, C. Chae, C. Joishi, J. Hwang and S. Rajan, Phys. Status Solidi RRL, 2024, 18, 2400042 CrossRef CAS.
- W. R. Lopes, H. F. A. Medeiros, G. S. Santos, T. C. Araujo, J. F. Carvalho, P. V. dos Santos and M. T. de Araujo, J. Opt. Soc. Am. A, 2018, 35, 1919–1928 CrossRef CAS PubMed.
- S. Chandrappa, S. N. Myakala, N. A. Koshi, S. J. Galbao, S.-C. Lee, S. Bhattacharjee, D. Eder, A. Cherevan and D. H. K. Murthy, ACS Appl. Mater. Interfaces, 2024, 16, 8763–8771 CrossRef CAS PubMed.
- T. M. Inerbaev, A. U. Abuova, Z. Y. Zakiyeva, F. U. Abuova, Y. A. Mastrikov, M. Sokolov, D. Gryaznov and E. A. Kotomin, Molecules, 2024, 29, 2707 CrossRef CAS PubMed.
- Y. Y. Huang, Y. L. Yang, L. Y. Zhang, V. Laletin, V. Shur, R. Y. Jing and L. Jin, J. Alloys Compd., 2024, 1006 Search PubMed.
- M. K. Mahata, T. Koppe, K. Kumar, H. Hofsäss and U. Vetter, Sci. Rep., 2020, 10, 8775 CrossRef CAS PubMed.
- J. Hao, Y. Zhang and X. Wei, Angew. Chem., Int. Ed., 2011, 50, 6876–6880 CrossRef CAS PubMed.
- X. Tian, Z. Wu, Y. Jia, J. Chen, R. K. Zheng, Y. Zhang and H. Luo, Appl. Phys. Lett., 2013, 102, 042907 CrossRef.
- H. Sun, X. Wu, D. F. Peng and K. W. Kwok, ACS Appl. Mater. Interfaces, 2017, 9, 34042–34049 CrossRef CAS PubMed.
- Y. Zhou, R. Xiong, P. Wang, X. Wu, B. Sa, C. Lin, M. Gao, T. Lin and C. Zhao, J Materiomics, 2022, 8, 586–595 CrossRef.
- E. Orhan, J. A. Varela, A. Zenatti, M. F. C. Gurgel, F. M. Pontes, E. R. Leite, E. Longo, P. S. Pizani, A. Beltràn and J. Andrès, Phys. Rev. B:Condens. Matter Mater. Phys., 2005, 71, 085113 CrossRef.
- T. Watanabe, D. Hoshi, M. Ishida and T. Ohba, Langmuir, 2018, 34, 10250–10253 CrossRef CAS PubMed.
- M.-S. Zhang, Z. Yin, Q. Chen, W. Zhang and W. Chen, Solid State Commun., 2001, 119, 659–663 CrossRef CAS.
- M. L. Moreira, M. F. C. Gurgel, G. P. Mambrini, E. R. Leite, P. S. Pizani, J. A. Varela and E. Longo, J. Phys. Chem. A, 2008, 112, 8938–8942 CrossRef CAS PubMed.
- L. Verlet, Phys. Rev., 1967, 159, 98–103 CrossRef CAS.
- T. M. Inerbaev, Y. Han, T. B. Bekker and D. S. Kilin, J. Phys. Chem. C, 2022, 126, 6119–6128 CrossRef CAS.
- T. M. Inerbaev, J. D. Hoefelmeyer and D. S. Kilin, J. Phys. Chem. C, 2013, 117, 9673–9692 CrossRef CAS PubMed.
- D. J. Vogel and D. S. Kilin, J. Phys. Chem. C, 2015, 119, 27954–27964 CrossRef CAS.
- Fatima, Y. Han, D. J. Vogel, T. M. Inerbaev, N. Oncel, E. K. Hobbie and D. S. Kilin, J. Phys. Chem. C, 2019, 123, 7457–7466 CrossRef CAS.
- D. R. Graupner and D. S. Kilin, J. Phys. Chem. C, 2024, 128, 3935–3944 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B, 1998, 57, 1505–1509 CrossRef CAS.
- F. Maldonado, S. Jácome and A. Stashans, Comput. Condens. Matter, 2017, 13, 49–54 CrossRef.
- P. E. Blöchl, Phys. Rev. B:Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- A. Savin, R. Nesper, S. Wengert and T. F. Fässler, Angew Chem. Int. Ed. Engl., 1997, 36, 1808–1832 CrossRef CAS.
- A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397–5403 CrossRef CAS.
- V. Wang, N. Xu, J.-C. Liu, G. Tang and W.-T. Geng, Comput. Phys. Commun., 2021, 267, 108033 CrossRef CAS.
- D. S. Kilin and D. A. Micha, J. Phys. Chem. Lett., 2010, 1, 1073–1077 CrossRef CAS.
- S. Huang and D. S. Kilin, J. Chem. Theory Comput., 2014, 10, 3996–4005 CrossRef CAS PubMed.
- V. B. Parmar, D. Raval, S. K. Gupta, P. N. Gajjar and A. M. Vora, Mater. Today: Proc., 2023 DOI:10.1016/j.matpr.2023.01.410.
- R. A. Evarestov and A. V. Bandura, J. Comput. Chem., 2012, 33, 1123–1130 CrossRef CAS PubMed.
- S. H. Wemple, Phys. Rev. B, 1970, 2, 2679–2689 CrossRef.
- H. Gao, J. Cao, L. Liu and Y. Yang, J. Mol. Struct., 2011, 1003, 75–81 CrossRef CAS.
- A. Forde, T. Inerbaev, E. K. Hobbie and D. S. Kilin, J. Am. Chem. Soc., 2019, 141, 4388–4397 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2025 |