‘Kick-in the head’: high-performance and air-stable mononuclear Dy^III single-molecule magnets with pseudo-D_6h symmetry from a [1 + 1] Schiff-base macrocycle approach

Abstract

Using the [1 + 1] condensation approach for the preparation of new macrocyclic scaffolds (L^N6_phen and L^N4O2_phen) with the rigid phenanthroline-based ‘head’ unit produces the air-stable mononuclear compounds [Dy(L^N6_phen)(Ph₃SiO)₂](PF₆) (1-L^N6_phen) and [Dy(L^N4O2_phen)(Ph₃SiO)₂](PF₆) (1-L^N4O2_phen) through a stepwise metal-ion templated synthesis. Both compounds exhibit pseudo-D_6h symmetry with different degrees of distortion from the ideal hexagonal bipyramidal geometry, depending on the planarity of the equatorial macrocycles and the intramolecular π–π stacking interactions between the phenyl groups of the apical siloxide ligand and the equatorial macrocycle. Both compounds are single-molecule magnets (SMMs) with large energy barriers for the magnetization reversal, exhibiting out-of-phase AC susceptibility signals up to 75 K or 90 K. The closer-to-ideal D_6h complex 1-L^N4O2_phen possesses a U_eff of 1360 K, which is the highest reported barrier among all mononuclear Dy^III SMMs synthesized using the [1 + 1] Schiff-base macrocycle approach. The experimental results are supported by ab initio calculations, which indicate relaxation of the magnetization via the first- or second-excited state for 1-L^N6_phen and 1-L^N4O2_phen, respectively. The results demonstrate the ability of Schiff-base macrocycles to facilitate the synthesis of high-performance and air-stable SMMs through a chemical modulation of the individual carbonyl ‘head’ and amine subunits, deciphering the factors which affect the magnetic dynamics of SMMs.

---

Introduction

Over the past decade, there has been a rapid increase in the number of studies on molecular compounds of f-elements that exhibit slow relaxation of their magnetic moment.¹ The motivation behind this growing interest is the potential to use stable magnetic moments for storing information in molecules.² Coordination compounds based on 4f-elements, particularly those containing dysprosium and terbium, are of great interest because their strong spin–orbit coupling and appreciable magnetic anisotropy can result in large and bistable magnetic moments separated by an energy barrier for the spin reversal (U_eff), thus leading to slow magnetization relaxation and single-molecule magnet (SMM) behavior.² SMMs can retain their magnetization even in the absence of an external magnetic field, mimicking the behavior observed in bulk magnetic materials but at the molecular level.³ This ability to control and manipulate magnetic states at such small scales could revolutionize areas such as quantum computing,⁴ spintronics,⁵ and information storage,⁶ where traditional extended solid materials may face limitations.

In lanthanide complexes, two critical factors influence their magnetic properties, namely the symmetry and strength of the ligand field that surrounds the 4f-metal ions.⁷ These factors contribute to the onset of significant crystal-field splitting, which in turn leads to large effective energy barriers for magnetization reorientation and high blocking temperatures (T_B), both essential parameters for preserving magnetic information.⁸ One of the most promising approaches for developing high-performance and air-stable lanthanide SMMs is the synthesis of mononuclear Dy^III complexes, where the metal center exhibits axial crystal-field (CF) symmetry, and adopts pentagonal bipyramidal (D_5h) or hexagonal bipyramidal (D_6h) coordination geometries.^7,8 The primary intention of the CF symmetry is to eliminate, or at least significantly reduce, the transverse CF components that accelerate magnetic relaxation through quantum tunneling of the magnetization (QTM). Simultaneously, the strong axial CF is mandatory in the case of the oblate-shaped Dy^III ion for achieving large energy separation of the CF-induced m_J states and high U_eff values.⁹

Although it is difficult to modulate the arrangement of the donor-atoms around a lanthanide ion and obtain perfect local symmetry, synthetic chemists have invented ways through ligand design and basic principles of molecular inorganic chemistry that result in the metal center adopting geometries with a near-ideal D_5h or D_6h symmetry. In this vein, there are three different synthetic strategies based on the preferences of the oblate-shaped electron density of Dy^III, which requires strong metal–ligand interactions along the z-axis and weak interactions in the xy plane.⁹ The first strategy involves the coordination of five weakly bound monodentate ligands (e.g. pyridine, THF, H₂O) in the equatorial plane in conjunction with two strong and bulky axial ligands (e.g. alkoxides, phenoxides or phosphine oxides) that reside along the z-axis. This approach prevents other ligands from coordinating with the metal, leading to almost perfect pentagonal bipyramidal compounds with remarkably high U_eff and T_B values.¹⁰ The second approach is based on the rotating degrees of freedom and the twisting of the polydentate organic chelate (e.g. H₂bbpen and its derivatives; H₂bbpen = N,N′-bis(2-hydroxybenzyl)-N,N′-bis(2-methylpyridyl)ethylenediamine) that has the ability to coordinate both equatorially and axially to the metal center, providing the appropriate axial ligand field (RO⁻ groups) around the oblate-shaped Dy^III ions.¹¹ The last route comprises the use of macrocyclic molecules with certain cavity sizes and numbers of donor-atoms, such as Schiff-bases and crown ethers. The latter encapsulate the lanthanide ion and promote a soft equatorial ligation, rendering the apical positions amenable to interact strongly with anionic O-donor ligands, such as phenoxides and siloxides.¹² This synthetic strategy has yielded a variety of Dy^III coordination compounds with D_5h or D_6h local symmetries,¹² and record U_eff values for the magnetization reversal,¹³ comparable to the landmark dysprosium-metallocene SMMs.¹⁴

A common method to synthesize Schiff-base macrocyclic complexes involves a condensation reaction of a dicarbonyl (‘head’ unit) and diamine compounds in the presence of a template metal-ion that can foster the cyclization of the resulting product.¹⁵ Depending on the ratio of diamine to dicarbonyl, the amine chain length, the donor atoms, the ionic radius of the metal, and the cavity size, the reaction can yield [1 + 1], [2 + 2], or [3 + 3] macrocyclic products.^15,16 Trivalent lanthanide ions (Ln^III) have been employed as metal templates in the condensation reactions of diamines and dicarbonyl compounds to produce various [1 + 1] and [2 + 2] macrocyclic complexes, with a pyridine ‘head’ unit usually located at the macrocyclic scaffold.¹⁶ More specifically, the [2 + 2] products have led to a plethora of mononuclear Dy^III complexes exhibiting D_6h symmetry and enhanced SMM properties with extremely high U_eff values;¹⁷ this is mainly due to the ability of these large macrocycles to accommodate sizeable 4f-metal ions without suffering from significant bond strain within their combined carbonyl and amine units. In contrast, the [1 + 1] products can also yield Dy^III complexes with D_5h or D_6h symmetries in a more designable manner, albeit the resulting coordination compounds are often more distorted than the [2 + 2] analogues, deviating from the ideal geometries.¹⁸ As a result, most of the high-performance hexagonal bipyramidal Dy^III SMMs reported in the literature, have stemmed from the [2 + 2] approach, whereas only two examples have been reported that contain the [1 + 1] condensation reaction.^18d,e

In this direction, we decided to utilize the metal-ion assisted [1 + 1] cyclocondensation approach by implementing the more robust phenanthroline-based ‘head’ unit to produce Dy^III Schiff-base macrocyclic complexes with D_6h symmetries and investigate their overall magnetic dynamics. To the best of our knowledge, phenanthroline-based dicarbonyl compounds have never been previously used in the coordination chemistry of lanthanide/Schiff-base macrocyclic complexes (Table S1†). Herein, we report the synthesis of two hexagonal bipyramidal Dy^III complexes: [Dy(L^N6_phen)(Ph₃SiO)₂](PF₆) (1-L^N6_phen) and [Dy(L^N4O2_phen)(Ph₃SiO)₂](PF₆) (1-L^N4O2_phen), which bear the macrocycles L^N6_phen and L^N4O2_phen (Scheme 1), surrounding the equatorial plane of the metal centers, while two bulky triphenylsiloxide (Ph₃SiO⁻) ligands occupy the apical positions. The two new, structurally similar, macrocycles have resulted from the [1 + 1] condensation reaction of 1,10-phenanthroline-2,9-dicarbaldehyde with either triethylenetetramine or 1,2-bis(2-aminoethoxy)ethane, yielding the all-N₆ or the mixed-donor N₄O₂ scaffolds, respectively, with dissimilar equatorial environments, electronic properties, and degrees of distortion.

Scheme 1 Structural representation of the ‘head’ units (top) and the new [1 + 1] Schiff-base macrocyclic ligands L^N6_phen and L^N4O2_phen (bottom) discussed in this work.

Interestingly, both Dy^III complexes exhibit SMM behavior up to 75 K (1-L^N6_phen) and 90 K (1-L^N4O2_phen), albeit with distinctly different U_eff values depending on the deviation of the macrocyclic ligands from the perfect planar conformation and the overall distortion from the ideal D_6h local symmetry. Apparently, the replacement of the –NH groups by the etheric O-donor atoms within the macrocycle scaffolds has yielded a substantial increase in the U_eff value, thus rendering 1-L^N4O2_phen as a record holder in energy barriers amongst all reported [1 + 1] macrocycle-based Dy^III SMMs.

Results and discussion

Synthesis and molecular structures

We recently reported the mononuclear complexes [Dy(L^N6_py)(Ph₃SiO)₂](PF₆) and [Dy(L^N3O3_py)(Ph₃SiO)₂](PF₆), which feature pseudo-D_6h symmetry and exhibit enhanced SMM properties with U_eff values up to 1300 K.^18e The two air-stable compounds have resulted from the [1 + 1] Schiff-base macrocyclic approach, utilizing the macrocycles derived from the condensation of the well-known 2,6-diacetylpyridine ‘head’ unit (Table S1†) with either tetraethylenepentamine (L^N6_py) or 1,11-diamino-3,6,9-trioxaundecane (L^N3O3_py). In the present study, we decided to shift from pyridine to phenanthroline ‘head’ unit, thus exploiting several new opportunities, such as the offer of an additional N-donor atom from the ‘head’ unit for coordination to the metal center, as well as the rigidity, bulkiness and planarity of phenanthroline over pyridine groups. Further, we have retained the Ph₃SiO⁻ groups as strong axial ligands for directing the magnetic anisotropy along the Ising-type axis.

The new phenanthroline-based compounds 1-L^N6_phen and 1-L^N4O2_phen were prepared by following a well-known synthetic protocol (Scheme 2), which was firstly introduced by Murrie and coworkers for the synthesis of [1 + 1] Dy^III complexes with D_5h symmetries.^18c In particular, the stoichiometric reaction of 1,10-phenanthroline-2,9-dicarbaldehyde and the respective diamine was carried out in the presence of DyCl₃·6H₂O as a template agent to form the Dy^III/Cl⁻/macrocycle precursor. Subsequently, the bulky triphenylsilanol pro-ligand (Ph₃SiOH) was used, which upon deprotonation with Et₃N, can occupy the axial sites of the Dy^III center and replace the weakly bound Cl⁻ ions and/or the coordinated solvate molecules (i.e., MeOH, H₂O). Finally, an anion metathesis reaction with NH₄PF₆ or KPF₆ was performed to aid crystallization, resulting in pale yellow plate-like crystals of the mononuclear complexes [Dy(L^N6_phen)(Ph₃SiO)₂](PF₆) (1-L^N6_phen) and [Dy(L^N4O2_phen)(Ph₃SiO)₂](PF₆) (1-L^N4O2_phen).

Scheme 2 General synthetic route for the preparation of complexes 1-L^N6_phen (X = NH and A⁺ = NH₄⁺) and 1-L^N4O2_phen (X = O and A⁺ = K⁺).

Both 1-L^N6_phen and 1-L^N4O2_phen are thermally robust, with a high decomposition temperature approaching 250 °C (Fig. S3†). The powder X-ray diffraction patterns of both compounds show good agreement with the simulated ones, confirming the phase purity of the samples (Fig. S4 and S5†).

Single-crystal X-ray diffraction revealed that complexes 1-L^N6_phen and 1-L^N4O2_phen crystallize in the orthorhombic P2₁2₁2₁ and triclinic P1̄ space groups, respectively (Fig. S6†). Crystallographic details for both complexes are presented in Table S2.† Selected interatomic distances and angles for complexes 1-L^N6_phen and 1-L^N4O2_phen are listed in Tables S3 and S4,† respectively. For the sake of brevity, only important metrical parameters will be discussed in the main text. The molecular structure of 1-L^N6_phen is composed of the mononuclear cationic complex [Dy(L^N6_phen)(Ph₃SiO)₂]⁺ (Fig. 1A) counterbalanced by a PF₆⁻ ion. The Dy^III center is encapsulated in the cavity of the L^N6_phen Schiff-base macrocycle, which provides an equatorial N₆ coordination environment, whereas the axial positions are occupied by two strongly bound Ph₃SiO⁻ ligands, leading to an overall N₆O₂ coordination environment. The eight-coordinate Dy^III center adopts a significantly distorted hexagonal bipyramidal geometry according to the SHAPE program (Fig. 1B),¹⁹ as indicated by the large Continuous Shape Measure (CShM) value of 4.35 (Table S5†). Values of CShM greater than 3 correspond to a significant distortion from the ideal coordination geometry. The relatively large Dy–N_equatorial bond distances, which fall into the range of 2.558(8)–2.695(9) Å, in conjunction with the two short and strong Dy–O_axial bond lengths of 2.159(5) and 2.163(5) Å, demonstrate the compressed D_6h local symmetry favoring the axial crystal-field required for an oblate-shaped Dy^III ion. Additionally, the O–Dy–O bond angle of 164.6(2)° significantly deviates from the ideal angle of 180° for a perfect hexagonal bipyramid, as well as the O–Dy–N bond angles, which diverge from the ideal angle of 90° (Table S3†), corroborating the distorted polyhedron of 1-L^N6_phen.

Fig. 1 Structures of the cationic complexes 1-L^N6_phen (A), 1-L^N4O2_phen (C), and the distorted hexagonal bipyramidal coordination polyhedra of the Dy centers (B and D). The PF₆⁻ counterions, and the H-atoms of both compounds are omitted for clarity. The smaller white spheres define the vertices of the corresponding ideal polyhedron. Color scheme: Dy, yellow; O, red; N, blue; C, grey; Si, olive.

On the other hand, the Dy^III center in 1-L^N4O2_phen (Fig. 1C) is equatorially coordinated by the L^N4O2_phen mixed-donor macrocycle via two pyridine N-atoms and two N-atoms of the secondary amine (–NH–) groups (same as in 1-L^N6_phen), as well as two ether-type O-donors in place of the secondary amine N-atoms in 1-L^N6_phen. Likewise, two axial triphenylsiloxide ligands, each located above and below the DyN₄O₂ plane, complete the overall N₄O₄ coordination environment. In contrast to 1-L^N6_phen, the O_ax–Dy–O_ax angle of 174.52(7) and the O_ax–Dy–N_eq/O_eq bond angles within 1-L^N4O2_phen are closer to the ideal 180° and 90°, respectively, for a perfect hexagonal bipyramid (Table S4†), resulting in a CShM value of 1.74 (Table S5†), implying a smaller distortion from ideal D_6h symmetry (Fig. 1D). Moreover, the Dy–O_ax bonds are 2.142(2) and 2.153(2) Å, noticeably shorter than the analogous bonds in 1-L^N6_phen, while the Dy–N_eq/O_eq lie in the range of 2.570(2)–2.628(2) Å.

A closer inspection of the degree of planarity of the equatorial plane, according to the relative positions of the donor atoms with respect to the hexagonal plane, revealed that the macrocycle L^N4O2_phen exhibits a more planar conformation than L^N6_phen. This observation was validated by the strikingly different CShM values regarding the ideal hexagon between 1-L^N6_phen and 1-L^N4O2_phen (CShM = 4.13 vs. 1.32) (Fig. S7†). The packing diagram of neighboring monomeric complexes revealed that the shortest intermolecular Dy⋯Dy distance is 10.848(4) Å for 1-L^N6_phen and 8.015(5) Å for 1-L^N4O2_phen (Fig. S8 and S9†).

Attempting to rationalize the observed differences in the macrocycles’ planarity and the O_ax–Dy–O_ax angles, it is worth noting that the phenyl rings of the triphenylsilanolate ligands interact through π–π stacking and C–H⋯π intramolecular interactions with the phenanthroline moiety of the macrocyclic scaffold in both compounds (Fig. S10†). More specifically, the strength of the C–H⋯π interactions is of the same magnitude for both complexes, as indicated by the relatively long C52–H52⋯Ar1 centroid (1-L^N6_phen) and C21–H21⋯Ar1 centroid (1-L^N4O2_phen) distances of 2.936 Å and 2.935 Å, respectively. However, the π–π stacking interactions within 1-L^N6_phen are much stronger than 1-L^N4O2_phen, as demonstrated by the centroid⋯centroid distances of 3.538 Å (Ar2⋯Ar4) for the former and 3.719 Å (Ar1⋯Ar4) for the latter. This discrepancy may be responsible for the tilting of the axial triphenylsilanolate ligand towards the macrocycle, thus leading to a more bent hexagonal bipyramidal coordination geometry and less axial O_ax–Dy–O_ax angle in 1-L^N6_phen.

Magnetic properties

To probe the static magnetic properties of the two complexes, direct current (dc) magnetic susceptibility studies were conducted on analytically pure microcrystalline samples in the temperature range of 2–300 K under an applied field of 0.1 T (Fig. 2). The room temperature χ_MT values of 14.10 (1-L^N6_phen) and 14.06 (1-L^N4O2_phen) cm³ mol⁻¹ K are very close to the theoretical value of 14.17 cm³ mol⁻¹ K for an isolated Dy^III ion (⁶H_15/2, S = 5/2, L = 5, g = 4/3). For both complexes, the χ_MT product decreases smoothly upon cooling until ∼14 K, and then more sharply reaching values of 12.49 (1-L^N6_phen) and 10.00 (1-L^N4O2_phen) cm³ mol⁻¹ K at 2 K. The abrupt decrease of the χ_MT products can be attributed to the depopulation of the low-lying crystal-field m_J states of the ground ⁶H_15/2 state as the temperature is lowering, combined with the onset of magnetic blocking on approaching the low temperature limit of the experiment.

Fig. 2 Temperature dependence of the χ_MT product for complexes 1-L^N6_phen (black circles) and 1-L^N4O2_phen (red circles).

The isothermal field (H) dependence of the magnetization (M) was measured at 2, 3, and 5 K for both complexes in the range of 0–7 T (Fig. S11 and S12†). The M(H) curves at 2 K are similar for both complexes, exhibiting an abrupt increase of magnetization at low fields while remaining almost constant at high fields. The magnetization values at the maximum applied field of 7 T and the lowest temperature of 2 K are 5.30 (1-L^N6_phen) and 5.07 Nμ_B (1-L^N4O2_phen), much lower than the expected saturation value (M_S) for one free Dy^III ion (M_S/Nμ_B = 10Nμ_B); this can be ascribed to the crystal field effects that induce significant magnetic anisotropy.

To assess the slow magnetization relaxation phenomena and the SMM behavior of 1-L^N6_phen and 1-L^N4O2_phen, alternating current (ac) magnetic susceptibility studies were performed under zero applied dc field and a weak ac field of 3.0 Oe, oscillating with frequencies ranging from 10 to 10000 Hz. Interestingly, both compounds exhibit frequency-dependent in-phase (Fig. S13†) and out-of-phase (Fig. 3A and Fig. 4A) peaks of signals with well-defined maxima up to 75 and 90 K for 1-L^N6_phen and 1-L^N4O2_phen, respectively. The appearance of the out-of-phase magnetic susceptibility signals denotes the presence of slow magnetization relaxation due to an energy barrier for the spin-reversal consistent with SMM behavior. Furthermore, the detection of the frequency dependence of the out-of-phase susceptibility up to this high-temperature regime suggests the existence of significant magnetization reversal barriers for both complexes. The ac frequency at which the maximum occurs in the corresponding 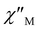vs. v plots shows a slight variation below 10 K, suggesting the presence of quantum tunneling of magnetization (QTM) relaxation process. At elevated temperatures, this maximum becomes significantly dependent on temperature, shifting to higher frequencies as the temperature increases, indicating a relaxation process driven by thermal activation.²⁰

Fig. 3 (A) Frequency-dependence of the out-of-phase magnetic susceptibility under zero applied dc field over the temperature range of 2–75 K for complex 1-L^N6_phen. (B) Temperature-dependence of relaxation times (τ) for complex 1-L^N6_phen. The circles correspond to experimental data and the lines to the best-fit of the data.

Fig. 4 (A) Frequency-dependence of the out-of-phase magnetic susceptibility under zero applied dc field over the temperature range of 2–90 K for complex 1-L^N4O2_phen. (B) Temperature-dependence of relaxation times (τ) for complex 1-L^N4O2_phen. The circles correspond to experimental data and the lines to the best-fit of the data.

To obtain the temperature-dependence of relaxation times (τ) and derive the operating relaxation processes, we constructed the Arrhenius plot (ln τ vs. 1/T) by fitting the data through the equation:

τ⁻¹ = τ₀⁻¹e^−U_eff/kT + CTⁿ + τ_QTM⁻¹, (1)

where the pre-exponential factor, τ₀, and the effective energy barrier (U_eff) correspond to the thermally-assisted Orbach relaxation process, C and n are the parameters of the Raman relaxation process, while τ_QTM represents the relaxation time through the quantum tunnelling of the magnetization (QTM).²¹ As depicted in Fig. 3B and Fig. 4B, the non-linear regime of the Arrhenius plots supports the substantial role of the Raman and QTM mechanisms as the temperature is lowered. In particular, at intermediate temperatures, the relaxation time seems to be dominated by the Raman process as indicated by the curvature of the ln τ vs. 1/T plots, while below 10 K the relaxation time becomes temperature-independent for both complexes.^20,21 Accordingly, in the high-temperature regime, the thermally-activated Orbach process becomes the dominant relaxation pathway and the relaxation time shows an exponential dependence on temperature (linear region in ln τ vs. 1/T plots).^20,21 Therefore, the best-fit to the experimental data afforded the following parameters: U_eff = 779 (54) K, τ₀ = 9.98 × 10⁻¹⁰ s, C = 0.5477 (0.045) s⁻¹ K⁻ⁿ, n = 2.42 (0.03), τ_QTM = 1.57 × 10⁻² (2.19 × 10⁻⁴) s for complex 1-L^N6_phen and U_eff = 1360 (21) K, τ₀ = 5.88 × 10⁻¹² s, C = 0.0777 (0.01) s⁻¹ K⁻ⁿ, n = 2.45 (0.06), τ_QTM = 1.77 × 10⁻² (6.94 × 10⁻⁴) s for complex 1-L^N4O2_phen. The values of the parameters τ₀, C, and n are within the expected range for mononuclear Dy^III-based SMMs,^10,11,17,18 while the exponent n of the Raman process takes a significantly smaller value than the expected for a Kramers ion (n = 9). However, it has been reported that deviations in n values suggest the mixing of optical and acoustic phonons, most probably due to the presence of low energy optical phonons that contribute to the Raman demagnetization.^17,18,21,22 The obtained U_eff for compound 1-L^N4O2_phen is the highest effective energy barrier yet reported among all mononuclear Dy^III SMMs, which have derived from the [1 + 1] Schiff-base macrocycle approach (Table S1†). Li, Yin and coworkers have recently reported the complex [Dy(L^N6₁)(Ph₃SiO)₂](BPh₄) with a pseudo-D_6h symmetry, bearing the neutral hexaaza macrocyclic Schiff base ligand derived from the [1 + 1] condensation of 6,6′-diformyl-2,2′-bipyridyl and triethylenetetramine.^18d This complex behaves as an SMM with a U_eff of ∼584 K, much smaller than the corresponding values of 1-L^N6_phen and 1-L^N4O2_phen, which is rationalized in terms of the severe distortion from the ideal D_6h symmetry (CShM = 3.91) and the significant deviation from the perfect axiality (O–Dy–O = 169.1°) and equatorial hexagonal plane (best mean angle of N–Dy–N = 50.8°).

To further examine the distribution of relaxation times (α) across the entire temperature range, the Cole–Cole plots (Fig. S14†) of both complexes were fitted using a generalized Debye model (eqn (S1) and (S2), see ESI† for details). The non-semicircular shape of the plots indicates a wide distribution of relaxation times, most probably due to overlapping of different relaxation mechanisms. Indeed, the large α values span the range 0.35–0.18 for 1-L^N6_phen (Table S6†) and 0.33–0.11 for 1-L^N4O2_phen (Table S7†), corroborating the above hypothesis. In particular, the largest α values are observed in the low-T regime, denoting the coexistence of Raman and QTM relaxation processes as the temperature is lowered.

To verify the blocking temperature of both compounds, magnetization (M) vs. field (H) hysteresis studies were performed at an average field sweep rate of 40 Oe s⁻¹ and different low temperatures by sweeping the field between −5 and 5 T (Fig. 5A and Fig. S15†). Both compounds showed butterfly-shaped loops, characteristics of the fast tunneling near zero field, which results in small coercivities.²³ In particular, complexes 1-L^N4O2_phen and 1-L^N6_phen exhibit opening of the hysteresis loops up to 9 K (Fig. 5B) and 5 K (Fig. S15†), respectively, thus implying a smaller transverse anisotropy and a higher pseudo-D_6h symmetry for the former compound, in agreement with the results obtained from the ab initio calculations (vide infra).

Fig. 5 Magnetic hysteresis loops for complex 1-L^N4O2_phen measured at a temperature range of 2–9 K with a mean field sweep rate of 40 Oe s⁻¹ (A) and enlargement of the zero-field region from 5 to 9 K (B).

Ab initio calculations

Detailed insight into the magnetic properties of 1-L^N6_phen and 1-L^N4O2_phen was obtained through ab initio calculations, using the SINGLE_ANISO approach implemented in the ORCA 5.0.2 software package^24a (see the ESI† for details), to further analyze the mechanism that governs magnetization relaxation in both complexes. As expected from the strong axial ligand field, the Dy^III ions in both compounds exhibit large crystal-field splitting of 1854 K (1-L^N6_phen) and 2126 K (1-L^N4O2_phen) (Table S8†). The calculated energies of the eight lowest Kramer Doublets (KDs) of the ⁶H_15/2 ground multiplet of the Dy^III centers along with the principal components of the g-tensors and the angles between the ground and excited KDs of 1-L^N6_phen and 1-L^N4O2_phen are tabulated in Tables S9 and S10,† respectively. The ground KDs in both complexes possess strong axial magnetic anisotropy, which can be reflected in the wavefunction composition of nearly 100% of the m_J = 15/2, as well as the respective g-tensors approaching the Ising limit (g_x = 3.3 × 10⁻⁴, g_y = 5.7 × 10⁻⁴, g_z = 19.85 for 1-L^N6_phen and g_x = 6.8 × 10⁻⁴, g_y = 8.0 × 10⁻⁴, g_z = 19.87 for 1-L^N4O2_phen). In addition, the calculated orientations of the ground state anisotropic axes in both complexes point towards the axial Dy–O bonds of the triphenylsilanolate ligands (Fig. 6C/D). Moreover, the anisotropic axes of the ground doublet for both compounds are almost collinear with those of the first two excited doublets, exhibiting angles of 0.462° and 0.99° with the second KD and 1.413° and 3.07° with the third KD for 1-L^N6_phen and 1-L^N4O2_phen, respectively. Although the high purity of the first excited doublet (m_J = ±13/2) for 1-L^N6_phen can be validated by the relative wavefunction composition of 99.4%, the axial g-tensor is significantly lower (g_z = 16.92) and the transversal components of the g-tensor are also small but non-negligible (g_x = 0.1176, g_y = 0.1195). In contrast, complex 1-L^N4O2_phen exhibits a purer and more anisotropic first excited doublet composed of 99.67% of the m_J = ±13/2, while the values of the g-tensors are: g_z = 16.94, g_x = 0.081, and g_y = 0.089. However, the third KD in 1-L^N4O2_phen is an admixture of m_J = ±11/2 (96.47%) and m_J = ±1/2 (2.60%), while the low axiality within this KD is corroborated by the significant contribution of the transverse g-components (g_x = 0.106, g_y = 0.298) along with the decreased value of the axial component (g_z = 13.77). These observations suggest that the g_z-component is not sufficiently axial to suppress the through-barrier relaxation mechanisms within the second KD in 1-L^N6_phen and the third KD in 1-L^N4O2_phen. This is further confirmed by the experimentally determined U_eff values following the calculated energies of the second KD in 1-L^N6_phen and the third in KD 1-L^N4O2_phen which are located at 680 K and 1352 K, respectively. In detail, the experimental U_eff value of 1360 K for 1-L^N4O2_phen is in excellent agreement with the calculated energy of the third KD (1352 K), whereas the experimental U_eff value of 779 K for 1-L^N6_phen is slightly higher than the calculated energy state of the second KD (680 K). The small deviation between the energy of the second KD and the experimentally observed U_eff in 1-L^N6_phen most likely results from neglecting electron correlation outside the 4f orbital space in the CASSCF calculations.^14a Therefore, we applied an alternative fit to the experimental data for 1-L^N6_phen in the temperature range of 10–75 K, discarding the QTM term from eqn (1). This was due to the relaxation time becoming temperature-independent below 10 K, and indeed the alternative fit gave a U_eff value of 653(27) K (Fig. S16;† see the caption for additional fit parameters), very close to the computed energy of the second KD in 1-L^N6_phen.

Fig. 6 Single_Aniso computed energy of the KDs (A and B) and orientation of the ground state anisotropic axis highlighted with purple color for 1-L^N6_phen (C) and 1-L^N4O2_phen (D). Dark red arrows show the most probable relaxation route and light red arrows indicate less significant but non-negligible matrix elements between different m_J states.

Fig. 6 illustrates the probability of the magnetic relaxation pathways where the most intense red arrows show the most probable relaxation route. According to the above observations, combined with the magnitudes of the transition moment matrix elements (Tables S11 and S12†), which show transitions between different KDs, the crossing of the magnetization relaxation barrier is predicted to proceed through the second and third KDs in 1-L^N6_phen and 1-L^N4O2_phen, respectively. In the case of 1-L^N6_phen the predicted barrier of 473 cm⁻¹ is somewhat lower than the experimental barrier of 541 cm⁻¹, although, based on the appreciable transverse components of the g-tensors in the first-excited KD, relaxation via any higher-lying states seems unlikely. The discrepancy in the experimental and calculated barriers could be a consequence of electron correlation effects outside of the 4f orbital manifold not being captured by the calculations. For 1-L^N4O2_phen, the first-excited KD at 512 cm⁻¹ has more pronounced axial character, increasing the probability of reaching the second-excited KD at 940 cm⁻¹, where a barrier-crossing transition then occurs. If valid, this analysis provides a good match with the experimental barrier of 945 cm⁻¹.

To further quantify the axiality of both compounds and the magnitude of the crystal-field induced energy separation between the ground and the low-lying excited states, we calculated the crystal-field parameters by implementing SINGLE_ANISO module (Table S13, see ESI† for details). To calculate the crystal-field parameters was used the following Hamiltonian:^24b,c

where Ô^k_q are the extended Stevens operators, B^k_q the crystal-field (CF) parameters, and k is the rank of the ITO (2,4,6) and q is the component of the ITO, taking values of −k, −k + 1, … 0, 1, … k. Furthermore, the crystal-field Hamiltonian in D_6h symmetry can be simplified by the following equation:

Ĥ_CF = B⁰₂Ô⁰₂+ B⁰₄Ô⁰₄+ B⁰₆Ô⁰₆+ B⁶₆ (Ô⁶₆ + Ô⁻⁶₆), (3)

where the axial crystal-field parameters are coined as B^k_q (k = 0, q = 2, 4, 6) and the transverse ones as B^k_q (k ≠ 0, q = 2, 4, 6).²⁵ For both compounds, the axial CF parameters clearly dominate over the transversal ones, as expected due to the strong ligation provided by the hard O-donor atoms of the triphenylsilanolates along the easy axis (Table S13,† highlighted values in bold). More specifically, the magnitude of the |B⁰₂| term determines the axiality of the molecular compound and the scale of the crystal-field splitting. The greater the magnitude of the |B⁰₂|, the larger the energy separation between the ground KD and the excited ones, thus leading to higher U_eff values, as well as lower operational QTM process at low temperatures.^13,26 The |B⁰₂| term for compound 1-L^N6_phen takes a value of 6.786, whereas for compound 1-L^N4O2_phen exhibits a greater value of 7.773. The variation between these values is due to the more linear O–Dy–O bond angle and the higher D_6h symmetric local coordination environment of the Dy^III center in complex 1-L^N4O2_phen. This noticeable difference is further translated to the larger energy splitting of the m_J states in 1-L^N4O2_phen than 1-L^N6_phen (Table S8† and Fig. 6), thereby leading to an almost two-fold increase of the magnetic anisotropy barrier (i.e., from 779 to 1360 K).

Conclusions

In summary, we have synthesized two new air-stable Dy^III macrocyclic complexes with hexagonal bipyramidal geometries by implementing for the first time a phenanthroline-based ‘head’ unit through the metal-ion assisted [1 + 1] Schiff-base cyclocondensation reaction. Both compounds 1-L^N6_phen and 1-L^N4O2_phen behave as zero-field SMMs with high energy barriers stemming from the strongly axial ligand fields in conjunction with the weak coordination from the all N-donor L^N6_phen macrocycle in complex [Dy(L^N6_phen)(Ph₃SiO)₂](PF₆) and the mixed N/O-donor L^N4O2_phen macrocycle in complex [Dy(L^N4O2_phen)(Ph₃SiO)₂](PF₆). The replacement of the secondary amine groups in L^N6_phen with etheric O-atoms in L^N4O2_phen seems to have a significant impact on the overall planarity of the equatorial plane, as well as improved magnetic axiality, thereby leading to a closer-to-ideal D_6h symmetry for complex 1-L^N4O2_phen. Additionally, it appears that the strength of the intramolecular π–π stacking interactions between the aromatic groups of the apical and equatorial ligands has its own effect on the geometric and electronic structures of the two compounds via modulating not only the planarity of the Schiff-base macrocycle but also the axial O–Dy–O tilt. Theoretical studies have shed light on the magnetization relaxation mechanisms of both complexes, presaging a dominant relaxation pathway through the first excited doublet for 1-L^N6_phen and the second excited doublet for 1-L^N4O2_phen. Furthermore, the larger value of the axial CF parameter |B⁰₂|, when shifting from 1-L^N6_phen to 1-L^N4O2_phen, was in agreement with the experimental results, and particularly the 2-fold enhancement of the U_eff value from 779 K in compound 1-L^N6_phen to 1360 K in compound 1-L^N4O2_phen. The latter U_eff is a record value among all (D_5h and D_6h) previously reported mononuclear Dy^III SMMs resulted from the [1 + 1] Schiff-base macrocyclic approach.

Ongoing research involves the enrichment of the family of [1 + 1] Schiff-base macrocyclic Dy^III complexes through the designed synthesis and use of macrocycles with reduced equatorial binding strength and improved planarity by modulating either the carbonyl ‘head’ or the amine(s) units, or both. In turn, the implementation of aliphatic instead of aromatic substituted O-donor axial ligands, as a means of eliminating the intramolecular π–π stacking interactions, can lead to more linear O–Dy–O bond angles and increase the axial magnetic anisotropy of the Dy^III ions, and the energy barrier for the magnetization reorientation.

Author contributions

Th. C. S. conceived the research idea. A. S. A. designed the structures and performed their synthesis and characterization. A. M., S. R. G., D. I. A. and J. T. made contributions to the data acquisition and analysis (XRD, magnetism, ab initio calculations). R. A. L. and Th. C. S. wrote the paper, with contributions from all the co-authors.

Data availability

The data supporting this article have been included as part of the ESI.† Crystallographic data for 1-L^N6_phen and 1-L^N4O2_phen have been deposited at the Cambridge Crystallographic Data Centre (CCDC) under 2393281 and 2393282, respectively.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

A. M. and R. A. L. thank the UK EPSRC (grants EP/V003089/1, EP/X036626/1) for financial support. J. T. acknowledges the National Natural Science Foundation of China (grant 92261103).

References

1. K. Bernot, Get under the Umbrella: A Comprehensive Gateway for Researchers on Lanthanide-Based Single-Molecule Magnets, Eur. J. Inorg. Chem., 2023, 26, e202300336.
2. (a) D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Lanthanide Single-Molecule Magnets, Chem. Rev., 2013, 113, 5110–5148; (b) L. Sorace, C. Benelli and D. Gatteschi, Lanthanides in molecular magnetism: old tools in a new field, Chem. Soc. Rev., 2011, 40, 3092–3104; (c) M. Atzori and R. Sessoli, The second quantum revolution: role and challenges of molecular chemistry, J. Am. Chem. Soc., 2019, 141, 11339–11352.
3. A. Zabala-Lekuona, J. M. Seco and E. Colacio, Single-Molecule Magnets: From Mn12-ac to dysprosium metallocenes, a travel in time, Coord. Chem. Rev., 2021, 441, 213984.
4. (a) S. Thiele, F. Balestro, R. Ballou, S. Klyatskaya, M. Ruben and W. Wernsdorfer, Electrically driven nuclear spin resonance in single-molecule magnets, Science, 2014, 344, 1135–1138; (b) R. Vincent, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Electronic read-out of a single nuclear spin using a molecular spin transistor, Nature, 2012, 488, 357–360; (c) E. Moreno-Pineda and W. Wernsdorfer, Measuring molecular magnets for quantum technologies, Nat. Rev. Phys., 2021, 3, 645–659.
5. (a) A. Candini, S. Klyatskaya, M. Ruben, W. Wernsdorfer and M. Affronte, Graphene Spintronic Devices with Molecular Nanomagnets, Nano Lett., 2011, 11, 2634–2639; (b) I. S. Zlobin, Y. V. Nelyubina and V. V. Novikov, Molecular Compounds in Spintronic Devices: An Intricate Marriage of Chemistry and Physics, Inorg. Chem., 2022, 61, 12919–12930; (c) M. Ganzhorn and W. Wernsdorfer, in Molecular Magnets, ed. J. Bartolomé, F. Luis and J. F. Fernández, Springer Berlin Heidelberg, Berlin, Heidelberg, 2014, pp. 319–364; (d) M. Urdampilleta, N.-V. Nguyen, J.-P. Cleuziou, S. Klyatskaya, M. Ruben and W. Wernsdorfer, Molecular Quantum Spintronics: Supramolecular Spin Valves Based on Single-Molecule Magnets and Carbon Nanotubes, Int. J. Mol. Sci., 2011, 12, 6656–6667.
6. (a) M. D. Korzyński, Z. J. Berkson, B. Le Guennic, O. Cador and C. Copéret, Leveraging Surface Siloxide Electronics to Enhance the Relaxation Properties of a Single-Molecule Magnet, J. Am. Chem. Soc., 2021, 143, 5438–5444; (b) G. Gabarró-Riera, G. Aromí and E. C. Sañudo, Magnetic molecules on surfaces: SMMs and beyond, Coord. Chem. Rev., 2023, 475, 214858; (c) E. Coronado, Molecular magnetism: from chemical design to spin control in molecules, materials and devices, Nat. Rev. Mater., 2019, 5, 87–104; (d) M. Mannini, F. Pineider, P. Sainctavit, C. Danieli, E. Otero, C. Sciancalepore, A. M. Talarico, M.-A. Arrio, A. Cornia, D. Gatteschi and R. Sessoli, Magnetic memory of a single-molecule quantum magnet wired to a gold surface, Nat. Mater., 2009, 8, 194–197.
7. (a) T. G. Ashebr, H. Li, X. Ying, X.-L. Li, C. Zhao, S. Liu and J. Tang, Emerging Trends on Designing High-Performance Dysprosium(III) Single-Molecule Magnets, ACS Mater. Lett., 2022, 4, 307–319; (b) S. K. Gupta and R. Murugavel, Enriching lanthanide single-ion magnetism through symmetry and axiality, Chem. Commun., 2018, 54, 3685–3696.
8. (a) V. Vieru, S. Gómez-Coca, E. Ruiz and L. F. Chibotaru, Increasing the Magnetic Blocking Temperature of Single–Molecule Magnets, Angew. Chem., Int. Ed., 2024, 63, e202303146; (b) Z. Zhu and J. Tang, Lanthanide single-molecule magnets with high anisotropy barrier: where to from here?, Natl. Sci. Rev., 2022, 9, nwac194.
9. (a) J.-L. Liu, Y.-C. Chen and M.-L. Tong, Symmetry strategies for high performance lanthanide-based single-molecule magnets, Chem. Soc. Rev., 2018, 47, 2431–2453; (b) J. D. Rinehart and J. R. Long, Exploiting single-ion anisotropy in the design of f-element single-molecule magnets, Chem. Sci., 2011, 2, 2078–2085.
10. (a) L.-L. Li, H.-D. Su, S. Liu, Y.-C. Xu and W.-Z. Wang, A new air-and moisture-stable pentagonal-bipyramidal DyIII single-ion magnet based on the HMPA ligand, Dalton Trans., 2019, 48, 2213–2219; (b) Y. Ding, T. Han, Y. Zhai, D. Reta, N. F. Chilton, R. E. P. Winpenny and Y.-Z. Zheng, A Study of Magnetic Relaxation in Dysprosium(III) Single–Molecule Magnets, Chem. – Eur. J., 2020, 26, 5893–5902; (c) S. K. Gupta, T. Rajeshkumar, G. Rajaraman and R. Murugavel, An air-stable Dy(III) single-ion magnet with high anisotropy barrier and blocking temperature, Chem. Sci., 2016, 7, 5181–5191; (d) A. B. Canaj, M. K. Singh, C. Wilson, G. Rajaraman and M. Murrie, Chemical and in silico tuning of the magnetisation reversal barrier in pentagonal bipyramidal Dy(III) single-ion magnets, Chem. Commun., 2018, 54, 8273–8276; (e) S. K. Gupta, S. Dey, T. Rajeshkumar, G. Rajaraman and R. Murugavel, Deciphering the Role of Anions and Secondary Coordination Sphere in Tuning Anisotropy in Dy(III) Air–Stable D_5h SIMs, Chem. – Eur. J., 2022, 28, e202103585; (f) Y. Chen, J. Liu, Y. Lan, Z. Zhong, A. Mansikkamäki, L. Ungur, Q. Li, J. Jia, L. F. Chibotaru, J. Han, W. Wernsdorfer, X. Chen and M.-L. Tong, Dynamic Magnetic and Optical Insight into a High Performance Pentagonal Bipyramidal DyIII Single–Ion Magnet, Chem. – Eur. J., 2017, 23, 5708–5715; (g) K.-X. Yu, J. G. C. Kragskow, Y.-S. Ding, Y.-Q. Zhai, D. Reta, N. F. Chilton and Y.-Z. Zheng, Enhancing magnetic hysteresis in single-molecule magnets by ligand functionalization, Chem, 2020, 6, 1777–1793; (h) Y. Ma, Y. Zhai, Q. Luo, Y. Ding and Y.-Z. Zheng, Ligand Fluorination to Mitigate the Raman Relaxation of DyIII Single–Molecule Magnets: A Combined Terahertz, Far–IR and Vibronic Barrier Model Study, Angew. Chem., Int. Ed., 2022, 61, e202206022; (i) Y. Ding, N. F. Chilton, R. E. P. Winpenny and Y.-Z. Zheng, On Approaching the Limit of Molecular Magnetic Anisotropy: A Near-Perfect Pentagonal Bipyramidal Dysprosium(III) Single-Molecule Magnet, Angew. Chem., Int. Ed., 2016, 55, 16071–16074; (j) X. Ding, Q. Luo, Y. Zhai, X. Zhang, Y. Lv, X. Zhang, C. Ke, C. Wu and Y.-Z. Zheng, Rigid Dysprosium(III) Single–Molecule Magnets Exhibit Preserved Superparamagnetism in Solution, Chin. J. Chem., 2022, 40, 563–570; (k) Y.-C. Chen, J.-L. Liu, L. Ungur, J. Liu, Q.-W. Li, L.-F. Wang, Z.-P. Ni, L. F. Chibotaru, X.-M. Chen and M.-L. Tong, Symmetry-Supported Magnetic Blocking at 20 K in Pentagonal Bipyramidal Dy(III) Single-Ion Magnets, J. Am. Chem. Soc., 2016, 138, 2829–2837; (l) I. F. Díaz-Ortega, J. M. Herrera, S. Dey, H. Nojiri, G. Rajaraman and E. Colacio, The effect of the electronic structure and flexibility of the counteranions on magnetization relaxation in [Dy(L)₂(H₂O)₅]³⁺ (L = phosphine oxide derivative) pentagonal bipyramidal SIMs, Inorg. Chem. Front., 2020, 7, 689–699.
11. (a) L. Zhu, B. Yin, P. Ma and D. Li, Tuning the Equatorial Crystal-Field in Mononuclear DyIII Complexes to Improve Single-Molecule Magnetic Properties, Inorg. Chem., 2020, 59, 16117–16121; (b) L. Zhu, Y. Dong, B. Yin, P. Ma and D. Li, Improving the single-molecule magnet properties of two pentagonal bipyramidal Dy³⁺ compounds by the introduction of both electron-withdrawing and -donating groups, Dalton Trans., 2021, 50, 12607–12618; (c) Z. Jiang, L. Sun, Q. Yang, B. Yin, H. Ke, J. Han, Q. Wei, G. Xie and S. Chen, Excess axial electrostatic repulsion as a criterion for pentagonal bipyramidal DyIII single-ion magnets with high U_eff and TB, J. Mater. Chem. C, 2018, 6, 4273–4280; (d) J. Liu, Y.-C. Chen, J.-L. Liu, V. Vieru, L. Ungur, J.-H. Jia, L. F. Chibotaru, Y. Lan, W. Wernsdorfer, S. Gao, X.-M. Chen and M.-L. Tong, A Stable Pentagonal Bipyramidal Dy(III) Single-Ion Magnet with a Record Magnetization Reversal Barrier over 1000 K, J. Am. Chem. Soc., 2016, 138, 5441–5450.
12. Y. Gil, A. Castro-Alvarez, P. Fuentealba, E. Spodine and D. Aravena, Lanthanide SMMs Based on Belt Macrocycles: Recent Advances and General Trends, Chem. – Eur. J., 2022, 28, e202200336.
13. W.-J. Xu, Q.-C. Luo, Z.-H. Li, Y.-Q. Zhai and Y.-Z. Zheng, Bis-Alkoxide Dysprosium(III) Crown Ether Complexes Exhibit Tunable Air Stability and Record Energy Barrier, Adv. Sci., 2024, 11, 2308548.
14. (a) F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, A Dysprosium Metallocene Single-Molecule Magnet Functioning at the Axial Limit, Angew. Chem., Int. Ed., 2017, 56, 11445–11449; (b) F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Magnetic hysteresis up to 80 kelvin in a dysprosium metallocene single-molecule magnet, Science, 2018, 362, 1400–1403; (c) F.-S. Guo, M. He, G.-Z. Huang, S. R. Giblin, D. Billington, F. W. Heinemann, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Discovery of a Dysprosium Metallocene Single-Molecule Magnet with Two High-Temperature Orbach Processes, Inorg. Chem., 2022, 61, 6017–6025.
15. W. Radecka-Paryzek, V. Patroniak and J. Lisowski, Metal complexes of polyaza and polyoxaaza Schiff base macrocycles, Coord. Chem. Rev., 2005, 249, 2156–2175.
16. (a) V. Alexander, Design and Synthesis of Macrocyclic Ligands and Their Complexes of Lanthanides and Actinides, Chem. Rev., 1995, 95, 273–342; (b) D. E. Fenton and P. A. Vigato, Macrocyclic Schiff base complexes of lanthanides and actinides, Chem. Soc. Rev., 1988, 17, 69–90.
17. (a) M. S. Raju, K. Paillot, I. Breslavetz, G. Novitchi, G. L. J. A. Rikken, C. Train and M. Atzori, Optical Readout of Single-Molecule Magnets Magnetic Memories with Unpolarized Light, J. Am. Chem. Soc., 2024, 146, 23616–23624; (b) A. B. Canaj, S. Dey, E. R. Martí, C. Wilson, G. Rajaraman and M. Murrie, Insight into D_6h Symmetry: Targeting Strong Axiality in Stable Dysprosium(III) Hexagonal Bipyramidal Single-Ion Magnets, Angew. Chem., 2019, 131, 14284–14289; (c) Z. Li, Y. Zhai, W. Chen, Y. Ding and Y.-Z. Zheng, Air-Stable Hexagonal Bipyramidal Dysprosium(III) Single-Ion Magnets with Nearly Perfect D_6h Local Symmetry, Chem. – Eur. J., 2019, 25, 16219–16224; (d) Z. Zhu, C. Zhao, Q. Zhou, S. Liu, X.-L. Li, A. Mansikkamäki and J. Tang, Air-Stable Dy(III)-Macrocycle Enantiomers: From Chiral to Polar Space Group, CCS Chem., 2022, 4, 3762–3771; (e) Z. Zhu, C. Zhao, T. Feng, X. Liu, X. Ying, X.-L. Li, Y.-Q. Zhang and J. Tang, Air-Stable Chiral Single-Molecule Magnets with Record Anisotropy Barrier Exceeding 1800 K, J. Am. Chem. Soc., 2021, 143, 10077–10082; (f) C. Zhao, Z. Zhu, X.-L. Li and J. Tang, Air-stable chiral mono- and dinuclear dysprosium single-molecule magnets: steric hindrance of hexaazamacrocycles, Inorg. Chem. Front., 2022, 9, 4049–4055; (g) S. Liu, Y. Gil, C. Zhao, J. Wu, Z. Zhu, X.-L. Li, D. Aravena and J. Tang, A conjugated Schiff-base macrocycle weakens the transverse crystal field of air-stable dysprosium single-molecule magnets, Inorg. Chem. Front., 2022, 9, 4982–4989.
18. (a) B. Zhang, X. Guo, P. Tan, W. Lv, X. Bai, Y. Zhou, A. Yuan, L. Chen, D. Liu, H.-H. Cui, R. Wang and X.-T. Chen, Axial Ligand as a Critical Factor for High-Performance Pentagonal Bipyramidal Dy(III) Single-Ion Magnets, Inorg. Chem., 2022, 61, 19726–19734; (b) J.-L. Wang, J.-T. Chen, H. Yan, T.-T. Wang, Y.-Q. Zhang and W.-B. Sun, Constructing high axiality mononuclear dysprosium molecular magnets via a regulation-of-co-ligands strategy, Dalton Trans., 2024, 53, 10982–10990; (c) A. B. Canaj, S. Dey, C. Wilson, O. Céspedes, G. Rajaraman and M. Murrie, Engineering macrocyclic high performance pentagonal bipyramidal Dy(III) single-ion magnets, Chem. Commun., 2020, 56, 12037–12040; (d) S. Jia, X. Zhu, B. Yin, Y. Dong, A. Sun and D. Li, Macrocyclic Hexagonal Bipyramidal Dy(III)-Based Single-Molecule Magnets with a D_6h Symmetry, Cryst. Growth Des., 2023, 23, 6967–6973; (e) A. S. Armenis, A. Mondal, S. R. Giblin, C. P. Raptopoulou, V. Psycharis, D. I. Alexandropoulos, J. Tang, R. A. Layfield and Th. C. Stamatatos, Unveiling new [1 + 1] Schiff-base macrocycles towards high energy-barrier hexagonal bipyramidal Dy(III) single-molecule magnets, Chem. Commun., 2024, 60, 12730–12733.
19. M. Llunell, D. Casanova, J. Girera, P. Alemany and S. Alvarez, SHAPE, version 2.0, Universitat de Barcelona, Barcelona, Spain, 2010.
20. (a) J. Tang and P. Zhang, Lanthanide Single Molecule Magnets, Springer Berlin Heidelberg, Berlin, Heidelberg, 2015; (b) R. A. Layfield and M. Murugesu, Lanthanides and Actinides in Molecular Magnetism, John Wiley & Sons, Ltd, 2015.
21. S. T. Liddle and J. Van Slageren, Improving f-element single molecule magnets, Chem. Soc. Rev., 2015, 44, 6655–6669.
22. (a) E. Garlatti, A. Chiesa, P. Bonfà, E. Macaluso, I. J. Onuorah, V. S. Parmar, Y.-S. Ding, Y.-Z. Zheng, M. J. Giansiracusa, D. Reta, E. Pavarini, T. Guidi, D. P. Mills, N. F. Chilton, R. E. P. Winpenny, P. Santini and S. Carretta, A Cost-Effective Semi-Ab Initio Approach to Model Relaxation in Rare-Earth Single-Molecule Magnets, J. Phys. Chem. Lett., 2021, 12, 8826–8832; (b) J. G. C. Kragskow, A. Mattioni, J. K. Staab, D. Reta, J. M. Skelton and N. F. Chilton, Spin–phonon coupling and magnetic relaxation in single-molecule magnets, Chem. Soc. Rev., 2023, 52, 4567–4585; (c) A. Lunghi, F. Totti, R. Sessoli and S. Sanvito, The role of anharmonic phonons in under-barrier spin relaxation of single molecule magnets, Nat. Commun., 2017, 8, 14620; (d) S. Dey, T. Sharma and G. Rajaraman, Unravelling the role of spin–vibrational coupling in designing high-performance pentagonal bipyramidal Dy(III) single ion magnets, Chem. Sci., 2024, 15, 6465–6477; S. Mondal and A. Lunghi, Unraveling the contributions to spin-lattice relaxation in Kramers single-molecule magnets, J. Am. Chem. Soc., 2022, 144, 22965–22975.
23. F. Ortu, D. Reta, Y.-S. Ding, C. A. P. Goodwin, M. P. Gregson, E. J. L. McInnes, R. E. P. Winpenny, Y.-Z. Zheng, S. T. Liddle, D. P. Mills and N. F. Chilton, Studies of hysteresis and quantum tunnelling of the magnetisation in dysprosium(III) single molecule magnets, Dalton Trans., 2019, 48, 8541–8545.
24. (a) F. Neese, Software Update: The ORCA Program System—Version 5.0. WIREs Computational Molecular Science, 202212e1606; (b) K. W. H. Stevens, The theory of paramagnetic relaxation, Rep. Prog. Phys., 1967, 30, 189–226; (c) K. W. H. Stevens, Matrix elements and operator equivalents connected with the magnetic properties of rare earth ions, Proc. Phys. Soc. A, 1952, 65, 209–215.
25. J. Li, S. Gómez-Coca, B. S. Dolinar, L. Yang, F. Yu, M. Kong, Y.-Q. Zhang, Y. Song and K. R. Dunbar, Hexagonal Bipyramidal Dy(III) Complexes as a Structural Archetype for Single-Molecule Magnets, Inorg. Chem., 2019, 58, 2610–2617.
26. H. Liu, J.-F. Li and B. Yin, The coexistence of long τQTM and high U_eff as a concise criterion for a good single-molecule magnet: a theoretical case study of square antiprism dysprosium single-ion magnets, Phys. Chem. Chem. Phys., 2022, 24, 11729–11742.

---

Footnote

† Electronic supplementary information (ESI) available: Synthetic procedures, single-crystal X-ray data, IR, p-XRD, TGA, structural and magnetism plots, and ab initio calculations. CCDC 2393281 and 2393282. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4qi02756f

---