DOI:
10.1039/D5PY00185D
(Paper)
Polym. Chem., 2025,
16, 2291-2297
Mechanism and modelling of photo-mediated RAFT step-growth polymerization†
Received
24th February 2025
, Accepted 4th April 2025
First published on 9th April 2025
Abstract
Here, we report the modelling of photo-mediated RAFT step-growth polymerization kinetics of maleimide and acrylate monomers with bifunctional RAFT agents bearing tertiary carboxyalkyl stabilized fragementable R groups. We demonstrate that the kinetics for both photo-iniferter and PET-RAFT step-growth polymerizations display a three-half order dependence on monomer conversion. Modelling photo-iniferter RAFT step-growth for both monomer classes discloses that acrylate monomers exhibit lower kapp values compared to maleimide monomers; however, modelling PET-RAFT step-growth indicates that acrylate monomers exhibit higher kapp values compared to maleimide monomers. Furthermore, with the kinetics of thermally-initiated RAFT step-growth, we compare and summarize the kinetic trends based on monomer class, solvent selection, and initiation methods.
Introduction
Reversible addition fragmentation chain transfer (RAFT) polymerization is a controlled radical polymerization technique that governs uniform chain growth through a degenerative chain transfer mechanism.1–3 Despite the many advantageous aspects of RAFT polymerization (such as the user friendly nature and high functional group tolerance), the polymers are predominantly limited to all carbon backbones, thus limiting their potential applications.3 On the other hand, step-growth polymerization proceeds through the reaction of two functional groups to generate polymers in a stepwise manner, allowing desired functionality to be incorporated into the backbone. However, traditionally, step-growth polymerization requires harsh conditions to achieve high monomer conversion and molecular weight polymers.4
RAFT step-growth synergistically combines the user-friendly nature and high functional group tolerance of RAFT with the versatility in backbone functionality from step-growth, allowing for highly functional polymers to be synthesized with ease.5–11 RAFT step-growth employs bifunctional chain transfer agents (CTA) and monomers that proceeds through a single unit monomer insertion (SUMI) mechanism (Scheme 1). Initial reports of RAFT step-growth employed heat and exogenous radical sources (e.g., azo initiators) to generate the radicals used in the RAFT step-growth cycle, akin to thiol–ene polymerization.5–7,9,11–14 More recently, light as an initiation technique both with and without a photocatalyst has emerged as a viable alternative to initiate RAFT step-growth (Scheme 1A and B).8,15 As RAFT agents can directly absorb light to generate radicals, they can directly initiate polymerizations without the use of exogenous radical sources or photocatalyst (Scheme 1A).16–20 This principle, introduced by Otsu, employs thiocarbonylthio compounds as the initiator source, transfer agent, and terminating source (photo-iniferter) under UV light.16 On the other hand, photo-induced electron/energy transfer (PET) RAFT employs a photocatalyst that, in an excited state, either transfers an electron or triplet energy to the RAFT agent, subsequently fragmenting the RAFT agent to generate the radicals initiating the polymerization (Scheme 1B).21
 |
| | Scheme 1 (A) Photo-iniferter RAFT step-growth mechanism. (B) PET-RAFT step-growth mechanism. (C) Relative radical stability of backbone derived radical (M˙) and RAFT agent derived radical (R˙) (D) monomers used in this study. | |
In previous work, we developed a kinetic model for thermally initiated RAFT step-growth of maleimides and acrylate monomers using CTAs bearing tertiary carboxyalkyl fragmentable R groups.22 In that model, we demonstrated that these monomer classes follow first order kinetics with respect to monomer concentration when polymerized in the presence of exogenous radical sources, such as AIBN. Furthermore, it was demonstrated that acrylates exhibit lower apparent rate constants (kapp) compared to maleimide monomers. Additionally, rate of polymerization for both monomer classes was shown to have [I]1/2 dependence on initiator concentration.
Here, we extend the kinetic analysis to photo-iniferter and PET-RAFT step-growth for maleimides and acrylates with trithiocarbonates (Scheme 1D). Identifying rate order with respect to monomer provides valuable and necessary insight for optimizing reaction conditions. These systems involve two activation pathways (Scheme 1A and B): cleavage of the end-group RAFT agent (activation pathway I) and cleavage of the backbone RAFT agent (activation pathway II).8 The radicals generated by these activation pathways differ in stability, with the end-group cleavage producing a tertiary stabilized radical, whereas backbone RAFT agent yields a secondary radical of lower stability (Scheme 1C). Consequently, activation pathway I is expected to be the dominant pathway.
Results and discussion
ESR spin trapping studies to elucidate initiation mechanism for photo-iniferter and PET-RAFT step-growth
To verify this preference for activation pathway I, we performed electron spin resonance (ESR) spectroscopy spin trapping experiments using 5,5-dimethyl-1-pyrroline-N-oxide (DMPO) as a spin trap to form stable radical adducts detectable by ESR.23 We employed 3 equivalence of DMPO and 1 equivalence of RAFT agent, and this mixture was then irradiated with light at λmax = 405 nm for 15 minutes before recording the X-band ESR spectra. Two series of six hyperfine lines were observed for 2-(butylthiocarbonothioylthio)-2-methylpropanoic acid (BDMAT) in both 1,4-dioxane and toluene, indicating that direct photolysis of the end group RAFT agent (activation pathway I) occurs (Fig. 1A and S2†). In contrast, no discernible signals were detected for the maleimide SUMI adduct or (propanoic acid)yl butyl trithiocarbonate (PABTC), corresponding to the RAFT agent on the maleimide backbone and acrylate backbone, respectively, suggesting that photolysis of the backbone RAFT agent (activation pathway II) does not occur (Fig. 1B and C). Additionally, control experiments were performed by separately irradiating either DMPO or the RAFT agent with λmax = 405 nm for 15 minutes, where no obvious signals were observed (Fig. S3–S8†). Notably, these ESR experiments were conducted at different wavelengths compared to the RAFT step-growth polymerizations (λmax = 458, 514, and 625 nm), so differences in radical generation may vary slightly under the polymerization conditions. Nevertheless, these results strongly suggest that activation pathway I is the predominant mechanism in photo-mediated RAFT step-growth, enabling the simplification of the reaction mechanism by excluding activation pathway II.
 |
| | Fig. 1 X-band electron spin resonance (ESR) spectra of 5,5-dimethyl-1-pyrroline-N-oxide (DMPO) and different RAFT agents: (A) BDMAT in toluene, (B) SUMI adduct in 1,4-dioxane, and (C) PABTC in toluene, after irradiation with light at λmax = 405 nm for 15 minutes, [DMPO]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [RAFT agent]0 = 1 [RAFT agent]0 = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, [RAFT agent]0 = 0.25 M. 3, [RAFT agent]0 = 0.25 M. | |
Derivation of rate of polymerization (Rp) for photo-iniferter and PET RAFT step-growth
We next investigated the mechanism and observed kinetics for photo-iniferter RAFT step-growth further by developing a kinetic model based on the proposed mechanism (Scheme 1A), involving 5 species: the monomer (M), RAFT agent (CTA), as well as three radical species generated by the cycle (backbone derived radical (M˙), RAFT agent derived radical (R˙), and chain transfer intermediate adduct radical (CTA˙)). For simplicity, we did not consider thiocarbonyl thionyl radical intermediates formed by RAFT agent photolysis, nor any related termination, reversible deactivation, or side reactions. Additionally, we excluded the reverse chain-transfer process because the end-group CTA bears a more stabilized fragmentable group (R˙) compared to the monomer-derived radical (M˙).
In our previous work on thermally initiated RAFT step-growth, we defined a set of eqn (1)–(5) to represent each species involved. Eqn (1) and (2) describe the consumption of monomer via addition to the R˙ radical and the consumption of RAFT agent via addition to the M˙ radical, respectively. In the photo-iniferter context, eqn (2) also includes an additional term to account for RAFT agent consumption through activation pathway I. Meanwhile, eqn (3)–(5) outline the concentration profiles of the three intermediate radical species in the RAFT step-growth cycle, encompassing initiation (in eqn (4)), termination, and the overall generation and consumption of radicals.
| | 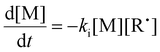 | (1) |
| |  | (2) |
| | 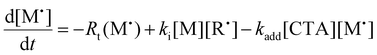 | (3) |
| | 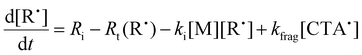 | (4) |
| | 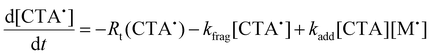 | (5) |
The initiation rate (Ri) accounted for in eqn (3) is defined by eqn (6), where kPI is the rate of photoactivation of the end group RAFT agent, and [CTA] is the concentration of RAFT agent. Rates of termination (Rt(M˙), Rt(R˙), and Rt(CTA˙)) or consumption of radical intermediates by radical–radical termination are shown below in eqn (7)–(9). Notably, all termination events are assumed to be equally likely, thus (kt1, kt2, kt3, kt4, kt5, and kt6) are all equal and can be further defined by a general termination kinetic parameter (kt). Furthermore, eqn (7)–(9) can be summed together to give a general rate of termination (Rt) (eqn (10)).
| | | Rt(M˙) = 2kt1[M˙]2 + kt2[M˙][R˙] + kt3[M˙][CTA˙] | (7) |
| | | Rt(R˙) = kt2 [M˙][R˙] + 2kt4[R˙]2 + kt5[R˙][CTA˙] | (8) |
| | | Rt(CTA˙) = kt3 [M˙][CTA˙] + kt5[R˙][CTA˙] + 2kt6[CTA˙]2 | (9) |
| | | Rt = Rt(M˙) + Rt(R˙) + Rt(CTA˙) | (10) |
The rate of polymerization (Rp) can be analytically solved using eqn (1)–(10). Consumption rates of monomer and RAFT agent can be assumed to be equal, and therefore, eqn (1) and (2) can be set equal. Furthermore, the steady state approximation can be adopted, allowing for eqn (3)–(5) to be set equal to zero, giving eqn (11). A more detailed derivation of eqn (11) can be found in the ESI.†
| |  | (11) |
Eqn (11) can be simplified by assuming that monomer addition to R˙ species is the rate limiting step (kadd, kfrag ≫ ki). This assumption is supported by previous studies on RAFT step-growth of acrylate and maleimide monomers with tertiary stabilized fragmentable carboxyalkyl RAFT agent.10,22 Under this assumption, eqn (11) reduces to eqn (12). Note, the monomer and RAFT agent concentrations are set equal ([M] = [CTA]) to each other as RAFT step-growth requires stoichiometric balance.
| |  | (12) |
Eqn (12) indicates that the rate of polymerization for photo-iniferter RAFT step-growth is proportional to monomer concentration raised to the three-half power (Rp ∝ [M]3/2). Furthermore, an apparent rate constant (kapp,PI) can be derived from eqn (12) as shown in eqn (13) below.
| |  | (13) |
Integrating eqn (12) gives the following time dependent expression (eqn (14)), which is consistent with established literature for kinetic modelling of photo-mediated RAFT SUMI processes.24
| |  | (14) |
A similar approach can be applied to model PET-RAFT step-growth kinetics. In this case, eqn (S10)–(S19)† describe the mechanism in Scheme 1B, where kd is the rate of photo-dissociation and [PC*] is the concentration of photocatalyst. As with the photo-iniferter system, activation pathway II is considered negligible and is therefore omitted. These equations can be analytically solved to give the rate of polymerization (Rp), which can be further simplified by assuming ki as the rate limiting step (eqn (15)). A more detailed derivation of Rp is provided in the ESI.†
| |  | (15) |
Akin to photo-iniferter RAFT step-growth, PET-RAFT step-growth displays a three-half order dependance on monomer concentration (Rp ∝ [M]3/2). Furthermore, an apparent rate constant for PET-RAFT can be defined (kapp,PET) in eqn (16). Again, integrating eqn (15) gives the same time dependent relationship seen with photo-iniferter RAFT step-growth (eqn (14)).24
| |  | (16) |
Kinetic analysis of photo-iniferter RAFT step-growth
Experimental photo-iniferter RAFT step-growth polymerization data for maleimide and acrylate monomers (Scheme 1D) can be fit using the model predictions from eqn (14) (Fig. 2). As a result, experimental data of RAFT step-growth polymerization of CTA2 with N,N′-(1,4-phenylene)dimaleimide, M2A, under blue, green, and red light (458 nm, 514 nm, and 625 nm, respectively) in tetrachloroethane (TCE) ([M2]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [CTA2]0 = 0.5
[CTA2]0 = 0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 M) was plotted with linear regressions applied from 0 to 16.0 hours (Fig. 2A, Table S1, and Fig. S9†).8 Both blue and green light conditions displayed kapp,PI values of 0.27 M−1/2 h−1 with R2 values above 0.98; on the other hand, the red light condition resulted in a much slower rate with a kapp,PI value of 0.03 M−1/2 h−1 and an R2 value of 0.99. The reduced rate for the red light condition is a result of the minimal overlap of the n–π* symmetry forbidden transition of the RAFT agent.8,25 Interestingly, all three light conditions display a plateau in the kinetics at increasing monomer conversion, which may result from competing light absorption by newly formed backbone CTA species and the progressively lower end-group CTA concentration (Fig. 2A, Table S1, and Fig. S9†).
0.5 M) was plotted with linear regressions applied from 0 to 16.0 hours (Fig. 2A, Table S1, and Fig. S9†).8 Both blue and green light conditions displayed kapp,PI values of 0.27 M−1/2 h−1 with R2 values above 0.98; on the other hand, the red light condition resulted in a much slower rate with a kapp,PI value of 0.03 M−1/2 h−1 and an R2 value of 0.99. The reduced rate for the red light condition is a result of the minimal overlap of the n–π* symmetry forbidden transition of the RAFT agent.8,25 Interestingly, all three light conditions display a plateau in the kinetics at increasing monomer conversion, which may result from competing light absorption by newly formed backbone CTA species and the progressively lower end-group CTA concentration (Fig. 2A, Table S1, and Fig. S9†).
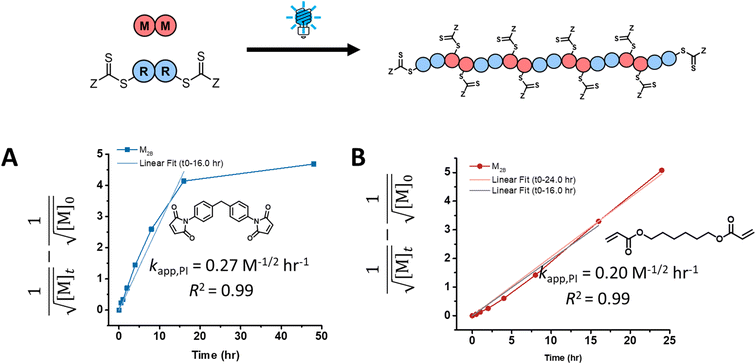 |
| | Fig. 2 Kinetic analysis of photo-iniferter RAFT step-growth under blue light irradiation (458 nm) with CTA2 and (A) M2A, a bismaleimide, and (B) M2B, a diacrylate. | |
Similarly, experimental data of photo-iniferter RAFT step-growth for 1,6-hexanediol diacrylate with CTA2 under blue and green light (458 nm and 514 nm, respectively) in dimethyl formamide (DMF) ([M2]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [CTA2]0 = 1.0
[CTA2]0 = 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.0 M) can be plotted and fitted with linear regressions from 0 to 24.0 hours (Fig. 2B, Table S2 and Fig. S10†).15 Both blue and green light conditions displayed kapp,PI values of approximately 0.2 M−1/2 h−1 with R2 values above 0.99. The observed lower kapp value for the polymerization of acrylates compared to maleimide monomers tracks with previous results seen for these monomer classes under thermally initiated RAFT step-growth conditions,22 which can be attributed to slower monomer addition to the R˙ species for acrylates compared to maleimides. Interestingly, unlike monomer M2A, monomer M2B did not display a plateau in the kinetics at high monomer conversion, which we attribute to some degree of homopropagation as was reported previously for this monomer.15
1.0 M) can be plotted and fitted with linear regressions from 0 to 24.0 hours (Fig. 2B, Table S2 and Fig. S10†).15 Both blue and green light conditions displayed kapp,PI values of approximately 0.2 M−1/2 h−1 with R2 values above 0.99. The observed lower kapp value for the polymerization of acrylates compared to maleimide monomers tracks with previous results seen for these monomer classes under thermally initiated RAFT step-growth conditions,22 which can be attributed to slower monomer addition to the R˙ species for acrylates compared to maleimides. Interestingly, unlike monomer M2A, monomer M2B did not display a plateau in the kinetics at high monomer conversion, which we attribute to some degree of homopropagation as was reported previously for this monomer.15
Kinetic analysis of PET-RAFT step-growth
Next, we fit experimental PET-RAFT step-growth polymerization data for maleimide and acrylate monomers (Scheme 1D) using the model predictions from eqn (14) (Fig. 3). Experimental data for PET-RAFT step-growth polymerization of M2A with CTA2 and zinc tetraphenyl porphyrin (ZnTPP) as the photocatalyst under blue, green, and red light (458 nm, 514 nm, and 625 nm, respectively) in TCE ([M2]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [CTA2]0
[CTA2]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [ZnTPP]0 = 0.5
[ZnTPP]0 = 0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5
0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.005 M) can be plotted with linear regressions applied from 0 to 48.0 hours (Fig. 3A, Table S3 and Fig. S11†).8 All three light conditions displayed kapp,PET values of approximately 0.1 M−1/2 h−1 with R2 values of 0.99. Interestingly, PET-RAFT step-growth of maleimides results in reduced polymerization rate compared to photo-iniferter RAFT step-growth, which contrasts the observed kinetics for chain-growth, where PET-RAFT is faster than RAFT-iniferter.26 In literature, computational data has shown that ZnTPP forms a precomplex with trithiocarbonate RAFT agents for the electron transfer process.27 Thus, we reason that maleimide monomers may interfere with or disrupt this precomplex, thereby reducing the polymerization rate.
0.005 M) can be plotted with linear regressions applied from 0 to 48.0 hours (Fig. 3A, Table S3 and Fig. S11†).8 All three light conditions displayed kapp,PET values of approximately 0.1 M−1/2 h−1 with R2 values of 0.99. Interestingly, PET-RAFT step-growth of maleimides results in reduced polymerization rate compared to photo-iniferter RAFT step-growth, which contrasts the observed kinetics for chain-growth, where PET-RAFT is faster than RAFT-iniferter.26 In literature, computational data has shown that ZnTPP forms a precomplex with trithiocarbonate RAFT agents for the electron transfer process.27 Thus, we reason that maleimide monomers may interfere with or disrupt this precomplex, thereby reducing the polymerization rate.
 |
| | Fig. 3 Kinetic analysis of PET-RAFT step-growth under red light irradiation (625 nm) with ZnTPP, CTA2 and (A) M2A, a bismaleimide, (B) M2B, a diacrylate, and (C) M2C, another diacrylate. | |
Additionally, experimental polymerization data for CTA2 with M2B (a diacrylate) and ZnTPP under red light (625 nm) in 1,4-dioxane ([M2]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [CTA2]0
[CTA2]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [ZnTPP]0 = 1.0
[ZnTPP]0 = 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.0
1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.0025 M) was fitted with a linear regression applied from 0 to 8.0 hours, giving a kapp,PET value of 0.69 M−1/2 h−1 and R2 value of 0.99 (Fig. 3B and Table S4†). Opposite to the case with maleimides, PET-RAFT step-growth with acrylates results in a faster polymerization rate compared to RAFT-iniferter step-growth. Furthermore, polymerization data for polyethylene glycol diacrylate (M2C) with CTA2 and ZnTPP in 1,4-dioxane under red light was also fitted, and a linear regression was applied from 0 to 16.0 hours, resulting in a kapp,PET value of 0.34 M−1/2 h−1 and R2 value of 0.99 (Fig. 3C).
0.0025 M) was fitted with a linear regression applied from 0 to 8.0 hours, giving a kapp,PET value of 0.69 M−1/2 h−1 and R2 value of 0.99 (Fig. 3B and Table S4†). Opposite to the case with maleimides, PET-RAFT step-growth with acrylates results in a faster polymerization rate compared to RAFT-iniferter step-growth. Furthermore, polymerization data for polyethylene glycol diacrylate (M2C) with CTA2 and ZnTPP in 1,4-dioxane under red light was also fitted, and a linear regression was applied from 0 to 16.0 hours, resulting in a kapp,PET value of 0.34 M−1/2 h−1 and R2 value of 0.99 (Fig. 3C).
We further plotted and applied linear regressions to PET-RAFT step-growth polymerization data for CTA2 with M2B and M2C under red light in DMF (Fig. S12 and Table S5†). Interestingly, rate of polymerization in DMF was much faster compared to 1,4-dioxane with kapp,PET values of 1.10 M−1/2 h−1 and 0.58 M−1/2 h−1 for monomers M2B and M2C, respectively. This solvent dependency trend for PET-RAFT step-growth with ZnTPP follows that seen with chain-growth PET-RAFT.21
Comparison of photo-mediated and thermally-initiated RAFT-step growth kinetics
We have summarized key results in Table 1, comparing the kinetics of photo-mediated RAFT step-growth polymerization to that of thermally-initiated RAFT step-growth polymerization for various monomers with CTA2.22 Both photo-iniferter and PET-RAFT step-growth polymerizations display a three-half order dependence with respect to monomer concentration (Table 1). This reaction order is a result of the initiation of the polymerization, which involves the direct photocleavage of the RAFT agent in the case of photo-iniferter and photocatalyst assisted cleavage of the RAFT agent in the case of the PET mechanism. In contrast, the kinetics of thermal-initiated RAFT step-growth displays first order dependence with respect to monomer concentration (Table 1),22 since the radicals are generated by thermal decomposition of an exogenous initiator (such as azo-initiators), resulting in lower reaction order with respect to monomer concentration.5–7,9,10,22 However, as radical generation is dependent on the decomposition of thermal initiators, we previously demonstrated a [I]1/2 dependence of Rp for thermally-initiated RAFT step-growth, where [I] is initiator concentration.22
Table 1 Comparison of rate order and rate constants for different monomer classes and initiation methods of RAFT step-growth polymerization
| Monomer |
Initiation |
Solvent |
[M2]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [CTA2]0 [CTA2]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [I/PC]0 (M)a [I/PC]0 (M)a |
Time (h) |
Reaction order |
Rate constant (k)b,c |
|
AIBN was used as an initiator for thermal initiation at 70 °C, while ZnTPP was used as the photocatalyst for PET-RAFT.
Rate constant (k) units for first order reaction = h−1.
Rate constant (k) units for three half order reaction = M−1/2 h−1.
|
|
Thermal |
TCE |
0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.05 0.05 |
4 |
1 |
2.27 |
| Photoiniferter |
TCE |
0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0 |
48 |
3/2 |
0.27 |
| PET-RAFT |
TCE |
0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.005 0.005 |
48 |
3/2 |
0.13 |
| |

|
Thermal |
Dioxane |
1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.0 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.05 0.05 |
4 |
1 |
0.98 |
| Photoiniferter |
Dioxane |
1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.0 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0 |
24 |
3/2 |
0.20 |
| PET-RAFT |
Dioxane |
1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.0 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.0025 0.0025 |
8 |
3/2 |
0.69 |
| PET-RAFT |
DMF |
1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.0 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.0025 0.0025 |
8 |
3/2 |
1.10 |
| |

|
PET-RAFT |
Dioxane |
1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.0 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.0025 0.0025 |
16 |
3/2 |
0.34 |
| PET-RAFT |
DMF |
1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.0 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.0025 0.0025 |
16 |
3/2 |
0.58 |
Furthermore, under photo-iniferter RAFT step-growth conditions, acrylate monomers exhibited slightly lower kapp values compared to maleimide monomers (kapp = 0.20 M−1/2 h−1 and 0.27 M−1/2 h−1, respectively) (Table 1). Similarly, under thermally initiated RAFT step-growth conditions, acrylate monomers display lower kapp values compared to maleimide monomers (kapp = 0.98 h−1 and 2.27 h−1 for acrylate and maleimide monomers, respectively) (Table 1).22 Conversely, for PET-RAFT step-growth, we found that acrylate monomers exhibit higher kapp values compared to maleimide monomers (kapp = 0.69 M−1/2 h−1 and 0.13 M−1/2 h−1, respectively) (Table 1), subject to a plausible impact from the solvent used (i.e., TCE vs. 1,4-dioxane). Furthermore, in the case of PET-RAFT step-growth polymerization of acrylate monomers, we observed solvent dependency on the rate of the polymerization, where polymerizations conducted in DMF resulted in higher kapp values compared to 1,4-dioxane. This solvent dependency with ZnTPP follows previously reported trends for PET-RAFT chain-growth with ZnTPP.21 Overall, thermally-initiated RAFT step-growth polymerization for both monomer classes demonstrated higher kapp values compared to photo-mediated RAFT step-growth polymerization.
Conclusions
In summary, we successfully modelled the photo-mediated RAFT step-growth polymerization kinetics of maleimide and acrylate monomers with bifunctional RAFT agents with tertiary carboxyalkyl stabilized fragmentations. By analytically solving the governing equations for these polymerizations, we determined that the kinetics follow a three-half order dependence with respect to monomer concentration. This is attributed to the initiation of the polymerization, where the radicals are generated via the direct photocleavage of the RAFT agent in the case of photo-iniferter and photocatalyst assisted cleavage of the RAFT agent in the case of PET mechanism. Furthermore, after modelling photo-iniferter RAFT step-growth for maleimide and acrylate monomers, we found that acrylate monomers exhibit lower kapp values compared to maleimide monomers. On the other hand, in the case of PET-RAFT step-growth, we found that acrylate monomers exhibit higher kapp values compared to maleimide monomers, which we attribute to maleimide monomers interacting with the photocatalyst-trithiocarbonate precomplex. Together with the kinetics data of the thermal-initiated RAFT step-growth polymerization, we summarized the trend and observations based on monomer class, solvent, and initiation methods, offering insightful guidance when choosing appropriate RAFT step-growth polymerizations.
Author contributions
The manuscript was written through contributions of all authors.
Data availability
Data for this article, including all syntheses and characterization data, and mathematical derivations/fittings, are available in the ESI.†
Conflicts of interest
The authors declare the following competing financial interest(s): J. T. and W. Y. are named inventors on a patent application owned by UNC-Chapel Hill (PCT/US2022/042087) which laid the foundation for this work. Dr You is also a co-founder of Delgen Biosciences, a startup company that has licensed this UNC patent application.
Acknowledgements
This work was financially supported by the National Science Foundation (NSF) under Award CHE-2108670. This material is based upon work supported by the National Science Foundation Graduate Research Fellowship Program under Grant No. (NSF DGE-2439854). Bruker AVANCE III Nanobay 400 MHz NMR Spectrometer was supported by NSF under Grant No. CHE-0922858, and Bruker NEO 600 MHz NMR spectrometer was supported by NSF under Grant No. CHE-1828183. Authors thank Dr Marc A. ter Horst from University of North Carolina's Department of Chemistry NMR Core Laboratory for the use of the NMR spectrometers.
References
- S. Perrier, Macromolecules, 2017, 50, 7433–7447 CrossRef CAS.
- J. Chiefari, Y. K. Chong, F. Ercole, J. Krstina, J. Jeffery, T. P. T. Le, R. T. A. Mayadunne, G. F. Meijs, C. L. Moad, G. Moad, E. Rizzardo and S. H. Thang, Macromolecules, 1998, 31, 5559–5562 CrossRef CAS.
- C. L. Moad and G. Moad, Chem. Teach. Int., 2021, 3, 3–17 CrossRef.
- L. Billiet, D. Fournier and F. Du Prez, Polymer, 2009, 50, 3877–3886 CrossRef CAS.
- J. Tanaka, N. E. Archer, M. J. Grant and W. You, J. Am. Chem. Soc., 2021, 143, 15918–15923 CrossRef CAS PubMed.
- P. Boeck, N. Archer, J. Tanaka and W. You, Polym. Chem., 2022, 13, 2589–2594 RSC.
- N. E. Archer, P. T. Boeck, Y. Ajirniar, J. Tanaka and W. You, ACS Macro Lett., 2022, 11, 1079–1084 CrossRef CAS PubMed.
- S. M. Clouthier, J. Tanaka and W. You, Polym. Chem., 2022, 13, 6114–6119 RSC.
- P. T. Boeck, J. Tanaka, W. You, B. S. Sumerlin and A. S. Veige, Polym. Chem., 2023, 14, 2592–2598 RSC.
- J. Tanaka, J. Li, S. M. Clouthier and W. You, Chem. Commun., 2023, 59, 8168–8198 RSC.
- S. M. Clouthier, J. Li, J. Tanaka and W. You, Polym. Chem., 2024, 15, 17–21 RSC.
- N. B. Cramer, T. Davies, A. K. O'Brien and C. N. Bowman, Macromolecules, 2003, 36, 4631–4636 CrossRef CAS.
- N. B. Cramer, S. K. Reddy, A. K. O'Brien and C. N. Bowman, Macromolecules, 2003, 36, 7964–7969 CrossRef CAS.
- S. K. Reddy, N. B. Cramer and C. N. Bowman, Macromolecules, 2006, 39, 3673–3680 CrossRef CAS.
- S. M. Clouthier, J. Li, J. Tanaka and W. You, Macromol. Rapid Commun., 2024, e2400602, DOI:10.1002/marc.202400602.
- T. Otsu and M. Yoshida, Macromol. Rapid Commun., 1982, 3, 127–132 CrossRef CAS.
- T. Otsu and M. Yoshida, Polym. Bull., 1982, 7, 197–203 CAS.
- T. Otsu, M. Yoshida and A. Kuriyama, Polym. Bull., 1982, 7, 45–50 CAS.
- T. Otsu, J. Polym. Sci., 2000, 38, 2121–2136 CrossRef CAS.
- M. Hartlieb, Macromol. Rapid Commun., 2022, 43, e2100514 CrossRef PubMed.
- S. Shanmugam, J. Xu and C. Boyer, J. Am. Chem. Soc., 2015, 137, 9174–9185 CrossRef CAS PubMed.
- S. M. Clouthier, J. Tanaka and W. You, Polym. Chem., 2025, 16, 266–271 RSC.
- J. Li, M. Zhang, J. Zhu and X. Zhu, Polymers, 2019, 11, 1722 CrossRef CAS PubMed.
- L. Zhang, R. Liu, Z. Huang and J. Xu, Polym. Chem., 2021, 12, 581–593 RSC.
- A. Aerts, R. W. Lewis, Y. Zhou, N. Malic, G. Moad and A. Postma, Macromol. Rapid Commun., 2018, 39, e1800240 CrossRef PubMed.
- C. A. Figg, J. D. Hickman, G. M. Scheutz, S. Shanmugam, R. N. Carmean, B. S. Tucker, C. Boyer and B. S. Sumerlin, Macromolecules, 2018, 51, 1370–1376 CrossRef CAS.
- P. Seal, J. Xu, S. Luca, C. Boyer and S. C. Smith, Adv. Theory Simul., 2019, 2, 1900038 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Jiajia
Li
a,
Jiajia
Li
 ab,
Joji
Tanaka
ab,
Joji
Tanaka
 *a and
Wei
You
*a and
Wei
You
 *a
*a
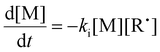

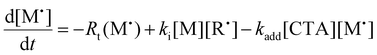
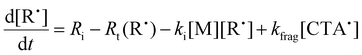
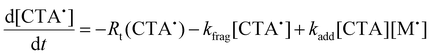






![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [CTA2]0 = 0.5
[CTA2]0 = 0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 M) was plotted with linear regressions applied from 0 to 16.0 hours (Fig. 2A, Table S1, and Fig. S9†).8 Both blue and green light conditions displayed kapp,PI values of 0.27 M−1/2 h−1 with R2 values above 0.98; on the other hand, the red light condition resulted in a much slower rate with a kapp,PI value of 0.03 M−1/2 h−1 and an R2 value of 0.99. The reduced rate for the red light condition is a result of the minimal overlap of the n–π* symmetry forbidden transition of the RAFT agent.8,25 Interestingly, all three light conditions display a plateau in the kinetics at increasing monomer conversion, which may result from competing light absorption by newly formed backbone CTA species and the progressively lower end-group CTA concentration (Fig. 2A, Table S1, and Fig. S9†).
0.5 M) was plotted with linear regressions applied from 0 to 16.0 hours (Fig. 2A, Table S1, and Fig. S9†).8 Both blue and green light conditions displayed kapp,PI values of 0.27 M−1/2 h−1 with R2 values above 0.98; on the other hand, the red light condition resulted in a much slower rate with a kapp,PI value of 0.03 M−1/2 h−1 and an R2 value of 0.99. The reduced rate for the red light condition is a result of the minimal overlap of the n–π* symmetry forbidden transition of the RAFT agent.8,25 Interestingly, all three light conditions display a plateau in the kinetics at increasing monomer conversion, which may result from competing light absorption by newly formed backbone CTA species and the progressively lower end-group CTA concentration (Fig. 2A, Table S1, and Fig. S9†).

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [CTA2]0 = 1.0
[CTA2]0 = 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.0 M) can be plotted and fitted with linear regressions from 0 to 24.0 hours (Fig. 2B, Table S2 and Fig. S10†).15 Both blue and green light conditions displayed kapp,PI values of approximately 0.2 M−1/2 h−1 with R2 values above 0.99. The observed lower kapp value for the polymerization of acrylates compared to maleimide monomers tracks with previous results seen for these monomer classes under thermally initiated RAFT step-growth conditions,22 which can be attributed to slower monomer addition to the R˙ species for acrylates compared to maleimides. Interestingly, unlike monomer M2A, monomer M2B did not display a plateau in the kinetics at high monomer conversion, which we attribute to some degree of homopropagation as was reported previously for this monomer.15
1.0 M) can be plotted and fitted with linear regressions from 0 to 24.0 hours (Fig. 2B, Table S2 and Fig. S10†).15 Both blue and green light conditions displayed kapp,PI values of approximately 0.2 M−1/2 h−1 with R2 values above 0.99. The observed lower kapp value for the polymerization of acrylates compared to maleimide monomers tracks with previous results seen for these monomer classes under thermally initiated RAFT step-growth conditions,22 which can be attributed to slower monomer addition to the R˙ species for acrylates compared to maleimides. Interestingly, unlike monomer M2A, monomer M2B did not display a plateau in the kinetics at high monomer conversion, which we attribute to some degree of homopropagation as was reported previously for this monomer.15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [CTA2]0
[CTA2]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [ZnTPP]0 = 0.5
[ZnTPP]0 = 0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5
0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.005 M) can be plotted with linear regressions applied from 0 to 48.0 hours (Fig. 3A, Table S3 and Fig. S11†).8 All three light conditions displayed kapp,PET values of approximately 0.1 M−1/2 h−1 with R2 values of 0.99. Interestingly, PET-RAFT step-growth of maleimides results in reduced polymerization rate compared to photo-iniferter RAFT step-growth, which contrasts the observed kinetics for chain-growth, where PET-RAFT is faster than RAFT-iniferter.26 In literature, computational data has shown that ZnTPP forms a precomplex with trithiocarbonate RAFT agents for the electron transfer process.27 Thus, we reason that maleimide monomers may interfere with or disrupt this precomplex, thereby reducing the polymerization rate.
0.005 M) can be plotted with linear regressions applied from 0 to 48.0 hours (Fig. 3A, Table S3 and Fig. S11†).8 All three light conditions displayed kapp,PET values of approximately 0.1 M−1/2 h−1 with R2 values of 0.99. Interestingly, PET-RAFT step-growth of maleimides results in reduced polymerization rate compared to photo-iniferter RAFT step-growth, which contrasts the observed kinetics for chain-growth, where PET-RAFT is faster than RAFT-iniferter.26 In literature, computational data has shown that ZnTPP forms a precomplex with trithiocarbonate RAFT agents for the electron transfer process.27 Thus, we reason that maleimide monomers may interfere with or disrupt this precomplex, thereby reducing the polymerization rate.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [CTA2]0
[CTA2]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [ZnTPP]0 = 1.0
[ZnTPP]0 = 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.0
1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.0025 M) was fitted with a linear regression applied from 0 to 8.0 hours, giving a kapp,PET value of 0.69 M−1/2 h−1 and R2 value of 0.99 (Fig. 3B and Table S4†). Opposite to the case with maleimides, PET-RAFT step-growth with acrylates results in a faster polymerization rate compared to RAFT-iniferter step-growth. Furthermore, polymerization data for polyethylene glycol diacrylate (M2C) with CTA2 and ZnTPP in 1,4-dioxane under red light was also fitted, and a linear regression was applied from 0 to 16.0 hours, resulting in a kapp,PET value of 0.34 M−1/2 h−1 and R2 value of 0.99 (Fig. 3C).
0.0025 M) was fitted with a linear regression applied from 0 to 8.0 hours, giving a kapp,PET value of 0.69 M−1/2 h−1 and R2 value of 0.99 (Fig. 3B and Table S4†). Opposite to the case with maleimides, PET-RAFT step-growth with acrylates results in a faster polymerization rate compared to RAFT-iniferter step-growth. Furthermore, polymerization data for polyethylene glycol diacrylate (M2C) with CTA2 and ZnTPP in 1,4-dioxane under red light was also fitted, and a linear regression was applied from 0 to 16.0 hours, resulting in a kapp,PET value of 0.34 M−1/2 h−1 and R2 value of 0.99 (Fig. 3C).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [CTA2]0
[CTA2]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [I/PC]0 (M)a
[I/PC]0 (M)a
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5
0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.05
0.05![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5
0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0
0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5
0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.005
0.005
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.0
1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.05
0.05![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.0
1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0
0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.0
1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.0025
0.0025![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.0
1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.0025
0.0025
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.0
1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.0025
0.0025![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.0
1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.0025
0.0025

