Insights into the structural features of crumpling graphene nanoribbons

Abstract

The exploration of graphene nanoribbons (GNRs) offers promising prospects by leveraging their unique physical properties and expanding their versatile applications. Here, we investigate the crumpling behavior of GNRs via coarse-grained molecular dynamics (CG-MD) simulations. By systematically varying the size and geometry (i.e., width and the aspect ratio), we systematically examine the potential energy, configuration, mechanical state, and internal structure of crumpled GNRs in detail. Our findings indicate that as the size of GNRs increases, the self-adhering and self-folding behaviors during the crumpling process become more pronounced. Crumpled GNRs with large sizes exhibit greater adhesion energy but lower out-of-plane strain energy due to the formation of more planar regions and fewer sharp crumples compared to smaller GNRs. By evaluating the relative shape anisotropy and representative configuration during crumpling, we identify two aspect ratio-dependent crumpling modes for GNRs, namely the edge-bending-dominated (EBD) and sliding- and folding-dominated (SFD) crumpling modes, respectively. Notably, the width-dependent critical aspect ratio controlling the transition between these modes provides valuable insights into understanding and predicting the crumpling behavior of GNRs with varying geometries. Moreover, our assessment of curvature and stress distributions and the cross-sectional patterns of crumpled GNRs further reveals a reduction of mechanical heterogeneity with increased sheet size. Our study highlights the critical role of geometry in the crumpling behavior of GNRs, which has significant implications for the tailored design of crumpled ribbon-like sheet materials.

---

1. Introduction

Quasi-one-dimensional (Q1D) nanomaterials have recently garnered considerable attention due to their intriguing physical properties for extensive applications.^1,2 As a notable example, atomically thin graphene nanoribbons (GNRs) exhibit anisotropic mechanical properties,³ boundary-dependent electronic properties,⁴ ultra-high thermal conductivity,⁵ light absorption capabilities,⁶ and promising applications in composites,⁷ optical materials,⁸ sensors,⁹ catalysts,¹⁰etc. Over recent decades, GNRs have been realized from theoretical modeling^11,12 to large-scale preparation.^13–16 Specifically, GNRs are strips of graphene less than 100 nm in width, featuring a honeycomb structure composed of carbon atoms with sp²-orbitals.¹⁷ This nanostructure endows GNRs with more flexible and tunable physical properties compared to graphene, e.g., width-dependent band gaps and all-semiconducting characteristics,¹⁸ due to quantum confinement and edge effects.^19,20 GNRs with varying shapes and sizes can be fabricated using multiple approaches, including electron-beam lithography,²¹ chemical vapor deposition,²² sonochemical exfoliation,¹⁸ gas-phase etching,²³ squashing carbon nanotubes,²⁴ epitaxial synthesis on semiconductor substrates,²⁵etc. Despite promising aspects of GNRs in various practical applications, inevitably, flaky and ribbon-like graphene with low out-of-plane bending stiffness often exhibits significant ripples, wrinkles, and crumples in reality due to its thermal fluctuations,²⁶ structural defects,²⁷ polycrystalline nature,²⁸ and edge effects.²⁹ Such conformational versatility affects the physical performance of graphene in different shapes, such as mechanical performance³⁰ and carrier mobility,³¹ making the exploration of rippled, wrinkled, and crumpled graphene a focus of research in recent years.

Considerable efforts have been made toward understanding the structural behavior, mechanical properties, and applications of crumpled graphene sheets.^32,33 Typically, factors such as size,³⁴ defect type,^35–37 functional groups,^38,39 stickiness,⁴⁰ and processing conditions (e.g., temperature and crumpling rate)⁴¹ influence the crumpling pattern of graphene sheets by affecting their self-folding behavior during the crumpling process. The resulting crumpled sheets with varying internal structures have remarkably different mechanical properties. For instance, sticky crumpled sheets possess a larger effective compressive modulus than the non-sticky ones,⁴² and crumpled graphene with grain boundaries and reconstructed vacancy defects exhibits a larger bulk modulus than pristine ones,^35,36 making them promising additives for functional nanocomposites.⁴³ Moreover, crumpled graphene boasts considerable packing efficiency, solvent accessible surface area, aggregation resistance, and self-dispersion, which are advantageous for supercapacitor and tribological applications.^44–47

Previous studies on crumpled materials primarily focused on graphene sheets with a relatively low aspect ratio close to ∼1. Given the larger aspect ratio of GNRs, their crumpling behavior is expected to vary with sheet sizes and geometries. The successful preparation of straight GNRs with smooth edges, fewer defects, and large aspect ratios (∼387) on liquid metal substrates has laid the foundation for the fundamental study of GNRs.⁴⁸ Notably, GNRs detached from the substrate and suspended in a solvent tend to develop significant wrinkles and curls due to thermal fluctuations. Studies have shown that the size, aspect ratio, and surface modifications control the three main conformations of graphene sheets in equilibrium, i.e., planar membrane-like, ribbon-like, and scroll-like conformations.⁴⁹ Despite the progress made, the crumpling behavior of graphene sheets with different aspect ratios under hydrostatic pressure has not been well understood.

To unravel the relationship between sheet geometry (e.g., width and the aspect ratio) and crumpling modes, in this study, we perform a series of coarse-grained (CG) molecular dynamics (MD) simulations to provide insights into the size-dependent crumpling patterns of GNRs. Specifically, we study the evolution of the total potential energy and its contribution to GNRs with different geometries during the crumpling process and in various crumpled states, which emphasizes the effect of geometry on the self-adhering and self-folding effects of crumpled GNRs. Moreover, we analyze the relative shape anisotropy of GNRs to gain insight into the effect of sheet geometry on their structural changes upon crumpling. Remarkably, we identify two distinct geometry-dependent crumpling modes of GNRs, i.e., edge-bending-dominated (EBD) and sliding-and folding-dominated (SFD) crumpling modes, along with the critical aspect ratio for the transition between them as a function of width. Finally, our exploration of the local curvature, stresses, and cross-section patterns of the crumpled GNRs further reveals the geometry-dependent mechanical states. Our research emphasizes the pivotal role of sheet geometry in shaping the crumpling mechanism of GNRs. This newfound understanding paves the way for the meticulous design of intricately crumpled ribbon-like materials.

2. Methods

2.1. Overview of the coarse-grained modeling

CG-MD modeling, which not only overcomes the spatiotemporal limitations of all-atom (AA) MD simulations and greatly improves computational efficiency, but also preserves the essential characteristics of molecules, has been increasingly applied in recent years to study various complex systems at extended length and time scales.^50–52 Here, GNRs are represented by a CG model with the hexagonal lattice derived based on the AA model, where each CG bead represents four carbon atoms, with a mass of 48 g mol⁻¹ (Fig. 1(a)). The CG force field developed based on the strain energy conservation approach includes interactions from bonds V_b, angles V_a, dihedrals V_d, and pairwise non-bonded interaction V_nb.^53,54 The CG force field parameters were calibrated employing the mechanical properties of graphene (e.g., in-plane Young's and shear moduli, bending rigidity per unit width, and adhesion energy per surface area) obtained from experiments and density functional theory. The functional forms and parameters of the CG force field are listed in Table S1 in the ESI.† This CG model not only effectively captures the mechanical behavior of graphene, such as large deformation, fracture, interlayer anisotropic shear response, and nonlinear elastic deformation, but also significantly improves the computational speed and access to greater spatiotemporal scales compared with AA simulations^53,55 and has been applied to MD simulation studies of structures such as nanostructured or architected sheet assembly systems,^56,57 multilayer graphene assemblies,^58,59 graphene-reinforced polymers,^43,60etc. Refer to our previous study for details on the building of the CG model.⁵³

Fig. 1 CG model of the GNRs considered and the setup of the crumpling simulation. (a) CG model of a GNR with width W and length L (L > W). The zoom-in shows the 4-to-1 mapping scheme of the CG model, where one CG bead (brick red bead) represents four connected carbon atoms (the gray atoms highlighted in the green region). (b) Lengths and widths corresponding to all GNR models considered in this work. The color bar indicates the aspect ratio a (a = L/W)) of the model. Models with the same a can be fitted by a dashed line with a matching color to a, e.g., a = 1, a = 10, and a = 60. (c) Conformational evolution of the GNR during the crumpling process. R_g0, R_g, and R_g1 represent the radii of gyration of GNRs in the initial wrinkled (IW) state, during the crumpling process, and in the final crumpled (FC) state, respectively. R_c denotes the radius of the confining sphere. ρ_g is the compaction ratio (0 ≤ ρ_g ≤ 1), and a smaller value implies a greater degree of compaction of the model.

The geometry of a graphene nanoribbon (GNR) is defined by its width W and aspect ratio a, as shown in Fig. 1(a). It should be noted that a = L/W and L is the length of the GNR (L > W); moreover, as the edge shapes of graphene sheets along the length direction (x-direction), i.e., armchair, zigzag, and chiral, have very minor influences on their structural and mechanical properties,⁶¹ we only focus on GNRs with zigzag edges along the length direction in this work. We study GNRs with W and a ranging from 10 nm to 35 nm and 1 to 60 (Fig. 1(b)), respectively, avoiding the GNRs from forming a scroll-like structure at the initial equilibrium state.⁴⁹ Taking advantage of our CG model, we are able to test the GNR having a wide range of length up to ∼1 μm.

2.2. Coarse-grained molecular dynamics simulation details

All CG-MD simulations in this study were conducted using large-scale atomic/molecular massively parallel simulator (LAMMPS) software,⁶² and the visualization of the CG-MD simulations was realized using visual molecular dynamics (VMD).⁶³ In our CG-MD simulation, the flat GNR model without any wrinkles was initially laid in the xy plane (Fig. 1(a)) and was located at the center of the simulation box (1200 nm × 1200 nm × 1200 nm). The simulations were performed using periodic boundary conditions (PBCs) in all directions with a time step of 6 fs and a temperature of 300 K, which are consistent with our prior studies.^36,40 Once the initial system was set up, the energy of the system was minimized according to an iterative conjugate gradient algorithm.⁶⁴ Then, equilibrium simulation with a time duration of 2 ns was carried out using the NVT ensemble until the total potential energy of the system became independent of time. Following this, as shown in Fig. 1(c), we employed a pseudo “confining spherical volume” to compact the GNR from the initial wrinkled (IW) state (i.e., state after equilibrium simulation) to the final crumpled (FC) state. This crumpling process is inspired by the mechanical compaction observed in aerosol evaporation experiments. While graphene in such experiments typically stays on the surface of a shrinking droplet,^46,65–68 in our model, the GNR adheres to the inner surface of a spherical boundary. This analogy captures a key physical feature: the droplet acts as a curved substrate and evaporation-induced surface tension generates a quasi-spherical inward driving force. Despite this idealization, our simulation approach facilitates a systematic exploration of geometry-dependent crumpling mechanisms, in line with previous computational studies.^34,36 Specifically, the boundary of the confining sphere, which completely encompasses the GNR model, exerts a repulsive force F perpendicular to the surface of the confining sphere at a certain cutoff distance, which can be written as:where r_i, R_c, and K_c denote the distance between the i^th bead and the center of the confining sphere, the radius of the confining sphere, and the spring force constant (K_c = 2.31 × 10⁵ kcal (mol nm³)⁻¹), respectively. The GNR model is progressively compacted into a crumpled state as the radius of the confining sphere decreases at a rate of 50 m s⁻¹. The spring force constant and compaction rate are adopted from previous studies on crumpling of graphene via spherical confinement⁴⁴ and provide a balance between effective compression and numerical stability, despite the fact that neither of them corresponds directly to an experimental value (e.g., capillary force or evaporation rate).⁶⁸ Moreover, according to previous tests, we found that the compaction rate of 50 m s⁻¹ can improve the computational speed of the simulation while capturing the basic crumpling behavior of the sheet at low velocities. Note that the density of the crumpled GNR in the FC state is equal to the bulk density of graphite (i.e., 2.267 g cm⁻³), and no further compaction was performed to avoid amorphous collapse or damage of the model, which is consistent with the modeling protocol in our recent studies.^34,36,37,40 We emphasize that the compaction here does not aim to replicate the exact pressure conditions in aerosol evaporation but rather to achieve a representative crumpled structure for analyzing geometry-dependent behaviors. Refer to our previous studies for more details on the crumpling simulation of the nanosheets.^34,36 Moreover, we have provided additional analyses in the ESI,† including the effects of temperature, post-crumpling relaxation at different relaxation rates, and relaxation timescales in the quasi-equilibrium state. We also discuss the comparison between CG-MD and AA-MD simulations, where the AA-MD simulations use the adaptive interatomic reactive empirical bond-order (AIREBO) potential.^69,70 Additionally, we examine the influence of GNR edge type on crumpling behavior. These results are presented in Fig. S1–S5 in the ESI.†

2.3. Property calculations

We calculated the radius of the gyration tensor R_g² of the GNR model at each time step to obtain the compaction ratio ρ_g and the relative shape anisotropy κ² of the system upon crumpling. Briefly, R_g² can be expressed as:and the radius of gyration R_g can be obtained as follows:where Λ_k (k = 1, 2, 3) are the principal eigenvalues of R_g² and Λ₁ ≤ Λ₂ ≤ Λ₃.

The compaction ratio ρ_g in our work is given as:

where R_g,IW and R_g,FC are the radii of gyration of the model in the IW and FC states, respectively. As the crumpling simulation proceeds, ρ_g of the system decreases from 1 to 0, i.e., a smaller value of ρ_g indicates a more compacted GNR.

Moreover, the relative shape anisotropy κ² can be obtained using the following formula:

Note that 0 ≤ κ² ≤ 1, and κ² = 0, κ² = 0.25, and κ² = 1 represent the ideal spherical structure, the ideal symmetrical flat sheet, and the ideal straight rod, respectively.

Additionally, the von Mises stress σ_v can be calculated as:

where σ_ij (i, j = 1, 2, 3) are the components of the stress tensor. The von Mises stress is commonly used as a yielding criterion rather than a real stress and is normalized with respect to the volume of the system in this paper. Besides, the effective stress σ_e can be calculated as:where σ_v,i is the von Mises stress of the i^th bead with the local curvature satisfying K ≥ 0.1 Å⁻¹; N is the total number of beads with K ≥ 0.1 Å⁻¹ in the crumpled model. The threshold K ≥ 0.1 Å⁻¹ is selected to isolate highly crumpled regions that dominate internal stress accumulation while minimizing contributions from nearly flat areas that are mechanically inactive. This curvature-based filtering approach is consistent with prior observations that link the high local curvature to the stress concentration in crumpled 2D materials.⁷¹

3. Results and discussion

3.1. Potential energy evolution upon crumpling

We first explore the total potential energy change during the crumpling process for GNRs with different widths W and aspect ratios a, aiming to better understand the influence of geometry on the crumpling behavior of GNRs at the molecular level. ΔPE_total considered in Fig. 2 is the total potential energy increment per unit area of the GNR, defined as ΔPE_total = (PE − PE_initial)/A, where A is the surface area of the flat GNR, and PE and PE_initial are the total potential energy of the system during the crumpling process and in the IW state, respectively. Moreover, we introduce the compaction ratio ρ_g to describe the degree of crumpling of GNRs. Note that ρ_g decreases from a value of 1 in the IW state to 0 in the FC state during the crumpling process, and thus a smaller ρ_g corresponds to a more compacted crumpled system.

Fig. 2 Total potential energy increment of crumpled GNRs in different states. (a) Evolution of change of the total potential energy increment per unit area ΔPE_total with the compaction ratio ρ_g for GNRs (W = 35 nm) having different aspect ratios ranging from 1 to 25. The orange and black arrows exemplify the quasi-equilibrium state (QE state) and the FC state of the GNR during the crumpling process, respectively. The shaded areas correspond to the standard deviation from three independent crumpling simulations for each specific case. ΔPE_total of the crumpled GNRs in the (b) QE state and (c) the FC state as a function of width W and aspect ratio a, respectively. The black line indicates the standard deviation.

Fig. 2(a) shows the evolution of ΔPE_total for GNRs (W = 35 nm) with different a values during the crumpling process. It can be found that the GNRs of different a values all have relatively steady ΔPE_total at the beginning of the crumpling, as none of the GNRs have formed the sharp fundamental crumples (e.g., folds, bends, developable cones, and stretching ridges) at the early stage.^34,36,72 In the intermediate stage of crumpling, the ΔPE_total values of GNRs with large a values (e.g., a = 10 and a = 25) decrease significantly to reach a valley, and this process is mainly influenced by the self-adhering and self-folding behaviors of the system.^40,73 Subsequently, the ΔPE_total values of all GNRs increase dramatically at the later stage of crumpling, which can be explained by the fact that the sheet is further compacted, causing the potential energy of the system to increase sharply.³⁴ In addition to the final crumpled (FC) state, we define the quasi-equilibrium state (QE state) of the crumpled GNR as the state of the system when the ΔPE_total value reaches a local minimum trough, at which the self-adhering and self-folding behaviors of the GNR basically saturate.⁴⁴ As observed in Fig. 2(a), the ρ_g of GNRs at the QE state decreases with increasing a.

Moreover, we analyze the effect of W and a on the ΔPE_total of crumpled GNRs in the QE state (Fig. 2(b)) and the FC state (Fig. 2(c)). Clearly, ΔPE_total in both states decreases with increasing W and a. This is attributed to the significant self-adhering and self-folding behaviors of GNRs with large sizes that fold more easily upon crumpling compared to small sizes, resulting in a low total potential energy of the system.^34,74 This trend is further supported by the localization factor calculated for the GNRs in the QE state, which increases with both W and a, indicating the formation of more extensive and localized interfacial contact in larger GNRs (Fig. S6 in the ESI†). Meanwhile, Fig. 2(c) reveals that the GNRs with a large width and large aspect ratio are easier to be compacted and crumpled into a spherical shape as less energy is required.

To gain further insights, we analyze the contribution of bond, angle, dihedral, and pairwise non-bonded potential energies characterizing the in-plane deformation, out-of-plane deformation, and adhesion properties of the model, respectively, to the total potential energy increment of crumpled GNRs. In our CG model, in-plane deformation is primarily governed by bond and angle energies, while out-of-plane deformation is captured by the dihedral energy contribution.⁵³ Taking the crumpled GNRs with W = 35 nm as a representative case, as shown in Fig. 3(a), increasing a has no marked influence on the bond and angle potential energies of the system in the QE state; however, the dihedral and non-bonded potential energies decrease slightly and increase significantly with increasing a, respectively; these trends are more pronounced when a becomes smaller. In addition, the crumpled GNRs with larger W have relatively smaller dihedral potential energy ΔPE_d (Fig. 3(b)) and larger non-bonded potential energy ΔPE_nb (Fig. 3(c)) in comparison with those with small W. According to the representative configurations of GNRs in the QE state, as shown in Fig. 3(d) and (e), it can be observed that, first, GNRs with larger a tend to develop scroll-like lamellar structures in the QE state and therefore have relatively large adhesion energy, while GNRs with smaller a tend to form comparatively sharper crumples (e.g., developable cones) and thus have large out-of-plane deformation potential energy. Second, GNRs with larger W form more planar regions and fewer crumpled regions than those with smaller W, resulting in larger ΔPE_nb and smaller ΔPE_d. The analysis of the configuration of crumpled GNRs in the QE state corroborates the previously reported configuration evolution of GNRs in the lowest energy state, i.e., GNRs transform from a bent-folded configuration to a rolled structure as the length increases.⁷⁵

Fig. 3 Contribution of the total potential energy increment for the crumpled GNRs and two crumpling regimes of GNRs from the QE state to the FC state. (a) Contribution of the total potential energy increment ΔPE as a function of the aspect ratio a for GNRs with W = 35 nm in the QE state. Here, the contributions of the bond, angle, dihedral, and pairwise non-bonded interactions to the total potential energy increment were analyzed. The non-bonded potential energy is taken in absolute value. Relationship between (b) the dihedral potential energy increment ΔPE_d and (c) the pairwise non-bonded potential energy increment ΔPE_nb with respect to a for crumpled GNRs with different widths in the QE state. Representative configurations of crumpled GNRs with (d) W = 10 nm and (e) W = 35 nm and different a values in the QE state. The gray line represents the scale bar. (f) ΔPE as a function of a for GNRs with W = 35 nm in the FC state. Relationship between (g) ΔPE_d and (h) ΔPE_nb with respect to a for crumpled GNRs with different widths in the FC state. The black dashed and solid lines indicate the power function fittings. (i) Illustration of two distinct regimes of crumpled GNRs from the QE state to the FC state. In regime I, the diameter d_fc of the crumpled GNR in the FC state is smaller than the width W of the GNR, while in regime II, d_fc is larger than W. As examples, the blue, cyan, and green colors emphasize the configuration of the strip lattices along the width direction of GNRs in the QE and FC states, respectively. (j) The d_fc/W ratio of GNRs of different W values as a function of a.

Fig. 3(f)–(h) show the total potential energy increment contribution of GNRs in the FC state, where the GNRs form highly crumpled spherical structures. It can be found that all the potential energies are negatively correlated with a except for the non-bonded potential energy of the system which is positively correlated with a, and the increase of W leads to smaller ΔPE_d and larger ΔPE_nb. Similar to the QE state, increasing the a and W values of GNRs enables the system in the FC state to have more laminated structures while causing a relative decrease in the sharp crumples formed per unit area, resulting in an increase and decrease in the adhesion energy and out-of-plane strain energy of the system, respectively. Interestingly, for the adhesion energy (ΔPE_nb) of the system in the QE and FC states (Fig. 3(c) and (h)), it has different rates of change for small and large a values, which is relevant to the internal laminar structure of crumpled GNRs. In particular, the adhesion energy reaches a saturation state when a is large enough in the QE state (Fig. 3(c)). Furthermore, it is meaningful to introduce two different crumpling regimes of scroll-like crumpled GNRs in the late crumpling process (from the QE state to the FC state) defined based on the sheet width and the diameter of the system in the FC state (d_fc). As shown in Fig. 3(i), further compaction makes the lattice along the width direction of the system (as examples, the strip lattices emphasized by blue, cyan, and green colors) undergo significant fold deformation as d_fc < W (i.e., regime I), while only slight bending of the lattice along the width direction appears when d_fc > W (i.e., regime II). Note that the d_fc/W ratio as a function of a for all the GNR models studied in this study is presented in Fig. 3(j). One can note that in different regimes, the lattices of the crumpled GNRs have different levels of folding, which affects the out-of-plane deformation energy of the whole system, resulting in different decrease rates of ΔPE_d as a function of a of the system in the FC state (see the different fitted lines in Fig. 3(g)). In general, the geometry of graphene nanoribbons controls the potential energy of the system by influencing its internal structures, e.g., sharp crumples and scroll-like laminated structures. The above analysis helps us to gain a deeper understanding of the contribution of various potential energies in the crumpled GNRs.

3.2. Shape descriptor of crumpled structures

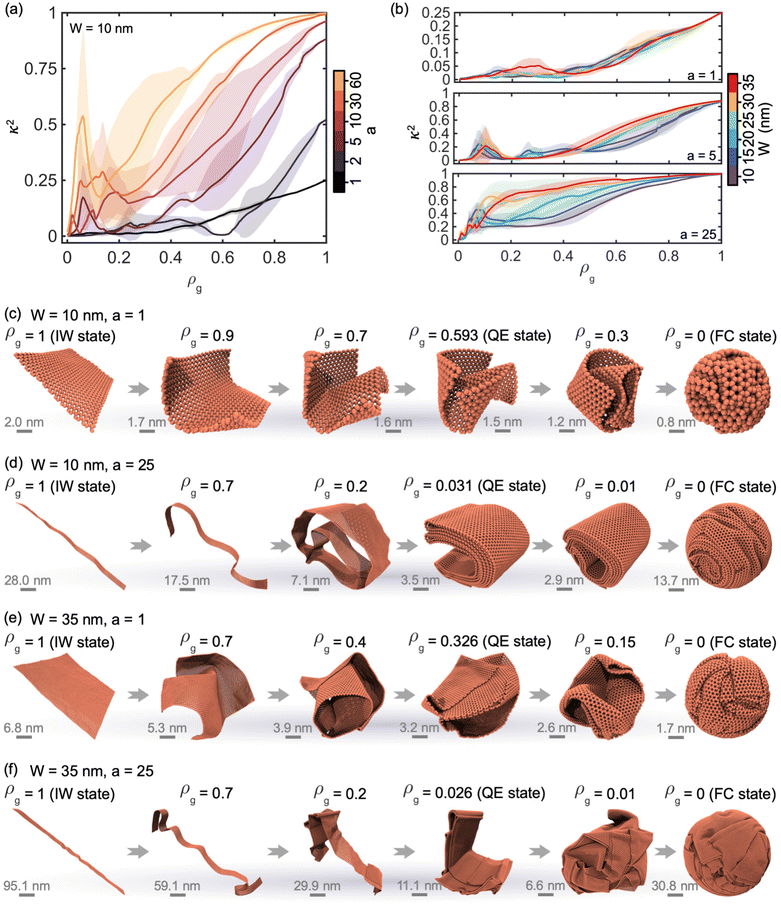
Evaluating the shape descriptor, i.e., relative shape anisotropy κ², of GNRs during the crumpling process helps us to better characterize the effect of geometry on the structural features of the system. κ² is commonly adopted to describe characteristics such as symmetry and dimensionality of the structure and ranges from 0 to 1.^56,76,77 In particular, κ² is equal to 1, 0.25, and 0 for ideal straight rods, ideal symmetrical flat sheets, and ideal spherical structures, respectively. Fig. 4(a) and (b) exhibit the evolution of κ² with decreasing compaction ratio ρ_g for crumpled GNRs with different widths W and aspect ratios a, and Fig. 4(c)–(f) show the representative configurations of the models during the crumpling process. As shown in Fig. 4(a), increasing a raises the κ² value of GNRs (W = 10 nm) at ρ_g = 1 (IW state), suggesting that, in comparison with a square sheet (a = 1), the larger the a, the more the system tends to the ideal rod shape at this state (Fig. 4(c) and (d)). Moreover, κ² of all cases shows a decreasing trend as the crumpling proceeds, and the larger the a, the smaller the ρ_g of the system compacted into a planar-like structure (κ² ≈ 0.25). The continuous compaction causes the crumpled GNRs to show a tendency to shift toward a rod-like configuration, which is known from the rebounded κ² when 0.07 ≲ ρ_g ≲ 0.2, and the system with larger a has a larger increase in κ². This is mainly due to the adhesion energy that makes systems with large a more prone to exhibit self-adhering and self-folding behaviors, forming scroll-like laminar structures and making their κ² rebound (Fig. 4(d)). Further compaction leads all systems to a sphere-like crumpled structure (κ² ≈ 0). κ² of GNRs with large a is overall larger than that of GNRs with small a during the crumpling process.

Fig. 4 Shape descriptor and representative configurations of GNRs during the crumpling process. Relative shape anisotropy κ² as a function of the compaction ratio ρ_g for GNRs with (a) W = 10 nm having different aspect ratios a and (b) a = 1, 5, and 25, respectively, having different W values. The shaded areas of the curves correspond to the standard deviation. Representative configurations of crumpled GNRs for different compaction ratios ranging from 0 to 1 with (c) W = 10 nm and a = 1, (d) W = 10 nm and a = 25, (e) W = 35 nm and a = 1, and (f) W = 35 nm and a = 25. The gray arrow indicates the process of crumpling from the IW state to the QE state and then to the FC state. The gray line represents the scale bar for the configuration size.

Meanwhile, the analysis of the effect of width on κ² evolution reveals that the increase in W for square graphene nanosheets (a = 1) makes the κ² of the system rebound significantly at the late stage of crumpling, as shown in Fig. 4(b). This can be attributed to the fact that graphene sheets with large W form relatively more planar regions (e.g., the QE state in Fig. 4(c) and (e)) under the effect of adhesion energy, which affects κ². However, for GNRs with larger a, especially when a = 25, as shown in Fig. 4(b), the increase in width allows the system to have a highly rod-like conformation during the crumpling process, and a laminated structure is developed at the late stage of crumpling (Fig. 4(f)). Overall, GNRs with small W and a tend to form bent structures that occupy 3D space upon crumpling, and their κ² curves have no apparent rebound.³⁴ In contrast, GNRs with large W and a commonly exhibit remarkable self-adhering and self-folding behaviors,⁴⁰ making their crumpled configurations tend to be laminated rod-like with relatively large κ².

The analysis of the crumpling process of GNRs with different geometries reveals two distinct crumpling modes. In general, GNRs with small aspect ratios are first bent up out-of-plane on all four edges upon crumpling, and then the developed crumpled structures occupying 3D space are further compacted into crumpled spheres (Fig. 4(c) and (e)). Based on this observation, we classify the crumpling mode of GNRs with a small aspect ratio as the edge bending-dominated (EBD) crumpling mode. Moreover, as the aspect ratio is sufficiently large, GNRs tend to bend and wrinkle along the length direction under the action of the confining sphere, followed by local sliding and self-folding due to adhesion and forming scroll-like laminated structures, and finally the GNRs are compacted into spherical crumpled structures (Fig. 4(d) and (f)). This crumpling mode of GNRs with large aspect ratios is classified as the sliding- and folding-dominated (SFD) crumpling mode. We can trace the mechanical mechanisms of the above two crumpling modes from the previous studies.⁷⁸ Specifically, for the EBD crumpling mode (corresponding to GNRs with small aspect ratios), the strain in the corner region of GNRs is larger than that in the middle region, and the corners buckle first under compression, followed by buckling in the middle regions. For the SFD crumpling mode (corresponding to GNRs with large aspect ratios), the distance from the corners to the middle of the edges in the width direction is shorter, and their buckling is synchronized so that buckling along the length direction is developed under compression to form a rolled structure. Understanding these two crumpling modes will provide deeper insights into the crumpling behavior and structural features of GNRs. Therefore, it is essential to study the transition between these two crumpling modes.

3.3. Transition of crumpling modes

To determine the transition between the EBD crumpling mode and the SFD crumpling mode, we introduce a parameter d̄_W/W that characterizes these two crumpling modes. Here, d̄_W is the average distance between the upper and lower edges of the crumpled GNRs, and d̄_W ≈ W for the system in the IW state. In the EBD crumpling mode, the four edges of crumpled GNRs bend upward in the QE state, resulting in d̄_W/W < 1. Conversely, the crumpled GNRs in the SFD crumpling mode have d̄_W/W ≈ 1 in the QE state, which is attributed to the fact that the system forms a scroll-like laminated structure in the QE state without significant deformation along the width direction. As shown in Fig. 5(a), the crumpled systems (QE state) with the EBD crumpling mode and the SFD crumpling mode satisfy d_W < W and d_W ≈ W, respectively, where d_W is the distance between the two ends of the highlighted strip lattices. The analysis of the effect of a on d̄_W/W in Fig. 5(b) reveals that d̄_W/W increases first with increasing a and then reaches a constant value of 1, following an exponential evolution relationship with a. Here, we define that the system experiences the EBD crumpling mode when d̄_W/W < 0.9 and the SFD crumpling mode when d̄_W/W ≥ 0.9. Thus, we can obtain the critical aspect ratio a_c for the transition from the EBD crumpling mode to the SFD crumpling mode, and a_c increases with increasing W (Fig. 5(b)).

Fig. 5 Two distinct crumpling modes of GNRs. (a) Illustration of two crumpling modes, i.e., the edge bending-dominated (EBD) crumpling mode and the sliding- and folding-dominated (SFD) crumpling mode. As examples, the blue, cyan, and green colors emphasize the configuration of the strip lattices of GNRs along the width direction. These highlighted strip lattices have endpoint spacings (i.e., the distance between the upper and lower edges) of W and d_W in the IW and QE states, respectively. (b) The average distance between the upper and lower edges (normalized by W) as a function of aspect ratio a of the crumpled GNRs with W = 10 nm and W = 35 nm, respectively, in the QE state. The blue dotted lines denote the critical aspect ratio a_c. (c) Change in the critical aspect ratio a_c as a function of sheet width W. The black dashed lines in (b) and (c) indicate the exponential fitting.

Remarkably, the evolution of the critical aspect ratio with respect to the sheet width is obtained in this work, as shown in Fig. 5(c). The relationship between a_c and W can be described by the exponential function:

a_c = b₁e^b₂W + d₁e^d₂W (8)

where b₁ = 1.431 ± 6.969, b₂ = −0.0818 ± 1.170, d₁ = 1.131 ± 4.473, and d₂ = 0.0415 ± 0.097 are adjustable constant coefficients from the fitting (R² = 0.9903). Notably, GNRs exhibit the EBD crumpling mode when a < a_c, while they show the SFD crumpling mode when a > a_c. It is significant to explore the crumpling modes of GNRs since different modes inevitably lead to different internal crumpled patterns. The above analyses allow us to have more in-depth simulation-based insights for predicting the crumpled structure of GNRs.

3.4. Mechanical heterogeneity

To facilitate a better understanding of the internal structure of crumpled GNRs and provide insights into their mechanical states, we proceed to analyze the local curvature K, local von Mises stress σ_v, effective stress σ_e, and cross-section patterns of crumpled GNRs in the FC state. Fig. 6(a)–(c) show the distributions of K and σ_v as well as their probability profiles of crumpled GNRs with W = 10 nm and different aspect ratios a. Here, K and σ_v are mapped to a 2D planar model for better visualization. It can be observed that the high curvature regions correspond to the high stress regions for all cases (Fig. 6(a)); the peaks of the probability distributions of K and σ_v (skewed Gaussian distributions) tend to increase and shift to smaller K and σ_v as a increases, and their distributions become concentrated and narrower, which implies that the degree of mechanical heterogeneity of crumpled GNRs decreases with the increase of a (Fig. 6(b) and (c)). These curvature distribution profiles also serve as the basis for a principal component analysis (PCA) to quantitatively classify the crumpled morphologies (Fig. S7 in the ESI†). Moreover, the heterogeneous stress distributions observed in Fig. 6(a) are mainly attributed to the fundamental building blocks that constitute the crumpled system,^36,42 such as bends, developable cones, and stretching ridges, as shown in Fig. 6(d). Briefly, the fundamental structures constituting the crumpled GNRs are mostly developable cones and stretching ridges when a is small (see a = 1 and 5 in Fig. 6(a)); for larger a, such as a = 25, the internal structures are mostly bends as GNRs form scroll-like laminated structures through the SFD crumpling mode (Fig. 6(a) and 5(c)). That is, the sharp crumples increase the stress heterogeneity of the system. Fig. 6(e) shows the distribution of K versus σ_v for the crumpled GNRs (W = 10 nm) with different aspect ratios. It can be verified that the overall K and σ_v are smaller for the crumpled system with larger a; K and σ_v maintain a certain correlation, i.e., small K corresponds to small σ_v and large K corresponds to large σ_v.

Fig. 6 Mechanical state of crumpled GNRs in the FC state. (a) Maps of the local curvature K and local von Mises stress σ_v distributions for crumpled GNRs (W = 10 nm) with aspect ratios a = 1, 5, and 25, respectively. Probability distribution of (b) K and (c) σ_v for crumpled GNRs having various a values. (d) Representative configurations of the three fundamental building blocks found in crumpled GNRs (W = 10 nm), i.e., bend, developable cone, and stretching ridge, which are recreated by origami. These three representative configurations are sequentially located in the rectangular regions (i), (ii), and (iii) in panel (a). (e) Distribution of K versus σ_v for crumpled GNRs (W = 10 nm) with a = 1, 5, and 25, respectively. (f) Effective stress σ_e as a function of a for crumpled GNRs having different W values. (g) Schematic for analyzing the cross-section pattern of the crumpled GNR. The cutting plane passes the center of mass of the model and is perpendicular to the y-axis. (h) Cross-section patterns of crumpled GNRs having various a values. Here, the black line represents the scale bar b.

Fig. 6(f) presents the power-law scaling relationship between σ_e and a for the crumpled GNRs with different widths. Here, σ_e is defined as the average of the von Mises stresses of all CG beads with curvature greater than or equal to 0.1 Å⁻¹. It is evident that σ_e decreases approximately linearly with increasing a and that the width of the sheet is negatively related to σ_e. This can be explained by the fact that sharp crumples (e.g., developable cones and stretching ridges), commonly observed in crumpled GNRs with relatively small widths and aspect ratios, possess higher stresses, whereas crumpled GNRs with larger initial sizes have comparatively low stresses due to their internal structures, which are mainly composed of bends.³⁶ We point out here that the effective stress is somehow positively correlated with the mechanical properties (e.g., bulk modulus and effective compressive modulus) of the crumpled system.

To gain a deeper understanding of the effect of aspect ratio on the internal structure of a crumpled system, we analyze the cross-section patterns of the crumpled GNRs (W = 10 nm) with various aspect ratios by cutting the models with the virtual cutting plane (Fig. 6(g)). From Fig. 6(h), it can be found that the cross-section of crumpled GNRs with a small aspect ratio (e.g., a = 1 and 2) shows a disordered folding pattern, which is due to the EBD crumpling mode that the system possesses (a < a_c). However, for the systems with large aspect ratios (e.g., a = 25 and 60), the cross-section exhibits a scroll-like laminated and highly ordered pattern, which is attributed to the SFD crumpling mode of the system (a > a_c). In addition, although some systems (e.g., a = 5 and 10) possess the SFD crumpling mode, their cross-sections exhibit a relatively disordered layered pattern, and this is because the crumpling process of the systems being compacted from the QE state to the FC state falls into regime I (d_fc < W), making the scroll-like laminated structures highly squeezed and deformed (see Fig. 3(i) and (j)). Overall, the increase of the aspect ratio can improve the structural ordering and packing of crumpled GNRs.

4. Conclusions

In the present study, we investigated the crumpling behavior of graphene nanoribbons (GNRs) via CG-MD simulations by systematically varying the width of GNRs and their aspect ratio at a fixed sheet width. Our findings reveal that at the molecular level, the geometries of GNRs strongly impact several key aspects, including their potential energy, configuration, mechanical state, and internal structure. Specifically, the total potential energy per unit area of GNRs decreases with the increase of their width and aspect ratio in the intermediate and late stages of the crumpling process, attributed to the enhanced self-adhering and self-folding behaviors of larger GNRs. Analysis of the total potential energy contribution indicates that smaller sheets tend to form sharper crumples with higher dihedral energy that characterizes the out-of-plane deformation properties, whereas larger GNRs develop more planar regions due to their self-adhering and self-folding behaviors, leading to higher adhesion energy. By systematically evaluating the relative shape anisotropy and conformational features, we identify two aspect ratio-dependent crumpling modes for GNRs: the edge-bending-dominated (EBD) mode for smaller aspect ratios and the sliding- and folding-dominated (SFD) mode for larger aspect ratios. The investigation of the transition between these two crumpling modes determines the width-dependent critical aspect ratio, offering insights for the design of crumpled graphene nanostructures. Remarkably, increasing the aspect ratio of the crumpled GNRs reduces the mechanical heterogeneity and effective stress, facilitating the compact formation of crumpled structures. Furthermore, the analysis of cross-section patterns highlights the shift in the internal structures of the crumpled systems from disordered crumples to ordered scroll-like laminated structures as the aspect ratio increases. Our study highlights the critical role of geometry (i.e., width and the aspect ratio) in shaping the crumpling dynamics of GNRs, facilitating the tailored design of ribbon-like materials.

Author contributions

Yangchao Liao: methodology, software, formal analysis, validation, writing – original draft, and writing – review & editing. Long Chen: software, formal analysis, validation, and writing – review & editing. Wenjie Xia: conceptualization, supervision, project administration, funding acquisition, resources, and writing – review & editing.

Data availability

The data that support the findings of this study are available upon reasonable request from the authors.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

The authors acknowledge the support from the National Science Foundation (NSF) under CMMI award no. 2237063. L. C. and W. X. also acknowledge the support from the Department of Aerospace Engineering at Iowa State University.

References

1. K. Peng and M. B. Johnston, Appl. Phys. Rev., 2021, 8, 41314.
2. T. Li, W. Zeng and Z. Wang, Sens. Actuators, B, 2015, 221, 1570–1585.
3. S. K. Georgantzinos, G. I. Giannopoulos, D. E. Katsareas, P. A. Kakavas and N. K. Anifantis, Comput. Mater. Sci., 2011, 50, 2057–2062.
4. A. K. Singh and B. I. Yakobson, Nano Lett., 2009, 9, 1540–1543.
5. J. Hu, X. Ruan and Y. P. Chen, Nano Lett., 2009, 9, 2730–2735.
6. K. I. Sasaki, K. Kato, Y. Tokura, K. Oguri and T. Sogawa, Phys. Rev. B:Condens. Matter Mater. Phys., 2011, 84, 085458.
7. M. A. Rafiee, W. Lu, A. V. Thomas, A. Zandiatashbar, J. Rafiee, J. M. Tour and N. A. Koratkar, ACS Nano, 2010, 4, 7415–7420.
8. Y. Y. He, J. Chen, X. L. Zheng, X. Xu, W. Q. Li, L. Yang and W. Q. Tian, ACS Appl. Nano Mater., 2019, 2, 1648–1654.
9. U. Rajaji, R. Arumugam, S. M. Chen, T. W. Chen, T. W. Tseng, S. Chinnapaiyan, S. Y. Lee and W. H. Chang, Int. J. Electrochem. Sci., 2018, 13, 6643–6654.
10. Y. Gong, H. Fei, X. Zou, W. Zhou, S. Yang, G. Ye, Z. Liu, Z. Peng, J. Lou, R. Vajtai, B. I. Yakobson, J. M. Tour and P. M. Ajayan, Chem. Mater., 2015, 27, 1181–1186.
11. M. Fujita, K. Wakabayashi, K. Nakada and K. Kusakabe, J. Phys. Soc. Japan, 1996, 65, 1920–1923.
12. K. Nakada, M. Fujita, G. Dresselhaus and M. S. Dresselhaus, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 17954–17961.
13. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669.
14. P. V. Fedotov, D. V. Rybkovskiy, A. I. Chernov, E. A. Obraztsova and E. D. Obraztsova, J. Phys. Chem. C, 2020, 124, 25984–25991.
15. Z. Chen, A. Narita and K. Müllen, Adv. Mater., 2020, 32, 2001893.
16. A. Berdonces-Layunta, F. Schulz, F. Aguilar-Galindo, J. Lawrence, M. S. G. Mohammed, M. Muntwiler, J. Lobo-Checa, P. Liljeroth and D. G. De Oteyza, ACS Nano, 2021, 15, 16552–16561.
17. R. Saito, M. Fujita, G. Dresselhaus and M. S. Dresselhaus, Appl. Phys. Lett., 1992, 60, 2204–2206.
18. X. Li, X. Wang, L. Zhang, S. Lee and H. Dai, Science, 2008, 319, 1229–1232.
19. L. Yang, C. H. Park, Y. W. Son, M. L. Cohen and S. G. Louie, Phys. Rev. Lett., 2007, 99, 186801.
20. X. Wang, Y. Ouyang, X. Li, H. Wang, J. Guo and H. Dai, Phys. Rev. Lett., 2008, 100, 0206803.
21. M. Y. Han, B. Özyilmaz, Y. Zhang and P. Kim, Phys. Rev. Lett., 2007, 98, 206805.
22. M. Pan, E. C. Girão, X. Jia, S. Bhaviripudi, Q. Li, J. Kong, V. Meunier and M. S. Dresselhaus, Nano Lett., 2012, 12, 1928–1933.
23. X. Wang and H. Dai, Nat. Chem., 2010, 2, 661–665.
24. C. Chen, Y. Lin, W. Zhou, M. Gong, Z. He, F. Shi, X. Li, J. Z. Wu, K. T. Lam, J. N. Wang, F. Yang, Q. Zeng, J. Guo, W. Gao, J. M. Zuo, J. Liu, G. Hong, A. L. Antaris, M. C. Lin, W. L. Mao and H. Dai, Nat. Electron., 2021, 4, 653–663.
25. M. H. Oliveira, J. M. J. Lopes, T. Schumann, L. A. Galves, M. Ramsteiner, K. Berlin, A. Trampert and H. Riechert, Nat. Commun., 2015, 6, 1–7.
26. P. Xu, M. Neek-Amal, S. D. Barber, J. K. Schoelz, M. L. Ackerman, P. M. Thibado, A. Sadeghi and F. M. Peeters, Nat. Commun., 2014, 5, 1–7.
27. H. S. Seung and D. R. Nelson, Phys. Rev. A, 1988, 38, 1005–1018.
28. O. V. Yazyev and Y. P. Chen, Nat. Nanotechnol., 2014, 9, 755–767.
29. V. B. Shenoy, C. D. Reddy, A. Ramasubramaniam and Y. W. Zhang, Phys. Rev. Lett., 2008, 101, 245501.
30. J. Zhang, T. Ragab and C. Basaran, Int. J. Damage Mech., 2019, 28, 325–345.
31. J. Jia, X. Sun, X. Lin, X. Shen, Y. W. Mai and J. K. Kim, ACS Nano, 2014, 8, 5774–5783.
32. W. M. A. El Rouby, RSC Adv., 2015, 5, 66767–66796.
33. S. Deng and V. Berry, Mater. Today, 2016, 19, 197–212.
34. Y. Liao, Z. Li, Fatima and W. Xia, Carbon, 2021, 174, 148–157.
35. M. Becton, L. Zhang and X. Wang, Phys. Chem. Chem. Phys., 2015, 17, 6297–6304.
36. Y. Liao, Z. Li, W. Nie and W. Xia, Forces Mech., 2022, 6, 100057.
37. Y. Liao, Z. Li, L. Chen, A. B. Croll and W. Xia, Nano Lett., 2023, 23, 3637–3644.
38. C. Chen and F. L. Duan, Acta Phys. Sin., 2020, 69, 193102.
39. Y. Liao, O. Molares Palmero, A. Arshad, L. Chen and W. Xia, ACS Appl. Nano Mater., 2024, 7, 7802–7811.
40. Y. Liao, Z. Li, S. Ghazanfari, Fatima, A. B. Croll and W. Xia, Langmuir, 2021, 37, 8627–8637.
41. M. Becton, L. Zhang and X. Wang, Phys. Chem. Chem. Phys., 2014, 16, 18233–18240.
42. A. B. Croll, Y. Liao, Z. Li, W. M. A. Jayawardana, T. Elder and W. Xia, Matter, 2022, 5, 1792–1805.
43. Y. Wang and Z. Meng, Carbon, 2021, 177, 128–137.
44. S. W. Cranford and M. J. Buehler, Phys. Rev. B:Condens. Matter Mater. Phys., 2011, 84, 205451.
45. I. Giordanelli, M. Mendoza, J. S. Andrade, M. A. F. Gomes and H. J. Herrmann, Sci. Rep., 2016, 6, 1–6.
46. X. Ma, M. R. Zachariah and C. D. Zangmeister, Nano Lett., 2012, 12, 486–489.
47. X. Dou, A. R. Koltonow, X. He, H. D. Jang, Q. Wang, Y. W. Chung and J. Huang, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 1528–1533.
48. L. Cai, W. He, X. Xue, J. Huang, K. Zhou, X. Zhou, Z. Xu and G. Yu, Natl. Sci. Rev., 2021, 8, nwaa298.
49. Z. Xu and M. J. Buehler, ACS Nano, 2010, 4, 3869–3876.
50. S. Ghazanfari, H. M. N. Faisal, K. S. Katti, D. R. Katti and W. Xia, Langmuir, 2022, 38, 4859–4869.
51. A. Alesadi and W. Xia, Macromolecules, 2020, 53, 2754–2763.
52. Z. Li, Y. Liao, Y. Zhang, Y. Zhang and W. Xia, Extreme Mech. Lett., 2022, 50, 101519.
53. L. Ruiz, W. Xia, Z. Meng and S. Keten, Carbon, 2015, 82, 103–115.
54. Z. Meng, R. A. Soler-Crespo, W. Xia, W. Gao, L. Ruiz, H. D. Espinosa and S. Keten, Carbon, 2017, 117, 476–487.
55. X. Wei, Z. Meng, L. Ruiz, W. Xia, C. Lee, J. W. Kysar, J. C. Hone, S. Keten and H. D. Espinosa, ACS Nano, 2016, 10, 1820–1828.
56. W. Xia, F. Vargas-Lara, S. Keten and J. F. Douglas, ACS Nano, 2018, 12, 5427–5435.
57. Z. Shen, H. Ye, C. Zhou, M. Kröger and Y. Li, Nanotechnology, 2018, 29, 104001.
58. H. Li, H. Zhang and X. Cheng, Phys. E, 2017, 85, 97–102.
59. W. Xia, L. Ruiz, N. M. Pugno and S. Keten, Nanoscale, 2016, 8, 6456–6462.
60. C. Shao and S. Keten, Sci. Rep., 2015, 5, 1–12.
61. Z. Xu, J. Comput. Theor. Nanosci., 2009, 6, 625–628.
62. S. Plimpton, J. Comput. Phys., 1995, 117, 1–19.
63. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
64. M. C. Payne, M. P. Teter, D. C. Allan, T. A. Arias and J. D. Joannopoulos, Rev. Mod. Phys., 1992, 64, 1045–1097.
65. Q. Liu, J. Huang and B. Xu, J. Mech. Phys. Solids, 2019, 133, 103722.
66. J. Yang, H. Sun, H. Liang, H. Ji, L. Song, C. Gao and H. Xu, Adv. Mater., 2016, 28, 4606–4613.
67. Q. Liu and B. Xu, ACS Appl. Mater. Interfaces, 2020, 12, 43058–43064.
68. W. N. Wang, Y. Jiang and P. Biswas, J. Phys. Chem. Lett., 2012, 3, 3228–3233.
69. S. J. Stuart, A. B. Tutein and J. A. Harrison, J. Chem. Phys., 2000, 112, 6472–6486.
70. D. W. Brenner, O. A. Shenderova, J. A. Harrison, S. J. Stuart, B. Ni and S. B. Sinnott, J. Phys.: Condens. Matter, 2002, 14, 783.
71. W. M. A. Jayawardana, Y. Liao, Z. Li, W. Xia and A. B. Croll, Soft Matter, 2023, 19, 1081–1091.
72. A. B. Croll, T. Twohig and T. Elder, Nat. Commun., 2019, 10, 1–8.
73. Z. Zhang and T. Li, Nanoscale Res. Lett., 2011, 6, 1–11.
74. Y. Wang and Z. Liu, Nanoscale, 2018, 10, 6487–6495.
75. R. D. Yamaletdinov and Y. V. Pershin, Sci. Rep., 2017, 7, 1–9.
76. H. Arkin and W. Janke, J. Chem. Phys., 2013, 138, 54904.
77. M. Bishop and J. P. J. Michels, J. Chem. Phys., 1986, 85, 5961–5962.
78. A. P. Sgouros, G. Kalosakas, K. Papagelis and C. Galiotis, Sci. Rep., 2018, 8, 1–13.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5nr00805k

‡ These authors contributed equally to this work.

---