Rayleigh streaming phenomena at the physical origin of cellulose nanocrystals orientations during combined ultrasound and ultrafiltration processes

Abstract

Rayleigh acoustic streaming, a phenomenon resulting from the interaction of ultrasound (US) with a fluid, was revealed for the first time during simultaneous frontal filtration and US processes on a cellulose nanocrystal (CNC) suspension. According to in situ small-angle X-ray scattering (SAXS) and particle image velocimetry (PIV) measurements, channel-type filtration cells coupled with US were developed to simultaneously generate a vertical acoustic force via an ultrasonic vibrating blade at the top and to concentrate the CNCs under a transmembrane pressure force at the bottom. SAXS measurements under different transmembrane pressures demonstrated a change in CNCs orientation as a function of the distance from the membrane surface to the vibrating blade. These measurements led to the appearance of an orthotropic organization: CNCs were vertically oriented near the vibrating blade, then had an isotropic organization in the middle, and exhibited horizontal orientations near the membrane surface. This orthotropic organization appeared above a threshold in transmembrane pressure of ∼0.6 × 10⁵ Pa. Concurrently, in situ micro-PIV measurements revealed the formation of Rayleigh acoustic streaming in the CNCs suspension, for the same threshold in transmembrane pressure and same US conditions, thereby highlighting the origin of the orthotropic organization. We propose that this threshold allows for sufficient accumulation of CNCs near the membrane surface, thus enabling confined flow, to generate acoustic streaming. This work highlights the interplay between acoustic streaming and orientations of CNC particles, thereby advancing understanding of the manipulation of liquid crystal-like suspensions in microfluidic applications.

---

1. Introduction

Acoustic streaming, studied for over 50 years,^1–3 is a type of macroscopic flow caused by an acoustic field in a viscous fluid.⁴ If an acoustic wave propagates in a fluid, it causes oscillations in particle pressure and velocity. In an ideal fluid, the mean particle displacement is zero; however in a real fluid, viscosity causes this displacement to become non-zero, creating a continuous flow.⁵ This flow has a range of a few centimeters to a few tens of centimeters⁶ and a velocity of between 1 and 100 cm s⁻¹, varying with ultrasound (US) power and frequency.^7,8 Acoustic streaming can be broadly categorized into several types depending on the mechanism of acoustic energy dissipation: Schlichting streaming and Rayleigh streaming (driven by the boundary layer), Eckart streaming (dissipation of bulk fluid), and cavitation microstreaming (near-oscillating bubbles). Under the conditions of the present study, characterized by low-frequency US (20 kHz) and the absence of isolated bubbles or significant bulk dissipation, Rayleigh acoustic streaming was the most relevant mechanism. This type of streaming arises from viscous dissipation of acoustic energy in the boundary layer of a fluid along solid surfaces. In standing waves, this dissipation creates a constant momentum flux, generating vortices in the fluid, with Schlichting streaming confined to the boundary layer and Rayleigh streaming dominating the outer regions of the fluid.⁵ Nevertheless, acoustic streaming is difficult to characterize completely due to its many mechanisms and forms. However, it is particularly pronounced if⁹ λ ≫ h ≫ δ, where λ is the wavelength (m), h is the characteristic length scale of the fluid chamber (m), and δ_ν is the viscous penetration depth (m), which in an oscillating flow is given by (where ν is the kinematic viscosity and ω is the angular frequency of the acoustic wave).⁵ Over the past two decades, interest in acoustic streaming has been renewed by the application of US to manipulate fluids and suspended particles in microfluidic systems.¹⁰ Acoustic streaming is thus used for ultrasonic cleaning, dispersion, mixing, and non-contact driving.⁴ Furthermore, if used correctly, acoustic streaming can be an extremely useful phenomenon that overcomes many of the challenges presented by low Reynolds number flows in microfluidics,⁵ and its experimental characterization in terms of modification of velocity fields remains crucial.

Various techniques can be used to observe fluid movement, such as micro-particle image velocimetry (PIV),¹¹ laser Doppler velocimetry (LDV),¹² magnetic resonance velocimetry (MRV)¹³ or holographic particle velocimetry (HPV).¹⁴ Micro-PIV uses microscopic particles that are introduced into the fluid to be studied.¹⁵ These particles are small enough (generally sub-micrometer in size) to faithfully follow the movements of the fluid. The moving fluid (and therefore the particles in the fluid) is then illuminated by a light source, often a pulsed laser. The light pulses freeze the positions of the particles at precise instants. Images of the illuminated particles are then captured at very short time intervals by a high-resolution, high-frequency camera. Micro-PIV is used in microfluidics,¹⁶ biomedicine,¹⁷ and has previously been used in our research team to understand the mechanisms involved in the formation of concentration polarization and fouling phenomena during the cross-flow ultrafiltration of colloidal suspensions of LAPONITE® clay¹⁸ and cellulose nanocrystals (CNCs).¹⁹

CNCs have attracted significant interest across disciplines, from chemistry and physics to materials science and engineering, due to their renewable origin and intrinsic properties. If organized appropriately, CNC-based materials can exhibit high-value functional properties such as iridescence, enhanced stiffness, resistance to crack propagation, and excellent gas barrier performance. These characteristics open the door to a wide range of advanced applications, including pressure-sensitive screens and photovoltaics in microelectronics,^20,21 multilayered tissue scaffolds in regenerative medicine,²² and sustainable packaging solutions for the bio- and agri-food industries.²³ A critical challenge in developing such materials lies in the precise control of CNC orientation and organization over large spatial scales. This requires not only mastering the interactions among CNCs and between CNCs and their surrounding medium (aqueous or polymeric) but also efficiently applying external forces during processing to direct their alignment and unlock their full functional potential.

The orientation of CNCs nanoparticles within the fluid can be observed using different techniques such as small-angle X-ray scattering (SAXS)²⁴ or small-angle neutron scattering (SANS).²⁵ For example. SAXS uses X-rays (wavelengths of the order of a few angstroms) to probe matter. The X-rays are directed at the sample to be studied. If they encounter variations in the electron density of the sample, they are scattered in different directions. The scattered radiation is then captured by a detector placed at a certain distance from the sample. Depending on the scattering intensity measured, it is possible to extract different information on the size, shape and spatial distribution of the particles in the sample.^26,27 SAXS is used in many fields, such as biology (to analyze the structure of proteins²⁸), chemistry (to characterize emulsions²⁹) and materials science (to study nanoparticles^30–32). Previously in our research team, this technique has been used to study the effects of US on cross-flow ultrafiltration of skimmed milk,³³ the breakdown and buildup mechanisms in concentrated CNC suspensions under shear and during relaxation upon cessation of shear³⁴ and, more recently, to highlight the typical orthotropic structure of articular cartilage obtained on a CNC suspension subjected to ultrafiltration combined with US.³⁵

In the present study, we developed a channel-type filtration cell combining frontal ultrafiltration (FU) with low-frequency US, building on our previous works,^33–35 which enabled in situ SAXS and micro-PIV measurements. This cell was designed to create an US pressure wave that produces a vertical acoustic radiation force via a vibrating blade at the top of the channel. Simultaneously, it concentrated the CNCs suspension through an ultrafiltration membrane at the bottom of the channel under transmembrane pressure. Based on in situ micro-PIV measurements, Rayleigh acoustic streaming was revealed on a CNC suspension. Streamlines, velocity fields and particle velocities were calculated, demonstrating the influence of transmembrane pressure on acoustic streaming. In situ SAXS measurements, 2D patterns and anisotropy calculations enabled observation of the corresponding changes in CNC orientations over the entire height of the cell, depending on the transmembrane pressure applied.

2. Materials and methods

2.1. Materials

2.1.1. Preparation of CNC suspensions. An aqueous suspension of CNCs from UMaine Development Center (University of Maine, Orono, ME, USA) was used at a stock concentration of 12.2 wt%. From this stock suspension, dilution in deionized water and NaCl (0.01 mol L⁻¹) was carried out, and mechanical agitation during 2 h was applied. Sonication with a maximum power output of 250 W was then applied with a Branson Digital sonifier (Marshall Scientific, Hampton, NH, USA). A suspension (250 mL) was sonicated by applying an output power of 0.5 W cm⁻² with a 30% duty cycle under magnetic stirring. The normalized energy dose of sonication per liter of suspension (43.7 kJ L⁻¹) was calculated by the procedure given by Taurozzi and colleagues,³⁶ and normalized by the concentration and volume of the suspension as described by Johns et al. and Girard and colleagues.^37,38 Previous work³⁹ allowed to describe the morphology of the CNCs considered in this work and their phase diagram in aqueous suspension. In particular, SAXS data have allowed evaluation of the average dimension of sonicated CNCs in a dilute suspensions at rest, given calculated dimensions of 121 × 20 × 5 nm³, assuming a parallelepipedal shape.^34,40 The concentration of CNC suspensions filtered in this work was fixed at 10 wt% (6.25 vol%). For micro-PIV measurements, polystyrene microbeads (5 μm in diameter) coated with rhodamine were added as passive tracers. These particles, with a density of 1.05 g cm⁻³ and emitting light at 607 nm, helped track fluid motion while minimizing reflection effects near the filtration membrane (PES membrane at 100 kDa (Orélis Environnement, Paris, France)).

2.2. Experimental methods

2.2.1. In situ SAXS during FU–US processing. To monitor in situ the changes in the dynamical structural organization, time-resolved SAXS were performed in a FU–US-SAXS cell, as described previously.^35,41,42 A cell with a parallelepipedal channel 4 mm in width (x), 8 mm in depth (z) and length (y) of 100 mm was made of transparent polycarbonate. A titanium vibrating blade (3 mm-wide and 100 mm-long) was immersed from the upper part of the channel to define the depth (5600 μm from the ultrafiltration membrane surface) where the suspension was structured by FU–US processing. This blade was connected to a sonotrode (Sodeva TDS, Méry, France) consisting of a piezoelectric transducer attached to a metal rod. It allowed application of an acoustic radiation force along the vertical direction z, generating ultrasonic waves at a frequency f_US = 20 kHz with an amplitude a_US.^35,41–43 This amplitude was previously measured to be a_US = 1.6 μm³⁵.

An FU–US protocol was applied. Briefly, the feed suspension, referred to as the “retentate” (1 in Fig S1†), was pumped with a syringe (2 in Fig S1†) from a tank containing the CNC suspension and allowed to fill-up the entire channel (Fig S1†). Different valves placed at the inlet and outlet of the filtration cell allowed control of the flow rate in the channel (3 and 4 in Fig S1†). Compressed air (5 in Fig S1†) was used to control the pressure in the loop. A pressure gauge (FP110; FGP Sensors & Instruments) placed at the inlet of the cell allowed measurement of the applied transmembrane pressure. A T-junction (6 in Fig S1†) was placed between the outlet vane and outlet of the filtration cell. Compressed air was applied from the upper part of the T-junction. During filling of the channel, the pressure vane (8 in in Fig S1†) permitted protection of the air circuit from the suspension. The permeate (9 in Fig S1†) was recollected in a small tank. The mass variation of this reservoir was measured every 10 s with an accuracy of 0.001 g using a precision scale (Balance Series 400 M; Precisa), allowing monitoring of the permeate flux J.

SAXS measurements were accomplished at the TRUSAXS ID02 beamline (ESRF, Grenoble, France).⁴⁴ Measurements at room temperature were completed with a sample-to-detector distance of 10 m and an X-ray energy of E = 12.230 keV (wavelength λ = 0.1014 nm). The corresponding range of scattering wave vector magnitude, q, was 0.005–0.7 nm⁻¹, where q = (4π/λ) sin(θ/2) with θ the scattering angle. This q range allowed exploration of a nominal length scale l (∼2π/q) range of ∼10 nm ≤ l ≤ 1200 nm. The pinhole collimation setup available at ID02 permitted reduction of the beam size at the sample position. All measurements were made using a beam cross-section (FWHM) of ∼35 μm vertically and 150 μm horizontally. The incident beam passed through the sample in the FU–US-SAXS cell. Two-dimensional scattered intensity patterns were recorded on a high-resolution pixel array detector (Eiger2-4M; Dectris, Baden, Switzerland). Following the standard procedure, measured scattering patterns were normalized to an absolute scale.⁴⁴ During experimentation, the X-ray beam was directed along the x-direction perpendicular to the walls of the cell positioned in the middle of the channel (y = 50 mm) through a window of 3 mm × 5.5 mm × 0.3 mm (width × height × thickness, respectively). To align the incident beam parallel to the membrane surface, a rotational stage was used, and positioned between the sample table and the FU–US-SAXS-cell. To probe the structure at different z-positions above the membrane surface, a vertical translation table was used.

The analysis of the normalized SAXS patterns recorded in the FU–US-SAXS cell was the same as that described in previous works.^{18,19,35,42,45} Four regions were defined by measuring the transmitted X-ray signal as a function of the distance z through the FU–US-SAXS cell. This analysis allowed detection of the minimal distance z above which the permeate channel and membrane surface scattering did not influence the scattered intensity of the CNC suspensions. This z₀ position was defined as the origin (z = 0). Then, z = 100 μm was the minimal distance above which the SAXS data were usable (determined by the planarity and roughness of the membrane). Vertical scans along z were systematically performed during FU–US processing, with SAXS pattern acquisitions every 50 μm from z = 100 to 500 μm and every 100 μm from z = 500 to 5600 μm. The one-dimensional scattered intensity profile I(q) was obtained by azimuthally averaging the normalized scattering patterns. The normalized background scattering of the cell was recorded with a cell filled with demineralized water. This scattering background was systematically subtracted from the scattering of the CNC suspensions. After patching the gaps between the detector modules using SAXSutilities software, the azimuthal averages of the scattering patterns were calculated.⁴⁶ Using MATLAB-based Small-Angle Scattering Evaluation Tool (SASET) software, the anisotropy analysis was performed from the 2D-SAXS patterns.⁴⁷ Specifically, the model-free principal component analysis (PCA) method was chosen. This method provides values for anisotropy ranging from 0 for isotropic suspensions to 1 for fully aligned systems and, depending on the system, it is quantitatively comparable with the commonly used order parameter.⁴⁷ Via PCA in the q-range of 0.071–0.368 nm⁻¹, the anisotropy and direction of maximum scattering ψ₀ were calculated. These calculations allowed quantification of the relative effect of FU and US on the degree of anisotropy referred to as “PCA anisotropy” and on the orientation [maximum scattering direction (ψ₀)] of the CNCs during FU–US processing as a function of time t and distance z from the membrane surface. The CNC concentration profile as a function of filtration times and distance z from the membrane surface was deduced with the same analysis described in our previous work.³⁵ Briefly, first, a calibration curve was established from several CNC samples at different known CNC concentrations in static conditions. This calibration curve allowed determination of the relationship between the mass concentration C and mean interparticle distance d. Second, the apparent structure factor, S(q) was calculated at each time t and distance z from the membrane surface. The apparent structure factor, S(q) was obtained by dividing the scattering intensity I(q) at a given position in the FU–US cell by the form factor. Then, the average interparticle distance d = 2π/q_peak at each time t and distance z from the membrane surface was evaluated from these S(q) values. Finally, using the calibration curve, the corresponding local mass concentration C(z,t) was calculated.

2.2.2. In situ micro-PIV: velocity field measurements during FU–US. A Plexiglas™ (PMMA) cross-flow filtration cell was specifically designed to allow complete visualization of the flow field within the entire cell during FU–US. The micro-PIV technique was implemented to measure the velocity field from the membrane surface to the US blade. The dimensions of the feed channel were the same as for the cell used for SAXS measurements (4 mm × 8 mm × 100 mm (width × depth × length, respectively)). The same US blade and sonotrode were used in exactly the identical conditions of SAXS. The 3 mm-wide and 100 mm-long titanium vibrating blade was immersed from the upper part of the channel to a z distance = 5600 μm from the membrane surface to define the depth of the region where the suspension was structured by FU under US. Micro-PIV measurements were accessible all along the length of the channel thanks to the design of the cell (Fig. 1).

Fig. 1 In situ micro-PIV measurements under FU–US (schematic).

The device for velocity field measurement consisted of a FlowSense EO 4-million-pixel camera, 2000 × 2000 pixels in full resolution, where each pixel corresponds to 21.7 μm. For the experiments, the resolution was reduced to 2079 × 351 pixels to optimize storage on the computer hard drive. The Milvus 2/100 M reflex lens (minimum focal length of 100 mm; Zeiss, Oberkochen, Germany) was added to the camera, as well as a high-pass filter (545–800 nm; LaVision, Göttingen, Germany) to visualize only the wavelengths emitted by the fluorescent particles (and thus be able to characterize the hydrodynamic field within the cell channel). The seeding particles used were polystyrene microbeads coated with rhodamine that re-emit light at 607 nm. Rhodamine was used to limit the effects of wall reflections, especially near the filtration membrane. These particles are made of polystyrene and coated with rhodamine, with an average diameter of 5 μm. These particles have a density of 1.05 g cm⁻³, very close to those of the studied suspension and are considered to be passive tracers. Indeed, the tracers must have a density close to that of the fluid to be investigated so that their displacement follows as closely as possible that of the fluid. Moreover, they must not modify the rheological behavior of the fluid to be studied. The Stokes number is used as a criterion in the choice of the diameter and density. The Stokes number shows the ratio between the kinetic energy of the particle and the energy it dissipates by friction in a fluid, described by the equation 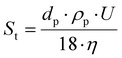, where d_p is the diameter of the fluorescent particles (m), U the average velocity of the flow (m s⁻¹), ρ_p the density of the fluorescent particles, (kg m⁻³), and η the dynamic viscosity (Pa s). A low Stokes number indicates that a particle follows the flow correctly and is therefore a good passive tracer. The Stokes number for the selected particles, and for the smallest velocity measured in the experiments (U = 1 mm s⁻¹), which is most prone to sedimentation, was 2.06 × 10⁻⁴ for CNC suspensions.

This system was set up to acquire image pairs during flow without being hindered by reflections near the membrane surface. The camera was synchronized with the laser at a frequency of 15 Hz, and driven by micro-PIV software (Dynamic Studio; Dantec Dynamics, Skovlunde, Denmark). It was placed orthogonal to the laser plane. The camera was placed in front of the filtration cell and placed on a micrometric table for accurate motion in x, y and z directions, as well as rotation, allowing it to be perpendicular to the flow direction. To illuminate the CNC suspension containing rhodamine particles, a pulsed Nd–Yag laser (Dantec Dynamics) with a wavelength of 532 nm (green) and power of 400 mJ per pulse was used. This laser provided the illumination necessary to visualize correctly the CNCs during FU–US and to deduce velocity fields by subsequent analyses. The laser sheet generator was placed on the side of the cell so that the sheet can pass through the cell in the x (flow) direction. It was also placed on a micrometric table allowing displacements in the y direction, as well as rotation in order to be parallel to the flow direction. The laser sheet (Dantec Dynamics) was a horizontal plane generated by a lens (Dantec Dynamics), with a working distance range of 20 cm to 4 m, a width of ∼1 cm and a thickness of ∼1 mm.

To determine the velocity field, knowing the time between images, an adaptive method was used to optimize the quality of the images when the investigated particle had a certain opacity, and to have the most reliable possible result. This method consisted of performing several passes of cross-correlation calculation on variable sizes of the region of interest. The interrogation window size was 170 × 375 pixels, with an overlap of 50%, and the calculation was performed in three passes: the first pass with 16 × 16 pixels, followed by a second pass with 8 × 8 pixels, and a final pass with 4 × 4 pixels. The calculation for the velocity field was executed over 500 images to ensure statistical convergence of the field. From the instantaneous vector fields, statistical analyses were performed to obtain the mean field (in the Reynolds point of view) and higher order moments for the velocity fluctuations in the case of turbulent flow. The longitudinal velocity U and vertical velocity V in the (x,y) plane were thus obtained, either in the form of velocity iso-contours, or in the form of the velocity profile U(y) and velocity gradients.

2.2.3. Experimental protocol. FU–US processing consisted of a specific procedure. First, the cell was filled with the CNC suspension with an initial concentration C = 10 wt% containing rhodamine particles. Inlet and outlet valves were opened at the extremities of the channel, the pressure valve was closed, and the suspension was pumped from the tank with the syringe to fill-up the entire channel. Then, the inlet and outlet valves were closed, and the pressure valve was opened so that compressed air was injected from the T junction, allowing FU to start at time t = 0 under the imposed transmembrane pressure. Simultaneously, US was activated. Description of the experimental procedure (ultrasonic power (%), transmembrane pressure) is presented in Fig. 2.

Fig. 2 Monitoring of US power and transmembrane pressure during experimentation.

For all the measurements presented in this work, only one acoustic radiation force was applied with a fixed acoustic amplitude a_US = 1.6 μm. This corresponded to an acoustic pressure P = 2πρvf_USa_US ≅ 300 kPa and an acoustic power P_a = P²/ρv ≅ 6 W cm⁻², where ρ = 1000 kg m³ is the water density and v = 1480 m s⁻¹ is the speed of sound in water, as described previously.³⁵ Cavitation was not observed. During the first phase, entitled “Step 1” (Fig. 2), the transmembrane pressure was kept constant and equal to ΔP = 1.2 10⁵ Pa. FU–US processing was applied for a total duration of 90 min. To evaluate the relaxation pressure under US and the relative strength of US over FU transmembrane pressure on the structural organization of the CNCs in the cell, “Step 2” of the procedure was applied. First, the transmembrane pressure was reduced to zero at time t = 90 min and then increased to four consecutive values of ΔP = (0.3, 0.6, 0.9 and 1.2) × 10⁵ Pa for a few minutes and then reduced again to zero and time t = 125 min, as described in Fig. 2. Meanwhile, evolution of the 2D SAXS pattern was monitored. The same experiment conducted in SAXS was then reproduced in in situ micro-PIV.

3. Results and discussion

3.1. Observation of steady-state acoustic streaming, orienting CNC

In a previous study,³⁵ we demonstrated an orthotropic organization of CNCs under the combined effect of US and FU for different filtration times using SAXS measurements. Close to the membrane surface, the 2D SAXS pattern exhibited anisotropy with a vertical elongation, indicating horizontal alignment of CNCs driven by frontal ultrafiltration (Fig. 3a). Close to the US blade, the SAXS patterns displayed horizontal elongation, revealing vertical alignment of the director of CNCs along the direction of the US wave propagation. At the boundary between these two regions, the SAXS patterns appeared isotropic, indicating a randomly distributed orientation of CNCs. These initial results corresponded to Step 1 (Fig. 2). First, we explored the appearance of the streaming phenomena observed in Step 1 in comparison with the orientations studied by SAXS in previous results and confirmed in this work. Then, we enlarged these data in terms of filtration/US conditions explored during Step 2.

Fig. 3 Comparison of (a) 2D-SAXS patterns and schematic representation of the orientation of CNCs, and (b) velocity field for two similar states (ΔP = 1.2 × 10⁵ Pa and P_a = 6 W cm⁻²) and different times of filtration, such as Step 1 (t_f1 = 88 min) and Step 2 (t_f2 = 19 min).

For Step 1, the filtration time was equal to the time of experience because the entire step was performed under transmembrane pressure ΔP = 1.2 × 10⁵ Pa (Fig. 2). However, for Step 2, after t = 90 min, the pressure was released and at t = 97 min, the I(q) signal showed that the concentration profile was completely lost. Hence, at this stage, the concentration had become homogeneous, at ∼15 wt%, across the whole cell (Fig. S2†). This redistribution occurred because US was maintained even in the absence of pressure, facilitating the redispersion and breakup of the concentrated deposit formed in Step 1. Consequently, when pressure was increased again in Step 2, the starting concentration was no longer 10 wt% as at the start of Step 1, but around 15 wt%. Nevertheless, the concentration was homogeneous throughout the cell, and therefore, the filtration time counter in Step 2 was reset to zero. Filtration started when the transmembrane pressure was no longer zero, which corresponded to the experiment time t = 105 min, corresponding to t_f2 = 0 min. It is important to note, however, that we started Step 2 with a slightly higher initial concentration than at the beginning of Step 1 due to the concentrating effect of FU.

During the application of FU–US in Step 1, the phenomenon of acoustic streaming was observed for the first time by in situ micro-PIV for different times of filtration (see movie in ESI Data†). This streaming phenomenon occurred under specific conditions, where the interaction between acoustic waves and the confined geometry of the flow generated Rayleigh streaming. According to the theoretical framework, Rayleigh streaming arises when the relationship λ_a ≫ h ≫ δ_ν is fulfilled, with λ_a representing the acoustic wavelength, h the characteristic dimension of the chamber, and δ_ν the thickness of the viscous boundary layer. In our setup, these criteria were met: λ_a = 7.5 cm, h varied between 3800 μm and 5600 μm, and δ_ν ranged from 40 μm to 126 μm, depending on the viscosity of the CNC suspension (ν = 10⁻³ to 10⁻⁴ Pa s). At the surface of the walls, the boundary layer (in green in Fig. S3†) formed due to friction between the fluid and solid wall (Fig. S3†). This boundary layer was characterized by slower fluid flow near the wall and faster flow away from it. Within the fluid, the interaction between the acoustic wave and flow geometry generated Rayleigh streaming (in orange in Fig. S3†).

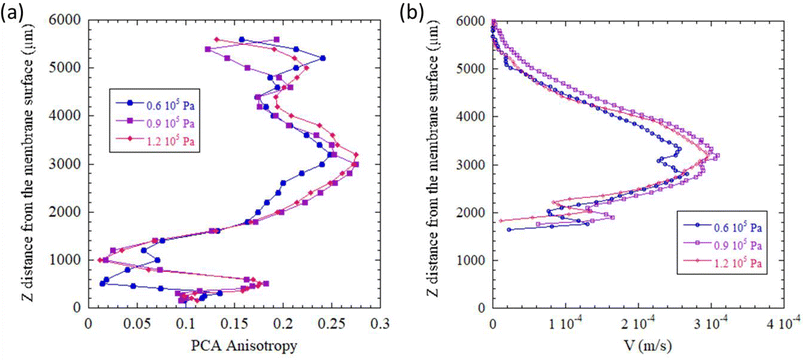
Initially, we studied the reversibility of the streaming acoustic phenomenon. To do so, we compared the SAXS spectra (Fig. 3a), the resulting PCA anisotropy, and the vertical velocity V (Fig. 3b) determined by in situ micro-PIV of two similar states (ΔP = 1.2 × 10⁵ Pa and P_a = 6 W cm⁻²) obtained for a filtration time of t_f1 = 88 min (Step 1), and then for a filtration time of t_f2 = 19 min (Step 2) after undergoing a gradual increase in transmembrane pressure (Step 2). The SAXS patterns for those two conditions for a different distance z from the membrane surface are shown in Fig. 3a. The entire z-scan for those two conditions are represented in Fig. S4.† As can be seen, the same 2D-SAXS patterns (and consequently the same CNCs orientation) were obtained for those two conditions.

The PCA anisotropy measured at the center of the cell, from the membrane surface to the US blade (Fig. 4a), overlapped for both similar states (Step 1 (t_f1 = 88 min) and Step 2 (t_f2 = 19 min)). The same phenomenon was observed for the vertical velocity V calculated by micro-PIV (Fig. 4b). These results demonstrated a quite stable and reproducible physical phenomenon even though, due to the first step, the suspensions had reached a constant concentration of ∼15 wt% (Fig. S2†) in the whole sample agitated by US. At the beginning of Step 2, the initial concentration before applying a transmembrane pressure was slightly higher (15 wt%) in the wall cell than that in Step 1 (10 wt%). It was also interesting to notice that the equilibrium pressure (ΔP = 1.2 × 10⁵ Pa for the two steps) elicited the same structural organization of the CNC suspension between the membrane surface and US blade even though the way the pressure had been applied during this time was not the same. This observation could be explained by the liquid crystal behavior of CNC suspensions. In Step 1 t_f1 = 88 min, a transmembrane pressure of ΔP = 1.2 × 10⁵ Pa had been applied continuously whereas for Step 2 t_f2 = 19 min, the pressure had been gradually increased from ΔP = 0.3 × 10⁵ Pa to ΔP = 1.2 × 10⁵ Pa regularly, as shown in Fig. 2. This observation reinforced the fact that an equilibrium had been reached between the acoustic forces and transmembrane pressure forces for these two measuring points at the same US and filtration (ΔP = 1.2 × 10⁵ Pa) conditions but with a different history.

Fig. 4 Comparison of (a) PCA anisotropy and (b) vertical velocity V (m s⁻¹) measured from the membrane surface to the ultrasonic blade for two similar states (ΔP = 1.2 × 10⁵ Pa and P_a = 6 W cm⁻²) such as Step 1 (t_f1 = 88 min) and Step 2 (t_f2 = 19 min). The standard deviation of the measured velocity was 5.4 × 10⁻⁵ m s⁻¹ for Step 1 and 6.3 × 10⁻⁵ m s⁻¹ for Step 2.

3.2. Effect of transmembrane pressure on acoustic streaming

As for Step 1, the 2D-SAXS patterns were monitored during time in Step 2. The first interesting phenomenon was that, immediately after the release of pressure, the effect of the orientation of US near the blade was reduced, but not completely lost, and slight orientation of the 2D-SAXS patterns (Fig. 5) was detected. In the meantime, near the membrane surface, the parallel orientation of the CNC director was also preserved but the level of orientation was reduced, and the orientation was more chaotic (Fig. S5†). One could infer that the streaming Rayleigh phenomenon responsible for the CNC orientation along the US radiation propagation was less efficient. Moreover, when comparing velocity fields (Fig. 5b) with the one from Fig. 3b, two regions of high flow were observed for the case without transmembrane pressure whereas, under ΔP = 1.2 × 10⁵ Pa, only one well-defined region could be identified.

Fig. 5 (a) 2D-SAXS patterns and (b) velocity field obtained at a time of experience of 97 min, with ΔP = 0 Pa and P_a = 6 W cm⁻².

Theoretically, the appearance of the Rayleigh streaming phenomenon requires specific boundary conditions and confined flow.^5,48 Under pressure, the presence of well-oriented particles near the membrane surface can provide a good reflection surface for the propagation and reflection of US waves. However, if the pressure is released, the consistency of the concentrated layer at the membrane surface is not suitable for surface reflection anymore, inducing a condition for which the streaming phenomena is less established and unstable (as can be seen in Fig. 6 in micro-PIV images). The porous membrane surface would leave a free boundary towards atmospheric pressure, which would allow the propagation wave of US to be damped by the membrane rather than being reflected by a solid wall. This phenomenon could explain this weakening effect of US. Fig. 6 shows the difference between the in situ micro-PIV velocity streamlines obtained without (Fig. 6a) and with (Fig. 6b) transmembrane pressure. Without transmembrane pressure, the particles exhibited a circular motion, as indicated by the streamlines. In contrast, with transmembrane pressure, the particles displayed a completely different motion with vertical field lines aligned parallel to the incident US wave.

Fig. 6 Comparison of velocity streamlines obtained from in situ micro-PIV under US waves for the same area in the filtration cell (block A in red) (a) without and (b) with transmembrane pressure. (a) Step 1 (time of experiment t = 97 min; ΔP = 0 Pa and P_a = 6 W cm⁻²). (b) Step 2 (t_f2 = 19 min; ΔP = 1.2 × 10⁵ Pa and P_a = 6 W cm⁻²).

These data align with what has been proposed previously:⁴⁹ US orients the CNCs by a phenomenon of streaming rather than a phenomenon of elastic nature due to the anisotropy of sound absorption.

Furthermore, an interesting effect was the influence of transmembrane pressure on the acoustic streaming and orthotropic orientation of the CNCs. Fig. 7 shows the 2D-SAXS patterns for different distances from the membrane surface to the vibrating blade, at different conditions of filtration (ΔP varying from 0 to 1.2 × 10⁵ Pa) with a constant acoustic power of P_a = 6 W cm⁻². In the absence of transmembrane pressure (ΔP = 0 Pa), the 2D-SAXS patterns did not present a clear orientation all along the z position, with several light orientations of the SAXS patterns in different directions. Only near the membrane surface did a vertical orientation of the 2D-SAXS patterns seemed to be preserved due to the previous structuring by filtration during Step 1 and not completely de-structured by US. The orthotropic structure had thus almost disappeared, and acoustic streaming did not take place. As the transmembrane pressure increased (ΔP = 0.3 × 10⁵ Pa), anisotropic spectra were observed in the upper part of the cell (from 1400 μm). Hence, a preferential orientation of CNCs was taking shape, but had not yet stabilized. Further increases in transmembrane pressure (ΔP = (0.6, 0.9 and 1.2) × 10⁵ Pa) revealed the orthotropic structure discussed above, characterized by vertical anisotropic 2D-SAXS patterns near the membrane, isotropic between 600 to 1400 μm, and then horizontal anisotropic at the top of the cell. Hence, near the ultrasonic blade, the CNCs were oriented perpendicular to the blade surface. Vertical acoustic streaming could then take place because, under pressure, the presence of well-oriented particles near the membrane surface could act as a good reflective surface for the propagation and reflection of US waves, as explained above. From the SAXS patterns and corresponding I(q), the concentration as a function of the distance from the membrane surface z was calculated and is presented in Fig. S6.† As described above, a pronounced vertical concentration gradient was established due to the concentration polarization layer formed during membrane ultrafiltration.^40–42,45 In this work, the increase in transmembrane pressure from 0 to 1.2 × 10⁵ Pa corresponding to Step 2 revealed both an increase in concentration in the accumulated layer and increase of its thickness at increasing ΔP (no layer at ΔP = 0 Pa versus 800 μm at ΔP = 1.2 × 10⁵ Pa). This observation was in accordance with the fact that CNCs accumulated not only at the membrane surface but also in the bulk at increasing layers from the membrane surface. In this case, where US was applied at the same time of increasing ΔP, this concentration phenomenon was reinforced by the local agitation induced by US near the membrane surface, which permitted reaching quicker and higher levels of concentration near the membrane surface, as discussed in previous works.^41,42

Fig. 7 Comparison of 2D-SAXS patterns for five filtration conditions (P_a = 6 W cm⁻² and ΔP varying from 0 to 1.2 × 10⁵ Pa) with the corresponding filtration time during Step 2 (t_f2 = 0, 4, 9, 14 and 19 min). The schematic orientation of CNCs deduced from 2D-SAXS patterns on the right corresponds to t_f2 = 19 min.

The study of velocity fields obtained by micro-PIV also confirmed the observations made by SAXS. Fig. 8 shows the evolution of velocity fields and streamlines as a function of transmembrane pressure. Without transmembrane pressure (ΔP = 0 Pa), the particles followed circular streamlines in the observation plane, and two regions of high-velocity fields could be identified near 1000 μm and 4000 μm. As the transmembrane pressure increased, this phenomenon of circular streamlines disappeared regularly and led to some descending and increasing velocity movements without a clear direction. However, a pressure threshold of 0.6 × 10⁵ Pa was required for the acoustic streaming phenomenon to appear clearly, with the presence of vertical streamlines. The observation of velocity fields suggested also a transition to two regions of streaming to a large one located at a distance between 3000 and 5000 μm. This acoustic velocity fields tended to stabilize at 1.2 × 10⁵ Pa.

Fig. 8 Variation in velocity fields and the corresponding streamlines calculated in block A (same position as in Fig. 6) for different transmembrane pressures by in situ micro-PIV. P_a = 6 W cm⁻² and ΔP = (0; 0.3; 0.6; 0.9; 1.2) × 10⁵ Pa.

This observation was also confirmed when comparing the values of PCA anisotropy and vertical velocity V (Fig. 9). Indeed, stabilization of the PCA anisotropy curve was observed from ΔP = 0.6 × 10⁵ Pa (Fig. 9a). The corresponding curves for ΔP = 0.9 × 10⁵ Pa and ΔP = 1.2 × 10⁵ Pa overlapped for all z distances except near the vibrating blade, for which the motion phenomenon related to the boundary layer gave a random direction of orientations and non-accurate level of anisotropy. Evolution of PCA anisotropy as a function of z was consistent with observations from 2D-SAXS patterns (Fig. 7) and the streamlines in micro-PIV (Fig. 8). Similarly, the velocity curves (Fig. 9b) depicting evolution of the vertical velocity V as a function of distance z from the membrane surface also overlapped for the two highest transmembrane pressure conditions (ΔP = 0.9 × 10⁵ Pa and ΔP = 1.2 × 10⁵ Pa).

Fig. 9 Comparison of (a) PCA anisotropy and (b) vertical velocity V (m s⁻¹) for different transmembrane pressures (0.6, 0.9 and 1.2 × 10⁵ Pa) as a function of the distance z from the membrane surface. The standard deviation of the measured velocity was 6.3 × 10⁻⁵ m s⁻¹, 6.7 × 10⁻⁵ m s⁻¹, and 6.3 × 10⁻⁵ m s⁻¹ for transmembrane pressures of 0.6, 0.9, and 1.2 × 10⁵ Pa, respectively.

These results confirmed our first hypothesis. When the pressure threshold is high enough and in the presence of a concentrated layer at the membrane surface, acoustic streaming is generated in the top part of the filtration channel at a distance between 3000 and 5000 μm from the membrane surface. The direction of the velocity fields is orientated vertically parallel to the incident US wave. In this region, the CNCs are then orientated vertically due to this flow field. If moving closer from the membrane surface, a balance between the acoustic force and pressure force can be revealed. Acoustic streaming was not observed below z = 2000 μm, and the parallel orientation of CNCs in the vicinity of the membrane surface was thus induced by the concentration phenomenon due to membrane ultrafiltration.

Numerical simulations and experimental studies offer complementary perspectives on comprehension of acoustic streaming phenomena for the application of membrane filtration. Our experimental work, based on SAXS and micro-PIV, provides direct observations of streaming flows under real-world conditions. In contrast, some studies, such as the one by Tang and Hu,⁴ employed finite element method (FEM) simulations to explore the impact of parameters such as frequency, vibrating source geometry, and fluid temperature on the diversity of eddy patterns and streaming. Their study revealed how these factors shape both the complexity and velocity of the streaming field. While those simulations offer predictive frameworks to understand these mechanisms, our experiments validate and enrich these findings by observing this behavior in a precise acoustic field. For a given fluid temperature (298 K), particle size (5 μm), US frequency (20 kHz) and size of the ultrasonic source (3 mm wide), our results consistently align with theoretical predictions, confirming the expected behavior. By integrating these approaches, we gain a more comprehensive understanding of acoustic streaming and its potential for advancing micro- and nanoscale applications.

4. Conclusions

We demonstrated the Rayleigh acoustic streaming phenomenon in a membrane filtration cell coupled with low-frequency US using in situ SAXS and micro-PIV on CNCs suspensions. In situ micro-PIV experiments revealed characteristic streamlines of Rayleigh acoustic streaming, identified as the key mechanism at the origin of the orthotropic organization induced by simultaneous FU–US processes applied to a CNC suspension.

SAXS experiments complemented this result by revealing the particular orientation of CNCs near the US blade as transmembrane pressure increased. A critical transmembrane pressure threshold of 0.6 × 10⁵ Pa was necessary to establish the confined flow conditions required for acoustic streaming appearance, which was demonstrated by the streamlines in micro-PIV. Indeed, above this threshold, particles accumulated near the membrane, as demonstrated in SAXS by the orientation of the CNCs parallel to the membrane surface.

These results demonstrate the main role of transmembrane pressure in enabling acoustic streaming and controlling CNC orientation. The combined use of micro-PIV and SAXS provided a comprehensive understanding of how confined flow conditions influence CNC alignment. This work underscores the potential of FU–US processes to precisely “tailor” the orientation of CNCs, paving the way for advanced material-designed strategies.

Abbreviations

FU	Frontal ultrafiltration
US	Ultrasound
SAXS	Small-angle X-ray scattering
CNC	Cellulose nanocrystal
ESRF	European synchrotron radiation facility
PCA	Principal component analysis
PIV	Particle image velocimetry.

Author contributions

Fanny Bosson: writing (original draft, reviewing and editing) and data analyses. Mathilde Challamel: investigation. Mohamed Karrouch: technical design and investigation. Nicolas Hengl: investigation, data analyses, and writing (reviewing and editing). Henda Djeridi: investigation, data analyses, and writing (reviewing and editing). Frédéric Pignon: conceptualization, methodology, writing (draft, reviewing and editing), investigation, and data analyses.

Data availability

Data from ESRF can be found online at https://doi.org/10.15151/ESRF-ES-450400240.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We sincerely thank Emilie Guilbert, Samuel Mandin (Laboratoire Rhéologie et Procédés), Bruno Jean (Cermav), Thomas Gibaud (ENS Lyon), William Chèvremont and Theyencheri Narayanan (ESRF) for constructive discussions and for their kind help in scattering experiments. We are obliged to Jean-Jacques Lasserre (Dantec Dynamics) for productive discussions and for his help in the micro-PIV measurements. We thank Jacques Gorini (ESRF), Didier Blésès, Frédéric Hugenell and Eric Faivre (Laboratoire Rhéologie et Procédés) for technical assistance. ESRF is acknowledged for provision of synchrotron beamtime (proposal SC-5110).

The authors acknowledge the support of the French Agence Nationale de la Recherche (ANR) under grant ANR-20-CE43-0015 (ANISOFILM). LRP is part of Institut Carnot PolyNat (ANR-16-CARN-0025-01), LabEx Tec21 (ANR-11-LABX-0030) and Glyco@Alps programme (ANR-15-IDEX-02).

References

1. T. G. Leighton, Ultrason. Sonochem., 1995, 2, S123–S136.
2. T. G. Leighton, Prog. Biophys. Mol. Biol., 2007, 93, 3–83.
3. W. L. Nyborg, Br. J. Cancer, Suppl., 1982, 5, 156.
4. Q. Tang and J. Hu, Ultrasonics, 2015, 58, 27–34.
5. M. Wiklund, R. Green and M. Ohlin, Lab-on-a-Chip, 2012, 12, 2438–2451.
6. M. O. Lamminen, H. W. Walker and L. K. Weavers, J. Membr. Sci., 2004, 237, 213–223.
7. B.-G. Loh, S. Hyun, P. I. Ro and C. Kleinstreuer, J. Acoust. Soc. Am., 2002, 111, 875–883.
8. S. Nomura, A. Yamamoto and K. Murakami, Jpn. J. Appl. Phys., 2002, 41, 3217.
9. R. Barnkob, P. Augustsson, T. Laurell and H. Bruus, Phys. Rev. E:Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2012, 86, 056307.
10. H. Bruus, J. Fluid Mech., 2017, 826, 1–4.
11. M. Raffel, C. E. Willert, F. Scarano, C. J. Kähler, S. T. Wereley and J. Kompenhans, in Particle Image Velocimetry: A Practical Guide, ed. M. Raffel, C. E. Willert, F. Scarano, C. J. Kähler, S. T. Wereley and J. Kompenhans, Springer International Publishing, Cham, 2018, pp. 367–411.
12. R. Huang, X. Nie and J. Zhou, Measurement, 2019, 134, 286–292.
13. K. John, S. Jahangir, U. Gawandalkar, W. Hogendoorn, C. Poelma, S. Grundmann and M. Bruschewski, Exp. Fluids, 2020, 61, 27.
14. N. Chen, C. Wang and W. Heidrich, Laser Photonics Rev., 2021, 15, 2100008.
15. M. R. Abdulwahab, Y. H. Ali, F. J. Habeeb, A. A. Borhana, A. M. Abdelrhman and S. M. A. Al-Obaidi, J. Adv. Res. Fluid Mech. Therm. Sci., 2020, 65, 213–229.
16. D. A. M. de Winter, K. Weishaupt, S. Scheller, S. Frey, A. Raoof, S. M. Hassanizadeh and R. Helmig, Transp. Porous Media, 2021, 136, 343–367.
17. S. Ravikumar, M. Fedrizzi, R. Prabhakar, R. Pocock, M. K. O'Bryan and J. Soria, bioRxiv, 2020, preprint,  DOI:10.1101/2020.06.16.119396.
18. C. Rey, N. Hengl, S. Baup, M. Karrouch, A. Dufresne, H. Djeridi, R. Dattani and F. Pignon, J. Membr. Sci., 2019, 578, 69–84.
19. C. Rey, N. Hengl, S. Baup, M. Karrouch, E. Gicquel, A. Dufresne, H. Djeridi, R. Dattani, Y. Jin and F. Pignon, ACS Sustainable Chem. Eng., 2019, 7, 10679–10689.
20. B. Frka-Petesic, H. Radavidson, B. Jean and L. Heux, Adv. Mater., 2017, 29, 1606208.
21. M. Mitov, Soft Matter, 2017, 13, 4176–4209.
22. R. M. A. Domingues, M. E. Gomes and R. L. Reis, Biomacromolecules, 2014, 15, 2327–2346.
23. H. Kargarzadeh, J. Huang, N. Lin, I. Ahmad, M. Mariano, A. Dufresne, S. Thomas and A. Galęski, Prog. Polym. Sci., 2018, 87, 197–227.
24. T. Rosén, C. Brouzet, S. V. Roth, F. Lundell and L. D. Söderberg, J. Phys. Chem. C, 2018, 122, 6889–6899.
25. D. Zákutná, K. Graef, D. Dresen, L. Porcar, D. Honecker and S. Disch, Colloid Polym. Sci., 2021, 299, 281–288.
26. H. Nirschl and X. Guo, Chem. Eng. Res. Des., 2018, 136, 431–446.
27. S. Koizumi, H. Hasegawa and T. Hashimoto, Macromolecules, 1994, 27, 7893–7906.
28. T. W. Gräwert and D. I. Svergun, J. Mol. Biol., 2020, 432, 3078–3092.
29. Y.-T. Lee, D. S. Li, J. Ilavsky, I. Kuzmenko, G.-S. Jeng, M. O'Donnell and L. D. Pozzo, J. Colloid Interface Sci., 2019, 536, 281–290.
30. F. L. d. O. Paula, Condens. Matter, 2019, 4, 55.
31. T. Rattanawongwiboon, S. Soontaranon, K. Hemvichian, P. Lertsarawut, S. Laksee and R. Picha, Radiat. Phys. Chem., 2022, 191, 109842.
32. K. Tsukimura, Y. Miyoshi, T. Takagi, M. Suzuki and S. Wada, Sci. Rep., 2021, 11, 6997.
33. Y. Jin, N. Hengl, S. Baup, F. Pignon, N. Gondrexon, M. Sztucki, G. Gésan-Guiziou, A. Magnin, M. Abyan, M. Karrouch and D. Blésès, J. Membr. Sci., 2014, 470, 205–218.
34. F. Pignon, M. Challamel, A. De Geyer, M. Elchamaa, E. F. Semeraro, N. Hengl, B. Jean, J.-L. Putaux, E. Gicquel and J. Bras, Carbohydr. Polym., 2021, 260, 117751.
35. F. Pignon, E. Guilbert, S. Mandin, N. Hengl, M. Karrouch, B. Jean, J.-L. Putaux, T. Gibaud, S. Manneville and T. Narayanan, J. Colloid Interface Sci., 2024, 659, 914–925.
36. J. S. Taurozzi, V. A. Hackley and M. R. Wiesner, Nanotoxicology, 2011, 5, 711–729.
37. M. Girard, D. Vidal, F. Bertrand, J. R. Tavares and M.-C. Heuzey, Ultrason. Sonochem., 2021, 71, 105378.
38. M. A. Johns, C. Lam, B. Zakani, L. Melo, E. R. Grant and E. D. Cranston, Cellulose, 2023, 30, 8259–8274.
39. E. Gicquel, J. Bras, C. Rey, J.-L. Putaux, F. Pignon, B. Jean and C. Martin, Cellulose, 2019, 26, 7619–7634.
40. E. Semeraro, N. Hengl, M. Karrouch, L. Michot, E. Paineau, B. Jean, J.-L. Putaux, C. Lancelon-Pin, L. Sharpnack and F. Pignon, Colloids Surf., A, 2020, 584, 124030.
41. Y. Jin, N. Hengl, S. Baup, F. Pignon, N. Gondrexon, M. Sztucki, A. Romdhane, A. Guillet and M. Aurousseau, Carbohydr. Polym., 2015, 124, 66–76.
42. Y. Jin, N. Hengl, S. Baup, F. Pignon, N. Gondrexon, A. Magnin, M. Sztucki, T. Narayanan, L. Michot and B. Cabane, J. Membr. Sci., 2014, 453, 624–635.
43. T. Gibaud, N. Dagès, P. Lidon, G. Jung, L. C. Ahouré, M. Sztucki, A. Poulesquen, N. Hengl, F. Pignon and S. Manneville, Phys. Rev. X, 2020, 10, 011028.
44. T. Narayanan, M. Sztucki, T. Zinn, J. Kieffer, A. Homs-Puron, J. Gorini, P. Van Vaerenbergh and P. Boesecke, J. Appl. Crystallogr., 2022, 55, 98–111.
45. F. Pignon, M. Abyan, C. David, A. Magnin and M. Sztucki, In Situ Characterization by SAXS of Concentration Polarization Layers during Cross-Flow Ultrafiltration of LAPONITE® Dispersions|Langmuir, https://pubs-acs-org.sid2nomade-2.grenet.fr/doi/full/10.1021/la201492z, (accessed August 3, 2023).
46. M. Sztucki, SAXSutilities2 (version 1.024), Zenodo, 2021.
47. M. Muthig, S. Prevost, R. Orglmeister and M. Gradzielski, J. Appl. Crystallogr., 2013, 46, 1187–1195.
48. L. K. Zarembo, in High-Intensity Ultrasonic Fields, ed. L. D. Rozenberg, Springer US, Boston, MA, 1971, pp. 135–199.
49. F. Pignon, E. F. Semeraro, W. Chèvremont, H. Bodiguel, N. Hengl, M. Karrouch and M. Sztucki, J. Phys. Chem. C, 2021, 125, 18409–18419.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5nr00521c

---